Hybrid organic–inorganic mononuclear lanthanoid single ion magnets†
Walter
Cañón-Mancisidor
 *ab,
Matias
Zapata-Lizama
ab,
Patricio
Hermosilla-Ibáñez
*ab,
Matias
Zapata-Lizama
ab,
Patricio
Hermosilla-Ibáñez
 ab,
Carlos
Cruz
bc,
Diego
Venegas-Yazigi
ab,
Carlos
Cruz
bc,
Diego
Venegas-Yazigi
 ab and
Guillermo
Mínguez Espallargas
ab and
Guillermo
Mínguez Espallargas
 *d
*d
aUniversidad de Santiago de Chile, Depto. de Química de los Materiales, Santiago, Chile. E-mail: walter.canon@usach.cl
bCenter for the Development of Nanoscience and Nanotechnology, CEDENNA, Chile
cUniversidad Andres Bello, Facultad de Ciencias Exactas, Departamento de Ciencias Químicas, Chile
dInstituto de Ciencia Molecular (ICMol), Universidad de Valencia, Valencia, Spain. E-mail: guillermo.minguez@uv.es
First published on 22nd November 2019
Abstract
The first family of hybrid mononuclear organic–inorganic lanthanoid complexes is reported, based on [PW11O39]7− and 1,10-phenanthroline ligands. This hybrid approach causes a dramatic improvement of the relaxation time (×1000) with a decrease of the optimal field while maintaining the Ueff of the inorganic analogues.
The plasticity of the coordination chemistry of lanthanoid ions (Ln) has allowed the design of novel coordination compounds with appealing physical properties, including the presence of slow relaxation of the magnetization.1,2 The first Single Ion Magnet (SIM) was obtained as a “sandwich type” complex in which two phthalocyaninate ligands coordinate a Ln ion.3 After this seminal contribution, different types of Ln molecular complexes with SIM behaviour have been obtained through a rational approach using coordination chemistry.4,5 Most of these compounds are based on organic ligands,6–8 allowing a fine-tuning of the dynamic response through chemical modification of the organic moieties,9 and can find applications as spin valves and qubits.8,10 The inorganic analogues, i.e., mononuclear SIMs in which the organic ligands have been replaced by inorganic ones, have also been described using different types of lacunary polyoxometalates (LPOMs),11–15 resulting in more robust systems with applications in quantum computation;16,17 this is a consequence of the magnetic insulation from the other neighbouring magnetic molecules of the crystal lattice caused by the inorganic moieties.18,19 On the other hand, theoretical studies have shown that heteroleptic coordination compounds formed by anionic and neutral ligands favour the SMM behaviour in DyIII complexes compared to homoleptic systems.20
The optimum coordination environment for the appearance of SMM behaviour in lanthanoid complexes is D4d symmetry,21,22 although other unconventional geometries such as pentagonal bipyramid Ln complexes have resulted in breakthrough energy barriers of ca. 1200 cm−1.23 More recently, different dysprosium metallocenes have shown magnetic hysteresis at temperatures of up to 80 K.24–26
Conversely, despite the exquisite control of coordination chemistry, the preparation of mononuclear hybrid organic–inorganic Ln complexes with SMM behaviour remains elusive. These hybrid materials could benefit from the combination of the ease of functionalization of the organic ligands with the robustness of the inorganic moieties. However, all the attempts in this direction have been unsuccessful, producing dinuclear and polynuclear systems.27–31
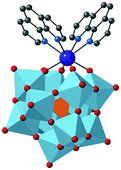
Herein we present the first isostructural family of mononuclear hybrid organic–inorganic lanthanoid complexes that present SMM behavior, [n-NBu4]3[LnH(PW11O39)(phen)2]·H2O, denoted as LM4-1-Ln‡ (Ln = Dy, Er, Gd and Dy0.25Y0.75, see Scheme 1).
 | ||
| Scheme 1 Representation of octacoordinated SIMs based on organic, inorganic and hybrid organic–inorganic ligands. | ||
The combination of the neutral phenanthroline ligand and the anionic inorganic lacunary Keggin POM ligand under hydrothermal synthesis at 160 °C after 48 h yields a molecular heteroleptic complex, LM4-1-Ln. Under this experimental condition, the pH becomes more acidic, due to the deprotonation of the inorganic ligand. Single crystals of LM4-1-Dy, LM4-1-Er and LM4-1-Gd suitable for X-ray diffraction were obtained, revealing that all compounds are isostructural, crystallizing in the monoclinic P21/c space group (Table S2, ESI†). Compound LM4-1-DyY was obtained as a microcrystalline material but thorough characterization indicates that LM4-1-DyY has the same chemical formula and crystalline phase than the other complexes (see Sections S1 and S2 in the ESI†).
Three [NBu4]+ cations can be clearly identified in the crystal structure, and electroneutrality is achieved by the presence of one proton that is delocalized over the LPOM.32 The BVS calculations for all oxygen atoms of the [PW11O39]7− show values close to 2, as expected for a non-protonated bridging oxido groups (Table S4, ESI†).33 The anionic complex of formula [LnH(PW11O39)(phen)2]3− is formed by two types of ligands, an inorganic POM and two organic phenanthrolines, forming an octacoordinated complex (Fig. 1). The inorganic ligand corresponds to the Keggin lacunary polyoxometalate, [PW11O39]7−, which can be defined as a more rigid ligand compared to the two phenanthroline molecules. The distances between the Ln centre and the coordinated oxygen atoms are in the range 2.225(14)–2.358(11) Å in the [PW11O39]7− moiety, whereas the Ln to nitrogen distances of the phenanthrolines are in the range 2.545(14)–2.646(16) Å.
Continuous shape measurement (CShM's) calculations, performed using the SHAPE code,34,35 reveal that the geometry of the Ln complexes can be best described as a square antiprism, thus implying that the Ln centres present a pseudo-D4d symmetry as observed for the fully inorganic analogue, LnIII(LPOM)2 (see Section S2.4, ESI†).13,32
Magnetic dc susceptibility measurements were carried out between 2 and 300 K at 1 kG for all complexes (see Fig. 2 and Section S3, ESI†). The susceptibility values of all the complexes are in good agreement with the expected values for mononuclear complexes. The χT values decrease at low temperatures due to the thermal depopulation of the Stark sublevels,36 as the absence of any dipolar magnetic exchange interaction is confirmed with the measurement of isotropic LM4-1-Gd compound, which shows a constant χT value in all the temperature range (see Fig. 2). Magnetization measurements were done for all the compounds at 2 K between 0 to 90 kG, with no saturation observed for LM4-1-Dy, LM4-1-Er and LM4-1-DyY. On the contrary, the magnetization is close to saturation for LM4-1-Gd (6.95 Nβ), further confirming the paramagnetic character of this system (see Fig. S8, ESI†). For compounds LM4-1-Dy and LM4-1-Er the non-superposition of the iso-field lines shows the anisotropic character of the system with the dysprosium complex (LM4-1-Dy) presenting a butterfly magnetic hysteresis suggesting the presence of slow magnetic relaxation and Quantum Tunnelling of Magnetization (QTM). This indicates the presence of a dynamic response, as also observed for other lanthanoid SIMs (see Fig. S9 and S10, ESI†).4,5
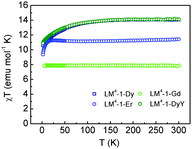 | ||
| Fig. 2 Experimental χT vs. T plots from 2 to 300 K of compounds LM4-1-Dy (dark blue), LM4-1-Er (blue), LM4-1-Gd (green) and LM4-1-DyY (dark green). | ||
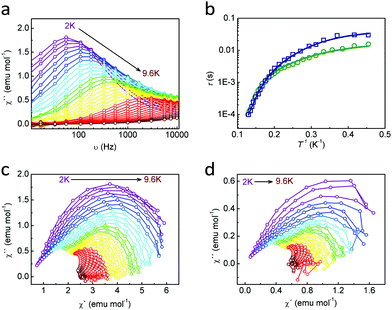
The magnetic characterization of LM4-1-Dy and LM4-1-Er was completed by alternate current (ac) measurements (see Section S3.2, ESI†). LM4-1-Dy presents an out-of-phase signal (χ′′) in the absence of an external dc field, which is frequency-dependent, although no maxima are observed (see Fig. S11, ESI†). This behaviour could be due to the existence of fast relaxation of the magnetization through a quantum tunnelling mechanism, which has been quenched by applying an optimal external field of 2 kG (see Fig. S12, ESI†).37 Importantly, the ac-susceptibility versus frequencies measurements show a single maximum related to the relaxation process of this system (Fig. 3 and Fig. S13, ESI†).
In order to rationalize the relaxation process of single ion magnets, the relaxation mechanisms can be explained as originated by the energy exchange between the paramagnetic centres and the phonon radiations, i.e., direct, Raman and Orbach mechanisms.38 Furthermore, there is a relaxation mechanism that is independent of the temperature of the system, caused by the existence of transverse anisotropy induced by the distortion from the axial symmetry, which is referred as Quantum Tunnelling of Magnetization (QTM).1 Thus, the relaxation times τ can be quantitative explained using eqn (1) to model the magnetic data:36,39–42
 | (1) |
For LM4-1-Dy and LM4-1-DyY the Ueff value obtained are 36.4 cm−1 and 36.3 cm−1, respectively, considering the Orbach relaxation mechanism under an optimal field of 2 kG. Upon comparison of the magnetic dynamic properties of the hybrid organic–inorganic LM4-1-Dy with the purely inorganic analogue, i.e. [DyIII(PW11O39)2]9−, it is possible to observe an improvement in the dynamic response. First, it presents maxima at a lower dc field (2 kG for LM4-1-Dyvs. 3 kG for [DyIII(PW11O39)2]9−); and second, the relaxation time (τ0) is improved 3 orders of magnitude (5.3 × 10−9 s for LM4-1-Dyvs. 9.6 × 10−12 s for [DyIII(PW11O39)2]9−).32 Importantly, the energy of the magnetization is maintained unaffected around 36 cm−1. This reflects that the addition of organic ligands has an effect on the dynamic of the magnetic properties. In some extension, this fact tends to confirm that the inclusion of an organic ligand improves the magnetization dynamics in DyIII-POM compounds.
This behaviour can be due to the fact that the LM4-1-Dy complex is an heteroleptic system that can favour SMM behaviour compared to the inorganic analogue, which is an homoleptic system.20 Moreover, if a comparison is made between the most common eight-coordinated SIMs3,32,46 (see Table S5, ESI†), it is possible to observe that the heteroleptic organic complex shows the highest Ueff. The highest τ0 values are observed for the homoleptic and heteroleptic organic complexes, thus no clear correlation can be observed. It is clear that this field remains an open subject.
The distribution of the relaxation times can be studied by plotting χ′′ versus χ′ in an Argand plot, also known as Cole–Cole plots. The fit of the data to a general Debye model47 (eqn (S1), ESI†) results in adequate description of the experimental points. These plots were used to extrapolate the α value for LM4-1-Dy (see Fig. 3). At low temperatures, the α value is around 0.3, suggesting that multiple relaxation mechanism are present like direct, Raman, and QTM at low temperatures. When increasing the temperature, the α value decreases to 0.12 inferring that the Orbach mechanism becomes dominant at higher temperatures (see Fig. S14 and Table S6, ESI†).
Moreover, LM4-1-Er presents frequency dependent signals when a dc field is applied, making this Erbium compound a field induced Single Ion Magnet (SIMs), an uncommon situation compared to the DyIII ones.40,48 However, the QTM phenomenon in this system cannot be suppressed even when applying different dc fields since no maxima can be observed. (see Fig. S15–S17, ESI†).49 In order to study the dynamic magnetic relaxation of this compound, an approach to the Arrhenius equation was used.50–52 A good fit was achieved with energy barriers of the relaxations of the magnetization at different frequencies, being the average Ueff = 7.5(2) cm−1 and an average for τ0 = 3.5(7) × 10−6 s−1 (Fig. S18, ESI†). ErIII SIMs are scarce since there are a few compared to DyIII SIMs. However, at least one example of ErIII(LPOM)2 exists in the literature,13 having an energy barrier of magnetization of 37 cm−1 obtained at zero dc field. LM4-1-Er, the first ErIII SIM system based on hybrid organic–inorganic ligands, has, on the contrary, a small value of Ueff under an applied dc field.
In summary, a family of mononuclear hybrid organic–inorganic compounds with SMM behaviour has been successfully obtained using a lacunary Keggin POM and phenanthroline as inorganic and organic ligands, respectively. The optimal field of the hybrid LM4-1-Dy is 2 kG, lower than the purely inorganic analogues of formula Ln(POM)2. In addition, the relaxation times obtained for the hybrid compounds are 1000 slower than the pure inorganic system, proving that the addition of organic ligands is a suitable approach to lower the relaxation times. Since the systems improve some aspects of their magnetic response, this opens the way to the design of novel hybrid materials, in which the modification of the organic ligand will allows to deposit these molecules onto surfaces for potential applications in spintronics and/or as spin qubits.
W. C.-M. thanks FONDECYT 11160830 and REDI170277 for financial support. The authors also thank partial support from ACT-1404 (IPMaG) and Financiamiento Basal FB0807 (CEDENNA) and CONICYT-FONDEQUIP/EQM130086-EQM140060. This work was done under the LIA-M3-1027 CNRS Collaborative Program. The present work has been also funded by the Spanish MICINN (Unidad de Excelencia “María de Maeztu” MDM-2015-0538 and project CTQ2017-89528-P), and the Generalitat Valenciana (PROMETEU/2019/066). G. M. E. acknowledges MICINN for a Ramón y Cajal contract.
Conflicts of interest
There are no conflicts to declare.References
-
J. Tang and P. Zhang, Lanthanide Single Molecule Magnets, Springer Berlin Heidelberg, Berlin, Heidelberg, 2015 Search PubMed
.
- S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC
.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed
.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS
.
- A. Dey, P. Kalita and V. Chandrasekhar, ACS Omega, 2018, 3, 9462–9475 CrossRef CAS
.
- S. Da Jiang, B. W. Wang, G. Su, Z. M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448–7451 CrossRef
.
- W. Cañon-Mancisidor, S. G. Miralles, J. J. Baldoví, G. M. Espallargas, A. Gaita-Ariño and E. Coronado, Inorg. Chem., 2018, 57, 14170–14177 CrossRef
.
- S. G. Miralles, A. Bedoya-Pinto, J. J. Baldoví, W. Cañon-Mancisidor, Y. Prado, H. Prima-Garcia, A. Gaita-Ariño, G. Mínguez Espallargas, L. E. Hueso and E. Coronado, Chem. Sci., 2018, 9, 199–208 RSC
.
- Y. Bi, Y.-N. Guo, L. Zhao, Y. Guo, S.-Y. Lin, S.-D. Jiang, J. Tang, B.-W. Wang and S. Gao, Chem. – Eur. J., 2011, 17, 12476–12481 CrossRef CAS
.
- K. Katoh, H. Isshiki, T. Komeda and M. Yamashita, Chem. – Asian J., 2012, 7, 1154–1169 CrossRef CAS PubMed
.
- C. Boskovic, Acc. Chem. Res., 2017, 50, 2205–2214 CrossRef CAS PubMed
.
- M. Vonci and C. Boskovic, Aust. J. Chem., 2014, 67, 1542–1552 CrossRef CAS
.
- M. A. AlDamen, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, C. Martí-Gastaldo, F. Luis and O. Montero, Inorg. Chem., 2009, 48, 3467–3479 CrossRef CAS PubMed
.
- M. A. AlDamen, J. M. Clemente-Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874–8875 CrossRef CAS PubMed
.
- P. Ma, F. Hu, R. Wan, Y. Huo, D. Zhang, J. Niu and J. Wang, J. Mater. Chem. C, 2016, 4, 5424–5433 RSC
.
- A. Gaita-Ariño, H. Prima-García, S. Cardona-Serra, L. Escalera-Moreno, L. E. Rosaleny and J. J. Baldoví, Inorg. Chem. Front., 2016, 3, 568–577 RSC
.
- M. D. Jenkins, Y. Duan, B. Diosdado and J. J. Garc, Phys. Rev. B, 2017, 064423 CrossRef
.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351 CrossRef CAS PubMed
.
- J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Chem. Soc. Rev., 2012, 41, 7464–7478 RSC
.
- D. Aravena and E. Ruiz, Inorg. Chem., 2013, 52, 13770–13778 CrossRef CAS PubMed
.
-
J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Lanthanides and Actinides in Molecular Magnetism, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2015, pp. 27–60 Search PubMed
.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC
.
- Y. S. Ding, N. F. Chilton, R. E. P. Winpenny and Y. Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074 CrossRef CAS PubMed
.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed
.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef CAS PubMed
.
- F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed
.
- P. Ma, F. Hu, R. Wan, Y. Huo, D. Zhang, J. Niu and J. Wang, J. Mater. Chem. C, 2016, 4, 5424–5433 RSC
.
- J. Niu, K. Wang, H. Chen, J. Zhao, P. Ma, J. Wang, M. Li, Y. Bai and D. Dang, Cryst. Growth Des., 2009, 9, 4362–4372 CrossRef CAS
.
- S. Zhang, Y. Wang, J. Zhao, P. Ma, J. Wang and J. Niu, Dalton Trans., 2012, 41, 3764–3772 RSC
.
- P. Ma, R. Wan, Y. Si, F. Hu, Y. Wang, J. Niu and J. Wang, Dalton Trans., 2015, 44, 11514–11523 RSC
.
- L. Xiao, T.-T. Zhang, Z. Liu, X. Shi, H. Zhang, L. Yin, L.-Y. Yao, C.-C. Xing and X.-B. Cui, Inorg. Chem. Commun., 2018, 95, 86–89 CrossRef CAS
.
- P. Ma, F. Hu, Y. Huo, D. Zhang, C. Zhang, J. Niu and J. Wang, Cryst. Growth Des., 2017, 17, 1947–1956 CrossRef CAS
.
- D. Zhang, Y. Zhang, J. Zhao, P. Ma, J. Wang and J. Niu, Eur. J. Inorg. Chem., 2013, 1672–1680 CrossRef CAS
.
- D. Casanova, J. Cirera, M. Llunell, P. Alemany, D. Avnir and S. Alvarez, J. Am. Chem. Soc., 2004, 126, 1755–1763 CrossRef CAS PubMed
.
- D. Casanova, M. Llunell, P. Alemany and S. Álvarez, Chem. – Eur. J., 2005, 11, 1479–1494 CrossRef CAS
.
- P. Cen, X. Liu, J. Ferrando-Soria, Y.-Q. Zhang, G. Xie, S. Chen and E. Pardo, Chem. – Eur. J., 2019, 25, 3884–3892 CrossRef CAS PubMed
.
- N. Ishikawa, M. Sugita and W. Wernsdorfer, J. Am. Chem. Soc., 2005, 127, 3650–3651 CrossRef CAS PubMed
.
- R. Orbach, Proc. R. Soc. London, Ser. A, 1961, 264, 458–484 CrossRef CAS
.
- M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, Chem. Sci., 2016, 7, 155–165 RSC
.
- K. S. Pedersen, L. Ungur, M. Sigrist, A. Sundt, M. Schau-Magnussen, V. Vieru, H. Mutka, S. Rols, H. Weihe, O. Waldmann, L. F. Chibotaru, J. Bendix and J. Dreiser, Chem. Sci., 2014, 5, 1650–1660 RSC
.
- L.-F. Wang, J.-Z. Qiu, J.-L. Liu, Y.-C. Chen, J.-H. Jia, J. Jover, E. Ruiz and M.-L. Tong, Chem. Commun., 2015, 51, 15358–15361 RSC
.
- E. Lucaccini, L. Sorace, M. Perfetti, J.-P. Costes and R. Sessoli, Chem. Commun., 2014, 50, 1648–1651 RSC
.
- H.-H. Zou, T. Meng, Q. Chen, Y.-Q. Zhang, H.-L. Wang, B. Li, K. Wang, Z.-L. Chen and F. Liang, Inorg. Chem., 2019, 58, 2286–2298 CrossRef CAS PubMed
.
- X. Zhang, N. Xu, W. Shi, B.-W. Wang and P. Cheng, Inorg. Chem. Front., 2018, 5, 432–437 RSC
.
- K. N. Shrivastava, Phys. Status Solidi, 1983, 117, 437–458 CrossRef CAS
.
- G.-J. Chen, C.-Y. Gao, J.-L. Tian, J. Tang, W. Gu, X. Liu, S.-P. Yan, D.-Z. Liao and P. Cheng, Dalton Trans., 2011, 40, 5579–5583 RSC
.
- C. Dekker, A. Arts, H. de Wijn, A. van Duyneveldt and J. Mydosh, Phys. Rev. Lett., 1988, 61, 1780–1783 CrossRef CAS
.
- L. Chen, J. Zhou, A. Yuan and Y. Song, Dalton Trans., 2017, 46, 15812–15818 RSC
.
- J. Dreiser, J. Phys.: Condens. Matter, 2015, 27, 183203 CrossRef CAS PubMed
.
- A. Adhikary, J. A. Sheikh, S. Biswas and S. Konar, Dalton Trans., 2014, 43, 9334–9343 RSC
.
- J. Bartolomé, G. Filoti, V. Kuncser, G. Schinteie, V. Mereacre, C. E. Anson, A. K. Powell, D. Prodius and C. Turta, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 1–16 Search PubMed
.
- F. Luis, J. Bartolomé, J. F. Fernández, J. Tejada, J. M. Hernández, X. X. Zhang and R. Ziolo, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 11448–11456 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional figures, schemes and tables and X-ray crystallographic file in CIF format for compound 1-Dy, 1-Er and 1-Gd. CCDC 1951515 (1-Dy), 1951516 (1-Er) and 1951519 (1-Gd). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9cc07868a |
| ‡ LM4 = Laboratory of Molecular Magnetism and Molecular Materials. |
| This journal is © The Royal Society of Chemistry 2019 |