Measurement of the triplet exciton diffusion length in organic semiconductors†

Deepesh Rai and Russell J. Holmes *
Department of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, Minnesota 55455, USA. E-mail: rholmes@umn.edu

First published on 25th April 2019

---

---

Introduction

Exciton spin plays a central role in the behavior of organic semiconductor thin films and the design of associated devices. Short-lived spin singlet excitons are responsible for fluorescence in organic light-emitting devices (OLEDs) and also form the majority of active materials used for photoconversion in organic photovoltaic cells (OPVs). Long-lived spin triplet excitons are frequently non-radiative, but play important roles as energetic intermediates in OLEDs (as in delayed fluorescence),^1–8 and also as potential active materials in OPVs (via singlet fission).^9–14 In all of these applications, exciton migration plays an important role in the ability to spatially confine or transport energy. For singlets, the direct probing of exciton migration is made possible through photoluminescence measurements.^15,16 For non-radiative triplet excitons, direct photoluminescence-based techniques are not applicable, and alternate methods must be employed.^17–19

Frequently, device-based measurements are used to indirectly probe triplet diffusion via the byproducts of their dissociation or transfer to a luminescent species. Specifically, these include the fitting of external quantum efficiency spectra in OPVs,^14,20–23 photovoltage measurements,^24–26 photoconductivity measurements,²⁷ microwave spectroscopy,^28,29 and a variety of measurements in OLED configurations.^30–35 While capable of yielding a value for the exciton diffusion length (L_D), intrinsic values of L_D can only be obtained by carefully accounting for unknown recombination losses and interfacial energy transfer rates.²³ Further, the roles of triplet–triplet annihilation, triplet–polaron quenching, exciton formation zone migration, and the contribution from singlet diffusion are also difficult to evaluate. Consequently, there is frequently disagreement among different methods of measurement for the triplet L_D. Non-device-based methods such as delayed fluorescence spread^36,37 and transient absorption spectroscopy^38,39 are capable of probing the intrinsic diffusion length of non-radiative triplets however, their implementation often involves more involved instrumentation. It is for these reasons that the direct probing of non-radiative triplets using a phosphorescent sensitizer^40,41 is of particular interest, due to its ability to distinguish between singlet and triplet transport, as well as prevent bimolecular triplet quenching mechanisms. However, in this method, the quenching efficiency of triplet excitons by the phosphorescent sensitizer is seldom known quantitatively, and hence can cause inaccuracy in reported values. Here, we develop a methodology to resolve this issue and apply the technique to extract the triplet L_D for a variety of materials.

Fig. 1a shows a phosphorescent sensitizer-based methodology for measuring dark triplet excitons in organic semiconductor thin films. Singlet excitons are optically generated in a thin phosphorescent injection layer which undergoes rapid intersystem crossing due to spin–orbit coupling.⁴² The resulting triplets are injected directly into the triplet energy level (E_T) of an adjacent transport layer (i.e. the material of interest), with transfer from the injection layer to the singlet level of the transport layer being frustrated by its endothermicity.⁴³ Triplet excitons that diffuse through the full thickness of the transport layer may undergo energy transfer to a low-energy phosphorescent sensitizer layer, leading to measurable photoluminescence.^41,44 Exciton diffusion in the transport material is therefore characterized by a transport efficiency (η_T), defined as the ratio of the exciton collection rate by the sensitizer and the exciton injection rate into the transport layer. Experimentally, η_T is calculated based on the reduction (increase) of photoluminescence (PL) from the injector (sensitizer) in the presence of the transport layer versus a wide energy gap exciton blocking layer (ΔPL^Injector and ΔPL^Sensitizer, respectively) as:

	(1)

In eqn (1), η^PL_Injector and η^PL_Sensitizer are the outcoupled PL efficiencies of the injector and sensitizer layers. The outcoupled PL efficiencies are determined experimentally as discussed in the ESI† and Fig. S1.

In eqn (1), the assumption is made that any changes in PL from the injector and sensitizer layers come from the transport of excitons through the material of interest. For this to be accurate, the short-range quenching of excitons in the material of interest by the sensitizer must be efficient. Without knowledge of the quenching efficiency, the extracted L_D may not reflect the intrinsic behavior of the material. Here, we extract the transfer rate (k_Q) from the transport layer to the phosphorescent sensitizer by varying the concentration of the sensitizer in a non-quenching host. In this way, the number of quenching sites (and the quenching efficiency) at the interface is also varied in a predictable manner. Increasing the sensitizer concentration leads to a concomitant increase in η_T until the quenching efficiency reaches unity.

In this work, η_T is measured as function of thickness in order to track the injected triplet exciton density reaching the sensitizer layer. In parallel, measurements of η_T as a function of sensitizer concentration are used to extract k_Q, and determine an appropriate boundary condition for the exciton density. A previously published kinetic Monte Carlo (KMC) formalism is used to model the dependence of η_T and extract the triplet diffusion length of the transport layer.^45,46 The injected triplet exciton density in the transport layer is kept small (∼10¹⁵ cm⁻³) to avoid triplet–triplet annihilation.⁴⁷ The triplet diffusion length is probed in thin films of the archetypical organic semiconductors N,N′-di(1-naphthyl)-N,N′-diphenyl-(1,1′-biphenyl)-4,4′-diamine (NPD), tris-(8-hydroxyquinoline)aluminum (Alq₃) and bis-(8-hydroxy-2-methylquinoline)-(4-phenylphenoxy)aluminum (BAlq). The method is validated against thickness dependent photoluminescence quenching measurements for singlet exciton diffusion in both Alq₃ and 2,3,6,7-tetrahydro-1,1,7,7,-tetramethyl-1H,5H,11H-10(2-benzothiazolyl)quinolizine[9,9a,1gh] coumarin (C545T).

Experimental

All thin films were deposited using vacuum thermal sublimation (base pressure <7 × 10⁻⁷ Torr) at a total rate of 0.1 nm s⁻¹ on glass substrates. Substrates were pre-cleaned by sequentially sonicating in tergitol solution, deionized water, and acetone, followed by rinsing in isopropanol. Material optical constants and film thicknesses were measuring using a J. A. Woollam variable-angle spectroscopic ellipsometer (Cauchy model). Active materials of N,N′-di-1-naphthalenyl-N,N′-diphenyl [1,1′:4′,1′′:4′′,1′′′-quaterphenyl]-4,4′′′-diamine (4P-NPB), tris[2-phenylpyridinato-C2,N]iridium(III) (Ir(ppy)₃), tris(4-carbazoyl-9-ylphenyl)amine (TCTA), 1,3-bis(N-carbazolyl)benzene (mCP), NPD, C545T and Alq₃ were purchased from Luminescence Technology Corporation; BAlq was purchased from Sigma Aldrich, and platinum octaethylporphyrin (PtOEP) and platinum tetra-phenyl-tetra-benzo-porphyrin (PtTPTBP)^48,49 were purchased from Frontier Scientific. The 1,4,5,8,9,11-hexaazatriphenylene hexacarbonitrile (HATCN)⁵⁰ used as a quencher for measuring the singlet L_D of Alq₃ and C545T was purchased from Luminescence Technology Corporation. In this work, the quenching efficiency of HATCN is assumed to unity, due to its favorable energy offset for electron transfer.⁵¹ Photoluminescence spectra were measured under N₂ purge using a Photon Technology International QuantaMaster 400 Fluorometer equipped with a photomultiplier detection system. Samples were excited at an angle of 70° to sample normal using a monochromatic Xe lamp. The incident light intensity was measured using a S2281 silicon photodiode with a mask of 0.36 cm² area. To check for the presence of triplet–triplet annihilation in our measurements, PL spectra were collected at two different pump intensities using a neutral density filter (OD = 0.5). The experimental data was fit using a non-linear least squares methodology where fit error in the calculation of L_D represents a 95% confidence interval. To detect any crystallinity in the transport layers, X-ray diffraction measurements were carried out at an incident angle of 8 degrees, while samples were scanned using a 2D detector which spans from 2θ = 1 degree to 53 degrees. Triplet energy levels for Ir(ppy)₃ and the sensitizer molecules were determined from room temperature phosphorescence spectra. All other triplet energy levels referenced in this work were determined using the first peak of the phosphorescence taken from literature.^33,52–54

Results and discussion

To demonstrate the validity of the phosphorescent sensitizer-based technique, the method was first applied to measure the singlet diffusion length of Alq₃ and the result compared to well-established thickness-dependent PL quenching-methods.¹⁵ In the generalized scheme of Fig. 1a, singlet excitons are injected from fluorescent 4P-NPB into Alq₃ by optical pumping at a wavelength of λ = 380 nm, where absorption occurs mainly in 4P-NPB (Fig. S2b, ESI†). An injector layer of 4P-NPB is chosen due to its favorable spectral overlap with the absorption spectrum of Alq₃ (see Fig. S2 for active material emission and absorption spectra, ESI†), enabling efficient Förster energy transfer. Excitons migrate through Alq₃ and are detected by monitoring phosphorescence from a sensitizer layer of PtTPTBP at λ = 770 nm. The exciton transport efficiency is extracted by comparing changes in PL from PtTPTBP and 4P-NPB (Fig. 2a) in the case when the injector layer of 4P-NPB is present, and where it is replaced by a non-absorbing, wide energy gap spacer layer of mCP. In this way, the increase in photoluminescence from PtTPTBP due to energy transfer from 4P-NPB can be isolated from direct optical excitation (i.e. where the injection layer of 4P-NPB is replaced with mCP). The η_T is calculated using eqn (1) and the associated architecture for measurement is shown in Fig. S2a (ESI†). The KMC modelling of experimentally measured η_T as a function of Alq₃ thickness results in a single L_D of (5.9 ± 0.6) nm (Fig. 2b).

The architecture for comparing the phosphorescent sensitizer technique against thickness-dependent PL quenching for Alq₃ singlets is shown in Fig. S2a (ESI†). This method requires the measurement of PL from the material of interest both with and without an adjacent quenching layer, with the ratio of these two quantities fit as a function of thickness for L_D. Here, the sensitizer layer is replaced by a top quenching layer of HATCN or an exciton blocking layer of mCP for the quenched and unquenched samples, respectively. Singlets are generated in Alq₃ by optical pumping at a wavelength of λ = 440 nm, where absorption occurs mainly in Alq₃ (Fig. S2b, ESI†). A PL ratio is calculated as a function of Alq₃ layer thickness as the ratio of the integrated PL spectrum with and without an adjacent quenching layer (Fig. 2c). The analytical modelling of the experimentally measured PL ratio also yields a singlet L_D of (5.6 ± 0.4) nm (Fig. 2d),⁵⁵ validating the sensitizer-based technique. The method was also verified for the organic fluorescent dye C545T which results in a L_D of (12.2 ± 0.7) nm as discussed in the ESI† (Fig. S3).

Triplet exciton diffusion is examined for three archetypical organic molecules: NPD, Alq₃ and BAlq. Thin films show no scattering peaks in X-ray diffraction, consistent with previous reports showing that as-grown films of these materials are amorphous.^56,57 All three of these materials are used frequently as transport layers in OLEDs and there is disagreement among the reported L_D values for both NPD and Alq₃.¹⁷ Here, the case of NPD is considered first to demonstrate the methodology in detail using the architecture of Fig. 3a. Using a phosphorescent injector layer of Ir(ppy)₃ (E_T = 2.4 eV),³³ the system is pumped at a wavelength of λ = 470 nm, where absorption only occurs in Ir(ppy)₃ and no singlet excitons are generated in NPD (Fig. 3b). Triplets are injected into NPD and those that migrate through the layer may undergo energy transfer to a sensitizer layer of PtOEP (E_T = 1.9 eV)³³ doped in a wide energy gap host of TCTA (E_T = 2.8 eV).⁵² The η_T is extracted by comparing the photoluminescence from PtOEP and Ir(ppy)₃ in the case when the transport layer of NPD is present, and where it is replaced by a wide gap spacer layer of TCTA (Fig. 3c). The photoluminescence spectra in Fig. 3c are deconvoluted using the separately measured photoluminescence spectra of PtOEP and Ir(ppy)₃ (Fig. 3b). The decrease in photoluminescence from Ir(ppy)₃ when adjacent to NPD reflects triplet exciton injection into NPD. Similarly, the corresponding increase in photoluminescence from PtOEP reflects triplet excitons that diffuse through NPD and undergo energy transfer into the sensitizer layer. The boundary condition at the interface between NPD and the sensitizer layer is determined by increasing the concentration of PtOEP molecules from 0.5 wt% to 30 wt%. In Fig. 3d, the experimentally measured values of η_T as a function of NPD thickness are similar for PtOEP concentrations >5 wt%, signifying that all excitons reaching the interface are quenched. The boundary condition is implemented in the KMC model by varying k_Q to the sensitizer layer with respect to energy transfer (k_T) within the layer. The k_T can linked to the exciton diffusivity (D) and L_D as:

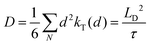	(2)

where d is the intermolecular spacing assuming a cubic lattice, τ is the exciton lifetime and N is the number of molecular hopping sites.^18,58 The KMC modelling of the experimentally measured dependence of η_T on NPD thickness yields L_D = (29.8 ± 1.1) nm for the triplet of NPD (Fig. 3b). The measured L_D is larger than that previously obtained by fitting device photocurrent, likely reflecting device specific recombination losses.²⁰ The measured L_D for NPD is smaller than the previous related work which has doped a discontinuous sensitizer layer into the transport layer and assumed that the sensitizer does not significantly perturb the underlying triplet density.⁴¹ The current work suggests that accurate determination of the triplet L_D depends upon both the sensitizer concentration and boundary condition assumptions. Inaccurate assumptions for a given sensitizer concentration can lead to either overestimation or underestimation of L_D. For example, in the current work, the incorrect assumption of perfect quenching by 0.5 wt% PtOEP would yield an underestimated triplet L_D = 12 nm. Similarly, assuming that the sensitizer does not perturb the exciton density in the case of quenching by 15 wt% PtOEP yields an overestimated triplet L_D = 52 nm.

The triplet exciton diffusion lengths of Alq₃ and BAlq are similarly determined using a sensitizer of PtTPTBP (E_T = 1.6 eV) doped in mCP (E_T = 2.9 eV).⁵³ The triplets are injected by optically pumping Ir(ppy)₃ at a wavelength of λ = 470 nm. Triplets diffusing through the transport layer are probed for two different concentrations of sensitizer (5 wt% and 15 wt% PtTPTBP) in order to check the quenching efficiency of excitons reaching the sensitizer interface. The η_T is calculated using eqn (1) from the measured photoluminescence of PtTPTBP and Ir(ppy)₃ for the case when the transport layer of BAlq or Alq₃ is present, and when it is replaced by a wide gap spacer layer of mCP. The KMC modelling of the experimentally determined η_T as a function of BAlq and Alq₃ thickness yield L_D values of (16.6 ± 1.0) nm and (15.2 ± 0.9) nm, respectively (Fig. 4). The agreement in η_T for two different sensitizer concentrations suggests efficient quenching at the transport layer and sensitizer interface. The measured L_D for Alq₃ is consistent with the value of (14 ± 9) nm previously reported by Baldo et al.³³ using transient analysis of phosphorescence in an OLED.

In addition to offering a means to accurately probe the diffusion of dark triplet excitons, the phosphor sensitized methodology is attractive for its ability to separately probe singlet or triplet exciton transport. Indeed, by simply varying the injecting layer, either the singlet or triplet of the material of interest can be excited. For example, in Alq₃ we find here a singlet diffusion length of L_D = (5.9 ± 0.6) nm and a triplet diffusion length of L_D = (15.2 ± 0.9) nm in the same architecture, simply by changing the injection layer from 4P-NPB to Ir(ppy)₃. Certainly, the Alq₃ triplets have long L_D compared to the singlets due to an increased lifetime.^17–19 However, the corresponding increase in L_D is likely throttled by slow short-range Dexter energy transfer for amorphous organic semiconductor thin films.⁵⁹ By coupling measurements of this type with additional time-domain investigations, additional insight can be gained into the factors that impact singlet and triplet migration. Further, the ability to selective pump the singlet and triplet states should have great utility in decoupling the more complex exciton transport that exists in materials exhibiting singlet fission or TADF.⁶⁰ The tri-layer stack used in current work may also be extended to solution-processed active materials. For example, the use of orthogonal solvents is increasingly being demonstrated to prevent re-dissolving in multilayer stacks.^61–66 Further, the combination of a solution-processed bottom layer and vapor-processed top layer would reduce the issue of re-dissolving to only the bottom interface.

Conclusions

We present a phosphorescent sensitizer-based methodology to accurately extract the exciton diffusion length of non-radiative triplet excitons in organic semiconductor thin films. In order to confirm the validity of the technique, we first extract the L_D of luminescent singlet excitons in thin films of Alq₃ and C545T, comparing the result to conventional photoluminescence measurements. For measurement of non-radiative triplet excitons, excitons are injected by energy transfer from an adjacent phosphorescent layer. By measuring the transport efficiency of excitons across the material of interest, triplet L_D values in the range of 15–30 nm are obtained. The method is also attractive in that values for the singlet and triplet L_D can be extracted for a given material in a common architecture by varying only the exciton injecting material.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by National Science Foundation (NSF) Electronics, Photonics and Magnetic Devices under ECCS-1509121. The authors acknowledge C. Clark for X-ray diffraction measurement of as-grown thin films of active materials.

References

1. H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS PubMed .
2. D. Di, A. S. Romanov, L. Yang, J. M. Richter, J. P. H. Rivett, S. Jones, T. H. Thomas, M. A. Jalebi, R. H. Friend, M. Linnolahti, M. Bochmann and D. M. Credgington, Science, 2017, 356(6334), 159–163 CrossRef CAS PubMed .
3. N. A. Kukhta, T. Matulaitis, D. Volyniuk, K. Ivaniuk, P. Turyk, P. Stakhira, J. V. Grazulevicius and A. P. Monkman, J. Phys. Chem. Lett., 2017, 8, 6199–6205 CrossRef CAS PubMed .
4. Z. Yang, Z. Mao, Z. Xie, Y. Zhang, S. Liu, J. Zhao, J. Xu, Z. Chi and M. P. Aldred, Chem. Soc. Rev., 2017, 46, 915 RSC .
5. T. Hosokai, H. Matsuzaki, H. Nakanotani, K. Tokumaru, T. Tsutsui, A. Furube, K. Nasu, H. Nomura, M. Yahiro and C. Adachi, Sci. Adv., 2017, 3, 5 Search PubMed .
6. T. J. Penfold, F. B. Diasb and A. P. Monkman, Chem. Commun., 2018, 54, 3926 RSC .
7. M. Y. Wong and E. Z. Colman, Adv. Mater., 2017, 29, 1605444 CrossRef PubMed .
8. D. Di, L. Yang, J. M. Richter, L. Meraldi, R. M. Altamimi, A. Y. Alyamani, D. Credgington, K. P. Musselman, J. L. MacManus-Driscoll and R. H. Friend, Adv. Mater., 2017, 29, 1605987 CrossRef PubMed .
9. A. Rao and R. H. Friend, Nat. Rev. Mater., 2017, 2, 17063 CrossRef CAS .
10. D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. V. Voorhis and M. A. Baldo, Science, 2013, 340(6130), 334–337 CrossRef CAS PubMed .
11. A. Rao, M. W. B. Wilson, J. M. Hodgkiss, S. Albert-Seifried, H. Bässler and R. H. Friend, J. Am. Chem. Soc., 2010, 132(36), 12698–12703 CrossRef CAS PubMed .
12. J. Lee, P. Jadhav, P. D. Reusswig, S. R. Yost, N. J. Thompson, D. N. Congreve, E. Hontz, T. V. Voorhis and M. A. Baldo, Acc. Chem. Res., 2013, 46(6), 1300–1311 CrossRef CAS PubMed .
13. M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed .
14. M. Tabachnyk, B. Ehrler, S. Bayliss, R. H. Friend and N. C. Greenham, Appl. Phys. Lett., 2013, 103, 153302 CrossRef .
15. P. Peumans, A. Yakimov and S. R. Forrest, J. Appl. Phys., 2003, 93, 3693 CrossRef CAS .
16. R. R. Lunt, N. C. Giebink, A. A. Belak, J. B. Benziger and S. R. Forrest, J. Appl. Phys., 2009, 105, 053711 CrossRef .
17. O. V. Mikhnenko, P. W. M. Blom and T.-Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867–1888 RSC .
18. S. M. Menke and R. J. Holmes, Energy Environ. Sci., 2014, 7, 499–512 RSC .
19. G. J. Hedley, A. Ruseckas and I. D. W. Samuel, Chem. Rev., 2017, 117(2), 796–837 CrossRef CAS PubMed .
20. W. A. Luhman and R. J. Holmes, Appl. Phys. Lett., 2009, 94, 153304 CrossRef .
21. B. Siegmund, M. T. Sajjad, J. Widmer, D. Ray, C. Koerner, M. Riede, K. Leo, I. D. W. Samuel and K. Vandewal, Adv. Mater., 2017, 29, 1604424 CrossRef PubMed .
22. B. P. Rand, S. Schols, D. Cheyns, H. Gommans, C. Girotto, J. Genoe, P. Heremans and J. Poortmans, Org. Electron., 2009, 10(5), 1015–1019 CrossRef CAS .
23. T. Zhang, D. B. Dement, V. E. Ferry and R. J. Holmes, Nat. Commun., 2019, 10, 1156 CrossRef PubMed .
24. T. K. Mullenbach, I. J. Curtin, T. Zhang and R. J. Holmes, Nat. Commun., 2017, 8, 14215 CrossRef CAS PubMed .
25. I. J. Curtin and R. J. Holmes, Adv. Energy Mater., 2018, 8(13), 1702339 CrossRef .
26. T. Zhang and R. J. Holmes, J. Mater. Chem. C, 2017, 5(45), 11885–11891 RSC .
27. H. Najafov, B. Lee, Q. Zhou, L. C. Feldman and V. Podzorov, Nat. Mater., 2010, 9, 938–943 CrossRef CAS PubMed .
28. J. E. Kroeze, T. J. Savenije, L. P. Candeias, J. M. Warman and L. D. A. Siebbeles, Sol. Energy Mater. Sol. Cells, 2005, 85, 189–203 CrossRef CAS .
29. T. J. Savenije, A. J. Ferguson, N. Kopidakis and G. Rumbles, J. Phys. Chem. C, 2013, 117(46), 24085–24103 CrossRef CAS .
30. J. Wünsche, S. Reineke, B. Lüssem and K. Leo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 245201 CrossRef .
31. M. A. Baldo, D. F. O’Brien, M. E. Thompson and S. R. Forrest, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 14422 CrossRef CAS .
32. Y. Luo and H. Aziz, J. Appl. Phys., 2010, 107, 094510 CrossRef .
33. M. A. Baldo and S. R. Forrest, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 10958 CrossRef CAS .
34. M. Lebental, H. Choukri, S. Chenais, S. Forget, A. Siove, B. Geffroy and E. Tutis, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165318 CrossRef .
35. Y. C. Zhou, L. L. Ma, J. Zhou, X. M. Ding and X. Y. Hou, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 132202 CrossRef .
36. G. Akselrod, P. Deotare, N. Thompson, J. Le, W. Tisdale, M. Baldo, V. Menon and V. Bulović, Nat. Commun., 2014, 5, 3646 CrossRef CAS PubMed .
37. P. Irkhin and I. Biaggio, Phys. Rev. Lett., 2011, 107, 017402 CrossRef PubMed .
38. A. D. Poletayev, J. Clark, M. W. B. Wilson, A. Rao, Y. Makino, S. Hotta and R. H. Friend, Adv. Mater., 2014, 26, 919–924 CrossRef CAS PubMed .
39. C. Grieco, G. S. Doucette, R. D. Pensack, M. M. Payne, A. Rimshaw, G. D. Scholes, J. E. Anthony and J. B. Asbury, J. Am. Chem. Soc., 2016, 138, 16069–16080 CrossRef CAS PubMed .
40. N. C. Giebink, Y. Sun and S. R. Forrest, Org. Electron., 2006, 7, 375–386 CrossRef CAS .
41. O. V. Mikhnenko, R. Ruiter, P. W. M. Blom and M. A. Loi, Phys. Rev. Lett., 2012, 108, 137401 CrossRef PubMed .
42. M. A. Baldo, D. F. O’Brien, Y. You, A. Shoustikov, S. Sibley, M. E. Thompson and S. R. Forrest, Nature, 1999, 395, 151–154 CrossRef .
43. M. Wu, D. N. Congreve, M. W. B. Wilson, J. Jean, N. Geva, M. Welborn, T. V. Voorhis, V. Bulović, M. G. Bawendi and M. A. Baldo, Nat. Photonics, 2016, 10, 31–34 CrossRef CAS .
44. N. J. Thompson, M. W. B. Wilson, D. N. Congreve, P. R. Brown, J. M. Scherer, T. S. Bischo, M. Wu, N. Geva, M. Welborn, T. V. Voorhis, V. Bulovic, M. G. Bawendi and M. A. Baldo, Nat. Mater., 2014, 13, 1039–1043 CrossRef CAS PubMed .
45. S. M. Menke, T. K. Mullenbach and R. J. Holmes, ACS Nano, 2015, 9, 4543–4552 CrossRef CAS PubMed .
46. D. Rai and R. J. Holmes, Phys. Rev. Appl., 2019, 11, 014048 CrossRef CAS .
47. B. W. Caplins, T. K. Mullenbach, R. J. Holmes and D. A. Blank, J. Phys. Chem. C, 2015, 119(49), 27340–27347 CrossRef CAS .
48. K. W. Hershey, J. Suddard-Bangsund, G. Qian and R. J. Holmes, Appl. Phys. Lett., 2017, 111, 113301 CrossRef .
49. N. C. Erickson and R. J. Holmes, Adv. Funct. Mater., 2013, 23, 5190–5198 CrossRef CAS .
50. S. M. Menke and R. J. Holmes, ACS Appl. Mater. Interfaces, 2015, 7(4), 2912–2918 CrossRef CAS PubMed .
51. Y. Kim, J. W. Kim and Y. Park, Appl. Phys. Lett., 2009, 94, 063305 CrossRef .
52. T. Kato, T. Mori and T. Mizutani, Thin Solid Films, 2001, 393, 109 CrossRef CAS .
53. R. J. Holmes, S. R. Forrest, Y.-J. Tung, R. C. Kwong, J. J. Brown, S. Garon and M. E. Thompson, Appl. Phys. Lett., 2003, 82, 2422 CrossRef CAS .
54. S. Tokito and I. Tanaka, Electrochemistry, 2008, 76, 24–31 CrossRef CAS .
55. L. A. A. Pettersson, L. S. Roman and O. Inganas, J. Appl. Phys., 1999, 86, 487–496 CrossRef CAS .
56. M. Brinkmann, G. Gadret, M. Muccini, C. Taliani, N. Masciocchi and A. Sironi, J. Am. Chem. Soc., 2000, 122(21), 5147–5157 CrossRef CAS .
57. J. Ding, Q. Wang, L. Zhao, D. Ma, L. Wang, X. Jinga and F. Wanga, J. Mater. Chem., 2010, 20, 8126–8133 RSC .
58. R. C. Powell and Z. G. Soos, J. Lumin., 1975, 11, 1 CrossRef CAS .
59. S. R. Yost, E. Hontz, S. Yeganeh and T. V. Voorhis, J. Phys. Chem. C, 2012, 116, 17369–17377 CrossRef CAS .
60. S. M. Menke and R. J. Holmes, J. Phys. Chem. C, 2016, 120(16), 8502–8508 CrossRef CAS .
61. B. E. Lassiter, J. D. Zimmerman and S. R. Forrest, Appl. Phys. Lett., 2013, 103, 123305 CrossRef .
62. N. Aizawa, Y. J. Pu, M. Watanabe, T. Chiba, K. Ideta, N. Toyota, M. Igarashi, Y. Suzuri, H. Sasabe and J. Kido, Nat. Commun., 2014, 5, 5756 CrossRef PubMed .
63. Z. Hu, F. Huang and Y. Cao, Small Methods, 2017, 1, 1700264 CrossRef .
64. S. Wang, B. Zhang, Y. Wang, J. Ding, Z. Xiea and L. Wang, Chem. Commun., 2017, 53, 5128–5131 RSC .
65. T. L. Murrey, K. Guo, J. T. Mulvey, O. A. Lee, C. Cendra, Z. I. Bedolla-Valdez, A. Salleo, J. F. Moulin, K. Hong and A. J. Moulé, J. Mater. Chem. C, 2019, 7, 953–960 RSC .
66. Q. Dao, A. Fujii and M. Ozaki, Jpn. J. Appl. Phys., 2016, 55, 03DB01 CrossRef .

---

Footnote

† Electronic supplementary information (ESI) available: Methodology to measure outcoupled photoluminescence efficiency ratio for the architectures probed in this study. Absorption coefficient and normalized photoluminescence spectrum of the materials probed in this study. Architectures for extracting the ηT as a function of transport layer thickness. See DOI: 10.1039/c9tc00686a

This journal is © The Royal Society of Chemistry 2019