Highly sensitive optical ratiometric thermal sensing based on the three-photon upconversion luminescence of Y₂O₃:Yb³⁺,Er³⁺ nano-thermometers

Leipeng Li ^a, Feng Qin ^b, Lu Li ^b, Hong Gao ^c and Zhiguo Zhang *^ab
aSchool of Physics, Harbin Institute of Technology, Harbin, 150001, P. R. China. E-mail: zhangzhiguo@hit.edu.cn
^bCondensed Matter Science and Technology Institute, School of Instrumentation Science and Engineering, Harbin Institute of Technology, Harbin, 150001, P. R. China
^cKey Laboratory for Photonic and Electronic Bandgap Materials, Ministry of Education, School of Physics and Electronic Engineering, Harbin Normal University, Harbin, 150025, P. R. China

First published on 15th May 2019

---

---

Introduction

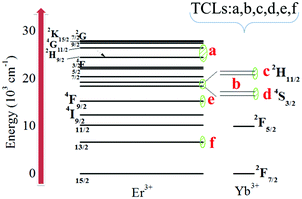
Due to the significance of temperature in a number of fields, lots of methods have emerged for thermal sensing in recent years.^1–8 This is evidenced by the fact that temperature sensing devices own the majority of the global sensor-market share.^9,10 Undeniably, thermocouple and thermal resistance-based sensors, due to their attractive features, such as reliable performance and relatively low manufacturing cost, are regarded as the most popular temperature detection devices for general purposes and are widely used in modern society.⁹ However, with the development of nano-science and nano-technology, these traditional devices no longer apply in more domains, for instance, in monitoring the temperature of a moving object or a tissue at the nano-meter scale.¹⁰ In order to solve these problems, optical thermometry has gained considerable attention because it features a non-contact working pattern, short response time, high thermal sensitivity and temperature resolution, and so forth.¹¹

In the field of optical thermometry, rare earth ions are especially attractive due to their unique properties.^12–20 For instance, they have the ability of converting low energy and long wavelength NIR excitation into high energy and short wavelength light, which is known as the upconversion (UC) process. This is especially useful in biological and medical fields as the commonly used NIR excitation, such as the 980 nm laser, can not only provide a relatively larger penetration depth, but also minimize the effect of the auto-fluorescence of tissues. So far, up to ten kinds of rare earth ions, including Er³⁺, Ho³⁺, Tm³⁺, Nd³⁺, Yb³⁺, Pr³⁺, Sm³⁺, Eu³⁺, Gd³⁺ and Dy³⁺ ions, have been demonstrated to be potential candidates for optical ratiometric thermal sensing because they have, at least, one pair of thermally coupled levels (TCLs), and the populations and thus the luminescence intensity ratio (LIR) between them can be described well by a Boltzmann distribution.^11,21–28 Among these lanthanides, the Er³⁺ ion is especially attractive as it has been confirmed to possess at least six pairs of TCLs, which are the ⁴G_11/2/²H_9/2–⁴I_15/2 TCL, the ²H_11/2/⁴S_3/2–⁴I_15/2 TCL, and the two Stark components of the ²H_11/2, ⁴S_3/2, ⁴F_9/2, and ⁴I_13/2 levels, respectively, just as presented in Fig. 1 (labelled as a–f). (i) The ²H_11/2/⁴S_3/2–⁴I_15/2 levels may be the most well-known TCLs and have been investigated in a variety of hosts for more than thirty years.¹¹ The energy gap between the ²H_11/2 and ⁴S_3/2 TCLs is, however, relatively small, ca. 700 cm⁻¹. According to the expression Sr = ΔE/kT², where ΔE is the energy difference between TCLs, k is the Boltzmann constant and T is the absolute temperature; the relative sensitivity, Sr, for the ²H_11/2 and ⁴S_3/2 TCLs is estimated to be 1.09% K⁻¹ at room temperature. This value is not ideal for achieving a better temperature resolution under the same experimental setup. It should be mentioned here that Marciniak et al. once reported a large relative sensitivity on the basis of the ²H_11/2/⁴S_3/2–⁴I_15/2 levels.¹² However, it was achieved by taking the pulsed 980 nm laser as the excitation source, which exceeds the scope of our work. Here, we only discuss the case where the continuous wave 980 nm laser is utilized to excite the samples as this is the most common case. (ii) The two Stark components of the ²H_11/2, ⁴S_3/2, ⁴F_9/2, and ⁴I_13/2 levels can separately constitute four pair of TCLs, which has been confirmed by several groups.^29,30 Nonetheless, the gap that spaces the two Stark components of a certain level of rare earth ions is, in general, quite narrow. For these four pairs of TCLs, the gaps are calculated to be around 86, 88, 74 and 116 cm⁻¹, respectively. Accordingly, their relative thermal sensitivities are 0.13, 0.13, 0.11 and 0.18% K⁻¹, respectively, at room temperature (see Table 1). These values are quite small and are thus not good for the practical application of these four pairs of TCLs. (iii) In general, the safe threshold of the energy gap that ensures a thermal equilibrium between TCLs is around 2000 cm⁻¹, as firstly suggested by Wade et al.¹¹ Although Zheng et al. once demonstrated that the ⁴D_7/2 and ⁴G_9/2 levels of the Er³⁺ ion could be used for temperature measurement through the LIR technology, the gap between these two levels is approximately equal to 2800 cm⁻¹, being much larger than the above-mentioned safe threshold.³¹ Therefore, it is difficult to populate the ⁴D_7/2 level at the expense of the lower ⁴G_9/2 one by thermal equilibrium. Accordingly, the relative sensitivity for this pair of levels was only 0.41% K⁻¹ at room temperature. In order to overcome the limitations of these TCLs, the ⁴G_11/2/²H_9/2 levels have, thus, become the better choice as the gap between them is slightly smaller than the safe threshold but much larger than the foregoing gaps.^32,33 Using this pair of levels is expected to achieve a highly sensitive thermal sensing via the LIR method. Nonetheless, in previous work, it was found that their relative sensitivity was only 0.46% K⁻¹ at 303 K in a CaWO₄ host, which largely goes beyond the expected maximum sensitivity.³² Therefore, searching for a more suitable material for the ⁴G_11/2/²H_9/2 TCLs becomes meaningful.

---

Aiming to achieve the maximum performance of the ⁴G_11/2/²H_9/2–⁴I_15/2 transitions of the Er³⁺ ion, here, we wish to report a kind of optical nano-thermometer, the Y₂O₃:X%Yb³⁺,1%Er³⁺ (X = 1, 5, 10 and 15) nano-phosphors. It is demonstrated that the relative sensitivity of the ⁴G_11/2/²H_9/2 TCLs in Y₂O₃:1%Yb³⁺,1%Er³⁺ nano-thermometers can reach up to 2.05% K⁻¹ at 303 K. It is, to the best of our knowledge, the maximum value reported so far for the ⁴G_11/2/²H_9/2–⁴I_15/2 transitions and for the Er³⁺ ion. Moreover, this value is also among the highest sensitivities achieved based on different kinds of TCLs of rare earth ions.

Experimental

Yb₂O₃, Er₂O₃, Y₂O₃ (purity: 99.999%, Aladdin Co., Ltd), nitric acid (analytical purity) and NaOH (analytical purity, Aladdin Co., Ltd) were used as purchased, without any further purification. The specific synthesis processes for Y₂O₃:X%Yb³⁺,1%Er³⁺ (X = 1, 5, 10 and 15) nano-phosphors could be described as follows. Firstly, Yb(NO₃)₃, Er(NO₃)₃ and Y(NO₃)₃ solutions (0.5 mol L⁻¹) were prepared with the use of Yb₂O₃, Er₂O₃, and Y₂O₃ powders and nitric acid. Secondly, stoichiometric Yb(NO₃)₃, Er(NO₃)₃ and Y(NO₃)₃ solutions (the mole ratio of Yb(NO₃)₃ to Er(NO₃)₃ was X:1 where X = 1, 5, 10 and 15) were added into a 50 ml beaker, forming a mixture. This was followed by the addition of excess NaOH. The solution mixture was then kept under strong magnetic stirring for 24 h. After centrifugation, the white powders were obtained successfully. After washing three times, the white powders were dried in an oven at 60 °C for one day. Finally, these powders were sintered at 1150 °C for 6 h to form the final products.

Powder X-ray diffraction (XRD) patterns of the prepared nano-phosphors were recorded using a diffractometer (Rigaku D/MAX-2600/PC with Cu Kα radiation, λ = 1.5406 Å) at room temperature. Scanning electron microscopy (SEM) images of the prepared nano-phosphors were obtained by using a Hitachi S-4300. A continuous wave 980 nm laser diode (ITC-4005, Thorlabs) was used as the excitation source. A spectrometer (SBP-300, Zolix Instruments Co., Ltd) was used for wavelength discrimination. A photomultiplier (PMTH-S1-CR131, Zolix Instruments Co., Ltd) connected to an acquisition card was used to collect the emission spectra of the samples at different temperatures over the range between 303 and 783 K. The samples were heated by a home-made heating chamber with an accuracy of ±0.3 K in the experimental temperature range.

Results and discussion

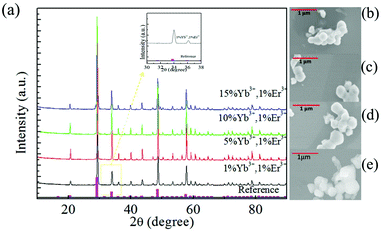
Fig. 2(a) shows the XRD patterns of the prepared Y₂O₃:X%Yb³⁺,1%Er³⁺ (X = 1, 5, 10 and 15) nano-phosphors and the standard data with number 43-1036 from the JCPDS, which is the representative standard cubic phase Y₂O₃. As can be observed, all the prepared Y₂O₃:X%Yb³⁺,1%Er³⁺ (X = 1, 5, 10 and 15) nano-phosphors’ diffraction peaks are in good agreement with the reference data. This is an indication that the samples had been successfully prepared and held the cubic phase. The inset in Fig. 2(a) shows the enlarged part marked by the yellow rectangle that covers the 2θ range of 30–38 degrees. One can see that the diffraction peak of the samples shifts slightly toward a larger 2θ degree, indicating that there is shrinkage for the host. This is because the radius of the Y³⁺ ion (0.0893 nm) is slightly larger than that of Yb³⁺ (0.0858 nm) and Er³⁺ (0.0881 nm) ions. Fig. 2(b–e) present the SEM images of the prepared Y₂O₃:X%Yb³⁺,1%Er³⁺ (X = 1, 5, 10 and 15) nano-phosphors, respectively. It can be seen that the samples are of a non-uniform round shape, with the radius ranging from 120 to 240 nm.

Fig. 3(a) shows the UC emission spectra of Y₂O₃:X%Yb³⁺,1%Er³⁺ (X = 1, 5, 10 and 15) nano-phosphors, which were obtained at room temperature, following the NIR excitation by a 980 nm continuous wave laser diode. For comparison, the experimental setups were kept unchanged upon obtaining the emission spectra of the prepared nano-phosphors. As can be observed, each spectrum is mainly made up of two emission bands, peaking at ca. 387 and 410 nm, respectively. According to the literature, the two emission bands are separately ascribed to the ⁴G_11/2–⁴I_15/2 and ²H_9/2–⁴I_15/2 transitions of the Er³⁺ ion.^32,33 It should be mentioned that the green and the red UC luminescence of the Er³⁺ ion, separately attributed to the ²H_11/2/⁴S_3/2–⁴I_15/2 and ⁴F_9/2–⁴I_15/2 transitions, has long been observed and studied. There are quite a large number of references reporting these luminescence bands and are therefore not discussed here.^34–40 In contrast, the ⁴G_11/2–⁴I_15/2 and ²H_9/2–⁴I_15/2 ones were rarely studied previously.^32,33 In fact, similar to the former two transitions, the ⁴G_11/2–⁴I_15/2 and ²H_9/2–⁴I_15/2 ones are also of significance.^41,42 Thus, it is meaningful to study the ⁴G_11/2–⁴I_15/2 and ²H_9/2–⁴I_15/2 emission bands. From Fig. 3(a), it can be seen that at the low doping concentration of Yb³⁺ ions, it is hard to detect the 387 and 410 nm emission bands by a commonly used photomultiplier under the experimental setup. Upon increasing the Yb³⁺ ion concentration, the emission intensities of these two bands increase markedly. When the Yb³⁺ doping concentration is boosted to 10%, there is a quite good signal to noise ratio for luminescence spectral detection. Moreover, the emission band intensity reaches its maximum. With the further increase of the Yb³⁺ doping concentration up to 15%, the spectrum undergoes a sharp decrease. Therefore, the optimized doping concentration for Yb³⁺ ions is ca. 10%.

By integrating the 380–400 and 400–420 nm spectral ranges, the emission intensities for the 387 and 410 nm lines were obtained. Fig. 3(b) presents the 387 and 410 nm emission line intensities of Y₂O₃:10%Yb³⁺,1%Er³⁺ nano-phosphors as a function of the power density, with the double logarithmical plot. Based on the theory, the UC luminescence intensity, I, can be expressed as I = qPⁿ, where q is a constant, P is the power density and n is the photon number that is needed to populate the emitting state of a certain ion.⁴³ It is found that the slopes of the two linear fits for the 387 and 410 nm lines shown in Fig. 3(b) are all close to three, being an indication that these two emission bands are probably from the three-photon UC mechanism. On the basis of these results, the specific processes for the two emission bands are depicted in Fig. 3(c). Firstly, the Yb³⁺ ions at the ²F_7/2 ground state absorb the NIR photons of the 980 nm laser diode and jump to the higher ²F_5/2 excited state. Secondly, the continuous energy transfers from the Yb³⁺ ions at the ²F_5/2 state occur, exciting the Er³⁺ ions at the ⁴I_15/2 ground state to the higher ⁴I_11/2/⁴F_7/2/²G_7/2 excited states. This is followed by the non-radiative relaxation for the Er³⁺ ions at the ²G_7/2 state to the adjacent lower ⁴G_11/2 and ²H_9/2 states. Finally, the radiative transitions ⁴G_11/2–⁴I_15/2 and ²H_9/2–⁴I_15/2 take place, leading to the 387 and 410 nm emission bands, respectively.

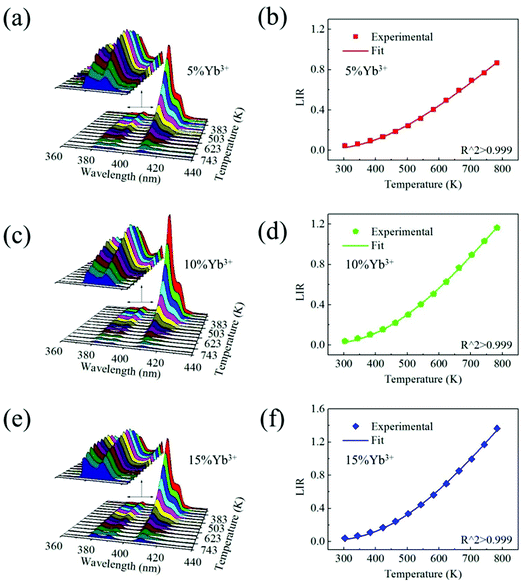
The thermal sensing ability using the 387 and 410 nm emission bands, on the basis of LIR thermometry, was then investigated. Fig. 4(a, c and e) show the UC luminescence of Y₂O₃:5%Yb³⁺,1%Er³⁺, Y₂O₃:10%Yb³⁺,1%Er³⁺ and Y₂O₃:15%Yb³⁺,1%Er³⁺ nano-phosphors, respectively, as a function of temperature in the range between 303 and 783 K with a 40 K step. As can be observed, upon increasing the temperature from 303 to 783 K, the 387 nm emission band increases first and then decreases. By comparison, the 410 nm one always decreases in the experimental temperature range. Fig. 4(b, d and f) present the LIR between the 387 and 410 nm emission bands of Y₂O₃:5%Yb³⁺,1%Er³⁺, Y₂O₃:10%Yb³⁺,1%Er³⁺ and Y₂O₃:15%Yb³⁺,1%Er³⁺ nano-phosphors, respectively. According to the Boltzmann distribution, the LIR between the populations of the two closely separated states can be expressed as^44–48

	(1)

where I₁ and I₂ are the emission intensities for the two bands from the upper and lower thermally coupled states, respectively, A is a constant and ΔE is the gap between TCLs. It is found that all the experimental data depicted in Fig. 4(b, d and f) are in good accordance with eqn (1). For the LIR between the 387 and 410 nm emission lines of Y₂O₃:10%Yb³⁺,1%Er³⁺ nano-phosphors, the parameters A and ΔE/k are fitted to be 12.8 and 1875 K, respectively. In contrast, they are separately fitted to be 8.0 and 1739 K for the LIR between the 387 and 410 nm emission lines of Y₂O₃:5%Yb³⁺,1%Er³⁺ nano-phosphors. For Y₂O₃:15%Yb³⁺,1%Er³⁺ nano-phosphors, the fitted results are A = 16.4 and ΔE/k = 1960 K. Therefore, the 387 and 410 nm emission bands can be used for thermal sensing through ratiometric technology. It was noticed that the fitted pre-exponential factor varies with the Yb³⁺ doping concentration. A similar phenomenon has been previously reported in other cases. Although the physical and chemical explanations are still not clear, it may be understood as follows. For one thing, there is the error in the fitting process for the pre-exponential factor considering that the pre-exponential factor is a fitting value. For another, the spontaneous emission probabilities for the 387 and 410 nm emitting levels may also vary with the Yb³⁺ doping concentration as the pre-exponential factor in eqn (1) is strongly related with the spontaneous emission probability ratio between the two emission lines.

For a temperature sensor, the relative sensitivity, Sr, is a very significant parameter to evaluate its performance. Its original definition is^49–52

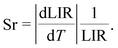	(2)

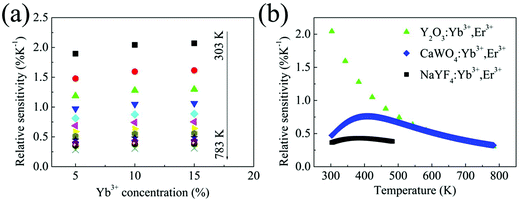
The relative sensitivities for Y₂O₃:5%Yb³⁺,1%Er³⁺, Y₂O₃:10%Yb³⁺,1%Er³⁺ and Y₂O₃:15%Yb³⁺,1%Er³⁺ nano-phosphors were obtained, as shown in Fig. 5(a). As can be observed, for each sample, the relative sensitivity decreases monotonically as the temperature was increased. Moreover, over the experimental temperature range, the three relative sensitivities are quite close to each other. The relative sensitivity does not show an evident dependence on the Yb³⁺ doping concentration. For the sensitivity of Y₂O₃:10%Yb³⁺,1%Er³⁺ nano-phosphors, its maximum value is achieved to be 2.05% K⁻¹ at 303 K, and it decreases gradually upon the increase of temperature from 303 to 783 K. In our previous work, it was shown that based on the 387 and 410 emission bands, CaWO₄:Yb³⁺,Er³⁺ and NaYF₄:Yb³⁺,Er³⁺ phosphors were also promising candidates for ratiometric thermal sensing.^32,33 For comparison, the relative sensitivities based on these two kinds of thermometers are also presented in Fig. 5(b). One can see that at 303 K, their relative sensitivities are 0.47 and 0.36% K⁻¹, respectively. Both values are much smaller than 2.05% K⁻¹ for Y₂O₃:10%Yb³⁺,1%Er³⁺ nano-phosphors. As shown in Fig. 5(b), compared with the NaYF₄:Yb³⁺,Er³⁺ nano-thermometers, using the Y₂O₃:10%Yb³⁺,1%Er³⁺ material boosts the relative sensitivity by 5.7 times at room temperature. Moreover, in the temperature range between 303 and 500 K, the relative sensitivity for Y₂O₃:10%Yb³⁺,1%Er³⁺ nano-phosphors is always larger than that for CaWO₄:Yb³⁺,Er³⁺ and NaYF₄:Yb³⁺,Er³⁺ phosphors. At relatively high temperatures, their sensitivities are quite similar. This suggests, undoubtedly, that Y₂O₃:10%Yb³⁺,1%Er³⁺ nano-phosphors are promising nano-thermometers on the basis of the 387 and 410 nm emission bands. It was noticed that Huang et al. recently reported a kind of nano-thermometer based on the emissions of Er³⁺ ion.⁵³ The maximum sensitivity can reach 3.3% K⁻¹ when an impulse pump was utilized in their experiment. However, under the continuous wave 980 nm laser excitation used in our work, the sensitivity becomes 1.6% K⁻¹, which is smaller than the maximum relative sensitivity obtained here at room temperature.

With the help of eqn (1) and (2), we have

	(3)

where I₁ and I₂ are the 387 and 410 nm emission band intensities, respectively, and Sr₁ and Sr₂ are the relative sensitivities on the basis of these two emission bands, separately. As can be observed from Fig. 4(a), over the whole temperature range, the 410 nm emission band always decreases, meaning that Sr₂ is smaller than zero all the way. In contrast, the 387 nm emission band first increases in the range of 303–463 K and then decreases upon the further increase of temperature between 463 and 783 K. This means that Sr₂ decreases gradually from a certain value to zero with increasing the temperature from 303 to 463 K. At temperatures higher than 463 K, Sr₂ is smaller than zero. Therefore, on the basis of these analyses and eqn (3), one can conclude that using the 387 and 410 nm emission band intensity ratio will achieve a thermal sensing more sensitive than solely using the 387 nm emission band or the 410 nm one in the range of 303–463 K. However, at temperatures higher than 463 K, using solely the 410 nm emission band is expected to achieve a higher relative sensitivity than using the 387 and 410 nm emission band intensity ratio.

Fig. 6(a) shows the integral intensity for the 410 nm emission band as a function of temperature. Considering that there might be several mechanisms imposed on the ²H_9/2 state, it is difficult to describe the 410 nm emission band as a function of temperature using a certain physical model. Therefore, an empirical function is used here. It is found that the experimental data are in good accordance with the following expression:

	(4)

where I₄₁₀ is the intensity of the 490 nm emission band, and A₀, B and C are constants. These three parameters are found to be −2158, 2.4 × 10⁶ and 128, respectively. On the basis of eqn (2), the relative sensitivity for the 410 nm emission band can be calculated, as presented in Fig. 6(b). For comparison, the relative sensitivity for the 387 and 410 nm emission bands is also shown. It decreases markedly upon the increase of temperature. At 783 K, this value is as small as 0.30% K⁻¹, which is only one seventh that achieved at 303 K. It is known that the temperature resolution, δ_T, can be expressed as

	(5)

According to the literature, δLIR/LIR is dependent on the experimental setup. Therefore, the larger the Sr, the smaller the δ_T. Obviously, using the 387 and 410 nm emission bands is bad for achieving a better temperature resolution at relatively high temperatures due to the relatively small sensitivity. In contrast, it can be seen that the sensitivity for the 410 nm emission band increases continuously from 0.78 to 1.27% K⁻¹ as the temperature is increased from 303 to 783 K. At 783 K, this sensitivity is four times larger than that based on the 387 and 410 nm emission bands. Moreover, the typical value of the relative sensitivity for the mostly studied ²H_11/2/⁴S_3/2–⁴I_15/2 transitions of Er³⁺ ion is also presented in Fig. 6(b). As can be observed, this sensitivity is smaller than that based on the 410 nm emission band nearly in the whole experimental temperature range. It decreases markedly from 1.00 to 0.15% K⁻¹ with increasing the temperature from 303 to 783 K. At 783 K, the relative thermal sensitivity for the 410 nm emission band is even one order of magnitude higher than that based on the conventional ²H_11/2/⁴S_3/2–⁴I_15/2 transitions. It thus suggests that the 410 nm emission band may find its application for thermal sensing in the future. It should be underlined that although using the single 410 emission band will be beneficial for temperature sensing over a certain temperature range, the emission intensity of the single band depends on many experimental conditions, such as the excitation source, the illuminated area, the concentration of the luminescent center, and so forth. Therefore, single band-based optical thermometry provides stringent requirements for the experimental setup. Based on the above discussion and eqn (3), the 410 nm emission band is most likely to be used as the “diminishing” band when designing new-generation luminescent ratiometric nanothermometers.

Finally, the influence of power density on the relative sensitivity of the prepared nano-phosphors is studied. Fig. 7(a) presents the emission spectra of the samples under different excitation conditions, which have been normalized to 410 nm. As can be observed, when the excitation power is increased, the 387 nm emission band increases markedly. The LIR between the 387 and 410 nm emission bands under the different excitation conditions can be calculated, as presented in Fig. 7(b). One can see that the higher the excitation power, the larger the LIR. With the use of eqn (1), the temperature increase induced by the laser heating effect was calculated, which is shown in Fig. 7(c). It can be seen that a larger excitation power leads to a matching higher temperature. Fig. 7(d) shows the relative sensitivity as a function of power density. As can be seen, as the power density is increased, the thermal sensitivity decreases monotonically. When the power density is ca. 106 mW mm⁻², the relative sensitivity goes down to 1.29% K⁻¹, only 65 percent of the value obtained at a lower power density. Therefore, in a real case, it is important to select a small power density if the signal to noise of the emission bands involved is ideal.

Conclusions

To sum up, it is shown that the ⁴G_11/2–⁴I_15/2 and ²H_9/2–⁴I_15/2 transitions of Er³⁺ can be used for sensitive temperature measurement via the ratiometric method. At 303 K, the relative sensitivity based on these two emission lines reaches to 2.05% K⁻¹, which is among the reported highest sensitivities that depend on the thermally coupled states of different kinds of lanthanides. Moreover, this sensitivity is independent of the Yb³⁺ doping concentration. Therefore, Y₂O₃:X%Yb³⁺,1%Er³⁺ (X = 5, 10 and 15) phosphors are promising candidates for thermal sensing, which may find their application in the future. In addition, using solely the 410 nm emission band for temperature measurement features high relative sensitivity at relatively high temperatures. At 783 K, the thermal sensitivity is found to be 1.27% K⁻¹. This may provide a possible solution for the long lasting problem that the relative sensitivity sharply decreases upon raising the temperature.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (NSFC) (Grant No. 81571720 & 61505045).

References

1. M. Quintanilla and L. M. Liz-Marzán, Nano Today, 2018, 19, 126–145 CrossRef CAS .
2. M. Quintanilla, E. Cantelar, F. Cussó, M. Villegas and A. C. Caballero, Appl. Phys. Express, 2011, 4, 022601 CrossRef .
3. D. Jaque and F. Vetrone, Nanoscale, 2012, 4, 4301–4326 RSC .
4. J. Rocha, C. D. S. Brites and L. D. Carlos, Chem. – Eur. J., 2016, 22, 1–15 CrossRef .
5. X. Wang, Q. Liu, Y. Bu, C.-S. Liu, T. Liu and X. Yan, RSC Adv., 2015, 5, 86219–86236 RSC .
6. V. K. Rai, Appl. Phys. B: Lasers Opt., 2007, 88, 297–303 CrossRef CAS .
7. X. Wang, O. S. Wolfbeis and R. J. Meier, Chem. Soc. Rev., 2013, 42, 7834–7869 RSC .
8. G. Gao, D. Busko, S. Kauffmann-Weiss, A. Turshatov, I. A. Howard and B. S. Richards, J. Mater. Chem. C, 2018, 6, 4163–4170 RSC .
9. P. R. N. Childs, J. R. Greenwood and C. A. Long, Rev. Sci. Instrum., 2000, 71, 2959 CrossRef CAS .
10. C. D. S. Brites, S. Balabhadra and L. D. Carlos, Adv. Opt. Mater., 2018, 1801239 Search PubMed .
11. S. A. Wade, S. F. Collins and G. W. Baxter, J. Appl. Phys., 2003, 94, 4743 CrossRef CAS .
12. L. Marciniak, K. Waszniewska, A. Bednarkiewicz, D. Hreniak and W. Strek, J. Phys. Chem. C, 2016, 120, 8877–8882 CrossRef CAS .
13. L. Marciniak, K. Prorok and A. Bednarkiewicz, J. Mater. Chem. C, 2017, 5, 7890–7897 RSC .
14. P. Du, L. Luo, H.-K. Park and J. S. Yu, Chem. Eng. J., 2016, 306, 840–848 CrossRef CAS .
15. H. Suo, C. Guo, J. Zheng, B. Zhou, C. Ma, X. Zhao, T. Li, P. Guo and E. M. Goldys, ACS Appl. Mater. Interfaces, 2016, 8, 30312–30319 CrossRef CAS PubMed .
16. H. Suo, C. Guo and T. Li, J. Phys. Chem. C, 2016, 120, 2914–2924 CrossRef CAS .
17. B. Dong, B. Cao, Y. He, Z. Liu, Z. Li and Z. Feng, Adv. Mater., 2012, 24, 1987–1993 CrossRef CAS PubMed .
18. B. Dong, R. N. Hua, B. S. Cao, Z. P. Li, Y. Y. He, Z. Y. Zhang and O. S. Wolfbeis, Phys. Chem. Chem. Phys., 2014, 16, 20009–20012 RSC .
19. D. Chen, Z. Wan, Y. Zhou, X. Zhou, Y. Yu, J. Zhong, M. Ding and Z. Ji, ACS Appl. Mater. Interfaces, 2015, 7, 19484–19493 CrossRef CAS PubMed .
20. D. Chen, W. Xu, S. Yuan, X. Li and J. Zhong, J. Mater. Chem. C, 2017, 5, 9619–9628 RSC .
21. L. Tong, X. Li, J. Zhang, S. Xu, J. Sun, H. Zheng, Y. Zhang, X. Zhang, R. Hua, H. Xia and B. Chen, Opt. Express, 2017, 25, 16047–16058 CrossRef CAS PubMed .
22. G. Sui, B. Chen, J. Zhang, X. Li, S. Xu, J. Sun, Y. Zhang, L. Tong, X. Luo and H. Xia, J. Lumin., 2018, 198, 77–83 CrossRef CAS .
23. S. F. León-Luis, V. Monteseguro, U. R. Rodríguez-Mendoza, I. R. Martín, D. Alonso, J. M. Cáceres and V. Lavín, J. Lumin., 2016, 179, 272–279 CrossRef .
24. J. Cai, X. Wei, F. Hu, Z. Cao, L. Zhao, Y. Chen, C. Duan and M. Yin, Ceram. Int., 2016, 42, 13990–13995 CrossRef CAS .
25. R. Lei, D. Deng, X. Liu, F. Huang, H. Wang, S. Zhao and S. Xu, Opt. Mater. Express, 2018, 8, 3023–3035 CrossRef CAS .
26. Y. Cheng, Y. Gao, H. Lin, F. Huang and Y. Wang, J. Mater. Chem. C, 2018, 6, 7462–7478 RSC .
27. S. Liu, H. Ming, J. Cui, S. Liu, W. You, X. Ye, Y. Yang, H. Nie and R. Wang, Color-tunable upconversion luminescence and multiple temperature sensing and optical heating properties of Ba₃Y₄O₉:Er³⁺/Yb³⁺ Phosphors, J. Phys. Chem. C, 2018, 122, 16289–16303 CrossRef CAS .
28. S. Liu, S. Liu, M. Zhou, X. Ye, D. Hou and W. You, RSC Adv., 2017, 7, 36935–36948 RSC .
29. B. Cao, J. Wu, X. Wang, Y. He, Z. Feng and B. Dong, Sensors, 2015, 15, 30981–30990 CrossRef CAS PubMed .
30. N. Rakova and G. S. Maciel, J. Lumin., 2018, 199, 293–297 CrossRef .
31. K. Zheng, W. Song, G. He, Z. Yuan and W. Qin, Opt. Express, 2015, 23, 7653–7658 CrossRef CAS PubMed .
32. W. Xu, Z. Zhang and W. Cao, Opt. Lett., 2012, 37, 4865–4867 CrossRef CAS PubMed .
33. L. Li, F. Qin, Y. Zhou, Y. Zheng, H. Zhao and Z. Zhang, ACS Appl. Nano Mater., 2018, 1, 1912–1920 CrossRef CAS .
34. O. A. Savchuk, J. J. Carvajal, C. Cascales, M. Aguiló and F. Díaz, ACS Appl. Mater. Interfaces, 2016, 8, 7266–7273 CrossRef CAS PubMed .
35. R. G. Geitenbeek, P. T. Prins, W. Albrecht, A. van Blaaderen, B. M. Weckhuysen and A. Meijerink, J. Phys. Chem. C, 2017, 121, 3503–3510 CrossRef CAS PubMed .
36. X. Xu, Z. Wang, P. Lei, Y. Yu, S. Yao, S. Song, X. Liu, Y. Su, L. Dong, J. Feng and H. Zhang, ACS Appl. Mater. Interfaces, 2015, 7, 20813–20819 CrossRef CAS PubMed .
37. M. A. R. C. Alencar, G. S. Maciel, C. B. Araújo and A. Patra, Appl. Phys. Lett., 2004, 84, 4753 CrossRef CAS .
38. A. Huang, Z. Yang, C. Yu, J. Qiu and Z. Song, J. Am. Ceram. Soc., 2017, 100, 4994–4998 CrossRef CAS .
39. D. Avram and C. Tiseanu, Methods Appl. Fluoresc., 2018, 6, 025004 CrossRef PubMed .
40. S. F. Léon-Luis, U. R. Rodríguez-Mendoza, I. R. Martín, E. Lalla and V. Lavín, Sens. Actuators, B, 2013, 176, 1167–1175 CrossRef .
41. R. B. Anderson, S. J. Smith, P. S. May and M. T. Berry, J. Phys. Chem. Lett., 2014, 5, 36–42 CrossRef CAS PubMed .
42. M. T. Berry and P. S. May, J. Phys. Chem. A, 2015, 119, 9805–9811 CrossRef CAS PubMed .
43. J. F. Suyver, A. Aebischer, S. García-Revilla, P. Gerner and H. U. Güdel, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 125123 CrossRef .
44. M. D. Dramićanin, Methods Appl. Fluoresc., 2016, 4, 042001 CrossRef PubMed .
45. Y. Zhang, S. Xu, X. Li, J. Zhang, J. Sun, H. Xia, R. Hua and B. Chen, Opt. Mater. Express, 2018, 8, 368–384 CrossRef CAS .
46. G. Sui, B. Chen, J. Zhang, X. Li, S. Xu, J. Sun, Y. Zhang, L. Tong, X. Luo and H. Xia, J. Lumin., 2018, 198, 77–83 CrossRef CAS .
47. R. G. Geitenbeek, H. W. de Wijn and A. Meijerink, Phys. Rev. Appl., 2018, 10, 064006 CrossRef CAS .
48. S. F. Léon-Luis, V. Monteseguro, U. R. Rodríguez-Mendoza, M. Rathaiah, V. Venkatramu, A. D. Lozano-Gorrín, R. Valiente, A. Muñoz and V. Lavín, RSC Adv., 2014, 4, 57691–57701 RSC .
49. L. Marciniak, A. Bednarkiewicz, D. Hreniak and W. Strek, J. Mater. Chem. C, 2016, 4, 4327–4328 RSC .
50. Ł. Marciniak, A. Bednarkiewicz, M. Stefanski, R. Tomala, D. Hreniak and W. Strek, Phys. Chem. Chem. Phys., 2015, 17, 24315–24321 RSC .
51. L. Marciniak, A. Bednarkiewicz, D. Kowalska and W. Strek, J. Mater. Chem. C, 2016, 4, 5559–5563 RSC .
52. X. Tian, X. Wei, Y. Chen, C. Duan and M. Yin, Opt. Express, 2014, 22, 30333–30345 CrossRef .
53. F. Huang, T. Yang, S. Wang, L. Lin, T. Hu and D. Chen, J. Mater. Chem. C, 2018, 6, 12364–12370 RSC .

This journal is © The Royal Society of Chemistry 2019