Charge assisted halogen and pnictogen bonds: insights from the Cambridge Structural Database and DFT calculations†
Rosa M.
Gomila
 a and
Antonio
Frontera
a and
Antonio
Frontera
 *b
*b
aServeis Cientificotècnics, University of Balearic Islands, E-07122, Palma, Spain
bDepartament de Química, Universitat de les Illes Balears, Crta de Valldemossa km 7.5, 07122 Palma de Mallorca, Baleares, Spain. E-mail: toni.frontera@uib.es
First published on 31st March 2020
Abstract
This manuscript combines a search in the Cambridge Structural Database (CSD) and theoretical density functional theory (DFT) calculations to analyse the existence and importance of charge assisted pnictogen and halogen bonds involving halophosphonium cations. Trivalent pnictogen atoms typically have three σ-holes and are able to establish up to three pnictogen bonds (PnBs). In phosphonium salts, the phosphorus atom forms four covalent bonds and, consequently, four σ-holes are located at the extension of these bonds. Therefore, up to four charge assisted PnBs can be formed between these holes and the counterions or any electron rich atom. The covalent bond arrangement around the phosphorus atom is similar to that around tetravalent tetrel atoms and converts into a similar pattern of σ-hole interactions. We have found and described this type of charge assisted pnictogen bond in various halophosphonium crystal structures. Moreover, the competition of charge assisted PnBs with charge assisted halogen bonds (HaBs) has been also studied both theoretically and by analysing the CSD.
Introduction
Similar to hydrogen, elements of the p-block of the periodic table can behave as electrophiles and participate in attractive interactions with electron rich sites.1–6 In these p-block elements, the electron density distribution is normally anisotropic, especially when they are covalently bonded to elements of higher electronegativity, thus presenting both regions of positive and negative electron density.7,8 The location and number of positive regions (namely σ-holes) are associated with the position and number of the covalent bonds established by the p-block element.9 That is, the number of σ-holes depends on the number of covalent bonds. For example, halogen, chalcogen, pnictogen and tetrel atoms classically form one, two, three and four covalent bonds and σ-holes may be located opposite to these bonds.10 These regions of depleted charge typically form highly directional interactions which are named using the name of the p-block group, that is, halogen bonds (HaBs)1 for group 17, chalcogen bonds (ChBs)11 for group 16, pnictogen bonds (PnBs)3,12 for group 15 and tetrel bonds (TrBs) for group 14.13,14Attention to PnBs from the scientific community has increased in recent years.2,15,16 For instance, triple-pnictogen bonding has been used as a tool for supramolecular assembly17 and phosphonium–stibonium and bis-stibonium cations have been utilized as pnictogen-bonding catalysts for the hydrogenation of quinolines.18 Moreover, Matile's group has used pnictogen-bonding interactions for transmembrane anion transport and compared their characteristics with those of their chalcogen- and halogen-bonding analogs.19 The positive electrostatic potential energy value at the σ-holes increases going from the top to the bottom of group 15 because the polarizability of the pnicogen atom increases. In fact, pnictogen bonds involving antimony have materialized as the most promising ones for incorporation into functional systems.20
The utilization of the heavier pnictogen atoms to establish effective and competitive interaction in solution is a good strategy to succeed in the fields of supramolecular chemistry and catalysis.21 Another strategy is the utilization of tetravalent phosphorus cations as PnB donor sites (R4P+⋯:A). Tetrasubstituted phosphorus atoms should be able to afford particularly strong charge-assisted pnictogen bonds. Moreover, the presence of up to four σ-holes is expected for phosphorus, consequently enabling up to four PnBs to be established. For the chalcogen elements, the formation of three charge assisted chalcogen bonds involving sulfur,22,23 selenium and tellurium has been studied theoretically and analysed using the CSD.24 Moreover, charge assisted ChBs have been described in several biological systems like S-adenosyl-L-methionine dependent methyl-transferases25 and α-glucosidase inhibitors.24 Similarly, charge assisted halogen bonds have been described in halonium salts forming two charge assisted halogen bonds with anions26 or Lewis bases27,28 opposite to the two covalent bonds.
In this manuscript, we report a combined Cambridge Structural Database (CSD)29 and DFT study (PBE1PBE-D3/def2-TZVP) to analyse the existence and relevance of charge assisted PnBs in crystal structures and analyse their energetic features in some model compounds. Since we use several halophosphonium salts (X4P+, X = F, Cl, Br and I), we also analyse their competition with charge assisted HaBs. In particular, we have compared charge assisted PnBs and HaBs by analysing the X-ray structures present in the CSD and also by computing the energetic and geometric features of two families of complexes, using halophosphonium tetraborate salts as pnictogen/halogen bond donors and several Lewis bases as σ-hole acceptors (electron donors).
Results and discussion
Preliminary CSD search
We have firstly inspected the CSD, searching for X-ray structures of salts containing the RX3P+ cationic unit (X = halogen). As starting points, we have imposed the presence of at least three halogen atoms bonded to phosphorus for three main reasons: (i) to prevent as much as possible overcrowding around the tetrahedral pnictogen atom, (2) to prevent the possibility of establishing additional noncovalent interactions with the groups bonded to P and (iii) to analyse possible competition with charge-assisted halogen bonds. The reference codes (refcodes) of the X-ray structures found in the CSD are gathered in Table 1. Unfortunately, we have not found any structure containing the RX3P+ fragment for X = F. Therefore, we have expanded the search to structures with the (CH3)3XP+ fragment, that is, structures having one halogen atom and the smallest organic group to prevent as much as possible overcrowding around the tetrahedral P-atom. We have found three structures (X = F, Cl and I) that are represented in Fig. 1.| X = Cl | X = Br | X = I |
|---|---|---|
| BAMSAJ | HUHHUN | AHEMEH |
| LUWMIA | YAJTOV | GEKNAM |
| LUWNAT | YAJTUB | HEDGAY |
| SOZFUI | HEDGEC | |
| TCXPHC10 | HEDGIG | |
| TECNOE | HUHHOH | |
| QIRZOH | ||
| QIRZUN |
 | ||
| Fig. 1 X-ray solid state structures of [(CH3)3XP]+[PnF6]− (X = halogen, Pn = pnictogen) salts. (a) NUWTUW, X = F, (b) DITBIS, X = Cl and (c) RANQON, X = I. Distances in Å. | ||
It can be observed that for X = F (NUWTUW30) and Cl (DITBIS31), the O-atom belonging to the counterion is located opposite to the P–X bond at a distance that is shorter than the sum of van der Waals radii thus establishing a charge assisted pnictogen bonding interaction. In both structures, the O-atom also interacts with the H-atoms of the methyl groups thus establishing three C–H⋯O H-bonds that are significantly less directional than the PnB (the range of C–H⋯O distances is also indicated in Fig. 1 for both structures). Interestingly, the O⋯P distance is slightly shorter in the NUWTUW30 structure than in the DITBIS one, in agreement with the typical behaviour of σ-hole interactions. That is, with a given electron donor, the strength typically increases as the electron withdrawing ability of X increases. Remarkably, for X = I (RANQON32), the counterion interacts with the I-atom instead of the P-atom, thus forming a charge assisted halogen bond (HaB) instead of a PnB. A likely explanation is that I is the best halogen bond acceptor and the worse electron withdrawing element in the series.
Other examples of charge assisted PnBs in crystal structures involving the σ-hole opposite to the F–P bond are shown in Fig. 2 including also the aforesaid NUWTUW30 structure. Interestingly, it forms two different PnBs in the solid state (see Fig. 2a) that are highly directional and also a remarkable chalcogen bond where the F-atom is located exactly on the extension of the CF3–S bond (179°). Fig. 2 shows two additional examples, one corresponds to the refcode ENUVEQ33 where the O-atom of triflate interacts with the polarized P–F bond and the other one (refcode PAVSEN34) represents an example of an intramolecular charge assisted PnB.
 | ||
| Fig. 2 X-ray solid state structures as representative examples of highly directional charge assisted PnBs in R3FP+ salts. (a) NUWTUW, (b) ENUVEQ and (c) PAVSEN. Distances in Å. | ||
We have found seventeen structures of halophosphonium cations in the CSD where the P-atom is at least bonded to three halogen atoms (six for X = Cl, three for X = Br and eight for X = I), which are indicated in Table 1. In all these structures, either the P-atom or the halogen atom exhibits strong and directional charge assisted σ-hole interactions.
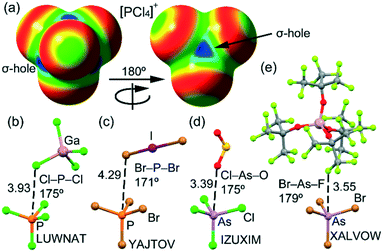
Several structures (indicated in bold in Table 1) correspond to tetrahalophosphonium salts that should present four symmetrically distributed σ-holes, as corroborated in Fig. 3a, where the molecular electrostatic potential (MEP) surface of [PCl4]+ is represented. Two of these X4P+ salts (refcodes LUWNAT35 and YAJTOV36) are represented in Fig. 3b and c and it can be observed that one atom of the counterion is indeed located opposite to one of the P–X bonds; however, the distance is very long, thus suggesting a very weak contribution of the PnB interaction. This can be due to the repulsion with the negative belts of the halogen atoms. We have compared the geometric features of these PnBs with those observed in the X-ray structure of [AsCl4]+ and [AsBr4]+ salts (Fig. 3d and e). Remarkably, in the case of [AsX4]+ salts, the PnB distances O⋯As and F⋯As (in IZUXIM37 and XALVOW,38 respectively) are significantly shorter than the sum of their corresponding van der Waals radii and also highly directional. This result reveals the greater ability of As to establish charge assisted PnBs, in line with the typical behaviour described for conventional PnBs involving trivalent pnictogen atoms.
The analysis of the X-ray structures in Table 1 shows that most of these compounds and especially the [RI3P]+ salts have a strong tendency to form three halogen bonds instead of the charge assisted PnB. Three illustrative examples are given in Fig. 4. In BAMSAJ,39 the trichloro-(4-ethoxyphenyl)-phosphonium cation establishes three strongly directional interactions with the chloride counterions with Cl⋯Cl distances that are shorter than the sum of van der Waals radii (ΣvdW = 3.50 Å). Similarly, in both methyl-tri-iodophosphonium (HEDGIG40) and t-butyl-tri-iodophosphonium (HEDGAY40) iodide salts, three short I⋯I halogen bonds are established with short distances (ΣvdW = 3.96 Å), thus confirming the importance of charge assisted halogen bonds in the solid state of these compounds.
 | ||
| Fig. 4 X-ray solid state structures of [P(X)3R]+ cations. (a) BAMSAJ, X = Cl, (b) HEDGIG, X = I and (c) HEDGAY, X = I. Distances in Å. | ||
MEP surface study
With the purpose of exploring the electron density anisotropy at the phosphorus and halogen atoms in the X4P+ salts, we have computed the molecular electrostatic potential (MEP) surfaces of the salts (compounds 1–4, Scheme 1) as representative models of tetrahalophosphonium salts. In the first series (a), we have used [X4P]+[BF4]− salts with a P–X bond pointing opposite to the [BF4]− anion which is thus suitable for establishing halogen bonding interactions at the opposite side of the anion. Another geometrical arrangement of the salt in this series has been also considered, where one B–F bond points to the P-atom of [X4P]+. However, this arrangement yields to nucleophilic attack of one fluoride atom of [BF4]− on the [X4P]+ cation. In the second series (b), we have used a different orientation where the P–X bond is pointing to the [BF4]− anion, thus suitable for establishing pnictogen bonding interactions. For this series, we have also considered another geometry of the salt, where one B–F bond points to the X–P bond, thus forming a HaB interaction. However, this combination was not used in this study because it is higher in energy than those depicted in Scheme 1.In Fig. 5, we present the MEP surfaces of compounds 1a–4a and in Fig. 6, those of compounds 1b–4b. The MEP values at the σ-holes of P and X for both series “a” and “b” are summarized in Table 2. For the “a” series, the σ-hole at the P-atom is very large for X = F due to the strong electron withdrawing effect of F. Moreover, the electron density is not anisotropic at the F-atom. For the rest of the halogen atoms, the distribution of electron density is anisotropic and the σ-hole slightly increases going from Cl to I. The change is small because the MEP value is largely dominated by the global positive charge of the [X4P]+ moiety. It is interesting to highlight that the size and intensity of the σ-hole at the P-atom significantly decreases going from the lighter to the heaviest halogen atom (see Fig. 5 and Table 2), thus strongly decreasing its ability to participate in noncovalent interactions. For the “b” series, the MEP surfaces evidence the existence of a σ-hole in the X = Cl, Br and I salts with a constant value of +51 kcal mol−1, thus confirming the fact that the cationic nature of the [X4P]+ fragment is masking the polarizability effect in the heavier halogen atoms. In contrast, the MEP value at the P-atom for X = F is very large (Vs,max = 109.2 kcal mol−1) and it significantly decreases going from F to I. This analysis agrees well with the CSD results, since for X = F, pnictogen bonding interactions are common (see Fig. 2); however, for phosphonium cations with heavier halogens, PnBs are rare and HaBs predominate in the solid state. In general, the MEP values are more positive in the “b” series because the counterion [BF4]− is located at a larger distance (longer P⋯B distance) due to the relative orientation of the [X4P]+ and [BF4]− moieties.
 | ||
| Fig. 5 MEP surfaces of compounds 1a (a), 2a (b), 3a (c) and 4a (d). Energies at selected points of the surface (0.001 a.u.) are given in kcal mol−1. | ||
 | ||
| Fig. 6 MEP surfaces of compounds 1b (a), 2b (b), 3b (c) and 4b (d). Energies at selected points of the surface (0.001 a.u.) are given in kcal mol−1. | ||
| Complex | V s,X | V s,P | Complex | V s,X | V s,P |
|---|---|---|---|---|---|
| 1a | 37.0 | 75.3 | 1b | 48.9 | 109.2 |
| 2a | 47.0 | 48.0 | 2b | 50.8 | 60.8 |
| 3a | 47.7 | 39.5 | 3b | 51.4 | 48.3 |
| 4a | 48.9 | 29.5 | 4b | 51.4 | 33.8 |
Energetic analysis
The interaction energies and equilibrium distances (PBE0-D3/def2-TZVP) for both series of complexes 5–24 (see Scheme 2) are gathered in Table 3. We have considered three neutral compounds with different donor abilities (CO, HCN and NH3) to evaluate the PnB without the large contribution of the pure electrostatic attraction between the counter-ions. In addition, we have used two different anions (SCN− and Br−) in order to investigate possible hypervalency of the P-atom upon complexation, especially in the fluorinated phosphonium salts that present very large values of MEP at the P-atom (see Fig. 6a).| Complex | X | Y | ΔEa | R | ρ(r) | H(r) |
|---|---|---|---|---|---|---|
| a For the calculation of the interaction energies, the [X4P+][BF4−] ion pair was considered as a subunit. b The bond paths connect Y to the X-atoms. | ||||||
| 5a | F | CO | −1.0 | 3.254 | 0.0039 | 0.0013 |
| 5b | F | CO | −4.1 | 3.335 | 0.0075 | 0.0009 |
| 6a | F | HCN | −3.5 | 2.923 | 0.0066 | 0.0022 |
| 6b | F | HCN | −11.7 | 2.905 | 0.0139 | 0.0012 |
| 7a | F | NH3 | −3.5 | 2.959 | 0.0079 | 0.0020 |
| 7b | F | NH3 | −23.6 | 1.972 | 0.1091 | −0.0895 |
| 8a | F | SCN− | −17.4 | 2.853 | 0.0110 | 0.0031 |
| 8b | F | SCN− | −36.9 | 3.072 | 0.0145 | 0.0006 |
| 9a | F | Br − | −24.4 | 2.913 | 0.0153 | 0.0023 |
| 9b | F | Br − | −85.2 | 2.319 | 0.1074 | −0.0600 |
| 10a | Cl | CO | −1.7 | 3.315 | 0.0067 | 0.0015 |
| 10b | Cl | CO | −2.0 | 3.943 | 0.0039b | 0.0019 |
| 11a | Cl | HCN | −4.7 | 3.021 | 0.0104 | 0.0023 |
| 11b | Cl | HCN | −6.2 | 3.585 | 0.0059b | 0.0015 |
| 12a | Cl | NH3 | −6.7 | 2.829 | 0.0195 | 0.0015 |
| 12b | Cl | NH3 | −6.3 | 3.560 | 0.0074b | 0.0013 |
| 13a | Cl | SCN− | −21.1 | 2.854 | 0.0216 | 0.0016 |
| 13b | Cl | SCN− | −28.2 | 3.644 | 0.0083b | 0.0015 |
| 14a | Cl | Br − | −41.4 | 2.637 | 0.0503 | −0.0063 |
| 14b | Cl | Br − | −49.8 | 2.417 | 0.0889 | −0.0375 |
| 15a | Br | CO | −2.1 | 3.315 | 0.0084 | 0.0014 |
| 15b | Br | CO | −1.4 | 3.907 | 0.0032b | 0.0009 |
| 16a | Br | HCN | −5.1 | 3.009 | 0.0130 | 0.0019 |
| 16b | Br | HCN | −5.0 | 3.715 | 0.0055b | 0.0011 |
| 17a | Br | NH3 | −8.6 | 2.729 | 0.0278 | 0.0000 |
| 17b | Br | NH3 | −5.2 | 3.668 | 0.0071b | 0.0010 |
| 18a | Br | SCN− | −22.7 | 2.844 | 0.0262 | 0.0002 |
| 18b | Br | SCN− | −26.1 | 3.758 | 0.0082b | 0.0010 |
| 19a | Br | Br − | −52.6 | 2.567 | 0.0655 | −0.0138 |
| 19b | Br | Br − | −45.3 | 2.428 | 0.0862 | −0.0346 |
| 20a | I | CO | −2.6 | 3.294 | 0.0112 | 0.0013 |
| 20b | I | CO | −1.8 | 4.108 | 0.0045 | 0.0007 |
| 21a | I | HCN | −6.0 | 2.978 | 0.0174 | 0.0015 |
| 21b | I | HCN | −4.0 | 3.854 | 0.0054 | 0.0010 |
| 22a | I | NH3 | −11.7 | 2.700 | 0.0355 | −0.0028 |
| 22b | I | NH3 | −4.5 | 3.739 | 0.0074b | 0.0007 |
| 23a | I | SCN− | −25.1 | 2.855 | 0.0317 | −0.0021 |
| 23b | I | SCN− | −23.7 | 3.844 | 0.0086b | 0.0009 |
| 24a | I | Br − | −61.6 | 2.662 | 0.0639 | −0.0159 |
| 24b | I | Br − | −38.0 | 3.728 | 0.0118b | 0.0006 |
The interaction energies and distances for complexes 5–24 are summarized in Table 3. The energetic results indicate that the CO complexes are the weakest ones in both series and the Br− complexes are the strongest ones. In fact, the equilibrium distances in some CO complexes are longer than the sum of van der Waals radii (complexes 10b, 15b and 20b) It is interesting to highlight that the interaction energies for the “b” series (PnBs) are larger (in absolute value) than those for the “a” series for X = F and X = Cl apart from complex 12 (Y = NH3). This result strongly agrees with the MEP analysis, since the MEP at the σ-hole at the P-atom is more intense in compounds 1b and 2b than that at the σ-hole at the X-atom in compounds 1a and 2a. For X = Br and I, the charge assisted HaBs are stronger than the charge assisted PnBs in line with the MEP surface analysis. For the “a” series, the interaction strengthens going from X = F to X = I, as is common for HaBs,1 and for the “b” series, the interaction weakens going from F to I, in line with the lower polarization of the P–X bond for the heavier halogens. As expected, the interaction energies involving the anionic donors are stronger than those with neutral donors.
The geometries of some representative complexes in both series are given in Fig. 7 and 8, where it can be observed that the tetrahedral geometry of the X4P+ unit is not changed upon complexation. However, in some complexes in the “b” series, nucleophilic attack of the electron rich atom on the P-atom occurs, changing from tetrahedral to trigonal pyramidal. These complexes are 7b (Y = NH3), 9b, 14b and 19b (Y = Br−). The geometries of three of them are given in Fig. 9. It can be observed that a covalent bond instead of a non-covalent bond is formed in these complexes, thus explaining the large interaction energies, especially for the Br− complexes. It is worthy to comment that in case of the NH3 molecule, the nucleophilic attack only occurs in the complex with the [X4P]+[BF4]− salt, in good agreement with the MEP surface plot shown in Fig. 6a that shows a very large MEP value at the phosphorus atom's σ-hole.
 | ||
| Fig. 7 PBE0-D3/def2-TZVP optimized geometries of complexes 8a (a), 12a (b), 15a (c) and 21a (d). Distances in Å. | ||
 | ||
| Fig. 8 PBE0-D3/def2-TZVP optimized geometries of complexes 6b (a), 10b (b), 17b (c) and 24b (d). Distances in Å. | ||
 | ||
| Fig. 9 PBE0-D3/def2-TZVP optimized geometries of complexes 7b (a), 9b (b) and 19b (c). Distances in Å. | ||
Characterization of the interactions in complexes 5–24 has been carried out using the quantum theory of “atoms-in-molecules” (QTAIM).41 For all complexes in the “a” series, the HaB is characterized by a bond critical point (CP) and bond path connecting the X-atom to the interacting atom of Y (marked in bold in Table 3). For the “b” series, the distribution of bond CPs and bond paths is more complicated. For X = F, the PnB interaction is characterized by a bond CP and bond path interconnecting the P-atom to the electron rich atom of Y. For X = Cl, Br and I, the interaction is characterized by three symmetrically equivalent bond CPs and bond paths connecting Y to three halogen atoms of the X4P+ unit. In these complexes, the complexation is further characterized by three ring CPs and a cage CP as a consequence of the formation of three supramolecular rings and one supramolecular cage (see Fig. 10 for a representative set of complexes for both series). The values of ρ(r) (electron charge density) at the bond CPs that characterize the HaBs in complexes 5a–24a are given in Table 3. The value of ρ(r) at the bond CP correlates well with the interaction energies.42 That is, for a given electron donor (Y), the ρ(r) values increase going from F to I. In contrast, for the “b” series, the values of ρ(r) decrease going from X = F to X = Br ≈ I, thus confirming the fact that PnBs are stronger for X = F and HaBs are stronger for X = I. In order to differentiate covalent and noncovalent interactions, we have also gathered in Table 3 the values of the total energy density [H(r)] at the bond CPs. Positive values of H(r) indicate noncovalent bonding, negative and small values of H(r) are indicative of partial covalent character, and large and negative values of H(r) along with large values of ρ(r) indicate covalent bonding.43,44 Examination of the values of H(r) in Table 3 reveals that most of the complexes are non-covalent in nature. Furthermore, halogen bonded complexes 14a, 22a and 23a present partial covalent character (values in italics in Table 3) in addition to the PnB complexes. The QTAIM analysis also confirms the covalent character of PnB complexes 7b, 9b, 14b and 19b, which presents a trigonal bipyramidal geometry around the P-atom (values in bold in Table 3) since they present large and negative values of H(r). Moreover, the HaB complexes 19a and 24a, involving an anionic electron donor in combination with the heavier halogens Br and I, also exhibit significant covalent character, in line with the strong σ-hole at the halogen atom (see Fig. 5).
Conclusions
In conclusion, analysis of the X-ray structures present in the CSD evidences the existence of directional charge assisted pnictogen and halogen bonds in tetravalent phosphonium cations. Theoretical DFT calculations show the presence of four σ-holes at the pnictogen atoms in tetrahalophosphonium cations similar to those observed in tetrels. The X4P+ tetrafluoroborate salts are capable of forming either charge assisted PnBs or HaBs. DFT evaluation of the interaction energies and QTAIM analysis evidence that the PnB should prevail over the HaB in the fluorinated salts. Both interactions are energetically similar in the chlorinated salts; however, experimentally, a HaB is more likely to occur due to the fact that the σ-hole at the halogen atom is significantly more accessible than that at the tetravalent Pn atom. For X = Br and I halophosphonium salts, the charge assisted HaB is stronger than the PnB as demonstrated by DFT calculations and also by the analysis of the X-ray structures of halophosphonium salts in the CSD.Theoretical methods
The energies of all complexes included in this study were computed at the PBE0-D3/def2-TZVP level of theory. The geometries have been fully optimized imposing C3v symmetry constraints by using the program Gaussian-16.45 The interaction energy (or binding energy in this work), ΔE, is defined as the energy difference between the optimized complex and the sum of the energies of the optimized monomers where one of the monomers is the salt. For the calculations, we have used the Weigend def2-TZVP46,47 basis set and the PBE1PBE48 DFT functional. The basis set superposition error (BSSE) has been corrected by using the counterpoise method.49 The MEP (molecular electrostatic potential) surface calculations have been carried out at the same level of theory and plotted using the 0.001 a.u. isosurface as the best estimate of the van der Waals surface. The QTAIM formalism has been used to analyse the topology of the electron density,43,44 using the same level of theory and making use of the AIMAll program.50Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We thank the MICIU/AEI (project CTQ2017-85821-R FEDER funds) for financial support. We thank the CTI (UIB) for computational facilities.References
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed
.
- P. Scilabra, G. Terraneo and G. Resnati, Acc. Chem. Res., 2019, 52, 1313–1324 CAS
.
- S. Scheiner, Acc. Chem. Res., 2013, 46, 280–288 CrossRef CAS PubMed
.
-
(a) A. Bauzá, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317–12321 CrossRef PubMed
; (b) A. Bauzá, S. K. Seth and A. Frontera, Coord. Chem. Rev., 2019, 384, 107–125 CrossRef
; (c) A. Bauzá, T. J. Mooibroek and A. Frontera, Chem. Commun., 2014, 50, 12626–12629 RSC
; (d) A. Bauzá, T. J. Mooibroek and A. Frontera, Chem. – Eur. J., 2014, 20, 10245–10248 CrossRef PubMed
.
-
(a) A. Bauzá and A. Frontera, Angew. Chem., Int. Ed., 2015, 54, 7340–7343 CrossRef PubMed
; (b) A. Bauzá and A. Frontera, Coord. Chem. Rev., 2020, 404, 213112 CrossRef
.
- S. Grabowski, J. Comput. Chem., 2018, 39, 472–480 CrossRef CAS PubMed
.
- P. Politzer and J. S. Murray, Crystals, 2017, 7, 212–226 CrossRef
.
- J. S. Murray, P. Lane, T. Clark, K. E. Riley and P. Politzer, J. Mol. Model., 2012, 18, 541–548 CrossRef CAS PubMed
.
- G. Cavallo, P. Metrangolo, T. Pilati, G. Resnati and G. Terraneo, Cryst. Growth Des., 2014, 14, 2697–2702 CrossRef CAS
.
-
(a) A. Bauzá, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496–2517 CrossRef PubMed
; (b) I. Alkorta, J. Elguero and A. Frontera, Crystals, 2020, 10, 180 CrossRef
.
- C. B. Aakeroy, D. L. Bryce, G. R. Desiraju, A. Frontera, A. C. Legon, F. Nicotra, K. Rissanen, S. Scheiner, G. Terraneo, P. Metrangolo and G. Resnati, Pure Appl. Chem., 2019, 91, 1889–1892 CAS
.
-
(a) J. Y. C. Lim and P. D. Beer, Chem, 2018, 4, 731–783 CrossRef CAS
; (b) P. Scilabra, G. Terraneo and G. Resnati, J. Fluorine Chem., 2017, 203, 62–74 CrossRef CAS
.
- M. Marín-Luna, I. Alkorta and J. Elguero, J. Phys. Chem. A, 2016, 120, 648–656 CrossRef PubMed
.
- D. Mani and E. Arunan, Phys. Chem. Chem. Phys., 2013, 15, 14377–14383 RSC
.
-
(a) D. J. Pascoe, K. B. Ling and S. L. Cockroft, J. Am. Chem. Soc., 2017, 139, 15160–15167 CrossRef CAS PubMed
; (b) S. Scheiner, Chem. – Eur. J., 2016, 22, 18850–18858 CrossRef CAS PubMed
.
- E. Alikhani, F. Fuster, B. Madebene and S. J. Grabowski, Phys. Chem. Chem. Phys., 2014, 16, 2430–2442 RSC
.
- S. Moaven, M. C. Andrews, T. J. Polaske, B. M. Karl, D. K. Unruh, E. Bosch, N. P. Bowling and A. F. Cozzolino, Inorg. Chem., 2019, 58, 16227–16235 CrossRef CAS PubMed
.
- M. Yang, M. Hirai and F. P. Gabbaï, Dalton Trans., 2019, 48, 6685–6689 RSC
.
- L. M. Lee, M. Tsemperouli, A. I. Poblador-Bahamonde, S. Benz, N. Sakai, K. Sugihara and S. Matile, J. Am. Chem. Soc., 2019, 141, 810–814 CrossRef CAS PubMed
.
- P. Vieira, M. Q. Miranda, I. Marques, S. Carvalho, L.-J. Chen, E. N. W. Howe, C. Zhen, C. Y. Leung, M. J. Spooner, B. Morgado, O. A. B. Cruz e Silva, C. Moiteiro, P. A. Gale and V. Félix, Chem. – Eur. J., 2020, 26, 888–899 CrossRef CAS PubMed
.
- M. Yang, D. Tofan, C.-H. Chen, K. M. Jack and F. P. Gabbaï, Angew. Chem., Int. Ed., 2018, 57, 13868–13872 CrossRef CAS PubMed
.
- U. Adhikari and S. Scheiner, J. Phys. Chem. A, 2014, 118, 3183–3192 CrossRef CAS PubMed
.
- S. Scheiner, J. Phys. Chem. A, 2015, 119, 9189–9199 CrossRef CAS PubMed
.
- B. Galmés, A. Juan-Bals, A. Frontera and G. Resnati, Chem. – Eur. J., 2020, 26, 4599–4606 CrossRef PubMed
.
- R. J. Fick, G. M. Kroner, B. Nepal, R. Magnani, S. Horowitz, R. L. Houtz, S. Scheiner and R. C. Trievel, ACS Chem. Biol., 2016, 11, 748–754 CrossRef CAS PubMed
.
-
(a) L. Catalano, G. Cavallo, P. Metrangolo, G. Resnati and G. Terraneo, Top. Curr. Chem., 2016, 373, 289–310 CrossRef CAS PubMed
; (b) G. Cavallo, J. S. Murray, P. Politzer, T. Pilati, M. Ursini and G. Resnati, IUCrJ, 2017, 4, 411–419 CrossRef CAS PubMed
.
- M. Ochiai, Y. Nishi, S. Goto, M. Shiro and H. J. Frohn, J. Am. Chem. Soc., 2003, 125, 15304–15305 CrossRef CAS PubMed
.
- M. Ochiai, T. Suefuji, K. Miyamoto, N. Tada, S. Goto, M. Shiro, S. Sakamoto and K. Yamaguchi, J. Am. Chem. Soc., 2003, 125, 769–773 CrossRef CAS PubMed
.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed
.
- S. S. Chitnis, A. P. M. Robertson, N. Burford, J. J. Weigand and R. Fischer, Chem. Sci., 2015, 6, 2559 RSC
.
- J. J. Weigand, N. Burford, A. Decken and A. Schulz, Eur. J. Inorg. Chem., 2007, 2007, 4868 CrossRef
.
- S. Maria, F. Stoffelbach, J. Mata, J.-C. Daran, P. Richard and R. Poli, J. Am. Chem. Soc., 2005, 127, 5946 CrossRef CAS PubMed
.
- K. Schwedtmann, R. Schoemaker, F. Hennersdorf, A. Bauzá, A. Frontera, R. Weiss and J. J. Weigand, Dalton Trans., 2016, 45, 11384 RSC
.
- I. Mallov, T. C. Johnstone, D. C. Burns and D. W. Stephan, Chem. Commun., 2017, 53, 7529 RSC
.
- J. J. Weigand, N. Burford, R. J. Davidson, T. S. Cameron and P. Seelheim, J. Am. Chem. Soc., 2009, 131, 17943 CrossRef CAS PubMed
.
- D. Hausmann, R. Köppe, S. Wolf, P. W. Roesky and C. Feldmann, Dalton
Trans., 2016, 45, 16526 RSC
.
- P. Bertocco, C. Bolli, J. Derendorf, C. Jenne, A. Klein and K. Stirnat, Chem. – Eur. J., 2016, 22, 16032 CrossRef CAS PubMed
.
- M. Gonsior and I. Krossing, Dalton Trans., 2005, 1203 RSC
.
- D. Mootz, W. Poll, H. Wunderlich and H.-G. Wussow, Chem. Ber., 1981, 114, 3499 CrossRef CAS
.
- W.-W. du Mont, V. Stenzel, J. Jeske, P. G. Jones, A. Sebald, S. Pohl, W. Saak and M. Batcher, Inorg. Chem., 1994, 33, 1502 CrossRef CAS
.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS
.
- A. Bauzá and A. Frontera, ChemPhysChem, 2020, 21, 26–31 CrossRef PubMed
.
- R. F. W. Bader, M. T. Carroll, J. R. Cheeseman and C. Chang, J. Am. Chem. Soc., 1987, 109, 7968–7979 CrossRef CAS
.
-
R. F. W. Bader, Atoms in Molecules, A Quantum Theory, Clarendon, Oxford, 1990 Search PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC
.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6169 CrossRef CAS
.
- S. F. Boys and F. Bemardi, Mol. Phys., 1970, 19, 553 CrossRef CAS
.
-
AIMAll (Version 17.11.14), T. A. Keith, TK Gristmill Software, Overland Park KS, USA, (http://aim.tkgristmill.com), 2013 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of all optimized complexes and salts. See DOI:10.1039/d0ce00220h |
| This journal is © The Royal Society of Chemistry 2020 |