Designing water splitting catalysts using rules of thumb: advantages, dangers and alternatives†

Oriol Piqué , Francesc Illas and Federico Calle-Vallejo *
Departament de Ciència de Materials i Química Física & Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, Martí i Franqués 1, 08028 Barcelona, Spain. E-mail: f.calle.vallejo@ub.edu

First published on 9th March 2020

---

---

Oriol Piqué

Oriol Piqué obtained his bachelor's degree in chemistry and MSc in computational modelling from Universitat de Barcelona in 2017 and 2018, respectively. Currently he is doing a PhD at the Institut de Química Teòrica i Computacional (IQTC). His research interests are in electrocatalysis, heterogeneous catalysis, and machine learning. He is currently working on the atomic-scale understanding and tuning of catalysts for CO2 electroreduction and the oxygen evolution reaction.

Francesc Illas

Francesc Illas has developed his professional activity at the Universitat de Barcelona, where he became Full Professor of Physical Chemistry in 1992. He spent several periods at IBM Almaden Research Center and Los Alamos National Laboratory and has been invited professor at Universita’ della Calabria (Italy) and Université Pierre et Marie Curie (France). He received the Distinguished Professor Mention for the University Research Promotion awarded by the Generalitat de Catalunya in 2001, the Bruker Physical Chemistry Research Award of the Spanish Royal Society of Chemistry in 2004, and the ICREA Academia Award in 2009 and 2015. He was elected Fellow of the European Academy of Sciences (2009) and of Academia Europeae (2017).

Federico Calle-Vallejo

Following an undergraduate degree in chemical engineering in Colombia at UPB, Federico Calle-Vallejo completed his PhD at the Technical University of Denmark with Jens K. Nørskov and Jan Rossmeisl. He has worked at both Leiden University with Marc Koper's group, and at École Normale Supérieure de Lyon with Philippe Sautet's group for several post-doctorates. Federico Calle-Vallejo is currently a Ramón y Cajal researcher at the University of Barcelona. Dr Calle-Vallejo's research focuses on the structure-sensitive computational simulation of electrocatalytic reactions such as: oxygen reduction and evolution, hydrogen evolution, CO2 and CO reduction, CO oxidation and nitrate and NO reduction.

---

Introduction

It is a well-known experimental fact that the oxygen evolution reaction (OER: 2H₂O → O₂ + 4H⁺ + 4e⁻) at the anode of proton-exchange membrane electrolyzers is sluggish.^1,2 This, in addition to the scarceness, unsatisfactory durability and high prices of the most active electrocatalysts (usually Ir- or Ru-based) have prevented the extensive use of such electrolyzers for the generation of hydrogen.³ While remarkable efforts have been made by experimenters to find new water-splitting catalysts^4,5 and other routes exist to split water (via photocatalysis, for instance),^6,7 the subject of this perspective is the computational modelling of the electrochemical OER and how it is currently dominated by an uncertain rule of thumb.

Before we write and discuss such rule of thumb in detail, it is advisable to present the thermodynamic framework it is based on. First, the energetics of proton–electron pairs are described using the computational hydrogen electrode,⁸ and it is assumed that all catalysts follow the same mechanistic pathway from H₂O to O₂:^9,10

* + H2O → *OH + H+ + e−	(1)

*OH→*O + H+ + e−	(2)

*O + H2O → *OOH + H+ + e−	(3)

*OOH →* + O2 + H+ + e−	(4)

There are three adsorbed intermediates in the mechanism, namely *O, *OH, and *OOH, so that the free energies of reaction (hereafter, referred to simply as energies) can be written as a function of those:

ΔG1 = ΔGOH	(5)

ΔG2 = ΔGO − ΔGOH	(6)

ΔG3 = ΔGOOH − ΔGO	(7)

ΔG4 = ΔGO2 − ΔGOOH	(8)

where ΔG_O2 = 4.92 eV corresponds to the sum of eqn (5)–(8), and is equivalent to the equilibrium potential (E⁰ = 1.23 V) multiplied by the total number of transferred electrons per catalytic cycle (1.23 V × 4e⁻ = 4.92 eV). Linear relations exist between the adsorption energies of those three intermediates on a wide variety of materials,^11–15 such that all reaction energies in eqn (5)–(8) can be written in terms of one of the three adsorption energies (either ΔG_O, ΔG_OH, or ΔG_OOH) or a linear combination of them (e.g. ΔG_O − ΔG_OH). In this model, the overpotential (in V) is determined by the largest positive reaction energy (in eV) in eqn (5)–(8):^9,10η_OER = max({ΔG_i})/e⁻− 1.23, with i = 1, 2, 3, 4. The electrochemical step with such energy is deemed the potential-limiting step, which may be different from the rate-determining step.¹⁶ To conclude this section, note that within this model a catalyst with all ΔG_i = 1.23 eV has null OER overpotential.

1. The upsides and downsides of adsorption-energy scaling relations

When aiming at understanding a physical and/or chemical phenomenon, a low number of degrees of freedom is advantageous, as the resulting model is likely simple and depends on a small set of independent parameters. Nevertheless, once the phenomenon is understood and the model is used for optimization purposes, a low number of degrees of freedom is problematic. Essentially, the linear dependence between certain parameters may prevent full optimization. As shown in Fig. 1, that is exactly what happens during the OER for ΔG_O, ΔG_OH, and ΔG_OOH. The figure contains theoretical data collected from the literature for 155 different compounds belonging to different families, including various types of oxides, porphyrins and functionalized graphitic materials (FGMs).^10,17–25 We note that other families of compounds, such as chalcogenides and nitrides^26,27 might as well be included in the plot and in the analysis shown in the final parts of this article. The mean absolute error (MAE) between the linear fit and the calculated data points is only 0.17 eV for ΔG_OOHvs. ΔG_OH, and 0.50 eV for ΔG_Ovs. ΔG_OH.

Ideally, all reaction steps should consume 1.23 eV for the overpotential to be null, but adsorption-energy scaling relations seem to forbid it. This was first proposed in 2011,^10,28 after it was noted that the scaling relation between *OH and *OOH has a near unity slope and an intercept of ∼3.2 ± 0.2 eV (see Fig. S1, ESI†).^10,17–25

The consequences of such constant separation are far-reaching. To illustrate the matter, consider the sum of eqn (2) and (3), and the corresponding sum of reaction energies in eqn (6) and (7):

*OH + H2O → *OOH + 2H+ + 2e−	(9)

ΔG2+3 = ΔGOOH − ΔGOH	(10)

For an ideal catalyst, ΔG₂₊₃ should be 1.23 V × 2e⁻ = 2.46 eV, given that all the steps involved are energetically identical. However, for a wide collection of catalysts it is usually in the range of 3.2 ± 0.2 eV,^10,17–25 see Fig. S2 (ESI†). This, in addition to the fact that the overpotential is normally determined by steps 2 or 3, led to the conclusion that there exists an intrinsic OER overpotential due to scaling relations. Such overpotential can be calculated as: η^SR_OER = (3.2 − 2.46) eV/2e⁻ = 0.37 V, where SR stands for scaling relations. In other words, the top of the so-called volcano plot is not located at 1.23 V but rather at 1.60 V. Note that a similar analysis holds, in principle, for the oxygen reduction reaction (ORR: O₂ + 4H⁺ + 4e⁻ → 2H₂O), where the top of the volcano is located at 0.86 V instead of 1.23 V.^17,29

2. A simple rule of thumb for OER electrocatalysis

If there is an overpotential attributable to the OOH vs. OH scaling, it is natural to hypothesize that its breaking will lead to enhanced OER electrocatalysis. The recipe is then to stabilize *OOH with respect to *OH.^10,30 This plausible yet unverified hypothesis quickly became a pervasive rule of thumb for the design of new OER electrocatalysts and the concept was extended to other electrocatalytic reactions.^31–34

The hypothesis was put to the test recently by plotting the calculated overpotential as a function of γ_OOH/OH (in V), which is a metric for the degree of breaking of the OOH vs. OH scaling relation (γ_OOH/OH = (ΔG_OOH − ΔG_OH − 2.46) eV/2e⁻). As γ_OOH/OH tends to zero, catalysts depart more and more from the scaling relation, which should correspond to a proportional lowering of the calculated OER overpotential. Unfortunately, as shown in Fig. 2, this is not the case for a great variety of catalysts compiled from the literature.

Given that a series of reasonable arguments led us to a visibly incorrect guess, namely that breaking scaling relations necessarily implies catalytic enhancement, it is worth finding the weak points in the analysis. One of them is the assumption of a sole reaction pathway for all materials. This is debatable but necessary to build an affordable framework wherein all catalysts can be directly compared. Nonetheless, we note that several alternative pathways have been proposed in the literature,^30,35–37 and that recent studies have shown that scaling relations can also be used to study competing pathways.³⁸ The structure- and composition-sensitive effects of solvation^20,39–41 are also worth incorporating in the model to improve its predictions, as *O, *OH, and *OOH are differently solvated depending on the material. Furthermore, if the potential- and rate-limiting steps of the reaction are different, the model might as well be misleading, as pointed out before.¹⁶ Other modelling approaches also exist including reaction kinetics,^42,43 and recent works have been devoted to finding a unifying approach that accounts for OER thermodynamics and kinetics.^44,45

Another weak point is the idea that stabilizing *OOH with respect to *OH indefectibly reduces η_OER. Looking at eqn (1)–(4), we conclude that this is only true for materials in which step 3 (*O + H₂O → *OOH + H⁺ + e⁻) is potential limiting. From the 155 compounds considered here, only 45% of them belong to this group.

There is no effect on materials where the first (* + H₂O → *OH + H⁺ + e⁻) and second (*OH → *O + H⁺ + e⁻) steps are potential-limiting because *OOH is not involved in those.^46,47 Among all materials considered, 12 and 43% are respectively limited by steps 1 or 2.

Strikingly, if step 4 (*OOH → * + O₂ + H⁺ + e⁻) is potential-limiting, stabilizing *OOH increases η_OER instead of decreasing it.^46,47 Although less than 1% of the materials considered in this work are limited by this step, it usually limits the ORR on numerous materials.⁴⁷

Therefore, the problem with the OOH–OH rule of thumb is that in at least 55% of the inspected cases it will likely have no effect on the overpotential or even increase it. Based on this, our conclusion is that one should probably focus on the actual potential-limiting step of the OER, which depends on every material, instead of trying to stabilize *OOH by default. The latter optimizes the sum of steps 2 and 3, which does not unambiguously result in a lowering of the calculated overpotential.

3. Electrocatalytic symmetry and a metric for it

As the OOH–OH rule of thumb is likely to fail in more than half of the cases, it is pertinent to ask if there are simple alternatives to evaluate and predict enhanced OER catalysts. As said before, the ideal catalyst has all ΔG_i = 1.23 eV, which implies that it indeed breaks the OOH vs. OH scaling relation and has null OER overpotential. Thus, at least from a thermodynamic point of view, it is reasonable to claim that the goal is for a catalyst to resemble as much as possible the ideal one. To quantitatively assess such resemblance, the electrochemical-step symmetry index (ESSI) was proposed: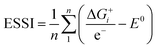

	(11)

where ΔG⁺_i corresponds to the reaction energies in eqn (1)–(4) that are larger than 1.23 eV, as only those can be potential-limiting, and E⁰ is the OER equilibrium potential (1.23 V). Examples of the assessment of ESSI can be found elsewhere.^{22–24,46,47}

The correlation between ESSI, which is a metric for electrocatalytic symmetry, and OER overpotentials is apparent in Fig. 3. In the analyzed set of 155 materials, the mean absolute error (MAE) for the prediction of η_OER is 0.20 V and the maximum absolute error (MAX) is 0.69 V. For comparison, a linear fit of the data in Fig. 2 provides a mean absolute error (MAE) of 0.38 V and a maximum absolute error (MAX) of 1.69 V. Besides, in Fig. 4 we observe that the linear combination of γ_OOH/OH and ESSI essentially follows the trends dictated by ESSI, and there are no substantial improvements in the MAE or the MAX (0.19 and 0.68 V, respectively).

To close this section, we note that, as ESSI is an average, it can be accompanied by error bars showing the dispersion of the data. In principle, catalysts with wide bars are easier to optimize than those with narrow bars.^46,47 Besides, ESSI can be calculated regardless of the presence or absence of scaling relations between reaction intermediates.

4. Quantitative prediction of catalytic enhancement

It is a common practice in experimental electrocatalysis to initially find a prospect material and subsequently engineer its structural and/or electronic properties to make it more active.^2,4 Intuitively, as a material approaches the top of the volcano plot, it gets progressively more difficult to further optimize it. However, how much a given material can be optimized is usually difficult to assess, so that the optimization of some may be slow and take many years.

A computational assessment of a given material's ease of improvement is provided by δ–ε optimization.⁴⁶ The procedure is simple and requires only the addition of two parameters in eqn (5)–(8): δ, which is scaling-dependent; and ε, which is scaling-free, as shown in eqn (12)–(15). Both parameters in eqn (12)–(15) are in the same units as the adsorption energies.

ΔG1 = ΔGOH + δ	(12)

ΔG2 = ΔGO − ΔGOH + δ	(13)

ΔG3 = ΔGOOH − ΔGO − δ + ε	(14)

ΔG4 = ΔGO2 − ΔGOOH − δ − ε	(15)

As it is the case for eqn (5)–(8), the sum of eqn (12)–(15) is ΔG_O2 = 4.92 eV, as required by the energy conservation principle applied over the catalytic cycle in eqn (1)–(4). Since ε is scaling-free, it only affects *OOH. Conversely, δ is scaling-dependent, so it proportionally affects *O, *OH and *OOH. Accordingly, if ΔG_OH is modified by δ, then ΔG_OOH is also modified by δ and ΔG_O is modified by 2δ, which is justified by the slopes of the scaling relations in Fig. 1. A positive value of δ causes a weakening of the adsorption energies, while a negative value of δ and ε causes their strengthening. Conservative ranges for δ and ε are [−0.3, 0.3] and [−0.3, 0] eV, respectively.⁴⁶ These imply that δ can either be a scaling-based destabilization or stabilization (via e.g. strain or geometric effects), while ε is a stabilization of *OOH (via tethering, nanoconfinement, ligand–adsorbate interactions).^30,46

To illustrate the aim of δ–ε optimization, let us consider three materials: Sr_1−xNa_xRuO₃, LaNiO₃, and Ru FGM.^{10,18,19,23,25} Their adsorption energies, reaction energies and calculated overpotentials before and after δ, ε and δ−ε optimization are shown in Table 1. We note that, although initially the OER overpotential of LaNiO₃ is lower than that of Sr_1−xNa_xRuO₃ (0.37 vs. 0.32 V), the latter is considerably easier to optimize. Indeed, upon δ optimization LaNiO₃'s overpotential decreases by 0.01 V, whereas that of Sr_1−xNa_xRuO₃ decreases by 0.17 V (0.31 vs. 0.21 V). Interestingly, in none of the two perovskites was ε optimization leading to lower OER overpotentials (thus, ε = 0 eV), which stems from the two unoptimized materials being limited by the second electrochemical step (*OH→*O + H⁺ + e⁻), in which *OOH is not involved.

---

The results for Ru FGM in Table 1 show that it benefits from δ, ε, and δ−ε optimizations. Separately, δ and ε optimizations lower the overpotential from 0.68 to 0.38 V, while their combination achieves 0.21 V. However, the difficulties for the experimental implementation of such optimizations likely increase from δ to ε to δ−ε, so that the former strategy is to be preferred over the latter two. Before closing this section, we emphasize that ESSI and δ−ε optimization can be used in conjunction, as recently shown in ref. 46.

5. Extension to other electrocatalytic reactions

The ESSI analysis and δ−ε optimization are not exclusively applicable to the OER but rather to all electrocatalytic reactions. Indeed, the ESSI analysis has also been applied to the ORR and correlations were found between ESSI_ORR and ESSI_OER.⁴⁷ Recently, the two descriptors were used to simultaneously assess the OER and ORR activities of oxides in the search for bifunctional electrocatalysts.²⁴ In Fig. 5 we present a combined plot for the ORR and the OER on a variety of oxides, including LSNMR (La_1.5Sr_0.5NiMn_0.5Ru_0.5O₆), a highly active double perovskite.

A simple metric for OER–ORR bifunctionality is the bifunctional index (BI),^48,49 which is defined as the positive difference between the potentials needed to achieve an OER current density of 10 mA/cm² and an ORR current density of −1 mA cm⁻². Following the analysis around eqn (1)–(8), the ideal ORR–OER bifunctional catalyst should have BI ≈ 0 V. The analysis around eqn (9) and (10) suggests that an optimal catalyst obeying scaling relations should have BI ≈ 1.60 − 0.86 ≈ 0.74 V (i.e. the difference between the two scaling-based limiting potentials). In practice, most catalysts display BIs larger than 1.0 V and those in the range of 0.8–0.9 V are regarded as highly bifunctional.^24,48,49

Interestingly, the bottom inset in Fig. 5 shows that the DFT-calculated BIs (BI_DFT = η_OER + η_ORR) are linearly correlated with the difference in ESSI (ΔESSI = ESSI_OER − ESSI_ORR). Furthermore, the top inset in Fig. 5 shows that DFT-calculated BIs are generally in good agreement with the experimental ones. Therefore, the two insets establish a useful connection between ESSI and experimental bifunctionality.

Summary and conclusions

Rules of thumb are rather common and helpful in many branches of chemistry, physics, and engineering. Although they can greatly facilitate analyses and designs, it is important when resorting to them not to forget where they come from, as they probably resulted from analyses in which several approximations and assumptions were made. Clearly, the ideal catalyst is not subject to scaling relations, but a compilation of data from the literature shows that breaking the OOH vs. OH scaling relation in real catalysts does not per se lead to enhanced oxygen evolution electrocatalysis.

Instead, the electrochemical-step symmetry index (ESSI, which can be calculated irrespective of the presence or absence of adsorption-energy scaling relations between intermediates) and the δ−ε optimization are reasonable alternatives for the scaling-based and scaling-free design of enhanced electrocatalysts. The two alternatives suggest that catalytic enhancement may result more likely from focusing on specific steps rather than on universal recipes. In sum, focusing on the actual potential-limiting steps seems a more advisable practice in electrocatalysis than using unverified rules of thumb.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work was supported by Spanish MICIUN's RTI2018-095460-B-I00 and María de Maeztu MDM-2017-0767 grants and, in part, by Generalitat de Catalunya 2017SGR13, XRQTC grants and by COST Action 18234, supported by COST (European Cooperation in Science and Technology). F. C. V. thanks the Spanish MICIUN for a Ramón y Cajal research contract (RYC-2015-18996) and F. I. acknowledges additional support from the 2015 ICREA Academia Award for Excellence in University Research. O. P. thanks the Spanish MICIUN for an FPI PhD grant (PRE2018-083811). We are thankful to Red Española de Supercomputación (RES) for super-computing time at SCAYLE (projects QS-2019-3-0018, QS-2019-2-0023, and QCM-2019-1-0034). The use of supercomputing facilities at SURFsara was sponsored by NWO Physical Sciences.

References

1. N.-T. Suen, S.-F. Hung, Q. Quan, N. Zhang, Y.-J. Xu and H. M. Chen, Chem. Soc. Rev., 2017, 46, 337–365 RSC .
2. T. Reier, H. N. Nong, D. Teschner, R. Schlögl and P. Strasser, Adv. Energy Mater., 2017, 7, 1601275 CrossRef .
3. C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS PubMed .
4. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, 146 CrossRef PubMed .
5. W. T. Hong, M. Risch, K. A. Stoerzinger, A. Grimaud, J. Suntivich and Y. Shao-Horn, Energy Environ. Sci., 2015, 8, 1404–1427 RSC .
6. X. Wang, J. Wang and M. Sun, Appl. Mater. Today, 2019, 15, 212–235 CrossRef .
7. F. E. Osterloh, Chem. Soc. Rev., 2013, 42, 2294–2320 RSC .
8. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2014, 108, 17886–17892 CrossRef .
9. J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS .
10. I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS .
11. F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105 CrossRef CAS PubMed .
12. F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Nat. Chem., 2015, 7, 403–410 CrossRef CAS PubMed .
13. M. M. Montemore and J. W. Medlin, Catal. Sci. Technol., 2014, 4, 3748–3761 RSC .
14. J. Greeley, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 605–635 CrossRef PubMed .
15. B. Garlyyev, J. Fitchner, O. Piqué, O. Schneider, A. S. Bandarenka and F. Calle-Vallejo, Chem. Sci., 2019, 10, 8060 RSC .
16. M. T. M. Koper, J. Solid State Electrochem., 2013, 17, 339–344 CrossRef CAS .
17. M. García-Mota, A. Vojvodic, H. Metiu, I. C. Man, H.-Y. Su, J. Rossmeisl and J. K. Nørskov, ChemCatChem, 2011, 3, 1607–1611 CrossRef .
18. F. Calle-Vallejo, J. I. Martínez and J. Rossmeisl, Phys. Chem. Chem. Phys., 2011, 13, 15639–15643 RSC .
19. F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, E. Abad and M. T. M. Koper, Surf. Sci., 2013, 607, 47–53 CrossRef CAS .
20. F. Calle-Vallejo, A. Krabbe and J. M. Garcia-Lastra, Chem. Sci., 2017, 8, 124–130 RSC .
21. F. Calle-Vallejo, N. G. Inoglu, H.-Y. Su, J. I. Martínez, I. C. Man, M. T. M. Koper, J. R. Kitchin and J. Rossmeisl, Chem. Sci., 2013, 4, 1245–1249 RSC .
22. M. Retuerto, F. Calle-Vallejo, L. Pascual, P. Ferrer, A. García, J. Torrero, D. Gianolio, J. L. G. Fierro, M. A. Peña, J. A. Alonso and S. Rojas, J. Power Sources, 2018, 404, 56–63 CrossRef CAS .
23. M. Retuerto, L. Pascual, F. Calle-Vallejo, P. Ferrer, D. Gianolio, A. G. Pereira, A. García, J. Torrero, M. T. Fernández-Díaz, P. Bencok, M. A. Peña, J. L. G. Fierro and S. Rojas, Nat. Commun., 2019, 10, 2041 CrossRef PubMed .
24. M. Retuerto, F. Calle-Vallejo, L. Pascual, G. Lumbeeck, M. T. Fernández-Díaz, M. Croft, J. Gopalakrishnan, M. A. Peña, J. Hadermann, M. Greenblatt and S. Rojas, ACS Appl. Mater. Interfaces, 2019, 11, 21454–21464 CrossRef CAS PubMed .
25. F. Calle-Vallejo, O. A. Díaz-Morales, M. J. Kolb and M. T. M. Koper, ACS Catal., 2015, 5, 869–873 CrossRef CAS .
26. G. A. Tritsaris, J. K. Nørskov and J. Rossmeisl, Electrochim. Acta, 2011, 56, 9783–9788 CrossRef CAS .
27. E. M. Fernández, P. G. Moses, A. Toftelund, H. A. Hansen, J. I. Martínez, F. Abild-Pedersen, J. Kleis, B. Hinnemann, J. Rossmeisl, T. Bligaard and J. K. Nørskov, Angew. Chem., Int. Ed., 2008, 47, 4683–4686 CrossRef PubMed .
28. M. T. M. Koper, J. Electroanal. Chem., 2011, 660, 254–260 CrossRef CAS .
29. M. Busch, N. B. Halck, U. I. Kramm, S. Siahrostami, P. Krtil and J. Rossmeisl, Nano Energy, 2016, 29, 126–135 CrossRef CAS .
30. Z.-F. Huang, J. Song, S. Dou, X. Li, J. Wang and X. Wang, Matter, 2019, 1, 1494–1518 CrossRef .
31. J. Pérez-Ramírez and N. López, Nat. Catal., 2019, 2, 971–976 CrossRef .
32. Y. Li and Q. Sun, Adv. Energy Mater., 2016, 6, 1600463 CrossRef .
33. A. A. Peterson and J. K. Nørskov, J. Phys. Chem. Lett., 2012, 3, 251–258 CrossRef CAS .
34. J. H. Montoya, C. Tsai, A. Vojvodic and J. K. Nørskov, ChemSusChem, 2015, 8, 2180–2186 CrossRef CAS PubMed .
35. R. R. Rao, M. J. Kolb, N. B. Halck, A. F. Pedersen, A. Mehta, H. You, K. A. Stoerzinger, Z. Feng, H. A. Hansen, H. Zhou, L. Giordano, J. Rossmeisl, T. Vegge, I. Chorkendorff, I. E. L. Stephens and Y. Shao-Horn, Energy Environ. Sci., 2017, 10, 2626–2637 RSC .
36. M. J. Craig, G. Coulter, E. Dolan, J. Soriano-López, E. Mates-Torres, W. Schmitt and M. García-Melchor, Nat. Commun., 2019, 10, 4993 CrossRef PubMed .
37. J. Hessels, R. J. Detz, M. T. M. Koper and J. N. H. Reek, Chem. – Eur. J., 2017, 23, 16413–16418 CrossRef CAS PubMed .
38. F. Calle-Vallejo and M. T. M. Koper, ACS Catal., 2017, 7, 7346–7351 CrossRef CAS .
39. V. Tripkovic, Phys. Chem. Chem. Phys., 2017, 19, 29381 RSC .
40. Z.-D. He, S. Hanselman, Y.-X. Chen, M. T. M. Koper and F. Calle-Vallejo, J. Phys. Chem. Lett., 2017, 8, 2243–2246 CrossRef CAS PubMed .
41. L. G. V. Briquet, M. Sarwar, J. Mugo, G. Jones and F. Calle-Vallejo, ChemCatChem, 2017, 9, 1261–1268 CrossRef CAS .
42. K. S. Exner and H. Over, Acc. Chem. Res., 2017, 50, 1240–1247 CrossRef CAS PubMed .
43. C. F. Dickens, C. Kirk and J. K. Nørskov, J. Phys. Chem. C, 2019, 123, 18960–18977 CrossRef CAS .
44. K. S. Exner, ACS Appl. Energy Mater., 2019, 2, 7991–8001 CrossRef CAS .
45. K. S. Exner and H. Over, ACS Catal., 2019, 9, 6755–6765 CrossRef CAS .
46. N. Govindarajan, M. T. M. Koper, E. J. Meijer and F. Calle-Vallejo, ACS Catal., 2019, 9, 4218–4225 CrossRef CAS .
47. N. Govindarajan, J. M. García-Lastra, E. J. Meijer and F. Calle-Vallejo, Curr. Opin. Electrochem., 2018, 8, 110–117 CrossRef CAS .
48. J. Masa, W. Xia, I. Sinev, A. Zhao, Z. Sun, S. Grützke, P. Weide, M. Muhler and W. Schuhmann, Angew. Chem., Int. Ed., 2014, 53, 8508–8512 CrossRef CAS PubMed .
49. K. Elumeeva, J. Masa, F. Tietz, F. Yang, W. Xia, M. Muhler and W. Schuhmann, ChemElectroChem, 2016, 3, 138–143 CrossRef CAS .

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp00896f

This journal is © the Owner Societies 2020