View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/D0CP05422D (Paper) Phys. Chem. Chem. Phys., 2021, 23, 1976-1983

Magnetic anisotropy in YbIII complex candidates for molecular qubits: a theoretical analysis†

Martín Amoza , Silvia Gómez-Coca and Eliseo Ruiz *
Departament de Química Inorgànica i Orgànica and Institut de Recerca de Química Teòrica i Computacional, Universitat de Barcelona, Diagonal 645, 08028 Barcelona, Spain. E-mail: eliseo.ruiz@qi.ub.es

Received 15th October 2020 , Accepted 16th December 2020

First published on 16th December 2020

Abstract

The magnetic properties of mononuclear YbIII complexes have been explored by using multiconfigurational CASPT2/RASSI calculations. Such complexes, in particular the case of [Yb(trensal)] complex, have been proposed as molecular qubits due to their spin dynamics properties. We have verified the accuracy of the theoretical approach to study such systems by comparing with experimental magnetic data. In order to have a wide overview of the magnetic properties of mononuclear YbIII complexes, we have considered simple charged and neutral models, [Yb(H2O)n]3+ and [Yb(OH)3(H2O)n−3], for many coordination modes. Thus, the results for more than 100 models allow extraction of some conclusions about the best ligand distributions in the coordination sphere to tailor the magnetic properties. Some low coordination, between 3 and 5, complexes that have no experimental magnetic data have been studied computationally to check if they can present high magnetic anisotropy.

1. Introduction

There are many technologies to provide qubit systems in order to build up quantum computers. A single qubit can be described as a system that can populate two states, at the classical level the system will be in one of them or the other, but the qubit is the coherent superposition of both states. Usually, to establish the requirements for a system to be a qubit DiVincenzo proposed five points:1 (i) scalability of the qubit system; (ii) simple initialization of the initial state; (iii) long coherence times; (iv) universal set of quantum gates and (v) qubit measurement capability. Long coherence times are crucial because they must be longer than the time of a single operation of the quantum computer. In some of the qubit technologies, the information support is the spin that can be a superposition of up |1〉 or down |0〉 configurations. In such cases, spin dynamics of the qubit is fundamental to control the coherence time that can be tuned by suppressing a series of relaxation mechanisms that induce a change in the spin direction, and consequently will change the superposition between the two states.2–5 There are two crucial time parameters to quantify the spin dynamics and the time coherence: the spin–lattice (or longitudinal) T1 and the spin–spin (or transversal) T2 relaxation times.6 The spin–lattice T1 relaxation corresponds to the dynamics in the z direction and it involves the interaction of the spin with the vibrations of the surrounding lattice, thus, T1 depends on the temperature. The T2 spin–spin relaxation time follows the temporal evolution of magnetization in the xy plane until recovery of thermal equilibrium. Usually, T2 is considerably smaller than T1, thus the spin reorientation in the xy plane is much faster than in the z axis. However, as T1 decreases with increasing temperature, in some cases at higher temperatures both magnitudes could be similar. The spin qubit can be based on magnetic molecules that offer a high degree of tunability being highly reproducible nanoobjects. One of the spin quantum computer technologies is based on superconducting microwave resonator devices,7–9 where the spin state of magnetic systems can be controlled via microwave photons trapped in superconducting on-chip resonators.

The challenge to have efficient molecular spin qubits is to increase the coherence times, and the spin–lattice T1 relaxation time, which can be improved by analysing the magnetic anisotropy and the spin–phonon coupling. For molecular qubits, very large magnetic anisotropy is not an essential ingredient because it would fix the spin in a single direction and this is a fundamental difference in comparison with single-molecule magnets. Usually, the most critical time is T2 (or the related phase memory time Tm) that corresponds to the spin relaxation through spin–spin interactions, either electron–electron or electron–nuclear. Hence, dilution in diamagnetic matrices or solution using solvents with elements with or without reduced nuclear spin, for instance CS2 or deuterated solvents, helps to increase time coherence values. For the practical application of the qubits a figure of merit is proposed as the w1·Tm product, where w1 is the microwave Rabi nutation frequency and the value of the product should be around 104–105.4,10,11 The usual microwave ω1 values are around 107 s−1 (10 MHz), thus Tm (or in general T2) must be larger than 10−4 s (0.1 ms). A record value was obtained in solution with a deuterated vanadium complex [Ph4P]2[V(C8S8)3] using a nuclear spin-free ligand (C8S82− dithiolene)2 and a nuclear spin-free solvent CS2, to give a Tm value of 0.7 ms at 10 K. However, despite this case in solution (far of the conditions of electronic devices), typical studies systems, which are usually low spin ions such as VIV or CuII,2,12–20 have values around of 0.01–0.001 ms.4,21 Among the lanthanide compounds, probably the most experimentally studied system is a molecular spin qubit based on YbIII cations coordinated to a Schiff base (trensal ligand).22,23 A diluted powder sample in the LuIII analogue presents a T2 value of 0.005 ms. The challenge is to improve the coherence time in magnetic molecules, however, coherence times for such a molecular systems are still relatively far from those obtained in NV centres by doping diamond and silicon with N (or also P atoms) with T2 values reaching 1–5 ms at room temperature.24–26

The direct calculation of the spin relaxation times T1 and T2 from electronic structure methods is still an open challenge.27–29 There are many different parameters such as lattice vibrations, magnetic anisotropy, temperature, electron spin–spin interactions, spin nuclear effects and so on that play a fundamental role. Thus, the main goal of this study is to analyse the magnetic anisotropy of mononuclear YbIII complexes, in particular the case of the [Yb(trensal)] complex,23,30 in order to predict which complexes could exhibit good properties as molecular qubits and also, to detect in which cases we can have large magnetic anisotropy despite the 4f13 configuration of such a cation.

2. Computational details

Electronic structure calculations were performed on a series of YbIII complexes using the experimental structures obtained by X-ray diffraction (see Fig. 1), some of them showing slow relaxation of the spin under an external magnetic field (single-molecule magnets), [Yb(trensal)],30 [YbCp*(DAD)(THF)]31 and [Yb(Tpz)2(Bpz)].32
image file: d0cp05422d-f1.tif
Fig. 1 The seven YbIII complexes studied, the first three systems are field-induced single-molecule magnets and the magnetic characterization of the other four systems has not been reported. Ytterbium, phosphorous, silicon, oxygen, nitrogen, carbon and boron atoms are represented in cyan, purple, dark grey, red, blue, light grey and pink, respectively. Hydrogen atoms have been hidden for simplicity.

The calculations were made at the CASPT2 level with the program MOLCAS 8.033 using an active space with seven f orbitals and 13 electrons. The effects of spin–orbit coupling were included through restricted active space state interaction (RASSI).34 The corresponding ANO-RCC basis sets including relativistic corrections35 with an orbital contraction at the TZV level were used for different elements: Yb {8s7p4d3f2g}, B, C, N, O {4s3p2d1f} and H {2s1p}. With the code SINGLE_ANISO,36–38 included in MOLCAS, the different spin relaxation paths were analysed (tunnelling effect through the fundamental state and the different excited states and the Orbach mechanism) these being the integral between the two states involved with the magnetic moment operator as proposed by Fermi's golden rule. Other spin relaxation mechanisms, such Raman or direct contributions, are not easily quantified using electronic structure calculations. Moreover, for these systems the tunnelling relaxation is the essential mechanism in most of the predicted systems. Furthermore, the crystalline field parameters of the fundamental multiplet of YbIII and the anisotropy of the g-tensor for the fundamental state were calculated. In addition, the magnetisation and susceptibility of the different compounds were also obtained with this code. Such magnitudes are calculated as an average of different directions so that it could be compared with the available experimental powder information to check the accuracy of the theoretical approach. Once the methodology was validated, the same CASPT2/RASSI/SINGLE_ANISO calculations were carried out in the models created ([Yb(H2O)n]3+ and [Yb(OH)3(H2O)n−3]).

Finally, a series of YbIII systems without experimental measures of spin relaxation were studied, [Yb(DBP)3],39 [YbCp3],40 [Yb(NPPh3)4]−41 and [Yb(CH2SiMe3)3(THF)2]42 (see Fig. 1). The calculations in the systems [Yb(DBP)3], [Yb(CH2SiMe3)3(THF)2] and [Yb(NPPh3)4]− were performed only at the CASSCF level because the calculation at the CASPT2 level becomes computationally inaccessible due to their size. The corresponding ANO RCC bases were used with the following orbital contractions Yb {8s7p4d3f2g}, Si, P {5s4p2d1f}, C, N, O {4s3p2d1f} and H {2s1p}.

3. Results and discussion

3.1 Validation of the theoretical approach

The electronic structure of the YbIII cations 2F7/2. (S = 1/2, L = 3, J = 7/2) has low magnetic anisotropy and the shape of the electron density for the mJ = 7/2 is slightly prolate that becomes gradually oblate for mJ = 1/2. The relative stabilization of the mJ state can be tuned by the spatial distribution of the ligands in order to reduce the electrostatic metal–ligand repulsion.43–45 Negative ligands in equatorial positions would stabilize the prolate mJ = 7/2 configuration while the opposite behavior should be found if the charged ligands are in axial positions. The calculation of the 13f configuration is more difficult than the usual SMM lanthanides, i.e. DyIII and TbIII cations due to the larger interelectronic repulsion due to the higher number of electrons in the f orbitals. Thus, if for DyIII and TbIII cations usually the CASSCF method is enough to have a proper description of the system, the inclusion of the dynamic correlation is usually required for YbIII complexes.5 In Fig. S1 (ESI†), the experimental and calculated magnetizations and susceptibilities are compared. A reasonable agreement is found. For the [Yb(trensal)] complex,23,30 more experimental information is available to perform the comparison with the theoretical data. EPR data (g⊥ = 3.80 and g‖ = 4.99) and the theoretical CASPT2/RASSI results (g = 2.90 and g = 4.29) show a similar ratio between both values but those calculated are smaller. In addition, an excellent agreement in the state energies is obtained from emission/absorption experiments (see Fig. 2).30
image file: d0cp05422d-f2.tif
Fig. 2 Representation of the gz component for the [Yb(trensal)] complex and the experimental energy for the excited states (blue) and the calculated CASPT2/RASSI values (red). The energy values correspond to the splitting of the four Kramers doublets of the 2F7/2 state (energy ordered by the mJ values, |mJ| = 7/2 being the most stable).

The gz component of the [Yb(trensal)] complex is aligned with the C3 axis (see Fig. 2) due to the longest axial Yb–N bond distance (2.705 Å) while the equatorial distances are shorter (Yb–O 2.166 Å and Yb–N 2.431 Å). This coordination sphere favors the orientation of the prolate f electron density with such a C3 axis to reduce the metal–ligand electron repulsion. These results confirm that such a compound does not have a large magnetic anisotropy (maximum gz value should be 8 for the YbIII configuration with J = 7/2) as it is required for qubit molecules.

3.2 Analysis of the magnetic anisotropy for different coordination modes

In this section, the goal is to analyze which ones are the usual coordination modes of the mononuclear YbIII complexes and to check the magnetic anisotropy for such structures. Thus, the first step is to search in the Cambridge Structural Database46 by the coordination number of such a cation and lately, with the help of the Shape program47,48 for each coordination number to classify the structures in their coordination polyhedron. The search in the database of the mononuclear YbIII complexes was performed using as a criterion discrete molecules containing only one metal cation (and neglecting the YbII cations). The results are indicated in Fig. 3, showing that the most abundant coordination numbers are from 6 to 9, coordination 8 being especially frequent. The analysis using the Shape code for each coordination number is included in the ESI,† and the most common systems are those included in Fig. 4 together with those coordination modes that we can expect should present appealing magnetic anisotropy properties.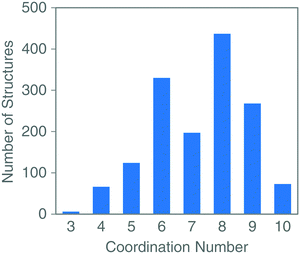
image file: d0cp05422d-f3.tif
Fig. 3 Number of mononuclear YbIII complexes for each coordination number found on the Cambridge Structural Database.

image file: d0cp05422d-f4.tif
Fig. 4 Selected coordination polyhedron to analyse the magnetic anisotropy using multiconfigurational methods with their coordination number (c.n.) and the number of structures (n.s.) found in the CSD.

For the selected structures shown in Fig. 4, we performed CASPT2/RASSI calculations using [Yb(H2O)n]3+ models to determine the g components and using the SINGLE_ANISO module we checked the main mechanism for spin relaxation. The results are presented in Fig. 5; there are 9 coordination modes where the gz value (or g‖, green dots in Fig. 5) is close to 8, and consequently they should present relatively large axial anisotropy. Such coordination modes would be those proposed to have large magnetic anisotropy, and they should be good candidates to present SMM behaviour. It is important to keep in mind that for qubits intermediate anisotropy values are required ([Yb(trensal)] has g‖ = 4.99); from Fig. 5, there are six coordination modes with g‖ in the range of around 4 to 6.


image file: d0cp05422d-f5.tif
Fig. 5 Histogram for all [Yb(H2O)n]3+ models as labelled in Fig. 4 showing the results obtained at the CASPT2/RASSI level. The g components (g‖, green dots; g⊥, orange dots). The horizontal lines correspond to the energy of Kramers doublets, highlighting in color the state through which the relaxation of the spin is taking place: (red) through the quantum tunneling effect; (blue) through the Orbach type mechanism; (violet) or a mixture of both. The black horizontal line at 0.5 g value highlights the limit of the g⊥ value from which the quantum tunneling effect starts to be relevant.

The analysis of the spin relaxation mechanism can also provide useful information. Thus, in Fig. 5 the main mechanism is indicated by colouring the states in the energy diagram. The spin relaxation mechanism is determined from the matrix elements of the transition magnetic moments49 between both states computed with the SINGLE_ANISO module. In most of the cases, the main mechanism is tunnelling in the ground state. If the g⊥ value is smaller than 0.5 (see the horizontal black line in Fig. 5) the tunnelling in the ground state is not the main mechanism. The analysis of the geometry of the six cases (see Fig. 6) with the g⊥ value is smaller than 0.5 indicates that structures with no axial ligands in the z direction, 31 and 41 are those with a higher spin inversion barrier close to 800 cm−1. These results fit well with the simple oblate/prolate model,43 because the prolate YbIII electron density can be aligned with the z direction with no electrostatic repulsions in the axial direction. Similar conclusions can be extracted from Table S1 (ESI†) with the systems with the highest axial anisotropy identified as those with a larger percentage of the MJ = 7/2 state in the ground state.


image file: d0cp05422d-f6.tif
Fig. 6 Geometries of the six coordination modes of [Yb(H2O)n]3+ models showing the spin relaxation mechanism through excited states predicted from CASPT2/RASSI calculations and that are expected to be good candidates to have SMM behavior (see Fig. 5).

Taking into account that experimentally in many cases the YbIII complexes are neutral, we have adopted a new model [Yb(OH)3(H2O)n−3]. Due to the large variety of modes to place the three hydroxo ligands in the coordination sphere a total number of 107 complexes were calculated (see Fig. S10 and Tables S2–S4, ESI†). There are 26 cases with a spin relaxation mechanism different than the quantum tunneling in the ground state (in black bold Tables S2–S4, ESI†). Among these, only in 4 of them the relaxation is via quantum tunneling through the first excited state. In the rest the Orbach mechanism also contributes to the relaxation pathway. Thus, such 4 cases are the best candidates to present SMM behavior even without an external field that cancels some quantum tunneling effects and are presented in Fig. 7.


image file: d0cp05422d-f7.tif
Fig. 7 (top) Four geometries of the coordination spheres of [Yb(OH)3(H2O)n−3] models for which the spin relaxation mechanism through excited states predicted from CASPT2/RASSI calculations and that are expected to be good candidates to have SMM behavior. The gray spheres indicate the position of the hydroxo ligands. (bottom) Representation of the g components (g‖, green dots; g⊥, orange dots). The horizontal lines correspond to the energy of Kramers doublets, highlighting in color the state through which the relaxation of the spin is taking place: (red) through the quantum tunneling effect; (blue) through the Orbach type mechanism; (violet) or a mixture of both. The black horizontal line at 0.5 g value marks the limit of the g⊥ value from which the quantum tunneling effect starts to be relevant.

The expected spin inversion barriers are relatively high, and it is worth to remark that logically the increase of the charge in the equatorial ligands, see for instance 31 cases (Fig. 5 and 7), results in an increase from 650 cm−1 for [Yb(H2O)3]3+ to 1400 cm−1 for [Yb(OH)3] due to the electrostatic metal–ligand repulsion. The inclusion of the charged hydroxo ligands results in an increase of the axiality, thus, among the 107 studied complexes (Tables S2–S4, ESI†) only six complexes show intermediate gz values (in the range of 4–6). From previous results, localization of the negatively charged ligands in equatorial positions leads to an increase of the axial character of the magnetic anisotropy. In Table 1, we have collected the reported magnetic data corresponding to the mononuclear YbIII complexes. No zero-field YbIII SMM have been reported among the experimental data; it is also worth remarking that [Yb(trensal)] has the largest effective barrier despite a moderate magnetic anisotropy and the short τ0 value. The relationship between these two magnitudes is not straightforward as pointed out by Castro-Alvarez et al.50 but such values are consistent with the ability to have slow spin dynamics at low temperatures because the Orbach contribution is only predominant above 6 K. Below such temperature other spin relaxation mechanisms such as Raman processes are leading. We have analyzed the distribution of charged ligands in the compounds reported in Table 1 (see Fig. S11, ESI†) but there are no complexes with all the charged ligands in the equatorial position that would enhance the axiality of the magnetic anisotropy.

Table 1 Reported mononuclear YbIII complexes showing field induced SMM (in Oe) indicating the coordination number, the geometry of the first coordination sphere according to the Shape program, the external field required Hdc for the SMM behavior, the inversion barrier Ueff (in cm−1) and the prefactor of the Orbach relaxation term (in s). See acronyms in the ESI
Complex N.C. Shape H dc U eff τ 0 Ref.
{[YbIII(3-pyridone)2(H2O)2][CoIII(CN)6]} 6 OC-6 1000 31 2.7 × 10−7 51
[YbFc3(THF)2Li2]− 6 TP-6 2000 6 9.0 × 10−5 52
[Yb(μ3-OH)(na)(pyzc)]n 7 CTPR-7 3000 10 2.1 × 10−7 53
[Yb(trensal)] 7 COC-7 2000 38 1.5 × 10−8 30
[Yb(C29H41N8O9)] 7 PBPY-7 1600 15 5.4 × 10−7 54
[Yb(BcrCOO)(acac)2(H2O)]n 7 PBPY-7 2000 25 1.5 × 10−7 55
[Yb(tta)2(L1)(L2)]2 8 TDD-8 2000 15 1.7 × 10−6 56
[Yb2L33(CH3OH)] 8 TDD-8 3000 15 1.6 × 10−6 57
[Yb2(DBM)6(L4)] 8 SAPR-8 2000 16 7.9 × 10−7 58
[Yb(Tpz)2(Bpz)] 8 BTPR-8 1500 20 2.0 × 10−8 32
[Yb{Mo5O13(OMe)4NNC6H4-p-NO2}2]3− 8 SAPR-8 1000 16 6.7 × 10−6 59
[Yb(dnbz)(acac)2(H2O)(EtOH)]2 8 SAPR-8 2000 18 2.8 × 10−7 60
[YbCp*(DAD)(THF)] 8 — 1500 14 1.7 × 10−6 31
[Yb2(2-FBz)6(phen)2] 8 BTPR-8 2000 5 9.3 × 10−6 61
β-Yb(2-qpH)(SO4)(H2O)2 8 TDD-8 2000 8 8.6 × 10−6 62
[{Yb(apdo)-(H2O)4}{Co(CN)6}]·2H2O 8 TDD-8 700 11 3.2 × 10−6 63
{[Yb(terpy)(H2O)3][Co(CN)6]·5H2O}n 8 TDD-8 1000 24 1.7 × 10−7 64
[Yb(tmh)3(μ3-HAT)] 8 SAPR-8 1000 15 3.7 × 10−7 65
[Yb(PyrCOO)(acac)2(H2O)2] 8 SAPR-8 2000 38 7.4 × 10−8 66
[Co2Yb2(OCH3)2(teaH)2(Piv)6] 8 SAPR-8 1500 23 2.1 × 10−6 67
[Yb2L3(OAc)4(CH3OH)2] 8 SAPR-8 JBTPR-8 3000 9 4.8 × 10−6 57
[Yb2L3L5L6(CH3OH)(H2O)2](ClO4)2 8 SAPR-8 JBTPR-8 3000 2 1.0 × 10−5 57
{[Yb(L7)(H2O)3(DMF)]·(HL7)·(H2O)}n 8 SAPR-8 1000 20 3.4 × 10−7 68
2 2.0 × 10−4
{[Yb2L3(OAc)4]·3H2O}n 8 9 TDD-8 MFF-9 3000 2 3.7 × 10−5 57
[Yb(H2O)5(NCS)3]·H2O 8 SAPR-8 2500 35 2.3 × 10−8 69
[Yb(H2O)(bpy)2(NCS)3]·0.5(bpy)·H2O 8 SAPR-8 1000 33 1.7 × 108 69
[Yb(H2O)(phen)2(NCS)3]·phen·0.5H2O 8 SAPR-8 1000 15 4.5 × 10−7 69
[Hphen][Yb(phen)2(NCS)4] 8 SAPR-8 1000 26 8.4 × 10−8 69
[Yb2(C114H70N4O12)] 9 CSAPR-9 1500 23 4.7 × 10−7 70
[Yb2(μ2-2-FBz)2(2-FBz)4(terpy)2]2(H-2-FBz)2(H2O) 9 CSAPR-9 1000 16 7.6 × 10−7 71
[YbL28(tmh)(CH3OH)]·nH2O·mCH3OH 9 CSAPR-9 1000 21 3.5 × 10−7 71
[YbL83]·CH3OH 9 CSAPR-9 1000 8 4.6 × 10−6 71
[YbL82(tta)(CH3OH)]·CH3OH 9 CSAPR-9 1000 21 2.0 × 10−7 71
[Yb2(μ2-9-AC)4(9-AC)2(bpy)2] 9 MFF-9 500 16 7.4 × 10−7 72
[Zn(μ-L9)(μ-OAc)Yb(NO3)2]·CH3CN 9 CSAPR-9 1000 13 5.5 × 10−8 73

Finally, we have analysed the structures of the reported YbIII mononuclear complexes that have no magnetic properties reported to look for good candidates to present appealing magnetic properties. According to previous results with the simplified structural model, we have focused on systems with low coordination numbers, the selected systems are [Yb(DBP)3],39 [YbCp3],40 [Yb(NPPh3)4]− (ref. 41) and [Yb(CH2SiMe3)3(THF)2]42 (see Fig. 1). The calculated results are collected in Fig. 8, three of the systems show a relatively axial character showing their spin relaxation through the first excited state, most notably the [Yb(DBP)3] complex that has three charged equatorial ligands has an expected inversion barrier of around 1000 cm−1. The magnetic properties of the [YbCp3] complex are considerably different, despite it being compared with a 3-cordinated complex, with a loss of the axial character due to the delocalization of the charge. The tetrahedral and trigonal bipyramid complexes have high axial character but the energy of their first excited state is lower than the one in the [Yb(DBP)3] complex.


image file: d0cp05422d-f8.tif
Fig. 8 Histogram for complexes [Yb(DBP)3], [YbCp3], [Yb(NPPh3)4]− and [Yb(CH2SiMe3)3(THF)2] labeled with the coordinated atoms YbO3, Yb(C5)3, YbN4 and YbC3O2, respectively with the results at CASPT2 or CASSCF/RASSI (see the Computational details section). Representation of the components for g are shown (g‖, green dots; g⊥, orange dots). The horizontal lines correspond to the energy of Kramers doublets, highlighting in color the state through which the relaxation of the spin is produced: (red) through the quantum tunneling effect; (blue) through the Orbach type mechanism; (violet) or a mixture of both. The black horizontal mark at the 0.5 g value marks the limit of the g⊥ value from which the quantum tunneling effect starts to be relevant.

4. Concluding remarks

YbIII complexes have been experimentally studied as molecular qubits, especially the [Yb(trensal)] complex. These compounds, despite having a 4f13 electron configuration and only one unpaired electron, are significantly different to usual S = 1/2 transition metal molecular qubits, such as those with VIV and CuII cations, because they must be described as J = 7/2 systems. The goal of our study was to explore different YbIII complexes to check their magnetic anisotropy, and consequently their spin dynamics. The first step was to verify with three experimental YbIII complexes, among them the [Yb(trensal)] complex, that the theoretical approach (CASPT2 including the spin–orbit effect with the RASSI method), can provide an accurate description of the magnetic properties of such systems. Once such verification was carried out, we have analysed in the Cambridge Structural Database the reported mononuclear YbIII complexes and their coordination sphere, focusing on the coordination number and the geometry of the coordination sphere. From this analysis, we have analysed the calculated magnetic properties for sixteen [Yb(H2O)n]3+ models. Such calculations indicate that in most cases, there is a strong spin relaxation through a quantum tunnelling mechanism in the ground state. This is consistent with the lack of zero-field single-molecule magnets in the family of mononuclear YbIII complexes. However, from such calculations a relatively high barrier above 600 cm−1 was predicted for trigonal planar and square planar YbIII complexes. Taking into account that many reported mononuclear YbIII complexes are neutral, we have also considered a [Yb(OH)3(H2O)n−3] model with three charged hydroxo ligands. The combination of water and hydroxo ligands, especially for the highest coordination numbers, results in a large number of possible complexes. Thus, one hundred seven systems were calculated, again few systems exhibit a spin relaxation through excited states: trigonal planar, trigonal bipyramid, square antiprism and triangular dodecahedron coordination modes. We have also analysed the distribution of the charged ligands in the reported mononuclear YbIII complexes with measured magnetic properties. There are no complexes with the same charge distribution that the synthetic targets predicted by our calculations. Hence, finally we have calculated four real complexes with no reported magnetic properties that, from what we have learnt from the model calculations, we expect they could present relatively high magnetic anisotropy. Among them, the [Yb(DBP)3] complex (DBP:2,6-di-t-butyl-phenoxide) with a trigonal planar coordination with three oxygen atoms seems to be the most promising prediction for some zero-field SMM candidates with a spin inversion barrier around 1000 cm−1. Finally, it is worth noting that lanthanide complexes with low coordination numbers have appealing magnetic properties. In some cases, as the popular DyIII complexes, the linear coordination74,75 geometry is the most interesting one, while in this case, with YbIII complexes, the trigonal planar structure seems more appealing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research reported here was supported by the Spanish Ministerio de Ciencia e Innovación (grants PGC2018-093863-B-C21 and MDM-2017-0767). E. R. thanks Generalitat de Catalunya for an ICREA Academia award and for the SGR2017-1289 grant. S. G.-C. thanks the Generalitat de Catalunya for a Beatriu de Pinós (grant 2017BP00080). M. A. acknowledges the Ministerio de Educación, Cultura y Deporte for an FPU predoctoral grant. The authors acknowledge computer resources, technical expertise and assistance provided by the CSUC.

References

  1. D. P. DiVincenzo, Fortschr. Phys., 2000, 48, 771–783 CrossRef .
  2. J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488–492 CrossRef CAS .
  3. E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef .
  4. M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS .
  5. D. Aravena and E. Ruiz, Dalton Trans., 2020, 49, 9916–9928 RSC .
  6. A. Abragam and B. Bleaney, Electron paramagnetic resonance of transition ions, Oxford Classic Texts, 2013 Search PubMed .
  7. M. D. Jenkins, D. Zueco, O. Roubeau, G. Aromí, J. Majer and F. Luis, Dalton Trans., 2016, 45, 16682–16693 RSC .
  8. C. Bonizzoni, A. Ghirri, K. Bader, J. van Slageren, M. Perfetti, L. Sorace, Y. Lan, O. Fuhr, M. Ruben and M. Affronte, Dalton Trans., 2016, 45, 16596–16603 RSC .
  9. C. Bonizzoni, A. Ghirri, M. Atzori, L. Sorace, R. Sessoli and M. Affronte, Sci. Rep., 2017, 7, 13096 CrossRef CAS .
  10. S. Bertaina, S. Gambarelli, A. Tkachuk, I. N. Kurkin, B. Malkin, A. Stepanov and B. Barbara, Nat. Nanotechnol., 2007, 2, 39–42 CrossRef CAS .
  11. Y.-S. Ding, Y.-F. Deng and Y.-Z. Zheng, Magnetochemistry, 2016, 2, 40 CrossRef .
  12. J. M. Zadrozny and D. E. Freedman, Inorg. Chem., 2015, 54, 12027–12031 CrossRef CAS .
  13. C. J. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 14678–14685 CrossRef CAS .
  14. M. S. Fataftah, M. D. Krzyaniak, B. Vlaisavljevich, M. R. Wasielewski, J. M. Zadrozny and D. E. Freedman, Chem. Sci., 2019, 10, 6707–6714 RSC .
  15. K. Bader, M. Winkler and J. van Slageren, Chem. Commun., 2016, 52, 3623–3626 RSC .
  16. S. Lenz, K. Bader, H. Bamberger and J. van Slageren, Chem. Commun., 2017, 53, 4477–4480 RSC .
  17. S. Lenz, B. Kern, M. Schneider and J. van Slageren, Chem. Commun., 2019, 55, 7163–7166 RSC .
  18. M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731–740 CrossRef CAS .
  19. L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Chem. Sci., 2016, 7, 2074–2083 RSC .
  20. L. Tesi, A. Lunghi, M. Atzori, E. Lucaccini, L. Sorace, F. Totti and R. Sessoli, Dalton Trans., 2016, 45, 16635–16643 RSC .
  21. S. Sproules, in Electron Paramagnetic Resonance, ed. V. Chechik and D. M. Murphy, 2017, vol. 25, pp. 61–97 Search PubMed .
  22. R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. S. Pedersen, R. De Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2018, 140, 9814–9818 CrossRef CAS .
  23. K. S. Pedersen, A. M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804 CrossRef CAS .
  24. M. V. G. Dutt, L. Childress, L. Jiang, E. Togan, J. Maze, F. Jelezko, A. S. Zibrov, P. R. Hemmer and M. D. Lukin, Science, 2007, 316, 1312–1316 CrossRef .
  25. A. Jarmola, V. M. Acosta, K. Jensen, S. Chemerisov and D. Budker, Phys. Rev. Lett., 2012, 108, 197601 CrossRef CAS .
  26. E. D. Herbschleb, H. Kato, Y. Maruyama, T. Danjo, T. Makino, S. Yamasaki, I. Ohki, K. Hayashi, H. Morishita, M. Fujiwara and N. Mizuochi, Nat. Commun., 2019, 10, 3766 CrossRef CAS .
  27. P. C. E. Stamp and I. S. Tupitsyn, Phys. Rev. B, 2004, 69, 014401 CrossRef .
  28. L. Escalera-Moreno and J. J. Baldovi, Front. Chem., 2019, 7, 662 CrossRef CAS .
  29. L. Escalera-Moreno, A. Gaita-Arino and E. Coronado, Phys. Rev. B, 2019, 100 Search PubMed .
  30. K. S. Pedersen, J. Dreiser, H. Weihe, R. Sibille, H. V. Johannesen, M. A. Sørensen, B. E. Nielsen, M. Sigrist, H. Mutka, S. Rols, J. Bendix and S. Piligkos, Inorg. Chem., 2015, 54, 7600–7606 CrossRef CAS .
  31. A. A. Trifonov, B. Shestakov, J. Long, K. Lyssenko, Y. Guari and J. Larionova, Inorg. Chem., 2015, 54, 7667–7669 CrossRef CAS .
  32. A. Lannes and D. Luneau, Inorg. Chem., 2015, 54, 6736–6743 CrossRef CAS .
  33. F. Aquilante, L. De Vico, N. Ferre, G. Ghigo, P. A. Malmqvist, P. Neogrady, T. B. Pedersen, M. Pitonak, M. Reiher, B. O. Roos, L. Serrano-Andres, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247 CrossRef CAS .
  34. P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS .
  35. B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS .
  36. L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137 Search PubMed .
  37. L. F. Chibotaru, in Molecular Nanomagnets and Related Phenomena, ed. S. Gao, 2015, vol. 164, pp. 185–229 Search PubMed .
  38. L. Ungur and L. F. Chibotaru, Chem. – Eur. J., 2017, 23, 3708–3718 CrossRef CAS .
  39. L. A. M. Steele, T. J. Boyle, R. A. Kemp and C. Moore, Polyhedron, 2012, 42, 258–264 CrossRef CAS .
  40. R. G. Denning, J. Harmer, J. C. Green and M. Irwin, J. Am. Chem. Soc., 2011, 133, 20644–20660 CrossRef CAS .
  41. T. Gröb, G. Seybert, W. Massa and K. Dehnicke, Z. Anorg. Allg. Chem., 2001, 627, 304–306 CrossRef .
  42. M. Niemeyer, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2001, 57, m553–m555 CrossRef CAS .
  43. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC .
  44. D. Aravena and E. Ruiz, Inorg. Chem., 2013, 52, 13770–13778 CrossRef CAS .
  45. N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551 CrossRef .
  46. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 2002, 58, 380–388 CrossRef .
  47. S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693 CrossRef CAS .
  48. M. Llunell, D. Casanova, J. Cirera, J. M. Bofill, P. Alemany, S. Alvarez, M. Pinsky and D. Avnir, SHAPE, Universitat de Barcelona, 2003 Search PubMed .
  49. L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Inorg. Chem., 2013, 52, 6328–6337 CrossRef CAS .
  50. A. Castro-Alvarez, Y. Gil, L. Llanos and D. Aravena, Inorg. Chem. Front., 2020, 7, 2478–2486 RSC .
  51. S. Chorazy, M. Rams, J. Wang, B. Sieklucka and S.-i. Ohkoshi, Dalton Trans., 2017, 46, 13668–13672 RSC .
  52. T. P. Latendresse, V. Vieru, A. Upadhyay, N. S. Bhuvanesh, L. F. Chibotaru and M. Nippe, Chem. Sci., 2020, 11, 3936–3951 RSC .
  53. Y. Li, J.-W. Yu, Z.-Y. Liu, E.-C. Yang and X.-J. Zhao, Inorg. Chem., 2014, 54, 153–160 CrossRef .
  54. M. Fondo, J. Corredoira-Vázquez, A. M. García-Deibe, J. Sanmartín-Matalobos, M. Amoza, A. M. P. Botas, R. A. S. Ferreira, L. D. Carlos and E. Colacio, Inorg. Chem. Front., 2020, 7, 3019–3029 RSC .
  55. A. V. Gavrikov, P. S. Koroteev, N. N. Efimov, Z. V. Dobrokhotova, A. B. Ilyukhin, A. K. Kostopoulos, A.-M. Ariciu and V. M. Novotortsev, Dalton Trans., 2017, 46, 3369–3380 RSC .
  56. F. Pointillart, B. L. Guennic, S. Golhen, O. Cador, O. Maury and L. Ouahab, Chem. Commun., 2013, 49, 615–617 RSC .
  57. T.-Q. Liu, P.-F. Yan, F. Luan, Y.-X. Li, J.-W. Sun, C. Chen, F. Yang, H. Chen, X.-Y. Zou and G.-M. Li, Inorg. Chem., 2014, 54, 221–228 CrossRef .
  58. O. Sun, P. Chen, H.-F. Li, T. Gao, W.-B. Sun, G.-M. Li and P.-F. Yan, CrystEngComm, 2016, 18, 4627–4635 RSC .
  59. J. J. Baldoví, Y. Duan, C. Bustos, S. Cardona-Serra, P. Gouzerh, R. Villanneau, G. Gontard, J. M. Clemente-Juan, A. Gaita-Ariño, C. Giménez-Saiz, A. Proust and E. Coronado, Dalton Trans., 2016, 45, 16653–16660 RSC .
  60. A. V. Gavrikov, N. N. Efimov, A. B. Ilyukhin, Z. V. Dobrokhotova and V. M. Novotortsev, Dalton Trans., 2018, 47, 6199–6209 RSC .
  61. B. Casanovas, M. Font-Bardía, S. Speed, M. S. El Fallah and R. Vicente, Eur. J. Inorg. Chem., 2018, 1928–1937 CrossRef CAS .
  62. D. Zeng, M. Ren, S.-S. Bao, Z.-S. Cai, C. Xu and L.-M. Zheng, Inorg. Chem., 2016, 55, 5297–5304 CrossRef CAS .
  63. S. Chorazy, M. Zychowicz, S.-i. Ohkoshi and B. Sieklucka, Inorg. Chem., 2018, 58, 165–179 CrossRef .
  64. S. P. Petrosyants, A. B. Ilyukhin, N. N. Efimov, A. V. Gavrikov and V. M. Novotortsev, Inorg. Chim. Acta, 2018, 482, 813–820 CrossRef CAS .
  65. I. F. Díaz-Ortega, J. M. Herrera, T. Gupta, G. Rajaraman, H. Nojiri and E. Colacio, Inorg. Chem., 2017, 56, 5594–5610 CrossRef .
  66. A. V. Gavrikov, N. N. Efimov, Z. V. Dobrokhotova, A. B. Ilyukhin, P. N. Vasilyev and V. M. Novotortsev, Dalton Trans., 2017, 46, 11806–11816 RSC .
  67. A. V. Funes, L. Carrella, Y. Rechkemmer, J. van Slageren, E. Rentschler and P. Alborés, Dalton Trans., 2017, 46, 3400–3409 RSC .
  68. A. Belio Castro, J. Jung, S. Golhen, B. Le Guennic, L. Ouahab, O. Cador and F. Pointillart, Magnetochemistry, 2016, 2, 26 CrossRef .
  69. S. P. Petrosyants, K. A. Babeshkin, A. V. Gavrikov, A. B. Ilyukhin, E. V. Belova and N. N. Efimov, Dalton Trans., 2019, 48, 12644–12655 RSC .
  70. B. Casanovas, S. Speed, O. Maury, M. Font-Bardía and R. Vicente, Polyhedron, 2019, 169, 187–194 CrossRef CAS .
  71. J.-R. Jiménez, I. F. Díaz-Ortega, E. Ruiz, D. Aravena, S. J. A. Pope, E. Colacio and J. M. Herrera, Chem. – Eur. J., 2016, 22, 14548–14559 CrossRef .
  72. B. Casanovas, S. Speed, O. Maury, M. S. El Fallah, M. Font-Bardía and R. Vicente, Eur. J. Inorg. Chem., 2018, 3859–3867 CrossRef CAS .
  73. I. Oyarzabal, B. Artetxe, A. Rodríguez-Diéguez, J. Á. García, J. M. Seco and E. Colacio, Dalton Trans., 2016, 45, 9712–9726 RSC .
  74. N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, Chem. Commun., 2015, 51, 101–103 RSC .
  75. S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289, 379–392 CrossRef .

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05422d
This journal is © the Owner Societies 2021
Click here to see how this site uses Cookies. View our privacy policy here.