Emerging investigator series: modeling of wastewater treatment bioprocesses: current development and future opportunities
Shiyun
Yao
 ,
Cheng
Zhang
,
Cheng
Zhang
 and
Heyang
Yuan
and
Heyang
Yuan
 *
*
Civil & Environmental Engineering, Department of Civil and Environmental Engineering, Temple University, 1947 N. 12th St, Philadelphia, PA 19122, USA. E-mail: heyang.yuan@temple.edu
First published on 9th December 2021
Abstract
For more than a half-century, modelers have developed various modeling strategies to facilitate the transition of wastewater treatment bioprocesses from lab-scale demonstration to full-scale applications. This review presents the mathematical fundamentals of mechanistic models, machine learning algorithms of data-driven models, and hybrid modeling strategies for different biological wastewater treatment systems including activated sludge processes, anaerobic digesters, anammox processes, and bioelectrochemical systems. The discussion is focused on the biological principles in those modeling strategies. The conventional Monod expressions are a prevailing tool to describe the mathematical connection between microbial kinetics and state variables in mechanistic models. Stoichiometric equations and steady-state conditions are also required for the mechanistic modeling approach to predict system performance such as the removal of carbon, nitrogen, and phosphorus. On the other hand, data-driven models statistically link the inputs and outputs for the prediction and optimization of system performance with a minimum requirement of a priori knowledge. Although this strategy shows outstanding learning ability of data interpolation, the predictions are often uninterpretable due to the black-box nature. Hybrid modeling strategies have the potential to address the inherent limitations of standalone models. Currently, the mechanistic and data-driven components in hybrid models are still structured based on microbial kinetics and trained with physical and biochemical data, respectively. This problem can be potentially solved by incorporating genomics data into model construction to link microbial kinetic to microbial population and functional dynamics. We discuss the perspectives of incorporating genomic data into model construction and propose genomics-enabled hybrid modeling strategies for future research.
Water impactWastewater treatment bioprocesses are conventionally modeled using mechanistic, data-driven, or hybrid models. Herein, we identify the knowledge gaps in those models. We also propose potential modeling strategies to incorporate genomic data for handling a large amount of the physical, biochemical, and microbiological data collected from biological wastewater treatment systems, with the overarching goal to achieve real-time monitoring and optimize system performance. |
1. Introduction
A variety of wastewater treatment systems are developed to harness microorganisms to remove organic contaminants and nutrients.1 These include activated sludge processes, anaerobic digesters, and membrane bioreactors that have been extensively applied in full-scale treatment plants, as well as emerging technologies such as anaerobic ammonium oxidation (anammox) and bioelectrochemical systems. By taking advantage of the metabolic versatility of microorganisms, some of those systems can be engineered to achieve sustainable treatment of complex waste streams. For example, anammox as an anaerobic and autotrophic process converts ammonia to nitrogen gas with little energy input,2 and bioelectrochemical systems can recover energy and resource from waste streams.3Biological wastewater treatment systems are commonly monitored using real-time biochemical data such as biological oxygen demand (BOD), chemical oxygen demand (COD), and mixed liquor volatile suspended solids (MLVSS) as an indication of biomass concentration.4–6 This is an operationally simple method that leads to a quick assessment of the microbiological activity and system performance. However, those macroscopic state variables sometimes do not help explain the inconsistency in treatment performance caused by environmental and operational perturbations, primarily because they are unable to reflect the complex microbial physiology, community structure, metabolism, and interspecies interactions in the systems.4 As conventional bioprocesses face challenges from emerging pollutants and more stringent discharge limits over the past decades,5 real-time monitoring and experimental trials are laborious and frequently fall short to provide insights into system optimization.
The high complexity of bioprocesses and the pressing need to develop more sustainable systems drive environmental researchers and engineers to build computational models to gain mechanistic and predictive understandings of the dynamic behaviors in the systems. A prevailing strategy is to build mechanistic models, also known as white-box or first-principle models, based on the mathematical expressions of the physical/chemical/biological principles of the processes involved.8 This modeling strategy starts with defining the model purpose followed by model structure selection, input identification, data collection/reconciliation, and model calibration/correction.9 To improve the robustness of mechanistic models, it is important to understand the fundamental microbial kinetics. Monod expressions are the most well-established tool for modeling microbial growth and substrate utilization kinetics and have been extensively applied to simulate many bioprocesses.10–15 The kinetic parameters in Monod equations are commonly derived from biochemical measurements.16 For ill-defined systems that are driven by uncharacterized functional populations, it becomes challenging to determine which biochemical indicators to measure to reliably reflect their growth and substrate utilization kinetics.
Data-driven models seek to establish statistical connections between the inputs and outputs and require little knowledge about the fundamental principles of the processes involved. This is of great interest to the modeling of bioprocesses, in which the lifestyles of many functional populations remain unknown.17 Data-driven modeling strategies started to attract environmental/biological engineers' attention in the early 90s with the practical implementation of artificial neural networks (ANNs) and major advances in machine learning.18–20 Using appropriate training datasets and network architecture, neural networks were trained to directly predict wastewater treatment performance,20,21 as well as the effects of sludge volume index and total nitrogen concentration on the effluent quality.22 Recent studies demonstrated the applicability of several machine learning algorithms, including support vector machine, random forest, extreme gradient boosting, and k-nearest neighbors, to full-scale digesters.23 Those algorithms have also been used to train models with biochemical data collected from literature, presenting a powerful tool for data mining.24 Despite the outstanding learning performance, data-driven models are black boxes that often generate uninterpretable predictions.25 This is particularly problematic for bioprocesses when the models are trained solely with physical and biochemical data.21–23,26
Hybrid models are built through the integration of mechanistic and data-driven sub-models to improve the shortcomings of those individual modeling strategies.27 Hybrid models are ideal for ill-defined systems in which only part of the process can be mechanistically described (e.g., the mass balance of measurable biochemical variables), while another part of the process is too complicated to be derived from first principles (e.g. microbial interactions).28 Depending on the significance of the known and unknown processes in a system, the mechanistic and data-driven sub-models can be integrated through parallel, in series, or a mix of both structures.29 Such integration allows the designer to structure the model more flexibly based on the availability of the a priori knowledge.28 Recent studies demonstrate that hybrid models are more accurate and flexible in predicting the dynamic behaviors of wastewater treatment bioprocesses.30,31
This review discusses the applications and drawbacks of major modeling approaches that have been developed for simulating wastewater treatment bioprocesses over the past 60 years in chronological order (Fig. 1). We first review the mechanistic modeling of several systems including activated sludge processes, anaerobic digesters, anammox, and bioelectrochemical systems. The discussion of this modeling strategy is focused on the biological principles, in particular microbial growth and substrate utilization kinetics. In the following sections, we review data-driven models capable of capturing the dynamic behaviors of bioprocesses, as well as hybrid models that take advantage of both modeling strategies (Fig. 2). We also discuss the potential of incorporating high-throughput sequencing data into model construction to unfold the underlying interactions among microbial kinetics, community structure, and functional dynamics. Finally, we propose a conceptual framework to build hybrid models with omics-based results for robust and interpretable prediction of microbial interactions and wastewater treatment performance.
2. Mechanistic modeling of wastewater treatment bioprocesses
2.1 Early development of microbial kinetic model
Microbial growth is impacted by several factors such as cell metabolic activity, substrate availability, oxygen concentration, temperature, etc. Among them, the substrate is arguably the most important one as it is directly involved in cell metabolism.32 To model the kinetic behaviors of microbial growth, a greater understanding of the effects of substrate concentration on metabolic quotients, specific growth rate, and yield is required. Between the 1920s and 1960s, many hypotheses and models were proposed to explain the biological mechanisms of substrate consumption for cellular metabolism and storage.33The Monod equation is a microbial kinetic model that describes the hyperbolic growth behavior of microbes in batch systems at exponential and steady-state phases.16 In the Monod equation, the specific growth rate of a culture is a function of the concentration of a given substrate,34 with the substrate saturation constant (i.e., the substrate concentration when the specific growth rate is half of the maximum specific growth rate) indicating the affinity of the substrate to cell growth.16 The Monod equation and its modified expressions were demonstrated to be robust for modeling different pure cultures under varied conditions.35 Since then, a variety of mechanistic models have been built on Monod expressions.10,13,36–38
Several studies pointed out the inadequacy of the original Monod expression in dealing with substrate inhibition, cell decay, diffusional limitation, etc.36,39 Substrate inhibition as a common issue arises when the complex composition in wastewater shows different affinity to microbial cells, leading to competition among functional populations and/or inhibition to cell growth. The Haldane–Andrews equation included an inhibition constant in the Monod expression to reflect substrate inhibition.36 However, because the constant is inferred through the generalized substrate inhibition model, a normal distribution method with an error range, such a modification does not reveal the actual impacts of substrate inhibition on microbial growth.40
2.2 Modeling of activated sludge processes
The activated sludge models have been developed for more than 70 years since the early 60s.11 Early mechanistic models were derived based on steady-state applications in which the cell growth rate remained constant.34 The biochemical parameters used to quantify cell growth were total organic carbon (TOC), total oxygen demand (TOD), and COD along with 5 day BOD.41 They are sufficient for modeling steady-state conditions but have severe limitations in real-time situations where cell growth behaves dynamically under the influence of substrate variation. Oxygen uptake rate and mixed liquor volatile suspended solid were later included to address the limitation.36,41 Mathematical techniques such as the feedforward–feedback strategy were also applied to control the flowrate disturbance. These modifications allowed mechanistic models to respond to dynamic situations with real-time biochemical data.41In 1982, the International Association on Water Pollution Research and Control published a preliminary model on activated sludge systems. Later, Dold and Marais incorporated the preliminary model to a final version called the Activated Sludge Model No. 1 (ASM1).12,42 ASM1 is considered a reference model and is generally accepted as a fundamental component for wastewater treatment modeling.43 In particular, the Monod equation in ASM1 was proven reasonably appropriate to describe the microbial growth and substrate utilization behaviors in wastewater.44
The microbiological principles of ASM1 include the growth of aerobic and anoxic heterotrophic organisms, the growth of aerobic autotrophic organisms, the decay of heterotrophs and autotrophs, hydrolysis of slowly biodegradable substrate, ammonification, and hydrolysis of organic nitrogen.10 In addition, the model also describes the following dynamic mass balances that have impacts on biomass concentration: 1) readily biodegradable substrates, 2) slowly biodegradable substrates, 3) inert particulate substances, 4) particulate organic nitrogen, 5) soluble organic nitrogen, 6) ammonia, 7) nitrate, and 8) oxygen.10 These state variables serve as explicit indicators of the nutrient removal processes. Among all parameters used in ASM1, the growth and decay rates are of key importance as they control the biomass concentration as a function of the influent substrate concentration. The full description of ASM1 and the comprehensive review of model development can be found elsewhere.8,10 The robustness of ASM1 has been demonstrated by numerous studies. Forty years after its first implementation, ASM1 is still playing a central role in the mechanistic modeling of bioprocesses and has been incorporated in commercial software as a core structure for the simulation of full-scale wastewater treatment plants.45
Advancing from ASM1, ASM2 incorporates polyphosphate-accumulating organisms (PAO), a functional population enriched during enhanced biological phosphorus removal in activated sludge systems. In addition to common microbial kinetics, the model structure for PAO also includes the storage of glycogen, polyhydroxyalkanoate, and polyphosphate, which are expressed as a function of oxygen availability according to their physiological traits.46 In the 1990s, ASM2d was developed based on ASM2 by including the ability of PAOs to use internal cellular materials for denitrification,10 thus linking the metabolism of nitrate and phosphorous under anoxic conditions. In the absence of oxygen, PAOs can use nitrate as a terminal electron acceptor for phosphorous uptake.10,47 In ASM2d, a fraction of the maximum growth rate of PAO is assigned to complete denitrification. The fraction varies depending on PAOs' activity including growth, denitrification, and anoxic phosphorus uptake.48 ASM2 and ASM2d are comprehensively reviewed by Henze et al.10
ASM3 was modified to improve the prediction of oxygen consumption, sludge production, nitrification, and denitrification. Key modifications include cellular storage of organic substrates and the consumption of dead cells through endogenous respiration (instead of the decay and recycling processes described by ASM1).37 With these modifications, ASM3 is more accurate in describing the substrate uptake and storage behaviors, but the enhanced prediction may not be relevant for most treatment plants where ASM1 is sufficient for simulation of general performance.46 Therefore, ASM3 is needed only when specific metabolic activities are modeled.
There are several commercial software packages available to simulate the activated sludge processes following the development of ASM1/2/3. Olsson and Newell provided a detailed overview of the simulator environments for the bioprocesses in wastewater treatment plants.49 Some of the simulators, such as MATLAB-based Simulink, serve a general purpose with high flexibility to complete simulation. Other simulators contain a library of predetermined models for specific bioprocesses, and the process configuration is a unit-based simulation environment. Examples of this type of simulator are AQUASIM, BioWin, EFOR, GPS-X, SIMBA, STOAT, and WEST. The computation package can solve mechanistic models with multiple mathematical equations simultaneously.50 BioWin, for example, is a flexible software tool that includes multiple microbial processes presented in ASMs and anaerobic digestor models (ADMs).51–55 It has been used to model the biological systems in full-scale wastewater treatment plants,52–55 including activated sludge,56 anaerobic digestion,57,58 and anammox processes.51 In some of the studies, BioWin provided a good match between the measured and predicted data (difference <10%) for both small-scale batch reactors and full-scale systems,56–58 and it can perform optimization of sludge retention time and nitrogen removal under different DO and return activated sludge flows.53 In most of the studies, however, model calibration is required to improve the prediction performance. Improper calibration, for example, with nitrogen, phosphorus, and other microbial inhibitory substances has been reported to cause inaccurate prediction of methane production in anaerobic digestion.58 Because commercial software still requires both in-depth knowledge of the bioprocess and expertise in modeling, it is not very user-friendly to treatment plant staff.
2.3 Modeling of anaerobic digesters
Anaerobic digesters have a highly complex microbial community composed of fermentative bacteria, syntrophs, acidogens/acetogens, and methanogens.59 The model structure in early models was improved with a greater understanding of the microbial kinetics of those functional populations and the associated biochemical reactions. For example, Andrews applied the Haldane function on the Monod expression to modify the substrate uptake function with inhibition under rate-limiting conditions,60 Andrews and Graef later proposed to include the effects of pH change and buffering through liquid–gas phase interaction and carbonate equilibrium, leading to more accurate modeling of microbial kinetics.61 Based on those studies, Hill and Barth further included a function that described the inhibition effects of volatile fatty acids (VFAs) and ammonia on methanogens, as well as charge balance to correct temperature-dependent pH.62After decades of study of the microbial ecology in anaerobic environments, a task group from the International Water Association consolidated the up-to-date knowledge and formulated Anaerobic Digester Model No. 1 (ADM1) as a common platform model for anaerobic processes.13 This model involves 4 typical digestion processes (hydrolysis, acidogenesis, acetogenesis, and methanogenesis) and several physicochemical steps including gas–liquid diffusion, ion association, and dissociation. ADM1 describes in total 29 processes and 32 variables at dynamic state, 24 of which are based on the Monod equation and first-order kinetics. The model also allows modifications for specific applications such as sulfate reduction, phosphorous conversion, and mineral precipitation.13 ADM1 has been successfully implemented to simulate effluent characteristics with various types of substrates and operating conditions. The most common function of this comprehensive model is to predict and optimize biogas production. Satpathy et al. applied ADM1 to simulate biogas production from rare substrates such as chicken manure.63 Other applications of ADM1 include the prediction of effluent quality from systems fed with winery wastewater64 or treating phenol from olive mill waste.65 For example, Ozkan-Yucel and Gökçay applied ADM1 to a full-scale anaerobic digester under varying organic loading rates to predict total VFAs and COD in the effluent.66 Modified ADM1 can also help troubleshoot operational problems caused by inhibition effects,48 in particular, the accumulation of VFAs.67,68
Despite successful implementation for specific applications, the extensions of sulfate reduction and mineral precipitation can cause a significant computational burden. This is because the precipitation of multiple components (CaHPO4, struvite, and other unknown compounds) and their release mechanisms involve a large number of processes, in which the fundamental knowledge is not available for the model to perform ab initio prediction.69 Another critical issue is that ADM1 is still not able to fully recapitulate the actual functional populations due to the lack of an in-depth understanding of the microbial community. Specifically, ADM1 is structured without considering the production of different short-chain VFAs, alcohols, and hydrogen. The model is thus not able to meet the growing interest in those value-added products.64 Shi et al. attempted to solve this problem by redefining the pseudo-stoichiometric dynamic parameters of VFAs and alcohols corresponding to the hydrogen partial pressure.70 The modified model successfully predicted the concentrations of acetate, propionate, butyrate, ethanol, and hydrogen with standard errors <0.04. However, there remains some discrepancy between the predicted and observed hydrogen levels and effluent COD when the system was fed with high-strength streams.70 In terms of methane production, the model did not include the methanogenic population via direct interspecies electron transfer,71 which was recently found to be a ubiquitous electron transfer mechanism in many engineered and natural environments.72 A reaction–diffusion-electrochemistry model composed of activation and ohmic losses predicted that methanogenesis could be an order of magnitude faster via direct interspecies electron transfer than via the classic route of interspecies hydrogen transfer.73 Modified ADM1 further predicted over one-third of the CH4 produced via this novel electron transfer mechanism,74 underpinning its critical role in methane production.
2.4 Modeling of emerging bioprocesses
Discovered in the 90s, anammox has been applied as an alternative technology for biological nitrogen removal.75 Anammox can be engineered as a single-step process, which is efficient in terms of energy, space, and cost compared with conventional two-step nitrification/denitrification.76 In anammox systems, part of the ammonium is oxidized by ammonium oxidizing bacteria through partial nitrification to nitrite, which serves as the electron acceptor for anammox bacteria to oxidize the remaining ammonium to nitrogen gas.77 Due to the unique bioprocesses, a previous study built an anammox model from fundamental processes including diffusion, hydrolysis, and microbial kinetics of anammox bacteria for simulation of long-term nitrogen and COD removal by a granular up-flow anaerobic sludge blanket reactor.15 Because the model only assumed cell growth under optimum conditions, the predicted and observed nitrogen removal did not correlate well. The anammox process was later modeled using modified ASM1. Through experimental calibration, the model yielded satisfactory prediction of nitrogen removal efficiency of a laboratory-scale bioreactor.78 Interestingly, anammox is better simulated when coupled to other bioprocesses, e.g., sulfur-driven denitrification,14 as the kinetic parameters in the model can be more accurately estimated by varying both sulfur (sulfite, sulfur, and sulfate) and nitrogen (ammonium, nitrogen, nitrite, and nitrate).14 Although the models have demonstrated the potential of anammox systems, the modeling of anammox is still challenging because the system performance is highly dependent on the dynamic interactions between ammonium/nitrite oxidizing bacteria and anammox bacteria.14 A reliable method is to calibrate the maximum growth rates of ammonium oxidizing bacteria, nitrite oxidizing bacteria, and anammox bacteria using experimental data from the full-scale bioreactors and validate the calibration based on the sensitivity analysis.79 In addition, the substrate affinity coefficients should be adjusted based on reported literature to fit the microbial substrate utilization under the possible effects of mass transfer in flocs.79In addition to predicting and optimizing the performance of well-developed bioprocesses such as anammox, mechanistic models can also be implemented for emerging biotechnology such as bioelectrochemical systems to gain an in-depth understanding of their potential and facilitate practical applications. A typical bioelectrochemical system is composed of a cathode and an anode in which the electrochemical reactions are catalyzed by microorganisms. It is challenging to model bioelectrochemical systems primarily because of the close yet uncharacterized connections among microbial kinetics, extracellular electron transfer mechanisms, and electrochemical factors (e.g., internal/external resistance).80 A few mathematical models for this novel system have been developed and reviewed elsewhere.17,81–83 Noticeably, the growth and substrate utilization rates of the functional groups are still based on the Monod expression and corrected with electron mediator concentration, which in turn is expressed as a function of the substrate utilization rate of electroactive bacterial.18,31,84–86 Meanwhile, the Nernst–Michaelis–Menten equation was used to calculate the electron transfer rate in the system87 and the Nernst–Planck equation was introduced to represent ion diffusion through the membrane between anode and cathode.88,89
2.5 Inherent drawbacks of mechanistic modeling
The model structure in response to intracellular biochemical reactions is oftentimes inadequate, which represents a major limitation of mechanistic models. Structural inadequacy stems from the generalization of microbial growth and substrate utilization kinetics with Monod expressions.8 Ideally, the Monod expression for the growth rate of a functional population should consider all degradable and inhibitory compounds and the corresponding factors. The substrates in practical applications (e.g., wastewater) contain various degradable and inhibitory compounds that result in highly complex microbial communities, in which many of the functional populations are uncharacterized.90–92 Therefore, it is not clear which substrates should be experimentally measured to reflect their growth and substrate utilization kinetics. The absence of expressions for novel methanogenesis mechanism via direct interspecies electron transfer is an example of inadequate model structure.57 Such an issue is more problematic for emerging bioprocesses. The models for bioelectrochemical systems were typically structured with fermentative, electroactive, and methanogenic populations. Although the microbial community in bioelectrochemical systems is much more diverse than those in anaerobic digestors,93,94 uncharacterized populations cannot be incorporated into the model structure because their physiological traits related to growth and substrate utilization are poorly understood.95–97Another challenge lies in the unmeasurable kinetic parameters in Monod expressions. Most of the kinetic parameters such as inhibition constant, maximum growth rates, half-saturation constants, and substrate utilization rates can only be derived from biochemical measurements (e.g., substrate concentration).98 From an experimental perspective, when microbial kinetics responds to changing influent characteristics in real-time, it is unrealistic to derive the kinetic parameters throughout the variation. As the operating condition changes, biochemical measurements can vary significantly, and the estimation of kinetic parameters becomes conditional.27 The identifiability of unmeasurable kinetic parameters, i.e., the possibility to derive a unique set of values for the parameters from experimental data, is then of great concern. Firstly, uncertainty issues arise because the derivation of the kinetic parameters is obtained through rate-controlling experiments with specific temperatures, pH, BOD, and COD, etc.,34 while in wastewater treatment processes, microbial cells are exposed to varied substrates. Those parameters need constant calibration. An uncalibrated model is not likely to yield accurate predictions. As a result, it is not certain to what extent the predictions can be used to explain the observed physical, chemical, and biological mechanisms.99 Secondly, to identify the kinetics parameters, the identification of the biochemical and physical parameters responsible for biomass concentrations must be achieved first. Flotats et al. applied the Taylor series expansion to four state variables (acetate, propionate, valerate, and methane) of ADM1 to identify the parameters related to valerate consumption and biomass concentration.100 Such a method has only been reported to solve simple models with a few unidentifiable parameters.101,102 For complex models such as second-order models, parameter identification was handled with the asymptotic behavior of the maximum likelihood estimator and multiple shooting approach described in Müller et al.103 Those previous studies collectively show that the identification and computation processes of kinetic parameters are cumbersome and uncertain in reality.
3. Data-driven modeling of wastewater treatment bioprocesses
3.1 Neural networks
Neural networks, first reported in 1943, are arguably the most prevailing data-driven models across various research fields.104,105 A neural network is composed of multiple layers of interconnected nodes (neurons), through which the inputs are propagated to the final output layer.106 Each input to a neuron has a weight factor that determines the interconnection strength to the next neuron. By adjusting the weight factors, a neural network can be properly trained to perform problem-solving. The training algorithm can be divided into three types: supervised, unsupervised, and hybrid training. In supervised training, neural networks are trained with a labeled dataset that provides feedback about the prediction accuracy.106 Unsupervised training allows networks to be trained with unlabeled data, and the algorithm extracts features and patterns on its own.106 The hybrid training strategy uses unsupervised training for the hidden neurons and supervised training for the output neurons.107Neural networks were first implemented for continuously stirred bioreactors to predict the fermentation products and pH in the effluent.108 Boger applied the modeling strategy to full-scale wastewater treatment plants and showed that neural networks could be a solution for simulating expert rules, a set of boundary values that confined the neural network prediction, from historical operating data.19 Traditionally, neural networks were trained in a feed-forward fashion, meaning that the feed was directed forward-only through layers of training. Yang and Linkenst found that the back-propagation method, which fed outputs from a random layer back to a previous layer, could help the network lower the error rate of prediction.109 Backpropagation thus became a prevailing algorithm of neural network modeling. Several studies used this method to predict effluent COD, biogas production, and NH4+-N removal in different biological wastewater treatment systems including activated sludge processes,21 up-flow anaerobic sludge blanket reactors,26 sequencing batch reactors,110 and anaerobic digesters.111
Previous studies have combined neural networks with other types of data-driven models to improve the simulation of ill-defined systems. One of the strategies is to use the genetic algorithm to select the initial dataset for downstream neural network training, thereby identifying the optimal training parameters and reducing the computational burden.112 Bagheri et al. have successfully applied the genetic algorithm to optimize the weights and thresholds of neural networks to accurately predict sludge volume index.22 Neural networks can also be coupled to particle swarm optimization, a population-based optimization technique that searches for optimal weights and biases through multiple iterations of particle positions in a given search space. This coupling approach was intended to lower the training time and computational cost for finding an optimal neural network structure.113 Compared to the genetic algorithm, neural networks coupled to particle swarm optimization is more memory-efficient in searching optimal weight parameters but is less practical because it has no crossover and mutation in its operator.114
Neural networks have been proven feasible for interpolation within the training data range.91 Insufficient training data can result in low prediction accuracy, particularly when prediction is performed with a dataset of fewer than 10 samples.93 Another issue is that the model structure is often determined based on a trial-and-error approach, leading to significant time consumption and computational cost.92 The fact that neural networks are black box built based on data fitting rather than the mechanistic understanding of the processes suggests that their outputs cannot be used to explain the mechanisms where the inputs are sourced.25
3.2 Random forest
Random forest was initially developed as a stochastic discrimination approach for classification purposes in the 90s.115 Later, the approach was extended to combine bagging and random selection features to construct a collection of decision-making trees with control variance.116 To use the random forest algorithm, the input data are classified through layers of tree branches consisting of a variety of features and classes, and multiple trees composed of the same number of features and classes are collectively used for prediction.116In the wastewater treatment field, the random forest algorithm has been implemented for activated sludge processes, anaerobic digesters, membrane bioreactors, and anammox processes.117–120 The main use of random forest-based models includes the prediction of system performance, fault finding, big data handling, model comparisons, and exploration of datasets with applicable reservations and constraints.121 Although random forest-based models, similar to other data-driven models, are not able to integrate biological principles, these models allow for the identification of key features and conditions that are most influential on the process. The inference can shed light on the underlying biochemical mechanisms. Song et al. implemented this modeling approach with wastewater treatment inputs as multivariate datasets to predict N2O emission from the aerated zones of activated sludge processes.118 Based on the model inference, they identified inorganic carbon concentration and specific ammonia oxidation activity as two of the dominant factors that determined treatment performance.118 The model was further used to identify the different mechanisms of N2O generation in oxic and anoxic environments and demonstrated the key role of N2O in those zones in promoting niche-specific biochemical reactions.122
Random forest can be combined with other algorithms such as principal component analysis (PCA) and neural networks to improve the prediction of effluent quality. Preprocessing of data using PCA could enhance the robustness of random forest-based models, leading to a more accurate prediction of membrane flux in membrane bioreactors as compared with neural networks.117 When coupled to neural networks, random forest-based models could be trained to predict the settleability in the biological reactor chamber,119 as well as to evaluate the effects of key operating factors on treatment performance.123 The results suggested that such a combined strategy could help achieve real-time monitoring and optimize operating conditions.124
3.3 Fuzzy logic
Fuzzy logic is an if-then algorithm that can be used to develop a set of flexible rules for diagnosis and control. A fuzzy logic-based system has four robust components: a fuzzifier, a fuzzy rule-base, an inference engine, and a defuzzifier.125 The fuzzifier is responsible for converting crisp inputs into fuzzy sets, which are mapped by the inference engine to produce another fuzzy set as the output. The fuzzy rule base is a collection of rules that guide the fuzzy engine to produce the outputs. Finally, the defuzzifier transfers the output fuzzy sets back to crisp values.125Fuzzy logic can be applied to numerous scenarios in wastewater treatment bioprocesses such as diagnosis and control of sequencing batch reactor processes,126 simulations and prediction of phosphorus removal,127 as well as design, evaluation, and decision optimization of activated sludge processes.128 Robles et al. developed a fuzzy logic-based controller to optimize biogas production and VFA concentration at varied influent flow rates.129 The designed controller was able to help prevent acidification in a closed-loop setting.129
A combination of fuzzy logic and neural networks could bring together the learning powers of both algorithms, enabling fault tolerance during the modeling of complex systems.107,108 For example, the adaptive neuro-fuzzy inference system that pairs neural networks with fuzzy logic allows modelers to insert a priori knowledge into the neural network structure as rules for training.130–133 The combined modeling strategy was used to predict suspended solids, COD, pH and DO levels in activated sludge systems.108–110 Using the adaptive neuro-fuzzy inference system, Essienubong et al. obtained a strong correlation between the experimental and predicted biogas production with temperature, pH, substrate/water ratio, and hydraulic retention time as the inputs.134 The work by Hosseinzadeh et al. also demonstrated a higher sensitivity of the adaptive neuro-fuzzy inference system when predicting water flux in an osmotic membrane bioreactor.135 In addition to neural networks, fuzzy logic was coupled to genetic algorithms and particle swarm optimization, which outperformed the adaptive neuro-fuzzy inference system during the prediction of BOD, ammonium, and suspended solids in specific bioprocesses.136
Although fuzzy logic models are powerful tools for predicting system outputs using observable environmental data and human-like logic, these data-driven models cannot capture the behaviors of the complex kinetic reactions in engineered biological bioprocesses, which presents the major criticism among other concerns of implementation.137 From an engineering point of view, detailed descriptions of the chemical, physical, and microbiological principles in bioprocesses and computing-based predictive methodology are equally important.138 Unfortunately, fuzzy logic systems, like most of the data-driven models, are incapable of providing mechanistic insight into troubleshooting and system optimization due to their black-box nature.
4. Hybrid models that address the limitations of conventional modeling strategies
The concept of combining mechanistic and data-driven sub-models for hybrid modeling was first proposed in the early 90s and immediately implemented for a fermentation bioprocess to reduce the dependence on microbial kinetics.29 Hybrid modeling strategies were further examined with activated sludge processes and anaerobic digesters through parallel or serial combinations of the mechanistic and data-driven components.139,140In a parallel structure, the outputs from the mechanistic and data-driven components are combined primarily through pure superposition (i.e., summation of the outputs).106,140–142 Weighing functions can be introduced to adjust the weight of the outputs, thereby improving the overall prediction accuracy.143 It should be noted that the prediction performance of a parallel-structured hybrid model is highly dependent on the robustness of the individual sub-models.141 In cases when a biological system is too dynamics/nonlinear and some of the biochemical data are too expensive to collect in real-time (e.g., H2 in anaerobic digesters), neither the mechanistic nor the data-driven components could predict accurately, leading to poor prediction performance of the hybrid model. It is therefore argued that the sub-models in a parallel structure are not well integrated due to the lack of interactions (e.g., cross-feeding of the outputs as done in a serial structure).
In a serial structure, the data-driven component acts as a parameter simulator and estimates kinetic parameters for the mechanistic component to complete simulation.29,140 Serial coupling of the sub-models leverages the prediction power of the data-driven component and is sometimes capable of extrapolating system outputs outside of the observation range. A mixture of both structures has been implemented for chemical systems but not bioprocesses.106 As the selection of the structures depends on the availability of the mechanistic information,142 we argue that with more functional populations being characterized in wastewater biological systems,144 a serial or mixed structure may better reflect the underlying biological mechanisms whilst accurately predicting the system performance.
One of the advantages of hybrid modeling is that unmeasurable mechanistic parameters, in particular microbial growth and substrate utilization rates, can be determined by the data-driven component (Fig. 2).29,145 This was done in the first study of hybrid modeling of engineered bioprocesses, in which a neural network was trained to estimate the specific growth rate of the overall microbial community, and the outputs were used to establish a biomass balance, resulting in more accurate predictions than those from a standalone neural network.29 Compared to conventional mechanistic models that perform one-time estimation of the kinetic parameters, the data-driven component in hybrid models allows the microbial kinetics to be updated in a timely manner based on the collected data, thereby making the hybrid model more robust under varied conditions.29 Another benefit is that the data-driven component can capture more dynamic data to compensate for the prediction of the mechanistic component. For instance, a neural network was used to estimate the operational data at time t + 1 based on the influent and operational data at time t, and the outputs were subsequently used to correct the mechanistic predictions at time t + 1.140 In this way, the hybrid model could capture the disturbance caused by shock loadings of toxic compounds and deliver more accurate prediction of the effluent composition.140
Similar to standalone mechanistic models, hybrid models still contain a Monod expression-based model structure. As previously discussed, Monod expressions approximate the physiological traits of functional populations (i.e., microbial growth and substrate utilization) by assuming a homogeneous culture.16,35 Real wastewater and sewage sludge are highly heterogeneous with various degradable and inhibitory compounds that result in diverse microbial populations.43,55 For well-characterized populations with known functions, unmeasurable kinetic parameters are predominantly derived from biochemical measurements.14,16,34,35,40 Although the data-driven component can help correct the estimates and improve the prediction performance, the estimated kinetic parameters do not necessarily reflect the actual activity of those populations. This is even more problematic for uncharacterized functional populations, whose microbial activity information can be inferred with the data-driven component but does not help interpret the final prediction because those populations are frequently overlooked in the mechanistic component. Therefore, conventional hybrid models constructed with biochemical and physical data still suffer from interpretation issues. A potential solution is to incorporate microbial population and functional dynamics directly into the mechanistic and data-driven components.
5. Genomics-enabled modeling strategies for accurate and interpretable prediction
5.1 Genomics-enabled data-driven modeling
The rapid development of high throughput sequencing techniques and bioinformatics has led to a greater understanding of the microbiomes in wastewater treatment bioprocesses.146–149 Recovering the 16s rRNA sequences allows us to unfold the taxonomy and phylogeny of the core populations in activated sludge, anaerobic digester, and many other systems.146 Meanwhile, metagenomic and meta-transcriptomic data have greatly advanced our knowledge about the genetic potential and functional dynamics of uncharacterized populations.147,148 The findings gained with those powerful tools have validated the mechanistic structure of existing models formulated with known functional populations.149 The million dollar question now is how to incorporate those genomic data into modeling in a more direct manner (Fig. 3). | ||
| Fig. 3 Incorporation of genomic data into model construction. The diagrams of S-, N-, and C-cycle are originated from the study of Wu and Yin.7 The figures of phylogenic trees, PCoA, and data-driven modeling analysis on functional expression are based on the study of Cheng et al.31 | ||
Two pioneering studies integrated 16S rRNA amplicon sequencing data with machine learning algorithms (neural networks and Bayesian networks) to reconstruct the microbial communities in natural ecosystems.150,151 Following similar strategies, several machine learning-based models were trained with microbial taxon abundance and generated semi-interpretable predictions of system performance and stability.152,153 The inferences suggested that for specific systems, classifying taxonomic data at the family level could enhance the prediction accuracy, whilst abundances of specific genera could act as better predictors, highlighting the potential to improve the prediction interpretability with proper data preparation. Before training Bayesian networks, Yuan et al. prepared the genomic data collected from a bioelectrochemical system by selecting dominant taxa at the phylum, genus (Fig. 4A), and operational taxonomic unit levels.154 The genomics-enabled data-driven modeling approach was rigorously cross-validated using three validation strategies.154 Firstly, the difference between the predicted and observed relative abundances of the selected populations remained within an acceptable range as indicated by a relative root-mean-square error (RMSE) of ∼20%. Secondly, the microbial communities reconstructed with the predicted abundances of the selected populations shared high Bray–Curtis similarity with the observed communities at all taxonomic levels. Finally, the predicted system outputs agreed well with the experimental data. For example, current production as the most important system performance for bioelectrochemical systems was predicted with high accuracy at the order level (R2 = 0.97 for prediction vs. observation, Fig. 4B). After validation, the model was used to predict current production as a function of operating conditions (e.g., substrate salinity, Fig. 4C) and provided practical insights into system optimization.
 | ||
| Fig. 4 (A) A Bayesian network trained with the microbial population dynamics at the order level in a bioelectrochemical system. (B) Predicted vs. observed current production. (C) Prediction of current production as a function of substrate salinity. Figures adapted from Yuan et al.154 | ||
Functional genomic data as the training input can improve prediction interpretability. A previous study trained ANNs with gene expression levels to infer metabolic behaviors, resulting in a plausible explanation of microbes' stress adaptation behaviors under environmental perturbations.155 Using a similar but more dynamic modeling strategy, Yuan et al. trained Bayesian networks with meta-transcriptomic data to explain the contribution of interspecies hydrogen transfer and direct interspecies electron transfer to methanogenesis.30 It is highly desired to develop a predictive understanding of the involvement of the two mechanisms due to the lack of measurement techniques.73,74 To prepare data for model training, the genes for alcohol metabolism, hydrogen metabolism, extracellular electron transfer, and methanogenesis were extracted from the metagenome-assembled genomes of the dominant microbes. A Bayesian network trained with those genes is composed of two components (Fig. 5A): upstream gene–gene interactions that predict the expression level of the relevant genes in methanogens, and a downstream sub-network that links the genes encoding methanogenesis to methane. A complete network could accurately predict methane production (R2 = 0.96 for prediction vs. observation, Fig. 5B). To statistically infer the contribution of the electron transfer mechanisms, relevant genes were manually silenced. When the simulation was performed without the genes for hydrogen metabolism, the prediction accuracy was significantly compromised as evidenced by the noticeable difference between the predicted and observed methane production and high RMSE (ΔIHT in Fig. 5B). In contrast, the prediction remained accurate with in silico knockout of the genes for direct interspecies electron transfer (ΔDIET in Fig. 5B). The results thus implied a more critical role of hydrogen-mediated electron transfer in methane production.
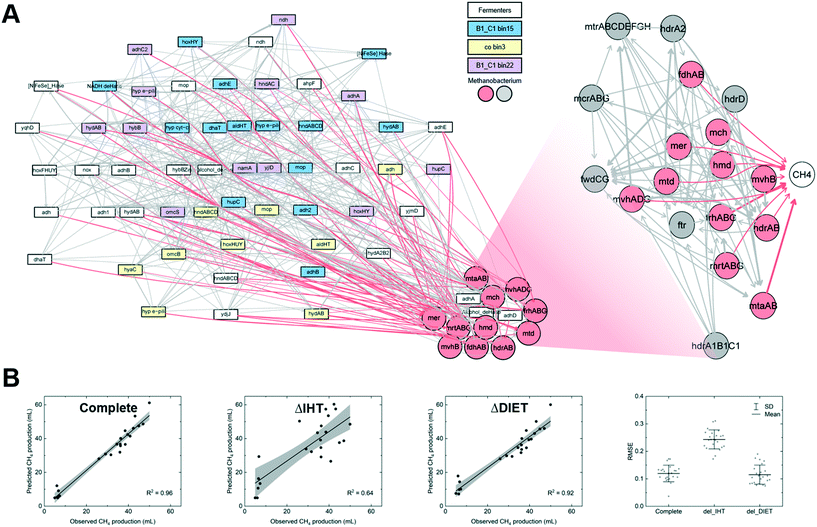 | ||
| Fig. 5 (A) A Bayesian network trained with the genes for alcohol metabolism, hydrogen metabolism, direct interspecies electron transfer, and methanogenesis from dominant microbes. (B) Prediction of methane production with a complete Bayesian network and in silico knockout of relevant genes. Figures adapted from Yuan et al.30 | ||
5.2 Genomics-enabled hybrid modeling
Thus far, genomic data have only been used to train data-driven models for semi-interpretable prediction. There is a growing interest to incorporate it into hybrid modeling to predict the underlying mechanisms for system design and optimization. One potential strategy is to infer unidentifiable kinetic parameters from microbial population and gene dynamics. The mechanistic component can be formulated following conventional modeling procedures to estimate kinetic parameters, and the estimates can be combined with microbial taxon abundance and operating conditions to train the data-driven component. The resulting hybrid model is therefore a kinetics simulator that statistically infers kinetic parameters, which can then be fed back to the mechanistic component for prediction of system performance.The concept has been proven valid by a recent study,31 in which a genomics-enabled hybrid model was implemented for bioelectrochemical systems based on 77 samples collected from 13 publications. The mechanistic component of the hybrid model was built to estimate the maximum growth and substrate utilization rates of three functional populations: fermentative, electroactive, and methanogenic microbes, which were subsequently combined with the relative abundances of 38 core taxa at the genus level to train a hybrid Bayesian network (Fig. 6A). When examined with six new samples that were not included in network training, the hybrid model achieved the most accurate prediction of current production (hybrid + mechanistic in Fig. 6B) compared with standalone data-driven models. The enhanced prediction performance of the hybrid model likely results from the close connection between population dynamics and microbial kinetics.
 | ||
| Fig. 6 (A) A Bayesian network as the data-driven component of the hybrid model was trained with microbial population dynamics and microbial kinetic parameters estimated from the mechanistic component (green oval nodes). (B) Predicted vs. observed current production. Figures adapted from Cheng et al.31 | ||
An alternative strategy to incorporate genomic data into hybrid modeling is to replace Monod expression-based model structures in conventional mechanistic models by simulating microbial population dynamics. This can be achieved with an iterative strategy, in which the data-driven component trained with processed genomic data infers instantaneous biochemical and microbial intermediates, and the intermediates are fed into the mechanistic component to predict steady-state biochemical outputs. This novel strategy mimics microbial community assembly driven by environmental perturbations in engineered systems:156–158 operating conditions and biochemical inputs impose selective pressure and together shape the microbial community structure, and the enriched functional populations produce biochemical intermediates that are rapidly mixed with the inputs to form a new steady-state, causing the community structure to further shift until the biochemical outputs reach equilibrium. The proposed strategy thus frees models from microbial kinetics-based structures, while the abiotic and microbial processes and their interplay are revealed in each iteration. Successful modeling with this strategy relies on the ability of hybrid models to act as a community simulator to predict microbial taxon abundance and reconstruct microbial communities in silico. For example, Bayesian networks could infer the relative abundances of dominant taxa, resulting in Bray–Curtis similarity of over 90% between the simulated and observed microbial communities at the phylum level.156 However, the similarity dropped to 83% at the order level and 69% at the OTU level, likely because of the presence of functionally redundant taxa in the small data pool. The potential of the proposed strategy warrants investigation with big data collected from global databases.
6. Conclusions
This review focuses on three major types of models: mechanistic, data-driven, and hybrid models. Mechanistic models can provide fundamental insights but need laborious calibration because the Monod-based model structure is inadequate to reflect the biological principles whilst the microbial kinetic parameters are largely unidentifiable. As a result, a mechanistic model built for a specific system frequently falls short when applied to other bioprocesses. Data-driven models can provide predictive insights but yield uninterpretable predictions due to their black-box nature. Hybrid models are believed to overcome the issues of structural inadequacy, parametric unidentifiability, and uninterpretable prediction of the standalone models. Recent biotechnological development such as high throughput sequencing data and omics-based analysis can further enable the incorporation of microbial population and functional dynamics into the model to directly reflect the biological principles. Genomics-enabled hybrid modeling strategies require the mechanistic and data-driven components to be integrated interactively. Two strategies are proposed: kinetics simulator and community simulator, and their applicability warrant further studies. Although hybrid models can potentially overcome the drawbacks of standalone models, the main rationale of modeling selection and design is largely dependent on its intended use. Additionally, the availability of omics-based data and computational cost require more effort in preparation, collection, process, and analysis, which demands technical labor, time, and financial investment. All these factors need to be taken into consideration when modelers design and modify existing models.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the U.S. Department of Agriculture [Award No. 2020-67019-31027].References
- USEPA, Emerging Technologies for Wastewater Treatment and In-Plant Wet Weather Management, U.S. Environmental Protection Agency, Fairfax, 2013 Search PubMed.
- J. Kuenen, Anammox bacteria: from discovery to application, Nat Rev Microbiol, 2008, 6, 320–326, DOI:10.1038/nrmicro1857
.
-
J. S. Seelam, S. A. Maesara, G. Mohanakrishna, S. A. Patil, A. Ter Heijne and D. Pant, in Waste Biorefinery: Potential and Perspectives, Elsevier, 2018, pp. 535–570 Search PubMed
.
- Module 16: the Activated sludge process part II, Pennsylvania Department of Environmental Protection, Harrisburg, 2014 Search PubMed.
- Biological Treatment: suspended growth processes study guide, Wisconsin Department of Natural Resouces, Madison, WI, 2015 Search PubMed.
- R. Snyder and D. Wyant, Activated sludge process control: training manual for wastewater treatment plant operators, State of Michigan Department of Environmental Quality Search PubMed.
- G. Wu and Q. Yin, Microbial niche nexus sustaining biological wastewater treatment, npj Clean Water, 2020, 3, 33, DOI:10.1038/s41545-020-00080-4
.
-
U. Jeppsson, Modelling Aspects of Wastewater Treatment Processes, PhD, Department of Industrial Electrical Engineering and Automation (IEA) Lund Institute of Technology (LTH), P.O. Box 118 S-221 00 LUND, Sweden, 1996, pp. 65–171 Search PubMed
.
- N. Hvala and J. Kocijan, Design of a hybrid mechanistic/Gaussian process model to predict full-scale wastewater treatment plant effluent, Comput. Chem. Eng., 2020, 140, 106934 CrossRef CAS
.
- M. Henze, W. Gujer, T. Mino, T. Matsuo, M. Wentzel, G. Marais and M. Loosdrecht, Activated sludge model No.2D, ASM2D, Water Sci. Technol., 1999, 39, 165–182 CrossRef CAS
.
- M. C. M. Van Loosdrecht, C. M. Lopez-Vazquez, S. C. F. Meijer, C. M. Hooijmans and D. Brdjanovic, Twenty-five years of ASM1: Past, present and future of wastewater treatment modelling, J. Hydroinf., 2015, 17, 697–718 CrossRef
.
-
M. Henze, W. Gujer, T. Mino and M. Van Loosedrecht, Activated sludge models ASM1, ASM2, ASM2d and ASM3, Water Intell. Online, 2006, vol. 5, pp. 47–77 Search PubMed
.
-
D. J. Batstone, J. Keller, I. Angelidaki, S. V. Kalyuzhnyi, S. G. Pavlostathis, A. Rozzi, W. T. M. Sanders, H. Siegrist and V. A. Vavilin, The IWA Anaerobic Digestion Model No 1 (ADM1), 2002 Search PubMed
.
- Y.-F. Deng, W.-T. Tang, H. Huang, J. Qian, D. Wu and G.-H. Chen, Development of a kinetic model to evaluate thiosulfate-driven denitrification and anammox (TDDA) process, Water Res., 2021, 198, 117155 CrossRef CAS PubMed
.
- B. J. Ni, Y. P. Chen, S. Y. Liu, F. Fang, W. M. Xie and H. Q. Yu, Modeling a granule-based anaerobic ammonium oxidizing (ANAMMOX) process, Biotechnol. Bioeng., 2009, 103, 490–499 CrossRef CAS PubMed
.
- J. Monod, The Growth of Bacterial Cultures, Annu. Rev. Microbiol., 1949, 3, 371–394 CrossRef CAS
.
- S. Luo, H. Sun, Q. Ping, R. Jin and Z. He, A Review of Modeling Bioelectrochemical Systems: Engineering and Statistical Aspects, Energies, 2016, 9, 1–27 Search PubMed
.
- Y. Liu, M. Qin, S. Luo, Z. He and R. Qiao, Understanding Ammonium Transport in Bioelectrochemical Systems towards its Recovery, Sci. Rep., 2016, 6, 1–10 CrossRef PubMed
.
- Z. Boger, Application of neural networks to water and wastewater treatment plant operation, ISA Trans., 1992, 31, 25–33 CrossRef CAS
.
- N. Bhat and T. J. McAvoy, Use of neural nets for dynamic modeling and control of chemical process systems, Comput. Chem. Eng., 1990, 14, 573–582 CrossRef CAS
.
- H. Moral, A. Aksoy and C. F. Gokcay, Modeling of the activated sludge process by using artificial neural networks with automated architecture screening, Comput. Chem. Eng., 2008, 32, 2471–2478 CrossRef CAS
.
- M. Bagheri, S. A. Mirbagheri, Z. Bagheri and A. M. Kamarkhani, Modeling and optimization of activated sludge bulking for a real wastewater treatment plant using hybrid artificial neural networks-genetic algorithm approach, Process Saf. Environ. Prot., 2015, 95, 12–25 CrossRef CAS
.
- D. De Clercq, D. Jalota, R. Shang, K. Ni, Z. Zhang, A. Khan, Z. Wen, L. Caicedo and K. Yuan, Machine learning powered software for accurate prediction of biogas production: A case study on industrial-scale Chinese production data, J. Cleaner Prod., 2019, 218, 390–399 CrossRef
.
- L. Wang, F. Long, W. Liao and H. Liu, Prediction of anaerobic digestion performance and identification of critical operational parameters using machine learning algorithms, Bioresour. Technol., 2020, 298, 1–9 Search PubMed
.
- C. Rudin, Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead, Nat. Mach. Intell., 2019, 1, 206–215 CrossRef
.
- C. Mendes, R. da Silva Magalhes, K. Esquerre and L. M. Queiroz, Artificial neural network modeling for predicting organic matter in a full-scale up-flow anaerobic sludge blanket (UASB) reactor, Environ. Model. Assess., 2015, 20, 625–635 CrossRef
.
- M. J. Wade, Not just numbers: Mathematical modelling and its contribution to anaerobic digestion processes, Processes, 2020, 8, 1–31, DOI:10.3390/PR8080888
.
-
T. Bohlin, Practical grey-box process identification: theory and applications, Springer, London, 2006 Search PubMed
.
- D. C. Psichogios and L. H. Ungar, A hybrid neural network-first principles approach to process modeling, AIChE J., 1992, 38, 1499–1511 CrossRef CAS
.
- H. Yuan, X. Wang, T.-Y. Lin, J. Kim and W.-T. Liu, Disentangling Syntrophic Electron Transfer Mechanisms in Methanogenesis Through Electrochemical Stimulation, Omics, and Machine Learning, Sci. Rep., 2021, 11, 1–22, DOI:10.21203/rs.3.rs-288821/v1
.
- Z. Cheng, S. Yao and H. Yuan, Linking population dynamics to microbial kinetics for hybrid modeling of bioelectrochemical systems, Water Res., 2021, 202, 117418, DOI:10.1016/j.watres.2021.117418
.
-
B. E. Rittmann and P. L. McCarty, Environmental biotechnology: Principles and applications, McGraw-Hill Education, 2001 Search PubMed
.
- J. E. McKee, G. M. Fair and L. S. Kraus, Load Distribution in the Activated Sludge Process, Sewage Works J., 1942, 14, 121–146 CAS
.
- K. Kovárová-Kovar and T. Egli, Growth kinetics of suspended microbial cells: from single-substrate-controlled growth to mixed-substrate kinetics, Microbiol. Mol. Biol. Rev., 1998, 62, 646–666 CrossRef PubMed
.
- J. Heijnen and B. Romein, Derivation of Kinetic Equations for Growth on Single Substrates Based on General Properties of a Simple Metabolic Network, Biotechnol. Prog., 1995, 11, 712–716 CrossRef CAS
.
- J. F. Andrews, A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates, Biotechnol. Bioeng., 1968, 10, 707–723 CrossRef CAS
.
- W. Gujer, M. Henze, T. Mino and M. Van Loosdrecht, Activated sludge model no. 3, Water Sci. Technol., 1999, 39, 183–193 CrossRef CAS
.
- J. Alex, L. Benedetti, J. Copp, K. V. Gernaey, U. Jeppsson, I. Nopens, M. N. Pons, L. Rieger, C. Rosen, J. P. Steyer, P. Vanrolleghem and S. Winkler, Benchmark Simulation Model no. 1 (BSM1), 2008, p. 62 Search PubMed.
- M. Mohammadi, A. R. Mohamed, G. D. Najafpour, H. Younesi and M. H. Uzir, Kinetic Studies on Fermentative Production of Biofuel from Synthesis Gas Using Clostridium ljungdahlii, Sci. World J., 2014, 2014, 1–9 Search PubMed
.
- G. C. Okpokwasili and C. O. Nweke, Microbial growth and substrate utilization kinetics, Afr. J. Biotechnol., 2005, 5, 305–317 Search PubMed
.
- M. K. Stenstrom, W. Kido, R. F. Shanks and M. Mulkerin, Estimating Oxygen
Transfer Capacity of a Full-Scale Pure Oxygen Activated Sludge Plant, J. - Water Pollut. Control Fed., 1989, 61, 208–220 CAS
.
- P. L. Dold, G. A. Ekama, G. Marais and G. R. Marais Van, A general model for the activated sludge process, Prog. Water Technol., 1980, 12, 47–77 CAS
.
- K. V. Gernaey, M. C. M. Van Loosdrecht, M. Henze, M. Lind and S. B. Jørgensen, Activated sludge wastewater treatment plant modelling and simulation: State of the art, Environ. Model. Softw., 2004, 19, 763–783 CrossRef
.
- J. H. Sherrard, R. O. Mines, J. E. Alleman and M. S. Kennedy, Activated Sludge, J. - Water Pollut. Control Fed., 1983, 55, 615–622 CAS
.
- P. J. Roeleveld and M. C. M. Van Loosdrecht, Experience with guidelines for wastewater characterisation in The Netherlands | Water Science & Technology, Water Sci. Technol., 2002, 45, 77–87 CrossRef CAS PubMed
.
- M. C. M. Van Loosdrecht, C. M. Lopez-Vazquez, S. C. F. Meijer, C. M. Hooijmans and D. Brdjanovic, Twenty-five years of ASM1: Past, present and future of wastewater treatment modelling, J. Hydroinf., 2015, 17, 697–718 CrossRef
.
-
N. Boontian, PhD. thesis, Cranfield University, 2012 Search PubMed
.
- Z. R. Hu, M. C. Wentzel and G. A. Ekama, Modelling biological nutrient removal activated sludge systems - A review, Water Res., 2003, 37, 3430–3444 CrossRef CAS PubMed
.
- G. Olsson and B. Newell, Wastewater Treatment Systems: Modelling, Diagnosis and Control, 2005, vol. 4 Search PubMed.
- A. Serdarevic and A. Dzubur, Wastewater process modeling, Coupled Syst. Mech., 2016, 5, 21–39 CrossRef
.
- A. G. Dorofeev, Yu. A. Nikolaev, M. N. Kozlov, M. V. Kevbrina, A. M. Agarev, A. Yu. Kallistova and N. V. Pimenov, Modeling of anammox process with the biowin software suite, Appl. Biochem. Microbiol., 2017, 53, 88–95 Search PubMed
.
- O. Oleyiblo, J. Cao, Q. Feng, G. Wang, X. Zhaoxia and F. Fang, Evaluation and improvement of wastewater treatment plant performance using BioWin, Chin. J. Oceanol. Limnol., 2014, 33, 468–476 CrossRef
.
- A. Elawwad, M. Matta, M. Abo-Zaid and H. Abdel-Halim, Plant-wide modeling and optimization of a large-scale WWTP using BioWin's ASDM model, J. Water Process. Eng., 2019, 31, 100819 CrossRef
.
-
K. Rathore, M.S. thesis, University of South Florida, 2018 Search PubMed
.
- C. Moragaspitiya, J. Rajapakse, W. Senadeera and I. Ali, Simulation of Dynamic Behaviour of a Biological Wastewater Treatment Plant in South East Queensland, Australia using Bio-Win Software, Eng. J., 2017, 21, 1–22 CrossRef CAS
.
- R. Vitanza, I. Colussi, A. Cortesi and V. Gallo, Implementing a respirometry-based model into BioWin software to simulate wastewater treatment plant operations, J. Water Process. Eng., 2016, 9, 267–275 CrossRef
.
- I. Hamawand and C. Baillie, Anaerobic Digestion and Biogas Potential: Simulation of Lab and Industrial-Scale Processes, Energies, 2015, 8, 454–474 CrossRef CAS
.
-
J. L. Callahan, Ph.D. thesis, Colorado School of Mines, 2018 Search PubMed
.
- K. Venkiteshwaran, B. Bocher, J. Maki and D. Zitomer, Relating Anaerobic Digestion Microbial Community and Process Function: Supplementary Issue: Water Microbiology, Microbiol. Insights, 2015, 8s2, MBI.S33593, DOI:10.4137/MBI.S33593
.
- J. F. Andrews, A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates, Biotechnol. Bioeng., 1968, 10, 707–723 CrossRef CAS
.
- J. F. Andrews and S. P. Graef, in Anaerobic Biological Treatment Processes, American Chemical Society, 1971, pp. 126–162 Search PubMed.
- D. T. Hill and C. L. Barth, A Dynamic Model for Simulation of Animal Waste Digestion on JSTOR, J. - Water Pollut. Control Fed., 1977, 49, 2129–2143 CAS
.
- P. Satpathy, S. Steinigeweg, F. Uhienhut and E. Siefert, Application of Anaerobic Digestion Model 1 (ADM1) for Prediction of Biogas Production, Int. J. Sci. Res., 2013, 4, 86–89 Search PubMed
.
- D. J. Batstone, M. Torrijos, C. Ruiz and J. E. Schmidt, Use of an anaerobic sequencing batch reactor for parameter estimation in modelling of anaerobic digestion, Water Sci. Technol., 2004, 50, 295–303 CrossRef CAS PubMed
.
- B. Fezzani and R. B. Cheikh, Extension of the anaerobic digestion model No. 1 (ADM1) to include phenolic compounds biodegradation processes for the simulation of anaerobic co-digestion of olive mill wastes at thermophilic temperature, J. Hazard. Mater., 2009, 162, 1563–1570 CrossRef CAS PubMed
.
- U. G. Ozkan-Yucel and C. F. Gökçay, Application of ADM1 model to a full-scale anaerobic digester under dynamic organic loading conditions, Environ. Technol., 2010, 31, 633–640 CrossRef CAS PubMed
.
- A. Ramachandran, R. Rustum and A. J. Adeloye, Review of anaerobic digestion modeling and optimization using nature-inspired techniques, Processes, 2019, 7(12), 1–12, DOI:10.3390/pr7120953
.
- J. Palatsi, J. Illa, F. X. Prenafeta-Boldú, M. Laureni, B. Fernandez, I. Angelidaki and X. Flotats, Long-chain fatty acids inhibition and adaptation process in anaerobic thermophilic digestion: Batch tests, microbial community structure and mathematical modelling, Bioresour. Technol., 2010, 101, 2243–2251 CrossRef CAS PubMed
.
- D. J. Batstone, M. Torrijos, C. Ruiz and J. E. Schmidt, Use of an anaerobic sequencing batch reactor for parameter estimation in modelling of anaerobic digestion, Water Sci. Technol., 2004, 50, 295–303 CrossRef CAS PubMed
.
- E. Shi, J. Li and M. Zhang, Application of IWA Anaerobic Digestion Model No. 1 to simulate butyric acid, propionic acid, mixed acid, and ethanol type fermentative systems using a variable acidogenic stoichiometric approach, Water Res., 2019, 161, 242–250 CrossRef CAS PubMed
.
- A. E. Rotaru, P. M. Shrestha, F. Liu, M. Shrestha, D. Shrestha, M. Embree, K. Zengler, C. Wardman, K. P. Nevin and D. R. Lovley, A new model for electron flow during anaerobic digestion: Direct interspecies electron transfer to Methanosaeta for the reduction of carbon dioxide to methane, Energy Environ. Sci., 2014, 7, 408–415 RSC
.
- D. R. Lovley, Syntrophy Goes Electric: Direct Interspecies Electron Transfer, Annu. Rev. Microbiol., 2017, 71, 643–664 CrossRef CAS PubMed
.
- T. Storck, B. Virdis and D. J. Batstone, Modelling extracellular limitations for mediated versus direct interspecies electron transfer, ISME J., 2016, 10, 621–631 CrossRef CAS PubMed
.
- Y. Liu, Y. Zhang, Z. Zhao, H. H. Ngo, W. Guo, J. Zhou, L. Peng and B. J. Ni, A modeling approach to direct interspecies electron transfer process in anaerobic transformation of ethanol to methane, Environ. Sci. Pollut. Res., 2017, 24, 855–863 CrossRef CAS PubMed
.
- A. Terada, S. Zhou and M. Hosomi, Presence and detection of anaerobic ammonium-oxidizing (anammox) bacteria and appraisal of anammox process for high-strength nitrogenous wastewater treatment: a review, Clean Technol. Environ. Policy, 2011, 13, 759–781 CrossRef CAS
.
- X. Chang, D. Li, Y. Liang, Z. Yang, S. Cui, T. Liu, H. Zeng and J. Zhang, Performance of a completely autotrophic nitrogen removal over nitrite process for treating wastewater with different substrates at ambient temperature, J. Environ. Sci., 2013, 25, 688–697 CrossRef CAS
.
- K. A. Third, A. O. Sliekers, J. G. Kuenen and M. S. M. Jetten, The CANON system (completely autotrophic nitrogen-removal over nitrite) under ammonium limitation: Interaction and competition between three groups of bacteria, Syst. Appl. Microbiol., 2001, 24, 588–596 CrossRef CAS PubMed
.
- G. Cema, A. Sochacki, J. Kubiatowicz, P. Gutwiński and J. Surmacz-Górska, Start-up, modelling and simulation of the anammox process in a membrane bioreactor, Chem. Process Eng. - Inz. Chem. Proces., 2012, 33, 639–650 CAS
.
- B.-J. Ni, A. Joss and Z. Yuan, Modeling nitrogen removal with partial nitritation and anammox in
one floc-based sequencing batch reactor, Water Res., 2014, 67(15), 321–329, DOI:10.1016/j.watres.2014.09.028
.
- D. Pant, A. Singh, G. Van Bogaert, S. Irving Olsen, P. Singh Nigam, L. Diels and K. Vanbroekhoven, RSC Adv., 2012, 2, 1248–1263 RSC
.
- C. Xia, D. Zhang, W. Pedrycz, Y. Zhu and Y. Guo, J. Power Sources, 2018, 373, 119–131 CrossRef CAS
.
- V. B. Oliveira, M. Simões, L. F. Melo and A. M. F. R. Pinto, Overview on the developments of microbial fuel cells, Biochem. Eng. J., 2013, 73, 53–64 CrossRef CAS
.
- V. M. Ortiz-Martíneza, M. J. Salar-Garcíaa, A. P. de los Ríosb, F. J. Hernández-Fernándeza, J. A. Egeac and L. J. Lozanoa, Developments in microbial fuel cell modeling, Chem. Eng. J., 2015, 271, 50–60 CrossRef
.
- R. P. Pinto, B. Srinivasan, A. Escapa and B. Tartakovsky, Multi-population model of a microbial electrolysis cell, Environ. Sci. Technol., 2011, 45, 5039–5046 CrossRef CAS PubMed
.
- R. P. Pinto, B. Srinivasan, M. F. Manuel and B. Tartakovsky, A two-population bio-electrochemical model of a microbial fuel cell, Bioresour. Technol., 2010, 101, 5256–5265 CrossRef CAS PubMed
.
- Q. Ping, C. Zhang, X. Chen, B. Zhang, Z. Huang and Z. He, Mathematical Model of Dynamic Behavior of Microbial Desalination Cells for Simultaneous Wastewater Treatment and Water Desalination, Environ. Sci. Technol., 2014, 48, 13010–13019 CrossRef CAS PubMed
.
- A. K. Marcus, C. I. Torres and B. E. Rittmann, Conduction-based modeling of the biofilm anode of a microbial fuel cell, Biotechnol. Bioeng., 2007, 98, 1171–1182 CrossRef CAS PubMed
.
- F. Harnisch, R. Warmbier, R. Schneider and U. Schröder, Modeling the ion transfer and polarization of ion exchange membranes in bioelectrochemical systems, Bioelectrochemistry, 2009, 75, 136–141 CrossRef CAS PubMed
.
- J. Kim, H. Kim, B. Kim and J. Yu, Computational fluid dynamics analysis in microbial fuel cells with different anode configurations, Water Sci. Technol., 2014, 69, 1447–1452 CrossRef CAS PubMed
.
- D. C. Vuono, J. Regnery, D. Li, Z. L. Jones, R. W. Holloway and J. E. Drewes, rRNA Gene Expression of Abundant and Rare Activated-Sludge Microorganisms and Growth Rate Induced Micropollutant Removal, Environ. Sci. Technol., 2016, 50, 6299–6309 CrossRef CAS PubMed
.
- L. Wu, D. Ning, B. Zhang, Y. Li, P. Zhang, X. Shan, Q. Zhang, M. Brown, Z. Li, J. D. Van Nostrand, F. Ling, N. Xiao, Y. Zhang, J. Vierheilig, G. F. Wells, Y. Yang, Y. Deng, Q. Tu, A. Wang, T. Zhang, Z. He, J. Keller, P. H. Nielsen, P. J. J. Alvarez, C. S. Criddle, M. Wagner, J. M. Tiedje, Q. He, T. P. Curtis, D. A. Stahl, L. Alvarez-Cohen, B. E. Rittmann, X. Wen and J. Zhou, Global diversity and biogeography of bacterial communities in wastewater treatment plants, Nat. Microbiol., 2019, 4, 1183–1195, DOI:10.1038/s41564-019-0426-5
.
- A. M. Saunders, M. Albertsen, J. Vollertsen and P. H. Nielsen, The activated sludge ecosystem contains a core community of abundant organisms, ISME J., 2016, 10, 11–20 CrossRef CAS PubMed
.
- S. Jung and J. M. Regan, Comparison of anode bacterial communities and performance in microbial fuel cells with different electron donors, Appl. Microbiol. Biotechnol., 2007, 77, 393–402 CrossRef CAS PubMed
.
- D. Pant, G. Van Bogaert, L. Diels and K. Vanbroekhoven, A review of the substrates used in microbial fuel cells (MFCs) for sustainable energy production, Bioresour. Technol., 2010, 101, 1533–1543 CrossRef CAS PubMed
.
- S. Ishii, S. Suzuki, T. M. Norden-Krichmar, A. Tenney, P. S. G. Chain, M. B. Scholz, K. H. Nealson and O. Bretschger, A novel metatranscriptomic approach to identify gene expression dynamics during extracellular electron transfer, Nat. Commun., 2013, 4, 1–10 Search PubMed
.
- B. E. Logan, Exoelectrogenic bacteria that power microbial fuel cells, Nat. Rev. Microbiol., 2009, 7, 375–381 CrossRef CAS PubMed
.
- Y. Xiao, Y. Zheng, S. Wu, E.-H. Zhang, Z. Chen, P. Liang, X. Huang, Z.-H. Yang, I.-S. Ng, B.-Y. Chen and F. Zhao, Pyrosequencing Reveals a Core Community of Anodic Bacterial Biofilms in Bioelectrochemical Systems from China, Front. Microbiol., 2015, 6, 1410 Search PubMed
.
- X. Zhao, L. Li, D. Wu, T. Xiao, Y. Ma and X. Peng, Modified Anaerobic Digestion Model No. 1 for modeling methane production from food waste in batch and semi-continuous anaerobic digestions, Bioresour. Technol., 2019, 271, 109–117 CrossRef CAS PubMed
.
- P. Reichert and N. Schuwirth, Linking statistical bias description to multiobjective model calibration, Water Resour. Res., 2012, 48, 2011WR011391 CrossRef
.
- X. Flotats, B. K. Ahring and I. Angelidaki, Parameter identification of thermophilic anaerobic degradation of valerate, Appl. Biochem. Biotechnol., 2003, 109, 47–62 CrossRef CAS PubMed
.
- N. Noykova, T. Müller, M. Gyllenberg and J. Timmer, Quantitative analyses of anaerobic wastewater treatment processes: identifiability and parameter estimation, Biotechnol. Bioeng., 2002, 78, 89–103 CrossRef CAS PubMed
.
- A. Donoso-Bravo, J. Mailier, C. Martin, J. Rodríguez, C. A. Aceves-Lara and A. V. Wouwer, Model selection, identification and validation in anaerobic digestion: A review, Water Res., 2011, 45, 5347–5364 CrossRef CAS PubMed
.
- T. G. Müller, N. Noykova, M. Gyllenberg and J. Timmer, Parameter identification in dynamical models of anaerobic waste water treatment, Math. Biosci., 2002, 177–178, 147–160 CrossRef
.
- Z. Boger, Application of neural networks to water and wastewater treatment plant operation, ISA Trans., 1992, 31, 25–33 CrossRef CAS
.
- J. Jawad, A. H. Hawari and S. Javaid Zaidi, Artificial neural network modeling of wastewater treatment and desalination using membrane processes: A review, Chem. Eng. J., 2021, 419(1), 129540, DOI:10.1016/j.cej.2021.129540
.
- S. Zendehboudi, N. Rezaei and A. Lohi, Appl. Energy, 2018, 228, 2539–2566 CrossRef CAS
.
- M. Ben Nasr and M. Chtourou, A hybrid training algorithm for feedforward neural networks, Neural Process. Lett., 2006, 24, 107–117 CrossRef
.
- J. Thibault, V. Van Breusegem and A. Chéruy, On-line Prediction of Fermentation Variables Using Neural Networks, Biotechnol. Bioeng., 1990, 36, 1041–1048 CrossRef CAS PubMed
.
- Y. Y. Yang and D. A. Linkenst, Modelling of continuous bioreactors via neural networks, Trans. Inst. Meas. Control, 1993, 15, 158–169 CrossRef
.
- P. Kundu, A. Debsarkar and S. Mukherjee, Artificial Neural Network Modeling for Biological Removal of Organic Carbon and Nitrogen from Slaughterhouse Wastewater in a Sequencing Batch Reactor, Adv. Artif. Neural Syst., 2013, 2013, 1–15, DOI:10.1155/2013/268064
.
- B. Mahanty, M. Zafar and H. S. Park, Characterization of co-digestion of industrial sludges for biogas production by artificial neural network and statistical regression models, Environ. Technol., 2013, 34, 2145–2153 CrossRef CAS PubMed
.
-
P. Koehn, M.S. thesis, University of Tennessee, 1994 Search PubMed
.
- M. Shariati, M. S. Mafipour, P. Mehrabi, A. Bahadori, Y. Zandi, M. N. A. Salih, H. Nguyen, J. Dou, X. Song and S. Poi-Ngian, Application of a hybrid artificial neural network-particle swarm optimization (ANN-PSO) model in behavior prediction of channel shear connectors embedded in normal and high-strength concrete, Appl. Sci., 2019, 9(24), 5534, DOI:10.3390/app9245534
.
-
H. Lu, J. Chen and L. Guo, in Comprehensive Energy Systems, Elsevier, 2018, vol. 5, pp. 258–314 Search PubMed
.
- H. Tyralis, G. Papacharalampous and A. Langousis, A brief review of random forests for water scientists and practitioners and their recent history in water resources, Water, 2019, 11, 910 CrossRef
.
- L. Breiman, Random forests-random features, 1999 Search PubMed.
- W. Li, C. Li and T. Wang, Application of machine learning algorithms in mbr simulation under big data platform, Water Pract. Technol., 2020, 15, 1238–1247 CrossRef
.
- M. J. Song, S. Choi, W. Bin Bae, J. Lee, H. Han, D. D. Kim, M. Kwon, J. Myung, Y. M. Kim and S. Yoon, Identification of primary effecters of N2O emissions from full-scale biological nitrogen removal systems using random forest approach, Water Res., 2020, 184, 116114, DOI:10.1016/j.watres.2020.116144
.
- B. Szeląg, A. Gawdzik and A. Gawdzik, Application of selected methods of black box for modeling the settlability process in wastewater treatment plant, Ecol. Chem. Eng. S, 2017, 24(1), 119–127, DOI:10.1515/eces-2017-0009
.
- B. Szeląg, J. Drewnowski, G. Łagód, D. Majerek, E. Dacewicz and F. Fatone, Soft sensor application in identification of the activated sludge bulking considering the technological and economical aspects of smart systems functioning, Sensors, 2020, 20(7), 1941, DOI:10.3390/s20071941
.
- H. Tyralis, G. Papacharalampous and A. Langousis, A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources, Water, 2019, 11, 910 CrossRef
.
- M. J. Song, S. Choi, W. B. Bae, J. Lee, H. Han, D. D. Kim, M. Kwon, J. Myung, Y. M. Kim and S. Yoon, Identification of primary effecters of N2O emissions from full-scale biological nitrogen removal systems using random forest approach, Water Res., 2020, 184, 116114 CrossRef PubMed
.
- D. Wang, S. Thunéll, U. Lindberg, L. Jiang, J. Trygg, M. Tysklind and N. Souihi, A machine learning framework to improve effluent quality control in wastewater treatment plants, Sci. Total Environ., 2021, 784, 147138 CrossRef CAS PubMed
.
-
G. Louppe, Ph.D. thesis, University of Liège, 2014 Search PubMed
.
- J. M. Mendel and G. C. Mouzouris, Designing Fuzzy Logic Systems, IEEE Trans. Circuits Syst., 1997, 44(11), 885–895, DOI:10.1109/82.644042
.
- L. Fan and K. Boshnakov, in Proceedings of the World Congress on Intelligent Control and Automation (WCICA), 2010, pp. 4142–4146 Search PubMed.
- H. Xu and R. Vilanova, in 2015 23rd Mediterranean Conference on Control and Automation, MED 2015 - Conference Proceedings, Institute of Electrical and Electronics Engineers Inc., 2015, pp. 545–550 Search PubMed.
- T. J. J. Kalker, C. P. van Goor, P. J. Roeleveld, M. F. Ruland and R. Babuška, Fuzzy control of aeration in an activated sludge wastewater treatment plant: design, simulation and evaluation, Water Sci. Technol., 1999, 39, 61–69 Search PubMed
.
- A. Robles, E. Latrille, M. V. Ruano and J. P. Steyer, A fuzzy-logic-based controller for methane production in anaerobic fixed-film reactors, Environ. Technol., 2016, 38(1), 42–52, DOI:10.1080/09593330.2016.1184321
.
- J. S. R. Jang, ANFIS: Adaptive-Network-Based Fuzzy Inference System, IEEE Trans. Syst. Man Cybern.: Syst., 1993, 23, 665–685 CrossRef
.
-
R. Rustum, Ph.D. thesis, Heriot-Watt University, 2009 Search PubMed
.
- T. Y. Pai, P. Y. Yang, S. C. Wang, M. H. Lo, C. F. Chiang, J. L. Kuo, H. H. Chu, H. C. Su, L. F. Yu, H. C. Hu and Y. H. Chang, Predicting effluent from the wastewater treatment plant of industrial park based on fuzzy network and influent quality, Appl. Math. Model., 2011, 35, 3674–3684 CrossRef
.
- M. Huang, J. Wan, K. Hu, Y. Ma and Y. Wang, Enhancing dissolved oxygen control using an on-line hybrid fuzzy-neural soft-sensing model-based control system in an anaerobic/anoxic/oxic process, J. Ind. Microbiol. Biotechnol., 2013, 40, 1393–1401 CrossRef CAS PubMed
.
- I. A. Essienubong, A.-I. Effiong Ndon and J. Etim, Fuzzy modeling and optimization of anaerobic co-digestion process parameters for effective biogas yield from bio-wastes, Int. J. Eng. Sci., 2020, 43–61 Search PubMed
.
- A. Hosseinzadeh, J. L. Zhou, A. Altaee, M. Baziar and X. Li, Modeling water flux in osmotic membrane bioreactor by adaptive network-based fuzzy inference system and artificial neural network, Bioresour. Technol., 2020, 310, 123391, DOI:10.1016/j.biortech.2020.123391
.
- M. Ansari, F. Othman and A. El-Shafie, Optimized fuzzy inference system to enhance prediction accuracy for influent characteristics of a sewage treatment plant, Sci. Total Environ., 2020, 722, 137878 CrossRef CAS PubMed
.
-
K. Yetilmezsoy, in Handbook of Environmental Materials Management, Springer International Publishing, 2019, pp. 2001–2046 Search PubMed
.
-
C. González-Figueredo, R. Alejandro Flores-Estrella and O. A. Rojas-Rejón, in Current Topics in Biochemical Engineering, IntechOpen, 2019 Search PubMed
.
- Y. D. Zhao, E. N. Yamoah and P. G. Gillespie, Regeneration of broken tip links and restoration of mechanical transduction in hair cells, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 15469–15474 CrossRef CAS PubMed
.
- D. S. Lee, C. O. Jeon, J. M. Park and K. S. Chang, Hybrid neural network modeling of a full-scale industrial wastewater treatment process, Biotechnol. Bioeng., 2002, 78, 670–682 CrossRef CAS PubMed
.
- D. S. Lee, P. A. Vanrolleghem and M. P. Jong, Parallel hybrid modeling methods for a full-scale cokes wastewater treatment plant, J. Biotechnol., 2005, 115, 317–328 CrossRef CAS PubMed
.
- M. von Stosch, R. Oliveira, J. Peres and S. Feyo de Azevedo, Hybrid semi-parametric modeling in process systems engineering: Past, present and future, Comput. Chem. Eng., 2014, 60, 86–101 CrossRef CAS
.
- S. Banihashemi, G. Ding and J. Wang, Developing a Hybrid Model of Prediction and Classification Algorithms for Building Energy Consumption, Energy Procedia, 2017, 110, 371–376 CrossRef
.
- S. J. McIlroy, A. M. Saunders, M. Albertsen, M. Nierychlo, B. McIlroy, A. A. Hansen, S. M. Karst, J. L. Nielsen and P. H. Nielsen, MiDAS: the field guide to the microbes of activated sludge, Database Search PubMed.
- N. Hvala and J. Kocijan, Design of a hybrid mechanistic/Gaussian process model to predict full-scale wastewater treatment plant effluent, Comput. Chem. Eng., 2020, 140, 106914, DOI:10.1016/j.compchemeng.2020.106934
.
- T. Větrovský and P. Baldrian, The Variability of the 16S rRNA Gene in Bacterial Genomes and Its Consequences for Bacterial Community Analyses, PLoS One, 2013, 8, 1–10, DOI:10.1371/journal.pone.0057923
.
- V. Aguiar-Pulido, W. Huang, V. Suarez-Ulloa, T. Cickovski, K. Mathee and G. Narasimhan, Evol. Bioinf. Online, 2016, 12, 5–16 Search PubMed
.
- K. Yu and T. Zhang, Metagenomic and metatranscriptomic analysis of microbial community structure and gene expression of activated sludge, PLoS One, 2012, 7, 38183 CrossRef PubMed
.
- L. Ye, R. Mei, W. T. Liu, H. Ren and X. X. Zhang, Machine learning-aided analyses of thousands of draft genomes reveal specific features of activated sludge processes, Microbiome, 2020, 8, 1–13 CrossRef PubMed
.
- P. E. Larsen, D. Field and J. A. Gilbert, Predicting bacterial community assemblages using an artificial neural network approach, Nat. Methods, 2012, 9, 621–625 CrossRef CAS PubMed
.
- J. L. Metcalf, Z. Z. Xu, S. Weiss, S. Lax, W. Van Treuren, E. R. Hyde, S. J. Song, A. Amir, P. Larsen, N. Sangwan, D. Haarmann, G. C. Humphrey, G. Ackermann, L. R. Thompson, C. Lauber, A. Bibat, C. Nicholas, M. J. Gebert, J. F. Petrosino, S. C. Reed, J. A. Gilbert, A. M. Lynne, S. R. Bucheli, D. O. Carter and R. Knight, Microbial community assembly and metabolic function during mammalian corpse decomposition, Science, 2016, 351, 158–162 CrossRef CAS PubMed
.
- K. L. Lesnik and H. Liu, Predicting Microbial Fuel Cell Biofilm Communities and Bioreactor Performance using Artificial Neural Networks, Environ. Sci. Technol., 2017, 51, 10881–10892 CrossRef CAS PubMed
.
- K. L. Lesnik, W. Cai and H. Liu, Microbial Community Predicts Functional Stability of Microbial Fuel Cells, Environ. Sci. Technol., 2020, 54(1), 427–436, DOI:10.1021/acs.est.9b03667
.
- H. Yuan, S. Sun, I. M. Abu-Reesh, B. D. Badgley and Z. He, Unravelling and Reconstructing the Nexus of Salinity, Electricity, and Microbial Ecology for Bioelectrochemical Desalination, Environ. Sci. Technol., 2017, 51, 12672–12682 CrossRef CAS PubMed
.
- J. Kuang, L. Huang, Z. He, L. Chen, Z. Hua, P. Jia, S. Li, J. Liu, J. Li, J. Zhou and W. Shu, Predicting taxonomic and functional structure of microbial communities in acid mine drainage, ISME J., 2016, 10, 1527–1539 CrossRef CAS PubMed
.
- H. Yuan, R. Mei, J. Liao and W. T. Liu, Nexus of stochastic and deterministic processes on microbial community assembly in biological systems, Front. Microbiol., 2019, 10, 1–12, DOI:10.3389/fmicb.2019.01536
.
- I. Vanwonterghem, P. D. Jensen, P. G. Dennis, P. Hugenholtz, K. Rabaey and G. W. Tyson, Deterministic processes guide long-term synchronised population dynamics in replicate anaerobic digesters, ISME J., 2014, 8, 2015–2028 CrossRef CAS PubMed
.
- J. S. Griffin and G. F. Wells, Regional synchrony in full-scale activated sludge bioreactors due to deterministic microbial community assembly, ISME J., 2017, 11, 500–511 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2022 |


