Superb energy density of PbHfO₃-based antiferroelectric ceramics via regulating the antiferroelectric–ferroelectric transition energy barrier†

Jiawen Hu‡ ^a, Zihao Zheng‡ ^c, Tao Zhang ^c, Ling Lv ^a, Zhixin Zhou ^a, Jinjun Liu ^a, Peng Li ^b, Yunye Cao *^a, Jinming Guo *^c and Zhongbin Pan *^a
aSchool of Materials Science and Chemical Engineering, Ningbo University, Ningbo, Zhejiang 315211, China. E-mail: panzhongbin@163.com; caoyunye@nbu.edu.cn
^bSchool of Materials Science and Engineering, Liaocheng University, Liaocheng, Shandong 252059, China
^cElectron Microscopy Center, Ministry-of-Education Key Laboratory of Green Preparation and Application for Functional Materials, School of Materials Science and Engineering, Hubei University, Wuhan 430062, China. E-mail: guojinming@hubu.edu.cn

First published on 30th August 2024

---

---

1. Introduction

Electrostatic capacitors based on dielectric materials are essential components in electronic devices and electrical power systems, valued for their ultrahigh power densities, ultrafast charging and discharging rates, high voltage endurance, and exceptional reliability.^1–4 However, the energy densities of current commercial dielectric capacitors are generally low, particularly given the miniaturization and integration needs of the electronics industry.^5–7

Energy storage in dielectric capacitors primarily depends on the dielectric materials, which traditionally include linear dielectrics, ferroelectrics (FE), relaxor ferroelectrics (RFE), and antiferroelectrics (AFE).^8,9 Among them, AFE materials show exceptional energy storage potential due to their unique field-induced AFE-FE phase transition, ¹⁰e.g. PbZrO₃ (PZO)-based,^11–14 AgNbO₃-based,¹⁵ and NaNbO₃-based AFE materials.^16,17 The first discovered AFE material of PZO has historically dominated research in this area. Since Kittel introduced the concept of antiferroelectricity in 1951,¹⁸ various AFE systems based on Pb(Zr, Ti)O₃ (PZT),¹⁹ (Pb, La) (Zr, Ti)O₃ (PLZT),¹² (Pb, La) (Zr, Sn, Ti)O₃ (PLZST),^9,20,21 and other PZO-based compositions have been developed. The Hf element as a homologous group element of Zr is expected to completely replace Zr in compositions to achieve higher energy storage performance. Despite the crystal structure similarity to PZO at room temperature, PbHfO₃ (PHO) has been less explored for energy storage due to its poor sinter ability and higher cost.²² Recently, Wei et al. prepared PHO ceramics by rolling process and obtained a high energy density (W_rec) of 7.6 J cm⁻³ at 270 kV cm⁻¹,²³ demonstrating the potential of PHO-based AFEs for energy storage applications. However, pure PHO faces limitations in energy storage performance due to its low phase switching field (E_AF/FA) and significant hysteresis width, indicating a need for further enhancement.

For typical AFE materials, the small energy difference between the nonpolar AFE phase and the polar FE phase makes the AFE-FE phase transition easy to occur under the influence of an external electric field. Consequently, polarization quickly reaches saturation when an electric field is applied. Doping with small-radius ions at the A-site of the perovskite structure can mitigate this issue.^24–29 By enhancing the energy barrier of the AFE-FE transition through small-radius ion doping, the AFE state can be stabilized, thereby optimizing the E_AF/FA. For example, Zhang et al. designed Sr-doped (Pb_0.97−xSr_xLa_0.02) (Zr_0.75Sn_0.195Ti_0.055)O₃ AFE ceramics, finding that as the Sr²⁺ content increased from 0 to 2.5 mol%, the E_AF increased from 120 to 245 kV cm⁻¹.³⁰ Similarly, Liu et al. demonstrated that doping Sr²⁺ doping in (Pb_{0.98 − x}La_0.02Sr_x) (Zr_0.9Sn_0.1)_0.995O₃ increased the E_AF from 235 to 315 kV cm⁻¹.²⁸ However, the enhanced stability of AFEs is often accompanied by a decreasing trend in the maximum polarization (P_max), which limits further improvements in energy storage performance.

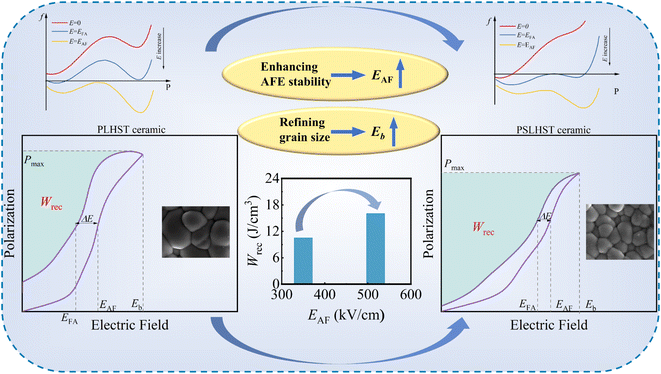
Here, Pb_0.925La_0.05(Hf_0.9Sn_0.1)O₃(PLHS) was chosen as the substrate to enhance the energy storage performance of the ceramics through the co-doping effect of Sr and Ti.^31,32 The introduction of Sr²⁺ ions at the A-site increased the AFE-FE phase transition barrier, while the introduction of Ti⁴⁺ at the B-site promotes the rapid transformation of the FE phase during the depolarization process, thereby compensating to some extent for the excessive decrease in P_max.^33,34 The performance optimization schematic is shown in Fig. 1. By coordinating the positions of the AFE and FE states in the energy path, a high P_max was achieved while stabilizing the AFE nature, resulting in a remarkable W_rec of 16.05 J cm⁻³. This paper provides a detailed analysis of the Pb_0.925−xSr_xLa_0.05(Hf_0.89Sn_0.1Ti_0.01) (PSLHST) AFE ceramics, highlighting their significant potential for energy storage device applications.

2. Experimental procedure

Pb_0.925−xSr_xLa_0.05(Hf_0.89Sn_0.1Ti_0.01)O₃ (x = 0.00 (Sr0), 0.04 (Sr4), 0.05 (Sr5), 0.06 (Sr6), 0.07 (Sr7)) ceramics were prepared using conventional solid-phase reaction methods. The raw materials, comprising Pb₃O₄ (98%), SrCO₃ (99%), La₂O₃ (99%), HfO₂ (99.9%), SnO₂ (99.5%), and TiO₂ (99%), were initially weighed according to the stoichiometric ratio and 2 mol% excess of Pb₃O₄ was added to compensate for the loss of lead during sintering. The weighed powder was ball-milled with ethanol for 24 h. The ball-milled slurry was dried and calcined at 900 °C for 3 h to form a perovskite structure. The samples were then prepared by the press-banding method and heated at 500 °C for 10 h to remove PVA. After that, all the samples were sintered at 1360 °C for 3 h. The ceramic samples were polished to a thickness of 30 μm after sintering and coated with gold electrodes with a diameter of 2 mm for the analysis of their performance and structure.

The ceramic samples underwent phase analysis using the PANalytical Empyrean X-ray diffractometer (XRD) from PANalytical, a Dutch company. Surface morphology characterization was conducted using the Regulus 8230 scanning electron microscope (SEM) from China Hitachi Corporation. The dielectric properties, including dielectric constant and dielectric loss, were characterized using the TH2838A dielectric test and analysis system from China Tonghui Corporation. The ferroelectric properties of the samples were tested using the TF Analyzer 2000 ferroelectric tester from Polyk Corporation in the United States. The testing temperature was controlled using the TLRS-003 high and low-temperature cooling and heating system from China Tongguo Corporation. The local structural features of samples were observed using transmission electron microscopy (TEM) (Talos F200X).

3. Results and discussion

Fig. 2a illustrates the XRD patterns of PSLHST ceramics with varying Sr²⁺ contents, all presenting a singular perovskite structure devoid of noticeable secondary phases. The characteristic splitting of diffraction peaks (200) and (002) signifies the orthorhombic spatial arrangement characteristics of this phase.³⁵ XRD refinement of PSLHST ceramics using orthogonal phase Pbam as a structural model, showcased in Fig. S1.† The attained R_wp values within the range of 5.89–6.78% and χ² ranging from 2.48–3.24. The variation trend of cell volume and lattice parameters (a, b, and c) related to Sr²⁺ content is detailed in Fig. 2b. As Sr²⁺ content increases, the unit cell volume decreases from 553.715 ų to 553.407 ų due to the substitution of the larger Pb²⁺ ion (1.49 Å) with the smaller Sr²⁺ ion (1.27 Å). The microstructure of the Sr5 ceramic was observed using TEM. The Pbam phase structure in the [001] direction fits well with the selected area electron diffraction (SAED) pattern within the I region of Fig. 2c, especially the 1/4 superlattice diffraction with obvious AFE characteristics can be observed, as marked by the red arrow in Fig. 2d. This corresponds to the antiparallel displacement of Pb²⁺ ions in the diagonal direction within the (001)pc (where pc designates pseudo-cubic) crystallographic plane. Combined with the results of XRD refinement, the ceramic's room-temperature phase structure is demonstrated to be an orthorhombic Pbam phase.

The Raman spectra of the PSLHST ceramics were measured at room temperature to delve into the influence of Sr²⁺ doping on the local structure of the ceramic samples, presented in Fig. 2f. Given the sensitivity of low-frequency modes to crystal structure changes and phase transitions, the analysis here focuses specifically on the variations of Raman peaks within the range of 0 to 200 cm⁻¹. Notably, the displacement Raman peak of oxygen ions concerning Pb²⁺ ions at 130 cm⁻¹ gradually widens with increasing Sr²⁺ content (Fig. S2†).³⁶ This phenomenon suggests a replacement of the A-site cations by smaller-radius ions, reducing cation disorder. Prior studies indicate that this structural adjustment might induce an antiparallel polar order in the AFE phase, potentially enhancing AFE stability.²⁷

Fig. 3f showcases the temperature-dependent characteristics of the dielectric constant in PSLHST ceramics with varying Sr²⁺ contents at a frequency of 1000 kHz. As the temperature increases, three prominent dielectric anomaly peaks, labeled as T₀, T₁, and T₂, emerge, corresponding to the AFE_I-AFE_II, AFE_II-multicell cubic (MCC), and MCC-PE phase transitions, respectively. The presence of the MCC state is attributed to the thermodynamic instability of the PbSnO₃ solid solution. ^29,37,38 Within this phase region, the ceramics demonstrate a relatively stable crystal structure characterized by an orderly and relatively fixed arrangement of electric dipoles, resulting in a dielectric constant that remains relatively stable and impervious to temperature fluctuations. The expansion of the MCC phase region with increasing x augments the stability of the AFE.³⁹ Simultaneously, the maximum dielectric constant diminishes as x increases, leading to a decrease in the electrostatic force received at the sample surface, facilitating the realization of high E_b. Based on the aforementioned analysis, the temperature-composition phase diagram for PSLHST ceramics was graphed, as depicted in Fig. S2a.† These diagrams facilitate the examination of the temperature range corresponding to each phase of PSLHST ceramics and the correlation between phase transition temperature and Sr²⁺ content.

The polarization electric field (P–E) hysteresis lines and current-electric field (I–E) loops of PSLHST ceramics with different Sr²⁺ contents at 100 Hz are shown in Fig. 4a and S2b.† Due to typical AFE properties, all ceramics exhibit near-zero remnant polarization (P_r). The multistage phase transition under the action of an electric field contributes to a large P_max.^40,41 As expected, the substitution of the large-radius ion Pb by the small-radius ion Sr²⁺ decreases the tolerance factor, thereby enhancing the stability of the AFE phase.³⁴ With increasing Sr²⁺ content, both the electric field for E_AF and E_FA are bolstered, elevating from 350 kV cm⁻¹ and 293 kV cm⁻¹ to 552 kV cm⁻¹ and 508 kV cm⁻¹, respectively (Fig. 4b). This augmentation in E_AF and E_FA expands the area between the phase-switching rings, amplifying the overall energy storage capability. Additionally, the reduced ΔE minimizes the hysteresis width, thereby enhancing energy storage efficiency (η). Introducing a small amount of Ti mitigates the decline in polarization caused by the substitution of Sr for Pb, as observed in Fig. 4c. Despite the decreasing trend in P_max with increasing Sr²⁺ content, it remains notably high at x = 0.05, reaching 47.07 μC cm⁻².

The enhanced AFE stability and P_max can be elucidated using a simplified Landau–Devonshire theoretical model. The corresponding polarization, energy, and electric field functions can be described as follows:

where G_o(T) is a temperature-only term, α, β, and γ are the thermodynamic coefficients, E is the electric field and P is the polarization. By constructing a pathway that describes the energy potential required for the gradual change of net polarization from 0 (AFE) to P (FE), it is investigated whether the energy gap between these two states can be thermally traversed by injecting electrostatic energy. In Fig. 4d, when P > 0, the three extreme points (∂G/∂P = 0) P₁, P₂, and P₃, correspond to three energy states: P₁ represents the AFE state, P₂ is the barrier state, and P₃ represents the FE state. When E = 0, the high intrinsic barrier makes the transition between P₁ and P₃ difficult to cross, stabilizing the system in the AFE state. As the E gradually increases, the FE state P₃ gradually tends to stabilize, and the barrier P₂ decreases accordingly. When the barrier between P₁ and P₂ becomes sufficiently low, the AFE-FE transition begins. At this point, the system begins to occupy a steady state dominated by the FE state P₃, resulting in a peak in polarization. After removing the electric field, the electric dipole moments in the lattice are rearranged, when the barrier between P₃ and P₂ can be thermally overcome, the reverse FE-AFE transition occurs. Therefore, this structural model can be used to solve the problem of AFE-FE transition.

In this paper, the introduction of Sr²⁺ stabilizes the AFE phase, leading to an increase in the energy barrier at state P₂, and the E_AF and E_FA are enhanced as designed (Fig. 4e). However, the increased P₁ steady state is accompanied by a leftward deviation of the path, which weakens the P_max to some extent and is not conducive to the overall energy storage performance. Conversely, a moderate amount of Ti⁴⁺ introduction appears to compensate for the excessive reduction in P_max to some degree. As illustrated in Fig. 4f, this compensation is associated with increased barriers at P₂ and the FE state P₃. Although the introduction of Ti⁴⁺ reduced the E_AF and E_FA, the resulting polarization amplification proved to be more conducive to the enhancement of the overall energy storage. In summary, adjusting the positions of P₁, P_2, and P₃ in the energy path allows for the significant enhancement of key parameters including E_AF, E_FA, ΔE, and P_max, thereby improving the overall energy storage performance of the system.

Fig. 5a shows W_rec, W_tol, and η across various Sr²⁺ contents under the E_b. With the increase of Sr²⁺ content, W_rec reaches a maximum value of 16.05 J cm⁻³ at x = 0.05, with η reaching 81%. Subsequently, W_rec gradually decreases while η remains stable at around 80%. Fig. 5b–d shows the specific characteristics of P_max, W_rec, η, and ΔP (P_max − P_r) as a function of the electric field. Notably, P_max, W_rec, and ΔP exhibit rapid increases with the onset of the AFE-FE phase transition, while at the same time, η shows a tendency to decrease first and then increase slightly before decreasing continuously. Fig. 5e summarizes the energy storage performance of ceramics of other systems reported in recent years, compared with other systems, PSLHST ceramics possess a high W_rec (16.05 J cm⁻³) and moderate η (81%), indicating significant potential for energy storage and pulsed power applications. These excellent properties are closely related to having a large E_b value. The E_b value can be evaluated using the Weibull distribution,⁴² where a higher slope parameter β indicates better fitting confidence (Fig. 5f). With the increase of Sr²⁺ content, β, and E_b increases from 7.37 and 557 kV cm⁻¹ to 16.51 and 748 kV cm⁻¹. These fitting results align well with the actual E_b values, indicating that the distribution model is fully applicable to the estimation of the electrical breakdown strength of PSLHST ceramics.

The size of the grain size is a critical factor affecting the size of the E_b value of ceramics. Fig. S3† shows an SEM image of PSLHST ceramics, All samples showcase a uniform and compact structure devoid of noticeable voids. Upon introducing Sr²⁺, a gradual refinement in grain size is observed, reducing the average grain size from 1.54 μm to 0.93 μm. This reduction in grain size significantly enhances the E_b. According to the relationship (E_b = 1/√G),⁴³ smaller grain sizes correspond to a greater value of E_b, as a decrease in grain size leads to a higher density of grain boundaries (Fig. 6a). Consequently, when an electric field is applied, charge accumulates at these boundaries, intensifying the E_b of the material. Using COMSOL, we visualize the dielectric breakdown process based on the SEM results. As depicted in Fig. 6b, high electric fields concentrate at grain boundaries, serving as the primary defense layer against dielectric breakdown. As the grain size decreases, the number of grain boundaries increases, resulting in a more uniform distribution of the electric field. However, over time, the electric field intensity at grain boundaries significantly escalates, causing a non-uniform potential distribution. Consequently, the equipotential lines gradually distort towards the lower boundary, and the electric tree gradually grows. Ultimately, the electric tree breaches the equipotential lines, and breakdown occurs at the point of the highest electric field.²⁷ Simulation results reveal that, within the same timeframe, the Sr4 sample experiences breakdown first (Fig. 6b and S4†), exhibiting the smallest nominal electric field value (Fig. 6c). This observation aligns with previous studies.^44–46

From a practical application standpoint, the stability of energy storage performance holds significant importance for capacitors intended for harsh environments. As shown in Fig. 7a and b, in a cyclic stability test of 10⁴ at 600 kV cm⁻¹, the P–E circuit consistently maintains a slender shape with stable P_max (W_rec variation rate less than 3.09%, η variation rate less than 2.35%), highlighting the exceptional fatigue resistance of Sr5 ceramics. After varying the frequency of the applied electric field from 10–100 Hz, the ceramic has a W_rec variation of less than 0.34% and an η variation of less than 2.62% (Fig. 7c and d), indicating that the ceramic has both a good frequency reliability.

The practical energy storage capabilities of Sr5 ceramics were evaluated through RLC circuits, focusing on their charging and discharging attributes. In Fig. 8a, the discharge waveforms under various electric fields illustrate significant increases in peak current (I_max), P_D, and current density (C_D) as the DC voltage rises from 40 kV cm⁻¹ to 600 kV cm⁻¹. Specifically, the I_max surged from 0.97 A to 20.25 A, both P_D and C_D escalated from their initial readings of 0.62 MW cm⁻³ and 30.9 A cm⁻² to final values of 193.5 MW cm⁻³ and 644.9 A cm⁻² (Fig. 8b), respectively. The calculations for W_dis were performed using the overdamped charge/discharge curve,^47–49 as shown in Fig. 8c. With a significant increase in time, W_dis reaches a plateau in a relatively short period. Fig. 8d shows W_dis and t_0.9 for each electric field. At a DC voltage of 600 kV cm⁻¹, the Sr5 ceramic displayed a large W_dis of 12.7 J cm⁻³ and a rapid discharge time of 106 ns. These findings strongly signify the considerable potential of Sr5 ceramics for applications in pulsed power capacitors.

4. Conclusion

In this study, Pb_0.925−xSr_xLa_0.05(Hf_0.89Sn_0.1Ti_0.01) AFE ceramics were synthesized via solid phase sintering. The introduction of Sr²⁺ ions at the A-site increases the AFE-FE phase transition barrier, thereby significantly enhancing AFE stability. Concurrently, grain size refinement strengthened the breakdown strength. Remarkably, P_max remained consistently high (>47.07 μC cm⁻²) under the influence of trace Ti⁴⁺ ions, even with Sr²⁺ content as high as 5 mol%. The results show that Sr5 ceramics exhibit excellent performance under an applied electric field of 640 kV cm⁻¹, achieving a large W_rec of 16.05 J cm⁻³ and an impressive η of 81%, surpassing most reported bulk ceramics. Additionally, the ceramic displayed robust fatigue resistance over 10000 cycles and demonstrated remarkable frequency stability W_rec variation <0.34 at 1–100 Hz. It also exhibited remarkable W_dis (12.7 J cm⁻³), P_D (193.5 MW cm⁻³), and rapid discharge time (t_0.9 = 106 ns) in practical applications. These advantages underscore the effectiveness of synergistically optimizing energy storage performance, significantly contributing to the development of ceramic capacitors with comprehensive energy storage capabilities.

Data availability

The data are available from the corresponding author on reasonable request.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

J. H., and Z. Z. contributed equally to this work. This work was supported by National Natural Science Foundation of China, China (Grant no. 52472126), Natural Science Foundation of Zhejiang Province, China (Grant no. LY21E020002), Guangdong Basic and Applied Basic Research Foundation, China (Grant no. 2022A1515140004) Natural Science Foundation of Ningbo City, China (Grant no. 2023J377).

References

1. Y. Cheng, Y. Feng, Z. B. Pan, P. Wang, J. J. Liu, L. Liang, J. H. Yu, J. W. Zhai and Q. Wang, Energy Environ. Sci., 2023, 16, 5881–5890 RSC .
2. H. Wu, F. Zhuo, H. Qiao, L. Kodumudi Venkataraman, M. Zheng, S. Wang, H. Huang, B. Li, X. Mao and Q. Zhang, Energy Environ. Mater., 2022, 5, 486–514 CrossRef CAS .
3. H. H. Wu, J. Zhu and T. Y. Zhang, Nano Energy, 2015, 16, 419–427 CrossRef CAS .
4. Z. B. Pan, L. M. Yao, J. W. Zhai, X. Yao and H. Chen, Adv. Mater., 2018, 30, 1705662 CrossRef PubMed .
5. M. Hoffmann, F. P. G. Fengler, B. Max, U. Schroeder, S. Slesazeck and T. Mikolajick, Adv. Energy Mater., 2019, 9, 1901154 CrossRef CAS .
6. H.-J. Kim, S. Morita, K. N. Byun, Y. Shi, T. Taniguchi, E. Yamamoto, M. Kobayashi, Y. Ebina, T. Sasaki and M. Osada, Nano Lett., 2023, 23, 3788–3795 CrossRef CAS PubMed .
7. W. Wang, Y. Yang, J. Qian, W. Shi, Y. Huang, R. Jing, L. Zhang, Z. Pan, V. Laletin, V. Shur, J. Zhai and L. Jin, Chem. Eng. J., 2024, 488, 151043 CrossRef CAS .
8. L. M. Tang, Z. B. Pan, J. H. Zhao, Y. H. Shen, X. Q. Chen, H. H. Li, P. Li, J. J. Liu and J. W. Zhai, Chem. Eng. J., 2023, 455, 140524 CrossRef CAS .
9. H. Wan, Z. Liu, F. Zhuo, J. Xi, P. Gao, K. Zheng, L. Jiang, J. Xu, J. Li and J. Zhang, J. Mater. Chem. A, 2023, 11, 25484–25496 RSC .
10. J. Yang, G. Ge, C. Chen, B. Shen, J. Zhai and X. Chou, Acta Mater., 2023, 257, 119186 CrossRef CAS .
11. Z. Fu, X. Chen, Z. Li, T. Hu, L. Zhang, P. Lu, S. Zhang, G. Wang, X. Dong and F. Xu, Nat. Commun., 2020, 11, 3809 CrossRef CAS PubMed .
12. K. Shang, W. Shi, Y. Yang, Y. Huang, V. Shur, V. Laletin, L. Zhang, R. Jing and L. Jin, ACS Appl. Mater. Interfaces, 2024, 16, 20458–20496 Search PubMed .
13. H. Zhao, R. Xu, M. J. Wang, G. Wang, H. C. Sun, X. Z. Wang, Q. S. Zhu, X. Y. Wei, Y. J. Feng and Z. Xu, Adv. Funct. Mater., 2024, 2316674 CrossRef CAS .
14. P. Zhao, S. Wang, H. Tang, X. Jian, X. Zhao, Y. Yao, T. Tao, B. Liang and S. G. Lu, Scr. Mater., 2021, 200, 113920 CrossRef CAS .
15. L. Zhao, J. Gao, Q. Liu, S. Zhang and J. F. Li, ACS Appl. Mater. Interfaces, 2017, 10, 819–826 CrossRef PubMed .
16. X. Yang, F. Zhuo, C. Wang, Y. Liu, Z. Wang, H. Tailor, C. He and X. Long, J. Mater. Chem. A, 2019, 7, 8414–8422 RSC .
17. A. Xie, H. Qi and R. Zuo, ACS Appl. Mater. Interfaces, 2020, 12, 19467–19475 CrossRef CAS PubMed .
18. C. Kittel, Phys. Rev., 1951, 82, 729–732 CrossRef CAS .
19. G. Shirane, K. Suzuki and A. Takeda, J. Phys. Soc. Jpn., 1952, 7, 12–18 CrossRef CAS .
20. Y. J. Feng, Z. Xu and X. Yao, J. Mater. Sci. Eng. B, 2003, 99, 499–501 CrossRef .
21. S. Jiang, L. Zhang, G. Zhang, S. Liu, J. Yi, X. Xiong, Y. Yu, J. He and Y. Zeng, Ceram. Int., 2013, 39, 5571–5575 CrossRef CAS .
22. B. Jaffe, R. S. Roth and S. Marzullo, J. Res. Natl. Bur. Stand., 1955, 55, 239–254 CrossRef CAS .
23. J. Wei, T. Yang and H. Wang, J. Eur. Ceram. Soc., 2019, 39, 624–630 CrossRef CAS .
24. W. Chao, L. Tian, T. Yang, Y. Li and Z. Liu, Chem. Eng. J., 2022, 433, 133814 CrossRef CAS .
25. G. Ge, K. Huang, S. Wu, F. Yan, X. Li, B. Shen and J. Zhai, Energy Storage Mater., 2021, 35, 114–121 CrossRef .
26. S. Jiang, J. Zhang, J. Wang, S. Wang, J. Wang and Y. Wang, Scr. Mater., 2023, 235, 115602 CrossRef CAS .
27. C. Li, M. Yao and X. Yao, J. Mater. Chem. A, 2023, 11, 18689–18701 RSC .
28. X. Liu, T. Yang and W. Gong, J. Mater. Chem. A, 2022, 10, 4137–4145 RSC .
29. H. Wang, Y. Liu, T. Yang and S. Zhang, Adv. Funct. Mater., 2019, 29, 1807321 CrossRef .
30. Q. Zhang, H. Tong, J. Chen, Y. Lu, T. Yang, X. Yao and Y. He, Appl. Phys. Lett., 2016, 109, 262901 CrossRef .
31. Y. Yu, Y. Zhang, K. Zou, G. Chen, Y. Zhang, H. Li, Y. Lu, Q. Zhang and Y. He, Ceram. Int., 2019, 45, 24419–24424 CrossRef .
32. Y. J. Zhang, P. Liu, K. R. Kandula, W. R. Li, M. Shen, Y. F. Qin, H. B. Zhang and G. Z. Zhang, J. Eur. Ceram. Soc., 2021, 41, 360–367 CrossRef CAS .
33. Y. Bao, M. Zhou, S. Yan, F. Cao, X. Dong and G. Wang, J. Eur. Ceram. Soc., 2019, 39, 4785–4793 CrossRef CAS .
34. X. Liu, Y. Li and X. Hao, J. Mater. Chem. A, 2019, 7, 11858–11866 RSC .
35. G. Shirane and R. Pepinsky, Phys. Rev., 1953, 91, 812–815 CrossRef CAS .
36. K. Huang, G. Ge, F. Yan, B. Shen and J. Zhai, Adv. Electron. Mater., 2020, 6, 1901366 CrossRef CAS .
37. D. Viehland, D. Forst and J. F. Li, J. Appl. Phys., 1994, 75, 4137–4143 CrossRef CAS .
38. Y. Zhao, X. J. Meng and X. H. Hao, Scr. Mater., 2021, 195, 113723 CrossRef CAS .
39. Y. Lu, S. S. Jiang, X. Y. Zhao, S. Guo, J. Zhang, K. D. Zhou and L. He, Ceram. Int., 2023, 49, 37881–37887 CrossRef CAS .
40. S. S. Jiang, J. Zhang, J. J. Wang, S. H. Wang, J. Wang and Y. J. Wang, Scr. Mater., 2023, 235, 115602 CrossRef CAS .
41. Y. Lu, S. Jiang, X. Zhao, S. Guo, J. Zhang, K. Zhou and L. He, Ceram. Int., 2023, 49, 37881–37887 CrossRef CAS .
42. A. Kishimoto, K. Koumoto and H. Yanagida, J. Mater. Sci., 1989, 24, 698–702 CrossRef CAS .
43. D. Li, D. Xu, W. Zhao, M. Avdeev, H. Jing, Y. Guo, T. Zhou, W. Liu, D. Wang and D. Zhou, Energy Environ. Sci., 2023, 16, 4511–4521 RSC .
44. X. Chen, Z. Sun, H. Li, J. Liu, P. Li, J. Zhai and Z. Pan, J. Eur. Ceram. Soc., 2024, 44, 2121–2127 CrossRef CAS .
45. X. Q. Chen, M. K. Wang, Z. B. Pan, H. H. Li, J. H. Zhao, L. M. Tang, J. J. Liu, P. Li, H. Z. Xie and J. W. Zhai, Chem. Eng. J., 2023, 467, 143395 CrossRef CAS .
46. J. Zhao, T. Hu, Z. Fu, Z. Pan, L. Tang, X. Chen, H. Li, J. Hu, L. Lv, Z. Zhou, J. Liu, P. Li and J. Zhai, Small, 2023, 19, 2206840 CrossRef CAS PubMed .
47. L. Lv, Z. Pan, J. Hu, Z. Zhou, H. Li, X. Chen, J. Liu, P. Li and J. Zhai, J. Mater. Chem. A, 2024, 12, 16108–16115 RSC .
48. W. B. Li, D. Zhou, L. X. Pang, R. Xu and H. H. Guo, J. Mater. Chem. A, 2017, 5, 19607–19612 RSC .
49. J. Hu, Z. Pan, L. Lv, Z. Zhou, X. Chen, H. Xie, J. Liu, P. Li and J. Zhai, Inorg. Chem. Front., 2024, 11, 4187–4196 RSC .

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta04971c.

‡ Co-authors.

This journal is © The Royal Society of Chemistry 2024