View PDF Version
 
DOI: 10.1039/D5CP01692D (Paper) Phys. Chem. Chem. Phys., 2025, Advance Article

Beyond the static picture: a machine learning and molecular dynamics insight on singlet fission†

Natalia Szczepkowska‡ , Iga Pręgowska‡, Diana Radovanovici and Luis Enrique Aguilar Suarez*
Amsterdam University College, Science Park 113, 1098 XG Amsterdam, The Netherlands. E-mail: l.e.aguilarsuarez@auc.nl; Tel: +31 020-525 8170

Received 5th May 2025 , Accepted 14th July 2025

First published on 16th July 2025

Abstract

Singlet fission (SF) is a promising mechanism to overcome the current efficiency limit in solar cells. Theoretical studies have focused extensively on static pairs of molecules, the minimum system where SF can occur. Our work presents a complementary two-step approach. First, we developed a neural network model to investigate correlations between selected descriptors and the SF driving force across a library of organic molecules. SHAP analysis suggests that ionization potential (IP) and the second-to-lowest triplet (T2) are the most influential features. Notably, SF-active and SF-inactive molecules exhibit distinct energy ranges: 2.0–3.0 eV vs. 3.7–4.5 eV for T2 and 5.0–6.5 eV vs. 8.0–9.5 eV for IP. Second, we performed a molecular dynamics simulation on the α-polymorph of 1,3-diphenylbenzofurane, which is SF-active. We followed the evolution of the electronic states and calculated electronic couplings within a diabatic framework. Values of electronic couplings suggest a charged-transfer mediated mechanism, with the largest electronic couplings (20 meV) observed in inter-stack pairs, and intra-stack pairs exhibiting lower values. This work attempts to illustrate how machine learning can uncover relationships that may be relevant in the design of SF materials, and highlight the role of structural changes in modulating electronic couplings.

1 Introduction

The conversion of sunlight to electricity has been extensively studied as a means of transitioning to more renewable methods for energy generation.1 However, a theoretical radiative efficiency limit of around 30% has been proposed for current inorganic-based solar cells with a single p–n junction,2 prompting exploration of different approaches in other families of organic and inorganic compounds. In addition to this search, several ongoing works have been dedicated to overcoming the efficiency limit by experimenting with new architectures. Examples of these approaches include multi-junction solar cells with stacked inorganic layers,3 the incorporation of perovskites4 and quantum dots,5–7 bio-inspired solar cells,8 and the development of organic photovoltaics. Within the latter category,9 particular attention has been paid to organic materials that exhibit multiple exciton generation (MEG).

Observed originally in 1965 in anthracene,10 and three years later in tetracene,11 singlet fission (SF)12,13 is a MEG and spin-allowed process that occurs in organic crystals. In this process, two free charge carriers may be formed upon absorption of a photon; a photochemically excited molecule transfers part of its energy to a neighboring molecule, resulting in the formation of a state in which two triplets are coupled. Fig. 1 shows a schematic representation in which a molecule in the first singlet excited state (S1) and a neighbor molecule in the ground state (S0) undergo SF to generate the 1TT state. This coupled state will eventually separate into two independent triplets (T1) that will move away from each other until they are harvested.14 SF is thermodynamically favored if the condition E(S1) ≳ 2E(T1) is met, i.e. the process is slightly exothermic, where E represents the energy of the corresponding excited state.


image file: d5cp01692d-f1.tif
Fig. 1 Depiction of the singlet fission process. Two neighboring molecules, one in the first singlet excited state (S1) and one in the ground state (S0) undergo the spin-allowed process to form two coupled triplets (1TT). The process may occur throughout different channels: (a) direct, (b) a two step mechanism by the formation of the cation (D+) and anion (D−), or (c) mediated by charge transfer states.

The underlying mechanism of the process has been debated, and experimental and theoretical evidence has been presented in an effort to determine the mechanistic pathways that are taking place. In Fig. 1 we can differentiate between: (a) a direct transfer mechanism in which the conversion occurs in a single step, (b) a two-step mechanism in which the cation (D+) and anion (D−) are formed and the process goes through these intermediaries, and finally (c) a charge-transfer (CT) mediated-mechanism15 in which the CT states are not involved directly in the process, but rather mixed with the singlet and triplet states facilitating the conversion.

In this simple picture, the excited states of most interest are S1 and T1 since these are the ones directly involved in the process. Nevertheless, there are some additional energetic considerations that must be taken into account when looking for new SF materials. For example, to avoid triplet–triplet loss it is crucial that the second triplet state (T2) lies higher in energy than S1, i.e. E(S1) < E(T2). If the process would occur via CT intermediates then E(S1) ≥ E(CT) ≥ 2E(T1). For this reason, it is necessary to understand and study the influence that these additional electronic states and structural parameters have on the SF process. In this context, machine learning (ML) algorithms offer the possibility to aid us in uncovering patterns or relationships within data that may be unapparent at first sight. This task can be achieved by not only evaluating the predictive power of the model, but also by analyzing the relative importance that the different descriptors have in describing our quantity of interest.

Previous works have demonstrated the applicability and predictive power of ML algorithms to study SF. Examples of these works include the use of a hierarchical approach, namely the sure-independence-screening-and-sparsifying-operator algorithm, to identify potential SF candidates from a library of 101 polycyclic aromatic hydrocarbons.16 Another work employed a random forest classifier on a library of four million cibalackrot17 derivatives to explore the influence of chemical substitution on the electronic properties of this indigo derivative.18 Moreover, binary classification models (namely support vector machines and decision trees) in combination with K-means clustering have been used to identify SF candidates, based on their biradical character, from a library of nearly half a million compounds.19 A recent model has studied the extrapolation of complete active-space self-consistent field (CASSCF) in pentacene crystals to have an understanding of the evolution of the SF process.20

Theoretical studies on SF have focused mainly on a static picture of a pair of molecules in vacuum, since, in principle, it is the smallest system where SF can occur.21 Studies exploring the dynamics of the process are needed to offer a deeper understanding of how SF occurs and, ultimately, offer guidance on the design of SF materials. Recent works have gone beyond the static pair model either by including the influence of the environment, studying larger ensembles22 and following the dynamics of the process. Sousa et al. studied the differences in electronic couplings for pairs and trimers, finding that similar conclusions can be drawn from both structural models.23 Furthermore, López et al. analyzed the evolution of electronic couplings due to vibrations and thermal motions in pentacene and doped B,N-pentacene.24

Our work focuses on applying a ML algorithm to identify correlations between input features and a target variable. For our purposes, the target variable of interest is the so-called driving force (DF) of the SF process which is mathematically defined as DF = E(S1) − 2E(T1). To achieve our goals, we have set up the following procedure: first, a neural network (NN) architecture was built to determine which of the explored input features have an influence on the target quantity DF. We built our own dataset of 150 different molecules that represent a broad range of chemical families. We have included examples of molecules previously pointed out in the literature as potential SF candidates. We also incorporated compounds that do not exhibit SF to verify that the NN is capturing accurately those compounds that do. For each of these compounds, we have chosen the following features: the second lowest singlet (S2), the second lowest triplet state (T2), electron affinity (EA), ionization potential (IP), as well as the number of total atoms as a sanity check.

To determine the influence of each parameter on DF, we used the Shapley additive explanations25 (SHAP) values. This analysis offers an insight into the importance that each descriptor has on the model, how it affects the target variable and its relative contribution with respect to other descriptors. We then performed a molecular dynamics (MD) simulation on a section of the α crystalline structure of 1,3-diphenylisobenzofuran (DPBF, Fig. 2), the known form exhibiting SF.26,27 With this, we studied how the vibrational motions in the crystal influence the evolution of electronic states as well as the effective electronic couplings in a diabatic representation. These couplings are a measurement of the probability of the process to occur. Our work focuses on studying how conformational changes during the ground-state dynamics affect the magnitude of the electronic coupling.


image file: d5cp01692d-f2.tif
Fig. 2 Chemical structure of diphenylbenzofurane; a polymorph of this compound exhibits singlet fission.

This paper is structured as follows: in Section 2 we outline the details for the generation of the dataset, the architecture of the NN, and the calculation of the SHAP values. We also present the outline of the setup for the MD simulations, the snapshot selection, and the calculation of the different parameters and electronic couplings. In Section 3, we discuss the results of the NN and the evolution of the electronic states and effective couplings throughout the simulation. Finally, we summarize our findings, discuss limitations, and present lines for future work.

2 Computational details

2.1 Dataset construction

Structures for 150 molecules, shown in Fig. S1–S6 in the ESI,† were optimized28–31 using density functional theory (DFT) at the ωB97X-D332/6-311G** level of theory. Vibrational analyses were performed to confirm that these optimized structures corresponded to local minima. Following this, the excitation energies for ten singlets and triplets in each compound were obtained with time-dependent DFT (TD-DFT) at the same level of theory as the geometry optimizations. The EA and IP were calculated as the energy difference between the neutral molecule and its anionic and cationic forms, respectively.

For each molecule, we calculated its corresponding DF using the S1 and T1 excitation energies and used this quantity as the target variable. The input features used for the ML model, which we will refer to as descriptors, were T2, S2, IP, EA, and number of atoms. All calculations were performed with the open-source ORCA33 package. The full dataset is available for download as a CSV file in the GitLab repository (link provided in the ESI†).

2.2 Neural network architecture and hyperparameter tuning

For our predictive model of the DF, we employed a feedforward NN implemented in PyTorch.34 We have explored three architectures: (a) a single-hidden layer model, (b) a two-hidden layer model, and (c) a two-hidden layer model with dropout regularization after the first layer. For architecture (a), we varied the size from 2 to 100 to identify differences in performance. For the extended architectures (b) and (c), we tested 64 and 32 nodes as the first and second hidden layer sizes, respectively.

For each of these architectures, we further evaluated ReLU, LeakyReLU, ELU as activation functions, in combination with three loss functions: mean squared error (MSE), mean absolute error (MAE) and Huber loss (see their mathematical definitions in Notes and references).§ The models were optimized with the adaptive moment estimation (Adam),35 and three training/testing splits were analyzed: 90/10, 80/20 and 70/30. To avoid overfitting and reduce training time, we implemented an early stopping if the value of the loss function did not improve after 20 consecutive epochs. The results of these runs are presented in Fig. S7–S35 in ESI.†

One architecture was chosen based on lower variability in MAE and coefficient of determination (R2) values across the different runs, and the configuration that consistently yielded the lowest values of MAE. To further test the robustness of the model, we employed a 5-fold cross-validation and explored five different learning rates: 0.01, 0.005, 0.001, 0.0005, and 0.0001. The optimal learning rate was chosen based on the lowest average validation loss.

For all the explored NN configurations, we computed the SHAP values to assess the importance of the features and the interpretability of the model. Beeswarm plots were generated to visualize the contribution of each of the descriptors (Fig. S7–S35 in ESI†). As a baseline comparison, we also performed a multiple linear regression to test whether the relationship between the features is predominantly linear or not.

2.3 Snapshots of the dynamics

The MD simulations for the DPBF crystal were performed using the GROMACS36 software. The initial crystal structure was obtained from the Cambridge Structural Database with deposition number 1428159.26 The force field for the DPBF molecule was generated and validated with the Q-Force37 software. The simulation box was constructed by replicating the unit cell along the three lattice vectors (2 × 2 × 2) to ensure proper periodic boundary conditions and preserve the crystalline environment. Energy minimization was performed using the steepest descent algorithm. Then, we performed an NVT equilibration at 300 K for 500 ps using the V-rescale thermostat, followed by an equilibration under NPT conditions (1 atm, 300 K) for 500 ps with the Parrinello–Rahman barostat. One MD production simulation was then carried out for 10 ns with a 2 fs time step. For the calculation of the electronic states we have recorded 100 snapshots (every 0.1 ns) and identified a single molecule in the center of the crystal as our reference for these calculations. For calculation of electronic couplings, due to limited computational resources, we selected five snapshots (every 2 ns) and in each of these, we identified three different pairs of molecules that are representative of the inter and intra-stack interactions.

2.4 Effective electronic couplings

The calculation of effective electronic couplings was performed using the GronOR38 package, in which a non-orthogonal configuration interaction approach is implemented.

As the first step of this methodology, we carried out individual state-specific CASSCF(6,6)/ANO-S-VDZP for the monomers in the identified pairs by performing state-average calculations and setting the weights to zero for those states that were not relevant. For each monomer, we described the S0, S1, T1, D+ and D− states. These molecular calculations were performed in the conformation arising from the MD simulations without optimization in order to retain the influence of structural changes. This first step allows us to account for orbital relaxation and non-dynamical electron correlation for the localized states resulting in non-orthogonal orbital sets. The CASSCF calculations were carried out with the OpenMolcas39 software.

Then, we constructed six many-electron basis functions (MEBFs) as (spin-adapted) anti-symmetrized products of the molecular wavefunctions to describe the states of interest in the pairs. These states are S0S0, S0S1, S1S0, 1TT, D+D−, and D−D+. The electronic couplings (V) between these diabatic states were estimated by:

 
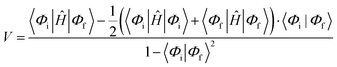image file: d5cp01692d-t1.tif(1)
where Ĥ represents the electronic Hamiltonian, and Φi and Φf denote the initial and final diabatic electronic states, i.e., the MEBFs. The influence of the CT states in the system was explored by allowing the CT states to mix with the photochemically excited states.

The reason behind calculating electronic couplings for only five snapshots is the limited resources available at our disposal since GronOR is intended for massively parallel computations.

3 Results and discussion

3.1 Machine learning algorithms and feature importance

3.1.1 Hyperparameter tuning and output of the model. The multiple linear regression (Fig. S36 in ESI†) led to an R2 = 0.2800 suggesting a non-linear relationship between the input features and the target variable, prompting the use of the NN to uncover potential non-linear patterns.

The results of the systematic NN exploration are summarized in Tables S1–S3 in the ESI.† In the following analysis, we examine the differences in MAE and R2 across variations in activation functions, loss functions and training/testing splits.

For architecture (a), which consists of a single hidden layer, the use of LeakyReLU generally resulted in modestly higher R2 values and lower MAE across all training/testing splits. For example, with a 70/30 split and MSE as the loss function, the MAE and R2 values were 0.2821 eV and 0.8132 (ReLU), 0.2804 eV and 0.8585 (LeakyReLU), and 0.3181 eV and 0.8488 (ELU). A similar trend was observed for the MAE values across the other two loss functions.

When comparing loss functions, no strong trends were observed among comparable runs (i.e., with a fixed activation function and training/testing split). However, Huber loss often achieved the lowest MAE, which is in line with its role as a balance between MSE and MAE.

Overall, the results for the three activation and loss functions in architecture (a) suggest similar performance across runs, with only a marginal advantage when using LeakyReLU.

For architecture (b), LeakyReLU again demonstrated the most stable and consistent performance across most splits and loss functions. In particular, for the 70/30 runs using MSE as the loss function, the registered MAE values were 0.2249 eV (ReLU), 0.2167 eV (LeakyReLU) and 0.2654 eV (ELU). Similarly, the use of Huber loss yielded the lowest MAE when in combination with the ReLU function.

For architecture (c), we observed a comparable performance between the ReLU and LeakyReLU activation functions with similar MAE and R2 values across runs. In this particular setting, Huber loss did not outperform the other two loss functions, and the ELU activation function showed the weakest performance. The latter may indicate that this activation function is less robust in the current architecture and for the explored hyperparameters in our dataset.

Comparison of performance among the three architectures shows that (b) and (c) achieved lower MAE and higher R2 values for runs with similar settings (training/testing, activation and loss functions). The performance of (b) shows lower variability than (c) which may indicate greater robustness and stability. In this regard, for the purposes of this study we prioritize robustness of the model rather than marginal gains in the R2 and MAE.

Based on the previous observations, we selected the following configuration for further testing by varying the learning rate and using 5-fold cross-validation: architecture (b), LeakyReLU as activation function and MSE as the loss function. Based on the results of the 5-fold cross validation, a learning rate of 0.005 was chosen.

Fig. 3 aggregates all the predicted and actual DF values obtained from the 5-fold cross validation on the selected configuration. The model achieved an average R2 of 0.8179 ± 0.0539.


image file: d5cp01692d-f3.tif
Fig. 3 Actual vs. predicted driving force (DF, in eV) obtained from the selected neural network model (architecture with two hidden layers, LeakyReLu, MSE loss function) trained with 5-fold cross validation. Predictions are aggregated across all folds. The red dashed line indicates the linear agreement.

A closer examination of the results reveals that the model appears to distinguish between compounds that exhibit SF, characterized by a DF close to zero, and those that do not, with values as large as −4.0 eV. For instance, the predicted DF for pentacene (compound 33 in Fig. S2 in ESI†) and tetracene (compound 34 in Fig. S2 in ESI†), both of which are known to undergo SF in the crystalline phase, are −0.20 eV and −0.42 eV, respectively. In contrast, compounds that do not exhibit the process, such as 4-methylphenol (compound 61 in Fig. S3 in ESI†) and 1-phenylethanone (compound 77 in Fig. S4 in ESI†) show larger predicted DFs of −3.13 eV and −2.97 eV, respectively.

Nevertheless, the model is unable to accurately predict DF for compounds with subtle DF differences. To illustrate this limitation, Fig. 4 compares the descriptors for compounds 31 and 32 (code used in Fig. S2 of the ESI†) as well as their predicted and calculated DF. Based on the calculated S1 and T1 energies, their calculated DFs differ by 0.063 eV. The model predicts nearly identical values, with a difference of only 0.003 eV, suggesting limited sensitivity to such changes. An inspection of the input descriptors reveals that the energies of the S2 and T2 states are nearly identical, with a difference of 0.017 eV and 0.001 eV, respectively. The number of atoms is also nearly identical. The largest differences arise in their IP (0.448 eV) and EA (0.671 eV). In the following section, we discuss the feature importance analysis which indicates that our model places a larger importance on IP than EA when predicting the DF.


image file: d5cp01692d-f4.tif
Fig. 4 Chemical structures of two molecules in the library that differ in their functional groups, a nitro substituent (31) and a nitrile group (32). The values of their descriptors are listed in the table. Excitation energies, electron affinity (EA) and ionization potential (IP) in units of eV.

These findings highlight the need to explore additional architectures beyond the presented NN, in order to construct a model that could fully capture the subtle differences arising from positional isomers and chemical substitutions. Additionally, expanding input features that reflect the crystal packing may help improve the current model.

3.1.2 Feature importance. One of the goals of this study is to identify trends among the molecular descriptors and the DF. These observations may inform the design of SF materials. In order to interpret the relationships captured by our NN model, we employed SHAP values to quantify the contribution that each descriptor had on the DF.

Fig. 5 presents a representative SHAP beeswarm plot (fold 1 of 5-fold cross validation) in which the descriptors are ordered top-to-bottom by their average absolute SHAP value. Additional plots for the remaining folds are presented in Fig. S37–S40 of the ESI.†


image file: d5cp01692d-f5.tif
Fig. 5 Beeswarm plot in which the descriptors have been ranked based on their mean absolute SHAP value. The following electronic states are represented: second triplet (T2), second singlets (S2), electron affinity (EA), ionization potential (IP) and total number of atoms (NumAtom). The feature value color scale represents the range of each feature. The presented plot is for fold 1 of cross-validation.

The SHAP plots reveal that IP and T2 are consistently the two most influential features. This ranking remained stable across all the cross-validation folds as well as across the runs exploring activation and loss functions (Fig. S7–S35 in ESI†). We calculated the mean SHAP values and standard deviations for each descriptor across the folds (Table 1). These results confirm that IP (0.8412 ± 0.1206) and T2 (0.4571 ± 0.0767) are the main features in the model prediction. In comparison, the EA, S2 and number of atoms exhibited lower average SHAP values and variable ranking, which suggests that their influence is dependent on the configuration of the model.

Table 1 Mean absolute SHAP values and standard deviation for each descriptor across 5 cross-validation folds
Descriptor SHAP Standard deviation
IP 0.8412 0.1206
T2 0.4571 0.0767
EA 0.2164 0.0264
Number of atoms 0.1476 0.0548
S2 0.0529 0.0154

To explore possible reasons for the influence of IP and T2 in our model, we examined the IP values for two representative samples of molecules from our library, one group with the molecules known to exhibit SF and the second with molecules that do not. Table 2 presents examples of both groups to illustrate the general trends.

Table 2 Descriptors for four representative molecules. Tetracene and pentacene are SF-active while 4-methylphenol and 1-phenylethanone are not. Units of the different electronic states are given in eV. The desriptors used as input features are presented in italics
Descriptor Tetracene Pentance 4-Methylphenol 1-Phenylethanone
S1 3.42 2.91 5.34 4.11
S2 3.94 3.69 6.35 5.34
T1 1.74 1.29 4.08 3.59
T2 2.94 2.35 4.29 3.83
IP 5.23 6.45 8.02 9.26
EA 1.68 1.17 1.75 0.23
Number of atoms 30 38 16 17

Our initial observations for the SF-active molecules suggest that the energy of the T2 states lies roughly within a range of 2.0–3.0 eV. For SF-inactive molecules in our set, these energies oscillated in a higher range between 3.7–4.5 eV. For SF-active molecules the T2 states are higher in energy than the S1 states; for example 1.20 eV for tetracene and 1.06 eV for pentacene. Opposite to this, T2 states in SF-inactive molecules lay closer to the corresponding S1 states (0.11 eV for 4-methylphenol and 0.24 eV for 1-phenylethanone). Experimentally, this may be beneficial since higher T2 states may reduce triplet–triplet annihilation. Nevertheless, further investigation is needed.

Regarding IP, we observed larger differences between the two groups. For SF-active molecules, these values lie within a range of 5.0–6.5 eV while for SF-inactive molecules it ranged from 8.0–9.5 eV. We speculate that these different ranges may contribute to the higher importance of this descriptor in the model.

Such differences in value ranges between the two molecular groups were not observed for EA. With the exception of 1-phenylethanone, which exhibited the lowest EA value (0.23 eV), both groups of molecules had values ranging between 1.0–2.0 eV. This lack of differentiation may explain the relative lower impact on the model. Similarly, the number of atoms was the second-to-last feature in terms of importance with S2 having the lowest (mean) SHAP value.

At present, we do not have a clear chemical interpretation of the observation that the number of atoms had a higher relative importance than S2, which may reflect limitations of the current model in our data set. Additionally, expanding our analysis to feature interactions may reveal further non-linear patterns within the molecular descriptors.

3.1.3 Evolution of electronic states and effective couplings. The average values for T2 (in Table 3) show that this state is higher in energy (3.50 ± 0.03 eV) than S1 (3.29 ± 0.07 eV), which is one of the energetic requirements proposed for SF to take place. The values throughout the simulation are consistent with the overall SF requirement in which E(S1) ≈ 2E(T1). However, this is not the case for all levels of theories and methodologies explored and presented in Table 3 highlighting the importance of further benchmarking.
Table 3 Vertical excitation energies of the S1, S2, T1 and T2 electronic states, and the electron affinity (EA) and ionization potential (IP) for an optimized structure of DPBF calculated at different levels of theory and in units of eV. Not available (NA)
Method S1 S2 T1 T2 EA IP
B3LYP 3.18 3.95 1.90 3.28 0.35 6.45
BHANDLYP 3.44 4.54 1.89 3.37 0.20 6.40
CAM-B3LYP 3.47 4.54 1.98 3.44 0.33 6.97
ωB97X-D 3.28 4.77 1.46 3.54 0.23 6.68
ADC(2) 3.52 3.84 2.30 NA — —
Experimental40 3.16 NA 1.47 NA NA NA

Table 4 collects the average values and standard deviations across 100 different snapshots, of vertical excitation energies, EA and IP of a single molecule in vacuum taken from the crystal during the MD simulation. The standard deviations below 0.1 eV suggest that the changes due to vibrational modes had a negligible influence on the energies of the different states. It is worth stressing that we have considered a single molecule of DPBF in vacuum for these calculations, and that inclusion of the environment could point towards another direction since additional intermolecular interactions could play a significant role.

Table 4 Average values and standard deviations of different electronic states (in eV) calculated at the ωB97X-D/cc-pVDZ level of theory for 100 conformations of a single molecule of DPBF in the crystal structure
State Average value Standard deviation
S1 3.29 0.07
S2 3.89 0.04
T1 1.50 0.06
T2 3.50 0.03
EA 0.26 0.04
IP 6.66 0.02

In this work, we focused on studying the α-polymorph of DPBF, which is known to exhibit SF. We selected three pairs in the crystal structure as shown in Fig. 6. The first pair consists of monomers I and II that are representative of a π–π intra-stack interaction. The second pair corresponds to the one formed by monomers I and III; this represents an inter-stack interaction in which monomer III has an orthogonal disposition with respect to monomer I. The third pair is formed by monomers I and IV which also represents an inter-stack interaction. However, the monomers in the latter pair do not overlap. The difference between these dispositions is further exemplified by the distance of separation (ds) between the centers of mass of the different monomers: for pair I–II, ds = 5.59 Å, ds = 7.08 Å for pair I–III, and ds = 12.66 Å for pair I–IV.


image file: d5cp01692d-f6.tif
Fig. 6 (a) Representation of a portion of the crystal structure in which the three pair arrangements are indicated. Monomers I and II represent a pair with intra-stack interaction, while the pairs involving molecules I and III, and I and IV represent inter-stack dispositions. (b) Individual depictions of the dispositions between the pairs of molecules.

Table 5 collects the effective electronic couplings between the pairs (in vacuum) for the five different snapshots recorded during the ground-state MD simulation. These electronic couplings are divided into two sets: (1) one in which the CT states are not allowed to mix, and (2) one set in which these states were allowed to do so.

Table 5 Direct (not mixing allowed) and-charge transfer (CT) mediated electronic couplings (in meV) between the electronic states S0S1 and 1TT for each of the pairs identified in the crystal structure of 1,3-diphenylbenzofurane. The CT states were allowed to mix with these states for the calculation of the CT-mediated couplings
Snapshot Not mixing Mixing of CT states
I–II I–III I–IV I–II I–III I–IV
1 2.1 7.0 0.0 11.4 23.2 0.1
2 2.3 5.9 0.0 15.4 25.1 0.2
3 3.1 6.3 0.0 9.8 21.5 1.1
4 2.7 6.2 0.0 8.7 25.8 0.6
5 1.0 5.8 0.0 5.0 18.3 0.2

The magnitudes of the electronic couplings in set (2) are higher than those in set (1). This suggests that, in these snapshots, the mechanism appears to be CT-mediated, i.e., the CT states mix with the S0S1, S1S0, and 1TT states to facilitate the conversion.

The highest CT-mediated couplings are consistently observed for the I–III pair throughout the snapshots (with values ranging from 18.3 to 25.8 meV), and it corresponds to an inter-stack spatial conformation. Smaller electronic couplings, in the range 5.0–15.4 meV, are observed in the I–II pair that represents the π–π intra-stack interaction. Finally, pair I–IV shows a negligible coupling all across the snapshots with values closer to 0 meV. This observation on pair I–IV could be related to its inter-stack disposition where the monomers have a large distance of separation (12.66 Å) which suggests an unfavorable disposition for electronic transfer.

The CT-mediated electronic couplings differ in approximately 10 and 7 meV for pairs I–II and I–III, respectively. These large differences in the couplings for a pair illustrate that subtle structural differences due to vibrational modes may have an impact on the coupling. A closer look at the structures of the pairs in snapshots 1 and 5, which presents the lower coupling value, reveals that in the latter, the phenyl rings of the structure are bent out-of-plane, as depicted in Fig. 7 when compared against the pair in snapshot 1. This bending could be related to a lower coupling due to less overlap. In the original experimental study,26 the authors suggested that this property was probably related to the inter-stack rather than intra-stack interactions. This is supported by the calculated electronic couplings presented in Table 5.


image file: d5cp01692d-f7.tif
Fig. 7 Superposition of the identified I–III pair in snapshots 1 (red) and 5 (blue) depicting the structural differences between the arrangements captured by the molecular dynamics simulation due to vibrational modes.

These coupling values also provide a qualitative estimation of the timescale over which SF may occur. For comparison, a previous study employed a fragment spin difference scheme to estimate SF rates based on calculated effective electronic couplings on pentacene.41 Their findings pointed to estimated SF rates of 239 and 37 fs for couplings of 15.21 and 37.30 meV, respectively. While our methodology differs, it provides a basis for interpreting the calculated couplings. Although we cannot predict SF rates by analogy, the magnitudes of our couplings (18.3 to 25.8 meV) suggest a sub-picosecond scale which is in line with the reported timescales in DPBF of around 10–30 ps.27 Moreover, the magnitude of the couplings computed in this work is comparable to previously reported NOCI couplings calculated for known SF molecules and potential candidates, which support the hypothesis that CT-mediated couplings could facilitate SF in DPBF.24

Conclusions

In this work, we adopted a combined computational approach to contribute to the discussion of how dynamics affect the singlet fission process. In this regard, we explored whether electronic states beyond S1 and T1 correlate with the driving force of the process. For this purpose, we constructed a library of 150 different molecules consisting of SF active and inactive compounds.

We trained a neural network model to analyze the influence on the driving force of the following features: S2, T2, EA, IP, and number of atoms. Our model distinguishes between SF-active and inactive molecules. However, it shows limitations when predicting DF for molecules that have subtle functional group variations and, hence, similar magnitudes of the input features. SHAP analysis suggests IP and T2 as the most influential features in the model, and subsequent inspection revealed non-overlapping value ranges for these two descriptors.

To improve the robustness of our model, we plan to expand the molecular library to account for a larger variety of chemical families. Additionally, we aim to incorporate additional features, particularly those that reflect molecular packing and crystalline properties to better reflect the environment in which SF occurs.

As an illustrative example, we studied the α-polymorph of 1,3-diphenylbenzofurane, a crystalline structure that exhibits singlet fission. We performed a molecular dynamics simulation in order to capture the vibrational motions, to study the effect that these have on electronic states and effective electronic couplings. Due to computational limitations, we calculated electronic couplings for pairs in five snapshots with the aim of providing a case study of how structural conformations influence the magnitude of the couplings.

The average and standard deviations calculated along the simulation for S1, S2, T1, T2, EA and IP of a molecule in the vacuum suggest that vibrational motions had little effect on the energies of the different electronic states. Nevertheless, further studies are needed in which the crystal environment is included to clarify whether this is indeed the case for DPBF.

In this study, we have selected three different pairs of DPBF molecules; one of which represents an intra-stack π–π interaction, and two other molecular pairs that represent the unique inter-stack interactions within the crystal. We have employed a non-orthogonal configuration interaction to calculate electronic couplings, within a diabatic framework, for five snapshots during the simulation. Our results reveal that for the crystalline structure, the strongest values are found in inter-stack pairs (defined in Fig. 6 as I and III) rather than in the intra-stack pair between molecules I and II.

Author contributions

Luis Suarez: conceptualization, methodology, formal analysis, investigation, supervision, writing – original draft. Natalia Szczepkowska: investigation, formal analysis, writing – neural network modeling. Iga Pręgowska: investigation, formal analysis, writing – linear regression modeling. Diana Radovanovici: investigation, writing – structured data analysis for electronic properties.

Conflicts of interest

There are no conflicts to declare.

Data availability

The supporting data for this article including: (a) the structures of the 150 molecules (as XYZ files), (b) the dataset constructed for the machine learning analysis (as a CSV file), (c) the neural network and multiple linear regression codes (as Python files), (d) the initial structure for the MD simulations as well as the corresponding MDP files and thr protocol used, (e) the coordinate files of the 100 snapshots used in the excited stated calculations and the 5 snapshots used for the coupling calculations(in XYZ format) are available in the following public GitLab repository: https://uva-hva.gitlab.host/l.e.aguilarsuarez/singletfission. ESI† (in PDF format) contains the chemical structures of the molecules studied, as well as additional information in the hyperparametrization tuning of the neural network and the results of the linear regression model.

Acknowledgements

The authors would like to express gratitude to Rubi Zarmiento Garcia for the fruitful discussion as well for the technical advice and support on the molecular dynamics simulations. This research was conducted using resources provided by the Amsterdam University College.

Notes and references

  1. M. Roelfsema, H. L. van Soest, M. Harmsen, D. P. van Vuuren, C. Bertram, M. den Elzen, N. Höhne, G. Iacobuta, V. Krey, E. Kriegler, G. Luderer, K. Riahi, F. Ueckerdt, J. Després, L. Drouet, J. Emmerling, S. Frank, O. Fricko, M. Gidden, F. Humpenöder, D. Huppmann, S. Fujimori, K. Fragkiadakis, K. Gi, K. Keramidas, A. C. Köberle, L. Aleluia Reis, P. Rochedo, R. Schaeffer, K. Oshiro, Z. Vrontisi, W. Chen, G. C. Iyer, J. Edmonds, M. Kannavou, K. Jiang, R. Mathur, G. Safonov and S. S. Vishwanathan, Nat. Commun., 2020, 11, 2096 CrossRef CAS PubMed .
  2. W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS .
  3. M. Yamaguchi, Phys. E, 2002, 14, 84–90 CrossRef CAS .
  4. D. Weber, Z. Naturforsch. B, 1978, 33, 1443–1445 CrossRef .
  5. Z. A. Peng and X. Peng, J. Am. Chem. Soc., 2001, 123, 183–184 CrossRef CAS PubMed .
  6. A. G. Pattantyus-Abraham, I. J. Kramer, A. R. Barkhouse, X. Wang, G. Konstantatos, R. Debnath, L. Levina, I. Raabe, M. K. Nazeeruddin, M. Grätzel and E. H. Sargent, ACS Nano, 2010, 4, 3374–3380 CrossRef CAS PubMed .
  7. L. Hu, Q. Zhao, S. Huang, J. Zheng, X. Guan, R. Patterson, J. Kim, L. Shi, C.-H. Lin, Q. Lei, D. Chu, W. Tao, S. Cheong, R. D. Tilley, A. W. Y. Ho-Baillie, J. M. Luther, J. Yuan and T. Wu, Nat. Commun., 2021, 12, 466 CrossRef CAS PubMed .
  8. C. Li, F. Wang and J. C. Yu, Energy Environ. Sci., 2011, 4, 100–113 RSC .
  9. X. Yang and J. Loos, Macromolecules, 2007, 40, 1353–1362 CrossRef CAS .
  10. S. Singh, W. J. Jones, W. Siebrand, B. P. Stoicheff and W. G. Schneider, J. Chem. Phys., 1965, 42, 330–342 CrossRef CAS .
  11. C. Swenberg and W. Stacy, Chem. Phys. Lett., 1968, 2, 327–328 CrossRef CAS .
  12. M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed .
  13. D. Casanova, Chem. Rev., 2018, 118, 7164–7207 CrossRef CAS PubMed .
  14. K. Miyata, F. S. Conrad-Burton, F. L. Geyer and X. Y. Zhu, Chem. Rev., 2019, 119, 4261–4292 CrossRef CAS PubMed .
  15. N. Monahan and X.-Y. Zhu, Annu. Rev. Phys. Chem., 2015, 66, 601–618 CrossRef CAS PubMed .
  16. X. Liu, X. Wang, S. Gao, V. Chang, R. Tom, M. Yu, L. M. Ghiringhelli and N. Marom, npj Comput. Mater., 2022, 8, 70 CrossRef .
  17. J. L. Ryerson, A. Zaykov, L. E. Aguilar Suarez, R. W. A. Havenith, B. R. Stepp, P. I. Dron, J. Kaleta, A. Akdag, S. J. Teat, T. F. Magnera, J. R. Miller, Z. Havlas, R. Broer, S. Faraji, J. Michl and J. C. Johnson, J. Chem. Phys., 2019, 151, 184903 CrossRef PubMed .
  18. F. Weber and H. Mori, npj Comput. Mater., 2022, 8, 176 CrossRef CAS .
  19. L. Borislavov, M. Nedyalkova, A. Tadjer, O. Aydemir and J. Romanova, J. Phys. Chem. Lett., 2023, 14, 10103–10112 CrossRef CAS PubMed .
  20. Z. Li, F. J. Hernández, C. Salguero, S. A. Lopez, R. Crespo-Otero and J. Li, Nat. Commun., 2025, 16, 1194 CrossRef CAS PubMed .
  21. M. F. S. J. M. Luis Enrique Aguilar Suarez and S. Faraji, Mol. Phys., 2020, 118, e1769870 CrossRef .
  22. L. E. Aguilar Suarez, C. de Graaf and S. Faraji, Phys. Chem. Chem. Phys., 2021, 23, 14164–14177 RSC .
  23. C. Sousa, A. Sánchez-Mansilla, R. Broer, T. P. Straatsma and C. de Graaf, J. Phys. Chem. A, 2023, 127, 9944–9958 CrossRef CAS PubMed .
  24. X. López, T. P. Straatsma, A. Sánchez-Mansilla and C. de Graaf, J. Phys. Chem. C, 2023, 127, 16249–16258 CrossRef PubMed .
  25. S. M. Lundberg and S.-I. Lee, Advances in Neural Information Processing Systems 30, Curran Associates, Inc., 2017, pp. 4765–4774 Search PubMed .
  26. J. L. Ryerson, J. N. Schrauben, A. J. Ferguson, S. C. Sahoo, P. Naumov, Z. Havlas, J. Michl, A. J. Nozik and J. C. Johnson, J. Phys. Chem. C, 2014, 118, 12121–12132 CrossRef CAS .
  27. J. N. Schrauben, J. L. Ryerson, J. Michl and J. C. Johnson, J. Am. Chem. Soc., 2014, 136, 7363–7373 CrossRef CAS PubMed .
  28. F. Neese, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS PubMed .
  29. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS .
  30. B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109 CrossRef CAS PubMed .
  31. F. Neese, J. Comput. Chem., 2022, 1–16 Search PubMed .
  32. Y.-S. Lin, G.-D. Li, S.-P. Mao and J.-D. Chai, J. Chem. Theory Comput., 2013, 9, 263–272 CrossRef CAS PubMed .
  33. F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2022, 12, e1606 Search PubMed .
  34. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Köpf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, PyTorch: An Imperative Style, High-Performance Deep Learning Library, arXiv, 2019, preprint, arxiv:1912.01703 DOI:10.48550/arxiv.1912.01703.
  35. D. P. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, arXiv, 2017, preprint, arxiv:1412.6980 DOI:10.48550/arxiv.1412.6980.
  36. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef .
  37. S. Sami, M. F. S. J. Menger, S. Faraji, R. Broer and R. W. A. Havenith, J. Chem. Theory Comput., 2021, 17, 4946–4960 CrossRef CAS PubMed .
  38. T. P. Straatsma, R. Broer, A. Sanchez-Mansilla, C. Sousa and C. de Graaf, J. Chem. Theory Comput., 2022, 18, 3549–3565 CrossRef CAS PubMed .
  39. G. Li Manni, I. Fdez Galván, A. Alavi, F. Aleotti, F. Aquilante, J. Autschbach, D. Avagliano, A. Baiardi, J. J. Bao, S. Battaglia, L. Birnoschi, A. Blanco-González, S. I. Bokarev, R. Broer, R. Cacciari, P. B. Calio, R. K. Carlson, R. Carvalho Couto, L. Cerdán, L. F. Chibotaru, N. F. Chilton, J. R. Church, I. Conti, S. Coriani, J. Cuéllar-Zuquin, R. E. Daoud, N. Dattani, P. Decleva, C. de Graaf, M. G. Delcey, L. De Vico, W. Dobrautz, S. S. Dong, R. Feng, N. Ferré, M. Filatov(Gulak), L. Gagliardi, M. Garavelli, L. González, Y. Guan, M. Guo, M. R. Hennefarth, M. R. Hermes, C. E. Hoyer, M. Huix-Rotllant, V. K. Jaiswal, A. Kaiser, D. S. Kaliakin, M. Khamesian, D. S. King, V. Kochetov, M. Krośnicki, A. A. Kumaar, E. D. Larsson, S. Lehtola, M.-B. Lepetit, H. Lischka, P. López Ros, M. Lundberg, D. Ma, S. Mai, P. Marquetand, I. C. D. Merritt, F. Montorsi, M. Mörchen, A. Nenov, V. H. A. Nguyen, Y. Nishimoto, M. S. Oakley, M. Olivucci, M. Oppel, D. Padula, R. Pandharkar, Q. M. Phung, F. Plasser, G. Raggi, E. Rebolini, M. Reiher, I. Rivalta, D. Roca-Sanjuán, T. Romig, A. A. Safari, A. Sánchez-Mansilla, A. M. Sand, I. Schapiro, T. R. Scott, J. Segarra-Mart, F. Segatta, D.-C. Sergentu, P. Sharma, R. Shepard, Y. Shu, J. K. Staab, T. P. Straatsma, L. K. Sørensen, B. N. C. Tenorio, D. G. Truhlar, L. Ungur, M. Vacher, V. Veryazov, T. A. Voß, O. Weser, D. Wu, X. Yang, D. Yarkony, C. Zhou, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2023, 19, 6933–6991 CrossRef CAS PubMed .
  40. A. F. Schwerin, J. C. Johnson, M. B. Smith, P. Sreearunothai, D. Popović, J. Černý, Z. Havlas, I. Paci, A. Akdag, M. K. MacLeod, X. Chen, D. E. David, M. A. Ratner, J. R. Miller, A. J. Nozik and J. Michl, J. Phys. Chem. A, 2010, 114, 1457–1473 CrossRef CAS PubMed .
  41. C.-H. Yang and C.-P. Hsu, J. Phys. Chem. Lett., 2015, 6, 1925–1929 CrossRef CAS PubMed .

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01692d
‡ These authors contributed equally to this work.
§ Here we provide the mathematical equations describing the three loss functions ([script L]) used during the tuning of our model.

(a) Mean squared error (MSE)

image file: d5cp01692d-t2.tif

(b) Mean absolute error

image file: d5cp01692d-t3.tif

(c) Huber loss (also known as smooth mean absolute error)

image file: d5cp01692d-t4.tif
where DFi denotes the reference value of DF for compound i, image file: d5cp01692d-t5.tif represents the corresponding predicted value by our model, N is the total number of compounds in the data set, and δ is a threshold parameter that determines the when the function transitions from MSE to MAE. In our case, the default value used was 1.0.

This journal is © the Owner Societies 2025
Click here to see how this site uses Cookies. View our privacy policy here.