The mechanism of high pressure-induced phase transition in titanium dioxide: ab initio molecular dynamics simulations†
Zihe Caoa,
Yidong Zhaoa,
Zonghu Mab,
Xiaolu Chena,
Kai Lia,
Qiang Lu a and
Bing Zhang
a and
Bing Zhang *a
*a
aNational Engineering Research Center of New Energy Power Generation, North China Electric Power University, Beijing 102206, China. E-mail: zhangb@ncepu.edu.cn
bChina Huadian Engineering Co., Ltd, Beijing 100160, China
First published on 30th July 2025
Abstract
The phase transition behavior of anatase TiO2 nanocrystals under high pressure has attracted considerable attention; however, systematic understanding of the atomic-scale mechanism of the solid–solid phase transition remains unclear. Therefore, in the current work, TiO2 supercells of different sizes were constructed and the atomic rearrangement processes were investigated through ab initio molecular dynamics (AIMD) simulations. Under high pressure, TiO2 undergoes a structural phase transition from the anatase phase to the baddeleyite phase, accompanied by the coordination polyhedron transformation from [TiO6] octahedra to [TiO7] mono-capped trigonal prisms, following a non-diffusive transition pathway. The simulations reveal distinct structural transformation behaviors: the larger supercell exhibits a layer-by-layer transition with a reduced energy barrier (0.26 eV) compared to the smaller one. These findings contribute to the mechanistic understanding of structural phase transformations in TiO2 and provide insights into the rational design of pressure-sensitive crystalline materials.
1. Introduction
TiO2 exhibits excellent photocatalytic activity, as well as chemical and biological inertness,1–3 making it widely applicable in lithium-ion batteries,4 solar cells,5,6 and gas sensors.7,8 This material exhibits multiple polymorphic forms with at least ten reported phases.9 The connectivity patterns of [TiOx] polyhedra vary across different crystal phases, resulting in distinct properties.10 For instance, rutile features edge-sharing [TiO6] octahedra forming linear chains,11 while columbite arranges these octahedra in zig-zag chains. Anatase, rutile, and brookite are the primary ambient phases. Under high pressure, bulk anatase, rutile, or brookite undergoes a similar phase transition pathway: anatase/rutile/brookite → columbite → baddeleyite → TiO2-OI → TiO2-OII.12–14 These high-pressure phases show considerable potential for applications in photocatalysis, water splitting, and energy conversion, attributed to their narrow band gaps and exceptional photoelectric properties.15Under varying temperature and pressure conditions, TiO2 demonstrates complex and diverse phase transition behaviors.16–20 Temperature-driven transitions occur through nucleation and diffusion,19–21 while pressure-induced transformations require diamond anvil compression, shock waves, or laser effects.22 Kusaba et al.23 found that shock along the [100] direction most readily induces rutile-to-columbite transition. They also proposed a displacive rutile-to-fluorite mechanism, where the [100] and [001] directions of rutile transform into the [001] and [1−10] directions of fluorite, respectively. More recently, Jacqueline et al.24 elucidated the anatase–columbite transformation under high-pressure torsion through a shear strain model describing the (001) plane movement along the b-axis, with computational results suggesting an intermediate phase.
Furthermore, studies indicated that the crystal size of anatase significantly affects its high-pressure phase transition behavior.25–27 Particles smaller than 10 nm transform into an amorphous phase, 12 to 50 nm particles transition to the baddeleyite phase, and those larger than 50 nm transform into the columbite phase.28 Park et al.29 found that rice-shaped anatase nanoparticles showed a decreased bulk modulus while rod-shaped particles exhibited an increased bulk modulus under compression. Liu et al.25 compared hollow and solid anatase microspheres of identical diameters, observing the same anatase–baddeleyite–columbite sequence but different transition pressures (13.6 GPa and 11.5 GPa for hollow and solid spheres). Additionally, nanocrystals with various morphologies, such as TiO2 nanotubes30 and TiO2 nanowires,31 similarly exhibit distinct responses under high pressures.32
In recent years, computational approaches have been employed to address experimental limitations in capturing rapid transition dynamics. Lee et al.33 simulated anatase compression from 0 GPa to 70 GPa at different temperatures using machine learning potentials. At 300 K, highly ordered collective motion with {010} plane sliding produced a monoclinic baddeleyite phase at 20 GPa. At 2000 K, the transition involved both collective motion and diffusion of oxygen atoms, forming a cotunnite phase. Liu et al.34 induced rutile-to-columbite transition through applied shear strain, finding that strains exceeding 20.5% caused significant distortions, with Ti atoms shuffling along the 〈0−11〉 direction and dragging O atoms to new positions. However, microscopic understanding of phase transition pathways remains limited because empirical and machine learning potentials rely on pre-fitted parameters that may not accurately represent the structure changes and bond reorganization occurring during transitions.
Given the need for detailed microscopic understanding of phase transition mechanisms, AIMD simulations were employed to investigate pressure-induced structural evolution in anatase, using supercells of two different sizes to examine size effects. Cell parameters, Ti–O bond lengths, and structural changes in TiO2 during the dynamic process were analyzed to elucidate the mechanisms of the anatase-to-baddeleyite transformation. Furthermore, stress–strain analysis and changes in the formation energy of the system reveal the critical role of cell size in the high-pressure phase transitions of nanomaterials. This study offers theoretical insights into designing and optimizing anatase nanocrystals by exploring their high-pressure response mechanisms.
2. Computational methods
As shown in Fig. 1, 2 × 2 × 1 (48 atoms) and 2 × 2 × 3 (144 atoms) anatase TiO2 supercells were used as initial structures in the present work. Anatase TiO2 features a tetragonal structure, where [TiO6] octahedra are elongated along the [001] direction. Each octahedron is edge-sharing with four surrounding octahedra, forming zig-zag chains along the a and b-axes. The ratio of shared vertices to shared edges in the octahedra is 1 (4/4).35AIMD simulations were conducted using the Car–Parrinello Molecular Dynamics (CPMD) module36 in the Quantum ESPRESSO package.37 The exchange–correlation interactions between atoms were described using Vanderbilt ultrasoft pseudopotentials38 and the Perdew–Burke–Ernzerhof (PBE) functional39 within the generalized gradient approximation (GGA). The kinetic energy cutoffs for the smooth part of the electronic wave functions and the augmented electronic density were set to 40 Ry and 400 Ry,40 respectively. A fictitious electron mass of 400 a.u. and an integration time step of 5 a.u. were employed. All simulations were conducted under unbiased pressure, and the system was initialized at 300 K and then evolved without any thermostat. All atoms in the system were allowed to move freely. Experimental studies indicate that anatase TiO2 began to undergo a phase transition at 5 GPa.41 Dynamic simulations were performed for the 2 × 2 × 1 supercell at specific pressures within the range of 5–20 GPa and for the 2 × 2 × 3 supercell at 12 GPa.
Structural snapshots of the dynamic process over a simulation duration of 20 ps were extracted at 0.1 ps intervals. All static calculations were performed using the Vienna Ab initio Simulation Package (VASP).42,43 The stress–strain method was used to calculate elastic constants.44 To capture the structural characteristics of TiO2 at specific times and analyze any associated changes, the snapshot structures were not geometrically optimized. The Perdew–Burke–Ernzerhof (PBE) functional was used to characterize the non-local electron exchange–correlation interactions, while projected augmented wave (PAW) pseudopotentials45 were employed to represent the interactions between ionic cores and valence electrons. The cutoff energy for the plane-wave basis set was set to 600 eV, and k-point meshes were generated using the Monkhorst–Pack scheme. For the 2 × 2 × 1 supercell, an 8 × 8 × 6 k-point mesh was used, while a 5 × 5 × 1 k-point mesh was applied for the 2 × 2 × 3 supercell.
The X-ray diffraction (XRD) simulations of intermediate structures during the phase transition were conducted using the Reflex module in the Materials Studio software. The simulations employed Cu-Kα radiation (λ = 1.5418 Å) as the incident source, with a step size of 0.1°.
3. Results and discussion
3.1. Structural changes at different pressures
The anatase TiO2 supercell containing 48 atoms was dynamically simulated under pressures ranging from 5 to 20 GPa, with structural changes shown in Fig. 2.As the pressure increased from 5 GPa to 11 GPa, the supercell volume decreased linearly from 94% to 89% (Fig. 3a), while lattice parameter a only decreased by approximately 5% (Fig. S1, ESI†). This indicates that the overall shape of the supercell remained largely unchanged. Furthermore, the coordination numbers of Ti and O atoms, as well as the connectivity of the [TiO6] octahedra, remained consistent (Fig. 2a), suggesting that no phase transition occurred. Fig. S2 and S3 (ESI†) illustrate additional simulation details for pressure ranging from 5 to 11 GPa.
 | ||
| Fig. 3 (a) The volume of the 48-atom supercell at different pressures. RMSD curves of the (b) 48-atom system at 12 GPa, (c) 48-atom system at 20 GPa, and (d) 144-atom system at 12 GPa. | ||
When the pressure reached 12 GPa, the TiO2 system exhibited significant structural changes. The curve illustrating root mean square deviation (RMSD) of atomic motion (Fig. 3b) began to rise at 3 ps and stabilized at approximately 1.2 Å by 5 ps. The volume change, as shown in Fig. 3a, sharply dropped from 89% at 11 GPa to 82% at 12 GPa, suggesting a sudden alteration in the shape of the supercell. Ultimately, the coordination number of Ti atoms in the TiO2 crystal increased from 6 to 7, while the coordination numbers of O atoms were 3 and 4. Additionally, layers of three-fold- and four-fold-coordinated O atoms alternately arranged along the c-axis. Each [TiO7] polyhedron was connected to eight neighboring [TiO7] polyhedra via edge-sharing (Fig. 2b), with a vertex/edge-sharing ratio of 0.25 (2/8). When the pressure reached 19 GPa, the volume further dropped to 79%. The structure is shown in Fig. 2c, and the vertex/edge-sharing ratio of the [TiO7] polyhedron is 1 (6/6), indicating a phase transition. Although the atomic coordination numbers are identical to those in the baddeleyite phase, the connectivity of the [TiO7] polyhedra differs. In baddeleyite, each [TiO7] polyhedron connects to seven neighboring [TiO7] polyhedra through edge-sharing, with a vertex/edge-sharing ratio of 0.57 (4/7).46 According to the results of the experimental study by Catalin et al.,47 the transition structures may represent an intermediate state in the anatase–baddeleyite phase transition. (After structural optimization, the structure transforms to columbite, and further computational details are provided in Fig. S4, ESI.†)
Under a pressure of 20 GPa, the RMSD curve of atomic movements (as shown in Fig. 3c) sharply increased at 3 ps and reached a peak of approximately 2 Å at 3.5 ps. This finding implies that under high pressure, Ti and O atoms underwent simultaneous displacement and responded abruptly, leading to a rapid structural transformation of the system. After 3.5 ps, the RMSD curve slightly decreased and stabilized at around 1.5 Å by 4.5 ps, indicating that the atoms began to undergo local adjustments, with the movements of Ti and O atoms gradually diminishing and the structure starting to stabilize. The structure at 20 ps is shown in Fig. 2d, where the coordination number of Ti atoms is 7, and that of O atoms is 3 and 4. Alternating layers of three-fold- and four-fold-coordinated O atoms can be observed along the a, b, and c crystal orientations. Each [TiO7] polyhedron is connected to seven neighboring [TiO7] polyhedra via edge-sharing, with a vertex/edge-sharing ratio of 0.57 (4/7). It can be concluded that the baddeleyite phase has formed.
Additionally, we further dynamically simulated the 144-atom system under a pressure of 12 GPa. The RMSD curve of atomic movements began to oscillate and increase from 2 ps (Fig. 3d), indicating that under the current pressure, the atoms in the TiO2 system gradually adjusted their positions and reached a new equilibrium state. Ultimately, the curve stabilized at approximately 2.5 Å by 7 ps, and the coordination numbers of atoms in the phase transition product, as well as the connectivity of [TiO7] polyhedra, coincided with those observed in the 48-atom system at 20 GPa (the supercell structure is illustrated in Fig. S5, ESI†).
To further confirm the phase transition products, XRD simulations were performed on the structures of the 48-atom system at 20 GPa and the 144-atom system at 12 GPa after 20 ps. As shown in Fig. 4, the XRD diffraction peaks of both the 144-atom and 48-atom systems closely match those of the baddeleyite phase in terms of intensity and position.48,49 The diffraction peaks observed in the 48-atom system were relatively disordered. This was attributed to the sudden structural transformation under high pressure, preventing the atoms from adequately adjusting their positions and resulting in minor defects in the phase transition products.21 In contrast, at lower pressures, the atomic movement was slower and the phase transition took slightly longer, allowing the structure to gradually adjust to a stable state. Consequently, the 144-atom system exhibited a noticeable decrease in spurious peaks and a higher degree of crystallographic order. This finding indicates that smaller supercells have limitations in accommodating interatomic interactions during reactions,50 thereby influencing the crystal phase transition. These results revealed that under high-pressure conditions, anatase undergoes a phase transition to baddeleyite.
 | ||
| Fig. 4 XRD patterns of (a) anatase and (b) baddeleyite from ICSD; simulated XRD patterns of the (c) 144-atom structure and (d) 48-atom structure at 20 ps. | ||
3.2. Mechanism of the phase transition of anatase–baddeleyite
The size of the supercell plays a crucial role in high-pressure phase transitions.51 The cell evolution processes in different systems were further analyzed. As shown in Fig. 5a, the cell volumes of the 48-atom and 144-atom systems were decreased by 21% and 20%, respectively, both significantly higher than the theoretical volume reduction of 15%52 for the anatase–baddeleyite phase transition reported by Hearne et al. This discrepancy arises from the differences between the bulk structure and the nanostructure, as the theoretical calculations are based on bulk structures. As the volume decreases, the energy of the system increases, as shown in Fig. 5b. In the 48-atom system, the molecular energy of TiO2 increased by 0.72 eV, indicating an energy barrier of 0.72 eV for lattice deformation and Ti–O bond rearrangement. This value is very close to the density functional theory (DFT) calculation result of 0.71 eV53 reported by Song et al. In contrast, the 144-atom system exhibited an energy increase of 0.46 eV, corresponding to a decrease in the phase transition barrier by 0.26 eV. This finding suggests that larger anatase nanocrystals facilitate easier phase transitions.54 Furthermore, even after the phase transition is complete, the energy does not decrease due to the formation of a stable crystal phase but remains in a high-energy state. This partially explains why the baddeleyite phase cannot be preserved under ambient pressure. | ||
| Fig. 5 Variations in (a) the supercell volumes and (b) the potential energy of TiO2 during the phase transition; lattice parameter evolution for the (c) 48-atom system and (d) 144-atom system. | ||
At 4.5 ps, the supercell volumes of both systems had stabilized. However, at 4.3 ps, the lattice parameters α, β, and γ began to change significantly (Fig. 5c and d), indicating the onset of spontaneous supercell twisting. By 7 ps, the supercell shapes began to stabilize, with angles α, β, and γ for the 48-atom system being 86°, 94°, and 86°, respectively, and those for the 144-atom system being 94°, 94°, and 93°, respectively. The stabilized lattice parameters signify the completion of the phase transition process. In contrast, under pressures ranging from 12 to 19 GPa, the angles remained stable at around 90° (Fig. S6, ESI†), suggesting that the transition under such conditions leads to an intermediate phase. This observation highlights the critical role of lattice distortion in the phase transition pathway. Building upon Jacqueline et al.'s24 DFT calculations showing that shear deformation facilitates the phase transition, our dynamic simulations reveal that spontaneous lattice twisting naturally occurs during the transition, providing direct evidence that shear-related distortions are dynamically inevitable.
To further elucidate the microscopic mechanisms of the phase transition, we extracted structural snapshots from the dynamic simulations and observed the atomic reorganization process. In the initial stage of the phase transition for the 144-atom system (2–4.2 ps), the RMSD curve exhibited a significant increase; however, the Ti–O bond connections remained unchanged. The initial structure and the structure at 3.5 ps are shown in Fig. 6. In contrast to diffusional phase transitions observed at high temperatures, where the RMSD curve can exceed 20 Å,21 atomic movements under high pressure are non-diffusive, and the RMSD curve does not surpass 3 Å (Fig. 3d).
 | ||
| Fig. 6 (a) TiO2 structures (initial and 3.5 ps) and (b) and (c) partial TiO2 structures (initial and 3.5 ps). | ||
Analysis indicates that the amplitudes of Ti atomic movements across different {001} crystal planes differ. As shown in Fig. S7a (ESI†), the RMSD values for Ti4 and Ti8 reach up to 4 Å, whereas the RMSD values for Ti28 and Ti32 reach around 1 Å. The variation in the activity of Ti atom movements is manifested through the relative displacement of the {001} crystal planes. For instance, the atomic layers containing Ti17 and Ti21 move in the negative direction along the a-axis, while the layers containing Ti42 and Ti46 shift in the positive directions along both the a-axis and the c-axis (as indicated by the yellow arrows in Fig. 6a). During the structural evolution process, as shown in Fig. 6b and c, particularly, the O60 and O61 atoms are bound to the Ti32 atom. In the initial supercell, the O60–Ti32–O61 bond angle is 180°. Starting at 2 ps, with the sliding of the atomic layer, Ti32 moves 0.86 Å along the c-axis, thereby dragging the connected O60 and O61 atoms in the same direction. Concurrently, because O61 is also bonded to Ti30 and Ti22, Ti30 and Ti22 move 1.09 Å and 0.81 Å along the a-axis, respectively, subsequently pulling O61 some 1.27 Å along the a-axis, while O60 experiences only a displacement of 0.02 Å along the a-axis. Similarly, although O58 is also bound to Ti30, it is simultaneously bound to Ti24. Since Ti24 and Ti32 move in the same direction, the displacement of O58 is more significantly affected. These observations demonstrate that Ti and O atoms are mutually constrained, and through synergistic effects, they restrict the direction of sliding of the atomic layers. This ultimately results in a reduction of the supercell volume by approximately 20%.
From 4.3 ps onwards, the supercell continuously twists, with lattice parameters α and β varying by approximately 10°. Under strong perturbations, the atoms no longer exhibit collective displacement but instead show region-specific changes. We calculated the variations in the Ti–O bond length for each Ti atom (Fig. 7), from its initial [TiO6] octahedron to its final [TiO7] polyhedron, using 2.5 Å as the critical Ti–O bond length threshold.53 The crystal structure can be divided into two regions based on four distinct patterns of Ti–O bond length evolution. In the outer layer region (e.g. Ti36), between 4.3 and 4.5 ps, a new Ti–O bond is formed; after about 1 ps, one old Ti–O bond is broken while another new bond is generated. In the inner layer region (e.g. Ti30), between 4.6 and 4.9 ps, two new Ti–O bonds are formed simultaneously with the rupture of an old bond. Ti atoms at the boundary between the outer and inner layers, as highlighted in Fig. 8a, show two patterns. Specifically, in each plane containing four Ti atoms, two Ti atoms do not break any existing Ti–O bonds but directly form new ones, whereas the other two break two old bonds and simultaneously form three new bonds. These marked differences in the formation and rupture of Ti–O bonds suggests that the phase transition proceeds in a non-uniform manner, as different regions respond differently to high-pressure perturbations.
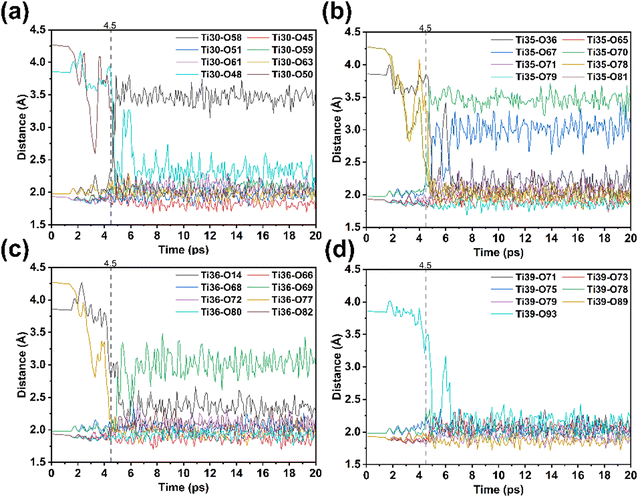 | ||
| Fig. 7 Changes in the (a) Ti30–O, (b) Ti35–O, (c) Ti36–O and (d) Ti39–O bond length during the phase transition. | ||
 | ||
| Fig. 8 (a) 144-atom supercell; TiO2 structures during the phase transition of the 144-atom system at (b) 4.5 ps, (c) 5 ps and (d) 20 ps. | ||
Analysis of the structures at 4.5 ps, 5 ps, and 20 ps (Fig. 8b–d) reveals distinct stages of the phase transition. At 4.5 ps, the Ti–O–Ti bond angles in the outer region are already very close to those observed at 20 ps, implying that the [TiOx] polyhedral connections have largely stabilized. For instance, in the outer layer region, the Ti48–O74–Ti40 bond angle at 4.5 ps differs by only about 5° from that in the 20 ps structure, whereas in the inner region, the Ti32–O42–Ti24 bond angle differs by approximately 32°. Correspondingly, the [TiOx] polyhedra around Ti48 and Ti40 share edges, whereas those around Ti32 and Ti24 share O atoms. By 5 ps, the Ti–O bonds in the inner region have undergone full reconfiguration, and all [TiO7] polyhedra are formed, which generally coincides with the connectivity of the baddeleyite. At 7 ps, the supercell shape becomes stable, and the Ti–O bonding network subsequently stabilizes, ultimately yielding a stable monoclinic baddeleyite phase.
The 48-atom system exhibits a more rapid strain response under 20 GPa, characterized by a significant reduction in unit cell volume and the formation of a plateau between 3.3 and 4.3 ps. Similar to the dynamic process observed in the 144-atom system, slippage occurs across different crystal planes (Fig. 9a and b), resulting in a decrease in the volume. Due to the higher applied pressure, the mobility of Ti atoms on various crystal planes becomes comparable (Fig. S7b, ESI†), leading to significant atomic displacements uniformly across the system. At 4.5 ps, the unit cell parameters α and β change abruptly, with the twisting of the unit cell facilitating the formation of new Ti–O bonds and the establishment of a metastable structure in a single step. The resultant TiO2 structure remains stable within the 4.5–6.5 ps timeframe, with the vertex/edge-sharing ratio of the [TiO7] polyhedra measured at 0.57, matching the structural characteristics of baddeleyite. However, the Ti–O bonds that form the tetragonal pyramids within the polyhedra are unstable. Consequently, at 6.5 ps, the supercell undergoes another twisting event, altering the connections of the Ti–O bonds within the [TiO7] polyhedra. As shown in Fig. 9c and d, in the metastable structure, Ti16 is connected to O12, and Ti11 is connected to O19. Due to shear deformation, the Ti16 atom detaches from the left-hand O12 atom and forms a new Ti–O bond with the right-hand O19 atom. Similarly, the Ti11 atom establishes a new Ti–O bond with the O12 atom. Throughout this process, the positions of Ti and O atoms are only slightly adjusted without significant atomic displacements, ultimately completing the phase transition and forming a stable baddeleyite phase.
 | ||
| Fig. 9 TiO2 structures during the phase transition of the 48-atom system at (a) 3.3 ps, (b) 4.3 ps, (c) 4.5 ps and (d) 6.5 ps. | ||
The comprehensive analysis indicates that phase transition is affected by both energy variations and dynamic processes. When the supercell size is tripled along the c-axis, the phase transition pressure decreases from 20 GPa to 12 GPa, and the transition barrier is reduced by 0.26 eV, while the volume change remains comparable. At the initial stage of the phase transition, atoms exhibit vigorous movements, and the {001} crystal planes undergo slippage. As the volume contracts and energy accumulates, the necessary force driving the phase transition is provided, promoting crystal deformation and ultimately completing the phase transition.
3.3. Stress–strain analysis
The uniform pressure applied during the dynamic process induces crystal cell twisting due to differential stress responses along various crystal orientations within the cell. Elastic constants, which characterize the mechanical response of a crystal, were analyzed at 4.2 ps, before significant changes in cell angles arose. The results are summarized in Table 1. At 20 GPa, the elastic constants of the 48-atom system increased, with C11 and C33 both approximately 530 GPa, indicating near isotropic behavior. Similarly, C12 and C13 were close in magnitude, both being around 230 GPa. This uniform stress distribution across all directions suggests that higher pressures are required to induce deformation. In contrast, the 144-atom system exhibited significant anisotropy. Specifically, C11 and C33 were 542.44 GPa and 366.52 GPa, respectively, with a difference of approximately 175 GPa. Notably, C33 decreased by about 60 GPa. Furthermore, C12 and C13 were 99.67 GPa and 186.83 GPa, respectively, with C13 being approximately double C12. This pronounced anisotropy suggests a tendency to shear deformation, which facilitates the phase transition at a lower pressure of 12 GPa. Additionally, in the 48-atom system, C33 and C66 are increased by 91.55 GPa and 102.15 GPa, respectively, while in the 144-atom system, C33 decreased by 59.09 GPa and C66 increased by only 20.53 GPa. These lower elastic constants in the 144-atom system indicate that its crystal cell is more susceptible to deformation, thereby promoting the phase transition.| Atom pressure | Time (ps) | C11 | C33 | C12 | C13 | C44 | C66 |
|---|---|---|---|---|---|---|---|
| 48–20 | 0 | 491.59 | 435.73 | 39.52 | 147.30 | 98.45 | 58.53 |
| 4.2 | 532.74 | 527.28 | 232.00 | 225.59 | 102.79 | 160.68 | |
| 48–12 | 4.2 | 457.53 | 507.11 | 234.57 | 190.52 | 107.54 | 179.93 |
| 144–12 | 0 | 489.83 | 425.61 | 37.55 | 145.45 | 98.61 | 58.55 |
| 4.2 | 542.44 | 366.52 | 99.67 | 186.83 | 102.47 | 79.08 | |
| 20 | 612.86 | 448.67 | 185.96 | 201.79 | 122.94 | 161.41 | |
The dynamic process of the 48-atom system under 12 GPa was further analyzed. Similar to the anatase–baddeleyite phase transition, the sliding of atomic layers leads to an 18% reduction in the volume. During the sliding process, new Ti–O bonds are directly formed between adjacent Ti atoms due to the large displacement distances. By approximately 4 ps, these newly formed bonds stabilize and establish robust connections (Fig. S8, ESI†). Since variations of the Ti–O–Ti angles can characterize structural distortion,47,55 the variations of Ti–O–Ti bond angles along a- and b-axis directions are analyzed separately (Fig. S9, ESI†). At around 4 ps, the Ti–O–Ti angles in the 144-atom system are significantly larger than those in the 48-atom system. The formation of new Ti–O bonds, together with the anisotropic variation of the Ti–O–Ti bond angles along the a- and b-axes, may constrain further cell torsion. Additionally, stress–strain analysis of the structure at 4.2 ps reveals significant increases in the elastic constants C12 and C66, by approximately 200 GPa and 120 GPa, respectively, which are much larger than those in the 144-atom system. This indicates that the structure is relatively stable and less prone to shear deformation under these conditions.
4. Conclusions
In this study, the transformation of anatase to baddeleyite through a non-diffusional phase transition was systematically investigated using AIMD simulations. The main findings are as follows:1. Under high pressure, Ti and O atoms exhibit cooperative displacements, leading to an abrupt reduction in the cell volume, an increase in the energy in the system, and a significant redistribution of internal stress. The consequent shear deformation facilitates structural rearrangements of the supercell and the formation of new Ti–O bonds, ultimately completing the transition to the baddeleyite phase.
2. Increasing the grain size can reduce the energy barrier for the phase transition. Under higher pressures, the 48-atom supercell undergoes a single-step transformation, whereas the 144-atom supercell follows a layer-by-layer mechanism with a lower energy barrier.
Our dynamical simulations reveal a direct transition from the anatase phase to the baddeleyite phase without the formation of the intermediate columbite phase, consistent with the experimental studies on anatase nanocrystals under high pressure. While our research successfully captures the atomic-level mechanisms of phase transition, we acknowledge that real materials contain lattice defects, which can significantly influence the stability and kinetics of high-pressure phases. Future research requires more accurate and efficient methodologies to incorporate defect features, ultimately providing a more robust theoretical foundation for understanding and regulating high-pressure crystal growth in technological applications.
Conflicts of interest
The authors declare no competing financial interest.Data availability
The data used to support the findings of this study are available from the corresponding author upon request.Acknowledgements
The authors acknowledge the financial support from the National Natural Science Foundation of China (52436009 and 62175063) and the Fundamental Research Funds for the Central Universities (2025JG008).References
- J. Roy, J. Ind. Eng. Chem., 2022, 106, 1–19 CrossRef CAS
.
- K. Nakata and A. Fujishima, J. Photochem. Photobiol., C, 2012, 13, 169–189 CrossRef CAS
.
- J. Schneider, M. Matsuoka, M. Takeuchi, J. Zhang, Y. Horiuchi, M. Anpo and D. W. Bahnemann, Chem. Rev., 2014, 114, 9919–9986 CrossRef CAS PubMed
.
- M. Yao, L. Li, T. Yao, D. Wang, B. Liu and H. Wang, J. Alloys Compd., 2022, 926, 166943 CrossRef CAS
.
- J. Nam, J. H. Kim, C. S. Kim, J.-D. Kwon and S. Jo, ACS Appl. Mater. Interfaces, 2020, 12, 12648–12655 CrossRef CAS PubMed
.
- M. Grätzel, J. Photochem. Photobiol., C, 2003, 4, 145–153 CrossRef
.
- X. Gao and T. Zhang, Sens. Actuators, B, 2018, 277, 604–633 CrossRef CAS
.
- S. Cao, N. Sui, P. Zhang, T. Zhou, J. Tu and T. Zhang, J. Colloid Interface Sci., 2022, 607, 357–366 CrossRef CAS PubMed
.
- Q.-J. Liu, Z. Ran, F.-S. Liu and Z.-T. Liu, J. Alloys Compd., 2015, 631, 192–201 CrossRef CAS
.
- X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891–2959 CrossRef CAS PubMed
.
- K. M. Glassford and J. R. Chelikowsky, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 1284 CrossRef CAS PubMed
.
- W. Liu, J. Chen, X. Zhang, J. Yan, M. Hou, M. Kunz, D. Zhang and H. Zhang, ACS Earth Space Chem., 2019, 3, 844–853 CrossRef CAS
.
- Y. Al-Khatatbeh, K. K. Lee and B. Kiefer, J. Phys. Chem. C, 2012, 116, 21635–21639 CrossRef CAS
.
- N. A. Dubrovinskaia, L. S. Dubrovinsky, R. Ahuja, V. B. Prokopenko, V. Dmitriev, H.-P. Weber, J. Osorio-Guillen and B. Johansson, Phys. Rev. Lett., 2001, 87, 275501 CrossRef CAS PubMed
.
- D. Bedghiou, F. H. Reguig and A. Boumaza, Comput. Mater. Sci., 2019, 166, 303–310 CrossRef CAS
.
- X. Chen, S. N. Hosseini and M. A. Van Huis, ACS Appl. Nano Mater., 2022, 5, 1600–1606 CrossRef CAS PubMed
.
- Q. Mao, Y. Ren, K. H. Luo and S. Li, J. Phys. Chem. C, 2015, 119, 28631–28639 CrossRef CAS
.
- Y. Liu, Z.-Y. Jiang, X.-D. Zhang, W.-X. Wang and Z.-Y. Zhang, Ceram. Int., 2024, 50, 37900–37907 CrossRef CAS
.
- W. Lu, H. Zhu, B. Birmingham, N. Craft, J. Hu, K. Park and Z. Zhang, Phys. Chem. Chem. Phys., 2023, 25, 3199–3210 RSC
.
- S. Wu, X. Luo, Y. Long and B. Xu, IOP Conf. Ser.: Mater. Sci. Eng., 2019, 493, 012010 CrossRef CAS
.
- B. Zhang, S. Chen, Y. Yang, R. Luo, Y. Xia, X. Wang, Q. Lu and B. Hu, Phys. Chem. Chem. Phys., 2023, 25, 23024–23032 RSC
.
- S.-Y. Chen and P. Shen, Jpn. J. Appl. Phys., 2004, 43, 1519 CrossRef CAS
.
- K. Kusaba, M. Kikuchi, K. Fukuoka and Y. Syono, Phys. Chem. Miner., 1988, 15, 238–245 CrossRef CAS
.
- J. Hidalgo-Jiménez, T. Akbay, Y. Ikeda, T. Ishihara and K. Edalati, J. Mater. Sci., 2024, 59, 5995–6007 CrossRef
.
- F. Liu, Z. Dong and L. Liu, J. Phys.: Condens. Matter, 2019, 31, 395403 CrossRef CAS PubMed
.
- Q. Li, B. Cheng, B. Tian, R. Liu, B. Liu, F. Wang, Z. Chen, B. Zou, T. Cui and B. Liu, RSC Adv., 2014, 4, 12873–12877 RSC
.
- X. Zhang, H. Tian, W. Li, W. Liu, J. Chen, J. Liu, X. Han, B. Yan, Z. Chen, H. Gou, K. Li, H. Jiang, D. Zhang, M. Kunz and H. Zhang, J. Phys. Chem. C, 2020, 124, 1197–1206 CrossRef CAS
.
- V. Swamy, A. Kuznetsov, L. S. Dubrovinsky, R. A. Caruso, D. G. Shchukin and B. C. Muddle, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 184302 CrossRef
.
- S. Park, J. Jang, J. Cheon, H.-H. Lee, D. R. Lee and Y. Lee, J. Phys. Chem. C, 2008, 112, 9627–9631 CrossRef CAS
.
- Q. Li, R. Liu, T. Wang, K. Xu, Q. Dong, B. Liu, J. Liu and B. Liu, AIP Adv., 2015, 5, 097128 CrossRef
.
- Q. Li, B. Cheng, X. Yang, R. Liu, B. Liu, J. Liu, Z. Chen, B. Zou, T. Cui and B. Liu, J. Phys. Chem. C, 2013, 117, 8516–8521 CrossRef CAS
.
- L. Meng, S. Duwal, J. M. D. Lane, T. Ao, B. Stoltzfus, M. Knudson, C. Park, P. Chow, Y. Xiao, H. Fan and Y. Qin, MRS Bull., 2022, 47, 455–460 CrossRef CAS
.
- J. G. Lee, C. J. Pickard and B. Cheng, J. Chem. Phys., 2022, 156, 074106 CrossRef CAS PubMed
.
- Y. Liu, W.-X. Wang, Z.-Y. Jiang and Z.-Y. Zhang, J. Alloys Compd., 2021, 878, 160452 CrossRef CAS
.
- M. E. Arroyo-de Dompablo, A. Morales-García and M. Taravillo, J. Chem. Phys., 2011, 135, 054503 CrossRef CAS PubMed
.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS PubMed
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed
.
- K. Laasonen, A. Pasquarello, R. Car, C. Lee and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 10142–10153 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- K. Kaur and C. V. Singh, Energy Procedia, 2012, 29, 291–299 CrossRef CAS
.
- K. Lagarec and S. Desgreniers, Solid State Commun., 1995, 94, 519–524 CrossRef CAS
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed
.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed
.
- J. Muscat, V. Swamy and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 224112 CrossRef
.
- C. Popescu, J. A. Sans, D. Errandonea, A. Segura, R. Villanueva and F. Sapiña, Inorg. Chem., 2014, 53, 11598–11603 CrossRef CAS PubMed
.
- A. Reinhardt, C. J. Pickard and B. Cheng, Phys. Chem. Chem. Phys., 2020, 22, 12697–12705 RSC
.
- M. Horn, C. Schwebdtfeger and E. Meagher, Z. Kristallogr. – Cryst. Mater., 1972, 136, 273–281 CrossRef CAS
.
- P. Ball, Nat. Mater., 2022, 21, 1341 CrossRef CAS PubMed
.
- Z. Fu, Y. Liang, S. Wang and Z. Zhong, Phys. Status Solidi B, 2013, 250, 2206–2214 CrossRef CAS
.
- G. R. Hearne, J. Zhao, A. M. Dawe, V. Pischedda, M. Maaza, M. K. Nieuwoudt, P. Kibasomba, O. Nemraoui, J. D. Comins and M. J. Witcomb, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 134102 CrossRef
.
- M. Song, Z. Lu and D. Li, Nanoscale, 2020, 12, 23183–23190 RSC
.
- H. Razavi-Khosroshahi, K. Edalati, M. Arita, Z. Horita and M. Fuji, Scr. Mater., 2016, 124, 59–62 CrossRef CAS
.
- H. Fan, R. Wang, Z. Xu, H. Duan and D. Chen, J. Non-Cryst. Solids, 2021, 571, 121049 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01805f |
| This journal is © the Owner Societies 2025 |


