Precisely tuning band gaps of graphene/h-BN lateral heterostructures toward enhanced photocatalytic hydrogen evolution†

Huizhong Ma^a, Yulong Wang^a, Lingling Sun^a, Chunyan Wang^a, Liwei Wang^a, Zhuang Ma^a, Honglei Yuan*^a and Jin Feng*^b
aSchool of Physics and Telecommunication Engineering, Zhoukou Normal University, Zhoukou 466001, China. E-mail: yhl@zknu.edu.cn
^bKey Laboratory of Life-Organic Analysis of Shandong Province, School of Chemistry and Chemical Engineering, Qufu Normal University, Qufu 273100, China. E-mail: fengjinzuibang@163.com

First published on 22nd July 2025

---

---

1. Introduction

Photocatalytic hydrogen production represents an ideal pathway for clean energy generation, with the development of efficient photocatalysts being central to its realization.^1–4 An optimal photocatalyst must exhibit an appropriate band gap to ensure sufficient visible-light absorption, optimal absolute energy level positions to provide adequate thermodynamic driving force for the hydrogen evolution reaction (HER), and robust electron–hole separation capability to enhance HER kinetics.^5,6 To fulfill these criteria, researchers have employed diverse strategies for catalyst design and optimization, including defect engineering, elemental doping, heterostructure construction etc.^7–13 Although these methods can moderately improve photocatalytic performance, they generally lack precision in fine-tuning the band gap and energy level alignment, thereby limiting the potential to achieve optimal catalytic states. Consequently, developing catalysts capable of precise structural modulation to realize gradient band gap and energy-level evolution represents a critical research direction.

Two-dimensional (2D) graphene/hexagonal boron nitride (h-BN) lateral heterostructures have recently emerged as a promising platform to simultaneously fulfill all aforementioned requirements.^14–16 These heterostructures consist of graphene and h-BN with compatible hexagonal lattices exhibiting minimal lattice mismatch (∼1.7%). Compared to vertical configurations, lateral heterostructures demonstrate enhanced interfacial contact through seamless atomic stitching, reduced defect density due to direct growth without layer transfer, and improved charge carrier mobility enabled by in-plane transport pathways.^17,18 Importantly, these heterostructures can effectively combine the thermal stability of h-BN with the exceptional electrical conductivity of graphene, potentially endowing them with superior electron mobility, thus effectively promoting HER catalysis.^19–23 Furthermore, as a heterostructure system, they theoretically exhibit enhanced electron–hole separation efficiency compared to their individual components. However, previous theoretical and experimental studies have predominantly focused on their applications in electronic and optoelectronic devices,^15,24 while limited attention has been paid to their photocatalytic HER applications. The primary reason lies in the fact that the inherent electronic constraints of these materials—graphene's gapless Dirac cone and h-BN's wide band gap (∼6 eV)—establish a fundamental “materials gap” that intrinsically limits their direct utilization in photocatalysis.^25,26

To harness the HER potential of these graphene/h-BN lateral heterostructures, developing effective band gap engineering strategies to achieve broad-spectrum visible-light absorption have become imperative. Notably, both experimental observations and theoretical analyses indicate that the band gap exhibits a size-dependent sensitivity.^15,27–30 For example, Ci et al. observed that domain size variation in graphene/h-BN hybrids leads to band gap modulation.²⁹ Wang et al. further reported that graphene nanoribbon width reduction results in quantized band gap opening.³⁰ Additionally, Liu et al. found that controlled heterostructure dimensions can influence electronic properties while preserving interface quality.¹⁵ However, these studies are limited by insufficiently precise domain size modulation and by focusing solely on graphene domain size while ignoring the influence of h-BN domain size. The studied configurations lacked diversity, preventing clear identification of band gap evolution trends. A systematic investigation of how precisely controlling the relative domain sizes of graphene and h-BN influences the band gap and energy level alignment in these heterostructures would provide fundamental insights essential for guiding the experimental design of high-performance HER photocatalysts through targeted structural engineering.

In this work, we achieve precise control over both graphene and h-BN domain sizes to construct 2D lateral heterostructures with systematically varied graphene domains embedded in h-BN matrices. To identify optimal configurations, we implement a computational strategy that rigorously evaluates band gap characteristics and HER driving forces across progressively scaled heterostructure dimensions. The band structure of the target heterostructure (denoted as 66BN-33Gr, see Fig. S1, ESI†), as determined through our DFT calculations, is predicted to facilitate efficient visible-light absorption while preserving a sufficient driving force for the HER, thereby promoting favorable reaction kinetics. By employing advanced many-body Green's function theory (the GW approximation combined with the Bethe–Salpeter equation), we further rigorously characterize the electronic and optical properties of the target heterostructure.^31,32 The results demonstrate that the target heterostructure exhibits enhanced electron–hole separation capability, overcoming the characteristic high exciton binding energy that fundamentally limits conventional nonmetallic 2D photocatalysts.^33,34 Furthermore, systematic investigation of HER mechanisms reveals exceptionally low excited-state reaction energy barriers, suggesting a highly efficient photocatalytic process in this system. Collectively, these theoretical insights into electronic structure, optical properties, and reaction mechanisms establish a design framework for experimentally achieving high-efficiency hydrogen production using graphene/h-BN lateral heterostructures with optimized domain configurations.

2. Computational details

This work optimized all structural configurations using the plane-wave basis Vienna Ab initio Simulation Package (VASP).³⁵ The interactions between electrons and ions were described using the projector-augmented-wave (PAW) method,³⁶ while exchange–correlation effects were treated with the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA).³⁷ The plane-wave energy cutoff was fixed at 550 eV, and the convergence criteria for energy and force were set to <10⁻⁵ eV and 0.01 eV Å⁻¹, respectively, during the relaxation of atomic positions. To account for van der Waals interactions in adsorption systems, the semiempirical DFT-D3 approach was utilized.³⁸ The Monkhorst–Pack k-point meshes were carefully selected and tested for force convergence to 0.01 eV Å⁻¹, ensuring their suitability for different lattice structures. Spin polarization was explicitly incorporated in the calculations when investigating the HER mechanism. The HER performance was characterized by calculating the Gibbs free energy change of hydrogen adsorption (ΔG) using the following equation:

ΔG = ΔEH* + ΔEZPE − TΔSH* + ΔGpH

The hydrogen adsorption energy (ΔE_H*) was determined by the equation ΔE_H* = E_H* − E − 1/2E_H2, where E_H*, E, and E_H2 represent the total energies of the catalyst with an adsorbed hydrogen atom, the pristine catalyst, and gaseous H₂, respectively. The zero-point energy correction (ΔE_ZPE) and entropy change (ΔS_H) for adsorbed species were obtained using the VASPKIT code.³⁹ The temperature was set to 298.15 K, and additional corrections for pH (ΔG_pH) were included, with ΔG_pH = k_BTln10pH. In this study, a pH value of zero was assumed.

Our computational workflow consisted of two stages: (i) DFT-based structure optimization and electronic characterization using VASP, followed by (ii) many-body Green's function theory (MBGFT) calculations incorporating both the GW approximation and the Bethe–Salpeter equation (BSE) for ground- and excited-state properties.^31,32 While MBGFT provides superior electronic structure accuracy, preliminary structural optimization was conducted using VASP because force calculations in MBGFT would demand thousands of GW + BSE evaluations per optimization step—a computationally prohibitive task. This integrated workflow has proven effective for investigating electronic and optical properties in diverse material systems, including both periodic and non-periodic structures, as demonstrated in recent studies.^40–45 Critical parameters for the present study, particularly optical absorption spectra, exciton binding energies, and excitation energies, can be reliably determined through this approach. In detail, our GW calculations were performed at the one-shot G₀W₀ level, using DFT under the local density approximation (LDA) as the starting point. The GW physical quantities were constructed based on LDA eigenvalues and eigenfunctions, while a rigid scissor shift was applied to the LDA eigenvalues of unoccupied orbitals to achieve quasiparticle corrections that match the band gap.^46,47 The dielectric function was computed within the random-phase approximation, and its dynamical effects were approximated using the plasmon-pole model proposed by von der Linden and Horsch.⁴⁸ The GW + BSE calculations were carried out using a code with Gaussian orbitals as the basis set,^49,50 with decay constants (in atomic units) of 0.25, 0.75, 2.25, and 6.75 for carbon atoms, 0.2, 0.5, 1.25, and 3.2 for nitrogen and boron atoms, and 0.2 and 0.8 for hydrogen atoms. This basis set was extensively validated to ensure converged results. A vacuum layer of 45 Å was introduced to minimize interlayer interactions and guarantee convergence. Converged Monkhorst–Pack k-point meshes were utilized for different properties, specifically 1 × 1 × 1 for the dielectric function, 3 × 3 × 1 for self-energy, and 6 × 6 × 1 for BSE excitons. In the context of HER excited-state reaction mechanisms, the lowest excitation energy computed by BSE was directly considered as the energy difference between the ground state and the excited state, as MBGFT is computationally prohibitive for calculating excited-state forces. This methodology has been successfully applied in previous studies, demonstrating excellent agreement with experimental data and other theoretical excited-state calculations.^44,51,52

3. Results and discussion

3.1. Band gap engineering in size-controlled graphene/h-BN 2D lateral heterostructures

It is well established that an appropriate band gap is a prerequisite for efficient utilization of solar energy. Both our theoretical calculations and prior experimental studies confirm that when graphene and h-BN are arranged in different layers, the resulting heterostructure exhibits a near-zero band gap, rendering it unsuitable for photocatalytic applications (Fig. S2, ESI†).^53–55 This finding underscores the importance of investigating graphene/h-BN lateral heterostructures with both components in the same plane. As mentioned earlier, the size effect holds significant potential in modulating the excessively narrow band gap of graphene and the overly wide band gap of h-BN. Therefore, we designed diverse graphene/h-BN 2D lateral heterostructures through precise control over the domain sizes of graphene and h-BN. In our computational approach, the domain sizes of graphene and h-BN are quantified using supercell dimensions, a simplification adopted to facilitate systematic analysis. To streamline the structural description, we introduce the nomenclature “xyBN-zmGr” for the size-controlled graphene/h-BN 2D lateral heterostructures in this work. Here, “xyBN-zmGr” denotes a heterostructure formed by embedding a z × m × 1 graphene domain into an x × y × 1 h-BN domain. A representative example is provided in Fig. S1 (ESI†), which illustrates the design and nomenclature of 66BN-33Gr. Structurally, 66BN-33Gr consists of a 3 × 3 × 1 graphene domain embedded within a 6 × 6 × 1 h-BN domain. Since the graphene domain is fully encapsulated by h-BN and does not reside at the lattice boundaries of the new xyBN-zmGr structure, all graphene boundary atoms are explicitly incorporated in the model.

We analyzed the band gap variation trends in xyBN-zmGr heterostructures. Given the vast possible combinations of x, y, z, and m, we initially restricted our study to structures with x = y < 10 and z = m < x − 2 to balance computational cost and structural simplicity. Using DFT-PBE, we systematically investigated the band gap evolution in these configurations. To evaluate the graphene size effect on band gap modulation, we fixed the h-BN domain as a 9 × 9 × 1 supercell while varying the graphene dimensions from 1 × 1 × 1 to 6 × 6 × 1, generating six heterostructures (denoted as 99BN-11Gr, 99BN-22Gr, 99BN-33Gr, 99BN-44Gr, 99BN-55Gr, and 99BN-66Gr, illustrated in Fig. S3, ESI†). Our calculations revealed an inverse correlation between graphene domain size and band gap magnitude (Fig. 1a), which can be attributed to weakened quantum confinement effects in larger graphene domains, with the smallest band gap found in 99BN-66Gr. Similarly, for other xyBN-zmGr structures (x = y < 9), 88BN-55Gr, 77BN-44Gr, 66BN-33Gr, 55BN-22Gr, and 44BN-11Gr are predicted to exhibit their respective minimal band gaps within their series, with corresponding DFT-PBE values provided in Fig. S3 (ESI†). Considering the well-known underestimation of band gaps by DFT-PBE functionals and the requirement for broad visible-light absorption in photocatalytic applications, we targeted band gap range of 0.5–2 eV based on established literature.^56–58 Among these, the 66BN-33Gr heterostructure, with an intermediate band gap of 1.24 eV, was selected as a representative model for further investigation—a choice that balances computational constraints (particularly relevant for more accurate but expensive MBGFT calculations) with the need for reliable representation of fundamental electronic properties.

To provide practical guidance for experimentally screening xyBN-zmGr structures with optimal band gaps, we further investigated the influence of carbon concentration on both the band gap and energy level alignment in graphene/h-BN 2D lateral heterostructures. For the 9 × 9 × 1 h-BN substrate, we observed a clear trend of decreasing band gap with increasing embedded carbon concentration. However, this relationship did not hold universally across all studied xyBN-zmGr configurations, prompting us to examine a broader range of heterostructures. As illustrated in Fig. 1b, we confirmed that under consistent h-BN dimensions, the band gap indeed decreases progressively with increasing carbon concentration. This trend strictly requires identical h-BN substrate sizes; for heterostructures with varying h-BN dimensions, the correlation does not necessarily apply. Our analysis revealed that at fixed carbon concentrations, larger h-BN domains yield smaller band gaps. Interestingly, we discovered that band gaps also depend on the geometric shape of embedded graphene domains. As shown in Fig. S4 (ESI†), structures with comparable carbon concentrations but different graphene geometries—specifically comparing a square (2 × 2 × 1) versus rectangular (1 × 4 × 1) configuration (99BN-22Gr vs. 99BN-14Gr)—exhibit significant band gap differences (∼0.62 eV). Our calculations demonstrate that the band gap remains consistently intermediate between graphene and h-BN across all carbon concentrations and geometric configurations, establishing a general strategy for band gap engineering in analogous materials. Further examination of carbon concentration effects on the absolute energy levels of valence band maximum (VBM) and conduction band minimum (CBM) (Fig. S5, ESI†) reveals that within identical h-BN substrates, increasing carbon concentration elevates the VBM while lowering the CBM. Fig. S5 (ESI†) demonstrates that 66BN-33Gr possesses sufficiently high HER driving force. Combined with its optimal band gap characteristics (Fig. 1a), these findings confirm that 66BN-33Gr represents a rational and representative model system for photocatalytic applications. The front and side views of the 66BN-33Gr structure are presented in Fig. 2a and b.

Comprehensive evaluation of 66BN-33Gr's structural integrity and stability was conducted through systematic analysis of its geometric parameters and ab initio molecular dynamics (AIMD) simulations, revealing excellent structural preservation and thermal stability. Specifically, our calculations show that the lattice constant of 66BN-33Gr exhibits negligible deviation (<0.1 Å) compared to pristine hexagonal boron nitride (6 × 6 × 1 supercell), demonstrating excellent lattice matching at the interface region which suggests favorable formation feasibility through stitching process. Further investigation of bond lengths focused on four distinct bond types (B–C, B–N, C–N, and C–C), as presented in Fig. S6 (ESI†). The data indicate that these bond lengths remain generally comparable, with maximum variations below 0.2 Å. These computational results (1.40–1.53 Å bond lengths) align with experimental measurements of covalent bonding in such heterostructures, with the sp²-hybridized state of all elements being specifically verified.^15,29 Notably, the bond length differences between B–N (C–C) bonds near and far from the stitching interface are less than 0.04 Å (0.05 Å), suggesting that both h-BN and graphene largely retain their intrinsic properties after stitching. The newly formed C–N bonds measure 1.40–1.42 Å, while the C–B bonds range from 1.52 to 1.53 Å, all falling within typical bond length ranges for these chemical bonds. Furthermore, we assessed the thermal stability of 66BN-33Gr through AIMD simulations in the NVT ensemble⁵⁹ at 298 K, 500 K, and 1000 K, with each 15 ps simulation employing a 1 fs time step. The AIMD results demonstrate excellent structural preservation of 66BN-33Gr throughout the simulations (Fig. 2c, d and Fig. S7, S8, ESI†). While the initially planar structure becomes curved at elevated temperatures, it recovers its predominantly flat configuration upon subsequent relaxation. Additionally, it should be noted that although current experimentally synthesized graphene/h-BN lateral heterostructures primarily exhibit randomly distributed large domains, recent advances have successfully demonstrated controlled fabrication of heterostructures with specific domain sizes.^15,60,61 This progress confirms the feasibility of experimentally realizing our theoretically optimized 66BN-33Gr structure through appropriate synthetic strategies.

3.2. Electronic and optical properties of 66BN-33Gr

We performed GW calculations to obtain quantitatively accurate electronic properties and evaluate the catalytic potential of 66BN-33Gr. The GW calculation yields a band gap of 2.63 eV for 66BN-33Gr, while the PBE method significantly underestimates this value at 1.24 eV, demonstrating a 1.39 eV discrepancy between the two approaches (Fig. 3a and Fig. S9a, ESI†). Both the VBM and CBM are located at the Γ high-symmetry point, confirming the direct band gap nature of this material. This characteristic electronic configuration facilitates efficient photon absorption under solar irradiation through momentum-conserved electron transitions.^6,62,63 Orbital composition analysis indicates that the VBM and CBM primarily derive from π orbitals localized on the embedded carbon atoms (Fig. 3b), suggesting carbon-dominated charge carrier dynamics. In theoretical catalysis studies, the absolute energy level of the catalyst's CBM relative to the HER potential serves as a crucial criterion for evaluating HER kinetics. As shown in Fig. 3a, the HER driving force of 2.17 eV demonstrates the strong potential of 66BN-33Gr for facilitating hydrogen evolution. Additionally, the working mechanism of the 66BN-33Gr lateral heterostructure photocatalyst for hydrogen generation is schematically illustrated in Fig. 3b. The heterostructure exhibits type-I band alignment, with both the VBM and CBM predominantly localized on the graphene component, while the charge-localized energy levels of h-BN reside at deeper positions.

The solar spectrum utilization of the proposed 66BN-33Gr heterostructure demonstrates remarkable enhancement compared to pristine h-BN. As shown in Fig. 4a, the optical spectrum of pristine h-BN calculated using BSE yields an optical band gap of 5.96 eV, in excellent agreement with previously reported experimental values.^64,65 Nevertheless, this large optical absorption edge (5.96 eV) makes pristine h-BN unsuitable for practical photocatalytic applications. In striking contrast, the optimized 66BN-33Gr heterostructure exhibits significantly reduced optical band gap (2.00 eV, Fig. 4a), rendering it highly responsive to visible light, which is particularly advantageous for practical photocatalytic applications. Spectral analysis confirms prominent absorption features across the 400–600 nm visible region, suggesting enhanced light-harvesting capability under solar illumination. Further examination of electron–hole distribution at optical absorption edge reveals that both charge carriers predominantly localize within embedded graphene domains, while showing negligible distribution in original h-BN regions, directly accounting for the substantial optical band gap reduction in 66BN-33Gr compared to pristine h-BN (Fig. S10, ESI†).

The electron–hole separation capability, quantitatively characterized by exciton binding energy as a theoretical metric, plays a pivotal role in determining photocatalytic performance under photoexcitation.^66–69 As a prototypical 2D non-metallic material, h-BN suffers from prohibitively large exciton binding energies (1.68 eV at the optical absorption edge), which severely hinder charge dissociation. However, constructing planar heterojunctions by embedding graphene into h-BN (denoted as 66BN-33Gr) achieves exciton binding energies of 0.80 eV at the optical absorption edge, significantly below the typical range (>1 eV) observed in conventional 2D non-metal semiconductors.^33,34 Strikingly, 66BN-33Gr hosts numerous excitons with binding energies <0.2 eV that coexist with substantial oscillator strengths in the visible spectrum (Fig. 4b and c), consistent with the reported graphene induced reduction of exciton binding energies in 2D material systems.^70,71 These weakly bound excitons exhibit diminished coulomb interactions between electrons and holes, thereby promoting efficient charge separation, which consequently enhances photocatalytic performance. Furthermore, we systematically analyzed the excitonic behavior of representative excited states in both h-BN and 66BN-33Gr. Specifically, we examined the lowest excited states (α state for h-BN and β state for 66BN-33Gr), as well as an excited state in 66BN-33Gr (γ state) characterized by a weakly bound exciton (0.23 eV) and a high oscillator strength (1.06) (Fig. 4b and c). To assess electron–hole separation, we fixed the hole position within the central unit and mapped the spatial distribution of the electron. For the α state of h-BN, both electron and hole remain tightly confined within the same lattice unit (Fig. 4d), indicative of poor charge separation. In contrast, for the β and γ states of 66BN-33Gr, the electrons are predominantly localized on carbon atoms (Fig. S10a and b, ESI†), with minimal distribution on boron and nitrogen atoms. This pronounced carbon localization can enable efficient charge transport through the embedded graphene network.^72,73 In the β-state, the electron can migrate to adjacent lattice units (Fig. 4e). More remarkably, for the γ-state with its lower exciton binding energy, the electron within the central unit undergoes significant displacement, migrating over a distance of approximately 38 Å (Fig. 4f). This extended separation distance signifies near-complete decoupling of the electron–hole pair, which is critically advantageous for enabling their independent participation in photocatalytic redox reactions.

3.3. HER mechanism of 66BN-33Gr

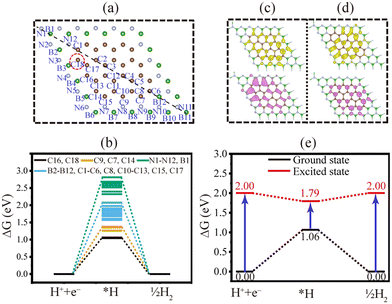
To further explore the HER mechanisms of 66BN-33Gr, the free energy of the hydrogen-adsorbed monolayers was calculated. Owing to the symmetry of the 66BN-33Gr structure, 42 distinct possible H adsorption sites were considered in the free energy calculations (Fig. 5a). The calculated HER free energies at these sites exhibit significant variations (Fig. 5b). H adsorption on nitrogen atoms yields the highest energy barrier (ΔG = 2.32–2.81 eV), whereas adsorption on boron and carbon atoms shows relatively lower barriers. Specifically, carbon sites display a range of ΔG values (1.04–1.87 eV), which are generally more favorable than those of boron sites (1.58–2.52 eV). This trend correlates well with the primary electron density distribution on carbon atoms, as shown in Fig. 5c. Among all investigated sites, the most thermodynamically favorable HER sites are site C16 and C18, exhibiting the lowest ground-state energy barrier of 1.04 eV and 1.06 eV respectively.

Given that photocatalytic HER proceeds through an excited-state mechanism, it is essential to evaluate the reaction energy barriers in the excited state. Our BSE calculations revealed a substantial decrease in the excited-state reaction energy barrier relative to the ground state. The HER excited-state free energies at site C16 and C18 are presented in Fig. 5e and Fig. S11 (ESI†) respectively. Notably, site C18 exhibits the lowest excited-state reaction barrier of 0.21 eV, indicating spontaneous HER under photocatalytic conditions (Fig. 5e). To further understand this phenomenon, we analyzed the electron–hole distributions in both the initial and intermediate states (Fig. 5c and d). Our analysis reveals that upon hydrogen atom adsorption on the substrate, the electronic transition shifts from π → π* to n → π*. Additionally, the spatial separation between electrons and holes is markedly enhanced. As a result, these factors collectively contribute to a lower excitation energy for 66BN-33Gr after hydrogen adsorption, which in turn leads to the reduced excited-state reaction energy barrier for HER.

3.4. Properties of layered 66BN-33Gr

The newly designed 66BN-33Gr, a 2D material with controlled B–N–C hybridization, represents a promising platform for investigating stacking-dependent electronic properties, particularly in the context of previously demonstrated layer-sensitive band structure modifications in 2D lateral heterostructures.^74,75 Based on previous reports of analogous systems, the multilayer configurations can be classified into two primary stacking modes: the AA stacking pattern where atoms are perfectly aligned between layers, and the AB stacking pattern where atoms in one layer are positioned directly above the center of hexagonal rings in the adjacent layer (Fig. 6a and b).^76–78 Therefore, we primarily examined the energy and band gap variations in multilayer 66BN-33Gr under these two distinct stacking modes, namely AA and AB. Our calculations based on DFT-PBE show that the AB stacking mode is more stable than the AA mode, with a stability difference of approximately 0.004–0.005 eV per atom (Fig. 6c). Regarding band gap modulation, AB-stacked multilayers display a gradual reduction in band gap with increasing layer number (Fig. 6d). For instance, the bulk 66BN-33Gr exhibits only a 0.27 eV band gap reduction compared to its monolayer counterpart. In contrast, AA-stacked systems undergo drastic band gap narrowing: a 0.44 eV decrease from monolayer to bilayer, 0.64 eV for trilayer, and 0.99 eV for bulk. The substantial band gap tunability in AA-stacked 66BN-33Gr (spanning ∼1 eV range across layer numbers) suggests its potential as a broadband absorber in the visible to near-infrared spectrum. Remarkably, Fig. S9b (ESI†) shows that the transition from monolayer 66BN-33Gr to its AA-stacked bulk counterpart induces a direct-to-indirect band gap shift, a phenomenon analogous to that observed in 2D transition metal dichalcogenides.⁷⁹ The emergence of an indirect band gap in bulk structures may suppress the recombination of photogenerated electron–hole pairs, thereby potentially enhancing photocatalytic activity.^80,81

4. Conclusion

This study comprehensively investigates the potential of graphene/h-BN 2D lateral heterostructures, tailored through size modulation, for photocatalytic HER via advanced theoretical frameworks. The analysis highlights that precise manipulation of the domain dimensions of graphene and h-BN enables effective band gap engineering, optimizing their performance for visible light absorption. For instance, the 66BN-33Gr heterostructure exhibits an optical band gap of 2.00 eV (as determined by the BSE), accompanied by outstanding light absorption characteristics. Additionally, the exciton binding energy of 66BN-33Gr is below 0.80 eV at the optical absorption edge, surpassing that of most non-metallic 2D photocatalysts, thereby highlighting its superior electron–hole separation efficiency—a critical factor for enhancing photocatalytic activity. Crucially, the investigation into the HER mechanism reveals an exceptionally low reaction energy barrier of 0.21 eV under excited states, indicating the feasibility of spontaneous HER under photocatalytic conditions. These insights establish a robust theoretical basis for leveraging graphene/h-BN heterostructures in photocatalytic hydrogen evolution, advancing their application in sustainable energy technologies.

Our work further elucidates several characteristic trends in 2D lateral graphene/h-BN heterostructures. The computational results demonstrate that the band gap of these heterostructures depends not only on carbon concentration but also on the h-BN domain size and the geometric arrangement of embedded graphene domains, revealing lateral heterojunction engineering as a transformative approach for band gap modification. Moreover, different stacking configurations display distinct band gap evolution patterns and can facilitate direct-to-indirect band gap transitions, suggesting potential variations in light absorption ranges and excited-state dynamics. Importantly, our study not only predicts these phenomena but also provides mechanistic explanations for the computed trends. These theoretical insights could offer valuable guidance for experimentally synthesizing graphene/h-BN 2D lateral heterostructures with tunable properties for various applications.

Author contributions

Huizhong Ma: conceptualization, methodology, investigation, writing – original draft. Yulong Wang: investigation, formal analysis, validation. Lingling Sun: Investigation, formal analysis, validation. Chunyan Wang: investigation, Validation. Liwei Wang: investigation, validation. Zhuang Ma: investigation, validation. Honglei Yuan: writing – review & editing, funding acquisition. Jin Feng: supervision, writing – review & editing.

Conflicts of interest

The authors declared that there is no conflict of interest.

Data availability

The data supporting this article have been included as part of the ESI.†

Acknowledgements

This work was supported by the Key Technologies R&D Program of Henan Province (Grant 252102241034) and the Natural Science Foundation of Henan Province (Grants 242300420674 and 232300420399).

References

1. X. Chen, S. Shen, L. Guo and S. S. Mao, Semiconductor-Based Photocatalytic Hydrogen Generation, Chem. Rev., 2010, 110, 6503–6570 CrossRef CAS PubMed .
2. Q. Wang, T. Hisatomi, Q. Jia, H. Tokudome and M. Zhong, et al., Scalable Water Splitting on Particulate Photocatalyst Sheets with a Solar-to-Hydrogen Energy Conversion Efficiency Exceeding 1%, Nat. Mater., 2016, 15, 611–615 CrossRef CAS PubMed .
3. Y. Zhang, Y. Li, X. Xin, Y. Wang and P. Guo, et al., Internal Quantum Efficiency Higher than 100% Achieved by Combining Doping and Quantum Effects for Photocatalytic Overall Water Splitting, Nat. Energy, 2023, 8, 504–514 CrossRef CAS .
4. P. Zhou, I. A. Navid, Y. Ma, Y. Xiao and P. Wang, et al., Solar-to-Hydrogen Efficiency of More than 9% in Photocatalytic Water Splitting, Nature, 2023, 613, 66–70 CrossRef CAS PubMed .
5. W.-J. Ong, L.-L. Tan, Y. H. Ng, S.-T. Yong and S.-P. Chai, Graphitic Carbon Nitride (g-C₃N₄)-Based Photocatalysts for Artificial Photosynthesis and Environmental Remediation: Are We a Step Closer To Achieving Sustainability?, Chem. Rev., 2016, 116, 7159–7329 CrossRef CAS PubMed .
6. H. Jin, H. Zhang, J. Li, T. Wang and L. Wan, et al., Data-Driven Systematic Search of Promising Photocatalysts for Water Splitting under Visible Light, J. Phys. Chem. Lett., 2019, 10, 5211–5218 CrossRef CAS PubMed .
7. S. Bai, N. Zhang, C. Gao and Y. Xiong, Defect Engineering in Photocatalytic Materials, Nano Energy, 2018, 53, 296–336 CrossRef CAS .
8. M. A. Khan, S. Mutahir, I. Shaheen, Y. Qunhui and M. Bououdina, et al., Recent Advances over the Doped g-C₃N₄ in Photocatalysis: A Review, Coord. Chem. Rev., 2025, 522, 216227 CrossRef CAS .
9. X. Pan, F. Kong and M. Xing, Spatial Separation of Photo-Generated Carriers in g-C₃N₄/MnO₂/Pt with Enhanced H₂ Evolution and Organic Pollutant Control, Res. Chem. Intermed., 2022, 48, 2837–2855 CrossRef CAS .
10. M. Meng, W. Qin, C. Li, K. Xu and L. Xu, et al., Synergistic Effect of Photonic Crystals and Oxygen Vacancies on Photoelectrochemical Water Splitting of TiO₂ Nanotube, J. Nanoelectron. Optoelectron., 2020, 15, 226–230 CrossRef CAS .
11. X. Zhu, E. Zhou, X. Tai, H. Zong and J. Yi, et al., g-C₃N₄ S-Scheme Homojunction through van der Waals Interface Regulation by Intrinsic Polymerization Tailoring for Enhanced Photocatalytic H₂ Evolution and CO₂ Reduction, Angew. Chem., Int. Ed., 2025, e202425439 CAS .
12. H. Zhang, Q. Li, B. Weng, L. Xiao and Z. Tian, et al., Edge Engineering of Platinum Nanoparticles via Porphyrin-Based Ultrathin 2D Metal–Organic Frameworks for Enhanced Photocatalytic Hydrogen Generation, Chem. Eng. J., 2022, 442, 136144 CrossRef CAS .
13. H. Zhang, Y. Chen, X. Zhu, H. Zhou and Y. Yao, et al., Mn²⁺-doped Zn₂GeO₄ for Photocatalysis Hydrogen Generation, Int. J. Energy Res., 2019, 43, 5013–5019 CrossRef CAS .
14. M. P. Levendorf, C.-J. Kim, L. Brown, P. Y. Huang and R. W. Havener, et al., Graphene and Boron Nitride Lateral Heterostructures for Atomically thin Circuitry, Nature, 2012, 488, 627–632 CrossRef CAS PubMed .
15. Z. Liu, L. Ma, G. Shi, W. Zhou and Y. Gong, et al., In-Plane Heterostructures of Graphene and Hexagonal Boron Nitride with Controlled Domain Sizes, Nat. Nanotechnol., 2013, 8, 119–124 CrossRef CAS PubMed .
16. H. Guo, A. Garro-Hernandorena, A. J. Martínez-Galera and J. M. Gómez-Rodríguez, Lateral Heterostructures of Graphene and h-BN with Atomic Lattice Coherence and Tunable Rotational Order, Small, 2023, 19, 2207217 CrossRef CAS PubMed .
17. J. Wang, Z. Li, H. Chen, G. Deng and X. Niu, Recent Advances in 2D Lateral Heterostructures, Nano-Micro Lett., 2019, 11, 48 CrossRef PubMed .
18. Y. Gong, J. Lin, X. Wang, G. Shi and S. Lei, et al., Vertical and In-Plane Heterostructures from WS₂/MoS₂ Monolayers, Nat. Mater., 2014, 13, 1135–1142 CrossRef CAS PubMed .
19. W. Che, W. Cheng, T. Yao, F. Tang and W. Liu, et al., Fast Photoelectron Transfer in (C_ring)–C₃N₄ Plane Heterostructural Nanosheets for Overall Water Splitting, J. Am. Chem. Soc., 2017, 139, 3021–3026 CrossRef CAS PubMed .
20. A. Du, S. Sanvito, Z. Li, D. Wang and Y. Jiao, et al., Hybrid Graphene and Graphitic Carbon Nitride Nanocomposite: Gap Opening, Electron–Hole Puddle, Interfacial Charge Transfer, and Enhanced Visible Light Response, J. Am. Chem. Soc., 2012, 134, 4393–4397 CrossRef CAS PubMed .
21. N. T. Padmanabhan, N. Thomas, J. Louis, D. T. Mathew and P. Ganguly, et al., Graphene Coupled TiO₂ Photocatalysts for Environmental Applications: A Review, Chemosphere, 2021, 271, 129506 CrossRef CAS PubMed .
22. Q. Xiang, J. Yu and M. Jaroniec, Graphene-Based Semiconductor Photocatalysts, Chem. Soc. Rev., 2012, 41, 782–796 RSC .
23. G. Ramalingam, N. Perumal, A. K. Priya and S. Rajendran, A Review of Graphene-Based Semiconductors for Photocatalytic Degradation of Pollutants in Wastewater, Chemosphere, 2022, 300, 134391 CrossRef CAS PubMed .
24. B. Lyu, J. Chen, S. Wang, S. Lou and P. Shen, et al., Graphene Nanoribbons Grown in h-BN Stacks for High-Performance Electronics, Nature, 2024, 628, 758–764 CrossRef CAS PubMed .
25. G. Cassabois, P. Valvin and B. Gil, Hexagonal Boron Nitride is an Indirect Bandgap Semiconductor, Nat. Photonics, 2016, 10, 262–266 CrossRef CAS .
26. K. S. Novoselov, V. I. Fal′ko, L. Colombo, P. R. Gellert and M. G. Schwab, et al., A Roadmap for Graphene, Nature, 2012, 490, 192–200 CrossRef CAS PubMed .
27. O. Olaniyan, L. Moskaleva, R. A. Mahadi, E. Igumbor and A. Bello, Tuning the Electronic Structure and Thermodynamic Properties of Hybrid Graphene-Hexagonal Boron Nitride Monolayer, FlatChem, 2020, 24, 100194 CrossRef CAS .
28. E. M. O’Sullivan, N. Grobert and M. Swart, Density Functional Theory Investigation of 2D Phase Separated Graphene/Hexagonal Boron Nitride Monolayers; Band Gap, Band Edge Positions, and Photo Activity, J. Phys. Chem. C, 2024, 129, 638–647 CrossRef PubMed .
29. L. Ci, L. Song, C. Jin, D. Jariwala and D. Wu, et al., Atomic Layers of Hybridized Boron Nitride and Graphene Domains, Nat. Mater., 2010, 9, 430–435 CrossRef CAS PubMed .
30. H. S. Wang, L. Chen, K. Elibol, L. He and H. Wang, et al., Towards Chirality Control of Graphene Nanoribbons Embedded in Hexagonal Boron Nitride, Nat. Mater., 2021, 20, 202–207 CrossRef CAS PubMed .
31. X. Leng, F. Jin, M. Wei and Y. Ma, GW Method and Bethe–Salpeter Equation for Calculating Electronic Excitations, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 532–550 CAS .
32. M. Zhang, Y. Liu, Y.-N. Jiang and Y. Ma, Many-Body Green's Function Theory for Electronic Excitations in Complex Chemical Systems, J. Phys. Chem. Lett., 2023, 14, 5267–5282 CrossRef CAS PubMed .
33. J.-H. Choi, P. Cui, H. Lan and Z. Zhang, Linear Scaling of the Exciton Binding Energy versus the Band Gap of Two-Dimensional Materials, Phys. Rev. Lett., 2015, 115, 066403 CrossRef PubMed .
34. Z. Jiang, Z. Liu, Y. Li and W. Duan, Scaling Universality Between Band Gap and Exciton Binding Energy of Two-Dimensional Semiconductors, Phys. Rev. Lett., 2017, 118, 266401 CrossRef PubMed .
35. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed .
36. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed .
37. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed .
38. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed .
39. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS .
40. J. Feng, C.-W. Tseng, T. Chen, X. Leng and H. Yin, et al., A New Energy Transfer Channel from Carotenoids to Chlorophylls in Purple Bacteria, Nat. Commun., 2017, 8, 71 CrossRef PubMed .
41. X. Zhang, H. Ma, M. Zhang and Y. Ma, Interfacial Charge-Transfer Excitons Help the Photoreduction of CO₂ on TiO₂, ACS Catal., 2022, 12, 11024–11035 CrossRef CAS .
42. H. Yin, Y. Ma, J. Mu, C. Liu and M. Rohlfing, Charge-Transfer Excited States in Aqueous DNA: Insights from Many-Body Green's Function Theory, Phys. Rev. Lett., 2014, 112, 228301 CrossRef PubMed .
43. T. Chen, Y.-n Hao, F. Jin, M. Wei and J. Feng, et al., Origin of the Deep Band-Gap State in TiO₂(110): ddσ Bonds Between Ti-Ti Pairs, Phys. Rev. B, 2018, 98, 205135 CrossRef CAS .
44. H. Ma, X. Zhang, F. Jin, H. Zhou and J. Zhang, et al., Crucial Roles of Triazinic-N = O and C = O Groups in Photocatalytic Water Splitting on Graphitic Carbon Nitride, J. Mater. Chem. A, 2021, 9, 5522–5532 RSC .
45. H. Ma, L. Sun, Y. Ma, H. Yuan and H. Song, et al., Graphene with Suitable-Size Nitrogen-Doped Cavity Being an Excellent Photocatalyst for Proton-Coupled Electron Transfer in Water Splitting, Carbon, 2024, 230, 119626 CrossRef CAS .
46. X. Qian, P. Umari and N. Marzari, First-Principles Investigation of Organic Photovoltaic Materials C₆₀, C₇₀, [C₆₀]PCBM, and Bis-[C₆₀]PCBM Using a Many-Body G₀W₀-Lanczos Approach, Phys. Rev. B, 2015, 91, 245105 CrossRef .
47. M. R. Filip and F. Giustino, GW Quasiparticle Band Gap of the Hybrid Organic-Inorganic Perovskite CH₃NH₃PbI₃: Effect of Spin-Orbit Interaction, Semicore Electrons, and Self-Consistency, Phys. Rev. B, 2014, 90, 245145 CrossRef .
48. W. von der Linden and P. Horsch, Precise Quasiparticle Energies and Hartree-Fock Bands of Semiconductors and Insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 8351–8362 CrossRef CAS PubMed .
49. M. Rohlfing, P. Krüger and J. Pollmann, Efficient Scheme for GW Quasiparticle Band-Structure Calculations with Applications to Bulk Si and to the Si(001)-(2 × 1) surface, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 1905–1917 CrossRef CAS PubMed .
50. M. Rohlfing, P. Krüger and J. Pollmann, Quasiparticle Band-Structure Calculations for C, Si, Ge, GaAs, and SiC Using Gaussian-Orbital Basis Sets, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 17791–17805 CrossRef CAS PubMed .
51. Y. Liu, X. Zhang, Y.-N. Jiang, M. Zhang and Y. Ma, Critical Role of Empty in-Gap States in the Photocatalytic Water Splitting on Carbon Nitride Nanosheets, Appl. Surf. Sci., 2024, 644, 158806 CrossRef CAS .
52. F. Jin, X. Zhang, M. Wei, T. Chen and H. Ma, et al., Critical Role of the Defect State in the Photo-Oxidation of Methanol on TiO₂(110), J. Mater. Chem. A, 2020, 8, 20082–20090 RSC .
53. B. Hunt, J. D. Sanchez-Yamagishi, A. F. Young, M. Yankowitz and B. J. LeRoy, et al., Massive Dirac Fermions and Hofstadter Butterfly in a van der Waals Heterostructure, Science, 2013, 340, 1427–1430 CrossRef CAS PubMed .
54. J. Jung, A. M. DaSilva, A. H. MacDonald and S. Adam, Origin of Band Gaps in Graphene on Hexagonal Boron Nitride, Nat. Commun., 2015, 6, 6308 CrossRef CAS PubMed .
55. E. Wang, X. Lu, S. Ding, W. Yao and M. Yan, et al., Gaps Induced by Inversion Symmetry Breaking and Second-Generation Dirac Cones in Graphene/Hexagonal Boron Nitride, Nat. Phys., 2016, 12, 1111–1115 Search PubMed .
56. J. Zhang and X. Wang, Solar Water Splitting at λ = 600 nm: A Step Closer to Sustainable Hydrogen Production, Angew. Chem., Int. Ed., 2015, 54, 7230–7232 CrossRef CAS PubMed .
57. K. Maeda and K. Domen, Photocatalytic Water Splitting: Recent Progress and Future Challenges, J. Phys. Chem. Lett., 2010, 1, 2655–2661 CrossRef CAS .
58. X. Wang, K. Maeda, A. Thomas, K. Takanabe and G. Xin, et al., A Metal-Free Polymeric Photocatalyst for Hydrogen Production from Water Under Visible Light, Nat. Mater., 2009, 8, 76–80 CrossRef CAS PubMed .
59. S. Nosé, A Unified Formulation of the Constant Temperature Molecular Dynamics Methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef .
60. M. Li, Y. Sun, X. Xue, X. Lu and Z. Guo, et al., Growth and Etching of Centimeter-Scale Self-Assembly Graphene–h-BN Super-Ordered Arrays: Implications for Integrated Electronic Devices, ACS Appl. Nano Mater., 2022, 5, 774–781 CrossRef CAS .
61. D. Geng, I. Abdelwahab, X. Xiao, A. Cernescu and W. Fu, et al., One-Pot Confined Epitaxial Growth of 2D Heterostructure Arrays, ACS Mater. Lett., 2021, 3, 217–223 CrossRef CAS .
62. Y. Wang, G. Brocks and S. Er, Data-Driven Discovery of Intrinsic Direct-Gap 2D Materials as Potential Photocatalysts for Efficient Water Splitting, ACS Catal., 2024, 14, 1336–1350 CrossRef CAS .
63. Y. Wang, M. C. Sorkun, G. Brocks and S. Er, ML-Aided Computational Screening of 2D Materials for Photocatalytic Water Splitting, J. Phys. Chem. Lett., 2024, 15, 4983–4991 CrossRef CAS PubMed .
64. K. Watanabe, T. Taniguchi and H. Kanda, Direct-Bandgap Properties and Evidence for Ultraviolet Lasing of Hexagonal Boron Nitride Single Crystal, Nat. Mater., 2004, 3, 404–409 CrossRef CAS PubMed .
65. R. Y. Tay, M. H. Griep, G. Mallick, S. H. Tsang and R. S. Singh, et al., Growth of Large Single-Crystalline Two-Dimensional Boron Nitride Hexagons on Electropolished Copper, Nano Lett., 2014, 14, 839–846 CrossRef CAS PubMed .
66. Z.-A. Lan, G. Zhang, X. Chen, Y. Zhang and K. A. I. Zhang, et al., Reducing the Exciton Binding Energy of Donor–Acceptor-Based Conjugated Polymers to Promote Charge-Induced Reactions, Angew. Chem., Int. Ed., 2019, 58, 10236–10240 CrossRef CAS PubMed .
67. Z. Gu, Z. Shan, Y. Wang, J. Wang and T. Liu, et al., Tuning the Exciton Binding Energy of Covalent Organic Frameworks for Efficient Photocatalysis, Chin. Chem. Lett., 2024, 35, 108356 CrossRef CAS .
68. G. Li, P. Fu, Q. Yue, F. Ma and X. Zhao, et al., Boosting Exciton Dissociation by Regulating Dielectric Constant in Covalent Organic Framework for Photocatalysis, Chem. Catal., 2022, 2, 1734–1747 CAS .
69. W. Zhang, Z. Deng, J. Deng, C.-T. Au and Y. Liao, et al., Regulating the Exciton Binding Energy of Covalent Triazine Frameworks for Enhancing Photocatalysis, J. Mater. Chem. A, 2022, 10, 22419–22427 RSC .
70. G. Wang, A. Chernikov, M. M. Glazov, T. F. Heinz and X. Marie, et al., Colloquium: Excitons in Atomically Thin Transition Metal Dichalcogenides, Rev. Mod. Phys., 2018, 90, 021001 CrossRef CAS .
71. A. Raja, A. Chaves, J. Yu, G. Arefe and H. M. Hill, et al., Coulomb Engineering of the Bandgap and Excitons in Two-Dimensional Materials, Nat. Commun., 2017, 8, 15251 CrossRef PubMed .
72. A. Kaplan, Z. Yuan, J. D. Benck, A. Govind Rajan and X. S. Chu, et al., Current and Future Directions in Electron Transfer Chemistry of Graphene, Chem. Soc. Rev., 2017, 46, 4530–4571 RSC .
73. K. I. Bolotin, K. J. Sikes, Z. Jiang, M. Klima and G. Fudenberg, et al., Ultrahigh Electron Mobility in Suspended Graphene, Solid State Commun., 2008, 146, 351–355 CrossRef CAS .
74. C. Zhang, Y. Chen, J.-K. Huang, X. Wu and L.-J. Li, et al., Visualizing Band Offsets and Edge States in Bilayer–Monolayer Transition Metal Dichalcogenides Lateral Heterojunction, Nat. Commun., 2016, 7, 10349 CrossRef PubMed .
75. X. Huang, R. Xiong, C. Hao, P. Beck and B. Sa, et al., 2D Lateral Heterojunction Arrays with Tailored Interface Band Bending, Adv. Mater., 2024, 36, 2308007 CrossRef CAS PubMed .
76. L. Zhang, K. Liu, A. B. Wong, J. Kim and X. Hong, et al., Three-Dimensional Spirals of Atomic Layered MoS₂, Nano Lett., 2014, 14, 6418–6423 CrossRef CAS PubMed .
77. Y. Yu, Y. Zhao, S. Li, C. Zhao and W. Liu, et al., Determine the Complete Configuration of Single-Walled Carbon Nanotubes by One Photograph of Transmission Electron Microscopy, Adv. Sci., 2023, 10, 2206403 CrossRef CAS PubMed .
78. S. Behzad and R. Chegel, Investigation of Effects of Interlayer Interaction and Biaxial Strain on the Phonon Dispersion and Dielectric Response of Hexagonal Boron Arsenide, Sci. Rep., 2023, 13, 21339 CrossRef CAS PubMed .
79. A. Splendiani, L. Sun, Y. Zhang, T. Li and J. Kim, et al., Emerging Photoluminescence in Monolayer MoS₂, Nano Lett., 2010, 10, 1271–1275 CrossRef CAS PubMed .
80. Y. Deligiannakis, Nanomaterials for Environmental Solar Energy Technologies: Applications & limitations, KONA Powder Part J., 2018, 35, 14–31 CrossRef CAS .
81. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Atomically Thin MoS₂: A new Direct-Gap Semiconductor, Phys. Rev. Lett., 2010, 105, 136805 CrossRef PubMed .

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp02176f

This journal is © the Owner Societies 2025