Open Access Article
Open Access ArticleBoron beats nitrogen: strained boron–boron bonds as (molecular) proton sponges†‡
Ibon Alkorta *a,
José Elguero
*a,
José Elguero a,
M. Merced Montero-Campillo
a,
M. Merced Montero-Campillo *b,
Otilia Mó
*b,
Otilia Mó b and
Manuel Yáñez
b and
Manuel Yáñez b
b
aInstituto de Química Médica, CSIC, C/Juan de la Cierva, 3, 28006 Madrid, Spain. E-mail: ibon@iqm.csic.es
bDepartamento de Química, Módulo 13, Facultad de Ciencias, and Institute of Advanced Chemical Sciences (IAdChem), Universidad Autónoma de Madrid, Campus de Excelencia UAM-CSIC, Cantoblanco, 28049 Madrid, Spain. E-mail: mm.montero@uam.es
First published on 14th July 2025
Abstract
Although boron usually behaves as a Lewis acid, some molecular structures containing B–B bonds can act as electron donors. Inspired in reported crystalline structures, the basicity and the hydrogen bond (HB) acceptor capability of diborane derivatives of dipyrazole 1 have been studied theoretically using M06-2x and CCSD(T) computational methods. The topology of the electron density and molecular electrostatic potential of compound 1 reveal that the richest electron region is located above the B–B bond, making it suitable to be a strong donor and a very effective proton catcher. A key finding is the remarkably high proton affinity of the parent derivative, which exceeds that of very strong nitrogen-containing organic bases such as guanidines. In line with this finding, the hydrogen-bonded complexes exhibit binding energies up to 37 kJ mol−1, which is a significant interaction considering the electronegativity of boron in comparison with elements typically involved in hydrogen bonds. We have also designed substituted structures where the inductive effect improves the proton affinity and HB acceptor capabilities. The proton affinities of 1b reach 1096 kJ mol−1, among the highest reported for molecules in the gas-phase.
1. Introduction
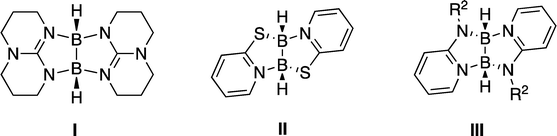
The small boron atom is one of the most versatile of the periodic table, showing a rich variety of bonding patterns beyond the common trivalent monomeric compounds. For instance, the diborane (B2H6) structure with bridging hydrogens is well known for being the paradigm of three centre-two electron (3c–2e) bonds.1 Another interesting example is the highly stable species B12H122−, closoborane, which exhibits an icosahedral Ih symmetry.2,3 In this structure, each boron atom is surrounded by five atoms: four other borons and one hydrogen.Single B–B bonds, are found, among other systems, in diboron(4) compounds. The structure of its parent compound, B2H4, has been in debate for years. Several experimental and high-level theoretical studies have proved it belongs to the C2v symmetry group.4,5 The ability of the B–B bond of this molecule to act as a HB acceptor has been explored by some of us,6 and the reactivity and electronic characteristics of diboron(4) and some of its simple derivatives have been reviewed recently.7 The growing interest on boron chemistry and its applications to synthesis made us explore the physicochemical properties of strained boron–boron compounds, with the aim of finding out what were the limits they could reach in particular for the acid–base behaviour.
In the search of promising donors of this kind, we found a set of reported structures achieved by dehydrogenation of dimers of borane derivatives, and characterized by X-ray crystallography, where polycyclic structures I–III with B–B bonds are stabilized by dative bonds (Scheme 1).8–11 The central core of these structures present two five-membered rings with a common B–B bond. The theoretical analysis of I shows that the HOMO orbital is located on this bond, and the protonation of its derivatives proceeds with its breakdown, placing the new hydrogen atom between the two boron atoms.12 Following these evidences, the dehydrogenation of pyrazobole IV could yield compound 1, which contains a B–B bond leading to two four membered rings (Scheme 2). Because of this, we hypothesized that this highly strained bond could exhibit better donor qualities than the previously described ones.
In the present article, we will study the donor properties of the abovementioned tetracyclic structure 1 with three different substituents on the boron atom (see Scheme 3), to consider a range of inductive effects. For each of them, the protonation and the HB complexes with five typical HB donors (HF, HCl, HBr, HCN and HCCH) are studied at the CCSD(T)-F12c and M06-2X computational levels, leading to a survey of 18 complexes fully characterized at a high level of theory.
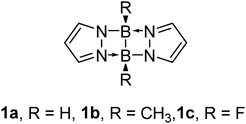 | ||
| Scheme 3 The three derivatives of 1 considered in the present article, to be combined with HF, HCl, HBr, HCN and HCCH hydrogen-bond donors. | ||
2. Computational methods
The geometries of the whole set of molecules and complexes have been optimized with the M06-2X method13 and the aug-cc-pVTZ basis set,14 an approach that provides a reliable treatment of electron correlation and noncovalent interactions for this type of complexes.15,16 Frequency calculations were carried out at the same computational level to verify that the structures correspond to energetic minima. In addition, the complexes of the parent compound 1a were reoptimized at the CCSD(T)-F12c/VDZ-F12 level.17 The CCSD (T) method is known as the gold-standard in quantum chemistry.18,19 The DFT calculations were carried out with the Gaussian-16 program20 and the CCSD(T) ones with the Molpro package.21 The optimized geometries are collected in Table S1 of the ESI.†The electronic properties of the systems have been analysed through the molecular electrostatic potential (MEP),22 electron localization function (ELF),23,24 natural bond orbital (NBO) theory,25 quantum theory of atoms in molecules (QTAIM),26,27 and electron density shift (EDS).28 MEP regions with negative values (isosurfaces coloured in red) indicate parts of the molecules suitable to react or interact with electron deficient systems, as it is the case in protonation or forming intermolecular hydrogen bonds. The ELF maps reflect localized electron pairs in the space for a given system, offering a Lewis-like picture through the partition of the molecular electron density into basins. They are especially useful to evaluate the electron population of a given bond or a lone pair. The NBO method also provides a Lewis-like description from an orbitalic point of view, including hyperconjugation (charge transfer) between occupied and empty orbitals. The Natural energy decomposition analysis (NEDA),29 which is based on the NBO theory, has been performed to obtain information on the most important components of the interaction energy of the complexes. QTAIM analyses the topology of the electron density, for which the critical points are classified based on the number of positive or negative curvatures as nuclear attractor (3,−3), bond (3,−1), ring (3, +1), and cage critical points (3, +3). In particular, the properties of the bond critical points (BCP) are useful to characterize and quantify the interatomic interactions. Finally, the EDS shows how the electron density is reorganized in the complex with respect to the isolated molecules.
3. Results and discussion
We present our results divided in three parts, where the first section focusses on the properties of the isolated parent compound 1a, paying attention to electronic characteristics and proton affinity; the second explores the hydrogen bonded complexes of 1a, and the third and final section discusses the inductive effect of the substituents, specifically 1b and 1c, in terms of their proton affinity values and ability to form hydrogen bond complexes. This approach allows a quite systematic exploration of the relationship between structure and donor properties of the prototype strained boron–boron bond.3.1. Properties of 1 (R = H)
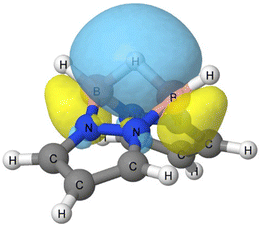
Depicted in Fig. 1, the isolated compound 1a exhibits C2v symmetry with a roof-like shape. According to the MEP and in agreement with what observed for compound I, the most negative region in 1 is located above the B–B bond (the ridgepole of the roof), while the positive regions are associated to the hydrogen atoms of the pyrazole rings. The richest electron region between the two borons appears in the ELF analysis represented by a disynaptic basin populated by 2.25 e, and the same interatomic region viewed through QTAIM analysis presents a B–B BCP with a high electron density (ρBCP = 0.15 a.u.) and negative Laplacian (∇2ρBCP = −0.36 a.u.), which are together the fingerprints of a covalent bond.30 The HOMO corresponds precisely to the same B–B basin region, as shown in the last image of Fig. 1.It is evident from this set of results that the B–B bond is the most basic region and protonation occurs at this bond, leading to its cleavage. In fact, the calculated proton affinity (PA), 1065 kJ mol−1 at the CCSD-F12c computational level (1060 kJ mol−1 at M06-2X), is considerably larger than that of guanidine (986, 979, and 982 kJ mol−1 for the experimental,31 M06-2X, and CCSD(t)-F12c values, respectively), and even larger than that of 1,8-bis(dimethylamino)naphthalene (1028.2 kJ mol−1), which is considered a prototype proton sponge.31 The protonated geometry we obtained for 1a is consistent with the reported experimental protonated structure of I, were the additional hydrogen is positioned between the two boron atoms.32 This protonation can be reversed, regenerating the neutral form of molecule I.33 Attempts to protonate 1a on the B–H bond with dissociation of H2, as described for other borane derivatives,34 rearrange to the structure shown in Fig. 2.
The B–B bond cleavage induced by protonation results in an energetic distortion of the structure amounting to 95 kJ mol−1, calculated as the energy difference of the isolated monomer and the protonated structure excluding the additional proton atom. Nevertheless, the substantial stabilization observed upon protonation, as indicated by the value of PA, can be attributed to the formation of a 3c–2e bond that links the B–H–B group, as depicted in Fig. 2. According to NBO calculations, this 3c–2e bond is richly populated with 1.94 e, with each boron contributing 25% and the bridging hydrogen accounting for 49%, and only 1% from remaining atoms.
At this point, it is interesting to compare neutral 1a with others mentioned in the Introduction, such as diborane(4). Recalling the disynaptic ELF B–B basin described in Fig. 1, diborane(4) exhibits a monosynaptic basin between boron atoms populated with 2 e,6 but instead of a BCP diborane(4) presents a non-nuclear attractor at the same place. The MEP of both structures are pretty similar, but the curvatures of the density are not ((3,−1) vs. (3, +3) critical points). In this sense, borons in diborane(4) are tricoordinated and the monosynaptic basin between them resembles a lone pair, whereas tetracoordinated boron atoms behaviour in 1a are closer to π donors. Nonetheless, the topology when connecting with HB donors such as HF is completely analogous, as we will see in the following section.
3.2. Hydrogen bonded complexes with 1a
In view of the basicity of the system, it is not surprising that hydrogen bond donors interact with 1a through the strained B–B bond. Consequently, complexes with linear proton donors H–X belong as well to the C2v symmetry group, with the H–X molecule pointing towards the middle of the B–B bond. This latter point is a BCP of the B–B bond, as shown by the molecular graph in Fig. 3(a), which is connected through an intermolecular bonding path with the hydrogen atom of HF. This path is similar to that described for HB complexes with π-systems as HCCH and H2CCH;35 as in those cases, the description of the electron density topology corresponds to a conflict catastrophe, since a small perturbation of the systems breaks the H⋯(B–B) BCP bond path. Two examples are included in Fig. S2 (ESI†). | ||
| Fig. 3 (a) Molecular graph of 1a:HF. (b) NBO orbitals involved in the formation of the 1a:HF complex. Green and red dots of the molecular graph correspond to the location of the BCPs and RCPs, respectively. The molecular graphs of the set of complexes are illustrated in Table S1 (ESI†). The values of the electron density at the intermolecular and the B–B bcp's are indicated in au. | ||
Despite being boron an archetype of electrodeficient atom, the accumulation of electron density due to the formation of the B–B bond results into quite high dissociation energies, as it is important to remind that we are just dealing with neutral complexes in the gas phase. The dissociation values are shown in Table 1, ranging between 34 and 13 kJ mol−1 at the CCSD(T)-F12c level, and between 37 and 12 kJ mol−1 at the M06-2X level. The similarity between both methods is not surprising, given that the geometries are almost identical (linear regression, “M06-2x distance” = 0.0285 + 0.9874 “CCSD(T)F12c distance”, R2 = 0.999, n = 5). The stability order of the complexes follows the sequence HF ≫ HCl > HCN > HBr ≫ HCCH, in line with the dipole moment and polarizability exhibited by the set of HB donors, what is reflected in a significantly shorter intermolecular distance (2.03 Å) for the strongest complex with respect to the others.
For a reader unfamiliar with the strength expected for gas-phase neutral complexes of this kind, it might seem that the 1a:HCCH interaction is quite weak. However, it is important to put this result in an appropriate context. A comparison with results reported in the literature at the CCSD(T)-F12c level36 for nonpolar HCCH and cyclopropane as HB acceptor (paradigm of strained cycle), shows that 1a is a stronger HB acceptor. For instance, the dissociation energy values for the complexes of HF with HCCH, cyclopropane and 1a are 17.6, 17.9 and 33.9 kJ mol−1, respectively. Regarding the impact of the interaction, it should be mentioned that the donor molecule essentially keeps its geometrical features and suffers very small distortions, whereas the largest deformation energy is only 2.30 kJ mol−1 in the HF complex. The complex formation produces the elongation of the B–B bond and a small increment of the roof angle of 1a (see Table S2 and Fig. S1, ESI†). Excellent linear correlations (R2 > 0.97) are obtained between the three geometrical parameters analysed (H⋯CB dist., ΔB–B bond, and Δroof angle) (Fig. S1, ESI†). Shorter H⋯X distances correspond to larger increments of the B–B bonds (up to 0.035 Å in the strongest complex, the HF one, along with an increment of 1.6° in the roof angle of 1a).
Because of the bond elongation, the electron density of the B–B orbital (Fig. 3(b)) decreases, and accordingly a part of its density is transferred to the antibonding σ* (HX) molecular orbital, resulting in a net charger transfer. The charge transfer (CT) stabilization is precisely the most important attractive component in the natural energy decomposition analysis (NEDA), shown in Table 2. When looking at the different components of the interaction energy, the CT contribution ranges between the 46–33% of the attractive terms, being larger in the most stable complexes and smaller in the least one [1a:HCCH]. The rest of the stabilizing components are mostly electrostatic, but polarization and even more exchange have significant contributions. As expected, the strongest interactions are accompanied by the largest electronic deformation of the monomers, which oppose to binding. The effects of the charge transfer can be quantified as well looking at the increment of the dipole moment of the complex (last column in Table 2), and the molecular regions contributing the most visualized through EDS maps (Fig. 4). For the case illustrated in the latter figure, the dipole moment enhancement Δμ is 1.42 D, which is due to the population of the HB region and the electron gaining in the fluorine lone pairs.
| Complex | CT | ES | POL | XC | Def 1a | Def HX | Δμ (D) |
|---|---|---|---|---|---|---|---|
| 1a:HF | −65.3 | −46.3 | −8.1 | −22.3 | 48.0 | 55.4 | 1.42 |
| 1a:HCl | −57.3 | −34.6 | −15.1 | −24.3 | 52.6 | 53.1 | 1.57 |
| 1a:HBr | −63.4 | −34.1 | −17.3 | −26.0 | 63.4 | 54.0 | 1.77 |
| 1a:HCN | −34.4 | −29.3 | −12.9 | −16.7 | 37.8 | 30.9 | 1.40 |
| 1a:HCCH | −19.1 | −14.5 | −10.8 | −13.6 | 26.8 | 19.7 | 0.84 |
 | ||
| Fig. 4 Electron density shift of the 1a:HF complex. Red and grey regions correspond to poorer and richer electron regions upon complexation, respectively. | ||
3.3. Enhancing basicity by inductive effect on the boron–boron bond.
Going back to the question of the limits of boron bonds as donors, it is obvious from a chemical point of view that the effects of substitution need to be explored. There is a clear inductive effect evidenced by the PA values of these molecules, which are 1128.4 kJ mol−1 for 1b and 1064.8 kJ mol−1 for 1c; in other words, 36 kJ mol−1 larger and 28 smaller, respectively, than the one obtained for the parent compound 1a, 1092.6 kJ mol−1. It is more than well documented the positive inductive effect that methyl groups have on regular C–C bonds, and the same is observed here on a B–B bond. Regarding the hydrogen-bond acceptor capabilities (see Table 3), and in good agreement with the proton affinities (Table 1), the ranking of dissociation energies is 1b:HX > 1a:HX > 1c:HX. Note that the strongest complex, 1b:HF, has a dissociation energy of almost 40 kJ mol−1, together with a bonding distance below 2 Å. Even the complex with the weakest HB donor, HCCH, is reinforced, and the corresponding distance decreases by ∼0.1 Å.| 1b | 1c | |||
|---|---|---|---|---|
| Complex | De | H⋯CB | De | H⋯CB |
| a These complexes show almost negligible imaginary frequencies (8i cm−1 in 1:HCl and 5i and 3i cm−1 in 1:HCCH). The C2v geometries of all the systems will be considered for consistency. | ||||
| 1:HF | 39.8 | 1.991 | 20.8 | 2.168 |
| 1:HCl | 28.4 | 2.151 | 15.2a | 2.332 |
| 1:HBr | 27.0 | 2.108 | 14.3 | 2.348 |
| 1:HCN | 27.2 | 2.324 | 18.7 | 2.456 |
| 1:HCCH | 15.5 | 2.481 | 8.0a | 2.634 |
Some further chemical insight from the De values can be obtained using a combination of a Free-Wilson matrix37,38 (Table S3, ESI†) and the nucleophilicity and electrophilicity indexes, whose relationship is based on the eqn (1) proposed by Legon:39,40
| De = c·NbEHX | (1) |
| Molecule | Nb | Molecule | EHX |
|---|---|---|---|
| 1a | 5.9 | HF | 6.0 |
| 1b | 6.7 | HCl | 4.2 |
| 1c | 3.7 | HBr | 3.9 |
| HCN | 4.2 | ||
| HCCH | 2.2 |
As long as the Nb values of the ligands follow the sequence 1b > 1a > 1c, and EHX reflects the electrophilicity of H in the HB acceptor according to the order HF > HCl ∼ HCN > HBr > HCCH, we can say that the results are fully in line with the dissociation energies previously observed, to the point that the fitted values using the derived from the Nb and EHX vs. the calculated De energies are linearly correlated with a R2 value larger 0.98 (see Fig. S3, ESI†). We can hypothesize that the inductive effects we generally predict for sigma carbon bonds are expected to be followed here as well, opening a door for tunning donor abilities in a predictable manner. Similar conclusions could be followed by analysing the topology of the electron density of the complexes, explained in detail in Fig. S4 (ESI†).
Again, it is useful to remember that derivatives of diborane(4) compounds, such as those synthesized and characterized by Horn and collaborators,12 can also be tuned by the choice of the substituents, improving the nucleophilicity of the system.
4. Conclusions
Novel structures including a strained B–B bond are proposed in this article, for which we have explored the protonation and hydrogen bond acceptor properties using the CCSD(T)-F12c and DFT (M06-2X) computational methods. These systems exhibit proton affinities greater than those of well-known organic bases, such as guanidines or 1,8-bis(dimethylamino)naphthalene (1028.2 kJ mol−1), which is considered a prototype proton sponge. Furthermore, their complexes with proton donors are highly stable, as evidenced by the dissociation energy of −34 kJ mol−1 for the 1a:HF complex. We find these results relevant, as we are dealing with electrodeficient atoms behaving as electron donors and proton sponge qualities better than nitrogen donors, which is a result that was not easily predictable. Moreover, the modulation of their properties seems to be affordable. Replacing the hydrogen atoms bonded to the boron atoms in 1a with methyl groups or fluorine atoms reveals significant inductive effects, reaching PA values higher than 1096 kJ mol−1. We have also observed that the protonation of these systems leads to the cleavage of the B–B bond and the subsequent formation of a 3c–2e B–H–B bond.As occurs with classical lone-pair donor atoms, the strained B–B bond can form hydrogen bonds, as observed when studying the hydrogen-bonded complexes with a set of representative compounds. The interaction takes place at the centre of the B–B bond, consistent with the position of the MEP minima and the HOMO orbital of the isolated 1a molecule. The electron density characteristics of these complexes indicate a catastrophic instability, like that observed in π systems. The stability of the complexes has been correlated with the nucleophilicity and electrophilicity indexes using eqn (1) proposed by Legon. The nucleophilicity results for the three derivatives of 1 align with the characteristics of their substituents in typical carbon chemistry.
Conflicts of interest
There are no conflicts of interest to declare.Data availability
The data supporting this article have been included as part of the ESI.†Acknowledgements
This work was carried out with financial support from Projects PID2021-125207NB-C31 and PID2021-125207NB-C32 of the Ministerio de Ciencia, Innovación y Universidades of Spain (MICINN).References
- S. H. Bauer, J. Am. Chem. Soc., 1937, 59, 1096–1103 CrossRef CAS
.
- H. C. Longuet-Higgins, M. D. V. Roberts and H. J. Emeleus, Proc. R. Soc. London, Ser. A, 1955, 230, 110–119 CAS
.
- A. R. Pitochelli and F. M. Hawthorne, J. Am. Chem. Soc., 1960, 82, 3228–3229 CrossRef CAS
.
- B. Ruščic, M. Schwarz and J. Berkowitz, J. Chem. Phys., 1989, 91, 4576–4581 CrossRef
.
- S.-L. Chou, J.-I. Lo, Y.-C. Peng, M.-Y. Lin, H.-C. Lu, B.-M. Cheng and J. F. Ogilvie, Chem. Sci., 2015, 6, 6872–6877 RSC
.
- I. Alkorta, I. Soteras, J. Elguero and J. E. Del Bene, PCCP, 2011, 13, 14026–14032 RSC
.
- E. C. Neeve, S. J. Geier, I. A. I. Mkhalid, S. A. Westcott and T. B. Marder, Chem. Rev., 2016, 116, 9091–9161 CrossRef CAS PubMed
.
- A. Ahmad, S. Gayen, S. Mishra, Z. Afsan, S. Bontemps and S. Ghosh, Inorg. Chem., 2024, 63, 3376–3382 CrossRef CAS PubMed
.
- O. Ciobanu, P. Roquette, S. Leingang, H. Wadepohl, J. Mautz and H.-J. Himmel, Eur. J. Inorg. Chem., 2007, 4530–4534 CrossRef CAS
.
- É. Rochette, N. Bouchard, J. Légaré Lavergne, C. F. Matta and F.-G. Fontaine, Angew. Chem., Int. Ed., 2016, 55, 12722–12726 CrossRef PubMed
.
- O. Ciobanu, F. Allouti, P. Roquette, S. Leingang, M. Enders, H. Wadepohl and H.-J. Himmel, Eur. J. Inorg. Chem., 2008, 5482–5493 CrossRef CAS
.
- J. Horn, A. Widera, S. Litters, E. Kaifer and H.-J. Himmel, Dalton Trans., 2018, 47, 2009–2017 RSC
.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed
.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS
.
- M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600 CrossRef CAS PubMed
.
- B. Nepal and S. Scheiner, Chem. Phys., 2015, 463, 137–144 CrossRef CAS
.
- G. D. Purvis, III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef
.
- A. G. Donchev, A. G. Taube, E. Decolvenaere, C. Hargus, R. T. McGibbon, K.-H. Law, B. A. Gregersen, J.-L. Li, K. Palmo, K. Siva, M. Bergdorf, J. L. Klepeis and D. E. Shaw, Sci. Data, 2021, 8, 55 CrossRef CAS PubMed
.
- J. Řezáč and P. Hobza, J. Chem. Theor. Comput., 2013, 9, 2151–2155 CrossRef PubMed
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg
Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, USA, 2016 Search PubMed
.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS
.
- E. Scrocco and J. Tomasi, in Advances in Quantum Chemistry, ed. P.-O. Löwdin, Academic Press, 1978, vol. 11, pp. 115–193 Search PubMed
.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS
.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS
.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed
.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS
.
- P. L. A. Popelier, Atoms In Molecules. An introduction, Prentice Hall, Harlow, England, 2000 Search PubMed
.
- I. Iribarren, G. Sánchez-Sanz, I. Alkorta, J. Elguero and C. Trujillo, J. Phys. Chem. A, 2021, 125, 4741–4749 CrossRef CAS PubMed
.
- E. D. Glendening and A. Streitwieser, J. Chem. Phys., 1994, 100, 2900–2909 CrossRef CAS
.
- I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154–11161 CrossRef CAS
.
- S. G. Lias, J. E. Bartmess, J. F. Liebman, J. L. Holmes, R. D. Levin and W. G. Mallard, NIST Chemistry WebBook, NIST Standard Reference Database, eds.P. J. Linstrom and W. G. Mallard, Gaithersburg MD, 2023 Search PubMed
.
- O. Ciobanu, E. Kaifer, M. Enders and H.-J. Himmel, Angew. Chem., Int. Ed., 2009, 48, 5538–5541 CrossRef CAS PubMed
.
- A. Wagner, S. Litters, J. Elias, E. Kaifer and H.-J. Himmel, Chem. – Eur. J., 2014, 20, 12514–12527 CrossRef CAS PubMed
.
- M. Yáñez, O. Mó, M. M. Montero-Campillo, I. Alkorta and J. Elguero, J. Comput. Chem., 2025, 46, e27509 CrossRef PubMed
.
- I. Rozas, I. Alkorta and J. Elguero, J. Phys. Chem. A, 1997, 101, 9457–9463 CrossRef CAS
.
- I. Alkorta and A. Legon, Chem. Phys. Lett., 2023, 833, 140929 CrossRef CAS
.
- S. M. Free and J. W. Wilson, J. Med. Chem., 1964, 7, 395–399 CrossRef CAS PubMed
.
- I. Alkorta, F. Blanco and J. Elguero, Tetrahedron, 2008, 64, 3826–3836 CrossRef CAS
.
- A. C. Legon and D. J. Millen, J. Am. Chem. Soc., 1987, 109, 356–358 CrossRef CAS
.
- I. Alkorta and A. C. Legon, Molecules, 2017, 22, 1786 CrossRef PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp02320c |
| ‡ Dedicated to Professor Resnati, celebrating a career in fluorine and noncovalent chemistry on the occasion of his 70th birthday. |
| This journal is © the Owner Societies 2025 |