Amorphous solid water prevails inside the spherical nanopores of the MIL-101(Cr) framework below 200 K: PALS, XRD and BDS studies†
Vivek Sudhira,
Debarati Dasbc,
Pranav Utpallad,
Siddhartha Kolayce,
Manvendra Narayan Singhf and
Dhanadeep Dutta *bc
*bc
aCochin University of Science and Technology, Cochin – 682022, Kerala, India
bRadiochemistry Division, Bhabha Atomic Research Centre, Trombay, Mumbai-400085, India. E-mail: deep@barc.gov.in
cHomi Bhabha National Institute, Anushaktinagar, Mumbai-400094, India
dSchool of Chemistry, University of Hyderabad, Hyderabad-500046, India
eChemistry Division, Bhabha Atomic Research Centre, Trombay, Mumbai-400085, India
fSynchrotron Utilization Section, Raja Ramanna Centre for Advanced Technology, Indore-452013, India
First published on 24th July 2025
Abstract
The glass transition of nano-confined supercooled water is still a vivid topic of discussion. Previous calorimetric studies on nano-confined water have reported that no glass transition is visible for water confined within nanopores having size less than 2 nm due to a lack of network formation [M. Oguni et al, J.Phys. Chem. B, 2011, 115, 14023-14029]. According to literature reports, a sharp increase in heat capacity [G. P. Johari, J. Chem. Phys., 2009, 130, 124518] or a cross-over in relaxation [J. Swenson et al., Phys Rev. Letts 2006, 96, 247802] of water inside the nanopores (size ∼1–1.8 nm) in the temperature range of 210–180 K was due to pre-melting of fine ice crystals, fragile to strong transitions or non-cooperative relaxation. In the present study, we have carried out low-temperature Positron Annihilation Lifetime Spectroscopy (PALS), synchrotron-based X-ray diffraction and Broadband Dielectric Spectroscopy (BDS) on water confined within the nanopores (size ∼0.7–1.8 nm) of the synthesized MIL-101(Cr) metal organic framework (MOF) to clearly understand the low-temperature phase transition of confined water. The PALS spectra have shown three different slopes at three different temperatures. At high temperature, the change in the slope of the ortho-positronium (o-Ps) pick-off lifetime (τo-Ps) profile near 280 K corresponds to the structural rearrangement of water molecules in the liquid phase. At around 230 K, a slight change in the slope of the τo-Ps profile corresponds to partial crystallization of confined supercooled water. The XRD pattern showed the evolution of short range crystalline peaks below 230 K, confirming partial crystallization of water under confinement. At around 200 K, the τo-Ps profile showed a sharp change in the slope, and below 200 K, τo-Ps remains almost constant. Interestingly, XRD peaks did not show any noticeable change at 200 K, suggesting that the transition at 200 K is not associated with any crystallization change. Rather, the weak temperature dependence of τo-Ps (∼0.5 ns) below 200 K corresponds to o-Ps annihilation in the free volume associated with amorphous solid water (ASW) inside the MIL-101(Cr) nanopores. The dielectric relaxation of confined water showed a cross-over from Vogel–Fulcher–Tammann (VFT) to Arrhenius dependence at around 190 K, indicating a transition from a fragile glass forming liquid to an ASW like strong glassy phase inside the nanopores. Hence, a combined study using XRD, PALS and BDS confirms that the supercooled liquid transforms into to an ASW glassy phase at 200–190 K inside the nanopores of MIL-101(Cr) having pore size distribution around 0.7–1.8 nm.
1. Introduction
The anomalous properties of water in its supercooled phase have spurred extensive research into its structural, dynamical, and thermodynamical properties over the past few decades. Certain thermo-physical response functions such as the coefficient of thermal expansion, isothermal compressibility, and isobaric heat capacity of supercooled water have shown a diverging trend at an extrapolated temperature of 228 K known as the singularity temperature (Tc).1–3 However, before reaching Tc, supercooled bulk water crystallizes at a higher temperature around 235 K known as the homogeneous nucleation temperature (TH), thus making it difficult to experimentally reach the Tc below the TH to study the supercooled liquid phase. Hence, the temperature region below TH is known as “no man's land”.1,4 Nevertheless, crystallization of water at 235 K may be avoided, if bulk water is cooled extremely rapidly to reach a glassy phase below a commonly accepted glass transition temperature of Tg = 136 K at ambient pressure.1 However, Angell and his coworkers suggested that true glass transition temperature may be assigned at 169 K by comparing the behavior of some thermodynamical parameters (enthalpy relaxation) of water with other normal liquids.5 Nevertheless, the assignment of the glass transition temperature of water is still a controversial issue because glassy water inevitably crystallizes while heating at 150 K,4 making it difficult to directly observe the reassigned Tg = 169 K. Another approach to circumvent ice crystallization at low temperatures is to confine water within nanopores.1,4,6 Depending on the extent of size and shape of confinement, water can remain in a supercooled liquid state below the homogeneous nucleation temperature.1,4,6 Thus, nanoconfined water provides an excellent platform to be deeply cooled until it reaches its glass transition temperature. Several studies have reported that severe confinement can be used to suppress crystallization, enabling the study of the glass transition and related dynamics of water.7–9 However, in many previous studies on nano-confined water, a clear calorimetric result of glass transition has not been obtained due to a lack of hydrogen bonding network formation inside the nanopores having pore sizes less than 2.1 nm.7,10 It was thus necessary to have a water hydrogen bonding network larger than 2.1 nm but avoid crystallization to observe the calorimetric result of glass transition. Several studies have been carried out by changing the pore topology and the surface chemistry of the pores to observe the calorimetric step for glass transition.11–13 Depending upon the pore size and the measurement techniques, the transition temperature of water has been reported within the range of 180–220 K.14–20 However, the assignment of the transition within this temperature range is still controversial. Some authors attributed this transition to a dynamical cross-over from high-temperature Vogel–Fulcher–Tammann (VFT) relaxation of fragile water molecules to low-temperature Arrhenius relaxation of strong water molecules. Thus, this cross-over transition was also ascribed to a fragile to strong transition of the confined supercooled water. It was also suggested that this transition might be recognized as a transition from a high-density liquid (HDL) to a low-density liquid (LDL). Nonetheless, this dynamical crossover or the fragile to strong cross-over was suggested as the general phenomenon of glass forming water in its supercooled state. Oguni et al. have shown that the water confined within MCM41 nanopores exhibits three discrete glass transition temperatures, namely, 115 K, 165 K, and 210 K, with increasing pore diameter within the range of 1.5–5.0 nm.7 They have suggested that the glass transition temperature for bulk water is 210 K, at which water molecules aggregate through the formation of hydrogen-bond networks, thus freezing the conformational flexibility. This is the highest glass transition temperature reported so far for water forming four bonds per molecule in a developed hydrogen-bond network.7 Despite numerous works in confined water investigating its dynamics and glass transition through molecular dynamics simulations21,22 and various experimental methods,23–25 a clear and comprehensive picture of the glass transition and associated dynamics is still lacking. In the present study, Positron Annihilation Lifetime Spectroscopy (PALS) has been utilized to understand the nature of the transition occurring at around 200 K for supercooled water confined within MIL-101(Cr) MOF nanopores (pore size within 1–2 nm) by investigating the changes in the local free volume of the nano-confined water molecules during the phase transition. We have compared the PALS result with those of synchrotron based XRD and Broadband Dielectric Spectroscopy (BDS) to obtain a comprehensive picture of the structure and dynamic changes occurring during the phase transition at around 200 K. The evolution of local free volume during the transition investigated using the PALS technique can be considered as the manifestation of the reorientation of water molecules or the freezing of cooperative motion of water molecules inside the confinement. Hence, PALS can reliably provide an indication of the glass transition and has thus been used extensively to study several simple glass-forming systems in confinement and bulk.26–33 PALS shows direct correspondence with other techniques like coherent neutron scattering and - BDS used for investigating the dynamics of nano-confined water.34 Using PALS, Bartos and Kristiak have shown the correlation of the “fragility” of simple glass forming liquids with the free volume microstructure in a series of elastomeric polymers by measuring the lifetime of the metastable electron–positron bound state known as positronium (Ps) formed in the matrix.35 The temperature-dependent Ps lifetime has been shown in the literature to be correlated with the free volume, density and dielectric relaxation behavior of different glass forming liquids.36–38The sensitivity of positron/positronium to changes in local electron density at the site of annihilation facilitates its use in identifying the microscopic structural modification following the phase transition of the confined liquid. In a dielectric porous medium, energetic positron after being injected into the medium loses its energy through excitation and ionization of the molecular substance. After being thermalized, or during the slowdown process, a fraction of positrons may annihilate freely with electrons from the surrounding medium with a short lifetime (∼0.1–0.2 ns). Another fraction may get trapped in open volume defects/pores present in the matrix and annihilate with a longer lifetime (∼0.4 ns). The remaining fraction of thermalized positrons may form a metastable Ps state by capturing an electron from the medium. This state may energetically favor localization in pre-existing free volume in molecular solids, or it may create a cavity/bubble in liquids due to exchange repulsion with the surrounding electrons and gets trapped into it before annihilation.39 The Ps exists in two spin states: the spin singlet para-Ps (p-Ps), which decays through two-photon emission with a very short intrinsic lifetime of 0.125 ns (in vacuum), and the spin triplet ortho-Ps (o-Ps), which annihilates through three-photon emission with a much longer average lifetime of 142 ns in vacuum. However, in the presence of matter, o-Ps can annihilate via a two-photon mode through a process known as pick-off annihilation, whereby the positron in o-Ps seeks an electron of opposite spin from the surrounding medium and annihilates through the emission of two photons with a lifetime of 1–10 ns. The pick-off component of the positron annihilation spectrum can be correlated to the average free-volume size, its distribution, surface chemistry of the free volume, etc. inside the molecular medium.40 Hence, in the present experiment, the temperature dependence of the trapped positron/o-Ps lifetime and intensity in confined water has been measured to understand the low temperature phase transition behavior of water in nano-confinement.
A metal–organic framework (MOF) having uniform pores with a highly porous lattice structure and a high specific surface area formed through self-assembly of metal (oxides) clusters linked via organic ligands of tunable length may act as an ideal host matrix for the nano-confinement study. One of the stable MOFs under humid conditions is chromium terephthalate [popularly known as MIL-101(Cr)] comprising trimeric chromium(III) octahedral clusters interconnected by 1,4-benzenedicarboxylates.41 MIL-101(Cr) having nano-porous spherical cages with a high specific surface area and specific pore volume has displayed excellent hydrothermal and chemical stability.42–45 Theoretically, MIL-101(Cr) has a zeolite-type network structure with the connectivity of the spherical pores through pentagonal (1.2 nm) or hexagonal (1.6 nm) windows. The sizes of two spherical pores as calculated from the original crystallographic structure are 2.7 nm and 3.9 nm. Details of the structure of the MIL-101(Cr) MOF can be obtained from ref. 42 and 44.
2. Experimental methods
2.1. Synthesis of the MIL-101(Cr) framework
The synthesis route of the three-dimensional chromium terephthalate-based framework MIL-101(Cr) was adopted from a reported method.42,45 First, Cr(NO3)3·9H2O (8.0 g, 20 mmol) was dissolved in 100 ml of distilled water and then terephthalic acid (3.32 g, 20 mmol) was added to it and intensively stirred for 30 minutes at room temperature, followed by dropwise addition of 0.84 ml of HNO3 and stirring for an additional 30 minutes. Subsequently, the mixture was transferred to a Teflon-lined stainless steel autoclave and heated at 483 K for 8 hours with a ramp-up/down rate of 2 K min−1. After heating, the green powder was collected by centrifugation and subsequently washed with water. After washing, the powder was treated with dimethylformamide (DMF), water and ethanol separately for 6 hours at 80 °C and separated from the supernatant by centrifugation each time. The green powder of MIL-101(Cr) was dried at 393 K for 12 hours under vacuum.2.2. Characterization of the MIL-101(Cr) framework
Formation of the framework was confirmed using the powder X-ray diffraction technique. The powder diffraction pattern matches well with the simulated pattern generated from the single crystal XRD data file, as shown in Fig. S1 ESI.†Notably, the major peaks align precisely with those of the standard pattern of MIL-101(Cr). The high intensities observed in the pattern signify the high crystallinity of the product, while the presence of peaks at lower angles suggests the abundance of pores within its structure.
The BET N2 gas adsorption–desorption isotherm technique was utilized to estimate the average pore size, specific pore surface area and pore volume of the MIL-101(Cr) MOF.
2.3. Loading with water
Calculated amounts of Millipore water corresponding to the specific pore volume (∼1.21 cm3 g−1 as estimated from the BET N2 gas adsorption–desorption isotherm) was injected into the MIL-101(Cr) framework at room temperature. The sample was sonicated in a water bath for 10 minutes to ensure uniform adsorption of water in the pores of the framework. The prepared samples were kept for 16 h for homogenization. The exact amount of loaded water was then confirmed using thermogravimetric analysis (TGA; Setsys Evolution 1750) with a heating rate of 5 K min−1 under an argon gas atmosphere.2.4. Synchrotron based XRD measurements
Synchrotron-based X-ray diffraction (XRD) was carried out using an angle dispersive X-ray diffraction (ADXRD) beamline (BL-12) at the Indus-2 Synchrotron Radiation Facility, India. The dry and water loaded MIL-101(Cr) samples were separately enclosed in a capillary tube having a diameter of 0.5 mm and then mounted on a rotating holder. To prevent frost formation on the exterior of the capillary, it was cooled with a stream of liquid nitrogen along with dry nitrogen gas. After reaching the target temperature, the sample was stabilized for 30 minutes prior to the measurements.The XRD measurements were conducted in transmission mode using a Mar 345-Dtb area detector. We employed monochromatic X-rays with a wavelength of 0.07878 nm. The accuracy of the X-ray wavelength and the distance between the sample and the detector were ensured by calibrating the setup with the XRD pattern of a LaB6 NIST standard under identical conditions. Each temperature point involved exposing the sample to X-rays for approximately 1 to 3 seconds after a 30-minute equilibration period, with the diffraction data being recorded on an image plate detector.
2.5. Positron annihilation lifetime spectroscopy (PALS)
The 22Na positron source (10 μCi, sealed within 5 mm × 5 mm × 8 μm Kapton foil) embedded in a water loaded MIL-101(Cr) powder sample was hermetically sealed in a copper sample holder. The sample holder was mounted on the cold head of a Sumitoma closed cycle helium cryostat. The measurements were carried out within the temperature range of 150–300 K at 5 K intervals (during the cooling cycle) with a temperature accuracy of ±0.01 K. The temperature dependent PALS measurements were carried out using two BaF2 scintillation detectors connected to a fast–fast coincidence system, which consists of two Constant Fraction Differential Discriminators (CFDD), an ns delay, a Time-to-Amplitude Converter (TAC) and a Multichannel Analyzer (MCA). The time resolution measured with 60Co in 22Na energy windows was 278 ps, and the time calibration was 25 ps per channel. The positron annihilation lifetime spectra were analyzed for discrete lifetime components using the PALSfit analysis program.46 Detailed data analysis is shown in the ESI.†2.6. Broad band dielectric spectroscopy (BDS)
Broad band dielectric spectroscopy (BDS) within the temperature range of 120–300 K on water confined within MIL-101(Cr) was carried out in a broad frequency range of 1.0 × 10−1–1.0 × 107 Hz using an impedance analyzer (Novocontrol, Germany) coupled with a Quatro Cryo system. The sample was first cooled at 120 K and then slowly heated up to 300 K. There was no hysteresis observed during the cooling and heating cycles. The temperature stability during the measurement was maintained at ±0.1 K using a flow of dry N2. Circular powder samples with a diameter of 1.8 mm and a thickness of approximately 1 mm were used for the BDS measurements. The samples were positioned between standard circular gold-plated parallel electrodes and an ac voltage of 0.2 V was applied to the electrodes. BDS measures the complex dielectric function, ε*(ω) = ε′(ω) − iε′′(ω), where ε′ and ε′′ are the real and imaginary parts of permittivity, respectively. In order to determine the characteristic relaxation time (τ), the frequency dependent imaginary part of permittivity (ε′′) was fitted using Havriliak–Negami (HN) functions.473. Results and discussion
3.1. Confirmation of water loading
Confirmation of water loading was carried out using the TGA method and the results are shown in Fig. S2 (ESI†). The complete desorption of water from the loaded MIL-101(Cr) framework takes place near 200 K. Beyond 200 K, there is no weight loss observed due to the complete desorption of water. The percentage weight loss can be expressed as , where MH2O is the mass of water desorbed from the initially water-loaded MIL-101(Cr) matrix and MMIL-101 is the mass of the bare MIL-101(Cr) framework. The percentage volume fraction (vol%) of water loaded into the framework can be calculated as [volH2O/volpore] × 100, where volH2O represents the volume of desorbed water and volpore is the specific pore volume of the MIL-101(Cr) framework. The calculated value of the volume fraction is 73.5 vol% of water in the MIL-101(Cr) nanopores. Henceforth, the dry MIL-101(Cr) framework and water loaded framework will be called S0 and S1, respectively.
, where MH2O is the mass of water desorbed from the initially water-loaded MIL-101(Cr) matrix and MMIL-101 is the mass of the bare MIL-101(Cr) framework. The percentage volume fraction (vol%) of water loaded into the framework can be calculated as [volH2O/volpore] × 100, where volH2O represents the volume of desorbed water and volpore is the specific pore volume of the MIL-101(Cr) framework. The calculated value of the volume fraction is 73.5 vol% of water in the MIL-101(Cr) nanopores. Henceforth, the dry MIL-101(Cr) framework and water loaded framework will be called S0 and S1, respectively.
3.2. Estimation of pore size from BET and PALS
Although theoretically the MIL-101(Cr) framework has two different pore sizes, namely, 2.7 nm and 3.9 nm,44 the BET N2 gas adsorption–desorption isotherm shows a distribution of pore sizes in the synthesized MIL-101(Cr) framework. The pore size distribution is within the range of about 0.7–1.8 nm as estimated using the BJH (Barrett–Joyner–Halenda) method. The specific pore surface area is ∼2564 m2 g−1 and the specific pore volume is ∼1.21 cm3 g−1. The BET N2 gas adsorption–desorption isotherm and the histogram of estimated pore size distribution are shown in Fig. S3 and S4 (ESI†), respectively. The theoretically calculated pore sizes from crystallographic dimensions are observed to be higher than that estimated using the BET N2 gas adsorption–desorption isotherm. The inhouse synthesis of the framework might cause the appearance of small defects in the sample, which could possibly be the source of smaller pore sizes in the sample as compared to that obtained from theoretical calculations.The room temperature PALS study was carried out on dry (S0) and water-loaded (S1) MIL-101(Cr) frameworks. In the pristine framework (S0) sample, the PAL spectrum was best fitted with five lifetime components (from τ1 to τ5 with ascending values). The fitted PAL spectrum of S0 in vacuum at room temperature is shown in Fig. 1. The last three components (namely, τ3, τ4 and τ5) with increasing order correspond to o-Ps annihilation in smaller pores, larger pores and in intergranular meso-porous regions, respectively, as shown in Table 1. The first two components (τ1 and τ2, not shown in Table 1) do not correspond to a long-lived o-Ps state. The first component (τ1) corresponds to free positron and p-Ps annihilation in the bulk, whereas the second component (τ2) is attributed to positron annihilation from small trapping sites (crystal defects) as mentioned before. From the τ3 (= 3.75 ± 0.30 ns) and τ4 (= 13.27 ± 0.63) components, we calculated the pore sizes using the extended Tao–Eldrup (ETE) model.48 The estimated pore sizes are ∼1 nm and 1.6 nm, respectively, which are close to the values estimated from the BET method. These values show a lower limit of the true pore sizes, as a major fraction of o-Ps diffuses out of the crystal grains to the intergranular space. The τ5 component, which arises due to o-Ps diffusion and annihilation at the intergranular space, does not correspond to any intrinsic pore size. When the MIL-101(Cr) framework was loaded with water (S1), the PALS histogram was best fitted with three lifetime components (τ1, τ2 and τ3) with the longest-lived component τ3 corresponding to o-Ps pick-off annihilation in confined water (τ3 ≈ 1.96 ns), whereas the components τ1 and τ2 carry the same information as described above for S0. The fitted lifetime components of o-Ps and their corresponding intensity values in S1 are shown in the last row of Table 1.
| Samples (vol% water loading) | τ3 (ns) | I3 (%) | τ4 (ns) | I4 (%) | τ5 (ns) | I5 (%) |
|---|---|---|---|---|---|---|
| S0 (0%) | 3.75 ± 0.30 | 4.60 ± 0.36 | 13.27 ± 0.63 | 11.25 ± 0.29 | 50.93 ± 0.75 | 18.46 ± 0.34 |
| S1 (73.5%) | 1.96 ± 0.03 | 4.93 ± 0.13 | — | — | — | — |
The typical pick-off lifetime of o-Ps from the self-trapped bubble state in bulk water is around 1.8 ns.49 However, the pick-off lifetime value of o-Ps in confined water inside the MIL-101(Cr) framework is observed to be higher than that in bulk water, which may be ascribed to the lower surface tension of water in nano-confinement (pore size < 2 nm) based on Tolman's equation.50,51
3.3. Low temperature PALS
The low temperature PALS measurements were carried out on the fully hydrated framework sample (S1) within the temperature range of 150–300 K (during the cooling cycle). The variation of PALS spectra with temperature is shown in Fig. S5 (ESI†). The PALS spectra were well fitted with three lifetime components (τ1, τ2, and τ3) above 200 K (as shown in Fig. S6, ESI†). However, below 200 K, fitting the spectra with three components resulted in poorer agreement; rather the data were better described using a two-component fit. The details of fitted lifetime data are given in Table S1 (ESI†). The larger lifetime component obtained from the two-component fitting below 200 K appears to be a low temperature extension of the τ3 profile of three-component fitting above 200 K. Therefore, the larger lifetime component with a value around 0.4–0.5 ns below 200 K is also assigned the label τ3. The variation of τ3 with temperature is shown in Fig. 2. It is seen that the temperature profile of the o-Ps pick-off annihilation lifetime (τ3) component exhibits a quasi-sigmoid curve as shown in Fig. 2. The quasi-sigmoid behavior of o-Ps lifetime is generally observed in glass forming liquids, which indicates that water confined within the nanopores of the MIL-101(Cr) framework undergoes glassy state formation at low temperature.32It can be seen from Fig. 2 that, with decreasing temperature, the τ3 component shows an abrupt decrease at 273 K, indicating the freezing of water present at the bulk/intergranular spaces of the sample.52 Below 273 K, water confined within the nanopores remains in a supercooled liquid state showing a steady decrease in the τ3 value. At around 230 K, a slight change in the slope of the τ3 profile is observed, which is attributed to the partial freezing of core water molecules present inside the cylindrical nanopores.53 However, the surface bound water molecules at the pore wall remain unfrozen (deeply cooled) up to about 200 K due to the significant surface forces, preventing the arrangement of water molecules in a regular tetrahedral ice-like structure.52 However, below 200 K, a clear slope change occurs and τ3 shows very weak temperature dependence up to the lowest temperature studied (150 K). The transition at around 200 K, below which τ3 remains practically constant with very feeble temperature dependence, can be attributed to the formation of an amorphous glass-like structure with a disordered hydrogen bonding network, which does not significantly alter its free-volume structure with a decrease in temperature.49 Hence, the transition at around 200 K can be identified as the glass transition of confined water in the MIL-101(Cr) framework having pore size with a narrow distribution of 0.7–1.8 nm.
This value of τ3 below 200 K may be considered as the combination of o-Ps pick-off lifetime and the trapped positron lifetime in glassy ice. The intensity (I3) of this larger component increases to about 75% at the lowest temperature studied, while the intensity of the o-Ps pick-off annihilation was on average 7–8% above 200 K. The sudden jump in intensity below 200 K indicates a significant contribution of trapped positron annihilation along with o-Ps pick-off annihilation to I3 in the amorphous glassy phase of ice below the glass transition at 200 K. The variation of this intensity component (I3) is shown in Fig. S7 (ESI†).
The value of the smaller lifetime of the two-component fitting below 200 K is also identified as the low temperature extension of the τ2 profile of three-lifetime-component fitting above 200 K, and hence the smaller component below 200 K is labeled as τ2. The variation of τ2 above and below 200 K in combination is shown in Fig. 3, which also exhibits a quasi-sigmoidal dependence with temperature. Above 200 K, τ2 corresponds to the average lifetime of the trapped positron in water and in the MIL-101(Cr) framework system, whereas below 200 K it represents the mean value of trapped positron lifetime in the small defects present in glassy ice, the MIL-101(Cr) framework surface and the reduced lifetime of free positron annihilation while diffusing into the defects, as well as p-Ps lifetime inside the ice filled MIL-101(Cr) framework. The profile of τ2 (Fig. 3) reflects the structural variation of the annihilation sites of trapped positron with the decrease in temperature. There is a gradual decrease in the τ2 value below 273 K and a mild change in the slope was observed at around 230 K. A sharp change in the slope was observed at around 200 K, almost identical to the temperature behavior of τ3 (Fig. 2) as mentioned above. A slower decrease in τ2 with the reduction in temperature below 200 K signifies the poor thermal response of the local trapping sites of positron after glassy phase formation of confined water, identical to the poor thermal response of free volume in glassy ice as observed through the variation of τ3.
 | ||
| Fig. 3 Variation in trapped positron lifetime (τ2) with temperature. The shaded boundaries are shown in Fig. 2. The solid lines are a guide to the eye. | ||
3.4. Low temperature synchrotron XRD
The X-ray diffraction (XRD) pattern of water adsorbed in the MIL-101(Cr) framework, as shown in Fig. 4 illustrates the crystalline behavior of water (after subtraction of the dry MIL-101(Cr) [S0] contribution) in 73.5 vol% hydrated sample while decreasing the temperature from 300 K (RT) to 150 K. The broad diffraction patterns (in black) obtained from RT down to 230 K are characteristic of liquid water, confirming the presence of water in a supercooled liquid state inside the nanopores of the MIL-101(Cr) framework below its bulk freezing temperature of 273 K. The sharp Bragg's peaks (in red) riding on the broad background are observed to appear below 230 K. The appearance of sharp Bragg's peaks clearly indicates the formation of crystalline ice inside the nanopores of the MIL-101(Cr) framework below 230 K. The diffraction peaks are observed to remain unchanged from 230 K down to the temperature 150 K, signifying that there is no further crystalline phase transition below 230 K during cooling.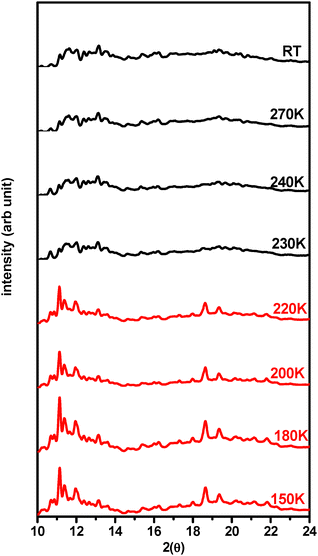 | ||
| Fig. 4 Variation of the XRD pattern of water confined within MIL-101(Cr) framework pores with temperature. The crystalline peaks of ice appear below 230 K. | ||
The sharp Bragg's peaks, which align with those of crystalline ice, indicate the emergence of a mixed phase of cubic ice (ice Ic) that corresponds to three peaks at 2θ = 11.24°, 18.5° and 21.82° and hexagonal ice (ice IH) peaks at 2θ = 10.69°, 11.33°, 12.07°, 15.67°, 18.51°, 20.17° and 21.83° for temperatures below 230 K as illustrated in Fig. 5. The fraction of the crystalline part of frozen water inside the nanopores of MIL-101(Cr) at a temperature of 150 K has been approximated by calculating the ratio of area under the diffraction peak to the total area of the diffraction pattern over the scattering angular range 10°–25° (as shown in Fig. S8, ESI†). It is seen that only about 24 vol% of confined water has crystalline nature, implying that a major fraction of the confined water at a temperature of 150 K is in the amorphous ice state, which is consistent with our previous XRD and neutron diffraction results on nano-confined water.45,53 The phase transition at 200 K as observed through PALS could not be identified by the XRD measurement, confirming the transition at 200 K is not related to the crystalline phase change of confined ice. The transition at 200 K may therefore be attributed to the liquid-to-amorphous phase transition or the glass transition of supercooled water inside the nanopores. Since the free volume of confined water below 200 K remains almost constant up to 150 K as observed through PALS, it is definite that the water is transformed into a solid amorphous phase below 200 K inside the nanopores of the MIL-101(Cr) framework. The crystalline peaks, as observed through XRD, were identified as a mixture of cubic (ice Ic) and hexagonal (ice IH) phases of ice formed inside the pore as indicated in Fig. 5. It is interesting to note that the peaks corresponding to the ice Ic are more intense than the peaks of ice IH, supporting our earlier result of high cubicity of nano-confined ice.45
3.5. BDS measurement
In order to gain a deeper understanding of the dynamical nature of the 200 K glassy ice phase transition inside the nanopores, BDS measurement within the temperature range of 120–300 K on water confined within MIL-101(Cr) has been carried out in a broad frequency range of 10−1–107 Hz. Fig. 6a and b, respectively, show the profile of the real (ε′) and imaginary (ε′′) parts of the complex permittivity (ε = ε′ − iε′′) of water loaded MIL-101(Cr) at some of the selected temperatures in a broad frequency range. Clear signatures of different relaxation processes have been observed through the step-like features in the real part (ε′) and the peaks/shoulders in the imaginary part (ε′′), both shifting to lower frequencies with decreasing temperature as shown in Fig. 6a and b, respectively. This shift indicates a continuous slowdown of the molecular dynamics, characteristic of glassy freezing.54,55 For the dry MIL-101(Cr) framework (S0), the profiles of ε′ and ε′′ have been observed to be featureless as shown in Fig. S9a and b (ESI†).The glass forming materials exhibit diverse relaxation dynamics due to their disordered nature.54 The dynamics of the supercooled water molecules confined within the nanopores of MIL-101(Cr) can be identified by observing the dielectric relaxation processes. Three prominent relaxation processes (marked as 1, 2 and 3) in ε′ and four prominent processes along with a weak relaxation process (process 5) at very low temperature in ε′′ spectra are identified within the experimental frequency window of 10−1–107 Hz (Fig. 6a and b). The feature-less spectrum in the blank MIL-101(Cr) sample proves that the relaxation processes are solely the representatives of the dynamics of confined supercooled water. Process 1 shows a strong power-law increase for both ε′ and ε′′ at low frequencies, which is attributed to the non-intrinsic electrode polarization (EP) effect caused by the unavoidable ionic charge transport through the hydrated samples, which are blocked at the electrodes, pore walls, grain boundaries, etc. in the materials.56 Process 2 is clearly visible as steps in ε′ and peaks in ε′′, which are observed to be much slower than the relaxation dynamics of other systems like bulk supercooled water,14,56,57 aqueous solutions,58 crystallized ice14 and water confined within larger (>2.1 nm) sized pores.56,59 Process 3, visible as a valley in ε′′ spectra, is also slower than the relaxation of bulk supercooled water. The slower dynamics corresponding to relaxation processes 2 and 3 may therefore be ascribed to the dynamics of water molecules directly interacting with the pore walls of two different pore sizes. On the other hand, the time scale of process 4 in ε′′ lies almost within the time scale of bulk-like supercooled water, which is therefore attributed to the hydrogen bonded network of water molecules not directly interacting with the pore walls. The slowdown of process 4 with decreasing temperature can be ascribed to the modification of the hydrogen-bond network of the water molecules under confinement as compared to bulk-like water as well as the development of cooperative length of water molecules up to the pore size and beyond.56 Relaxation process 5 occurring at temperatures below 140 K in the loss spectra (ε′′) in the higher frequency range (above 104 Hz) is faster than the relaxation of supercooled bulk water, which can be ascribed to the relaxation of confined water not being able to develop intermolecular cooperativity.47 This type of faster process (relaxation time < 10−5 s at 140–120 K) has also been attributed to the secondary relaxation known as Johari–Goldstein (JG) β-relaxation.12,59,60 However, this process is very weak and is resolvable only in the limited temperature range (below 140 K). This process may not have a significant effect on the glassy freezing of supercooled water. We will not further discuss relaxation process 5 in the present study. In order to determine the relaxation time (τ) corresponding to relaxation processes 2, 3 and 4, ε′′(ω) at different temperatures has been fitted to the following equation:
 | (1) |
Fig. 7 shows the variation of multiple relaxation time components of water confined within MIL-101(Cr) pores with the variation of temperature, as obtained from the best fitting of ε′′ with the HN function within the studied frequency range. The two slow relaxation processes corresponding to the relaxation time τA and τB may be attributed to the relaxation behavior of interfacial water interacting with the pore wall as well as with the adjacent water layer inside the pores. The appearance of two different slow dynamics of interfacial water may indicate the presence of inhomogeneity in the pore size distribution, which causes the variation in interfacial environment of different pores. The two relaxation times represent the average relaxation dynamics of interfacial water in smaller and larger pore scales having pore size distribution of ∼0.7–1.8 nm. The interfacial water inside the smaller pore may exhibit relatively slower dynamics with relaxation time τA, as compared to the interfacial water inside the larger pores showing relaxation time τB. Interestingly, the third relaxation time τC, faster than both τA and τB, appears below 230 K, which may be attributed to process 4, i.e. the relaxation of the core water having partial crystalline structure inside both types of the pore sizes. It is appealing to see that both the slow relaxation time components (τA and τB) of interfacial water for both the smaller and larger sides of pores follow the VFT equation of relaxation as described below:
 | (2) |
 , where τ0 is the pre-exponential factor, Ea is the activation energy and k is the Boltzmann constant, showing that the relaxation dynamics follow a simple activated process (Arrhenius behavior) as the temperature goes below 190 K. The cross-over at around 190 K from VFT to Arrhenius type behavior with the temperature decrease signifies the change from fragile to strong glass forming nature of the water confined within MIL-101(Cr) pores. The crossover from VFT to Arrhenius behavior is often ascribed to a transition from α-like to β-relaxation dynamics, or alternatively, to a change in β-relaxation alone.10,58,66,67 A further alternative explanation for this cross-over in a confined glass-forming liquid is based on the fact that the cooperativity length scale of confined hydrogen bonded water molecules reaches the limit of confining pore size and thus cannot grow beyond the pore size with further decreasing temperature, resulting in a dynamical crossover of α relaxation at the crossover temperature.68,69 As the cooperativity length of the hydrogen bonded water molecules reaches its limit of the order of pore size at Tcr, the cooperativity length remains almost temperature independent with further cooling below Tcr. Hence, the energy barrier for relaxation of water molecules below Tcr does not increase and exhibits Arrhenius behavior unlike VFT dynamics.68,69 Above Tcr, the VFT fitted curves of τC are observed to diverge, signifying rapid slowdown of the dynamics of core water with the decrease in temperature, and reach the extrapolated value of 100 s at an extrapolated temperature of about 170 K, suggesting the glass transition of the core water according to the usual definition of τ(Tg) = 100 s as reported by Angell for bulk water.61 However, the extrapolated glass transition temperature (170 K) is observed to be lower than the cross-over temperature (190 K) from the VFT to Arrhenius behavior of confined water in MIL-101(Cr). The cross-over (at 190 K) above the extrapolated glass transition temperature suggests the glassy freezing of the α-like dynamics of water inside the pore above 170 K.56 The relaxation dynamics of the confined water below 190 K is complex in nature arising from the combined effects of water–substrate and water–water interactions in the interfacial region, which hinders the formation of an ice-like arrangement, as well as the relaxation of core water having partially crystalline ice, which, on average, shows Arrhenius behavior following a simple activation process with temperature. The activation energy calculated from the Arrhenius fitting at low temperature is 25 ± 5 kJ mol−1, which is observed to be less than that calculated in MCM-41.64 The value of the activation energy may depend on the pore size, the degree of pore filling as well as the interaction of water molecules among themselves and with the substrate.64 The lower activation energy in the present case may be a consequence of the small pore size, where a long range hydrogen bond network is not formed due to spatial restrictions. It should be mentioned that the cooperativity length of water molecules reached its maximum value of the dimension of the pore size (average of ∼1 nm within the pore size distribution) at the cross-over temperature of 190 K, below which the Arrhenius-like relaxation behavior suggests temperature independent cooperativity of the glassy water inside nanopores, which is in accordance with Adams–Gibbs theory.56,70
, where τ0 is the pre-exponential factor, Ea is the activation energy and k is the Boltzmann constant, showing that the relaxation dynamics follow a simple activated process (Arrhenius behavior) as the temperature goes below 190 K. The cross-over at around 190 K from VFT to Arrhenius type behavior with the temperature decrease signifies the change from fragile to strong glass forming nature of the water confined within MIL-101(Cr) pores. The crossover from VFT to Arrhenius behavior is often ascribed to a transition from α-like to β-relaxation dynamics, or alternatively, to a change in β-relaxation alone.10,58,66,67 A further alternative explanation for this cross-over in a confined glass-forming liquid is based on the fact that the cooperativity length scale of confined hydrogen bonded water molecules reaches the limit of confining pore size and thus cannot grow beyond the pore size with further decreasing temperature, resulting in a dynamical crossover of α relaxation at the crossover temperature.68,69 As the cooperativity length of the hydrogen bonded water molecules reaches its limit of the order of pore size at Tcr, the cooperativity length remains almost temperature independent with further cooling below Tcr. Hence, the energy barrier for relaxation of water molecules below Tcr does not increase and exhibits Arrhenius behavior unlike VFT dynamics.68,69 Above Tcr, the VFT fitted curves of τC are observed to diverge, signifying rapid slowdown of the dynamics of core water with the decrease in temperature, and reach the extrapolated value of 100 s at an extrapolated temperature of about 170 K, suggesting the glass transition of the core water according to the usual definition of τ(Tg) = 100 s as reported by Angell for bulk water.61 However, the extrapolated glass transition temperature (170 K) is observed to be lower than the cross-over temperature (190 K) from the VFT to Arrhenius behavior of confined water in MIL-101(Cr). The cross-over (at 190 K) above the extrapolated glass transition temperature suggests the glassy freezing of the α-like dynamics of water inside the pore above 170 K.56 The relaxation dynamics of the confined water below 190 K is complex in nature arising from the combined effects of water–substrate and water–water interactions in the interfacial region, which hinders the formation of an ice-like arrangement, as well as the relaxation of core water having partially crystalline ice, which, on average, shows Arrhenius behavior following a simple activation process with temperature. The activation energy calculated from the Arrhenius fitting at low temperature is 25 ± 5 kJ mol−1, which is observed to be less than that calculated in MCM-41.64 The value of the activation energy may depend on the pore size, the degree of pore filling as well as the interaction of water molecules among themselves and with the substrate.64 The lower activation energy in the present case may be a consequence of the small pore size, where a long range hydrogen bond network is not formed due to spatial restrictions. It should be mentioned that the cooperativity length of water molecules reached its maximum value of the dimension of the pore size (average of ∼1 nm within the pore size distribution) at the cross-over temperature of 190 K, below which the Arrhenius-like relaxation behavior suggests temperature independent cooperativity of the glassy water inside nanopores, which is in accordance with Adams–Gibbs theory.56,70
The XRD results show that there is a crystalline phase transition below 230 K, and only about 23 vol% of the total confined water undergoes a crystalline phase transition. The crystalline part is a combination of cubic and hexagonal phases, the major part of which is cubic as shown in our previous study using the neutron diffraction technique.45 The dielectric relaxation exhibits an additional fast relaxation component (τC) below 230 K, which is attributed to the dynamics of core water having a partial short range crystalline structure. A large fraction of confined water below the temperature of 230 K remains in the liquid phase up to about 200 K as observed through PALS. Below 200 K, PALS results show almost temperature independent lifetime components (both τ2 and τ3) of o-Ps, signifying the frozen water state with a nearly static molecular free volume inside the confinement. However, the XRD results do not show any change in crystallinity below 200 K, indicating that the freezing of water in this temperature region leads to the formation of an amorphous solid phase. Nonetheless, the dielectric relaxation time does not show any alteration in the relaxation dynamics of water at 200 K, rather it shows a cross-over from VFT to Arrhenius behavior at a lower temperature of 190 K, indicating a transition from a fragile glass forming liquid into a glassy amorphous ice state. Thus, the transition observed at around 200 K through PALS may be considered as the onset of amorphous ice formation through the creation of static molecular free volume, which is completed at 190 K. Thus, within the temperature range of 190–200 K, water remains in a mixed state of amorphous solid and liquid water, with static free volume inside the core of the MIL-101(Cr) nanopores. The coexistence of crystalline and liquid phases has already been reported in the case of water confined within a hydrogel.65 In the present case, within a pore size distribution of 0.7–1.8 nm, only partial crystallinity of water below 230 K is observed. A large fraction of confined water is transformed into an amorphous solid below 200 K. The phase transition within the temperature range of 190–200 K may therefore be ascribed to the formation of an amorphous glassy phase of solid water inside the nanopores. The static free volume formed by the hydrogen bonded water molecules below 200 K, as observed through PALS, corroborates the temperature independence of the cooperativity length of water molecules below the cross-over temperature inside the nanopores.
The dielectric strength of three relaxation processes A (core water), B (water in larger pore walls) and C (water in smaller pore walls) in the MIL-101(Cr) framework is shown in Fig. S11 (ESI†). The amplitude of process C is observed to be two orders of magnitude higher than those of processes A and B. The large surface-to-volume ratio of the smaller pores may suggest that the number of water molecules attached to the pore surface undergoing relaxation is indeed very high.23 Interestingly, the amplitude of relaxation process A is observed to become temperature independent below 200 K, signifying that the number of water dipoles responding to the applied electric field remains almost constant after solid water formation.
4. Summary
In summary, the transformation of supercooled water into an amorphous form of ice within the nano-confinement is detected using a combination of PALS, XRD and BDS. In general, amorphous ice or amorphous solid water (ASW) in bulk is formed by cooling water very fast (105 K s−1) or depositing water vapor onto an ultracold surface of any substrate.71 However, our result shows that water confined within nanopores (0.7–1.8 nm) undergoes glassy freezing below 200 K with a moderate cooling rate and transforms into an ASW phase. PALS, which is used to investigate the changes in the molecular free volume of confined liquid with temperature, is thus proven to be a unique tool to distinguish the solid amorphous form of water from a supercooled liquid phase at low temperature, which was corroborated by the XRD and BDS results. The cross-over temperature at around 190 K, as obtained by the BDS study, corresponds to a transition from a fragile liquid to glassy solid phase. It should be noted that the ASW phase is an important constituent in interstellar clouds. The ASW is formed at the surface of interstellar sub-micron dust particles like silicate and carbonaceous materials. The porous ASW can trap molecules and gases to act as catalysts for the formation of complex organic molecular structures at interstellar molecular clouds, which plays an important role in astrochemistry. Our simple method of producing ASW under nano-confinement will be helpful for characterizing the catalytic behavior of the model ASW phase in the laboratory.Conflicts of interest
There are no conflicts of interest to declare.Data availability
The positron annihilation lifetime and the XRD data supporting this article have been included as part of the ESI.†Acknowledgements
The authors gratefully acknowledge the technical support from Dr Archana Sagdeo, Synchrotron Utilization Section, RRCAT, India for carrying out low temperature XRD experiments. The technical support from Mr. Nitin Gumber, FCD, BARC, India for BET N2 adsorption isotherm analysis is also thankfully acknowledged.References
- O. Mishima and H. E. Stanley, The relationship between liquid, supercooled and glassy water, Nature, 1998, 396, 328–335 CrossRef
.
- R. J. Speedy and C. A. Angell, Isothermal compressibility of supercooled water and evidence for a thermodynamic singularity at −45C, J. Chem. Phys., 1976, 65, 851–858 CrossRef CAS
.
- C. A. Angell, in Water: A Comprehensive Treatise, ed. F. Franks, Plenum Press, New York, 1982, vol. 7, pp. 1–81 Search PubMed
.
- P. G. Debenedetti and H. E. Stanley, Supercooled and glassy water, Phys. Today, 2003, 56(6), 40–46 CrossRef CAS
.
- V. Velikov, S. Borick and C. A. Angell, The glass transition of water, based on hyperquenching experiments, Science, 2001, 294, 2335 CrossRef CAS PubMed
.
- E. B. Moore and V. Molinero, Structural transformation in supercooled water controls the crystallization rate of ice, Nature, 2011, 479, 506–509 CrossRef CAS PubMed
.
- M. Oguni, et al., Calorimetric study of water's glass transition in nanoscale confinement, suggesting a value of 210 k for bulk water, J. Phys. Chem. B, 2011, 115, 14023–14029 CrossRef CAS PubMed
.
- A. Nagoe, et al., Findings of Cp Maximum at 233 K for the Water within Silica Nanopores and Very Weak Dependence of the T max on the Pore Size, J. Phys. Chem. B, 2010, 114, 13940–13943 CrossRef CAS
.
- M. Oguni, et al., Glass Transitions of Ordinary and Heavy Water within Silica-Gel Nanopores, Chem. – Asian J., 2007, 2, 514–520 CrossRef CAS PubMed
.
- J. Swenson, Possible Relations between Supercooled and Glassy Confined Water and Amorphous Bulk Ice, Phys. Chem. Chem. Phys., 2018, 20, 30095–30103 RSC
.
- H. E. Stanley and J. Teixeira, Interpretation of the Unusual Behavior of H2O and D2O at Low Temperatures: Tests of a Percolation Model, J. Chem. Phys., 1980, 73, 3404–3422 CrossRef CAS
.
- R. Bergman and J. Swenson, Dynamics of Supercooled Water in Confined Geometry, Nature, 2000, 403, 283 CrossRef CAS PubMed
.
- S. Wu, X. Liang, Y. Lei, L. Yang, L. Wang and J. Feng, Dynamics and Glass Transition of Supercooled Water Confined in Amphiphilic Polymer Films, J. Phys. Chem. Lett., 2020, 11, 6039–6044 CrossRef CAS PubMed
.
- J. Sjöström, et al., Investigating hydration dependence of dynamics of confined water: Monolayer, hydration water and Maxwell–Wagner processes, J. Chem. Phys., 2008, 128, 154503 CrossRef PubMed
.
- K. Ito, C. T. Moynihan and C. A. Angell, Thermodynamic determination of fragility in liquids and a fragile-to-strong liquid transition in water, Nature, 1999, 398, 492–495 CrossRef CAS
.
- S.-H. Chen, L. Liu, E. Fratini, P. Baglioni, A. Faraone and E. Mamontov, Observation of fragile-to-strong dynamic crossover in protein hydration water, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9012–9016 CrossRef CAS PubMed
.
- R. Shi, J. Russo and H. Tanaka, Origin of the emergent fragile-to-strong transition in supercooled water, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9444–9449 CrossRef CAS
.
- C. E. Bertrand, Y. Zhang and S.-H. Chen, Deeply-cooled water under strong confinement: neutron scattering investigations and the liquid–liquid critical point hypothesis, Phys. Chem. Chem. Phys., 2013, 15, 721–745 RSC
.
- M. Sattig and M. Vogel, Dynamic crossovers and stepwise solidification of confined water: A 2H NMR study, J. Phys. Chem. Lett., 2014, 5, 174–178 CrossRef CAS PubMed
.
- X.-Q. Chu, et al., Observation of a dynamic crossover in water confined in double-wall carbon nanotubes, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2007, 76, 021505 CrossRef PubMed
.
- J. Faeder and B. M. Ladanyi, Molecular dynamics simulations of the interior of aqueous reverse micelles, J. Phys. Chem. B, 2000, 104, 1033–1046 CrossRef CAS
.
- P. A. Pieniazek, Y.-S. Lin, J. Chowdhary, B. M. Ladanyi and J. L. Skinner, Vibrational spectroscopy and dynamics of water confined inside reverse micelles, J. Phys. Chem. B, 2009, 113, 15017–15028 CrossRef CAS PubMed
.
- J. Swenson, H. Jansson and R. Bergman, Relaxation processes in supercooled confined water and implications for protein dynamics, Phys. Rev. Lett., 2006, 96, 247802 CrossRef PubMed
.
- P. Berntsen, R. Bergman, H. Jansson, M. Weik and J. Swenson, Dielectric and calorimetric studies of hydrated purple membrane, Biophys. J., 2005, 89, 3120–3128 CrossRef CAS PubMed
.
- F. Mallamace, et al., Transport properties of supercooled confined water, Eur. Phys. J.: Spec. Top., 2008, 161, 19–33 Search PubMed
.
- D. Kilburn, et al., Confinement induces both higher free volume and lower molecular mobility in glycerol, Appl. Phys. Lett., 2008, 92, 033109 CrossRef
.
- J. Bartoš, et al., Positron annihilation response and broadband dielectric spectroscopy: Propylene carbonate, J. Non-Cryst. Solids, 2010, 356, 794–799 CrossRef
.
- J. Bartoš, Positron annihilation response and viscosity of a glass-forming system within the two-order parameter model of liquids, J. Phys.:Condens. Matter, 2008, 20, 285101 CrossRef
.
- J. Bartoš, et al., Positron annihilation and relaxation dynamics from dielectric spectroscopy and nuclear magnetic resonance: Cis–trans-1, 4-poly (butadiene), J. Chem. Phys., 2011, 134, 164507 CrossRef PubMed
.
- J. Bartoš, et al., Positron-annihilation-lifetime response and broadband dielectric relaxation spectroscopy: Diethyl phthalate, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2007, 76, 031503 CrossRef
.
- J. Bartoš, et al., Positron annihilation lifetime response and relaxation dynamics in glycerol, J. Non-Cryst. Solids, 2005, 351, 2599–2604 CrossRef
.
- J. Bartoš, et al., Free volume factor in supercooled liquid dynamics, J. Non-Cryst. Solids, 2002, 307, 417–425 CrossRef
.
- J. Bartoš, et al., Free-volume microstructure of glycerol and its supercooled liquid-state dynamics, J. Phys.:Condens. Matter, 2001, 13, 11473 CrossRef
.
- K. L. Ngai, L.-R. Bao, A. F. Yee and C. L. Soles, Correlation of positron annihilation and other dynamic properties in small molecule glass-forming substances, Phys. Rev. Lett., 2001, 19, 215901 CrossRef PubMed
.
- J. Bartoš and J. Krištiak, Free volume aspects of the strong–fragile classification of polymer liquids, J. Non-Cryst. Solids, 1998, 235, 293–295 CrossRef
.
- R. A. Pethrick, F. M. Jacobsen, O. E. Mogensen and M. Eldrup, Positron lifetime study of the transition from glassy to normal liquid state for two phenyl ether, J. Chem. Soc., Faraday Trans. 2, 1980, 76, 225–232 RSC
.
- B. D. Malhotra and R. A. Pethrick, Correlation of dielectric relaxation and positron annihilation in glass-forming liquids, Phys. Rev. B:Condens. Matter Mater. Phys., 1983, 28, 1256 CrossRef CAS
.
- B. D. Malhotra and R. A. Pethrick, Positron annihilation studies of supercooled liquids. Ortho-terphenyl, J. Chem. Soc., Faraday Trans. 2, 1982, 78, 297–306 RSC
.
- R. A. Ferrell, Long lifetime of positronium in liquid helium, Phys. Rev., 1957, 108, 167 CrossRef CAS
.
- Y. Kobayashi, K. Ito, T. Oka and K. Hirata, Positron chemistry in porous materials, Radiat. Phys. Chem., 2007, 76, 224 CrossRef CAS
.
- S. Bhattacharjee, C. Chen and W.-S. Ahn, Chromium terephthalate metal–organic framework MIL-101: functionalization, and applications for adsorption and catalysis, RSC Adv., 2014, 4, 52500–52525 RSC
.
- T. Zhao, F. Jeremias, I. Boldog, B. Nguyen, S. K. Henninger and C. Janiak, High-yield, fluoride-free and large-scale synthesis of MIL-101(cr), Dalton Trans., 2015, 44, 16791–16801 RSC
.
- K. Leus, et al., Systematic study of the chemical and hydrothermal stability of selected “stable” Metal Organic Frameworks, Microporous Mesoporous Mater., 2016, 226, 110–116 CrossRef CAS
.
- G. Férey, C. Mellot-Draznieks, C. Serre, F. Millange, J. Dutour, S. Surblé and I. Margiolaki, A Chromium Terephthalate–Based Solid with Unusually Large Pore Volumes and Surface Area, Science, 2005, 309, 2040 CrossRef PubMed
.
- D. Dutta, et al., High cubicity of D2O ice inside spherical nanopores of MIL-101 (Cr) framework: a neutron diffraction study, Phys. Chem. Chem. Phys., 2022, 24, 11872–11881 RSC
.
- P. Kirkegaard, et al., PALSfit, Roskilde: Danmarks Tekniske Universitet, Risø National laboratoriet for BæredygtigEnergi. Denmark. ForskningscenterRisoe. Risoe-R, 2009, vol. 1652 Search PubMed
.
- S. Havriliak and S. Negami, A complex plane analysis of α-dispersions in some polymer systems, J. Polym. Sci., Part C, 1966, 14, 99–117 CrossRef
.
- T. L. Dull, W. E. Frieze, D. W. Gidley, J. N. Sun and A. F. Yee, Determination of Pore Size in Mesoporous Thin Films from the Annihilation Lifetime of Positronium, J. Phys. Chem. B, 2001, 105, 4657–4662 CrossRef CAS
.
- M. Eldrup, O. Mogensen and G. Trumpy, Positron Lifetimes in Pure and Doped Ice and in Water, J. Chem. Phys., 1972, 57, 495–504 CrossRef CAS
.
- R. C. Tolmann, The effect of droplet size on surface tension, J. Chem. Phys., 1949, 17, 333 CrossRef
.
- F. O. Koenig, On the thermodynamic relation between surface tension and curvature, J. Chem. Phys., 1950, 18, 449–459 CrossRef CAS
.
- P. Maheshwari, D. Dutta, S. Mukherjee, P. K. Madhu, K. R. Mote and P. K. Pujari, Positron annihilation and nuclear magnetic resonance study of the phase transition of water confined in mesopores at different levels of hydration, Phys. Chem. Chem. Phys., 2016, 18, 12886 RSC
.
- T. Muthulakshmi, P. Maheshwari, D. Dutta, A. K. Bera, M. N. Singh, A. K. Sinha, S. M. Yusuf and P. K. Pujari, Evolution of confined ice nano structure at different levels of pore filling: a synchrotron based X-ray diffraction study, Phys. Chem. Chem. Phys., 2020, 22, 14309–14317 RSC
.
- P. Lunkenheimer, U. Schneider, R. Brand and A. Loidl, Contemp. Phys., 2000, 41, 15–36 CrossRef CAS
.
- A. Schönhals and F. Kremer, in Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, Springer, Berlin, 2003, pp. 59–98 Search PubMed
.
- J. K. H. Fischer, P. Sippel, D. Denysenko, P. Lunkenheimer, D. Volkmer and A. Loidl, Supercooled water confined in a metal-organic framework, Commun. Phys., 2020, 3, 95 CrossRef CAS
.
- H. Jansson and J. Swenson, Dynamics of water in molecular sieves by dielectric spectroscopy, Eur. Phys. J. E:Soft Matter Biol. Phys., 2003, 12, 51–54 CrossRef PubMed
.
- S. Cerveny, F. Mallamace, J. Swenson, M. Vogel and L. Xu, Confined water as model of supercooled water, Chem. Rev., 2016, 116, 7608–7625 CrossRef CAS PubMed
.
- S. Capaccioli, K. L. Ngai, S. Ancherbak, M. Bertoldo, G. Ciampalini, M. S. Thayyil and L.-M. Wang, The JG β-relaxation in water and impact on the dynamics of aqueous mixtures and hydrated biomolecules, J. Chem. Phys., 2019, 151, 034504 CrossRef CAS PubMed
.
- G. P. Johari and M. Goldstein, Viscous liquids and the glass transition. II. Secondary relaxations in glass of rigid molecules, J. Chem. Phys., 1970, 53, 2372–2388 CrossRef CAS
.
- C. A. Angell, in Relaxation in complex Systems, ed. K. L. Ngai and G. B. Wright, Naval Research Laboratory, Washington DC, 1985, pp. 3–12 Search PubMed
.
- P. Lunkenheimer, M. Köhler, S. Kastner and A. Loidl, in Structural Glasses and Supercooled Liquids: Theory, Experiment, and Applications, ed. P. G. Wolynes and V. Lubchenko, Wiley, Hoboken, 2012, pp. 115–149 Search PubMed
.
- R. Böhmer, K. L. Ngai, C. A. Angell and D. J. Plazek, Non exponential relaxations in strong and fragile glass formers, J. Chem. Phys., 1993, 99, 4201–4209 CrossRef
.
- F. Bruni, R. Mancinelli and M. A. Ricci, Multiple relaxation processes versus the fragile-to-strong transition in confined water, Phys. Chem. Chem. Phys., 2011, 13, 19773–19779 RSC
.
- K. Pathmanathan and G. P. Johari, Relaxation and crystallization of water in a hydrogel, J. Chem. Soc., Faraday Trans., 1994, 90, 1143 RSC
.
- J. Swenson and S. CCerveny, Dynamics of deeply
supercooled interfacial water, J. Phys.: Condens. Matter, 2015, 27, 033102 CrossRef CAS PubMed
.
- S. Cerveny, F. Barroso-Bujans, A. Alegira and J. Colmenero, Dynamics of wtare intercalated in graphite oxide, J. Phys. Chem. C, 2010, 114, 2604–2612 CrossRef CAS
.
- M. Uhl, et al., Glycerol confined in zeolitic imidazolate frameworks: The temperature dependent cooperativity length scale of glassy freezing, J. Chem. Phys., 2019, 150, 024504 CrossRef CAS PubMed
.
- M. Arndt, R. Stannarius, H. Groothues, E. Hempel and F. Kremer, Phys. Rev. Lett., 1997, 79, 2077 CrossRef CAS
.
- G. Adam and J. H. Gibbs, On the temperature dependence of cooperative relaxation properties in glass forming liquids, J. Chem. Phys., 1965, 43, 139–146 CrossRef CAS
.
- K. L. Bachmann, A. Hallbrucker, E. Mayer and T. Loerting, Liquid-like relaxation in hyperquenched water at ≤ 140 K, Phys. Chem. Chem. Phys., 2005, 7, 3210–3220 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp02453f |
| This journal is © the Owner Societies 2025 |





