View PDF Version

Open Access Article
This Open Access Article is licensed under a Creative Commons Attribution-Non Commercial 3.0 Unported Licence
DOI: 10.1039/D5DD00128E (Paper) Digital Discovery, 2025, Advance Article

Combining DeepH with HONPAS for accurate and efficient hybrid functional electronic structure calculations with ten thousand atoms

Yifan Kea, Xinming Qin*a, Wei Hu*a and Jinlong Yang*b
aHefei National Research Center for Physical Sciences at the Microscale, University of Science and Technology of China, Hefei, Anhui 230026, China. E-mail: xmqin03@ustc.edu.cn; whuustc@ustc.edu.cn
bKey Laboratory of Precision and Intelligent Chemistry, University of Science and Technology of China, Hefei, Anhui 230026, China. E-mail: jlyang@ustc.edu.cn

Received 29th March 2025 , Accepted 6th August 2025

First published on 11th August 2025

Abstract

Density functional theory (DFT) calculations of hybrid functionals have traditionally been limited to small systems containing hundreds of atoms due to substantial computational constraints. In this work, we introduce an interface between DeepH, a machine learning-based Hamiltonian approach, and HONPAS, a density functional theory software package. By leveraging DeepH's ability to bypass self-consistent field (SCF) iterations, DFT calculations in HONPAS become significantly more efficient, including computationally intensive hybrid functional calculations. This combined approach is particularly advantageous for twisted van der Waals systems, as demonstrated through examples of twisted bilayer graphene and twisted bilayer MoS2. The substantial reduction in computation time for the HSE06 functional suggests that our method effectively addresses the efficiency-accuracy trade-off in DFT calculations, making high-accuracy calculations feasible for large systems containing more than ten thousand atoms.

1 Introduction

The Kohn–Sham density functional theory (DFT)1 is a foundational method in ab initio simulations, where the complex many-body Schrödinger equation is reduced to a series of single-particle equations. To approximate the exchange–correlation energy, a hierarchy of functionals has been developed, each balancing accuracy and computational efficiency. These include the local density approximation (LDA), generalized gradient approximation (GGA), meta-GGA, hybrid functionals, and the random phase approximation (RPA), arranged in ascending order of computational complexity. Hybrid functionals, which combine LDA or GGA with a fraction of Hartree–Fock exchange,2 are particularly noteworthy for their high accuracy in predicting excited states, reaction barriers, and weak interactions.3–6 Their computational cost lies between meta-GGA and RPA. While they are more demanding than meta-GGA, hybrid functionals are significantly less expensive than RPA, which relies on response functions to calculate exchange–correlation energy and is particularly effective for capturing long-range interactions and van der Waals forces.7–11 Owing to their optimal trade-off between accuracy and efficiency, hybrid functionals have become widely adopted for a broad range of material simulations.

Neural network models are increasingly being integrated into material science research to enhance computational efficiency and predictive accuracy.12–18 Extensive efforts have been dedicated to applying machine learning in materials science research. To effectively model and predict DFT results, previous training targets have primarily focused on charge density or wave functions. These studies predominantly advocate for the use of surrogate models, where atomic structures serve as inputs and electron densities as outputs.19,20 For instance, DeePHF efficiently predicts Hartree–Fock orbitals and density matrices,21 while DeePKS explores generalized functionals applicable to diverse chemical systems.22 Deep density employs the deep potential neural network framework to map atomic structures to electron densities.23,24 Chemception applies deep convolutional neural networks directly to 2D molecular images, achieving competitive performance with expert-designed QSAR/QSPR models without relying on explicit chemical descriptors or domain knowledge.25 In the context of materials science, machine learning can also be integrated by training tight-binding Hamiltonians extracted from ab initio data.26 For instance, DeePTB employs deep neural networks to generate transferable tight-binding models across diverse atomic configurations, enabling efficient and accurate band structure predictions for a wide range of materials.27 Additionally, a kernel-based machine learning approach has been developed to predict DFT Hamiltonians directly from atomic environments. This method offers an accurate, transferable, and scalable alternative to traditional semi-empirical approximations for electronic structure calculations.28 Meanwhile, DeePMD leverages neural networks to fit interatomic potential surfaces, significantly accelerating molecular dynamics simulations with accuracy comparable to DFT.23,29 In efforts to study large-scale materials, such as twisted van der Waals interfaces, the Deep Hamiltonian (DeepH) framework30 and its specialized variants, including DeepH-E3,31 DeepH-Hybrid,32 xDeepH,33 and DeepH-PW,34 represent a significant advancement in Hamiltonian prediction for complex systems. By leveraging machine learning, DeepH makes use of the nearsightedness of pseudo-atomic orbital (PAO) bases,35 transforming what would typically be a global optimization problem into a series of localized calculations that align well with the locality of neural network layers. DeepH applies graph neural networks (GNNs) to represent materials, a technique that has been effectively used in AI for material studies.13 Similarly, HamGNN also utilizes GNNs to efficiently predict Hamiltonians.36 Compared to wavefunctions and charge densities, DeepH-E3 leverages equivariant neural networks to efficiently train local environments and predict the Hamiltonian, providing a more comprehensive representation of the system with smaller model sizes. It also enables density functional perturbation theory calculations37 and contributes to the development of a universal model applicable to all materials.38 The integration of AI with DFT further expands the scope of material design, particularly by advancing molecular dynamics simulations.23,29,39,40 This progress represents a significant milestone in computational materials science, fostering new insights and broadening applications in the study of complex material systems.

Among the various DFT software, HONPAS (Hefei Order-N Packages for Ab Initio Simulations) stands out as a robust tool, especially notable for implementing the HSE06 hybrid functional.41 The HSE06 functional, developed by Jochen Heyd, Gustavo E. Scuseria, and Matthias Ernzerhof, combines Hartree–Fock exchange with DFT correlation, making it effective for accurately predicting electronic structures in systems with challenging van der Waals interactions.42 HONPAS has been successfully applied to materials simulations involving systems with more than 10[thin space (1/6-em)]000 atoms, demonstrating its robustness and scalability for large-scale electronic structure calculations.43–47 However, despite optimizations such as NAO2GTO for efficient computation of the Hartree–Fock exchange (HFX) matrix,48,49 hybrid functional calculations remain computationally demanding and require extensive parallelization, typically limiting practical applications to systems with fewer than a hundred atoms.

Even when generalized to plane-wave DFT, reconstruction from plane-wave Hamiltonians to atomic orbital Hamiltonians remains necessary in DeepH-PW.34 Due to the locality of the DeepH scheme, it currently depends on atomic orbital-based DFT packages. Examples of such software include SIESTA,50 HONPAS,49 FHI-aims,51 OpenMX,52,53 and ABACUS,54 among others. At present, DeepH supports only OpenMX and ABACUS. Therefore, in this work, we extend its compatibility to HONPAS. Like HONPAS, OpenMX utilizes low-scaling methods and achieves excellent parallel performance, although its most accurate functional support is limited to the GGA level. In contrast, HONPAS supports HSE06 functional with a parallelization implementation. Compared to ABACUS, which utilizes the LCAO technique based on atomic orbitals,54,55 HONPAS adopts the NAO2GTO approach and ISDF method for the HFX calculations.48,49,56 These methods significantly improve the efficiency in handling two-electron integrals and hybrid functional calculations, thereby streamlining the dataset preparation process. Built upon SIESTA, HONPAS shares a similar input/output structure and workflow, which facilitates adoption by the large existing SIESTA user community. In DFT calculations, common basis sets include plane waves and atomic orbitals, with the latter well-suited for large-scale parallel computations.51,57,58 For typical materials, double-zeta (DZ) and double-zeta polarized (DZP) basis sets are often used.

Given the well-established hybrid functional capabilities of HONPAS, the DeepH + HONPAS combination is well-suited for machine learning-assisted material calculations, particularly for systems requiring the accuracy of hybrid functionals. Our work leverages the strengths of both HONPAS and DeepH by creating an interface that facilitates hybrid functional calculations.

However, utilizing DeepH effectively requires a solid understanding of material structure and the mechanisms of DFT, as setting its input parameters demands physical insight. To address this, we first introduce the DeepH + HONPAS architecture. We then present our code implementation and performance testing. Finally, we apply this code to predict electronic properties in twisted van der Waals bilayer systems, specifically comparing twisted bilayer graphene and twisted bilayer MoS2. Notably, the hybrid HSE06 functional produces a larger band gap than the PBE functional in gapped MoS2 and at the Γ point in graphene systems.

2 Overview of DeepH and HONPAS

We begin by reviewing the fundamental concept and architecture of the DeepH method. In density functional theory (DFT), the central problem is solving the Schrödinger equation, H|ψ〉 = E|ψ〉, where H represents the Kohn–Sham Hamiltonian, E is the eigenvalue, and |ψ〉 is the eigenstate.1 In ab initio DFT calculations, the H matrix is derived through self-consistent field (SCF) iterations. According to the Hohenberg–Kohn theorem, the Hamiltonian H is uniquely determined by the material's atomic structure,1 meaning that for any given structure, there exists a unique solution for H.

The SCF iterations, however, constitute the most time-consuming component of DFT calculations. To bypass this bottleneck, DeepH leverages machine learning techniques to learn the Hamiltonian features of a wide range of materials, enabling it to predict the Hamiltonian for new materials with similar chemical composition. The validity of this approach is grounded in the one-to-one mapping between the material structure image file: d5dd00128e-t1.tif and the Hamiltonian image file: d5dd00128e-t2.tif, provided that the predicted Hamiltonian is consistent with the one obtained from SCF iterations.

In their work on DeepH, He Li et al. emphasized the importance of directly training the Hamiltonian, not merely because it underlies ab initio DFT, but because this approach bypasses intermediate quantities such as total energies or forces and allows for a more physically interpretable and transferable model, especially in electronic structure prediction tasks.30 To facilitate learning the Hamiltonian, DeepH introduces a cutoff radius, Rc, in the Hamiltonian matrix, defining a local environment that typically comprises only a few atoms. This locality and nearsightedness are ensured by the destructive interference between the many-particle eigenstates.59,60 Leveraging this locality, large Hamiltonians can be related to smaller ones through covariant transformations, where physical quantities transform covariantly. Consequently, the information within these local environments can effectively capture the behavior of the entire Hamiltonian when transformed back.

The local environment Hamiltonian matrix, denoted as H′, can be trained independently and then transformed back into the full Hamiltonian matrix H through a rotation transformation:

 
image file: d5dd00128e-t3.tif(1)
where Ri represents the rotation transformation between the local and global coordinates. The target of the neural network model is the Hamiltonian matrix element Hij = 〈ϕi|Ĥ|ϕj〉, where |ϕi〉 denotes the atomic orbital basis functions, expressed in terms of radial functions and spherical harmonic functions.

In HONPAS, numerical atomic orbitals (NAOs) are fitted to Gaussian type orbitals (GTOs) to capture the non-local features of hybrid functionals. GTOs are particularly useful since they decay more slowly over long-range distances, facilitating more accurate calculations. The approximation is given by:

 
image file: d5dd00128e-t4.tif(2)

This approach is highly efficient for evaluating two-electron integrals:

 
image file: d5dd00128e-t5.tif(3)
which is frequently encountered in HSE06 functional calculations.

The basis functions remain fixed throughout the DeepH procedure. For the prediction of large-scale structures, necessary information, such as atomic positions, basis sets, and bonds, is represented by the overlap matrix Sij = 〈ϕi|ϕj〉, which encapsulates non-SCF material information. This overlap matrix serves as the initial feature in the input layer, which is then mapped to the Hamiltonian matrix through the trained neural network model:

 
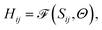image file: d5dd00128e-t6.tif(4)
where Θ represents the set of weights trained in the model.

The core architecture of DeepH's neural network is a message-passing neural network (MPNN) constructed on a crystal graph representation of the material. In this setup, DeepH transforms the material structure into a crystal graph, where each atom is represented by a vertex, vi, and each atom pair by an edge, eij. The initial vertex feature vectors are derived from elemental embeddings, while edge feature vectors are based on Gaussian-type distances. Edge features in DeepH are further represented using real spherical harmonics, Ylm: l = 0 represents distance, while higher l values incorporate relative directional information and Hamiltonian elements, or hoppings, between atoms.

In the message-passing (MP) layers, both vertex and edge features are iteratively updated, with the final edge output representing the Hamiltonian matrix element, Hij. According to the original DeepH paper, the model uses five MP layers and one local coordinate message-passing (LCMP) layer. The neural network contains 471, 409 + 129 × Nout parameters, where Nout is the number of selected orbital pairs.

3 Code implementation of DeepH + HONPAS

As a machine learning approach, the prediction of large-scale Hamiltonians in DeepH involves three primary steps: preprocessing, training, and inference. These steps encompass dataset preparation, neural network model training, and the final prediction, transforming bare structural data into Hamiltonians. DFT calculations are required during both the preprocessing and inference phases. We illustrate the workflow of the DeepH + HONPAS integration in Fig. 1. Among these steps, dataset preparation has a substantial impact on the final output. This is due to DeepH's assumption of a local environment with a cutoff radius rc, where the relative positions of neighboring atoms and overlapping orbitals constitute the primary input data.
image file: d5dd00128e-f1.tif
Fig. 1 Schematic workflow of DeepH + HONPAS. In the “preprocess” phase, Hamiltonian matrices of various structures are computed via HONPAS self-consistent field (SCF) calculations and are rearranged into smaller components representing local Hamiltonians. In the “train” phase, each Hamiltonian element, image file: d5dd00128e-t7.tif, serves as the target at the output layer of the model. The equivariant neural network iteratively updates its weights to minimize the loss associated with predicting image file: d5dd00128e-t8.tif. During the “inference” phase, the overlap matrix of a large-scale structure is obtained from HONPAS calculations without requiring SCF iterations. This overlap matrix is then fed into the trained neural network as input. The predicted and reassembled Hamiltonian matrix, Hij, can subsequently be used for electronic band structure calculations.

For a previously unseen structure, creating an effective dataset can be challenging. Consequently, dataset preparation demands physical intuition and a deep understanding of the material structure to make accurate predictions. For instance, in a two-dimensional bilayer system, it is appropriate to randomly shift the top layer in-plane by distances on the order of the unit cell length to simulate various stacking patterns. Alternatively, datasets can be generated from molecular dynamics trajectories. These perturbations on atomic positions incorporate factors like stacking order, interlayer folding, and bond length variations. Thus, this model is capable of predicting similar materials with different bond lengths or interlayer configurations.

The data structure used in DeepH primarily consists of HDF5 (.h5) files. To convert DFT data into a format suitable for neural network input, a preprocessing step is required. This can be executed using the deeph-preprocess tool after configuring the preprocess.ini file. For datasets generated from HONPAS, four essential files are required for each structure: .STRUCT_OUT, .HSX, .ORB_INDX, and .XV. Additionally, an assertion line is added in DeepH to ensure that the DFT output files are located in the correct directory. It is recommended to name the output file as output when running HONPAS, which can be achieved by executing the following command:

image file: d5dd00128e-u1.tif

In this line, the MPI parallel execution is enabled, and the output file name is set to “output”. Additionally, to save the .HSX file in the output directory, the flag SaveHS .true. is set in the input.fdf file. The .HSX file contains the Hamiltonian and overlap matrices, which are essential for training since the Hamiltonian elements, image file: d5dd00128e-t9.tif, are the targets. In the HONPAS input configuration, selecting the appropriate size of the atomic orbitals is crucial as it impacts both the accuracy and computational cost. For example, for carbon atoms, the SZ (single-zeta) basis includes 4 orbitals (one 2s and three 2p orbitals), while the DZP (double-zeta polarized) basis includes 13 orbitals (two 2s, six 2p, and five 3d orbitals). This information, including detailed global positions and symmetries, is available in the .ORB_INDX file.

For the training process, it is recommended to utilize a GPU to accelerate computations, although DeepH is also compatible with the CPU version of PyTorch. Similar to preprocessing, training is conducted using the “deeph-train” command with settings specified in the train.ini configuration file. Two key parameters for the training phase are “atom_fea_len” and “edge_fea_len”, which define the embedding for atomic features and interatomic distances, respectively. These parameters control the dimensionality of the graph neural network. Additionally, the orbital parameter plays an essential role. This parameter is structured as a dictionary that lists all the Hamiltonian elements for the desired orbital pairs. Below is an example showcasing simple SZ orbital overlaps in graphene:

image file: d5dd00128e-u2.tif

In the dictionary configuration, the key “6 6” represents a pair of carbon atoms, while the entry “[1, 2]” specifies the Hamiltonian matrix element at position (2, 3) for these two atoms, each having 4 orbitals. For a larger basis set or when different elements are included, the dictionary will adjust in dimension according to the number of orbitals assigned to describe each atom. The DeepH package provides a script to automatically generate all orbital pairs in dictionary format.

During training, the learning rate is adapted based on the decay rate of the validation loss. Starting at an initial rate of 0.001, it is progressively reduced to 0.0004, then to 0.0002, each time the loss plateaus. For extended training sessions, DeepH includes options for “pretrained_model” and “resume” to continue from a saved state, while all training history is stored in the specified “train_dir”.

In the prediction phase, the “deeph-inference” code is used to apply the trained model to a new structure for inference. The “inference.ini” file contains a “task” list parameter, which includes the following steps: (1) parse overlap, (2) obtain local coordinates, (3) compute the predicted Hamiltonian, (4) rotate back, and (5) perform sparse calculations. These tasks can be executed sequentially.

Since DeepH requires the overlap matrix of the final large structure, we set the maximum number of self-consistency field (SCF) iteration steps to 1 in HONPAS, ensuring that no SCF calculation is performed during the DFT run. This approach minimizes the time required to obtain the overlap matrix, which is stored in the .HSX file. To retrieve only the overlap, the following settings in the input.fdf file are necessary:

image file: d5dd00128e-u3.tif

The “ForceAuxCell” flag is activated to ensure that the diagonal elements of the overlap matrix are set to 1 during the single Gamma point calculation. The .HSX file contains both the Hamiltonian and overlap matrix, which can be parsed using the same code as in the preprocessing stage. After task (4), the predicted Hamiltonian is stored in the working directory. To verify the prediction, the band structure is calculated in task (5). In the interface, we output the .bands file in HONPAS format, which is generated after performing sparse matrix diagonalization of the band Hamiltonians. Additionally, we also output a result.mat file containing the band structure, making it easy to read using MATLAB and eliminating the need to search for post-processing scripts specific to the DFT package.

4 Results

In this section, we present examples that highlight the high efficiency and accuracy of DeepH + HONPAS in large-scale material calculations. In twisted moiré materials, one of the most notable features is the change in electronic structures as the twist angles are adjusted. Band structures of PBE and HSE06 functionals are provided for twisted bilayer graphene (TBG) and twisted bilayer MoS2 (TBMoS2). We conclude that HSE06 functional restores band gaps which are underestimated by PBE functional. The predicted bands align well with direct DFT bands of both functionals.

4.1 Twisted bilayer graphene

The band structure of TBG exhibits significant variations under different twist angles. In the small angle range of less than 10°, the typical Dirac cone of graphene is modified by the twisting, resulting in a reduction of Fermi velocity, band flattening, and an enhancement of the local density of states near the Fermi level.63–66 We study this phenomenon by performing DFT calculations on TBG at three twist angles: 7.34°, 4.41°, and 2.88°. The continuous evolution of the bands near the Fermi level reflects the influence of twisting and suggests the emergence of the magic angle flat bands at 1.05°. The atom counts for these three structures are 244, 676, and 1588, respectively. The corresponding unit cells are illustrated in Fig. 2(a)–(c). We performed an uncertainty evaluation across a broader range of twist angles using the energy difference between the first valence band and the first conduction band at the Γ point. The resulting mean absolute error (MAE) is 0.046 eV, and the root mean square error (RMSE) is 0.052 eV, demonstrating the model's strong generalization ability in predicting a wider range of previously unseen structures.
image file: d5dd00128e-f2.tif
Fig. 2 (a)–(c) Moiré unit cells of twisted bilayer graphene (TBG) with twist angles of 7.34°, 4.41°, and 2.88°. (d)–(f) PBE band structures for TBG with the same twist angles obtained using the DeepH + HONPAS framework. (g)–(i) PBE band structures for TBG with twist angles of 7.34°, 4.41°, and 2.88°, calculated with DeepH-E3 + HONPAS. Notably, the same overlap matrix of the large-scale structure is applicable to both DeepH and DeepH-E3. However, DeepH-E3 demonstrates superior memory efficiency compared to DeepH.

We highlight that, through the machine learning approach, we can significantly reduce the computational cost, enabling the calculation of such structures on personal computers rather than relying on supercomputers. In Fig. 2, we present the band structures of TBG at the three twist angles, calculated directly from HONPAS and predicted by the trained model. The bands are well-aligned, demonstrating the remarkable ability of the model to predict unseen structures accurately. Fig. 2(d)–(f) display the band structures predicted using the DeepH framework, while Fig. 2(g)–(i) present results obtained with the DeepH-E3 framework. Both approaches exhibit similar performance; however, the DeepH-E3 framework features a smaller model size, leading to reduced memory consumption during training. Additionally, our implementation includes scripts for utilizing the DeepH-E3 framework.

We prepare the HONPAS dataset based on the published dataset from DeepH's work.67 For reproduction of the result of this work, we also publish the HONPAS dataset.68 The graphene dataset consists of 300 4 × 4 bilayer graphene cells (Fig. 3(a)), which were generated from molecular dynamics simulations of AA-stacked bilayer graphene at T = 300 K. These structures are then calculated directly in HONPAS to produce their Hamiltonians, overlap matrices, and band structures for benchmarking. The k-points are sampled using the Monkhorst–Pack method with a 4 × 4 × 1 grid. The pseudo-atomic orbital (PAO) basis set is chosen to be DZ to ensure accuracy. We adopt the generalized gradient approximation (GGA) exchange–correlation functional, parameterized by Perdew, Burke, and Ernzerhof (PBE). The convergence threshold for the density matrix is set to 10−5 eV.


image file: d5dd00128e-f3.tif
Fig. 3 (a) A dataset consisting of 300 distinct 4 × 4 bilayer graphene (BG) cells used for training. Each structure contributes a Hamiltonian matrix to the dataset. (b) Heatmap of the converged validation loss function for interactions between carbon atoms, with a convergence threshold of 1 × 10−4 for the learning rate. (c) The moiré pattern of magic-angle twisted bilayer graphene (MATBG) at a twist angle of 1.05°, with the frame indicating its unit cell, which contains 11[thin space (1/6-em)]908 carbon atoms. (d) Predicted electronic band structure of MATBG, calculated using the DeepH + HONPAS framework with the PBE functional. Continuum model and tight binding model results are also presented. In the BM-type continuum model, the hopping energy is set to 110 meV.61 In the tight binding model, the Slater–Koster type hopping is adopted, where V0ppπ = −2.7 eV and V0ppσ = 0.48 eV.62

The dimension of the overlap matrix for each pair of atoms is uniformly 8 × 8, as only carbon element is present in the material, and the DZ basis set for carbon contains 8 orbitals. To highlight the performance advantage of GPU acceleration in our workflow, we benchmarked training times on the bilayer graphene dataset using both CPU and CUDA backends. Specifically, we compared a CPU workstation with two Hygon C86 7285 32-core processors (PyTorch 2.1.0+cpu) and a desktop equipped with an Intel i9-10850K and an NVIDIA RTX 4090 GPU (PyTorch 2.1.0+cu121). When using 32 CPU threads, the training time per epoch ranged from 280 to 300 seconds. In contrast, with GPU acceleration and 8 CPU threads, the training time was reduced to approximately 10 seconds per epoch. This >25× speedup underscores the practical necessity of CUDA support for efficiently handling large or high-resolution datasets in our framework. Typically, convergence can be achieved at 2000 to 3000 epochs, depending on the cutoff radius and accuracy. The preprocessing time is typically in the range of hundreds of seconds (e.g., 262.96 s with 10 threads). Therefore, the combined time cost of preprocessing and training is practically negligible, and this process only needs to be performed once, provided the predicting structure shares the same element species and similar dimensions as the dataset.

Using the model trained on the bilayer graphene dataset, we study larger-scale TBG systems, including magic-angle twisted bilayer graphene (MATBG) and twisted trilayer graphene (MATTG). The twisting configuration of MATBG is (32, 31) with a twist angle of 1.05°, containing 11[thin space (1/6-em)]908 carbon atoms (Fig. 3(a)) and that of MATTG (ABA) is near (22, 21) 1.54° with 8322 carbon atoms (Fig. 4(a)). Here pairs of integers (32, 31) and (22, 21) denote the commensurate rotation vector with graphene unit cell vectors as bases. The theoretically predicted magic angle for ABA stacking trilayer graphene is near 1.5°, image file: d5dd00128e-t10.tif times that of bilayer counterpart. ABA stacking MATTG is predicted to host both flat bands and Dirac cone as well as superconductivity.69–75 In Fig. 3(b), the validation loss at the final step of training has a maximum amplitude of 0.1300 meV, indicating that the neural network model has converged and has an acceptable error margin of 10−4 eV. The largest matrix element, located at position (3, 3), corresponds to the hopping between py orbitals of carbon atoms. Other significant elements correspond to hoppings between the in-plane orbitals, px and py, where the z-axis is defined as the out-of-plane direction perpendicular to the material. The model's ability to predict large structures, as shown in Fig. 3(c), demonstrates DeepH's excellent transferability for unseen structures with similar chemical compositions. In Fig. 3(d), we present the flat band structure of magic-angle graphene. The predicted bands near the zero-energy Fermi level are flat, which is consistent with the continuum model, the tight-binding (TB) model, and qualitatively with experimental observations.65


image file: d5dd00128e-f4.tif
Fig. 4 (a) ABA-stacked MATTG structure, where the top and bottom layers are AA-stacked, while the middle layer is twisted by 1.54° relative to the other layers. (b) Predicted electronic band structure of MATTG, obtained using the DeepH + HONPAS framework with the PBE functional.

We also show the predicted electronic band structure of MATTG, which contains a set of flat bands and a Dirac cone (Fig. 4(b)). Though the localized environment surrounding a particular atom of TTG is difference from that of TBG, they both can be accounted by interlayer and intralayer hoppings. Therefore, MATTG Hamiltonian can still be predicted by the neural network model trained with bilayer graphene dataset.

Hybrid functional Hamiltonians are fundamentally different from the LDA or GGA ones, as the nonlocal exact exchange part modifies both the matrix elements and the optimized cutoff radius for training. We prepare the dataset by performing HSE06 functional calculations on 300 bilayer graphene structures using HONPAS. The cutoff radius is optimized to 5.8 bohr to achieve the best electronic band structure fitting. The fitted bands for TBG are shown in Fig. 5. In panel (a), direct DFT calculations of 7.34° TBG using PBE and HSE06 are carried out to highlight the slight difference at the Γ point. The gap at the Γ point obtained by HSE06 (2.52 eV) is larger than that of PBE (2.15 eV). In Fig. 5(b)–(d), band structures for 7.34°, 4.41°, and 2.88° TBG, obtained by both HONPAS and DeepH + HONPAS, are presented. As a result, the neural network is able to capture the differences between functionals, as long as the corresponding dataset is prepared properly.


image file: d5dd00128e-f5.tif
Fig. 5 (a) Band structure of 7.34° TBG calculated directly with HONPAS using the PBE and HSE06 functionals. The HSE06 functional captures the subtle difference in Fermi velocity at the K point. (b)–(d) HSE06 band structures of 7.34°, 4.41°, and 2.88° TBG obtained from the DeepH + HONPAS framework, compared to the direct results from HONPAS.

4.2 Twisted bilayer MoS2

In addition to carbon-based materials, DeepH + HONPAS also performs well for more complex materials. We construct a dataset of 500 4 × 4 bilayer MoS2 (BMoS2) unit cells (as shown in Fig. 6(a)) to facilitate large-scale twisted bilayer MoS2 (TBMoS2) studies. The training process achieves convergence with a maximum validation loss of less than 0.0371 meV (Fig. 6(b)). In Fig. 6(c), we present the band structure of a single layer 8 × 8 MoS2 supercell (SMoS2), while Fig. 6(d)–(f) depict the predicted band structures of TBMoS2 with twist angles of 7.34°, 4.41°, 2.88°.
image file: d5dd00128e-f6.tif
Fig. 6 (a) A total of 500 4 × 4 bilayer MoS2 (BMoS2) cells are used for training. (b) Validation loss of the trained model for Mo and S. Both elements use the DZ basis set, with Mo described by 12 orbitals and S by 8 orbitals. (c) PBE band structure of a single-layer 8 × 8 MoS2 extended cell. (d)–(f) PBE band structures of TBMoS2 with twist angles of 7.34°, 4.41°, and 2.88°, respectively.

Hybrid functionals play a more important role in gapped semiconductors, where the PBE functional underestimates band gaps. In Fig. 7, the HSE06 band structures of 7.34° TBMoS2 calculated using both HONPAS and DeepH + HONPAS show excellent agreement at the valence and conduction band edges. The deviations away from the band edges are due to the necessary cutoff radius in the crystal graph neural network, which needs to be balanced between efficiency and accuracy due to the inherent nearsightedness in neural network training. Also, band gap of PBE functional (1.18 eV) in Fig. 6(d) is smaller than that of HSE06 (1.69 eV) functional in Fig. 7.


image file: d5dd00128e-f7.tif
Fig. 7 HSE06 band structures of TBMoS2. The band fitting parameters are provided in the SI. The predicted HSE06 band gap is 0.51 eV larger than the PBE results.

4.3 Performance

We here present some details regarding the time cost of the inference step and compare it with the traditional approach of directly calculating the self-consistent field (SCF) using a DFT package. While HONPAS offers significant advantages in handling systems with thousands of atoms, DeepH + HONPAS demonstrates even greater potential by further reducing the computational cost while maintaining high precision. In Fig. 8, we present the detailed time costs of five substeps in the inference process, including (1) parsing the overlap matrix, (2) obtaining local coordinates, (3) predicting the Hamiltonian, (4) rotating back, and (5) performing sparse matrix calculations. In the parsing step, the large overlap matrix is represented as a crystal graph for further prediction, similar to the preprocessing of raw DFT datasets. This step is the most time-consuming due to binary file I/O and the use of serial processing. By the time the code reaches the fourth step, which involves rotating the local Hamiltonians back to the full Hamiltonian, the Hamiltonian prediction is already completed. The fifth step is solely dedicated to electronic band structure calculations. Although band structure calculations can be time-consuming, this difficulty is mitigated in larger systems, where sparse matrix diagonalization algorithms perform efficiently. This step employs the Lanczos method, implemented in the Julia code for diagonalization.76
image file: d5dd00128e-f8.tif
Fig. 8 Detailed single-CPU time breakdown across five substeps in the inference phase. Inference times for graphene materials were recorded on three different computing systems: (a) a system featuring a single Intel i9-10850K 10-core processor and an NVIDIA RTX 4090 GPU. (b) The same system as in (a), but with the GPU disabled. (c) A CPU workstation equipped with two Hygon C86 7285 32-core processors. The “parse” step accounts for the largest portion of the total runtime, particularly for large systems. Additionally, the time required for band structure calculations (“sparse calc”) significantly exceeds the time needed for Hamiltonian acquisition, highlighting the computational bottleneck for large-scale inference tasks.

In Fig. 9, we present a comparison of single-core CPU time between DeepH + HONPAS and HONPAS. This time cost includes the first three substeps of the inference process. DeepH + HONPAS shows a remarkable improvement in efficiency, accelerating the acquisition of the Hamiltonian matrix by nearly 100 times for PBE to 500 times for HSE06. This efficiency also enables the study of larger systems, where machine learning can offer even greater advantages over traditional DFT calculations.


image file: d5dd00128e-f9.tif
Fig. 9 (a) Time cost for calculations using the PBE functional. For TBG and TBMoS2 systems, the combined DeepH/DeepH-E3 + HONPAS framework demonstrates superior performance compared to standalone HONPAS calculations. (b) Time cost for calculations using the HSE06 functional. Direct HSE06 calculations for larger systems of TBMoS2 (with twist angles below 7.34°) are infeasible on current computational platforms, highlighting the efficiency of the DeepH framework.

5 Summary

DeepH + HONPAS stands as a robust and efficient methodology for integrating hybrid density functionals into the DeepH framework, enabling large-scale electronic structure calculations with improved accuracy and computational efficiency. We demonstrated the ability of machine learning predictions to reproduce HONPAS band structures of twisted bilayer graphene and MoS2. The time required for acquiring the Hamiltonian matrix is reduced by nearly 100 to 500 times and can be further decreased for larger systems. The slight differences between the PBE and HSE06 functionals can be captured by the machine learning model simply by feeding the neural network with the DFT Hamiltonians of corresponding functionals as the dataset. Since HONPAS also utilizes the NAO2GTO and ISDF techniques, it is efficient for hybrid functional calculations, which further accelerates dataset preparation. After improving accuracy, future directions include applying graph neural networks to molecular dynamics.39 To further improve scalability and efficiency, future developments will target the optimization of HONPAS, including accelerated ERI computations and enhanced parallelization. DeepH + HONPAS opens new avenues for the application of deep learning methods in advanced electronic structure theories.

Conflicts of interest

There are no conflicts to declare.

Data availability

The dataset and source code supporting the findings of this study are publicly available at Zenodo: https://doi.org/10.5281/zenodo.14979348. This record includes both the DeepH-HONPAS codebase (version 1.0, corresponding to the main branch used in this work) and all datasets used in our calculations. Further details on data access and usage are provided in the manuscript. For additional inquiries, please contact the corresponding author.

The SI includes model training validation errors, statistical analyses, band fitting parameters, and the effects of cutoff radius selection. See DOI: https://doi.org/10.1039/d5dd00128e.

Acknowledgements

This work is partly supported by the Innovation Program for Quantum Science and Technology (2021ZD0303306), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB0450101, XDB1170000), the National Natural Science Foundation of China (22288201, 22173093, 21688102), by the Anhui Provincial Key Research and Development Program (2022a05020052), the National Key Research and Development Program of China (2016YFA0200604, 2021YFB0300600), the Fundamental Research Funds for the Central Universities (No. WK2320000061), and the CAS Project for Young Scientists in Basic Research (YSBR-005). The authors declare no competing financial interest.

Notes and references

  1. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef .
  2. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS .
  3. H.-D. Saßnick and C. Cocchi, Electron. Struct., 2021, 3, 027001 CrossRef .
  4. P. Deák, B. Aradi, T. Frauenheim, E. Janzén and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 153203 Search PubMed .
  5. A. J. Garza and G. E. Scuseria, J. Phys. Chem. Lett., 2016, 7, 4165–4170 Search PubMed .
  6. B. J. Abdullah, Mater. Sci. Semicond. Process., 2022, 137, 106214 CrossRef CAS .
  7. D. Bohm and D. Pines, Phys. Rev., 1953, 92, 609 Search PubMed .
  8. X. Ren, P. Rinke, C. Joas and M. Scheffler, J. Mater. Sci., 2012, 47, 7447–7471 CrossRef CAS .
  9. A. Heßelmann and A. Görling, Mol. Phys., 2011, 109, 2473–2500 Search PubMed .
  10. A. Grüneis, M. Marsman, J. Harl, L. Schimka and G. Kresse, J. Chem. Phys., 2009, 131, 154115 CrossRef PubMed .
  11. F. Karlicky and M. Otyepka, J. Chem. Theory Comput., 2013, 9, 4155–4164 CrossRef CAS PubMed .
  12. T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed .
  13. C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 Search PubMed .
  14. K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed .
  15. K. Choudhary and B. DeCost, npj Comput. Mater., 2021, 7, 185 CrossRef .
  16. K. T. Schütt, M. Gastegger, A. Tkatchenko, K.-R. Müller and R. J. Maurer, Nat. Commun., 2019, 10, 5024 CrossRef PubMed .
  17. Y. Zhuo, A. Mansouri Tehrani and J. Brgoch, J. Phys. Chem. Lett., 2018, 9, 1668–1673 CrossRef CAS PubMed .
  18. J. Lee, A. Seko, K. Shitara, K. Nakayama and I. Tanaka, Phys. Rev. B, 2016, 93, 115104 CrossRef .
  19. J. R. Moreno, G. Carleo and A. Georges, Phys. Rev. Lett., 2020, 125, 076402 CrossRef CAS PubMed .
  20. B. G. del Rio, B. Phan and R. Ramprasad, npj Comput. Mater., 2023, 9, 158 CrossRef .
  21. Y. Chen, L. Zhang, H. Wang and W. E, J. Phys. Chem. A, 2020, 124, 7155–7165 Search PubMed .
  22. Y. Chen, L. Zhang, H. Wang and W. E, J. Chem. Theory Comput., 2020, 17, 170–181 CrossRef PubMed .
  23. L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed .
  24. L. Zepeda-Núñez, Y. Chen, J. Zhang, W. Jia, L. Zhang and L. Lin, J. Comput. Phys., 2021, 443, 110523 Search PubMed .
  25. G. B. Goh, C. Siegel, A. Vishnu, N. O. Hodas and N. Baker, arXiv, 2017, preprint, arXiv:1706.06689,  DOI:10.48550/arXiv.1706.06689.
  26. Z. Wang, S. Ye, H. Wang, J. He, Q. Huang and S. Chang, npj Comput. Mater., 2021, 7, 11 CrossRef CAS .
  27. Q. Gu, Z. Zhouyin, S. K. Pandey, P. Zhang, L. Zhang and W. E, Nat. Commun., 2024, 15, 6772 Search PubMed .
  28. G. Hegde and R. C. Bowen, Sci. Rep., 2017, 7, 42669 Search PubMed .
  29. H. Wang, L. Zhang, J. Han and E. Weinan, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS .
  30. H. Li, Z. Wang, N. Zou, M. Ye, R. Xu, X. Gong, W. Duan and Y. Xu, Nat. Comput. Sci., 2022, 2, 367–377 CrossRef PubMed .
  31. X. Gong, H. Li, N. Zou, R. Xu, W. Duan and Y. Xu, Nat. Commun., 2023, 14, 2848 CrossRef CAS PubMed .
  32. Z. Tang, H. Li, P. Lin, X. Gong, G. Jin, L. He, H. Jiang, X. Ren, W. Duan and Y. Xu, Nat. Commun., 2024, 15, 8815 CrossRef CAS PubMed .
  33. H. Li, Z. Tang, X. Gong, N. Zou, W. Duan and Y. Xu, Nat. Comput. Sci., 2023, 3, 321–327 Search PubMed .
  34. X. Gong, S. G. Louie, W. Duan and Y. Xu, Nat. Comput. Sci., 2024, 4, 752–760 CrossRef PubMed .
  35. T. L. Beck, Rev. Mod. Phys., 2000, 72, 1041 CrossRef CAS .
  36. Y. Zhong, H. Yu, M. Su, X. Gong and H. Xiang, npj Comput. Mater., 2023, 9, 182 CrossRef .
  37. H. Li, Z. Tang, J. Fu, W.-H. Dong, N. Zou, X. Gong, W. Duan and Y. Xu, Phys. Rev. Lett., 2024, 132, 096401 CrossRef CAS PubMed .
  38. Y. Wang, Y. Li, Z. Tang, H. Li, Z. Yuan, H. Tao, N. Zou, T. Bao, X. Liang and Z. Chen, et al., Sci. Bull., 2024, 69, 2514–2521 CrossRef CAS PubMed .
  39. C. Zhang, Y. Zhong, Z.-G. Tao, X. Qin, H. Shang, Z. Lan, O. V. Prezhdo, X.-G. Gong, W. Chu and H. Xiang, Nat. Commun., 2025, 16, 2033 CrossRef CAS PubMed .
  40. Y. Zhong, H. Yu, J. Yang, X. Guo, H. Xiang and X. Gong, Chin. Phys. Lett., 2024, 41, 077103 CrossRef .
  41. X. Qin, H. Shang, L. Xu, W. Hu, J. Yang, S. Li and Y. Zhang, Int. J. High Perform. Comput. Appl., 2020, 34, 159–168 CrossRef .
  42. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS .
  43. W. Hu, L. Lin, C. Yang and J. Yang, J. Chem. Phys., 2014, 141, 214704 CrossRef PubMed .
  44. W. Hu, Y. Huang, X. Qin, L. Lin, E. Kan, X. Li, C. Yang and J. Yang, npj 2D Mater. Appl., 2019, 3, 17 CrossRef .
  45. W. Hu, L. Lin, C. Yang, J. Dai and J. Yang, Nano Lett., 2016, 16, 1675–1682 CrossRef CAS PubMed .
  46. X. Liu, X. Qin, X. Li, Z. Ding, X. Li, W. Hu and J. Yang, Nano Lett., 2021, 21, 9816–9823 CrossRef CAS PubMed .
  47. Y. Ke, L. Wan, X. Qin, W. Hu and J. Yang, Nano Lett., 2024, 24, 4433–4438 CrossRef CAS PubMed .
  48. H. Shang, Z. Li and J. Yang, J. Chem. Phys., 2011, 135, 034110 CrossRef PubMed .
  49. X. Qin, H. Shang, H. Xiang, Z. Li and J. Yang, Int. J. Quantum Chem., 2015, 115, 647–655 Search PubMed .
  50. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 Search PubMed .
  51. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS .
  52. T. Ozaki and H. Kino, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045121 Search PubMed .
  53. T. Ozaki, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155108 CrossRef .
  54. M. Chen, G. Guo and L. He, J. Phys.: Condens. Matter, 2010, 22, 445501 Search PubMed .
  55. P. Li, X. Liu, M. Chen, P. Lin, X. Ren, L. Lin, C. Yang and L. He, Comput. Mater. Sci., 2016, 112, 503–517 Search PubMed .
  56. X. Qin, J. Liu, W. Hu and J. Yang, J. Phys. Chem. A, 2020, 124, 5664–5674 Search PubMed .
  57. B. Delley, J. Chem. Phys., 1990, 92, 508–517 Search PubMed .
  58. J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola and H. Hansen, et al., J. Phys.: Condens. Matter, 2010, 22, 253202 Search PubMed .
  59. W. Kohn, Phys. Rev. Lett., 1996, 76, 3168 Search PubMed .
  60. E. Prodan and W. Kohn, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11635–11638 CrossRef CAS PubMed .
  61. R. Bistritzer and A. H. MacDonald, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 12233–12237 CrossRef CAS PubMed .
  62. J. C. Slater and G. F. Koster, Phys. Rev., 1954, 94, 1498 Search PubMed .
  63. A. Kerelsky, L. J. McGilly, D. M. Kennes, L. Xian, M. Yankowitz, S. Chen, K. Watanabe, T. Taniguchi, J. Hone and C. Dean, et al., Nature, 2019, 572, 95–100 Search PubMed .
  64. S. Fang and E. Kaxiras, Phys. Rev. B, 2016, 93, 235153 CrossRef .
  65. Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50 Search PubMed .
  66. M. Koshino, N. F. Yuan, T. Koretsune, M. Ochi, K. Kuroki and L. Fu, Phys. Rev. X, 2018, 8, 031087 CAS .
  67. H. Li, Version v1, Zenodo, 2022,  DOI:10.5281/zenodo.6555484 .
  68. Y. Ke, Version v1, Zenodo, 2025,  DOI:10.5281/zenodo.14979348 .
  69. E. Khalaf, A. J. Kruchkov, G. Tarnopolsky and A. Vishwanath, Phys. Rev. B, 2019, 100, 085109 CrossRef CAS .
  70. J. M. Park, Y. Cao, L.-Q. Xia, S. Sun, K. Watanabe, T. Taniguchi and P. Jarillo-Herrero, Nat. Mater., 2022, 21, 877–883 Search PubMed .
  71. Z. Liu, W. Shi, T. Yang and Z. Zhang, J. Mater. Sci. Technol., 2022, 111, 28–34 Search PubMed .
  72. Y. Zhang, R. Polski, C. Lewandowski, A. Thomson, Y. Peng, Y. Choi, H. Kim, K. Watanabe, T. Taniguchi and J. Alicea, et al., Science, 2022, 377, 1538–1543 CrossRef CAS PubMed .
  73. J. M. Park, Y. Cao, K. Watanabe, T. Taniguchi and P. Jarillo-Herrero, Nature, 2021, 590, 249–255 CrossRef CAS PubMed .
  74. Z. Hao, A. Zimmerman, P. Ledwith, E. Khalaf, D. H. Najafabadi, K. Watanabe, T. Taniguchi, A. Vishwanath and P. Kim, Science, 2021, 371, 1133–1138 CrossRef CAS PubMed .
  75. H. Kim, Y. Choi, C. Lewandowski, A. Thomson, Y. Zhang, R. Polski, K. Watanabe, T. Taniguchi, J. Alicea and S. Nadj-Perge, Nature, 2022, 606, 494–500 CrossRef CAS PubMed .
  76. R. B. Lehoucq, D. C. Sorensen and C. Yang, ARPACK Users' Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods, SIAM, 1998 Search PubMed .
This journal is © The Royal Society of Chemistry 2025
Click here to see how this site uses Cookies. View our privacy policy here.