View PDF Version

Open Access Article
This Open Access Article is licensed under a
Creative Commons Attribution 3.0 Unported Licence
DOI: 10.1039/D5DT01115A (Paper) Dalton Trans., 2025, Advance Article

X-ray crystallographic and computational studies of quaternary ammonium chloride salt complexes with uranyl–salophen compounds†

Marco Saccone*a, Arto Valkonenb, Kari Rissanenb and Massimo Cametti*c
aUniversità degli Studi del Piemonte Orientale “Amedeo Avogadro”, Dipartimento di Scienze e Innovazione Tecnologica, Viale Teresa Michel 11, 15121, Alessandria, Italy. E-mail: marco.saccone@uniupo.it
bDepartment of Chemistry, University of Jyvaskyla, P.O. Box 35, 40014 Jyväskylä, Finland
cDepartment of Chemistry, Materials and Chemical Engineering “Giulio Natta”, Politecnico di Milano, Via Luigi Mancinelli 7, 20131, Milano, Italy. E-mail: massimo.cametti@polimi.it

Received 12th May 2025 , Accepted 7th July 2025

First published on 10th July 2025

Abstract

This study investigates salophen–UO2 complexes 1 and 2 assembled with four tetraalkylammonium chloride salts of various cation sizes: tetramethyl (TMA), dimethyl-dipropyl (DMDPA), dimethyl-dibutyl (DMDPA), and tetrabutylammonium (TBA). Single-crystal X-ray diffraction (SC-XRD) and computational analyses such as Hirshfeld surface and DFT analyses and interaction region indicator (IRI) representation provided a comprehensive view on how packing and the overall assembly of the complexes are affected by the size of the ammonium cation and on the interplay among different intermolecular forces responsible for the solid-state structures observed, with a particular focus on the role of cation–π interactions.

Introduction

Salophen–UO2 compounds are kinetically robust complexes formed by reacting the linear dioxido UO22+ cation with salophen ligands, an established class of organic Schiff-base ligands structurally related to salens.1,2 They are characterized by the U(VI) center coordinated on the equatorial plane by the tetradentate doubly deprotonated NNOO salophen ligand, while the two uranyl oxygens tightly bound to the U atom, formally via triple bonds, reside on the apical positions. By usually adopting a pentagonal bipyramidal coordination geometry, the U atom in these complexes can establish an additional coordination interaction, which is consequently seized by a Lewis base substrate or the solvent. In the absence of the latter, dimeric species can also be obtained.3 Overall, in the solid state, with few documented exceptions,4 these compounds adopt a hallmark curvature. This feature, which is also retained in solution, although characterized by a concomitant dynamic flipping motion usually limited in the solid state, can impart chirality to the system if the ligand lacks any plane of symmetry.5 Given all the above-mentioned properties, since the early 1990s, uranyl–salophen compounds have been studied in more detail, aiming at several applications, such as catalysis and recognition, following seminal works by Reinhoudt et al.6,7

More recently, mono- and bis-uranyl salophen compounds have been reported to achieve among the highest affinity and selectivity for fluoride anions in polar aprotic organic media.8,9 They have also been successfully employed as ion pair receptors in solution and in the solid state, where they have been reported to bind and assemble with quaternary ammonium and alkali metal halide salts.10–12 In this context, salophen–UO2 complexes have been used to study cation–π interactions13,14 and are recognized among the most relevant examples of abiotic systems where these weak interactions have been determined and evaluated experimentally in both solution and in the solid state, as recently highlighted by Mahadevi et al.15 However, no study has yet firmly established the energetic role of cation–π interactions as a driving force in the packing of these complexes in the solid state, despite UO2–salophen complexes being among the most relevant supramolecular systems featuring cation–π interactions reported to date. One plausible reason for this gap is the difficulty in the computational treatment of the actinide atom paired with a large-sized ligand. Thus, until recently, computational studies on salophen–actinyl compounds have been scarce. Some reports describe non-symmetric uranyl–salophen compounds interacting with α,β-unsaturated aldehydes and ketones and with a specific drug.16,17 Others focus on more classic, symmetric salophen–NpO2 compounds, providing detailed analysis of the bonding from a molecular orbital perspective.18 However, a detailed elucidation and dissection of the forces driving the solid-state assembly of these systems, especially regarding the contribution of cation–π interactions in ion-pair receptor systems, is missing. In this work, we report on the solid-state structures of receptor 1 with dimethyl-dipropyl (DMDPA) and dimethyl-dibutyl (DMDBA) ammonium chlorides (Scheme 1). These complexes have been characterized by SC-XRD analysis and described in comparison with the previously reported complexes with tetramethylammonium (TMA) and tetrabutylammonium (TBA) salts.11,12 For comparison, the structure of the adduct formed between [TMA]Cl and 2, a salophen–UO2 compound devoid of the lateral side arms and thus less effective in establishing cation–π interactions, is also considered. The description of the crystal structures, complemented by Hirshfeld surface analysis (HSA),19 is paired with a quantitative evaluation of intermolecular interactions. This allows us to elucidate the role of cation–π interactions and other packing–driving forces in the complexes, also by visualization of interaction region indicator (IRI) isosurface maps. Furthermore, we provide insights into the electronic structure of compound 1 by performing an extensive computational study on it and two of its derivatives: the neutral complex [1-MeCN] and the anionic species [1-Cl]−.


image file: d5dt01115a-s1.tif
Scheme 1 The salophen−UO2 complexes 1 and 2 and the tetraalkylammonium chloride salts [TMA]Cl, [DPDMA]Cl, [DBDMA]Cl and [TBA]Cl considered in the present work. The ring code is attributed assuming compounds 1 and 2 facing the reader with their convex side (see also Fig. 1a).

Experimental and computational details

Caution! The DPDMA[1-Cl] and DBDMA[1-Cl] salts prepared in this study contained depleted uranium. Standard precautions for handling radioactive materials or heavy metal salts such as uranyl acetate were followed.

Receptor 1 was synthesized according to the original publication by Reinhoudt et al.6 [DMDPA]Cl and [DMDBA]Cl salts were prepared by following the original publication by Ropponen et al.20 Single crystals of DMDPA[1-Cl] and DMDBA[1-Cl] were obtained by slow evaporation of an acetone solution of 1 in the presence of an excess of the corresponding chloride salt. SC-XRD data for both complexes were collected with a Bruker Nonius Kappa CCD diffractometer (APEX II detector) using graphite monochromatized Mo Kα radiation (λ = 0.71073 Å). The structures were solved by direct methods, and full-matrix least-squares refinements on F2 were performed. The reflections were corrected for Lorentz polarization, and multi-scan absorption correction was applied. More SC-XRD structure determination details and the software used can be found in the ESI (crystallographic Tables S1, S2 and Fig. S4, S5†). Crystallization of TMA[1-Cl] (CSD refcode ELUFUM) and TBA[1-Cl] (ELUGAT) has been described before,11,12 and their X-ray structures were retrieved from the CSD: these are discussed again geometrically and computationally here. The [TMA][2-Cl] salt was not synthesized: its geometrical coordinates were retrieved from the CSD (refcode HEYXUF) and used only for the computational study.

All calculations were performed at the DFT level using the GAUSSIAN 16 (Rev. C.01) quantum-chemistry package21 and the B3LYP functional.22 For geometry optimizations and vibrational frequency analysis performed in the last section of the manuscript, the pcseg-2 basis set of Jensen of triple-ζ-quality and optimized for DFT calculations,23 was used for all atoms except for uranium. For the latter, the def2-TZVP basis set was used, along with an associated relativistically contracted effective core potential, which replaced 60 core electrons on the uranium center.24 Subsequent single-point calculations performed on the optimized structures employed the all-electron cc-pVTZ-DK basis set for all atoms including uranium.25 Scalar relativistic effects were modeled using the second-order Douglas–Kroll–Hess Hamiltonian.26,27 Ours are closed-shell, high-valent complexes of uranyl(VI) where the f orbital occupation is low, so we did not include the effects of spin–orbit interactions in this work.28 In order to stabilize the anionic electronic structures, geometries were optimized using default optimization criteria in the presence of a continuum aqueous solvent, defined using the COSMO model (radii: H, 1.30 Å; C, 2.00 Å; N, 1.83 Å; O, 1.72 Å; Cl, 2.05 Å; U, 2.23 Å).29 To account for anharmonicity effects, the B3LYP-predicted spectra were scaled by 0.97.30 All-electron DKH densities were used as the starting point for further analysis including IRI31 and QTAIM32 employing AIMAll (version 11.05.16)33 and Multiwfn (version 3.8) software.34 For both the IRI and QTAIM analyses, a grid with an ultra-high resolution of 5 pm was employed. VMD (version 1.9.4) software was used for visualization purposes.35 For the calculation of intermolecular energies from the experimentally derived X-ray data, we used a semiempirical approach, popularized by Gavezzotti with the PIXEL method,36 and recently revamped by Spackman et al., who developed the CrystalExplorer suite,37 which we also used for the HSA. The interaction energy is decomposed into the sum of the following terms, Etot = Eele + Epol + Edis + Erep, which have already been discussed by Gavezzotti and explained in detail by Turner et al. in their implementation.38 Monomer electron densities used to compute Eele, Epol, and Erep were obtained at the B3LYP/6-31G(d,p) level of theory with the GAUSSIAN software, and Edis is the Grimme D2 dispersion correction, summed over all intermolecular atom pairs. For these calculations, geometries were taken from crystallographic coordinates. Before the calculations at the geometries determined by X-ray started, C–H distances were restrained to the values obtained from neutron diffraction studies of small molecules.39 This methodology has recently been used to rationalize the aggregation-induced-emission behavior of a series of aromatic thioethers40 and to explain subtle differences in the liquid crystalline behavior of supramolecular liquid crystals.41

Results and discussion

SC-XRD data: general considerations

A general view of the four ion-pair complexes as determined by SC-XRD analysis is shown in Fig. 1. As far as the molecular complexes are concerned, defined as the closest cation⋯[1-Cl] unit, the four species are similar but exhibit important differences. While the central salophen moiety comprising the UO2-Cl unit remains practically unchanged within the series, the lateral arms show a much greater degree of flexibility, adjusting to the different size and shape of the cations. In particular, the receptors front the cations with their convex side, with the exception of the [TBA][1-Cl] case, where it is the concave side of the salophen–UO2 compound that faces the closest cation. Overall the conformation of the alkyl chains of the anions is all trans for [DMDPA][1-Cl], while for [DMDBA][1-Cl] and TBA[1-Cl], one of the butyl arms exhibits a gauche conformation. Furthermore, as far as cation–π interactions are concerned, while in [TMA][1-Cl] the cation mainly interacts with only one aromatic ring belonging to the side arm, in [DMDPA][1-Cl] and [DMDBA][1-Cl], the cations interact with two aromatic rings, one from the side arm and one from the salophen moiety core.
image file: d5dt01115a-f1.tif
Fig. 1 Capped stick views of UO2−salophen 1 complexed with quaternary ammonium chlorides: (a) [TMA][1-Cl]; (b) [DMDPA][1-Cl]; (c) [DMDBA][1-Cl]; and (d) [TBA][1-Cl]; color code: H = light grey, C = dark gray, O = red, N = violet, U = cyan, and Cl = green. Cations are represented in orange. In the case of [DMDPA][1-Cl] and [DMDBA][1-Cl], the solvent present is omitted for clarity.

In [TBA][1-Cl], however, the bulkiest cation shows multiple contacts with three aromatic rings. The structure of [1-Cl]− has been described in detail in previous studies;10 however it is important, in the context of molecular recognition, to discuss the role of the γ and δ rings as they can freely rotate to accommodate the cation. In particular, the angle between the planes containing the C atoms of the γ and δ rings increase in the series [TMA][1-Cl] (20.13°) < [DMDPA][1-Cl] (49.96°) < [DMDBA][1-Cl] (58.57°) < [TBA][1-Cl] (60.71°). This allows the anion to maximize the π-interactions with the cation as it enlarges. Relevant cation–π distances as determined by metric analysis on the X-ray data are reported in Table S1 in the ESI.† C–H bond distances were restrained as stated above. Depending on the packing (vide infra), each [(1-Cl)]− anion might have additional cations located near its aromatic ring, and the corresponding contacts are also reported for each complex in Table S1.† For [DMDPA][1-Cl] and [DMDBA][1-Cl], we analyzed the geometrical contacts in detail, while we briefly comment on them in the other structures which have been already reported.

Although the molecular complexes of all species are quite similar, their packing is considerably different and, in our view, this is a direct effect of the ammonium cation size. We wish to point out that dispersive interactions among the [(1-Cl)]− anions and the cations are difficult to understand in terms of short contacts and they are best approached through interaction region indicator (IRI) analysis, which also reveal covalent bonds (see below).

[DMDPA][1-Cl]. As explained in the previous section, the closest dimethyl-dipropyl ammonium cation strongly interacts with the anion. One of the main sources of interactions is constituted by aspecific electrostatic forces between the two ion partners. This is easily visualized by checking the shortest cation⋯[(1-Cl)]− contacts (C42–H⋯Cl1 = 2.57 Å and C45–H⋯O2 = 2.40 Å). This is explained by the fact that the aforementioned atoms belong to the part of the anion with the lowest molecular electrostatic potential (ESP) and so its most negative part (Fig. S1 in the ESI†). This cation also forms short cation–π interactions with γ and δ rings of the salophen ligand: C44–H⋯C34 (Table S1†). Another cation also interacts strongly with the uranyl moiety from the convex side of the [(1-Cl)]− anion, with short C42–H⋯O2 and C45–H⋯O2 contacts of 2.205 Å and 2.66 Å, respectively. The last cation approaches the [(1-Cl)]− unit from the concave side, featuring short cation–π contacts with the γ ring (Table S1†). Interestingly, the solvent molecule interacts with the anion via C–H⋯Nsaloph contacts (Fig. 2).
image file: d5dt01115a-f2.tif
Fig. 2 (a) Capped stick representation of [DMDPA][1-Cl], surrounded by an additional close cation and the solvent. Cations are shown in orange and the solvent in blue. Cyan lines represent short intermolecular contacts below the sum of the van der Waals radii of the respective atoms. Hydrogen atoms involved in short contact interactions are represented as isotropic spheres. (b) Mixed ball-and-stick/spacefill view of a [[DMDPA][1-Cl]]2 unit representative of packing elements in the lattice. Color chart: grey = C, white = H, blue = N, red = O, green = Cl, and light blue = U. Disorder is omitted for clarity.

The importance of such ion−solvent interactions is often overlooked in the literature.42 Several other short intermolecular contacts, although repulsive in nature, are present in this structure, which belong to the “approach preferences”43 caused by anion−anion “collateral damage” interactions (see below).

[DMDBA][1-Cl]. As in the previous case, there are strong aspecific interactions between the two closest cations and the [(1-Cl)]− anion. This is reflected by very short C–H⋯O(uranyl) contacts of 2.18 Å (C46–H⋯O1), 2.52 Å (C42–H⋯O1) and 2.56 Å (C46–H⋯O1), together with a 2.68 Å C–H⋯Cl (C46–H⋯Cl1) contact between the closest cations and the [1-Cl−] unit. Even in this case, the contacts occur between the cation and the most negative ESP area of the anion (Fig. S1, ESI†). Many cation–π interactions are present in this structure. Among these we especially note those with the δ ring (Table S1†). Interestingly, at variance with [DMDPA][1-Cl], the solvent interacts with the anion via a charge assisted C–H–π interaction. Collateral damage approach preferences between the anion pairs are also present in this structure. In both [DMDBA][1-Cl] and [DMDPA][1-Cl], the observed assemblies can be described as head to tail arranged chloride-bound salophen−UO2 dimers encapsulating two cation units. Overall, this assembly is centrosymmetric (Fig. 2b and 3b).
image file: d5dt01115a-f3.tif
Fig. 3 (a) Capped stick representation of [DMDBA][1-Cl], surrounded by neighboring cations and the solvent. Cations are shown in orange and the solvent in blue. Cyan lines represent short intermolecular contacts below the sum of the van der Waals radii of the respective atoms. Hydrogen atoms involved in short contact interactions are represented as isotropic spheres. (b) Mixed ball-and-stick/spacefill view of a [[DMDBA][1-Cl]]2 unit representative of the packing element in the structure. Color chart: grey = C, white = H, blue = N, red = O, green = Cl, and light blue = U. Disorder is omitted for clarity.
[TMA][1-Cl]. We note important CH⋯Cl contacts in the range 2.69–2.88 Å (C40–H⋯Cl1 and C43-H⋯Cl1), C–H⋯O(uranyl) contacts of 2.65 Å (C43–H⋯O2) and C40–H⋯Osaloph of 2.43 Å (C40–H⋯O10), with three surrounding tetramethylammonium cations, which are an indication of ionic interactions (Fig. 4a). Also, significant cation–π interactions in the range 2.71–2.87 Å (C–H⋯C) are present among the cations and the α, γ and δ rings (Table S1†).
image file: d5dt01115a-f4.tif
Fig. 4 (a) Capped stick representation of [TMA][1-Cl], surrounded by neighboring cations. Cations are shown in orange. Cyan lines represent short intermolecular contacts below the sum of the van der Waals radii of the respective atoms. Hydrogen atoms involved in short contact interactions are represented as isotropic spheres; (b) mixed capped stick/spacefill view of one of the tetrameric [[TMA][1-Cl]]4 units representative of the packing elements in the structure. Color chart: grey = C, white = H, blue = N, red = O, green = Cl, and light blue = U.

Packing in [TMA][1-Cl] has been previously described. Briefly, it results from the assembly of ion-clusters made of four TMA cations, located at the vertices of isosceles tetrahedra and tightly encapsulated by shells made of four [(1-Cl)]− units (Fig. 4b). Overall, spherical adducts with a diameter of approx. 18.5 Å are found.

[TBA][1-Cl]. This structure features two independent cations and anions in the asymmetric unit, and due to the increased size of the cation (largest in the series), cation–π contacts increase in number. In fact, we observe contacts between the cations and all the aromatic rings of the salophen ligand with C–H⋯C contacts as short as 2.60 Å (Table S1†). Nevertheless, interactions which are less specific are reflected in the C–H⋯O(uranyl) contacts of 2.33 Å and 2.62 Å (C54B–H⋯O1B and C57B–H⋯O2B, Fig. 5a).11
image file: d5dt01115a-f5.tif
Fig. 5 (a) Capped stick representation of [TBA][1-Cl] surrounded by neighboring cations. Cations are shown in orange. Cyan lines represent short intermolecular contacts below the sum of the van der Waals radii of the respective atoms. Hydrogen atoms involved in short contact interactions are represented as isotropic spheres; (b) mixed ball-and-stick/spacefill view of a stacked chloride-bound receptor/TBA cation columnarly stacked units representative of the packing in the structure. Color chart: grey = C, white = H, violet = N, red = O, green = Cl, and light blue = U.

Finally, in this case the packing is different from what was seen in the other cases, for the TBA cations are found stacked between [(1-Cl)]− units (Fig. 5b). In all the above-mentioned cases, it is important to note that the lateral side arms in 1 are mainly responsible for the cation–π interactions observed.

As a useful comparison, the structure of salophen–UO2 compound 2, devoid of these adjunct binding sites, is shown in Fig. 6.


image file: d5dt01115a-f6.tif
Fig. 6 (a) Capped stick representation of [TMA][2-Cl] surrounded by the closest cation. Cations are shown in orange. Cyan lines represent short intermolecular contacts below the sum of the van der Waals radii of the respective atoms. Hydrogen atoms involved in short contact interactions are represented as isotropic spheres; (b) mixed capped stick/spacefill view of one of the hexameric [[TMA][2-Cl]]6 units representative of the packing elements in the structure. Color chart: grey = C, white = H, blue = N, red = O, green = Cl, and light blue = U.

No TMA cation can be found on top of any aromatic ring (Fig. 6a) and therefore limited cation–π interactions can be identified (see Table S1†). Packing is also better described by open hexameric assemblies in which the UO2-bound chloride points towards an interior filled with six TMA cations and a MeCN solvent (Fig. 6b).

Hirshfeld surface analysis

Hirshfeld surface analyses were performed on all structures with the aim of gathering quantitative insights into the intermolecular interactions in relation to the nature of the present cation. We mapped the Hirshfeld surface of 1 in all the different structures over the shape index,19 and quantitatively analyzed the most significant interactions (viz., H⋯H, C⋯H, C⋯C and so on). The shape index on the Hirshfeld surface allows the identification of complementary, interacting regions of two molecular entities represented as hollows (red) and bumps (blue). In Fig. 7, the two-dimensional fingerprint plots show the difference between the intermolecular interaction patterns and the relative contributions (in percentage) of the significant intermolecular interactions associated with the four analyzed compounds. Intermolecular interactions become visible as distinct spikes in the two-dimensional fingerprint plots. Complementary regions are observable in the fingerprint plots where one molecule acts as a donor (de > di, red regions) and the other as an acceptor (de < di, blue regions). The structural differences in the Hirshfeld analysis appear to be very significant in the whole series: the H⋯H contact percentage increases from 46.3% to 55.6% from the small TMA salt to the big TBA salt which is an almost 10% increase in absolute terms and 20% in relative terms. An opposite but equally significant trend is observed for the C⋯H/H⋯C contacts. These numbers are very large, especially considering that the only molecule that changes in our structures is the cation and that the salophen anion remains the same.
image file: d5dt01115a-f7.tif
Fig. 7 Fingerprint plots of the molecule 1-Cl−, resolved into different interactions showing the percentages of contacts contributing to the total Hirshfeld surface area of the anion.

From the Hirshfeld analysis, it appears that the size of cation is directly correlated to the percentage of H⋯H contacts (R2 = 0.99) and inversely correlated to the percentage of C⋯H/H⋯C contacts (R2 = 0.99).44 This trend is not maintained in the O⋯H/H⋯O contacts where, although [TMA][1-Cl] has a higher number of contacts compared to [TBA][1-Cl], the two intermediate-sized cations have higher contacts than both the others (with [DMDBA][1-Cl] > [DMDPA][1-Cl]). However, this can be explained by the fact that these two compounds are found as acetone solvates and therefore there is an extra oxygen that contributes to the overall O⋯H/H⋯O contacts. The Cl⋯H contacts are less important percentage-wise, with [TMA][1-Cl] having the lowest % count, [DMDBA][1-Cl] and [DMDPA][1-Cl] the highest, with [TBA][1-Cl] found in between. As to [TMA][2-Cl], H⋯H are reduced to 38% in comparison with the 46.3% in case of [TMA][1-Cl], while the C⋯H/H⋯C contacts are calculated to be 30.3 vs. 32.2% (Fig. S2† in the ESI†). To get a clearer quantification of the propensity for various types of intermolecular contacts and for a straightforward interpretation of bond formation tendencies within the crystal structure, we calculated the enrichment ratios from the fingerprint data. The enrichment ratio (E) is the ratio of actual contacts in the crystal to the calculated contacts having the same probability of formation.45 Therefore, the pairs exhibiting an enrichment ratio above 1 have a high tendency to form interactions within the crystal packing. On the other hand, the pairs exhibiting an enrichment ratio below 1 have a low tendency to form interactions.46 The results, summarized in Table S2,† clearly show a strong enrichment of O⋯H and Cl⋯H contacts, which can be considered as charge assisted hydrogen bonds. This enrichment is stronger as the cation size decreases. This is due to the fact that a small cation has an easy access to the anion surface including O and Cl atoms. The H⋯H contacts are somewhat disfavored but approximately follow the trend of the cation size, which means the highest for TBA and lowest for TMA and DMDPA.

Computational studies on complexes [TMA][1-Cl], [DMDPA][1-Cl], [DMDBA][1-Cl], [TBA][1-Cl], and [TMA][2-Cl]: structural determinants

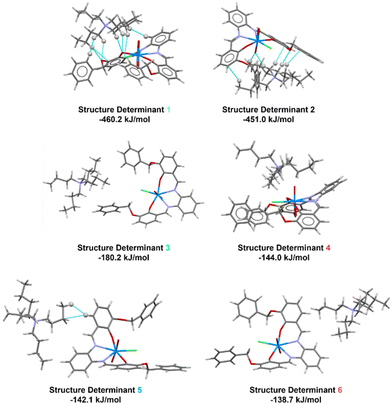
We performed a detailed computational study on the quaternary ammonium salts of 1 described previously in terms of geometrical analyses based on SC-XRD data, in order to understand the different factors responsible for the observed solid-state architectures. In particular, we analyzed to which extent cation–π interactions and cation–[(1-Cl)]− anion aspecific interactions were modulated by the increasing size of the quaternary ammonium cation in the series, a fact that has already been put forward from the Hirshfeld analysis. Therefore, a reference molecule in the crystalline packing was defined (as provided by CrystalExplorer) and then molecule pairs with surrounding molecules were analysed with respect to their intermolecular interactions. Unless otherwise stated, the reference molecule considered is the [1-Cl]− anion. In this respect, we selected the six most significant pairs (Fig. 8–11). These pairs are called structure determinants (SDs) and are identified by a color code, a symmetry operator joining the two molecules, the number N of identical pairs having the same energy and by a distance between centers of mass (R). The color code associated in each SD in each figure in the manuscript directly correlates with the color code on the respective table in the ESI.† Full details about these quantities for each structure determinant are provided in Tables S3–S6 in the ESI.† The SDs are thus extracted from experimental X-ray data. In each SD, the interaction energies are decomposed into physically meaningful and familiar terms as described before (Tables S3–S6, ESI† for each individual contribution).
image file: d5dt01115a-f8.tif
Fig. 8 Supramolecular hierarchy of the six most stabilizing interactions in [TMA][1-Cl] as obtained using CrystalExplorer. Cyan lines represent short intermolecular contacts below the sum of the van der Waals radii of the respective atoms. Hydrogen atoms involved in short contact interactions are represented as isotropic spheres. Color chart: grey = C, white = H, violet = N, red = O, green = Cl, and light blue = U.

image file: d5dt01115a-f9.tif
Fig. 9 Supramolecular hierarchy of the six most stabilizing interactions in [DMDPA][1-Cl] as obtained using CrystalExplorer. Cyan lines represent short intermolecular contacts below the sum of the van der Waals radii of the respective atoms. Hydrogen atoms involved in short contact interactions are represented as isotropic spheres. Color chart: grey = C, white = H, violet = N, red = O, green = Cl, and light blue = U.

image file: d5dt01115a-f10.tif
Fig. 10 Supramolecular hierarchy of the nine most stabilizing interactions in [DMDBA][1-Cl] as obtained using CrystalExplorer. Cyan lines represent short intermolecular contacts below the sum of the van der Waals radii of the respective atoms. Hydrogen atoms involved in short contact interactions are represented as isotropic spheres. Color chart: grey = C, white = H, violet = N, red = O, green = Cl, and light blue = U.

image file: d5dt01115a-f11.tif
Fig. 11 Supramolecular hierarchy of the six most stabilizing interactions in [TBA][1-Cl] as obtained using CrystalExplorer. Cyan lines represent short intermolecular contacts below the sum of the van der Waals radii of the respective atoms. Hydrogen atoms involved in short contact interactions are represented as isotropic spheres. Color chart: grey = C, white = H, violet = N, red = O, green = Cl, and light blue = U.
[TMA][1-Cl]. Only three cations are at short range (contacts below 3.8 Å) from the [1-Cl]− anion, so SD 1–3 are the only stabilizing interaction modes in this structure. In SD 1, there is a combination of cation⋯π, cation⋯Osaloph and cation⋯Cl interactions: indeed, the Cl atom has the lowest local electrostatic potential surface in [1-Cl]− anion. In SD 2, cation⋯Cl and cation⋯Osaloph interactions are present, while in SD 3, only cation⋯π interactions are present. This finding is reflected in the weakening of the electrostatic component of the interaction energy in the series SD 1 → SD 3 (Table S3 ESI†). All the other SDs are for destabilizing anion−anion interactions (Fig. 8).
[DMDPA][1-Cl]. From this structure, all the SDs become stabilizing, a fact that is determined by the increasing size of the cation, which doubles in terms of volume with respect to the TMA, making possible at least six cation–anion interactions at short range. In this case, a situation similar to the [TMA][1-Cl] occurs in the case of SD 1 and SD 2, with SD 1 having strong cation⋯π interactions and cation⋯Cl interactions, and SD 2 having only cation⋯Cl and cation⋯Osaloph interactions. In this case, however, although the stabilization is similar for these two determinants, compared to the [TMA][1-Cl] counterparts, the components of the interaction change, with the electrostatic component reduced and the dispersive component increased. We attribute this to the fact that the DMDPA cation is much larger than the TMA cation and therefore has a charge which is spread over a larger volume. SD 3 shows several cation⋯π interactions, while the other SDs have only nonspecific ionic interactions (Fig. 9).
[DMDBA][1-Cl]. For this structure, similar considerations apply compared to the previous one, with the structural determinants very similar to those of [DMDPA][1-Cl]. In this case, the energy differences are more marked. In addition to the non-specific interactions, it is also worth mentioning (which also applies to the previous structure) that the interaction energy between the anion and acetone is 69 kJ mol−1 and ranks ninth in the SD hierarchy. Since these are ion⋯dipole interactions, the value is well in line with this type of interactions, having in this case an equal electrostatic and dispersive component (Fig. 10).
[TBA][1-Cl]. Given the considerable size of the TBA cation, which is three times that of the TMA cation, the dispersive contribution to cation–anion interactions starts to have a significant weight even in the first two SDs for which, although dominated by electrostatics, the dispersive component reaches a third of the electrostatic one (for comparison in [TMA][1-Cl] the dispersive component does not exceed 12%). In the first three structural determinants there are also notable cation⋯π interactions, which are the main forces directing the packing together with the aspecific ionic interactions (Fig. 11).

A view of the whole picture of interactions can be appreciated by looking at Fig. 12 where all energetic contributions are plotted against the cations volume (Å3).


image file: d5dt01115a-f12.tif
Fig. 12 Plot of the energy contribution for each term (electrostatic, polarization, dispersion and repulsion) based on SDs for all complexes against the cation volume. Energies are normalized relative to those related to the largest cation (TBA) and averaged over the two highest SDs.

Energies are normalized relatively to those related to the largest cation in the series (and averaged over the two main SDs). The electrostatic contribution slightly diminishes in the series, following an increase of the cation size. Conversely, dispersion interactions increase. The same trend is observed for the repulsion interactions, which however contribute positively (stabilizing) to the assembly. Polarization forces instead have less marked changes and a more complex trend, with an initial decrease, and a subsequent increase for the TBA cation. This can be probably explained by the fact that polarizability increases for bigger cations but, at the same time, a more diffuse charge is less polarizing.

As for [TMA][2-Cl], the six most relevant SDs are shown in Fig. 13 (see also Table S7†).


image file: d5dt01115a-f13.tif
Fig. 13 Supramolecular hierarchy of the six most stabilizing interactions in [TMA][2-Cl] as obtained using CrystalExplorer. Cyan lines represent short intermolecular contacts below the sum of the van der Waals radii of the respective atoms. Hydrogen atoms involved in short contact interactions are represented as isotropic spheres. Color chart: grey = C, white = H, violet = N, red = O, green = Cl, and light blue = U.

As easily discernible by looking at the lower stabilization energies (average 350 vs. 420 kJ mol−1), at the type of interactions (mainly CHalk⋯O, or CHalk⋯Cl) and at the fact that relevant SDs are four and all of very similar stability (in the 321–378 kJ mol−1 range), it can be reasonably proposed that, in this case, the contribution of cation–π interactions is definitely less relevant compared to that in [TMA][1-Cl]. Although the electrostatic contribution of the main SDs is reduced by ca. 15% compared to that in the analogous [TMA][1-Cl], the polarization and dispersion forces are more significantly lessened (by 35–40%). The ESP of [TMA][2-Cl] in Fig. S3† is similar to that of [TMA][1-Cl].

These considerations are also in line with solution studies where the association constants in CDCl3 were measured and found to be significantly smaller for 2 than for 1, of a factor of ca. 10, and of ca. 4 with [TMA]Cl and [TBA]Cl, respectively.11

IRI surface representations

As previously noted, despite the wide interest in the complexation of uranyl(VI) ion,47,48 and the importance of salophen–UO2 complexes, the role of cation⋯π interactions in these large systems was never fully established by computation. Sherrill recently reviewed and summarized the status of the computations on cation⋯π interactions,49 and found that (together with electrostatics and dispersion) the polarization contribution has a sizeable role in the whole interaction energy balance, especially in off-axis interactions, based on highly accurate Na+⋯benzene SAPT calculations.50 Interestingly, although performed at a slightly lower level of theory as imposed by the significantly larger systems investigated, our data too bring about the importance of polarization contributions, as indicated, for example, by the first two SDs of each structure (Tables S2–S5 in the ESI†). Moreover, our analysis points towards the fact that, by increasing the size of the cation, dispersive interactions increase as well. As these dispersive interactions occur between the cation and the π-cloud of the aromatic rings and cannot be interpreted in terms of short contacts, we performed the IRI analysis and present here the results which show how pervasive this phenomenon is (Fig. 14).
image file: d5dt01115a-f14.tif
Fig. 14 Isosurface maps of IRI = 1 for all structures computed from crystallographic coordinates. Blue regions are associated with covalent or coordination bonds, green regions with dispersive interactions and red regions with repulsive interactions. Color chart: H = white, C = grey, N = violet, O = red, Cl = lime, U = light blue.

Indeed, by looking at the snapshots of the IRI isosurfaces of [TMA][1-Cl] and [TBA][1-Cl] structures, some unambiguous observations can be made. First of all, dispersive interactions are ubiquitous, involving areas between the anions and cations which are not directly involved in short contacts: for example, the TMA cation shows interactions with the entire γ ring, and not with only one C atom of that ring as the geometrical analysis seems to indicate. Secondly, while the smaller TMA cation interacts only with one ring, the bigger TBA cation interacts with all the rings, except for the α ring. This is a clear sign of the increase of the cation⋯π interactions in the series [TMA][1-Cl] → [TBA][1-Cl]. The [DMDPA][1-Cl] and the [DMDBA][1-Cl] represent intermediate cases interacting with two and three rings respectively, and ideally collocate between the smallest and the largest cation. As far as [TMA][2-Cl] is concerned, the IRI results supports the view of TMA interacting with two rings (β and ε, Scheme 1), however, the isosurface associated with vdW interactions is very small compared to that of [TMA][1-Cl], again highlighting a lesser role of these interactions in the smaller host 2 compared to 1 which has two additional, and suitably positioned, aromatic rings.

The salophen–UO2 unit and its fifth equatorial coordination site

Finally, a more detailed computational study focusing on the salophen–UO2 unit in its neutral form, 1, was carried out. Also, its complexes with MeCN, a neutral molecule, and with chloride anion (the [(1-Cl)]− unit), as found in the four crystal structures described above, were taken into consideration. These findings were then compared with the results obtained for the bare UO22+ dication. The aim of this analysis was to elucidate how the uranyl unit is affected by the presence of the salophen ligand and in turn, how 1 responds to an extra ligand, neutral or charged, placed at the available fifth equatorial coordination site, and completing the pentagonal bipyramidal coordination geometry commonly observed in these systems. In this respect, the B3LYP functional was found to be especially suitable.51 The results of our findings, which are based in this section on geometrically optimized structures as described in the computational details above, and which gather both a vibrational frequency analysis and a QTAIM analysis,52–55 are summarized in Table 1.
Table 1 Vibrational frequency analysis and QTAIM analysis for the complexed and uncomplexed salophen–UO2 unit 1 as compared to UO22+
  UO22+ 1 [1-MeCN] [1-Cl]−
Stret. symm. 1016.45 cm−1 851.29 cm−1 848.47 cm−1 844.48 cm−1
Stret. asymm. 1096.04 cm−1 928.33 cm−1 924.02 cm−1 921.15 cm−1
U–Oyl bond length 1.682 Å 1.756 Å 1.758 Å 1.759 Å
ρ (at BCP U–Oyl) 0.389 au 0.321 au 0.320 au 0.319 au
ρ (at BCP U–Nsalo) NA 0.053 au 0.046 au 0.037 au
ρ (at BCP U–Osalo) NA 0.090 au 0.085 au 0.074 au
H (at BCP U–Oyl) −0.912 au −0.649 au −0.602 au −0.587 au
H (at BCP U–Nsalo) NA −0.116 au −0.108 au −0.099 au
H (at BCP U–Osalo) NA −0.048 au −0.042 au −0.039 au
Binding energies — — 13.37 kcal mol−1 45.43 kcal mol−1

The [(1-Cl)]− unit has been previously studied both experimentally and computationally,56 and our computed results are in excellent agreement with the experimental data for the symmetric and asymmetric O[double bond, length as m-dash]U[double bond, length as m-dash]O stretching. The agreement between our theoretical data and their experimental data is in fact far better compared to their theoretical/experimental data. This is due to the higher level of the calculations used in this work. The computed binding energy also agrees (within 5%) with the previously calculated result.56 The theoretical results which we obtained for the symmetric and asymmetric O[double bond, length as m-dash]U[double bond, length as m-dash]O stretching in the neutral [1-MeCN] system, also compares very well with the experimental results for similar salen complexes.57

Several interesting facts can be readily deduced from the data. The most important one is that the chemical environment at the uranyl core greatly affects the wavenumber of certain vibrational modes. As far as the U–O(yl) bond lengths in Table 1 are concerned, the value of the electron density ρ and energy density H at the bond critical points (BCP) decreases proportionally to the red shift observed for the U–O(yl) symmetric and asymmetric stretching in the vibrational spectra (R2 = 0.99, Table 1). Such a decrease in ρ would suggest a weakening of the bond due to the introduction of the salophen tetradentate ligand first, forming the complex 1, and then by the coordination with MeCN and Cl− anion to 1. The U electron density from the U–O(yl) bond is thus partially transferred to the ligands, a fact that is also reflected in the increase of the U–O(yl) bond length in the UO22+ → [(1-Cl)]− anion series. This effect is the axial equatorial π-competition,58 where a fraction of the electronic density is transferred from the axial bonding region towards both the uranyl oxygen atoms and the equatorial bonding region, effectively weakening the U–O(yl) bond. Our data are in excellent agreement with those that Kerridge et al. obtained on smaller UO22+ systems having 4–6 identical ligands.59 Furthermore, we noted a decrease in the values of ρ at the U–Nsal and U–Osal BCPs, which is a clear indication of electron density transfer from the salophen ligand to the ligand in the fifth equatorial site which gives rise to the pentagonal bipyramidal complexes.

Conclusions

In this study, we investigated the supramolecular assembly made of uranyl–salophen receptors 1 and 2 complexed with tetraalkylammonium chloride salts of different cation sizes, focusing on the hierarchy of intermolecular forces responsible for their structures observed in the solid state. By utilizing both experimental and newly developed computational methodologies which include ultrahigh level calculations, we highlighted the significant role of cation–π interactions within these systems. Our findings indicate that cation–π interactions are the primary specific interactions among the intermolecular forces at play, becoming increasingly important as the size of the cation grows from tetramethylammonium (TMA) to tetrabutylammonium (TBA). Through single-crystal X-ray diffraction (SC-XRD) and Hirshfeld surface analyses, we provided detailed insights into the geometric and interaction patterns of the complexes and recognized how the size of the cation shapes the overall assembly. Indeed, salophen units are found to wrap around ionic quadruplexes or octaplexes (viz., two or four ion pairs) or simply form a stacked columnar arrangement. The computational analyses, employing density functional theory (DFT) and the energy decomposition method, further supported these observations by quantifying the interaction energies and decomposing them into their electrostatic, polarization, dispersive, and repulsive components. Our results demonstrated that as the size of the quaternary ammonium cation increases, the dispersive interactions become more pronounced, a trend that is also reflected in the IRI surface representations. The repulsion term also behaves similarly. For the electrostatic contribution, a direct comparison between receptors 1 and 2 was possible in the case of [TMA]Cl and it reinforces the role of the pendant sidearms in establishing cation–π interactions, with an interesting parallel with what was demonstrated from previous investigations in solution. This study not only enhances our understanding of UO2-based supramolecular receptors for ion-pairs but also sets the stage for future explorations into cation–π interactions in larger and more complex supramolecular systems. It also highlights the importance of combining crystallographic data with computational tools to dissect and understand the forces driving the assembly of supramolecular architectures. Given the interest in the coordination of actinides and in the development of new materials with specific binding properties, the knowledge gained here also contributes to the broader field of ion recognition and its applications.

Conflicts of interest

There are no conflicts to declare.

Data availability

Data are available in the ESI.†

Acknowledgements

All authors thank Dr Laura Ilander for the crystallization studies which yielded [DMDPA][1-Cl] and [DMDBA][1-Cl]. M. S. thanks CINECA (Project BIFROST) for computational resources and Dr Ciro A. Guido for reading the manuscript.

References

  1. J. L. Sessler, P. J. Melfi and G. D. Pantos, Coord. Chem. Rev., 2006, 250, 816 Search PubMed .
  2. L. Leoni and A. Dalla Cort, Inorganics, 2018, 6, 42,  DOI:10.3390/inorganics6020042 .
  3. K. Takao and Y. Ikeda, Inorg. Chem., 2007, 46, 1550–1562 Search PubMed .
  4. A. Valkonen, G. Lombardo, K. Rissanen, F. Punzo and M. Cametti, Dalton Trans., 2017, 46, 5240–5249 Search PubMed .
  5. A. Dalla Cort, L. Mandolini, G. Palmieri, C. Pasquini and L. Schiaffino, Chem. Commun., 2003, 2178–2179 Search PubMed .
  6. A. R. van Doorn, M. Bos, S. Harkema, J. van Eerden, W. Verboom and D. N. Reinhoudt, J. Org. Chem., 1991, 56, 2371 Search PubMed .
  7. M. M. G. Antonisse and D. N. Reinhoudt, Chem. Commun., 1998, 443–448 Search PubMed .
  8. M. Cametti, A. Dalla Cort, L. Mandolini, M. Nissinen and K. Rissanen, New J. Chem., 2008, 32, 1113–1116 Search PubMed .
  9. M. Cametti, Y. Sakata, J. Martí-Rujas and S. Akine, Inorg. Chem., 2019, 58(21), 14871–14875 Search PubMed .
  10. M. Cametti, M. Nissinen, A. Dalla Cort, L. Mandolini and K. Rissanen, J. Am. Chem. Soc., 2005, 127, 3831–3837 Search PubMed .
  11. M. Cametti, M. Nissinen, A. Dalla Cort, L. Mandolini and K. Rissanen, J. Am. Chem. Soc., 2007, 129, 3641–3648 Search PubMed .
  12. M. Cametti, L. Ilander, A. Valkonen, M. Nieger, M. Nissinen, E. Nauha and K. Rissanen, Inorg. Chem., 2010, 49(24), 11473–11484 Search PubMed .
  13. J. C. Ma and D. A. Dougherty, Chem. Rev., 1997, 97, 1303–1324 Search PubMed .
  14. N. Kumar, N. S. Gaur and G. N. Sastry, J. Chem. Sci., 2021, 133, 97 Search PubMed .
  15. A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2013, 113(3), 2100–2138 Search PubMed .
  16. W. Z. Sun, L. L. Dai, X. H. Kong, Y. Mao, Z. L. Wu, L. F. Liao, X. L. Xiao and C. M. Nie, Appl. Organomet. Chem., 2020, 34, e5486 Search PubMed .
  17. W. B. Lan, X. F. Wang, L. P. He, Y. B. Meng, J. Li, B. Qiu and C. M. Nie, Appl. Organomet. Chem., 2018, 32, e4137 Search PubMed .
  18. B. E. Klamm, C. J. Windorff, C. Celis-Barros, M. L. Marsh and T. E. Albrecht-Schmitt, Inorg. Chem., 2020, 59, 23 Search PubMed .
  19. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 Search PubMed .
  20. J. Ropponen, M. Lahtinen, S. Busi, M. Nissinen, E. Kolehmainen and K. Rissanen, New J. Chem., 2004, 28, 1426 Search PubMed .
  21. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed .
  22. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 Search PubMed .
  23. F. Jensen, J. Chem. Theory Comput., 2014, 10, 1074–1085 Search PubMed .
  24. W. Küchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535 Search PubMed .
  25. K. A. Peterson, J. Chem. Phys., 2015, 142, 074105 Search PubMed .
  26. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 Search PubMed .
  27. B. A. Hess, Phys. Rev. A, 1986, 33(6), 3742–3748 Search PubMed .
  28. N. Kaltsoyannis, Chem. Soc. Rev., 2003, 32, 9–16 Search PubMed .
  29. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 Search PubMed .
  30. I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887 Search PubMed .
  31. T. Lu and Q. Chen, Chem.:Methods, 2021, 1, 231–239 Search PubMed .
  32. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 Search PubMed .
  33. T. A. Keith, AIMAll (Version 11.05.16), TK Gristmill Software, Overland Park KS, USA, 2011, https://aim.tkgristmill.com Search PubMed .
  34. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 Search PubMed .
  35. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 Search PubMed .
  36. A. Gavezzotti, New J. Chem., 2016, 40, 6848–6853 Search PubMed .
  37. P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011 Search PubMed .
  38. M. J. Turner, S. Grabowsky, D. Jayatilaka and M. A. Spackman, J. Phys. Chem. Lett., 2014, 5, 4249–4255 Search PubMed .
  39. F. H. Allen and I. Bruno, Acta Crystallogr., Sect. B:Struct. Sci., 2010, 66, 380–386 Search PubMed .
  40. M. Saccone, S. Riebe, J. Stelzer, C. Wölper, C. G. Daniliuc, J. Voskuhl and M. Giese, CrystEngComm, 2019, 21, 3097–3105 Search PubMed .
  41. F. Malotke, M. Saccone, C. Wölper, R. Y. Dong, C. A. Michal and M. Giese, Mol. Syst. Des. Eng., 2020, 5, 1299–1306 Search PubMed .
  42. T. H. Rehm and C. Schmuck, Chem. Soc. Rev., 2010, 39, 3597–3611 Search PubMed .
  43. A. Gavezzotti, Acta Crystallogr., Sect. B:Struct. Sci., 2010, 66, 396–406 Search PubMed .
  44. Volumes of the cations are: 122 Å3 for TMA, 254 Å3 for DPDMA, 279 Å3 for DBDMA and 380 Å3 for TBA, respectively (see computational details).
  45. C. Jelsch, K. Ejsmont and L. Huder, IUCrJ, 2014, 1, 119–128 Search PubMed .
  46. S. S. Hasanova, E. A. Yolchueva, A. Q. Mashadi, S. Muhammad, M. Ashfaq, M. E. Muhammed, K. S. Munawar, M. N. Tahir, A. G. Al-Sehemi and S. S. Alarfaji, ACS Omega, 2023, 8, 8530–8540 Search PubMed .
  47. A. C. Sather, O. B. Berryman and J. Rebek, J. Am. Chem. Soc., 2010, 132(39), 13572–13574 Search PubMed .
  48. D. M. T. Eralie, J. Ducilon and A. E. V. Gorden, Inorg. Chem., 2025, 64(2), 767–784 Search PubMed .
  49. C. D. Sherrill, Acc. Chem. Res., 2013, 46, 1020–1028 Search PubMed .
  50. M. S. Marshall, R. P. Steele, K. S. Thanthiriwatte and C. D. Sherrill, J. Phys. Chem. A, 2009, 113, 13628–13632 Search PubMed .
  51. V. Vallet, U. Wahlgren and I. Grenthe, J. Phys. Chem. A, 2012, 116, 12373–12380 Search PubMed .
  52. P. Dey, A. Hossain and S. K. Seth, J. Mol. Struct., 2024, 1295(P2), 136642 Search PubMed .
  53. S. Islam, P. Dey and S. K. Seth, Polyhedron, 2023, 242, 116514 Search PubMed .
  54. P. Dey, S. Islam and S. K. Seth, J. Mol. Struct., 2023, 1284, 135448 Search PubMed .
  55. O. Sarkar, M. Roy, N. R. Pramanik, P. Dey, S. K. Seth, M. G. Drew and S. Chakrabarti, J. Mol. Struct., 2024, 1301, 137125 Search PubMed .
  56. E. Bodo, A. Ciavardini, A. Dalla Cort, I. Giannicchi, F. Y. Mihan, S. Fornarini, S. Vasile, D. Scuderi and S. Piccirillo, Chem. – Eur. J., 2014, 20, 11783–11792 Search PubMed .
  57. E. M. Nour, A. A. Taha and I. S. Alnaimi, Inorg. Chim. Acta, 1988, 141, 139–144 Search PubMed .
  58. S. Fortier and T. W. Hayton, Coord. Chem. Rev., 2010, 254, 197–214 Search PubMed .
  59. P. Di Pietro and A. Kerridge, Inorg. Chem., 2016, 55, 573–583 Search PubMed .

Footnote

† Electronic supplementary information (ESI) available. CCDC 2390012 and 2390013. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5dt01115a
This journal is © The Royal Society of Chemistry 2025
Click here to see how this site uses Cookies. View our privacy policy here.