Unconventional S-orbital state of Tb and cooperative Ru(4d)–Tb(4f) spin-ordering in the strongly correlated 4d–4f system Ba₃TbRu₂O₉†

E. Kushwaha ^a, G. Roy ^a, A. M. dos Santos ^b, M. Kumar ^a, S. Ghosh ^a, T. Heitmann ^c and T. Basu *^a
aDepartment of Sciences and Humanities, Rajiv Gandhi Institute of Petroleum Technology, Jais, Amethi, 229304, Uttar Pradesh 229305, India. E-mail: tathamay.basu@rgipt.ac.in
^bNeutron Scattering Division, Oak Ridge National Lab, Oak Ridge, TN 37831, USA
^cThe Missouri Research Reactor, University of Missouri, Columbia, Missouri 65211, USA

First published on 12th June 2025

---

---

1. Introduction

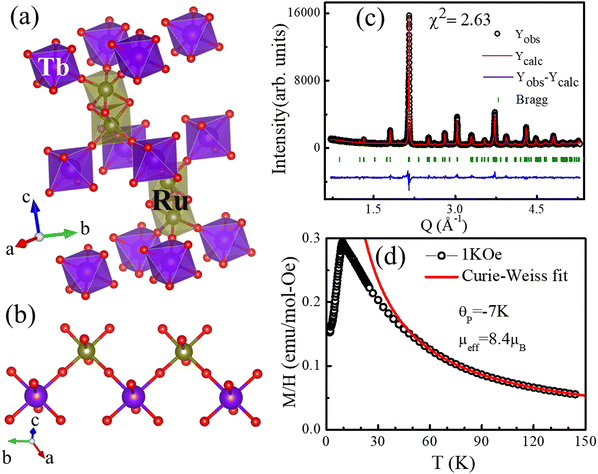
The 6H-perovskite system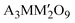 (where A = Ca, Sr, or Ba; M = Li, Bi, a 3d-transition metal, or a lanthanide metal ion (Ln); M′ = a 4d/5d-transition metal ion) exhibits a variety of exotic magnetic ground states arising from strong metal–metal (M–M′) electronic correlations and high magnetic frustration, leading to various quantum phenomena, such as quantum spin liquid behavior, molecular-type magnetism or spin-driven ferroelectricity.^1–8 The Ba₃LnRu₂O₉ system has attracted significant attention owing to strong Ru(4d)–Ln(4f) interactions, strong spin–orbit coupling (SOC), the large crystal electric field (CEF) of Ru (4d)-orbitals, and rare-earth anisotropy.^9–12 In such 6H perovskite systems, Ru₂O₉ dimers, consisting of two face-sharing distorted RuO₆-octahedra, are connected through corner-sharing regular LnO₆ octahedra (Fig. 1a and b). For non-magnetic lanthanide ions (Ln = Y, La, Eu, or Lu), the compound behaves like a magnetic dimer, exhibiting a broad hump in temperature-dependent magnetic susceptibility.^3,10 Conversely, the presence of a magnetic rare-earth metal introduces long-range magnetic ordering. Interestingly, the Nd member of this family shows ferromagnetic (FM) ordering at 24 K, which is in sharp contrast to other rare earth elements (Sm, Gd, Tb, Ho, Dy, and Er) that exhibit long-range antiferromagnetic (AFM) ordering at 9–12 K.^4,5,11–14 Recently, systems with heavy rare-earth elements (R = Ho and Tb) were characterized as magnetodielectric and showed potential as hosts of multiferroicity.^4,11 This intriguing magnetism and spin-driven ferroelectricity are well established in Ba₃HoRu₂O₉.⁶

It is clear that lanthanide ions play a decisive role in establishing the magnetic ground state of this family. The lanthanide contraction across the series modifies Ln–O–Ru bond angles and Ru–Ru distances, which in turn influence magnetic exchange interactions. For example, in Ba₃YRu₂O₉, ruthenium exhibits an S = 1/2 ground state owing to strong metal–metal bonding.³ Replacing yttrium with the larger lanthanum modifies the Ru–Ru distance, which results in an S = 3/2 orbital-selective Mott ground state for Ba₃LaRu₂O₉, arising from different degrees of Ru–Ru hybridization.¹⁰ Conversely, for Ba₃NdRu₂O₉, the 4f orbital of Nd is less localized and closer to the Fermi level than those of other heavy rare-earth ions in this family. This might result in the unique observation of the ferromagnetic ordering of the Nd members.^11,12 In most d–f correlated systems, the d-orbital ions are magnetically ordered at high temperatures because of their extended bonding character, whereas the more shielded, f-orbitals are magnetically ordered at lower temperatures. In contrast with this observation, cooperative Ru(4d)–Ho(4f) spin ordering was already observed in Ba₃HoRu₂O₉ at temperatures below 50 K.⁵ Furthermore, a reduced Ru moment compared with its spin-only (S = 2) value was observed for the Nd and Ho members in this series.^5,12 The exact ruthenium moment and nature of its ground state are also ambiguous in other R-members of this family. This overview highlights how the magnetic ground states of Ru and R ions vary significantly across the lanthanide series. In these oxides, the magnetic rare-earth ions are trivalent (R³⁺) such that the Ru₂O₉ dimers have mixed valence Ru⁴⁺/Ru⁵⁺ states. The only exceptions are for Ba₃CeRu₂O₉ and Ba₃TbRu₂O₉, in which Ce/Tb can adopt a tetravalent (Ce⁴⁺/Tb⁴⁺) configuration, resulting in a single valence Ru⁴⁺ state. A recent neutron scattering experiment confirmed that Ce⁴⁺ has a non-magnetic ground state and that Ru does not magnetically order down to 2 K.¹⁵ An earlier study on Ba₃TbRu₂O₉ reported long-range AFM ordering at 9.5 K, suggesting the magnetic ordering of the Tb moment but with no contribution ascribed to ruthenium.¹⁴ Therefore, a detailed magnetic structure describing both the Tb and Ru ground states remains absent from the literature.

The ruthenium ground state often varies significantly due to small changes in the environment (such as hybridization and lattice distortions), resulting from the competition between the crystal field effect and spin–orbit coupling. For example, in the Ba₄Ru₃O₁₀, which consists of Ru₃O₁₀ trimers, the central Ru⁴⁺ ion exhibits a non-magnetic ground state (S = 0), whereas the ground state of the edge Ru⁴⁺ ions in the trimer is magnetic (S ≠ 0).¹⁶ It has also been demonstrated that different RuO₆ octahedral distortions, even in the same structure, play a significant role in determining the magnetic ground state, yielding an intriguing magnetic structure in the same family.^16,17 The role of R-ions in local MO₆ octahedral distortion and complex magnetism has also been documented in many 3d–4f systems, for example, in canonical RMnO₃ perovskites.¹⁸ Thus, an understanding of the ground states of Ru and Tb and the 4d–4f correlation in the Ba₃TbRu₂O₉ compound is essential for understanding the consequences of the subtle interplay of the lattice-orbital-magnetic degrees of freedom in these compounds.

In this study, we performed a detailed time-of-flight neutron diffraction experiment over a wide momentum transfer (Q_min < 1 Å⁻¹), which allowed us to resolve the spin structure and magnetic ground state of both Tb and Ru. The results reveal that in Ba₃TbRu₂O₉, an unconventional spin-only ground state emerges, with Tb (orbital moment L = 0, J = S = 7/2) and spin-only moment of Ru (S = 2, L = 0).

2. Experimental details

The compound Ba₃TbRu₂O₉ was synthesized by solid-state reaction using mixtures of high-purity (>99.9%) precursors: BaCO₃, RuO₂, and Tb₄O₇, which were mixed thoroughly using an agate mortar and pestle. The homogenized mixture was then pressed into pellets and subjected to a series of calcination steps. The initial firing was carried out at 900 °C for 12 h, followed by successive heating at 1100 °C for 48 h, 1150 °C for 24 h, and a final sintering at 1180 °C for 12 h. After each heating cycle, the pellets were reground and repalletized to ensure homogeneity.¹⁴ To check the phase purity of the powder, X-ray diffraction was carried out using a Panalytical diffractometer fitted with a Cu-Kα source. Magnetization measurements were performed as a function of temperature and magnetic field using a Quantum Design Superconducting Quantum Interference Device (SQUID, Quantum Design). Time-of-flight (TOF) neutron diffraction data were collected at the SNAP beamline using a diffractometer at the Spallation Neutron Source (SNS) in Oak Ridge National Laboratory (ORNL), USA. The magnetic structure was determined using the FULLPROF and SARAH programs.^19,20 X-ray Photoelectron Spectroscopy (XPS) measurements were carried out using a Thermo Fisher Scientific K-Alpha spectrometer equipped with a monochromatic Al Kα source (1486.6 eV, 10 kV, 10 mA). Scanning Electron Microscopy (SEM) imaging was conducted using a JEOL JXA-8230 electron probe microanalyzer operated at an accelerating voltage of 20 kV. High-resolution, high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) was performed on a JEM-ARM200F instrument operating at 200 kV. For sample preparation, a small amount of finely ground powder was dispersed in ethanol using ultrasonication for uniform mixing. A drop of the resulting suspension was then deposited onto a carbon-coated copper grid and allowed to dry at room temperature before imaging.

3. Results and discussion

3.1. Structural analysis and magnetic susceptibility measurements

The Rietveld refinement of the X-ray diffraction pattern is shown in Fig. 1c, confirming the purity of the sample. A representation of the crystal structure obtained from the Rietveld refinement and the Tb–O–Ru–O–Tb super-exchange paths is shown in Fig. 1a and b. The Ru–Ru distance and Ru–O–Ru angle within the dimers are 2.56 Å and 79.26°, respectively, indicating that the short Ru–Ru direct exchange interaction and the Ru–O–Ru super-exchange interactions are competing within the Ru₂O₉ dimers. However, these dimers are magnetically connected via terbium. The Ru–O–Tb angle is 179.180°, implying a stronger AFM super-exchange path, over the Ru–O–Ru exchange interaction. Therefore, the Ru–O–Tb–O–Ru super-exchange path is responsible for the magnetic ordering.

To confirm the elemental composition and homogeneous distribution of constituent elements in the Ba₃TbRu₂O₉ powder sample, we performed scanning electron microscopy (SEM) with energy-dispersive X-ray spectroscopy (EDS) and high-resolution high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM). The SEM-EDS and HAADF-STEM images are shown in Fig. S1–S3 in the ESI.† The SEM-EDS and HAADF-STEM elemental maps confirm a uniform spatial distribution of Ba, Ru, Tb, and O across the sample, confirming the homogeneity of the sample. The EDS results show that the atomic percentage ratio for Ba:Tb:Ru:O is 22.0:7.2:15.5:60.6 (≈3.1:1:2.1:8.4), which agrees with the stoichiometry of the compound within the resolution limit of the instrument.

The temperature-dependent magnetic susceptibility under a 1 kOe magnetic field under zero-field-cooled conditions is shown in Fig. 1d. The results revealed antiferromagnetic (AFM) ordering below 9.5 K (T_N), consistent with an earlier report.¹⁴ The Curie–Weiss fitting in the paramagnetic region yielded an effective moment (μ_eff) of 8.4 μ_B. This low value of μ_eff is not consistent with Tb³⁺ (effective quantum number J = 6, μ_eff ∼ 9.72 μ_B). Terbium adopts a Tb⁴⁺ valence with a spin configuration of S = 7/2 and L = 0 for a half-filled shell. This result is consistent with the theoretical value of 7.94 μ_B for S = 7/2. The experimentally calculated effective magnetic moment per Ru atom was approximately 1.94 μ_B based on the following relation:

μeff2 = μTb2 + 2μRu2

To determine the oxidation states of Tb and Ru, XPS was performed on the sample (shown in Fig. S4, ESI†). The binding values of Tb 4d_5/2 are 150.3 eV and 4d_3/2 are 157.8 eV and for Ru 3p_3/2 is 461.7 eV and 3p_1/2 is 484.2 eV, which are close to the values reported in the literature.^21,22 However, it should be noted that the binding energy difference between the two oxidation states of Ru-atoms is only nearly 1 eV, and such a small difference may also arise for the same oxidation state in different crystallographic environments.^23,24 However, if the valence state is a mixture of +4 and +5, we would observe two separate nearby peaks or a very broad peak, whereas here we observe a single peak due to a single valence state, as similarly observed in the literature.^21–24

3.2. Time-of-flight neutron diffraction and magnetic structure

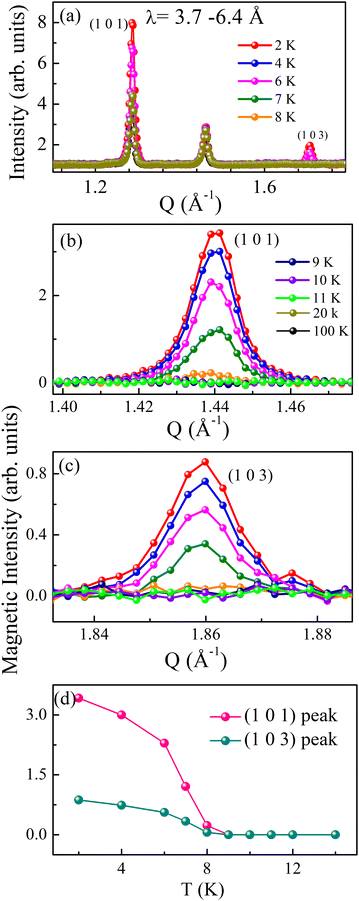
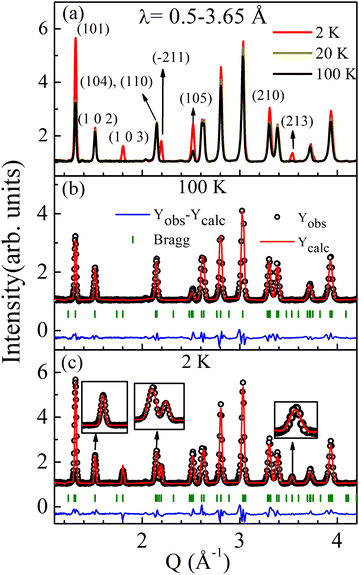
To determine the magnetic structure, we performed temperature-dependent (2, 4, 6, 7, 8, 9, 10, 12, 14, 16, 20, 50, and 100 K) time-of-flight neutron diffraction (ND) measurements and collected data over a wavelength band covering 3.7–6.5 Å, corresponding to a momentum transfer coverage between 1 Å⁻¹ and 2 Å⁻¹ (shown in Fig. 2a). A significant enhancement of the intensity of the (101) and (103) Bragg peaks (at Q = 1.44 Å⁻¹ and 1.86 Å⁻¹ respectively) is observed below T_N. No change in diffraction intensity was observed above T_N. The magnetic reflections of both the Bragg peaks ((101) and (103)) at various temperatures are shown in Fig. 2b and c. The magnetic intensities were calculated by subtracting the data collected at 2–11 K from the 100 K data, which contains the purely nuclear contribution. The temperature dependence of the integrated magnetic intensity is shown in Fig. 2d, which represents the magnetic order parameter. The magnetic intensity increased as the temperature decreased below T_N due to the typical saturation of magnetic moments with decreasing temperature. We did not observe any additional magnetic Bragg reflections at low temperatures within this Q-range. Therefore, we further performed the experiments over a broader Q-range (for wavelength range 0.5–3.65 Å) at a few selected temperatures (100, 50, 20, and 2 K). Interestingly, the 2 K diffraction profile shows a few extra peak intensities at Q = 1.44, 1.86, 2.19, 2.52, 3.30 and 3.53 Å⁻¹ corresponding to reflections (101), (103), (211), (105), (213) and (210) respectively, compared to the high-temperature diffraction profile above T_N, shown in Fig. 3a.

The neutron diffraction profile measured at 100 K in the paramagnetic region was well-fitted to the reported space group P6₃/mmc, confirming the phase purity of the sample (see Fig. 3b). The additional magnetic reflections can be indexed using the propagation vector k = (0 0 0).

The Wyckoff positions of the magnetic Tb and Ru ions were 2a (0, 0, 0) and 4f (0.33333, 0.66667, 0.16223), respectively. To evaluate the possible magnetic structures consistent with crystallographic symmetry, we performed irreducible representational analysis using the SARAh program.¹⁹ The resulting irreducible representations (IRs) and basis vectors (BVs) for the Ru and Tb sites are presented in Tables S1 and S2 (ESI†). There are four irreducible representations for Tb and eight for Ru. The magnetic representation is given by

Γmag(Tb) = 1Γ13 + 1Γ17 + 1Γ29 + 1Γ211

Γmag(Ru) = 1Γ12 + 1Γ13 + 1Γ16 + 1Γ17 + 1Γ29 + 1Γ210 + 1Γ211 + 1Γ212

Since neutrons interact with the magnetic moment component perpendicular to the momentum transfer (Q), the significant difference in intensity of the (1 0 1), (1 0 3), (1 0 4), (1 1 0), (1 0 5), (2 1 0) Bragg peaks between 2 K and 100 K suggests that the magnetic moment should have a dominant contribution along the b-axis. However, the presence of strong magnetic reflection for (2 1 0) and (−2 1 1) indicates that there should be a magnetic component along the c-axis.

We could not achieve a suitable refined structure considering Γ₂, Γ₆, Γ₁₀ and, Γ₁₂, ruling out the possibility of a non-magnetic terbium (because, only ruthenium contributes to these particular basis vectors, obtained from SARAh analysis). We attempted to fit the data using Γ₃, Γ₇, Γ₉ and Γ₁₁, where both Tb and Ru moments contribute. For terbium, Γ₉(Ψ₅) and Γ₁₁(Ψ₅) have a magnetic moment in the b-plane, Γ₉(Ψ₄) and Γ₁₁(Ψ₆) have a magnetic moment in the ab-plane and Γ₃(Ψ₁) and Γ₇(Ψ₂) have a magnetic moment in the c-axis (Table S1, ESI†). For ruthenium, Γ₉(Ψ₅) and Γ₁₁(Ψ₉) have magnetic moment along the b-axis, Γ₉(Ψ₆) and Γ₁₁(Ψ₁₀) have a magnetic moment in ab-plane and Γ₃(Ψ₂) and Γ₇(Ψ₄) have a magnetic moment in the c-axis (Table S2, ESI†). The best fit to the data was achieved using a combination of Γ₁₁(Ψ₅) for Ru and Γ₇(Ψ₂), Γ₁₁(Ψ₅) for Tb. The corresponding Shubnikov space group, which is the magnetic space group of the paramagnetic space group P6₃/mmc with k = (0, 0, 0), is .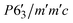

The Rietveld refinement of the 2 K data is shown in Fig. 3c. An enlarged view of the selected nuclear and magnetic peaks is shown in the insets of Fig. 3c and Fig. S5 of ESI.† The fittings parameters are: χ² = 9.8, R_p = 2.87, R_wp = 4.27, R_exp = 1.11, and the magnetic R-factor, R_mag = 5.14, which indicates good fitting of the data. The magnetic structure obtained by this refinement is shown in Fig. 4a.

The results reveal that the Ru moments are ordered along the b-direction with a magnetic moment of 1.96 μ_B, and the Tb moments are ordered in the bc-plane (small canting of 15.9° with c-axis) with a magnetic moment of 6.18 μ_B. The moments associated with terbium and ruthenium are listed in Table S3 in ESI.† The fit of the magnetic structure was further checked by setting the Ru moment to zero and refining the Tb moments, thereby allowing it to achieve its maximum value; this, however, does not result in a good fit. The refined magnetic structure results in terbium with 6.18 ± (0.04) μ_B (close to S = 7/2) and a spin-only moment of ruthenium (S = 1).

In most of the d–f coupled systems, the transition metal ion is first ordered at higher temperatures, followed by rare-earth ordering at lower temperatures.^25–30 Interestingly, we observed the rare cooperative ordering of Ru(4d) and Tb(4f) moments below T_N, which is attributed to strong 4d–4f coupling in this system.

The Ru-moments are collinearly arranged antiferromagnetically along the b-axis of the title compound (Fig. 4a). For the Ba₃HoRu₂O₉ compound, the ruthenium network exhibits a canted AFM spin-structure within the Ru₂O₉ dimers below magnetic ordering.⁵ The Ru spins are ferromagnetically arranged within Ru₂O₉ dimers for Nd-members, and the ferromagnetic dimers are antiferromagnetically arranged.¹² The strong spin–orbit coupling and strong 4d–4f correlation are reported for the heavy-rare-earth member Ba₃HoRu₂O₉. Surprisingly, being a heavy rare-earth member, Tb possesses an S = 7/2 ground state (f⁷) with zero orbital moments, adopting an unusual +4 valence state, which is characterized as an s-state, more commonly observed for Gd³⁺ ions, which have f⁷ electronic configurations.

Tb possesses a +4 valence state, contrary to the usual +3 valence state of R-ions in this whole family. Most likely, the energy is minimized by adopting a spin configuration similar to the related Gd³⁺. The spin configurations of the Tb and Ru spins are shown in Fig. 4b and c, respectively.

The slightly smaller value of the refined Tb moment compared to its theoretical spin-only value of 7/2 could be due to two reasons: (i) the Landé g-factor might be slightly lower than 2 (the ideal value for a free electron's spin-only moment) in this strongly correlated electron system with complex magnetic interaction; and/or (ii) the moments may not be fully saturated even at 2 K, although this is unlikely. Interestingly, unlike other R-members in this series where a reduced Ru-moment is generally observed, our results yield an almost full moment for Ru (1.96 μ_B).^5,12 We did not observe any molecular-like magnetic state, as observed in Ba₃YRu₂O₉, or a selective-orbital state similar to Ba₃LaRu₂O₉.^3,10

4. Conclusion

In summary, we resolved the spin-structure of the Ba₃TbRu₂O₉ compound and observed a unique magnetic ground state for both terbium and ruthenium in Ba₃TbRu₂O₉, which is distinct from all other lanthanide members in this series. The 4f orbitals of Tb behave similarly to those of an s-state ion, exhibiting zero orbital moment (L = 0). Our neutron diffraction results revealed that the magnetic moment of Ru atoms was almost 2 μ_B, manifesting as an S = 1 magnetic ground state, in contrast to the reduced moment of ruthenium in all other members of this family. We also report the cooperative spin-ordering of both Ru and Tb, which is not commonly observed in d–f coupled systems.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the ESI.†

Acknowledgements

T. B. greatly acknowledges the Science and Engineering Research Board (SERB) (Project No.: SRG/2022/000044), and UGC-DAE Consortium for Scientific Research (CSR) (Project No CRS/2021-22/03/544), Government of India, and SEED Grant, RGIPT, for research funding. A portion of this research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. The beam time was allocated to the SNAP instrument on proposal number IPTS-33740.1. We acknowledge Dr Jhuma Sannigrahi, IIT Goa for the fruitful discussion. T. B. thanks the Central Instrumentation Facilities (CIF), RGIPT. M. K. thanks the University Grant Commission (UGC), India, for the research fellowship.

References

1. Y. Ishiguro, K. Kimura, S. Nakatsuji, S. Tsutsui, A. Q. Baron, T. Kimura and Y. Wakabayashi, Nat. Commun., 2013, 4, 2022 CrossRef PubMed .
2. J. Hwang, E. Choi, F. Ye, C. Dela Cruz, Y. Xin, H. Zhou and P. Schlottmann, Phys. Rev. Lett., 2012, 109, 257205 CrossRef CAS PubMed .
3. D. Ziat, A. A. Aczel, R. Sinclair, Q. Chen, H. Zhou, T. J. Williams, M. B. Stone, A. Verrier and J. Quilliam, Phys. Rev. B, 2017, 95, 184424 CrossRef .
4. T. Basu, V. Caignaert, S. Ghara, X. Ke, A. Pautrat, S. Krohns, A. Loidl and B. Raveau, Phys. Rev. Mater., 2019, 3, 114401 CrossRef CAS .
5. T. Basu, V. Caignaert, F. Damay, T. Heitmann, B. Raveau and X. Ke, Phys. Rev. B, 2020, 102, 020409 CrossRef CAS .
6. E. Kushwaha, G. Roy, M. Kumar, A. Dos Santos, S. Ghosh, D. Adroja, V. Caignaert, O. Perez, A. Pautrat and T. Basu, Phys. Rev. B, 2024, 109, 224418 CrossRef CAS .
7. S.-J. Kim, M. D. Smith, J. Darriet and H.-C. Zur Loye, J. Solid State Chem., 2004, 177, 1493–1500 CrossRef CAS .
8. W. Miiller, M. Avdeev, Q. Zhou, A. J. Studer, B. J. Kennedy, G. J. Kearley and C. D. Ling, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 220406 CrossRef .
9. S. Hayashida, H. Gretarsson, P. Puphal, M. Isobe, E. Goering, Y. Matsumoto, J. Nuss, H. Takagi, M. Hepting and B. Keimer, Phys. Rev. B, 2025, 111, 104418 CrossRef CAS .
10. Q. Chen, A. Verrier, D. Ziat, A. Clune, R. Rouane, X. Bazier Matte, G. Wang, S. Calder, K. M. Taddei and C. D. Cruz, et al. , Phys. Rev. Mater., 2020, 4, 064409 CrossRef CAS .
11. T. Basu, A. Pautrat, V. Hardy, A. Loidl and S. Krohns, Appl. Phys. Lett., 2018, 113 Search PubMed .
12. M. S. Senn, S. A. Kimber, A. M. Arevalo Lopez, A. H. Hill and J. P. Attfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 134402 CrossRef .
13. Y. Doi and Y. Hinatsu, J. Mater. Chem., 2002, 12, 1792–1795 RSC .
14. Y. Doi, M. Wakeshima, Y. Hinatsu, A. Tobo, K. Ohoyama and Y. Yamaguchi, J. Mater. Chem., 2001, 11, 3135–3140 RSC .
15. Q. Chen, S. Fan, K. M. Taddei, M. B. Stone, A. I. Kolesnikov, J. Cheng, J. L. Musfeldt, H. Zhou and A. A. Aczel, J. Am. Chem. Soc., 2019, 141, 9928–9936 CrossRef CAS PubMed .
16. J. Sannigrahi, A. Paul, A. Banerjee, D. Khalyavin, A. Hillier, K. Yokoyama, A. Bera, M. R. Lees, I. Dasgupta and S. Majumdar, et al. , Phys. Rev. B, 2021, 103, 144431 CrossRef CAS .
17. T. Basu, F. Wei, Q. Zhang, Y. Fang and X. Ke, Phys. Rev. Mater., 2020, 4, 114401 CrossRef CAS .
18. G. Maris, V. Volotchaev and T. Palstra, New J. Phys., 2004, 6, 153 CrossRef .
19. J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef .
20. A. S. Wills, Phys. B, 2000, 276, 680–681 CrossRef .
21. L. Jozwiak, J. Balcerzak and J. Tyczkowski, Catalysts, 2020, 10, 278 CrossRef CAS .
22. E. G. Sogut, H. Acidereli, E. Kuyuldar, Y. Karatas, M. Gulcan and F. Sen, Sci. Rep., 2019, 9, 15724 CrossRef PubMed .
23. Z. Cao, C. Wang, Y. Sun, M. Liu, W. Li, J. Zhang and Y. Fu, Chem. Sci., 2024, 15, 1384–1392 RSC .
24. X. Mao, Z. Liu, C. Lin, J. Li and P. K. Shen, Inorg. Chem. Front., 2023, 10, 558–566 RSC .
25. L. Chang, M. Prager, J. Perßon, J. Walter, E. Jansen, Y. Chen and J. Gardner, J. Phys.: Condens. Matter, 2010, 22, 076003 CrossRef CAS PubMed .
26. N. Taira, M. Wakeshima and Y. Hinatsu, J. Mater. Chem., 2002, 12, 1475–1479 RSC .
27. C. Wiebe, J. Gardner, S.-J. Kim, G. Luke, A. Wills, B. Gaulin, J. Greedan, I. Swainson, Y. Qiu and C. Jones, Phys. Rev. Lett., 2004, 93, 076403 CrossRef CAS PubMed .
28. Y. Doi, Y. Hinatsu, K.-I. Oikawa, Y. Shimojo and Y. Morii, J. Mater. Chem., 2000, 10, 797–800 RSC .
29. D. Adroja, S. Sharma, C. Ritter, A. Hillier, D. Le, C. Tomy, R. Singh, R. Smith, M. Koza and A. Sundaresan, et al. , Phys. Rev. B, 2020, 101, 094413 CrossRef CAS .
30. Y. Doi, Y. Hinatsu, A. Nakamura, Y. Ishii and Y. Morii, J. Mater. Chem., 2003, 13, 1758–1763 RSC .

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc01652e

This journal is © The Royal Society of Chemistry 2025