Enhanced water splitting for hydrogen production via Z-scheme heterostructures of Mo@CTF-0, HfS₂, and HfSSe monolayers†

Qing-Guo Sun^a, Chuan-Lu Yang*^ac, Xiaohu Li^bc, Yuliang Liu^a, Wenkai Zhao^a and Feng Gao^d
aSchool of Physics and Optoelectronic Engineering, Ludong University, Yantai 264025, China. E-mail: ycl@ldu.edu.cn
^bXinjiang Astronomical Observatory, Chinese Academy of Science, Urumqi 830011, China
^cKey Laboratory of Radio Astronomy, Chinese Academy of Science, Urumqi 830011, China
^dDepartment of Physics, Southern University and A&M College, LA70813, USA

First published on 4th July 2025

---

---

1. Introduction

Amid the global energy crisis and environmental pollution, photocatalytic overall water splitting (OWS) for hydrogen production has become a prominent research focus in energy and environmental science.^1–3 Since the groundbreaking discovery by Fujishima and Honda⁴ of hydrogen production via photocatalytic water splitting using TiO₂, researchers have made significant strides in identifying photocatalysts with high solar-to-hydrogen (STH) efficiency. Two-dimensional (2D) covalent organic frameworks (COFs) have garnered considerable attention for their potential applications in photocatalysis^5–9 and electrocatalysis^10–12 owing to their outstanding characteristics, such as a high specific surface area, adjustable porosity, ease of functionalization, thermochemical stability, and extended π-conjugation.^13–15

However, the photocatalytic OWS performance of COFs is still hindered by the rapid recombination of photogenerated electron–hole (e–h) pairs^16,17 and wide band gap.^17–19 Thus, to overcome these limitations, numerous strategies have been proposed. For instance, a CHF-7²⁰ framework exhibited an STH efficiency of 12.04%. A covalent triazine-based framework (CTF-1)¹⁹ exhibited a low band gap of 2.81 eV, yielding an STH efficiency of 3.70%. A self-contained, unbiased photoelectrochemical (PEC) tandem device incorporating photoelectrodes coated with CTF-BTh also achieved a similar STH efficiency of 3.70%.²¹ Furthermore, the STH efficiencies of S@CTF-0/β-Sb and Se@CTF-0/β-Sb heterostructures²² were previously reported to reach 13.28% and 12.17%, respectively. However, there is significant room for improvement in the STH efficiencies of these COF-based systems.

Constructing heterostructures with a photocatalytic direct Z-scheme is a promising strategy for enhancing the separation of photogenerated charges and achieving high redox potential.^23–25 Additionally, extensive research has demonstrated that transition metal doping can not only narrow the bandgap of semiconductors to enhance light absorption but also provide active sites for the hydrogen evolution reaction (HER).^26,27 The two-dimensional covalent triazine-based framework CTF-0²⁸ has been reported to possess band edge positions suitable for OWS and can be synthesized via microwave-assisted and ionothermal methods. However, to date, no CTF-0-based system demonstrating high catalytic performance has been reported.

This work aims to achieve efficient photocatalytic OWS for hydrogen evolution based on CTF-0 by synergistically constructing heterostructures through doping with transition metal atoms (Ti, Zr, Hf, Cr, Mo, W, Ru, Os, Pd, and Pt). The band gaps of the doped monolayers (TM@CTF-0) were in the range of 0.17 eV to 2.36 eV. Among them, the Mo@CTF-0 monolayer exhibited a moderate indirect band gap of 1.60 eV, with its conduction band minimum (CBM) spanning the reduction potential for HER (−4.44 eV vs. vacuum level), while its valence band maximum (VBM) fails to cover the oxidation potential for OER (−5.67 eV vs. vacuum level), suggesting it is well-suited for photocatalytic HER. HfS₂ and HfSSe monolayers have already been confirmed to be effective OER half-reaction catalysts in heterostructures for photocatalytic OWS.^29–32 Consequently, the Mo@CTF-0 monolayer was incorporated into van der Waals heterostructures with HfS₂ and HfSSe monolayers. First-principles calculations were employed to investigate the electronic properties and STH efficiencies of the Mo@CTF-0/HfS₂, Mo@CTF-0/α-HfSSe, and Mo@CTF-0/β-HfSSe heterostructures. At present, ultrafast dynamics^33–35 and non-adiabatic molecular dynamics (NAMD) simulations³⁶ have become the core approaches for studying photogenerated carrier dynamics. In this work, NAMD simulations were performed to explore the interlayer charge transfer and recombination of photogenerated carriers. The results showed that the STH efficiencies of the Mo@CTF-0/HfS₂, Mo@CTF-0/α-HfSSe, and Mo@CTF-0/β-HfSSe heterostructures were 11.76%, 20.18%, and 20.36%, respectively. The Gibbs free energy calculations indicated that both the HER and OER processes can occur spontaneously within a suitable pH range for all three heterostructures. NAMD simulations further revealed that the photocatalytic Z-scheme in the Mo@CTF-0/α-HfSSe heterostructure is more efficient than that in Mo@CTF-0/HfS₂ and Mo@CTF-0/β-HfSSe. As a result, the Mo@CTF-0/α-HfSSe heterostructure emerged as the most promising candidate for driving photocatalytic OWS to produce hydrogen.

2. Computational methods

The electronic property calculations were performed using the Vienna Ab Initio Simulation Package (VASP),³⁷ employing density functional theory (DFT) and projector augmented wave (PAW) pseudopotentials. The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE)^38,39 functional was used for geometric optimization and ab initio molecular dynamics (AIMD) simulations, while for the calculation of the other properties, such as band structures, density of states (DOS), light absorption, carrier mobility, strain, and Gibbs free energy, the Heyd–Scuseria–Ernzerhof (HSE06)⁴⁵ hybrid functionals to account for exchange–correlation interactions. In the case of both optimization and static calculations, a 6 × 6 × 1 k-point mesh was used for the primitive cells, while a 5 × 3 × 1 k-point mesh was applied in the band structure calculations and strain analysis. The DFT-D4 method^40,41 was employed to include van der Waals interactions. A plane-wave cutoff energy of 600 eV was used for all calculations. A vacuum space of greater than 15 Å was introduced to prevent interactions between adjacent heterostructures. The convergence criteria of energy and force were set to 1 × 10⁻⁶ eV and 0.01 eV Å⁻¹, respectively. AIMD simulations were performed using 2 × 2 × 1 supercells of the primitive cells, applying both the canonical (NVT) and constant-volume (NVE) ensembles at 300 K to assess thermodynamic stability and generate wave functions for the subsequent NAMD simulations.⁴² The Hefei-NAMD code³⁶ was used to study the dynamics of the photo-excited carriers. In the decoherence-induced surface hopping (DISH) simulations,^36,43 1000 random initial configurations were sampled, with 2000 surface-hopping trajectories, and the maximum simulation times for the carrier transfer and recombination processes were set to 50 ps and 300 ps, respectively.

3. Result and discussion

3.1. Electronic properties of TM@CTF-0, HfS₂, and HfSSe monolayers

Fig. 1a, b and Fig. S2 (ESI†) show that ten transition metal atoms (TM = Ti, Zr, Hf, Cr, Mo, W, Ru, Os, Pd, and Pt) were incorporated on the outer surface of the triazine ring in the CTF-0 framework. The lattice constants of the TM@CTF-0 monolayers, as summarized in Table S1 (ESI†), range from 7.25 to 7.38 Å. The band structures and DOS for these systems are shown in Fig. 2a–j, respectively. Notably, Ti@CTF-0 and Zr@CTF-0 exhibit direct bandgaps, while the remaining materials show indirect bandgap semiconducting behavior. The bandgaps, as detailed in Table S1 (ESI†), vary between 0.17 and 2.38 eV, representing a significant reduction compared to the bandgap of 3.70 eV of the intrinsic CTF-0 monolayer.²² In particular, Mo@CTF-0 has a moderate bandgap of 1.60 eV, which not only broadens its light absorption range but also provides a favorable overpotential for OWS. Further analysis in Fig. 2e and Fig. S3a (ESI†) reveals that the CBM of Mo@CTF-0 is largely influenced by the Mo-s and Mo-p orbitals, while the VBM is predominantly derived from the Mo-d orbitals. Fig. 1c and d depict the crystal structures of HfS₂ and HfSSe, with lattice constants of 3.61 and 3.68 Å, respectively, which are in agreement with the reported values of 3.63 and 3.65 Å for the HfS₂ monolayer^29,30 and 3.68 Å for HfSSe monolayers.³¹ The band structures in Fig. 2k and l show that both HfS₂ and HfSSe are direct bandgap semiconductors, with bandgaps of 1.98 and 1.40 eV, respectively. Both materials exhibit their CBM and VBM at the Γ point, consistent with earlier findings.⁴⁴ In the case of HfS₂ and HfSSe, their CBM arises from the Hf-d orbitals, while their VBM is contributed by the S-p and Se-p orbitals, as shown in Fig. 2k, l and Fig. S3b, c (ESI†), respectively.

The absolute band edge positions were calculated using the following formula:

EAbsCBM/VBM = EHSE06CBM/VBM − Evac	(1)

where E^HSE06_CBM/VBM represent the energies of CBM/VBM and E_vac the vacuum energy level. The E^HSE06_CBM/VBM values for Mo@CTF-0, HfS₂, and HfSSe, calculated using the HSE06 hybrid functional, are presented in Table S1 (ESI†). The E_vac was determined from the static potential curves (Fig. S4, ESI†). As shown in Fig. S4a (ESI†), the Mo@CTF-0 monolayer exhibits surface asymmetry, leading to a differential static potential across its surface. Given that both the CBM and VBM are primarily contributed by the Mo orbitals, the E_vac used for these calculations is denoted as E_vac2. This approach was also applied to HfS₂ and HfSSe. The results indicate that the E^Abs_CBM of Mo@CTF-0 spans the HER potential of −4.44 eV (at pH = 0), yielding a large overpotential, χ(H₂), of 2.64 eV. However, the E^Abs_VBM does not reach the OER potential of −5.67 eV (at pH = 0). In contrast, the E^Abs_VBM of both HfS₂ and HfSSe aligns with the OER potential, with overpotentials, χ(O₂), of 1.30 and 0.65 eV, respectively, while their E^Abs_CBM fails to meet the HER potential. These findings suggest that constructing heterostructures by combining Mo@CTF-0 with HfS₂ and HfSSe is a promising approach for achieving efficient photocatalytic OWS.

3.2 Geometrical structures and stabilities of the Mo@CTF-0/HfS₂, Mo@CTF-0/α-HfSSe, and Mo@CTF-0/β-HfSSe heterostructures

Mo@CTF-0/HfS₂, Mo@CTF-0/α-HfSSe and Mo@CTF-0/β-HfSSe (where the prefix α or β denotes the S or Se atoms of the HfSSe monolayer on the inner surface of the heterostructure, respectively) were constructed by combining the Mo@CTF-0 monolayer with 2 × 2 × 1 supercells of HfS₂ and HfSSe monolayers.

The lattice mismatch ratios can be calculated using the following formula:

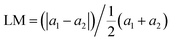	(2)

where a₁ and a₂ are the lattice constants of the two monolayers. The calculated lattice mismatch ratios used were 1.90%, 0.27%, and 0.27%, respectively, indicating high lattice compatibility. Then, based on maintaining the lattice mismatch, a total of 27 potential configurations was constructed by flipping one or both of the monolayers in the heterostructures by 180° along the x or y direction of the lattice.⁴⁵ The symbols M/M_x/M_y, D/D_x/D_y, E/E_x/E_y, and denote the stacking patterns using positional flipping of Mo@CTF-0, HfS₂, α-HfSSe, and β-HfSSe monolayers within the heterostructures, respectively.

The formation energies of the heterostructures were calculated as follows:

Ef = (Et − E1 − E2)/SA	(3)

where E_t is the total energy of the heterostructure, E₁ and E₂ are the energies of the individual monolayers, and S_A is the area of the heterostructure. As shown in Tables S3 and S4 (ESI†), except for the configuration obtained by flipping the Mo@CTF-0 monolayer along the x-direction, the formation energies are within the range of the van der Waals interaction energies (4.146–41.457 meV Å⁻²)⁴⁶ and the interlayer distances of these configurations fall within the van der Waals interaction range (3–5 Å).⁴⁷ Next, the initial configurations, MD, ME, and ME', as well as three configurations, M_yD_x, ME_y, and M_yE_x, which have more negative formation energies compared to their respective initial configurations after flipping, were selected for further study. The top and side views of these six heterostructures after full optimization are shown in Fig. 3.

3.3. Photocatalytic OWS Z-scheme and STH Efficiency of the Heterostructures

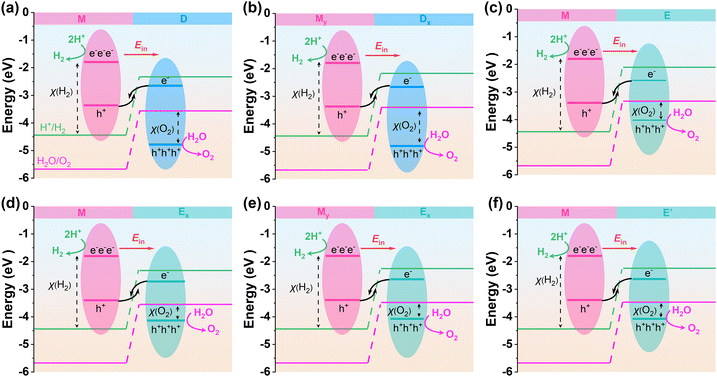
The band structures presented in Fig. 4a–f demonstrate the staggered band alignments for all six configurations, which are crucial features for facilitating photocatalytic OWS with a direct Z-scheme. In these heterostructures, their CBMs can be attributed to the HfS₂ or HfSSe monolayers, while their VBMs can be attributed to the Mo@CTF-0 monolayer. Conversely, the vacuum energy levels and work function differences of the heterostructures are shown in Fig. S5 (ESI†). The band gaps were determined using the projected energy levels onto the respective monolayer and summarized in Table S5 (ESI†).

The formation of the photocatalytic Z-scheme is driven by a built-in electric field (E_in), which plays a vital role in charge separation and transport. As shown in the differential charge densities in Fig. S6 (ESI†), charge depletion occurs on the Mo@CTF-0 monolayer, while charge accumulation is observed on the HfS₂ (or HfSSe) monolayers. The work function (Φ) was calculated as follows:

Φ = Evac − EF	(4)

where E_F represents the Fermi energy of the respective monolayer. As shown in Fig. S4a–c (ESI†), the work function of the Mo@CTF-0 monolayer (5.24eV) is lower than that of the HfS₂ (6.75 eV) and HfSSe (6.10 eV) monolayers. This difference indicates that the charge will flow from Mo@CTF-0 to HfS₂ or HfSSe when a heterostructure is formed, confirming the existence of a built-in electric field. Based on these findings, the photocatalytic Z-scheme for all six configurations was established, as depicted in Fig. 5a–f, with the overpotentials χ(H₂) and χ(O₂) for HER and OER summarized in Table S5 (ESI†), respectively. The values for the MD, M_yD_x, ME, ME_x, M_yE_x, and ME′ configurations were calculated to be 11.76%, 10.73%, 20.18%, 19.42%, 19.47%, and 20.36%, respectively. The bandgap values of the single layers with larger bandgaps in M_yD_x, ME_x, and M_yE_x are all greater than that of their corresponding initial configurations. Additionally, the OER overpotentials χ(O₂) of the ME_x and M_yE_x configurations are lower than that of the initial ME configuration. These factors contribute to the flipped configurations exhibiting lower efficiency compared to their respective initial configurations. The values of these heterostructures are significantly higher than the 0.28% reported for the CTF-0 monolayer in our previous work,²² and approach or exceed the efficiencies reported for other CTF-based monolayers and heterostructures (3.70–15.8%).^19–22,48 Therefore, the three initial configurations MD, ME, and ME′ were selected for subsequent studies.

To further validate the thermodynamic stability of the three heterostructure configurations, we performed AIMD simulations using a 2 × 2 × 1 supercell at 300 K for 10 ps. As shown in Fig. S7a–c (ESI†), respectively, the energies of the three heterostructures remained stable with minimal fluctuation throughout the simulation, and no obvious deformations were recognized, which can be used to confirm the thermodynamic stability of the heterostructures.

We investigated the influence of biaxial tensile and compressive strain (ranging from −4% to +4%) on the band edges and values. The strain energy (E_s) was calculated as follows:^49,50

Es = (Estrained – Eunstrained)/n	(5)

where n is the total number of atoms in the heterostructure. As shown in Fig. 6a, the strain energy of each heterostructure follows a quadratic curve under strain from −4% to +4%, confirming that the elasticity and stability of the heterostructures can be maintained within this strain range. As shown in Fig. 6b–d and Tables S6–S8 (ESI†), the effect of strain on the band gap was also explored, where with an increase in compressive strain, the band gaps of the monolayers narrow, whereas they widen under tensile strain, respectively. In contrast, the vacuum level difference exhibited the opposite trend. In the case of the HfS₂/Mo@CTF-0 heterostructure, the values increase as the band gap narrows, reaching the maximum value of 17.42% under −4% strain and a minimum value of 8.4% under +4% strain. This suggests that tensile stress should be avoided in practical applications. In the case of the two heterostructures comprised of the Mo@CTF-0 and HfSSe monolayers, both compressive and tensile strain led to a reduction in . As explained in the ESI,† the decrease in due to compressive and tensile strain can be attributed to the changes in χ(O₂) and the widening of the band gap, respectively. Nevertheless, the lowest STH efficiencies observed (15.01% for Mo@CTF-0/α-HfSSe and 13.24% for Mo@CTF-0/β-HfSSe) remained above 10%, ensuring that these heterostructures maintain a reasonable performance even under biaxial strain.

The optical absorption of each monolayer in the heterostructures was calculated and shown in Fig. S8 (ESI†). The optical absorption coefficients of all the monolayers in both the visible and ultraviolet regions exceed 10⁴ cm⁻¹, confirming the efficient photon absorption and utilization in these heterostructures. The carrier mobilities of the monolayers in the heterostructures and the CTF-0 monolayer are listed in Table S9 (ESI†), providing insight into their charge transport properties. The electron mobility (μ_e) of the Mo@CTF-0, HfS₂, and HfSSe monolayers in the x-direction are 14433.56, 9670.98, and 8984.98 cm² V⁻¹ S⁻¹, while in the y-direction, they are 16679.16, 4686.16, and 9890.13 cm² V⁻¹ S⁻¹, respectively. These values are significantly higher than the theoretical mobilities of several other 2D catalysts proposed for water splitting, such as MoS₂ (∼200 cm² V⁻¹ S⁻¹),⁵¹ PdSP (∼312 cm² V⁻¹ S⁻¹),⁵² SnSe (2486.93 cm² V⁻¹ S⁻¹)⁵³ and SnS₂ (2181.96 cm² V⁻¹ S⁻¹).⁵³ It is worth noting that the electron mobility in the x and y directions of Mo@CTF-0 (14433.56/16679.16 cm² V⁻¹ S⁻¹) is significantly enhanced compared to that of pristine CTF-0 (883.39/883.39 cm² V⁻¹ S⁻¹). The higher electron mobility facilitates the rapid separation of photogenerated electron–hole pairs and their effective participation in redox reactions. In addition, the hole mobilities (μ_h) of all the monolayers are considerably lower than their electron mobilities. This discrepancy helps to suppress the intralayer carrier recombination, thereby enhancing the transport of photogenerated interlayer carriers to a certain extent.⁵⁴

3.4. Thermodynamic feasibility of HER and OER

For photocatalytic OWS to occur spontaneously under illumination, it is essential that the photogenerated electrons and holes provide sufficient oxidation (eU_h) and reduction (eU_e) potentials to suppress the Gibbs free energy barriers ( and ΔG_max) for HER and OER,^55,56 respectively. Specifically, eU_e corresponds to χ(H₂) and eU_h to χ(O₂) + 1.23 eV. In all the heterostructures, HER takes place on the Mo@CTF-0 monolayer, as demonstrated in Fig. 7a–c. The computed values at the N sites are 0.60, 0.63, and 0.64 eV for Mo@CTF-0/HfS₂, Mo@CTF-0/α-HfSSe, and Mo@CTF-0/β-HfSSe, respectively. Meanwhile, the values at the Mo sites are 0.59, 0.58, and 0.58 eV for these heterostructures, respectively. These values are all smaller than the corresponding reduction overpotentials, eU_e, of 2.65, 2.64, and 2.65 eV, respectively, indicating that HER can proceed spontaneously under solar light for all heterostructures. Moreover, the results suggest that the incorporation of Mo atoms introduces additiosnal active sites, which lower the energy barrier for photocatalytic HER. In the case of OER, the reaction occurs on the HfS₂ or HfSSe monolayers through a four-step process involving intermediate products such as OH*, O*, and OOH*.^20,57 The Gibbs free energy changes in these intermediate steps are illustrated in Fig. 7d–f, respectively, and Table S10 (ESI†). The rate-limiting step of the Mo@CTF-0/HfS₂ and Mo@CTF-0/β-HfSSe heterostructures occurs in the third step with the OOH* intermediate, whereas it takes place in the first step with the OH* intermediate in the case of Mo@CTF-0/α-HfSSe. The ΔG_max values are 2.89, 2.34, and 2.65 eV for Mo@CTF-0/HfS₂, Mo@CTF-0/α-HfSSe, and Mo@CTF-0/β-HfSSe, all exceeding the oxidation overpotential (eU_h) of 2.62, 1.92, and 1.83 eV at pH = 0, respectively. However, the pH range necessary for spontaneous OWS in these heterostructures can be determined using the following equations:

|eUe| − pH × 0.059 > |ΔGH*|	(6)

|eUh| + pH × 0.059 > |ΔGmax|	(7)

Based on these calculations, the pH range required for spontaneous OWS under illumination is 4.58 < pH ≤ 14 for Mo@CTF-0/HfS₂, 7.12 < pH ≤ 14 for Mo@CTF-0/α-HfSSe, and 13.89 < pH ≤ 14 for Mo@CTF-0/β-HfSSe. Thus, the Mo@CTF-0/HfS₂ and Mo@CTF-0/α-HfSSe heterostructures can achieve spontaneous photocatalytic OWS over a broader pH range compared to the Mo@CTF-0/β-HfSSe heterostructure.

The pH range required for the spontaneous occurrence of OWS in the Mo@CTF-0/HfS₂, Mo@CTF-0/α-HfSSe and Mo@CTF-0/β-HfSSe heterostructures under illumination was calculated to be 4.58 < pH ≤ 14, 7.12 < pH ≤ 14 and 13.89 < pH ≤ 14, respectively. Therefore, Mo@CTF-0/HfS₂ and Mo@CTF-0/α-HfSSe can achieve spontaneous photocatalytic OWS in a wider pH range compared to the Mo@CTF-0/β-HfSSe heterostructure.

3.3. Migration of the photogenerated carriers

From the perspective of photogenerated carrier dynamics, an effective photocatalytic Z-scheme needs to satisfy two conditions simultaneously. Firstly, the interlayer charge transfer process (processes ① and ② labeled in Fig. 8a–c) should be slow enough to maintain a long lifetime of photogenerated carriers. Secondly, an effective recombination process (process ③ labeled in Fig. 8a–c) of interlayer electrons and holes.^49,58 Therefore, NAMD simulations were performed for the Mo@CTF-0/HfS₂, Mo@CTF-0/α-HfSSe and Mo@CTF-0/β-HfSSe heterostructures to understand the transfer and recombination of the photogenerated carries.

The average nonadiabatic coupling (NAC) matrix elements associated with the carrier transfers and recombination processes are defined as follows:⁴⁰

	(8)

where H represents the Kohn–Sham Hamiltonian. Meanwhile, the symbols φ_i/j and ε_i/j stand for the wavefunctions and eigenvalues corresponding to φ_i/j, respectively. Additionally, Ṙ_I denotes the nuclear velocity. As a result, d_ij is positively correlated with the electron–phonon (e–ph) coupling φ_i|∇_ṘIĤ|φ_j and the nuclear velocity Ṙ_I, and negatively correlated with the energy gap ε_j − ε_i. Also, in general, a larger NAC favors more rapid carrier recombination or transfer processes. Fig. 8g–i show the NAC values for the charge transfer and e–h recombination processes.

The amplitude of the electron energy level oscillations is directly related to the strength of the e–ph coupling φ_i|∇_ṘIĤ|φ_j.⁵⁹ The time-dependent energies of the Kohn–Sham orbitals in Fig. 8a–c show that the electron transfer occurs on CBM + 3, which is projected to the CBM of the Mo@CTF-0 monolayer, for all the heterostructures, while the hole transfer occurs on VBM-9, projected to the VBM of the HfS₂ monolayer, for the Mo@CTF-0/HfS₂ heterostructure and occurs on VBM-4, which is projected to the VBM of the HfSSe monolayer, for both Mo@CTF-0/α-HfSSe and Mo@CTF-0/β-HfSSe. As shown in Fig. 8d–f, the Fourier transforms of the normalized autocorrelation function of the energy difference fluctuation between the donor and acceptor states were calculated using the optical response theory. In the case of the electron transfer process (process ①) in Fig. 8a–c, the oscillation amplitudes of the corresponding energy levels for all the heterostructures are similar, but these energy gaps exhibit significant differences of Mo@CTF-0/α-HfSSe > Mo@CTF-0/HfS₂ > Mo@CTF-0/β-HfSSe, showing the opposite trends in NACs, as observed in Fig. 8g–i, respectively. Regarding the hole transfer process (process ②), the extremely small energy gap of the Mo@CTF-0/HfS₂ heterostructure results in the largest NAC, whereas in the case of the Mo@CTF-0/α-HfSSe and Mo@CTF-0/β-HfSSe heterostructures, with similar energy gaps, the larger oscillation amplitude of the energy levels of the latter leads to a NAC that is twice that of the former, as shown in Fig. 8g–i, respectively. Otherwise, in the case of the e–h recombination process (process ③), Fig. 8g–i show that the NAC for the Mo@CTF-0/β-HfSSe is significantly smaller than that of the other two heterostructures, respectively. However, in Fig. 8a–c, all the heterostructures exhibit similar oscillation amplitudes and energy gaps, indicating that e–ph coupling φ_i|∇_ṘIĤ|φ_j and energy gap ε_j–ε_i are not the primary factors leading to this significant difference in NACs.

The Fourier transforms of the normalized autocorrelation function of the energy difference fluctuation between the donor and acceptor states were calculated using the optical response theory. All the charge transfer processes exhibit peaks in the low-frequency regions of 66.71, 100.07 and 133.43 cm⁻¹. The difference occurs in the hole transfer processes, where the Mo@CTF-0/HfS₂ and Mo@CTF-0/β-HfSSe heterostructures exhibit peaks at higher frequencies of 266.85 and 233.49 cm⁻¹, respectively. However, considering Fig. 8g–i collectively, this is not the dominant factor leading to the differences in NACs. In the e–h recombination processes, compared to Mo@CTF-0/HfS₂ and Mo@CTF-0/α-HfSSe, the absence of peaks at 133.43, 166.78 and 200.14 cm⁻¹ for Mo@CTF-0/β-HfSSe indicates its smallest nuclear velocity, Ṙ_I, which is the main factor leading to the significantly smaller NAC in this heterostructure compared to the other two. Moreover, Fig. S13 (ESI†) demonstrates that the out-of-plane vibrations of the Hf–S (or Hf–Se), C–C, C–N, and Mo–N bonds and in-plane vibrations of the Hf–S (or Hf–Se) and Mo–N bonds contributed all the vibration modes, which implies that the Ṙ_I values of the carrier processes are not substantially different.

In summary, the e–ph coupling φ_i|∇_ṘIĤ|φ_j energy gap ε_j–ε_i and nuclear velocity Ṙ_I jointly influence the carrier dynamics processes. When the e–ph coupling strength and nuclear velocity are similar, the energy gap size dominates the NAC values during the electron transfer process. In the case of the hole transfer process, the significant differences in e–ph coupling strength and energy gap between heterostructures dominate the variations in NACs. Furthermore, when the e–ph coupling strength and energy gap for all the heterostructures are similar in e–h recombination, the differences in nuclear velocity lead to variations in the NAC values.

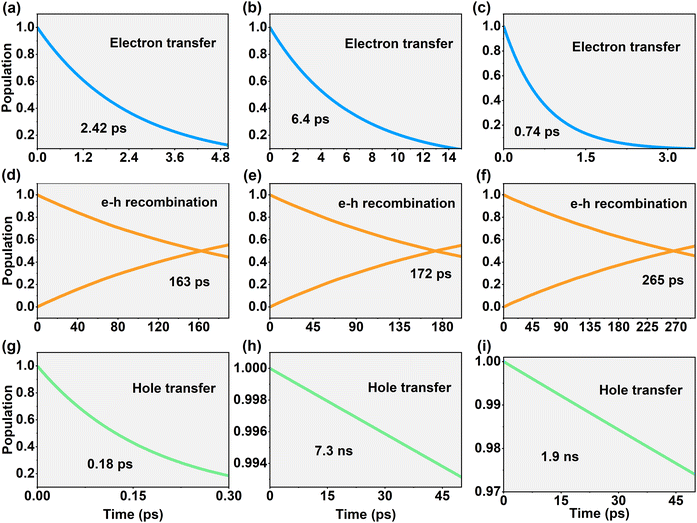
Based on the obtained NACs, NAMD simulations were performed using DISH.^36,43 As shown in Fig. 9, the dynamics of the photogenerated carriers reveal their lifetimes, determined by fitting the decay profiles to an exponential function, f(t) = e^−t/τ. Additionally, the e–h recombination timescales were assessed by analyzing the intersection points of the time-evolution trajectories for holes at VBM and electrons at CBM. Fig. 8g–i and 9a–i demonstrate that the differences in carrier lifetimes during the charge transfer process and the e–h recombination times are consistent with the NAC values, respectively. As shown in Fig. 9a–c and g–i, the photogenerated electron and hole lifetimes of Mo@CTF-0/α-HfSSe (6.4 ps and 7.3 ns) are significantly longer than that of the Mo@CTF-0/HfS₂ (2.42 ps and 0.18 ps) and Mo@CTF-0/β-HfSSe heterostructures (0.74 ps and 1.9 ns), respectively, indicating that the reducing ability provided by the photogenerated electrons and the oxidizing ability provided by the photogenerated holes in Mo@CTF-0/α-HfSSe are both well-preserved. Fig. 9d–f show that the interlayer e–h recombination times for Mo@CTF-0/α-HfSSe and Mo@CTF-0/β-HfSSe are close, at 163 ps and 172 ps, respectively, both of which are faster than the 265 ps observed for the Mo@CTF-0/β-HfSSe heterostructure. Otherwise, all these recombination times are significantly shorter than that of the BCN/In₂S₃ (11.03 ns) and BCN/Ga₂S₃ (14.99 ns) heterostructures with a direct Z-scheme,⁵⁸ confirming that effective e–h recombination occurs in all the heterostructures. In short, Mo@CTF-0/α-HfSSe is believed to achieve a more effective Z-scheme in comparison with the Mo@CTF-0/HfS₂ and Mo@CTF-0/β-HfSSe heterostructures.

4. Conclusions

In summary, the photocatalytic performance of the Z-scheme with the Mo@CTF-0/HfS₂, Mo@CTF-0/α-HfSSe, and Mo@CTF-0/β-HfSSe heterostructures was systematically analyzed based on their electronic properties. The introduction of transition metal doping into the CTF-0 monolayer effectively modulated its band structure, with Mo@CTF-0 exhibiting a moderate indirect bandgap of 1.60 eV and a suitable CBM for HER. By integrating Mo@CTF-0 with HfS₂ or HfSSe monolayers, a series of van der Waals heterostructures was constructed, among which six configurations, MD, M_yD_x, ME, ME_x, M_yE_x, and ME′, were identified as representative cases for further investigation. The calculated values for these configurations range from 10.73% to 20.36%, indicating their potential for favorable STH efficiency. AIMD simulations proved the thermodynamic stabilities of the MD, ME, and ME′ configurations, while the electronic transport analysis suggested that high carrier mobility enhances the separation performance of photogenerated hole–electron pairs. Optical absorption revealed that the constituent monolayers within these heterostructures exhibit absorption coefficients in the range of 10⁴–10⁵ cm⁻¹ in the ultraviolet-visible region, ensuring efficient photon capture and carrier generation. Furthermore, the Gibbs free energies show that the pH range for spontaneous photocatalytic OWS varies among these heterostructures, with Mo@CTF-0/α-HfSSe exhibiting the widest pH range (7.12 < pH ≤ 14) for simultaneous HER and OER. NAMD simulations provided further insights into the carrier dynamics, revealing that the electron–hole recombination times in Mo@CTF-0/HfS₂ and Mo@CTF-0/α-HfSSe (163 ps and 172 ps, respectively) are shorter than in Mo@CTF-0/β-HfSSe (265 ps). Notably, the lifetimes of photogenerated holes for OER and electrons for HER in Mo@CTF-0/α-HfSSe (7.30 ns and 6.40 ps, respectively) are significantly extended compared to that in the other two heterostructures. These findings indicate that the Mo@CTF-0/α-HfSSe heterostructure exhibits superior photocatalytic efficiency within the Z-scheme, making it a potential candidate for solar-driven water splitting applications.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

The datasets generated and analyzed during the current study are available from the corresponding author upon reasonable request.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 12374232 and 12473025). C. L. Yang thanks the Xinjiang Tianchi Talent Program (2023).

References

1. M. M. Rahman and K. Alam, Renewable Energy, 2021, 172, 1063–1072 CrossRef CAS .
2. M. W. Zafar, M. Shahbaz, A. Sinha, T. Sengupta and Q. Qin, J. Cleaner Prod., 2020, 268, 122149 CrossRef .
3. A. D. A. Bin Abu Sofian, H. R. Lim, H. Siti Halimatul Munawaroh, Z. Ma, K. W. Chew and P. L. Show, Sustainable Dev., 2024, 32, 3953–3978 CrossRef .
4. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed .
5. T. Luo, L. Gilmanova and S. Kaskel, Coord. Chem. Rev., 2023, 490, 215210 CrossRef CAS .
6. R. K. Sharma, P. Yadav, M. Yadav, R. Gupta, P. Rana, A. Srivastava, R. Zbořil, R. S. Varma, M. Antonietti and M. B. Gawande, Mater. Horiz., 2020, 7, 411–454 RSC .
7. M. Traxler, S. Gisbertz, P. Pachfule, J. Schmidt, J. Roeser, S. Reischauer, J. Rabeah, B. Pieber and A. Thomas, Angew. Chem., Int. Ed., 2022, 61, e202117738 CrossRef CAS PubMed .
8. L. Li, X. Lv, Y. Xue, H. Shao, G. Zheng and Q. Han, Angew. Chem., Int. Ed., 2024, 63, e202320218 CrossRef CAS PubMed .
9. Y. Luo, B. Zhang, C. Liu, D. Xia, X. Ou, Y. Cai, Y. Zhou, J. Jiang and B. Han, Angew. Chem., Int. Ed., 2023, 62, e202305355 CrossRef CAS PubMed .
10. M. Lu, M. Zhang, C.-G. Liu, J. Liu, L.-J. Shang, M. Wang, J.-N. Chang, S.-L. Li and Y.-Q. Lan, Angew. Chem., Int. Ed., 2021, 60, 4864–4871 CrossRef CAS PubMed .
11. X. Zhao, P. Pachfule and A. Thomas, Chem. Soc. Rev., 2021, 50, 6871–6913 RSC .
12. C.-Y. Lin, D. Zhang, Z. Zhao and Z. Xia, Adv. Mater., 2018, 30, 1703646 CrossRef PubMed .
13. Y.-N. Gong, X. Guan and H.-L. Jiang, Coord. Chem. Rev., 2023, 475, 214889 CrossRef CAS .
14. S. S. A. Shah, M. S. Javed, T. Najam, M. A. Nazir, A. Ur Rehman, A. Rauf, M. Sohail, F. Verpoort and S.-J. Bao, Mater. Today, 2023, 67, 229–255 CrossRef CAS .
15. Y. Luo, Y. Qin, C. Ni, C. Liu, H. Yan, Y. Tao, W. Du and J. Zou, Chem. Eng. J., 2024, 497, 154941 CrossRef CAS .
16. C. Cui, X. Xu, X. Zhao, N. Xi, M. Li, X. Wang, Y. Sang, X. Yu, H. Liu and J. Wang, Nano Energy, 2024, 126, 109632 CrossRef CAS .
17. H. Zhang, H. Gu, Y. Huang, X. Wang, L. Gao, Q. Li, Y. Li, Y. Zhang, Y. Cui, R. Gao and W.-L. Dai, J. Colloid Interface Sci., 2024, 664, 916–927 CrossRef CAS PubMed .
18. Y. Chen, X. Luo, J. Zhang, L. Hu, T. Xu, W. Li, L. Chen, M. Shen, S.-B. Ren, D.-M. Han, G.-H. Ning and D. Li, J. Mater. Chem. A, 2022, 10, 24620–24627 RSC .
19. C.-F. Fu, C. Zhao, Q. Zheng, X. Li, J. Zhao and J. Yang, Sci. China: Chem., 2020, 63, 1134–1141 CrossRef CAS .
20. Y. Zhao, C. Wang, X. Han, Z. Lang, C. Zhao, L. Yin, H. Sun, L. Yan, H. Ren and H. Tan, Adv. Sci., 2022, 9, 2202417 CrossRef CAS PubMed .
21. Y. Zhang, H. Lv, Z. Zhang, L. Wang, X. Wu and H. Xu, Adv. Mater., 2021, 33, 2008264 CrossRef CAS PubMed .
22. Q.-G. Sun, C.-L. Yang, X. Li, Y. Liu, W. Zhao and X. Ma, Colloids Surf., A, 2024, 703, 135437 CrossRef CAS .
23. H. Li, W. Tu, Y. Zhou and Z. Zou, Adv. Sci., 2016, 3, 1500389 CrossRef PubMed .
24. S. Wang, B. Zhu, M. Liu, L. Zhang, J. Yu and M. Zhou, Appl. Catal., B, 2019, 243, 19–26 CrossRef CAS .
25. S. Lu, S. Zhang, L. Li, C. Liu, Z. Li and D. Luo, Chem. Eng. J., 2024, 483, 149058 CrossRef CAS .
26. F. Zhou, Y. Zhang, J. Wu, W. Yang, X. Fang, T. Jia, Y. Ling, P. He, Q. Liu and J. Lin, Appl. Catal., B, 2024, 341, 123347 CrossRef CAS .
27. J. Du, J. Chen, C. Zhang and G. Jiang, Inorg. Chem., 2023, 62, 1001–1006 CrossRef CAS PubMed .
28. D. Kong, X. Han, J. Xie, Q. Ruan, C. D. Windle, S. Gadipelli, K. Shen, Z. Bai, Z. Guo and J. Tang, ACS Catal., 2019, 9, 7697–7707 CrossRef CAS PubMed .
29. L. He, X. Long, L. Wang, C. Mi, C. Zhang, K. Ma, L. She and M. Yu, J. Catal., 2024, 436, 115606 CrossRef CAS .
30. Q. Feng, D. Hu, B. Li, X. Xiang, W. Liu, H. Deng, W. Zhou and X. Zu, Int. J. Hydrogen Energy, 2024, 83, 378–386 CrossRef CAS .
31. W. Tang, G. Wang, C. Fu, B. Wang, H. Yuan and H. Chen, Appl. Surf. Sci., 2023, 626, 157247 CrossRef CAS .
32. J. Wang, G. Liu, L. Wei, J. Zhao and G. Zhang, Int. J. Hydrogen Energy, 2024, 81, 785–794 CrossRef CAS .
33. C. Wang, M. Sun, H. Wang and G. Zhao, J. Phys. Chem. Lett., 2023, 14, 164–169 CrossRef CAS PubMed .
34. C. Wang, H. Wang, M. Sun and G. Zhao, CCS Chem., 2023, 5, 1982–1988 CrossRef CAS .
35. C. Wang, J. Feng, D. Wang and J. Wang, J. Lumin., 2025, 281, 121213 CrossRef CAS .
36. Q. Zheng, W. Chu, C. Zhao, L. Zhang, H. Guo, Y. Wang, X. Jiang and J. Zhao, WIREs Comput. Mol. Sci., 2019, 9, e1411 CrossRef CAS .
37. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS .
38. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed .
39. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed .
40. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed .
41. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed .
42. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed .
43. Y. Wang and R. Long, J. Phys. Chem. Lett., 2020, 11, 1601–1608 CrossRef CAS PubMed .
44. Q. Zhao, Y. Guo, K. Si, Z. Ren, J. Bai and X. Xu, Phys. Status Solidi B, 2017, 254, 1700033 CrossRef .
45. Q.-K. Yin, C.-L. Yang, M.-S. Wang and X.-G. Ma, J. Mater. Chem. C, 2021, 9, 12231–12238 RSC .
46. T. Björkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2012, 108, 235502 CrossRef PubMed .
47. D. L. Duong, S. J. Yun and Y. H. Lee, ACS Nano, 2017, 11, 11803–11830 CrossRef CAS PubMed .
48. H. Lv, D. Wang and X. Wu, J. Phys. Chem. C, 2024, 128, 18759–18766 CrossRef CAS .
49. X.-Q. Wan, C.-L. Yang, X.-H. Li, Y.-L. Liu and W.-K. Zhao, J. Mater. Chem. A, 2024, 12, 2359–2372 RSC .
50. X.-H. Li, B.-J. Wang, G.-D. Wang and S.-H. Ke, Sustainable Energy Fuels, 2020, 4, 5277–5283 RSC .
51. Y. Cai, G. Zhang and Y.-W. Zhang, J. Am. Chem. Soc., 2014, 136, 6269–6275 CrossRef CAS PubMed .
52. Y. Jing, Y. Ma, Y. Wang, Y. Li and T. Heine, Chem. – Eur. J., 2017, 23, 13612–13616 CrossRef CAS PubMed .
53. X. Li, X. Zuo, X. Jiang, D. Li, B. Cui and D. Liu, Phys. Chem. Chem. Phys., 2019, 21, 7559–7566 RSC .
54. R. Sun, C.-L. Yang, M.-S. Wang and X.-G. Ma, Int. J. Hydrogen Energy, 2023, 48, 38699–38707 CrossRef CAS .
55. Y. Xu and M. A. A. Schoonen, Am. Mineral., 2000, 85, 543–556 CrossRef CAS .
56. M. Qiao, J. Liu, Y. Wang, Y. Li and Z. Chen, J. Am. Chem. Soc., 2018, 140, 12256–12262 CrossRef CAS PubMed .
57. Y. Zhao, J. Gu and Z. Chen, Adv. Funct. Mater., 2019, 29, 1904782 CrossRef CAS .
58. A. Shi, D. Sun, X. Zhang, S. Ji, L. Wang, X. A. Li, Q. Zhao and X. Niu, ACS Catal., 2022, 12, 9570–9578 CrossRef CAS .
59. L. Xu, H. Zheng, B. Xu, G. Liu, S. Zhang and H. Zeng, Nano Lett., 2023, 23, 1954–1960 CrossRef CAS PubMed .

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc02212f

This journal is © The Royal Society of Chemistry 2025